Construction Material Selection by Using Multi-Attribute Decision Making Based on q-Rung Orthopair Fuzzy Aczel–Alsina Aggregation Operators

Abstract

A contribution of this article is to introduce new q-rung Orthopair fuzzy (q-ROF) aggregation operators (AOs) as the consequence of Aczel–Alsina (AA) t-norm (TN) (AATN) and t-conorm (TCN) (AATCN) and their specific advantages in handling real-world problems. In the beginning, we introduce a few new q-ROF numbers (q-ROFNs) operations, including sum, product, scalar product, and power operations based on AATN and AATCN. At that point, we construct a few q-ROF AOs such as q-ROF Aczel–Alsina weighted averaging (q-ROFAAWA) and q-ROF Aczel–Alsina weighted geometric (q-ROFAAWG) operators. It is illustrated that suggested AOs have the features of monotonicity, boundedness, idempotency, and commutativity. Then, to address multi-attribute decision-making (MADM) challenges, we develop new strategies based on these operators. To demonstrate the compatibility and performance of our suggested approach, we offer an example of construction material selection. The outcome demonstrates the new technique’s applicability and viability. Finally, we comprehensively compare current procedures with the proposed approach.

1. Introduction

Decision making (DM) is a helpful technique for choosing the best option from multiple lists of options. To acquire the best findings, several researchers gave a variety of concepts. MADM is an important part of decision sciences that can offer ranking outcomes for limited options based on the attribute values of various alternatives. In the last few years, the growth of construction businesses and social DM in all aspects have been linked to the issue of MADM. Therefore, it has become extensively used on various grounds, such as the assessment of sustainable housing affordability by Mulliner et al. [1] and fuzzy hybrid techniques for management of construction engineering by Fayek [2]. An important difficulty in the real-world DM process is expressing attribute value more accurately and efficiently. Zadeh [3] presented the fuzzy set (FS) notion to fill this gap. It was a significant accomplishment with several applications in various ambiguous environments. FS is essentially composed of just membership degree (MD) that fall into the $\left[0, 1\right]$ range. FS is a helpful tool for analyzing uncertain ambiguous data.

Researchers have been paying increasing attention to these approaches in recent decades and have effectively used them in the DM process in several situations. The concept of FS was further developed by Atanassov [3], intuitionist fuzzy set (IFS). It consists of MD ${}^{\prime }{\alpha }^{\prime }$ and non-membership degree (NMD) ${}^{\prime }{\beta }^{\prime }$ such that $0\le \alpha +\beta \le 1.$ When the value of MD is $0.3$ and NMD is $0.8,$ then IFS cannot clearly define how to handle such a circumstance. Then, Yager [4] developed the concept of the Pythagorean fuzzy set (PyFS) to address these issues by providing the condition for MD ${}^{\prime }{\alpha }^{\prime }$ and NMD ${}^{\prime }{\beta }^{\prime }$ such that $0\le {\alpha }^2+{\beta }^2\le 1.$ In addition, Yager [5], the q-ROF set (q-ROFS) can be used to generalize IFS and PyFS. The q-ROFS gives greater freedom for expressing their opinions and gives the conditions on MD ${}^{\prime }{\alpha }^{\prime }$ and NMD ${}^{\prime }{\beta }^{\prime }$ such that $0\le {\alpha }^q+{\beta }^q\le 1.$ The q-ROFS structure has the ability to deal with the sum of qth power of MD and NMD, and it always gives the answer within the range of $\left[0, 1\right]$. The results of this fuzzy structure are more accurate than previous fuzzy structures. Due to this important factor, we select this structure for the data aggregation.

In MADM, a hot debate is generated when trying to select the best option from ambiguous data or information. For MADM issues, the aggregation of data is the primary technique. A variety of AOs is based on different TCN and TN. The debate on arithmetic AOs has a long history among these AOs; many AOs have been examined in numerous contexts. For example, various authors have investigated Einstein AOs based on Einstein TNs, such as Munir et al. [6], who studied Einstein’s interactive AOs of a t-Spherical fuzzy set (TSFS), and Wang and Liu [7], who investigated Einstein geometric AOs of IFS. Intuitionistic fuzzy (IF) hybrid arithmetic AOs are proposed by Ye et al. [8], and Ullah [9] proposed picture fuzzy Maclaurin symmetric AOs. Mahmood [10] studied the applications of bipolar soft sets in MADM, and Wei [11] proposed IF trapezoidal fuzzy arithmetic AOs. The concept of Hamacher TNs, which led to the invention of Hamacher AOs and their use in MADM issues, has also been researched by several researchers in fuzzy mathematics. Hamacher AOs for IFSs based on Entropy are developed by Garg [12], while Ullah et al. [13] analyze the t-spherical fuzzy (TSF), Hamacher AOs for analyzing the performance of rescue robots. Various other TNs and TCNs, such as Dombi TNs and Dombi TCNs by Dombi [14], have been extensively investigated and led to the invention of Dombi AOs. Seikh and Mandal [15] and Jana et al. [16] developed the concepts of Dombi AOs in the context of IFSs and Dombi AOs in the Pythagorean fuzzy (PyF) system, respectively. Jana et al. [17] also investigated difficulties caused by Dombi AOs in q-ROFS. In this research article, we developed a few latest AOs for q-ROFS and examined the MADM issue.

Aczel–Alsina TN and TCN were presented by Aczel and Alsina [18] in 1982. The AATN and AATCN give more reliable and accurate results than other existing TN and TCN in fuzzy environments. They have good applicability in MADM under FS construction due to the high focus on parameter changeability. Menger [19] first proposed the concept of triangular norms in his theory of probabilistic fuzzy metric spaces. For FS, it has been discovered that TNs and their corresponding TCNs are significant operations, such as Archimedean TCNs and TNs [20], Frank TCNs and TNs [21], Dombi TCN and TN [22], Einstein TCN and TN [14], and Hamacher TCN and TN [23].

MADM algorithms are also used extensively in dealing with construction engineering problems, such as the modeling risk evaluation in construction management by Nasirzadeh et al. [24]. Wen et al. [25] discussed the applications of MADM algorithms in civil engineering. Dend and Zhang [26] used clustering algorithms based on fuzzy information to design and analyze construction engineering. The performance evaluation of construction companies by using VIKOR modeling was discussed by Lam et al. [27]. Chen et al. [28] presented the method of selecting sustainable materials for construction. Mohamed and Tran gave the idea of an inspection of concrete pavement for construction [29]. Demir [30] gave the model in the fuzzy environment for the financial comparison of Turkish cement companies with other companies. The evaluation of risk on small-level construction work by Topal and Atasoylu [31]. Baghdadi and Rahman [32] studied the stability of dunes during highway construction. The evaluation of construction material equipment by using the hybrid fuzzy technique was studied by Ghorabaee et al. [33]. Wudhikarn et al. [34] gave the idea of the improved construction material service provider strategy. The developed intellectual capital indicators in financial service companies using the best-worst method presented by Lu and Wudhikarn [35].

When we select the building material for the construction, the following features play a significant role: life of the material, the fineness of the material, the cost of the material, storage handling of the material, and the effect of climate on the material. Therefore, it is hard to measure which one is the best company to supply the best material. Because of the above considerations, we realize that DM problems are getting increasingly complicated in reality. It is necessary to explain the doubtful data in a far more beneficial approach to select the best option for the MADM concerns. The main goal of this informative article is to propose a q-ROFAAWA and q-ROFAAWG operator based on q-ROF information and to study their application in construction engineering problems.

The article provides the following information: In the next section, we discuss some basic concepts for Aczel–Alsina (AA) triangular norms and q-ROFSs. The AA operational laws for the q-ROFNs are intensely discussed in Section 3. Section 4 describes the q-ROFAAWA operator, q-ROFAAWG operator, q-ROFAAOWA operator, q-ROFAAOWG operator, q-ROFAAHWA operator, and q-ROFAAHWG operator, as well as a few useful features. In Section 5, we use the q-ROFAAWA operator to provide an algorithm for dealing with the MADM problem. Section 6 provides a numerical example for the best alternative selection by utilizing the proposed technique. Section 7 compares the newly developed method to existing methods to see whether the developed strategy is adequate. In the end, some conclusions and future research areas are mentioned in Section 8.

2. Preliminaries

This segment briefly explains some main concepts that help us understand this article.

2.1. q-Rung Orthopair Fuzzy Set

The notion of q-ROFS was proposed by Yager [5], where uncertain information is expressed in terms of MD and NMD with complete independency and accuracy. This notion of qROFS can handle information that IFSs and PyFSs cannot handle.

For better understanding, we construct Table 1, which discusses all symbols we used in the manuscript.

Table 1. Explanation of symbols.

Symbols	Explanation	Symbols	Explanation
$X$	Universal set	$x$	Element of universal set
$\tau$	q-ROF Set	$\beta$	Non-membership degree of q-ROF Set
$\alpha$	Membership degree of q-ROF set	$P\left(x\right)$	Hesitancy degree
$q$	$q\in {\mathbb{Z}}^{+}, q\ge 1$	$\mathcal{S}$	score function (SF)
$\lambda$	Any scalar number	${\zeta }_i$	Weight vector
$\mathcal{W}\left(\tau \right)$	Accuracy function (AF) of q-ROF Set

Definition 1.

[5], Let$X$be a universal set, then q-ROFS in the form of$\tau =\left\{x\left(\alpha ,\beta \right):0\le sum \left({\alpha }^q\left(x\right),{\beta }^q\left(x\right)\right)\le 1, q\in {\mathbb{Z}}^{+}\right\}$. The hesitancy degree for the pair$\left(\alpha ,\beta \right),x\in X$of q-ROFN is given by

$$P\left(x\right)=\sqrt[q]{1-sum\left({\alpha }^q\left(x\right),{\beta }^q\left(x\right)\right)}$$

Here,$\tau$represents q-ROFS and$\left(\alpha ,\beta \right)$denote a q-ROFN.

Definition 2.

The q-ROFNs’ sum, product, scalar multiplication, and power operations are defined as:[5], let${\tau }_1=\left({\alpha }_1, {\beta }_1\right)$and${\tau }_2=\left({\alpha }_2, {\beta }_2\right)$be the two q-ROFNs, here$\kappa$be any scalar number with a condition such as$\kappa >0$. Then

• ${\tau }_1\oplus {\tau }_2=\left(\sqrt[q]{{\alpha }_1^q+{\alpha }_2^q-{\alpha }_1^q.{\alpha }_2^q}, {\beta }_1.{\beta }_2\right)$
• ${\tau }_1\otimes {\tau }_2=\left( {\alpha }_1.{\alpha }_2,\sqrt[q]{{\beta }_1^q+{\beta }_2^q-{\beta }_1^q.{\beta }_2^q}\right)$
• $\kappa .\tau =\left(\sqrt[q]{1-{\left(1-{\alpha }^q\right)}^{\kappa }}, {\beta }^{\kappa } \right)$
• ${\tau }^{\kappa }=\left({\alpha }^{\kappa },\sqrt[q]{1-{\left(1-{\beta }^q\right)}^{\kappa }}\right)$

Definition 3.

[36], Let$\left({\alpha }_i, {\beta }_i\right)$where$i=1, 2, \dots , n$be the q-ROFNs. Then score function (SF) denoted by$\mathcal{S}$is given by:

$$\mathcal{S}\left(\tau \right)={\alpha }_i^q-{\beta }_i^q, Sco\left(\tau \right)\in \left[-1, 1\right]$$

(1)

and an accuracy function (AF) $\mathcal{W}$is

$$\mathcal{W}\left(\tau \right)={\alpha }_i^q+{\beta }_i^q, Acc\left(\tau \right)\in \left[0, 1\right]$$

(2)

Let${\tau }_1=\left({\alpha }_1, {\beta }_1\right)$and${\tau }_2=\left({\alpha }_2, {\beta }_2\right)$be the two q-ROFNs and$\mathcal{S}\left(\tau \right)$is the SF of${\tau }_i$and$\mathcal{W}\left(\tau \right)$is the AF of${\tau }_i$then${\tau }_1>{\tau }_2$where the symbol$“>”$means “preferred to” if either$\mathcal{S}\left({\tau }_1\right)>\mathcal{S}\left({\tau }_2\right)$or$\mathcal{S}\left({\tau }_1\right)=\mathcal{S}\left({\tau }_2\right)$and$\mathcal{W}\left({\tau }_1\right)>\mathcal{W}\left({\tau }_2\right)$holds.

2.2. Aczel–Alsina t-Norm & t-Conorm

Definition 4.

[19], A function$Z:{\left[0, 1\right]}^2\to \left[0, 1\right]$is called TN if for$r, s, p ϵ \left[0, 1\right],$ $Z$satisfy the following properties of Symmetry$Z\left(r, s\right)=T\left(s, r\right)$; Monotonicity$Z\left(r, s\right)\le Z\left(s, p\right)$if$s\le p$; Associativity$Z\left(r, Z\left(s, p\right)\right)=Z\left(Z\left(r, s\right), p\right)$; and one identity$Z\left(r, 1\right)=r$.

Examples 1.

A few examples of TN, such as Product of TN, is$Z_P\left(r, s\right)=r.s$; Minimum TN is$Z_M\left(r, s\right)=min\left(r.s\right)$; Lukasiewicz TN is$Z_L\left(r, s\right)-min\left(r+s-1, 0\right)$; and Drastic TN is given by:

$$Z_D=\left(r, s\right)=\{ \begin{array}{c}r if s=1\\ s if r=1\\ 0 \mathrm{otherwise}\end{array} \forall r, s\in \left[0,1\right].$$

Definition 5.

[37]A function$H:{\left[0, 1\right]}^2\to \left[0, 1\right]$is called TCN if$\forall r, s, p ϵ \left[0, 1\right],$ $H$satisfy the following properties of Symmetry$H\left(r, s\right)=H\left(s, r\right)$; Monotonicity$H\left(r, s\right)\le H\left(s, p\right)$if$s\le p$; Associativity$H\left(r, H\left(s, p\right)\right)=H\left(H\left(r, s\right), p\right)$; and null identity$H\left(r, 0\right)=r$.

Examples 2.

Few examples of TN, such as a probable sum of TCN$H_P\left(r, s\right)=r+s-r.s$; Maximum TCN$H_M\left(r, s\right)=max\left(r.s\right)$; Lukasiewicz TCN$H_L\left(r, s\right)-min\left(r+s-1\right)$; and Drastic TCN is given by:

$$H_D=\left(r, s\right)=\{\begin{array}{c}r if s=0\\ s if r=0\\ 1 \mathrm{otherwise}\end{array} \forall r, s\in \left[0,1\right].$$

Ref. [37], When $H$ is TCN and $T$ is TN then $H\left(r,s\right)\ge \max \left(r,s\right)$ and $H\left(r,s\right)\ge \min \left(r,s\right)\forall r,s \in \left[0, 1\right]$, respectively.

Definition 6.

Aczel et al. [18,38] proposed these TNs and TCNs classes for functional equations in the early 1980s.

The AATN is given by $\left(Z_A^{\lambda } \right)=\{\begin{array}{c}{Z}_D\left(r, s\right) if \lambda =0\\ min\left(r, s\right) if \lambda =\infty \\ e^{-{\left({\left(-\ln \left(r\right)\right)}^{\lambda }+{\left(-\ln \left(s\right)\right)}^{\lambda }\right)}^{1/\lambda }} \mathrm{otherwise}\end{array}$

The AATCN is given by $\left(H_A^{\lambda } \right)=\{\begin{array}{c}{H}_D\left(r, s\right) if \lambda =0\\ max\left(r, s\right) if \lambda =\infty \\ e^{-{\left({\left(-\ln \left(1-r\right)\right)}^{\lambda }+{\left(-\ln \left(1-s\right)\right)}^{\lambda }\right)}^{1/\lambda }} \mathrm{otherwise}\end{array}$

Cases: $Z_A^0=Z_D, Z_A^1=Z_P, Z_A^{\infty }=min,H_A^0=H_D, H_A^1=H_P, H_A^{\infty }=max \forall \lambda \in \left[0, 1\right]$, the TN $Z_A^{\lambda }$ and TCN $H_A^{\lambda }$ are twice each other. The number of AATNs is steadily increasing, while the number of AATCNs is steadily decreasing.

3. Aczel–Alsina Operational Laws for q-ROFN

We demonstrate the AA operations on q-ROFN and discuss some fundamental properties of these operations.

Definition 7.

Let${\tau }_1=\left({\alpha }_{{\tau }_1}, {\beta }_{{\tau }_1}\right)$and${\tau }_2=\left({\alpha }_{{\tau }_2}, {\beta }_{{\tau }_2}\right)$be two q-ROFNs and let$Z$and$H$denote the AATN and AATCN. Then, the generalized union and intersection$P$and$Q$are defined as:

$${\tau }_1\otimes {\tau }_2=\left( Z_A\left\{{\alpha }_{{\tau }_1},{\alpha }_{{\tau }_2}\right\},H_A\left\{{\beta }_{{\tau }_1},{\beta }_{{\tau }_2}\right\}\right)$$

$${\tau }_1\oplus {\tau }_2=\left( H_A\left\{{\beta }_{{\tau }_1},{\beta }_{{\tau }_2}\right\},Z_A\left\{{\alpha }_{{\tau }_1},{\alpha }_{{\tau }_2}\right\}\right)$$

Definition 8.

Let$\tau =\left({\alpha }_{\tau }, {\beta }_{\tau }\right), {\tau }_1=\left({\alpha }_{{\tau }_1}, {\beta }_{{\tau }_1}\right),$and${\tau }_2=\left({\alpha }_{{\tau }_2}, {\beta }_{{\tau }_2}\right)$be three q-ROFNs,$\mathcal{N}\ge 1$and$\lambda \ge 0$($\mathcal{N}$and$\lambda$are any scalar number). Then, the AATN and AATCN are defined as:

• $$\begin{gathered} {\alpha }_{{\tau }_1}\oplus {\beta }_{{\tau }_2}= \\ \left(\sqrt[q]{1-e^{-{\left({\left(-\ln \left(1-{\left({\alpha }_{{\tau }_1}\right)}^q\right)\right)}^{\mathcal{N}}+{\left(-\ln \left(1-{\left({\alpha }_{{\tau }_2}\right)}^q\right)\right)}^{\mathcal{N}} \right)}^{\frac{1}{\mathcal{N}}}}},e^{-{\left({\left(-\ln \left({\beta }_{{\tau }_1}\right)\right)}^{\mathcal{N}}+{\left(-\ln \left({\beta }_{{\tau }_2}\right)\right)}^{\mathcal{N}} \right)}^{\frac{1}{\mathcal{N}}}}\right) \end{gathered}$$
• $$\begin{gathered} {\alpha }_{{\tau }_1}\otimes {\beta }_{{\tau }_2}= \\ \left(e^{-{\left({\left(-\ln \left({\alpha }_{{\tau }_1}\right)\right)}^{\mathcal{N}}+{\left(-\ln \left({\alpha }_{{\tau }_2}\right)\right)}^{\mathcal{N}} \right)}^{\frac{1}{\mathcal{N}} }},\sqrt[q]{1-e^{-{\left({\left(-\ln \left(1-{\left({\beta }_{{\tau }_1}\right)}^q\right)\right)}^{\mathcal{N}}+{\left(-\ln \left(1-{\left({\beta }_{{\tau }_2}\right)}^q\right)\right)}^{\mathcal{N}} \right)}^{\frac{1}{\mathcal{N}} }}}\right) \end{gathered}$$
• $\lambda \tau =\left(\sqrt[q]{1-e^{-{\left(\lambda {\left(-\ln \left(1-{\left({\alpha }_{\tau }\right)}^q\right)\right)}^{\mathcal{N}} \right)}^{\frac{1}{\mathcal{N}} }}},e^{-{\left(\lambda {\left(-\ln \left({\beta }_{\tau }\right)\right)}^{\mathcal{N}} \right)}^{\frac{1}{\mathcal{N}}}}\right)$
• ${\tau }^{\lambda }=\left(e^{-{\left(\lambda {\left(-\ln \left({\alpha }_{\tau }\right)\right)}^{\mathcal{N}} \right)}^{\frac{1}{\mathcal{N}}}},\sqrt[q]{1-e^{-{\left(\lambda {\left(-\ln \left(1-{\left({\beta }_{\tau }\right)}^q\right)\right)}^{\mathcal{N}} \right)}^{\frac{1}{\mathcal{N}}}}}\right)$

Examples 3.

Let$\tau =\left(0.83,0.62\right), {\tau }_1=\left(0.77, 0.66\right),$and${\tau }_2=\left(0.67, 0.85\right)$be three q-ROFNs subjects to$q=3$and let$\mathcal{N}=3, \lambda =2$. Then AATN and AATCN are defined as:

$$\begin{gathered} {\alpha }_{{\tau }_1}\oplus {\beta }_{{\tau }_2}=\left(\sqrt[3]{1-e^{-{({(-\ln (1-{\left(0.77\right)}^3))}^3+{(-\ln (1-{\left(0.67\right)}^3))}^3 )}^{\frac{1}{3}}}},e^{-{({(-\ln \left(0.66\right))}^3+{(-\ln \left(0.85\right))}^3 )}^{\frac{1}{3}}}\right) \\ =\left(0.15903, 0.65465\right) \end{gathered}$$

$$\begin{gathered} {\alpha }_{{\tau }_1}\otimes {\beta }_{{\tau }_2}=\left(e^{-{({(-\ln \left(0.77\right))}^3+{(-\ln \left(0.67\right))}^3 )}^{\frac{1}{\mathcal{N}}}},\sqrt[3]{1-e^{-{({(-\ln (1-{\left(0.66\right)}^3))}^3+{(-\ln (1-{\left(0.85\right)}^3))}^3 )}^{\frac{1}{3}}}}\right) \\ =\left(0.64752, 0.20251\right) \end{gathered}$$

$$\begin{gathered} 2\tau =\left(\sqrt[3]{1-e^{-{(2{(-\ln (1-{\left(0.83\right)}^3))}^3 )}^{\frac{1}{3}}}},e^{-{(2{(-\ln \left(0.62\right))}^3 )}^{\frac{1}{3}}}\right) \\ =\left(0.21883, 0.54755\right) \end{gathered}$$

$$\begin{gathered} {\tau }^2=\left(e^{-{(2{(-\ln \left(0.83\right))}^3 )}^{\frac{1}{3}}},\sqrt[3]{1-e^{-{(2{(-\ln (1-{\left(0.62\right)}^3))}^3 )}^{\frac{1}{3}}}}\right) \\ =\left(0.79076, 0.09678\right) \end{gathered}$$

Theorem 1.

Let$\tau =\left({\alpha }_{\tau }\oplus {\beta }_{\tau }\right), {\tau }_1=\left({\alpha }_{{\tau }_1}, {\beta }_{{\tau }_1}\right),$and${\tau }_2=\left({\alpha }_{{\tau }_2}, {\beta }_{{\tau }_2}\right)$be three q-ROFNs where$\lambda ,{\lambda }_1, {\lambda }_2>0$. Then

• ${\tau }_1\oplus {\tau }_2={\tau }_2\oplus {\tau }_1$
• ${\tau }_1\otimes {\tau }_2={\tau }_2\otimes {\tau }_1$
• $\lambda \left({\tau }_1\oplus {\tau }_2\right)=\lambda {\tau }_1\oplus \lambda {\tau }_2$
• $\left({\lambda }_1+{\lambda }_2\right)\tau =\tau {\lambda }_1\oplus \tau {\lambda }_2$
• ${\left({\tau }_1\otimes {\tau }_2\right)}^{\lambda }={\tau }_1^{\lambda }\otimes {\tau }_2^{\lambda }$
• ${\tau }_1^{{\lambda }_1}\otimes {\tau }_2^{{\lambda }_2}={\tau }^{\left({\lambda }_1+{\lambda }_2\right)}$

Proof. 

Take three q-ROFNs $\tau , {\tau }_1, {\tau }_2$ and $\lambda , {\lambda }_1, {\lambda }_2$. Then

$$\begin{gathered} {\tau }_1\oplus {\tau }_2=\left( \sqrt[q]{1-e^{-{\left({\left(-\ln \left(1-{\left({\alpha }_{{\tau }_1}\right)}^q\right)\right)}^{\mathcal{N}}+{\left(-\ln \left(1-{\left({\alpha }_{{\tau }_2}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}} ,}{e}^{-{\left({\left(-\ln \left({\beta }_{{\tau }_1}\right)\right)}^{\mathcal{N}}+{\left(-\ln \left({\beta }_{{\tau }_2}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}}\right) \\ =\left( \sqrt[q]{1-e^{-{\left({\left(-\ln \left(1-{\left({\alpha }_{{\tau }_2}\right)}^q\right)\right)}^{\mathcal{N}}+{\left(-\ln \left(1-{\left({\alpha }_{{\tau }_1}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}} ,}{e}^{-{\left({\left(-\ln \left({\beta }_{{\tau }_2}\right)\right)}^{\mathcal{N}}+{\left(-\ln \left({\beta }_{{\tau }_1}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}}\right) \\ ={\tau }_2\oplus {\tau }_1 \end{gathered}$$

Similar to part 1.

$$\begin{gathered} \lambda \left({\tau }_1\oplus {\tau }_2\right)=\lambda \left( \sqrt[q]{1-e^{-{\left({\left(-\ln \left(1-{\left({\alpha }_{{\tau }_1}\right)}^q\right)\right)}^{\mathcal{N}}+{\left(-\ln \left(1-{\left({\alpha }_{{\tau }_2}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}} ,}{e}^{-{\left({\left(-\ln \left({\beta }_{{\tau }_1}\right)\right)}^{\mathcal{N}}+{\left(-\ln \left({\beta }_{{\tau }_2}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}}\right) \\ =\left( \sqrt[q]{1-e^{-{\left(\lambda \left({\left(-\ln \left(1-{\left({\alpha }_{{\tau }_1}\right)}^q\right)\right)}^{\mathcal{N}}+{\left(-\ln \left(1-{\left({\alpha }_{{\tau }_2}\right)}^q\right)\right)}^{\mathcal{N}}\right)\right)}^{\frac{1}{\mathcal{N}}}} ,}{e}^{-{\left(\lambda \left({\left(-\ln \left({\beta }_{{\tau }_1}\right)\right)}^{\mathcal{N}}+{\left(-\ln \left({\beta }_{{\tau }_2}\right)\right)}^{\mathcal{N}}\right)\right)}^{\frac{1}{\mathcal{N}}}}\right) \\ =\left(\begin{array}{c}\left( \sqrt[q]{1-e^{-{\left(\lambda {\left(-\ln \left(1-{\left({\alpha }_{{\tau }_1}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}} ,}{e}^{-{\left(\lambda {\left(-\ln \left({\beta }_{{\tau }_1}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}}\right)\\ \oplus \left( \sqrt[q]{1-e^{-{\left(\lambda {\left(-\ln \left(1-{\left({\alpha }_{{\tau }_2}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}} ,}{e}^{-{\left(\lambda {\left(-\ln \left({\beta }_{{\tau }_2}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}}\right)\end{array}\right) \\ =\lambda {\tau }_1\oplus \lambda {\tau }_2 \end{gathered}$$

$$\begin{gathered} {\lambda }_1\tau \oplus {\lambda }_2\tau =\left(\begin{array}{c}\left( \sqrt[q]{1-e^{-{\left({\lambda }_1{\left(-\ln \left(1-{\left({\alpha }_{\tau }\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}} ,}{e}^{-{\left({\lambda }_1{\left(-\ln \left({\beta }_{\tau }\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}}\right)\\ \oplus \left( \sqrt[q]{1-e^{-{\left({\lambda }_2{\left(-\ln \left(1-{\left({\alpha }_{\tau }\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}} ,}{e}^{-{\left({\lambda }_2{\left(-\ln \left({\beta }_{\tau }\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}}\right)\end{array}\right) \\ =\left( \sqrt[q]{1-e^{-{\left(\left({\lambda }_2+{\lambda }_2\right){\left(-\ln \left(1-{\left({\alpha }_{\tau }\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}} ,}{e}^{-{\left(\left({\lambda }_2+{\lambda }_2\right){\left(-\ln \left({\beta }_{\tau }\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}}\right) \\ =\left({\lambda }_2+{\lambda }_2\right)\tau \end{gathered}$$

$$\begin{gathered} {\left({\tau }_1\otimes {\tau }_2\right)}^{\lambda }={\left( \sqrt[q]{e^{-{\left({\left(-\ln \left(1-{\left({\alpha }_{{\tau }_1}\right)}^q\right)\right)}^{\mathcal{N}}+{\left(-\ln \left(1-{\left({\alpha }_{{\tau }_2}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}} ,}1-e^{-{\left({\left(-\ln \left({\beta }_{{\tau }_1}\right)\right)}^{\mathcal{N}}+{\left(-\ln \left({\beta }_{{\tau }_2}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}}\right)}^{\lambda } \\ =\left( \sqrt[q]{1-e^{-{\left(\lambda \left({\left(-\ln {\left({\alpha }_{{\tau }_1}\right)}^q\right)}^{\mathcal{N}}+{\left(-\ln {\left({\alpha }_{{\tau }_2}\right)}^q\right)}^{\mathcal{N}}\right)\right)}^{\frac{1}{\mathcal{N}}}} ,}{e}^{-{\left(\lambda \left({\left(-\ln \left(1-{\beta }_{{\tau }_1}\right)\right)}^{\mathcal{N}}+{\left(-\ln \left(1-{\beta }_{{\tau }_2}\right)\right)}^{\mathcal{N}}\right)\right)}^{\frac{1}{\mathcal{N}}}}\right) \\ =\left(\begin{array}{c}\left( \sqrt[q]{e^{-{\left({\lambda }_1{\left(-\ln {\left({\alpha }_{{\tau }_1}\right)}^q\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}} ,}1-e^{-{\left({\lambda }_1{\left(-\ln \left(1-{\beta }_{{\tau }_1}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}}\right)\\ \otimes \left( \sqrt[q]{e^{-{\left({\lambda }_2{\left(-\ln {\left({\alpha }_{{\tau }_2}\right)}^q\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}} ,}1-e^{-{\left({\lambda }_2{\left(-\ln \left(1-{\beta }_{{\tau }_2}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}}\right)\end{array}\right) \\ ={\tau }_1^{\lambda }\otimes {\tau }_2^{\lambda } \end{gathered}$$

$$\begin{gathered} {\tau }_1^{{\lambda }_1}\otimes {\tau }_2^{{\lambda }_2}=\left(\begin{array}{c}\left( \sqrt[q]{e^{-{\left({\lambda }_1{\left(-\ln {\left({\alpha }_{\tau }\right)}^q\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}} ,}1-e^{-{\left({\lambda }_1{\left(-\ln \left(1-{\beta }_{\tau }\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}}\right)\\ \otimes \left( \sqrt[q]{e^{-{\left({\lambda }_2{\left(-\ln {\left({\alpha }_{\tau }\right)}^q\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}} ,}1-e^{-{\left({\lambda }_2{\left(-\ln \left(1-{\beta }_{\tau }\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}}\right)\end{array}\right) \\ =\left( \sqrt[q]{e^{-{\left(\left({\lambda }_2+{\lambda }_2\right){\left(-\ln {\left({\alpha }_{\tau }\right)}^q\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}} ,}1-e^{-{\left(\left({\lambda }_2+{\lambda }_2\right){\left(-\ln \left(1-{\beta }_{\tau }\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}}\right) \end{gathered}$$

□

4. q-ROF Aczel–Alsina Aggregation Operators

This portion elaborates on some q-ROF average AOs utilizing AA operations. We discuss q-ROFAAWA, q-ROFAAWG, q-ROFAAOWA, q-ROFAAOWG, q-ROFAAHA, and q-ROFAAHG operators in detail.

Definition 9.

Let${\tau }_i=\left({\alpha }_i, {\beta }_i\right)$be some q-ROFNs and${\zeta }_i={\left({\zeta }_1, {\zeta }_2, \dots , {\zeta }_n\right)}^T$be the weight vector (WV) of${\tau }_i$, having condition${\zeta }_i\ge 0$and${\displaystyle \sum }_{i=1}^n{\zeta }_i=1.$Then, the q-ROFAAWA operator is the function:$M^{*}{}^n\to M^{*}$, defined as:

$$q-ROFAAWA \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)=\stackrel{n}{\underset{i=1}{\oplus }}\left({\zeta }_i{\tau }_i\right)={\zeta }_1{\tau }_1\oplus {\zeta }_2{\tau }_2\oplus \dots \oplus {\zeta }_n{\tau }_n$$

By using the AA operations on q-ROFNs, we derive the following theorem.

Theorem 2.

Let${\tau }_i=\left({\alpha }_i, {\beta }_i\right)$denote some q-ROFNs. Then aggregated values of${\tau }_i^{\prime }s$utilizing the q-ROFAAWA AOs is also known as a q-ROFN and given by:

$$\begin{array}{l}q-ROFAAWA \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)\\ =\left(\sqrt[q]{1-e^{-\left({\displaystyle \sum }_{i=1}^n\left({\left({\zeta }_i{\left(-\ln \left(1-{\left({\alpha }_{{\tau }_i}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)} ,}{e}^{-\left({\displaystyle \sum }_{i=1}^n\left(\left({\left({\zeta }_i{\left(-\ln \left({\beta }_{{\tau }_i}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)\right) }\right)\end{array}$$

(3)

Proof. 

By using the induction of mathematics rule:

For $n=2$,

$${\zeta }_1{\tau }_1=\left( \sqrt[q]{1-e^{-{\left(\left({\zeta }_1{\left(-\ln \left(1-{\left({\alpha }_{{\tau }_1}\right)}^q\right)\right)}^{\mathcal{N}}\right)\right)}^{\frac{1}{\mathcal{N}}}} ,}{e}^{-{\left({\zeta }_1{\left(-\ln \left({\beta }_{{\tau }_1}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}}\right)$$

$${\zeta }_2{\tau }_2=\left( \sqrt[q]{1-e^{-{\left(\left({\zeta }_2{\left(-\ln \left(1-{\left({\alpha }_{{\tau }_2}\right)}^q\right)\right)}^{\mathcal{N}}\right)\right)}^{\frac{1}{\mathcal{N}}}} ,}{e}^{-{\left({\zeta }_2{\left(-\ln \left({\beta }_2\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}}\right)$$

By Definition 5, we obtain

$$\begin{gathered} q-ROFAAWA \left({\tau }_1,{\tau }_2\right)={\zeta }_1{\tau }_1\oplus {\zeta }_2{\tau }_2 \\ =\left(\begin{array}{c}\left(\sqrt[q]{1-e^{-\left({\left({\zeta }_1{\left(-\ln \left(1-{\left({\alpha }_{{\tau }_1}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)} ,}{e}^{-\left(\left({\displaystyle \sum }_{i=1}^n{\left({\zeta }_1{\left(-\ln \left({\beta }_{{\tau }_1}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right) }\right)\\ \oplus \left(\sqrt[q]{1-e^{-\left({\left({\zeta }_2{\left(-\ln \left(1-{\left({\alpha }_{{\tau }_2}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)} ,}{e}^{-\left(\left({\displaystyle \sum }_{i=1}^n{\left({\zeta }_1{\left(-\ln \left({\beta }_{{\tau }_2}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right) }\right)\end{array}\right) \\ =\left(\begin{array}{c} \sqrt[q]{1-e^{-\left({\zeta }_1\left({\left({\left(-\ln \left(1-{\left({\alpha }_{{\tau }_1}\right)}^q\right)\right)}^{\mathcal{N}}+{\left(-\ln \left(1-{\left({\alpha }_{{\tau }_2}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)} ,}\\ e^{-{\left({\zeta }_1\left({\left(-\ln \left({\beta }_{{\tau }_1}\right)\right)}^{\mathcal{N}}+{\zeta }_2{\left(-\ln \left({\beta }_{{\tau }_2}\right)\right)}^{\mathcal{N}}\right)\right)}^{\frac{1}{\mathcal{N}}}}\end{array}\right) \\ =\left(\begin{array}{c}\sqrt[q]{1-e^{-\left({\displaystyle \sum }_{i=1}^2 \left({\zeta }_i{\left({\left(-\ln \left(1-{\left({\alpha }_{{\tau }_i}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)},}\\ e^{-\left({\displaystyle \sum }_{i=1}^2\left(\left({\zeta }_i{\left({\left(-\ln \left({\beta }_{{\tau }_i}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)\right) }\end{array}\right). \end{gathered}$$

For $n=k$

$$\begin{gathered} q-ROFAAWA\left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)=\stackrel{k}{\underset{\zeta =1}{\oplus }}\left({\zeta }_i{\tau }_i\right) \\ =\left(\begin{array}{c}\sqrt[q]{1-e^{-\left({\displaystyle \sum }_{i=1}^k \left({\zeta }_i{\left({\left(-\ln \left(1-{\left({\alpha }_{{\tau }_i}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)},}\\ e^{-\left({\displaystyle \sum }_{i=1}^k\left(\left({\left({\zeta }_i{\left(-\ln \left({\beta }_{{\tau }_i}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)\right) }\end{array}\right) \end{gathered}$$

Now for $n=k+1$, we obtain

$$\begin{gathered} q-ROFAAWA \left({\tau }_1, {\tau }_2, \dots ,{\tau }_k,{\tau }_{k+1}\right)=\stackrel{k}{\underset{\zeta =1}{\oplus }}\left({\zeta }_i{\tau }_i\right)\oplus \left({\zeta }_{k+1}{\tau }_{k+1}\right) \\ =\left(\begin{array}{c}\left(\begin{array}{c}\sqrt[q]{1-e^{-\left({\displaystyle \sum }_{i=1}^k \left({\zeta }_i{\left({\left(-\ln \left(1-{\left({\alpha }_{{\tau }_i}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)},}\\ e^{-\left({\displaystyle \sum }_{i=1}^k\left(\left({\left({\zeta }_i{\left(-\ln \left({\beta }_{{\tau }_i}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)\right) }\end{array}\right)\\ \oplus \left(\begin{array}{c} \sqrt[q]{1-e^{-\left({\zeta }_{k+1}{\left({\left(-\ln \left(1-{\left({\alpha }_{{\tau }_{k+1}}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)} ,}\\ e^{-{\left({\zeta }_1{\left(-\ln \left({\beta }_{{\tau }_1}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}}\end{array}\right)\end{array}\right). \\ =\left(\begin{array}{c}\sqrt[q]{1-e^{-\left({\displaystyle \sum }_{i=1}^{k+1} \left({\zeta }_i{\left({\left(-\ln \left(1-{\left({\alpha }_{{\tau }_i}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)},}\\ e^{-\left({\displaystyle \sum }_{i=1}^{k+1}\left(\left({\left({\zeta }_i{\left(-\ln \left({\beta }_{{\tau }_i}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)\right) }\end{array}\right) \end{gathered}$$

Hence, the result satisfies the condition for $n=k+1$.   □

Theorem 3.

(Idempotency) Let${\tau }_i=\left({\alpha }_i, {\beta }_i\right)=\left(\alpha , \beta \right)=\tau \forall i$. Then

$$\mathrm{q}-\mathrm{ROFAAWA} \left({\tau }_1, {\tau }_2, \dots ,{\tau }_k\right)=\tau$$

Proof. 

Since ${\tau }_i=\left({\alpha }_i, {\beta }_i\right); \left(i=1, 2, \dots , n\right)$.

$$\begin{gathered} \mathrm{q}-ROFAAWA \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)=\stackrel{k}{\underset{i=1}{\oplus }}\left({\alpha }_i, {\beta }_i\right) \\ =\left(\sqrt[q]{1-e^{-\left({\displaystyle \sum }_{i=1}^n \left({\zeta }_i{\left({\left(-\ln \left(1-{\left({\alpha }_{{\tau }_i}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)},}{e}^{-\left({\displaystyle \sum }_{i=1}^n\left(\left({\left({\zeta }_i{\left(-\ln \left({\beta }_{{\tau }_i}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)\right) }\right) \\ =\left(\sqrt[q]{1-e^{-{\left({\left(-\ln \left(1-{\left({\alpha }_{\tau }\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}},}{e}^{-{\left({\left(-\ln \left({\beta }_{\tau }\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}}\right) \\ =\left(\sqrt[q]{1-e^{\ln \left(1-{\alpha }^q\right)}},e^{\ln \left({\beta }^q\right)}\right)=\left(\alpha , \beta \right)=\tau \end{gathered}$$

□

Theorem 4.

(Boundedness) Let${\tau }_i=\left(\alpha , \beta \right)$be an accumulation of q-ROFNs. Let${\tau }^{-}=\min \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)$and${\tau }^{+}=\max \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)$. Then

$${\tau }^{-}\le q-ROFAAWA \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)\le {\tau }^{+}.$$

Proof. 

Let ${\tau }_i=\left(\alpha , \beta \right)$ be an accumulation of q-ROFNs. Let ${\tau }^{-}=\min \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)=\left({\alpha }_{\tau }^{-}, {\beta }_{\tau }^{-}\right)$ and ${\tau }^{+}=\max \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)=\left({\alpha }_{\tau }^{+}, {\beta }_{\tau }^{+}\right).$ We obtain ${\alpha }_{\tau }^{-}=\min \left({\alpha }_i\right), {\beta }_{\tau }^{-}=\max \left({\beta }_i\right),{\alpha }_{\tau }^{+}=\max \left({\alpha }_i\right), {\beta }_{\tau }^{+}=\min \left({\beta }_i\right).$ Hence, we obtained subsequent inequality as given below:

$$\begin{gathered} \sqrt[q]{1-e^{-\left({\displaystyle \sum }_{i=1}^n \left({\left({\zeta }_i\left(\left({\left(-\ln \left(1-{\left({\alpha }_{\tau }^{-}\right)}^q\right)\right)}^{\mathcal{N}}\right)\right)\right)}^{\frac{1}{\mathcal{N}}}\right)\right)}}\le \sqrt[q]{1-e^{-\left({\displaystyle \sum }_{i=1}^n \left({\left({\zeta }_i{\left(-\ln \left(1-{\alpha }_{{\tau }_i}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)}} \\ \le \sqrt[q]{1-e^{-\left({\displaystyle \sum }_{i=1}^n \left({\left({\zeta }_i{\left(-\ln \left(1-{\left({\alpha }_{\tau }^{+}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)}} \\ {e}^{-\left({\displaystyle \sum }_{i=1}^n{\left({\zeta }_i{\left(-\ln \left({\beta }_{\tau }^{-}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right) }\le e^{-\left({\displaystyle \sum }_{i=1}^n{\left({\zeta }_i{\left(-\ln {\beta }_{\tau }\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right) }\le e^{-\left({\displaystyle \sum }_{i=1}^n{\left({\zeta }_i{\left(-\ln \left({\beta }_{\tau }^{+}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right) } \end{gathered}$$

Therefore,

$${\tau }^{-}\le \mathrm{q}-\mathrm{ROFAAWA} \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)\le {\tau }^{+}$$

□

Theorem 5.

(Monotonicity) Let${\tau }_i=\left({\alpha }_i, {\beta }_i\right)$and${\tau }_i^{\prime }=\left({\alpha }_i^{\prime }, {\beta }_i^{\prime }\right) \left(i=1, 2, \dots , n\right)$be two q-ROFSs such that${\tau }_i\le {\tau }_i^{\prime }$i.e.,${\alpha }_i\le {\alpha }_i^{\prime } and {\beta }_i\ge {\beta }_i^{\prime } \forall i.$Then

$$q-ROFAAWA \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)\le q-ROFAAWA \left({\tau }_1^{\prime }, {\tau }_2^{\prime }, \dots ,{\tau }_n^{\prime }\right)$$

Proof. 

Consider two q-ROFSs ${\tau }_i=\left({\alpha }_i, {\beta }_i\right)$ and ${\tau }_i^{\prime }=\left({\alpha }_i^{\prime }, {\beta }_i^{\prime }\right) \left(i=1, 2, \dots , n\right)$. ${\tau }_i\le {\tau }_i^{\prime }$ implies that

$$\sqrt[q]{1-e^{-\left({\displaystyle \sum }_{i=1}^n \left({\zeta }_i{\left({\left(-\ln \left(1-{\left({\alpha }_{{\tau }_i}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)}}\le \sqrt[q]{1-e^{-\left({\displaystyle \sum }_{i=1}^n \left({\zeta }_i{\left({\left(-\ln \left(1-{\left({\alpha }_{{\tau }_i^{\prime }}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)}}$$

and

$$e^{-\left({\displaystyle \sum }_{i=1}^n\left(\left({\left({\zeta }_i{\left(-\ln \left({\beta }_{{\tau }_i}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)\right) }\ge e^{-\left({\displaystyle \sum }_{i=1}^n\left(\left({\left({\zeta }_i{\left(-\ln \left({\beta }_{{\tau }_i^{\prime }}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)\right) }$$

Implies that

$$q-ROFAAWA \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)\le q-ROFAAWA \left({\tau }_1^{\prime }, {\tau }_2^{\prime }, \dots ,{\tau }_n^{\prime }\right)$$

□

Definition 10.

Let${\tau }_i=\left({\alpha }_i, {\beta }_i\right)$be some q-ROFNs and${\zeta }_i={\left({\zeta }_1, {\zeta }_2, \dots , {\zeta }_n\right)}^T$be the WV of${\tau }_i$. Then, the q-ROFAAOWA operator is the function:$M^{*}{}^n\to M^{*}$, defined as:

$$q-ROFAAOWA \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)=\stackrel{n}{\underset{i=1}{\oplus }}\left({\zeta }_i{\tau }_{p\left(i\right)} \right)$$

where,$\left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)$are the permutation such that${\tau }_{i-1}\ge {\tau }_i \forall \left(i=1, 2, \dots , n\right).$Using AA operations on q-ROFNs, we demonstrate the following theorem.

Theorem 6.

Let${\tau }_i=\left({\alpha }_i, {\beta }_i\right)$denote some q-ROFNs. Then aggregated values of${\tau }_i^{\prime }s$utilizing the q-ROFAAOWA AOs is also known as a q-ROFN given by:

$$q-ROFAAOWA \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)=\left(\sqrt[q]{1-e^{-\left({\displaystyle \sum }_{i=1}^n\left({\left({\zeta }_i{\left(-\ln \left(1-{\left({\alpha }_{{\tau }_{p\left(i\right)}}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)} ,}{e}^{-\left({\displaystyle \sum }_{i=1}^n\left(\left({\left({\zeta }_i{\left(-\ln \left({\beta }_{{\tau }_{p\left(i\right)}}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)\right) }\right)$$

(4)

Definition 11.

Let${\tau }_i$be an accumulation of q-ROFNs. A q-ROFAAHA operator of dimension$n$is mapping$q-ROFAAHA:M^{*}{}^n\to M^{*}$such that

$$q-ROFAAHA \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)=\stackrel{n}{\underset{i=1}{\oplus }}\left({\zeta }_i\dot{{\tau }_i}\right)$$

where$\zeta ={\left({\zeta }_1, {\zeta }_2, \dots ,{\zeta }_n\right)}^T$are the WV of the q-ROFAAHA operator having conditions such that${\zeta }_i=\left[0, 1\right]$and${\displaystyle \sum }_{i=1}^n{\zeta }_i=1; \dot{{\tau }_i}=n{\zeta }_i{\tau }_i, \left(\dot{{\tau }_1}, \dot{{\tau }_2}, \dots ,\dot{{\tau }_n}\right)$is any permutation of the collection of weighted q-ROFNs such that${\dot{\tau }}_{i-1}\ge \dot{{\tau }_i} \forall i;\zeta ={\left({\zeta }_1, {\zeta }_2, \dots , {\zeta }_n\right)}^T$. Here$n$is the coefficient of balancing, which is responsible for maintaining equilibrium.

We can prove the following theorem using AA procedures using q-ROFNs information.

Theorem 7.

Consider${\tau }_i=\left({\alpha }_i, {\beta }_i\right)$denote some q-ROFNs. Then aggregated values of${\tau }_i\prime s$. utilizing the q-ROFAAHG operator also give a q-ROFN.

$$q-ROFAAHA \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)=\stackrel{n}{\underset{i=1}{\otimes }}\left({\zeta }_i\dot{{\tau }_i}\right)$$

Further,

$$q-ROFAAHA \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)=\left(\sqrt[q]{1-e^{-{\left({\displaystyle \sum }_{i=1}^n\left({\left({\left(-\log \left(1-{\left(\dot{{\alpha }_{{\tau }_i}}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)}^{{\zeta }_i}}}, e^{-{\left({\displaystyle \sum }_{i=1}^n{\left({\left(-\log \left(\dot{{\beta }_{{\tau }_i}}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}} } \right)}^{{\zeta }_i}}\right)$$

(5)

We can prove the following theorem using AA procedures using q-ROFNs information. It is also the same as Theorem 3.

Now, we propose some geometric aggregation operators based on AA operations for q-ROFNs.

Definition 12.

Let${\tau }_i=\left({\alpha }_i, {\beta }_i\right)$be some q-ROFNs and${\zeta }_i={\left({\zeta }_1, {\zeta }_2, \dots , {\zeta }_n\right)}^T$be the WV of${\tau }_i$, having condition${\zeta }_i\ge 0$and${\displaystyle \sum }_{i=1}^n{\zeta }_i=1.$Then, the q-ROFAAWG operator can be described in the form of a function:$M^{*}{}^n\to M^{*}$, defined as:

$$q-ROFAAWG \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)=\stackrel{n}{\underset{i=1}{\otimes }}\left({\tau }_i^{{\zeta }_i}\right)$$

By using the AA operations on q-ROFNs, we derive the following theorem.

Theorem 8.

Consider${\tau }_i=\left({\alpha }_i, {\beta }_i\right)$denote some q-ROFNs. Then aggregation results of${\tau }_i\prime s$utilizing the q-ROFAAWG operator also gives a q-ROFN.

$$q-ROFAAWG \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)=\stackrel{n}{\underset{i=1}{\otimes }}\left({\tau }_i^{{\zeta }_i}\right)=\left(e^{-{\left({\displaystyle \sum }_{i=1}^n\left({\left({\left(-\ln {\left({\alpha }_{{\tau }_i}\right)}^q\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)}^{{\zeta }_i},}\sqrt[q]{1-e^{-{\left({\displaystyle \sum }_{i=1}^n\left({\left({\left(-\ln \left(1-{\beta }_{{\tau }_i}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)}^{{\zeta }_i}}}\right)$$

(6)

The proof follows the same pattern as Theorem 2.

Definition 13.

Let${\tau }_i=\left({\alpha }_{{\tau }_i}, {\beta }_{{\tau }_i}\right)$be an accumulation of q-ROFNs. An q-ROFAAOWG operator of dimension$n$is mapping q-ROFAAOWG:$M^{*}{}^n\to M^{*}$with the corresponding WV,${\zeta }_i={\left({\zeta }_1, {\zeta }_2, \dots , {\zeta }_n\right)}^T$such that${\zeta }_i\ge 0$and${\displaystyle \sum }_{i=1}^n{\zeta }_i=1$, as follows:

$$q-ROFAAOWG \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)=\stackrel{n}{\underset{i=1}{\otimes }}\left({\tau }_{p\left(i\right)}^{{\zeta }_i}\right)$$

Theorem 9.

Let${\tau }_i=\left({\alpha }_{{\tau }_i}, {\beta }_{{\tau }_i}\right)$be the collection of q-ROFNs. The aggregation finding by using the q-ROFAAOWG operator is also q-ROFNs given by:

$$q-ROFAAOWG \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)=\stackrel{n}{\underset{i=1}{\otimes }}\left({\tau }_{p\left(i\right)}^{{\zeta }_i}\right)$$

Definition 14.

Let${\tau }_i$be an accumulation of q-ROFNs. A q-ROFAAHG operator of dimension$n$is mapping$q-ROFAAHG:M^{*}{}^n\to M^{*}$such that

$$q-ROFAAHG \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)=\stackrel{n}{\underset{i=1}{\otimes }}{\dot{{\tau }_i}}^{{\zeta }_i}$$

where$\zeta ={\left({\zeta }_1, {\zeta }_2, \dots ,{\zeta }_n\right)}^T$are the WV of the q-ROFAAHG operator with${\zeta }_i=\left[0, 1\right]$and${\displaystyle \sum }_{i=1}^n{\zeta }_i=1; \dot{{\tau }_i}=n{\zeta }_i{\tau }_i, \left(\dot{{\tau }_1}, \dot{{\tau }_2}, \dots ,\dot{{\tau }_n}\right)$is any permutation of the collection of weighted q-ROFNs such that${\dot{\tau }}_{i-1}\ge \dot{{\tau }_i} \forall i;\zeta ={\left({\zeta }_1, {\zeta }_2, \dots , {\zeta }_n\right)}^{\tau }$. Here$n$is the coefficient of balancing, which is responsible for maintaining equilibrium.

Theorem 10.

Let${\tau }_i$be the collection of q-ROFNs. The aggregation finding by using the q-ROFAAHG operator is also a q-ROFNs given by:

$$\begin{gathered} q-ROFAAHG\left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)=\stackrel{n}{\underset{i=1}{\otimes }}\left({\zeta }_i\dot{{\tau }_i}\right) \\ =\left(e^{-{\left({\displaystyle \sum }_{i=1}^n{\left({\left(-\log \left({\dot{\alpha }}_{{\tau }_i}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}} } \right)}^{{\zeta }_i}}, \sqrt[q]{1-e^{-{\left({\displaystyle \sum }_{i=1}^n\left({\left({\left(-\log \left(1-{\left(\dot{{\beta }_{{\tau }_i}}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)}^{{\zeta }_i}}}\right) \end{gathered}$$

5. MADM Algorithm Based on q-ROFAAWA

This section contains information using q-ROSF data to design a methodology and apply the proposed operators in MADM.

Consider $a=\left\{a_1,a_2,\dots ,a_m\right\}$ are $m$ alternatives for selection, let $J=\left\{j_1,j_2,\dots ,j_n\right\}$ are $n$ attributes with WV,$\zeta$. Let the q-ROSF data be $H={\left({\tau }_{ij}\right)}_{m\times n}$ in the form of a matrix where q-ROFN ${\tau }_{ij}=\left({\alpha }_{ij}, {\beta }_{ij}\right)$ represents the value of the characteristic that the decision-maker (DM) provides for the alternate $j_n$.${\tau }_{ij}=\left({\alpha }_{ij},{\beta }_{ij}\right)$ show alternative evaluation values where $0\le {\alpha }_{ij}{}^q+{\beta }_{ij}{}^q\le 1$. As a result, the q-ROF decision matrix $H={\left({\tau }_{ij}\right)}_{m\times n}$ is formed with the help of q-ROF information.

In this scenario, to select the best possible option, we construct the algorithm by using the q-ROFAAWA and q-ROFAAWG operators to explain the MADM issue in the q-ROF environment. The following steps of this algorithm are discussed below:

Step 1.

First, the q-ROF decision matrix is formed, which is further into the normalized decision matrix.

$$\overline{{\tau }_{ij}}=\{\begin{array}{c}{\tau }_{ij} \mathrm{benefit} \mathrm{attribute}\\ {\tau }_{ij}^c \mathrm{cost} \mathrm{attribute}\end{array}$$

Let ${\tau }_{ij} \mathrm{and} {\tau }_{ij}^c$ be the benefit and cost attributes of the decision matrix, respectively. There is no need to change any of the attributes if they are of the same type. Both categories must be changed if there are two different categories (cost and benefit).

Step 2.

For alternatives ${\zeta }_i$ aggregate all the values of ${\tau }_i$ with the help of q-ROFAAWA operator is given by:

$$\begin{gathered} q-ROFAAWA \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)=\stackrel{n}{\underset{\zeta =1}{\oplus }}\left({\zeta }_i{\tau }_i\right) \\ =\left(\sqrt[q]{1-e^{-\left({\displaystyle \sum }_{i=1}^n\left({\left({\zeta }_i{\left(-\ln \left(1-{\left({\alpha }_{{\tau }_i}\right)}^q\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)} ,}{e}^{-\left({\displaystyle \sum }_{i=1}^n\left(\left({\left({\zeta }_i{\left(-\ln \left({\beta }_{{\tau }_i}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)\right) }\right) \end{gathered}$$

And

$$\begin{gathered} q-ROFAAWG \left({\tau }_1, {\tau }_2, \dots ,{\tau }_n\right)=\stackrel{n}{\underset{i=1}{\otimes }}\left({\tau }_i^{{\zeta }_i}\right) \\ =\left(e^{-{\left({\displaystyle \sum }_{i=1}^n\left({\left({\left(-\ln {\left({\alpha }_{{\tau }_i}\right)}^q\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)}^{{\zeta }_i},}\sqrt[q]{1-e^{-{\left({\displaystyle \sum }_{i=1}^n\left({\left({\left(-\ln \left(1-{\beta }_{{\tau }_i}\right)\right)}^{\mathcal{N}}\right)}^{\frac{1}{\mathcal{N}}}\right)\right)}^{{\zeta }_i}} }\right) \end{gathered}$$

Step 3.

Calculate the score value by applying this SF provided by Liu et al. [36], which is given by:

$$\mathcal{S}\left(\tau \right)={\alpha }_i^q-{\beta }_i^q$$

Step 4.

We arrange the ranking values of all of the options to choose the best one while keeping ${\zeta }_i$ in mind.

6. Numerical Example

We handle a real-world construction material selection problem in this part by using the q-ROFAAWA and q-ROFAAWA aggregation operations. An explanation of the problem is as follows.

A sound product is possible only with sound materials; materials are the key to everything. The selection of the best building material is essential for the long life of the building. This article discusses the case study for selecting cement companies from the list of companies as cement is one of the essential constituents of construction material. In the global market, competition between cement companies is increasing day by day, and all companies are trying to produce high-quality cement. The selection of the best cement company is a challenging problem that can be accomplished with the help of the MADM procedure by keeping in mind the expert’s opinion under uncertain situations.

Example 4.

Consider we are selecting the cement company from the list of five companies like${\mathfrak{a}}_i=\left(i=1, 2, \dots , 5\right)$. We have the following attributes considered such as:$G_1$is the life of the cement,$G_2$is the fineness of the cement,$G_3$is the handling storage of cement,$G_4$is the effect of climate on cement. The attribute weight as$\zeta =\left(0.34, 0.26, 0.24, 0.16\right)$distributed by the DMs. The DMs will evaluate the five cement companies${\mathfrak{a}}_i=\left(i=1, 2, \dots , 5\right)$in ambiguity with q-ROF data under the following four attributes$G_i=\left(i=1, 2, 3, 4\right)$as presented inTable 2. It is noted that initially, we take parameters$q=3$and$\mathcal{N}=1$for q-ROFAAWA and q-ROFAAWG AOs. Furthermore, we also discuss the effect of the changeability in parameters$q$and$\mathcal{N}$.

Table 2. q-ROF decision matrix.

	${\mathfrak{a}}_1$	${\mathfrak{a}}_2$	${\mathfrak{a}}_3$	${\mathfrak{a}}_4$	${\mathfrak{a}}_5$
$G_1$	$\left(0.31, 0.89\right)$	$\left(0.29, 0.78\right)$	$\left(0.56, 0.88\right)$	$\left(0.33, 0.95\right)$	$\left(0.96, 0.50\right)$
$G_2$	$\left(0.32, 0.88\right)$	$\left(0.77, 0.28\right)$	$\left(0.87, 0.57\right)$	$\left(0.94, 0.30\right)$	$\left(0.95, 0.34\right)$
$G_3$	$\left(0.30, 0.86\right)$	$\left(0.28, 0.76\right)$	$\left(0.57, 0.86\right)$	$\left(0.30, 0.92\right)$	$\left(0.93, 0.32\right)$
$G_4$	$\left(0.28, 0.85\right)$	$\left(0.26, 0.71\right)$	$\left(0.55, 0.88\right)$	$\left(0.28, 0.89\right)$	$\left(0.90, 0.21\right)$

Step 1.

First, we construct the decision matrix by collecting the data from the five cement companies and provide all the data collection in the form of a matrix to experts for DM. We have considered four attributes with weight as follows: $G_1$ is the life of the cement $0.34$, $G_2$ is the fineness of the cement $0.26$, $G_3$ is the handling storage of cement $0.24$, $G_4$ is the effect of climate on cement $0.16$. The collection of the data is represented in Table 2.

Step 2.

In this step, we aggregate the information the DMs provide by using the q-ROFAAWA and q-ROFAAWG AOs. The aggregation findings are presented in Table 3. (Note that at the start, we take parameters $q=3$ and $\mathcal{N}=1$ during the aggregation.)

Table 3. Aggregation findings by using proposed q-ROFAAWA and q-ROFAAWG operators.

	q-ROFAAWA	q-ROFAAWG
${\mathfrak{a}}_1$	$\left(0.3185, 0.8525\right)$	$\left(0.6538, 0.9611\right)$
${\mathfrak{a}}_2$	$\left(0.2986, 0.7145\right)$	$\left(0.6378, 0.9189\right)$
${\mathfrak{a}}_3$	$\left(0.5675, 0.8619\right)$	$\left(0.8173, 0.9575\right)$
${\mathfrak{a}}_4$	$\left(0.3384, 0.8919\right)$	$\left(0.6538, 0.9827\right)$
${\mathfrak{a}}_5$	$\left(0.9590, 0.2159\right)$	$\left(0.9017, 0.4983\right)$

Step 3.

To apply the score values formula discussed in Definition 3. to check the best option from five companies. The score values are shown in Table 4. For better understanding, the findings of SF are represented geometrically in Figure 1.

Table 4. Scores of aggregated information.

	q-ROFAAWA	q-ROFAAWG
${\mathfrak{a}}_1$	$-0.5873$	$-0.8917$
${\mathfrak{a}}_2$	$-0.3380$	$-0.4557$
${\mathfrak{a}}_3$	$-0.4573$	$-0.5138$
${\mathfrak{a}}_4$	$0.6707$	$-0.8343$
${\mathfrak{a}}_5$	$0.6489$	$0.6094$

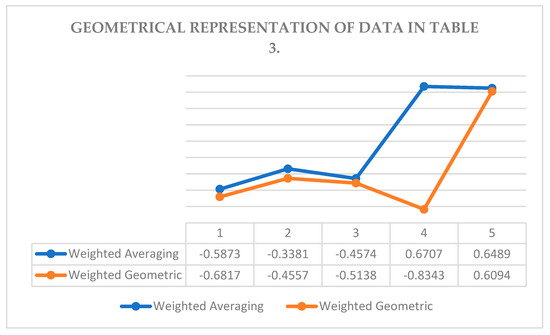Figure 1. The score values are represented geometrically. Where blue lines show the score values of WA while orange lines show the score value of WG aggregation.

For clarity and better understanding, we depict the score values in Figure 1.

Step 4.

Sort the five companies in order of preference based on their scores in Table 4. It is found that ${\mathfrak{a}}_4$ and ${\mathfrak{a}}_5$ are the best among the listed alternatives by applying the proposed q-ROFAAWA and q-ROFAAWG operators, respectively. The results are displayed in Table 5 below.

Table 5. Ranking of the score function.

	Ordering
q-ROFAAWA	${\mathfrak{a}}_4>{\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1$
q-ROFAAWG	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_4>{\mathfrak{a}}_1$

The results obtained by utilizing the q-OFAAWA and q-OFAAWG operators show that ${\mathfrak{a}}_5$ is the suitable alternative. Additionally, aggregated results from WA and WG operators do not always need to give the same rankings. However, it depends upon the DMs which WA and WG operators they select for the data aggregation.

6.1. The Effect of Parameters

As we saw in Section 3, all of the AOs proposed in this study depend on the two restrictions $\mathcal{N}$ and q. We observe the changeability effect of parameters ($\mathcal{N}$ and q) on the ranking order of our proposed AOs.

6.1.1. The Effect of $\mathcal{N}$

In our numerical example, we can see the value of the parameter $\mathcal{N}=1$. However, a change in the value $\mathcal{N}$ may influence the ranking results. We observed that when we change the value of parameter $\mathcal{N}$ in our proposed q-ROFAAWA and q-ROFAAWG operators, a significant variation occurs in the ranking sequence of alternatives. Such changes can be seen in Table 6 and Table 7.

Table 6. Ranking of score values by changing in $\mathcal{N}$ q-ROFAAWA.

Ranking of Score Values of q-ROFAAWA
$\mathcal{N}$	Ordering	$\mathcal{N}$	Ordering
1	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$	2	No result identified
3	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$	4	No result identified
5	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$	6	No result identified
7	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$	8	No result identified
9	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$	10	No result identified
13	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$	20	No result identified
15	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$	40	No result identified
17	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$	60	No result identified
19	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$	80	No result identified
99	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$	100	No result identified

Table 7. The ranking order of score function by changing in $\mathcal{N}$ q-ROFAAWG operator.

Ranking of Score Values of q-ROFAAWG
$\mathcal{N}$	Ordering	$\mathcal{N}$	Ordering
1	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$	2	No result identified
3	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$	4	No result identified
5	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$	6	No result identified
7	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$	8	No result identified
9	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$	10	No result identified
13	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$	20	No result identified
15	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$	40	No result identified
17	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$	60	No result identified
19	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$	80	No result identified
99	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$	100	No result identified

The aggregation findings of Table 5. are further represented in Figure 2. We can easily observe from the data there is no change in aggregation findings with the variations in $\mathcal{N}$. It is also observed that there when we take $\mathcal{N}$ as an even number, then there is no result identified.

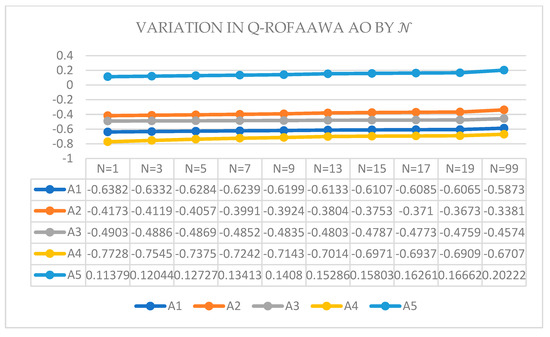
Figure 2. The graphical representation of score value, variation by $\mathcal{N}$.

All rankings in Table 6. can be observed in Figure 2. It can be noticed that in the q-ROFAAWA operator, there is no change when we take $\mathcal{N}$ as odd numbers. It is also observed that when we take $\mathcal{N}$ as even, no result will be identified.

Now, we also change the parameter $\mathcal{N}$ for q-ROFAAWG operators, and all the findings obtained are presented in Table 6, as given below.

The ranking of Table 7. can be seen geometrically in Figure 3, as given below. We noticed no change in a ranking order by the variation in $\mathcal{N}.$ It is also a highly significant factor; when we take $\mathcal{N}$ as an even number, then no result is identified.

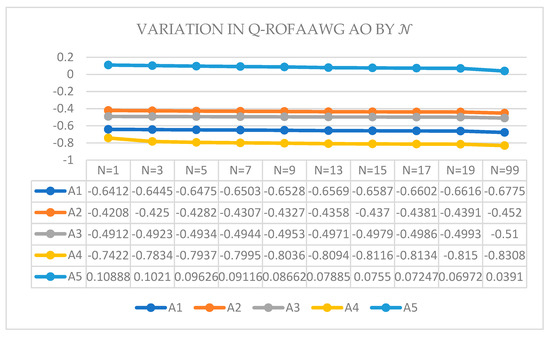
Figure 3. The graphical representation of score function, variation by $\mathcal{N}$, where the lines represent the raking of score value.

It is observed that when we take a variation of $\mathcal{N}$ as odd, then the sequence of listed five companies comes out to be the same, but this is not always guaranteed. On the other hand, when we take the variation of $\mathcal{N}$ even then, no result is identified.

6.1.2. The Effect of q

We take parameter q = 3 in the proposed numerical example and aggregate the data by utilizing the q-ROFAAWA and q-ROFAAWG AOs. If DMs can vary the value of parameter q, the ranking sequence also changes with the variation in q. We observed that the behavior of our proposed q-ROFAAWA and q-ROFAAWG AOs depends upon the parameter q for the interpretation of raking results. When we change the value of parameter q in the proposed q-ROFAAWA and q-ROFAAWG AOs, raking results are also affected by the changing of parameter q, which can be observed in Table 8 and Table 9, respectively.

Table 8. Ranking of score values by changing q.

q	Ranking of Score Values of q-ROFAAWA
3	${\mathfrak{a}}_1>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_5>{\mathfrak{a}}_4$
6	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$
9	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_1>{\mathfrak{a}}_3>{\mathfrak{a}}_4$
12	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_1>{\mathfrak{a}}_3>{\mathfrak{a}}_4$
15	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_1>{\mathfrak{a}}_4>{\mathfrak{a}}_3$
18	${\mathfrak{a}}_1>{\mathfrak{a}}_2>{\mathfrak{a}}_5>{\mathfrak{a}}_4>{\mathfrak{a}}_3$
36	${\mathfrak{a}}_1>{\mathfrak{a}}_2>{\mathfrak{a}}_5>{\mathfrak{a}}_3>{\mathfrak{a}}_4$

Table 9. Ranking of score values by changing q.

Q	Ranking of Score Values of q-ROFAAWG
3	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$
6	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$
9	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$
12	${\mathfrak{a}}_5>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_2>{\mathfrak{a}}_4$
15	${\mathfrak{a}}_5>{\mathfrak{a}}_3>{\mathfrak{a}}_2>{\mathfrak{a}}_1>{\mathfrak{a}}_4$
18	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$
36	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$

The ranking values of Table 8 are geometrically represented in Figure 4, as given below. Here, the range of score values describes vertically, and lines on horizontal lines show different values of the q.

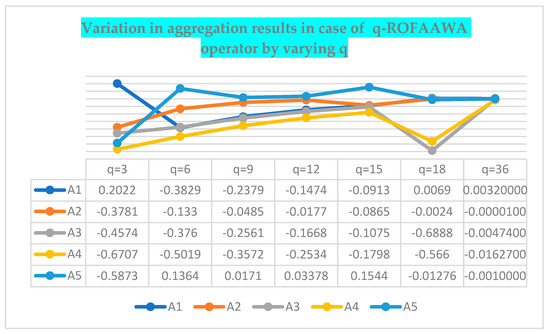
Figure 4. The geometric representation of score value, variation by q. Lines on horizontal lines represent the raking of score values, and here vertical line shows the range of score values of $\left[-1, 1\right]$.

.

The geometrical illustration of the ranking order in Table 9 is presented in Figure 5. Here, lines on horizontal lines represent the values of the SF, and vertical lines denote the range of score values of $\left[-1, 1\right]$.

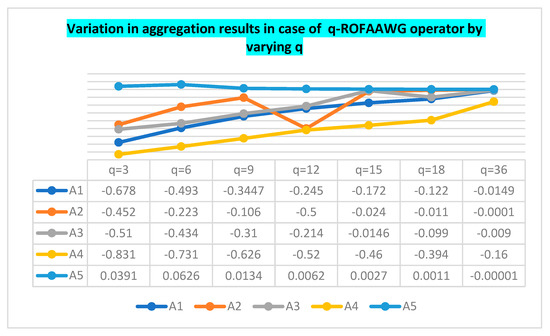
Figure 5. The graphical representation of score value, variation by q.

It is found that, in the sequence of the alternatives, when we take $\mathrm{q}=3$, we obtain the sequence of the listed five alternate values as follows ${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$. It is also a highly observable thing; when we take the parameter $q=12$, then the ranking of alternatives also varies due to changes in q; the variation in the sequence of alternatives is as follows ${\mathfrak{a}}_5>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_2>{\mathfrak{a}}_4$. Therefore, we can confidently say that the variation in the parameter q also changes the sequence of alternatives.

7. Comparative Analysis

In this part, we compared the aggregated findings produced with q-ROFAAWA and q-ROFAAWG operators to the aggregated results obtained with Dombi WA and WG AOs for q-ROFS by Jana et al. [17], q-ROF Yage WA (q-ROFYHA) and q-ROF Yager WG (q-ROFYWG) by Akram and Shahzadi [39], q-ROF weighted averaging (q-ROFWA), and geometric (q-ROFWG) operators by Liu and Wang [36]. All the results are shown in Table 10. We also showed that most of the AOs fail to aggregate the information provided in the form of q-ROFNs. These AOs include:

Table 10. Comparative analysis with existing operators.

Methods	Operators	Score Values	Ranking Results
Proposed operators	q-ROFAAWA	$\mathbb{S}\left(c_1\right)=-0.5873,\mathbb{S}\left(c_2\right)=-0.3380,$ $\mathbb{S}\left(c_3\right)=-0.4573,\mathbb{S}\left(c_4\right)=0.6707,$ $\mathbb{S}\left(c_5\right)=0.6489$	${\mathfrak{a}}_4>{\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1$
	q-ROFAAWG	$\mathbb{S}\left(c_1\right)=-0.8917,\mathbb{S}\left(c_2\right)=-0.4557,$ $\mathbb{S}\left(c_3\right)=-0.5138,\mathbb{S}\left(c_4\right)=-0.8343,$ $\mathbb{S}\left(c_5\right)=0.1223$	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_4>{\mathfrak{a}}_1$
Jana. et al. [17]	Dombi WA	$\mathbb{S}\left(c_1\right)=-0.6342, \mathbb{S}\left(c_2\right)=-0.411,$ $\mathbb{S}\left(c_3\right)=-0.4889, \mathbb{S}\left(c_4\right)=-0.7604,$ $\mathbb{S}\left(c_5\right)=0.1223$	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$
	Dombi WG	$\mathbb{S}\left(c_1\right)=-0.6460, \mathbb{S}\left(c_2\right)=-0.4250$, $\mathbb{S}\left(c_3\right)=-0.4928$, $\mathbb{S}\left(c_4\right)=-0.7954,$ $\mathbb{S}\left(c_5\right)=0.1024$	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$
Akram and Shahzadi [39]	q-ROFYHWA	$\mathbb{S}\left(c_1\right)=-0.3024, \mathbb{S}\left(c_2\right)=-0.5319,$ $\mathbb{S}\left(c_3\right)=-0.1609,\mathbb{S}\left(c_4\right)=-0.1580,$ $\mathbb{S}\left(c_5\right)=0.2885$	${\mathfrak{a}}_5>{\mathfrak{a}}_4>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_2$
	q-ROFYHWG	$\mathbb{S}\left(c_1\right)=0.3022, \mathbb{S}\left(c_2\right)=0.5318$, $\mathbb{S}\left(c_3\right)=0.1607,\mathbb{S}\left(c_4\right)=0.1574,$ $\mathbb{S}\left(c_5\right)=0.2875$	${\mathfrak{a}}_2>{\mathfrak{a}}_1>{\mathfrak{a}}_5>{\mathfrak{a}}_3>{\mathfrak{a}}_4$
Liu and Wang [36]	q-ROFWA	$\mathbb{S}\left(c_1\right)=-0.3062,\mathbb{S}\left(c_2\right)=-0.2487,$ $\mathbb{S}\left(c_3\right)=-0.3560,\mathbb{S}\left(c_4\right)=-0.4298,$ $\mathbb{S}\left(c_5\right)=0.0913$	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_1>{\mathfrak{a}}_3>{\mathfrak{a}}_4$
	q-ROFWG	$\mathbb{S}\left(c_1\right)=-0.6411, \mathbb{S}\left(c_2\right)=-0.4208$, $\mathbb{S}\left(c_3\right)=-0.4912, \mathbb{S}\left(c_4\right)=-0.7820,$ $\mathbb{S}\left(c_5\right)=0.1088$	${\mathfrak{a}}_5>{\mathfrak{a}}_2>{\mathfrak{a}}_3>{\mathfrak{a}}_1>{\mathfrak{a}}_4$
Senapati et al. [40]	IFAAFWA IFAAFWG	Unable to specify	Not applicable
Senapati et al. [41]	IVIFAAWA IVIFAAWG	Unable to specify	Not applicable
Hussain et al. [42]	PyFAAWA PyFAAWG	Unable to specify	Not applicable
Wei et al. [43]	PyFS WA PyFS WG	Unable to specify	Not applicable

• IF Aczel–Alsina WA (IFAAWA), and Aczel–Alsina WG (IFAAWG) operators by Senapati et al. [40].
• Interval-valued IFAAWA (IVIFAAWA) and interval-valued IFAAWA (IVIFAAWG) by Senapati et al. [41].
• PyF Aczel–Alsina weighted averaging (PyFAAWA) and geometric (PyFAAWG) operators by Hussain et al. [42].
• PyF weighted averaging (PyFWA) and geometric (PyFSWG) operators by Wei et al. [43].

Their structure is not allowed to aggregate the data. A short review of the aggregated outcomes of this article with other existing AOs is represented below in Table 10 and its geometrical representation in Figure 6.

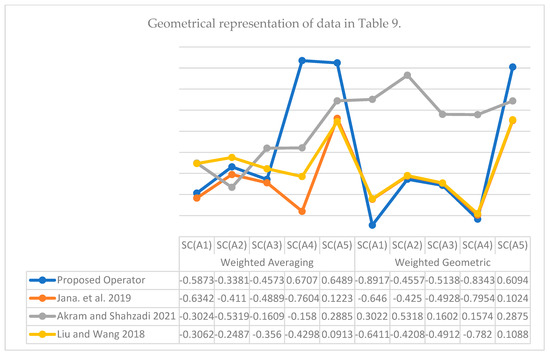
Figure 6. The comparative analysis is represented geometrically in the above graph, where lines show the score values. The results given in row 3 are from Jana et al. [18], the results given in row 5 are from Liu and Wang [35] while the results given in row 4 are from Akram and Shahzadi [38].

The results of Table 9 are described in Figure 6 for further clarity.

In Table 10 and Figure 6, we compared our results with Jana et al. [17], Akram and Shahzadi [39], Liu and Wang [36] by applying the AOs discussed in those references in our example. Since the work in Jana. et al. [17], Akram and Shahzadi [39], Liu and Wang [36] are based on Dombi, Yager, and algebraic TN and TCN, while our proposed work is based on AATN and AATCN. By keeping in mind that AATN and AATCN work significantly more than other discussed TNs, as suggested by [44]. Due to this fact, we believe that the proposed work is better than the previous work. We also discussed the limitations of several other AOs proposed by Senapati et al. [40], Senapati et al. [41], Hussain et al. [42], and Wei et al. [43]. The AOs discussed in [40,41,42,43] fail to aggregate the information provided in the form of q-ROFNs.

8. Conclusions

A decision-making strategy is one of the most critical and valuable techniques for evaluating the best optimal form for selecting preferences. The main conclusions of this analysis are described below:

• We pioneered AA operational laws for q-ROFSs and justified them with the help of examples.
• We diagnosed the theory of q-ROFAAWA, q-ROFAAWG, q-ROFAAOWA, q-ROFAAOWG, q-ROFAAHA, and q-ROFAAHG operators.
• We evaluated some properties (“Idempotency, Monotonicity, and Boundedness”) and the results of the evaluated approaches.
• We illustrated a MADM technique based on diagnosed information and also described the comparison between the proposed work and some prevailing information to enhance the worth of the evaluated theory.
• Geometrical representation of the proposed information is also part of this manuscript.

The future aspects of the work include the following:

• We aim to try to utilize the proposed concept in wastewater management system [45], VIKOR method [46], lane-keeping systems [47], construction material [48], controlled distribution [49], detection of driver fatigues during traveling [50], pattern recognition [51], similarity measure [52], risk evaluation [53], and transportation systems [54].
• We also aim to associate the proposed work with complex TSFs power AOs [55], Power AOs [56], hybrid decision-making [57], and complex TSFs [58].