Time Series and Non-Time Series Models of Earthquake Prediction Based on AETA Data: 16-Week Real Case Study
Abstract
:1. Introduction
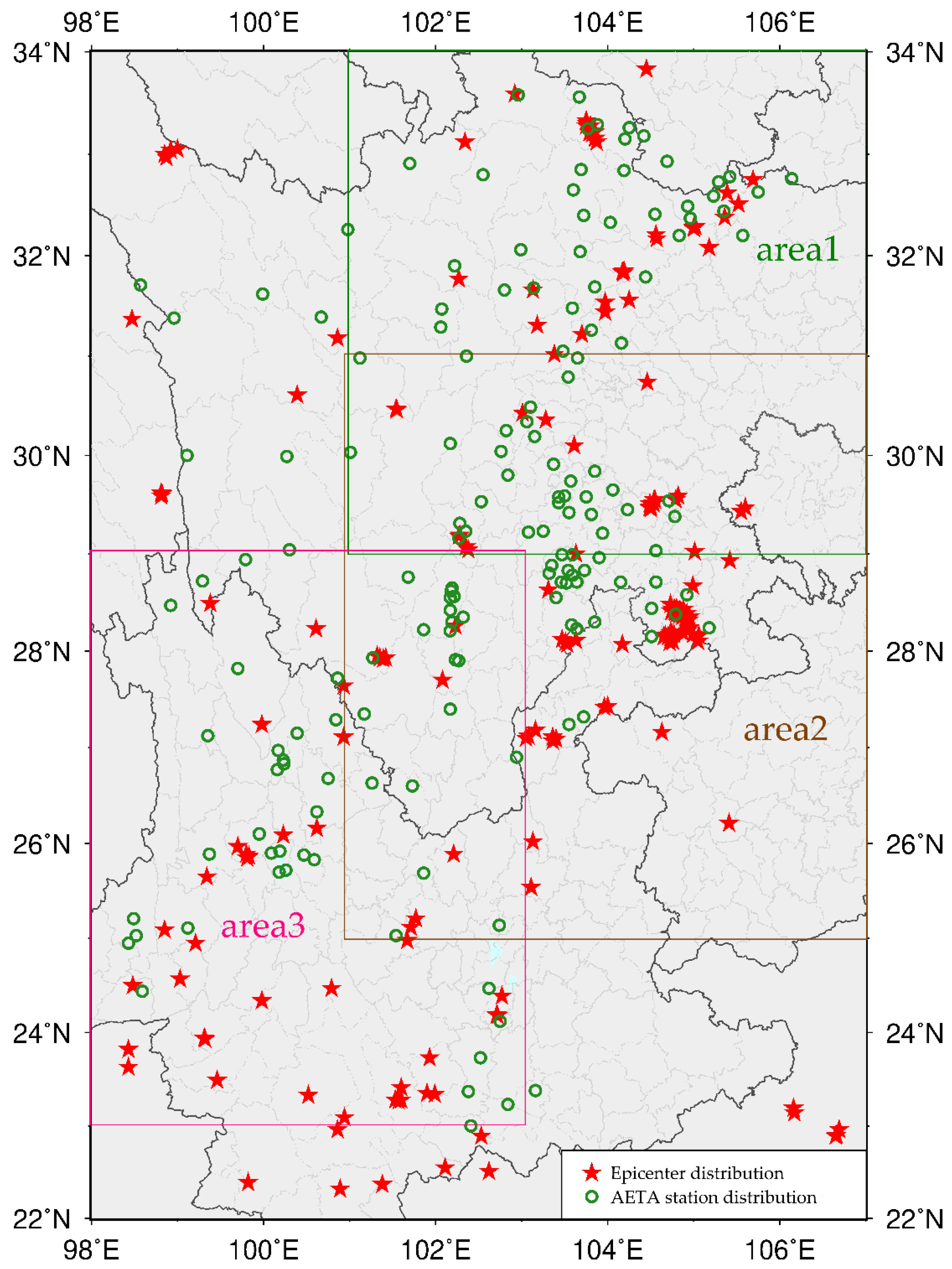
2. AETA System
2.1. AETA Devices and Data Acquisition
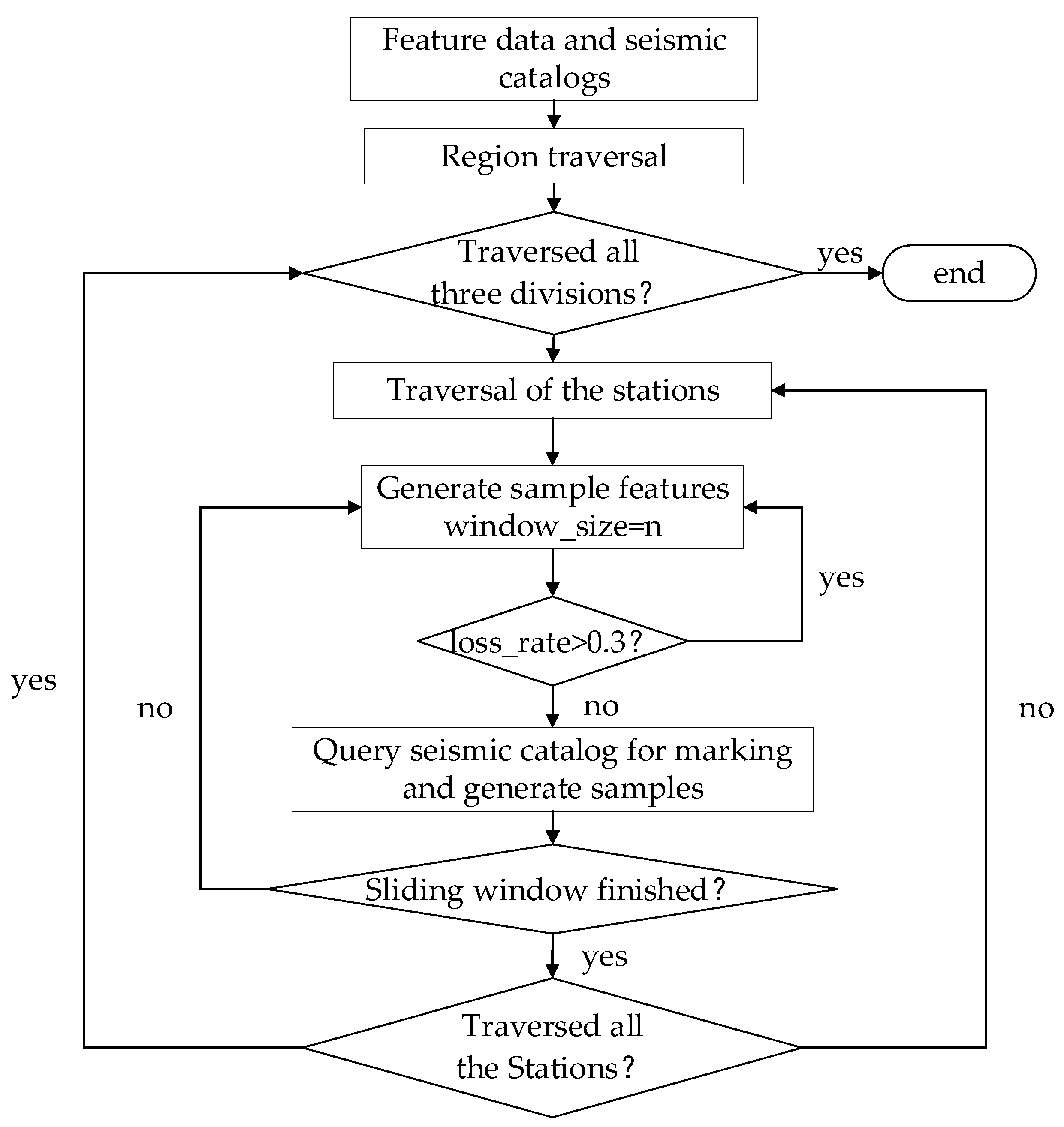
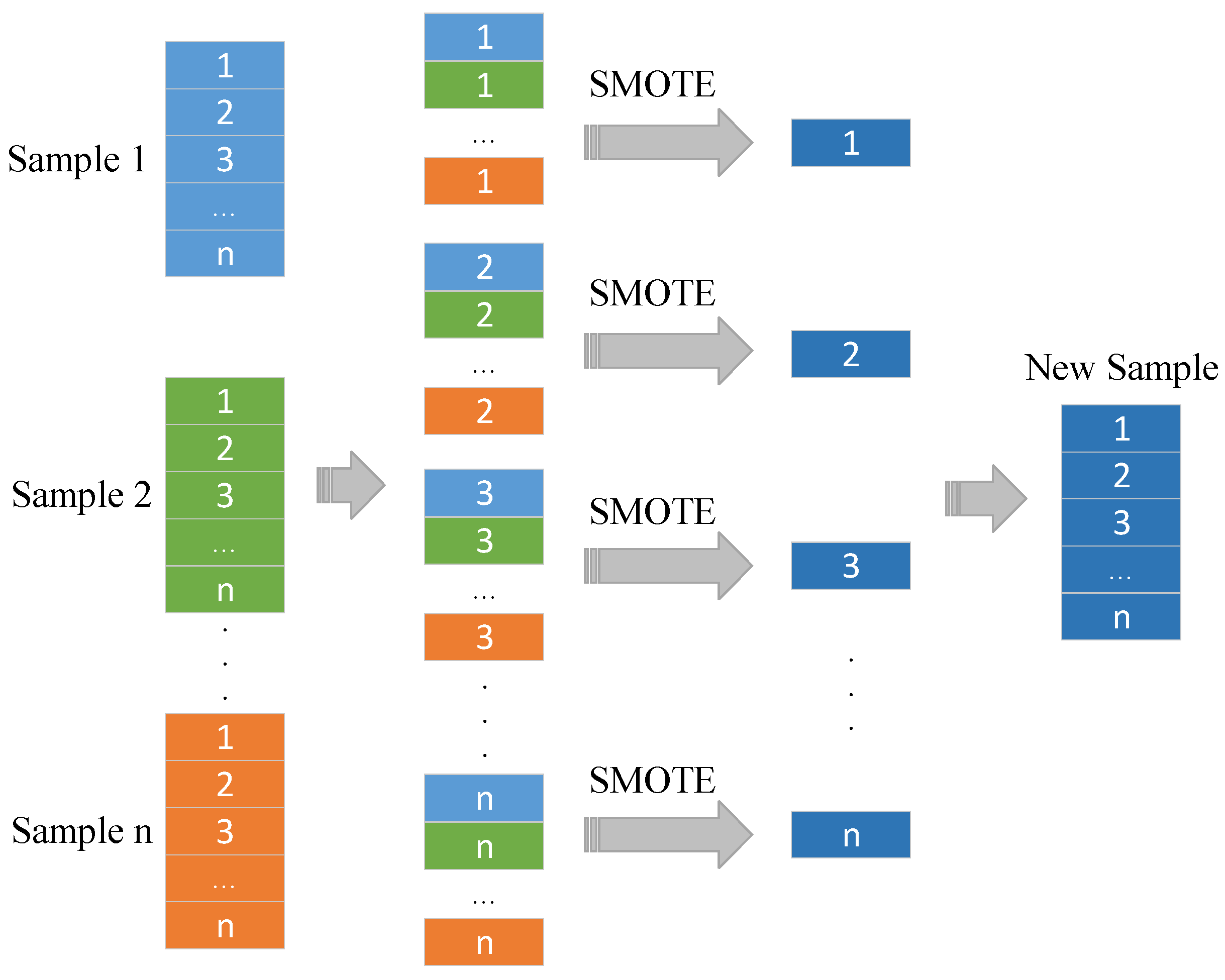
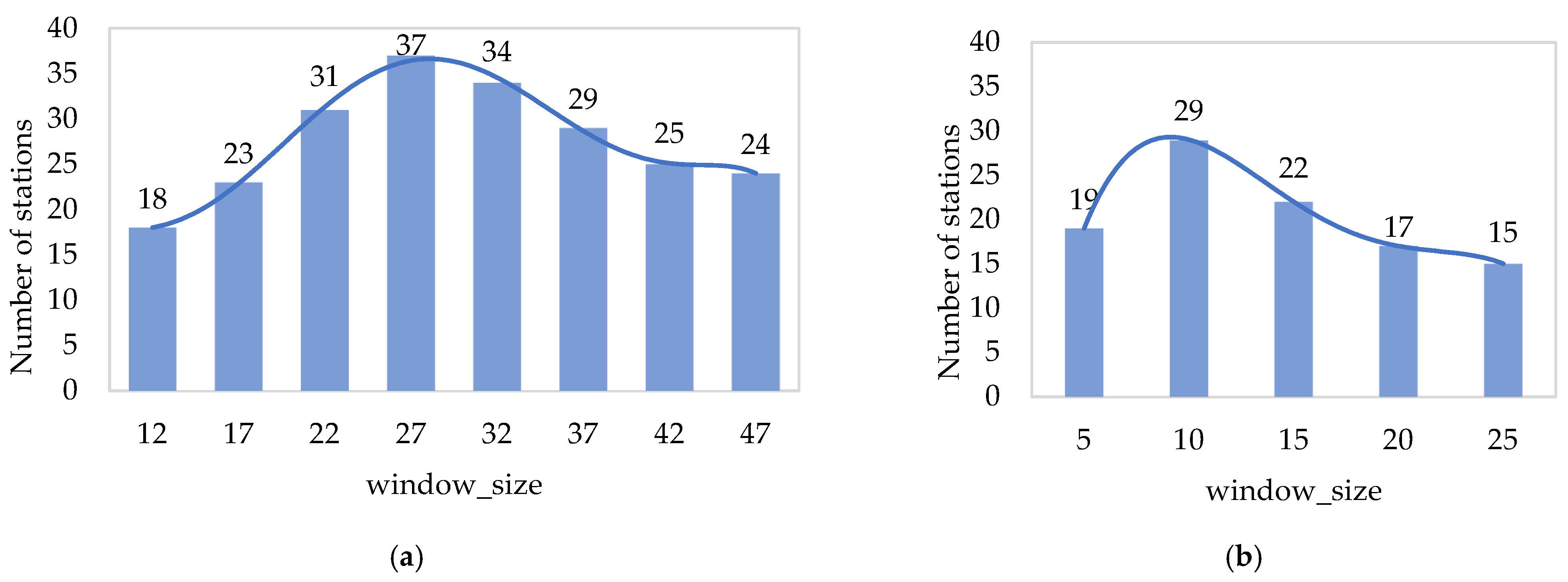
2.2. Data Set Construction
3. Model Construction
3.1. Non-Time Series Prediction Model
3.1.1. LightGBM
3.1.2. NN
3.1.3. Other Models
3.2. Time-Series Prediction Models
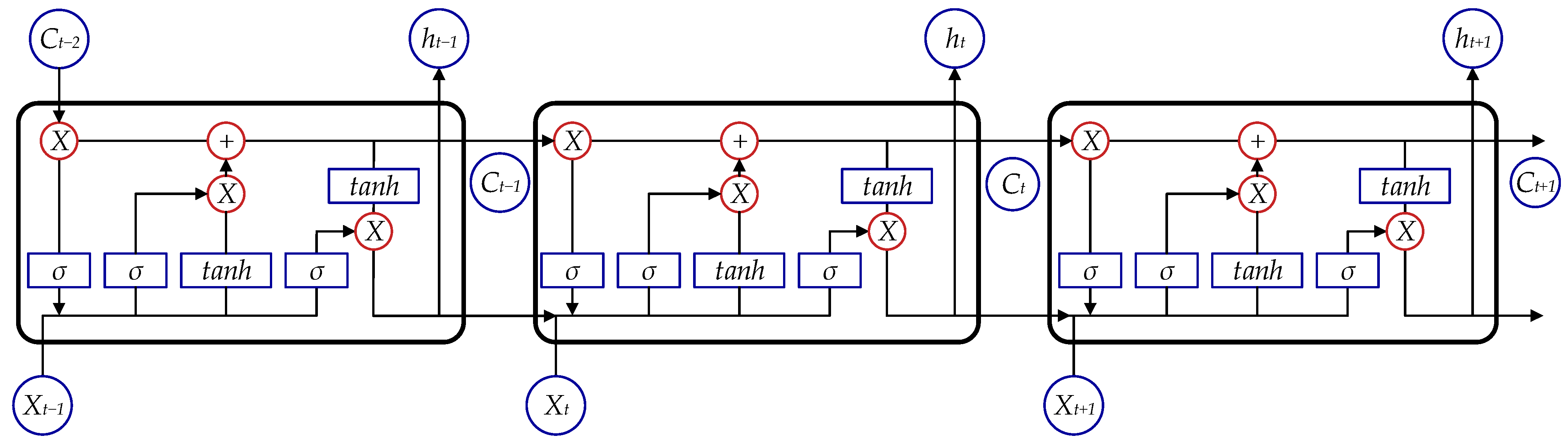
3.2.1. LSTM
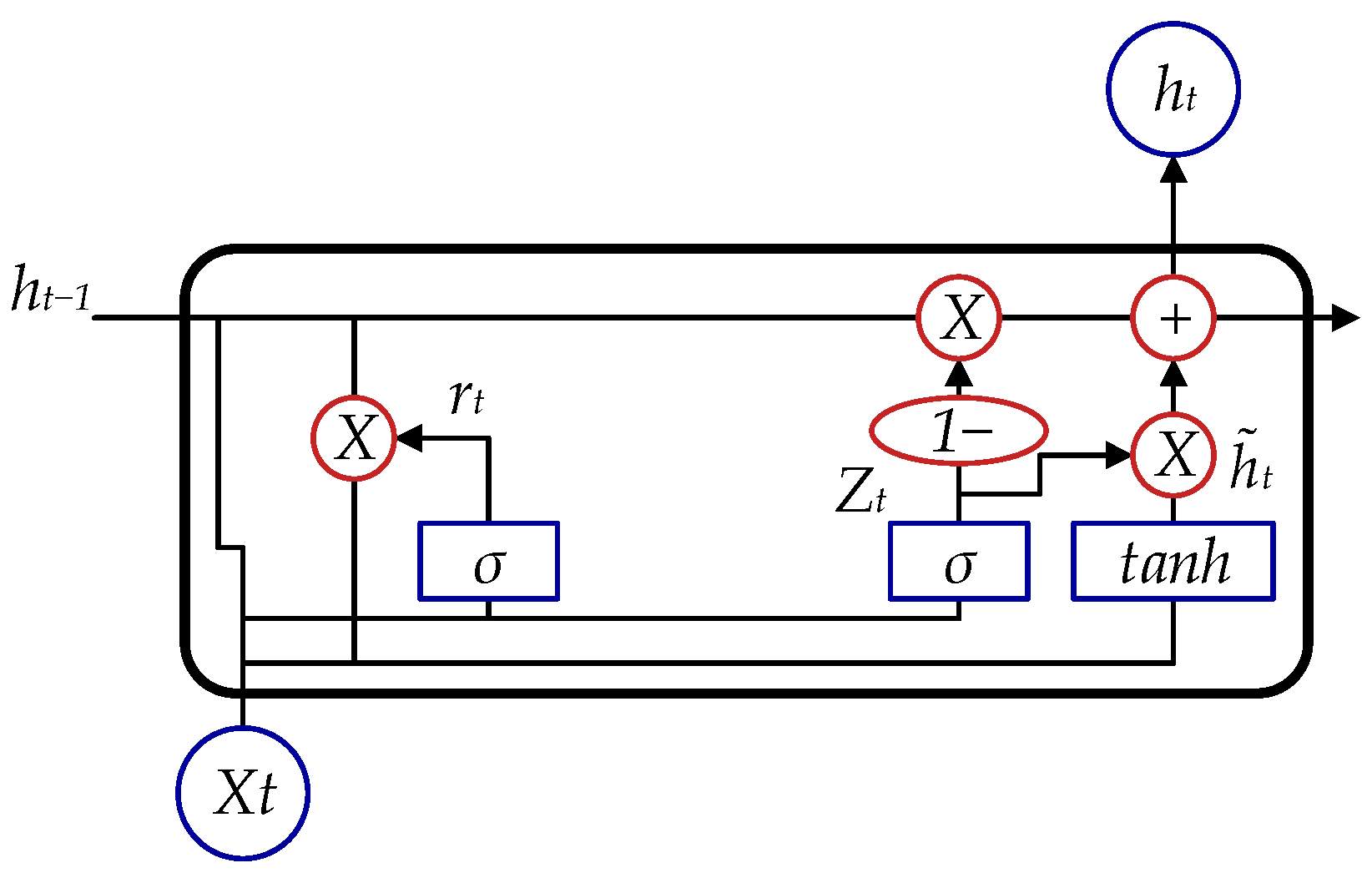
3.2.2. GRU
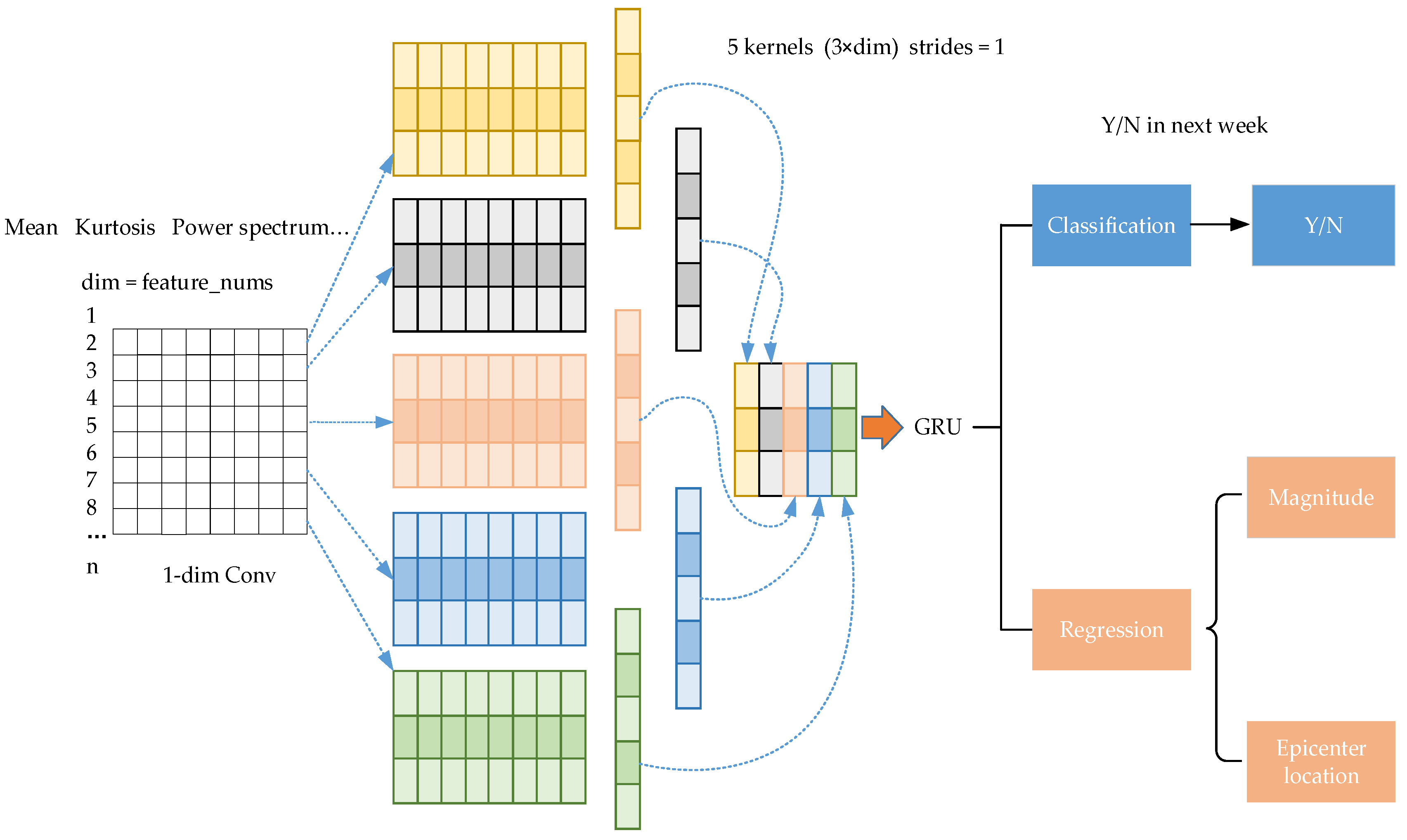
3.2.3. CNN+GRU
3.3. Model Parameters
3.4. Softmax-AUC Index Weighting Method
3.5. Model Evaluation Indicators
4. Results
4.1. Prediction Results of Non-Time Series Models
4.2. Prediction Results of the Time Series Models
5. Discussion
5.1. Comparison of Non-Time Series Models and Time Series Models
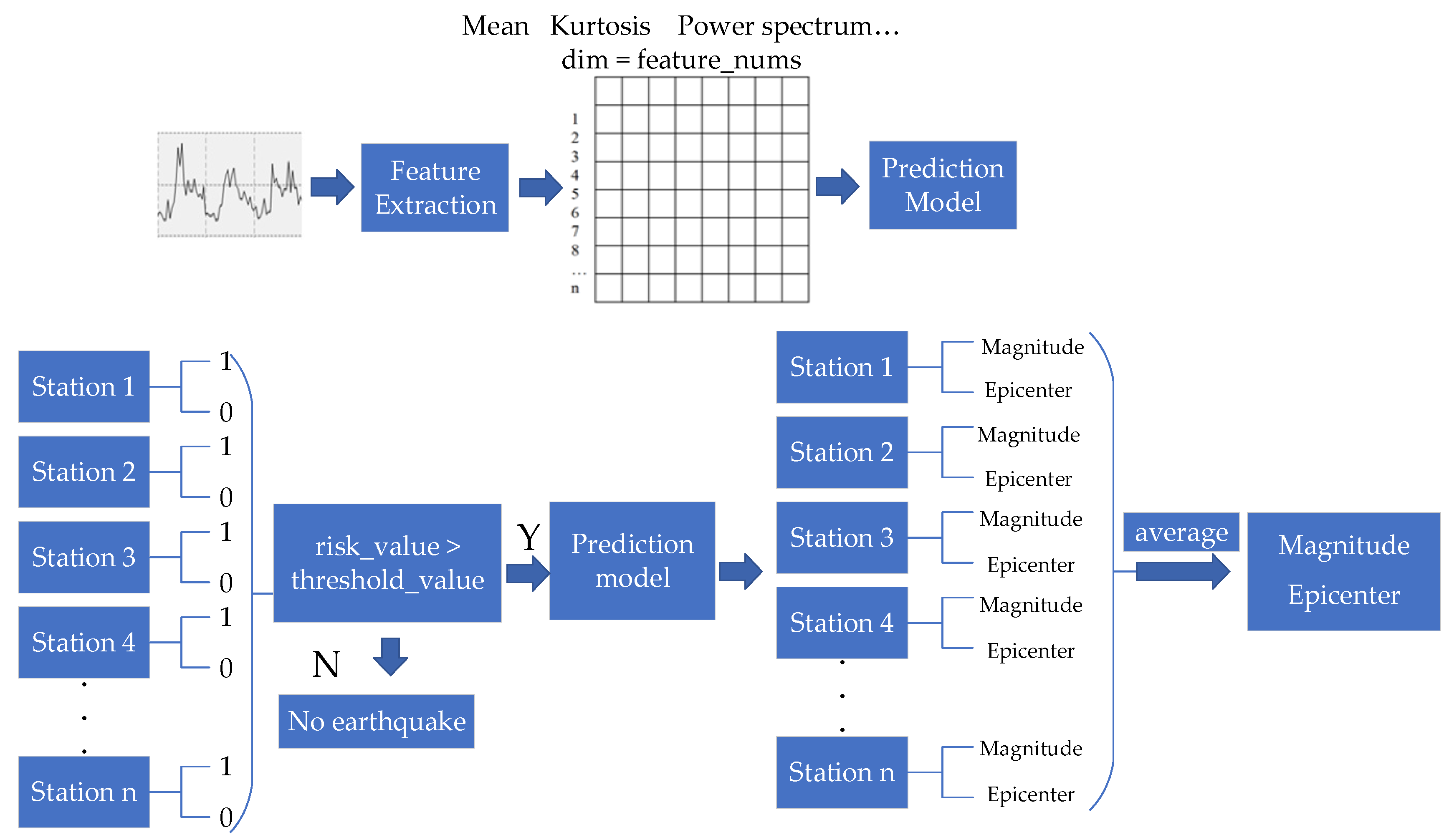
5.2. Real-Earthquake Prediction
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Type | Feature | Meaning | Number of EM Feature | Number of GA Feature |
|---|---|---|---|---|
| Time domain features | abs_mean | Mean of absolute value | 2 | 2 |
| var | Variance | 2 | 1 | |
| power | Power | 2 | 1 | |
| skew | Skewness | 2 | 1 | |
| kurt | Kurtosis | 2 | 1 | |
| abs_max | Maximum absolute value | 2 | 1 | |
| abs_top_x | Absolute maximum x% of position | 4 | 2 | |
| energy_sstd | standard deviation of short-time energy | 2 | 1 | |
| energy_smax | Short-time maximum energy | 2 | 1 | |
| s_zero_rate | Short-time average over-zero rate | 0 | 1 | |
| s_zero_rate_max | Short-time maximum over-zero rate | 0 | 1 | |
| Frequency domain features | power_rate_atob | Power from a~bHz in the frequency spectrum | 11 | 11 |
| frequency_center | Center of gravity frequency | 1 | 1 | |
| mean_square_frequency | Mean square frequency | 1 | 1 | |
| variance_frequency | Frequency variance | 1 | 1 | |
| frequency_entropy | Entropy of the spectrum | 1 | 1 | |
| Wavelet transforms | levelx_absmean | Mean value after the reconstruction of layer x | 4 | 4 |
| levelx_energy | Energy after the reconstruction of layer x | 4 | 4 | |
| levelx_energy_svar | Variance of the energy value after the reconstruction of layer x | 4 | 4 | |
| levelx_energy_smax | Maximum value of energy after the reconstruction of layer x | 4 | 4 | |
| Total | 51 | 44 |
Appendix B
| No. | Station | AUC | PA | PP | RP | PN | RN |
|---|---|---|---|---|---|---|---|
| 1 | DJY | 0.68 | 0.68 | 0.64 | 0.81 | 0.74 | 0.55 |
| 2 | SMSD | 0.68 | 0.68 | 0.60 | 1.00 | 1.00 | 0.37 |
| 3 | QC | 0.69 | 0.69 | 0.69 | 0.71 | 0.69 | 0.67 |
| 4 | WC | 0.67 | 0.67 | 0.73 | 0.55 | 0.62 | 0.79 |
| 5 | BX | 0.78 | 0.78 | 0.83 | 0.71 | 0.74 | 0.85 |
| 6 | GZYJ | 0.80 | 0.80 | 0.87 | 0.71 | 0.75 | 0.89 |
| 7 | EB | 0.66 | 0.66 | 0.60 | 1.00 | 1.00 | 0.33 |
| 8 | GYCT | 0.68 | 0.69 | 0.66 | 0.84 | 0.75 | 0.53 |
| 9 | JC | 0.82 | 0.82 | 0.76 | 0.96 | 0.94 | 0.69 |
| 10 | DF | 0.76 | 0.76 | 0.69 | 1.00 | 1.00 | 0.52 |
| 11 | QCYD | 0.76 | 0.77 | 0.96 | 0.54 | 0.70 | 0.98 |
| 12 | QCPS | 0.78 | 0.78 | 0.87 | 0.67 | 0.72 | 0.90 |
| 13 | CZ | 0.81 | 0.81 | 0.73 | 1.00 | 1.00 | 0.62 |
| 14 | PWHY | 0.78 | 0.77 | 0.94 | 0.60 | 0.68 | 0.95 |
| 15 | SPMJ | 0.68 | 0.68 | 0.72 | 0.59 | 0.66 | 0.77 |
| 16 | PWBM | 0.74 | 0.75 | 0.68 | 1.00 | 1.00 | 0.49 |
| 17 | JCAN | 0.66 | 0.66 | 0.96 | 0.33 | 0.60 | 0.99 |
| 18 | YAYJ | 0.69 | 0.69 | 0.70 | 0.67 | 0.68 | 0.71 |
| 19 | HS | 0.77 | 0.77 | 0.69 | 1.00 | 1.00 | 0.55 |
| 20 | MXDX | 0.69 | 0.70 | 0.89 | 0.44 | 0.63 | 0.95 |
| 21 | JZG4 | 0.71 | 0.71 | 0.72 | 0.67 | 0.70 | 0.75 |
| 22 | JZG5 | 0.73 | 0.73 | 0.71 | 0.80 | 0.75 | 0.65 |
| 23 | JZG2 | 0.70 | 0.70 | 0.65 | 0.82 | 0.77 | 0.57 |
| 24 | PWNB | 0.69 | 0.68 | 0.65 | 0.75 | 0.72 | 0.62 |
| 25 | JZG1 | 0.68 | 0.68 | 0.68 | 0.71 | 0.68 | 0.66 |
| 26 | WXZZ | 0.80 | 0.80 | 0.72 | 1.00 | 1.00 | 0.60 |
| 27 | HYA | 0.67 | 0.65 | 0.58 | 1.00 | 1.00 | 0.34 |
| 28 | DL | 0.80 | 0.80 | 0.79 | 0.76 | 0.81 | 0.83 |
| 29 | BK | 0.68 | 0.68 | 0.70 | 0.64 | 0.66 | 0.72 |
| 30 | HBY | 0.72 | 0.72 | 0.75 | 0.65 | 0.70 | 0.79 |
| 31 | REG | 0.88 | 0.88 | 0.83 | 0.96 | 0.95 | 0.79 |
| 32 | EMHW | 0.95 | 0.95 | 0.91 | 1.00 | 1.00 | 0.90 |
| 33 | JYZJJ | 0.93 | 0.93 | 0.87 | 1.00 | 1.00 | 0.86 |
| 34 | LSSW | 0.69 | 0.70 | 0.82 | 0.47 | 0.65 | 0.91 |
| 35 | RXCS | 0.96 | 0.96 | 0.93 | 1.00 | 1.00 | 0.93 |
| 36 | ZGDA | 0.77 | 0.77 | 0.68 | 1.00 | 1.00 | 0.55 |
| 37 | MYBC | 0.86 | 0.86 | 0.77 | 1.00 | 1.00 | 0.72 |
| No. | Station | AUC | PA | PP | RP | PN | RN |
|---|---|---|---|---|---|---|---|
| 1 | MB | 0.65 | 0.65 | 0.59 | 0.73 | 0.72 | 0.58 |
| 2 | LB | 0.76 | 0.76 | 0.77 | 0.79 | 0.75 | 0.72 |
| 3 | ML | 0.73 | 0.75 | 0.81 | 0.57 | 0.72 | 0.89 |
| 4 | EMS | 0.70 | 0.68 | 0.59 | 0.89 | 0.85 | 0.50 |
| 5 | XJX | 0.66 | 0.66 | 0.60 | 0.68 | 0.72 | 0.64 |
| 6 | DF | 0.65 | 0.65 | 0.68 | 0.66 | 0.62 | 0.65 |
| 7 | XCXM | 0.65 | 0.65 | 0.70 | 0.59 | 0.61 | 0.71 |
| 8 | LDDZ | 0.65 | 0.66 | 0.69 | 0.54 | 0.64 | 0.77 |
| 9 | YAYJ | 0.66 | 0.68 | 0.62 | 1.00 | 1.00 | 0.32 |
| 10 | LSBS | 0.69 | 0.69 | 0.78 | 0.52 | 0.64 | 0.85 |
| 11 | HYA | 0.85 | 0.84 | 0.75 | 1.00 | 1.00 | 0.70 |
| 12 | MSQS | 0.67 | 0.70 | 0.68 | 0.52 | 0.71 | 0.83 |
| 13 | EMGQ | 0.68 | 0.73 | 0.95 | 0.37 | 0.69 | 0.99 |
| 14 | MBMZ | 0.68 | 0.63 | 0.92 | 0.41 | 0.53 | 0.95 |
| 15 | MBRD | 0.75 | 0.76 | 0.77 | 0.80 | 0.75 | 0.70 |
| 16 | MBYJ | 0.69 | 0.69 | 0.65 | 0.63 | 0.73 | 0.74 |
| 17 | WTQ | 0.77 | 0.77 | 0.69 | 0.79 | 0.83 | 0.74 |
| 18 | NJWYYLZ | 0.66 | 0.66 | 0.61 | 0.71 | 0.71 | 0.60 |
| 19 | YBYX | 0.98 | 0.98 | 0.95 | 1.00 | 1.00 | 0.95 |
| 20 | LSFZJZ | 0.75 | 0.76 | 0.76 | 0.65 | 0.75 | 0.84 |
| 21 | ZGDA | 0.75 | 0.75 | 0.69 | 0.76 | 0.80 | 0.74 |
| No. | Station | AUC | PA | PP | RP | PN | RN |
|---|---|---|---|---|---|---|---|
| 1 | TH | 0.69 | 0.69 | 0.62 | 1.00 | 1.00 | 0.38 |
| 2 | CX | 0.80 | 0.80 | 0.71 | 1.00 | 1.00 | 0.61 |
| 3 | QJ | 0.68 | 0.69 | 0.68 | 0.73 | 0.69 | 0.64 |
| 4 | LJSD | 0.78 | 0.78 | 0.78 | 0.79 | 0.78 | 0.77 |
| 5 | SPI | 0.85 | 0.86 | 0.78 | 1.00 | 1.00 | 0.71 |
| 6 | DHZ | 0.68 | 0.67 | 0.62 | 0.87 | 0.79 | 0.49 |
| 7 | DR | 0.73 | 0.73 | 0.87 | 0.53 | 0.66 | 0.92 |
| 8 | DLSL | 0.77 | 0.74 | 0.63 | 0.96 | 0.95 | 0.58 |
| 9 | JN | 0.85 | 0.85 | 0.86 | 0.85 | 0.85 | 0.86 |
| 10 | YX | 0.68 | 0.68 | 0.90 | 0.40 | 0.62 | 0.95 |
| 11 | KM | 0.70 | 0.71 | 0.83 | 0.50 | 0.66 | 0.90 |
| 12 | LJYS | 0.67 | 0.67 | 0.61 | 1.00 | 1.00 | 0.33 |
| 13 | LJDZ | 0.76 | 0.76 | 0.68 | 1.00 | 1.00 | 0.52 |
| 14 | JZS | 0.91 | 0.91 | 0.97 | 0.86 | 0.87 | 0.97 |
| 15 | LJLD | 0.69 | 0.69 | 0.86 | 0.47 | 0.62 | 0.92 |
| 16 | TC | 0.79 | 0.79 | 0.73 | 0.93 | 0.90 | 0.65 |
| 17 | DQZ | 0.68 | 0.68 | 0.67 | 0.73 | 0.70 | 0.63 |
| 18 | JP | 0.87 | 0.87 | 0.79 | 1.00 | 1.00 | 0.73 |
| 19 | HH | 0.83 | 0.83 | 0.75 | 1.00 | 1.00 | 0.66 |
| 20 | TCMZ | 0.80 | 0.80 | 0.90 | 0.67 | 0.75 | 0.93 |
| 21 | LJNL | 0.68 | 0.68 | 0.77 | 0.53 | 0.63 | 0.83 |
| 22 | YYLG | 0.65 | 0.64 | 0.57 | 1.00 | 1.00 | 0.31 |
| 23 | XCH | 0.87 | 0.87 | 0.79 | 1.00 | 1.00 | 0.74 |
| 24 | DLHZ | 0.92 | 0.91 | 0.84 | 1.00 | 1.00 | 0.83 |
| 25 | XGLL | 0.90 | 0.90 | 0.83 | 1.00 | 1.00 | 0.79 |
Appendix C
| No. | Station | Mag_Mae | Distance_Average (km) |
|---|---|---|---|
| 1 | DJY | 0.26 | 98.83 |
| 2 | SMWJ | 0.16 | 57.97 |
| 3 | LXSM | 0.44 | 119.46 |
| 4 | WC | 0.12 | 96.04 |
| 5 | GYCT | 0.08 | 102.62 |
| 6 | SP | 0.32 | 50.16 |
| 7 | QCYD | 0.27 | 100.69 |
| 8 | QCPS | 0.08 | 50.48 |
| 9 | YAYJ | 0.14 | 50.47 |
| 10 | QCCB | 0.18 | 44.30 |
| 11 | HS | 0.25 | 47.65 |
| 12 | JZG2 | 0.15 | 19.53 |
| 13 | LSBS | 0.15 | 50.04 |
| 14 | MSQS | 0.40 | 48.30 |
| 15 | HBY | 0.17 | 82.37 |
| 16 | REG | 0.38 | 72.72 |
| 17 | WTQ | 0.26 | 26.32 |
| 18 | NJWYYLZ | 0.13 | 26.88 |
| 19 | JYZJJ | 0.09 | 14.30 |
| 20 | LSSW | 0.13 | 18.91 |
| 21 | RXCS | 0.27 | 63.67 |
| 22 | LSFZJZ | 0.10 | 16.96 |
| 23 | LSJJRMZF | 0.08 | 13.22 |
| 24 | ZGDA | 0.08 | 21.58 |
| 25 | MYBC | 0.10 | 95.15 |
| 26 | SMAS | 0.13 | 95.60 |
| No. | Station | Mag_Mae | Distance_Average (km) |
|---|---|---|---|
| 1 | CX | 0.25 | 77.79 |
| 2 | SMWJ | 0.25 | 80.03 |
| 3 | QW | 0.40 | 82.78 |
| 4 | GAX | 0.20 | 93.71 |
| 5 | YYYT | 0.13 | 97.71 |
| 6 | EB | 0.57 | 79.23 |
| 7 | MS | 0.22 | 85.35 |
| 8 | DF | 0.33 | 75.27 |
| 9 | YM | 0.13 | 96.95 |
| 10 | LDDZ | 0.50 | 79.81 |
| 11 | KM | 0.21 | 60.83 |
| 12 | CZ | 0.40 | 60.74 |
| 13 | MNLZ | 0.19 | 94.53 |
| 14 | HYA | 0.46 | 88.26 |
| 15 | YSHX | 0.13 | 96.26 |
| 16 | MBQB | 0.17 | 97.19 |
| 17 | MBMZ | 0.39 | 57.86 |
| 18 | MBSK | 0.41 | 37.05 |
| 19 | GYCT | 0.18 | 80.16 |
| 20 | SMAS | 0.22 | 91.43 |
| 21 | MBYJ | 0.15 | 85.54 |
| 22 | JYZJJ | 0.24 | 73.20 |
| 23 | RXCS | 0.30 | 58.51 |
| 24 | LSFZJZ | 0.22 | 83.11 |
| 25 | LSJJRMZF | 0.22 | 78.03 |
| 26 | ZGDA | 0.20 | 78.62 |
| 27 | YBCNQXJ | 0.64 | 59.24 |
| 28 | YBXWSHC | 0.27 | 96.84 |
| No. | Station | Mag_Mae | Distance_Average (km) |
|---|---|---|---|
| 1 | TH | 0.06 | 42.34 |
| 2 | XC | 0.26 | 101.01 |
| 3 | DC | 0.15 | 99.96 |
| 4 | DHZ | 0.23 | 42.08 |
| 5 | XCXM | 0.68 | 117.21 |
| 6 | DLSL | 0.27 | 113.03 |
| 7 | YL | 0.30 | 55.52 |
| 8 | YM | 0.31 | 44.14 |
| 9 | HA | 0.06 | 109.35 |
| 10 | YX | 0.16 | 79.27 |
| 11 | LJYS | 0.05 | 78.47 |
| 12 | LJGC | 0.04 | 54.87 |
| 13 | DQZ | 0.03 | 59.05 |
| 14 | HH | 0.03 | 14.53 |
| 15 | LJDD | 0.06 | 42.34 |
| 16 | TCMZ | 0.26 | 101.01 |
| 17 | LJHP | 0.15 | 99.96 |
| 18 | TCRH | 0.23 | 42.08 |
| 19 | LJNL | 0.68 | 117.21 |
| 20 | XCH | 0.27 | 113.03 |
References
- Wang, X.; Yong, S.; Xu, B.; Liang, Y.; Bai, Z.; An, H.; Zhang, X.; Huang, J.; Xie, Z.; Lin, K.; et al. Research and Implementation of Multi-component Seismic Monitoring System AETA. Acta Sci. Nat. Univ. Pekin. 2018, 54, 487–494. [Google Scholar]
- Varotsos, P.; Alexopoulos, K. Physical properties of the variations of the electric field of the earth preceding earthquakes, I. Tectonophysics 1984, 110, 73–98. [Google Scholar] [CrossRef]
- Frasersmith, A.C.; Bernardi, A.; McGill, P.R.; Ladd, M.E.; Helliwell, R.A.; Villard, O.G. Low-frequency magnetic-field measurements near the epicenter of the ms-7.1 Loma-Prieta earthquake. Geophys. Res. Lett. 1990, 17, 1465–1468. [Google Scholar] [CrossRef]
- Huang, Q.; Ikeya, M. Seismic electromagnetic signals (SEMS) explained by a simulation experiment using electromagnetic waves. Phys. Earth Planet. Inter. 1998, 109, 107–114. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Magnetic field variations associated with SES. Proc. Jpn. Acad. Ser. B Phys. Biol. Sci. 2001, 77, 87–92. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Electric Fields that “Arrive’’ before the Time Derivative of the Magnetic Field prior to Major Earthquakes. Phys. Rev. Lett. 2003, 91, 148501. [Google Scholar] [CrossRef]
- Huang, Q. Controlled analogue experiments on propagation of seismic electromagnetic signals. Chin. Sci. Bull. 2005, 50, 1956–1961. [Google Scholar] [CrossRef]
- Uyeda, S.; Nagao, T.; Kamogawa, M. Short-term earthquake prediction: Current status of seismo-electromagnetics. Tectonophysics 2009, 470, 205–213. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Identifying long-range correlated signals upon significant periodic data loss. Tectonophysics 2011, 503, 189–194. [Google Scholar] [CrossRef]
- Potirakis, S.M.; Karadimitrakis, A.; Eftaxias, K. Natural time analysis of critical phenomena: The case of pre-fracture electromagnetic emissions. Chaos 2013, 23, 23117. [Google Scholar] [CrossRef]
- Han, P.; Hattori, K.; Hirokawa, M.; Zhuang, J.; Chen, C.-H.; Febriani, F.; Yamaguchi, H.; Yoshino, C.; Liu, J.-Y.; Yoshida, S. Statistical analysis of ULF seismomagnetic phenomena at Kakioka, Japan, during 2001–2010. J. Geophys. Res. Space Phys. 2014, 119, 4998–5011. [Google Scholar] [CrossRef]
- Hayakawa, M.; Schekotov, A.; Potirakis, S.; Eftaxias, K. Criticality features in ULF magnetic fields prior to the 2011 Tohoku earthquake. Jpn. Acad. Ser. B Phys. Biol. Sci. 2015, 91, 25–30. [Google Scholar] [CrossRef] [PubMed]
- Han, P.; Hattori, K.; Huang, Q.; Hirooka, S.; Yoshino, C. Spatiotemporal characteristics of the geomagnetic diurnal variation anomalies prior to the 2011 Tohoku earthquake (Mw 9.0) and the possible coupling of multiple pre-earthquake phenomena. J. Asian Earth Sci. 2016, 129, 13–21. [Google Scholar] [CrossRef]
- Sarlis, N.V. Statistical Significance of Earth’s Electric and Magnetic Field Variations Preceding Earthquakes in Greece and Japan Revisited. Entropy 2018, 20, 561. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Varotos, P.A.; Skordas, E.S.; Uyeda, S.; Zlotnicki, J.; Nagao, T.; Rybin, A.; Lazaridou-Varotsos, M.S.; Papadopoulou, K.A. Seismic electric signals in seismic prone areas. Earthq. Sci. 2018, 31, 44–51. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Order Parameter and Entropy of Seismicity in Natural Time before Major Earthquakes: Recent Results. Geosciences 2022, 12, 225. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, H.; Yin, W.; Zhao, Z.; Ran, Q. Detection Method of Earthquake Disaster Image Anomaly Based on SIFT Feature and SVM Classification. J. Seismol. Res. 2019, 42, 265–272. [Google Scholar]
- Jozinovic, D.; Lomax, A.; Stajduhar, I.; Michelini, A. Rapid prediction of earthquake ground shaking intensity using raw waveform data and a convolutional neural network. Geophys. J. Int. 2020, 222, 1379–1389. [Google Scholar] [CrossRef]
- Xiong, P.; Long, C.; Zhou, H.Y.; Battiston, R.; Zhang, X.M.; Shen, X.H. Identification of Electromagnetic Pre-Earthquake Perturbations from the DEMETER Data by Machine Learning. Remote Sens. 2020, 12, 3643. [Google Scholar] [CrossRef]
- Wang, L.; Wu, J.; Zhang, W.; Wang, L.; Cui, W. Efficient Seismic Stability Analysis of Embankment Slopes Subjected to Water Level Changes Using Gradient Boosting Algorithms. Front. Earth Sci. 2021, 9, 807317. [Google Scholar] [CrossRef]
- Saad, O.M.; Chen, Y.F.; Trugman, D.; Soliman, M.S.; Samy, L.; Savvaidis, A.; Khamis, M.A.; Hafez, A.G.; Fomel, S.; Chen, Y.K. Machine Learning for Fast and Reliable Source-Location Estimation in Earthquake Early Warning. IEEE Geosci. Remote Sens. Lett. 2022, 19, 8025705. [Google Scholar] [CrossRef]
- Kanarachos, S.; Christopoulos, S.R.G.; Chroneos, A.; Fitzpatrick, M.E. Detecting anomalies in time series data via a deep learning algorithm combining wavelets, neural networks and Hilbert transform. Expert Syst. Appl. 2017, 85, 292–304. [Google Scholar] [CrossRef]
- Zhou, Y.; Yue, H.; Kong, Q.; Zhou, S. Hybrid Event Detection and Phase-Picking Algorithm Using Convolutional and Recurrent Neural Networks. Seismol. Res. Lett. 2019, 90, 1079–1087. [Google Scholar] [CrossRef]
- Titos, M.; Bueno, A.; Garcia, L.; Benitez, M.C.; Ibanez, J. Detection and Classification of Continuous Volcano-Seismic Signals with Recurrent Neural Networks. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1936–1948. [Google Scholar] [CrossRef]
- Jena, R.; Pradhan, B.; Alamri, A.M. Susceptibility to Seismic Amplification and Earthquake Probability Estimation Using Recurrent Neural Network (RNN) Model in Odisha, India. Appl. Sci. 2020, 10, 5355. [Google Scholar] [CrossRef]
- Xu, Y.; Lu, X.; Cetiner, B.; Taciroglu, E. Real-time regional seismic damage assessment framework based on long short-term memory neural network. Comput. Aided Civil Infrastruct. Eng. 2021, 36, 504–521. [Google Scholar] [CrossRef]
- Yan, X.; Shi, Z.M.; Wang, G.; Zhang, H.; Bi, E. Detection of possible hydrological precursor anomalies using long short-term memory: A case study of the 1996 Lijiang earthquake. J. Hydrol. 2021, 599, 126369. [Google Scholar] [CrossRef]
- Huang, Y.; Han, X.; Zhao, L. Recurrent neural networks for complicated seismic dynamic response prediction of a slope system. Eng. Geol. 2021, 289, 106198. [Google Scholar] [CrossRef]
- Xue, J.; Huang, Q.; Wu, S.; Nagao, T. LSTM-Autoencoder Network for the Detection of Seismic Electric Signals. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5917012. [Google Scholar] [CrossRef]
- Yong, S.; Wang, X.; Zhang, X.; Guo, Q.; Wang, J.; Yang, C.; Jiang, B.H. Periodic electromagnetic signals as potential precursor for seismic activity. J. Cent. South Univ. 2021, 28, 2463–2471. [Google Scholar] [CrossRef]
- Bao, Z.; Zhao, J.; Huang, P.; Yong, S.; Wang, X. Deep Learning-Based Electromagnetic Signal for Earthquake Magnitude Prediction. Sensors 2021, 21, 4434. [Google Scholar] [CrossRef] [PubMed]
- Yong, S.; Wang, X.; Pang, R.; Jin, X.; Zeng, J.; Han, C.; Xu, B.X. Development of Inductive Magnetic Sensor for Multi-component Seismic Monitoring System AETA. Acta Sci. Nat. Univ. Pekin. 2018, 54, 495–501. [Google Scholar]
- Carmona-Cabezas, R.; Gomez-Gomez, J.; de Rave, E.G.; Jimenez-Hornero, F.J. A sliding window-based algorithm for faster transformation of time series into complex networks. Chaos 2019, 29, 103121. [Google Scholar] [CrossRef] [PubMed]
- Bao, Z.; Yong, S.; Wang, X.; Yang, C.; Xie, J.; He, C. Seismic Reflection Analysis of AETA Electromagnetic Signals. Appl. Sci. 2021, 11, 5869. [Google Scholar] [CrossRef]
- Hussein, A.S.; Li, T.R.; Yohannese, C.W.; Bashir, K. A-SMOTE: A New Preprocessing Approach for Highly Imbalanced Datasets by Improving SMOTE. Int. J. Comput. Intell. Syst. 2019, 12, 1412–1422. [Google Scholar] [CrossRef]
- Liang, W.; Luo, S.; Zhao, G.; Wu, H. Predicting Hard Rock Pillar Stability Using GBDT, XGBoost, and LightGBM Algorithms. Mathematics 2020, 8, 765. [Google Scholar] [CrossRef]
- Zhang, D.; Gong, Y. The Comparison of LightGBM and XGBoost Coupling Factor Analysis and Prediagnosis of Acute Liver Failure. IEEE Access 2020, 8, 220990–221003. [Google Scholar] [CrossRef]
- Abdi, H. A neural network primer. J. Biol. Syst. 1994, 2, 247–281. [Google Scholar] [CrossRef]
- Tsang, I.W.; Kwok, J.T.; Cheung, P.M. Core vector machines: Fast SVM training on very large data sets. J. Mach. Learn. Res. 2005, 6, 363–392. [Google Scholar]
- Speiser, J.L.; Miller, M.E.; Tooze, J.; Ip, E. A comparison of random forest variable selection methods for classification prediction modeling. Expert Syst. Appl. 2019, 134, 93–101. [Google Scholar] [CrossRef]
- Zhang, W.; Li, H.; Tang, L.; Gu, X.; Wang, L.; Wang, L. Displacement prediction of Jiuxianping landslide using gated recurrent unit (GRU) networks. Acta Geotech. 2022, 17, 1367–1382. [Google Scholar] [CrossRef]
- Liu, Y.; Yong, S.; He, C.; Wang, X.; Bao, Z.; Xie, J.; Zhang, X. An Earthquake Forecast Model Based on Multi-Station PCA Algorithm. Appl. Sci. 2022, 12, 3311. [Google Scholar] [CrossRef]
- Christ, M.; Braun, N.; Neuffer, J.; Kempa-Liehr, A.W. Time Series Feature Extraction on basis of Scalable Hypothesis tests (tsfresh-A Python package). Neurocomputing 2018, 307, 72–77. [Google Scholar] [CrossRef]
- Santos, M.S.; Soares, J.P.; Abreu, P.H.; Araujo, H.; Santos, J. Cross-Validation for Imbalanced Datasets: Avoiding Overoptimistic and Overfitting Approaches. IEEE Comput. Intell. Mag. 2018, 13, 59–76. [Google Scholar] [CrossRef]
- Hosmer, D.W.; Lemeshow, S. Applied Logistic Regression; John Wiley & Sons, Ltd.: New York, NY, USA, 2000. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Pattern Recogn. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Christopoulos, S.R.G. Visualization of the significance of Receiver Operating Characteristics based on confidence ellipses. Comput. Phys. Commun. 2014, 185, 1172–1176. [Google Scholar] [CrossRef] [Green Version]



| Model | ||||
|---|---|---|---|---|
| LightGBM | 68 | 43 | 52 | 36 |
| NN | 57 | 49 | 47 | 39 |
| SVM | 51 | 39 | 43 | 41 |
| GBDT | 36 | 42 | 39 | 43 |
| RF | 45 | 37 | 41 | 32 |
| Model | ||||
|---|---|---|---|---|
| LSTM | 84 | 55 | 64 | 47 |
| GRU | 82 | 58 | 61 | 48 |
| CNN+GRU | 79 | 49 | 56 | 40 |
| Actual Magnitude | Predicted Magnitude | Actual Epicenter | Predicted Epicenter | |
|---|---|---|---|---|
| 1th week (5 April 2021–11 April 2021) | N | N | N | N |
| 2th week (12 April 2021–18 April 2021) | N | Ms4.0 | N | |
| 3th week (19 April 2021–25 April 2021) | N | N | N | N |
| 4th week (26 April 2021–2 May 2021) | N | N | N | N |
| 5th week (3 May 2021–9 May 2021) | Ms3.6 | N | N | |
| 6th week (10 May 2021–16 May 2021) | Ms4.7 | N | N | |
| 7th week (17 May 2021–23 May 2021) | Ms6.4 | Ms3.9 | ) | |
| 8th week (24 May 2021–30 May 2021) | Ms4.1 | Ms4.5 | ) | |
| 9th week (31 May 2021–6 June 2021) | N | Ms4.1 | N | |
| 10th week (7 June 2021–13 June 2021) | Ms5.1 | N | N | |
| 11th week (14 June 2021–20 June 2021) | Ms4.2 | Ms4.2 | ) | |
| 12th week (21 June 2021–27 June 2021) | Ms3.8 | Ms4.0 | ) | |
| 13th week (28 June 2021–4 July 2021) | Ms4.6 | Ms3.9 | ) | |
| 14th week (5 July 2021–11 July 2021) | Ms4.7 | N | N | |
| 15th week (12 July 2021–18 July 2021) | Ms4.8 | Ms3.9 | ) | |
| 16th week (19 July 2021–25 July 2021) | Ms4.1 | Ms4.0 | ) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Li, C.; Yong, S.; Wang, X.; Yang, C. Time Series and Non-Time Series Models of Earthquake Prediction Based on AETA Data: 16-Week Real Case Study. Appl. Sci. 2022, 12, 8536. https://doi.org/10.3390/app12178536
Wang C, Li C, Yong S, Wang X, Yang C. Time Series and Non-Time Series Models of Earthquake Prediction Based on AETA Data: 16-Week Real Case Study. Applied Sciences. 2022; 12(17):8536. https://doi.org/10.3390/app12178536
Chicago/Turabian StyleWang, Chenyang, Chaorun Li, Shanshan Yong, Xin’an Wang, and Chao Yang. 2022. "Time Series and Non-Time Series Models of Earthquake Prediction Based on AETA Data: 16-Week Real Case Study" Applied Sciences 12, no. 17: 8536. https://doi.org/10.3390/app12178536
APA StyleWang, C., Li, C., Yong, S., Wang, X., & Yang, C. (2022). Time Series and Non-Time Series Models of Earthquake Prediction Based on AETA Data: 16-Week Real Case Study. Applied Sciences, 12(17), 8536. https://doi.org/10.3390/app12178536





