Analysis and Suppression of Self-Excited Oscillations in Pressure Servo Valve System

Abstract

In this paper, the phenomenon of pressure servo valve system self-excited oscillation is studied, the dynamic model of the system is established, and the validity of the model is verified by experimental analysis. On this basis, it is concluded that the pressure oscillation with constant amplitude and nondecaying is caused by self-excited oscillation. Such a phenomenon comes from unreasonable structure design of pressure servo valve. Moreover, the factors affecting pressure oscillation are evaluated qualitatively. In order to suppress the pressure self-excited oscillation, this paper proposes a pressure servo valve structure optimization method based on weakening the positive feedback effect of the backpressure. The simulation results show that the method can effectively eliminate the system self-excited oscillation. The stability margin analysis shows that after the structure optimization, the pressure servo valve system has adequate stability margin.

1. Introduction

A pressure servo valve is a special jet pipe hydraulic servo valve, which can realize the feedback control of output pressure through the internal flow channel. Therefore, a control system using the pressure servo valve can realize the accurate control of output pressure in open-loop condition (without pressure sensor). Pressure servo valves are widely used in aircraft wheel braking systems with the advantage of easy control and high reliability. As a key component of large aircraft wheel brake servo control system, the pressure servo valve plays a very significant role in bearing impulse load and providing braking force [1,2]. However, the feedback structure inside the pressure servo valve can also cause positive feedback, which can lead to the nonlinear self-excited oscillation of aircraft wheel braking system and cause serious safety accidents [3].

At present, much research on self-excited oscillation of hydraulic valves and valve-controlled servo systems has been carried out. To solve the self-excited oscillation of the check valve, Grinis et al. have carried out a lot of theoretical analysis and experimental research, and finally determined that the inducement of check valve self-excited oscillation is the fluid-solid coupling between spool and fluid during the rotation of the ball valve [4]. Hayashi et al. established the nonlinear dynamic model of the pilot pressure control valve system, and the effect of valve inlet pressure on the spool self-excited oscillation had been investigated [5]. A nonlinear dynamic model of the pneumatic cartridge valve considering gas compressibility was established by Misra et al., and the pneumatic cartridge valve self-excited oscillation is attributed to the water hammer effect in the upstream/downstream pipeline of the valve [6]. Ye et al. established a nonlinear dynamic model of pilot electromagnetic pneumatic valve considering fluid-solid coupling, and clarified the influence of working parameters on valve self-excited oscillation [7]. Liu et al. established a model to describe the nonlinear dynamic behavior of the check valve system, and the method of increasing damping to suppress the self-excited oscillation had been put forward [8]. Wang et al. established the pneumatic check valve self-excited oscillation dynamic model, and solved the characteristic roots of linear equations based on the principle of small disturbance, and the stable working range of the check valve system without self-excited oscillation has been obtained [9]. Yan et al. established a finite element model of a pressure servo valve torque motor considering the thermal field, and concluded that a high temperature is more likely to cause resonance [10]. Jiang et al. established a nonlinear dynamic model of relief valve, and the influence of system parameters on the relief valve nonlinear dynamic behavior had been obtained [11].

Through mathematical modeling and experimental research, the self-excited oscillation in many hydraulic systems has been analyzed. However, for the self-excited oscillation mechanism of the pressure servo valve system (PSVS), there is a lack of relevant research work.

To address this situation, the mechanism and influencing factors of PSVS self-excited oscillations has been analyzed in depth, starting from the establishment of PSVS accurate dynamic model. The structure of this paper is as follows:

In the second part, the PSVS dynamic model is established, and the accuracy of the model is verified by experiments. Meanwhile, the PSVS nonlinear self-excited oscillation phenomenon is analyzed. In the third part, the nonlinear self-excited oscillation mechanism of the PSVS is obtained, and the influencing factors of the oscillation are also evaluated qualitatively in this part. In the fourth part, based on the above study, the pressure servo valve structure optimization method is proposed, and PSVS nonlinear self-excited oscillation is eliminated effectively. After that, it is concluded that the optimized PSVS is a stable dynamic system with sufficient stability margin.

2. Dynamic Model of the PSVS

The hydraulic schematic diagram of PSVS is shown in Figure 1. And the structural schematic diagram of the pressure servo valve is shown in Figure 2. The parameters in Figure 2 are described in the Table 1.

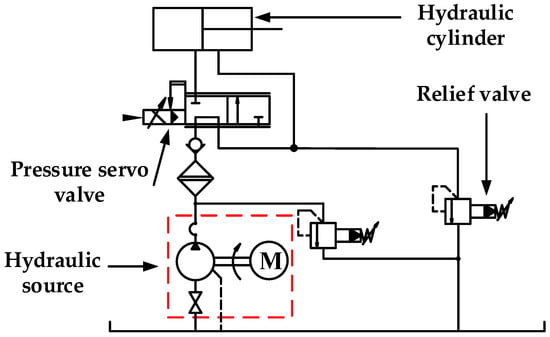
Figure 1. The hydraulic schematic diagram of PSVS.

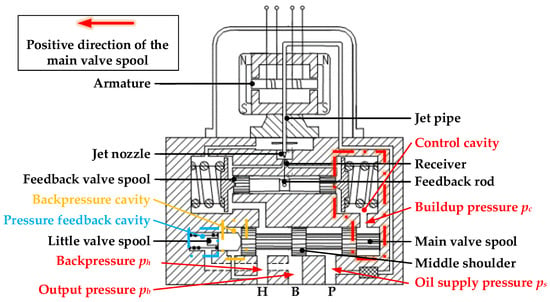
Figure 2. The structural schematic diagram of the pressure servo valve.

Table 1. The parameters.

Parameter	Definition	Unit
Δi	Input current	mA
Kt	Electromagnetic moment coefficient	Nm/rad
Km	Magnetic torque spring stiffness	Nm/rad
ψ	Jet pipe rotation angle	rad
Ja	Rotational inertia of jet pipe	kg·m2
Ba	Damping coefficient of jet pipe	Nm/rad/s
Ka	Stiffness of jet pipe	Nm/rad
Kfg	Stiffness of the feedback rod	N/m
r	Distance from feedback rod rotation center to nozzle	m
kq	Linearized flow gain coefficient of jet nozzle	m2/s
kc	Linearized flow pressure coefficient of jet nozzle	m3/sPa
xs	Displacement of jet nozzle	m
xc	Displacement of the second stage spool	m
pc	Buildup pressure	Pa
ps	Oil supply pressure	Pa
ph	Backpressure of the system	Pa
ρ	Oil density	kg/m3
β	Volumetric modulus of elasticity of oil.	Pa
Vcv	Volume of the control cavity	m3
Ac	Area of feedback valve spool	m2
Kc	Feedback spring stiffness	N/m
mc	Mass of the feedback spool	kg
Bc	Damping coefficient of the feedback spool	Nm/rad/s
Av	Effective area of buildup pressure	m2
pb	Output pressure	Pa
Ab	Effective area of output pressure	m2
Ah	Effective area of backpressure	m2
Kf	Steady-state flow force stiffness of main valve spool	N/m
xv	Displacement of power stage valve spool	m
xv0	Initial compression of power stage spring	m
Mv	Mass of power stage valve spool	kg
Bv	Damping coefficient of power stage valve spool	Nm/rad/s
K	Spring stiffness of power stage valve spool	N/m
Cd	Flow coefficient of main valve spool	-
W	Area gradient of the main valve spool	m
QL	Load flow	m3/s
y	Displacement of cylinder piston rod	m
Ag	Effective area of cylinder piston	m2
Vgb	Work cavity	m3
Cb	Leakage coefficient of cylinder	m3/s/Pa
Mg	Mass of cylinder piston	kg
Bg	Damping coefficient of cylinder	Nm/rad/s
Kg	Spring stiffness of cylinder	N/m
Vh	Volume of the oil return cavity	m3
Cdj	Flow coefficient of the relief valve	-
Qout	Flow of the relief valve	m3/s
xj	Displacement of relief valve spool	m
D	Valve port diameter of relief valve	m
α	Semi-cone angle of valve spool	rad
pcj	Relief valve control pressure	Pa
Vcj	Volume of the relief valve control cavity	m3
Rc	Impedance of relief valve damping hole	m3/s/Pa
Aj	Effective area of relief valve control pressure	m2
Mj	Mass of relief valve spool	kg
Kj	Spring stiffness of relief valve	N/m
Bj	Damping coefficient of relief valve	Nm/rad/s
xj0	Initial compression of relief valve spool	m
kj	Linearized flow gain coefficient of relief valve	m2/s
kqv	Linearized flow gain coefficient of main valve spool	m2/s
kcv	Linearized flow pressure coefficient of main valve spool	m3/sPa
ks	Steady-state flow force coefficient of relief valve spool	N/m/Pa

2.1. Working Principle of the System

The hydraulic schematic diagram of PSVS is shown in Figure 1. The hydraulic cylinder is used to simulate the load, and the relief valve is used to adjust the backpressure of the system.

The structure of the pressure servo valve is shown in Figure 2.

When the main valve spool moves to the left, the high-pressure oil from port P enters port B through the throttle window on the right side of the middle shoulder. At this time, the high-pressure oil will enter the hydraulic cylinder rod less cavity, pushing the piston to move against the spring force. At the same time the output pressure is formed, which acts on the left of the little valve spool, forming negative feedback to the main spool. On the contrary, when the main spool moves to the right, the oil in the hydraulic cylinder rod less cavity will enter the backpressure cavity through the throttle window on the left side of the middle shoulder (as p_b > p_h), resulting in the pressure increase of the backpressure cavity.

2.2. Dynamic Model of the PSVS

The PSVS dynamic model includes the pressure servo valve model, load cylinder model and backpressure model. Among them, the backpressure is usually regulated by a relief valve, therefore the backpressure is not an ideal constant value but a time variable that changes dynamically in a certain range. The author discusses the modeling process of PSVS in detail in his doctoral dissertation [12], and the model is as follows:

(1) Pressure servo valve model.

The pressure servo valve model consists of three parts: the jet amplifier model, the feedback valve spool model, and the main valve spool model.

(i). Jet amplifier model.

The pressure servo valve adopts a permanent magnet torque motor. The modeling method of such a torque motor is described in detail in the reference [13]. It should be noted that since the pressure servo valve has a three-stage structure, and the effect of the feedback valve spool on the feedback rod assembly needs to be considered when establishing the dynamic model of the torque motor.

$$T_d=K_t\Delta i+K_m\psi$$

(1)

$$T_d=J_a\frac{{\mathrm{d}}^2\psi }{\mathrm{d}{t}^2}+B_a\frac{\mathrm{d}\psi }{\mathrm{d}t}+K_a\psi +T_r$$

(2)

$$T_r=K_{fg}\left(r\psi +x_c\right)r$$

(3)

The linearized jet nozzle flow is as follows [14].

$$Q_{jetnozzle}=k_q{x}_s-k_c{p}_c$$

(4)

When the flow enters the control cavity, it will push the feedback valve spool and the main valve spool to the left, and the formula is as follows.

$$k_q{x}_s-k_c{p}_c=A_c\frac{\mathrm{d}{x}_c}{\mathrm{d}t}+A_v\frac{\mathrm{d}{x}_v}{\mathrm{d}t}+\frac{V_{cv}}{\beta }\frac{\mathrm{d}{p}_c}{\mathrm{d}t}$$

(5)

In Formula (5), x_s ≈ r·sinψ is the displacement of the end of the jet nozzle.

(ii). Feedback valve spool model.

The feedback valve spool is in a dynamic force balance state under the combined action of buildup pressure p_c, back pressure p_h, and feedback rod.

$$\left(p_c-p_h\right)A_c-K_{fg}\left(r\psi +x_c\right)-2K_c{x}_c=m_c{\ddot{x}}_c+B_c{\dot{x}}_c$$

(6)

(iii). Main valve spool model.

The main valve spool is in a dynamic force balance state under the combined action of buildup pressure p_c, output pressure p_b, and the back pressure p_h.

$$p_c{A}_v-p_b{A}_b-p_h{A}_h=M_v{\ddot{x}}_v+B_v{\dot{x}}_v+\left(K+K_f\right)x_v+K{x}_{v0}$$

(7)

(2) Load cylinder model

When the main valve spool moves along the positive direction, the oil enters the rod-less cavity of the hydraulic cylinder through the throttling window of the main valve spool. On the contrary, when the power stage spool moves in the negative direction, the oil in the rod-less chamber of the hydraulic cylinder enters the backpressure cavity. Therefore, the sign function (sign(x_v)) needs to be used to establish the load flow Equation.

$$Q_L=C_{d}W{x}_v\sqrt{\frac{2}{\rho }\left(\frac{1+sign(x_v)}{2}{p}_s+\frac{-1+sign(x_v)}{2}{p}_b-sign(x_v)p_h\right)}$$

(8)

Under the action of load flow and hydraulic cylinder leakage flow, the hydraulic cylinder piston will move along the positive or negative direction

$$Q_L-C_b{p}_b=A_g\frac{\mathrm{d}y}{\mathrm{d}t}+\frac{V_{gb}}{\beta }\frac{\mathrm{d}{p}_b}{\mathrm{d}t}$$

(9)

In the process, the hydraulic cylinder piston is in a dynamic force balance state under the action of the output pressure p_b.

$$A_g{p}_b=M_g\frac{{\mathrm{d}}^{2}y}{\mathrm{d}{t}^2}+B_g\frac{\mathrm{d}y}{\mathrm{d}t}+K_{g}y$$

(10)

(3) Dynamic backpressure model.

The backpressure of PSVS is provided by a relief valve, and its working principle is shown in Figure 3.

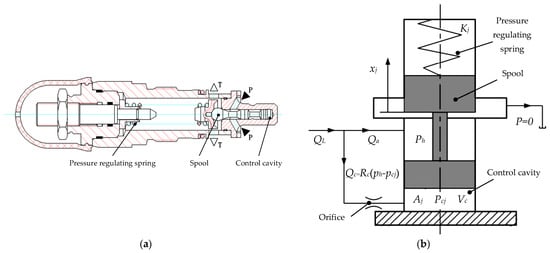
Figure 3. The relief valve: (a) The structure of relief valve, (b) The simplified principle of relief valve.

The channel P of the relief valve is connected to the port H of the pressure servo valve through the pipeline, and the backpressure acts on the control cavity through the internal orifice, forming a control pressure p_cj opposite to the pressure regulating spring. If the control pressure p_cj exceeds the setting value of the pressure regulating spring, the spool will move along the positive direction (x_j > 0). At this time, the part of the load flow enters the oil return channel through the relief valve, and the change of backpressure can be calculated according to the flow continuity Equation which is shown below.

$${\dot{p}}_h=\frac{\beta }{V_h}\left(C_{d}W{x}_v\frac{1-sign(x_v)}{2}\sqrt{\frac{2}{\rho }\left(p_b-p_h\right)}-R_c\left(p_h-p_{cj}\right)-Q_{out}\right)$$

(11)

The flow exiting through the relief valve can be calculated as follows [11].

$$Q_{out}=\pi D{x}_j\sin \alpha C_{dj}\sqrt{\frac{2}{\rho }{p}_h}$$

(12)

The control pressure p_cj can be calculated according to the flow continuity equation of the control cavity.

$${\dot{p}}_{cj}=\frac{\beta }{V_{cj}}\left[R_c\left(p_h-p_{cj}\right)-A_j{\dot{x}}_j\right]$$

(13)

The spool is in a dynamic force balance state under the action of the control pressure p_cj and pressure regulating spring.

$$p_{cj}{A}_j=M_j{\ddot{x}}_j+B_j{\dot{x}}_j+K_j{x}_j+K_j{x}_{j0}$$

(14)

According to the above formulas, the PSVS model is built in the Simulink software as shown in Figure 4.

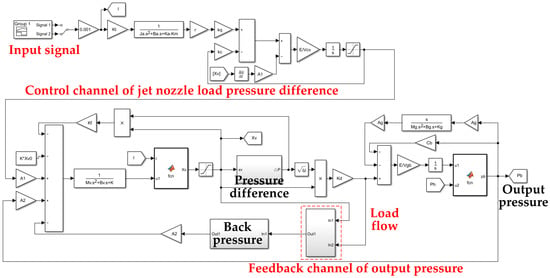
Figure 4. The structure schematic diagram of the pressure servo valve.

2.3. Simulation Analysis and Experiment

2.3.1. Test Platform

In order to verify the accuracy of PSVS dynamic model, an experimental platform is built in this paper. The hydraulic schematic diagram of the experimental platform is shown in Figure 5.

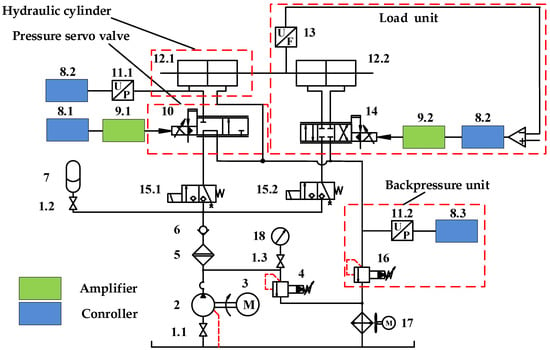
Figure 5. Hydraulic principle of experimental platform.

The output pressure p_b can be measured by the pressure sensor 11.1. The load unit is used to simulate the dynamic load of the hydraulic cylinder. The backpressure unit consists of a pressure sensor and a relief valve.

The experimental platform parameters are shown in Table 2.

Table 2. The parameters of experimental platform.

Oil Supply Pressure	System Flow	Output Pipe (m)	Oil Return Pipe (m)	Backpressure	Load Stiffness	Load Damping
15 MPa	6.25 × 10−4 m3/s	Φ0.006 × 1.50	Φ0.006 × 1.01	0.6 MPa	1 × 106 N/m	50 Ns/m

Figure 6 shows the experimental platform.

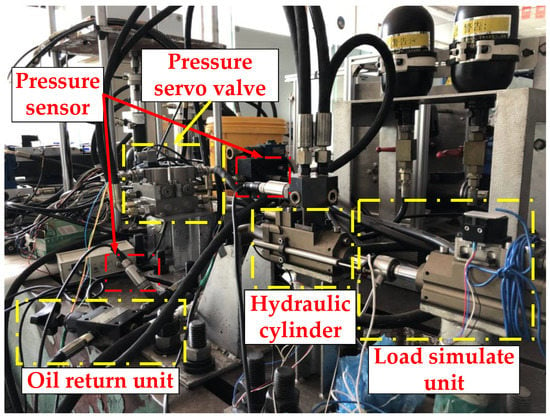
Figure 6. Pressure servo valve experimental platform.

The pressure sensor used in this paper is shown below which is provided by measurement SPECIALTIES. The range of the pressure sensor is 40 MPa, and the accuracy is 0.25% of F.S. (Figure 7).

Figure 7. The pressure sensor.

2.3.2. The Comparison between Simulation and Experiment

When the step current signal of 40 mA is given, and the output pressure measured experimentally is shown in Figure 8.

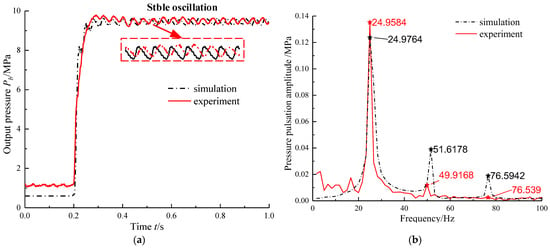
Figure 8. Experimental results of output pressure under step signal: (a) Time domain curve, (b) FFT spectrum of output pressure.

According to Figure 8, the following conclusions can be drawn:

Under the action of step signaling, the output pressure oscillates stably with constant amplitude, and its peak-to-peak value is about 0.40 MPa. Under the condition of a frequency range of 0~100 Hz and a sampling frequency of 60 Hz, the FFT spectrum of stable oscillation pressure can be obtained as shown in Figure 8b. It can be seen that the main frequency of pressure oscillation is about 25 Hz.

Table 3 It can be seen that the system dynamic model has high simulation accuracy.

Table 3. Comparison of output pressure oscillation.

	Peak-Peak Value (Mpa)	Main Frequency (Hz)
Experiment	0.319	24.9584
Simulation	0.347	24.9764
Error	8.8%	0.072%

After the ramp current signal of 40mA is input to PSVS, similar pressure oscillations still exist, as shown in Figure 9.

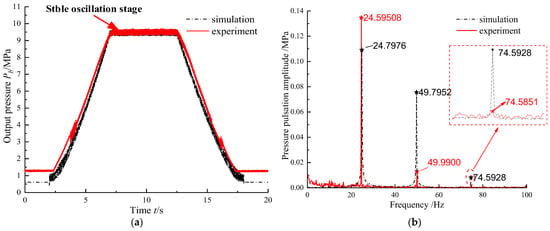
Figure 9. Experimental results of output pressure under ramp signal: (a) Time domain curve, (b) FFT spectrum of output pressure.

3. Pressure Oscillation Mechanism Analysis

PSVS shows the periodic oscillation in simulation and experiment. However, PSVS has neither an excitation source nor a resonance component and structural parameters that change periodically. However, there is a large number of feedback and regulation loops inside the system. Therefore, according to the mechanism of oscillation induction, the pressure oscillation is most likely to be self-excited oscillation, which is very common in nonlinear systems.

If self-excited oscillation occurs in a nonlinear system, an essential nonlinear factor exists in the system consequently. The principle of pressure servo valve power stage is shown below.

The pressure servo valve inevitably overshoots its output pressure under the action of step signaling. The overshoot pressure (which is higher than expected output pressure) will disrupt the dynamic force balance of the main spool, and the main valve spool will generating negative displacement (x_v < 0). At this time, port B in Figure 10 will connect to port H. Additionally, due to the differential pressure, the oil that comes from the cylinder will flow into the oil return cavity through the power stage spool window. This oil will be divided into two paths. The oil that goes along path 1 will enter the closed cavity (which is shown in Figure 10), causing a sudden pressure increase in the cavity. The oil that goes along path 2 will enter the oil return cavity (formed by the hose between the pressure servo valve and relief valve), causing a sudden pressure increase in said cavity. To further illustrate the pressure dynamics in the oil return cavity, a model is built, as shown in Figure 11.

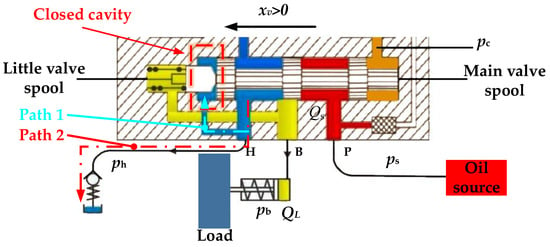
Figure 10. Pressure servo valve power stage.

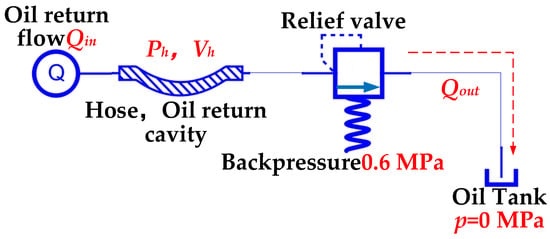
Figure 11. Model of the oil return cavity.

The relationship between the pressure gradient and the flow is as follows

$${\dot{p}}_h=\frac{\beta }{V_h}\left(Q_{in}-Q_{out}\right)$$

(15)

For the relief valve, there is an approximately linear relationship between the output flow and the pressure p_h.

$$Q_{out}=k_j{p}_h$$

(16)

Therefore, the following formula can be obtained.

$${\dot{p}}_h=\frac{Q_{in}}{k_j}\left(1-e^{-\frac{\beta k_j}{V_h}t}\right)$$

(17)

From the above formula, it can be seen that

(1) The volume of the oil return cavity V_h determines the time constant. The smaller V_h is, the faster the backpressure changes.

(2) The input flow Q_in determines the amplitude of the dynamic backpressure. The larger Q_in is, the farther the backpressure deviates from the set value of 0.6 MPa. Therefore, the larger the negative x_v is, the more obvious the backpressure p_h changes.

The sudden change of backpressure will cause the resultant force (along the negative direction, x_v < 0) which acts on the main valve spool increases furtherly. In addition, the positive feedback will form to force the main valve spool to move to the right side, until the output pressure drops more to form a new force balance state. This process can be represented by the control block diagram shown in the Figure 12.

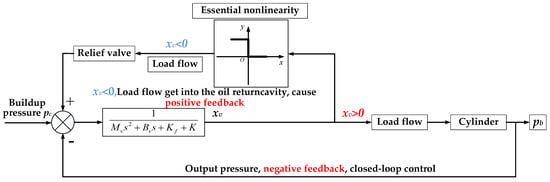
Figure 12. Pressure servo valve power stage feedback control block diagram.

According to the definition given by physicist A.A. Harkevich, a self-excited oscillation system is a closed-loop system consisting of a main oscillation subject, an energy source, a controller and a feedback unit, which is shown in Figure 13.

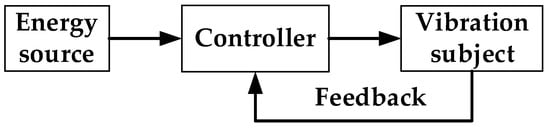
Figure 13. Self-excited oscillation feedback mechanism.

In PSVS, the buildup pressure p_c in Figure 10 is the energy source, the main valve spool is the main oscillation subject, and the positive feedback formed by the backpressure is the internal feedback information to maintain the energy replenishment. Therefore, the structure of power stage meets the structural characteristics of self-excited oscillation system. Therefore, the pressure oscillation of the PSVS is the self-excited oscillation caused by backpressure positive feedback.

4. Oscillation Suppression of PSVS

4.1. Oscillation Suppression Method

As described in the previous section, when x_v < 0, the oil from the cylinder enters the closed cavity which is shown in Figure 14. Since the closed cavity has only one flow path, the cavity is very sensitive to the changes in flow; that means even small changes in flow can cause dramatic pressure oscillation in that cavity. Additionally, it will triggering a backpressure positive feedback on the main spool valve.

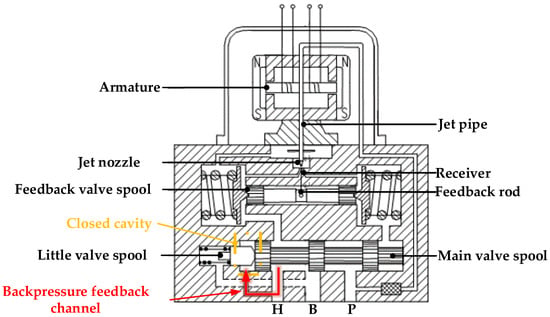
Figure 14. Pressure servo valve structure.

Therefore, in order to reduce the backpressure positive feedback effect of the main spool, two structure optimization methods are taken. First, the closed cavity is connected to the cavity at the left end of the feedback valve spool to transform the closed cavity into an open cavity. Therefore, the volume of the cavity increases, and the sensitivity of the cavity to the flow gradient is reduced. Secondly, a damping hole is added between the backpressure feedback channel and Prot H to achieve the attenuation of the backpressure oscillation, so that the pressure in front of the backpressure feedback channel tends to be smooth. The principle of the structure-optimized servo valve is shown in Figure 15.

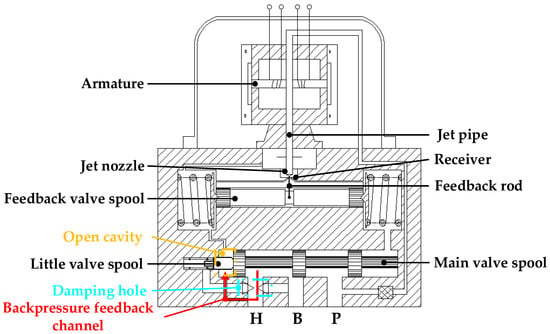
Figure 15. Principle of structure-optimized pressure servo valve.

To illustrate the attenuation effect of damping holes on backpressure oscillations, a simulation model of pressure oscillations with damping holes is established in the Amesim software, as shown in Figure 16.

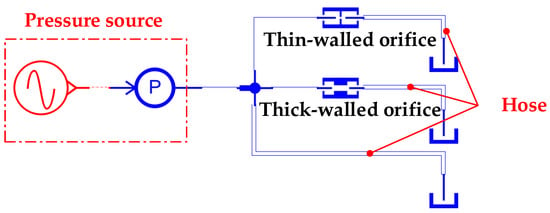
Figure 16. Simulation model of pressure oscillation with damped orifice.

The parameters in the simulation model are as same as those in Table 2. The orifice parameters are shown in Table 4.

Table 4. Orifice parameters.

	Diameter	Length	Diameter of Inlet Runner	Model
Thin-walled	1 mm	--	2 mm	$\xi =f\left(\mathrm{Re},\frac{A_c}{A_1}\right)$
Thick-walled	1 mm	10 mm	2 mm	$\xi =f\left(\mathrm{Re},\frac{A_c}{A_1},\frac{l}{D_h}\right)$

When the pressure source signal is $p=9.5+0.5\sin \left(2\pi \times 25t\right)$, the input pressure and the pressure in the hose are shown in Figure 17.

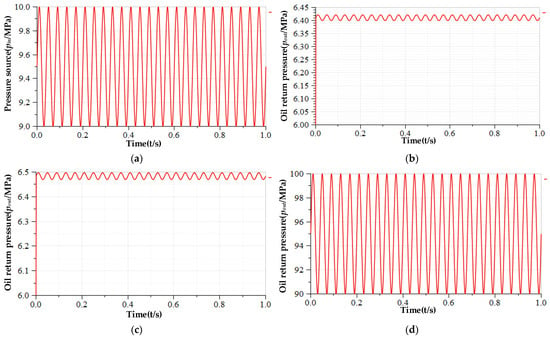
Figure 17. Pressure in the hose under the action of the sinusoidal pressure source: (a) pressure source; (b) pressure in hose (after thin-walled orifice); (c) pressure in hose (after thick-walled orifice); (d) pressure in hose (without orifice).

It can be seen that the sinusoidal pressure oscillation from the pressure source is greatly attenuated after passing through the orifice: the peak-to-peak value drops from 10 MPa to 0.3 MPa. Moreover, it is observed that the attenuation of pressure oscillations by the thin-walled orifice is better than that by the thick-walled orifice.

Therefore, it can be said that the pressure in the backpressure feedback channel can be approximated as a constant value (p_h = 0.6 MPa) after passing through the orifice. At this time, the dynamic model of the PSVS is as follows.

$$T_d=K_t\Delta i+K_m\psi$$

(18)

$$T_d=J_a\frac{{\mathrm{d}}^2\psi }{\mathrm{d}{t}^2}+B_a\frac{\mathrm{d}\psi }{\mathrm{d}t}+K_a\psi +T_r$$

(19)

$$T_r=K_{fg}\left(r\psi +x_c\right)r$$

(20)

$$k_q{x}_s-k_c{p}_c=A_c\frac{\mathrm{d}{x}_c}{\mathrm{d}t}+A_v\frac{\mathrm{d}{x}_v}{\mathrm{d}t}+\frac{V_{cv}}{\beta }\frac{\mathrm{d}{p}_c}{\mathrm{d}t}$$

(21)

$$\left(p_c-p_h\right)A_c-K_{fg}\left(r\psi +x_c\right)-2K_c{x}_c=m_c{\ddot{x}}_c+B_c{\dot{x}}_c$$

(22)

$$p_c{A}_v-p_b{A}_b-0.6A_h=M_v{\ddot{x}}_v+B_v{\dot{x}}_v+\left(K+K_f\right)x_v+K{x}_{v0}$$

(23)

$$Q_L=C_{d}W{x}_v\sqrt{\frac{2}{\rho }\left(\frac{1+sign(x_v)}{2}{p}_s+\frac{-1+sign(x_v)}{2}{p}_b-sign(x_v)p_h\right)}$$

(24)

$$Q_L-C_b{p}_b=A_g\frac{\mathrm{d}y}{\mathrm{d}t}+\frac{V_g+V_b}{\beta }\frac{\mathrm{d}{p}_b}{\mathrm{d}t}$$

(25)

$$A_g{p}_b=M_g\frac{{\mathrm{d}}^{2}y}{\mathrm{d}{t}^2}+B_g\frac{\mathrm{d}y}{\mathrm{d}t}+K_{g}y$$

(26)

4.2. Verification of Oscillation Suppression Method

4.2.1. Simulation Analysis

When a step and ramp current signal of 40 mA is given, the output pressure of PSVS is shown in Figure 18.

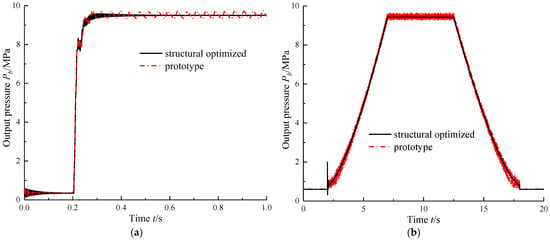
Figure 18. Output pressure with different input signal: (a) step input signal, (b) ramp input signal.

It can be seen that, compared with the prototype system, the output pressure of the PSVS does not oscillate under either the step signal or the ramp signal input, which means that the self-excited oscillation of PSVS is effectively eliminated.

4.2.2. Stability Margin Analysis

(1) Block diagram of pilot stage.

Take the Laplace transform of Formula (18)~Formula (21) as follows.

$$K_t\Delta \tilde{i}=\left(J_a{s}^2+B_{a}s+K_a-K_m\right)\tilde{\psi }+{\tilde{T}}_r$$

(27)

$${\tilde{T}}_r=K_{fg}\left(r\tilde{\psi }+{\tilde{x}}_c\right)\left(r+b\right)$$

(28)

$$k_q{\tilde{x}}_s-k_c{\tilde{p}}_c=A_{c}s{\tilde{x}}_c+A_{v}s{\tilde{x}}_v+\frac{V_{cv}}{\beta }s{\tilde{p}}_c$$

(29)

where the symbol “~” indicates the variable after Laplace transformation.

Therefore, the control block diagram of the control current Δi to buildup pressure p_c can be obtained as shown in Figure 19.

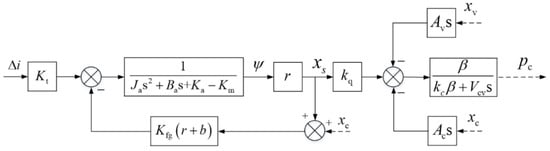
Figure 19. Control block diagram from control current to buildup pressure.

(2) Feedback stage control block diagram.

It can be seen that there is a negative feedback control channel in the pilot stage control loop, which comes from the feedback valve spool displacement x_c. Take the Laplace transform of Formula (22) as follows.

$$\left({\tilde{p}}_c-{\tilde{p}}_h\right)A_c-K_{fg}\left(r\tilde{\psi }+{\tilde{x}}_c\right)-2K_c{\tilde{x}}_c=M_c{s}^2{\tilde{x}}_c+B_{c}s{\tilde{x}}_c$$

(30)

Therefore, the control block diagram from the buildup pressure p_c to the feedback valve spool displacement x_c is shown in Figure 20.

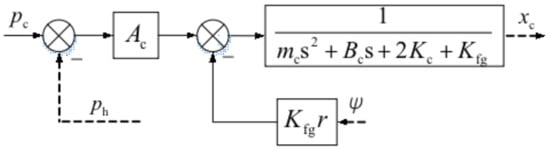
Figure 20. Control block diagram from buildup pressure to feedback stage spool displacement.

(3) Power stage control block diagram.

Take the Laplace transform of Formula (23) as follows.

$${\tilde{p}}_c{A}_v-{\tilde{p}}_b{A}_b-{\tilde{p}}_h{A}_h-K{x}_{v0}=\left(m_v{s}^2+B_{v}s+K_f+K\right){\tilde{x}}_v$$

(31)

The control block diagram from the buildup pressure p_c to the main valve spool displacement x_v can be obtained as shown in Figure 21.

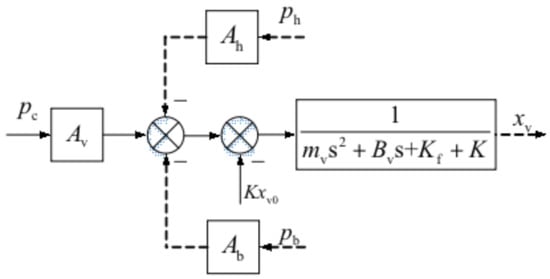
Figure 21. Control block diagram from buildup pressure to power stage spool displacement.

Therefore, it is necessary to establish the transfer relationship from the power stage spool displacement x_v to the output pressure p_b.

As can be seen from the Formula (24), there is a nonlinear relationship, which makes it difficult to build up the transfer relationship from x_v to p_b. Therefore, a linearization method is adopted, and the load flow can be calculated approximatively as follows.

$$Q_L=k_{qv}{x}_v-k_{cv}{p}_L$$

(32)

The linearized flow gain coefficient and linearized flow pressure coefficient in the above formula can be calculated by Formulas (33) and (34).

$$k_{qv}=\frac{\partial Q_L}{\partial x_v}=C_{d}W\sqrt{\frac{1}{\rho }\Delta p}$$

(33)

$$k_{cv}=-\frac{\partial Q_L}{\partial p_L}=\frac{C_{d}W{x}_v\sqrt{\frac{1}{\rho }\Delta p}}{2\left(\Delta p\right)}$$

(34)

When considering the leakage of cylinder, there is

$$\Delta Q=k_{qv}{x}_v-k_{cv}{p}_L-C_b{p}_b=A_g\frac{\mathrm{d}y}{\mathrm{d}t}+\frac{V_g+V_b}{\beta }\frac{\mathrm{d}{p}_b}{\mathrm{d}t}$$

(35)

When x_v > 0, the load differential pressure of main valve spool is p_L = p_s − p_b, and ΔQ > 0 means that the load flow comes from the oil source enters the cylinder. When x_v < 0, the load differential pressure of main valve spool is p_L = p_b − p_h, and ΔQ < 0 means that the load flow comes from the cylinder enters the oil return cavity.

Take the Laplace transform of Formulas (35) and (26) as follows.

$$k_{qv}{\tilde{x}}_v-k_{cv}{\tilde{p}}_L-C_b{\tilde{p}}_b=A_{g}s\tilde{y}+\frac{V_g+V_b}{\beta }s{\tilde{p}}_b$$

(36)

$$A_g{\tilde{p}}_b=\left(M_g{s}^2+B_{g}s+K_g\right)\tilde{y}$$

(37)

The control block diagram from the power stage spool displacement x_v to the output pressure p_b can be obtained as shown in Figure 22.

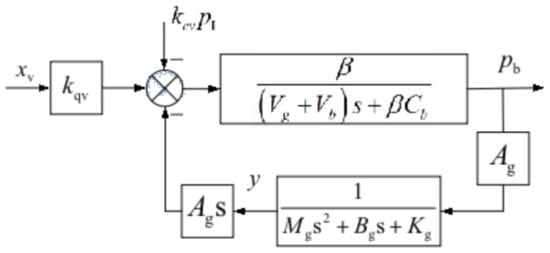
Figure 22. Control block diagram from main valve spool displacement to output pressure.

(4) Block diagram of PSVS.

According to the control block diagram above, the control block diagram of PSVS (from control current Δi to output pressure p_b) can be obtained, as shown in Figure 23.

Figure 23. Block diagram of PSVS.

As can be seen from Figure 23, the PSVS is a typical closed-loop control system, and there are complex cross-feedback loops and feedforward loops. Therefore, it is extremely difficult to solve the system open-loop transfer function directly. To solve the stability margin of the PSVS, this paper divides the system into two parts and makes reasonable simplification to establish their respective transfer function models, namely, the pre-stage stability transfer function model and the power stage transfer function model. When judging the stability of the system, both parts are taken into consideration.

(1) Pre-stage stability margin analysis.

In this paper, the pressure servo valve pre-stage includes two parts: jet amplifier and feedback stage, where the structure is shown in Figure 24a. Its working principle is similar to that of the force feedback two-stage hydraulic servo valve, as shown in Figure 24b.

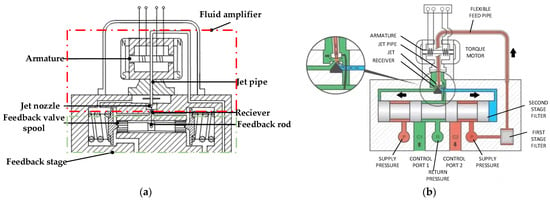
Figure 24. Servo valve force feedback structure: (a) Pressure servo valve pre-stage, (b) Jet pipe force feedback two-stage hydraulic servo valve.

Therefore, the pressure servo valve pre-stage transfer function can be established with reference to the jet pipe force feedback two-stage hydraulic servo valve.

The control block diagram of pre-stage is shown in Figure 25. It can be seen that when establishing the feedback valve spool force balance equation, the force of the feedback rod is ignored because the spring stiffness at both ends of the feedback valve spool is much larger than the feedback rod stiffness.

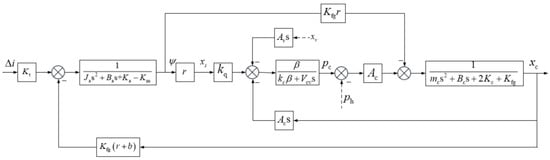
Figure 25. Block diagram of pressure servo valve pre-stage.

After ignoring some factors that have little influence, such as p_h (because $p_c\gg p_h$), the transfer function (from the displacement of jet pipe x_s to the displacement of feedback valve spool x_c) can be obtained below.

$${\tilde{x}}_c=\frac{\beta A_c{k}_q}{\left(k_c\beta +V_{cv}s\right)\left(m_c{s}^2+B_{c}s+2K_c\right)}{\tilde{x}}_s$$

(38)

The pressure servo valve pre-stage Bode diagram is shown in Figure 26.

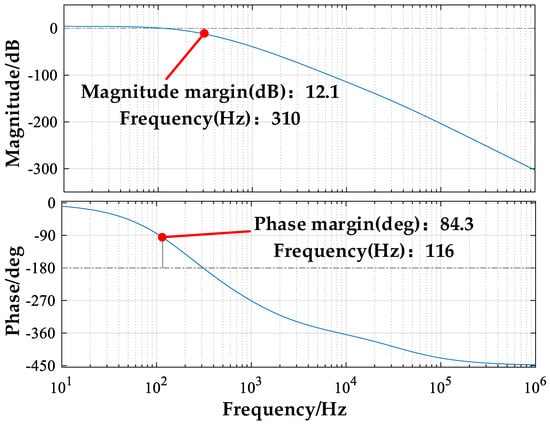
Figure 26. Bode diagram of the pre-stage.

It can be seen that the pressure servo valve pre-stage has a large amplitude margin (12.1 dB > 6 dB) and phase angle margin (84.3 deg > 30 deg), which can maintain stability under certain external disturbances.

(2) Pressure servo valve power stage stability margin analysis.

The control block diagram from buildup pressure p_c to output pressure p_b is as shown in Figure 27.

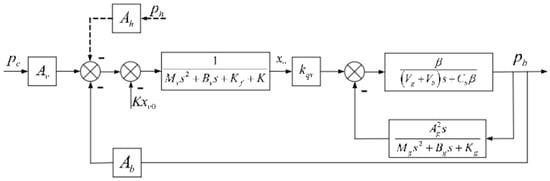
Figure 27. Power stage control block diagram.

The load differential pressure takes different values in the case of x_v > 0 and x_v < 0. From the analysis in subSection 4.2.1, it can be obtained that p_b ≈ 9.5 MPa. Therefore, the linearized flow gain coefficient of the main valve spool can be taken as

$$k_{qv+}=C_{d}W\sqrt{\frac{2\left(p_s-p_b\right)}{\rho }}$$

(39)

$$k_{qv-}=C_{d}W\sqrt{\frac{2\left(p_b-p_h\right)}{\rho }}$$

(40)

In order to simplify the block diagram some measures are adopted.

(1) The cylinder is a load with large stiffness, which has a spring force much larger than the inertia and damping forces. Therefore, only the spring stiffness is considered in the analysis.

(2) The fixed backpressure is an interfering term which does not affect the transmission function and can be ignored in the simplification.

The simplified block diagram of power stage can be obtained as shown in Figure 28.

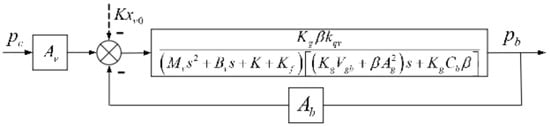
Figure 28. Simplified control block diagram of power stage.

The transfer function can be obtained in Formula (41). When taking Formula (39) or Formula (40) into Formula (41), the open-loop gain can be obtained in Formula (42).

$$W\left(\mathrm{s}\right)=\frac{K_g\beta k_{qv}{A}_b}{\left(M_v{s}^2+B_{v}s+K+K_f\right)\left[\left(K_g{V}_{gb}+\beta A_g^2\right)s+K_g{C}_b\beta \right]}$$

(41)

$$K_0=\frac{C_{d}W{A}_b}{C_b\left(K+K_f\right)}\sqrt{\frac{2p_L}{\rho }}$$

(42)

It can be seen that the open-loop gain of the power stage is related to the operating point of the pressure servo valve. It means that the open-loop gain of the power stage is changing with different load differential pressure.

According to Formula (41), the Bode diagram of the power stage is shown in Figure 29.

Figure 29. Bode diagram of pressure servo valve power stage.

The stability margin of the power stage is shown in Table 5.

Table 5. Power stage stability margin.

	Magnitude Margin (dB)	Phase Margin (deg)
Kqv = 2.001	31.4	87.5
Kqv = 2.545	29.4	86.8

It can be seen that the power stage is a stable system and has a sufficient stability margin to resist external disturbances. Furthermore, it can be seen that the system has a higher stability margin when x_v > 0.

Therefore, it can be judged that the PSVS is a stable dynamical system and has sufficient stability margin to maintain stability under certain external disturbances. This is also consistent with the time domain analysis results of the PSVS in Section 4.2.1.

5. Conclusions

In this paper, the dynamic model of PSVS ha been established and the correctness of the model has been verified by experiment. On this basis, the mechanism of pressure oscillation has been analyzed and an oscillation suppression method for the pressure servo valve has been proposed. The following conclusions can be drawn.

(1) The pressure oscillation of PSVS is the self-excited oscillation caused by backpressure positive feedback.

(2) The backpressure positive feedback can be suppressed by the open cavity and the orifice between Port H and the backpressure feedback channel.

(3) Based on the basic principle of weakening the positive feedback, the pressure servo valve structure optimization method has been proposed. The optimized PSVS has sufficient stability margin to maintain stable pressure output under certain external disturbance.

This paper solves the oscillation problem in the brake pressure control system of large aircraft, and the results provide a clear technical method for the optimal design of this kind of pressure control system.