SPEEDY Quantum Circuit for Grover’s Algorithm

Abstract

In this paper, we propose a quantum circuit for the SPEEDY block cipher for the first time and estimate its security strength based on the post-quantum security strength presented by NIST. The strength of post-quantum security for symmetric key cryptography is estimated at the cost of the Grover key retrieval algorithm. Grover’s algorithm in quantum computers reduces the n-bit security of block ciphers to $\frac{n}{2}$ bits. The implementation of a quantum circuit is required to estimate the Grover’s algorithm cost for the target cipher. We estimate the quantum resource required for Grover’s algorithm by implementing a quantum circuit for SPEEDY in an optimized way and show that SPEEDY provides either 128-bit security (i.e., NIST security level 1) or 192-bit security (i.e., NIST security level 3) depending on the number of rounds. Based on our estimated cost, increasing the number of rounds is insufficient to satisfy the security against quantum attacks on quantum computers.

1. Introduction

With the development of quantum computers, public key cryptography and symmetric key cryptography are vulnerable against quantum algorithms. It is expected that cryptography will no longer be secure when large-scale quantum computers that have reached the quantum resources required for target cryptography attacks are released [1]. Grover’s search algorithm is a well-known quantum algorithm that can accelerate the exhaustive key search against symmetric key cryptography [2]. Grover’s algorithm can reduce the computational complexity from $O\left(N\right)$ to $O\left(\sqrt{N}\right)$ for symmetric key cryptography using an n-bit key (i.e., $N=2^n$) in a quantum computer.

The National Institute of Standards and Technology (NIST) held a competition on post-quantum cryptography with the goal of setting standards for post-quantum cryptography to prepare for the post-quantum era, and presented an estimate of the strength of security for symmetric key cryptography [3]. Block ciphers are not guaranteed to be secure in quantum computers by Grover’s algorithm as well. In order to evaluate the safety of the target cipher in the post-quantum era, it is necessary to estimate the required quantum resources by implementing the target cipher as a quantum circuit. As a result, NIST presented the cost of key retrieval using Grover’s algorithm as an indicator of security strength in the post-quantum era. As a result, estimating the Grover key retrieval cost of symmetric key cryptography is an interesting area of research [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20].

SPEEDY is a block cipher proposed by CHES’21 [21] that operates with the block size, key length, and the number of rounds as variables. Since SPEEDY targets 6-bit S-boxes and 64-bit CPUs, the least common multiple of 6 and 64 (i.e., 192) is used as the default block size and key length. SPEEDY for a length of 192 bits and rounds of r is called SPEEDY-r-192. SPEEDY provides 128 bits of security when $r=6$ and achieves full security of 192 bits at $r=7$.

In this paper, we implement the SPEEDY block cipher as a quantum circuit and check the post-quantum security strength by estimating the resources to be applied to Grover’s algorithm. To the best of our knowledge, this is the first implementation of SPEEDY in quantum circuits. Grover’s algorithm operates by repeating oracle and diffusion operations, and the quantum circuit of the target cipher is essential in oracle. We used the proposed quantum circuit to estimate the quantum resources needed for Grover’s algorithm. Furthermore, we decomposed the estimated resource into the lower-level $Clifford+T$ gate to check the post-quantum security strength. We estimated the quantum resource by increasing r to see how the number of rounds affects the post-quantum security strength. SPEEDY-7-192 provided 192-bit security on classic computers, but showed a security strength of level 1 (i.e., the AES-128 level) on quantum computers. The post-quantum security strength did not increase even after a larger increase in rounds. In other words, estimating the quantum cost according to various rounds, it was confirmed that SPEEDY provided level 1 (AES-128) post-quantum security, and that the increase in rounds did not significantly affect the quantum security strength. Our results show that increasing the number of rounds can improve security for classical computers, but it is not enough for quantum computers. Finally, it was confirmed through comparison with other lightweight ciphers (i.e., LEA, CHAM, HIGHT, and PIPO) that the increase in rounds did not significantly affect the post-quantum security strength and that increasing the key length affects the security strength. We used IBM’s ProjectQ platform to implement and simulate quantum circuits.

Contributions of This Paper

• Implementation of the first quantum circuit for SPEEDY block cipher: To the best of our knowledge, this is the first quantum circuit implementation of SPEEDY. In the S-box implementation, an efficient Algebraic Normal Form (ANF) S-box was adopted in terms of quantum resources to reduce quantum resources, and separate quantum resources were not used through logical swap in ShiftColumns and Key Schedule.
• Estimating the cost of Grover key search for SPEEDY: We estimated the Grover algorithm’s quantum resource for the SPEEDY block cipher. Estimated quantum resources are decomposed into a lower-level $Clifford+T$ gate to lay the foundation for quantum security level analysis. Finally, we confirmed the post-quantum security strength through quantum cost calculation.
• Post-quantum security evaluation and analysis of SPEEDY block cipher: We evaluated post-quantum security for SPEEDY based on the Grover key retrieval cost presented by NIST. Additionally, we noted the change in security strength with increasing rounds of cipher. Based on these attempts, we discussed the differences in cipher security between classical and quantum computers.

2. Related Work

2.1. Quantum Background

A quantum computer uses qubit, similar to the bit used in classic computer operations [22]. While bits have fixed values of 0 and 1, qubit can have values of 0 and 1 at the same time [23]. The calculation can be performed quickly. Due to the nature of these qubits, a $2^n$ time brute-force attack in a classic computer can be performed only $\lfloor \frac{\pi }{4}{2}^{\frac{n}{2}}\rfloor$ times on a quantum computer. In quantum computing, all changes except measurements must be reversible. It is possible to return to the initial value only with the result value without additional information.

2.1.1. Quantum Gates

Quantum gates exploit the quantum entanglement and superposition states of qubits [24,25]. In quantum computing, the state of a qubit is changed with a quantum gate that can perform reversible operations. Figure 1 shows some of the quantum gates.

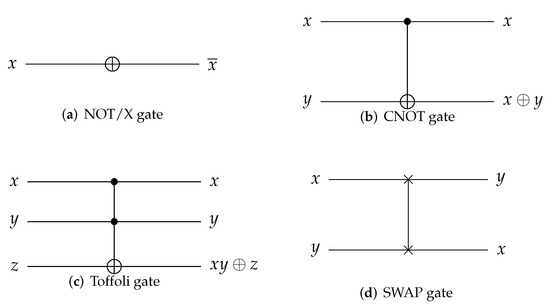
Figure 1. Quantum gates.

(1)

$NOT/X-gate$, X(x) = $\overline{x}$: The X gate inverts the state of a single qubit.

(2)

$CNOTgate$, CNOT(x, y) = (x, $x\oplus y$): One of the two input qubits becomes the control qubit, and the other becomes the target qubit. When the control bit is set to one, the state of the target qubit is inverted. If the control qubit x is one, target qubit y is inverted.

(3)

$Toffoligate$, Toffoli($x,y,z$) = $(x,y,x·y\oplus z)$: Two of the three input qubits become the control qubits, and the other becomes the target qubit. When all control bits are one, the state of the target qubit is inverted. If both control qubits (x and y) are one, the target qubit z is inverted.

(4)

$SWAPgate$, SWAP(x, y) = (y, x): This changes the state of two qubits.

2.1.2. Grover’s Algorithm for Key Search

An exhaustive key search using Grover’s algorithm described in Figure 2 can recover an n-bit key with only $2^{n/2}$ searches. The classical key search performs $2^n$ searches in the worst case (i.e., $O\left(2^n\right)$). Grover key search always repeats $2^{n/2}$. The Grover’s algorithm operates with oracle and diffusion operation and increases the probability of finding the correct key through repetition. The oracle in Grover’s algorithm finds the correct key. The quantum circuit of the target cipher is used. The diffusion operation in Grover’s algorithm operates to increase the probability of measuring the correct key. The following describes the operation process for Grover’s algorithm:

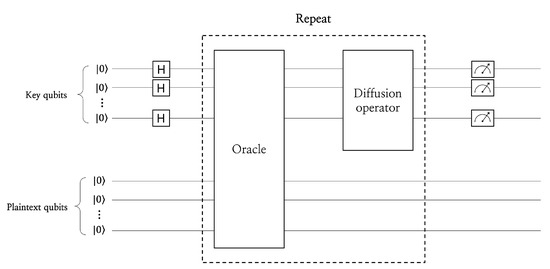
Figure 2. Exhaustive key search in Grover’s algorithm.

• n-qubits are prepared to find a key of length n.
           ${|0⟩}^{\otimes n}={|0⟩}_0\otimes {|0⟩}_1\otimes \cdots \otimes {|0⟩}_n$.
• All n qubits are placed in a superposition state by a Hadamard gate.
           ${|\psi ⟩}^{\otimes n}={|\psi ⟩}_0\otimes {|\psi ⟩}_1\otimes \cdots \otimes {|\psi ⟩}_n$.
• If the ciphertext generated by the input n-qubits (i.e., key) matches the known ciphertext, the sign of the key in that state is inverted.
• The amplitude of the solution key is amplified through the diffusion operator.
• Steps 3 and 4 are repeated $\sqrt{2^n}$ times to increase the key search probability.

2.1.3. Grover’s Algorithm for SPEEDY

The oracle in Grover’s algorithm performs a known plaintext attack (KPA), and the attack is possible when it knows one plaintext–ciphertext pair. Figure 3 shows the oracle in Grover’s algorithm. To perform KPA in oracle, a quantum circuit for the target cipher is required, and our SPEEDY quantum circuit performs encryption within oracle. For the SPEEDY quantum circuit, it performs encryption using a superposition key and finds the key value when the encryption result is the same as the known ciphertext. When these conditions are satisfied, the key is correct. In the SPEEDY block cipher, a known plaintext of length $6l$ and a 192-bit superposition key is input to perform the encryption function $Enc$. After storing the encryption result for the SPEEDY quantum circuit in the plaintext qubit, it is compared with the known ciphertext to find the correct key. Thus, this increases the observation probability of the correct key through the diffusion operation. Since the Grover’s algorithm repeats this operation, the encrypted plaintext state is returned to the previous state through the decryption (i.e., inverse) function $En{c}^{†}$.

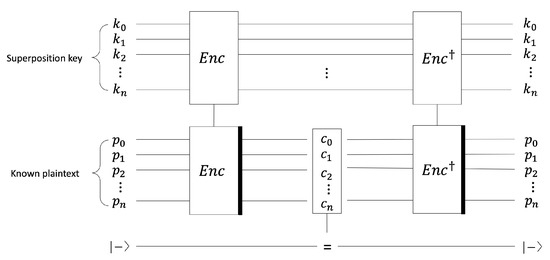
Figure 3. Oracle in Grover’s algorithm.

2.2. SPEEDY: Family of Block Ciphers

The SPEEDY block cipher is a family of ultra-low-latency block ciphers proposed at the CHES’21 [21]. It can use different block sizes and key lengths, and the number of rounds determines the level of security. SPEEDY is also an ultra-low-latency block cipher suite dedicated to the design of integrated circuits based on standard cells developed for very high execution speeds in CMOS hardware. SPEEDY aims to be a secure architecture for CPUs that require very-low-latency encryption, such as secure cache, dedicated hardware expansion, memory encryption, and pointer authentication. SPEEDY is noted as SPEEDY -r-6l for block size 6$\times l$ and number of rounds r. The internal state is represented as a $l\times$6 array. Since the SPEEDY block cipher targets 6-bit S-boxes and 64-bit high-end CPUs, it uses the least common multiple of 6 and 64 (i.e., SPEEDY-r-192) as a default block size and key length. Therefore, in this paper, SPEEDY is described based on the SPEEDY-r-192 representation. The operations in SPEEDY-r-192 work on a 32 × 6 array. In SPEEDY, it works with functions such as round function (R), S-box ($SB$), ShiftColumns ($SC$), MixColumns ($MC$), AddRoundKey ($A_{k_r}$), and AddRoundConstant ($A_{c_r}$). Each function of SPEEDY operates in the following order, except for the last round: $A_{k_r}$, $SB$, $SC$, $MC$$A_{c_r}$, KeySchedule. The last round is an exception and operates in the following order: $A_{k_r}$, $SB$, $SC$, $SB$, KeySchedule, $A_{k_r}$.

2.2.1. S-Box (SB)

The S-box in the SPEEDY block cipher is a 6-to-6-bit box with a 6-bit output ($y_0$ to $y_5$) for a 6-bit input ($x_0$ to $x_5$). It operates as a combination of NOT gate and NAND gate, as shown in Equation (1).

$$\begin{array}{c}{y}_0=(x_3\wedge {\overline{x}}_5)\vee (x_3\wedge x_4\wedge x_2)\vee ({\overline{x}}_3\wedge x_1\wedge x_0)\vee (x_5\wedge x_4\wedge x_1)\hfill \\ y_1=(x_5\wedge x_3\wedge {\overline{x}}_2)\vee ({\overline{x}}_5\wedge x_3\wedge {\overline{x}}_4)\vee (x_5\wedge x_2\wedge x_0)\vee ({\overline{x}}_3\wedge {\overline{x}}_0\wedge x_1)\hfill \\ y_2=({\overline{x}}_3\wedge x_0\wedge x_4)\vee (x_3\wedge x_0\wedge x_1)\vee ({\overline{x}}_3\wedge {\overline{x}}_4\wedge x_2)\vee ({\overline{x}}_0\wedge {\overline{x}}_2\wedge {\overline{x}}_5)\hfill \\ y_3=({\overline{x}}_0\wedge x_2\wedge {\overline{x}}_3)\vee (x_0\wedge x_2\wedge x_4)\vee (x_0\wedge {\overline{x}}_2\wedge x_5)\vee ({\overline{x}}_0\wedge x_3\wedge x_1)\hfill \\ y_4=(x_0\wedge {\overline{x}}_3)\vee (x_0\wedge {\overline{x}}_4\wedge {\overline{x}}_2)\vee ({\overline{x}}_0\wedge x_4\wedge x_5)\vee ({\overline{x}}_4\wedge {\overline{x}}_2\wedge x_1)\hfill \\ y_5=(x_2\wedge x_5)\vee ({\overline{x}}_2\wedge {\overline{x}}_1\wedge x_4)\vee (x_2\wedge x_1\wedge x_0)\vee ({\overline{x}}_1\wedge x_0\wedge x_3)\hfill \end{array}$$

(1)

2.2.2. ShiftColums ($SC$)

In ShiftColumns(SC), the j-th column of the state is rotated upside by j bits. The process is shown in Equation (2).

$$\begin{array}{c}{y}_{[i,j]}=x_{[i+j,j]}(0\le i<l,0\le j<6)\hfill \end{array}$$

(2)

2.2.3. MixColumns ($MC$)

MixColumns performs a CNOT operation with a shift in a column. The shift follows the order of the given constant $\alpha$ = $[{\alpha }_0$, ${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$, ${\alpha }_4$, ${\alpha }_5]$. In Equation (3) of MixColumn, i and j are rows and columns.

$$\begin{array}{c}{y}_{i,j}=x_{[i,j]}\oplus x_{[i+{\alpha }_1,j]}\oplus x_{[i+{\alpha }_2,j]}\oplus x_{[i+{\alpha }_3,j]}\oplus x_{[i+{\alpha }_4,j]}\oplus x_{[i+{\alpha }_5,j]}\oplus x_{[i+{\alpha }_6,j]}{}_{0\le i<l,0\le j<6}\hfill \end{array}$$

(3)

2.2.4. AddRoundKey ($A_{k_r}$)

The length of the key $k_r$ is equal to the length of $6·l$, and $k_r$ performs an XOR operation with x on the same bit position. The AddRoundKey ($A_{k_r}$) operation is as follows:

$$\begin{array}{c}{y}_{i,j}=x_{[i,j]}\oplus k_{r[i,j]},\forall i,j\hfill \end{array}$$

(4)

2.2.5. AddRoundConstant ($A_{c_r}$)

The constant $c_r$ of $6l$ bits operates XOR with x on the same bit position. The round constants are chosen as the binary number of $\pi -3=0.1415\dots$. The AddRoundConstant ($A_{c_r}$) operation is as follows:

$$\begin{array}{c}{y}_{i,j}=x_{[i,j]}\oplus c_{r[i,j]}\forall i,j\hfill \end{array}$$

(5)

2.2.6. KeySchedule

In KeySchedule, the 0-th round key $k_0$ is initialized to a specific value. Then, r round key $k_r$ is computed as in Equation (6). The $k_r$ uses the permutation P to change the bit position.

$$\begin{array}{c}{k}_{r+1[i^{\prime },j^{\prime }]}=k_{r[i,j]}\hfill \\ \\ (i^{\prime },j^{\prime }):=P(i,j)with(6·i^{\prime }+j^{\prime })\equiv (\beta ·(6·i+j)+\gamma )mod6\hfill \end{array}$$

(6)

2.2.7. Round Function

The SPEEDY block cipher repeats the round to proceed with encryption. In r-round encryption, operations are performed in the same way from 0 to $r-1$. In the last round, MixColumn ($MC$) and ShiftColumn ($SC$) are performed once each. The operation of the round function R follows Equation (7):

$$R_n=\left\{\begin{array}{c}{A}_{c_n}\circ MC\circ SC\circ SB\circ A_{k_n}(0<n<r-2)\hfill \\ A_{k_{n+1}}\circ SB\circ SC\circ SB\circ A_{k_n}(n=r-1)\hfill \end{array}\right.$$

(7)

3. Quantum Circuit for SPEEDY

In this section, we describe our proposed SPEEDY quantum circuit. The quantum circuit is designed based on SPEEDY-7-192. It is used to estimate the resources required for Grover’s algorithm. The overall quantum circuit operation sequence is shown in Figure 4. As shown in Figure 5, a $32\times 6$ array (i.e., $x_{\left[i\right]\left[j\right]},0\le i<6,0\le j<32$) in a classical computer is implemented by a $1\times 192$ array (i.e., $x_{\left[i\right]},0\le i<192$) in a quantum computer. We note the quantum circuits for the main algorithms of SPEEDY: S-box ($SB$), ShiftColumns ($SC$), MixColumns ($MC$), AddRoundKey ($A_{k_r}$), and AddRoundConstant ($A_{c_r}$). The SPEEDY quantum circuit operates for rounds 0 to $r-1$, and the operation is different only in the last round. In the quantum circuit, rounds 0 to $r-2$ operate in the following order: AddRoundKey, S-box, ShiftColumn, MixColumn, AddRoundConstant, KeySchedule. The last round $r-1$ operates in the order of AddRoundKey, S-box, ShiftColumn, S-box, KeySchedule, AddRoundKey.

Figure 4. Operation sequence for SPEEDY quantum circuit.

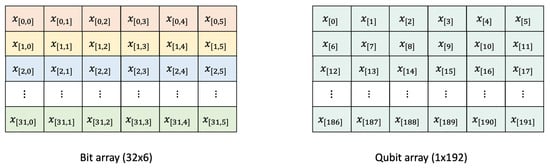
Figure 5. Bit array on classical computer and qubit array on quantum computer.

The SPEEDY quantum circuit uses the quantum gates described in Section 2.2.1 and additionally uses a multi-controlled X gate. The multi-controlled X gates used in the SPEEDY quantum circuit are represented as follows:

• CCCX($x_0$, $x_1$, $x_2$, $y_0$)=($x_0$, $x_1$, $x_2$, ($x_0·x_1·x_2)\oplus y_0$) : $x_0$, $x_1$, and $x_2$ are the control qubits and $y_0$ is a target qubit. When all control qubits are 1, the X gate is used to $y_0$.
• CCCCX($x_0$, $x_1$, $x_2$, $x_3$, $y_0$)=($x_0$, $x_1$, $x_2$, $x_3$, ($x_0·x_1·x_2·x_3)\oplus y_0$) : $x_0$, $x_1$, $x_2$, and $x_3$ are the control qubits and $y_0$ is a target qubit. When all control qubits are 1, the X gate is used to $y_0$.
• CCCCCX($x_0$, $x_1$, $x_2$, $x_3$, $x_4$, $y_0$)=($x_0$, $x_1$, $x_2$, $x_3$, ($x_0·x_1·x_2·x_3·x_4)\oplus y_0$) : $x_0$, $x_1$, $x_2$, $x_3$, and $x_4$ are the control qubits and $y_0$ is a target qubit. When all control qubits are 1, the NOT gate is used to $y_0$.

3.1. S-Box (SB)

The SPEEDY S-box uses NAND and OAI gates best suited for ultra-low latency. Therefore, the operation of the S-box follows Equation (1), expressed in disjunctive normal form (DNF). However, DNF is inefficient in terms of resources in the quantum circuit. In quantum circuits, NAND and OAI operations must allocate as many qubits as the number of operations to store intermediate values. To solve this problem, we reduced the quantum resources by using Algebraic Normal Form (ANF), which is performed as XOR gates. ANF is expressed using a combination of XOR and AND. The equation of the S-box expressed as ANF can be found in detail in [21]. Algorithm 1 shows our S-box quantum circuit implemented using CNOT and multi-controlled X gates. Furthermore, we have schematically shown the operation of Algorithm 1 as a quantum circuit in Figure 6. Here, we reduce the quantum resource by omitting the extra qubits for intermediate values. Since the SPEEDY S-box uses a lot of multi-controlled X gates, the gate cost is the highest part of the overall operation. In the S-box, the results of inputs $x_0$ to $x_5$ are output in ancilla $y_0$ to $y_5$. At the input ancilla, qubit y should initially be set to zero, and at the end of the circuit, it stores the 6-bit result of the S-box. Input x is the result of ShiftColumn and is the target of the S-box operation. That is, the S-box execution result of x is stored in y.

Algorithm 1 Quantum circuit of S-box (SB)
Input:  $x_0,x_1,x_2,x_3,x_4,x_5$ Output:  $y_0,y_1,y_2,y_3,y_4,y_5$
1: $y_0\leftarrow$ CNOT($x_3$, $y_0$) 2:          Toffoli($x_5$, $x_3$, $y_0$) 3:          CCCCX($x_5$, $x_4$, $x_3$, $x_2$, $y_0$) 4:          CCCX($x_5$, $x_4$, $x_1$, $y_0$) 5:          CCCCCX($x_5$, $x_4$, $x_3$, $x_2$, $x_1$, $y_0$) 6:          Toffoli($x_1$, $x_0$, $y_0$) 7:          CCCCX($x_5$, $x_4$, $x_1$, $x_0$, $y_0$) 8:          CCCX($x_3$, $x_1$, $x_0$, $y_0$) 9:          CCCCCX($x_5$, $x_4$, $x_3$, $x_1$, $x_0$, $y_0$) 10: $y_1\leftarrow$ CNOT($x_3$, $y_1$) 11:          Toffoli($x_4$, $x_3$, $y_1$) 12:          CCCX($x_5$, $x_4$, $x_3$, $y_1$) 13:          CCCX($x_5$, $x_3$, $x_2$, $y_1$) 14:          CNOT($x_1$, $y_1$) 15:          Toffoli($x_3$, $x_1$, $y_1$) 16:          CCCX($x_5$, $x_2$, $x_0$, $y_1$) 17:          Toffoli($x_1$, $x_0$, $y_1$) 18:          CCCX($x_3$, $x_1$, $x_0$, $y_1$) 19: $y_2\leftarrow$ NOT($y_2$) 20:          CNOT($x_5$, $y_2$) 21:          Toffoli($x_5$, $x_2$, $y_2$) 22:          Toffoli($x_4$, $x_2$, $y_2$) 23:          Toffoli($x_3$, $x_2$, $y_2$) 24:          CCCX($x_4$, $x_3$, $x_2$, $y_2$) 25:          CNOT($x_0$, $y_2$) 26:          Toffoli($x_5$, $x_0$, $y_2$) 27:          Toffoli($x_4$, $x_0$, $y_2$) 28:          CCCX($x_4$, $x_3$, $x_0$, $y_2$) 29:          Toffoli($x_2$, $x_0$, $y_2$) 30:          CCCX($x_5$, $x_2$, $x_0$, $y_2$) 31:          CCCX($x_3$, $x_1$, $x_0$, $y_2$) 32: $y_3\leftarrow$ CNOT($x_2$,$y_3$) 33:          Toffoli($x_3$, $x_2$, $y_3$) 34:          Toffoli($x_3$, $x_1$, $y_3$)	35:          Toffoli($x_5$, $x_0$, $y_3$) 36:          Toffoli($x_2$, $x_0$, $y_3$) 37:          CCCX($x_5$, $x_2$, $x_0$, $y_3$) 38:          CCCX($x_4$, $x_2$, $x_0$, $y_3$) 39:          CCCX($x_3$, $x_2$, $x_0$, $y_3$) 40:          CCCX($x_3$, $x_1$, $x_0$, $y_3$) 41: $y_4\leftarrow$ Toffoli($x_5$, $x_4$, $y_4$) 42:          CNOT($x_1$, $y_4$) 43:          Toffoli($x_4$, $x_1$, $y_4$) 44:          Toffoli($x_2$, $x_1$, $y_4$) 45:          CCCX($x_4$, $x_2$, $x_1$, $y_4$) 46:          CNOT($x_0$, $y_4$) 47:          CCCX($x_5$, $x_4$, $x_0$, $y_4$) 48:          CCCX($x_4$, $x_3$, $x_0$, $y_4$) 49:          CCCX($x_3$, $x_2$, $x_0$, $y_4$) 50:          CCCCX($x_4$, $x_3$, $x_2$, $x_0$, $y_4$) 51:          Toffoli($x_1$, $x_0$, $y_4$) 52:          CCCX($x_4$, $x_1$, $x_0$, $y_4$) 53:          CCCX($x_2$, $x_1$, $x_0$, $y_4$) 54:          CCCCX($x_4$, $x_2$, $x_1$, $x_0$, $y_4$) 55: $y_5\leftarrow$ CNOT($x_4$, $y_5$) 56:          Toffoli($x_5$, $x_2$, $y_5$) 57:          Toffoli($x_4$, $x_2$, $y_5$) 58:          Toffoli($x_4$, $x_1$, $y_5$) 59:          CCCX($x_4$, $x_2$, $x_1$, $y_5$) 60:          Toffoli($x_3$, $x_0$, $y_5$) 61:          CCCX($x_4$, $x_3$, $x_0$, $y_5$) 62:          CCCCX($x_5$, $x_3$, $x_2$, $x_0$, $y_5$) 63:          CCCCX($x_4$, $x_3$, $x_2$, $x_0$, $y_5$) 64:          CCCX($x_3$, $x_1$, $x_0$, $y_5$) 65:          CCCCX($x_4$, $x_3$, $x_1$, $x_0$, $y_5$) 66:          CCCX($x_2$, $x_1$, $x_0$, $y_5$) 67:          CCCCX($x_5$, $x_2$, $x_1$, $x_0$, $y_5$) 68:          CCCCCX($x_5$, $x_3$, $x_2$, $x_1$, $x_0$, $y_5$) 69:          CCCCCX($x_4$, $x_3$, $x_2$, $x_1$, $x_0$, $y_5$) 70: return$y_0,\cdots y_5$

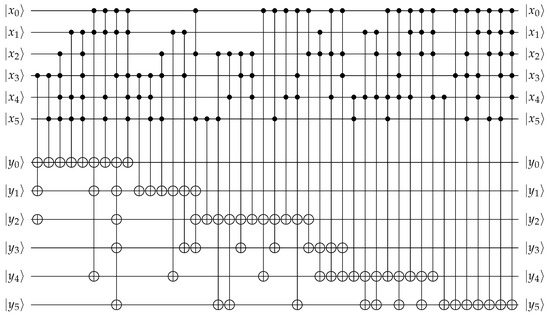
Figure 6. Quantum circuit for S-box.

3.2. ShiftColumns (SC)

ShiftColumns in the quantum circuit perform column shifts. It is implemented assuming that 6 qubits are arranged in 32 rows for a 1 × 192 qubit array. Assuming that the qubits are arranged as in Figure 7, each column of qubits shifts in the order $\delta =0,1,2,3,4,5$. That is, a shift of 1 in a column is a shift of index 6 in a qubit array. Here, we used logical swap to rotate the columns. In quantum circuits, swap gate only changes the position of the qubit. As a result, we do not use additional quantum resources in ShiftColumn ($SC$). Algorithm 2 shows the quantum circuit operation of ShiftColumn. It rearranges the input into $new\_array$ according to the operation. Then, it changes the index of the input as arranged in $new\_array$.

Algorithm 2 Quantum circuit of ShiftColumns ($SC$)

Input:  192-qubit array $=[x_0,x_1,\cdots ,x_{192}]$ Output:  192-qubit array $=[x_0,x_7,x_{14},\cdots ,x_{29}]$  1: $new\_array=$ [ ]  2: for$i=0$to 31 do  3:    for $j=0$ to 5 do  4:         $new\_array$ [$6·i+j$] ←$x_{(6·(i+j)+j)}$  5:      end for  6:    end for  7:    return $new\_array$

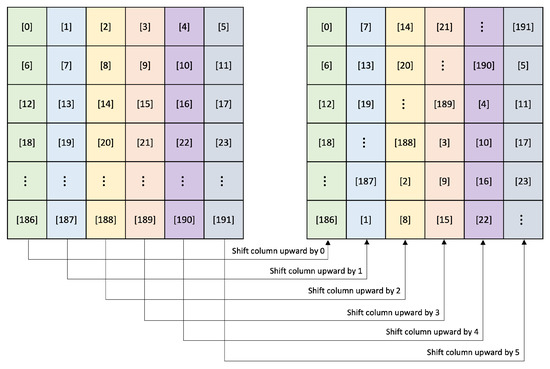
Figure 7. ShiftColumns (SC) operation process.

3.3. MixColumns (MC)

MixColumns repeats the XOR operation by shifting the index of the qubits. The MixColumn quantum circuit works with Algorithm 3. In Algorithm 3, the result is stored in the input qubit $x_k$, and $tem{p}_k$ is used as the temporary storage qubit. First, we use the CNOT gate to store the original x in $tem{p}_k$. Then, the CNOT gate for temp and x is performed during the shift in the index of temp. The standard of shift follows the order of $\alpha$ ($\alpha$ = 1, 5, 9, 15, 21, 26). The operation is stored in x, so no additional qubits are needed to store the result.

Algorithm 3 Quantum circuit of MixColumns ($MC$)

Input:  $x_k,tem{p}_k(k=0,\dots ,191),\alpha =[1,5,9,15,21,26]$ Output:  $x_k(k=0,\dots ,191)$  1: for$i=0$to 191 do  2:    $tem{p}_i\leftarrow$ CNOT($x_i$, $tem{p}_i$) // copy target qubit(x) to temporary qubit($temp$).  3:  end for  4:  for $i=0$ to 31 do  5:      for $j=0$ to 5 do  6:         $x_{6·i+j}\leftarrow$ CNOT($tem{p}_{6·(i+\alpha [0\left]\right)+j}$,$x_{6·i+j}$) // $x_{6·i+j}$ = $x_{6·i+j}\oplus x_{6·(i+\alpha [0\left]\right)+j}$  7:         $x_{6·i+j}$← CNOT($tem{p}_{6·(i+\alpha [1\left]\right)+j}$,$x_{6·i+j}$) // $x_{6·i+j}$ = $line6\oplus x_{6·(i+\alpha [1\left]\right)+j}$  8:         $x_{6·i+j}$← CNOT($tem{p}_{6·(i+\alpha [2\left]\right)+j}$,$x_{6·i+j}$) // $x_{6·i+j}$ = $line7\oplus x_{6·(i+\alpha [2\left]\right)+j}$  9:         $x_{6·i+j}$← CNOT($tem{p}_{6·(i+\alpha [3\left]\right)+j}$,$x_{6·i+j}$) // $x_{6·i+j}$ = $line8\oplus x_{6·(i+\alpha [3\left]\right)+j}$  10:       $x_{6·i+j}$← CNOT($tem{p}_{6·(i+\alpha [4\left]\right)+j}$,$x_{6·i+j}$) // $x_{6·i+j}$ = $line9\oplus x_{6·(i+\alpha [4\left]\right)+j}$  11:       $x_{6·i+j}$← CNOT($tem{p}_{6·(i+\alpha [5\left]\right)+j}$,$x_{6·i+j}$) // $x_{6·i+j}$ = $line10\oplus x_{6·(i+\alpha [5\left]\right)+j}$  12:     end for  13:  end for  14:  return $x_0,\cdots ,x_{191}$ =0

3.4. AddRoundKey ($A_{k_r}$)

AddRoundKey($A_{k_r}$) in the quantum circuit is assigned a qubit k (i.e., key) of length equal to the input length. In qubit k, the key value is stored in advance. The input qubit x operates the CNOT gate with k of the same index. We performed the XOR operation according to Equation (4). Since the constant is already known, there is no need to allocate qubits for it.

3.5. AddRoundConstant ($A_{c_r}$)

In AddRoundConstant ($A_{c_r}$), XOR uses the input x and a constant value. Since the constant is already known, there is no need to allocate qubits for it. Therefore, the X gate shifts to x at the position where the constant value is one, without using the CNOT gate. An X gate operating with a single qubit has a lower gate cost than a CNOT gate operating with two qubits. Therefore, our choice is efficient in terms of quantum resources, saving the gate cost. The X gate is used only where the value in the constant is one, so the X gate is used as much as the Hamming weight. Algorithm 4 shows the operation for AddRoundConstant ($A_{c_r}$).

Algorithm 4 Quantum circuit of AddRoundConstant ($A_{c_r}$)

Input:  $constant$, $x_0,\cdots ,x_{191}$ Output:  $x_0,\cdots ,x_{191}$  1: for$i=0$to 191 do  2:    if( $constant$ & 1 = 1 )  3:          $x_i$← X($x_i$)      $constant$ = $constant$≫ 1  4:  end for  5:  return $x_0,\cdots ,x_{191}$

4. Evaluation

In this section, we estimate the resources of Grover’s algorithm for a SPEEDY block cipher implemented as a quantum circuit. Resources estimated by the quantum simulator are used to evaluate the security strength in the quantum computer. The cost is calculated as (total gates × total depth) and the total gate is the sum of T and $Clifford$ gate. We decompose the non-Clifford gates into $T+Clifford$ gates to obtain the total gate [26]. Finally, we show that SPEEDY-7-192, which achieved a security strength of 192 length in the classic computer, does not achieve a security strength in the quantum computer. The block cipher security strength is evaluated based on the estimate of the post-quantum security strength presented by NIST [3].

4.1. Resource Estimation

Table 1 shows the quantum circuit resource estimation results for SPEEDY encryption. We estimated resources for rounds 6, 14, and 28 other than round 7 to evaluate the strength of security for each round. Based on SPEEDY-7-192, 4224 qubits, 1792 CCCCCX gates, 3584 CCCCX gates, 10752 CCCX gates, 10,304 Toffoli gates, 13,632 CNOT gates, and 2118 X gates were used. The estimated quantum resource is proportional to the number of rounds.

Table 1. Quantum resources for SPEEDY.

Cipher	r	Qubits	Gates						Depth
			CCCCCX	CCCCX	CCCX	Toffoli	CNOT	X
SPEEDY-r-192	6	3648	1536	3072	9216	8832	11,520	855	859
	7	4224	1792	3584	10,752	10,304	13,632	1018	1002
	14	8256	3584	7168	21,504	20,608	28,416	2118	2011
	28	16,320	7168	14,336	43,008	41,216	57,984	4346	4029

4.2. Security Strength Analysis for SPEEDY

The post-quantum security strength for SPEEDY is evaluated based on the security strength category presented by NIST [3]. We calculate the cost with the same calculation as Grassl et al. [4]. That is, the cost is calculated to (total gate × total depth). In NIST, the cost of AES-128, 196, and 256, which are security strength standards, was estimated as AES-128:$2^{170}$, AES-196:$2^{233}$, AES-256:$2^{298}$. The following are security strength categories presented by NIST based on AES-128, 196, 256:

• Level 1: Block ciphers using a 128-bit key (e.g., AES 128) require computational resources that are greater than or comparable to those required for key search.
• Level 3: Block ciphers using a 192-bit key (e.g., AES 192) require computational resources that are greater than or comparable to those required for key search.
• Level 5: Block ciphers using a 256-bit key (e.g., AES 256) require computational resources that are greater than or comparable to those required for key search.

Grover’s algorithm can reduce the computational complexity from $O\left(N\right)$ to $O\left(\sqrt{N}\right)$ for symmetric key cryptography with an n-bit key (i.e., $N=2^n$). This search algorithm increases the probability of finding the right key by repeating oracle and diffusion, and the quantum circuit is used in the oracle operation for encryption and decryption. Since the quantum circuit is a reversible circuit, decryption can be performed by reverse operation (i.e., encryption resource = decryption resource). Therefore, the total quantum resource used in the Grover’s algorithm is calculated as ⌈key size/block size⌉ $\times (Encryption+Decryption) \times$ number of iterations (i.e., $R \times 2 \times$ Table 1$\times \lfloor \frac{\pi }{4}{2}^{\frac{n}{2}}\rfloor$).

The Grover’s algorithm resource for SPEEDY is shown in Table 2. We compute the Grover’s key search cost by decomposing the non-$Clifford$ gate into the $T+Clifford$ gate from the estimated resource. Since the X gate and CNOT gate are the $Clifford$ gates, only the Toffoli gate and multi-controlled X gate are decomposed into $T+Clifford$ gates. One Tofffoli gate is decomposed into 7 T gates and 8 $Clifford$ gates, and multi-controlled X gates are decomposed into $(32\times C-$84) T gates (C: number of control qubits).

Table 2. Cost estimation for Grover’s algorithm.

Cipher	r	Gates		Total Gates	Total Depth	Cost	Security
		$\mathit{T}$	$\mathit{Clifford}$
SPEEDY-r-192	6	$1.27\times 2^{115}$	$1.99\times 2^{112}$	$1.51\times 2^{115}$	$1.31\times 2^{106}$	$1.97\times 2^{221}$	Level 1
	7	$1.48\times 2^{115}$	$1.16\times 2^{113}$	$1.77\times 2^{115}$	$1.53\times 2^{106}$	$1.38\times 2^{222}$	Level 1
	14	$1.48\times 2^{116}$	$1.16\times 2^{114}$	$1.77\times 2^{116}$	$1.54\times 2^{107}$	$1.36\times 2^{224}$	Level 1
	28	$1.48\times 2^{117}$	$1.17\times 2^{115}$	$1.77\times 2^{117}$	$1.54\times 2^{108}$	$1.36\times 2^{226}$	Level 1
LEA-128/128 [27]		$1.13\times 2^{81}$	$1.92\times 2^{81}$	$1.195\times 2^{82}$	$1.247\times 2^{77}$	$1.491\times 2^{159}$	Not achieved
LEA-128/192 [27]	-	$1.67\times 2^{115}$	$1.42\times 2^{115}$	$1.775\times 2^{115}$	$1.455\times 2^{109}$	$1.292\times 2^{225}$	Level 1
LEA-128/256 [27]		$1.91\times 2^{147}$	$1.63\times 2^{148}$	$1.014\times 2^{148}$	$1.645\times 2^{141}$	$1.668\times 2^{289}$	Level 3
CHAM-64/128 [27]		$1.05\times 2^{81}$	$1.04\times 2^{82}$	$1.23\times 2^{81}$	$1.003\times 2^{76}$	$1.234\times 2^{157}$	Not achieved
CHAM-128/128 [27]	-	$1.10\times 2^{80}$	$1.11\times 2^{81}$	$1.304\times 2^{81}$	$1.018\times 2^{77}$	$1.328\times 2^{158}$	Not achieved
CHAM-128/256 [27]		$1.31\times 2^{146}$	$1.34\times 2^{146}$	$1.566\times 2^{146}$	$1.264\times 2^{146}$	$1.98\times 2^{287}$	Level 3
HIGHT-64/128 [27]	-	$1.05\times 2^{81}$	$1.04\times 2^{82}$	$1.384\times 2^{82}$	$1.901\times 2^{75}$	$1.316\times 2^{158}$	Not achieved
PIPIO-64/128 [8]	-	$1.68\times 2^{78}$	$1.31\times 2^{79}$	$1.07\times 2^{80}$	$1.52\times 2^{73}$	$1.62\times 2^{153}$	Not achieved
PIPIO-64/256 [8]		$1.09\times 2^{144}$	$1.72\times 2^{144}$	$1.40\times 2^{145}$	$1.99\times 2^{138}$	$1.39\times 2^{284}$	Level 3

In a classic computer, SPEEDY-r-192 provides 128-bit security when $r=6$ and 192-bit security when $r=7$. However, both SPEEDY-6-192 and SPEEDY-7-192 provided 128-bit security in a quantum computer. In response, we performed encryption with more rounds r to check the strength of security in quantum computers. However, even if the number of rounds of r was increased as in Table 2, security was maintained at level 1. Contrary to expectations, increasing the number of rounds did not provide higher security. In other words, it can be confirmed that it is difficult to increase the security strength in quantum computers by increasing the number of rounds of encryption. It is also very inefficient because the number of rounds r must increase exponentially to enhance security in quantum computers. Simply put, the classic method of increasing security by increasing the number of rounds does not apply to quantum computers.

On the other hand, looking at the LEA, CHAM, and PIPO ciphers evaluated by [8,27] in Table 2, security strength was not achieved with a 64-bit key, but was achieved with a 256-bit key length. HIGHT ciphers that only work with 64-bit keys do not achieve security strength. For the LEA cipher, LEA-128/128 (using 128-bit key) did not achieve the security strength, but LEA-128/192 (using 192-bit key) and LEA-128/256 (using 256-bit key) achieved level 1 and level 3, respectively. In the case of the CHAM cipher, CHAM-64/128 and CHAM-128/128 (using 128-bit key) did not achieve the security strength, but CHAM-64/256 (using 256-bit key) achieved level 3. In the case of the PIPO cipher, PIPO-64/128 (using 128-bit key) did not achieve the security strength, but PIPO-64/256 (using 256-bit key) achieved level 3.

From the above results, it was confirmed that it is difficult to increase the quantum security strength by increasing the number of rounds and the block length, but it can be increased through the key length. Therefore, in order to strengthen the security in quantum computers, it is necessary to consider measures to increase the number of iterations exponentially by increasing the key length.

5. Conclusions

In this paper, a quantum circuit for the SPEEDY block cipher is presented. We estimated the resources required to perform a key search attack based on SPEEDY-r-192 and obtained the cost required to evaluate the security strength. As a result, SPEEDY-7-192 provided 192-bit security in classic computers, but showed a security strength of level 1 (i.e., AES-128 level) in quantum computers. In other words, encryption that is secure in classic computers cannot be considered secure in quantum computers. We increased the number of rounds as a way to strengthen the security in the quantum computer, but it did not increase the security strength significantly. Based on the results in this paper, we propose a method to increase the key length to ensure the security of the target cipher (SPEEDY in this paper) in a quantum computer.