Estimation of Tidal Volume during Exercise Stress Test from Wearable-Device Measures of Heart Rate and Breathing Rate

Abstract

Tidal volume (TV), defined as the amount of air that moves in or out of the lungs with each respiratory cycle, is important in evaluating the respiratory function. Although TV can be reliably measured in laboratory settings, this information is hardly obtainable under everyday living conditions. Under such conditions, wearable devices could provide valuable support to monitor vital signs, such as heart rate (HR) and breathing rate (BR). The aim of this study was to develop a model to estimate TV from wearable-device measures of HR and BR during exercise. HR and BR were acquired through the Zephyr Bioharness 3.0 wearable device in nine subjects performing incremental cycling tests. For each subject, TV during exercise was obtained with a metabolic cart (Cosmed). A stepwise regression algorithm was used to create the model using as possible predictors HR, BR, age, and body mass index; the model was then validated using a leave-one-subject-out cross-validation procedure. The performance of the model was evaluated using the explained variance (R²), obtaining values ranging from 0.65 to 0.72. The proposed model is a valid method for TV estimation with wearable devices and can be considered not subject-specific and not instrumentation-specific.

1. Introduction

Tidal volume is defined as the amount of air that moves in or out of the lungs with each respiratory cycle [1]. Changes in tidal volume may reveal pathologies such as restrictive or obstructive lung diseases, acute respiratory distress syndrome, and diseases affecting the respiratory muscles [1]. Of note, the information provided by tidal volume may not be replaced by breathing rate [2,3]. Indeed, tidal volume and breathing rate are differentially regulated, with the regulation of tidal volume being mainly mediated by metabolic inputs [2,3]. The existence of an unbalanced interdependence between tidal volume and breathing rate has also been suggested, in which tidal volume continuously adjusts on the basis of breathing rate, but not vice versa [4]. For these reasons, tidal volume represents an important variable for the evaluation of the respiratory function, and its continuous monitoring may have clinical implications [5,6].

Traditional methodologies for the measure of tidal volume rely on spirometry and optoelectronic plethysmography, both requiring a laboratory setting. Spirometry consists in the measurement of the air flow produced during the respiration, when the subject is asked to breath into a mask; thus, it is objective, noninvasive, sensitive to early change, and reproducible [7,8]. On the contrary, optoelectronic plethysmography consists of a motion analysis system which measures the changes in the chest wall during breathing by modelling the thoraco-abdominal surface [9,10].

However, as recently reviewed [11], in the last decade attempts have been made to estimate tidal volume also outside the laboratory settings during either static (e.g., sitting, standing, or lying) or dynamic tasks (e.g., during exercise), with the latter generally providing higher estimation errors. Different wearable technologies have been exploited, including various stretch sensors (optical, resistive, inductive, and pressure/tactile) [12,13,14,15] or acoustic sensors that use the movements of the chest wall or the sound generated by air flow during breathing [16], respectively; in other cases, the estimation of tidal volume was indirectly achieved from the electrocardiogram (ECG) by extracting from it features such as the breathing rate, ECG-derived respiration, and the heart-rate variability [17,18]. As for these latter methodologies, multiple regression models were created using the features extracted from the ECG acquired using a Holter monitor [18] or an armband device [17] as predictors. In the first case, the estimation was performed during an exercise stress test, whereas in the second during a lab-controlled experiment. To the best of our knowledge, no study has provided an estimation of tidal volume from features such as heart rate and breathing rate directly acquired from a commercially available wearable device during an exercise stress test. This study aims to fill this gap by proposing a multiple regression model based on these features.

2. Materials and Methods

2.1. Subjects

The data belong to nine male, healthy, adult, and physically active volunteers recruited at the University of Rome “Foro Italico”. The characteristics of each volunteer are reported in Table 1. All volunteers provided written informed consent for the study. The investigation was conducted in accordance with the Declaration of Helsinki, and ethical approval was provided by the respective local ethical committee.

Table 1. Characteristics of the volunteers.

	Age (years)	Height (cm)	Weight (kg)	BMI (kg/m2)	BSA (m2)
1	42	170	69.9	24.2	1.81
2	51	180	81.0	25.0	2.01
3	52	184	75.0	22.0	1.97
4	45	176	72.8	23.5	1.86
5	53	180	73.5	22.7	1.93
6	46	171	65.2	22.3	1.76
7	27	175	64.2	21.0	1.78
8	26	169	68.8	24.1	1.79
9	40	179	77.2	24.1	1.96
All	42 ± 10	176 ± 5	78.0 ± 4.2	22.7 ± 2.1	1.87 ± 0.09

BMI: body mass index (kg/m²); BSA: body surface area (m²). Data of all subjects are reported as mean ± standard deviation.

2.2. Experimental Setting

Each subject was asked to exercise on a cycle ergometer, starting from an initial power output of 20 W, followed by a continuous ramped increase in power output of 30 W·min⁻¹ up to 380 W. Each subject was equipped with a wearable device (BioHarness 3.0 by Zephyr, Annapolis, MD, USA) [19,20] used to record the heart rate (HR_WD) and the breathing rate (BR_WD) with sampling frequency of 1 Hz. Moreover, each subject was also equipped with a metabolic cart (Quark CPET by Cosmed, Rome, Italy), a type of spirometer which is able to measure the oxygen consumption and carbon dioxide production.

This system was used to record breath-by-breath tidal volume (TV), heart rate (HR_REF), and breathing rate (BR_REF), which served as reference instrumentation.

2.3. Pre-Processing

Since breath-by-breath and wearable-device data had a different starting time of acquisition, wearable-device data were aligned with breath-by-breath data in order to have simultaneous series for HR_WD, BR_WD, TV, HR_REF, and BR_REF. Then, the data were filtered for errant breaths (i.e., values resulting from sighs, swallows, coughs, etc.). Specifically, a 20-sample moving window was considered and characterized using percentile computation. Samples with values greater than the 95th percentile or lower than the 25th percentile were considered outliers, and thus discarded.

2.4. Model Formulation

The model for the prediction of the tidal volume from wearable-device data ($\widehat{{\mathrm{TV}}_{\mathrm{WD}}}$) was formulated using a stepwise regression approach, which allows for the creation of a data-driven model by automatically selecting the set of most significant predictors. Wearable-device data (HR_WD and BR_WD) were used as predictors, together with age and BMI. A multiple linear regression model with interactions was hypothesized:

$$\widehat{{\mathrm{TV}}_{\mathrm{WD}}}=\alpha +{\sum }_{\mathrm{i}=1}^4{\mathrm{\beta }}_{\mathrm{i}}·{\mathrm{F}}_{\mathrm{i}}+{\sum }_{\mathrm{i}=1}^4{\sum }_{\begin{array}{c}\mathrm{j}=1\\ \mathrm{i}\ne \mathrm{j}\end{array}}^4{\mathrm{\gamma }}_{\mathrm{i},\mathrm{j}}·{\mathrm{F}}_{\mathrm{i}}·{\mathrm{F}}_{\mathrm{j}}$$

(1)

where $\mathrm{\alpha },\mathrm{\beta },\mathrm{and}\mathrm{\gamma }$ are the model parameters and $\mathrm{F}$ is the four predictors (age, BMI, HR_WD, or BR_WD).

2.5. Model Validation

Using the formulated model, the prediction of tidal volume was also obtained using data from the reference instrumentation ($\widehat{{\mathrm{TV}}_{\mathrm{REF}}}$). Moreover, the formulated model was validated by performing a leave-one-subject-out cross-validation procedure using either wearable-device data (HR_WD and BR_WD) or breath-by-breath data (HR_REF and BR_REF), in addition to age and BMI. Specifically, the model was trained on 8 subjects (one less than the total number of subjects) and tested on the remaining one; thus, the procedure was repeated nine times.

2.6. Statistics

Distributions of all variables were reported in terms of mean ± standard deviation. HR_WD and BR_WD were compared with HR_REF and BR_REF, respectively, using paired T-Student tests. Goodness of fit was assessed by computing the explained variance (R²). Comparisons between both $\widehat{{\mathrm{TV}}_{\mathrm{WD}}}$ and $\widehat{{\mathrm{TV}}_{\mathrm{REF}}}$ predictions and breath-by-breath TV were performed by test of equivalence, Bland–Altman plots, Persons’ correlation analysis, and linear regression analysis. The statistical significance level was set at 0.05. All data processing, modeling, and statistics acquisition were performed using the MATLAB^® software (Mathworks, version R2019a, Natick, MA, USA).

3. Results

The number of original samples and the number of samples considered reliable after pre-processing are reported in Table 2. After pre-processing, 2409 out of 2421 samples (99.5%) were considered reliable. Distributions of predictors for wearable-device data and reference instrumentation data are reported in Table 3; no statistical differences were observed between HR_WD and HR_REF (p-value > 0.05) and between BR_WD and BR_REF (p-value > 0.05). The final formulation of the model is described by the following equation:

$$\begin{gathered} \widehat{{\mathrm{TV}}_{\mathrm{WD}}}=0.30·\mathrm{Age}+0.39·\mathrm{BMI}-0.02·{\mathrm{HR}}_{\mathrm{WD}}+0.17·{\mathrm{BR}}_{\mathrm{WD}}-0.12·\mathrm{Age}·{\mathrm{HR}}_{\mathrm{WD}}-0.46·\mathrm{Age}·{\mathrm{BR}}_{\mathrm{WD}} \\ +0.20·\mathrm{BMI}·{\mathrm{HR}}_{\mathrm{WD}}-4.80·\mathrm{BMI}·{\mathrm{BR}}_{\mathrm{WD}}-0.35·{\mathrm{HR}}_{\mathrm{WD}}·{\mathrm{BR}}_{\mathrm{WD}}-11.46 \end{gathered}$$

(2)

Table 2. Number of original samples, number of samples considered reliable after pre-processing and data division for the leave-one-subject-out cross-validation procedure.

Subject	Original	Reliable	Training	Testing
1	200	199	2210	199
2	271	271	2138	271
3	239	233	2176	233
4	278	273	2136	273
5	285	285	2124	285
6	238	238	2171	238
7	288	288	2121	288
8	348	248	2061	348
9	274	274	2135	274

Table 3. Distributions of the predictors.

Subject	Age (years)	BMI (kg/m2)	Wearable Device		Reference Instrumentation
			HRWD (bpm)	BRWD (cpm)	HRREF (bpm)	BRREF (cpm)
1	42	24.2	137 ± 23	24 ± 7	133 ± 25	27 ± 9
2	51	25.0	146 ± 22	30 ± 12	142 ± 24	34 ± 17
3	52	22.0	139 ± 24	25 ± 5	141 ± 24	26 ± 6
4	45	23.5	156 ± 22	30 ± 9	157 ± 22	34 ± 15
5	53	22.7	128 ± 26	31 ± 7	129 ± 27	34 ± 12
6	46	22.3	146 ± 32	26 ± 9	147 ± 32	29 ± 12
7	27	21.0	149 ± 25	30 ± 7	150 ± 24	32 ± 10
8	27	24.1	164 ± 26	38 ± 9	160 ± 27	39 ± 14
9	40	24.1	134 ± 31	29 ± 9	130 ± 30	30 ± 9
All	41 ± 10	22.8 ± 1.3	145 ± 28	30 ± 10	144 ± 29	32 ± 13

BMI: body mass index (kg/m²); HR_WD: heart rate from the wearable device (bpm); BR_WD: breathing rate from the wearable device (cpm); HR_REF: heart rate from the reference instrumentation (bpm); BR_REF: breathing rate from the reference instrumentation (cpm). Data of all subjects are reported as mean ± standard deviation.

The values of the model parameters obtained by applying the stepwise linear regression approach are reported in Table 4; the R² value for model formulation is equal to 0.71. Bland–Altman plots and results of the linear regression analysis for the comparison between both $\widehat{{\mathrm{TV}}_{\mathrm{WD}}}$ and $\widehat{{\mathrm{TV}}_{\mathrm{REF}}}$ predictions and breath-by-breath TV are represented in Figure 1. Bland–Altman analysis confirmed very good $\widehat{{\mathrm{TV}}_{\mathrm{WD}}}$ estimations (confidence intervals: [−0.01; 0.01] L), and good $\widehat{{\mathrm{TV}}_{\mathrm{REF}}}$ estimations (confidence intervals: [0.05; 0.08] L).

Table 4. Values of the model parameters obtained by applying the stepwise linear regression approach with interactions.

$\mathbf{Constant}\left(\mathsf{\alpha }\right)$	−11.46 L (p < 10−21)
$\mathbf{Linear}\left(\mathsf{\beta }\right)$
	Age	BMI	HRWD	BRWD
	$0.30\frac{\mathrm{L}}{\mathrm{years}}$ (p < 10−73)	$0.39\frac{\mathrm{L}·{\mathrm{m}}^2}{\mathrm{kg}}$ (p < 10−16)	$-0.02\frac{\mathrm{L}}{\mathrm{bpm}}$ (p = 0.05)	$0.17\frac{\mathrm{L}}{\mathrm{cpm}}$ (p < 10−8)
$\mathbf{Interaction}\left(\mathsf{\gamma }\right)$
	Age	BMI	HRWD	BRWD
Age	-	-	$-0.12\frac{\mathrm{L}}{\mathrm{years}·\mathrm{bpm}}$ (p < 10−69)	$-0.46\frac{\mathrm{mL}}{\mathrm{years}·\mathrm{cpm}}$ (p < 10−6)
BMI	-	-	$0.20\frac{\mathrm{mL}·{\mathrm{m}}^2}{\mathrm{kg}·\mathrm{bpm}}$ (p < 10−7)	$-4.80\frac{\mathrm{mL}·{\mathrm{m}}^2}{\mathrm{kg}·\mathrm{cpm}}$ (p < 10−4)
HRWD	$-0.12\frac{\mathrm{L}}{\mathrm{years}·\mathrm{bpm}}$ (p < 10−69)	$0.20\frac{\mathrm{mL}·{\mathrm{m}}^2}{\mathrm{kg}·\mathrm{bpm}}$ (p < 10−7)	-	$-0.35\frac{\mathrm{mL}}{\mathrm{bpm}·\mathrm{cpm}}$ (p < 10−12)
BRWD	$-0.46\frac{\mathrm{mL}}{\mathrm{years}·\mathrm{cpm}}$ (p < 10−6)	$-4.80\frac{\mathrm{mL}·{\mathrm{m}}^2}{\mathrm{kg}·\mathrm{cpm}}$ (p < 10−4)	$-0.35\frac{\mathrm{mL}}{\mathrm{bpm}·\mathrm{cpm}}$ (p < 10−12)	-

HR_WD: heart rate from the wearable device (bpm); BR_WD: breathing rate from the wearable device (cpm); BMI: body mass index (kg/m²).

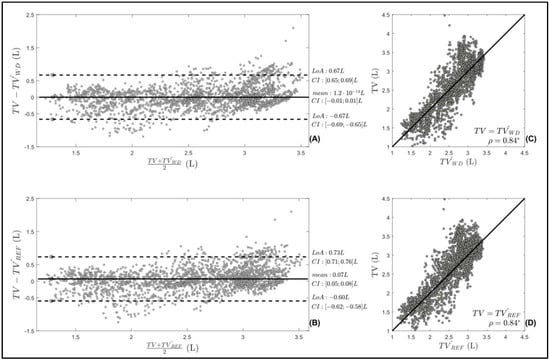
Figure 1. Bland–Altman plots for the comparison between: (A) prediction of tidal volume using wearable-device data ($\widehat{{\mathrm{TV}}_{\mathrm{WD}}}$) and breath-by-breath tidal volume (TV); (B) prediction of tidal volume using reference instrumentation ($\widehat{{\mathrm{TV}}_{\mathrm{REF}}}$) predictions and breath-by-breath TV; mean and limits of agreement (LoA) are reported, together with the related confidence interval (CI). Linear regression analysis for the comparison between: (C) prediction of tidal volume using wearable-device data ($\widehat{{\mathrm{TV}}_{\mathrm{WD}}}$) and breath-by-breath tidal volume (TV); (D) prediction of tidal volume using reference instrumentation ($\widehat{{\mathrm{TV}}_{\mathrm{REF}}}$) and breath-by-breath TV; correlation coefficient is reported (ρ), together with statistical significance (* indicates p < 0.05).

The data division for the leave-one-subject-out cross-validation procedure is reported in Table 2. The results of the leave-one-subject-out cross-validation procedure in terms of R², Pearson’s correlation coefficients, and predicted tidal volume using either wearable-device data ($\widehat{{\mathrm{TV}}_{\mathrm{WD}}}$) or reference instrumentation data ($\widehat{{\mathrm{TV}}_{\mathrm{REF}}}$) are reported in Table 5. Values of R² and correlation coefficients confirmed the goodness of fit. The results of the test of equivalence revealed a substantial equivalence between $\widehat{{\mathrm{TV}}_{\mathrm{WD}}}$ and TV and between $\widehat{{\mathrm{TV}}_{\mathrm{REF}}}$ and TV (Table 5), with an equivalence margin equal to 70% of a standard deviation.

Table 5. Distribution estimations and gold standard of the cross-validation.

		Wearable Device			Reference Instrumentation
Subject	TV (L)	$\widehat{{\mathbf{TV}}_{\mathbf{WD}}}\left(\mathbf{L}\right)$	${\mathit{R}}^2 \left(\mathbf{adi}\right)$	ρ (adi)	$\widehat{{\mathbf{TV}}_{\mathbf{REF}}}\left(\mathbf{L}\right)$	${\mathit{R}}^2 \left(\mathbf{adi}\right)$	ρ (adi)
1	2.5 ± 0.8	2.6 ± 0.4 *	0.66	0.91 §	2.6 ± 0.5 *	0.66	0.94 §
2	2.9 ± 0.7	2.4 ± 0.3 *	0.75	0.75 §	2.2 ± 0.4 *	0.78	0.83 §
3	2.7 ± 0.6	3.0 ± 0.6 *	0.65	0.97 §	3.1 ± 0.6 *	0.68	0.98 §
4	2.8 ± 0.5	3.0 ± 0.4 *	0.69	0.69 §	3.0 ± 0.4 *	0.69	0.76 §
5	2.4 ± 0.5	2.4 ± 0.5 *	0.65	0.93 §	2.2 ± 0.5 *	0.66	0.95 §
6	3.1 ± 0.6	2.7 ± 0.7 *	0.70	0.68 §	2.8 ± 0.7 *	0.70	0.73 §
7	2.5 ± 0.5	2.8 ± 0.4 *	0.66	0.93 §	2.8 ± 0.4 *	0.68	0.94 §
8	2.2 ± 0.4	3.2 ± 0.5 *	0.72	0.93 §	3.2 ± 0.6 *	0.75	0.93 §
9	2.4 ± 0.6	1.7 ± 0.8 *	0.69	0.96 §	1.8 ± 0.7 *	0.69	0.95 §

TV: breath-by-breath tidal volume (L); $\widehat{{\mathrm{TV}}_{\mathrm{WD}}}$: prediction of tidal volume using wearable-device data (L); $\widehat{{\mathrm{TV}}_{\mathrm{REF}}}$: prediction of tidal volume using reference instrumentation data (L); R²: explained variance. Data of all subjects are reported as mean ± standard deviation. * p-value < 0.05 assuming limits of equivalence equal to 70% of standard deviation. ^§ p-value < 0.05 for Pearson’s correlation analysis.

4. Discussion

This study proposed a multiple regression model for the indirect estimation of the tidal volume during an exercise stress test, using heart rate and breathing rate directly acquired from a commercially available wearable device, in addition to basic individual characteristics of the subject such as the age and the body mass index. The proposed approach appeared suitable for predicting tidal volume using wearable-device data, including when evaluated on new subjects. The reliability of the model formulation with respect to the selected predictors was also evaluated by considering predictors measured with reference instrumentation; the model appeared unaffected by the way in which heart rate and breathing rate were measured. On the basis of these considerations, the formulated model can be considered not subject-specific and not instrumentation-specific.

To the best of our knowledge, only the pilot study by Làzaro et al. [17] estimated the tidal volume using an approach similar to the one proposed by us. Although both approaches used wearable devices, our approach differs from that of Làzaro et al. [17] in two major respects. Firstly, the predictors used by Làzaro et al. [17] were based on electrocardiogram-derived respiration, whose extraction requires extensive processing of an acquired electrocardiogram; by contrast, in our approach, heart rate and breathing rate directly measured from the wearable device were used, without the need of additional extensive pre-processing. Secondly, in the study by Làzaro et al. [17], only tidal volume measured during a lab-controlled experiment was considered instead of dynamic conditions as the one characterizing exercise stress test. Thus, the very limited pre-processing required and the ability to deal with dynamic conditions represent the two main advantages of the proposed approach.

The multiple regression model formulated in our approach includes not only linear terms but also interactions, which is different from what was found in other studies not necessarily dealing with wearable devices [17,18]. Of note, previous studies did not consider the individual characteristics of the subjects (such as age and body mass index) as predictors. Their addition does not represent a particular issue, since these parameters can be easily provided. At the same time, the inclusion of such information may be important for tailoring the methodology on the basis of the subject’s characteristics. Indeed, both age and body mass index showed interaction effects with heart rate and breathing rate (see Table 3).

The importance of the selected predictors can be confirmed by the literature. Age and body composition were demonstrated as essential in the clinical assessment of tidal volume [21,22]. Of note, body composition may be estimated by several indexes, such as body mass index or body surface area. In the proposed approach, body mass index was selected as the clinical index of body composition, considering its wide diffusion and easy estimation. The body surface area is a measurement of the same physiological structure; it is thus highly correlated with body mass index [23] and was not included among the predictors. Gender is also known to affect tidal volume [21,22], but it was not possible to assess its effect in the present study since all the volunteers were males. Moreover, tidal volume has been shown to continuously adjust on the basis of breathing rate, but not vice versa [4,24]. Furthermore, despite intra-subject differences, tidal volume variations are also correlated with heart rate [25,26]. However, we cannot exclude the possibility that other factors not considered in this study may affect the ability of our model to estimate tidal volume. For instance, between-subject differences in exercise capacity may lead to different values of tidal volume that are not captured by age, body mass index, or breathing-rate or heart-rate values. In addition, our results may not necessarily be extended to other exercise protocols or modalities. Since the number of subjects included in the present study is quite limited—although still comparable with similar studies [17,18]—and their characteristics do not cover all the possible variety of conditions, further studies are needed to address these issues.

Heart rate and breathing rate can be simultaneously and reliably measured using commercially available wearable devices. These devices are usually associated with user-friendly software applications. Our model may be easily integrated in the associated software, guaranteeing an indirect real-time estimation of tidal volume for the user. In the present work, heart rate and breathing rate were acquired using BioHarness 3.0 by Zephyr (Annapolis, MD, USA), in which two sensing elements are present, one for the measure of the electrocardiogram and the other one for the measure of the breathing rate. This may represent a limitation of the proposed approach with respect to other approaches requiring only a single sensing element [17,18]. Thus, a possible extension of the proposed approach may deal with the estimation of the breathing rate from the electrocardiogram, in order to derive the two predictors from the same sensing element.

5. Conclusions

This study proposed a multiple regression model for the indirect estimation of the tidal volume during an exercise stress test, using features directly acquired from wearable devices in addition to basic individual characteristics, such as the age and the body mass index of the subject. The proposed model can be considered not subject-specific and not instrumentation-specific.