Abstract
In this paper, we present the concept of the Radio Environment Map (REM) designed to ensure electromagnetic situational awareness of cognitive radio networks. The map construction techniques based on spatial statistics are presented. The results of field tests done for Ultra High Frequency (UHF) range with different numbers of sensors are shown. Exemplary maps with selected interpolation techniques are presented. Control points where the signal from licensed users is correctly estimated are identified. Finally, the map quality is assessed, and the most promising interpolation techniques are selected.
1. Introduction
Radio environment map (REM) is a database that collects information on the radio signal levels at various points in the physical space as a function of time and frequency. It collects and stores information from a variety of available sources, such as radio monitoring stations and cognitive radios (CR). REM can be used as a source of information that allows us to estimate the signal level at any point in the space and to anticipate changes in the radio environment in the near future. There are different ways to use this information, both in civilian and military environments. One of the applications, which the authors of this publication are working on, is the Dynamic Spectrum Management (DSM). REM can be used to improve the efficiency of the centralized DSM (CDSM) mechanism [1] or to increase the Electromagnetic Environment Situational Awareness (EESA) for faster and more accurate local spectrum management in the autonomous manner, at the CR level. This article deals with the latter case. The attention is focused on radio networks operating at the tactical level, where the need for reliable and efficient communications systems poses a real challenge in terms of technical solutions. Such tactical networks must be operational despite high maneuverability of troops, lack of infrastructure, and in the presence of deliberate jamming. The concept of the Mobile Ad hoc Network (MANET) seems to be a promising response to the above requirements [2]. It is worth mentioning a subclass of MANET, known as Vehicular Ad hoc Network (VANET) [3], which is dedicated to the inter-vehicle communications (IVC) and is foreseen as the enabler for intelligent transportation systems (ITS) [4,5]. The key feature of MANETs is the support for the mobility of users and the ability to self-organize. Thanks to the routing mechanism, all the radios in MANETs play a dual role, that is the role of the end-user terminals and the role of the relay nodes. For this reason, the consideration of the REM application in the tactical environment seems to be much more complex than in the static scenario, e.g., with one TV transmitter and a group of receivers.
In the paper, we discuss the concept of the REM and the problem of how to estimate the signal level accurately. We also present exemplary maps created with different interpolation methods and analyze how the choice of interpolation technique and the number of sensors affect the quality of the maps.
The novelty of this paper can be summarized as follows:
I. The paper proposes a zonal approach to the analysis of the quality of the signal level estimation for spectrum awareness purposes, i.e., the division of the area into zones with respect to the distance from the transmitter. It is worth noting that in most research works, the analysis is limited to the case with a group of receivers deployed on a small area which is distant from the transmitter. As a result, the signal level measured within the area varies slightly, which considerably simplifies the process of the signal level estimation. This process is much more complex if it is needed to estimate the signal level in close proximity to the transmitter or for a wider area with the transmitter inside. In the paper, we show that it is beneficial to divide such a wider area into zones and that the accuracy of interpolation techniques for such zones varies and is closely related to the distance from the transmitter.
II. In our research work for the Inverse Distance Weighting (IDW) interpolation method, we extend the range of the power p up to 6, while in most cases this number is limited to 1 or 2. This is explained in detail in Section 3 (IDW method description) and Section 5 (the benefit of the application of IDW method with the power p higher than 2).
III. To assess the efficiency of interpolation techniques we combine two metrics: (a) Differences between estimated values and measured values; (b) the ratio between correct and incorrect estimations. This is explained in detail in Section 5.
2. Related Works
Licensed spectrum users, in the literature referred to as primary users (PUs), do not use radio spectrum in a continuous manner or use spectrum resources in all locations. This poses a very important technical and organizational challenge related to the efficiency of the usage of spectrum resources. A relatively new proposal in this field is the concept of cognitive radios, which is associated with the opportunistic access to the spectrum by secondary users (SUs) [6,7,8]. This approach concerns the detection problem of the transmission from PU [9,10,11] and the rules of sharing spectrum resources with, for example, cognitive radios. Reuse of the spectrum, however, must not interfere with the transmission made by PUs and must, therefore, be carried out in accordance with the principles of compatibility [12,13].
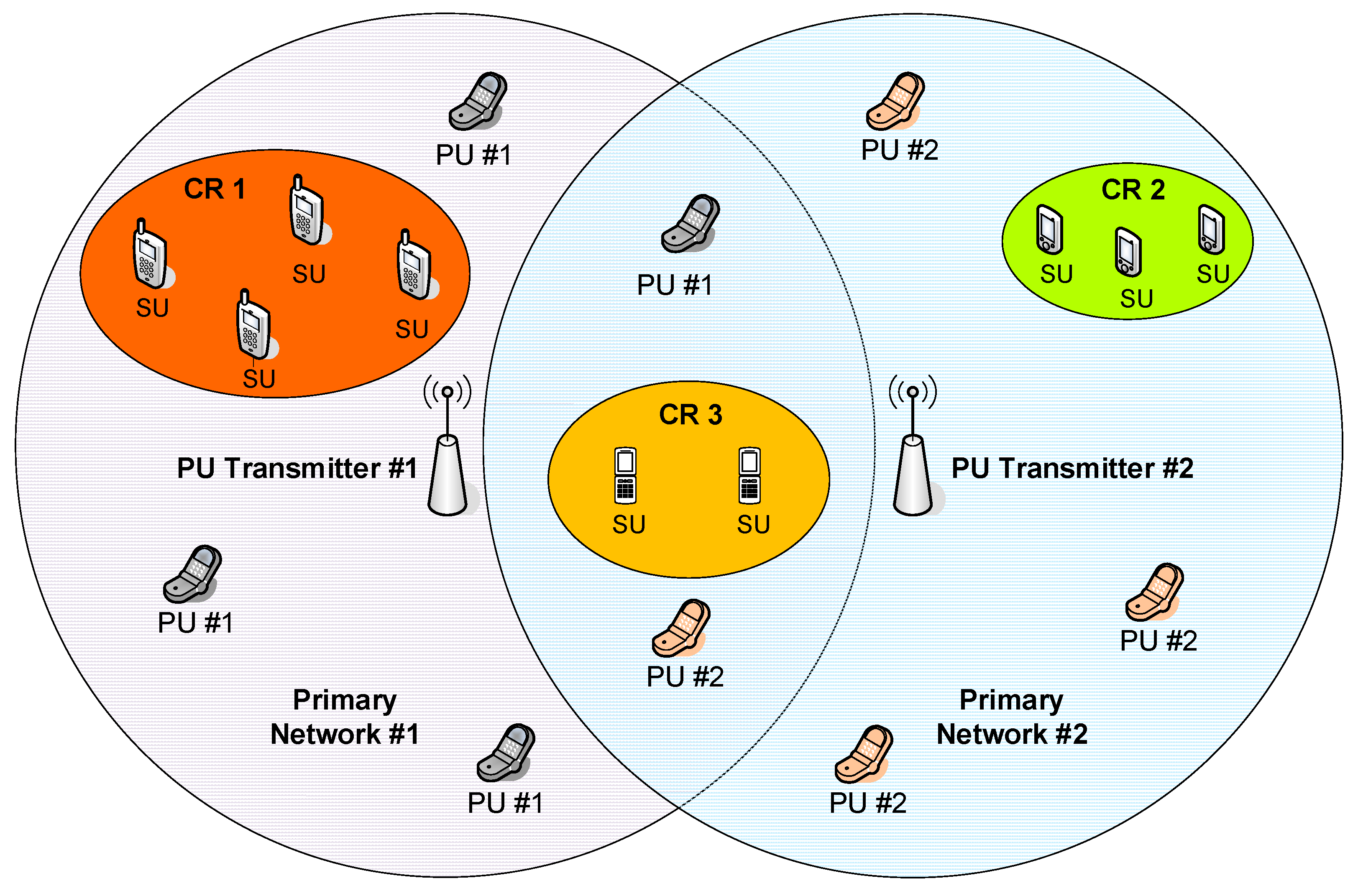
The generic idea of the coexistence between PUs and SUs is shown in Figure 1. Two primary networks are composed of PU transmitters and sets of PU receivers (PU #1 and PU #2). The range of Primary Network #1 is presented in purple color, while the range of Primary Network #2—in blue-grey color. There are three exemplary CR networks that do not overlap. CR 1 network is deployed within the range of Primary Network #1, while CR 2 network within the range of Primary Network #2. CR 3 network is arranged in the area that is covered by the ranges of both PU Transmitters. In general, SUs are allowed to use resources assigned to PUs operating in the same area, however, they must obey a set of specific rules to avoid disturbing PUs. As a minimum, cognitive radios have to know the transmission pattern of PUs or have to recognize the transmission from PUs.
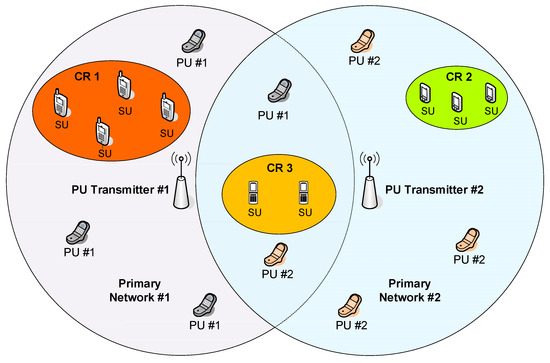
Figure 1.
The idea of sharing radio spectrum between primary users (PUs) and secondary users (SUs).
In early stages of CR concept development, the US federal regulations related to the reuse of the so-called TV White Spaces (TVWS) imposed a strict requirement that emissions coming from PU should be detected above the level of -114 dBm [14,15,16]. Such a rigorous demand practically precluded the reuse of radio spectrum by CRs. For this reason, in the second decade of this century, new solutions were sought. One of the subjects of the World Radiocommunication Conference WRC-12 were cognitive radios. The main conclusion was that for implementation of CRs, no additional global regulations were required and that the start-up of CRs may be carried out on the basis of the current ITU Radio Regulations. Moreover, in this regulation, it was stated that at least it is necessary to outline the rules for the protection of licensed users (systems) and to define the conditions for cross-border coordination of CR systems operating in neighboring countries [17,18].
One of the solutions aimed at making the operation of CRs possible was the concept of the centralized database, which would store all the registered transmitters with their geographical coordinates, characteristics, and transmission patterns [19]. Although such a concept created better opportunity for spectrum sharing, it took into account static PU transceivers only. On the other hand, the market of mobile devices is still growing and therefore, there is a need to include mobile transmitters in the database too. To meet the need the concept of the Radio Environment Map (REM) was proposed.
As a general rule, REM is considered as a database which provides comprehensive and up-to-date information on radio spectrum. It is assumed that this information is composed of results of measurements, geographical features, available services, spectral regulations, positions and activities of radios, policies adopted by the user and/or service providers, and knowledge from the past [20,21]. It is expected that measurements are conducted in a continuous manner to update the database regularly and to get a recent and reliable picture of the radio spectrum. For this reason, REMs are perceived as a useful and powerful tool supporting frequency assignment authorities.
In the literature on this topic, REM architecture is described as hierarchical, encompassing at least two levels, namely local REMs and global REM [21,22]. Local REMs are deployed on small areas, which enables us to limit the size of the database and the complexity of analysis. On the other hand, local REMs may include more detailed information on the radio environment. Global REM is supported by local REMs that provide data from many smaller areas. Global REM contains more complex radio environmental data and thus offers unique capabilities to the frequency management authority, e.g., detection of hidden terminals, localization of transmitters, and identification of those that are sources of interferences.
REMs are sometimes seen as a field of application for Big Data Analytics to enhance the Spectrum Awareness. This is for two reasons. The first one is the size of the input data, which is provided by measurement equipment and which is required to create REMs. The second reason is the amount and complexity of the output data, particularly at the global REM level. In [23], the authors presented an estimation of the amount of data stored in the database for the area of 20 km × 20 km with the terrain resolution of 20 m, under the assumption that the monitored band is limited to 120 MHz and measurements are taken with the step of 3 MHz. It was also assumed that the records of the radio environment state are done every 10 min and that each point on the map may be represented by 256 levels (8 bits). For such conditions, after 24 h of operation, there will be 5760 maps created, with the total size of 5.7 GB. Wider frequency range and higher resolution in both time and frequency domains will lead to the growth in the size of data by up to a million times.
As was mentioned above, REM needs measurement data delivered by sensors deployed in the area for which the map is being developed. Sensors are generally named Measurement Capable Devices (MCDs) [24]. In typical applications, the role of MCDs can be performed by various devices with measurement capabilities, such as simple mobile phones, smart phones, notebooks, etc. However, there are specific systems operating in dedicated bands, e.g., search and rescue or military systems. In such cases, spectrum measurements can be performed by cognitive radios, dedicated receivers, Electronic Warfare (EW) systems or Intelligence, Surveillance, Reconnaissance (ISR) systems [25].
The problem of the sensor network density and the deployment of sensors has been studied in the literature on the topic. Our approach to the problem of deployment of sensors in such an area is partly convergent with the scheme proposed in [26], as we also take into account a small number of trusted sensors creating the core part of the sensor network. The assumption of the small number of sensors results from the fact that we aim to reflect a small-scale network with a limited number of measurement devices.
The analysis presented in this paper is consistent with the methodology described in [27], i.e., some zones have to be occupied by sensors more densely. A slight difference is that for us, a constant number of sensors for a given scenario and a change of the location of some sensors are the only option possible. For this reason, we analyze the impact of the deployment of sensors on REM quality using selected interpolation techniques.
The main task of REM is to present an electromagnetic environment with the highest achievable quality. In the literature on the topic, the quality of such a presentation is expressed with different metrics, which enables us to compare the estimated value with the real value.
In [24,28,29], the authors proposed the Root Mean Square Error (RMSE), and the average RMSE (ARMSE) was applied in [30] as metrics computed for selected estimated values within the analyzed area. The RMSE shows a dissimilarity in Received Signal Strength (RSS) between the estimated values and real values. However, a drawback of such an approach lies in the fact that it is impossible to identify the reason why the SU could not take advantage of the spectrum opportunities [31]:
- When the RSS from PU was overestimated, the transmission from SU was needlessly restrained to avoid interferences,
- when the RSS from PU was underestimated, the transmission from SU was allowed and resulted in interferences.
To overcome the drawback of RMSE in [31,32], the Correct Detection Zone Ratio (CDZR) and False Alarm Zone Ratio (FAZR) were introduced. When on account of the inaccuracy of the estimation REM forbids the transmission, although it should be allowed, the area is named False Alarm Zone (FAZ). The area in which the spectrum is occupied but REM allows transmission because of the estimation imprecision is called a Missed Detection Zone (MDZ).
In our research, we have used quality measures similar to those presented above, and their description is given in the chapter devoted to the analysis of the results.
3. Map Construction Techniques
There are three main construction techniques suitable for REMs [33,34]:
- Indirect (transmitter location based methods)—applying transmitter location and propagation model to obtain the estimated value,
- direct (spatial statistics based methods)—applying interpolation techniques and sampled data,
- hybrid—combining the two approaches.
The selection of the most appropriate map construction technique depends on its specific application. In some research works, indirect methods are preferred due to the fact that they help to construct more accurate maps if the propagation model has been selected properly and if the terrain model is accurate. On the other hand, indirect methods require a set of input data, e.g., transmitter location, the TX power, and activity pattern of the transmitter as a minimum. Indirect methods are widely applied to predict the communication range of the wireless systems or to assign frequencies for specific scenarios.
Spatial statistics based methods use measurement data from many sensors. The collected measurement data is used as an input for the interpolation process, which enables us to get the data for the remaining points. Direct methods seem to be more relevant for spectrum monitoring and spectrum awareness systems. For this reason, in the following part of the paper, we deal with direct methods.
When REM is considered, the most promising interpolation techniques described in the literature are as follows: Nearest Neighbor (NN), Inverse Distance Weighting (IDW), and Kriging [35,36].
NN method uses Thiessen (or Voronoi) polygons, which are created around each point at which the measurement was taken. A characteristic feature of these polygons results from the fact that their borders are exactly in the middle of the distance between neighboring sensors. NN method is thought to be the simplest, and it offers little accuracy.
IDW is based on weighting factors wi that are inversely proportional to the distance between the given point x0 and the measurement point xi and raised to the power p. The power p defines how the influence of the weighting factors decreases with the distance. When the power p value is set high, the points which are closer have a stronger impact. If the power p value is set at zero, regardless of the distance, the weighting factors remain at the same level.
The typical formula for IDW method is [37,38]:
where:
- is the predicted signal level for point x0,
- N is the number of points at which the signal level was measured,
- 0) is the weighing factor for point x0,
- is the signal level measured at location xi.
The formula to determine the weights for wi is given below [37,38].
where hi is the distance between point xi and point x0, hk are distances between points xk and point x0, and p is the power. Usually, in the literature on the topic, the power p is set to 1 or 2. In our research, we have taken into account the power p up to 6. In the rest of the paper, we use the following notation for IDW method: IDW pα where α is the value of the power p, e.g., for IDW p3 the value of the power is equal to 3.
Kriging is one of the geostatic methods of interpolation [39,40]. Similarly to IDW method, Kriging also uses Equation (1) and weighting factors. However, these weighting factors are determined on the basis of the semivariogram that takes into account the distance between measurement points and the variation between measurements of signal levels as a function of the distance.
Semivariance is calculated according to the formula given below [41]:
where:
- h = xi–xj is the distance between points xi and xj,
- V(xi) and V(xj) are the levels of the signal measured at points xi and xj,
- N is the number of measurement points, while N(h) is the set of pairs of points separated by the distance h, and |N(h)| denotes its cardinality.
The detailed description of the weighting factors wi calculation for Kriging can be found in [40].
In many papers, Kriging is perceived as the most exact, though quite a complex method of interpolation. A more detailed description of the estimation techniques mentioned above is presented in [25,42].
4. Test Scenario and Exemplary Maps
In order to investigate the impact of the interpolation techniques on the REM quality, numerous tests were conducted for UHF frequency band. In total, there were 21 test frequencies assigned by the governmental authority. The comparative analysis for three selected frequencies, i.e., 303.05 MHz, 863.5 MHz, and 1997 MHz, is presented in [43]. The selection of frequencies was made in the following way: Two boundary frequencies and one frequency in the middle of the band. In this paper, we selected the highest frequency (1997 MHz), as it is the most adequate for broadband communication systems.
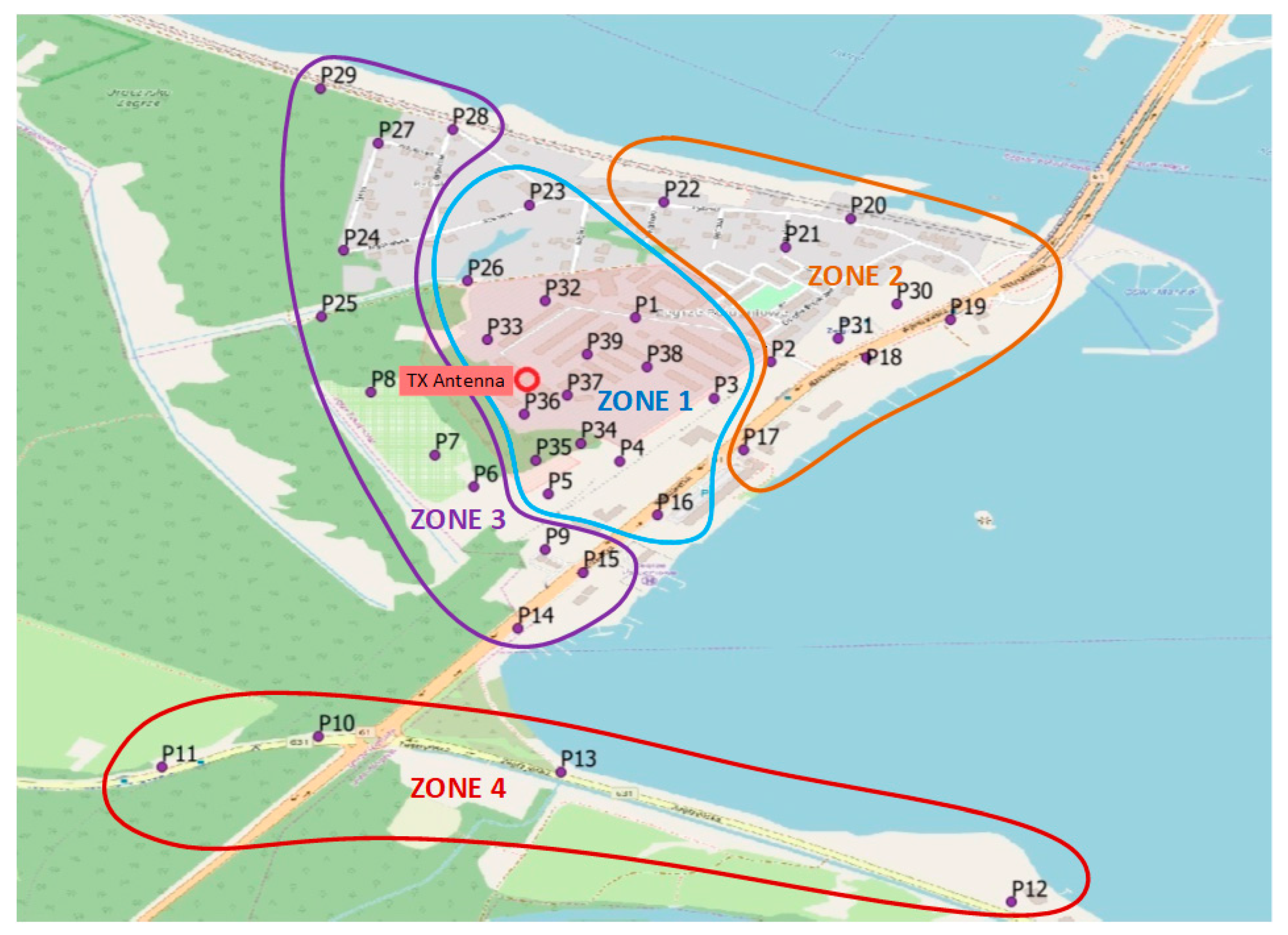
The experiment was conducted in the following way. First, measurements were taken in a real environment with 39 sensors to get input data, and then exemplary maps were created using different construction techniques. In the next step, the analysis of calculated RMSE for various arrangements of sensors was made. The initial distribution of 39 sensors is shown in Figure 2. There were Non-Line-of-Sight (NLOS) conditions for the following sensors:
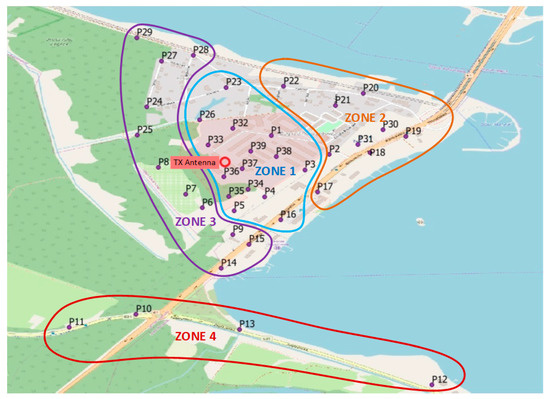
Figure 2.
Deployment of the sensors and position of the TX Antenna.
- P6–P8, P10, P11, P24, P25, P27, and P29—the average height of the forest separating sensors is about 25 m,
- P2, P18–P22, P30, and P31—the approximate height of the buildings separating sensors is between 12 m and 15 m,
- P1, P3–P5, P9, P12–P17, P23, P26, P28, P35, and P36—the approximate height of the buildings and single trees separating sensors ranges from 8 m to 10 m.
For the sensors P32–P34 and P37–P39, Line-of-Sight (LOS) conditions could be observed.
The area presented in Figure 2 was divided into four zones that reflect the distance of the sensors from the TX antenna and the signal levels measured by the sensors. Zone 1 represents the sensors located around the TX antenna with the received signal level higher than −90 dBm. Zone 2 includes sensors that measured a signal lower than −90 dBm and were deployed east of the TX antenna. This zone is an example of an urbanized area. Zone 3 also contains sensors with the signal level lower than −90 dBm, but located west of the TX antenna. This zone represents partly forested and partly rural area. Zone 4 was created at the bottom of the map and exemplifies a distant area at the edge of the radio range. All the sensors within this zone measured very low signal levels, lower than −100 dBm. This division of sensors into four zones was used in our further analysis.
To assess the quality of the maps created with the selected interpolation techniques, the calculated RMSE values were compared for three groups, each with a different number of measurement sensors used for interpolation, called: Scenario 26 (26 sensors out of 39), Scenario 20 (20 sensors out of 39), and Scenario 13 (13 sensors out of 39). The remaining sensors were used as control sensors to validate the result of the interpolation. Moreover, each of the three scenarios consisted of three tests (Test_a, Test_b, and Test_c) with different sets of measurement sensors used for interpolation. This means that there were three different deployments of measurement sensors for each scenario. Such an approach to the problem of data validation is known in the literature on the subject as the repeated random subsampling validation or Monte Carlo cross-validation. In order to be in line with this method of validation, measurement sensors were selected randomly for the interpolation process. Finally, for each test the difference between the measured and the interpolated signal level was compared for all the control sensors. It should be noted that the measurement (training) and control (validation) sensors did not overlap in any of the tests. The sets of the control (validation) sensors for each test are presented in Table 1.

Table 1.
Control (validation) sensors with respect to scenarios and tests.
The measurement system that was used to collect input data for the purpose of creation of REMs is presented below. The system was composed of its own source of radio emission working with the output power lower than that used by DVB-T transmitters, which are quite often used as a source of radio signal in these types of research works, and the mobile receiving node [44].
The receiving part of the testbed consisted of an antenna, a vector analyzer, and a computer controlling the receiving operation and recording the results. The receiving antenna was installed on a vehicle at the height of 3 m. The vehicle was moving within a preliminarily selected area presented in Figure 2 and took measurements in specific points (P1–P39). The transmitting part of the testbed was composed of a signal generator, an amplifier, an antenna, and a control computer. The antenna was mounted on the roof of a two-story building at the height of approximately 8 m. The detailed configuration of the measurement system is given in Appendix B.
The following configuration of the testbed was used: (a) Frequency: 1997 MHz; (b) modulation type: CW; (c) output power: 10 W; (d) measured parameter: average RSS; (e) number of averages: 10; (f) antenna type: Omnidirectional.
The measurements were taken in Central Europe (Poland) in the area of Zegrze Lake presented in Figure 2 (approx. 4 km2). The test area was diverse in terms of coverage, i.e., partly an open meadow neighboring a forest and partly an urbanized area with buildings of medium height.
The measurement results obtained for all 39 sensors are presented in Appendix A.
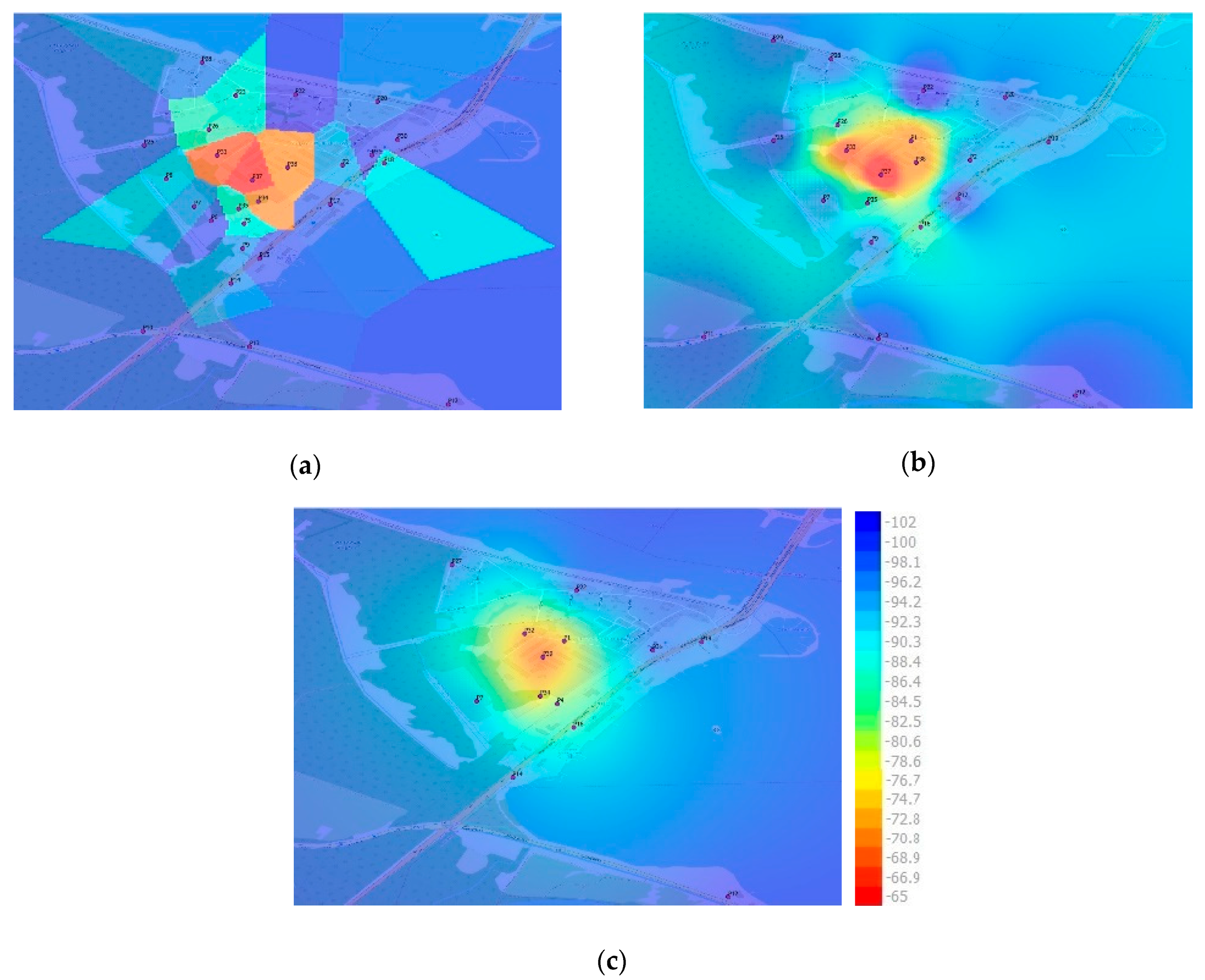
Some exemplary maps constructed with the selected interpolation techniques are presented in Figure 3.
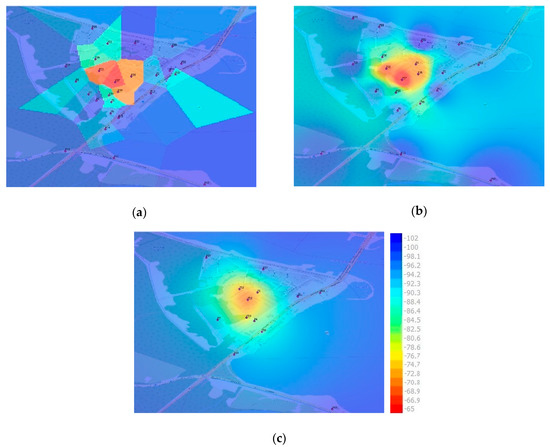
Figure 3.
Exemplary maps constructed for selected interpolation techniques and various number of sensors (signal level in dBm): (a) 26 sensors—Nearest Neighbor (NN); (b) 20 sensors—Inverse Distance Weighting (IDW) p3; (c) 13 sensors—Kriging.
The characteristic feature of the NN method (Figure 3a) are polygons created around each sensor. Within each polygon, the signal level takes the value measured by the sensor. For this reason, the signal level may change suddenly at the edges of the polygons, e.g., between the orange polygon in the center and the dark blue polygon at the top of the map (Figure 3a). It is worth noting that the size and the shape of the polygons depend on the density and deployment of neighboring sensors. The position of the TX antenna can be determined with little accuracy.
The map generated with the application of the IDW method is shown in Figure 3b. This method generates smoother maps when compared to NN. However, the drawback of the method is the bull’s-eye effect visible around each sensor. The size of eyes depends on the power p used in the interpolation process. The estimation of the signal level is quite accurate if the power p is set at 3 or higher and the sensors are deployed densely [25]. The location of the transmitter can be determined with moderate precision.
When the Kriging method is applied (Figure 3c), the signal level changes smoothly within the whole area. Neither bull’s-eye effects nor rapid changes in the signal value are observed even if the sensors are deployed sparsely or irregularly. For this reason, Kriging seems to be the method which is least sensitive to the deployment of the sensors [25]. The source of emission can be located with quite good accuracy. The red-orange zone in the center of the map has quite a regular shape of a circle.
The interpolation methods described above can be used to determine the likely location of the bigger number of transmitters working at the same time. Exemplary maps and analysis for the scenario with two transmitters are shown in [44].
5. Analysis of the Results
In this chapter, the results of the tests are discussed.
In the literature on the topic, the RMSE metric is the most commonly applied one to assess the fidelity of maps. In this paper, the RMSE is used to evaluate the quality of the signal strength representation for the global analyzed area and also separately for the four zones that were created with the aim to reflect the idea of the spectrum sharing among PUs and various SUs (Figure 1). The division of the area into zones may be treated as clustering of sensors or SUs with respect to their location and distance to the PU transmitter.
In the paper, the analysis of the RMSE metric was conducted from two perspectives:
- Globally, for the “lowest RMSE” test case for each scenario with 13, 20, and 26 sensors, i.e., for selected tests with the lowest RMSE value.
- Separately, for each of the zones presented in Figure 2.
In the next step, the analysis of the correctness of the signal level estimation was made separately for each control sensor for the “lowest RMSE” test case. This analysis was carried out with respect to selected interpolation techniques.
The RMSE was calculated according to the formula given below:
where:
- n is the number of control sensors,
- Sri is the signal level [dBm] measured by i-th control sensor,
- Soi is the signal level [dBm] interpolated for i-th control sensor,
- is the difference between measured and interpolated signal level [dB] for i-th control sensor,
- is the average value of .
The analysis of the dependency between the quality of maps and the density of the sensor network was provided in [45]. The general conclusion of this study was that the RMSE dropped as the number of sensors increased. This statement was valid for all interpolation techniques that were taken into account (NN, IDW, and Kriging). Analyzing our results, we also confirmed that the lowest ARMSE for each scenario was offered by Kriging and IDW with the power of 3 or 4.
The differences between the RMSE values obtained in individual tests for a given scenario were significant (up to 4.6 dB for the scenario with 26 sensors). A more thorough analysis revealed that this was due to unfavorable locations of some sensors, mainly terrain obstacles on the propagation path between the TX antenna and the sensors. Therefore, to minimize the impact of the arrangement of sensors on the results, for further analysis we selected the best test for each scenario. The best test is understood as this one of the three tests which has the lowest RMSE value calculated for all interpolation methods in a specific scenario prior to the division of sensors into four zones. In Table 2, we present the results of RMSE for all the tests with respect to the interpolation techniques. Note that the name of the test contains the number of sensors providing measurement data for the interpolation process. The tests with the lowest RMSE values are marked in bold in Table 2.

Table 2.
RMSE (Root Mean Square Error) for individual tests and various interpolation methods.
Below we present the list of the lowest RMSE tests for each scenario:
- Test_13a for the scenario with 13 sensors,
- Test_20c for the scenario with 20 sensors,
- Test_26a for the scenario with 26 sensors.
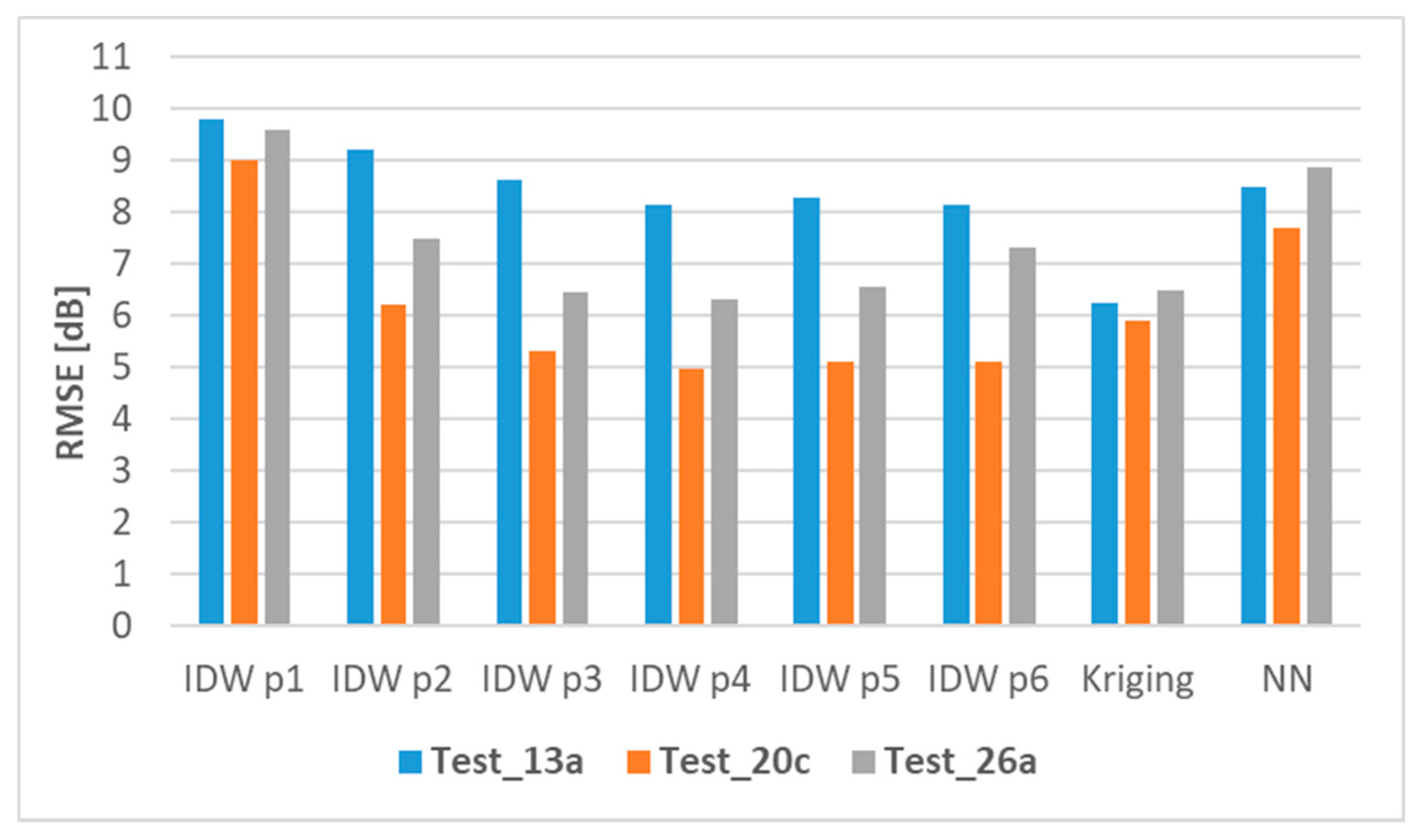
Figure 4 presents the results for selected tests with the lowest RMSE value. The RMSE is presented with respect to the eight interpolation techniques. These results generally confirm the statement given above since the lowest RMSE occurred for:
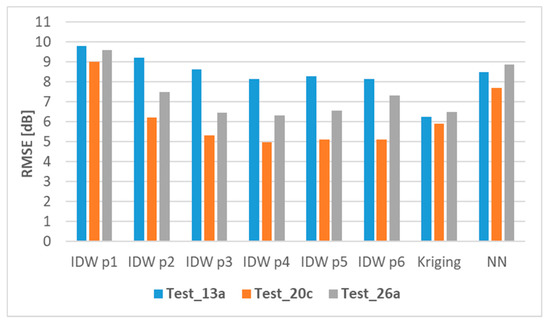
Figure 4.
RMSE (value in dB) for tests with 13, 20, and 26 sensors—lowest RMSE test case.
- Kriging in Test_13a (6.3 dB),
- IDW p4 in Test_20c (5.0 dB),
- IDW p4 in Test_26a (6.3 dB), and was comparable with the result for IDW p3 (6.4 dB) and for Kriging (6.5 dB).
It should be emphasized that, surprisingly, the lowest RMSE for Scenario 20 was lower than for other scenarios, especially for Scenario 26 with more sensors in the network. This effect may be explained in the following way: Although the number of sensors plays an important role in REM quality, another essential factor is the deployment of sensors. Therefore, in the case of a small number of sensors, the RMSE may be low when sensors were arranged properly. The analysis of this effect was presented in [46].
It is also worth noting that, independently of the scenario, the IDW p1 and NN interpolation techniques offered the worst REM quality when only the RMSE value was taken into account. For this reason it seems that, considering only the RMSE value, these methods should not be recommended for REM construction. On the other hand, irrespective of the scenario, the RMSE for Kriging oscillated at a low level (around 6 dB). This method of interpolation was the most stable, regardless of the number of sensors.
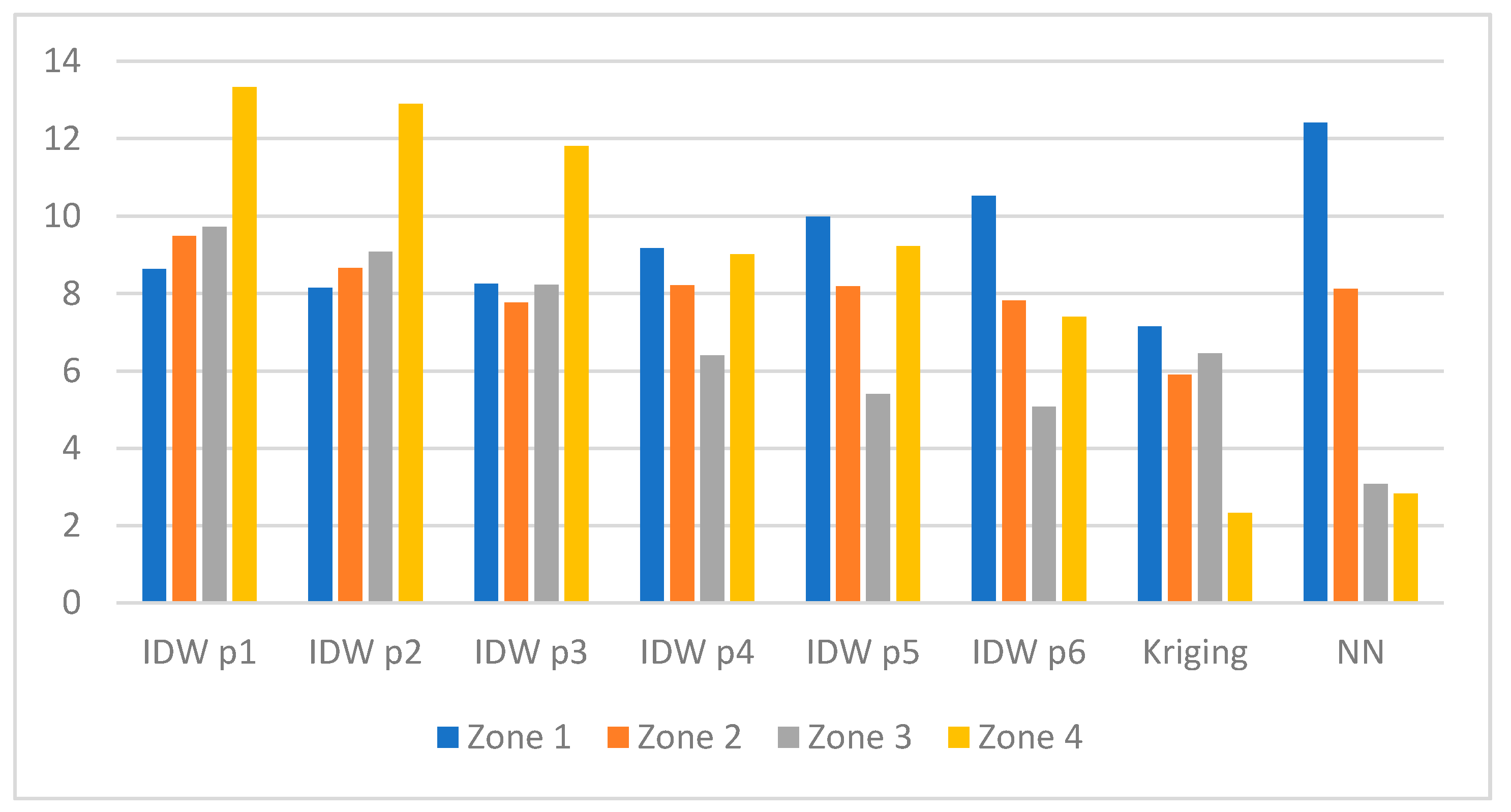
An in-depth analysis of RMSE values with respect to the four zones shown in Figure 2 and for tests with the lowest RMSE values is presented below:
- Figure 5—Test_13a, scenario with 13 measurement sensors,
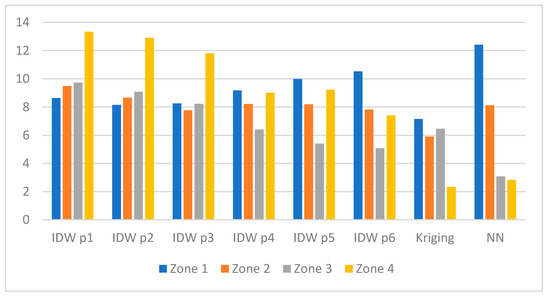 Figure 5. RMSE in zones (value in dB) for Test_13a.
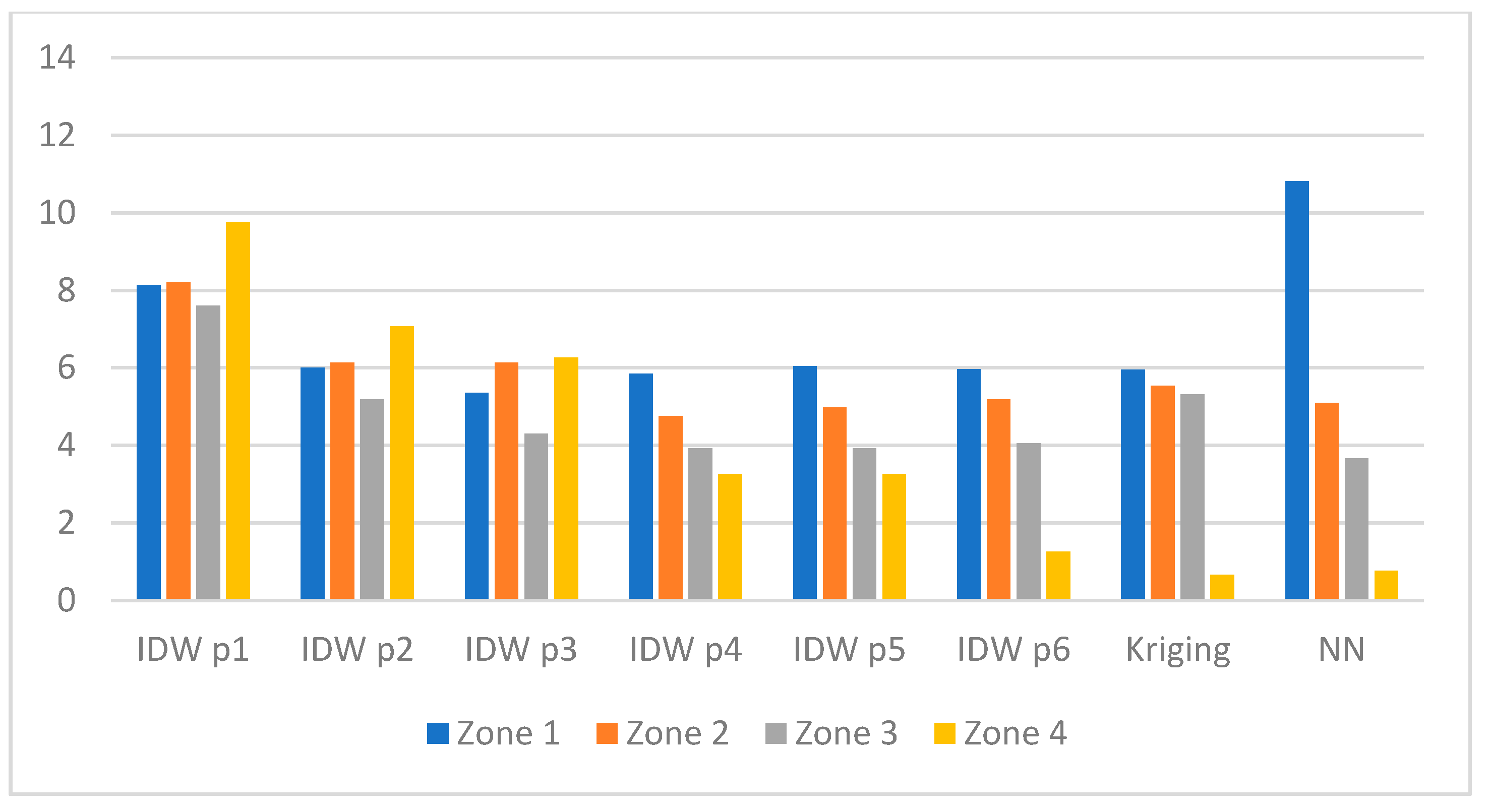
Figure 5. RMSE in zones (value in dB) for Test_13a. - Figure 6—Test_20c, scenario with 20 measurement sensors,
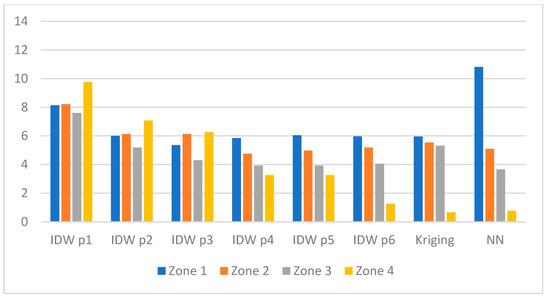 Figure 6. RMSE in zones (value in dB) for Test_20c.
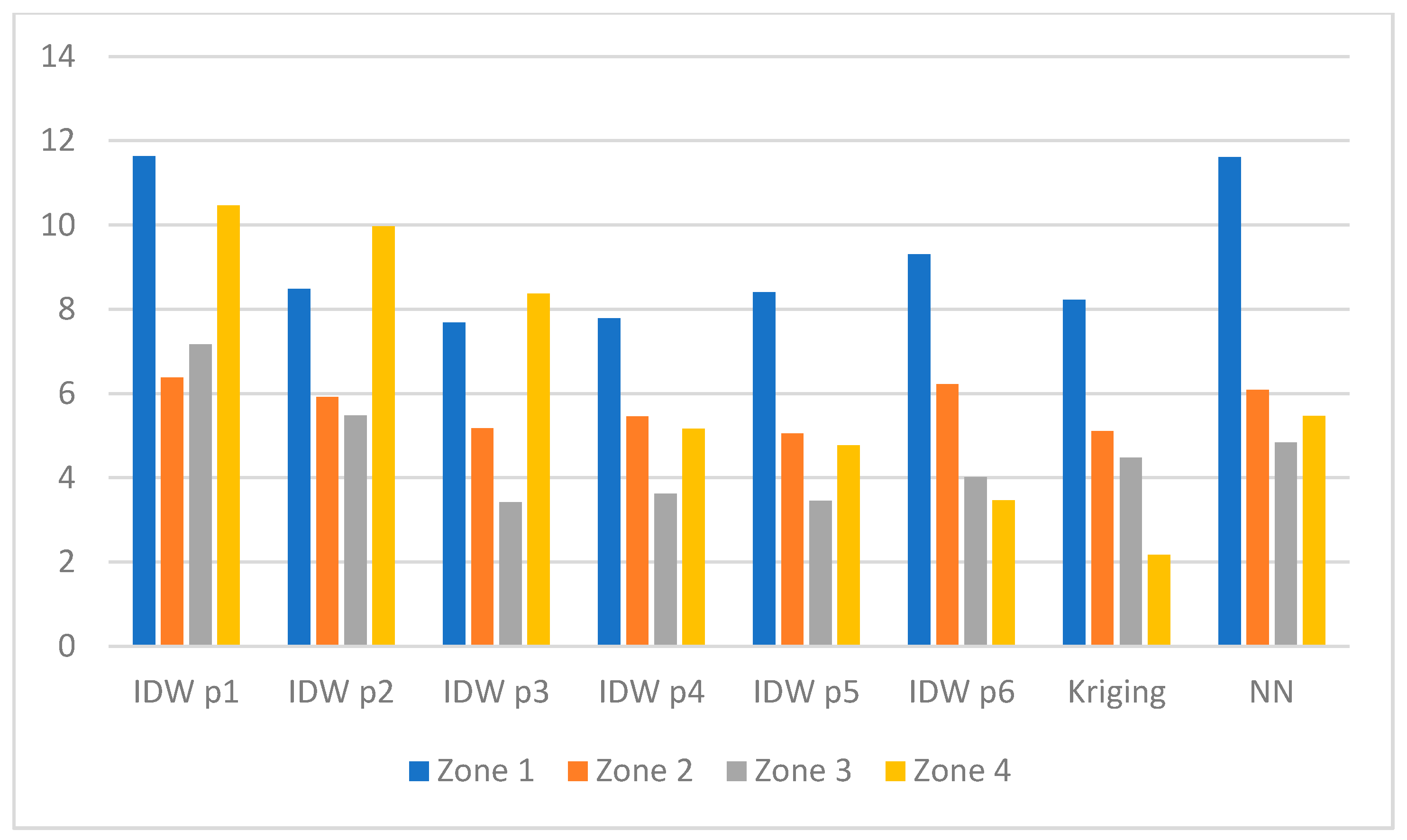
Figure 6. RMSE in zones (value in dB) for Test_20c. - Figure 7—Test_26a, scenario with 26 measurement sensors.
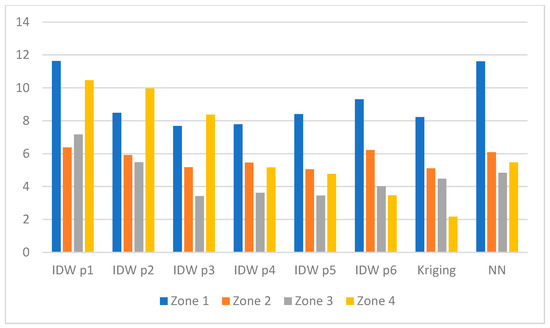 Figure 7. RMSE in zones (value in dB) for Test_26a.
Figure 7. RMSE in zones (value in dB) for Test_26a.
The analysis of the results presented in Figure 5 revealed that the lowest RMSE occurred for Zone 1 (7.15 dB), Zone 2 (5.9 dB), and Zone 4 (2.3 dB) for Kriging. Surprisingly, in Zone 3, NN method (RMSE approx. 3 dB) outperformed other interpolation techniques. Moreover, it is clearly visible that the application of IDW method with the power p from 1 to 3 resulted in the highest RMSE for Zone 4. In contrast, when IDW method with the power p from 4 to 6 was applied, the highest RMSE appeared for Zone 1. However, for Zone 1, the highest RMSE in this test occurred for NN method (12.4 dB).
Figure 6 shows that for most interpolation methods, the RMSE value did not exceed 6 dB in any of the zones. The specificity of this test case is that Kriging and IDW interpolation method with the power p ranging from 4 to 6 gave the smallest values of RMSE and similar trends of changes in RMSE values for individual zones. It is difficult to indicate here one interpolation method that would be the best for all the zones, because the lowest RMSE occurred for:
- IDW p3 method in Zone 1 (RMSE approx. 5.3 dB),
- IDW p4 method in Zone 2 (RMSE approx. 4.7 dB),
- NN method in Zone 3 (RMSE approx. 3.7 dB),
- Kriging method in Zone 4 (RMSE approx. 0.65 dB).
Nevertheless, the differences between the lowest RMSE values were quite insignificant and amounted to not more than 1.6 dB for almost all the zones except Zone 4, where Kriging outperformed the other interpolation techniques.
It is worth noting that the RMSE values were considerably above 6 dB for NN method in Zone 1, for IDW p2 method in Zone 4, and for IDW p1 method for all the zones. NN method performed not very well when interpolating radio signals in a close proximity to the transmitter, because in such conditions there were significant variations in the received signal levels, particularly in urban areas. The RMSE value reached 10.8 dB for NN method in Zone 1. On the other hand, NN method offered quite small RMSE values when applied for the interpolation of radio signal for distant areas, where the variance of the received signal level was low. The RMSE value amounted to 0.8 dB for NN method in Zone 4.
In Zone 4 (see Figure 7), Kriging offered the most accurate estimation of the signal strength (RMSE amounted to 2.1 dB). Moreover, in this zone we noticed a drop in the RMSE with the increase in the power p for IDW method, i.e., the highest RMSE occurred for IDW p1 (10.47 dB), while the lowest for IDW p6 (3.47 dB). In Zone 4, regardless of the number of sensors used for the interpolation, the highest RMSE values were obtained for IDW interpolation method with power p from 1 to 2 (approx. 10 dB). These methods do not seem to be suitable for REM maps for open areas located far away from the transmitter.
In Zone 2 and Zone 3, quite similar and low RMSE values were noticed for Kriging and for IDW interpolation methods with the power p from 1 to 5. The lowest RMSE values in these zones were as follows:
- Around 5.0 dB for IDW p5 and 5.1 dB for Kriging in Zone 2,
- approximately 3.4 dB for IDW p3 in Zone 3.
It is worth noting that the highest RMSE values for these two zones were obtained for IDW p1 method.
The analysis of the results revealed that for Test_26a, the highest RMSE values occurred for Zone 1, i.e., approximately 11.6 dB for IDW p1 and NN interpolation methods. The minimum RMSE value in Zone 1 amounted to 7.7 dB for IDW p3. A more thorough analysis of the RMSE values in Zone 1 showed that even for Kriging, the RMSE is reasonably high (8.2 dB). Moreover, the RMSE in Zone 1 with a smaller number of sensors (see the results for the Test_13a) was lower (7.2 dB). This comparison showed that even when the number of sensors was doubled, the RMSE in Zone 1 remained high. This observation may be explained in the following way. Firstly, effects like fading and shadowing, which are typical for radio transmission, make the received signal level change substantially. Unfortunately, these effects are not reflected in the interpolation methods. Secondly, although the number of sensors impacts the quality of the interpolation, the arrangement of sensors also plays an important role. An example of such a situation can be Test_20c, where the RMSE value in Zone 1 for Kriging method amounted to 6 dB, which is much lower than for Test_26a (8.2 dB). Thirdly, a characteristic feature of the interpolation methods under analysis is their inability to extrapolate the level of the radio signal, i.e., to estimate the level in the area closer to the transmitter if there were no measurement sensors located in the vicinity of the transmitter.
To overcome the drawback of RMSE, as the next step of the REM quality analysis, the differences between interpolated and true values were calculated. The results from the best tests (the lowest RMSE test cases) were selected for this study. These results are given in the tables below for various numbers of control points: Table 3 (scenario with 26 control points), Table 4 (scenario with 19 control points), and Table 5 (scenario with 13 control points). It should be noted that for the test with 26 control sensors, there were 13 measurement sensors providing data for the interpolation process, because there were 39 sensors in total. The same rule applies to the rest of the tests analyzed below. The following notation was applied for the calculated difference for each control point:

Table 3.
Difference between interpolated and true value for 26 control points and various interpolation methods (Test_13a).

Table 4.
Difference between interpolated and true value for 19 control points and various interpolation methods (Test_20c).

Table 5.
Difference between interpolated and true value for 13 control points and various interpolation methods (Test_26a).
- ±3 dB—Correct Estimation Point (CEP), green color,
- >3 dB—Overestimation Point (OEP), blue color,
- <−3 dB—Underestimation Point (UEP), orange color.
The results for the scenario with 26 control points are given in Table 3. It may be easily noticed that the biggest number of CEPs appeared for NN (12) and for Kriging (11), so these methods may be considered as promising for REM. For NN method 6, UEPs and 8 OEPs occurred while for Kriging 5 UEPs and 10 OEPs. As the smallest number of CEPs occurred for IDW p1 (3) and IDW p2 (4), these methods can be discarded in further analysis. For the remaining IDW methods the number of CEPs amounted from 7 to 9.
The above comparison showed that there were three control points (P5, P17, P35) for which all the methods overestimated the signal level. On the other hand, for P37, all the methods underestimated the signal value. There were two control points for which only one method gave the correct signal value, namely IDW p1 for P18 and NN for P33, while for the remaining interpolation techniques, the signal level was underestimated. This suggests that the deployment of control points plays a very important role, especially in the case of areas which are diverse in terms of coverage.
Additionally, for further analysis the control points were combined into four groups (zones) reflecting the distance of the sensors from the TX antenna, the direction to the TX antenna, and the signal levels measured by the sensors. These zones are also presented in Figure 2.
It is clearly visible in Table 3 that there were more UEPs in Zone 1 than in the other zones. It is worth noting that the sensors in Zone 1 were located closely to the TX antenna and therefore, the signal levels measured by these sensors were the highest. The two control sensors P33 and P37 measured the highest levels of the signal. However, in the interpolation process the measurement data from the remaining sensors placed in this zone was taken into account. As in the input data for the interpolation process, the signal levels were lower than for the two control sensors, and assuming that the interpolation methods flatten the results, it is obvious that the estimated levels for these control sensors were much lower than the measured levels.
In Zone 2, there was only one control point, namely P18, with dominating UEP. For this point, nearly all the interpolation techniques, except for IDW p1, underestimated the signal level by approximately 10 dB. This effect can be explained in the following way. The signal levels measured for all the neighboring sensors in this zone were much lower than for P18, and as a result, the interpolated signal level was much lower than the level measured by the control sensor P18.
In Zone 2, there was one control point P17 for which all the interpolating techniques overestimated the signal level by approximately 15 dB. The analysis revealed that the measurement points neighboring P17 (P3, P4, and P16) measured much higher signal levels. There were no points surrounding P17 that measured comparable or lower signal levels than P17. In consequence, the estimated signal level for P17 is much higher than the measured level.
The results presented in Table 3 reveal that Zone 3 was dominated by OEPs and CEPs, while OEPs prevailed in Zone 4.
It is worth mentioning that there were no such control points for which all the interpolation methods would give the correct signal level.
The results for the scenario with 19 control points (20 sensors used for the interpolation process) are given in Table 4. The biggest number of CEPs occurred for NN (10). For Kriging and IDW p6, there were 8 CEPs.
It is worth noting that in this case there was only one control point (P3) for which all the methods underestimated the signal level, and two control points (P5, P23) with the correct estimation for all the methods. The number of green fields in the table is much higher than in Table 3. The explanation of this effect is very simple: Fewer control points, means more points used for the interpolation process and as a result, an increase in accuracy, see results in Table 3.
The comparison of the results presented in Table 4 showed that there were three control points (P15, P30, P31) for which all the methods overestimated the signal level. There were two control points (P6 and P21) for which only NN gave the correct signal value, while for the remaining interpolation techniques the signal level was overestimated. Additionally, there were two control points for which one method only gave the correct signal value, namely IDW p1 for P18 and IDW p4 for P34, while for the remaining interpolation techniques, the signal level was underestimated.
The analysis of the results showed that Zone 1 was very diverse and there were 29 CEPs, 24 UEPs, and 11 OEPs. Consequently, it is hard to determine which trend dominates. In contrast, Zone 2 was dominated by OEPs, however the results for P18 were significantly different (depending on the interpolation technique there are 7 UEPs and 1 CEP). The results shown in Table 4 revealed that in Zone 3 and Zone 4 CEPs and OEPs prevailed.
The results for the scenario with 13 control points (26 points used for the interpolation) are given in Table 5. It can be easily noticed that the number of CEPs was the highest for Kriging (8) and IDW p1 (6) while for the remaining interpolation methods the number of CEPs did not exceed 4.
The comparison showed that there was only one control point (P37) for which all the methods underestimated the signal level. There were two control points for which one method only gave the correct signal value, namely Kriging for P13 and IDW p6 for P15, while for the remaining interpolation techniques the signal level was overestimated. Additionally, there were two control points for which one method only gave the correct signal value, namely IDW p1 for P18 and NN for P33, while for the remaining interpolation techniques the signal level was underestimated.
It is worth mentioning that there were no such control points for which all the interpolation methods would give the correct or overestimated signal level.
The analysis of the results for the scenario with 13 control sensors confirmed that Zone 1 is very diverse. There were 17 OEPs, 16 UEPs, and 15 CEPs. Zone 2 is also varied as there were 6 OEPs, 9 UEPs, and 9 CEPs. In Zone 3 CEPs (11) prevailed, while Zone 4 was dominated by OEPs (7).
A general conclusion from the analysis above was that for areas distant from the transmitter, the effect of overestimation occurred, while for areas very close to the transmitter, the correctness of estimation was hard to define as there were no dominating trends.
The analysis of the differences between interpolated and measured values for Zone 4 showed that there was the effect of constant overestimation for IDW method, except for IDW p6 for the scenario with 20 sensors, when the signal level was correctly estimated. The scale of the overestimation depended on the number of measurement sensors. For IDW methods with the power p3 and p4, which were assessed as promising on the basis of the RMSE comparison, the maximum values of these differences were quite significant and amounted to:
One of the solutions to the above problem could be constant correction of the interpolated level for distant zones.
When Kriging was applied, the results of interpolation for Zone 4 reflected the results of measurements well, as there were four CEPs and one OEP with the overestimation that amounted to 3.5 dB only.
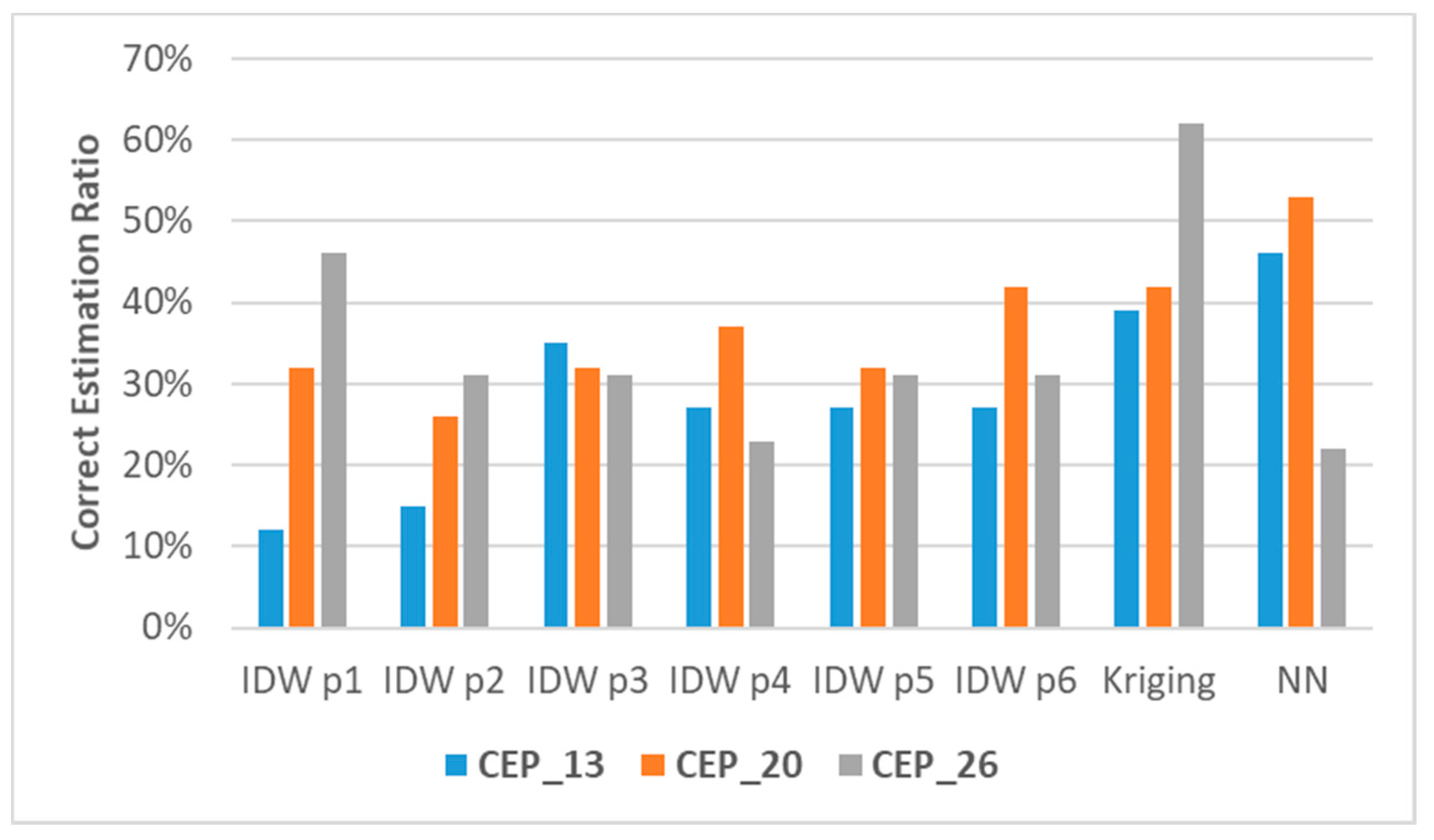
Figure 8 shows the comparison of CEPs expressed as a percentage of the total number of control points. These results are presented with respect to different numbers of measurement sensors and interpolation techniques, see Table 3, Table 4, and Table 5. The following notation was applied: CEP_xx, where xx denotes the number of measurement sensors providing data for the interpolation process.
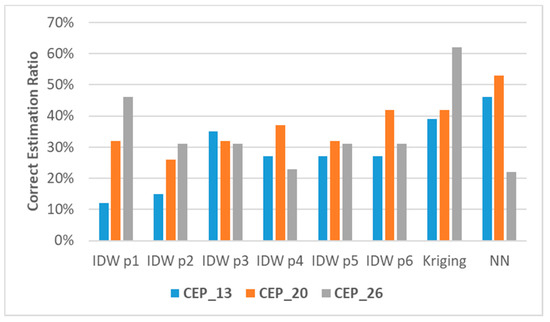
Figure 8.
Correct estimation ratio for selected interpolation techniques for lowest RMSE tests.
It can be easily noticed that in most cases, the highest correct estimation ratio appeared for Kriging and NN, while the lowest ratio was observed for IDW p1 and IDW p2. The highest correct estimation ratio (approx. 62%) occurred for the scenario with 26 points applied for the interpolation process.
Table 6 presents the comparison of the ratio of CEPs, OEPs, and UEPs for selected interpolation techniques and lowest RMSE tests.

Table 6.
The comparison of the ratio of Correct Estimation Points (CEPs), Overestimation Points (OEPs), and Underestimation Points (UEPs) for selected interpolation methods and lowest RMSE tests.
It can be easily noticed that for the scenario with the lowest number of measurement sensors providing data for the interpolation process (Test_13a), OEPs prevailed. It means that for a small number of measurement sensors, the signal level was overestimated for nearly all the interpolation techniques, except for NN. In fact, NN estimated quite well for a small and medium number of sensors used for interpolation. Surprisingly, for the highest number of measurement sensors, NN performed worse.
In general, OEPs outnumbered UEPs for each scenario and for all the interpolation techniques. It is worth noting that when two factors were taken into account together, namely the number of CEPs and the trend of CEPs with the increased number of sensors, Kriging outperformed the other interpolation methods. The number of CEPs increased from 39% for Test_13a to 62% for Test_26a.
Table 7 presents the comparison of the ratio of CEPs in zones for selected interpolation techniques and lowest RMSE tests. Unlike Table 6, the results shown in Table 7 are generalized for three scenarios. For Zone 1, IDW p1 and Kriging outperform other interpolation techniques. For Zone 2, there are no dominating interpolation techniques. The highest number of CEPs reaches 31% for three methods: IDW p1, IDW p2, and IDW p3. The reason for this poor performance could be the multi-path effect in urbanized Zone 2. For Zone 3, the highest number of CEPs occur for Kriging and NN (59%), and for IDW p3 (53%). For Zone 4, Kriging and NN outperform other interpolation methods. In this zone, the number of CEPs is the highest and amounts to 80%.

Table 7.
The comparison of CEPs in zones for selected interpolation methods and lowest RMSE tests.
A general conclusion from this analysis is that Kriging is the most accurate interpolation method for REM construction. Kriging offers the best performance in terms of the number of CEPs in three out of the four zones examined.
The zonal approach to the REM analysis revealed that all the interpolation techniques perform worse in the zone close to the transmitter. A possible solution to this problem could be the development of a more complex algorithm for REM construction, i.e., identifying such zones and excluding them from the analysis. Another possible option could be the application of the hybrid method, like the one presented in [34].
6. Conclusions
The quality of radio environment maps depends on several factors, among others, on the regularity of deployment of sensors, the number of sensors, the propagation environment, and the interpolation technique.
In general, an increased number of sensors in the network is beneficial since the RMSE drops significantly. If the number of sensors in the network is limited, more attention should be paid to the optimum deployment of sensors. In the literature on the topic, several methods are presented, although the most promising one seems to be the deployment algorithm based on the stratified approach, which assumes that in some zones the sensor network is more densely covered with sensors than in others. Such deployment of sensors seems to be reasonable in diverse areas, like the one presented in this paper, where RMSE values for the scenario with 20 sensors were much lower than for the scenario with 26 sensors.
It should be emphasized that, independently of the scenario, IDW p1 and NN interpolation techniques offered the highest RMSE, which also means the worst REM quality. The highest values of RMSE observed for NN and IDW p1 resulted from high uncertainty in estimating the signal level, even above 20 dB, which is a significant difference when compared to the other interpolation techniques. This effect results from a sudden and deep change in the interpolated signal level between neighboring areas. Consequently, even if the number of miscalculated estimations is low, the range of errors of estimation makes the value of RMSE high. For this reason, these methods should not be recommended for REM construction.
It is worth noting that for the lowest RMSE case, irrespectively of the scenario, the RMSE for Kriging oscillated at a low level of around 6 dB. IDW p3 and IDW p4 methods offer RMSE at levels that are comparable with RMSE for Kriging, particularly for tests with 20 measurement sensors and more. In our previous research work, these interpolation techniques were assessed as promising for REM application.
On the other hand, the main conclusion from the zone analysis is that Kriging outperforms the other interpolation techniques. Even if in some cases IDW method was better than Kriging, differences between RMSE levels were negligible. We also noticed that for all the interpolation techniques, the quality of estimation was lower in the area close to the transmitter than in other zones. This results from the fact that interpolation methods are not able to extrapolate the signal level, i.e., to estimate well the signal level in the area close to the transmitter if all measurement results are provided by distant sensors only. Another conclusion is that for areas far away from the transmitter, all the analyzed interpolation methods overestimated the signal level. Therefore, such areas may be interpreted as FAZs. One of the possible solutions to this problem is the assessment of the coefficient by which the signal level is overestimated and recalculation of the estimated level for distant areas to get the level closer to the real value.
The analysis of the differences between interpolated and measured levels shows that the number of CEPs is higher for Kriging than for the other interpolation methods. Furthermore, it is for Kriging interpolation method only that an increase in the number of measurement sensors causes the percentage of correct estimations to grow, which in turn leads to the minimalization of the risk of the FAZ and the MDZ. It must be emphasized that, contrary to the statement based on the RMSE analysis only, IDW method is less accurate than Kriging. In our previous analyses, IDW p3 and IDW p4 methods were assessed as promising and comparable with Kriging in some cases. The zonal approach and analysis of CEPs revealed that Kriging outperforms the IDW method. Nevertheless, Kriging is much more complex than the IDW method and requires much higher computational power. For this reason, in some applications IDW p3 or IDW p4 may be preferable and sufficiently accurate.
Taking into account both the RMSE and the number of Correct Estimation Points, the interpolation technique based on Kriging should be recommended for the Electromagnetic Situational Awareness of Cognitive Radios supported by REM.
As future work, it would be worthwhile to investigate the influence of the semivariogram selection on the quality of the signal level estimation with the application of Kriging. We would also like to pay attention to the problem of the REM construction for zones that are close to the transmitter. Thus, the development of the hybrid method of REM construction seems to be valuable.
Author Contributions
All the authors have contributed to collecting results, performing analysis and creating this article. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article in Appendix A.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The measurement results collected for all the 39 points (sensors) are presented in the table below. The geographical coordinates and sensor IDs correspond to the deployment of the sensors shown in Figure 2. The average levels of measured signals are expressed in dBm. The variance was about 3 dB2 for most of the sensors and reached 7.4 dB2 in the worst case.

Table A1.
Results of measurements.
Table A1.
Results of measurements.
| Sensor ID | LATITUDE | LONGITUDE | Signal Level [dBm] | Sensor ID | LATITUDE | LONGITUDE | Signal Level [dBm] |
|---|---|---|---|---|---|---|---|
| P1 | 52.45390833 | 21.00674833 | −72.087 | P21 | 52.45544333 | 21.01000833 | −101.29 |
| P2 | 52.45294833 | 21.00970667 | −94.82 | P22 | 52.456415 | 21.00738333 | −104.27 |
| P3 | 52.45216833 | 21.00846667 | −77.935 | P23 | 52.456365 | 21.00446 | −87.69 |
| P4 | 52.4508 | 21.00642 | −88.057 | P24 | 52.45536333 | 21.00042833 | −93.598 |
| P5 | 52.45008167 | 21.00486167 | −88.625 | P25 | 52.453935 | 20.99994167 | −100.31 |
| P6 | 52.450235 | 21.003245 | −100.77 | P26 | 52.45470667 | 21.003115 | −86.089 |
| P7 | 52.450935 | 21.00240833 | −96.821 | P27 | 52.45770167 | 21.00118167 | −98.633 |
| P8 | 52.45229167 | 21.00102 | −93.106 | P28 | 52.45799667 | 21.00278667 | −97.605 |
| P9 | 52.44887833 | 21.00480167 | −96.386 | P29 | 52.45889 | 20.99992167 | −98.734 |
| P10 | 52.44482 | 20.99988167 | −100.76 | P30 | 52.45421 | 21.01242667 | −100.80 |
| P11 | 52.44415833 | 20.996475 | −100.73 | P31 | 52.45346 | 21.01116 | −101.11 |
| P12 | 52.44123 | 21.01492667 | −102.20 | P32 | 52.45427333 | 21.004795 | −69.633 |
| P13 | 52.44405 | 21.005135 | −100.97 | P33 | 52.45342833 | 21.00353667 | −67.873 |
| P14 | 52.44716167 | 21.004205 | −96.756 | P34 | 52.451185 | 21.00557333 | −70.594 |
| P15 | 52.448385 | 21.00562833 | −100.3 | P35 | 52.45081667 | 21.00459667 | −87.471 |
| P16 | 52.44962333 | 21.00723 | −85.686 | P36 | 52.45181167 | 21.004345 | −80.195 |
| P17 | 52.45104 | 21.0091 | −99.576 | P37 | 52.45222167 | 21.005275 | −59.779 |
| P18 | 52.45305333 | 21.01176333 | −90.147 | P38 | 52.45284167 | 21.00700333 | −71.768 |
| P19 | 52.453865 | 21.01358833 | −95.426 | P39 | 52.45311167 | 21.005705 | −64.569 |
| P20 | 52.45606667 | 21.011425 | −97.96 | - | - | - | - |
Appendix B
The transmitting part of the testbed (Figure A1) was located in the main building of our Institute. The receiving part of the testbed (Figure A2) was mounted on the vehicle that took measurements in specific locations. The measurement system was controlled by our own software and synchronized by a GPS receiver.
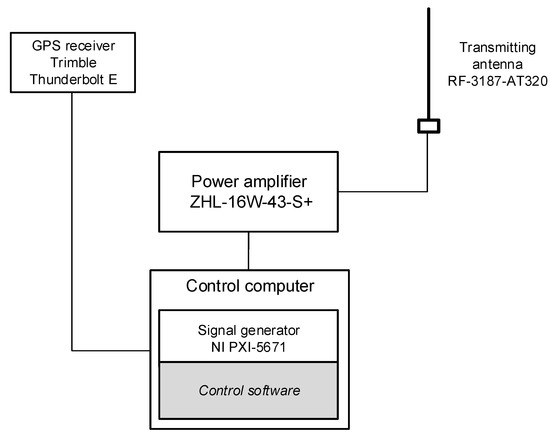
Figure A1.
The transmitting part of the testbed for UHF band.
Figure A1.
The transmitting part of the testbed for UHF band.
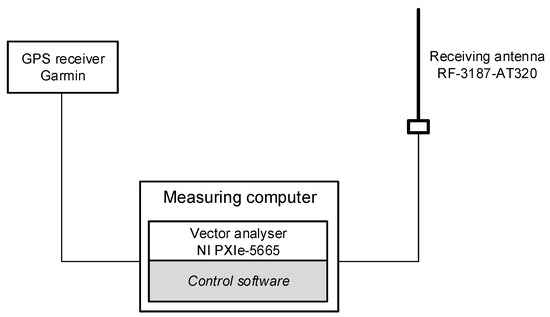
Figure A2.
The receiving part of the testbed for UHF band.
Figure A2.
The receiving part of the testbed for UHF band.
References
- Matyszkiel, R.; Grochowina, B.; Namiotko, R.; Wiśniewski, M.; Dobkowski, A.; Pater, G. The Tool to Support the Frequency Planning Process in the HF Range. In Proceedings of the 2018 New Trends in Signal Processing (NTSP), Demanovska Dolina, Slovakia, 10–12 October 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Romanik, J.; Golan, E.; Zubel, K.; Kaniewski, P. Electromagnetic Situational Awareness of Cognitive Radios supported by Radio Environment Maps. In Proceedings of the 2019 Signal Processing Symposium (SPSympo), Krakow, Poland, 17–19 September 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Luo, G.; Shi, M.; Zhao, C.; Shi, Z. Hash-Chain-Based Cross-Regional Safety Authentication for Space-Air-Ground Integrated VANETs. Appl. Sci. 2020, 10, 4206. [Google Scholar] [CrossRef]
- IEEE Standard for Information technology—Local and metropolitan area networks—Specific requirements—Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications Amendment 6: Wireless Access in Vehicular Environments. In IEEE Std 802.11p-2010; (Amendment to IEEE Std 802.11-2007 as amended by IEEE Std 802.11k-2008, IEEE Std 802.11r-2008, IEEE Std 802.11y-2008, IEEE Std 802.11n-2009, and IEEE Std 802.11w-2009); IEEE: New York, NY, USA, 2010; pp. 1–1465.
- Paul, A.; Chilamkurti, N.; Daniel, A.; Rho, S. Intelligent Vehicular Networks and Communications: Fundamentals, Architectures and Solutions; Elsevier: Amsterdam, The Netherlands; Boston, MA, USA; Heidelberg, Germany, 2017; ISBN 9780128092668. [Google Scholar]
- IEEE Standard—Information Technology—Telecommunications and information exchange between systems—Wireless Regional Area Networks—Specific requirements—Part 22: Cognitive Wireless RAN MAC and PHY specifications: Policies and Procedures for Operation in the Bands that Allow Spectrum Sharing where the Communications Devices May Opportunistically Operate in the Spectrum of Primary Service. In IEEE Std 802.22-2019; (Revision of IEEE Std 802.22-2011); IEEE: New York, NY, USA, 2020; pp. 1–1465.
- Bahaghighat, M.; Motamedi, S.A.; Xin, Q. Image Transmission over Cognitive Radio Networks for Smart Grid Applications. Appl. Sci. 2019, 9, 5498. [Google Scholar] [CrossRef]
- Garcia, C.E.; Camana, M.R.; Koo, I. Secrecy Energy Efficiency Maximization in an Underlying Cognitive Radio–NOMA System with a Cooperative Relay and an Energy-Harvesting User. Appl. Sci. 2020, 10, 3630. [Google Scholar] [CrossRef]
- Kustra, M.; Kosmowski, K.; Suchański, M. Hybrid sensing method of real OFDM signal. In Proceedings of the 2018 International Conference on Military Communications and Information Systems (ICMCIS), Warsaw, Poland, 22–23 May 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Kosmowski, K.; Prawdzik, K.; Baranowski, G. Immunity of automatic modulation classification algotithms against inaccurate estimation of signal parameters. In Proceedings of the 2017 Communication and Information Technologies (KIT), Vysoke Tatry, Slovakia, 4–6 October 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Arshid, K.; Hussain, I.; Bashir, M.K.; Naseem, S.; Ditta, A.; Mian, N.A.; Zahid, M.; Khan, I.A. Primary User Traffic Pattern Based Opportunistic Spectrum Handoff in Cognitive Radio Networks. Appl. Sci. 2020, 10, 1674. [Google Scholar] [CrossRef]
- Erdogan, E.; Çolak, S.; Alakoca, H.; Namdar, M.; Basgumus, A.; Durak-Ata, L. Interference Alignment in Multi-Hop Cognitive Radio Networks under Interference Leakage. Appl. Sci. 2018, 8, 2486. [Google Scholar] [CrossRef]
- Arjoune, Y.; Mrabet, Z.; Kaabouch, N. Multi-Attributes, Utility-Based, Channel Quality Ranking Mechanism for Cognitive Radio Networks. Appl. Sci. 2018, 8, 628. [Google Scholar] [CrossRef]
- Yilmaz, H.B.; Tugcu, T. Location estimation-based radio environment map construction in fading channels: REM construction in fading channels. Wirel. Commun. Mob. Comput. 2015, 15, 561–570. [Google Scholar] [CrossRef]
- IEEE Standard for Information technology—Telecommunications and information exchange between systems—Local and metropolitan area networks—Specific requirements—Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications Amendment 5: Television White Spaces (TVWS) Operation. In IEEE Std 802.11af-2013; (Amendment to IEEE Std 802.11-2012, as amended by IEEE Std 802.11ae-2012, IEEE Std 802.11aa-2012, IEEE Std 802.11ad-2012, and IEEE Std 802.11ac-2013); IEEE: New York, NY, USA, 2014; pp. 1–198.
- Corral-De-Witt, D.; Ahmed, S.; Awin, F.; Rojo-Álvarez, J.L.; Tepe, K. An Accurate Probabilistic Model for TVWS Identification. Appl. Sci. 2019, 9, 4232. [Google Scholar] [CrossRef]
- International Telecommunication Union. Recommendation 76, Deployment and use of cognitive radio systems. In Final Acts WRC-12, World Radiocommunication Conference; ITU: Geneva, Switzerland, 2012; ISBN 978-92-61-14141-7. [Google Scholar]
- EN 301 598 V1.1.1 White Space Devices (WSD); Wireless Access Systems Operating in the 470 MHz to 790 MHz TV Broadcast Band; Harmonized EN Covering the Essential Requirements of Article 3.2 of the R&TTE Directive; ETSI: Valbonne, France, 2014.
- Zhang, J.; Zhao, Q.; Zou, J. The IEEE802.22 WRAN System Based on Radio Environment Map (REM). In Proceedings of the First International Workshop on Education Technology and Computer Science, Wuhan, China, 7–8 March 2009; pp. 98–101. [Google Scholar] [CrossRef]
- Pesko, M.; Javornik, T.; Kosir, A.; Stular, M.; Mohorcic, M. Radio Environment Maps: The Survey of Construction Methods. KSII TIIS 2014, 8. [Google Scholar] [CrossRef]
- Bednarek, P.; Bicki, D.; Łopatka, J. Radio Environment Map for the Cognitive Radio Network Simulator. INTL J. Electron. Telecommun. 2018, 64, 45–49. [Google Scholar] [CrossRef]
- Kliks, A.; Kryszkiewicz, P.; Umbert, A.; PéRez-Romero, J.; Casadevall, F.; Kułacz, Ł. Application of Radio Environment Maps for Dynamic Broadband Access in TV Bands in Urban Areas. IEEE Access 2017, 5. [Google Scholar] [CrossRef]
- Bi, S.; Lyu, J.; Ding, Z.; Zhang, R. Engineering Radio Maps for Wireless Resource Management. IEEE Wireless Commun. 2019, 26, 133–141. [Google Scholar] [CrossRef]
- Ureten, S.; Yongacoglu, A.; Petriu, E. A comparison of Interference Cartography Generation Techniques in Cognitive Radio Networks. In Proceedings of the IEEE International Conference on Communications, Ottawa, ON, Canada, 10–15 June 2012; pp. 1879–1883. [Google Scholar] [CrossRef]
- Suchański, M.; Kaniewski, P.; Romanik, J.; Golan, E. Radio environment maps for military cognitive networks: Construction techniques vs. map quality. In Proceedings of the 2018 International Conference on Military Communications and Information Systems (ICMCIS), Warsaw, Poland, 22–23 May 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, R. Secure crowdsourced radio environment map construction. In Proceedings of the 2017 IEEE 25th International Conference on Network Protocols (ICNP), Toronto, ON, Canada, 10–13 October 2017; pp. 1–10. [Google Scholar] [CrossRef]
- Phillips, C.; Ton, M.; Sicker, D.; Grunwald, D. Practical radio environment mapping with geostatistics. In Proceedings of the IEEE International Symposium on Dynamic Spectrum Access Networks, Bellevue, WA, USA, 16–19 October 2012; pp. 422–433. [Google Scholar] [CrossRef]
- Zhang, T.; Ji, X.; Zhuang, Z.; Xu, W. JamCatcher: A Mobile Jammer Localization Scheme for Advanced Metering Infrastructure in Smart Grid. Sensors 2019, 19, 909. [Google Scholar] [CrossRef]
- Mao, D.; Shao, W.; Qian, Z.; Xue, H.; Lu, X.; Wu, H. Constructing accurate Radio Environment Maps with Kriging Interpolation in Cognitive Radio Networks. In Proceedings of the 2018 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference (CSQRWC), Xuzhou, China, 21–24 July 2018; pp. 1–3. [Google Scholar] [CrossRef]
- Tomic, S.; Beko, M.; Camarinha-Matos, L.M.; Oliveira, L.B. Distributed Localization with Complemented RSS and AOA Measurements: Theory and Methods. Appl. Sci. 2019, 10, 272. [Google Scholar] [CrossRef]
- Yilmaz, H.B.; Chae, C.-B.; Tugcu, T. Sensor placement algorithm for radio environment map construction in cognitive radio networks. In Proceedings of the 2014 IEEE Wireless Communications and Networking Conference (WCNC), Istanbul, Turkey, 6–9 April 2014; pp. 2096–2101. [Google Scholar] [CrossRef]
- Pesko, M.; Javornik, T.; Vidmar, L.; Košir, A.; Štular, M.; Mohorčič, M. The indirect self-tuning method for constructing radio environment map using omnidirectional or directional transmitter antenna. EURASIP J. Wirel. Com. Netw. 2015, 50. [Google Scholar] [CrossRef]
- Yilmaz, H.; Tugcu, T.; Alagöz, F.; Bayhan, S. Radio environment map as enabler for practical cognitive radio networks. IEEE Commun. Mag. 2013, 51, 162–169. [Google Scholar] [CrossRef]
- Kosmowski, K.; Romanik, J. Hybrid Method of the Radio Environment Map Construction to Increase Spectrum Awareness of Cognitive Radios. In Theory and Applications of Dependable Computer Systems. DepCoS-RELCOMEX 2020; Zamojski, W., Mazurkiewicz, J., Sugier, J., Walkowiak, T., Kacprzyk, J., Eds.; Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2020; Volume 1173, pp. 378–388. [Google Scholar] [CrossRef]
- Reddy, K.B.; Ramana, P.V.; Sumiya, K. Comparative analysis of spatial interpolation methods of different field measurements for cognitive radio. In Proceedings of the 2017 2nd IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), Belgrade, Serbia, 22–24 November 2011; pp. 2212–2216. [Google Scholar] [CrossRef]
- Le Nir, V.; Scheers, B. Multiple jammer localization and transmission power estimation for radio environment map. In Proceedings of the 2018 International Conference on Military Communications and Information Systems (ICMCIS), Warsaw, Poland, 22–23 May 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Dwarakanath, R.C.; Naranjo, J.D.; Ravanshid, A. Modeling of interference maps for Licensed Shared Access in LTE-advanced networks supporting Carrier Aggregation. In Proceedings of the IFIP Wireless Days (WD), Valencia, Spain, 13–15 November 2013; pp. 1–6. [Google Scholar] [CrossRef]
- Denkovski, D.; Atanasovski, V.; Gavrilovska, L.; Riihijaervi, J.; Maehoenen, P. Reliability of a Radio Environment Map: Case of Spatial Interpolation Techniques. In Proceedings of the 7th International Conference on Cognitive Radio Oriented Wireless Networks, Stockholm, Sweden, 18–20 June 2012. [Google Scholar] [CrossRef]
- Xiang, T.; Wang, H. Research on Distributed 5G Signal Coverage Detection Algorithm Based on PSO-BP-Kriging. Sensors 2018, 18, 4390. [Google Scholar] [CrossRef] [PubMed]
- Boccolini, G.; Hernández-Peñaloza, G.; Beferull-Lozano, B. Wireless sensor network for Spectrum Cartography based on Kriging interpolation. In Proceedings of the IEEE 23rd International Symposium on Personal, Indoor and Mobile Radio Communications—(PIMRC), Sydney, NSW, Australia, 9–12 September 2012; pp. 1565–1570. [Google Scholar] [CrossRef]
- Roger, S.; Botella, C.; Pérez-Solano, J.J.; Perez, J. Application of Radio Environment Map Reconstruction Techniques to Platoon-based Cellular V2X Communications. Sensors 2020, 20, 2440. [Google Scholar] [CrossRef] [PubMed]
- Suchański, M.; Kaniewski, P.; Romanik, J.; Golan, E. Radio environment map to support frequency allocation in military communications systems. In Proceedings of the 2018 Baltic URSI Symposium (URSI), Poznan, Poland, 15–17 May 2018; pp. 230–233. [Google Scholar] [CrossRef]
- Romanik, J.; Zubel, K. Radio Environment Maps for Military Cognitive Networks: Analysis of Measurement-based Maps for UHF Band. In Proceedings of the 2019 Communication and Information Technologies (KIT), Vysoke Tatry, Slovakia, 9–11 October 2019. [Google Scholar] [CrossRef]
- Zubel, K.; Romanik, J.; Golan, E.; Wilgucki, K. Measurement method for construction of the radio environment maps supporting cognitive radios. In Proceedings of the Radioelectronic Systems Conference 2019; Kaniewski, P., Matuszewski, J., Eds.; SPIE: Jachranka, Poland, 2020; p. 29. [Google Scholar] [CrossRef]
- Suchański, M.; Kaniewski, P.; Romanik, J.; Golan, E.; Zubel, K. Radio environment maps for military cognitive networks: Density of small-scale sensor network vs. map quality. EURASIP J. Wirel. Com. Netw. 2020, 189. [Google Scholar] [CrossRef]
- Suchański, M.; Kaniewski, P.; Romanik, J.; Golan, E.; Zubel, K. Radio Environment Maps for Military Cognitive Networks: Deployment of Sensors vs. Map Quality. In Proceedings of the 2019 International Conference on Military Communications and Information Systems (ICMCIS), Budva, Montenegro, 14–15 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).