Structural Adversarial Variational Auto-Encoder for Attributed Network Embedding

Abstract

As most networks come with some content in each node, attributed network embedding has aroused much research interest. Most existing attributed network embedding methods aim at learning a fixed representation for each node encoding its local proximity. However, those methods usually neglect the global information between nodes distant from each other and distribution of the latent codes. We propose Structural Adversarial Variational Graph Auto-Encoder (SAVGAE), a novel framework which encodes the network structure and node content into low-dimensional embeddings. On one hand, our model captures the local proximity and proximities at any distance of a network by exploiting a high-order proximity indicator named Rooted Pagerank. On the other hand, our method learns the data distribution of each node representation while circumvents the side effect its sampling process causes on learning a robust embedding through adversarial training. On benchmark datasets, we demonstrate that our method performs competitively compared with state-of-the-art models.

1. Introduction

Networks are ubiquitous since their strong power to model real data, such as telecommunication networks, social networks, citation networks, and biological networks. There are many crucial networks analysis tasks to deal with, such as node classification, node clustering, link prediction, community detection, etc. Since a large portion of networks contain nodes with extra information, attributed networks are really worth to study. Earlier works suffer high computation and great space cost since they usually represent networks with adjacency matrix. Then, network embedding, also known as graph embedding or network representation learning is proposed, aiming to embed vertices into a low dimensional space where the network structural information and network properties are preserved, then it is easy to exploit off-the-shelf machine learning algorithms to analysis networks efficiently [1].

First kind of network embedding models are methods such as DeepWalk [2], node2vec [3] and LINE [4], which adopt language model word2vec [5] in network representation. Second kind of models are based on matrix factorization, such as HOPE [6], TADW [7], and MNF-M [8]. They construct a matrix first, then decompose it to get embeddings.

As for attribute network embedding, since Graph Neural Networks (GCNs) have achieved great success, many models combine the GCN to do network analysis tasks. VGAE [9] uses the auto-encoder framework and combines the Variational auto-encoders (VAE) ([10,11]) and GCN to learn great node representation. Then ARVGA [12] and CAN [13] improve it by adding GAN or changing learning aim. GCN-based models inherit some common defects. VGAE and ARVGA use variational auto-encoders (VAE) to encode the data distribution of the latent codes in graphs while suffering from the drawback of the sampling process in VAE, which makes the latent representation not repeatable for the same sample and harms the performance in related tasks. These typical methods mostly ignore the global information between nodes.

To overcome the deficits mentioned before, we propose a framework (SAVGAE) to encode the graph structure and node attribute of attributed networks into compact representation. We use the higher proximity metric Rooted PageRank to include the local and global information between each pair of nodes. We design a delicate structure to employ the strong learning ability of VAE while circumventing the effect brought by the inner core sampling process through an adversarial training module. The delicate structure makes the representation exclusive for each node and the adversarial training module prevents the performance declining it may cause. We evaluate our model on three typical graph analysis tasks including link prediction, node clustering, and graph visualization meanwhile get competitive performance. In summary, our contributions are as follows:

• We propose to use Rooted PageRank (RPR) rather than adjacency matrix as the reconstruction objective so as to preserve local and global proximity simultaneously in node representation.
• We develop a novel graph autoencoder model combining generative adversarial networks and variational autoencoder, where we use the great learning ability of VAE and avoid the side effect it may cause on learning graph embedding.
• We evaluate the proposed model over two tasks on three widely used graph benchmarks, and get competitive results.

We organize the rest of our paper as follows. In Section 2, we introduce the work related to our model. In Section 3, we detail our model SAVGAE. In Section 4, we introduce the experiments setup and experiments results. Finally, in Section 5, we draw our conclusions.

2. Related Work

In this section, we introduce the models related to our work. Firstly, we introduce the earlier network embedding methods, then we present attributed network embedding models. Finally, we introduce related models exploiting deep generative models.

2.1. Network Embedding

Network embedding assigns each node in the network a low dimensional representation while preserving the network information [14]. Earlier works were related to dimension reduction techniques such as Isomap [15], Locally Linear Embedding (LLE) [16], and Laplacian Eigenmap (LE) [17]. The time complexity of these methods is usually at least quadratic with respect to the number of nodes, thus suffering scalability issue [1]. Recent models are directly designed for representing networks rather than reducing the high dimensionality of the non-relational data.

2.2. Attributed Network Embedding

Attributed Network Embedding exploits the topological structure and the node content simultaneously. Yang et al. prove that DeepWalk is equivalent to matrix factorization, and propose TADW to incorporate text features of nodes into network embedding [7]. TriNDR [18] is a coupled neural network model to exploit network structure, node content, and node labels to learn node representation. However, these models shallow models are either DeepWalk variants or based on the mechanism of matrix factorization. Recently Graph Neural Networks (GNNs) achieve excellent performance due to their strong representation power, and there are some works that exploit GNN in network embedding, such as VGAE, incorporating GCN into variational autoencoder framework.

2.3. Deep Generative Models

Generative models are an important class of models in probability statistics and machine learning, referring to a set of models used to generate observable data randomly. Generative models have a wide range of applications, and can be used to model different kinds of data, such as images, text, sound, etc. Thus, it is promising to use generative models in network representation learning. Deep generative models take advantage of the ability of deep neural networks to approximate arbitrary functions to model a complex distribution, Variational Autoencoder (VAE) and Generative Adversarial Networks (GANs) are two excellent classes.

AAE [19] combines the GAN and autoencoder to perform variational inference. However, the model is not designed for networks. Recently, Dai et al. used the adversarial training in networks [20]. However, the model cannot handle networks with node attributes. ARVGA also combines the GAN with the graph auto-encoder structure. However it only uses the GAN as a regularizer to enhance an intrinsic hypothesis of prior distribution in VAE. In contrast, our model uses the adversarial mechanism to improve the defect of VAE in attribute network embedding. Ref. [21] also try to overcome the problem of VAE, but it aims at general data.

3. Model

In this section, we formalize the attribute network embedding task we focus on firstly. Then we present our Structural Adversarial Variational Graph Auto-Encoder (SAVGAE) model. Next we introduce the Structral Variational Graph Auto-Encoder(SVGA) module, which uses Rooted Pagerank to learn comprehensive topology structural information. Finally, we introduce the adversarial training module which overcomes the defects of the VAE.

3.1. Problem Definition

Definition  1

(Attibuted Network). A attributed network is defined as $\mathcal{G}=(\mathcal{V},\mathcal{E},\mathbf{X})$, where $\mathcal{V}=(v_1,v_2,...,v_N)$ is the set of nodes, and $\mathcal{E}$ denotes the sets of edges with $e_{i,j}=(v_i,v_j)\in \mathcal{E}$. $\mathbf{X}$ is the feature matrix with ${\mathbf{x}}_{\mathbf{i}}\in \mathbf{X}$ denoting the feature information associated with node $v_i$. Meanwhile the topology information of the network can be represented by adjacency matrix $\mathbf{A}$. All notations are summarized in Table 1.

Table 1. Main Notations.

Symbol	Description
$\mathcal{V}$	nodes
$\mathcal{E}$	edges
$\mathcal{G}$	attribute network
$\mathbf{X}$	attribute matrix
$\mathbf{A}$	adjacency matrix
$\mathbf{Z}$	embedding matrix
$\mathbf{P}$	transition matrix

Problem  1

(Attributed Network embedding). The goal is to project each node $v_i\in V$ to a low-dimension vector $z_i\in {\mathbb{R}}^{N\times D}$:

$$f:V\mapsto Z$$

(1)

where $D<<N$, such that embedding matrix Z should well preserve the topological structure and attribute information of the graph, given an attributed network denoted as $\mathcal{G}=(\mathcal{V},\mathcal{E},X)$.

3.2. Overall Architecture

In this section, we introduce the overall architecture of our model. As Figure 1 shows, our model consists of two modules. Firstly, the SVGAE module learns representations for nodes while preserving their overall structural information and attribute information. Then we propose adversarial training module to learn robust embeddings for nodes.

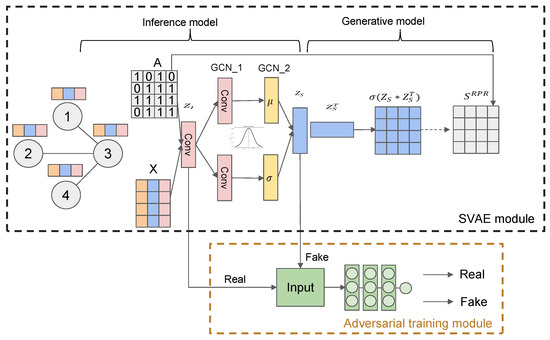
Figure 1. The proposed Structural Adversarial Variational Graph Auto-Encoder(SAVGAE). It consists of two modules. The SAVE module is a variational graph auto-encoder which encodes the network structure $\mathbf{A}$ and network attribute $\mathbf{X}$ into embedding ${\mathbf{Z}}_{\mathbf{S}}$ and reconstruct the Rooted Pagerank matrix ${\mathbf{S}}^{\mathbf{RPR}}$ to make ${\mathbf{Z}}_{\mathbf{S}}$ contain comprehensive network topological information. The adversarial training module reduces the information loss between ${\mathbf{Z}}_{\mathbf{I}}$ and ${\mathbf{Z}}_{\mathbf{S}}$ to guarantee ${\mathbf{Z}}_{\mathbf{I}}$ is exclusive and representative.

• Structural Variational Graph Auto-encoder module. SVGAE takes in adjacency matrix $\mathbf{A}$ and feature matrix $\mathbf{X}$ and gets embeddings ${\mathbf{Z}}_{\mathbf{S}}$, then reconstructs the Rooted Pagerank matrix.
• Adversarial training module. This module introduces the adversarial training based on the SVGAE to overcome the side effect of the VAE framework.

3.3. Structural Variational Graph Auto-Encoder Module

The Structural Variational Graph Auto-encoder consists of an inference model and a generative model. In our model, we adopt vanilla Graph Convolution Network layer [22] in our graph auto-encoder model. The layerwise transformation is denoted as follows:

$$\begin{array}{c}\hfill {\mathbf{Z}}^{l+1}=f({\mathbf{Z}}^{\left(l\right)},\mathbf{A}|{\mathbf{W}}^{\left(l\right)})\end{array}$$

(2)

where ${\mathbf{Z}}^l$ is the input layer, $\mathbf{A}$ is the adjacency matrix, and the $\mathbf{W}$ is the weights parameters to be learned in the training process. To be specific, our graph convolution here is defined as follows:

$$\begin{array}{c}\hfill f({\mathbf{Z}}^{\left(l\right)},\mathbf{A}|{\mathbf{W}}^{\left(l\right)})=\varphi \left({\stackrel{\sim }{\mathbf{D}}}^{-\frac{1}{2}}\stackrel{\sim }{\mathbf{A}}{\stackrel{\sim }{\mathbf{D}}}^{-\frac{1}{2}}{\mathbf{Z}}^{\left(l\right)}{\mathbf{W}}^{\left(l\right)}\right),\end{array}$$

(3)

where $\varphi$ is the Relu activation function, $\stackrel{\sim }{\mathbf{A}}=\mathbf{A}+\mathbf{I}$, $\stackrel{\sim }{{\mathbf{D}}_{\mathbf{ii}}}=\sum \stackrel{\sim }{{\mathbf{A}}_{\mathbf{ij}}}$.

3.3.1. Rooted PageRank

Here we choose a high-order proximity Rooted PageRank (RPR) $S_{RPR}$ [23] as an alternative to $\mathbf{A}$. As is defined in Equations (4) and (5), the $(i,j)$-th entry of $S_{RPR}$ defines the probability that if there is a random walk starting from node $v_i$, it will stop at node $v_j$ in the steady state. ${\beta }_{RPR}\in (0,1)$ is the parameter to control the probability of the current node walking to a neighbor node randomly rather than jumping back to the start node. $\mathbf{P}$ is transition matrix, and ${\mathbf{P}}_{i,j}=\frac{{\mathbf{A}}_{i,j}}{{\sum }_{k=1}^{\left|V\right|}{\mathbf{A}}_{i,k}}$. So we can use $S_{RPR}$ to describe the node-to-node proximity. Specifically, the i-th row of ${\mathbf{S}}_{RPR}$, can be used to represent the global structural information of node $v_i$.

$${\mathbf{S}}^{RPR}={\beta }_{RPR}·{\mathbf{S}}^{RPR}·\mathbf{P}+(1-{\beta }_{RPR})·\mathbf{I}$$

(4)

$${\mathbf{S}}^{RPR}=(1-{\beta }_{RPR}){(\mathbf{I}-{\beta }_{RPR}\mathbf{P})}^{-1}$$

(5)

3.3.2. Inference Model

In the inference model, we get hidden variable ${\mathbf{Z}}_S$ from the input adjacency matrix $\mathbf{A}$ and attribute matrix $\mathbf{X}$.

$$\begin{array}{cc}\hfill q\left({\mathbf{Z}}_S\right|\mathbf{X},\mathbf{A})=\prod _{i=1}^{N}q\left(z_s^{\left(i\right)}\right|\mathbf{X},\mathbf{A}),& \\ \hfill withq\left(z_s^{\left(i\right)}\right|\mathbf{X},\mathbf{A})=N\left(z_s^{\left(i\right)}\right|{\mu }_s^{\left(i\right)},diag\left({\sigma }_i^2\right))\end{array}$$

(6)

The inference model can also be seen as an encoder. $G({\mathbf{Z}}_S,\mathbf{A})=q\left({\mathbf{Z}}_S\right|\mathbf{X},\mathbf{A})$ which actually consists of two GCN layers.

$$\begin{array}{c}\hfill {\mathbf{Z}}_I=f_{Relu}(\mathbf{X},\mathbf{A}|{\mathbf{W}}^{\left(0\right)})\end{array}$$

(7)

$$\begin{array}{c}\hfill {\mathbf{Z}}^{\left(21\right)}=f_{Relu}({\mathbf{Z}}_I,\mathbf{A}|{\mathbf{W}}^{\left(11\right)})\end{array}$$

(8)

$$\begin{array}{c}\hfill {\mathbf{Z}}^{\left(22\right)}=f_{Relu}({\mathbf{Z}}_I,\mathbf{A}|{\mathbf{W}}^{\left(12\right)})\end{array}$$

(9)

$\mu ={\mathbf{Z}}^{\left(21\right)}$ and $log\sigma ={\mathbf{Z}}^{\left(22\right)}$ are matrix of mean vectors $z_i$ and matrix of log of the variance vectors respectively.

3.3.3. Generative Model

The generative model can also be seen as a decoder where traditional models aim at reconstructing the adjacency matrix $\mathbf{A}$ so the embedding matrix $\mathbf{Z}$ can preserve the information of graph $\mathbf{G}$. However, $\mathbf{A}$ just encode the one-order structural information of the graph which is not enough for learning comprehensive information of the graph structure. Therefore we adopt the ${\mathbf{S}}_{RPR}$ as the reconstruction aiming of the decoder. So the node embeddings preserve the comprehensive information of the network after loss function being optimized as it can reconstruct the Rooted Pagerank matrix to some extent.

$$\begin{array}{c}\hfill {\mathbf{Z}}_S=\mu \left({\mathbf{Z}}_I\right)+\sigma \left({\mathbf{Z}}_I\right)\ast ϵ,ϵ\sim \mathbf{N}(0,1)\end{array}$$

(10)

$$\begin{array}{cc}\hfill p\left(\widehat{\mathbf{S}}\right|{\mathbf{Z}}_S)=\prod _{i=1}^N\prod _{j=1}^{N}p\left(\widehat{S_{ij}}\right|z_s^{\left(i\right)},z_s^{\left(j\right)}),& \\ \hfill withp(\widehat{S_{ij}}=1|z_s^{\left(i\right)},z_s^{\left(j\right)})=\theta \left(z_s^{{\left(i\right)}^{\top }}{z}_s^{\left(j\right)}\right)\end{array}$$

(11)

3.3.4. Optimization

As a Variational graph auto-encoder model, we need optimize the variational lower bound

$$\mathcal{L}={\mathbb{E}}_{q\left({\mathbf{Z}}_S\right|\mathbf{X},\mathbf{A})}[logp\left(\widehat{\mathbf{S}}\right|{\mathbf{Z}}_S)]-KL[q\left({\mathbf{Z}}_S\right|\mathbf{X},\mathbf{A})\left|\right|p\left({\mathbf{Z}}_S\right)],$$

(12)

where the former indicates the reconstruction loss and the latter uses the Kullback-Leibler divergence as a regularizer of the variational auto-encoder.

3.4. Adversarial Training Module

In the previous section, we can find ${\mathbf{Z}}_S$ is suitable for represent the nodes of the network as illustrated in Figure 1. However, locating after the sampling process makes it not repeatable, so we decide to use ${\mathbf{Z}}_I$ for its stability, and using adversarial training module to decrease the information loss between ${\mathbf{Z}}_S$ and ${\mathbf{Z}}_I$ to guarantee the latter is representative.

In our adversarial training module, the input of the discriminator is latent code either from ${\mathbf{Z}}_I$(real) or ${\mathbf{Z}}_S$(fake) and the output is a scalar deciding whether the input is true or not. The cost of the discriminator is

$$\begin{array}{cc}\hfill -\frac{1}{2}{\mathbb{E}}_{x\sim p_x}[log\mathcal{D}\left(f(\mathbf{X},\mathbf{A})\right)]& \\ \hfill -\frac{1}{2}{\mathbb{E}}_{x\sim p_x}[log(1-\mathcal{D}\left(\mathcal{G}(\mathbf{X},\mathbf{A})\right))].\end{array}$$

(13)

Then the objective to train the encoder of SVGAE module with discriminator of the adversarial training module is as follows:

$$\begin{array}{cc}\hfill \underset{\mathcal{G}}{min}\underset{\mathcal{D}}{max}{\mathbb{E}}_{x\sim p_x}[log\mathcal{D}\left(f(\mathbf{X},\mathbf{A})\right)]& \\ \hfill +{\mathbb{E}}_{x\sim p_x}[log(1-\mathcal{D}\left(\mathcal{G}(\mathbf{X},\mathbf{A})\right))].\end{array}$$

(14)

3.5. Overall Algorithm

As in Algorithm 1, the SAVGAE model takes in the attributed network $\mathcal{G}$, and generates ${\mathbf{Z}}_I$ and ${\mathbf{Z}}_S$ through Equations (7) and (10) in step 2. Then it takes m samples from ${\mathbf{Z}}_I$ and ${\mathbf{Z}}_S$ and trains the discriminator in step 6. Finally, it trains the SAVGAE through updating Equation (12) in step 8 and gets the desired network embedding ${\mathbf{Z}}_I$.

Algorithm 1 Algorithm for SAVGAE

Input:$G=\{\mathbf{V},\mathbf{E},\mathbf{X}\}$: Graph; T: the number of iterations of training process; K: the number of steps for updating discriminator; d: the dimension of the embeddings

Output:${\mathrm{Z}}_I\in R^{n\times d}$

1: for iterator = 1 to T do

2:     Generate matrix ${\mathrm{Z}}_I$ and ${\mathrm{Z}}_S$ by Equations (7) and (10);

3:     for iterator = 1 to K do

4:       Sample m samples $\left\{a^{\left(1\right)},\dots ,a^{\left(m\right)}\right\}$ from ${\mathrm{Z}}_I$

5:       Sample m samples $\left\{b^{\left(1\right)},\dots ,b^{\left(m\right)}\right\}$ from ${\mathrm{Z}}_S$

6:       Update the discriminator with its stochastic gradient $$\nabla \frac{1}{m}\sum _{i=1}^m\left[log\mathcal{D}\left(a^i\right)+log\left(1-\mathcal{D}\left(b^i\right)\right)\right]$$

7:     end for

8:     Update the SVAE module by Equation (12)

9: end for

10: return ${\mathrm{Z}}_I\in R^{n\times d}$

4. Experiments

In this section, we evaluate the proposed model on two widely used tasks: link prediction and node clustering over 2 real-world datasets [24]. Meanwhile, we compare our methods with baseline algorithms.

4.1. Datasets and Baselines

We report experimental results on two attributed graph datasets: Cora and Citeseer. They are citation networks with varying sizes where nodes and edges represent publications and citations. Node attributes of Cora and Citeseer are bag-of-words representing the content of the publication. The statistics of the datasets are summarized in Table 2.

Table 2. Statistics of datasets.

Datasets	#Nodes	#Edges	#Attributes	#Lables
Cora	2708	5429	1433	7
Citeseer	3327	4732	3703	6

To validate and evaluate SAVGAE, we compare it with 7 baseline methods including DeepWalk, Spectral Clustering [25], node2vec, GAE, VGAE, ARGA, ARVGA in link prediction task. In node clustering task, we include 6 methods K-means, Graph Encoder [26], DNGR [27], RTM [28], RMSC [29], TADW besides baselines in link prediction task.

4.2. Experimental Setup and Evaluation Methods

We detail the experimental setup and evaluation methods for link prediction and node clustering respectively. Link prediction task aims at inferring the missing edges from the network which is not complete. Following the experimental settings of VGAE, each dataset is partitioned into the training set, the validatoin set and the test set. We randomly remove 5% edges for validation and 10% edges for test which serve as positive samples. Then we sample the same number of non-existing links as negative samples from the pairs of unconnected nodes. The model is trained on the residual network where attributes of nodes are kept. The model can be evaluated by the ability to classify the positive samples and negative samples, and we employ the AUC(the area under a receiver operating characteristic curve) and AP(average precision) as the metrics for evaluation.

For the node clustering task, we employ the K-means algorithm based on the node embeddings learned from the training phase. Then we employ accuracy (Acc), normalized mutual information (NMI), F-score (F1), precision, and average rand index (ARI) as metrics, compared to the true class labels of nodes.

4.3. Main Results

In this section, we detail our model performance on link prediction and node clustering experiments. Then we validate the effectiveness of different parts of SAVGAE through ablation studies. Finally, we visualize the node embeddings.

4.3.1. Link Prediction

The experimental results on the link prediction task are reported in Table 3. We can observe that SAVGAE achieves outstanding performance: consistently performs better than all baseline models. Compared with all the baselines, SAVGAE increased the AP score from around 2.9% compared with ARVGE, 3.9% compared with VGAE, 13.1% compared with VGAE without node features; 14.3% and 12.3% compared with Spectral Clustering and DeepWalk respectively.

Table 3. Results for Link Prediction. GAE* and VGAE* denote the variants of GAE and VGAE, which do experiments without using input features. Bold font indicates the best result.

Model	Cora		Citeseer
	AUC	AP	AUC	AP
SC	84.6	88.5	80.5	85.0
DW	83.1	85.0	80.5	83.6
node2vec	84.1	87.2	83.7	85.3
GAE*	84.3	88.1	78.7	84.1
VGAE*	84.0	87.7	78.9	84.1
GAE	91.0	92.0	89.5	89.9
VGAE	91.4	92.6	90.8	92.0
ARGE	92.4	93.2	91.9	93.0
ARVGE	92.4	92.6	92.4	93.0
SAVGAE(ours)	95.0	95.3	94.6	95.7

4.3.2. Node Clustering

After getting node embeddings, we apply K-means algorithm to do the node clustering task. The results on Cora and Citeseer datasets are reported in Table 4 and Table 5. The results illustrate that SAVGA has achieved a great improvement compared with all the other baselines. For example, on Cora dataset, SAVGAE has increased the accuracy from 40.2% compared with K-means to 88.0% compared with Spectral Clustering; increased the F1 score from 44.5% compared with TADW to 102.8% compared with DeepWalk; and increased NMI from 55.0% compared with K-means to 10.4% compared with ARVGE. The results has demonstrated the superiority of our SAVGAE.

Table 4. Clustering Results on Cora. Bold font indicates the best result.

Cora	Acc	NMI	F1	Precision	ARI
K-means	0.492	0.321	0.368	0.369	0.230
SC	0.367	0.127	0.318	0.193	0.031
GraphEncoder	0.325	0.109	0.298	0.182	0.006
DeepWalk	0.484	0.327	0.392	0.361	0.243
node2vec	0.526	0.343	0.413	0.393	0.284
DNGR	0.419	0.318	0.340	0.266	0.142
RTM	0.440	0.230	0.307	0.332	0.169
RMSC	0.407	0.255	0.331	0.227	0.090
TADW	0.560	0.441	0.481	0.396	0.332
GAE	0.596	0.429	0.595	0.596	0.347
VGAE	0.609	0.436	0.609	0.609	0.346
ARGE	0.640	0.449	0.619	0.646	0.352
ARVGE	0.638	0.450	0.627	0.624	0.374
SAVGAE(ours)	0.690	0.497	0.695	0.701	0.429

Table 5. Clustering Results on Citeseer. Bold font indicates the best result.

Cora	Acc	NMI	F1	Precision	ARI
K-means	0.540	0.305	0.409	0.405	0.279
SC	0.239	0.056	0.299	0.179	0.010
GraphEncoder	0.225	0.033	0.301	0.179	0.010
DeepWalk	0.337	0.088	0.270	0.248	0.092
node2vec	0.374	0.105	0.291	0.276	0.125
DNGR	0.326	0.180	0.300	0.200	0.044
RTM	0.451	0.239	0.342	0.349	0.203
RMSC	0.295	0.139	0.320	0.204	0.049
TADW	0.455	0.291	0.414	0.312	0.228
GAE	0.408	0.176	0.372	0.418	0.124
VGAE	0.344	0.156	0.308	0.349	0.093
ARGE	0.573	0.350	0.546	0.573	0.341
ARVGE	0.544	0.261	0.529	0.549	0.245
SAVGAE(ours)	0.582	0.352	0.573	0.596	0.364

4.3.3. Graph Visualization

Visualization is another intuitive and effective way to assess the performance of network embedding methods. We get node representations through SAVGAE model, then map these points into 2D space by t-SNE [30]. The color denotes the class label of the nodes in the dataset, which is not exploited in our unsupervised attributed network embedding. Therefore, nodes in the same color should locate closer to each other. As in Figure 2, the meaningful clustering layout demonstrates the performance of SAVGAE.

Figure 2. The visualization results of SAVGAE on Cora dataset.

4.4. Ablation Studies

To evaluate the performance of different parts of SAVGAE, we perform ablation studies on link prediction and node clustering task. “-RPR” means dicarding high-order proximity Rooted Pagerank and using adjacency matrix as learning objective. “-Adversarial training” means discarding adversarial training module. “-RPR and adversarial training” means discarding both Rooted Pagerank and adversarial training module. The results are illustrated in Table 6, Table 7 and Table 8. We find that the hybrid model performs best.

Table 6. Ablation results of link prediction experiments.

Model	Cora		Citeseer
	AUC	AP	AUC	AP
SAVGAE(ours)	95.0	95.3	94.6	95.7
-RPR	95.2	95.7	93.7	94.7
-Adversarial training	92.6	92.9	92.7	94.1
-RPR and adversarial training	91.4	92.6	90.8	92.0

Table 7. Ablation results of clustering experiments on Cora.

Cora	Acc	NMI	F1	Precision	ARI
SAVGAE(ours)	0.690	0.497	0.695	0.701	0.429
-RPR	0.655	0.465	0.628	0.635	0.393
-Adversarial training	0.642	0.462	0.640	0.632	0.282
-RPR and adversarial training	0.609	0.436	0.609	0.609	0.346

Table 8. Ablation results of clustering experiments on Citeseer.

Cora	Acc	NMI	F1	Precision	ARI
SAVGAE(ours)	0.582	0.352	0.573	0.596	0.364
-RPR	0.547	0.291	0.526	0.548	0.272
-Adversarial training	0.547	0.291	0.547	0.582	0.272
-RPR and adversarial training	0.344	0.156	0.308	0.349	0.093

5. Conclusions

In this paper, we propose SAVGAE, a novel attributed network embedding method, which preserves comprehensive topology structure and node content information of attributed network by modifying the VAE to handle graph data while integrating with generative adversarial networks. We use Rooted PageRank (RPR) rather than adjacency matrix as the reconstruction objective of the auto-encoder to preserve local and global proximity simultaneously in node representation while not increasing much model complexity. The sampling process is an indispensable part of VAE before getting a latent representation of the node, but it causes the problem that the node embeddings are not exclusive which may affect the downstream network analysis task. We modify the VAE structure and integrate with generative adversarial networks to learn an exclusive and robust embedding for each node to overcome the aforementioned problem. Empirically, we evaluate the generated network representations in a variety of network datasets and applications. The results demonstrate the superiority of our method compared with the state-of-the-art. Our future work will focus on proposing a generalized framework that can handle unseen nodes and networks rather than just learning embeddings on a single fixed network.