Simplified Plastic Hinge Model for Reinforced Concrete Beam–Column Joints with Eccentric Beams

Abstract

In nonlinear analysis for performance-based design of reinforced concrete moment frames, a plastic hinge spring element is predominantly used in order to simply and accurately describe the inelastic behavior of beam–column joints, including strength degradation. Although current design codes and guidelines provide various beam–column joint models, the focus is on concentric beam–column joints. Therefore, more studies are required for eccentric beam–column joints, which are also common in practice. In the present study, to consider the effect of beam eccentricity on the behavior of beam–column joints, a simplified plastic hinge model was proposed using the effective joint width of current design codes. The proposed model was compared to the cyclic loading test results of beam–column joints with/without beam eccentricity. The comparison showed that the simplified plastic hinge model with the effective joint width of NZS 3101-2006 or Eurocode 8 is considered acceptable for design purpose.

1. Introduction

For a safe and cost-effective design of building structures, the performance-based earthquake design is widely used. For the design approach, nonlinear behavior of structural components should be well described in analysis, including deformation capacity. In the case of reinforced concrete (RC) moment frames, the deformation capacity is significantly affected by shear damage and bar-slip at beam–column joints [1,2,3,4,5,6,7,8,9,10,11], and the joint shear damage and bar-slip are unavoidable even if the requirements of current seismic design codes [12,13,14,15] for beam–column joints are satisfied. Thus, to achieve a reliable design of RC moment frames, those characteristics affecting the nonlinear behavior of beam–column joints should be carefully considered in the analysis.

In practice, a lumped plastic hinge spring element is predominantly used for beam–column joints, because it is available in most of commercial software for nonlinear analysis [16,17]. Thus, it is reasonable to reflect those characteristics in the plastic hinge spring element. Meanwhile, joint shear strength degradation is also critical to the deformation capacity of beam–column joints. To address the nonlinear behavior of beam–column joints, a vast number of studies have been conducted: idealizing models, such as the strut–tie mechanism-based models [7,8,9,10,18,19,20] and the rotating-angle softened-truss model [21], and empirical equations [12,22,23] were proposed; the strain-increase in beam flexural bars due to cyclic loads was considered in the prediction of the joint shear strength degradation and deformation capacity [6]; the effects of joint shear demand, joint hoop bars, and yield strength of beam flexural bars on the joint deformation capacity were considered [24]; the effects of bar-slip, bar elongation, diagonal cracking, and shear deformation on the joint shear strength degradation were studied [8]; and the joint shear strength was defined as a function of target lateral drift ratio [9,10]. Although the existing studies provide a deep understanding on the behavior of beam–column joints, the majority of the existing studies focused on concentric beam–column joints. However, eccentric beam–column joints, in which the axis of beams framing into a joint does not lie on the column centerline, are also common in practice.

To investigate the effect of eccentric beams on the joint shear strength, several experimental studies were performed, and it was found that as the beam eccentricity increased, the shear strength capacity and ductility were decreased at interior [25,26,27,28,29,30,31] and exterior [32,33,34] beam–column joints. To consider the degradation in the shear strength of eccentric beam–column joints, a simple method of reducing the effective joint width was also proposed [27,28]. On the other hand, it was found that slabs can alleviate the shear strength degradation of eccentric beam–column joints [35,36]. Although the existing studies investigated the joint shear strength of eccentric beam–column joints, the deformation capacity and strength degradation were not evaluated, which were necessary for nonlinear analysis modeling.

Recently, for an improved performance-based design, Hwang and Park [37] developed an advanced plastic hinge model, which is applicable to interior and exterior beam–column joints. In the model, the effects of beam bar-slip and joint shear strength degradation were taken into account covering various design parameters, and the joint shear deformation and beam flexural deformation were also combined for simple modeling and computation. However, the existing models, including the model of Hwang and Park [37], were developed primarily for concentric beam–column joints. Thus, more studies are required for eccentric beam–column joints, considering the facts that a considerable number of RC structures are designed to have eccentric beam–column joints in practice and the design of RC structures is subjected to seismic and dynamic influences.

In the present study, for a safer and more economical design of RC structures, the effect of beam eccentricity on the behavior of beam–column joints was investigated. To this purpose, the effective joint width of current design codes and the plastic hinge model of Hwang and Park [36] were utilized with a modification, which can describe the nonlinear behavior of eccentric beam–column joints. For verification, the proposed method was compared to existing test results available in the literature.

2. Current Design Codes for Effective Joint Width

Current design codes, such as ACI 318-19 [12], ACI 352R-02 [13], and NZS 3101-2006 [14], specify the effective joint width b_s for concentric and eccentric beam–column joints (Figure 1). On the other hand, Eurocode 8 [15] does not consider the beam eccentricity in calculation of the effective joint width.

$$b_s=\min \left[b_b+2x,b_b+h_c,b_c\right] \mathrm{in} \mathrm{ACI} 318-19$$

(1)

$$b_s=\min \left[\frac{b_b+b_c}{2},b_b+{\displaystyle \sum m\frac{h_c}{2},b_c}\right] \mathrm{in} \mathrm{ACI} 352\mathrm{R}-02$$

(2)

$$b_s=\min \left[b_c,b_b+\frac{h_c}{2},\frac{b_b+b_c}{2}+\frac{h_c}{4}-e\right] \mathrm{in} \mathrm{NZS} 3101-2006$$

(3)

$$b_s=\min \left[b_c,b_b+0.5h_c\right] \mathrm{in} \mathrm{Eurocode} 8$$

(4)

where b_b is the beam width; h_c is the column depth; b_c is the column width; x is the smaller distance between the beam and column edges; m = 0.3 when the eccentricity e is greater than b_c/8 or m = 0.5 otherwise; and e is the eccentricity between the beam and column centerlines. In Equation (2), the value of mh_c/2 is limited to the distance between the beam and column edges at each side.

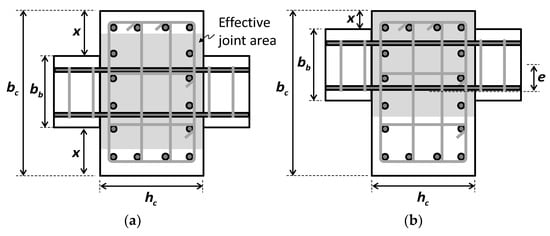
Figure 1. Effective joint area: (a) concentric beam–column joint; (b) eccentric beam–column joint.

Figure 2 compares the effective joint width b_s calculated by the current design codes (Equations (1)–(4)). As shown in the figure, for concentric beam–column joints (Figure 2a), the effective joint width was increased with the increase in the column width, and ACI 352R-02 [13] provided the smallest estimation. On the other hand, for eccentric beam–column joints (Figure 2b with x = 0), Eurocode 8 [15] ignoring the beam eccentricity provided the largest estimation, while ACI 318-19 [12] having a limitation of x = 0 provided the smallest estimation. As compared in Figure 2c, the effective joint width was decreased as the beam eccentricity increased (except Eurocode 8 [15]), and ACI 352R-02 [13] provided a smaller effective joint width than NZS 3101-2006 [14].

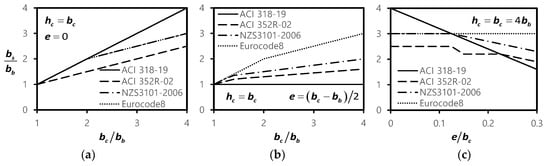
Figure 2. Comparison of effective joint widths in current design codes: (a) concentric beam–column joint; (b) eccentric beam–column joint; (c) effect of beam eccentricity.

3. Joint Shear Strength Degradation Model

Hwang and Park [37] proposed a simplified plastic hinge model for interior and exterior beam–column joints, which could predict the lateral load–drift ratio relationship, including strength degradation. Figure 3 shows the plastic hinge model for interior and exterior beam–column joints [37,38]. In the model, a joint is simplified using elastic beam–column elements, rotational spring elements, and rigid elements. The elastic beam–column elements are used to represent the elastic flexural deformation of beams and columns along their net length. The rigid elements are located at the center of the joint panel, and the rotational spring elements connect the beam–column elements and rigid elements at the joint interface and represent the sum of elastic joint shear deformation, plastic joint shear deformation, and plastic beam deformation.

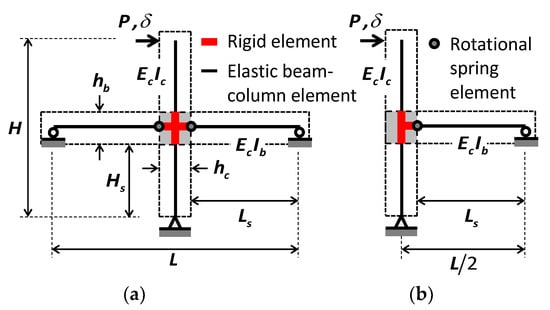
Figure 3. Plastic hinge model for beam–column joints: (a) interior beam–column joint; (b) exterior beam–column joint.

3.1. Lateral Load–Drift Ratio Relationship

Figure 4a shows the envelop curve of the simplified plastic hinge model [37] for a joint, and EY, EU, and EF in the figure indicate the yield, ultimate, and failure points, respectively. In the model, the lateral load P_y at EY corresponds to the nominal moment strength of the beam section at the joint interface. The lateral drift ratio δ_y at EY includes the elastic deformations of beams and columns framing into the joint (affected by effective flexural stiffness EI) and elastic joint shear deformation of the joint panel (affected by the rotation angle θ_jy [22]).

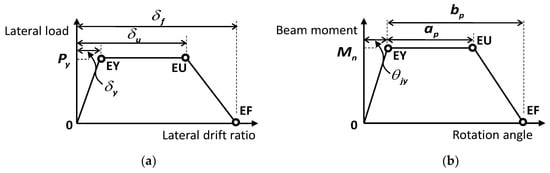
Figure 4. Load–displacement relationship of plastic hinge model: (a) lateral load–drift relationship of beam–column joint; (b) moment–rotation relationship of plastic hinge.

For interior beam–column joints,

$$P_y=\frac{L}{2H}\left(\frac{M^{+}+M^{-}}{L_s}\right)$$

(5)

$${\delta }_y=\frac{2P_y{H}_s^3}{3E_c{I}_c}\frac{1}{H}+\frac{2P_y{L}_s^3}{3E_c{I}_b}\frac{H}{L^2}+\frac{2{\mathsf{\theta }}_{jy}{L}_s}{L}$$

(6)

$${\mathsf{\theta }}_{jy}=8.4\times {10}^{-4}{\left({f^{\prime }}_c\right)}^{0.44}\frac{{\left(BI\right)}^{0.48}}{{\left(JI\right)}^{0.16}}\left(1-\frac{h_c}{2L}-\frac{h_b}{2H}\right)\frac{L}{2L_s}$$

(7)

For exterior beam–column joints,

$$P_y=\frac{L}{2H}\left(\frac{M^{-}}{L_s}\right)$$

(8)

$${\delta }_y=\frac{2P_y{H}_s^3}{3E_c{I}_c}\frac{1}{H}+\frac{4P_y{L}_s^3}{3E_c{I}_b}\frac{H}{L^2}+\frac{2{\mathsf{\theta }}_{jy}{L}_s}{L}$$

(9)

$${\mathsf{\theta }}_{jy}=5.2\times {10}^{-4}{\left({f^{\prime }}_c\right)}^{0.44}\frac{{\left(BI\right)}^{0.48}}{{\left(JI\right)}^{0.16}}\left(1-\frac{h_c}{2L}-\frac{h_b}{2H}\right)\frac{L}{2L_s}$$

(10)

$$BI=\frac{\left(A_s+{A^{\prime }}_s\right)f_y}{b_b{h}_b{f^{\prime }}_c}$$

(11)

$$JI=\max \left[0.0128,\frac{A_h{f}_{yh}}{b_c{h}_b{f^{\prime }}_c}\right]$$

(12)

where L is the beam length; H is the column height; H_s is the column shear span; L_s is the beam shear span; h_b is the beam height; M⁺ and M⁻ are the positive and negative moments of the beam section, respectively; A_s and A_s′ are the areas of tension and compression bars in the beam section, respectively; A_h and f_yh are the area and yield strength of joint hoop bars parallel to beam flexural bars, respectively; and f_c’ is the concrete compressive strength.

According to ASCE/SEI 41-17 [16], the effective flexural stiffness of beams (E_cI_b) and columns (E_cI_c) are defined as follows:

$$E_c{I}_b=0.3E_c{I}_{gb}$$

(13)

$$E_c{I}_c=0.3E_c{I}_{gc}\le \left(0.2+\frac{N_c}{b_c{h}_c{f^{\prime }}_c}\right)E_c{I}_{gc}\le 0.7E_c{I}_{gc}$$

(14)

where E_c is the elastic modulus of concrete (= 4700√f_c’); I_gb and I_gc are the second-order moments of inertia for gross section of beams and columns, respectively; and N_c is the axial force in columns.

The lateral drift ratios δ_u and δ_f at EU and EF are defined as follows:

$${\delta }_u={\delta }_y+a_p\frac{2L_s}{L}$$

(15)

$${\delta }_f={\delta }_y+b_p\frac{2L_s}{L}$$

(16)

where a_p (= a_j + a_f) and b_p (= b_j + b_f) are the plastic hinge rotation angles of a rotational spring element at EU and EF (Figure 4b), which represent the sum of the joint plastic shear angle and beam plastic rotation. The definitions of a_j, a_f, b_j, and b_f are given in the following section.

3.2. Plastic Hinge Model

3.2.1. Ultimate Point

According to Hwang and Park [37], the joint plastic shear angle a_j is defined as follows:

For interior beam–column joints,

$$a_j=0\le \frac{1}{1050}\left[\frac{1.1{\alpha }_c\left({\mathsf{\beta }}_c+0.2\right)\left(6-{\mathsf{\beta }}_j\right){f^{\prime }}_c\left(b_s{h}_c\right)}{V_u-V_T}-16\right]\le a_{mj}$$

(17)

$$a_{mj}=0.03-\frac{10.2a_j}{{\alpha }_t{f}_y\left(1-0.45h_b/L_s\right)\left(\mathsf{\kappa }-0.13\right)\left(3-5\mathsf{\kappa }\right)}>0.01$$

(18)

$$\mathsf{\kappa }=0.8\frac{h_c}{d_b}\frac{\sqrt{{f^{\prime }}_c}}{f_y}+0.05\le 0.6$$

(19)

$${\mathsf{\beta }}_c=\frac{\left(A_s+{A^{\prime }}_s\right)f_y}{0.85{f^{\prime }}_c{b}_b{h}_b}$$

(20)

$$V_u=\left(A_s+{A^{\prime }}_s\right)f_y-P_u$$

(21)

$$V_T=\min \left[A_h{f}_{yh},0.65A_s{f}_y\right]$$

(22)

$${\alpha }_t=0.24\left(1+\frac{A_h{f}_{yh}}{A_s{f}_y}\right)\le 0.6$$

(23)

For exterior beam–column joints,

$$a_j=0\le \frac{1}{1050}\left[\frac{2.8{\alpha }_c\left({\mathsf{\beta }}_c+0.1\right)\left(3-{\mathsf{\beta }}_j\right){f^{\prime }}_c\left(b_s{h}_c\right)}{V_u-V_T}-8\right]\le a_{mj}$$

(24)

$$a_{mj}=0.03-\frac{9a_j}{{\alpha }_t{f}_y\left(1-0.45h_b/L_s\right)\left(\mathsf{\kappa }-0.12\right)\left(3-5\mathsf{\kappa }\right)}>0.01$$

(25)

$$\mathsf{\kappa }=0.14\le 1.56\frac{l_{dh}}{d_b}\frac{\sqrt{{f^{\prime }}_c}}{f_y}-0.06\le 0.5$$

(26)

$${\mathsf{\beta }}_c=\frac{A_s{f}_y}{0.85{f^{\prime }}_c{b}_b{h}_b}$$

(27)

$$V_u=A_s{f}_y-P_u$$

(28)

where α_c is the strength increment factor due to the confinement effect of cross-beams (Figure 5); β_c is the compression zone depth ratio; β_j is the joint configuration ratio (= h_b/h_c); κ is the energy dissipation ratio of beam–column joints; l_dh is the development length of beam flexural bars anchored into the joint; and d_b is the diameter of beam bottom bars. Note that in the calculation of a_mj, the initial value of a_j is used without consideration of the limitation of a_mj.

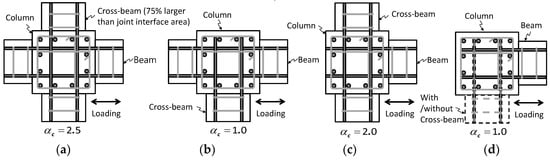
Figure 5. Confinement of beam–column joints: (a) interior beam–column joint with two-cross beams; (b) interior beam–column joint without two-cross beams; (c) exterior beam–column joint with two-cross beams; (d) exterior beam–column joint without two-cross beams.

On the other hand, the beam plastic rotation angle a_f is defined as a function of the energy dissipation ratio κ. [8,9,10,37]

$$a_f=\frac{3+5\mathsf{\kappa }}{3-5\mathsf{\kappa }}{a}_j\le a_{mf}$$

(29)

where a_mf is the maximum plastic rotation angle in order to consider the beam failure (= 0.003 to 0.025 rad) [16,37].

3.2.2. Failure Point

The joint plastic shear angle b_j is defined as follows, assuming linear strength degradation from EU to the point corresponding to 90% of the peak strength [37].

For interior beam–column joints,

$$b_j=\frac{1.1{\alpha }_c\left({\mathsf{\beta }}_c+0.2\right)\left(6-{\mathsf{\beta }}_j\right){f^{\prime }}_c\left(b_s{h}_c\right)V_u}{1050\left(0.9V_u-V_T\right)\left(V_u-V_T\right)}\le 2a_{mj}$$

(30)

For exterior beam–column joints,

$$b_j=\frac{2.8{\alpha }_c\left({\mathsf{\beta }}_c+0.1\right)\left(3-{\mathsf{\beta }}_j\right){f^{\prime }}_c\left(b_s{h}_c\right)V_u}{1050\left(0.9V_u-V_T\right)\left(V_u-V_T\right)}\le 2a_{mj}$$

(31)

In this study, to avoid the overestimation of deformation capacity in building structures and to address the minimum increase in the joint plastic shear angle, the joint plastic shear angle b_j was simplified as follows:

$$b_j=a_j+0.01$$

(32)

On the other hand, the beam plastic rotation angle b_f is defined as a function of the energy dissipation ratio κ [8,9,10,37].

$$b_f=\frac{3+5\mathsf{\kappa }}{3-5\mathsf{\kappa }}{b}_j\le b_{mf}$$

(33)

where b_mf is the maximum plastic rotation angle in order to consider the beam failure (= 0.01 to 0.05 rad) [16,36].

3.2.3. Summary of Parameters for Plastic Hinge Model

For modeling of the load–displacement relationship, the lateral load and drift ratios at point EY are determined from Equations (5) and (6) for interior beam–column joints (or Equations (8) and (9) for exterior beam–column joints), respectively. The drift ratios at points EU and EF are determined from Equations (15) and (16), respectively, and the lateral load at point EU is the same as that at point EY. The parameters for the plastic rotation angles used in Equations (15) and (16) are summarized in Table 1.

Table 1. Parameters for plastic rotation angles.

Parameters	Interior Beam–Column Joint	Exterior Beam–Column Joint
Plastic rotation angles	$a_p=a_j+a_f$ $b_p=b_j+b_f$
Plastic shear angle of the joint	$\begin{array}{l}{a}_j=\frac{1}{1050}\left[\frac{1.1{\alpha }_c\left({\mathsf{\beta }}_c+0.2\right)\left(6-{\mathsf{\beta }}_j\right){f^{\prime }}_c\left(b_s{h}_c\right)}{V_u-V_T}-16\right]\\ \le a_{mj}\end{array}$ $b_j=a_j+0.01$	$\begin{array}{l}{a}_j=\frac{1}{1050}\left[\frac{2.8{\alpha }_c\left({\mathsf{\beta }}_c+0.1\right)\left(3-{\mathsf{\beta }}_j\right){f^{\prime }}_c\left(b_s{h}_c\right)}{V_u-V_T}-8\right]\\ \le a_{mj}\end{array}$ $b_j=a_j+0.01$
Maximum shear angle	$a_{mj}=0.03\left(1-0.1\frac{a_j}{a_{jf}}\right)>0.01$
Partial bond failure	$a_{jf}={\alpha }_t{f}_y\frac{1-0.45h_b/L_s}{3400}\left(\mathsf{\kappa }-0.13\right)\left(3-5\mathsf{\kappa }\right)$	$a_{jf}={\alpha }_t{f}_y\frac{1-0.45h_b/L_s}{3000}\left(\mathsf{\kappa }-0.12\right)\left(3-5\mathsf{\kappa }\right)$
Plastic rotation angle of the beam end	$a_f=\frac{3+5\mathsf{\kappa }}{3-5\mathsf{\kappa }}{a}_j\le a_{mf}$ $b_f=\frac{3+5\mathsf{\kappa }}{3-5\mathsf{\kappa }}{b}_j\le b_{mf}$

Note: ${\alpha }_c$ = 2.5 for interior joints with two cross-beams, 2.0 for exterior joints with two cross-beams, or 1.0 otherwise; b_s = effective joint width in Equations (1)–(4); $V_u=\left(A_s+{A^{\prime }}_s\right)f_y-P_u$ for interior beam–column joint; $V_u=A_s{f}_y-P_u$ for exterior beam–column joint; $V_T=\min \left(A_h{f}_{yh},0.65A_s{f}_y\right)$; ${\beta }_j=h_b/h_c\ge 1$; ${\beta }_c=\left(A_s+{A^{\prime }}_s\right)f_y/\left(0.85{f^{\prime }}_c b_b{h}_b\right)$ for interior beam–column joint; and ${\beta }_c=A_s{f}_y/\left(0.85{f^{\prime }}_c b_b{h}_b\right)$ for exterior beam–column joint. Note that when calculating V_u and V_T in exterior beam–column joints, tension bars in a beam section are used under positive or negative moment.

4. Application of Simplified Plastic Hinge Model

4.1. Existing Test Results

To verify the simplified plastic hinge model, existing test results available in the literature were collected. Among those test results, cyclic loading tests for interior [25,30] and exterior [31,32,34] beam–column joints were used to compare predictions (envelope curves) with measurements (cyclic responses). Table 2 summarizes the primary test parameters of the test specimens. It is noted that the eccentricity ratio of beams e/b_c was in the range of 0–1/4, and the axial load ratio of columns (N_c/f_c’b_ch_c) was in the range of 0–0.20 in the collected test specimens.

Table 2. Test parameters of existing beam–column joint test specimens.

Specimens		Geometric Properties 1						Top Bar of Beam 2			Bottom Bar of Beam 2			Joint Hoop 3		fc′4	Nc/ (fc’bchc) 5	e/bc 6
		L	H	hb	bb	hc	bc	As	fy	db	As	fy	db	Ah	fyh
Joh et al. [25]	JXO-B1 JXO-B5	3000	1750	350	150	300	300	398	371	12.7	398	371	12.7	283	307	21.3 23.1	0.16	0 1/4
Kusuhara et al. [30]	JE-0 JE-55 JE-55S	2700	1350	300	180	280	320	710	387	9.5	710	387	9.5	320 320 604	364	27.0	0.00	0 11/64 11/64
Lee and Ko [31]	S0 S50 W0 W75 W150	4150	2700	450	300	600	400	1749	455	22.2	1749	455	22.2	426	471	29.5	0.10	0 1/8
		4150	2700	450	300	400	600	1749	455	22.2	1749	455	22.2	1065	471	29.5	0.10	0 1/8 1/4
Chen and Chen [32]	JC JE	5000	2840	500	300	500	500	2056	438	22.2	2056	438	22.2	1065	399	20.0	0.00	0 1/5
Ma et al. [34]	C0 E0 E2 E5	4000	2800	500	200	400	400	1511	452	20.0	686	436	18.0	101 0 101 251	378	23.8	0.20	0 1/4 1/4 1/4

¹L = beam length (mm); H = column height (mm); h_b = beam depth (mm); b_b = beam width (mm); h_c = column depth (mm); b_c = column width (mm). ² A_s = cross-sectional area of bars (mm²); f_y = yield strength of bars (MPa); d_b = bar diameter (mm). ³ A_h = area of hoop bars parallel to beam flexural bars (mm²); f_yh = yield strength of hoop bars (MPa). ⁴ Compressive strength of concrete. ⁵ Axial load ratio of columns. ⁶ Eccentricity ratio of beams.

In the application of the simplified plastic hinge model, the effective joint widths of the current design codes [12,13,14,15] were used. Table 3 compares the calculated effective joint widths for the test specimens.

Table 3. Calculated effective joint widths for existing test specimens.

Specimens		Geometric Properties (mm)			Effective Joint width, bs (mm)
		bb	bc	e	ACI 318-19, Equation (1)	ACI 352R-02, Equation (2)	NZS 3101-2006, Equation (3)	Eurocode 8, Equation (4)
Joh et al. [25]	JXO-B1	150	300	0	300	225	300	300
	JXO-B5			75	150	195	225	300
Kusuhara et al. [30]	JE-0	180	320	0	320	250	320	320
	JE-55			55	210	237	265	320
	JE-55S			55	210	237	265	320
Lee and Ko [31]	S0	300	400	0	400	350	400	400
	S50			50	300	350	400	400
	W0	300	600	0	600	450	500	500
	W75			75	450	450	475	500
	W150			150	300	360	400	500
Chen and Chen [32]	JC	300	500	0	500	400	500	500
	JE			100	300	375	425	500
Ma et al. [34]	C2	200	400	0	400	300	400	400
	E0			100	200	260	300	400
	E2			100	200	260	300	400
	E5			100	200	260	300	400

4.2. Comparison of Predictions to Test Results

Figure 6, Figure 7, Figure 8 and Figure 9 compare the test results (black cyclic responses) with the predictions by the simplified plastic hinge model (red envelope curves). It is noted that the comparison was made directly on the lateral load–drift ratio relationship. To examine the effect of the effective joint width, the predictions in each figure were made with a different design code: Figure 6 with ACI 318-19 [12] (or using Equation (1)), Figure 7 with ACI 352R-02 [13] (Equation (2)), Figure 8 with NZS 3101-2006 [14] (Equation (3)), and Figure 9 with Eurocode 8 [15] (Equation (4)). As shown in the figures, the predictions with different effective joint widths showed similar strength, which agreed well with the test results, but the deformation capacities (especially onset of strength degradation) varied. For concentric beam–column joint specimens (i.e., e/b_c = 0), the predictions with ACI 352R-02 [13] showed relatively earlier strength degradation after the peak strength. However, except specimen C2 (Figure 7m), the discrepancy was not significant. For eccentric beam–column joint specimens (i.e., e/b_c > 0), the predictions with ACI 318-19 [12] underestimated the deformation capacity, showing early strength degradation (Figure 6b,d,n,o,p). Compared to the predictions with ACI 318-19 [12], the predictions with ACI 352R-02 [13] showed better agreement, but slightly underestimated the deformation capacity in some specimens (Figure 7c,d,o,p). Overall, the simplified plastic hinge model using the effective joint width of NZS 3101-2006 [14] showed the best predictions for all test specimens (Figure 8). Unexpectedly, the predictions with Eurocode 8 [15], which does not consider the effect of the beam eccentricity on the effective joint width, also showed quite good agreement, except the test specimens E0, E2, and E5 (Figure 9n,o,p). From the comparison, it can be concluded that the simplified plastic hinge model with the effective joint width of NZS 3101-2006 [14] or Eurocode 8 [15] is considered acceptable for design purposes.

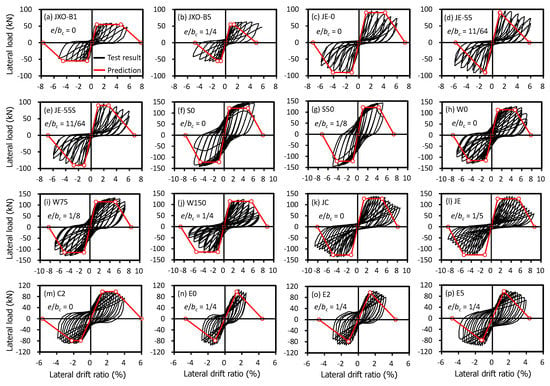
Figure 6. Comparison between test results and predictions with ACI 318-19.

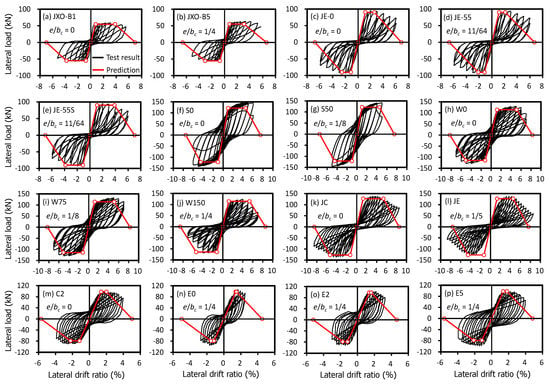
Figure 7. Comparison between test results and predictions with ACI 352R-02.

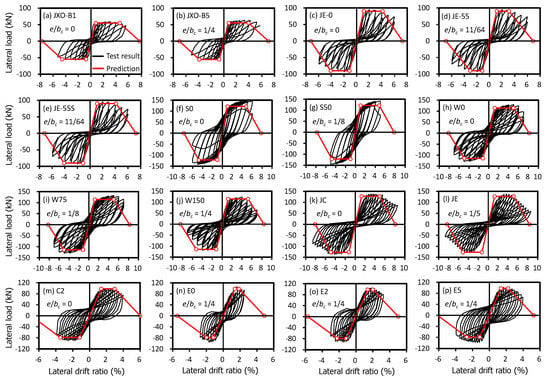
Figure 8. Comparison between test results and predictions with NZS 3101-2006.

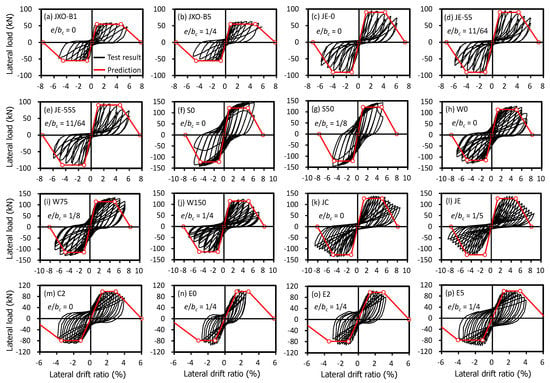
Figure 9. Comparison between test results and predictions with Eurocode 8.

More specifically, the deformation capacity δ_u by the predictions were quantitatively compared with the test results δ_T in Table 4: the deformation capacity δ_T of the test specimens was defined as the drift ratio corresponding to the nominal strength P_y (Equations (5) and (8)) in the post-peak response. As summarized in Table 4, the simplified plastic hinge model using the effective joint width of NZS 3101-2006 [14] or Eurocode 8 [15] matched well with the test results: the mean and COV (coefficient of variation) of δ_T/δ_u were 1.07 and 0.113 for the predictions with NZS 3101-2006, respectively, [14] or 0.97 and 0.177 for the predictions with Eurocode 8, respectively [15]. The underestimation of the predictions with ACI 318-19 [12] (1.45 and 0.474) or ACI 352R-02 [13] (1.25 and 0.165) was due to the underestimated effective joint width (Table 3): the effective joint width of the eccentric beam–column joint specimens was symmetrically decreased at both sides due to the beam eccentricity (x) in ACI 318-19 [12] (Equation (1)), and the effect of beam eccentricity was indirectly considered in ACI 352R-02 [13] by using a factor m (Equation (2)). On the other hand, NZS 3101-2006 [14] directly considered the beam eccentricity (e) in the calculation (Equation (3)), and the calculated effective joint width of NZS 3101-2006 [14] was larger than that of ACI 318-19 [12] or ACI 352R-02 [13] but less than that of Eurocode 2 [15] without consideration of the beam eccentricity (Table 3). For these reasons, the simplified plastic hinge model using the effective joint width of NZS 3101-2006 [14] showed the best predictions for all test specimens.

Table 4. Comparison of deformation capacity between test results and predictions.

Specimens		Test Results	Predictions with ACI 318-19		Predictions with ACI 352R-02		Predictions with NZS 3101-2006		Predictions with Eurocode 8
		δT (%)	δu (%)	δT/δu	δu (%)	δT/δu	δu (%)	δT/δu	δu (%)	δT/δu
Joh et al. [25]	JXO-B1	4.68	4.55	1.03	3.83	1.22	4.55	1.03	4.55	1.03
	JXO-B5	4.24	1.28	3.31	3.05	1.39	3.90	1.09	4.65	0.91
Kusuhara et al. [30]	JE-0	3.39	4.11	0.82	2.55	1.33	4.11	0.82	4.11	0.82
	JE-55	3.50	1.20	2.91	2.11	1.66	3.06	1.14	4.11	0.85
	JE-55S	3.50	2.74	1.28	3.85	0.91	4.11	0.85	4.55	0.77
Lee and Ko [31]	S0	6.03	4.79	1.26	4.50	1.34	4.79	1.26	4.79	1.26
	S50	5.02	4.21	1.19	4.50	1.11	4.79	1.05	4.79	1.05
	W0	6.01	4.67	1.29	5.10	1.18	4.96	1.21	4.96	1.21
	W75	6.01	5.10	1.18	5.10	1.18	5.03	1.19	4.96	1.21
	W150	5.03	5.53	0.91	5.36	0.94	5.25	0.96	4.96	1.01
Chen and Chen [32]	JC	5.52	4.92	1.12	5.22	1.06	4.92	1.12	4.92	1.12
	JE	5.20	5.51	0.94	5.29	0.98	5.14	1.01	4.92	1.06
Ma et al. [34]	C2	2.96	2.97	0.99	2.00	1.48	2.97	0.99	2.97	0.99
	E0	1.95	1.39	1.40	1.49	1.31	1.86	1.05	2.78	0.70
	E2	2.18	1.39	1.57	1.61	1.35	2.00	1.09	2.97	0.73
	E5	2.70	1.37	1.98	1.81	1.49	2.23	1.21	3.28	0.82
Mean		-		1.45		1.25		1.07		0.97
COV		-		0.474		0.165		0.113		0.177

It is noted that in eccentric beam–column joints, the joint shear strength could decrease due to additional torsion and stress concentration developed by eccentric beams at the joint interface. Moreover, when a wide column is used, the joint hoop bar stress close to the eccentric beam would be much higher than that far from the eccentric beam [31]. For these reasons, the use of total amount of joint hoop bars could overestimate the performance in the simplified plastic hinge model, particularly for the beam–column joints with a wide column and large beam eccentricity. Of the test specimens, W0, W75, and W150 used wide columns (Table 2 and Table 3). Among them, W150 had the widest column and largest beam eccentricity, and the overestimation in the onset of strength degradation in W150 may be caused by the use of total amount of joint hoop bars (Figure 6j, Figure 7j, Figure 8j and Figure 9j). However, to generalize the effect of joint hoop bars in the case of having a wide column and large beam eccentricity or to suggest an effective joint hoop bar area, existing test results relevant to the case are limited. Thus, further experimental studies are needed.

5. Conclusions

In the present study, the effect of beam eccentricity on the behavior of eccentric beam–column joints was investigated. A simplified plastic hinge model was proposed using the effective joint width of current design codes, and it was applied to existing test specimens. The principal findings can be summarized as follows:

(1)

Current design codes provide the effective joint widths for concentric and eccentric beam–column joints, but the effective joint widths vary widely.

(2)

In eccentric beam–column joints, the beam eccentricity reduces the effective joint shear area, which results in a decrease in the joint shear strength and more drastic strength degradation after the peak strength.

(3)

For nonlinear analysis of eccentric beam–column joints, a simplified plastic hinge model was proposed, addressing the beam eccentricity.

(4)

To verify the simplified plastic hinge model, the predictions with various code-specified effective joint widths were compared to the existing test results. The comparison showed that the simplified plastic hinge model with the effective joint width of NZS 3101-2006 matched best to eccentric beam–column joint specimens (for the deformation capacity, the mean and COV of test-to-prediction ratios were 1.07 and 0.113, respectively). Thus, for safer and more economical design of eccentric beam–column joints, the effective joint width of NZS 3101-2006 is recommended to be used in the simplified plastic hinge model.

Compared to concentric beam–column joints, previous experimental studies for eccentric beam–column joints are limited. Considering the fact that eccentric beam–column joints are also common in practice, further studies are needed to investigate the effects of beam eccentricity on the behavior of interior and exterior beam–column joints with various design parameters.