Abstract
In track cycling sprint events, optimal cadence PRopt is a dynamic aspect of fatigue. It is currently unclear what cadence is optimal for an athlete’s performance in sprint races and how it can be calculated. We examined fatigue-induced changes in optimal cadence during a maximal sprint using a mathematical approach. Nine elite track cyclists completed a 6-s high-frequency pedaling test and a 60-s isokinetic all-out sprint on a bicycle ergometer with continuous monitoring of crank force and cadence. Fatigue-free force-velocity (F/v) and power-velocity (P/v) profiles were derived from both tests. The development of fatigue during the 60-s sprint was assessed by fixing the slope of the fatigue-free F/v profile. Fatigue-induced alterations in PRopt were determined by non-linear regression analysis using a mono-exponential equation at constant slope. The study revealed that PRopt at any instant during a 60-s maximal sprint can be estimated accurately using a mono-exponential equation. In an isokinetic mode, a mean PRopt can be identified that enables the athlete to generate the highest mean power output over the course of the effort. Adding the time domain to the fatigue-free F/v and P/v profiles allows time-dependent cycling power to be modelled independent of cadence.
1. Introduction
In cycling, models are used to investigate the factors that determine performance and optimize competition outcomes. The sprint events in track cycling (i.e., team sprint, sprint, keirin, and 1000- or 500-m time trials) are approximately 15–60 s in duration and require maximal production of power over distances of 200–1000 m [1]. In races that are executed with all-out effort, such as sprint time trials or decisive phases of other sprint events in track cycling [1,2,3,4], the mechanical power applied by the athlete at any given time equals the maximum power achievable at the current cadence and state of exhaustion.
A decisive physiological determinant of performance in track cycling sprints is the ability to produce fatigue-free muscular power, which can be described by maximal force-velocity (F/v) and power-velocity (P/v) profiles (e.g., [1,4,5,6,7]). Although Hill [8] modelled the velocity with which muscle elements contract as a rectangular hyperbola, a strong linear relationship between the force generated and velocity of movement was established in the case of movements of large muscle groups engaging more than one joint [9]. The F/v relationship in cycling of mean pedal force and pedaling rate (PR) was also identified as linear and can be derived from short maximal sprints in the laboratory and in the field [5,10,11,12,13]. Multiplying the mean pedal force by the cadence results in a parabolic relationship between power output (P) and cadence (ibid.).
In cycling, the fatigue-free F/v and P/v profiles represent the maximal resistance an athlete can overcome at a certain cadence and the maximal power output at that cadence and allow important parameters of neuromuscular performance to be determined, including the theoretical maximal mean crank force (Fmax, as the F/v intersection of the y-axis) and cadence (PRmax, as the F/v intersection of the x-axis), maximum power output (Pmax, as the P/v apex), and optimal cadence (PRopt, as the pedaling rate corresponding to Pmax) [5].
With increasing duration of maximal exercise and with the onset of fatigue-induced impairment of performance, metabolic performance, interpreted as resistance to fatigue, becomes more and more important [14]. In contrast to the generalized representation of fatigue-free performance by F/v and P/v profiles, there is no mathematical model that describes the change in performance with the onset of fatigue in a generalized form to date, so that time-dependent maximal performance cannot be analyzed independent of the current cadence. To control for the effects of cadence on power decay during maximal sprints, an isokinetic test design is often used to diagnose anaerobic performance [15]. This limits current performance diagnostics to the analysis of an effort under fixed conditions and does not allow the general cadence-independent description of an athlete’s performance capacity. The development of such a model was recently re-identified as a specific research gap in the field of track cycling [1].
When performing at maximal level, elite track sprinters leave their fatigue-free F/v profile after less than 3 s in maximal sprints [16] and power output declines in an approximately exponential manner as a result of increasing fatigue [4]. In this process, accumulation of metabolites and the associated reduction in cellular pH may lead successively to an almost synchronous and uniform decline in force development (due to attenuated energy flow) and the velocity of contraction (reflecting reduced membrane excitability). Physiologically, this systematic reduction reflects the mechanical and metabolic properties of the different fiber types in the main propulsive muscles and their time-dependent contribution to power output (ibid.).
Mathematically, these fatigue-induced changes can be described by a parallel shift in the F/v profile towards the origin [17,18], whose time course should correspond to the exponential fatigue behavior described. By adding a time domain and incorporating the duration of exercise, two-dimensional F/v profiles should form a three-dimensional model. We proposed that it will be possible to describe the effect of fatigue and motion velocity on power output for any individual athlete, using a function of time in a mono-exponential equation. This model would provide a deeper insight into the physiology of fatigue-induced decline in performance and offer a mathematical approach to optimizing an athlete’s competitive performance.
With the parallel shift of the initial fatigue-free F/v profile, its characteristic parameters also decrease [7]. The optimal cadence is, therefore, not a static parameter, but a dynamic aspect of fatigue. Since it has not been possible to determine the changes in optimal cadence over the course of a race, it is currently unclear what cadence is optimal for an athlete’s performance in sprint races and how it can be calculated. As a special application of our approach with high practical relevance, we aimed to calculate the time-dependent optimal cadence and determine power output reserves in order to reveal unused potential for performance optimization.
2. Methods
Nine male elite track cycling sprinters (22.1 ± 4.2 yrs, 184.4 ± 4.6 cm, 89.2 ± 6.0 kg (means ± standard deviations)) performed a high-cadence, low-resistance pedaling test (motoric test), as well as a 60-s all-out test (sprint test) in a seated position on a bicycle ergometer. As very high neuromuscular and metabolic performance was required for the study, only athletes whose F/v profiles showed sufficiently high linearity (R2 > 0.95) in previous tests and who had experience with sprint time trials at national or international championships were tested.
All subjects used their own cycling shoes and pedals during these sprints. The settings of the ergometer were chosen to resemble the demands faced during actual competition.
The subjects were requested to refrain from consuming alcohol and from intense training during the 24-h period prior to the experimental session and asked to maintain their normal drinking and eating habits. All provided their written, informed consent to participate in this study, which was approved by the institute’s ethical committee and performed in accordance with the Declaration of Helsinki.
3. Exercise Protocol
The warm-up prior to both tests consisted of 6 min of low-intensity cycling (1–1.5 W kg−1 bodyweight), followed by a 3-s maximal sprint. Each athlete rested passively for 10 min between warm-up and testing.
Participants first performed 6 s of maximal high-cadence, low-resistance cycling (motoric test) on a specially prepared ergometer, from which the internal flywheel had been removed to minimize resistance. Reducing the overall momentum of the ergometer enabled the athlete to reach a cadence ≥160 rpm within the first 3 s to generate additional data points in the high-frequency cadence range for a valid determination of the F/v profiles by combining this data with the fatigue-free pedal revolutions from the acceleration phase of the 60-s sprint [19].
In order to determine the fatigue-induced drop in performance, after a further 10 min of rest, each athlete completed a 60-s sprint test in an isokinetic mode at a fixed cadence of 120 rpm, on another SRM cycle ergometer (Schoberer Radmesstechnik GmbH, Jülich, Germany) with a 9-kg flywheel, in seventh gear. As the test corresponded to the requirements of sprint time trials and the athletes were familiar with the settings from previous performance tests in the laboratory, no further familiarization was required.
The participants accelerated as rapidly as possible from a simulated rolling start (approx. 20 rpm) to 120 rpm at a self-selected instant and continued sprinting at this rate until the end of each effort, while receiving emphatic verbal encouragement to maintain maximal power output throughout the test.
In both tests, crank force and cadence were monitored continuously with a SRM power meter (Schoberer Radmesstechnik GmbH, Jülich, Germany).
4. Data Processing
Raw data from the ergometer were obtained at a sample rate of 10 Hz. The mean tangential force F (N) at both pedals, averaged over one revolution, as well as the corresponding mean pedal rate PR (rpm) were derived from these values.
From the first 3 s of the acceleration phase of the 60-s sprint, three or four cycles with linear decay in pedal force and one or two cycles at pedal rates above 160 rpm from the motoric test were evaluated to establish the fatigue-free F/v and P/v profiles. Since PR is directly proportional to the tangential speed of motion v at the pedal, they were based on the mean cadence PR and corresponding mean crank force F.
The force–velocity continuum was subjected to linear (F/v profile) and non-linear (P/v profile) regression analysis. The function
approximates the relationship between mean pedal force F and the movement velocity PR in the absence of fatigue.
P(v) was calculated by multiplying F(v) by PR:
For purposes of statistical analysis, the following indices of performance were calculated:
- theoretical maximal force ,
- theoretical maximal velocity of movement a−1,
- optimal cadence a)−1, and
- maximum power output b2a)−1.
To analyze the fatigue-induced performance loss during the 60s-sprint data, the slope derived from the fatigue-free force-velocity profile (1) was kept fixed, in accordance with Buttelli and colleagues [17]. When a time domain was added and the exercise duration was included, the two-dimensional F/v profiles yielded a three-dimensional model F:2→ in maximal sprints no longer than ~ 60 s in duration:
where F(v) is the fatigue-free F/v profile and τF denotes the time constant of its decline due to fatigue. Since the results of Burnley and Jones [20], among others, described a steady state of power output after an exponential drop, a limiting value c was included in the function to represent this steady state.
As the F/v profile shifted, the characteristic parameters of the fatigue-free profiles also decreased, allowing the three-dimensional model to be reduced to a two-dimensional model by eliminating the dependence on cadence. The fatigue-induced changes in the F/v can, therefore, be characterized by the alteration of a single parameter such as the optimal cadence. The calculation of the instantaneous F/v profile and theoretical optimal cadence for each data point i was based on the associated cadence and corresponding mean crank force :
The decay in PRopt during the sprint was approximated by an exponential function of time t:
Its parameters were determined by non-linear regression with , as the limiting value, and τ as the time constant.
A time delay (TD) was used to compensate for any delays in the onset of fatigue.
Theoretical mean power output Pmean(PRopt) was calculated as the mean power output that could be generated at the calculated mean optimal cadence.
To investigate the meaning of the mean optimal cadence mathematically, the cadence that maximizes power output was determined as follows by non-linear optimization:
5. Statistical Analyses
All data were checked for normality using the Shapiro–Wilk test and are presented as means SD. Linear regression analysis was used to study the relationship between measured and modelled data. The relative difference between the measured and modelled data was used to determine the bias of the measurements. The mean differences between parameters were compared using -tests for dependent samples. The Pearson product–moment correlation test was used to evaluate interrelationships between variables. Multiple regression analyses were conducted to identify the factors which exerted a major influence on a dependent variable. Pearson correlation coefficient r (small ≥ 0.1; medium ≥ 0.3; large ≥ 0.5) and Cohen’s d (small = 0.2; medium = 0.5; large = 0.8) were employed as a measure of effect size, with statistical significance being set at an alpha level of <0.05. The quality of the regression analyses was examined by calculating the coefficient of determination R2. For all tests, a post hoc power analysis was performed to determine the retrospective power of the observed effect based on the sample size at the indicated level of significance. All mathematical analyses and statistical tests were processed using IBM SPSS statistics version 24 Software for Windows (SPSS Inc., Chicago, IL, USA) and Office Excel 2016 (Microsoft Corporation, Redmond, WA, USA).
6. Results
Anthropometric data and the parameters of the fatigue-free F/v profile with corresponding model quality R2 are presented in Table 1 for all athletes.

Table 1.
Anthropometric data and model parameters of the linear fatigue-free F/v profile with corresponding model quality R2 of all participants.
The mean maximal force was 1266.89 ± 116.86 N, mean maximal crank velocity was 303.18 ± 21.23 rpm, and optimal pedaling rate was rpm, as determined from the fatigue-free F/v profile, which had a slope of . The coefficient of determination R2 for this profile was >0.98 for all athletes. The results of the procedure for generating the fatigue-free F/v and P/v profiles are depicted in Figure 1 for one athlete.
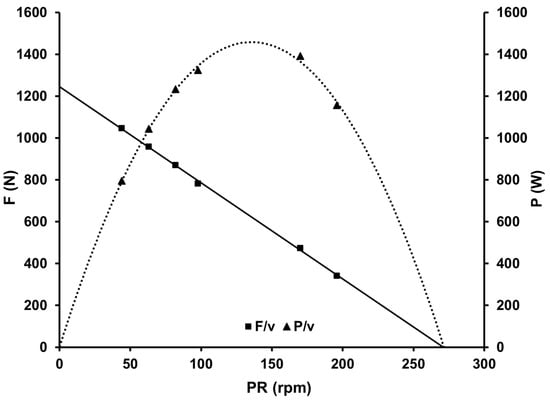
Figure 1.
The fatigue-free force-velocity and power-velocity profiles for a professional track cycling sprinter calculated on the basis of the force and velocity data derived from the first 3 s of acceleration during the motoric and the sprint test. The solid line represents the F/v and the dotted line represents the P/v function. The maximal mean pedal force was 1223 N and the maximal pedaling rate was 277 rpm, resulting in a fatigue-free optimal pedaling rate of 139 rpm. For both profiles, R2 was >0.99.
After a short period of acceleration, all of the athletes attained the specified cadence of 120 rpm and completed their 60-s sprints with an average power output of 735.15 ± 56.62 W. Figure 2 illustrates the typical time course of power output and corresponding cadence for one of the athletes.
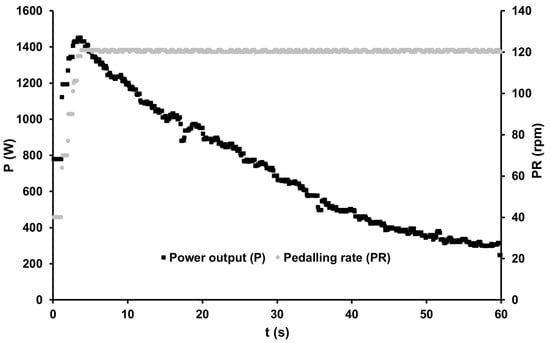
Figure 2.
Power output and pedaling rate of an elite male track cyclist during an isokinetic (120 rpm) all-out sprint on an SRM ergometer (sampling rate, 10 Hz).
Dynamic optimal cadence PRopt(t) showed an exponential decrease with time. Table 2 presents the parameters of PRopt(t) with corresponding model quality R2, as well as mean power output in the 60-s sprint Pmean and the theoretical mean power output Pmean(PRopt) for all participants.

Table 2.
Model parameters of the mono-exponential dynamic optimal cadence PRopt(t) with corresponding model quality R2 as well as mean power output Pmean and theoretical mean power output Pmean(PRopt) in the 60-s sprint for all participants.
The mean values of were , τ and . The high quality of the non-linear regression analysis was indicated by its mean coefficient of determination of R2 =. Figure 3a depicts a representative example of the fitting of the function describing the optimal dynamic pedaling rate to the data collected. The model was tested for correct reproduction of the time-specific optimal cadence. Figure 3b shows the deviation between modelled and measured data for the data points for all nine athletes. With a bias of <1% at a standard deviation of 4%, the overall agreement was found to be satisfactory.
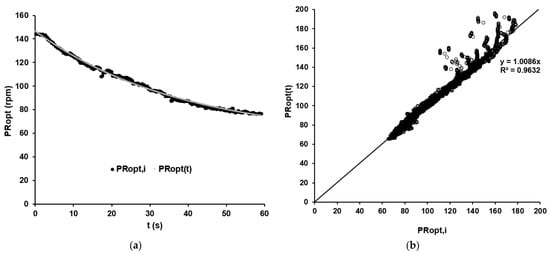
Figure 3.
(a) The optimal dynamic cadence as a function of time reflects the increase in fatigue with prolonged cycling. Black points: current optimal cadence calculated for data point i (PRopt,i) calculated using Equation (4). Grey curve: time-dependent optimal cadence (PRopt(t)) calculated using Equation (5). The amplitude A was 85 rpm, the time constant τ was 38.20 s, and the limiting value was c = 55.43 rpm with a time delay of 2.98 s. (b) Comparison of measured and modelled data via linear regression analysis.
The model was tested for correct reproduction of the time-specific optimal cadence. Figure 3b shows the deviation between modelled and measured data for the data points of all nine athletes. With a bias of <1% at a standard deviation of 4%, the overall agreement was found to be satisfactory. It can be seen that larger deviations between modelled and measured data occurred mainly in the high-cadence range, which represents the first few seconds of the sprint.
Mean power output Pmean was statistically significantly smaller than theoretical mean power output Pmean(PRopt) calculated on the mean optimal cadence (d = −0.872, p < 0.001). The cadence that maximizes the mean power output as a solution to the non-linear optimization problem was equal to the calculated mean optimal cadence. Figure 4a,b presents an example of the influence of cadence (a) and its optimization (b) on time-dependent power output and the work performed (calculated as the corresponding integral) in a 60-s isokinetic sprint test.
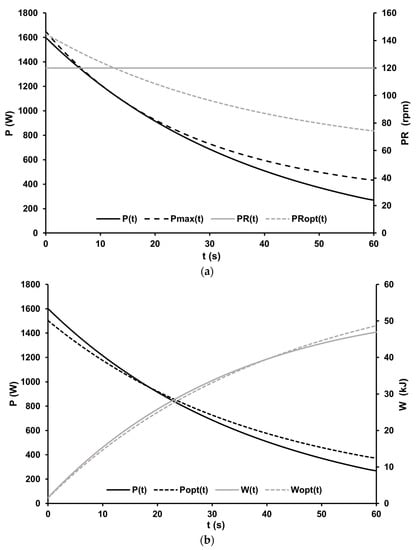
Figure 4.
(a) Time-dependent maximal power output (Pmax(t)) at dynamic optimal cadence (PRopt(t)) and power output (P(t)) during a 60-s all-out sprint at a cadence of 120 rpm (PR) on a cycle ergometer. (b) Comparison of the time-dependent power output (P(t)) at a pedaling rate of 120 rpm and the corresponding work performed (W(t)) to optimized power output (Popt(t)) at a mean optimal pedaling rate of 102 rpm and the corresponding work performed (Wopt(t)) during a 60-s all-out sprint on a cycle ergometer. In fact, free optimization of the mean power output by altering the cadence during the isokinetic test resulted in a calculated mean optimal pedaling rate of 102 rpm. Changing the cadence to 102 rpm would result in a 7% higher mean power output of the athlete in the isokinetic test mode.
There was a strong positive correlation between the average power Pmean and the values for Pmax (r = 0.704, p < 0.05), Fmax (r = 0.512, p < 0.05), and τ (r = 0.475, p < 0.05). Applying multiple linear regression analysis, the following statistically significant linear model could be utilized to estimate an athlete’s mean power output (R2 = 0.935, R2adj = 0.900):
The statistical power for the model quality was calculated to be >0.99. The reproduction of the quality of prediction stated was thus guaranteed, even with very small samples. The power of the other statistics ranged from 0.26 to 0.77. In order to be able to reproduce all results presented with a probability of at least 80%, we recommend choosing a sample size of ≥32.
7. Discussion
The findings presented in the current study confirmed that the decrease in optimal cadence due to fatigue during a 60-s maximal sprint by elite track cyclists can be described quite accurately by a mono-exponential equation.
By combining the fatigue-induced changes of the fatigue-free F/v profile with the time course of fatigue at maximal intensity, this approach allowed, for the first time, power output to be described in a cadence-independent, normalized form as a three-dimensional model. The relationship between F/v and P/v at maximal effort as a function of time is exemplified in Figure 5.
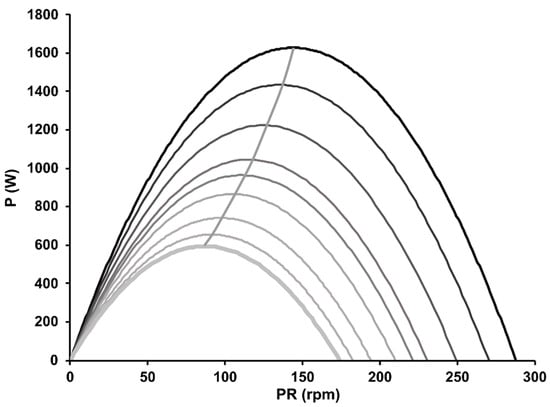
Figure 5.
A set of curves illustrating the time-course of the relationship between the force-velocity and power-velocity curves during a 60-s all-out sprint on a cycle ergometer. The profiles were derived from the data at every fifth second of the sprint test shown in Figure 2.
Assessment of fatigue or calculation of the decrement in fatigue in a normalized fashion is necessary for modelling the decay in performance during sprints. This model allowed both the evaluation of the different components of physiological performance and the simulation of scenarios to optimize competition performance, taking into account the physical characteristics of cycling.
Using Equation (5) to examine the effects of fatigue on the optimal cadence can help to optimize individual cadences and gear ratios. Dorel and co-workers [5] suggested that, during competition, when the difference between an athlete’s optimal (fatigue-free) cadence and the mean cadence is small, mean power output is maximal. In this context, our present findings indicate that the difference between the mean cadence and mean optimal dynamic cadence should be minimized in order to maximize mean power output. In fact, altering the cadence in the isokinetic test to the calculated mean optimal cadence would have resulted in a 4–12% higher mean power output. In track cycling sprint races with fixed gear ratios, where cadence also changes due to resistance and fatigue, there appears to be even greater potential for enhancing performance by reducing the discrepancy between cadence and individual dynamic optimal cadence [7].
Furthermore, this model allowed the exploration of the relationship between biomechanical and physiological performance. The systematic reduction in optimal cadence might correspond to the mechanical and metabolic properties of the various fiber types, with respect to specific characteristics of force development and contraction velocity, as well as of resistance to fatigue [4,21].
While force production by contractile units containing different types of fibers is similar, the maximal velocity of contraction by type IIx is approximately four-fold faster than that of type I muscle fibers [22,23,24]. IIx fibers derive their energy mainly from phosphates and glycolysis and are assumed to be completely fatigued after about 60 s of maximal power output [25]. The duration of maximal force production by predominantly glycolytic to predominantly oxidative IIa muscle fibers usually ranges from 3–6 min [26,27], whereas type I muscle fibers can work for as long as several hours without significant loss of power [28].
The maximal power output by a muscle can only be generated when it is moving at its own specific optimal velocity [8,29]. Although, practically, in connection with locomotion, velocity can only be determined globally for all the muscles involved, the importance of specific individual optimal velocities is unquestionable [21].
A variety of studies have demonstrated that maximal mechanical performance during cycling can only be achieved at the individual optimal cadence (e.g., [5,6,11,12,29,30,31]). In the case of maximally activated muscles, all fiber types (I, IIa, IIx) are expected to contribute to power output, so long as they are not completely fatigued and their maximal velocity of shortening is not exceeded [21].
The effect of fatigue on dynamic muscle function as expressed in the F/v and P/v profiles has rarely been investigated. Buttelli, Bogdanis, and their colleagues [17,18] reported that, with increasing fatigue, the F/v profile shifts in a parallel mode towards the origin, which corresponds to a linear decrease in velocity at constant resistance. A number of findings indicate that the parallel shift in the initially fatigue-free profile in maximal sprints is caused by an approximately simultaneous decrease in force development and in the contraction velocity of high-glycolytic fast-twitching muscle fibers, resulting in a decline in the number of active muscle fibers as they become fully fatigued [4,32,33,34].
If this is the case, the time course of the optimal cadence may reflect the time course of the recruitment of different types of muscle fibers as well as their metabolic state. As fatigue increases, the optimal cadence should approach the rate that can be sustained by all fibers with sufficient endurance to continue being activated (i.e., I and IIa). If the effort is prolonged, successive fatigue in IIa fibers will likely cause a further drop in the profile.
Assuming systematic changes in the force-velocity profile due to fatigue-related elimination of predominantly phosphatic and glycolytic fast-twitching muscle fibers during the first 60 s of all-out exercise, the combined optimal cadence of the fibers with sufficient endurance can be defined as the limiting value for the function modelling the optimal dynamic cadence (5). Here, c = describes the common optimal cadence of type I and IIa fibers, reflecting the optimal power generation for endurance events lasting only a few minutes. Based on our results, the cadence resulting in the greatest power output during maximal endurance exercise with maximal oxygen uptake appears to be approximately 62 rpm. This agrees with a number of other reports [29,35,36,37,38] that the cadence that generates power most efficiently during low- to moderate-intensity exercise is in the range of 42–71 rpm.
In endurance racing, professional cyclists prefer a cadence close to 90 rpm [6]. We assume that this is because during their regular training, they pedal at such rates, which results in improved motor coordination and reduced neuromuscular fatigue under these conditions [38]. Moreover, competing with the same cadence employed during training probably lowers the accumulation of metabolites during races lasting for several hours, due to shorter contractions and less restriction of blood flow [4].
Our findings reveal that the mean power during the sprint depends strongly on the fatigue-free maximal power and maximal force, as well as on the time constant in the function describing the time-dependent changes in optimal pedaling rate. Pmax and Fmax characterize an athlete`s fatigue-free level of performance, whereas τ represents his/her resistance to fatigue. With respect to the calculated linear influence of these parameters on Pmean, the fatigue-free level of power appears to exert a greater impact than the time constant of the loss of power induced by fatigue. Taking the resistances acting on an athlete during the different phases of a race into account further supports the proposal that, in races lasting 60 s or less, the fatigue-free level of performance is more important than resistance to fatigue [7]. Furthermore, Pmax (which is correlated to a cyclist’s maximal speed [4]) increases Pmean to a greater extent than does Fmax (which is associated with the ability to accelerate (ibid.)).
Assuming that our model is valid, it would become necessary to extend Henneman’s size principle [39] concerning metabolic thresholds to include the specific velocity of movement. This means that when planning training and controls, the zones of exercise intensity should not be presented in absolute terms, but as a function of the velocity of movement. Assuming that the limiting value of the model is the optimal cadence for exercises in which both type I and type IIa fibers contribute maximally to performance, it would be possible to generate fiber type-specific F/v profiles by combining the results of the 60-s all-out sprint with diagnostic isokinetic tests of maximal endurance. In our opinion, such differentiation could significantly improve specific development of the performance of the different types of muscle fibers. Furthermore, a fiber type-specific decline in the force-velocity and power-velocity profiles could be used to define reasonable maximal training loads.
8. Limitations
Valid determination of the fatigue-free F/v profiles of an athlete is the most important aspect in the calculation of performance reserves according to this approach. Shifts in the F/v profile during fatigue can only be correctly calculated and interpreted if the true fatigue-free profile parameters are known. The application of this model is currently limited to maximal sprints on the cycle ergometer with a duration of up to 60 s and has only been demonstrated on a small sample size. Performance predictions are only valid if the model proves to be valid and reliable. The transfer of our approach to other conditions and sports and the verification of its validity and reliability should be the subject of future investigation.
The quality of the model depends on the athlete’s neuromuscular performance. If an athlete is not able to activate all relevant motor units simultaneously, the power output will not correspond to the current maximum. The deviations between the measured data and the model at the beginning of the sprints prove that even elite athletes can have problems with muscle activation. However, this “inaccuracy” of our model can also be interpreted as an opportunity. With our model, deficits in neuromuscular performance can be detected and the athlete’s effort can be evaluated retrospectively.
9. Conclusions
The decrease in the optimal cadence due to fatigue during 60 s of all-out cycling can be described by utilizing a mono-exponential equation. Our explicit representation of the changes in an athlete’s performance with time in the form of F/v and P/v profiles at specific time points allows, for the first time, time-dependent biomechanical performance during track cycling to be modelled independently of cadence. Our model can be used to analyze various components of physiological performance as well as to optimize performance in competition by reducing the discrepancy between actual cadence and individual dynamic optimal cadence. In an isokinetic mode, the mean optimal cadence equals to the cadence at which the greatest mean power can be generated.
Author Contributions
A.K.D. designed and conducted the study and analyzed the data. A.K.D., R.G. and H.-C.H. were responsible for drafting the paper and revising it critically with respect to important intellectual content. All authors have read and agreed to the published version of the manuscript.
Funding
This research would not have been possible without the financial support from the BMI (Federal Ministry of the Interior and Community, Germany) for the more extensive project (AD-5-17) from which this investigation was derived.
Institutional Review Board Statement
The study was conducted according to the guidelines of the Declaration of Helsinki, and approved by the Institutional Ethics Committee of INSTITUTE FOR APPLIED TRAINING SCIENCE (ER_2020.18.12_11).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study. Written informed consent has been obtained from the subjects to publish this paper.
Data Availability Statement
The datasets generated during and/or analyzed during the current study can be obtained from the corresponding author upon reasonable request.
Conflicts of Interest
On behalf of all authors, the corresponding author states that we have no conflicts of interest.
Abbreviations
| F/v | Force-velocity |
| F | Force |
| P | Power |
| PR | Pedaling rate, cadence |
| P/v | Power-velocity |
| v | Velocity |
| rpm | Crank revolutions per minute |
| Pmax | Maximum power output |
| Pmax(t) | Time-dependent maximal power output |
| Fmax | Maximum force |
| PRmax | Maximum pedaling rate |
| Pmean | Mean power output |
| Pmean(PRopt) | Theoretical mean power output at mean optimal cadence |
| Popt(t) | Time-dependent power output at mean optimal cadence |
| PRopt | Optimal cadence, optimal pedaling rate |
| PRopt(t) | Optimal dynamic cadence; time-dependent optimal pedaling rate |
| PRoptI&IIa | Common optimal cadence of type I and type IIa muscle fibers |
| A | Amplitude of the dynamic optimal pedaling rate |
| τ | Time constant of the dynamic optimal pedaling rate |
| c | Limiting value for the dynamic optimal pedaling rate |
| Part. | Participant |
References
- Ferguson, H.A.; Harnsih, C.; Chase, J.G. Using field based data to model sprint track cycling performance. Sports Med. 2021, 7, 1–12. [Google Scholar] [CrossRef]
- De Koning, J.J.; Bobbert, M.F.; Foster, C. Determination of optimal pacing strategy in track cycling with an energy flow model. J. Sci. Med. Sport 1999, 2, 266–277. [Google Scholar] [CrossRef]
- Craig, N.P.; Norton, K.I. Characteristics of track cycling. Sports Med. 2001, 31, 457–468. [Google Scholar] [CrossRef] [PubMed]
- Douglas, J.; Ross, A.; Martin, J.C. Maximal muscular power: Lessons from sprint cycling. Sports Med. Open 2021, 7, 48. [Google Scholar] [CrossRef]
- Dorel, S.; Hautier, C.A.; Rambaud, O.; Rouffet, D.; van Praagh, E.; Lacour, J.-R.; Bourdin, M. Torque and power-velocity relationships in cycling: Relevance to track sprint performance in world-class cyclists. Int. J. Sports Med. 2005, 26, 739–746. [Google Scholar] [CrossRef]
- Abbiss, C.R.; Peiffer, J.J.; Laursen, P. Optimal cadance selection during cycling. Int. J. Sports Med. 2009, 10, 1–15. [Google Scholar]
- Dunst, A.K. Trends und Perspektiven im Radsport—Der Trend großer Übersetzungen und seine Konsequenz für das physiologische Anforderungsprofil im Bahnradsprint. Leistungssport 2021, 5, 34–37. [Google Scholar]
- Hill, A.V. The maximum work and mechanical efficiency of human muscles, and their most economical speed. J. Physiol. 1922, 56, 19–41. [Google Scholar] [CrossRef] [PubMed]
- Jaric, S. Force-velocity relationship of muscles performing multi-joint maximum performance tasks. Int. J. Sports Med. 2015, 36, 699–704. [Google Scholar] [CrossRef] [PubMed]
- Bertucci, W.; Taiar, R.; Grappe, F. Differences between sprint tests under laboratory and actual cycling conditions. J. Sports Med. Phys. Fit. 2005, 45, 277–283. [Google Scholar]
- Gardner, A.S.; Martin, J.C.; Martin, D.T.; Barras, M.; Jenkins, D.G. Maximal torque- and power-pedaling rate relationships for elite sprint cyclists in laboratory and field tests. Eur. J. Appl. Physiol. 2007, 101, 287–292. [Google Scholar] [CrossRef] [PubMed]
- Debraux, P.; Manolova, A.V.; Soudain-Pineau, M.; Hourdé, C.; Bertucci, W.M. Maximal torque and power pedaling rate relationships for high level BMX riders in field tests. J. Sci. Cycl. 2013, 2, 51–57. [Google Scholar]
- Rylands, L.; Roberts, S.; Hurst, H. Variability in laboratory versus field testing of peak power, torque and time of peak power production amongst elite BMX cyclists. J. Strength Cond. Res. 2015, 29, 2635–2640. [Google Scholar] [CrossRef] [PubMed]
- Dunst, A.K. Anwendung von Kraft-Geschwindigkeits-Profilen im Bahnradsport. In Kräftiger, Schneller, Ausdauernder—Entwicklung der Muskulären Leistung im Hochleistungstraining; Lehmann, F., Wenzel, U., Sandau, I., Eds.; Meyer&Meyer Verlag: Aachen, Germany, 2020; pp. 113–120. [Google Scholar]
- Martin, J.C.; Davidson, C.J.; Pardvjak, E.R. Understanding sprint-cycling performance: The integration of muscle power, resistance, and modelling. Int. J. Sports Physiol. Perform. 2007, 2, 5–21. [Google Scholar] [CrossRef] [PubMed]
- Dorel, S. Maximal force-velocity and power-velocity characteristics in cycling: Assessment and relevance. In Biomechanics of Training and Testing; Morin, J.B., Samozino, P., Eds.; Springer: Cham, Switzerland, 2018; pp. 7–31. [Google Scholar]
- Buttelli, O.; Seck, D.; Vandewalle, H.; Jouanin, J.C.; Monod, H. Effect of fatigue on maximal velocity and maximal torque during short exhausting cycling. Eur. J. Appl. Physiol. Occup. Physiol. 1996, 73, 175–179. [Google Scholar] [CrossRef] [PubMed]
- Bogdanis, G.C.; Papaspyrou, A.; Theos, A.; Maridaki, M. Influence of resistive load on power output and fatigue during intermittent sprint cycling exercise in children. Eur. J. Appl. Physiol. 2007, 101, 313–320. [Google Scholar] [CrossRef]
- Dunst, A.K.; Hesse, C. Trends und Perspektiven im Radsport—Geschwindigkeitsbasiertes Training in der Praxis; Leistungssport: Münster, Germany, 2022; p. 1. (in print) [Google Scholar]
- Burnley, M.; Jones, A.M. Power-duration relationship: Physiology, fatigue and the limits of human performance. Eur. J. Sport Sci. 2018, 18, 1–12. [Google Scholar] [CrossRef]
- Sargeant, A.J. Structural and functional determinants of human muscle power. Exp. Physiol. 2007, 92, 323–331. [Google Scholar] [CrossRef]
- MacIntosh, B.R.; Herzog, W.; Suter, E.; Wiley, J.P.; Sokolosky, J. Human skeletal muscle fibre types and force: Velocity properties. Eur. J. Appl. Physiol. Occup. Physiol. 1993, 67, 499–506. [Google Scholar] [CrossRef] [PubMed]
- Pette, D.; Staron, R.S. Transitions of muscle fiber phenotypic profiles. Histochem. Cell Biol. 2001, 115, 359–372. [Google Scholar] [CrossRef]
- Bottinelli, R.; Pellegrino, M.A.; Canepari, M.; Rossi, R.; Reggiani, C. Specific contributions of various muscle fibre types to human muscle performance: An in vitro study. J. Electromyogr. Kinesiol. 1999, 9, 87–95. [Google Scholar] [CrossRef]
- Bogdanis, G.C.; Nevill, M.E.; Boobis, L.H.; Lakomy, H.K.; Nevill, A.M. Recovery of power output and muscle metabolites following 30 s of maximal sprint cycling in man. J. Physiol. 1995, 482, 467–480. [Google Scholar] [CrossRef]
- Hultén, B.; Thorstensson, A.; Sjödin, B.; Karlsson, J. Relationship between isometric endurance and fibre types in human leg muscles. Acta Physiol. Scand. 1975, 93, 135–138. [Google Scholar] [CrossRef] [PubMed]
- Saltin, B.; Henriksson, J.; Nygaard, E.; Andersen, P.; Jansson, E. Fiber types and metabolic potentials of skeletal muscles in sedentary man and endurance runners. Ann. N. Y. Acad. Sci. 1977, 301, 3–29. [Google Scholar] [CrossRef] [PubMed]
- Monod, H.; Scherrer, J. The work capacity of a synergic muscular group. Ergonomics 1965, 8, 329–338. [Google Scholar] [CrossRef]
- Sargeant, A.J. Human power output and muscle fatigue. Int. J. Sports Med. 1994, 15, 116–121. [Google Scholar] [CrossRef]
- McCartney, N.; Heigenhauser, G.J.; Jones, N.L. Power output and fatigue of human muscle in maximal cycling exercise. J. Appl. Physiol. Respir. Environ. Exerc. Physiol. 1983, 55, 218–224. [Google Scholar] [CrossRef]
- Beelen, A.; Sargeant, A.J. Effect of fatigue on maximal power output at different contraction velocities in humans. J. Appl. Physiol. 1991, 71, 2332–2337. [Google Scholar] [CrossRef]
- Laube, W.; Kibittel, W.; Pieper, K.S. Is it possible to estimate the muscle fiber composition in a noninvasive way? In Sport und Medizin Pro und Contra/32. Deutscher Sportärzte-Kongress, München 1990; Zuckschwerdt: München, Germany, 1991; pp. 688–690. [Google Scholar]
- Hautier, C.A.; Linossier, M.T.; Belli, A.; Lacour, J.R.; Arsac, L.M. Optimal velocity for maximal power production in non-isokinetic cycling is related to muscle fibre type composition. Eur. J. Appl. Physiol. Occup. Physiol. 1996, 74, 114–118. [Google Scholar] [CrossRef]
- Hansen, E.A.; Andersen, J.L.; Nielsen, J.S.; Sjøgaard, G. Muscle fibre type, efficiency, and mechanical optima affect freely chosen pedal rate during cycling. Acta Physiol. Scand. 2002, 176, 185–194. [Google Scholar] [CrossRef]
- Brisswalter, J.; Hausswirth, C.; Smith, D.; Vercruyssen, F.; Vallier, J.M. Energetically optimal cadence vs. freely-chosen cadence during cycling: Effect of exercise duration. Int. J. Sports Med. 2000, 21, 60–64. [Google Scholar] [CrossRef] [PubMed]
- Kohler, G.; Boutellier, U. The generalized force–velocity relationship explains why the preferred pedaling rate of cyclists exceeds the most efficient one. Eur. J. Appl. Physiol. 2005, 94, 188–195. [Google Scholar] [CrossRef]
- Annaheim, S.; Boutellier, U.; Kohler, G. The energetically optimal cadence decreases after prolonged cycling exercise. Eur. J. Appl. Physiol. 2010, 109, 1103–1110. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Bessot, N.; Moussay, S.; Laborde, S.; Gauthier, A.; Sesboüé, B.; Davenne, D. The role of the slope of oxygen consumption and EMG activity on freely chosen pedal rate selection. Eur. J. Appl. Physiol. 2008, 103, 195–202. [Google Scholar] [CrossRef] [PubMed]
- Henneman, E.; Mendell, L.M. Functional organization of motoneurone pool and its inputs. In Handbook of Physiology, Section 1, The Nervous System, vol. II, Motor Control; Brookhart, J.M., Mountcastle, V.B., Brooks, V.B., Geiger, S.R., Eds.; American Physiological Society: Rockville, MD, USA, 1981; pp. 423–507. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).