Abstract
This article presents an efficient methodology for the calibration of a numerical model of a Sgnss freight railway wagon based on experimental modal parameters, namely natural frequencies and mode shapes. Dynamic tests were performed for two distinct static loading configurations, tare weight and current operational overload, under demanding test conditions, particularly during an unloading operation of the train and without disturbing its tight operational schedule. These conditions impose restrictions to the tests, especially regarding the test duration, sensor positioning and system excitation. The experimental setups involve the use of several high-sensitivity accelerometers strategically distributed along with the vehicle platform and bogies in the vertical direction. The modal identification was performed with the application of the enhanced frequency-domain decomposition (EFDD) method, allowing the estimation of 10 natural frequencies and mode shapes associated with structural movements of the wagon platform, which in some cases are coupled with rigid body movements. A detailed 3D FE model of the freight wagon was developed including the platform, bogies, wheelsets, primary suspensions and wheel–rail interface. The model calibration was performed sequentially, first with the unloaded wagon model and then with the loaded wagon model, resorting to an iterative method based on a genetic algorithm. The calibration process allowed the obtainment of the optimal values of eight numerical parameters, including a double estimation of the vertical stiffness of the primary suspensions under the unloaded and loaded static configurations. The results demonstrate that the primary suspensions present an elastic/almost elastic behaviour. The comparison of experimental and numerical responses before and after calibration revealed significant improvements in the numerical models and a very good correlation between the experimental and numerical responses after calibration.
1. Introduction
In recent years, rail freight traffic has experienced a significant rise in the total amount of transported goods, since railway operators have employed more efficient strategies, which include, for example, increasing the axle load, length and speed of trains, making this type of transport more competitive. Moreover, the European Union has increased its multi-annual budget to achieve more efficient and sustainable transportation systems, mainly the rail transportation. For rail freight, policy objectives for shifting goods from road to rail have been translated into a series of EU legislative measures ensuring non-discriminatory access to the market and promoting interoperability and safety [1]. In the case of Portugal, the investment in freight traffic has recently been assumed as a priority, with relevant investments planned for upgrading the existing railway corridors that connect the main Portuguese ports to the Spanish border.
The effects induced by freight trains on the railway infrastructure can be more severe than those caused by passenger trains. Despite circulating at lower speeds, these vehicles usually have higher axle loads, inducing relevant quasi-static and dynamic forces on the infrastructure that can potentially put the structural safety at risk. Field measurements conducted by Decroos et al. [2] revealed that freight trains induce higher dynamic forces on the lower ranges of frequencies in comparison to passenger trains. This behaviour is particularly critical for the railway infrastructure, especially in the case of structures with lower fundamental frequencies, such as medium-large-span bridges [3,4]. In these structures, there is a higher probability that the excitation frequency associated with the passage of regularly spaced groups of axles will coincide with the main structural frequencies, leading to a dynamic amplification of the responses and consequently making the infrastructure more susceptible to structural damages.
Aware of the potentially critical effects that these dynamic actions may impose on structures, engineers developed several powerful numerical tools capable of simulating the complex train–track dynamic interaction problem, as well as the wheel–rail contact interface [5,6,7]. In addition to a robust contact model, the efficiency of these numerical tools is closely related to the accuracy of both the track/structure and vehicle numerical models. Regarding these numerical models, recent studies confirm that their performance can be significantly improved using appropriate calibration strategies based on experimental data [8,9,10,11,12].
Regarding the vehicle modelling, two main approaches can be found in the literature. The first is based on multibody dynamics [13,14,15,16,17,18,19,20,21,22,23], and the second relies on finite element method (FEM) formulations [24,25,26,27,28,29,30,31].
Multibody modelling strategies consider all the vehicle components to be rigid and connected by elastic elements, typically suspensions, which are usually modelled as spring-dashpot assemblies [17]. Concentrated mass elements are positioned at the gravity centre of each vehicle component, which are then assigned with the corresponding inertial properties. Low computational costs and good accuracy in predicting the global vehicle response make these models very popular in the design process of new vehicles, as well as in running safety investigations [13,14,20,32].
Alternatively, finite element models (FEM) that consider the vehicle components flexibility through the use of shell, volume and beam elements are less widespread in modelling railway vehicles. This is especially due to high computational costs and difficulties in obtaining the vehicle design details due to the confidentiality reasons of the manufacturers. However, in problems where the influence of local modes of vibration is relevant, specifically related to the bending/torsion of vehicle components, the use of these models is required. Typically, the contribution of the local dynamic response is relevant in studies regarding the assessment of passenger comfort [27,33], fatigue-life prediction [29] and cargo stability [26,28].
One specificity on the dynamic analysis of rail freight vehicles is related to the adequate modelling of the different types of suspension systems (leaf, coil, etc.) which, in most situations, presents a nonlinear dynamic behaviour [15,34,35,36,37,38]. Another issue is the correct modelling of the overload, because in these wagons, the cargo load usually represents a significant portion of the total weight of the vehicle [28]. The high overload/tare mass ratio influences the dynamic behaviour of the wagon, forcing designers to include loaded and unloaded scenarios in their analysis [35]. Furthermore, the overload distribution requires special attention since it can change the position of the gravity centre of the vehicle [39].
Several works report the use of dedicated dynamic tests to experimentally evaluate the dynamic properties of the railway vehicles, particularly the natural frequencies, mode shapes and damping coefficients [25,30,40,41]. These tests can be executed when the vehicle is at its rest position or in motion, during its normal operation. When in rest position, an external excitation is usually applied to the structure by means of special equipment, such as an electrodynamic exciter, impact hammer, or even by people moving randomly over the vehicle [24,42,43]. Most of the authors perform the modal identification with the application of output-only techniques, also known as operational modal analysis [41].
Typically, the calibration of the numerical models of railway vehicles are based on experimental modal parameters derived from dynamic tests [24]. Model calibration strategies usually resort to iterative methodologies grounded in optimization algorithms, in which successive modifications of numerical parameters are performed, aiming to minimize an objective function [24]. In these type of problems, the objective function typically comprises weighted residuals derived from the natural frequencies and modal configurations [24]. The objective function must be properly constructed and the weights well selected in order to avoid ill-conditioned optimization problems [44]. Most algorithms used to solve these problems are the gradient-based algorithms, response surface methods and nature-inspired algorithms, such as the genetic algorithm and particle swarm optimization [31]. Several recent studies on damage identification problems based on modal parameters [45,46,47] demonstrated the great potential of recently developed nature-inspired algorithms, namely the Whale and the Moth-Flame optimization algorithms.
There is still a scarce number of studies regarding the experimental model calibration of freight vehicles [31,43], and most of the published works are focused on passenger vehicles [12,24,33]. Regarding the latter, Akiyama et al. [33] proposed an automatic calibration methodology based on a particle swarm optimization algorithm, aiming to reduce the maximum difference between numerical and experimental vibration frequencies. The experimental setup performed on a Shinkansen-type wagon involved 42 acceleration measurement points and an external excitation provided by an electrodynamic shaker. Six operational mode shapes were extracted using classical modal analysis based on frequency response functions. The model updating process involved 14 numerical parameters and resulted in a maximum difference of only 0.86% between numerical and experimental frequencies. Szafrański [12] proposed a simplified multibody single-level suspension model for the EN57 vehicle that was manually calibrated based on the stiffnesses and damping values of the suspensions. The calibration was based on the natural frequencies’ values, as well as the damping coefficients’ values, of the rolling and bouncing rigid-body modes of the car body. The modal configurations were identified by means of dynamic tests using the wedge excitation method.
Regarding the calibration of freight vehicles, Sichani et al. [43] updated a 3D FE numerical model of a freight wagon based on seven natural frequencies and corresponding modes of vibration. The model updating was performed using a two-step approach by means of a gradient-based method. Firstly, the suspension properties were tuned based on three rigid body modal parameters for the car body, and then the cross-section geometrical properties of specific structural elements of the car body were estimated based on four flexural modal parameters. Bragança et al. [31] calibrated and validated a 3D multibody model of a Laagrss-type freight wagon based on experimentally identified modal parameters obtained from dynamic tests performed with the vehicle on current operation and employing a minimalist layout of the sensors. The model validation was performed based on the direct comparison between simulated and measured accelerations and displacements on the car body and bogies.
This work intends to contribute to extending the existing knowledge about the dynamic behaviour of freight railway vehicles, presenting some innovative contributions, namely:
- -
- The calibration of a freight wagon numerical model considering both the loaded and unloaded configurations. This aspect is of the utmost importance when it comes to freight vehicles in which the towed load can be significantly higher than the vehicle tare weight, and consequently, can considerably change its dynamic behaviour.
- -
- The development of a FE numerical model of an existing freight vehicle. This detailed model is rarely found for freight vehicles, due to difficulties in obtaining technical details from the manufacturers; however, it can constitute a basis for a much more accurate evaluation of the wheel–rail contact forces and cargo stability in the scope of the dynamic analysis of the train–track–bridge system.
2. Freight Train
2.1. Description
The wagon studied is part of a railway composition operated by the Portuguese freight transport company Takargo. The train consists of 14 wagons of the Sgnss series, pulled by a EURO 4000 class diesel locomotive. These compositions operate on the Portuguese railway network transporting roundwood, usually of a eucalyptus type, connecting the wood-producing centres in Galicia (northern Spain) to the Portuguese pulp production plants. The locomotive has six axles, three per bogie, and an axle load of about 200 kN. The Sgnss wagon has two axles per bogie and a maximum axle load of 220 kN. Figure 1 shows an overview of the train in operation and the corresponding loading scheme.

Figure 1.
Freight train locomotive EURO 4000 with Sgnss type wagon: (a) general overview; (b) loading scheme (distances in metres and loads in kN).
2.2. The Sgnss Wagon
The Sgnss vehicle is a platform wagon originally designed for the transport of containers. Currently, this vehicle is adapted for transportation of roundwood with the addition of removable stanchions. The metallic stanchions are supported over the wagon platform, creating a specific stowage for the timber accommodation. Figure 2 presents an overview of this alternative vehicle layout as well as the original layout.

Figure 2.
Sgnss wagon: (a) layout for containers, (b) layout for timber transportation.
The wagon has a total length of 18.5 m, a width of 2.9 m and two bogies, spaced out by 12.4 m, and each has two axles spaced out by 1.8 m. The vehicle has a tare weight of 26.1 t and can carry a maximum load of 63.8 t, allowing a maximum permissible axle load of 220 kN.
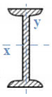
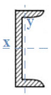
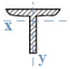
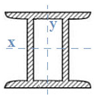
The vehicle platform is mainly composed by a grid of metallic girders, particularly: two central longitudinal main girders with I-section and variable web height; two longitudinal side beams, one on each side; and transversal girders embracing all the longitudinal girders, as presented in Figure 3. The vehicle platform only exists at both extremities of the wagon and is formed by a 2.0-millimetre-thick steel plate.

Figure 3.
Sgnss wagon: lateral view and plan of the platform (dimensions in mm).
Table 1 presents the main geometrical properties and cross-section schemes of the main structural elements of the Sgnss vehicle according to the numbering of Figure 3.

Table 1.
Geometrical characteristics of the main elements of the wagon platform.
The wagon is equipped with Y21-type bogies, which are a variant of the Y25 bogie [15], and is supplied with coil springs instead of leaf springs, allowing the bogie frame to be shorter and lighter. The Y21-type bogie (Figure 4a) has an axle distance equal to 2000 mm, a total weight of 4.72 t, a maximum wheelset load of 220 kN and a maximum operating speed of 100 km/h.

Figure 4.
Y21 bogie: (a) overview and main elements, (b) primary suspension detail, (c) cross-section in the transverse direction (adapted from [22]).
The semi-rigid connection between the wagon platform and the bogie is provided by a central spherical pivot, which releases the three rotational DOFs, complemented by two side bearings, as shown in Figure 4c. The side bearings constrain the roll movement between the car body and the bogie frame and provide frictional damping for the yaw movements of the bogie frame. The bogie frame rests on two sets of coil springs per axle box, totalling in eight coil springs. For each set of coil springs, one is connected to the bogie frame, more precisely to the spring holder, via an inclined link (Lenoir link). This link limits the opening of the spring in situations where a larger separation between the bogie frame and axle box occurs. Additionally, a bump stop is installed to provide a full-contact restraint concerning excessive approximation or separation of the coil springs. The primary suspension of the Y21 bogie is presented in detail in Figure 4b.
3. Dynamic Tests
3.1. Overview
This section describes the dynamic tests performed on the Sgnss wagon conducted at Navigator company, in Figueira da Foz (Portugal), aiming to identify modal parameters of the freight wagon, considering both the loaded and unloaded configurations. The tests were carried out during the train unloading operation, in the case of the loaded vehicle, or immediately after, in the case of the unloaded vehicle. Both tests were performed without disturbing the tight schedule of operations of these vehicles; however, there were some imposed restrictions to the tests, especially regarding the sensor positioning and the time window available for carrying out the work.
The study of the loaded and unloaded configurations was justified due to the high ratio between the maximum towed load (63.8 t) and tare weight of the wagon (26.2 t) equal to 2.6. This important mass increase conducts modifications to the modal properties of the wagon, which requires a detailed evaluation.
3.2. Loading Configurations
In the test performed on the loaded vehicle, one of the central stowage containers of timber was removed to allow the space needed for the installation of the data acquisition system (Figure 5a). The option of removing one of the central stowage containers, to the detriment of other stowage containers, aims to maintain an almost symmetrical mass distribution on the wagon. This is important since non-symmetric mass layouts can modify the modal configurations, as well as the natural frequencies, particularly in freight vehicles where the overload/tare mass ratio is high. Additionally, non-symmetric mass layouts are normally less representative of the real operating conditions of Sgnss wagons. Figure 5a presents a schematic representation of the loading configuration during the dynamic test and the corresponding mass values for each stowage container, weighted after the test. The weight on the central stowage container was only due to people and equipment, which is negligible in comparison to the total overload (Figure 5b).

Figure 5.
Dynamic tests of Sgnss wagon: (a) loaded configuration, (b) detail of the central stowage, (c) unloaded configuration.
In the test performed on the unloaded vehicle, the five remaining stowage containers of timber were removed (Figure 5c). The weight of the tested wagon was measured before and after the unloading process; the total weight was 81.85 t, and the net weight was 55.65 t.
3.3. Measurement Setup
Figure 6 shows a lateral and plan views of the measurement layout used in both dynamic tests considering the unloaded and loaded configurations. The dynamic tests were performed based on a technique that considers fixed reference points (marked in red in Figure 6) and mobile measuring points (marked in blue in Figure 6). The response was evaluated in terms of the accelerations in the vertical (z) direction, in four setups, totaling 20 measurement points (1 to 20): 14 located on the platform and 6 located on the bogies. The accelerometers located on the bogies allow scaling the movements of the bogies in relation to the movements of the vehicle platform.

Figure 6.
Dynamic tests of Sgnss wagon: measurement setup (reference points in red and mobile points in blue).
In total, 14 high-sensitivity piezoelectric accelerometers were used, PCB model 393B12, with a sensitivity equal to 10 V/g, a measurement range of ±0.5 g and a frequency range of 0.15–1000 Hz. The accelerometers were attached to the car body using metallic angles fixed to the vehicle with magnetic disks. The PC, data acquisition system (DAQ) and battery supplying system were located near the centre of the vehicle. The data acquisition was performed through the cDAQ-9172 system using modules NI 9233 for IEPE type accelerometers. The time series were acquired for 10 min periods, with a sampling frequency of 2048 Hz, posteriorly decimated to a frequency of 256 Hz. Figure 7 presents some details of the DAQ and the accelerometer connection to the vehicle platform and bogies.

Figure 7.
Dynamic tests of Sgnss wagon: DAQ and accelerometers on the platform and bogies.
The dynamic test was carefully planned to minimize the influence of noise in the measurements, which involved the use of shielded cables, insulated cable connectors, stable DC power supply from electrical batteries, denoise filters in the A/D conversion process and high-sensitivity accelerometers.
During the dynamic test, the vehicle was operating at slow and intermittent motion, or at rest, and so, a random external excitation, in time and space, was required to increase the vibration levels. The excitation was provided by means of a group of people jumping on the edges of the vehicle platform, as well as impacts induced by impulse hammers. This technique guarantees higher signal-to-noise ratios and consequently, an increase of the coherence between the measured signals.
3.4. Modal Identification
The identification of the modal parameters for the unloaded and loaded vehicle, particularly the natural frequencies, mode shapes and damping coefficients, was performed by the application of the enhanced frequency domain decomposition (EFDD) method implemented in the ARTeMIS software [48], which is a well-established and robust technology capable of providing accurate results even in the presence of noise on the measured data [49,50]. In this method, the natural frequencies are identified based on the peaks of the average and normalized singular values of the spectral matrices, and the modal configurations are derived from the corresponding singular vectors.
Figure 8 depicts the average and normalized singular values of the spectral matrices of all test setups, derived from the application of the EFDD method, and considering the unloaded (Figure 8a) and loaded (Figure 8b) configurations. The peaks corresponding to the five globally identified operational mode shapes are identified in the figure by dashed lines. The remaining peaks are possibly related to [51,52]: (i) local operational mode shapes not properly characterized by the sensors layout (vibrations of stanchions and elements of the wagon’s platform), (ii) presence of harmonics due to equipment in operation, (iii) influence of the excitation provided by people and impulse hammers, and (iv) noise on measured data or derived from the signal-processing operations.

Figure 8.
EFDD method—average normalized singular values of the spectral matrices: (a) unloaded configuration, (b) loaded configuration.
Figure 9a,b illustrate, in perspective, five identified operational mode shapes for the Sgnss vehicle considering the unloaded and loaded configurations, respectively. The deformed modal configurations are represented by red lines, in the case of the unloaded configuration, or blue lines, in the case of the loaded configuration, and the undeformed mesh are represented by grey lines. The average values of the natural frequencies and corresponding damping coefficients are also indicated.
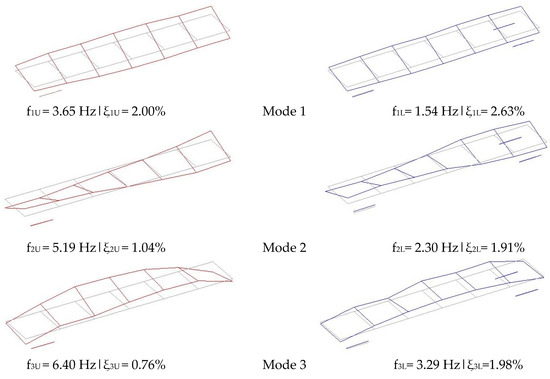

Figure 9.
Experimental modal parameters: (a) unloaded configuration, (b) loaded configuration.
Generally, the modal configurations have a very good definition and involve structural movements of the vehicle platform, which in some cases, to more or less extent, are coupled with rigid body movements. The modal configuration of the unloaded and loaded configurations are similar but have distinct modal ordinates, as can be observed in Figure 9a,b. Mode 1 is a rigid body mode associated with the rotation of the vehicle platform along its longitudinal axis (rolling). However, especially for the unloaded configuration, some coupling with the torsion movement of the vehicle platform is visible. Mode 2 is a flexural movement of the platform associated with its second torsion mode. Mode 3 involves the bending of the vehicle platform coupled with the rigid body bouncing movement. Mode 4 is associated with a higher-order torsion mode of the vehicle platform. Mode 5 is a local bending mode combined with rigid body pitching movement of the platform. In all the identified modal configurations, the movements of the bogies are negligible in comparison to the movements of the vehicle platform, with the exception of Mode 5, where a coupling effect was detected.
Additionally, as expected, due to the high ratio between towed load and tare weight, as is typical in this type of freight wagons, the natural frequencies for the loaded vehicle are significantly lower in comparison to the unloaded wagon. The range of frequency values is between 3.65 Hz and 16.63 Hz for the unloaded configuration, and between 1.54 Hz and 6.66 Hz for the loaded configuration.
The damping coefficients obtained for the loaded configuration (0.79% to 2.63%) are of the same order of magnitude but consistently higher, mode-by-mode, in comparison to the unloaded configuration (0.60% to 2.00%). This is probably due to the additional energy dissipation mechanisms associated with the cargo–platform interaction. However, in general, the damping coefficients are low, essentially due to the vehicle resting/low motion scenario in which the dynamic tests occurred, since the provided excitation was insufficient to induce large suspension movements. During an operational scenario, the suspensions were subjected to much larger displacements and, consequently, the suspension components would provide a higher damping due to their non-linear hysteretic behaviour [53,54].
4. Numerical Modelling
4.1. Description
A three-dimensional finite element model of the Sgnss wagon was developed in ANSYS [55] software, as presented in Figure 10. The FE model allows for the reproduction of the dynamic behaviour of the vehicle in the vertical (Z) direction. Some strategic degrees-of-freedom in the lateral (Y) and longitudinal (X) directions of the wagon platform were restrained to prevent movements in these two directions as well as yaw rotations.

Figure 10.
FE numerical model of the Sgnss vehicle including a detail of the bogie.
The vehicle’s main platform was modelled with beam finite elements (BEAM 188), taking into consideration their corresponding geometrical properties validated on field observations. The plates attached to the platform extremities were modelled through shell elements (SHELL 181) considering their real thickness. The bogie frames and axles were modelled using flexible beam elements based on their corresponding geometrical properties, and the axle boxes and spring holders were modelled using rigid beam elements, as shown in Figure 10. The suspensions were modelled as spring-dashpot assemblies using COMBIN14 elements in the vertical direction. The wheel–rail contact was modelled by a spring-dashpot assembly (COMBIN14), whose stiffness is estimated by the Hertz contact theory [56]. The vehicle tare mass was incorporated into the model by an equivalent density of the steel girders and plates to consider the extra mass associated with bolted/welded connections, strengthening plates, etc. Additionally, concentrated mass elements (MASS 21) were added to account for the mass of some non-structural elements, namely the stanchions for the roundwood accommodation (including or not including the timber, accordingly to the adopted loading scheme), suspensions and other bogie components, braking system, reservoirs, piping, on-board control equipment, wheelset and edges back stop and front stop. The positioning of the concentrated masses is presented in Figure 10, where a detail of one bogie is also shown.
The loaded numerical model considered the towel load configuration (load values and layout), similar to the one used during the dynamic test of the Sgnss wagon (Section 3). In the unloaded numerical model, no overload due to the eucalyptus roundwood was considered, but it included the masses of the stanchion structures. In the loaded model, the mass of the stanchions indirectly considers the effect of the masses distributed along its height, namely those related to the laterally supported towed overload. Thus, besides the towed load translational mass, the stanchions masses also include the rotary mass inertias dependent of the distance between the base of the stanchion and the towed mass levels.
Table 2 summarizes the geometric and mechanical parameters of the numerical model of the Sgnss wagon, including its designation, the adopted value and respective unit, as well as some references. Additionally, Table 2 lists the lower and upper limits of the parameters that were used in the model calibration phase (Section 5). The limits adopted for the steel deformability modulus indirectly consider the existing uncertainties on the dimensions of the steel sections (and corresponding geometrical properties) and on the type of connections between steel bars (assumed as rigid, but in some cases might have a semi-rigid behaviour). The vertical stiffness of each set of suspension springs, represented by the parameters K1 to K4, was considered independent since there was no guarantee that all the sets of coil springs had the same conservation state.

Table 2.
Main parameters of the numerical model of Sgnss wagon.
4.2. Modal Parameters
Figure 11 depicts five of the numerical mode shapes, and the corresponding natural frequencies, for the unloaded and loaded configurations. For each modal configuration, the figure presents a perspective complemented with a lateral view. For simplicity, and due to the similarity between the unloaded and loaded mode shapes, only the modal configurations associated with the unloaded vehicle are presented.
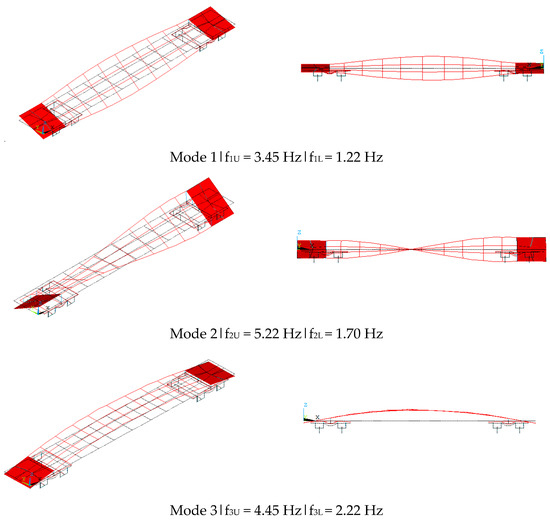

Figure 11.
Numerical modal parameters before calibration (undeformed mesh in grey and deformed mesh in red).
The modal configurations involve structural movements of the vehicle platform, namely bending and torsion, which in some of the cases, are coupled with specific rigid body movements particularly the rolling, bouncing and pitching. The presented mode shapes (1 to 5) are correspondent to the ones experimentally identified according to Figure 9. It should be noted that the order of the numerical modes is different from the order of the experimental modes, particularly in the case of Modes 2 and 3 for the unloaded configuration.
5. Calibration
The calibration of the numerical model of the Sgnss wagon was based on the results of the dynamic tests and involved a sensitivity analysis and an optimization based on a genetic algorithm. The automatic mode pairing between the numerical and experimental modes was performed based on the modal assurance criterion (MAC) [57]. The calibration was performed sequentially, first for the unloaded wagon model and then for the loaded wagon model. A correlation analysis allowed a comparison between the modal parameters obtained.
5.1. Sensitivity Analysis
The sensitivity analysis allowed for the selection of the numerical parameters that most influence the modal responses (five natural frequencies and five modal configurations) and so should be included in the subsequent optimization phase. In this study, 10 numerical parameters were selected and stochastically sampled by the Latin hypercube method. The samples generated based on uniform distributions within the limits of each parameter are given in Table 2.
The sensitivity analysis results are based on Spearman correlation coefficients (e) that express the monotonic correlation between two vectors of samples, x and y, based on their rank-order vectors, R(xi) and R(yi), by the expression:
in which (x) and (y) are the average values of the rank-order vectors R(xi) and R(yi), respectively, and n is the number of samples of each vector.
Figure 12 shows the results of the global sensitivity analysis based on a Spearman linear correlation matrix based on 750 samples obtained with the Latin hypercube method. The samples with a MAC value lower than 0.50 have been excluded from the total amount of samples. Additionally, the samples with a correlation coefficient within the range −0.30 to +0.30 were removed. This strategy allows us to properly identify only the parameters with a significant amount of correlation with the modal responses. Numerical parameters presenting Spearman correlation coefficients, in relation to the modal responses, higher than 0.50 were considered for the further optimization stage [58,59].

Figure 12.
Spearman correlation matrix: (a) unloaded configuration, (b) loaded configuration.
The results of the sensitivity analysis allowed us to identify specific numerical parameters that have an important influence on the modal responses, both on the unloaded and loaded models, particularly the side bearers’ vertical stiffness (e) and the stanchion masses (Mt). Curiously, there are other numerical parameters, namely the vertical stiffness of the primary suspensions (K1 to K4), that reveal a high sensitivity with the responses in the loaded model, particularly with the MAC values. The additional mass of the braking system (Mc) and the steel equivalent density (D) proved to have no influence, or negligible influence, on the modal responses, and, consequently, were not included in the optimization phase. Thus, from the 10 numerical parameters evaluated, 8 of them proved to have an influence on the modal responses, particularly on the side bearers’ vertical stiffness (Ks), the stanchion masses (Mt), the vertical stiffness of the suspensions (K1 to K4), the steel deformability modulus (ES) and the masses of the back stop and front stop (Me).
The stiffness parameters of each suspension showed enough sensitivity to be properly estimated in the optimization stage. This is particularly relevant, since in other studies (e.g., [12,31,33]), the reliable suspension stiffness estimation sometimes required the grouping of the suspension parameters, considering two sets or even four sets springs, since the individual stiffnesses per set of springs presented low correlation values.
Also, the mass parameters (D, Mc, Me, Mt) present a negligible sensitivity to the modal configurations, probably due to the symmetry/near symmetry of the vibration modes, which means that a variation in the values of these symmetrically positioned masses will not change its symmetrical configuration.
5.2. Optimization
The optimization of the numerical models (unloaded and loaded configurations) was performed using an iterative methodology based on a genetic algorithm. The implemented strategy relied on the interaction between two commercial softwares, MATLAB [60] and ANSYS [55], as presented in Figure 13.

Figure 13.
Model calibration strategy.
Firstly, in ANSYS, a numerical model was developed based on a set of initial numerical parameters randomly generated by the Latin hypercube method, considering the bounds of each individual parameter presented in Table 2. After, a numerical modal analysis was performed to evaluate the natural frequencies and mode shapes, which are exported to MATLAB through text files. In MATLAB, the mode pairing between numerical and experimental mode shapes was performed, associating each experimental mode with the correspondent numerical mode based on the highest MAC value. Finally, a new set of numerical parameters was estimated by means of a genetic algorithm aiming to minimize the residuals of an objective function. This process was repeated until the maximum number of iterations was reached. This stopping criterion has already been used in other similar applications of GA, since, typically, there have been small improvements on the residual of the objective function in the last generations, even in situations where apparently no upgrades were verified in the previous generations [24,31].
The optimization aimed to find the optimal values of the numerical parameters based on the modal responses. The level of agreement between numerical and experimental modal responses was evaluated based on the following objective function (f):
where a and b are the residuals weights, is the vibration frequency of the ith experimental mode, is the vibration frequency of the ith numerical mode and is the MAC value between the ith numerical and experimental modal configurations. The value of the weights a and b are assumed equal to 1.20 and 0.80, respectively, which gave more importance to the frequency residues. These weights consider the importance of each of the residues and the uncertainty that is associated with the experimental estimation of their dependent responses. Typically, the natural frequencies are more rigorously estimated than the mode shapes, and therefore its residues should have a higher weight [61].
The iterative process started with an initial population of 30 individuals, randomly generated by the Latin hypercube method, whose size has been maintained over 100 generations, totaling 3000 individuals. Each individual of the genetic algorithm is formed by a set of genes in correspondence with the numerical parameters of the optimization problem. The genetic algorithm requires some specific definitions for the selection crossover and mutation operators. The selection operator was based on the stochastic universal sampling (SUS) technique proposed by Baker [62]. This technique defines a line, in which each of the possible parents occupy a space proportional to its fitness. After, the algorithm moves along the line in equally spaced steps, where the step length is equal to the line length divided by the number of individuals to be selected. The position of the first step is chosen randomly between zero and the step length. For each step location, a parent is selected based on the corresponding section of the line.
Concerning the crossover, a scattered crossover operator was used. This operator relies on the random generation of a binary vector with the same number of genes of the parents. Each gene (i.e., numerical parameter) of the offspring is defined based on the values of the binary vector: if the value is 1 the gene will be derived from the first parent, and if the value is 0 it will be derived from the second parent. The crossover rate, which controls the probability that the binary vector will change its values from 1 to 0, was considered equal to 50% [59]. The mutation was performed by the Gaussian mutation operator. This operator adds to the value of each gene to a random value derived from a Gaussian distribution centered in zero and with standard deviation equal to the difference between the upper and lower bounds of the gene multiplied by a scale factor. In this study, this scale factor varied linearly from 0.10 (10%) to 0.01 (1%) from the first to the last generation. This strategy provides greater variability for the first generations and limits the variability of the good genes in the last generations [24,59]. Finally, the best individual of each generation was selected as an elite offspring and was automatically included in the population of the next generation.
5.2.1. Unloaded Vehicle
The first optimization process was conducted for the unloaded vehicle, considering the 8 numerical parameters and the 10 modal responses (5 natural frequencies and 5 MAC values).
The optimal values of the parameters were obtained based on the results of four independent optimization runs (GA1–GA4) with different initial populations. In Figure 14 are represented the ratios of the values of each numerical parameter relative to the bounds indicated in Table 2 for optimization runs GA1 to GA4. A ratio of 0% means that the parameter coincides with the lower limit. A ratio of 100% means that it coincides with the upper limit. Furthermore, the value of each individual numerical parameter is presented in brackets.
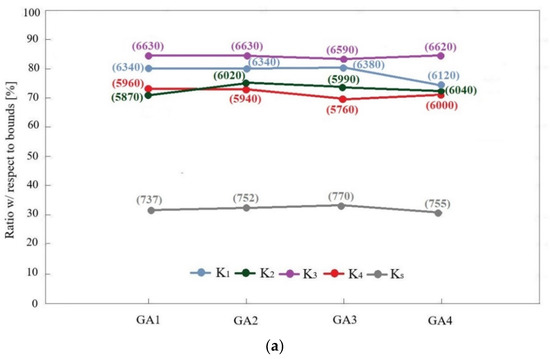

Figure 14.
Values of the optimal parameters for the optimization runs GA1–GA4 for the unloaded vehicle numerical model: (a) stiffness parameters, (b) additional mass parameters and steel deformability modulus.
The results show a very good stabilization for all the parameters estimates, with variations lower than 10% considering the distinct optimization runs. The values of the vertical stiffness of the different primary suspensions have comparable values, which predictably indicates a similar state of conservation of the different suspension sets. Moreover, none of the parameters reached their lower or upper bounds, which demonstrates the robustness and efficiency of the optimization process in the parameter estimation. Figure 15 shows the variation of the objective function residue throughout the optimization process. The optimal parameters are referred to the optimization run GA3, which presented the lowest value for the objective function.

Figure 15.
Residue of the objective function throughout the optimization process for the unloaded vehicle numerical model.
5.2.2. Loaded Vehicle
The second optimization process was performed for the loaded vehicle, considering only 5 numerical parameters, particularly the 4 vertical stiffness values of the primary suspensions (K1 to K4) and the vertical stiffness of the side bearers (Ks), as well as 10 modal responses.
The values of the remaining numerical parameters associated with the additional masses (Me and Mt) and steel deformability modulus (Es) were assumed as deterministic and derived from the optimization of the unloaded vehicle numerical model.
The proposed sequential optimization strategy allows limiting the extent of the optimization problem by reducing the number of design variables while incorporating the eventual modification of the vertical stiffness of the primary suspensions and side bearers in the optimization results, due to the eventual non-linear behaviour of these elastic components under higher load levels [53].
Thus, maintaining the same strategy of the unloaded vehicle optimization, Figure 16 represents the ratios of the values of each numerical parameter relative to the bounds indicated in Table 2 for four independent optimization runs, GA1 to GA4.

Figure 16.
Values of the optimal parameters for the optimization runs GA1–GA4 for the loaded vehicle numerical model.
Figure 17 shows the variation of the objective function residue during the optimization process. The optimal parameters are referred to the optimization run GA1, which presented the lowest value for the objective function.

Figure 17.
Residue of the objective function throughout the optimization process for the loaded vehicle numerical model.
Comparing the results obtained in the two optimization processes, and focusing on the primary suspension parameters, no significant variation on the vertical stiffness values were detected. Additionally, the estimated stiffness values are significantly higher in comparison to the nominal values usually found in the literature, which are typically evaluated considering the vehicle under operation and are in the range between 800 kN/m and 1000 kN/m [20,22,23,53]. As example, Figure 18a,b shows the evolution of the numerical parameter K1 as a function of the number of individuals and for the unloaded and loaded vehicle models, respectively.

Figure 18.
Variation of the optimal values of numerical parameter K1: (a) unloaded vehicle; (b) loaded vehicle.
These aspects are particularly relevant since as the vehicle was at rest, or almost at resting conditions, and the primary coil suspensions apparently kept their behaviour in an elastic or almost elastic regime, independently of the level of the vertical static loads, in this case the tare load (unloaded configuration) and a regular operation loading (loaded configuration). However, considering the vehicle in a real operation scenario, where, due to a variation on the movements of the suspension components due to the dynamic loading, non-linear behaviour of the suspensions is expected. This non-linear behaviour is due to the friction/slippage contact phenomenon that tends to occur in some of the suspension components, which justifies an overall stiffness reduction [36].
Regarding the vertical stiffness of the side bearers, an important increase in the vertical stiffness was detected, in comparison to the optimal values obtained with the unloaded configuration. This is probably associated with the pronounced non-linear behaviour of these components, since, under higher vertical forces, the force-displacement curve presents a higher tangent stiffness.
5.3. Correlation Analysis
Figure 19a shows the error values between numerical and experimental frequencies, before and after calibration, for the unloaded and loaded vehicle, taking as reference the values of the experimental frequencies. The relative errors on the natural frequencies were significantly reduced for all five modes, leading to a reduction in the average error from 11.8% before calibration to 3.2% after calibration, for the unloaded vehicle, and from 20.4% before calibration to 4.8% after calibration, for the loaded vehicle.

Figure 19.
Errors between experimental and numerical modal responses, before and after calibration: (a) natural frequencies, (b) MAC.
Figure 19b shows a comparison of the MAC values between the numerical mode shapes, before and after calibration, and experimental mode shapes. The average MAC value improved from 0.85 to 0.87, and from 0.82 to 0.85, in the unloaded and loaded configurations, respectively.
Figure 20 compares the experimental and numerical modal configurations after calibration, for the unloaded (Figure 20a) and loaded (Figure 20b) configurations. As can be observed, an evident similarity between numerical and experimental modal configurations was achieved after calibration.
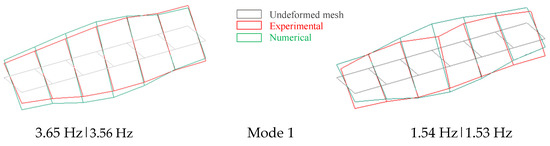

Figure 20.
Comparison between the experimental and numerical modal configurations after updating modal parameters: (a) unloaded configuration, (b) loaded configuration.
6. Conclusions
This paper presents an efficient model calibration methodology for a freight wagon based on experimental modal parameters, particularly natural frequencies and mode shapes. The wagon studied was a Sgnss type vehicle specifically designed for timber logs transport.
The identification of the modal parameters was based on dynamic tests performed at the Navigator company facilities for two distinct static loading configurations, tare weight and current operational overload. The experimental natural frequencies and their corresponding modal configurations were later used for calibrating the numeric model. The application of a modal identification technique based on the EFDD method allowed us to identify five operational modes with a very good definition involving structural movements of the vehicle platform, which in some cases, to more or less extent, are coupled with rigid body movements. The natural frequencies for the loaded vehicle are significantly lower in comparison to the unloaded wagon. The range of frequencies values is between 3.65 Hz and 16.63 Hz, for the unloaded configuration, and between 1.54 Hz and 6.66 Hz for the loaded configuration.
A detailed 3D numerical model of the freight wagon was developed resorting to the FE method, using a different type of finite elements (beam, shell, mass and spring-dashpot) in ANSYS software. The thickness and cross-sections of the shell and beam elements, respectively, were derived from technical drawings of the vehicle and validated with field observations. The loaded numerical model considered the towel load configuration (load values and layout), similar to the one used during the dynamic test, and for the unloaded numerical model, no overload was considered.
The model calibration was based on modal parameters and involved a sensitivity analysis and optimization. The sensitivity analysis allowed the selection of eight numerical parameters that most influence the modal responses, namely, the vertical stiffness of the side bearers, the stanchion masses, the vertical stiffnesses of the primary suspensions, the steel deformability modulus and the masses of the back stop and front stop. The optimization was performed by an iterative methodology using a genetic algorithm.
The optimization was performed sequentially, first for the unloaded wagon model and after for the loaded wagon model. The results prove that the vertical stiffness of the coil primary suspensions keeps their behaviour in an elastic or almost elastic regime, independently of the level of the vertical static loads, for unloaded and loaded configurations. On the other hand, the vertical stiffness of the side bearers presents quite distinct calibrated values on the unloaded and loaded wagon models, which is probably associated with the non-linear behaviour of these components. The comparison of experimental and numerical responses before and after calibration revealed significant improvements in the numerical models and a very good correlation between the experimental and numerical responses after calibration. The average error of the natural frequencies decreased from 11.8% before calibration to 3.2% after calibration for the unloaded case, and from 20.4% to 4.8% for the loaded case. The average MAC values improved from 0.85 to 0.87 and from 0.82 to 0.85 for the unloaded and loaded scenarios, respectively.
The calibrated loaded freight wagon model constitutes a very good basis for the dynamic analysis of the train–track system under operational conditions, particularly in evaluating the wheel–rail contact stability as well as the cargo stability. In that scenario, a non-linear behaviour of some suspension components is expected, due to the increase of the vibration amplitude under dynamic loading. Therefore, in future works, a recalibration of the loaded numerical model based on the measured dynamic responses under operational conditions should be performed. However, it is presently very difficult to gain authorisation from the railway operators for the dynamic test of the wagon in motion due to the interference it would cause to the tight schedule of operations of these vehicles. Additionally, for this new calibration scenario, the efficiency and robustness of other recent and advanced optimization algorithms (e.g., Whale and Moth-Flame algorithms) will be tested.
Author Contributions
Conceptualization, R.S. and D.R.; Methodology, R.S., D.R. and C.B.; Resources, C.C. and R.C.; Supervision, A.A.; Writing—original draft, R.S. and C.B.; Writing—review & editing, D.R. and C.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Fundação para a Ciência e a Tecnologia, grant number PD/BD/127812/.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to acknowledge the support of the Base Funding UIDB/04708/2020 and Programmatic Funding UIDP/04708/2020 of the CONSTRUCT (Instituto de I&D em Estruturas e Construções) funded by national funds through the FCT/MCTES (PIDDAC). The first author acknowledges the support provided by FCT PhD programme iRail based on the scholarship PD/BD/127812/2016. The authors express a special thanks to João Prina and Amilcar Ferreira from Navigator company, as well as Germán Fonseca from Takargo, for their authorization and collaboration on the experimental tests of the freight wagon. Finally, the authors’ gratitude is also expressed to Nuno Pinto, from LESE-FEUP laboratory, for his indispensable assistance during the preparation and execution of the experimental tests.
Conflicts of Interest
The authors declare no conflict of interest.
References
- ECA. Rail freight transport in the EU: Still not on the right track. In Special Report no 08/2016, E.C.O. AUDITORS; European Union: Luxembourg, 2016. [Google Scholar]
- Kris, D.; Patrick, V. Computational method for the efficiency determination of mitigation measures for railway induced low frequency ground borne vibrations. In Proceedings of the 13th World Congress in Computational Mechanics (WCCM XIII), New York, NY, USA, 23–27 July 2018. [Google Scholar]
- Costa, C.; Ribeiro, D.; Jorge, P.; Silva, R.; Arêde, A.; Calçada, R. Calibration of the numerical model of a stone masonry railway bridge based on experimentally identified modal parameters. Eng. Struct. 2016, 123, 354–371. [Google Scholar] [CrossRef]
- Costa, C.; Ribeiro, D.; Arêde, A.; Calçada, R. Experimental and numerical assessment of the modal parameters of Côa railway bridge. In Proceedings of the 7th International Conference on Arch Bridges, Trogir, Croatia, 2–4 October 2013. [Google Scholar]
- Wu, S.Y.; Yang, Y.-B.; Yau, J.-D. Three-Dimensional Analysis of Train-Rail-Bridge Interaction Problems. Veh. Syst. Dyn. 2001, 36, 1–35. [Google Scholar] [CrossRef]
- Montenegro, P.A.; Neves, S.; Calçada, R.; Tanabe, M.; Sogabe, M. Wheel–rail contact formulation for analyzing the lateral train-structure dynamic interaction. Comput. Struct. 2015, 152, 200–214. [Google Scholar] [CrossRef]
- Moreno Delgado, R.; Dos Santos, S.M. Modelling of Railway Bridge-Vehicle Interaction on High Speed Tracks. Comput. Struct. 1997, 63, 511–523. [Google Scholar] [CrossRef]
- Ribeiro, D.; Calçada, R.; Delgado, R.; Brehm, M.; Zabel, V. Finite element model updating of a bowstring-arch railway bridge based on experimental modal parameters. Eng. Struct. 2012, 40, 413–435. [Google Scholar] [CrossRef]
- Malveiro, J.; Sousa, C.; Ribeiro, D.; Calçada, R. Impact of track irregularities and damping on the fatigue damage of a railway bridge deck slab. Struct. Infrastruct. Eng. 2018, 14, 1257–1268. [Google Scholar] [CrossRef]
- Melo, L.R.T.; Ribeiro, D.; Calçada, R.; Bittencourt, T.N. Validation of a vertical train–track–bridge dynamic interaction model based on limited experimental data. Struct. Infrastruct. Eng. 2020, 16, 181–201. [Google Scholar] [CrossRef]
- Montenegro, P.A.; Calçada, R.; Carvalho, H.; Bolkovoy, A.; Chebykin, I. Stability of a train running over the Volga river high-speed railway bridge during crosswinds. Struct. Infrastruct. Eng. 2020, 16, 1121–1137. [Google Scholar] [CrossRef]
- Szafrański, M. A dynamic vehicle-bridge model based on the modal identification results of an existing EN57 train and bridge spans with non-ballasted tracks. Mech. Syst. Signal Process. 2021, 146, 107039. [Google Scholar] [CrossRef]
- Zhang, D.; Tang, Y.; Clarke, D.B.; Peng, Q.; Dong, C. An innovative method for calculating diagonal lashing force of cargo on railway wagons in a curve alignment. Veh. Syst. Dyn. 2021, 59, 352–374. [Google Scholar] [CrossRef]
- Ye, Y.; Ye, Y.; Sun, Y.; Dongfang, S.; Shi, D.; Hecht, M. Optimizing wheel profiles and suspensions for railway vehicles operating on specific lines to reduce wheel wear: A case study. Multibody Syst. Dyn. 2021, 51, 91–122. [Google Scholar] [CrossRef]
- Jönsson, P.-A.; Stichel, S.; Persson, I. New Simulation Model for Freight Wagons with UIC Link Suspension. Veh. Syst. Dyn. 2008, 46 (Suppl. S1), 695–704. [Google Scholar] [CrossRef]
- Piotrowski, J. Model of the UIC link suspension for freight wagons. Arch. Appl. Mech. 2003, 73, 517–532. [Google Scholar] [CrossRef]
- Bruni, S.; Vinolas, J.; Berg, M.; Polach, O.; Stichel, S. Modelling of suspension components in a rail vehicle dynamics context. Veh. Syst. Dyn. 2011, 49, 1021–1072. [Google Scholar] [CrossRef]
- Weidemann, C. State-of-the-Art Railway Vehicle Design with Multi-Body Simulation. J. Mech. Syst. Transp. Logist. 2010, 3, 12–26. [Google Scholar] [CrossRef][Green Version]
- Opala, M. Evaluation of bogie centre bowl friction models in the context of safety against derailment simulation predictions. Arch. Appl. Mech. 2018, 88, 943–953. [Google Scholar] [CrossRef]
- Buonsanti, M.; Leonardi, G. Dynamic Modelling of Freight Wagon with Modified Bogies. Eur. J. Sci. Res. 2012, 86, 274–282. [Google Scholar]
- Arvidsson, T.; Andersson, A.; Karoumi, R. Train running safety on non-ballasted bridges. Int. J. Rail Transp. 2019, 7, 1–22. [Google Scholar] [CrossRef]
- Pagaimo, J.; Magalhães, H.; Costa, J.N.; Ambrósio, J. Derailment study of railway cargo vehicles using a response surface methodology. Veh. Syst. Dyn. 2020, 1–26. [Google Scholar] [CrossRef]
- Bosso, N.; Gugliotta, A.; Soma, A. Multibody simulation of a freight bogie with friction dampers. In Proceedings of the ASME/IEEE Joint Railroad Conference, Washington, DC, USA, 23–25 April 2002. [Google Scholar]
- Ribeiro, D.; Calçada, R.; Delgado, R.; Brehm, M.; Zabel, V. Finite-element model calibration of a railway vehicle based on experimental modal parameters. Veh. Syst. Dyn. 2013, 51, 821–856. [Google Scholar] [CrossRef]
- Diana, G.; Cheli, F.; Collina, A.; Corradi, R.; Melzi, S. The Development of a Numerical Model for Railway Vehicles Comfort Assessment Through Comparison with Experimental Measurements. Veh. Syst. Dyn. 2002, 38, 165–183. [Google Scholar] [CrossRef]
- Harak, S.S.; Sharma, S.C.; Harsha, S.P. Structural Dynamic Analysis of Freight Railway Wagon Using Finite Element Method. Procedia Mater. Sci. 2014, 6, 1891–1898. [Google Scholar] [CrossRef]
- Zhang, Y.-W.; Zhao, Y.; Zhang, Y.H.; Lin, J.H.; He, X.W. Riding comfort optimization of railway trains based on pseudo-excitation method and symplectic method. J. Sound Vib. 2013, 332, 5255–5270. [Google Scholar] [CrossRef]
- Xue, R.; Ren, Z.; Fan, T.; Rakheja, S. Vertical vibration analysis of a coupled vehicle-container model of a high-speed freight EMU. Veh. Syst. Dyn. 2020, 1–25. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Y.; Xie, S.; Zhang, Q.; Guo, H. Fatigue failure analysis of express freight sliding side covered wagon based on the rigid-flexibility model. Int. J. Struct. Integr. 2021, 12, 98–108. [Google Scholar] [CrossRef]
- Kim, J.-S.; Jeong, J.-C. Natural frequency evaluation of a composite train carbody with length of 23 m. Compos. Sci. Technol. 2006, 66, 2272–2283. [Google Scholar] [CrossRef]
- Bragança, C.; Neto, J.; Pinto, N.; Montenegro, P.A.; Ribeiro, D.; Carvalho, H.; Calçada, R. Calibration and validation of a freight wagon dynamic model in operating conditions based on limited experimental data. Veh. Syst. Dyn. 2021, 1–27. [Google Scholar] [CrossRef]
- Evans, J.; Berg, M. Challenges in simulation of rail vehicle dynamics. Veh. Syst. Dyn. 2009, 47, 1023–1048. [Google Scholar] [CrossRef]
- Akiyama, Y.; Tomioka, T.; Takigami, T.; Aida, K.-I.; Kamada, T. A three-dimensional analytical model and parameter determination method of the elastic vibration of a railway vehicle carbody. Veh. Syst. Dyn. 2020, 58, 545–568. [Google Scholar] [CrossRef]
- Ling, L.; Zhang, Q.; Xiao, X.; Wen, Z.; Jin, X. Integration of car-body flexibility into train–track coupling system dynamics analysis. Veh. Syst. Dyn. 2018, 56, 485–505. [Google Scholar] [CrossRef]
- Iwnicki, S.; Stichel, S.; Orlova, A.; Hecht, M. Dynamics of railway freight vehicles. Veh. Syst. Dyn. 2015, 53, 995–1033. [Google Scholar] [CrossRef]
- Hoffmann, M. On the dynamics of European two-axle railway freight wagons. Nonlinear Dyn. 2008, 52, 301–311. [Google Scholar] [CrossRef]
- True, H.; Hoffmann, M.; Jönsson, P.-A. The Design and Performance of the European Freight Wagon Standard Suspensions. In Proceedings of the ASME 2005 International Mechanical Engineering Congress and Exposition, Orlando, FL, USA, 5–11 November 2005. [Google Scholar]
- Stichel, S. On freight wagon dynamics and track deterioration. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit. 1999, 213, 243–254. [Google Scholar] [CrossRef]
- Zhang, D.; Clarke, D.B.; Peng, Q.; Gao, H.; Dong, C. Effect of the combined centre of gravity on the running safety of freight wagons. Veh. Syst. Dyn. 2019, 57, 1271–1286. [Google Scholar] [CrossRef]
- Sun, W.; Zhou, J.; Gong, D.; You, T. Analysis of modal frequency optimization of railway vehicle car body. Adv. Mech. Eng. 2016, 8, 1687814016643640. [Google Scholar] [CrossRef]
- Ouyang, S.; Sui, F. Experimental modal analysis of high-speed railway carriage. In Proceedings of the 43rd International Congress on Noise Control Engineering, Melbourne, Australia, 16–19 November 2014. [Google Scholar]
- Tomioka, T.; Takigami, T.; Suzuki, Y. Numerical analysis of three-dimensional flexural vibration of railway vehicle car body. Veh. Syst. Dyn. 2006, 44 (Suppl. S1), 272–285. [Google Scholar] [CrossRef]
- Sichani, M.T.; Ahmadian, H. Identification of Railway Car Body Model Using Operational Modal Analysis. In Proceedings of the International Operational Modal Analysis Conference (IOMAC), Copenhagen, Danmark, 26–27 April 2006. [Google Scholar]
- Huang, M.-S.; Gül, M.; Zhu, H.-P. Vibration-Based Structural Damage Identification under Varying Temperature Effects. J. Aerosp. Eng. 2018, 31, 04018014. [Google Scholar] [CrossRef]
- Huang, M.; Cheng, X.; Lei, Y. Structural damage identification based on substructure method and improved whale optimization algorithm. J. Civ. Struct. Health Monit. 2021, 11, 351–380. [Google Scholar] [CrossRef]
- Huang, M.; Cheng, X.; Zhu, Z.; Luo, J.; Gu, J. A Novel Two-Stage Structural Damage Identification Method Based on Superposition of Modal Flexibility Curvature and Whale Optimization Algorithm. Int. J. Struct. Stab. Dyn. 2021, 21, 2150169. [Google Scholar] [CrossRef]
- Huang, M.; Li, X.; Lei, Y.; Gu, J. Structural damage identification based on modal frequency strain energy assurance criterion and flexibility using enhanced Moth-Flame optimization. Structures 2020, 28, 1119–1136. [Google Scholar] [CrossRef]
- ARTeMIS. ARTeMIS Extractor Pro—Academic Licence; Structural Vibration Solutions ApS: Aalborg, Denmark, 2009. [Google Scholar]
- Yang, Z.J.; Dutta, U.; Zhu, D.; Marx, E.; Biswas, N. Seasonal Frost Effects on the Soil-Foundation-Structure Interaction System. J. Cold Reg. Eng. 2007, 21, 108–120. [Google Scholar] [CrossRef]
- Brincker, R.; Zhang, L.; Andersen, P. Output-Only Modal Analysis by Frequency Domain Decomposition. In Proceedings of the ISMA25: 2000 International Conference on Noise and Vibration Engineering, Leuven, Belgium, 13–15 September 2000; pp. 717–723. [Google Scholar]
- Andersen, P.; Brincker, R.; Goursat, M.; Mevel, L. Automated Modal Parameter Estimation For Operational Modal Analysis of Large Systems. In Proceedings of the 2nd International Operational Modal Analysis Conference IOMAC 2007, Copenhagen, Denmark, 30 April–2 May 2007. [Google Scholar]
- Brincker, R.; Ventura, C. Introduction to Operational Modal Analysis, 1st ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2015. [Google Scholar]
- Molatefi, H.; Hecht, M.; Kadivar, M.H. Effect of suspension system in the lateral stability of railway freight trucks. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit. 2007, 221, 399–407. [Google Scholar] [CrossRef]
- Roy, R.; Craig, J.; Kurdila, A.J. Fundamentals of Structural Dynamics; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- ANSYS. Academic Research, Release 18.1, Help System, Ansys Fluent Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Hertz, H. Ueber die Berührung fester elastischer Körper (On Contact Between Elastic Bodies). J. Reine Angew. Math. 1882, 92. [Google Scholar]
- Allemang, R.J. The modal assurance criterion—Twenty years of use and abuse. Sound Vib. 2003, 37, 14–23. [Google Scholar]
- Brehm, M.; Zabel, V.; Unger, J.F. Stochastic Model Updating methods—A comparative study. In Proceedings of the IMAC XXVII—A Conference and Exposition on Structural Dynamics, Orlando, FL, USA, 9–12 February 2009. [Google Scholar]
- DYNARDO. optiSLang—The Optimizing Structural Language; DYNARDO: Weimar, Germany, 2008. [Google Scholar]
- MATLAB Optimization Toolbox 2020b. MATLAB User’s Guide; The MathWorks, Inc.: Natick, MA, USA, 2020.
- Jaishi, B.; Ren, W.-X. Structural Finite Element Model Updating Using Ambient Vibration Test Results. J. Struct. Eng. 2005, 131, 617–628. [Google Scholar] [CrossRef]
- Baker, J.E. Reducing bias and inefficiency in the selection algorithm. In Proceedings of the 2nd Annual Conference on Genetic Algorithms, Cambridge, MA, USA, 28–31 July 1985; pp. 14–21. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).