3DLEB-Net: Label-Efficient Deep Learning-Based Semantic Segmentation of Building Point Clouds at LoD3 Level

Abstract

In current research, fully supervised Deep Learning (DL) techniques are employed to train a segmentation network to be applied to point clouds of buildings. However, training such networks requires large amounts of fine-labeled buildings’ point-cloud data, presenting a major challenge in practice because they are difficult to obtain. Consequently, the application of fully supervised DL for semantic segmentation of buildings’ point clouds at LoD3 level is severely limited. In order to reduce the number of required annotated labels, we proposed a novel label-efficient DL network that obtains per-point semantic labels of LoD3 buildings’ point clouds with limited supervision, named 3DLEB-Net. In general, it consists of two steps. The first step (Autoencoder, AE) is composed of a Dynamic Graph Convolutional Neural Network (DGCNN) encoder and a folding-based decoder. It is designed to extract discriminative global and local features from input point clouds by faithfully reconstructing them without any label. The second step is the semantic segmentation network. By supplying a small amount of task-specific supervision, a segmentation network is proposed for semantically segmenting the encoded features acquired from the pre-trained AE. Experimentally, we evaluated our approach based on the Architectural Cultural Heritage (ArCH) dataset. Compared to the fully supervised DL methods, we found that our model achieved state-of-the-art results on the unseen scenes, with only 10% of labeled training data from fully supervised methods as input. Moreover, we conducted a series of ablation studies to show the effectiveness of the design choices of our model.

1. Introduction

The diffusion of buildings’ point clouds at a high Level of Detail (LoD) [1] such as LoD3 provides very detailed geometrical representation and semantic information [2], which enables and promotes new applications in a variety of fields such as cultural heritage documentation and preservation [3,4,5], construction engineering [6,7], emergency decision making [8] and smart cities [9]. However, point clouds of buildings generally provide the representation of the entire premises including only a few types of architectural elements with no semantic information, limiting the efficient exploitation in the abovementioned application domains [10]. Hence, it is essential to investigate the methods of extracting semantic information from buildings’ point clouds to acquire high-LoD models [11].

Thanks to the growing resolution and accuracy of 3D laser scanning sensors, point-cloud analysis has attracted a lot of interest in research. Inspired by the success of Deep Neural Networks (DNNs) used in Computer Vision (CV) to accomplish subset tasks (e.g., classification, detection and semantic segmentation), Deep Learning (DL) approaches have appeared in the last few years for understanding 3D point clouds [12]. Semantic segmentation is a fundamental task in 3D point-cloud analysis. As a result of the success in recent DL-based point-cloud analysis studies, DL-based approaches have been demonstrated to be a promising alternative to traditional segmentation methods. They aim to segment buildings by automatically learning features from labeled point clouds, rather than hand-crafted features. This principle has been successfully applied in numerous applications, such as indoor [13], urban [14] and buildings’ scenes [15]. Even though important results were achieved, the existing DL approaches for building point clouds are strongly supervised, and these methods have substantial demands for finely labeled data [16].

However, it is not feasible to create such an amount of labeled training data in many real-world problems. A building point cloud composed of thousands of 3D points would need to be individually annotated in the case of segmentation. This cumbersome process results in a lack of annotated 3D architectural datasets. For example, to the best of our knowledge, only the Architectural Cultural Heritage (ArCH) dataset [17] is publicly available to provide pointwise annotations and support for generating high-resolution LoD3 building models. Furthermore, in order to train a satisfactory segmentation network, billions of pointwise accurate labels are demanded [16], which is extremely time-consuming to obtain. For instance, some studies [3,5] on the application of DL in architectural semantic segmentation have been done only after the setup of the fine-labeled ArCH dataset.

In the CV domain, the problem of hunger for fine-labeled pointwise training data is often tackled by using unsupervised methods. Unsupervised learning plays an essential role in the CV field as it provides a way to pre-train feature extractors on large unlabeled datasets. The pre-trained extractor may initialize the parameters of downstream networks for more efficient and effective training on downstream tasks [18]. However, these approaches are mostly designed for 2D images, which are fundamentally different from unordered point clouds. Unlike 2D images that are projective observations from the built environment, 3D point clouds provide a metric reconstruction of the building scenes without scale ambiguity [19]. Furthermore, the application of label-efficient unsupervised learning to downstream tasks in the 3D field is still limited to either single-object or low-level tasks such as registration and classification [20]. Therefore, from a scientific viewpoint, it is still an open issue when using unsupervised DL-based methods in the semantic segmentation task of buildings’ point clouds.

For the abovementioned reasons, in this paper, we decided to put our efforts into developing an unsupervised DL method for high-level semantic segmentation of buildings’ point-clouds. We explored the possibility of learning a point-cloud segmentation network by only supplying limited task-specific labeled data. To conduct such a label-efficient unsupervised DL network (3DLEB-Net) we introduced the Autoencoder (AE) architecture to simultaneously learn reconstruction and discriminative features of the input 3D building point clouds without any label. To achieve this, we leveraged the Dynamic Graph Convolutional Neural Network (DGCNN) [21] as our encoder and FoldingNet [22] as decoder to acquire powerful embeddings from complex buildings’ point clouds without any labeled data. To this end, with limited labeled data, we designed three fully connected layers in an end-to-end segmentation network to achieve the downstream segmentation task.

In particular, our contributions may be summarized as follows:

• We proposed a novel AE network to learn powerful feature representations from a non-labeled complex-building point-cloud dataset, and the pre-trained AE may be used in the high-level downstream semantic segmentation task;
• We trained an end-to-end segmentation network for the buildings’ segmentation task. The output of our model is a semantically enriched LoD3 3D building representation; and
• We experimentally demonstrated how to exploit limited labeled point clouds to segment input point clouds of buildings. The result shows that our result either surpasses or achieves performance comparable to the one of recent state-of-the-art methods, with only 10% of training data.

2. Related Work

Laser scanning techniques are able to collect dense and accurate point clouds of buildings. At the same time, the massive amount of data requires a semantic interpretation at a high Level of Detail (LoD) in order to increase the exploitation of these datasets [23,24]. While several types of fully supervised Deep Neural Networks (DNNs) are continuously developed and improved in the analysis of 3D point clouds, fine-grained labels are always required in the training processes. These include pointwise labels and shape class labels for the semantic segmentation task and part-segmentation task, respectively. Thus, DNNs’ application to LoD3 buildings’ point clouds has been limited. This question has sparked the interest of various research on this problem. Several unsupervised approaches have emerged to tackle the scarcity of labeled data.

In this section, the state-of-the-art methods to figure out the possibility of unsupervised DL methods applied to buildings’ point clouds is dealt with. We review these approaches from two aspects as follows:

• Fully supervised methods on 3D point clouds; and
• Label-efficient unsupervised methods.

2.1. Fully Supervised Methods on 3D Point Clouds

Three-dimensional point clouds of buildings generally represent complex geometric structures, where the semantic content is not directly included. Therefore, semantic segmentation of it is still a challenging task. In traditional data-driven approaches [25,26], points with some notions of similarity are clustered together to map point clouds into classes by constructing feature descriptors (e.g., verticality, planarity and elevation). In conventional model-fitting approaches [27,28,29], some geometric models are sought to detect specific objects, such as houses, roofs, trees, etc. Despite the impressive performances from these traditional approaches, models or geometric descriptors cannot interpret the complexity of real data. Moreover, conventional semantic segmentation approaches heavily rely on hand-crafted features, making the generalization difficult. Thus, their efficient application to obtain high-LoD building models still remains quite challenging.

Due to these reasons, the chance of using DNN-based fully supervised learning to effectively and automatically extract features in an end-to-end fashion gives rise to the application of these promising methods for semantic segmentation of buildings’ point clouds. Based on the DNN input data format, existing point-cloud semantic segmentation methods can be grouped into direct and indirect methods. The latter usually first partition the 3D space into regular representations such as image [30,31,32] or voxel [33,34] data structures to take advantage of well-established 2D/3D DL networks for feature learning and semantic segmentation. However, due to point clouds’ inherent nature, the process of transferring point clouds to another intermediate representation degrades the resolution of the measured objects, which would result in quantization error and inefficiency [35]. In contrast, direct methods do not introduce explicit information loss [36]. More recently, the pioneering direct method PointNet [35] was proposed. It directly operates on point clouds, using a Multilayer Perceptron (MLP) to learn high-dimensional features for each point independently. Subsequently, pointwise features are stacked to a global feature through a max pooling layer. Since pointwise features are learned individually from each point in PointNet, the local context information between points is ignored. This work was subsequently extended in a variety of ways to extract local information within a point cloud. For example, Dynamic Graph Convolutional Neural Network (DGCNN) [21] improves the performance of segmentation by considering the relations between points in the local neighborhoods and by aggregating them into a global feature in the EdgeConv layers, which can be plugged into existing architectures. Since current state-of-the-art methods have shown that aggregating local and global information may increase the network’s capabilities of capturing context information, our network will exploit the feature extraction power of EdgeConv layers, which directly consumes points and incorporates the local neighbor information obtained from point clouds.

DL techniques for 3D point-cloud segmentation have been successfully applied in recent years, while the development in the built-environment domain has just started to be explored. A limited number of studies use DL methods to segment point clouds of buildings. Compared to the improvement of DL methods in indoor scenes, the segmentation methods of high-LoD buildings’ point clouds are still at the initial stage of development. Most existing studies focus on LoD1 [15,24,29,37,38], LoD2 [39,40] or one category of building elements [41].

Moreover, as was pointed out in the introduction of this paper, only the ArCH dataset [17] with pointwise annotations is publicly available. The process to acquire pointwise point clouds is also very time-consuming. For instance, the period required for manually labeling the ArCH dataset is one month [3]. The lack of semantic segmentation labels indicates the challenge for human beings to provide pointwise labels. Thus, there is also just a handful of DL-based research in higher-LoD building point-cloud (i.e., LoD3 and superior) segmentation tasks. Pierdicca [5] proposed to employ DGCNNs [21] for the point-cloud segmentation task applied on the ArCH dataset. By adding radiometric (HSV value) and normal features in DGCNN-Mod [5], they further improved the segmentation performance. Their work showed the potential offered by DL techniques for the segmentation task. By fusing spectral information and hand-crafted geometric features, DGCNN-Mod+3Dfeat [3] combines the positive aspects and advantages of machine learning and DL for semantic segmentation of point clouds in the field of cultural heritage. But 3D features in DGCNN-Mod+3Dfeat are hand-designed and extracted by machine-learning methods, and thus this solution is excluded from our consideration.

Despite the intensive efforts to improve the segmentation performance of buildings’ point clouds, (1) most existing algorithms are insufficient to model details (e.g., they can only be applied to the entire building or low LoDs) and are associated with a heavy workload, which meets current requirements in the development phase; (2) existing methods mostly use both 3D coordinates and hand-crafted features (i.e., geometric features) as their input to enhance performance; and (3) the aforementioned DL-based approaches for 3D point-cloud analysis are strongly supervised and rely on massive amounts of labeled 3D building data.

2.2. Label-Efficient Methods

Unsupervised learning does not require any human-annotated labels. Due to the scarcity of fine-labeled point-cloud datasets, unsupervised-learning methods have become popular alternatives to fully supervised learning to exploit the inherent and underlying information in large unlabeled data, which may dramatically decrease the need for labeled training data. Unsupervised Autoencoder (AE) methods on 3D point-cloud data is a relatively new research topic. Therefore, our review of the label-efficient unsupervised approach is not limited to the built-environment domain in this section.

2.2.1. Label-Efficient Methods for Images

Recently, some unsupervised methods have been proposed and achieved satisfactory performances in 2D CV tasks. There are many classes of unsupervised methods for learning representations: Generative Adversarial Networks (GANs) [42,43,44,45], Autoencoders (AEs) [44,46] and auto-regressive models [47]. Being much harder to annotate, 3D point-cloud analyses are potentially the biggest beneficiaries of unsupervised learning. Our work builds upon the AE, which is trained to learn a compressed representation by faithfully reconstructing original input data (i.e., image, point cloud). However, due to the irregular and unordered nature of point clouds, it is non-trivial to directly apply such image unsupervised methods to this type of data.

2.2.2. Label-Efficient Methods for Point Clouds

Following the impressive results that have been achieved with unsupervised learning in the image analysis, previous efforts to perform unsupervised learning on point clouds have been adaptations of these methods. Several unsupervised methods (e.g., GAN, AE) applied to 3D point clouds are reported in the literature, partly due to the common criticism that a huge amount of labeled data is required for training in a DNN. We provide a quick overview of both types of methods, GANs and AEs.

Generative Adversarial Networks (GANs). Typically, GANs consist of a generator that learns from a latent space to a data distribution of interest. A discriminator distinguishes generated point clouds produced by the generator from the true data distribution. For example, Achlioptas [48] investigated and compared GAN-based methods for generating point clouds in raw-data space and latent space of a pre-trained AE. Li [49] proposed a “sandwiching” reconstruction method that combines a modification of Wasserstein GAN [50] loss with Earth Mover’s Distance (EMD). AtlasNet [51] introduces a shape generation framework that represents a 3D shape as a collection of parametric surface elements by locally mapping a set of squares to the target surface of a 3D shape. Although impressive results were achieved, GAN-based methods focus more on generative models of point clouds, which aim to generate point clouds or complete shapes of point clouds.

Autoencoders (AEs). AE is one of the key ingredients in current state-of-the-art unsupervised visual representation learning. An AE is trained to learn a compressed representation by faithfully reconstructing an input original image/point cloud [52]. In FoldingNet [22], the authors adopted the idea of the folding-based decoder to deform a canonical 2D grid onto the underlying 3D object surface of a point cloud, in which the learned representation achieves high linear Support Vector Machines (SVM) classification accuracy on the ModelNet40 dataset. Built on the fully supervised PPFNet [53] and FoldingNet, in PPF-FoldNet [54], the authors improved their earlier solution by involving more features in their network in an unsupervised fashion. PPF-FoldNet achieves better reconstruction performance at rotations and different point densities, but their research focuses on reconstruction rather than downstream tasks. 3D-PointCapsNet [55] employed a dynamic routing scheme to extract discriminative representation while considering the geometric relations between parts, and the extracted representation can lead to improvements in point-cloud classification and part-segmentation tasks. BAE-NET [56] proposed a branched AE network that trains with a collection of objects from the ShapeNetPart dataset trained with a shape co-segmentation task.

Existing methods achieve state-of-the-art performances in their downstream tasks (i.e., classification, part-segmentation and co-segmentation). However, most of these existing unsupervised AE methods for 3D point clouds are: (1) trained and tested using simple 3D objects; and (2) designed for low-level tasks such as reconstruction, denoising and completion that are not designed for high-level downstream semantic segmentation.

Overall, learning to automatically generate powerful and robust representations from inhomogeneous point clouds, especially architectural point clouds with complex geometric structures, still poses a challenge. To address these mentioned issues, in this paper, we propose a novel label-efficient DL approach to benefit from the ability of AEs to learn features from unlabeled data, thereby reducing the need of pointwise labels of building point clouds. Moreover, our method improves the encoding capability of FoldingNet [22] by incorporating the local-region information and global-shape information using the EdgeConv layers, allowing unsupervised-learning methods to perform high-level downstream semantic segmentation tasks on point clouds of complex buildings.

3. Method

In FoldingNet [22], an AE is utilized to reconstruct input point clouds, whilst discriminative representations are learned without any labeled data. Inspired by this, our label-efficient method aims to: (1) extract features without any labeled data by constructing an AE network; and (2) with just 10 times fewer (3 scenes) labeled data of fully supervised methods, we train a segmentation network for the high-LoD (LoD3) buildings’ point-cloud semantic segmentation task. Specifically, we propose an AE network that can learn powerful representations by a dynamically updated graph-based encoder and folding-based decoder without any labels, thereby reducing our need for large amounts of fine labels in the building segmentation task.

Instead of the encoder in FoldingNet, we employed the EdgeConv layers in DGCNN [21] to exploit local geometric structures and generate discriminative representations. Then, we used the learned representations as input to our downstream task. In general, the proposed network architecture consists of three components: a DGCNN-based encoder, a folding-based decoder, and a segmentation network. The input of the encoder is given by the N coordinates $\left(x, y, z\right)$ of buildings’ points, and outputs are discriminative features, which are also the input of both decoder and the segmentation network. The outcomes are a matrix of size $\left(m, 3\right)$ representing the reconstructed point cloud and per-point classification scores $\left(N, n\_classes\right)$ for decoder and segmentation network, respectively, where m represents the number of points in the reconstructed point cloud and n_classes denotes the number of classes in the point cloud. The architecture of our AE is illustrated in Figure 1, and the illustration of the proposed segmentation network is shown in Figure 2.

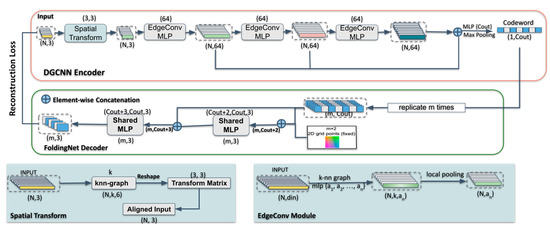
Figure 1. The architecture of our 3D Autoencoder (AE) branch, consisting of a DGCNN (Dynamic Graph Convolutional Neural Network)-based encoder module (top) and a folding-based decoder module (bottom).

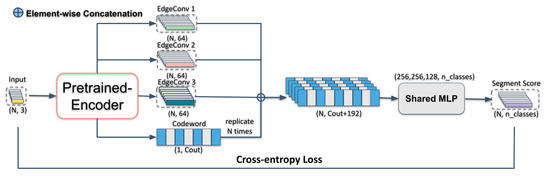
Figure 2. The architecture of semantic segmentation step of our label-efficient Deep Learning (DL) method.

3.1. DGCNN-Based Encoder

To capture the context information from discrete point sets, it is essential to extract the correlation of points inside the local neighborhood. Both encoders of FoldingNet and DGCNN use graph-based layers to extract the local geometric information in each point’s neighborhood and a max pooling layer to aggregate information. The local feature of FoldingNet at i-th vertex is computed as follows:

$${x^{\prime }}_i=\underset{j:\left(i,j\right)\in E}{\max }{h}_{\Theta }\left(x_j-x_i\right)$$

(1)

In the edge function $h_{\Theta }\left(x_j-x_i\right)$, $x_i$ is the central point belonging to point set $X=\left\{x_1, x_2,\cdots , x_n\right\} \subseteq \mathcal{R}$, $x_j$ is the local neighbor around the central point $x_i$, and $h_{\Theta }$ is implemented by a fully connected multi-perceptron layer, which includes learnable parameters. FoldingNet obtains the local information by encoding $x_j-x_i$ edge features. Then the learned local information is aggregated by a local $\max$ pooling operation on the constructed graphs $G=\left(V, E\right)$, where $V=\left\{1, 2, \cdots , N\right\}$ and $E \subseteq \left|\mathrm{V}\right|\times \left|\mathrm{V}\right|$ are the vertices and the edges, respectively, and $N$ is the number of vertices.

However, FoldingNet ignores the capture of the global-shape information. On the other hand, the operation on the constructed graph $G$ of DGCNN is the EdgeConv operation, which may extract both local geometric and global-shape information from the constructed graph. Firstly, the EdgeConv layer computes an edge feature set of size k for each input point cloud through an asymmetric edge function (Equation (2)):

$${\mathrm{e}}_{ij}=h_{\Theta }\left(x_i, x_j-x_i\right)$$

(2)

In this edge function, EdgeConv captures the global shape by encoding the coordinates of $x_i$ and then obtains the local information by encoding $x_j-x_i$. The output feature is aggregated by edge features from each connected vertex and itself in the constructed graph:

$${x^{\prime }}_i=\underset{j:\left(i,j\right)\in E}{\max }{h}_{\Theta }\left(x_i, x_j-x_i\right)$$

(3)

Thus, EdgeConv can explicitly combine the global-shape structure information with local neighborhoods’ information.

Furthermore, in FoldingNet, the graph is constructed by computing pairwise distances using initial input point coordinates. Hence their graph $G$ is fixed. In contrast, we calculate the pairwise distance in the feature space at each layer and choose the nearest $k$ points per each central point, and then we dynamically construct $G^l=\left(V^l, E^l\right)$ at layer $l$. Meanwhile, the receptive field becomes larger while such dynamic graph updates in each EdgeConv layer. The local information around central points and global information in different receptive fields are aggregated and stacked in the last layer before the max pooling layer.

The procedure for producing feature representations in DGCNN-based encoder is displayed in Figure 1. We remove the encoder of FoldingNet and replace it with three EdgeConv layers in the architecture of DGCNN. The outputs of the three EdgeConv layers are concatenated and then passed to a feature-wise max pooling layer to produce a ${\mathrm{C}}_{\mathrm{out}}$-dimensional “codeword” $\theta$. The outcomes of three EdgeConv layers and the “codeword” $\theta$ are stored in the pre-trained AE model, which will be the basis for our segmentation network.

3.2. Folding-Based Decoder

We use the “codeword” output from the DGCNN-based encoder and a 2D grid as input to our decoder. A folding-based decoder is then utilized to reconstruct input “codeword” with a 2D grid to 3D point clouds by two successive folding operations.

The folding-based decoder in our AE network is adopted from FoldingNet’s decoder that contains two successive folding operations. The first one folds the 2D manifold into 3D space, and the second one operates inside the 3D space directly. As shown in Figure 1, we modified the decoder of FoldingNet to make it usable with different sizes of input “codeword” $\theta$ (512-dimensional and 1024-dimensional) instead of a fixed-size 512-dimensional representation in FoldingNet. Before feeding the “codeword” into the folding-based decoder, we replicate the “codeword” $\theta$ m times and concatenate the replicated “codeword” $(m, C_{out})$ matrix with an $\left(m, 2\right)$ matrix, which contains the m grid points ($U$) on a square centered at the origin. As each row of $U$ is a 2D grid point, we define the $i$-th row of $U$ as $u_i$. Thus, the $i$-th row of the input matrix to the folding operation is $\left[u_i,C\right]$ after above concatenation, where $C=C_{out}+2$. The following two folding operations essentially form a universal 2D-to-3D mapping by two successive MLPs. The MLPs are applied in parallel to each row of the input matrix. We denote the $i$-th row of the output matrix as $f\left(\left[u_i,C\right]\right)$, where $f$ is approximated by the MLPs, which can be tuned by the input “codeword” and learn a “force” to reconstruct the input into arbitrary point-cloud surfaces. During the training process, as shown in Equation (4), we use Chamfer distance [57] as our reconstruction loss ${\mathcal{L}}_{rec}$, which measures the similarity of the reconstructed point cloud and the input point cloud:

$${\mathcal{L}}_{rec}\left(x,y\right)={\displaystyle \sum }_{x_i\in x}\underset{y_iϵy}{\mathit{min}}{\Vert x_i-y_i\Vert }_2^2+{\displaystyle \sum }_{y_i\in y}\underset{x_iϵx}{\mathit{min}}{\Vert x_i-y_i\Vert }_2^2$$

(4)

With the graph-based encoder and folding-based decoder, we learn a set of powerful and separable features and continue to the downstream semantic segmentation task (see next Section 3.3).

3.3. Semantic Segmentation Network Architecture

We create a semantic segmentation network to semantically segment buildings’ point clouds. The goal here is to assign a semantic label to each of the points given an input point cloud. Hence, we treat this semantic segmentation task as a per-point classification task. The output of the pre-trained encoder is a $C_{out}$-dimensional representation (“codeword”) and three stacked edge features, which are learned from non-labeled buildings’ point clouds. We replicate the codeword N times and concatenate it with the outputs of three EdgeConv layers in the pre-trained AE. A standard 3-layer shared MLP with a cross-entropy loss is then employed as our semantic segmentation classifier after the above concatenation. Considering the features obtained by the proposed AE are already distinctive, we chose this simplest MLP for the segmentation of the buildings’ point clouds. This semantic segmentation network is trained independently from the proposed AE. The procedure for acquiring per-point classification scores (N, n_classes) in the semantic segmentation network is illustrated in Figure 2.

3.4. Evaluation Matrix

To evaluate the performance of our model, the benchmark dataset is evaluated using the Overall Accuracy (OA) and the mean Intersection over Union (mIoU) score. OA is the percentage of points that were correctly classified and total number of points, ignoring incorrect classifications. In the semantics segmentation task, Intersection over Union (IoU) is the ratio of the intersection of the pointwise classification results with the ground truth to their union, and mIoU is the class-averaged IoU. Specifically, IoU (Equation (5)) and mIoU (Equation (6)) can be computed as:

$$\mathrm{IoU}=\frac{T{P}_c}{T{P}_c+F{P}_c+F{N}_c}$$

(5)

$$\mathrm{mIoU}=\frac{1}{C} {\displaystyle \sum }_{c=1}^c\frac{T{P}_c}{T{P}_c+F{P}_c+F{N}_c}$$

(6)

where $T{P}_c$is the number of true positives for class c, $F{P}_c$ is the number of false positives for class c, $F{N}_c$ is the number of false negatives belonging to that class, and C is the number of classes. Meanwhile, mIoU computes the class-averaged ratio of true positives to the sum of false positives (false alarms), false negatives (misses), and true positives.

As we can see, IoU and mIoU measures are more informative compared to OA because they take false alarms (incorrect classified points in point clouds) into consideration, whereas OA does not. Therefore, we use both OA and mIoU as evaluation criteria for segmentation results.

4. Experiment

4.1. Dataset

We qualitatively and quantitatively evaluated our method on the Architectural Cultural Heritage (ArCH) dataset [17]. In the state of the art, the most used datasets to train unsupervised learning are: ModelNet40 [13] with more than 100 k CAD models of objects from 40 different categories (e.g., table, chair, lamp, etc.) for classification tasks and ShapeNetPart [58] dataset with 31,693 meshes classified into 16 common object classes (e.g., plane, table, chair, etc.); each object has two to five parts for part-segmentation tasks. However, none of them can be used for the segmentation of buildings’ point-cloud. Other outdoor datasets used in this task, such as Semantic3D [59] and Oakland [60], feature LoD1 or LoD2 for the architectural elements. To date, there are no published datasets focusing on point clouds of urban buildings with a sufficient level of details, such as LoD3.

A building in LoD3 has detailed surface structures such as walls, roof and openings (doors and windows). The components of architectural heritage including detailed roof, façade structures, openings and some specific structures such as vaults, columns and front porches are similar to but more involved than in standard modern buildings. Networks trained on these kinds of datasets are easy to generalize to other building scenes. Therefore, we chose an immovable CH asset dataset with fine per-point labels, named ArCH dataset, to evaluate our method. For data acquisition techniques, it is acquired by static terrestrial laser scanners, namely a FARO Focus 3D X 120 and 130, and a Riegl VZ-400, and by applying structure-from-motion photogrammetry [61,62] based on images collected by Nikon D880E, D3100 and D3X cameras, and a DJI Phantom UAV platform equipped with a SONY ILCE 5100L camera.

The ArCH dataset consists of 17 indoor and outdoor labeled scenes, 15 for training and 2 for testing purposes, respectively. It includes different types of scenes such as rooms, churches, chapels, cloisters, pavilions, squares and porticoes. Many of these scenes are part of (or candidate to be listed in) the UNESCO World Heritage List (WHL- whc.unesco.org/en/list. Accessed on 24 September 2021). These scenes represent various historical periods and architectural styles of historical built heritage. As a consequence, the use of this kind of dataset as training data may improve the generalization ability of our network among various types of buildings.

Our primary motivation to study unsupervised classification problems was that the number of training data is limited. To test the performance when the number of unlabeled and labeled data is small, as shown in Figure 3, we select three small outdoor scenes (namely, “SMV_1”, “SMV_24”, “SMV_28”) from the 15 labeled scenes as the training data in both unsupervised AE training and supervised segmentation training stages. The training data in our experiment are only 10% of total number of points with respect to the standard of the state of the art [5], where all scenes are used as training data. Then we follow the settings adopted by [5] that removed the “others” category. Since validation data is used in deep learning to tune parameters, to choose features, and so on, the availability of validation data has no effect on our ability to evaluate the model’s performance. As a result, unlike [5], where “Scene A” and “Scene B” are used as validation and test sets, we use two unseen scenes (“A_SMG_portico” as “Scene_A” and “B_SMV_chapel_27to35” as “Scene_B”) as our test data (see Figure 3). It is worth mentioning that our training data include only the type of the outdoor chapel, but our test data include both indoor and outdoor and different types of architectural elements (“portico” and “chapel”), which is more challenging than the supervised methods including different types of scenes in their training data.

Figure 3. The network takes the three scenes in Architectural Cultural Heritage (ArCH) dataset as training data, in the top row, from (a–c): “SMV_1”, “SMV_24” and “SMV_28”. In the bottom row, from (d–f) are: “Scene_A”, “Scene_B south side” and “Scene_B indoor part”, which are employed as our test data. Copyright © 2021 ArCH dataset.

4.2. Implementation Details

We choose $1\times 1$ square-meter area as the block size for splitting each building scene into blocks along the horizontal direction to train. Prior to training, the input point clouds are aligned to a common reference frame. In addition, for training convenience, points in each block are sampled into a uniform number of 8192 points. During training, we randomly sampled n (2048 or 4096) points in each block on the fly. To train our AE network, we employed ADAM [63] as an optimizer with an initial learning rate of 0.001, batch size 16 and weight decay 10⁻⁶ with 250 epochs. The setting of hidden layers in our encoder is the same as the one of the DGCNN (github.com/WangYueFt/dgcnn. Accessed on 24 September 2021), but we removed those layers after the max pooling layer. The architecture of the encoder incorporates the following steps:

• Three EdgeConv layers to extract local and global geometric features. The EdgeConv layers take a tensor of shape n × f as input, where f is input features of point cloud, then acquire edge features for each point by applying an MLP with the number of layer neurons defined as $\left\{a_1,a_2,\dots ,a_n\right\}$. The number of nearest neighbors k is set as 20 at every EdgeConv layer;
• Features generated in three EdgeConv layers are concatenated to aggregate features in different receptive fields; and
• Lastly, the dimension of the MLP layer before the last max pooling layer is set as $C_{out}$ (512 or 1024) to globally aggregate a 1D global descriptor “codeword” $\theta$.

In our graph-based decoder, we used two consecutive three-layer MLPs to warp a fixed 2D grid into point-cloud surfaces as FoldingNet (ai4ce.github.io/publication/yang-2018-foldingnet. Accessed 24 Sepember 2021). Before feeding the “codeword” into the folding-based decoder, we replicated the “codeword” m times and concatenated the replicated $\left(m, C_{out}\right)$ matrix with a $\left(m, 2\right)$matrix. According to the input point-cloud size (2048 or 4096), m is set as 2025 or 4096. Then the size of two three-layer shared MLPs is $(C_{out}+2,$ $C_{out}, 3)$ and $(C_{out}+3,$ $C_{out}, 3)$, implemented by six 1D convolutional layers, each followed by a ReLU layer. The output is the reconstructed point cloud with size $\left(m, 3\right)$.

Similarly, in the semantic segmentation network, we also used ADAM as our optimizer (learning rate 0.01, batch size 8 or 16, 250 training epochs). According to the dimension of $C_{out}$, our shared MLPs are ($C_{out}+64+64+64, 512, 256, 128, n\_classes$) with layer output size ($512, 256, 128, n\_classes$) on each point. The evaluation matrix of Overall Point Accuracy (OA) and mean Intersection over Union (mIoU) are calculated on the ArCH dataset. The method was implemented using PyTorch. All experiments were conducted on an NVIDIA Tesla T4 GPU.

4.3. Results and Analysis

If the features obtained by the proposed AE are already distinctive, the required number of labeled data in the semantic segmentation network training process should be small. In this section, to demonstrate this intuitive statement, we report our experiment’s results for the ArCH dataset. We evaluated our model on two unseen scenes (“Scene_A” and “Scene_B”) for testing. In Table 1, the overall performances are reported and compared with respect to the state-of-the-art (SOTA) methods, i.e., PointNet [35], PointNet++ [64], PCNN [65] and DGCNN [21], which are trained with 10 scenes and retrieved from Pierdicca [5]. For a fair comparison, we maintain consistency of input features for all methods (including only x, y, z coordinates such as most SOTA methods). The DGCNN was improved in [5] by adding additional input features, which we will compare and analyze in Section 4.4.

Table 1. Our results vs. prior work on ArCH dataset. OA and mIoU denote Overall Accuracy and mean Intersection over Union, respectively. Our method performs best on mIoU with only 3 scenes (about 10% of total number of points in 10 scenes).

Method	Training Scenes	Test Scene	mIoU	OA
PointNet [35]	10 scenes	Scene_B	0.114	0.35
PointNet++ [64]	10 scenes	Scene_B	0.121	0.528
PCNN [65]	10 scenes	Scene_B	0.26	0.629
DGCNN [21]	10 scenes	Scene B	0.29	0.74
DGCNN [21]	15 scenes	Scene A	0.376	0.784
DGCNN [21]	15 scenes	Scene B	0.353	0.752
DGCNN [21]	3 scenes	Scene A	0.243	0.499
DGCNN [21]	3 scenes	Scene B	0.163	0.362
Ours	3 scenes	Scene_A	0.463	0.773
Ours	3 scenes	Scene_B	0.408	0.666

Note: The OA and mIoU of SOTA methods (PointNet, PointNet++, PCNN and DGCNN) that use 10 scenes (9 for training and 1 for validation) are retrieved from Tables 5 and 6 of Pierdicca [5], respectively. Performances of DGCNN that use 15 scenes are updated in ArCH dataset website (archdataset.polito.it/. Accessed on 24 September 2021).

Overall, with only about 10% of training data of the SOTA methods in both AE and segmentation network training stages, our model achieves the best results for the ArCH dataset with the same training strategy (only input x, y, z coordinates), as shown in Table 1. In particular, the test mIoU of “Scene_A” is 0.463, which overcomes the previous SOTA result (0.376). The mIoU of “Scene_B” is 0.408, which also outperforms the 0.353 of SOTA. As mIoU takes the false alarms and the unbalance of different categories into consideration, our mIoU is higher than SOTA methods, while OA is lower. Furthermore, we compared our results for “Scene_A” and “Scene_B” with the SOTA when training on the same subset (three scenes), as shown in Table 1. The results of “Ours” also outperform the ones from the SOTA methods.

The results of per-class quantitative evaluations for “Scene_B” are provided in Table 2. We can see that the proposed model performs better than other competitive methods in many classes. In particular, we achieve considerable gains in the arch, column, wall and vault categories. In the ArCH dataset, the vault is pasted onto the roof and difficult to delineate geometrically, but it is apparent from Figure 4 that our model can still segment them out.

Table 2. Our per-class IoU and class-averaged mIoU results vs. prior work on “Scene_B” of ArCH dataset. Each column represents the IoU of the category it belongs to. Our method performs better than others in many classes with only 3 scenes (about 10% of 10 scenes).

Method	mIoU	Arch	Column	Molding	Floor	Door–Window	Wall	Stair	Vault	Roof
PointNet [35]	0.114	0.000	0.000	0.001	0.294	0.000	0.411	0.000	0.337	0.094
PointNet++ [64]	0.121	0.000	0.000	0.002	0.009	0.000	0.514	0.000	0.074	0.608
PCNN [65]	0.26	0.072	0.062	0.198	0.482	0.004	0.581	0.082	0.468	0.658
DGCNN [21]	0.29	0.060	0.064	0.142	0.470	0.006	0.603	0.290	0.520	0.845
Ours	0.408	0.880	0.243	0.117	0.471	0.005	0.676	0.035	0.577	0.659

Note: The IoU of SOTA methods (PointNet, PointNet++, PCNN and DGCNN) that use 10 scenes (9 for training and 1 for validation) are retrieved from Table 6 of Pierdicca [5], and mIoU are calculated by Equitation (6).

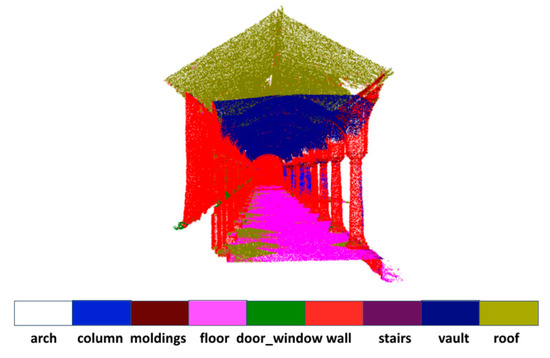
Figure 4. Qualitative results of a part of “Scene_B” of ArCH dataset. The vault is pasted onto the roof and difficult to delineate geometrically, but our model can still segment them out.

Figure 5 and Figure 6 describe the confusion matrices of the segmentation results when using nine features on “Scene_A” and “Scene_B”, respectively. Each row of the confusion matrix represents the instances in a predicted class, while each column represents the instances in an actual class. It is easy to see whether our model is confusing two categories by a confusion matrix. For example, in Figure 5, the column and molding classes are often confused with the wall, possibly due to the columns and moldings having a similar geometrical shape/appearance to walls. Meanwhile, the door_window class is also often confused with the wall, as the large-scale variation and their spatial distance are very close (e.g., door_window is inside of a wall, and the size of door_window is much smaller than a wall), which could result in the features being eliminated while training. The semantic segmentation’s qualitative results in the case of “Scene_A” and “Scene_B” are shown in Figure 7 and Figure 8, respectively. Our network is able to output smooth predictions.

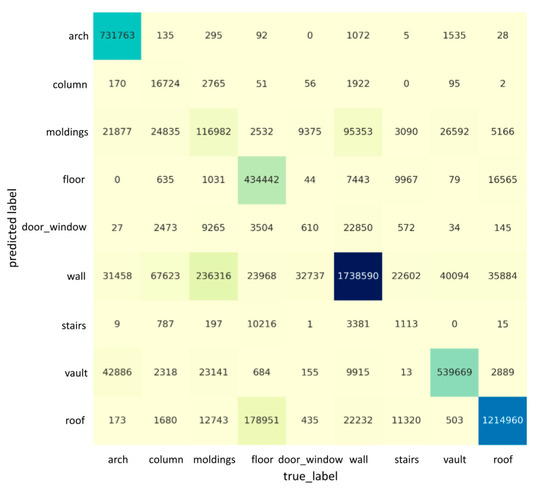
Figure 5. The confusion matrix for the segmentation result for the whole “Scene_A” of ArCH dataset. Each row represents the instances in a predicted class, and each column represents the instances in an actual class. The darkness of cells is proportional to the number of points labeled with the corresponding category.

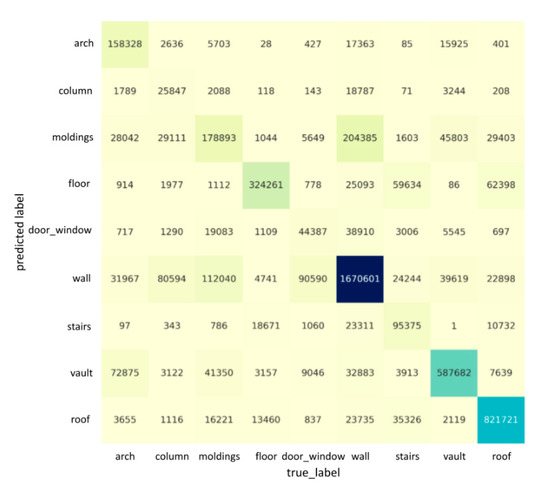
Figure 6. The confusion matrix for the segmentation result for the whole “Scene_B” of ArCH dataset. Each row represents the instances in a predicted class, and each column represents the instances in an actual class. The darkness of cells is proportional to the number of points labeled with the corresponding category.

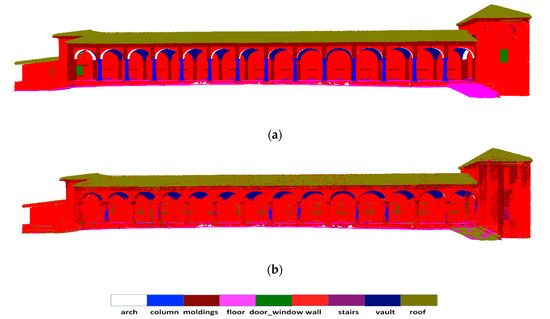
Figure 7. Qualitative results for semantic segmentation of “Scene_A” from ArCH dataset. The top row is the ground truth (a), and the second row is the prediction result (b). Different colors correspond to different classes of architectural elements. Same scenes are displayed from the same camera viewpoint.

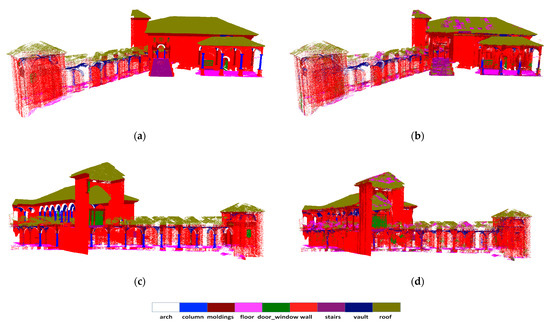
Figure 8. Qualitative results for semantic segmentation of “Scene_B” from ArCH dataset. The top row is the ground truth (a) and the prediction result (b) on the north side. The bottom row is the ground truth (c) and output semantic segmentation result (d) from another side. Different colors correspond to different classes. Scenes in the same row are displayed from the same camera viewpoint.

4.4. Ablation Study and Analysis

The following part of this paper describes in greater detail the design choices of our label-efficient model by a set of experiments. We also show the effects of our chosen hyper-parameters.

Effectiveness of DGCNN Encoder: In Table 3, we show the positive effects of our proposed DGCNN-based encoder. In order to compare the performance of FoldingNet’s encoder and our improved encoder on the semantic segmentation task, we set up two sets of controlled experiments. In the first set of experiments, we used one scene as training data, and in the second set, we used three scenes that we commonly used in this study as training data to compare the segmentation results.

Table 3. Comparison of semantic segmentation results for “Scene_B” of ArCH dataset using different encoders. “1 scene” (“SMV_24”) and “3 scenes” (“SMV_1”, “SMV_24”, “SMV_28”) in “Training Scenes” denote that we used it only for one scene or three scenes in both AE and segmentation network training stage.

Encoder	Training Scene	OA 1
FoldingNet	1 scene	0.425
FoldingNet	3 scenes	0.42
DGCNN-based	1 scene	0.493
DGCNN-based	3 scenes	0.561

¹ Note: This controlled experiment was carried out without any data augmentation, and reconstruction loss is modified Chamfer distance.

As shown in Table 3, compared to FoldingNet, the performance of the DGCNN-based encoder has a 7% boost while using one scene in the training stage and a 14% improvement while using three scenes in the training stage, testing on “Scene_B”.

Effectiveness of Data Augmentation: In Table 4, we demonstrate the positive effects of data augmentation. Compared to excluding translation (but using random rotation and jitter data augmentations), there is an 11% performance boost when all three augmentations are used together on “Scene_A”. In the same case, a 4% improvement is obtained when testing on “Scene_B”. Since “Scene_B” contains both indoor and outdoor elements, while our three training scenes contain only outdoor elements, it is more challenging to perform semantic segmentation on “Scene_B” than on “Scene_A”, and it is also harder to improve the performance. The following experiment was conducted with the data augmentation strategies.

Table 4. Ablation analysis of using or not data augmentation. Semantic segmentation results for the “Scene_A” and “Scene_B” of ArCH dataset. The names “wo_translation” and “w_translation” denote without using translation and using translation in the training process.

Data Augment	OA_Scene_A	OA_Scene_B
wo_translation	0.631	0.649
w_translation	0.747	0.681

Effectiveness of Reconstruction Loss: Table 5 demonstrates the positive effects of using original Chamfer Distance (CD) loss [57] as our reconstruction loss. Compared to using modified CD loss in FoldingNet [22], our performance on “Scene_A” of the ArCH dataset has a 6% boost while using a 512-dimensional codeword in the AE training stage and a 1% improvement while using a 1024-dimensional codeword and original CD loss in the AE training stage. The following experiment utilized the original CD loss as reconstruction loss.

Table 5. Ablation analysis of using various reconstruction losses, tested on the “Scene_A” of ArCH dataset in different settings. Acronyms “CD” and “CD_M” denote that we used Chamfer distance or modified Chamfer distance as our reconstruction loss in our training process. “Codeword_dims” denotes the dimension of the codeword. “Seg_n_points” represents the input point size in the segmentation network training phase. “AE_n_points” denotes input point size in the AE training stage.

Reconstruction_Loss	Codeword_Dims	AE_n_Points	Seg_n_Points 1	OA_Scene_A
CD	512	2048	4096	0.773
CD_M	512	2048	4096	0.71
CD	1024	2048	2048	0.722
CD_M	1024	2048	2048	0.71

¹ Note: The reason why we chose to set the different “Seg_n_points” in the second controlled experiment (4096 in the first controlled experiment and 2048 in the second controlled experiment) is that if “Codeword_dims” is set to 1024 and 4096 points used in the segmentation network training stage, the AE training time would take too long, and the improvement of performance would not be significant or even decrease.

Comparison with Different Dimensions of Codeword: We used a 512-dimensional codeword and a 1024-dimensional codeword as controlled experiments to compare the segmentation result of buildings’ point clouds. In the AE training phase, the input point-cloud size was fixed at 2048, and we set up two control groups to compare the segmentation results for different codeword dimensions:

• The input point size was 2048 in the segmentation training stage; and
• The input point size was 4096 in the segmentation training stage.

The semantic segmentation result of “Scene_A” is shown in Table 6. The model performs better when the dimension of the codeword is 512 than when the dimension of the codeword is 1024, regardless of whether the input point size is 2048 or 4096 in the semantic segmentation network.

Table 6. Ablation analysis of the varying codeword dimensions (512 and 1024) for codewords learned from AE. “Codeword_dims” was set as 512-dimensional codeword and 1024-dimensional codeword, respectively. Input point size in the AE training stage was fixed at 2048.

Codeword_Dims	Seg_n_Points	OA_Scene_A
512	2048	0.747
1024	2048	0.722
512	4096	0.773
1024	4096	0.694

Comparison with Different Input Point Size in AE and Segmentation Network: To optimize the hyper-parameters, we further investigated the effect of the different input point-cloud size (number of sampled points in each block) on the semantic segmentation results of the 3D buildings’ point cloud. For this purpose, we set up four sets of experiments, conducted in codeword dimensions at 512 and 1024, respectively:

• Trained on 2048 points with (x, y, z) coordinates when training the AE and segmentation network;
• Trained on 2048 points with (x, y, z) coordinates when training the AE, and segmentation network training with 4096 points;
• Trained on 4096 points with (x, y, z) coordinates when training the AE, and segmentation network training with 2048 points; and
• Trained on 4096 points with (x, y, z) coordinates when training the AE and segmentation network.

Table 7 shows the effect on the segmentation result of “Scene_A” with different input point size (2048 or 4096) in the AE and segmentation network training stages. This table is quite revealing in several ways:

Table 7. Ablation analysis of the varying number of input point size in the AE training stage and segmentation network training stage.

Seg_n_Points	AE_n_Points	Codeword_Dims	OA_Scene_A
2048	2048	512	0.747
4096	2048	512	0.773
2048	2048	1024	0.722
4096	2048	1024	0.694
2048	4096	512	0.497
4096	4096	512	0.494
2048	4096	1024	0.520
4096	4096	1024	0.502

• Comparing rows 1 and 5, rows 2 and 6, rows 3 and 7, and rows 4 and 8, we found that whether 2048 or 4096 points are used as input in the segmentation network with the codeword dimension 512 or 1024, using 2048 points as input in the AE performs much better than if 4096 points are used;
• When analyzing the effect of the input point size in the segmentation network, different results are found: when the dimension of the codeword is 1024, point-cloud size of 2048 in the segmentation network provides better results than 4096; however, when the dimension of the codeword is 512, the segmentation network with a point-cloud size of 4096 outperforms or draws the case of the point cloud with 2048 points; and
• The best overall accuracy (0.773) was achieved when the input point-cloud size was 2048 and 4096 in the AE and segmentation steps, respectively, and was 2.6% better than the second performing network, which had a point-cloud size of 2048 in both steps. However, considering that the training time of the network will be much longer when the input point-cloud size is 4096, in this paper, the experiments were mostly based on input point clouds of size 2048 in both steps.

Comparison with Different Number of Input Point Features in AE and Segmentation Network: We demonstrate the effects of involving more features of input in our model. The codeword dimensions for all four experiments were taken as 512. Input point size was 2048 both in the AE training stage and the segmentation network training stage. Results are described in Table 8.

Table 8. Ablation analysis of the varying number of input point-cloud features in the AE and the segmentation network training stage evaluated on “Scene_A” and “Scene_B” of ArCH dataset.

Input Feature	OA_Scene_A	mIoU	OA_Scene_B	mIoU
DGCNN 1	0.784	0.376	0.752	0.353
DGCNN-Mod 2	0.896	0.535	0.837	0.470
Ours:
$\left(x, y, z\right)$	0.747	0.459	0.681	0.383
$\left(x, y, z, r, g, b\right)$	0.700	0.433	0.693	0.384
$\left(x, y, z, r, g, b, normal\right)$	0.815	0.513	0.764	0.464
$\left(x, y, z, x^{\prime }, y^{\prime }, z^{\prime }, h, s, v, normal\right)$ 3	0.701	0.407	0.544	0.240

¹ DGCNN denotes only using coordinates and is trained with 15 scenes. ² DGCNN-Mod denotes using all 12 features and is trained with 15 scenes. ³ $x^{\prime }, y^{\prime }, z^{\prime }$ denotes normalized coordinates which following the setting in DGCNN-Mod.

• The input point feature only contains coordinates $\left(x, y, z\right)$;
• The input point feature contains coordinates and radiometric information $\left(x, y, z, r, g, b\right)$;
• The input point size contains coordinates, radiometric information and geometric information $\left(x, y, z, r, g, b, normal\right)$; and
• The input point size contains coordinates, normalized coordinates’ radiometric information and geometric information $\left(x, y, z, x^{\prime }, y^{\prime }, z^{\prime }, h, s, v, normal\right)$, where the normalized coordinate is following the setting in DGCNN_Mod [5].

From the data in Table 8, it is apparent that increasing the number of features per point is beneficial for training a good network in most cases. For example, by adding color features, our performance on “Scene_B” slightly goes up, and when adding color and normal features at each point, performance is optimal on both test scenes (0.513 and 0.464 of mIoU on “Scene_A” and “Scene_B”, respectively). It is worth noting that adding geometric information (normal) results has a more significant improvement than adding radiometric information (RGB values). However, the performance of our model will decrease rather than increase when involving too many input features (12 features per point). This is probably due to the fact that our training dataset is very small, and too many features will result in over-fitting our training process. Compared to the fully supervised DGCNN-Mod [5], our results are slightly lower than theirs when employing more features in our model. Our mIoU is 0.513 on “Scene_A” compared to 0.535 obtained from DGCNN-Mod, while the results of “Scene_B” are very close (0.464 vs. 0.470).

Comparison with Different Training Data Size: To evaluate the impact of the training data size (both labeled and unlabeled) we further provided more solid experiments on four aspects:

• To add one scene (“4_CA_church”, as shown in Figure 9) as unlabeled training data in the AE training stage;
  

  Figure 9. Photo of the church represented in the “4_CA_church” scene in ArCH dataset. Copyright © 2021 ArCH dataset.
• To add one scene (“4_CA_church”) as labeled training data in the segmentation network training stage;
• To add one scene (“4_CA_church”) both in the AE and the segmentation network training stage; and
• To decrease the labeled training data size whilst keeping one scene (“7_SMV_chapel_24”) in the segmentation network training stage.

The segmentation results of “Scene_A” are shown in Table 9. These achievements suggest that, if we add labeled training data in the segmentation network training stage, our performance could further improve. For instance, when we add one labeled scene in the segmentation network training stage, our performance on the AE pre-trained network increases by 1% and 3% on three scenes and four scenes, respectively. Furthermore, no increase was detected when we tried to add the unlabeled training data, which infers that training the AE from three scenes provides a good representation to learn. More importantly, we can further prove that our network is label efficient. Even if the labeled data were decreased to just one scene (4% of overall labeled data in the supervised method), our overall accuracy still remained at 0.695.

Table 9. Ablation analysis of the varying size of training data in the AE training stage and segmentation network training stage. Columns “AE_training_scene” and “Seg_training_scene” denote the number of scenes of ArCH dataset used in our AE and segmentation training phases, respectively.

AE_Training_Scene	Seg_Training_Scene	OA_Scene_A
3_scene	1_scene	0.695
3_scene	3_scene	0.747
3_scene	4_scene	0.76
4_scene	3_scene	0.743
4_scene	4_scene	0.772

5. Discussion

As mentioned in the literature review, previous DL-based approaches for 3D point-cloud analysis are strongly supervised and rely on a massive amount of labeled 3D building data. An initial objective of this paper was to identify if it is possible to reduce our need for a large amount of fine labels in point clouds of the building segmentation task. In response to the research purpose, in this study, the results indicate that nowadays it is possible to provide good results for semantic segmentation, while 10 times fewer labeled training data are provided. The most important relevant finding was, as reported in Table 1, that under the same training strategy, our method may achieve SOTA performance but with only approximately 10% of training data with respect to fully supervised methods in both AE and segmentation network training stages. An implication of this is the possibility that the proposed AE architecture may learn good representations from unlabeled data, and this learned representation may be further used in downstream tasks such as semantic segmentation. For more detailed analysis, we found: (1) considerable gains in the arch, column, wall and vault categories; (2) the worst performing classes—door-window, moldings and stairs—were also the categories with fewer labels (see Figure 10): the unbalances of the number of labels between these categories result in the lower performance.

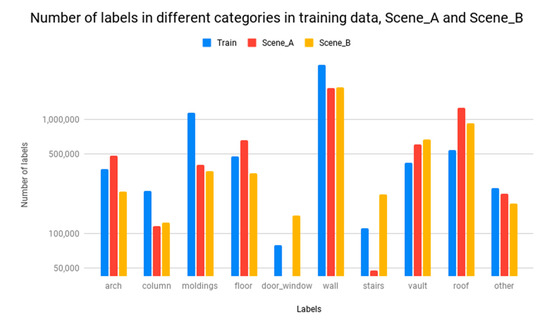
Figure 10. Comparison of the number of labels in different categories in selected training scenes from ArCH dataset, Scene_A and Scene_B.

In addition, as described in Section 4.4, we noticed that our results benefit from our network design choices, such as the use of a DGCNN-based encoder, data augmentation and reconstruction loss. It is worth noting that our results demonstrate (referring to Table 3) that the DGCNN-based encoder enables AE unsupervised learning to be exploited for downstream semantic segmentation tasks. Our improvement over the FoldingNet-based encoder (14% on “Scene_B”) demonstrates, on the other hand, the effective improvement on the AE architecture. Moreover, we further demonstrated the successful choice of our hyper-parameters, such as various dimension size of the codeword (referring to Table 6), different input point numbers in the AE and the segmentation training stage (referring to Table 7). We found that the representation size (dimension of the codeword) strongly influences the representation quality. Increasing the representation size might hurt representation usefulness in the few training data cases, which is in contrast with the observation in relatively large datasets. From this design and hyper-parameter choices, we achieved SOTA performances.

We further investigated the impact of the input feature number. With more features as input, our performances are comparable to the fully supervised method (referring to Table 8). For instance, by adding RGB and normal features at each point, the performance was optimal on both test scenes: 0.513 and 0.464 of mIoU on “Scene_A” and “Scene_B”, respectively. Intuitively, we believe that the segmentation performances should be better with more features involved in the training phase. What is surprising is that our experiments showed that our performances were degraded when we followed the SOTA setup in the supervised learning approach [5], which uses 12 features (coordinates, normalized coordinates, HSV and normal). As shown in Figure 11, our model shows over-fitting during the training process. The training accuracy was rapidly increased in the first 20 epochs, and the training accuracy reached more than 0.9 on epoch 40, while the test accuracy of “Scene_B” is just 0.544. It is easy to see that the model was trained to perfectly fit training data rather than unseen scenes, which is an obvious signal of over-fitting. This inconsistency may be due to the fact that we input too many features in the training data, which means that the classifier trained by the network will be inclined to distribute the training data. This result is especially exacerbated by the fact that we only used very few labeled data in the training process and graph-based DNNs typically have millions of parameters, as can be seen from the over-fitting results.

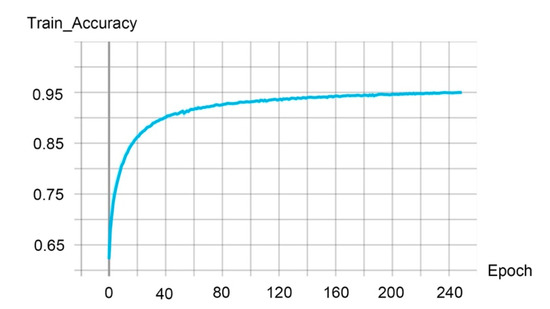
Figure 11. The training accuracy while using 12 features in input point cloud.

Another important finding was the impact of using different amounts of training data demanded in our model (both unlabeled and labeled data). The most obvious finding that emerged from the analysis is that from three unlabeled scenes, discriminative representation may be already learned in the pre-trained AE. Moreover, although segmentation results are increased or decreased by varying labeled training data in the segmentation network training stage, the magnitude of the change is very small. These results (referring to Table 9) further support the idea that our method is label-efficient in nature.

This combination of findings provides some support for the conceptual premise that our proposed AE architecture may learn powerful representations from unlabeled data, and these representations may be further used in our downstream tasks. Furthermore, the results of this study indicate the effectiveness of the design choices.

6. Conclusions

In this study, we presented an effective label-efficient unsupervised network for LoD3 buildings’ point-cloud semantic segmentation. The results in our experiment provide support that our proposed Autoencoder architecture may learn powerful representations from unlabeled data, and these representations may be further used in downstream tasks. Furthermore, our network supplies a unified approach for the segmentation task of building point clouds while obtaining equal or better results with respect to the state-of-the-art methods but on the basis of only 10% training data from the ArCH dataset. We also provided detailed ablation studies to validate our design choices.

However, our network has the following limitations: (1) In the data preprocessing stage, the block size is fixed. Thus, the network is trained on a small region of building scenes, and the performance is degraded, resulting in wrong segmentation. (2) The result of the proposed model is not enhanced when involving 12 features in input point clouds due to the limitation of training data size.

In future work, it might be possible to improve the performance by breaking through the input block size and incorporating more features of the input point cloud of buildings while using the very limited amount of labeled training data.