Remaining Useful Life Prediction of the Concrete Piston Based on Probability Statistics and Data Driven

Abstract

This paper proposes a method on predicting the remaining useful life (RUL) of a concrete piston of a concrete pump truck based on probability statistics and data-driven approaches. Firstly, the average useful life of the concrete piston is determined by probability distribution fitting using actual life data. Secondly, according to condition monitoring data of the concrete pump truck, a concept of life coefficient of the concrete piston is proposed to represent the influence of the loading condition on the actual useful life of individual concrete pistons, and different regression models are established to predict the RUL of the concrete pistons. Finally, according to the prediction result of the concrete piston at different life stages, a replacement warning point is established to provide support for the inventory management and replacement plan of the concrete piston.

1. Preface

Along with the continuous progress of modern manufacturing technology, the structure of mechanical and electrical systems is more and more complex, which brings new challenges to fault prediction and health management of the system. Parts are important components of mechanical and electrical product systems, once the parts fail, it may affect the healthy operation of the whole system, or even cause serious loss of life and property. Therefore, the remaining useful life (RUL) prediction of parts has become a key research issue of fault prediction and health management [1,2,3]. Lei Y et al. [4] provided a review on machinery prognostics following its whole program, i.e., from data acquisition to RUL prediction. Jay Lee et al. [5] provided a review on the system design of prognostics and health management, and gave a tutorial for the selection of RUL prediction approaches by comparing their advantages and disadvantages.

At present, a number of research on the RUL prediction of parts have reported [6,7,8], and approaches of RUL prediction can be roughly grouped into three categories. The first category is the prediction method based on physical models, which estimates the RUL of parts according to the degradation mechanism. Leser et al. [9] validated the crack growth modeling method using damage diagnosis data based on structural health monitoring, and a probabilistic prediction of RUL is formed for a metallic, single-edge notch tension specimen with a fatigue crack growing under mixed-mode conditions. Habib et al. [10] evaluated the stress of A310 aircraft wings during each loading cycle through a finite element analysis, and they predicted the RUL of A310 wings using the Paris Law technique based on linear elastic fracture mechanics. Chen et al. [11] developed a novel computational modelling technique for the prediction of crack growth in load bearing orthopaedic alloys subjected to fatigue loading, which can predict the RUL of parts through the crack path. The second category is the prediction method based on probability statistics, which fit the failure data of parts to obtain the characteristic distribution of life through a statistical distribution model. Wang et al. [12] proposed a novel method based on the three-parameter Weibull distribution proportional hazards model to predict the RUL of rolling bearings, the model is able to produce accurate RUL predictions for the tested bearings and outperforms the popular two-parameter model. Pan et al. [13] proposed a remanufacturability evaluation scheme based on the average RUL of the structural arm, and made a comprehensive evaluation by establishing the reliability parameter model of the structural arm. Xu et al. [14] discussed the influence of different distribution function values on the prediction results by analyzing different parameter estimation methods, and established the RUL prediction model based on the failure data of parts. Rong et al. [15] determined the average useful life of the pump truck boom based on the Weibull distribution function by using the failure data, and predicted the RUL of the boom by using the used time. The third category is the data-driven prediction method. Ren et al. [16] analyzed the time-domain and frequency-domain characteristics of rolling bearing vibration signals, and established the RUL prediction model of rolling bearing based on deep neural networks. Liu et al. [17] proposed an RUL prediction framework based on multiple health state assessments that divide the entire bearing life into several health states, where a local regression model can be built individually. Zio et al. [18] proposed a methodology for the estimation of the RUL of parts based on particle filtering. Sun et al. [19] used support vector machines to build degradation models for bearing RUL prediction. Maio et al. [20] proposed a combination of a relevance vector machine and model fitting as a prognostic procedure for estimating the RUL of degraded thrust ball bearings. Deutsch et al. [21] proposed a deep learning-based approach for the RUL prediction of rotating parts with big data.

With more and more information available to mechanical devices, many new methods have been applied to prediction models. Mad et al. [22] used a physical model to generate health indices whose evolution can be estimated and predicted online. Xu J et al. [23] combined the monitoring sensor data and integrated the strengths of the data-driven prognostics approach and the experience-based approach, while reducing their respective limitations.

The RUL prediction, based on physical model needs to establish accurate models to describe failure degradation mechanism of parts, while the RUL prediction, based on probability statistics, does not consider the actual working state of different parts, so the application of both methods is limited. With the support of modern information technology and the industrial Internet of Things technology, mechanical and electrical product systems are becoming more and more intelligent, so more and more data on the working status can be obtained, which brings great potential for data driven RUL prediction research [24].

A concrete pump truck is a kind of construction vehicle which uses hydraulic pressure to deliver concrete continuously through the pipeline. A concrete piston, which is located in the conveying cylinder of the pump truck, as shown in Figure 1, is an important part of the concrete pump truck. When the concrete piston is working, it reciprocates in the concrete medium of the conveying cylinder, provides pressure for the concrete, pumps the concrete to a remote place, and plays a sealing role at the same time. The working environment of the concrete piston is very harsh, and it is difficult to establish an accurate failure degradation model and obtain the operating state data directly. At present, there is limited research on the RUL prediction of the concrete piston. By using the condition monitoring data of the concrete pump truck and the replacement information data of the concrete piston, this paper puts forward an RUL prediction method of the concrete piston based on probability statistics and condition monitoring data, and the validity of the method is verified through the result analysis and model application.

Figure 1. Concrete pump truck and concrete piston.

Figure 2 shows the flowchart of the proposed methodology for RUL prediction. The methodology is divided into two phases: offline and online. In the offline phase, the replacement information data form different concrete pistons are used to fit features based on the Weibull distribution, the condition monitoring data from different concrete pump trucks are used to fit features based on regression algorithm, and the RUL prediction model is built. In the online phase, the RUL of the concrete piston is estimated based on the condition monitoring data from a new concrete pump truck and the real-time working life.

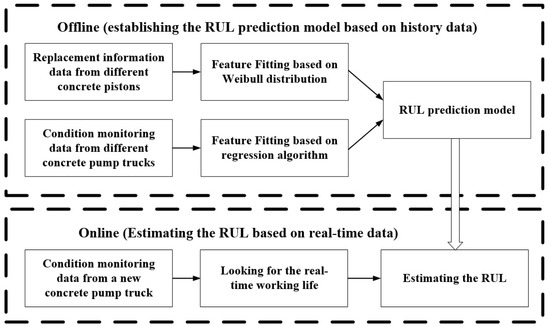
Figure 2. Flowchart of the RUL prediction.

The rest of the paper is organized as follows: Section 2 introduces the basic situation of the data. In Section 3, we establish the RUL prediction model of the concrete piston based on probability statistics and data-driven approaches. Section 4 discusses the prediction effect of different regression models, and we use the best prediction model to propose setting the replacement warning point of the concrete piston in Section 5, and conclusions are finally provided.

2. Data Overview

2.1. Data Source

The data studied in this paper were collected from 129 concrete pump trucks of a construction machinery enterprise from January to December 2019, including two types of data: condition monitoring data of the concrete pump truck and replacement information data of the concrete piston. The condition monitoring data of the concrete pump truck includes time, GPS latitude, GPS longitude, engine speed, hydraulic oil temperature, system pressure, pumping capacity, cumulative fuel consumption, reversing frequency, cumulative working time, and pump truck status, etc., which are uploaded to the enterprise’s networked operation and maintenance platform through the Internet of Things. The replacement information data, which refers to the actual working life of the concrete piston when it is replaced because of failure, is directly inputted into the networked operation and maintenance platform by the service engineer of the enterprise.

2.2. Data Description

According to the functional characteristics of the concrete piston, this paper studies five condition monitoring data related to the working state of the concrete pump truck, including engine speed, system pressure, pumping capacity, reversing frequency, and cumulative working time. The specific meaning of the condition monitoring data is shown in Table 1.

Table 1. Meanings of condition monitoring data of the concrete pump truck.

Name	Data Type	Unit	Scope	Meaning
Engine Speed	integral	RPM	0~2000	The speed of pump truck engine
System Pressure	integral	MPa	0~32	pump hydraulic pressure of pumping system
Pumping Capacity	integral	%	0~100	The percentage of pump truck in its maximum value
Reversing Frequency	integral	times/minute	0~30	Pump cylinder reversing times per minute
Cumulative Working Time	floating	hour	$\ge$0	Cumulative working time of pump truck

The condition monitoring data of the concrete pump truck includes “equipment number”, “parameter name”, “parameter value” and “server receiving time”, totaling more than 2.8 million pieces. The replacement information data of the concrete piston includes “equipment number”, “replacement timing” and “replacement date”, totaling 325 pieces.

2.3. Data Preprocessing

The condition monitoring data of the concrete pump truck studied in this paper are time series data collected by sensors. Due to factors such as the timing error of sensors or poor communication conditions, certain data are missed in the data set. For the four types of data, such as engine speed, system pressure, pumping capacity, and reversing frequency, the missing data may be very close to the data uploaded the previous time due to the high data collecting frequency, so the nearest complement method is adopted to fill in missed data. The cumulative working time is accumulated data; it can be assumed that the changing of the cumulative working time is slow and uniform, so the linear interpolation method is adopted to fill the missed data [25]. The original data of the engine speed in a certain period of time is shown in Figure 3, and the processed data is shown in Figure 4.

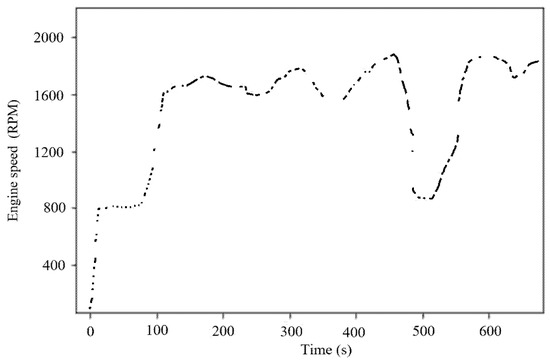
Figure 3. The original data.

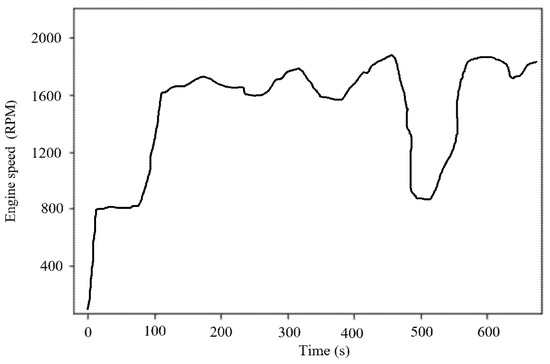
Figure 4. The processed data.

3. Model Building

3.1. Model Construction

If actual working life data of the concrete piston is known, the appropriate probability statistical distribution model can be selected to fit the data, and the characteristic distribution of the life can be obtained, which can be used to estimate the average useful life. During the operation of the concrete piston, the working state of the concrete pump truck will have an impact on its actual working life, so a concept of life coefficient is proposed based on the condition monitoring data of the concrete pump truck, and the RUL prediction model of the concrete piston is established, as shown in Equation (1).

$$M_r=\alpha ·M_t-M_0$$

(1)

where $M_r$ is the RUL of the concrete piston, α is the life coefficient of the concrete piston related to condition monitoring data of the concrete pump truck, $M_t$ is the average useful life of the concrete piston, and $M_0$ is the real-time working life of the concrete piston.

3.2. The Average Useful Life of the Concrete Piston

In the failure probability distribution function of parts, there are several kinds of common distribution functions: exponential distribution, normal distribution, lognormal distribution, Weibull distribution, etc. Among them, the Weibull distribution is the most widely used due to its high degree of fitting and good effect for parts which undergo notable degradation before final failure [25]. The main failure mode of the concrete piston is dissipation failure, so this paper uses the Weibull distribution to study the average useful life of the concrete piston.

The probability density function of the two-parameter Weibull distribution is:

$$f\left(x\right)=\frac{k}{\lambda }{\left(\frac{x}{\lambda }\right)}^{k-1}\exp \left[-{\left(\frac{x}{\lambda }\right)}^k\right],0\le x\le \infty ,\lambda >0,k>0$$

(2)

where $\lambda$ is the scale parameter, called the characteristic life, which is an average value of the life of the parts; $k$ is the shape parameter, which is the failure form of the parts.

The failure distribution function of the Weibull distribution is:

$$F\left(x\right)=1-\exp \left[1-{\left(\frac{x}{\lambda }\right)}^k\right]$$

(3)

The average useful life $M_t$ of the concrete piston is represented by the expected value of the failure distribution function:

$$M_t=\lambda \Gamma \left(1+\frac{1}{k}\right)$$

(4)

where Γ is the gamma function.

According to the replacement information data of the concrete piston, we can obtain the actual working life data, arrange it in increasing order, calculate it by the common median rank, and estimate the parameters of the Weibull distribution based on the least square method. The fitting results are shown in Figure 5, and the fitting error is not higher than 0.056.

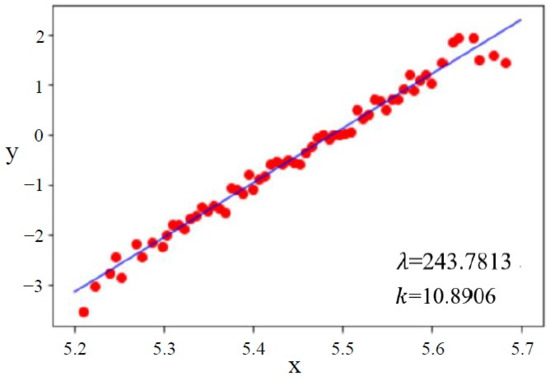
Figure 5. Least squares fitting diagram.

Substitute λ = 243.7813 and k = 10.8906 into Formula (4), the expected value of the Weibull distribution failure distribution function is obtained, and the average useful life of the concrete piston $M_t$ = 239.6256 h.

3.3. The Life Coefficient of the Concrete Piston

As the concrete piston is a mechanical part dominated by wear failure, it is expected to wear faster under a higher-strength working environment, so the working time of the concrete pump truck under a high-load working state has a greater impact on its life. Referring to the working environment and material properties of the concrete piston, the high-load working state is determined by parameters, such as engine speed, system pressure, pumping capacity, and reversing frequency. According to the actual performance parameters of the concrete pump truck, the definition of the high-load working state is shown in Table 2.

Table 2. Definition table of high-load working state of the concrete pump truck.

Name	Unit	Normal Range	High-Load Working State
Engine Speed	RPM	0~2000	≥1100
System Pressure	MPa	0~32	≥20
Pumping Capacity	%	0~100	≥40
Reversing Frequency	Times/minute	0~30	≥10

According to the definition of the high-load working state of the concrete pump truck, condition monitoring data of the concrete pump truck corresponding to the actual working life data of the concrete piston is statistically analyzed. The ratio of the high-load working state of the concrete piston in the life cycle of engine speed, system pressure, pumping capacity, and reversing frequency for 325 pieces is calculated respectively, which is recorded as A, B, C, D, as shown in Table 3. The life coefficient α is calculated by the average useful life $M_t$ and the real-time working life $M_0$ according to Formula (1), and the results are shown in Table 3.

Table 3. Dataset of the concrete piston life prediction.

Number	A	B	C	D	M0	α
1	0.5327	0.4649	0.2237	0.2131	275.7432	1.1507
2	0.4834	0.5586	0.2634	0.2056	258.7615	1.0779
3	0.4930	0.6394	0.2414	0.2527	232.4608	0.9701
4	0.4986	0.5002	0.1362	0.3006	257.3100	1.0738
5	0.6929	0.7160	0.3275	0.2343	269.2673	1.1237
6	0.5578	0.4718	0.3005	0.2156	236.1271	0.9854
7	0.4119	0.5886	0.2571	0.2779	263.5402	1.0998
8	0.4184	0.5829	0.2636	0.3029	259.3468	1.0823
9	0.4356	0.3802	0.2173	0.2318	264.6904	1.1046
10	0.7991	0.7307	0.3154	0.2297	229.6332	0.9583
11	0.6120	0.4617	0.1180	0.1447	256.2317	1.0693
12	0.6313	0.5106	0.3080	0.2707	254.0271	1.0601
13	0.4727	0.5465	0.1920	0.1924	264.5467	1.1040
14	0.3900	0.4855	0.2124	0.2814	261.2638	1.0903
15	0.5690	0.4688	0.3515	0.1846	258.9155	1.0805
16	0.3960	0.4253	0.1909	0.2327	265.2655	1.1070
17	0.6260	0.5851	0.1903	0.2584	220.7671	0.9213
18	0.4700	0.5367	0.1802	0.2610	264.2112	1.1026
19	0.5186	0.4900	0.3221	0.2101	240.6081	1.0041
20	0.3908	0.4339	0.1765	0.2387	256.1118	1.0688
21	0.4351	0.4570	0.1445	0.1752	253.8594	1.0594
22	0.3740	0.7600	0.4246	0.3216	214.8962	0.8968
23	0.5351	0.6035	0.3396	0.2556	233.5870	0.9748
24	0.4302	0.5646	0.2063	0.2923	236.6303	0.9875
25	0.5283	0.4452	0.2472	0.2426	244.3702	1.0198
26	0.6663	0.6448	0.2218	0.2453	228.8664	0.9551
27	0.5727	0.7697	0.3411	0.2537	219.0657	0.9142
28	0.6345	0.5055	0.2151	0.2957	232.2691	0.9693
29	0.5842	0.4344	0.2726	0.2262	253.6437	1.0585
30	0.6911	0.4715	0.2746	0.2917	244.1066	1.0187
31	0.5448	0.6426	0.2909	0.3201	233.3714	0.9739
32	0.3929	0.5887	0.2085	0.2582	238.4754	0.9952
33	0.5501	0.6243	0.1731	0.1468	247.1259	1.0313
34	0.5889	0.6195	0.2080	0.2483	252.7092	1.0546
35	0.7093	0.3554	0.3357	0.2742	247.8687	1.0344
36	0.3942	0.5236	0.2500	0.2306	253.4520	1.0577
37	0.7755	0.6721	0.3851	0.3027	237.2293	0.9900
38	0.4760	0.5225	0.1709	0.1920	252.3737	1.0532
39	0.5700	0.5270	0.3312	0.3010	239.8652	1.0010
40	0.7545	0.7045	0.3351	0.2761	228.3153	0.9528
41	0.5298	0.6320	0.3479	0.2816	224.8167	0.9382
42	0.5825	0.5987	0.2093	0.1327	227.9079	0.9511
43	0.5853	0.4876	0.1834	0.2694	217.8916	0.9093
44	0.5451	0.4701	0.3063	0.2326	252.9009	1.0554
45	0.4657	0.5438	0.2912	0.3321	245.7600	1.0256
46	0.5847	0.4798	0.3163	0.2012	235.1206	0.9812
47	0.7705	0.5957	0.2533	0.2740	230.4479	0.9617
48	0.6602	0.6436	0.3349	0.2553	232.0774	0.9685
49	0.5163	0.4518	0.2932	0.2523	280.4338	1.1703
50	0.4919	0.4107	0.1371	0.1977	248.3719	1.0365
51	0.5353	0.7071	0.3681	0.3211	213.4345	0.8907
52	0.6934	0.6488	0.3370	0.2824	233.9944	0.9765
53	0.6387	0.6471	0.3739	0.2274	241.2790	1.0069
54	0.4278	0.4885	0.1921	0.2458	246.6946	1.0295
55	0.6932	0.4207	0.2761	0.2872	242.2136	1.0108
56	0.5113	0.5023	0.1883	0.2215	253.3322	1.0572
57	0.5476	0.3089	0.1933	0.2920	252.1820	1.0524
58	0.6081	0.5186	0.3280	0.3104	231.7419	0.9671
59	0.3961	0.5079	0.2603	0.2196	260.6168	1.0876
60	0.3500	0.4500	0.1602	0.1790	263.3725	1.0991
61	0.5502	0.4101	0.3263	0.3634	249.2585	1.0402
62	0.5534	0.7115	0.2740	0.3103	230.5678	0.9622
63	0.4785	0.5300	0.2183	0.1731	260.3293	1.0864
64	0.5698	0.6483	0.2974	0.2842	235.8635	0.9843
65	0.3904	0.6349	0.3511	0.2974	233.3953	0.9740
66	0.7074	0.6328	0.2938	0.2446	231.8617	0.9676
67	0.5023	0.5521	0.3031	0.2701	238.1160	0.9937
68	0.6151	0.5705	0.2962	0.2476	234.2580	0.9776
69	0.6402	0.6849	0.3190	0.3735	235.0248	0.9808
70	0.5425	0.4229	0.3202	0.2349	259.1311	1.0814
71	0.3712	0.2922	0.2286	0.2336	247.1498	1.0314
72	0.6459	0.6576	0.2489	0.3010	231.8378	0.9675
73	0.4173	0.5811	0.4002	0.2432	241.3988	1.0074
74	0.5381	0.4812	0.2163	0.2784	246.9581	1.0306
75	0.5551	0.5284	0.3487	0.2546	242.4053	1.0116
76	0.5160	0.5578	0.3080	0.2523	242.2375	1.0109
77	0.5938	0.6039	0.3585	0.3144	234.3299	0.9779
78	0.6394	0.7066	0.3317	0.3065	225.4877	0.9410
79	0.3929	0.5261	0.2584	0.1987	249.4263	1.0409
80	0.3853	0.4664	0.1966	0.1815	254.3386	1.0614
81	0.5490	0.4925	0.1901	0.2395	255.7284	1.0672
82	0.4072	0.5081	0.1832	0.2050	268.5244	1.1206
83	0.4886	0.3629	0.2008	0.1686	271.1124	1.1314
84	0.7053	0.5604	0.3034	0.3427	216.3580	0.9029
85	0.4791	0.3072	0.2206	0.1546	253.4280	1.0576
86	0.5439	0.4260	0.1583	0.2440	250.6963	1.0462
87	0.4787	0.4619	0.2312	0.2319	270.0101	1.1268
88	0.5503	0.6096	0.2473	0.2190	250.5765	1.0457
89	0.6039	0.4221	0.2556	0.3442	234.9289	0.9804
90	0.5919	0.7085	0.2408	0.3349	214.0815	0.8934
91	0.4955	0.3821	0.3156	0.2506	248.3240	1.0363
92	0.5745	0.4788	0.2822	0.3193	231.8617	0.9676
93	0.6116	0.6443	0.2551	0.3027	234.6654	0.9793
94	0.6295	0.4652	0.3162	0.4058	225.7513	0.9421
95	0.5539	0.5181	0.2986	0.2226	247.7010	1.0337
96	0.6030	0.5657	0.3448	0.2144	237.2773	0.9902
97	0.4644	0.3807	0.1791	0.1555	272.2147	1.1360
98	0.6541	0.5545	0.4018	0.2551	240.7039	1.0045
99	0.4365	0.5885	0.3102	0.3304	242.4771	1.0119
100	0.6328	0.6943	0.3283	0.2597	234.9529	0.9805
101	0.5775	0.6414	0.2589	0.2481	225.5356	0.9412
102	0.4527	0.5211	0.2768	0.2113	240.4164	1.0033
103	0.5238	0.7210	0.3026	0.2791	228.6987	0.9544
104	0.6701	0.8097	0.2931	0.2319	211.7092	0.8835
105	0.5494	0.5042	0.1770	0.3102	243.0283	1.0142
106	0.5987	0.6512	0.3512	0.3089	225.9669	0.9430
107	0.5480	0.6019	0.3675	0.3097	236.6782	0.9877
108	0.6178	0.5802	0.3709	0.2382	232.1014	0.9686
109	0.5233	0.4629	0.2508	0.2647	264.5227	1.1039
110	0.5416	0.6134	0.2541	0.3603	229.9927	0.9598
111	0.6049	0.7044	0.2866	0.2677	233.7787	0.9756
112	0.7767	0.7459	0.3312	0.2980	224.0499	0.9350
113	0.7424	0.7940	0.2892	0.3641	229.4655	0.9576
114	0.4251	0.3137	0.1863	0.2582	255.2013	1.0650
115	0.4677	0.4836	0.2420	0.1943	247.6051	1.0333
116	0.4719	0.5506	0.1208	0.2607	249.9535	1.0431
117	0.7987	0.5091	0.2065	0.2828	244.6338	1.0209
118	0.6100	0.5015	0.3600	0.3276	241.5426	1.0080
119	0.6669	0.6183	0.2327	0.2860	238.7390	0.9963
120	0.5130	0.5522	0.1823	0.1880	256.2796	1.0695
121	0.5116	0.4400	0.2182	0.2465	265.7688	1.1091
122	0.5734	0.4599	0.2170	0.2026	239.1463	0.9980
123	0.5844	0.4862	0.2918	0.2739	213.8898	0.8926
124	0.6483	0.5492	0.3449	0.3031	233.2516	0.9734
125	0.3913	0.3401	0.1683	0.1353	262.7974	1.0967
126	0.5527	0.6217	0.2720	0.2031	229.3457	0.9571
127	0.5998	0.5637	0.2898	0.2458	236.9178	0.9887
128	0.5878	0.4996	0.3996	0.3000	272.6939	1.1380
129	0.5611	0.5380	0.2617	0.2755	241.4468	1.0076
130	0.4203	0.4602	0.2533	0.2163	288.0779	1.2022
131	0.5129	0.5617	0.3285	0.2422	235.8395	0.9842
132	0.4408	0.3256	0.1743	0.1156	263.5642	1.0999
133	0.6086	0.5302	0.3208	0.2517	241.1832	1.0065
134	0.4683	0.5353	0.2151	0.2366	254.7699	1.0632
135	0.5089	0.4360	0.1880	0.1649	263.9716	1.1016
136	0.6593	0.5301	0.3008	0.3063	229.8728	0.9593
137	0.6241	0.5892	0.3405	0.2801	234.7852	0.9798
138	0.4846	0.5178	0.3320	0.2457	263.4923	1.0996
139	0.4799	0.3837	0.2091	0.1693	270.0101	1.1268
140	0.7492	0.7146	0.3966	0.2981	203.3463	0.8486
141	0.5553	0.6123	0.2166	0.2633	227.1411	0.9479
142	0.6203	0.5740	0.3016	0.3028	224.2656	0.9359
143	0.6210	0.5310	0.2124	0.2406	253.7156	1.0588
144	0.5969	0.7138	0.4393	0.2870	229.7770	0.9589
145	0.6701	0.6351	0.2107	0.2495	245.9038	1.0262
146	0.5613	0.5360	0.2391	0.2374	244.9213	1.0221
147	0.5399	0.5594	0.2524	0.2649	258.5800	1.0791
148	0.6639	0.6073	0.2783	0.3198	223.2592	0.9317
149	0.5502	0.4978	0.2028	0.2773	235.4082	0.9824
150	0.6114	0.5488	0.3251	0.3126	222.3726	0.9280
151	0.5003	0.3057	0.1333	0.1959	250.6723	1.0461
152	0.5456	0.6012	0.3290	0.3119	233.7787	0.9756
153	0.5188	0.5440	0.3072	0.3005	240.8237	1.0050
154	0.3839	0.4064	0.1277	0.1674	274.0838	1.1438
155	0.5102	0.3532	0.1406	0.2123	261.3596	1.0907
156	0.6292	0.5956	0.2766	0.2094	205.7665	0.8587
157	0.5574	0.4750	0.2662	0.2037	254.0511	1.0602
158	0.5551	0.5952	0.2645	0.2576	234.3299	0.9779
159	0.5844	0.4964	0.2991	0.2398	269.4111	1.1243
160	0.5046	0.5260	0.2890	0.3293	268.7401	1.1215
161	0.5478	0.6837	0.3121	0.3214	218.9699	0.9138
162	0.6041	0.6057	0.2931	0.2927	227.0453	0.9475
163	0.5403	0.6416	0.3216	0.3729	239.9611	1.0014
164	0.7262	0.6158	0.3376	0.2182	225.9190	0.9428
165	0.5465	0.5881	0.2003	0.1856	263.9236	1.1014
166	0.5625	0.5929	0.3478	0.2767	226.0388	0.9433
167	0.4225	0.4387	0.2002	0.1501	261.0242	1.0893
168	0.6945	0.6719	0.3022	0.2703	205.6467	0.8582
169	0.5187	0.4585	0.2539	0.1418	260.0177	1.0851
170	0.4601	0.7740	0.3655	0.2495	251.0797	1.0478
171	0.6036	0.5835	0.3731	0.2935	231.8378	0.9675
172	0.5160	0.5574	0.2100	0.2328	265.6489	1.1086
173	0.5578	0.4984	0.2692	0.2352	230.6876	0.9627
174	0.4149	0.5973	0.3432	0.3339	225.8232	0.9424
175	0.5196	0.5593	0.2851	0.2697	260.8804	1.0887
176	0.5180	0.6140	0.3687	0.2659	241.6145	1.0083
177	0.5161	0.5074	0.2803	0.2277	262.1025	1.0938
178	0.4803	0.5122	0.2569	0.1834	288.5811	1.2043
179	0.5608	0.4847	0.2943	0.2037	234.4497	0.9784
180	0.3483	0.5307	0.2151	0.1520	276.1206	1.1523
181	0.4830	0.5920	0.2248	0.3274	237.4450	0.9909
182	0.5922	0.4822	0.2869	0.1430	306.8645	1.2806
183	0.6702	0.6951	0.3228	0.3498	233.3953	0.9740
184	0.6646	0.5053	0.2649	0.2604	215.0879	0.8976
185	0.6676	0.5642	0.3133	0.3632	225.6794	0.9418
186	0.6223	0.6392	0.2231	0.2530	214.0336	0.8932
187	0.6169	0.5294	0.2479	0.2073	263.9716	1.1016
188	0.6417	0.5766	0.3144	0.2674	209.7922	0.8755
189	0.4991	0.4622	0.3406	0.2389	255.1054	1.0646
190	0.5732	0.4733	0.2561	0.2080	248.7553	1.0381
191	0.4642	0.4482	0.1526	0.2511	278.2772	1.1613
192	0.4705	0.4710	0.2948	0.2380	248.4438	1.0368
193	0.3980	0.4314	0.2487	0.1844	270.2498	1.1278
194	0.5619	0.5153	0.3043	0.2721	241.0873	1.0061
195	0.5183	0.3431	0.1905	0.1427	255.5607	1.0665
196	0.5378	0.6151	0.2805	0.3287	229.1779	0.9564
197	0.6363	0.4785	0.2373	0.2320	254.3386	1.0614
198	0.6498	0.6442	0.2928	0.3814	213.7700	0.8921
199	0.4216	0.4310	0.1341	0.2889	265.1457	1.1065
200	0.7010	0.5817	0.2524	0.3164	209.6484	0.8749
201	0.5362	0.6251	0.2883	0.2724	218.4187	0.9115
202	0.4864	0.5794	0.2506	0.2725	235.5759	0.9831
203	0.6562	0.6062	0.2083	0.3454	255.9441	1.0681
204	0.3499	0.3902	0.1461	0.1384	268.9558	1.1224
205	0.6700	0.4900	0.2824	0.2015	229.6332	0.9583
206	0.5129	0.7297	0.3784	0.2789	214.5368	0.8953
207	0.5427	0.6054	0.2937	0.2557	228.7945	0.9548
208	0.4656	0.3771	0.2523	0.2204	258.2205	1.0776
209	0.5628	0.7643	0.3090	0.2544	229.8010	0.9590
210	0.3204	0.4247	0.2268	0.2008	248.8751	1.0386
211	0.4798	0.5539	0.1698	0.2075	265.8646	1.1095
212	0.5834	0.5282	0.3478	0.2868	236.7741	0.9881
213	0.5985	0.7345	0.3383	0.2557	234.4257	0.9783
214	0.5664	0.7624	0.3659	0.2459	231.1429	0.9646
215	0.5488	0.6883	0.2842	0.3029	211.3498	0.8820
216	0.6220	0.5906	0.3377	0.3362	228.0038	0.9515
217	0.4678	0.5518	0.2876	0.2269	258.2205	1.0776
218	0.5724	0.5558	0.3123	0.2871	240.9915	1.0057
219	0.5817	0.4938	0.3971	0.2734	231.0710	0.9643
220	0.6025	0.6517	0.3293	0.2192	236.6542	0.9876
221	0.4685	0.5601	0.2171	0.1900	262.4140	1.0951
222	0.6209	0.7014	0.2363	0.3432	229.6811	0.9585
223	0.4468	0.5704	0.3535	0.3161	249.2346	1.0401
224	0.6542	0.5667	0.3371	0.2738	232.3170	0.9695
225	0.6131	0.5116	0.3298	0.2219	231.8138	0.9674
226	0.5320	0.6009	0.2380	0.2300	252.3018	1.0529
227	0.4922	0.5774	0.3688	0.2073	244.8974	1.0220
228	0.3778	0.5247	0.1892	0.2118	252.3018	1.0529
229	0.5296	0.6142	0.3521	0.3223	241.1592	1.0064
230	0.6014	0.5301	0.3349	0.3462	230.7115	0.9628
231	0.4699	0.5192	0.2661	0.2243	240.2486	1.0026
232	0.3846	0.3595	0.1690	0.2545	265.1937	1.1067
233	0.4096	0.4316	0.2321	0.2468	252.5654	1.0540
234	0.5039	0.5834	0.2477	0.2505	241.9739	1.0098
235	0.6418	0.7229	0.2885	0.2730	251.0078	1.0475
236	0.6329	0.7621	0.4740	0.3463	229.0341	0.9558
237	0.4722	0.3236	0.1669	0.2484	259.2509	1.0819
238	0.4912	0.4438	0.2486	0.3104	245.9757	1.0265
239	0.5113	0.4463	0.1880	0.1897	249.0668	1.0394
240	0.5153	0.6013	0.3866	0.3206	234.4018	0.9782
241	0.6428	0.5521	0.3476	0.2764	223.1154	0.9311
242	0.6321	0.6634	0.2359	0.2585	238.5233	0.9954
243	0.5844	0.5470	0.2935	0.2552	240.1528	1.0022
244	0.3498	0.4925	0.2679	0.2633	230.5917	0.9623
245	0.3916	0.3891	0.1782	0.1629	243.2679	1.0152
246	0.5404	0.6057	0.3468	0.2711	232.0774	0.9685
247	0.4428	0.5545	0.1890	0.1716	257.5975	1.0750
248	0.3722	0.4015	0.2488	0.1196	257.9809	1.0766
249	0.4399	0.5011	0.1861	0.2124	260.2574	1.0861
250	0.5272	0.6077	0.2032	0.2845	239.7694	1.0006
251	0.6786	0.3383	0.2162	0.2228	235.3603	0.9822
252	0.4391	0.4175	0.2117	0.2774	251.8465	1.0510
253	0.3988	0.4560	0.1872	0.2227	246.8144	1.0300
254	0.6330	0.5616	0.3023	0.2692	226.6619	0.9459
255	0.6651	0.5741	0.2634	0.2190	225.6554	0.9417
256	0.4153	0.5895	0.2481	0.2455	230.8553	0.9634
257	0.4940	0.6101	0.2805	0.3141	212.0447	0.8849
258	0.5217	0.4009	0.1944	0.1861	282.0633	1.1771
259	0.6303	0.5292	0.2873	0.2560	252.7810	1.0549
260	0.5108	0.6170	0.2965	0.2150	252.1580	1.0523
261	0.5183	0.4238	0.2415	0.2348	263.6600	1.1003
262	0.5485	0.3874	0.1971	0.2004	264.0914	1.1021
263	0.6570	0.5258	0.2570	0.3183	232.1732	0.9689
264	0.4916	0.6562	0.3351	0.2652	232.7483	0.9713
265	0.5513	0.5241	0.2943	0.2734	242.9324	1.0138
266	0.5428	0.6279	0.2854	0.2430	220.5035	0.9202
267	0.6963	0.5806	0.2732	0.3194	232.9880	0.9723
268	0.3664	0.4032	0.1306	0.1917	264.5946	1.1042
269	0.6383	0.5060	0.3105	0.2282	277.2229	1.1569
270	0.5920	0.4225	0.2685	0.1743	268.5005	1.1205
271	0.5524	0.6838	0.1923	0.2678	221.7495	0.9254
272	0.5877	0.6777	0.3620	0.2749	232.0774	0.9685
273	0.5591	0.5969	0.3317	0.3499	247.5812	1.0332
274	0.5761	0.7042	0.2751	0.3200	229.1300	0.9562
275	0.6032	0.5553	0.3448	0.3193	254.0511	1.0602
276	0.4332	0.5580	0.1189	0.1600	246.5747	1.0290
277	0.5851	0.5439	0.3834	0.2520	246.9102	1.0304
278	0.5531	0.4472	0.2154	0.1032	253.4999	1.0579
279	0.5342	0.5928	0.2171	0.2931	232.7963	0.9715
280	0.7256	0.6209	0.3090	0.2353	213.4106	0.8906
281	0.6115	0.6997	0.2820	0.2711	230.9751	0.9639
282	0.6624	0.5737	0.2887	0.2871	240.6800	1.0044
283	0.5298	0.6562	0.2728	0.3122	215.4953	0.8993
284	0.6034	0.7123	0.2678	0.2319	236.5584	0.9872
285	0.6921	0.6675	0.3375	0.2408	225.7273	0.9420
286	0.3156	0.4856	0.1573	0.1467	245.1370	1.0230
287	0.4477	0.4241	0.1581	0.2325	262.8453	1.0969
288	0.6302	0.5184	0.2606	0.2911	232.1253	0.9687
289	0.4248	0.4548	0.1709	0.2443	264.1393	1.1023
290	0.6999	0.5557	0.3291	0.2522	241.3749	1.0073
291	0.5532	0.6686	0.2389	0.2439	238.5233	0.9954
292	0.5787	0.6172	0.3780	0.2663	233.8027	0.9757
293	0.4720	0.2747	0.1485	0.1831	271.3760	1.1325
294	0.6224	0.5788	0.2692	0.2930	207.7794	0.8671
295	0.6550	0.5699	0.2059	0.3384	243.5555	1.0164
296	0.6480	0.5499	0.2803	0.3288	230.5678	0.9622
297	0.5599	0.4991	0.2561	0.2912	256.5911	1.0708
298	0.6731	0.6333	0.3354	0.2925	235.6478	0.9834
299	0.3755	0.2417	0.1956	0.1674	270.7530	1.1299
300	0.5025	0.4791	0.3316	0.3000	241.9979	1.0099
301	0.5677	0.6050	0.2781	0.3094	216.5976	0.9039
302	0.4587	0.4341	0.2580	0.1742	258.1487	1.0773
303	0.3457	0.3740	0.1712	0.2576	255.2732	1.0653
304	0.6665	0.8054	0.2203	0.2670	236.5824	0.9873
305	0.6628	0.5363	0.3054	0.2917	243.1002	1.0145
306	0.6062	0.5330	0.2176	0.2317	234.0184	0.9766
307	0.4294	0.3416	0.1570	0.2334	271.5437	1.1332
308	0.5176	0.5744	0.2110	0.2575	258.1007	1.0771
309	0.6540	0.5509	0.3046	0.2460	227.0932	0.9477
310	0.6138	0.7034	0.2603	0.2930	235.7916	0.9840
311	0.4978	0.4038	0.2509	0.1538	264.5467	1.1040
312	0.5630	0.5215	0.2125	0.1738	242.3813	1.0115
313	0.5499	0.5871	0.2492	0.2572	243.2919	1.0153
314	0.5487	0.6291	0.2519	0.2663	236.5344	0.9871
315	0.5132	0.3572	0.2371	0.1984	246.6946	1.0295
316	0.6741	0.7068	0.3360	0.2874	213.4824	0.8909
317	0.5613	0.6079	0.2294	0.2608	227.7162	0.9503
318	0.6179	0.6208	0.3416	0.2625	231.8138	0.9674
319	0.5689	0.4891	0.2527	0.2139	249.4982	1.0412
320	0.4901	0.4874	0.1783	0.2603	276.5040	1.1539
321	0.4208	0.3983	0.1890	0.2137	265.9125	1.1097
322	0.6645	0.7621	0.2107	0.2571	215.5193	0.8994
323	0.6451	0.5535	0.3048	0.3276	206.1464	0.8602
324	0.4876	0.3694	0.2102	0.1315	288.4638	1.2038
325	0.6214	0.6292	0.3237	0.2590	230.1397	0.9601

The correlation coefficients between A, B, C, D and α are calculated respectively, and the results are −0.6548, −0.5583, −0.4863 and −0.5379. Obviously, the negative correlation between them are a little high.

Taking the four types of high-load working state proportions as inputs and the life coefficient α as outputs, a prediction model on α is established by different algorithms. Considering the number of datasets is only 325, Multiple linear regression (MLR), Support vector regression (SVR), and Random forest regression(RFR) are selected because of their good performance with a small amount of samples for RUL prediction.

3.3.1. MLR

MLR is used to predict the dependent variable as a linear combination of independent ones; it can map the relationship between a dependent variable and explanatory variables. The model is defined as:

$$y_i={\beta }_0+{\beta }_1{x}_{1i}+{\beta }_2{x}_{2i}+\cdots +{\beta }_k{x}_{ki}+{\epsilon }_i,\hspace{1em}i=1,2,\cdots ,n$$

(5)

where $y_i$ is response vector, $x_{ki}$ is regression matrix, ${\beta }_k$ is regression coefficient, ${\epsilon }_i$ is random error.

3.3.2. SVR

SVR is one of the applications of the Support Vector Machine (SVM). The SVM constructs a hyperplane in a high-dimensional space, which can be used for classification and regression. For a given dataset $\{(x_i,y_i), i=1,2, \cdots ,n\}$, where $x_i\in R^d, y_i\in R$, and $n$ is the capacity of samples, $x_i={\left[x_i^1,x_i^2,\cdots ,x_i^d\right]}^T$ are the input vectors, $y_i$ is the associated output value. The regression mode can be expressed as follows:

$$f\left(x\right)=\omega \widehat{A}·x+b$$

(6)

where $\omega$ is a d-dimensional vector and $b$ is the bias term.

3.3.3. RFR

RFR is an extension of the decision tree algorithm, in which decision trees are combined and each decision tree is independently trained. The training procedure was employed as follows:

(1) from the training dataset, a bootstrap sample was drawn as a randomized subset;

(2) each individual tree was grown using the randomized subset of predictor variables. Each tree model $f\left(x_i\right)$ was defined as $y_i=f\left(x_i\right)+{\epsilon }_i$. The trees were grown to the largest extent possible without pruning;

(3) repeat the step (2) until the number of trees was grown. Then the predicted results were aggregated by averaging them [26].

4. Result Analysis

The dataset of the concrete piston life prediction shown in Table 3 is randomly divided into a training set and a test set according to a ratio of 8:2. The three algorithms of MLR, SVR, and RFR are used to calculate the life coefficient α using the data of the training set. The derived α is then used to predict the life of the parts in the test set using the Formula (1) program in Python and invoking toolkits to calculate, analyze, and draw. The predicted life of the concrete piston calculated by each model is compared with the actual working life, as shown in Figure 6, Figure 7 and Figure 8.

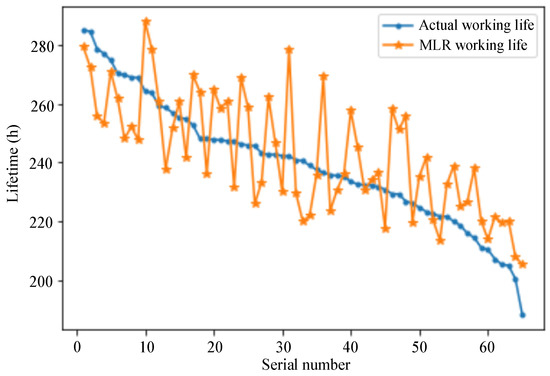
Figure 6. MLR model.

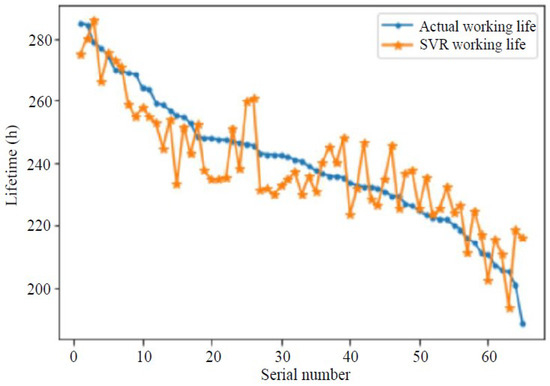
Figure 7. SVR model.

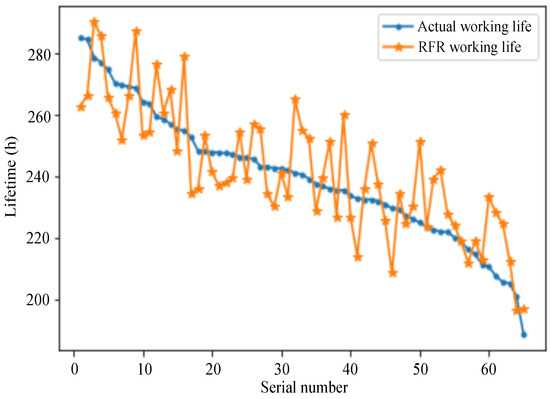
Figure 8. RFR model.

As can be seen from Figure 6, Figure 7 and Figure 8, among the three prediction models, the SVR model has the best prediction effect.

The root mean square error (RMSE), as shown in Formula (7), is used to evaluate the prediction results.

$$RMSE=\sqrt{\frac{1}{n}{{\displaystyle \sum }}_i^n{\left({\widehat{y}}_i-y_i\right)}^2}$$

(7)

where $\widehat{y}$ is the predicted capacity value, and $y$ is the real capacity value.

The RMSE refers to the square root of the mean of the square of all the errors in the estimated number $n$. A smaller RMSE value indicates a more accurate prediction.

In order to make a detailed comparison and analysis of the prediction accuracy of each model, a five-fold cross-validation is carried out. The dataset is divided into five subsets on average. Four subsets are selected as the training set and the remaining subset as the test set each time. A total of five validation calculations are carried out, and the RMSE values of each model are obtained, as shown in Figure 9. As can be seen from Figure 9, the prediction errors of each model are generally stable, among which the RMSE value of the SVR model is the lowest and the prediction effect is the best, so we chose the SVR model to predict the RUL of the concrete piston online.

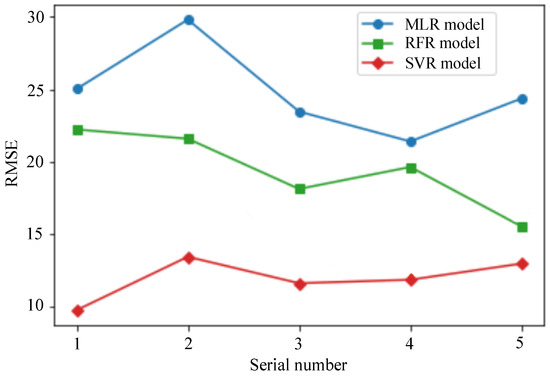
Figure 9. Comparison diagram of RMSE value of each model.

5. Dependence of RUL Prediction on Working Time

In order to further analyze the prediction effect of the life prediction model on different working times of the concrete piston, life prediction was performed at a step size of 5% of the actual working life, with a typical result of on $\alpha$ and RUL prediction shown in Table 4. In Table 4, $M_a$ is the actual RUL of the concrete piston.

Table 4. Data of a concrete piston at different life prediction points.

	0	5%	10%	15%	…	85%	90%	95%	100%
$M_0$	0	12.62	25.25	37.87	…	214.60	227.22	239.85	252.47
$M_a$	252.47	239.85	227.22	214.60	…	37.87	25.25	12.62	0
$\alpha$	1	1.0021	1.0082	1.0089	…	1.0479	1.0596	1.0778	1.1026
$M_r$	239.63	227.51	216.34	203.89	…	36.50	26.69	18.41	11.74

Three concrete pistons with an actual working life of 210, 240 and 270 h, respectively, were selected to analyze the prediction effect of the model, and all the data are calculated to draw the RMSE curve of the prediction results, as shown in Figure 10. From Figure 10a–c, it can be seen that the prediction effect is best when the actual working life reaches approximately 80%. The RUL of 325 concrete pistons is predicted using the proposed method, where the estimation error is less than 4.73%. Figure 10d shows the averaged RMSE value on the predicted RUL at different working times. It can be seen that, in the early-life stage of the concrete piston, the prediction has a large error due to less condition monitoring data. However, the prediction accuracy improves as the working time increases until the working time is at 80% of the actual working life. Then, the prediction accuracy becomes worse as the working time increases.

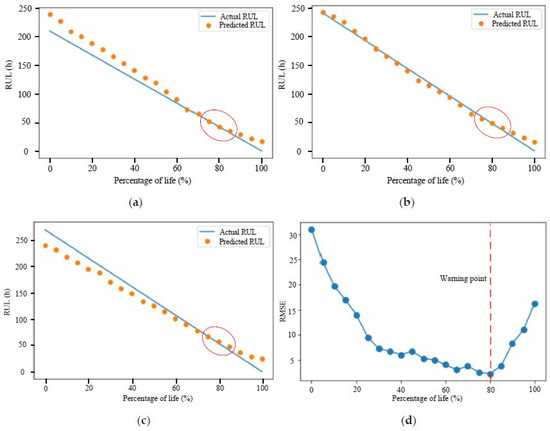
Figure 10. Prediction results. (a) Actual working life of 210 h; (b) Actual working life of 240 h; (c) Actual working life of 270 h; (d) RMSE curve.

At present, the concrete pistons of the concrete pump trucks are not replaced preventively due to the lack of supportive approaches. They are usually replaced after wearing until failure, which often leads to the unplanned downtime of the concrete pump truck, causing unnecessary economic losses and even affecting the project’s progress. To achieve preventive replacement, it is very important to choose an appropriate replacement time. Replacing too early will lead to increased costs, and replacing too late may lead to unplanned downtime. Therefore, it is necessary to develop a replacement plan when the working time is close to the actual working life and the prediction error is small. Through the research of this work, it is found that the RUL prediction model of the concrete piston based on probability statistics and data-driven methods has the best prediction effect when the concrete piston working life reaches 80% of the predicted RUL; this result can be used for the formulation of preventive replacement plans. It can be set as a replacement warning point, which can be used as the main basis for maintenance according to the situation, and a reasonable maintenance replacement and inventory management plan can be developed to reduce costs and economic losses.

6. Conclusions

This paper proposes a new method for predicting the RUL of the concrete piston based on probability statistics and data-driven methods. A life coefficient is proposed to link the actual life of individual concrete pistons and the average useful life derived from the actual replacement data of a set of concrete pistons. The life coefficient is considered to be mainly affected by the load working state, and it is found that support vector regression could provide a good estimation on the life coefficient. The RUL of 325 concrete pistons is predicted using the proposed method, where the estimation error is less than 4.73%. It is also found that that the prediction accuracy is best when the working life reaches 80% of the predicted useful life, which puts forward the replacement warning point to provide support for inventory management and a replacement plan of the concrete piston.