Abstract
Stability is a well-known challenge for rotating systems supported by hydrodynamic bearings (HDBs), particularly for the condition where the misalignment effect and the parametric uncertainty are considered. This study investigates the impact of misalignment and inherent uncertainties in bearings on the stability of a rotor-bearing system. The misalignment effect is approximately described by introducing two misaligned angles. The characteristics of an HDB, such as pressure distribution and dynamic coefficients, are calculated by the finite difference method (FDM). The stability threshold is evaluated as the intersection of run-up curve and borderline. Viscosity and clearance are considered as uncertain parameters. The generalized polynomial chaos (gPC) expansion is adopted to quantify the uncertainty in parameters by evaluating unknown coefficients. The unknown gPC coefficients are obtained by using the collocation method. The results obtained by the gPC expansion are compared with those of the Monte Carlo (MC) simulation. The results show that the characteristics of the HDB and the stability threshold are affected by misalignment and parameter uncertainties. As the uncertainty analysis using the gPC expansion is performed on a relatively small number of predefined collocation points compared with the large number of MC samples, the method is very efficient in terms of computation time.
1. Introduction
With the development of rotating machines, the hydrodynamic bearing (HDB) has attracted increasing attention as a critical component in some rotating systems. The HDB provides elastic support to the rotor and reduces wear between journal and bearing shell. However, it can also be a cause of instability in the system. Instabilities induced by an HDB are generally referred to oil whirl and oil whip [1,2,3]. These phenomena are self-excited vibrations, which often result in severe damage to the rotating system. Stability analysis is therefore crucial for maintaining safe operation of the rotor-bearing system.
Since the concept of stability threshold was realized, several studies have been conducted to determine the stability threshold speed of a rotating system. The most direct method is to observe the trajectory of the journal at different rotation speeds by experiment, whereby the stability threshold is the speed at which the trajectory starts to diverge [4,5]. Many theoretical methods have been developed on the basis of this realization. For instance, the Routh–Hurwitz criterion has been introduced to evaluate the stability threshold [6]. With this method, oil-film forces are linearized as functions of eight dynamic coefficients and coupled into the motion equation of the rotor. The stability of the system is then evaluated according to the Routh–Hurwitz stability array by considering coefficients of the characteristic equation. Abdel and Nasar [6] analyzed the whirl stability of a rotor-bearing system by using the Routh–Hurwitz criterion. They calculated the stability threshold by solving the eigenvalue problem of the rotating system. Since the real part of the eigenvalue represents the growth or decay of vibration, the stability threshold is determined when the real part of the eigenvalue is equal to zero. Based on this approach, Rho and Kim [7] predicted the stability threshold for an actively controlled HDB. Dyk et al. [8] discussed different HDB models in detail, including the Infinite Short (IS) model, the Infinite Long (IL) model, and the general finite length model, and then compared the stability threshold based on these models. Using a similar strategy, Huang et al. [9] studied the stability threshold by way of the dynamic coefficients with no coordinate transformation. Another commonly used approach is known as time series analysis, often also referred to as transient simulation [10,11,12]. As with the experimental method, in time series analysis, the stability threshold is generally estimated as the rotation speed at which the shaft leaves the steady equilibrium position. Castro et al. [3] numerically calculated the dynamic response of a rotor-bearing system during the run-up and run-down. The stability issue is determined according to the dynamic response, in which the HDB is assumed as short bearing and the bearing forces are considered as nonlinear. Smolík et al. [13] investigated both the stability threshold for a rigid rotor-bearing system using a numerical formulation and the impact of different HDB models. Furthermore, other nonlinear-theory-based methods have been employed to investigate the stability problem [14]. For instance, the numerical continuation method has been used to predict the stable and unstable limit cycles and Hopf bifurcation points [15,16]. The Liapunov direct method [17,18] or the Floquet and Bifurcation theories [19] have also been applied to analyze the stability threshold of a rotor-bearing system.
In previous studies, researchers have assumed that the center line of the journal is parallel to that of the bearing and that the rotor can be considered rigid [8,13]. Under these simplified conditions, the misalignment effect is neglected. However, in practical situations, the misalignment phenomenon is unavoidable for a number of reasons, such as deflection of the shaft, manufacturing error, or improper installation. Further, it is observed from the governing equation of the lubricated oil-film pressure that the pressure is determined by the thickness of the oil-film, while the thickness changes in the presence of the misalignment effect. Under this recognition, the misalignment effect is gradually taken into consideration. Sun and Changlin [20] studied the steady characteristics of an HDB considering the misalignment caused by deflection of the shaft. Herein, the misalignment effect is described by introducing two misaligned angles. The results show that the maximum pressure and the oil-film forces apparently vary with the misaligned angles. Zhang et al. [21] investigated the relationship between the load-carrying capacity and the misalignment angle for a misaligned water-lubricated HBD under different bearing parameters. Ebrat et al. [22] and Xu et al. [23] studied the influence of misalignment on the dynamic characteristics of an HDB. It can be concluded from these explorations that the characteristics of an HDB and the stability of the rotor-bearing system are affected by misalignment. Therefore, it is essential to consider the misalignment effect in a stability analysis of a rotor-bearing system. When the effect of misalignment is considered, there exist additional moments in the rotor-bearing system. In order to describe these moments, some researchers introduced the moments coefficients for a misaligned system [24,25]. However, after evaluating the moments’ coefficients, Mukherjee [26] and Rao [27] pointed out that the moments’ coefficients are generally insignificant and have little impact on the dynamic behavior of journal bearings. Further, the research of Ahmend and El-Shafei [28] demonstrated that the moments’ coefficients are much smaller than the force coefficients. Based on this evaluation, the moments’ coefficients are neglected in the following research [29]. Therefore, the stability analysis for a misaligned rotor-bearing system in this study only considers the conventional eight dynamic coefficients.
In addition, most previous research focused on deterministic analysis and ignored the inherent uncertainties in rotor-bearing systems caused by such factors as variations in wear and operating conditions. In such situations, the characteristics of the HDB, the dynamics response, and the stability of the rotor-bearing system all become uncertain due to the random nature of the input parameters. Hence, the effect of random parameters should also be taken into account to ensure the reliability of the system. In recent years, some uncertain quantification methods are introduced to evaluate the uncertainty in the rotor systems, such as interval methods [30,31], fuzzy models [32], probabilistic techniques [33,34], and hybrid approaches [35]. The selection of these methods depends on the available information of the uncertain system. In this study, it is assumed that the statistical information of the system has been obtained, which corresponds to the probabilistic approach and assumes aleatoric uncertainties. In this condition, several approaches have been developed to quantify the uncertainty, including sampling- and non-sampling-based methods. Monte-Carlo (MC) simulation is a conventional sampling-based method that addresses the stochastic problem. Generally, MC simulation can quantify the effect of uncertainty on dynamic response with considerable accuracy. However, this method converges only slowly and is thus rather inefficient, particularly for complex dynamic systems. In stability analysis, the computational costs of uncertainty quantification using MC simulation are acceptable when adopting simplified HDB models, such as IS and IL. Since these simplified models allow the analytical solution to be obtained for the characteristics of HDB, they can compensate for the high computational cost of MC simulation. Some related studies can be found in [36,37]. The behavior of the general finite-length HDB is governed by the Reynolds equation and is usually solved numerically. Uncertainty quantification using MC simulation would, in this case, become computationally very expensive. To achieve better computational efficiency, various non-sampling-based methods, such as generalized polynomial chaos (gPC) expansion, have received much attention in recent years [38,39,40]. In the gPC expansion method, the uncertain parameters are represented by a series of orthogonal polynomials with unknown coefficients [41,42]. Recently, Garoli et al. [43] demonstrated the application of the gPC expansion in a stochastic dynamic response analysis of a nonlinear rotor-bearing system, in which the nonlinear bearing forces are obtained using the IS model.
The literature review reveals that researchers have, for the most part, conducted deterministic stability analyses of rotor-bearing systems. However, a few studies are available that investigate the issue of uncertain stability on the basis of a simplified HDB model using a sampling-based method, such as MC simulation, but without considering the misalignment effect. This study reports an uncertain stability analysis for a rotor system supported by finite-length HDBs while taking into account the misalignment effect. We develop a stability analysis framework guided by the Routh–Hurwitz criterion. The characteristics of the HDB used for stability analysis are evaluated by solving the Reynolds equation numerically. Collocation-based gPC expansion is employed to determine the impact of uncertainties.
The paper is organized as follows: The next section introduces the theoretical background on characteristics of the general finite-length HDB. The process of determining the stability threshold is presented in Section 3, and the uncertain stability analysis based on the gPC expansion is presented in Section 4. Section 5 presents the numerical results of a rotor-bearing system under uncertainty. The paper’s conclusion then follows.
2. Governing Equations and Dynamic Coefficients
2.1. Reynolds Equation
The general HDB under consideration and the associated terminology are presented in Figure 1. A thin oil-film is sandwiched between the bearing shell and the rotating journal. Due to the relative motion of the two parts, pressure is generated in the oil-film that allows the HDB to provide support to the journal. Here, the support is commonly referred to as the bearing force. Due to the bearing forces and applied external load, the journal center displays an eccentricity e with respect to the bearing center . The position of the journal is usually determined by two coordinate systems, and , of which the former describes the journal center in terms of its eccentricity displacement and angle, and and the latter are the fixed horizontal and vertical coordinates.
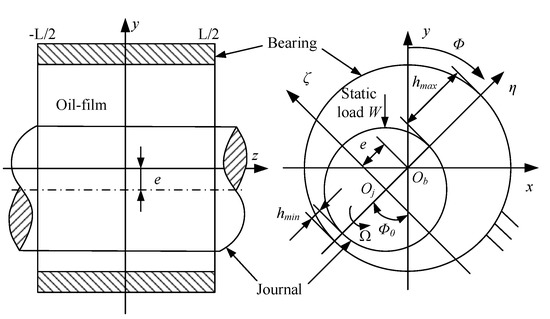
Figure 1.
General HDB and associated terminology.
The pressure of the oil-film is governed by the Reynolds equation derived from the Navier–Stokes equations [44], in which the lubricant oil is assumed to be a laminar, isothermal, and incompressible flow. The Reynolds equation is stated as in [45]
where p represents the oil-film pressure; R stands for the radius of the bearing; is the viscosity of the lubricant oil; and z represent the coordinates in circumferential and axial directions, respectively; is the rotation speed of the rotor; and are the velocity components of the rotating journal; and h denotes the thickness of the oil-film. According to the generally accepted Reynolds boundary conditions [46], the boundary of the oil-film begins approximately at the maximum film thickness and ends at the position where the pressure equals zero. In general, the thickness of the oil-film in a bearing without considering the misalignment effect is expressed approximately as [20]
in which c stands for the clearance; e represents the eccentricity; and denotes the attitude angle, which is used to depict the angle between the direction of the static load and the eccentricity line at equilibrium position. When the misalignment effect is considered, Equation (2) is no longer appropriate for describing the thickness of the oil-film since the thickness in axial direction has changed. The thickness is then given by introducing two misaligned angles as [20,23,47,48,49]
where is the eccentricity at mid-plane, and and are misaligned angles of rotor in the x-y plane and y-z planes, respectively, as shown in Figure 2.
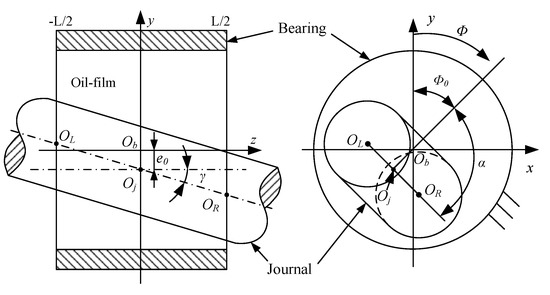
Figure 2.
Schematic diagram of a misaligned HDB.
The following dimensionless parameters are introduced to simplify computation
where is named as the eccentricity ratio. The reformulated Reynolds equation is rewritten by considering the dimensionless parameters as
The finite difference method (FDM) is adopted to solve the pressure of the lubricant oil. An over-relaxation iteration technique is employed to achieve good convergence of the solution [46]. Once the pressure has been computed, the bearing forces in the x- and y-directions are obtained by integrating the pressure over the whole area of the oil-film
where is the coefficient containing the parameters of the bearing. Theoretically, the vertical oil-film force should equal the static load W with the horizontal force equal to zero at the equilibrium position for the horizontal rotor. Accordingly, the following condition should be satisfied [46]
However, is not usually equal to zero, since the attitude angle is unknown before calculation. To reach the equilibrium position and to calculate the bearing forces accurately, the following procedures are adopted to determine the attitude angle. First, a predefined value is assumed as the initial attitude angle to calculate the initial bearing forces. Then, an error function is defined as
where k represents the kth iteration. The attitude angle is updated by a Newton–Raphson iteration such as
Eventually, the attitude angle is determined by using Equations (8) and (9) alternately, until Equation (7) is satisfied. The stopping criterion of the Newton–Raphson iteration is based on the error at the kth iteration. The attitude angle is determined if is satisfied, where is a prescribed error tolerance. The pressure distribution and the oil-film forces at equilibrium position are obtained. The Sommerfeld number representing the relationship of the major variables in the hydrodynamic lubrication analysis is calculated by
2.2. Dynamic Coefficients
According to Lund [45], the bearing forces are described by eight dynamic coefficients referring to the displacement and velocity. To calculate the dynamic coefficients, the bearing forces are characterized by reserving the first-order terms of a Taylor series expansion around the equilibrium position, i.e., [8,50]
in which and represent the bearing forces at the equilibrium position. The coefficients of displacement and velocity components are defined as dynamic coefficients in the form of
Conventionally, the following dimensionless form is adopted in the stability analysis
Similar to the bearing forces, the pressure of the oil-film under dynamic conditions is expanded as
where represents the pressure at the equilibrium position; indicates the increment of pressure caused by displacement and velocity under dynamic conditions; and , , , and are the corresponding perturbation pressures with respect to the displacement and velocity vectors . Further, the thickness of the oil-film is written as
By substituting Equations (14) and (15) into the Reynolds equation, five dimensionless equations are obtained as
The dynamic coefficients are estimated by integrating the perturbation pressures as
3. Stability Analysis
According to Krämer [51], the stability threshold for a specific rotor-bearing system is described by the intersection of the run-up curve and borderline. The run-up curve characterizes the eccentricity ratio at equilibrium position for different rotation speeds. The borderline indicates the rotation speed on the boundary of stability for different eccentricity ratios in dynamic conditions.
3.1. Run-Up Curve
For a symmetrical and horizontal rotor supported by two identical HDBs, it is known that the bearing forces equal the static load at equilibrium position (i.e., and ) [8,46]. Meanwhile, it can be seen from Equation (6) that the bearing forces are functions of rotation speed and eccentricity ratio. It is thus possible to plot the run-up curve depicting the relationship between rotation speed and eccentricity ratio. The rotation speed thus obtained is denoted by and expressed as
where and are bearing forces in the y direction of different dimensionless forms, and
3.2. Borderline and Stability Threshold
This paper considers a rotor-bearing system, as shown in Figure 3.
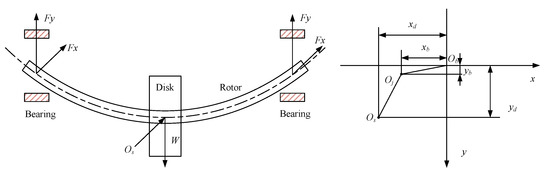
Figure 3.
Diagram of a rotor-bearing system and coordinates in the x-y plane.
Taking into account the flexibility of the rotor and referring to the coordinates shown in Figure 3, the motion is expressed as [51,52]
where m represents the mass of the rotor and disk; denotes the eccentricity of the unbalance mass; is the parameter used to describe the flexibility of the rotor; {} and {} represent the displacement components of the journal and disk center, respectively; and {} stands for the acceleration components of the disk center. In addition, combining with the linear bearing forces gives us [51]
The solutions of the homogeneous Equation (20) can be written in the form of
The characteristic equation for the system described by Equation (20) together with Equation (21) is then obtained by referring to Equation (22), as
in which are polynomials, as shown in Appendix A. The eigenvalue comprises the real part a and imaginary part as
At stability boundary, is purely imaginary, i.e., and . Thus, the rotation speed on the borderline denoted by is determined by [51]
where stands for the natural frequency of the flexible shaft, () represent polynomials as shown in Appendix A, and () are functions of the dimensionless dynamic coefficients shown in Equation (13). Meanwhile, it is known from Section 2 that dynamic coefficients are functions of the eccentricity ratio . It is therefore possible to conclude that is a function of by combining with Equation (25). Using this approach, it is possible to determine the borderline.
Finally, the deterministic stability analysis procedure is summarized as Algorithm 1.
| Algorithm 1 Deterministic stability analysis of rotor-bearing system |
|
4. Uncertainty Quantification
It was shown in the previous section that the stability threshold is affected by the parameters of the rotor-bearing system. The stability threshold is uncertain owing to the existence of inherent random parameters. In this situation, the uncertain stability threshold needs to be quantified to ensure that the rotating system is operating reliably. In view of the high computational costs of solving the characteristics of the finite-length HDB, the gPC expansion is employed to quantify uncertainty. The basic idea of a gPC expansion is to project a random variable onto a stochastic space, such that uncertain variables are represented by a series of orthogonal polynomials with unknown deterministic coefficients. Here, an uncertain variable Y defined in the random space is represented as
where denotes the unknown coefficients, represents the polynomials that are functions of the standard random variable vector , and N represents the finite number of truncated terms in the gPC expansion. This is identified from the expansion order m and the dimensionality n of the random vectors as
In general, the unknown deterministic coefficients are determined by a Galerkin projection
where stands for the inner product of the polynomials and represents the joint probability density function (PDF) of the vectors of random variables.
4.1. Determination of Orthogonal Polynomial Basis
If there is only one random variable (i.e., ), the gPC expansion for the random output can be directly constructed using Equation (26), where the orthogonal basis is the same as for the random input variable. However, the orthogonal basis for a multidimensional random vector results in tensor products of different polynomials representing each uncertain variable. For instance, let the random input variable follow the normal distribution with corresponding Hermite polynomials as , and let follow a uniform distribution represented by Legendre polynomials denoted as . Then, the polynomials of the random output are obtained by (cf. [41] for more details)
When the above random two-dimensional system (i.e., ) is used for a second-order gPC expansion (i.e., ), the orthogonal polynomials are represented as
The uncertain parameter Y is then approximated as
4.2. Calculation of Unknown Coefficients Using the Collocation Method
The collocation method is adopted [42] to determine the unknown coefficients in Equation (31). In this method, the numerical model is considered a black box. The responses at the collocation points are evaluated using the deterministic numerical model. The coefficients of the gPC expansion are then determined from these samples using a least squares minimization technique. The selection of the collocation points is critical for the accurate evaluation of the unknown coefficients. Once the order of the gPC expansion is known, the collocation points are generated as all combinations of roots of the next-higher-order polynomial basis. The origin (i.e., ) is added if it is not already included in the roots [42]. It is assumed that a set of response samples is generated at the collocation points . Substituting these in the gPC expansion of Y yields the following system of linear equations for calculating the coefficient vector as
where
The number of collocation points, q, is greater than the number of unknown coefficients for . The vector of coefficients, , is calculated using a least squares minimization technique as
4.3. Uncertain Stability Analysis
In this study, the viscosity and clearance c are considered random input parameters and represented by truncated gPC expansions as
Under the influence of the random input parameters, the static and dynamic characteristics of HDB become uncertain, as does the stability threshold of the coupled rotating system. On this basis, the uncertain characteristics of HDB, such as and , and the uncertain stability threshold are approximated by truncated gPC expansions as
where () represents the eccentricity ratio dependency. The step-by-step procedure for analyzing the stability of the rotor-bearing system under uncertainty is then summarized as Algorithm 2.
| Algorithm 2 Stability analysis of rotor-bearing system under uncertainty |
|
5. Numerical Study
The numerical study consists of two parts. In the first part, the characteristics of HDB are calculated and compared with published papers for validation. The results calculated are then used to conduct a stability analysis. In the second part, the influence of uncertainty on stability is investigated by applying gPC expansion. The accuracy of the gPC expansion is confirmed by comparing the results with those of a MC simulation.
The numerical study adopts the rotor-bearing systems, as shown in Figure 3. Table 1 shows the parameters of the rotor-bearing system. For the random input parameters, considering that the viscosity varies with variations in ambient temperature, it is assumed that viscosity is normally distributed. Clearance is considered to have uniform distribution due to the wear and deformation of the bearing shell and the journal. The statistical details of the random parameters are presented in Table 2.

Table 1.
Parameters of rotor-bearing system.

Table 2.
Details of distribution of random parameters.
5.1. Deterministic Analysis and Validation
5.1.1. Validation without Considering the Misalignment Effect
Using the present formulation, the static and dynamic characteristics of an HDB are calculated at a constant rotation speed of . To verify the present implementation, the results available from papers [45,46] are presented for comparison. The attitude angle and the Sommerfeld number S in terms of the eccentricity ratio are presented in Figure 4. The maximum pressures under various eccentricity ratios are listed in Table 3. These results show that the attitude angle and Sommerfeld number decrease as the eccentricity ratio increases, at a constant rotation speed, whereas the maximum pressure displays the opposite behavior.
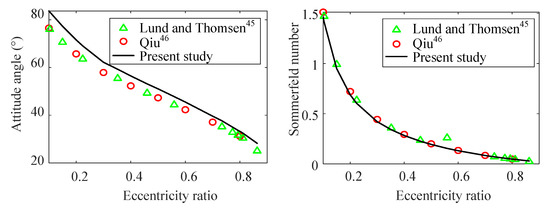
Figure 4.
Attitude angle and Sommerfeld number compared with references [45,46].

Table 3.
Maximum pressure for various eccentricity ratios.
The dimensionless dynamic coefficients are shown in Figure 5. The results are in good agreement with those of the references. This indicates that the present implementation produces reliable results, validating it for further use in this investigation.
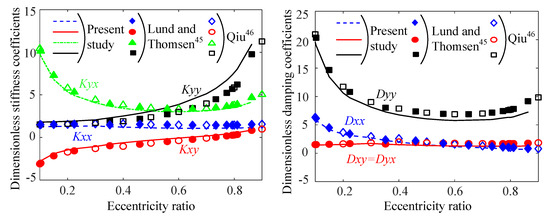
Figure 5.
Dimensionless stiffness and damping coefficients and comparison with references [45,46].
5.1.2. Validation for the Misalignment Effect
The above results are calculated while disregarding the misalignment effect. To clarify the impact of the misalignment effect, the parameters of the HDB provided by Sun and Changlin [20] are adopted for calculation. The parameter details are displayed in Table 4.

Table 4.
Parameters of HDB provided by Sun and Changlin [20].
Accordingly, the maximum pressures are calculated under various misaligned angles and shown in Table 5; they demonstrate that misalignment has a significant effect on maximum pressure. The results are compared with those presented by Sun and Changlin [20]. The comparison shows good agreement.

Table 5.
Maximum pressure taking into consideration the misalignment effect.
5.1.3. Stability Analysis
Next, the stability threshold is determined using the new implementation verified above. The parameters of the rotor-bearing system are adopted from Table 1. The misaligned angles are set as . Figure 6 shows the run-up curve and borderline calculated for both misaligned and aligned situations. These curves are used to determine the stability threshold of the rotor-bearing system. The run-up curves in both situations show that the eccentricity ratio decreases as the rotation speed increases. This implies that the journal center moves towards the bearing center (Figure 1) as the rotation speed increases.
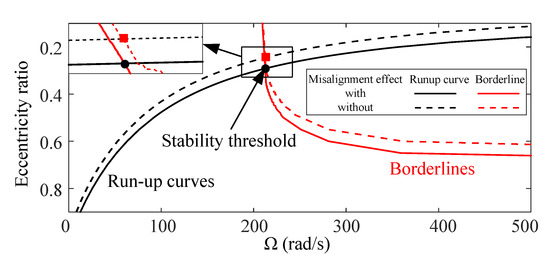
Figure 6.
The influence of the misalignment effect on run-up curve and borderline.
In the case of the borderline, the rotation speed increases as the eccentricity ratio increases. Moreover, it is observed that the gradient () increases with the increment of the eccentricity ratio.
By comparing the results from the misaligned and aligned conditions, it is observed that misalignment has an obvious influence on the run-up curve. The impact of misalignment varies over different parts of the borderline. It is observed that the impact is negligible when the eccentricity ratio remains small (approximately ), whereas it is evident for larger eccentricity ratios (approximately ). Furthermore, the intersections between the respective run-up curves and borderlines, i.e., the stability thresholds, are and under misaligned and aligned situations, respectively. To investigate the influence of the misaligned angle on the threshold, the thresholds are calculated under various misaligned angles, as listed in Table 6. It is found that the thresholds in the misaligned situation are greater than those in the aligned situation. In addition, the threshold increases as the misaligned angle increases. This implies that the misalignment improves the stability of the rotor-bearing system, which results in the same conclusion as that given by Qiu [46].

Table 6.
Threshold for various misaligned angles.
5.2. Uncertainty Analysis
A third-order gPC expansion is employed to represent the uncertain output, in which . Since the random parameters follow a normal and uniform distribution, the orthogonal polynomials of the system output are determined as the tensor products of Hermite and Legendre polynomials. The roots of the fourth-order Hermite polynomial are , while those of the Legendre polynomial are . By adding zero to the roots, 25 collocation points are produced with which to calculate the responses. These responses are used to determine the ten unknown coefficients by the least squares method. For uncertain parameters varying with the eccentricity ratios, such as the maximum pressure and dynamic coefficients, the responses and coefficients of the gPC expansion are calculated at different eccentricity ratios. To validate the accuracy of the constructed gPC expansion, the uncertainty analysis is also carried out by way of an MC simulation with 1000 samples. The convergence of the MC simulation is shown in Figure 7.
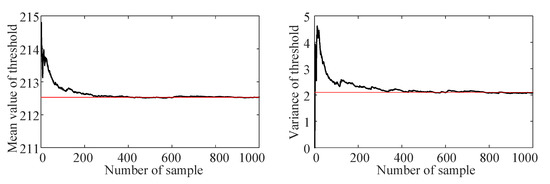
Figure 7.
Convergence of MC simulation.
It can be seen that the mean value and the variance of the stability threshold are well converged after adopting 500 samples, which shows that these results are suitable for validation use.
5.2.1. Characteristics of HDB under Uncertainty
As the characteristics of HDB vary with the eccentricity ratio, the probability distribution and mean values of static characteristics at are evaluated by the gPC expansion, as shown in Figure 8. The results obtained by the MC simulation are plotted in the same graph. It is observed that the distributions vary with the eccentricity ratio. The values corresponding to the maximum probability for each variable differ from their mean values. Some results show a limited agreement with the MC simulation, such as the PDF of at and at . This phenomenon results from the numerical iteration [53]. For a random system with an analytic expression avoiding the iterative approach, the consistency will be better. Generally, the PDF and mean values obtained by gPC expansion display good accordance with those obtained by the MC simulation. This indicates that the constructed third-order gPC expansion is accurate enough to approximate the random outputs. Furthermore, it is clearly known that the number of collocation points required for gPC expansion is much smaller than the number of sampling points required for MC simulation of similar accuracy.
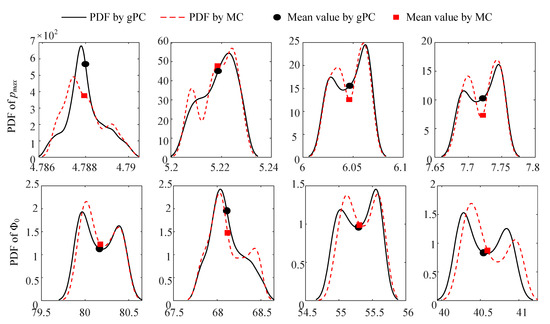
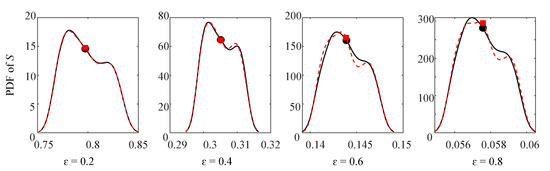
Figure 8.
PDF and mean values of maximum pressure of oil-film (unit: bar), attitude angle (unit: ), and Sommerfeld number at by gPC expansion and MC simulation.
Figure 9 shows the mean values of each variable with different eccentricity ratios, for the dimensionless dynamic coefficients. To illustrate the influence of random parameters, the values corresponding to the confidence interval are also plotted. It is revealed, for small eccentricity ratios, that the confidence intervals have a wider band for and large ratios for . This is because the sharp change in these dynamic coefficients for these regions makes them more sensitive to the eccentricity ratio.
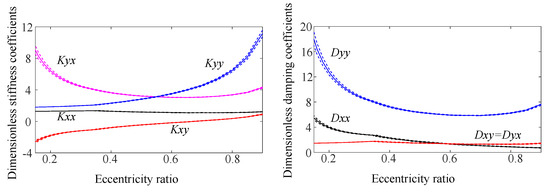
Figure 9.
Mean values of dimensionless dynamic coefficients by gPC expansion and their 95% confidence intervals plotted with dashed lines as the boundary.
5.2.2. Stability Threshold under Uncertainty
The mean values and the confidence intervals of the run-up curve and the borderline are shown in Figure 10. It is observed that the run-up curve is more sensitive to the random parameters than the borderline. It is also found that an intersection of the run-up curve and borderline may occur at any point within the region bounded by their 95% confidence intervals. The bounded region is surrounded by black and red dashed lines, respectively. This represents the possible zone within which the stability threshold can fall.
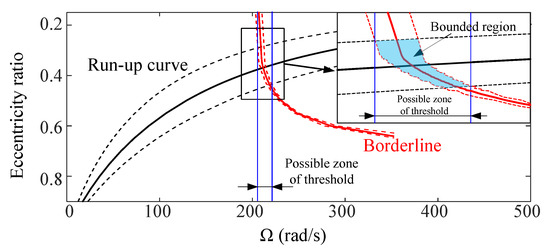
Figure 10.
Mean values of run-up curve and borderline by gPC expansion and their 95% confidence intervals plotted with dashed lines as the boundary.
The PDF, mean value, and 95% confidence interval of the stability threshold are evaluated using the gPC expansion, as presented in Figure 11. The PDF matches well with that of the MC simulation. The mean values of the stability threshold obtained by the gPC expansion and by MC simulation are and , respectively. These values are close to the deterministic result. However, the mean value of the stability threshold lies outside the maximum probability region. The 95% confidence interval of the stability threshold is from to , which means that the system should avoid this region during operation.
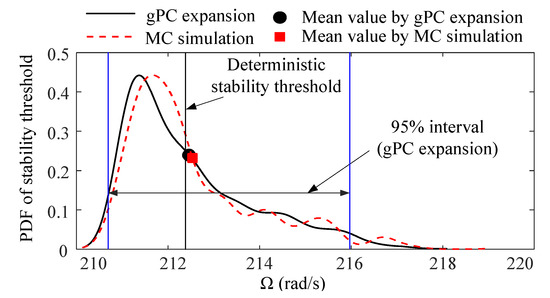
Figure 11.
PDF of stability threshold by gPC expansion and MC simulation.
6. Conclusions
This paper has presented a stability analysis of a rotor-bearing system taking into consideration the misalignment effect and uncertainty in a finite-length HDB. Determination of the stability threshold is guided by the Routh–Hurwitz method. The gPC expansion is used to quantify the impact of uncertainty. The characteristics of the HDB used to determine the stability threshold are calculated by numerical solving of the governing equations. The accuracy of the results is verified by comparison with those published in previous papers. The misalignment effect is investigated by introducing two misaligned angles in the expression of thickness of the oil-film. The results show that misalignment has a remarkable effect on the characteristics of the HDB and the run-up curve. The impact of misalignment on the borderline is negligible for a small eccentricity ratio, but evident for a larger eccentricity ratio. Moreover, the stability threshold increases as the misaligned angles increase. To study the influence of uncertainties on the stability threshold, clearance and viscosity are assumed as random parameters with predefined distribution. Using the collocation method, the gPC expansion is constructed by solving the responses at a series of specific collocation points using the deterministic code. MC simulation is implemented as a validation. The results show that the stability threshold becomes uncertain since the random input parameters can affect the static and dynamic characteristics of the system. By comparing the evaluated statistical properties of random outputs, it is apparent that gPC expansion is able to approximate the random parameters with reasonable accuracy. The results also illustrate that gPC expansion is more efficient, since it requires far fewer sample realizations.
In this study, the bearing force is considered linear and an analytical rotor is employed for the stability analysis. These are the main limitations of this study, which might limit its significance for direct industrial application. However, according to the previous studies, it is suggested that the developed framework is suitable to understand the performance of the rotor-bearing system. In addition, the interdisciplinary approach of combining stability analysis, misalignment effect, and uncertainty analysis using a gPC approach builds a bridge between these subjects. In the future, the nonlinear behavior of physical quantities and a complex rotor model will be simulated and investigated experimentally to close the gap between the purely numerical approach and a real physical model.
Author Contributions
Conceptualization, X.S.; methodology, X.S.; formal analysis, X.S.; writing—original draft preparation, X.S.; writing—review and editing, X.S., K.K.S. and S.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
Sourav Chandra is acknowledged for his suggestions regarding paper writing. The first author wishes to acknowledge the support received from the China Scholarship Council (File No. 201806450023).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HDB | Hydrodynamic bearing |
| FDM | Finite difference method |
| FEM | Finite element method |
| gPC | Generalized polynomial chaos |
| MC | Monte Carlo |
References
- Muszynska, A. Stability of whirl and whip in rotor/bearing systems. J. Sound Vib. 1988, 127, 49–64. [Google Scholar] [CrossRef]
- El-Shafei, A.; Tawfick, S.H.; Raafat, M.S.; Aziz, G.M. Some experiments on oil whirl and oil whip. ASME. J. Eng. Gas Turbines Power 2007, 129, 144–153. [Google Scholar] [CrossRef]
- De Castro, H.F.; Cavalca, K.L.; Nordmann, R. Whirl and whip instabilities in rotor-bearing system considering a nonlinear force model. J. Sound Vib. 2008, 317, 273–293. [Google Scholar] [CrossRef]
- Newkirk, B. Oil film whirl—An investigation of disturbances due to oil films in journal bearings. Trans. ASME 1956, 78, 21–27. [Google Scholar]
- Tondl, A. Experimental investigation of self-excited vibrations of rotors due to the action of lubricating oil film in journal bearings. Wear 1962, 5, 136–147. [Google Scholar] [CrossRef]
- El-Marhomy, A.A.; Abdel-Sattar, N.E. Stability analysis of rotor-bearing systems via Routh-Hurwitz criterion. Appl. Energy 2004, 77, 287–308. [Google Scholar] [CrossRef]
- Rho, B.; Kim, K.W. The effect of active control on stability characteristics of hydrodynamic journal bearings with an axial groove. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2002, 216, 939–946. [Google Scholar] [CrossRef]
- Dyk, Š.; Rendl, J.; Byrtus, M.; Smolík, L. Dynamic coefficients and stability analysis of finite-length journal bearings considering approximate analytical solutions of the Reynolds equation. Tribol. Int. 2019, 130, 229–244. [Google Scholar] [CrossRef]
- Huang, Y.; Tian, Z.; Chen, R.; Cao, H. A simpler method to calculate instability threshold speed of hydrodynamic journal bearings. Mech. Mach. Theory 2017, 108, 209–216. [Google Scholar] [CrossRef]
- Zhao, S.; Xu, H.; Meng, G.; Zhu, J. Stability and response analysis of symmetrical single-disk flexible rotor-bearing system. Tribol. Int. 2005, 38, 749–756. [Google Scholar] [CrossRef]
- Yadav, S.K.; Rajput, A.K.; Ram, N.; Sharma, S.C. Stability analysis of a rigid rotor supported by two-lobe hydrodynamic journal bearings operating with a non-Newtonian lubricant. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2019, 233, 884–898. [Google Scholar] [CrossRef]
- Wang, Y.; Xiong, X.; Hu, X. Vibration and Stability Analysis of a Bearing–Rotor System with Transverse Breathing Crack and Initial Bending. Machines 2021, 9, 79. [Google Scholar] [CrossRef]
- Smolík, L.; Rendl, J.; Dyk, Š.; Polach, P.; Hajžman, M. Threshold stability curves for a nonlinear rotor-bearing system. J. Sound Vib. 2019, 442, 698–713. [Google Scholar] [CrossRef]
- Chouchane, M.; Amamou, A. Bifurcation of limit cycles in fluid film bearings. Int. J. Non-Linear Mech. 2011, 46, 1258–1264. [Google Scholar] [CrossRef]
- Sghir, R.; Chouchane, M. Nonlinear stability analysis of a flexible rotor-bearing system by numerical continuation. J. Vib. Control 2016, 22, 3079–3089. [Google Scholar] [CrossRef]
- Amamou, A.; Chouchane, M. Nonlinear stability analysis of long hydrodynamic journal bearings using numerical continuation. Mech. Mach. Theory 2014, 72, 17–24. [Google Scholar] [CrossRef]
- El-Marhomy, A.A.J.; Schlack, A.L. Dynamic stability of elastic rotor-bearing systems via Liapunov’s direct method. J. Appl. Mech. 1991, 58, 1056–1063. [Google Scholar] [CrossRef]
- Al-Hussain, K. Dynamic stability of two rigid rotors connected by a flexible coupling with angular misalignment. J. Sound Vib. 2003, 266, 217–234. [Google Scholar] [CrossRef]
- Kim, Y.; Noah, S. Bifurcation analysis for a modified jeffcott rotor with bearing clearances. Nonlinear Dyn. 1990, 1, 221–241. [Google Scholar] [CrossRef]
- Sun, J.; Changlin, G. Hydrodynamic lubrication analysis of journal bearing considering misalignment caused by shaft deformation. Tribol. Int. 2004, 37, 841–848. [Google Scholar] [CrossRef]
- Zhang, X.; Yin, Z.; Jiang, D.; Gao, G.; Wang, Y.; Wang, X. Load carrying capacity of misaligned hydrodynamic water-lubricated plain journal bearings with rigid bush materials. Tribol. Int. 2016, 99, 1–13. [Google Scholar] [CrossRef]
- Ebrat, O.; Mourelatos, Z.P.; Vlahopoulos, N.; Vaidyanathan, K. Calculation of journal bearing dynamic characteristics including journal misalignment and bearing structural deformation. Tribol. Trans. 2004, 47, 94–102. [Google Scholar] [CrossRef]
- Xu, G.; Zhou, J.; Geng, H.; Lu, M.; Yang, L.; Yu, L. Research on the static and dynamic characteristics of misaligned journal bearing considering the turbulent and thermohydrodynamic effects. ASME. J. Tribol. 2015, 137, 024504. [Google Scholar] [CrossRef]
- Yu, H.; Adams, M.L. The linear model for rotor-dynamic properties of journal bearings and seals with combined radial and misalignment motions. J. Sound Vib. 1989, 131, 367–378. [Google Scholar] [CrossRef]
- Feng, H.; Jiang, S.; Ji, A. Investigations of the static and dynamic characteristics of water-lubricated hydrodynamic journal bearing considering turbulent, thermohydrodynamic and misaligned effects. Tribol. Int. 2019, 130, 245–260. [Google Scholar] [CrossRef]
- Mukherjee, A.; Rao, J.S. Stiffness and damping coefficients of an inclined journal bearing. Mech. Mach. Theory 1977, 12, 339–355. [Google Scholar] [CrossRef]
- Rao, J.S. Rotor Dynamics, 3rd ed.; New Age International (P) Limited: New Delhi, India, 2009; p. 191. [Google Scholar]
- Ahmed, A.M.; El-Shafei, A. Effect of misalignment on the characteristics of journal bearings. J. Eng. Gas Turbine. Power 2008, 130, 042501. [Google Scholar] [CrossRef]
- Rao, T. Stability characteristics of misaligned journal bearing. Adv. Vib. Eng. 2012, 11, 361–369. [Google Scholar]
- Fu, C.; Ren, X.; Yang, Y.; Xia, Y.; Deng, W. An interval precise integration method for transient unbalance response analysis of rotor system with uncertainty. Mech. Syst. Signal Process. 2018, 107, 137–148. [Google Scholar] [CrossRef]
- Fu, C.; Ren, X.; Yang, Y.; Lu, K.; Wang, Y. Nonlinear response analysis of a rotor system with a transverse breathing crack under interval uncertainties. Int. J. Non-Linear Mech. 2018, 105, 77–87. [Google Scholar] [CrossRef]
- Qiu, Y.; Singiresu, S.R. A fuzzy approach for the analysis of unbalanced nonlinear rotor systems. J. Sound Vib. 2005, 284, 299–323. [Google Scholar] [CrossRef]
- Griffini, D.; Salvadori, S.; Carnevale, M.; Montomoli, F. Uncertainty Quantification in Hydrodynamic Bearings. Energy Procedia 2018, 148, 884–891. [Google Scholar] [CrossRef]
- Didier, J.; Sinou, J.J.; Faverjon, B. Study of the non-linear dynamic response of a rotor system with faults and uncertainties. J. Sound Vib. 2012, 331, 671–703. [Google Scholar] [CrossRef] [Green Version]
- Fu, C.; Xu, Y.; Yang, Y.; Lu, K.; Gu, F.; Ball, A. Response analysis of an accelerating unbalanced rotating system with both random and interval variables. J. Sound Vib. 2020, 466, 115047. [Google Scholar] [CrossRef]
- Visnadi, L.B.; De Castro, H.F. Influence of bearing clearance and oil temperature uncertainties on the stability threshold of cylindrical journal bearings. Mech. Mach. Theory 2019, 134, 57–73. [Google Scholar] [CrossRef]
- Visnadi, L.B.; De Castro, H.F. Uncertainty analysis on stability of a rigid rotor with hydrodynamic bearings. In Proceedings of the ICVRAMISUMA uncertainties Congress, Curitiba, Brazil, 3–8 December 2017. [Google Scholar]
- Kronowetter, F.; Moheit, L.; Eser, M.; Sepahvand, K.K.; Marburg, S. Spectral Stochastic Infinite Element Method in Vibroacoustics. J. Theor. Comput. Acoust. 2020, 28, 2050009. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, W.; Sepahvand, K.K.; Wei, Y.; Marburg, S. A Three-Dimensional Ring Model for Uncertainty Quantification in Natural Frequencies and Sound Radiation Characteristics of Tires. J. Theor. Comput. Acoust. 2020, 28, 2050016. [Google Scholar] [CrossRef]
- Chikhaoui, K.; Bitar, D.; Kacem, N.; Bouhaddi, N. Robustness analysis of the collective nonlinear dynamics of a periodic coupled pendulums chain. Appl. Sci. 2017, 7, 684. [Google Scholar] [CrossRef]
- Sepahvand, K.; Marburg, S.; Hardtke, H.-J. Uncertainty quantification in stochastic systems using polynomial chaos expansion. Int. J. Appl. Mech. 2010, 2, 305–353. [Google Scholar] [CrossRef]
- Chandra, S.; Sepahvand, K.; Matsagar, V.; Marburg, S. Stochastic dynamic analysis of composite plate with random temperature increment. Compos. Struct. 2019, 226, 111159. [Google Scholar] [CrossRef]
- Garoli, G.Y.; De Castro, H.F. Analysis of a rotor-bearing nonlinear system model considering fluid-induced instability and uncertainties in bearings. J. Sound Vib. 2019, 448, 108–129. [Google Scholar] [CrossRef]
- Pinkus, O.; Sternlicht, B. Theory of Hydrodynamic Lubrication; McGraw-Hill: New York, NY, USA, 1961. [Google Scholar]
- Lund, J.; Thomsen, K. A calculation method and data for the dynamic coefficients of oil-lubricated journal bearings. In Topics in Fluid Film Bearing and Rotor Bearing System Design and Optimization; American Society of Mechanical Engineers: New York, NY, USA, 1978; pp. 1–28. [Google Scholar]
- Qiu, Z.L. A Theoretical and Experimental Study on Dynamic Characteristics of Journal Bearings. Ph.D. thesis, University of Wollongong, Wollongong, Australia, 1995. [Google Scholar]
- Vijayaraghavan, D.; Keith, T., Jr. Effect of cavitation on the performance of a grooved misaligned journal bearing. Wear 1989, 134, 377–397. [Google Scholar] [CrossRef]
- Guha, S. Analysis of steady-state characteristics of misaligned hydrodynamic journal bearings with isotropic roughness effect. Tribol. Int. 2000, 33, 1–12. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, L.; Huang, M.; Yue, X.; Xu, Q. Numerical investigation of journal misalignment on the static and dynamic characteristics of aerostatic journal bearings. Measurement 2018, 128, 314–324. [Google Scholar] [CrossRef]
- Wan, Z.; Wang, Y.; Chen, B.; Dou, Y.; Wei, X. The Vibration of a Transversely Cracked Rotor Supported by Anisotropic Journal Bearings with Speed-Dependent Characteristic. Appl. Sci. 2020, 10, 5617. [Google Scholar] [CrossRef]
- Krämer, E. Dynamics of Rotors and Foundations, 1st ed.; Springer: New York, NY, USA, 1993. [Google Scholar]
- Vervisch, B.; Stockman, K.; Loccufier, M. Estimation of the damping matrix in rotating machinery for the calculation of the stability threshold speed. Int. J. Struct. Stab. Dyn. 2014, 14, 1450012. [Google Scholar] [CrossRef]
- Sepahvand, K.; Marburg, S.; Hardtke, H.-J. Stochastic structural modal analysis involving uncertain parameters using generalized polynomial chaos expansion. Int. J. Appl. Mech. 2011, 3, 587–606. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).