Multi-Objective Production Scheduling of Perishable Products in Agri-Food Industry

Abstract

This paper deals with dynamic industry scheduling problem in agri-food production. The decision-making study in this paper is articulated around the management of perishable products under constrained resources. The scheduling of logistics operations is considered at the operational level. Two metaheuristics are proposed to solve dynamic scheduling under perturbations. The uncertainty sources considered in this study are the expiration date of product components and production delays. The proposed Genetic Algorithm (GA) and the Ant Colony Optimization Algorithm (ACO) take into consideration two objective functions: minimizing the makespan and reducing the number of perishable products. The algorithms are tested on a flow-shop agri-food system.

1. Introduction

The agri-food industry is highly dependent on changing consumer habits around the world and different international regulations. They must evolve themselves in terms of employment: workforce, qualification structure, skills, etc. Furthermore, globalization along with rapid demographic changes and evolving regulatory and legislative interventions dictate the increasing demand for high quality, value-added, and customized agri-food products for multitudes of finished products. Production requires efficient planning [1] to minimize costs in order to maximize profit generation while meeting the customer demand. Thus, an agri-food industry should have an efficient method for balancing customer demands and production decisions in order to optimize the inventory level [2,3].

Faced with those challenges, the evolution of this type of industries depends essentially on multiple strategies. The most important one concerns the company’s choices regarding organization of work, and coordination between functional and operational positions. This strategy has often been considered very important and even decisive for the majority of agri-food companies [4]. In this category of the industry, the quality changes imposed by the perishability phenomenon is noticeable by the entity receiving the products during the planning horizon. That is why some companies have made an effort to automate their manufacturing lines in order to better organize and control the flow of products [5,6]. Unlike other industrial products, agri-food products have a finite lifespan, with end-of-manufacturing dates. Each finished product is then associated with a consumption limit date. It should be noted that the sale of these products often passes through distribution areas that impose certain conditions on manufacturers, with the product being considered unsellable from a certain period before its expiry date  [7]. The production planner must then take account those criteria, considering production delays and resource capacities [8,9,10]. In this context, the design, development, and operation of an efficient agri-food supply chain have begun to be met with increased interest in modern management science [11,12]. The volatility of weather conditions, the complex food safety regulatory environment, the environmental concerns, and the plethora of stakeholders involved are then considered [13]. In particular, the uncertainty of the customer demands about the finished products with changing consumers’ lifestyle trends, the perishability of products, the production and distribution delays, and the constraints on production and storage capacities pose real, significant challenges towards the development of efficient and robust agri-food supply chains [14,15,16,17]. In this work, an exact method is applied; this is the Branch and Bound method and two approximate methods are also used—Algorithm Genetic [18] and Ant Colony Optimization [19]—to optimize the scheduling and the number of expired products. The rest of the paper is organized as follows: the state-of-the-art solutions to the scheduling and optimization problem under disruptions is given in Section 2. Section 3 deals with the agri-food scheduling problem description. In Section 4, the proposed GA and ACO to solve dynamic scheduling of perishable products in Agri-Food industry is detailed. The experimental results are developed in Section 5. Finally, the conclusions and some perspectives works are given in the last section.

2. Scheduling of Agri-Food Industry

2.1. Scheduling Problem Complexity

Scheduling logistic operations in a supply chain are, in general, optimization problems since their objective is to minimize (or maximize) an objective function while respecting certain criteria [20]. Some relatively large scheduling problems can have such a high level of complexity such that their resolution becomes very difficult [21]. In fact, jobs depending on the precedence constraints have to be satisfied [22]. In scheduling, the dominance concept of a subset of solutions is important in order to limit the algorithmic complexity associated with finding an optimal solution within a large set of solutions.

The complexity of the scheduling problems is defined according to the complexity of the resolution methods and that of the algorithms used [21]. The goal of complexity theory is to analyze the resolution costs, particularly in terms of computation time and of combinatorial optimization problems. Several researchers have focused on computing the time complexity of optimization scheduling algorithms [23,24,25,26]. This complexity increases more and more with the size of the problem to be solved, which leads to a number of exponential solutions difficult to calculate in a reduced time. Therefore, generally approximate optimization algorithms from operational research are used and the search space is reduced through the dominance rule [27].

2.2. Scheduling and Optimization Problems

The Multi-objective Optimization Problem (MOO), also called multi-criteria optimization, multi-performance, or vector optimization problem, has been defined in [28] as the problem of finding a vector of decision variables that satisfies the constraints and optimizes a vector function in which the elements represent the objective functions.

To find an optimal solution to MOO problems, constituting a set of points, it is necessary to define a relation order between these elements, called the dominance relationship, to identify the best compromises. The rule of dominance is a constraint that can be added to the initial problem without changing the value of the optimums. The most used is the one defined in the “Pareto sense” ([27,29]). Optimization problems, specially in the case of agri-food industry, are generally difficult to solve. Several methods are used to find a satisfactory answer to these problems. Jouglet and Carlier (2011) have defined the dominance rule as follows: “Dominance properties provide conditions under which certain potential solutions can be ignored”.

A formal definition of the dominance rule concept and a mathematical formulation is described as follow:

Given S is the solutions space, the dominance rule identifies a subset of S containing at least one optimal solution of S.

$P(\Omega )$⇒$P(\Omega )$ associates with a given subset S⊑$\Omega$ a subset $\delta$$\left(S\right)$⊑S such that $F\left(S\right)$⇒$O\left(S\right)\cap \delta$ (S).

The subset $\delta \left(S\right)$ is said to be a dominant subset of S, and its complementary with respect to S, i.e., $S\delta \left(S\right)$, is said to be dominated.

2.2.1. Exact Methods

The scheduling problems are solved using optimization methods considering the problem data as constraints to be satisfied and by proposing an optimal and permissible solution. The optimality of the decision variables is measured against the criteria and objectives established by the higher hierarchical decision level. We distinguish between the methods “Separation and Progressive Evaluation” or “Branch and Bound”, linear programming, and dynamic programming. These exact methods, in an implicit way, examine the totality research space and produce, in principle, an optimal solution [30]. When the computation time necessary to reach this solution is excessive, the approximate methods can provide a quasi-optimal solution after a reasonable calculation time.

2.2.2. Approximate Methods

These methods are considered for scheduling problems in which we do not find an optimal solution in a reasonable time. We distinguish between (i) methods based on heuristics and sets of knowledge resulting from the experiment, presenting EDD (Earliest Due Date), FIR (First In Random Out), SPT (Shorter Processing Time), etc. as a set of simple rules, and (ii) methods based on metaheuristics, such as neighborhood search methods, taboo search, genetic algorithms, colony algorithms, simulated annealing, etc. More precisely, we have the following:

2.2.3. Heuristic Methods

Heuristics are empirical methods that generally give good results without being demonstrable. They are based on simplified rules to optimize one or more criteria. The general principle of this category of methods is to integrate decision strategies to build a near optimal solution while trying to obtain a reasonable computation time [29].

2.2.4. Metaheuristic Methods

Metaheuristics are general research methods dedicated to difficult optimization problems. They are, in general, presented in the concepts form. We can cite taboo search, Genetic Algorithms, Ant Colony algorithms, etc. These methods, which are generally faster than the exact methods, give good results and have a relatively low cost. It is observed from the literature that metaheuristics hybridized with a local search procedure often give the best searching results ([19,31]). Another advantage is the ability to control the calculation time. Indeed, the quality of the solution found tends to improve gradually over time and the user is free to stop the execution at the moment chosen.

In this article, we focus on two methods that are the exact methods Brunch and Bound and the approximate methods Genetic Algorithms and Ant Colony Optimization algorithms. In the following section, the agri-food scheduling problem is described.

3. Agri-Food Scheduling Problem Description

3.1. Case Study

In agri-food system, the workshop is generally a flow-shop. We have m machines, noted $M_1$, $M_2$, …, $M_m$, and n jobs, noted $J_1$, $J_2$, …, $J_n$. Every job must be executed, in most, only once: on $M_1$, then $M_2$, etc.

Thus, the studied problem is formally defined as a flow-shop scheduling problem. We define the agri-food flow-shop scheduling problem formally with the following definitions. Hereafter, the parameters, decision variables, objective function, and constraints are described.

3.2. Parameters of the Model

• n: number of jobs, noted $J_i$, $i=\{1,\dots ,n\}$.
• m: number of machines, noted $M_j$, $j=1,\dots ,m$.
• $r_{ij}$: earliest starting time of the job $J_i$ on the machine $M_j$.
• ${\theta }_{ij}$: processing time of the job $J_i$ on the machine $M_j$.
• $v_{ij}$: validity limit date of the component used to execute the job $J_i$ on the machine $M_j$. To produce the job $J_i$, various components are necessary needed. Due to the validity dates of those components, each job has its validity limit date to be executed on the machine $M_j$.

3.3. Decision Variables

• $t_{ij}$: effective start time of the job $J_i$ on the machine $M_j$.
• ${\alpha }_{ij}$: completion time of the job $J_i$ on the machine $M_j$.
• $d{d}_i$: due date.

3.4. Objective Function

The objective of this study is to find the best solution with the best optimizing criterion. This problem corresponds to a flow-shop scheduling problem, and the algorithm must find an order of execution of the various jobs in a way that it minimizes $C_{max}$ and reduces the perishability product function. The value of this criterion depends on the makespan value that equals the completion time of the last job executed.

Our objective is to minimize the makespan ($C_{max}$) of these products while respecting these specific constraints bound to this type of industry. The $C_{max}$ is calculated as follows:

$$C_{max}=Max\left({\alpha }_{ij}\right),i=\{1,\dots ,n\},j=\{1,\dots ,m\}.$$

(1)

The perishability product function, represented by the number of expired products, is calculated as follows:

$$P{p}_{min}=\left\{\begin{array}{cc}\sum ({\alpha }_{ij}-v_{ij})/({\alpha }_{ij}-v_{ij}),if\hfill & {\alpha }_{ij}\ge v_{ij}\hfill \\ 0\hfill & ,\mathrm{outherwise}.\hfill \end{array}\right.$$

(2)

If $P{p}_{min}\le 0$, then we do not have any perishable products. Otherwise, there is at least one perishable product.

3.5. Constraints Formulation

$$t_{ij}\ge r_{ij}$$

(3)

$$r_{ij}\le v_{ij}\mathrm{otherwise}\mathrm{it}\mathrm{is}\mathrm{expired}$$

(4)

For a flow-shop system, the completion time of the job $J_i$ must be lower than the validity limit date of the following job $J_{i+1}$ on the same machine of the same product such that

$${\alpha }_{ij}\le v_{(i+1)j}$$

(5)

$${\alpha }_{ij}\ge Max({\alpha }_{(i-1)j},r_{ij})+{\theta }_{ij}$$

(6)

$$d{d}_i\ge Max\left({\alpha }_{ij}\right),j=\{1,\dots ,m\}$$

(7)

3.6. Constraints Description

Constraint (3) is used to calculate the effective starting time on the machine $M_j$. It ensures that the staring time should be equal or greater than the earliest starting time. Constraint (4) enables us to respect the perishable date of products. Constraint (5) calculates the completion time of job $J_i$. The precedence constraint is formulated in Equation (6). It is used to ensure precedence between jobs. In fact, the completion time of job $J_i$ on the machine $M_j$ should be greater or equal than the maximum between the completion time of the precedent job $J_{(i-1)}$ and the release time of the job $J_i$ and its processing time. Constraint (7) ensures that the completion time of each job respects its due date.

4. Proposed Approach

In this section, the GA and the ACO algorithms are described. The Figure 1 clearly describes the input and the output of both algorithms. The Branch and Bound algorithm was developed to obtain the lower bound value of the Cmax.

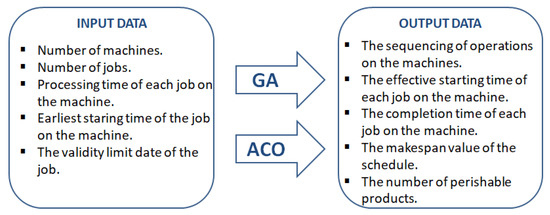
Figure 1. The input and the output of the propoed algorithms.

4.1. Branch and Bound Algorithm

The goal is to determine an optimal execution of n jobs on three machines to obtain the minimal makespan $C_{max}$ and the minimun perishable products. The principle is to evaluate two functions [32]:

-

$C_{max}$.

-

perishability: the sum of out-of-date products.

In the following, we develop each evaluation function mentioned below.

4.1.1. Evaluation of $C_{max}$

In order to determine a lower bound for a given solution, we need to calculate the makespan before proceeding to the resolution itself. Often, a job $J_i$ cannot begin before their earliest start time $r_{ij}$ and must be executed before the limited validity date $v_{ij}$.

Consider $\Gamma =J_1,J_2,\dots ,J_i,\dots ,J_k$ as the set of first supposed jobs to be executed in this order with $k\le n$ and U as the set with the rest of the jobs at any time.

We have the following:

• For $i=1$:
   
  ${\alpha }_{11}=t_{11}+{\theta }_{11}$;
  ${\alpha }_{12}=max({\alpha }_{11},r_{12})+{\theta }_{12}$;
  ${\alpha }_{13}=max({\alpha }_{12},r_{13})+{\theta }_{13}$.

• For $1<i\le k$:
   
  ${\alpha }_{i1}=max({\alpha }_{(i-1)1},r_{i1})+{\theta }_{i1}$;
  ${\alpha }_{i2}=max({\alpha }_{(i-1)2},{\alpha }_{i1},r_{i2})+{\theta }_{i2}$;
  ${\alpha }_{i3}=max({\alpha }_{(i-1)3},{\alpha }_{i2},r_{i3})+{\theta }_{i3}$.

   We now consider the last job $J_n$. The best case is that this job does not depend on the machine $M_2$ and the machine $M_3$. The makespan $C_{max}$ is then expressed by the following equation:

$$C_{max}={\alpha }_{k1}+\sum _{i\in U}{\theta }_{i1}+{\theta }_{n2}+{\theta }_{n3}$$

(8)

This leads to the following equations, considering the shortest processing time:

$$C_1\ge {\alpha }_{k1}+\sum _{i\in U}{\theta }_{i1}+\underset{j\in U}{min}({\theta }_{j2}+{\theta }_{j3}),$$

(9)

$$C_{max}\ge {\alpha }_{k2}+\sum _{i\in U}{\theta }_{i2}+\underset{j\in U}{min}\left({\theta }_{j3}\right),$$

(10)

and finally

$$C_{max}\ge {\alpha }_{k3}+\sum _{i\in U}{\theta }_{i3}.$$

(11)

Based on the results expressed by Equations $\left(2\right)$–$\left(4\right)$, the lower bound of $C_{max}$ can be expressed by the following inequality, with $j\in U$:

$$C_{max}\ge max\{C_1;C_2;C_3\}$$

(12)

with:

$$C_1={\alpha }_{k1}+\sum _{i\in U}{\theta }_{i1}+\underset{j\in U}{min}({\theta }_{j2}+{\theta }_{j3})$$

(13)

$$C_2={\alpha }_{k2}+\sum _{i\in U}{\theta }_{i2}+\underset{j\in U}{min}\left({\theta }_{j3}\right)$$

(14)

$$C_3={\alpha }_{k3}+\sum _{i\in U}{\theta }_{i3}$$

(15)

4.1.2. Evaluation Perishability Product Function

The perishability product function is calculated as follows:

$$P{p}_{min}=\left\{\begin{array}{cc}\sum ({\alpha }_{ij}-v_{ij})/({\alpha }_{ij}-v_{ij}),if\hfill & {\alpha }_{ij}\ge v_{ij}\hfill \\ 0\hfill & ,\mathrm{otherwise}.\hfill \end{array}\right.$$

(16)

4.2. The Proposed GA

Genetic Algorithms are iterative algorithms in which the goal is to optimize a predefined function, called “fitness”. To achieve this goal, the algorithm works on a set of points, called the population of individuals. Each individual or chromosome represents a possible solution to the given problem. It consists of elements called genes, which can take several values, called alleles [18].

The principle of Genetic Algorithms is based on an analogy between an individual in a population and the solution of a problem among a set of potential solutions: an individual (a solution) is characterized by a genetic structure (coding of the solutions of the problem). According to Darwin’s laws of survival, only the strongest individuals (the best solutions) survive and are able to give offspring. The operators of reproduction and mutation (recombination and mutation of the coding of the solutions) make it possible to move in the space of the solutions of the problem. From an initial population and after a certain number of generations, we obtain a population of strong individuals: good solutions of the considered problem.

In the following, we proposed a Genetic Algorithm optimizing $C_{max}$ and $P{p}_{min}$ of the agri-food workshop respecting special constraints of this type of industry within the following steps:

4.2.1. Coding of Individuals

The type of flow-shop considered in this work is $F3/r_i/C_{max}$: scheduling of non-preemtive jobs candidates for scheduling. The objective is to optimize the latest date of scheduling, the makespan, and the number of perishable products by respecting the constraints. The coding of the individual genes is based on two chromosomes i and j:

i: job number.

j: machine number.

An individual is coded by the first chromosome. i.e., the number i.

Example $\left[458973216\right]$ is an individual.

4.2.2. Generation of the Initial Population

Two hundred individuals are generated for our scheduling problem. These individuals generated randomly by respecting the constraints of starting time and validity date. This function is created to the test of the feasibility of the individual generated.

4.2.3. Calculation of $C_{max}$

The goal is to calculate $C_{max}$ of each individual generated.

4.2.4. Selection

Selection is a process where individuals are copied according to the value of their objective function. In this part, we have two steps:

-

Duplication of individuals by $C_{max}$.

-

Selection of the first 100 individuals, i.e., there is a minimum $C_{max}$.

4.2.5. Reproduction

Reproduction is a process where new individuals are formed by crossing two parents. It is based on this principle: we choose two random positions between [1, l − 1], where “l” is the length of the individual. The reproduction is performed by exchanging the bits between the two positions. Many cases can be obtained by applying this operator. These cases must be adapted to the coding solutions, and we choose the transmission of the right solutions from parents to children. The probability of reproduction is $0.8$; then, the crossing produces 80 individuals. The reproduction is performed using the following method: Consider two solutions X and Y selected among the solutions of good quality. A reproduction operator produces one or two new solutions $X^{\prime }$ and $Y^{\prime }$ by combining X and Y. If X and Y are two vectors, a classical reproduction operator is used to randomly select two positions in the vectors and to exchange the sequences contained between these two positions in both vectors.

For the scheduling problem with the encoding job list, this is not suitable.

Let us consider the example of Figure 2:

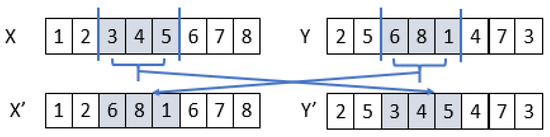
Figure 2. Example of reproduction.

When $X=12345678$ and $Y=25681473$, reproduction between the positions “after 2” and “after 5” would yield $X^{\prime }=12\left|681\right|678$ and $Y^{\prime }=25\left|345\right|473$, which are not permutations.

A specially designed reproduction operator for lists of data implements the following idea. The two parent solutions are “prepared” before the exchange of sequences located between two randomly selected positions.

In this example, the exchange zone of X is prepared to receive the sequence of jobs 6, 8, and 1 y.

In fact, we replace each job 6, 8, and 1 in the vector X by a void symbolized by $1\ast$ or $\ast 2\left|345\right|\ast 7\ast$, and beginning on the right of the exchange zone, one replace the remaining jobs of the permutation in the order of the permutation by forgetting $x\ast$, which gives $45\left|\ast \ast \ast \right|723.$

The * can be found therefore in the exchange zone, while the order of traversal of the other jobs has not changed. The same procedure for y = $2\ast \left|681\right|\ast 7\ast$ becomes $81\left|\ast \ast \ast \right|726$.

This is linked by the exchange of sequences, giving two children permutations $X^{\prime }$ and $Y^{\prime }$: $X^{\prime }=45\left|681\right|723$ and $Y^{\prime }=81\left|345\right|726$. A number of pairs of children are thus generated and replaces part of the parents selected from the least efficient ones. Thus, a mutation operation creates a child for this population to ensure diversity of the individuals [18]. Not to mention that an individual generated by this crossover operator should remain within the specified start date and date of perishability.

4.2.6. Mutation

Different values of mutation probability have been tested in order to select the best one providing better results. The best mutation probability in our case is 0.2, so the mutation produces 20 individuals. The individual generated by mutation must respect the constraints of time and start date of perishability.

4.2.7. Iteration

From the initial population comprising 200 individuals, we proceed with the creation of new populations using operations selection, crossover, and mutation, and we obtain a new population for each generation.

4.3. The Proposed ACO

Ant Colony Optimization algorithms (ACO) are part of the class of metaheuristics.The main objective of this approach is to find the shortest path between a nest and a source food. It was in 1992 that Marco Dorigo from University of Brussels [33] formulated this method. The advantage of this method lies in the strategies of research that achieves a compromise between exploitation and exploration [34].

The ACO algorithms are based on an analogy with natural phenomena and rely on the collective behavior of ants to organize the search for food [35]. Ants explore their environment by leaving behind volatile traces, called pheromone traces. They serve these traces to guide themselves and naturally tend to follow them.

Once the food is found, they use the traces they just deposited to determine the way back to the nest. During the journey, they leave traces of them in proportion to the interest of the food source. Ants that chose the shortest route perform more round trips, the amount of pheromones deposited are of higher importance, and this route will eventually be taken by all ants. The path is therefore strongly impregnated with pheromones and constitutes a track of choice for the ant colony [36]. The more the food source has been judged to be interesting, the more ants tend to follow this path. Therefore, little by little, the traces towards the sources of food are more and more marked. Colorni et al. [37] adapted this principle to the field of combinatorial optimization. To do this, they associated the neighborhood of the nest with the space of solutions. Each solution is similar to a food source in which the quality is provided by the evaluation function. Each ant is assimilated to a repetitive process of building solutions. The construction is biased by a global data set showing pheromone traces. This set provides a memory of the quality of the solutions and is regularly updated by the construction process and by a mechanism simulating the evaporation of the pheromone.

4.3.1. Coding of Scheduling Solution

The problem formulation is inspired from the Vehicule Routing Problem (VRP) [38]. Each selected job for scheduling is represented by a node in a graph G = (N, L), where N represents the number of nodes (N = n) and L represents the number of arcs that link the jobs. When an ant moves from a node i to a node j, it leaves a trace of pheromones on the arc $a_{ij}$.

For the scheduling problem, the information contained in the pheromone trace is based on the data (the validity date of components forming the job among others) and the constraints of the problem. This trace saves the information on the arc used (aij). In fact, the most used arc has a higher probability to be selected again.

4.3.2. Pseudo Code of the Proposed ACO

The pseudo code of the proposed algorithm (see the Algorithm 1 )for optimizing the objective function that represents the sum of the expired products is presented below.

Algorithm 1: pseudo code of the ACO algorithm

1: procedure INTIALIZATION 2:     Initialize the pheromone matrix ${\tau }_{ij}^k\left(0\right)\leftarrow {\tau }_0$ 3:     Initialize taboo list 4:     Realisation of a cycle: 5:     while $(Nc<N{c}_m)$ do 6:         for each job in $1\dots n$     $Type,Type2)$ 7:         for each ant in $1\dots m$ 8:         Choose a job $J_i$, randomly 9:         Update all available jobs 10:         Insert the Sk solution in the taboo list 11:         Select the following job according to $P_{ij}^k$ 12:         Update the pheromone matrix $\Delta {\tau }_i{j}^k$ according to the Sk solution 13:         Global update of the pheromone trace for each job in $1\dots n$      Evaluate the Sk solution according to the objective function       Update the matrix ${\tau }_{ij}^k$ 14:         End For 15:         End For 16:         End While 17:         $Nc\leftarrow Nc+1$

Upon initialization of the algorithm, the intensity of the pheromone trace for all the pairs of jobs (i,j) are set to a small positive value ${\tau }_0$. The parameter $\alpha ,\beta ,\gamma$ are used to determine the relative importance of the intensity of the trace and goals in the construction of a solution.

In addition, a taboo list is maintained to ensure that a job that has already been assigned to the sequence being built is not selected as in the old days. Each ant k therefore has its own taboo list, “$tabo{o}_k$”, which will keeps the jobs already selected in mind.

$$P_{ij}^k\left(t\right)=\left\{\begin{array}{cc}\frac{{\left[{\tau }_{ij}\left(t\right)\right]}^{\alpha }\ast {\left[{\varphi }_{ij}\right]}^{\beta }\ast {\left[{\psi }_{ij}\right]}^{\gamma }}{{\sum }_{h\notin tabo{u}_k}{\left[{\tau }_{ih}\left(t\right)\right]}^{\alpha }\ast {\left[{\varphi }_{ih}\right]}^{\beta }\ast {\left[{\psi }_{ih}\right]}^{\gamma }}\hfill & ,\mathrm{if}j\in \Omega \hfill \\ 0\hfill & ,\mathrm{else}.\hfill \end{array}\right.$$

(17)

$\Omega$ represents the set of available jobs; ${\varphi }_{ij}=\frac{1}{v_{ijk}}$; ${\psi }_{ij}=p_{ij}$; and $v_{ijk}$ and $p_{ij}$ represent, respectively, the date of validity of the component $c_{ijk}$ related to job i and the duration of execution (standardized), which have direct influences on the objective function. During an iteration of the algorithm, several ants build a role in turn, a solution represented by a sequence of jobs. At the end of each cycle, each of the m ants deposit a certain quantity of pheromones $\Delta {\tau }_{ij}^k\left(t\right)$ defined in the following equation; in its way, this quantity depends on the quality of the solution.

Let $P_{pmin}^k\left(t\right)$ be the evaluation of the objective to be optimized fpr the solution found by the $k^{eme}$ ant.

The contribution to updating the trace of the ant k is then calculated in the following way:

$$\Delta {\tau }_{ij}^k\left(t\right)=P_{pmin}^m/P_{pmin}^k\left(t\right)$$

where ${P_p^k}_{min}\left(t\right)$ is the number of perishable products associated with the ant k$\left(Sk\right)$ at the moment t, and ${P_p^m}_{min}$ represents the minimum number of perishable products obtained after the m ants have made their paths.

The algorithm performs an overall update of the intensity of the pheromone trace ${\tau }_{ij}^k$ at the end of each cycle to avoid premature convergence of the ACO algorithm. This update is influenced by an evaporation factor $\rho$, $0<\rho <1$, which decreases the quantity of pheromone present on all arcs (aij) [33]. This evaporation must not affect the tests: the solutions to the taboo list.

$${\tau }_{ij}^k=\rho \ast {\tau }_{ij}^k+\sum _{i=1}^m\Delta {\tau }_{ij}^l$$

5. Implementation and Experimental Results

5.1. Case Study

The specificity in the agri-food industry is the limited dates of the products and semi-finished products. It is a constraint specific to the agri-food industry. For the case study, we consider a flow-shop scheduling problem with $m=3$ machines, and we have n jobs to be executed (6–9 jobs). For each job $J_i$, $i=6\dots 9$, we specify the earliest start time $r_{ij}$, the processing time ${\theta }_{ij}$, and the validity limit date $v_{ij}$, as shown in Table 1. The following Table contains the details of the tested instances.

Table 1. Characteristics of the tested instances.

Job		Earliest Starting Time ${\mathit{r}}_{\mathit{ij}}$	Processing Time ${\mathit{\theta }}_{\mathit{ij}}$	Validity Limit Date ${\mathit{v}}_{\mathit{ij}}$
1	$M_1$	1	2	40
	$M_2$	3	4	44
	$M_3$	5	7	53
2	$M_1$	8	2	35
	$M_2$	9	1	40
	$M_3$	12	10	45
3	$M_1$	22	2	37
	$M_2$	21	3	43
	$M_3$	24	2	55
4	$M_1$	15	2	40
	$M_2$	16	3	45
	$M_3$	17	1	55
5	$M_1$	27	5	30
	$M_2$	29	4	35
	$M_3$	31	4	38
6	$M_1$	41	5	44
	$M_2$	44	10	50
	$M_3$	45	7	63
7	$M_1$	50	5	48
	$M_2$	55	4	55
	$M_3$	57	3	70
8	$M_1$	60	4	75
	$M_2$	65	3	65
	$M_3$	66	7	70
9	$M_1$	70	1	72
	$M_2$	75	2	80
	$M_3$	78	3	85

5.1.1. Parameterization of the GA Algorithm

To execute the proposed GA and ACO algorithms, a tuning procedure is used. As explained before, the probability of crossover is $0.8$. The mutation probability used in our case is $0.2$, so the mutation produces 20 individuals. The individual generated by mutation must respect the constraints of the earliest start time and start date of perishability. The size of the initial population comprises 200 individuals. A new populations is created using the selection, reproduction, and mutation operators.

5.1.2. Parameterization of the ACO Algorithm

The size of the set of ants equals 50. The number of tested cycles equals 100. The taboo list is updated in each iteration. The intensity of the pheromone trace is updated by the parameter $\rho$. The value of this parameter is dynamically changed ($0<\rho <1$).

6. Experimental Results

In this section, the experimental results are given. The instances were executed 10 times to calculate the average values of $C_{max}$ and the number of perishable products. The best scheduling solutions obtained by the two approaches are compared. Hereafter, the Gantt chart of best solutions obtained are given in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. The Figure 11 presents the best solution obtained by B&B algorithm.

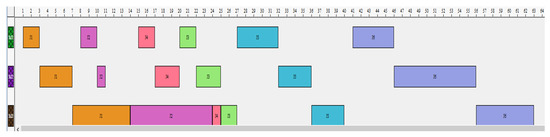
Figure 3. Gantt chart of the best solution with six jobs by GA.

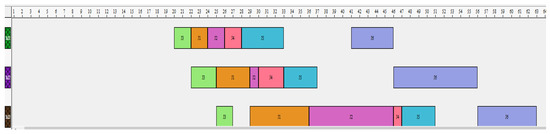
Figure 4. Gantt chart of the best solution with six jobs by ACO.

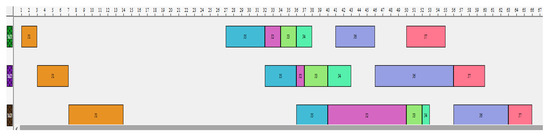
Figure 5. Gantt chart of the best solution with seven jobs by GA.

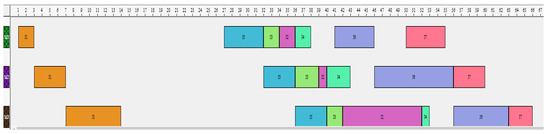
Figure 6. Gantt chart of the best solution with seven jobs by ACO.

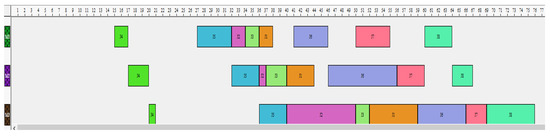
Figure 7. Gantt chart of the best solution with eight jobs by GA.

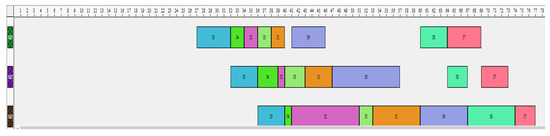
Figure 8. Gantt chart of the best solution with eight jobs by ACO.

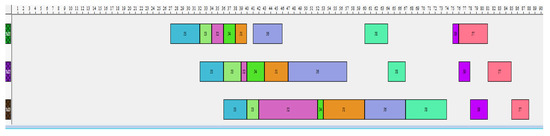
Figure 9. Gantt chart of the best solution with nine jobs by GA.

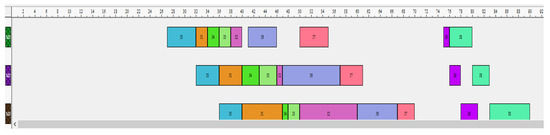
Figure 10. Gantt chart of the best solution with nine jobs by ACO.

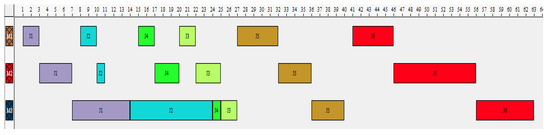
Figure 11. Gantt chart of the best solution with six jobs by B&B.

6.1. Comparative Study

To compare the robustness of the algorithms proposed, GA, ACO, and four instances were tested and compared with the results of the Branch and Bound method. Table 2 sum up the results obtained. From the results obtained, we can conclude that the GA and ACO give satisfactory results and near optimal solutions as with the Branch and Bound method. As we can see, the ACO and AG algorithms obtain the same makespan values in instances with six and seven jobs such as B&B. However, the ACO has not obtained the optimal number of perishable products (0 in the case of the instance with six jobs). From Table 2, we can remark that the GA algorithm gives the best solutions compared with ACO, except in the case with eight jobs ($P{p}_{min}=2$).

Table 2. Experimental results of the B&B, GA, and ACO algorithms.

Tested Instance	B & B			GA			ACO
	Best Solution	${\mathit{C}}_{\mathit{max}}$	${\mathit{Pp}}_{\mathit{min}}$	Best Solution	${\mathit{C}}_{\mathit{max}}$	${\mathit{Pp}}_{\mathit{min}}$	Best Solution	${\mathit{C}}_{\mathit{max}}$	${\mathit{Pp}}_{\mathit{min}}$
6_Jobs	124356	63	0	124356	63	0	312456	63	1
7_Jobs	1234567	66	1	1523467	66	1	1532467	66	1
8_Jobs	21345678	74	1	45231678	76	2	54231687	77	1
9_Jobs	321456789	77	2	532416897	88	2	514326798	90	4

Figure 12 and Figure 13 show the best average values, makespans, and number of perishable products obtained for two algorithms (GA and ACO).

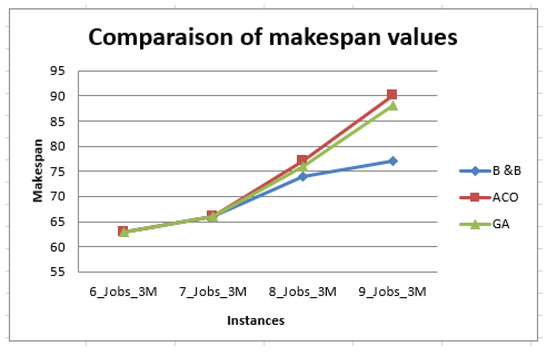
Figure 12. Comparison of the makespan values.

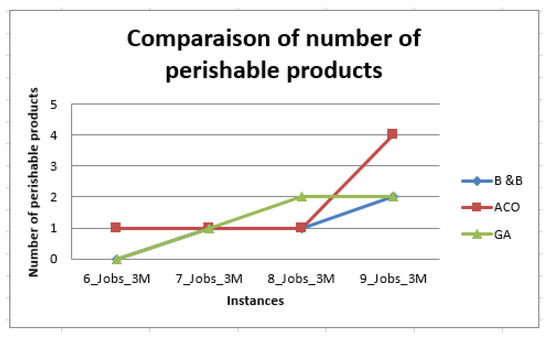
Figure 13. Comparison of the perishable products.

6.2. Interpretation

The schedule’s Gantt chart representation correspond to the best obtained solution found by the ACO and GA algorithms. The schedules in Figure 3 and Figure 4 are obtained after applying the proposed GA and ACO algorithms, respectively.

When considering deterministic scheduling with an objective to minimize makespan, there are no preferences in selecting one as both have the same makespan, which is 63 time units. However, when considering the number of perishable products, the schedule found by GA algorithm is better than the solution found by ACO. In fact, the GA algorithm gives a solution with a perishable product when solving the instance with six jobs and three machines.

For instance, with eight jobs and three machines, the ACO algorithm provides a better result in terms of the number of perishable products (only one) compared with the result found by the AG algorithm (two perishable products).

However, the makespan value of the best solution found by AG is better than that found by ACO, equals to 76 (see Figure 7 and Figure 8) For the instance with nine jobs and three machines, the GA algorithm provides a better result compared with that of ACO. The schedule in Figure 9 is more efficient than the schedule in Figure 10 since it has a lower makespan value and lower number of perishable products. The makespan value equals 88, which is better than the 90 found by ACO. Additionally, there are only two perishable products in the schedule in Figure 9, but with ACO, there are four perishable products.

The computational results indicate that the schedules generated using the proposed genetic algorithm GA have statically superior performances in terms of makespan and the number of perishable products compared with the ACO algorithm.

To complete our study and to assess the performance of our algorithms more, the B&B algorithm is used to obtain a lower bound. The computational results mentioned in the table below indicate that the performance of predictive schedules generated by the GA are similar to or near those found by the B&B algorithm. In fact, the GA provides similar schedule performances for the instances with six jobs and seven jobs to that of the B&B. When considering bigger instances with eight and nine jobs, the GA provides solutions with similar values of makespan (76 compared with 74 by the B & B) and similar values of the number of perishable products ($P{p}_{min}=2$ compared with $P{p}_{min}=1$ by B&B ).

7. Conclusion and Perspectives

This paper presents a Genetic Algorithm and an Ant Colony Optimization algorithm to solve the dynamic industry scheduling problem in agri-food production. The two meta-heuristics aim to find the best agri-food scheduling with the lowest value of makespan and the lowest number of perishable products. The algorithms were tested on a real case of the agri-food industry with three machines while varying the number of jobs from six to nine. The experimental results indicate that both algorithms are very effective compared to the B&B algorithm. However, the GA algorithm provides better results compared with the ACO algorithm. An interesting direction for future research is to take into consideration other real dynamic events such as the breakdown of the machines and the cancellation of the job. Additionally, we aim to design a new multi-agents decentralized GA and ACO suitable to communicate and collaborate with IoT applications.