EMP: Extended Kalman Filter Based Self-Adaptive Mold Protection Method on a Toggle Mechanism

Abstract

Nowadays, the plastic injection molding industry is ever-growing, crucial, and its plastic products can be seen everywhere. However, the mold damage problem still frustrates operators because of its high maintenance price and time-consuming maintenance process. This damage is commonly caused by foreign bodies in mold area, and the conventional mold protection method is insufficient for high-performance injection molding machines because of the uncertainty from many setting parameters. To improve detection precision of mold protection driven by a toggle mechanism ($TM$), this paper puts forward $EMP$, i.e., an extended Kalman filter ($EKF$) based self-adaptive mold protection method, wherein the $EKF$ is used in current curve optimization, and the self-adaptive method ($SAM$) is proposed to gain an safety range of current curve. The $EMP$ was verified in a 140-ton electric injection molding machine. Compared with a general method, the proposed method decreases the detected distance of mold protection by 22% under different thickness foreign bodies.

1. Introduction

Concepts of intelligent manufacturing [1], cyber-physical systems [2], etc., are widespread. Large equipment (e.g., CNC machining centers and injection molding machines) has crucial roles in these concepts, claiming many researchers’ interests [3,4,5] because of the equipment’s systematic complexity and costliness.

The injection molding machine ($IMM$) is a typical piece of large equipment, and the importance of $IMM\mathrm{s}$ has been ever-growing. $IMM\mathrm{s}$ produce plastic products occupying the main plastic market. Nowadays, $IMM\mathrm{s}$ tend toward high speed, precise control, and low energy consumption and noise. Many studies primarily focus on the control of robustness [6,7,8,9,10], trajectory planning [11,12,13], time optimization [14], and energy consumption [15,16,17]. Hence, the performance of $IMM\mathrm{s}$ has been enormously improved. Meanwhile, the mold protection ($MP$) issue is also serious. Figure 1 provides an example, where the toggle mechanism ($TM$) closes with the mold in less than two seconds and under high pressure. If there are some foreign bodies in the mold without a protection mechanism, the mold will be damaged directly. This problem always frustrates operators because of the high maintenance price and time-consuming maintenance process.

Figure 1. Electric injection molding machine with a mold. If there are some foreign bodies in the mold without protection, the mold will be damaged when the mold closes. Generally, the mold is expensive, and the maintenance is tedious.

At present, mold protection has attracted many researchers. One research direction is based on machine vision through comparing safe and unsafe situations to detect the foreign bodies. Wang et al. [18] presented a method that applied technologies, such as near infrared illumination technology, the background updating algorithm, and the region of interest, to fulfill $MP$. Yang et al. [19] applied key technologies, including the methods for pretreatment of the cavity image, template matching of the cavity image, and cross-correlation of an abnormal cavity situation, into $MP$. Chi et al. [20] proposed a system that was able to correctly detect the unsafe in-mold status of the stuck ejectors or pieces by the two approaches of offset correction and dynamic safe range learning. However, the above methods need to add a special vision system. In some high speed cases, processing speed also becomes the issue, and for getting a good effect from image processing, much effort should also be made to implement a customized visual program.

Other improving methods are to avoid failed production based on processing data and mathematical models to reduce the possibility of the entrance of foreign bodies. Based on the monitoring data, Ribeirol et al. [21] proposed an approach for fault detection in a thermoplastic injection molding process to assure a high level of quality control over the molded parts using neural networks. The properties in injection molding can also be controlled by neural networks in [22]. A study in [23] monitored the quality of molded parts in a process from the design and processing points of view. Ribeiro et al. [24] also proposed an approach of support vector machines for quality monitoring in a plastic injection molding process to monitor in-process data and thereby the unexpected process interferences could be responded quickly. These methods are good auxiliary but not the thorough ones for $MP$.

IMM controller venders (e.g., Techmation and KEBA) also have their own $MP$ methods. Those methods just compare electric current ($EC$) profiles simply, which need to set many parameters (e.g., $MP$ distance, upper deviation, lower deviation, left deviation, and right deviation). Using those methods, operators always take a long time adjusting parameters, and it is still possible that the mold will be damaged because of misjudgment.

To address the issue, we propose an extended Kalman filter based self-adaptive method. The contributions of this work are as follows:

• The mathematical model of the $TM$ driven by servo systems ($SS\mathrm{s}$) is built used for the process analysis and further researches.
• Through the mathematical model, this paper successfully proposes the $EMP$, which can be applied in any $TM$ driven by an $SS$.
• The proposed method was implemented in a 140-ton electric injection molding machine ($EIMM$), and decreased the detected distance of $MP$ by 22% compared with general one.

An extended Kalman filter ($EKF$) $EKF$ linearizes with an estimate of the current mean and covariance, which is a nonlinear kind of the Kalman filter [25,26]. It is widely used in various fields. Jana et al. [27] presented a hybrid FLC-EKF scheme for temperature control of a refinery debutanizer column. Charkhgard et al. [28] used neural networks and EKF to estimate the charging state for Lithium-ion batteries. Fang et al. [29] applied an EKF-based filter fusion method in a high-efficiency motion tracking system. Paolo proposed a two-stage EKF to build an observer for a sensorless control [30]. One key point for using the EKF is the choice of the elements of the covariance matrices, which affects both the performance and the convergence [31]. Many studies [32,33,34] have provided practical approaches and accounts. More details can be found in the surveys of [35,36,37]. However, none of these studies are involved in mold protection problems.

The remainder of this paper is structured as follows: Section 2 introduces the $TM$ system, $SS$ system, and $MP$ problem ($MPP$); Section 3 illustrates the $TM$ model driven by $SS$ and $EMP$; Section 4 presents the effect validation of $EMP$; and the last section concludes our work.

2. Control System of the Toggle Mechanism

A typical control system of $TM$ is shown in Figure 2. It consists of controller, servo driver, motor, and $TM$. The controller contained algorithms and logic programs send commands to the servo driver to drive the motor. The motor is connected to the $TM$ by a belt or lead screw. We define a servo driver working with a motor as an $SS$. In some special cases, two $SS\mathrm{s}$ can be used together to provide greater torque. Normally, the communication among the controller, servo driver, and motor adopts a real-time Ethernet bus (e.g., EtherCat).

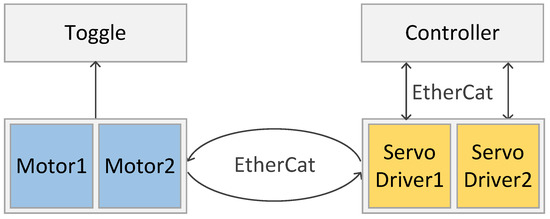
Figure 2. Control system of a toggle mechanism ($TM$), which consists of a controller, servo driver, motor, and $TM$. The controller embedded algorithms and logic programs send commands to the servo driver to drive the motor. The motor is connected with the $TM$ by a belt or lead screw.

A mold is commonly comprised of movable and fixed parts. The movable part is fastened on the $TM$. When the machine is power on, the servo system receives commands continuously form the controller to drive the $TM$ forward or backward. In the servo driver, an encoder is built-in to obtain the actual position and speed. Hence, the controller can gain the feedback (e.g., position, speed, $EC$) from the $SS$.

2.1. Mold Protection Problem

Every plastic product is molded by a specific mold. In production, an $IMM$ uses the mold to produce automatically, and every seamless mold close can produce a good product. However, as shown in Figure 3, there may exist a foreign body which will damage the mold. The $MPP$ is to detect the foreign body when a force is quickly pushing the movable mold on. As shown in Figure 3, we defined two key indicators of $MPP$ below.

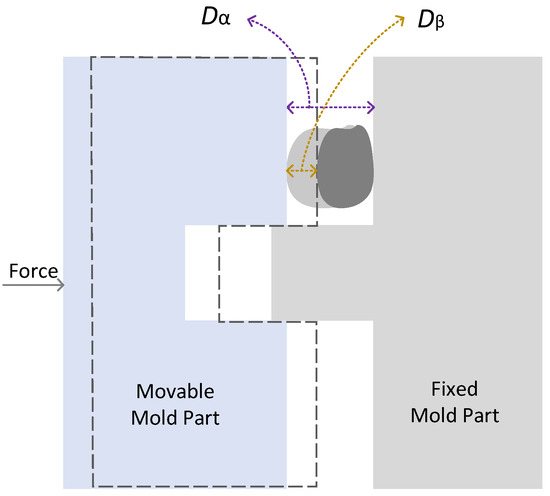
Figure 3. Damage distance and detected distance.

Definition 1.

(Damage distance$D_{\alpha }$):$D_{\alpha }$ donates the distance between the mold parts when the mold just contacts the foreign body.

Definition 2.

(Detected distance$D_{\beta }$):$D_{\beta }$ donates the pressed distance of a foreign body when it is detected.

Hence, the $MP$ intends to detect the foreign body at a smallest $D_{\beta }$ which also means less damage to the mold.

2.2. Servo System

$SS$ is the power system to drive the $TM$. Normally, it contains three closed loops: $EC$, speed, and position closed loop. Position closed loop is based on the speed closed loop, and speed closed loop is based on the $EC$ loop. $EC$ turns to torque and then provides a force on the actuator. Since the $TM$ fastened with the movable mold is driven by the force, the $EC$ should be the key factor for the proposed $MPP$. The $EC$ reflects the force on foreign body in the mold and herein could be used to detect the foreign body.

3. EKF Based Model

Regarding the fluctuation of $EC$, the $EKF$ is used to filter the $EC$. We can obtain the theoretical setting $EC$ from the user setting trajectory (prediction value), and the drive feedback current (measured value) from the $SS$.

3.1. Toggle Mechanism Model

We have shown the model in [13] and herein simply introduced it below.

From the geometry of Figure 4, we can obtain equations as follows:

$$\mathsf{\Phi }\left(\theta \right)=\left[\begin{array}{c}{r}_1{sin}_{{\theta }_1}+r_{3}sin\left({\theta }_2\right)-f\hfill \\ r_5{sin}_{{\theta }_5}+r_{4}sin({\theta }_1+\varphi )-h-f\hfill \end{array}\right]=0.$$

(1)

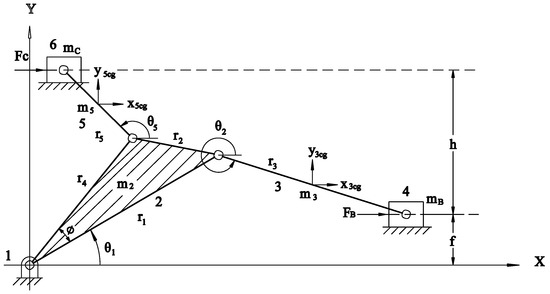
Figure 4. The physical model of $TM$. Establish a Cartesian coordinate system and set the origin at link one. $F_C$ and $F_B$ are the force on sliders B and C, respectively. $m_2$, $m_3$, $m_5$, $m_B$, and $m_C$ indicate the mass of links two, three, five, and sliders B and C, respectively. $r_1$, $r_2$, and $r_4$ indicate the three-side lengths of two, and $r_3$ and $r_5$ indicate the lengths of links three and five respectively; ${\theta }_1, {\theta }_2, \mathrm{and} {\theta }_5$ are the angular positions of link two, three, and five; h is the height between the two horizontal guides where sliders B and C travel; and f is an offset between links two and three [13].

$\mathsf{\Phi }\left(\theta \right)$ describes the parameter relationships in the $TM$ model. Then, we can obtain

$$x_B=r_{1}cos\left({\theta }_1\right)+{[r_3^2-{(f-r_{1}sin\left({\theta }_1\right))}^2]}^{\frac{1}{2}}.$$

(2)

Using Hamilton’s principle, we can obtain

$$\begin{array}{cc}0\hfill & ={\int }_{t_1}^{t_2}[\delta T_t+\delta W^A+\delta W^C]dt\hfill \\ \hfill & ={\int }_{t_1}^{t_2}\delta {\theta }^T\left[\frac{\partial T_t}{\partial \theta }+\frac{d}{dt}\frac{\partial T_t}{\partial \theta }-Q^A-Q^C\right]dt+{\left.\frac{\partial T_t}{\partial \theta }\delta \theta \right|}_{t_1}^{t_2},\hfill \end{array}$$

(3)

where $\delta W^A$ is the virtual work, and $\delta W^C=-\delta {\theta }^T{Q}^C,Q^C$ are the generalized constraint reaction forces.

We use energy method to gain dynamic motion equation. The total kinetic energy of the system is described below.

$$T_t=T_2+T_3+T_5+T_B+T_C,$$

(4)

where $T_2,T_3,T_5,T_B,T_C$ represent the kinetic energies of link two, three, five, and sliders B and C, respectively.

$Q^A,Q^C$ are calculated as follows:

$$Q_A=\left[\begin{array}{c}{F}_C{r}_5{sin}_{{\theta }_5}\hfill \\ F_B{r}_3{sin}_{{\theta }_2}\hfill \\ F_B{r}_1{sin}_{{\theta }_1}+F_C{r}_4{sin}_{{\theta }_1}+\varphi \hfill \end{array}\right],$$

(5)

where $\lambda$ is the Lagrange multiplier.

$$Q_C=-\lambda \left[\begin{array}{cc}0& r_{5}cos\left({\theta }_5\right)\\ r_{3}cos\left({\theta }_1\right)& 0\\ r_{1}cos\left({\theta }_1\right)& r_{4}cos\left({\theta }_1\right)+\varphi \end{array}\right].$$

(6)

Thus, the equation of motion for the $TM$ is

$$M\left(\ddot{\theta }\right)+N(\theta ,\dot{\theta })+\lambda {\mathsf{\Phi }}_{\theta }^T=Q_A.$$

(7)

Using the Equation (6) and trajectory $x_B$, we can obtain ${\dot{x}}_B,{\ddot{x}}_B,x_C,{\dot{x}}_C,{\ddot{x}}_C$, and $F_C$; for details see the previous paper [13].

3.2. Servo System Model

The $SS$ model is used to obtain theoretical setting $EC$ ($i_t$) form $F_C$. The $EC$ and torque can be described blew.

$${\tau }_e=K_{t}i\left(t\right),$$

(8)

where $i\left(t\right)$ is current and $K_t$ is stator torque constant.

The mechanical equation can be obtained as follows:

$${\tau }_e={\displaystyle \frac{F_C\times l}{2\times \pi \times \eta }},$$

(9)

where $F_C$ is the force on the slider C in Figure 4, l is the lead of ball screws, and $\eta$ is the screw drive efficiency.

Thus, we can gain the relation between current and force on slider C:

$$i\left(t\right)={\displaystyle \frac{F_C\times l}{2\times \pi \times \eta \times K_t}}.$$

(10)

3.3. Process of EKF

Recall that we use the $EC$ as the filter target, and regard $i_t$ and $h_t$ as the prediction value and measured value, respectively. Thus, we can obtain the equations of state time propagation and state measurement propagation as follows:

$$\left\{\begin{array}{c}X\left(t\right|t-1)=i(t)+r,\hfill \\ Z\left(t\right|t-1)=h(t)+q,\hfill \end{array}\right.$$

(11)

where r is the process standard deviation, and q is the measurement standard deviation.

Then we can get the Jacobian matrix $F_t$ and $H_t$.

$$\left\{\begin{array}{c}{F}_t={\displaystyle \frac{\partial i}{\partial t}},\hfill \\ H_t={\displaystyle \frac{\partial h}{\partial t}}.\hfill \end{array}\right.$$

(12)

The covariance updating equation of $P\left(t\right|t-1)$ is described below.

$$P\left(t\right|t-1)=F_{t}P(t-1|t-1)F_t+Q,$$

(13)

where $F_t$ is the transpose matrix of F, Q is the process variance.

According to the setting profile and feedback current, the current optimal estimation $X\left(t\right|t)$ can be obtained.

$$X\left(t\right|t)=X\left(t\right|t-1)+K_g\left(t\right)(Z\left(t\right|t-1)-H_{t}X\left(t\right|t-1)),$$

(14)

where $K_g\left(t\right)$ is Kalman gain, and it can be calculated using the following equation.

$$K_g\left(t\right)=P\left(t\right|t-1)H_t^T{(H_{t}P\left(t\right|t-1)H_t^T+R)}^{-1},$$

(15)

where R is the measurement variance.

To keep the $EKF$ running until the end of the system process, the covariance updating equation of $P\left(t\right|t)$ is needed.

$$P\left(t\right|t)=(I-Kg\left(t\right)H_t)P\left(t\right|t-1),$$

(16)

where I is a unit matrix.

The Equations (11)–(16) are the process of $EKF$ in the $MP$.

3.4. Self-Adaptive Model

The $EKF$ based self-adaptive method ($SAM$) is used to gain the safety range of the current curve. In $EKF$, according to mathematical model of $TM$ driven by $SS$, the setting profile is chosen as the prediction value, and the drive feedback current is chosen as the measurement value. At first, the $SAM$ should ensure the absence of foreign bodies, and then injection machine mold close and open automatically according to self-adaptive time n. Every $EKF$ current curve will be saved in a $m\times n$-dimensional matrix, $A_{m\times n}$. m is the time of sample, and the position of every sampled point is saved in a m-dimensional matrix, P. Equation (17) records the data to calculate the standard current curves.

$$\left\{\begin{array}{c}{A}_{m\times n}=[A_1,A_2\cdots A_k\cdots A_n],\hfill \\ P={[p_1,p_2,\cdots ,p_m]}^T,\hfill \end{array}\right.$$

(17)

where $A_k={[i_{k1},i_{k2},\cdots ,i_{km}]}^T$ is one time current curve optimized by $EKF$.

Then, we can get the safety range of current curve as follows.

$$\left\{\begin{array}{c}U={\mathcal{L}}_{max}(A_1,A_2\cdots A_k\cdots A_n)+\Delta ,\hfill \\ L={\mathcal{L}}_{min}(A_1,A_2\cdots A_k\cdots A_n)-\Delta ,\hfill \end{array}\right.$$

(18)

where ${\mathcal{L}}_{max}$ and ${\mathcal{L}}_{min}$ are functions to get the maximum and minimum values of every sampled point, respectively. U and L are upper deviation current curve and lower deviation current curve, respectively; and the dimension of U and L is m. $\Delta$ is true error.

Regarding Equation (18), the safety range at every position should be between the maximum and minimum currents within n self-adaptive processes. Note that $\Delta$ is necessary because the self-adaptive time n is limited. However, because of the unknown of the true error value, the error value is calculated by the Bessel formula below.

$$\Delta =\sqrt{{\displaystyle \frac{{\sum }_{k=1}^n{(A_k-\overline{A})}^2}{n-1}}},$$

(19)

where $\overline{A}={\displaystyle \frac{{\sum }_{k=1}^n{A}_k}{n}}$ is the arithmetic mean of n-time curves.

When the $IMM$ is running in $MP$ checking area, it will be checked whether the actual current curve is between the two curves. If not, the machine will stop closing and then open to protect the mold.

3.5. Process of the Self-Adaptive Method

The process of the self-adaptive method is divided two phases: training and applied phases; see Figure 5. From the perspective of the training phase, setting trajectory $x_B$ is executed in the $TM$ system several times, which must be under the condition without MMP. Every time $x_B$ is put into $TM$ system and our mathematical model, the $EKF$ can gain $h_t$ and $i_t$ to produce accurate EC. Then, the SAM uses the accurate ECs to produce safety range of current curve.

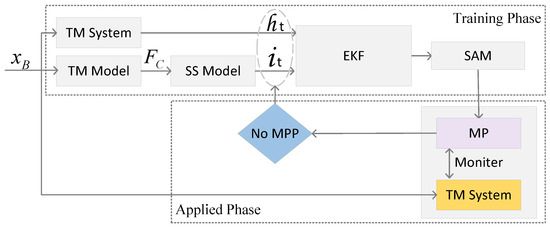
Figure 5. Process of the self-adaptive method.

After the training, the $SAM$ can be used to judge whether the MMP occurs—the applied phase. In this phase, the $x_B$ is put into $TM$ system. Meanwhile, the proposed $MP$ method monitors the $TM$ system as to whether any $MPP$ occurs or not. If no $MPP$ happens, the $i_t$ and $h_t$ produced can be used to update the $SAM$. Otherwise, the mold will open and give tips in the human machine interface (HMI).

4. Experimental Results

Experimental equipment and the control process are shown in Figure 6. The primary facility was a 140-ton $EIMM$, driven by $SS$. Data analysis was done in a Dell laptop which had a clock speed of 1.7 GHz and 4 GB DDR3 RAM. The controller was KEBA CP052 implemented the Ethercat protocol, and it used 24 v to control input and output. The servo drive was a Phase AXN 70.140.4, and the motor was a Phase U31013F.15.3 N7, whose maximum speed was 3000 RPM. An encoder built in the motor was used to feed back the position. In Figure 6, an experiment with a disposable cup is shown, which verifies the effectiveness of the method intuitively. Table 1 shows the parameters of the $TM$, $SS$, and $EKF$ in the experiment. Based on those parameters, the following experiments were done.

Figure 6. Experimental facility, control process, and effect of $MP$.

Table 1. Parameters of the $TM$, $SS$, and $EKF$ in the experiment.

Parameters	Value
$m_2,m_3,m_5$ (kg)	25, 30, 2.5
$m_B,m_C$ (kg)	80, 5
$r_1,r_2,r_3$ (m)	0.145, 0.07, 0.190
$r_4,r_5$ (m)	0.1, 0.055
$h,f$ (m)	0.08, 0.025
$\varphi$ (rad)	0.4499
$K_t$ (Nm/A)	0.621
l (mm)	40
$\eta$	0.873
q	0.01
r	0.02
Q	$1\times {10}^{-4}$
R	$4\times {10}^{-4}$

In our experiment, the s-curve was chosen as the start and stop slope. We set the speed and acceleration of mold open and mold close to 500 mm/s and 2 m/s², which are very fast times in real production. The displacement was set to 240 mm. In the section of $EKF$, the setting profile was chosen as the prediction value, and the drive feedback current was chosen as the measurement value.

Figure 7 shows the displacement, velocity, acceleration, and force on slider C, which were calculated from the setting profile.

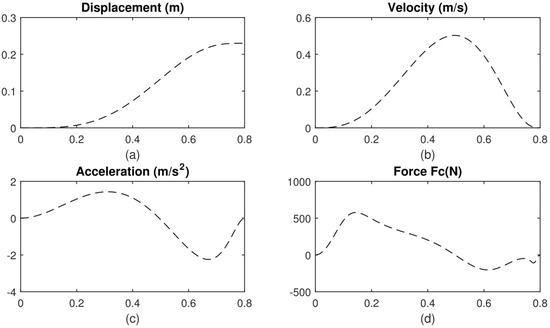
Figure 7. (a–d) The displacement, velocity, acceleration, and force on slider C, respectively, which all change over time.

When using $EKF$, the r was 0.01, q was 0.02, and protection monitor displacement was 7 mm. Then we tested the first effect of $EKF$, and Figure 8 is the effect of current profile filtered by $EKF$. Plus icons are measurement values. The green profile is the setting value after being calculated by our mathematical model. The blue profile is the optimized estimated value.

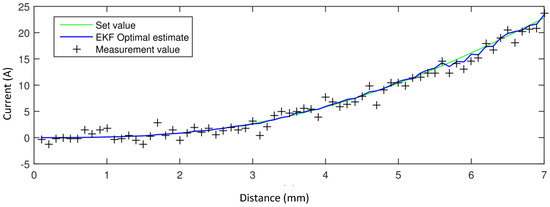
Figure 8. The effect of a current profile filtered by $EKF$.

In self-adaptive part, we set the learning time to 50. Figure 9 shows the result. The blue profiles are the 50 curves filtered by $EKF$. The red profile is the upper deviation curve, and the purple one is the lower deviation curve.

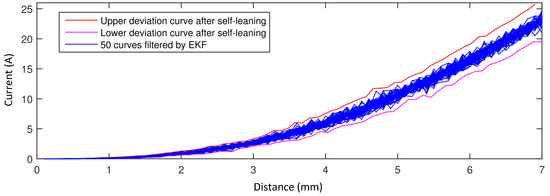
Figure 9. Result of self-adaptive mold protection method. The blue profiles are the 50 curves filtered by $EKF$. The red profile is upper deviation curve, and the purple one is the lower deviation curve.

In the next step, we took three experiments. In these experiments, we put three foreign bodies of different thicknesses into a mold individually, whose thicknesses ($D_{\alpha }$) were 1, 0.8, and 0.5 mm, respectively. Figure 10 shows the results. In case of 1 mm, it checked out the thickness was within a 0.16 mm range after touching the foreign body; i.e., $D_{\beta }$ = 0.16. In cases of 0.8 mm and 0.5 mm, the $D_{\beta }\mathrm{s}$ were 0.12 mm and 0.10 mm, respectively.

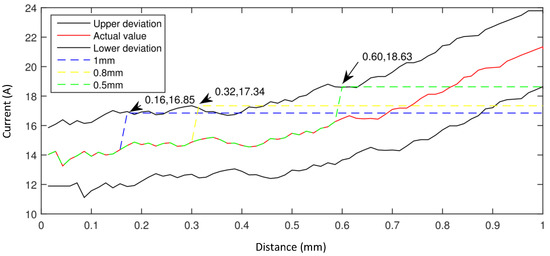
Figure 10. Current profiles when the mold closes with foreign bodies of different thicknesses.

In the last part, we compared precision of the proposed $EMP$ and general methods. In the contrast experiment, the thickness of each foreign body was arbitrary, and we tested the proposed method and the general one 100 times respectively. Figure 11 shows the results. In these 100 experiments, the average $D_{\beta }$ of proposed method was 0.94 mm, while the general one was 1.21 mm, which is a decrease of 22%.

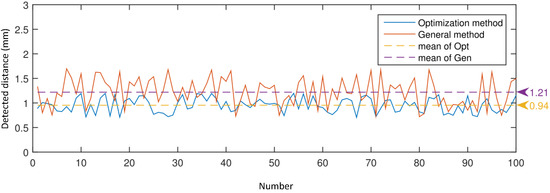
Figure 11. Detection precision comparison of the $EKF$ based self-adaptive $MP$ method and general one for 100 rounds. The thickness of each foreign body was arbitrary. Through 100 experiments, the average detected distance of the proposed method was 0.94 mm, while that of the general one was 1.21 mm. Namely, the detected distance of the proposed method was decreased by 22%.

5. Conclusions

The mold protection problem is bothering engineers because of the high maintenance price and time-consuming maintenance process. Vision-based methods need an additional vision system, and customized algorithms. Without a vision system, existing methods always take a lot of time for field engineers to adjust mold protection parameters. Therefore, we proposed an EKF-based self-adaptive method in this paper. We built a mathematical model for a toggle mechanism driven by servo systems. Using the rough values from the mathematical model and toggle mechanism system, we applied the EKF to obtain an accurate electric current. Then a self-adaptive method was proposed to obtain the safety current range. At last, the proposed method was implemented in a 140-ton $EIMM$, and the results showed that the detected distance of foreign bodies was decreased by 22% compared with the general method.

In future, a combination of the vision and proposed methods will be studied to further improve the robustness and sensitivity of the $MP$ for higher speed applications.