Mass Extinction Efficiency Approximation for Polydispersed Aerosol Using Harmonic Mean-Type Approximation

Abstract

Among many parameters characterizing atmospheric aerosols, aerosol mass extinction efficiency (MEE) is important for understanding the optical properties of aerosols. MEE is expressed as a function of the refractive indices (i.e., composition) and size distributions of aerosol particles. Aerosol MEE is often considered as a size-independent constant that depends only on the chemical composition of aerosol particles. The famous Malm’s reconstruction equation and subsequent revised methods express the extinction coefficient as a function of aerosol mass concentration and MEE. However, the used constant MEE does not take into account the effect of the size distribution of polydispersed chemical composition. Thus, a simplified expression of size-dependent MEE is required for accurate and conventional calculations of the aerosol extinction coefficient and also other optical properties. In this study, a simple parameterization of MEE of polydispersed aerosol particles was developed. The geometric volume–mean diameters of up to 10 µm with lognormal size distributions and varying geometric standard deviations were used to represent the sizes of various aerosol particles (i.e., ammonium sulfate and nitrate, elemental carbon, and sea salt). Integrating representations of separate small mode and large mode particles using a harmonic mean-type approximation generated the flexible and convenient parameterizations of MEE that can be readily used to process in situ observations and adopted in large-scale numerical models. The calculated MEE and the simple forcing efficiency using the method developed in this study showed high correlations with those calculated using the Mie theory without losing accuracy.

1. Introduction

The aerosol extinction coefficient b_ext is the key parameter that determines the aerosol optical depth by integrating over the light path; hence, it is important for the calculation of aerosol radiative forcing and the criterion of air pollution. The visibility is inversely proportional to the aerosol extinction coefficient and hence crucial for the safety and meteorological observations. Theoretically, with an assumption of the spherical shapes of the aerosol particles, the extinction coefficient of one species of distributed aerosol particles is calculated as

$$b_{ext}=\int Q_{ext}\frac{\pi }{4}{d}_p^{2}n(d_p)d{d}_p,$$

(1)

where b_ext is the extinction coefficient, Q_ext is the single particle extinction efficiency, d_p is the particle diameter, and n(d_p) is the number particle size distribution. The Mie theory-based calculations use Equation (1) for the extinction coefficient computation by integrating the Mie scattering libraries (e.g., Q_ext) over an observed particle size distribution.

Equation (1) can be rewritten as

$$b_{ext}=\int Q_{ext}\frac{\pi }{4}{d}_p^{2}n(d_p)d{d}_p=\int \frac{\pi {\rho }_p{d}_p^3}{6}n(d_p)Q_{ext}\frac{3}{2{\rho }_p{d}_p}d{d}_p,$$

(2)

where ρ_p is the particle density. Equation (2) implies that the aerosol extinction coefficient is a product of aerosol mass concentration and mass extinction efficiency (MEE, see also Figure 1), which is also known as the reconstruction method (e.g., [1,2]). Physically, aerosol MEE represents the amount of light extinction by aerosol for a given mass of aerosol in a unit volume of air [1,2]. Figure 1 shows the calculated extinction efficiency and mass extinction efficiency as a function of particle size for various aerosols using a Mie code [3] at a wavelength λ = 550 nm (Table 1). The strong dependence of both extinction efficiency (blue lines) and MEE (red lines) on the particle size and composition is revealed as also reported in previous studies (e.g., [4,5]).

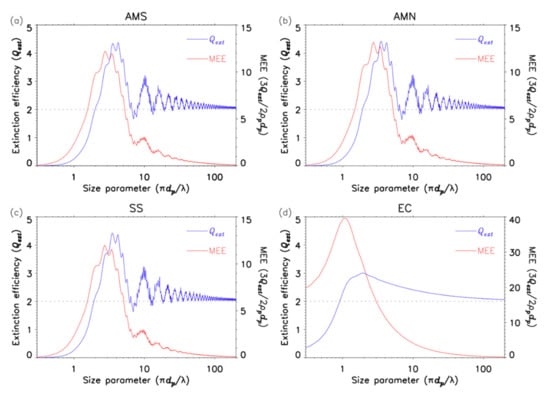
Figure 1. The calculated extinction efficiency (Q_ext, blue) and mass extinction efficiency (MEE, red) as a function of size parameter ($\pi d_p/\lambda$) for (a) ammonium sulfate (AMS), (b) ammonium nitrate (AMN), (c) sea salt (SS, NaCl), and (d) elemental carbon (EC). Mie code [3] was used for these calculations at a wavelength λ = 550 nm, and the corresponding refractive indices and density of aerosols are shown in Table 1.

Table 1. Aerosol refractive indices (m_r + im_i) at a wavelength of 550 nm [5,6] and densities for external mixing.

	Real Part (mr)	Imaginary Part (mi)	Density (g cm−3)
Ammonium sulfate	1.53	0.00	1.77
Ammonium nitrate	1.55	0.00	1.73
Elemental carbon	1.95	0.79	1.0
Sea salt	1.55	0.00	1.9

Several numerical models (e.g., the Community Multiscale Air Quality (CMAQ) modeling system [7]) provide empirical approaches, such as the reconstruction method (e.g., Equation (2)), that use mass concentrations of aerosol chemical compositions to calculate total aerosol optical depth with precalculated lookup tables. For example, Malm’s reconstruction method [8] of scattering and absorption by aerosol particles used in the Interagency Monitoring of Protected Visual Environments (IMPROVE) protocol is given by following form with an external mixing:

$$b_{ext}={{\displaystyle \sum }}_i{\mathrm{MEE}}_i\times {\mathrm{M}}_i=3f\left(\mathrm{RH}\right)\times \left[\mathrm{AMS}\right]+3f\left(\mathrm{RH}\right)\times \left[\mathrm{AMN}\right]+4\left[\mathrm{OC}\right]+10\left[\mathrm{EC}\right]+1\left[\mathrm{Soil}\right]+0.6\left[\mathrm{CM}\right],$$

(3)

where i indicates aerosol species and M_i is the mass concentration of species i. The scattering enhancement factor f(RH) is the ratio between dry and wet scattering as a function of relative humidity (RH) and wavelength. The constants of 3, 3, 4, 10, 1, and 0.6 are the MEE of ammonium sulfate (AMS), ammonium nitrate (AMN), organic carbon (OC), elemental carbon (EC), soil, and coarse mass (CM), respectively [6,8]. The square brackets indicate the mass concentration of each component. This equation assumes that contributions to total ambient light scattering are from ammonium sulfate, ammonium nitrate, organic carbon, soil, and coarse mass. Each species has the corresponding dry mass extinction (scattering; absorption) efficiency (m²g⁻¹), and the terms in the brackets correspond to mass concentrations (µg m⁻³).

Although Malm’s reconstruction method [8] is widely used to estimate the extinction coefficient, one of the main weaknesses of Malm’s equations is the assumption of size-independent mass extinction (scattering; absorption) efficiencies. Malm’s reconstruction method uses a constant MEE for each chemical species regardless of particle size, and thus, it does not take into account the size distribution of chemical compositions, which can cause visibility degradation. Thus, the extinction coefficient in Equation (3) is identical for the distributions of aerosol particles as long as their mass concentrations are identical, although there are wide variations in size distributions [9].

Figure 2 shows an example comparison of MEE as a function of geometric volume–mean diameter (d_gv) with varying geometric standard deviations (${\sigma }_g$). For AMS, AMN, sea salt (NaCl), and EC, the corresponding refractive indices and densities of externally mixed aerosols at a wavelength of 550 nm are shown in Table 1. It is clear that MEE has a strong dependence on the size distributions (i.e., different geometric standard deviations), as shown in Figure 2 and also in Figure 1. Thus, to consider the effect of particle size on the aerosol optical properties, Malm’s reconstruction method (i.e., Equation (2)) has often been modified. For example, Pitchford et al. [6] revised the Interagency Monitoring of Protected Visual Environments equation for fine and coarse particles using the Mie theory. In that study, the bimodal aerosol size distributions for AMS and AMN with two limited geometric mean diameters (geometric standard deviations) of 0.2 µm (2.2) and 0.5 µm (1.5) were used to represent fine and coarse modes, respectively. Thus, these modified expressions still could not fully describe the size-dependent mass efficiencies. Table 2 summarizes the constant mass extinction efficiencies determined in the original Malm’s equation [8] and in Pitchford’s revised method [6].

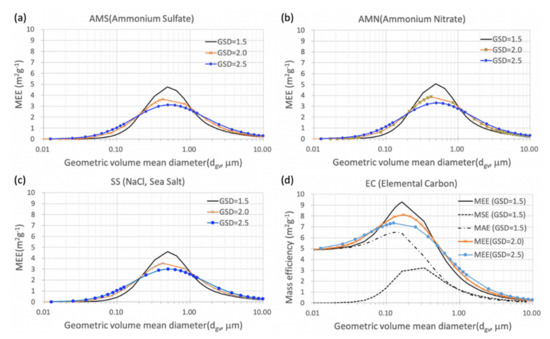
Figure 2. The calculated mass extinction efficiency (MEE) of (a) ammonium sulfate (AMS), (b) ammonium nitrate (AMN), (c) sea salt (SS, NaCl), and (d) elemental carbon (EC) as a function of geometric volume–mean diameter with varying geometric standard deviations (GSD) of 1.5, 2.0, and 2.5. For EC with GSD = 1.5, mass scattering efficiency (MSE) and mass absorption efficiency (MAE) are also embedded.

Table 2. The mass extinction efficiency (MEE, m²g⁻¹) determined in the original Malm’s equation [8] and Pitchford’s revised method [6].

MEE	Original Malm Equation	Pitchford Revised Method
		Aitken Mode	Accumulation Mode	Coarse Mode
Ammonium sulfate and ammonium nitrate	3	2.2	4.8
Organic carbon	4	2.8	6.1
Sea salt			1.7
Coarse mass	0.6			0.6
Elemental carbon	10	10	10

Another important factor to reconsider in Malm’s reconstruction method is the size-resolved parameterization of sea-salt particles. In the marine atmosphere, typical background aerosol comprises primarily produced sea-salt particles and secondarily produced particles consisting of non-sea salt sulfate and organic compounds [10]. Sea-salt particles dominate the super-micrometer fraction (d_p > 1 µm) of the aerosol size distributions. However, some primarily produced sea-salt particles contribute significantly to the sub-micrometer fraction of the particle size distribution [11,12]. In terms of the radiative forcing of the climate, the sub–micrometer size range is most relevant to light scattering because it comprises particles with diameters comparable to the wavelength of visible solar radiation. Measurements of the size-segregated chemical composition of aerosols over the Southern Ocean and the application of Mie scattering theory to those measurements confirmed the important role of sub-micrometer sea-salt particles. Sea-salt particles dominated both the chemical composition and aerosol light scattering of sub-micrometer particles [13,14]. In Malm’s original reconstruction method [8], sea-salt particles were regarded as coarse-mass particles with the constant MEE of 0.6 as shown in Equation (3). Thus, a new expression of MEE for sea-salt particles in the fine-mode size range should be developed.

Calculations of the extinction coefficient based on the Mie theory can yield more accurate results than the reconstruction method. However, it is hard to satisfy the multiple model requirements mainly because of their complexity, inconvenience, and computation time [15]. Thus, the development of a simple parameterization that accounts for the polydispersity and chemical composition of aerosol particles to calculate mass extinction (scattering; absorption) efficiency is necessary. To this end, Jung et al. [9] developed an analytic approach representing the MEE of each aerosol chemical component by fitting the calculated results to those with the Mie theory. However, the proposed approximated expression of the mass extinction (scattering; absorption) efficiencies was limited to an accumulation mode. Thus, simple but accurate new expressions of mass efficiencies for wider size ranges of atmospheric aerosols including nuclei and coarse modes are required and developed in this study.

2. Methodology

In this study, the MEE, mass scattering efficiency (MSE), and mass absorption efficiency (MAE) of polydispersed aerosol particles were calculated for the entire particle size ranges (i.e., nuclei, accumulation, and coarse modes) with varying geometric standard deviations between 1.5 and 2.5. An analytical approach to approximate an equation for the MEE with the chemical compositions was developed by fitting the calculated results obtained using the Mie theory with assumptions of lognormal aerosol size distribution and external mixture. Then, the mass efficiencies (i.e., MEE, MSE, or MAE) of all aerosol species for each size range were compared with the Mie theory-based calculations, and the parameterizations as a function of geometric volume–mean diameter in the form of a power law were developed. Subsequently, the coefficients of power-law equations were generalized as a function of geometric standard deviation. Finally, harmonic mean-type approximation was used to cover the polydispersed particle size range (up to d_gv = 10 μm). Figure 3 illustrates the methodological approach used in this study.

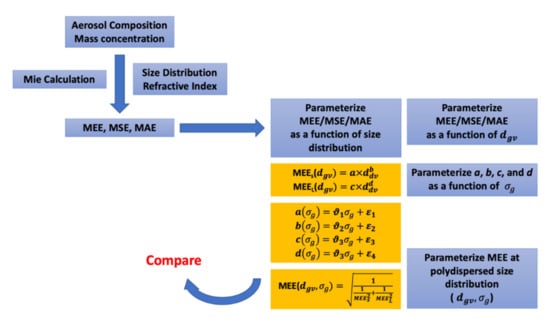
Figure 3. Schematic diagram for the calculations of mass extinction efficiency (MEE) approximation for polydisperse aerosol particles in this study. Mass scattering efficiency (MSE), mass absorption efficiency (MAE), MEE for small particle size range (MEE_S), MEE for large particle size range (MEE_L), geometric volume–mean diameter (d_gv), and geometric standard deviation (σ_g) are also specified.

2.1. Reconstruction Method vs. Mie Theory-Based Calculation

Two methods are conventionally used to calculate the optical properties of aerosols (e.g., extinction coefficient), namely the reconstruction method (e.g., Equations (2) and (3)) and the Mie-theory based calculation (e.g., Equation (1)). Aerosol mass concentrations are frequently available from numerical models and observations and, thus, the reconstruction method is more convenient than the Mie theory-based calculation because the reconstruction method can directly convert the aerosol mass concentrations to the optical properties, such as an extinction coefficient. However, the reconstruction method does not consider polydispersed particle size distribution as mentioned above. Theoretically, MEE for different sizes can be obtained based on Mie theory (i.e., Equation (1)). The Mie theory-based model calculates MEE from modeled aerosol physical characteristics including the refraction index, volume concentration, and aerosol size distribution. The Mie theory-based model yields accurate MEE if all the aerosol physical properties are known and correct. However, the reconstruction method (e.g., Equations (2) and (3)) is more widely used because of its simplicity and convenience. In this study, the modified reconstruction method was developed for deriving the parameterized MEE and the optical properties of polydispersed various species of atmospheric aerosol particles, and the results were compared with the Mie theory-based calculations.

2.2. Harmonic Mean-Type Approximation

Although the revised algorithm of Pitchford et al. [6] reduced biases by using the split–component MEE method for small and large particles, this approach still cannot fully describe the characteristics of polydispersed distributions of aerosol particles. Thus, additional modifications of the reconstruction method for polydispersed aerosol particles are required. A new approach is proposed in this study that MEE can be approximated as a power-law form of geometric volume–mean diameter that is a function of geometric standard deviation. In turn, the MEE is parameterized for various chemical compositions of aerosols with a multimodal lognormal size distribution as a function of geometric volume–mean diameter and geometric standard. In this study, the extinction coefficient of polydispersed aerosol particles are calculated as

$$\begin{gathered} b_{ext}\left(d_{gv},{\sigma }_g\right)={\mathrm{MEE}}_{AMS}\left(d_{gv},{\sigma }_g\right)\times f\left(\mathrm{RH}\right)\times \left[\mathrm{AMS}\right]+{\mathrm{MEE}}_{AMN}\left(d_{gv},{\sigma }_g\right)\times f\left(\mathrm{RH}\right)\times \\ \left[\mathrm{AMN}\right]+{\mathrm{MEE}}_{EC}\left(d_{gv},{\sigma }_g\right)\times \left[\mathrm{EC}\right]+{\mathrm{MEE}}_{SS}\left(d_{gv},{\sigma }_g\right)\times f\left(\mathrm{RH}\right)\times \left[\mathrm{SS}\right]+{\mathrm{MEE}}_{CM}\times \left[\mathrm{CM}\right], \end{gathered}$$

(4)

where the SS is sea salt (NaCl).

In this study, the harmonic mean-type approximation was adopted for calculating MEE over an entire particle size range for universal application. The harmonic mean-type approximation (half the harmonic mean) for MEE is described as follows

$$\mathrm{MEE}=\sqrt{\frac{1}{\frac{1}{{\mathrm{MEE}}_s^2}+\frac{1}{{\mathrm{MEE}}_L^2}}}.$$

(5)

The MEE for the small (MEE_S) and large (MEE_L) size ranges are represented in a power–law form of the geometric volume–mean diameter:

$${\mathrm{MEE}}_S=a\times d_{gv}^b \mathrm{and} {\mathrm{MEE}}_L=c\times d_{gv}^d$$

(6)

where a, b, c, and d are coefficients to be determined. In Equation (5), MEE converges to MEE_S and to MEE_L for small and large particle size ranges, respectively. In the intermediate region between small and large particle ranges, MEE is calculated as a harmonic mean-type approximation as described in Equation (5). The harmonic mean-type approximation has been used to estimate the coagulation and condensation kernel in the low Knudsen particle size region [15,16,17,18,19]. The main advantage of the harmonic mean-type approximation is that it enables the evaluation of an analytical expression for intermediate particle size ranges [18,19,20].

MEE is represented as a function of geometric volume–mean diameter as shown in Equations (5) and (6). A geometric volume–mean diameter (d_gv) is related with a geometric mean diameter (d_g) and a geometric standard deviation (${\sigma }_g$) as follows

$$\ln d_{gv}=\ln d_g+3{\ln }^2{\sigma }_g.$$

(7)

In this study, polydispersed size distributions of aerosol particles are represented by a lognormal distribution function

$$n\left(\ln d_p\right)=\frac{N}{\sqrt{2\pi }\ln {\sigma }_g}\exp \left[\frac{-{\ln }^2\left(d_p/d_g\right)}{2{\ln }^2{\sigma }_g}\right],$$

(8)

where N is the total number concentration of aerosol particles.

The coefficients a, b, c, and d in Equation (6) are represented as a linear expression of geometric standard deviation. For example, the coefficients a, b, c, and d are a function of geometric standard deviation and represented as

$$\begin{gathered} a={\vartheta }_1{\sigma }_g+{\epsilon }_1, \\ b={\vartheta }_2{\sigma }_g+{\epsilon }_2, \\ c={\vartheta }_3{\sigma }_g+{\epsilon }_3, \mathrm{and} \\ d={\vartheta }_4{\sigma }_g+{\epsilon }_4, \end{gathered}$$

(9)

where $\vartheta$ and $\epsilon$ are constants to be determined. The same procedure that is used for the calculation of MEE is applicable for those of MAE. In this study, EC was the only absorbing aerosol (see Table 1), and thus, MAE was calculated only for the EC.

3. Results

Figure 4 shows the comparison of the approximated MEE (long dashed red line) and that based on the Mie theory (solid black line) for AMS (left column) and AMN (right column). Geometric standard deviations of 1.5 (top row), 2 (middle row), and 2.5 (bottom row) were considered in these calculations. The MEE_S (MEE_L) for a small (large) size range is shown with the dotted blue (yellow) line in each panel. The MEE_S and MEE_L were approximated by fitting the Mie theory-based calculations (i.e., solid black line) in the form of a power law (i.e., Equation (6)) for $\frac{d\mathrm{MEE}}{d{d}_{gv}}>0$ and $\frac{d\mathrm{MEE}}{d{d}_{gv}}<0$, respectively.

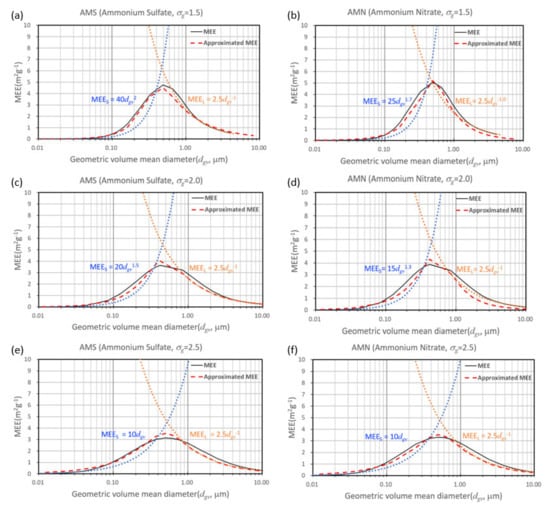
Figure 4. Comparison between the Mie-calculated mass extinction efficiency (MEE, solid black lines) and the approximated mass extinction efficiency (long-dashed red lines) of ammonium sulfate (AMS, left column) and ammonium nitrate (AMN, right column) for geometric standard deviations (${\sigma }_g$) of 1.5 (top row), 2.0 (middle row), and 2.5 (bottom row). The approximated mass extinction efficiency in each panel is calculated based on the MEE_S (dotted blue line) and the MEE_L (dotted yellow line) in each panel using Equation (5).

The MEE_S for AMS were approximated as ${\mathrm{MEE}}_S=40d_{gv}^2$, ${\mathrm{MEE}}_S=20d_{gv}^{1.5}$, and ${\mathrm{MEE}}_S=10d_{gv}^{1.0}$ for geometric standard deviations of 1.5, 2.0, and 2.5, respectively. For AMN, they were ${\mathrm{MEE}}_S=25d_{gv}^{1.7}$, ${\mathrm{MEE}}_s=15d_{gv}^{1.3}$, and ${\mathrm{MEE}}_s=10d_{gv}^{1.0}$. The MEE_L for both AMS and AMN was approximated as ${\mathrm{MEE}}_L=2.5d_{dv}^{-1}$ for all geometric standard deviations. For the intermediate size range, the MEE was determined by the harmonic mean-type approximation in Equation (5). It is shown that the Mie theory-based calculations of MEE and those approximated using the method proposed in this study are comparable without much loss of accuracy. It is also shown that the smooth transition from a small to large size range and vice versa is achieved by the approximated method.

A comparison between the approximated MEE (long dashed red line) and that based on the Mie theory (solid black line) for sea salt (left column) and EC (right column) for geometric standard deviations of 1.5 (top row), 2.0 (middle row), and 2.5 (bottom row) is shown in Figure 5.

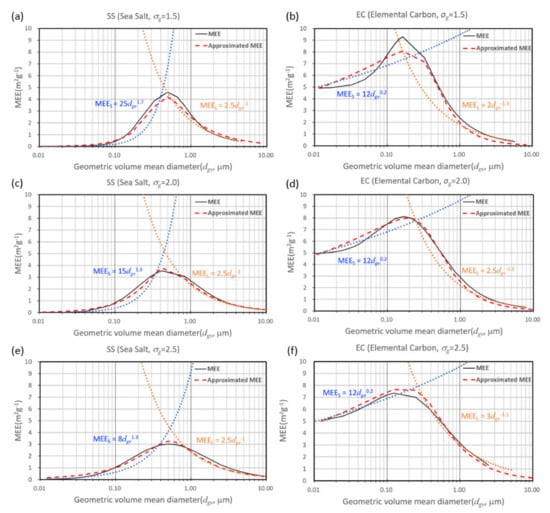
Figure 5. Same as Figure 4, but for sea salt (SS, left column) and elemental carbon (EC, right column).

For sea salt, the MEE_S was approximated as ${\mathrm{MEE}}_s=25d_{gv}^{1.7}$, ${\mathrm{MEE}}_s=15d_{gv}^{1.3}$, and ${\mathrm{MEE}}_s=8d_{gv}^{1.3}$ for geometric standard deviations of 1.5, 2.0, and 2.5, respectively, while the MEE_L was approximated as ${\mathrm{MEE}}_L=2.5d_{gv}^{-1}$ for all geometric standard deviations, as in the cases of AMS and AMN.

In contrast, for EC, the MEE_S was approximated as $12d_{gv}^{0.2}$ regardless of geometric standard deviation, while the MEE_L had different representations for different geometric standard deviations. The approximated MEE_L for EC was ${\mathrm{MEE}}_L=2d_{gv}^{-1.5}$, ${\mathrm{MEE}}_L=2.5d_{gv}^{-1.3}$, and ${\mathrm{MEE}}_L=3d_{gv}^{-1.1}$ for geometric standard deviations of 1.5, 2.0, and 2.5, respectively. The same procedure to determine MEE_S and MEE_L (Equation (6)) and MEE for intermediate size range by harmonic mean-type approximation (Equation (5)) for AMS and AMN in Figure 4 was also applied to sea salt and EC.

Figure 4 and Figure 5 show that the MEE can be estimated by using harmonic mean-type approximation for each size distribution. The power-law coefficients a and b are represented as a linear expression of geometric mean diameter as explained in Equation (9). Subsequently, the resultant approximated expression for MEE is as follows:

$$\begin{gathered} \mathrm{MEE}={\left({\left(a\times d_{gv}^b\right)}^{-2}+{\left(c\times d_{gv}^d\right)}^{-2}\right)}^{-\frac{1}{2}}={\left\{{\left(\left({\vartheta }_1{\sigma }_g+{\epsilon }_1\right)\times d_{gv}^{\left({\vartheta }_2{\sigma }_g+{\epsilon }_2\right)}\right)}^{-2}+ \\ {\left(\left({\vartheta }_3{\sigma }_g+{\epsilon }_3\right)\times d_{gv}^{\left({\vartheta }_4{\sigma }_g+{\epsilon }_4\right)}\right)}^{-2}\right\}}^{-\frac{1}{2}}. \end{gathered}$$

(10)

Figure 6 shows the determined MEE coefficients (a, b, c, and d) as a function of geometric standard deviation. For AMS (Figure 6a,b), AMN (Figure 6c,d), and sea salt (Figure 6e,f), the MEE_L values were approximated using the same equation (${\mathrm{MEE}}_L=2.5d_{gv}^{-1}$), which means that c and d were 2.5 and −1, respectively, regardless of geometric standard deviation. For EC, the MEE_S values were approximated to be ${\mathrm{MEE}}_s=12d_{gv}^{0.2}$ regardless of geometric standard deviation. The remaining coefficients (a and b for AMS, AMN, and sea salt, and c and d for EC) were linear as a function of geometric standard deviation, as shown in Figure 6. Table 3 summarizes the determined coefficients a, b, c, and d of each aerosol component as a function of geometric standard deviation. The determined coefficients of strongly absorbing EC were distinct from non-absorbing other aerosol species. Based on Figure 4, Figure 5 and Figure 6 and Table 3, the MEE can be approximated as analytical equations for each component of polydispersed aerosol particles. For example, the MEE_S and MEE_L values of AMS can be approximated as a simple form of

$${\mathrm{MEE}}_s=a\times d_{gv}^b=\left(-30{\sigma }_g+83.33\right)\times d_{gv}^{\left(-{\sigma }_g+3.5\right)} \mathrm{and} {\mathrm{MEE}}_L=c\times d_{gv}^d=2.5\times d_{gv}^{-1}.$$

(11)

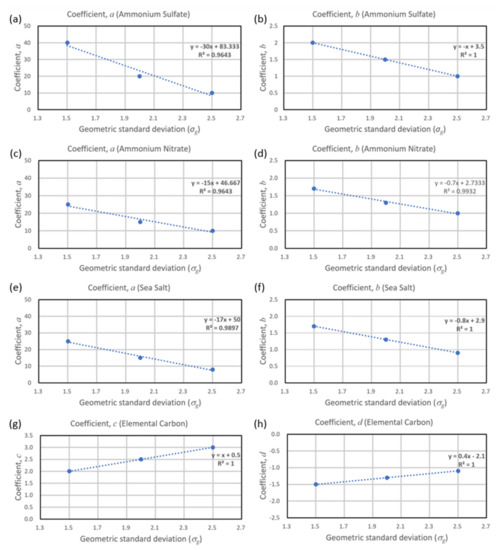
Figure 6. The determined mass extinction efficiency coefficients a and b as a function of geometric standard deviation in Equation (6) for ammonium sulfate (a,b), ammonium nitrate (c,d), and sea salt (e,f). For elemental carbon coefficients, c (g) and d (h) are determined.

Table 3. Determined coefficients (a, b, c, and d) of mass extinction efficiency in Equation (6) as a function of geometric standard deviation ${\sigma }_g$.

	$\mathit{a}$	$\mathit{b}$	$\mathit{c}$	$\mathit{d}$
Ammonium sulfate	$-30{\sigma }_g+83.33$	$-{\sigma }_g+3.5$	2.5	−1
Ammonium nitrate	$-15{\sigma }_g+46.67$	$-0.7{\sigma }_g+2.73$	2.5	−1
Sea salt	$-17{\sigma }_g+50$	$-0.8{\sigma }_g+2.9$	$2.5$	−1
Elemental carbon	12	0.2	${\sigma }_g+0.5$	$0.4{\sigma }_g-2.1$

The extinction coefficient now can be expressed as a function of the size distribution parameters (i.e., geometric volume–mean diameter and geometric standard deviation):

$$\begin{gathered} b_{ext}={{\displaystyle \sum }}_i{\mathrm{MEE}}_i\times M_i={{\displaystyle \sum }}_i{\left\{{\left(\left({\vartheta }_{1,i}{\sigma }_{g,i}+{\epsilon }_{1,i}\right)\times d_{gv,i}^{\left({\vartheta }_{2,i}{\sigma }_{g,i}+{\epsilon }_{2,i}\right)}\right)}^{-2}+{\left(\left({\vartheta }_{3,i}{\sigma }_{g,i}+{\epsilon }_{3,i}\right)\times \\ {d}_{gv,i}^{\left({\vartheta }_{4,i}{\sigma }_{g,i}+{\epsilon }_{4,i}\right)}\right)}^{-2}\right\}}^{-1/2}\times {\mathrm{M}}_i. \end{gathered}$$

(12)

To represent absorbing properties, the MAE of EC can also be approximated using the same approach of

$$b_{abs}={\mathrm{MAE}}_{EC}\times {\mathrm{M}}_{EC},$$

(13)

where MAE is expressed as follows:

$$\mathrm{MAE}={\left\{{\left(7\times d_{gv,i}^{0.08}\right)}^{-2}+{\left(\left(0.5{\sigma }_g+0.25\right)\times d_{gv,i}^{\left(0.6{\sigma }_g-2.6\right)}\right)}^{-2}\right\}}^{-\frac{1}{2}}.$$

(14)

Figure 7 shows the comparison of the approximated MAE and that using Mie theory for EC with varying geometric standard deviations of 1.5, 2.0, and 2.5 were considered to represent polydispersed aerosol size. The harmonic mean-type analytical expression for MAE proposed in this study (i.e., Equation (14)) also agreed with the results of the Mie theory-based calculations.

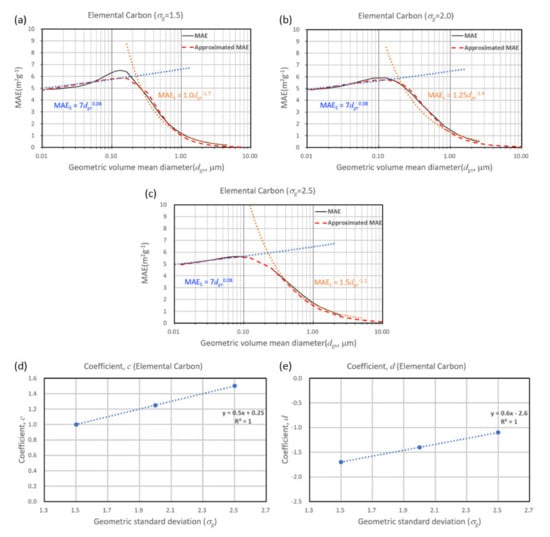
Figure 7. Comparison between the Mie theory-based calculation of mass absorption efficiency (MAE, solid black lines) and the approximated MAE (long-dashed red lines) of elemental carbon for geometric standard deviations (${\sigma }_g$) of (a) 1.5, (b) 2.0, and (c) 2.5. The approximated mass extinction efficiency in each panel is calculated based on the MAE_S (dotted blue line) and the MAE_L (dotted orange line) in each panel using Equation (5). The determined coefficients c and d of MAE as a function of geometric standard deviation in Equation (6) for elemental carbon are shown in panel (d,e).

To test the accuracy of the newly developed MEE approximation, the simple forcing efficiency (SFE) [5,21] of individual aerosol species was calculated. The simple forcing efficiency of chemical composition i based on direct aerosol radiative forcing at the top of the atmosphere is represented as follows:

$${\mathrm{SFE}}_i=-\frac{S_0}{4}{T}_{atm}^2\left(1-N\right)\left[{\left(1-\alpha \right)}^{2}2\beta {\mathrm{MSE}}_i-4\alpha {\mathrm{MAE}}_i\right],$$

(15)

where the unit of SFE is Wg⁻¹, S₀ is the solar constant (1370 W/m²), S₀/4 is the globally averaged incident solar flux at the top of the atmosphere, T_atm is the transmittance of the atmosphere above the aerosol layer (0.76), N is the fraction of sky covered by clouds (0.6), λ is the albedo of the underlying surface (0.15), and λ is the fraction of radiation scattered by aerosols into the upper hemisphere (0.125).

Figure 8 shows the comparison between the calculated SFE using the analytically approximated mass efficiency and that using the Mie theory with varying geometric standard deviations. The comparison is germane because calculations of radiative forcing by aerosols are of great interest in large-scale numerical models and hence climate studies. It is shown that the calculated SFE values using the analytically approximated mass efficiency and that using the Mie theory have large correlations (r² > 0.97) and small root mean square errors (RMSEs) for all aerosol species. These solid results do not depend on the variation of geometric standard deviations. For AMS, the r² is 0.986 (0.981; 0.983) for the geometric standard deviation of 1.5 (2.0; 2.5). These are 0.984 (0.961; 0.985) for AMN, 0.987 (0.990; 0.988) for SS, and 0.994 (0.998; 0.997) for EC. Thus, it is shown that the newly developed method that approximates MEE has comparable accuracy compared with the Mie theory-based calculations.

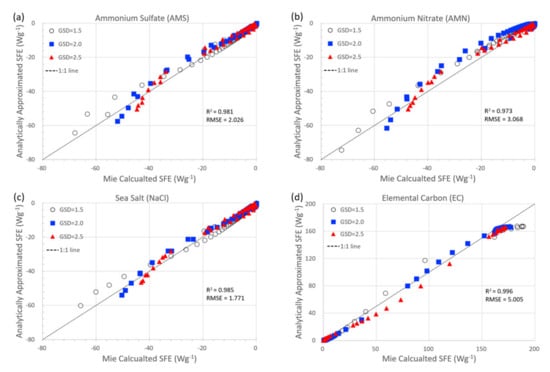
Figure 8. Comparison between the simple forcing efficiency (SFE) calculated using analytical approximation and those using Mie theory-based calculation for (a) ammonium sulfate (AMS), (b) ammonium nitrate (AMN), (c) sea salt (NaCl), and (d) elemental carbon (EC) with geometric standard deviations (GSD) of 1.5, 2.0, and 2.5. The correlation coefficient (r²) and root mean square error (RMSE) are embedded in each panel. The black dotted line in each panel is a 1:1 line.

4. Summary and Discussion

In this study, simple and flexible analytical expressions of mass extinction (scattering; absorption) efficiencies taking into account the effects of sizes and chemical compositions of aerosol particles were developed without losing accuracy compared with the Mie theory-based calculations. The polydispersed size range (i.e., geometric volume–mean diameters of up to 10 µm and geometric standard deviations of 1.5, 2.0, and 2.5) of aerosol particles was considered with lognormal size distributions for ammonium sulfate, ammonium nitrate, sea salt, and elemental carbon aerosols. The MEE (MSE and MAE) of each aerosol chemical composition was first determined by the separate fitting of the Mie theory-based calculations for small (MEE_S) and large (MEE_L) size ranges in the form of power-law relationships. The coefficients of the power-law relationships were represented as linear expressions of geometric standard deviation, which allowed flexible parameterizations of various size distributions. The MEE for the intermediate size range was determined using the MEE_S, MEE_L, and harmonic mean-type approximation. To test the accuracy of the newly developed MEE approximation, the simple forcing efficiency of aerosol was also examined. The calculated MEE and simple forcing efficiency using the newly developed method showed high correlations with those determined using the Mie theory-based calculations.

Conventional methods that calculate the aerosol extinction coefficient based on observations and outputs of numerical models depend exclusively on the reconstruction methods and their modifications. However, such methods do not take into account the effects of sizes and compositions of aerosol particles, while the newly developed method proposed in this study does. The flexible and convenient parameterizations of MEE developed in this study can be readily used to process in situ observations and adopted in large-scale numerical models. This method would be especially well suited to study the aerosol measurement in the ocean. A subsequent study will examine how the realistic non-spherical shapes of aerosol particles affects calculations of MEE and extinction coefficient and attempt to reduce errors in results between the reconstruction methods and the Mie theory-based calculations. The scattering enhancement factor f(RH) is of great interest and should be improved [22].