Featured Application
Aims to execute novel optimisation algorithms such as whale optimisation and lion optimisation to find the optimal Virtual_Ms on cloud environment as well as executing our model in different applications.
Abstract
Cloud computing has a significant role in healthcare services, especially in medical applications. In cloud computing, the best choice of virtual machines (Virtual_Ms) has an essential role in the quality improvement of cloud computing by minimising the execution time of medical queries from stakeholders and maximising utilisation of medicinal resources. Besides, the best choice of Virtual_Ms assists the stakeholders to reduce the total execution time of medical requests through turnaround time and maximise CPU utilisation and waiting time. For that, this paper introduces an optimisation model for medical applications using two distinct intelligent algorithms: genetic algorithm (GA) and parallel particle swarm optimisation (PPSO). In addition, a set of experiments was conducted to provide a competitive study between those two algorithms regarding the execution time, the data processing speed, and the system efficiency. The PPSO algorithm was implemented using the MATLAB tool. The results showed that the PPSO algorithm gives accurate outcomes better than the GA in terms of the execution time of medical queries and efficiency by 3.02% and 37.7%, respectively. Also, the PPSO algorithm has been implemented on the CloudSim package. The results displayed that the PPSO algorithm gives accurate outcomes better than default CloudSim in terms of final implementation time of medicinal queries by 33.3%. Finally, the proposed model outperformed the state-of-the-art methods in the literature review by a range from 13% to 67%.
1. Introduction
Currently, cloud computing is used in many Healthcare service (HCS) applications because of its ability to provide various medical services over the internet. Nevertheless, the optimal selection of virtual machines (Virtual_Ms) to process a medical request has always been a challenge. Optimal selection of Virtual_Ms provides a significant improvement of performance by reducing the execution time of medical requests and maximising utilisation of cloud resources. Cloud computing provides on-demand infrastructure services to large numbers of stakeholders. It supports large numbers of parallel requests and simultaneous accesses by stakeholders, in a dynamic way [1,2], to identify or predict disease in minimum time.
Healthcare service (HCS) applications can predict or diagnose diseases, such as kidney and heart diseases, cancer, and diabetes [3,4,5,6,7], and are used by large numbers of stakeholders. Healthcare service (HCS) applications can be used for hospital provisions, optometric examinations, surgical management, dental and complementary health facilities, and nursing [1,2]. From the technical point of view, the cloud is composed of datacentres, hosts, Virtual_Ms, resources, and storage that stakeholder’s access to predict or diagnose diseases [8,9]. Datacentres provide the housing for servers. Hosts are servers that host several Virtual_Ms that process and store medical resources and allow stakeholders to retrieve those resources. Cloud computing uses virtualisation to share the resources of a host between various stakeholders and organisations [10]. Virtualisation is divided into hardware, operating system (OS), and storage virtualisation. Hardware virtualisation allows multiple users to share the resources of a host [9,11]. Operating system virtualisation provides container isolation for running different applications on a single computer and storage virtualisation abstracts physical storage, allowing multiple aggregate devices into single storage [12,13].
Our primary objective is to find the best choice of Virtual_Ms to minimise the total execution time of medical requests on the cloud environment and maximise the utilisation of resources. Some of the swarm intelligence approaches used for optimal Virtual_Ms selection are bee colony optimisation (BCO), ant colony optimisation (ANT), bat optimisation [14,15,16], and particle swarm optimisation (PSO). Still, most of these approaches cannot use parallel computing. Bee colony optimisation (BCO) is a population-based algorithm which is inspired by the smart behaviour of honeybees but has two main disadvantages: (1) it has slow convergence and (2) many control parameters. ANT is used to identify the optimal solution from a set of solutions, based on the behaviour of ants probing food. Still, it is not appropriate to do a parallel search in a population. Particle swarm optimisation is used to find the best solution from a set of solutions by using particles to simulate population and swarm to reach a solution. Still, it also does not use parallel computation, and it cannot handle the problem of scattering. However, parallel particle swarm optimisation (PPSO) currently is used selecting Virtual_Ms for medical processing requests, which come from stakeholders and overcome the drawbacks of the existing system [9]. PPSO divides the population into sub-populations and applies the algorithm separately to these sub-populations to minimise execution time [2,17]. It is therefore suitable to process parallel requests from different stakeholders with good execution time.
Genetic algorithms can also be used to find high-quality solutions to optimisation and search problems inspired by biology. They have very good optimisation ability and internal implicit parallelism and can obtain the optimised solution and adjust the solution direction automatically through the optimisation method of probability [18,19]. They are part of evolutionary computing, which is inspired by Darwin’s theory about evolution. The algorithm is started with a set of solutions and tries to find the best solution through them according to their fitness—the more suitable they are, the more chances they have to reproduce, this is repeated until some condition is satisfied [20].
Currently, many healthcare applications that predict or diagnose diseases do not support real-time use, which maximises the time to respond to medical requests and remains a big challenge for most of the stakeholders in HCS [21]. Within this context, this paper aims to find the best choice of Virtual_Ms to reduce the total execution time of a medical request while easily accessing patient data and maximise the utilisation of resources. This paper proposes a new methodology for HCS based on cloud environment using parallel particle swarm optimisation (PPSO) and the genetic algorithm (GA) to optimise the Virtual_Ms selection.
- Firstly, we run both algorithms to select the Virtual_Ms to minimise the total execution time of medical requests on the cloud environment and maximise the utilisation of resources.
- Secondly, we compare both algorithms, and we select the best algorithm in terms of speedup and efficiency.
- Finally, we apply the best algorithm in the CloudSim package to verify the performance of this algorithm in a cloud environment. The objective function relies on three parameters which are turnaround time, waiting time, and CPU utilisation.
Most of the studies in related work have suggested the GA to select the optimal VM on the cloud environment. However, these studies did not reach optimal results to solve this problem. Therefore, this paper tries to explain GA results widely and compares it to another algorithm called PPSO to select the optimal algorithm between them.
This paper is organised as follows: Section 2 discusses the background and concepts of this study. Section 3 discusses the related work, and Section 4 describes the methodology used in this study. Section 5 presents the results and discussion of the experiments and, finally, Section 6 concludes the paper.
2. Related Work
In recent literature, several studies and approaches are using optimisation algorithms to select the optimal Virtual_Ms for reducing the execution time of a request, such as swarm intelligence approaches and multi-objective genetic algorithms.
Almezeini et al. [22] proposed a new method to improve and enhance task scheduling on a cloud computing environment using lion optimisation. In this study, the authors are trying to improve the performance of Virtual_Ms and maximise resources utilisation while reducing the server’s energy consumption. Ajith Sing et al. [1] proposed a new method of finding optimal Virtual_Ms placement in a datacentre in a cloud environment based on the honeybee algorithm with hierarchical clustering. In this study, the authors are trying to reach optimal Virtual_Ms placement to maximise resources utilisation and reduce energy consumption in servers using the Planet Lab tool.
Barlaskar et al. [23] introduced a new method of finding optimal Virtual_Ms placement based on the hierarchical cluster-based modified firefly algorithm (HCMFF). In this study, the authors are trying to get energy-efficient placement to optimise energy consumption in the cloud environment. The results of the simulation showed that HCMFF performs better than the honeybee algorithm and the original firefly algorithm. Fang et al. [24] proposed a new framework that detects the optimal Virtual_Ms placement on a cloud environment based on ant colony optimisation (ACO). This study tries to detect Virtual_Ms placement of datacentre to minimise energy cost and energy savings and to maximise the quality of Virtual_Ms.
Lei Chen et al. [10] presented a multitarget heuristic algorithm to solve the problem of Virtual_Ms placement by reducing the number of servers in the cloud and improving the efficiency of resource retrieval. In this study, the authors are focusing on efficient Virtual_Ms placement by reducing the energy consumption in servers, maximising resources utilisation and wastage rate in the datacentres. Shabeera et al. [25] introduced a model to find optimal Virtual_Ms on the cloud environment based on the ACO algorithm, reducing the energy consumption in servers, and enhancing data placement for data-intensive applications.
Dong et al. [26] introduced a new approach to detect the optimal Virtual_Ms placement in a cloud environment based on distributed parallel genetic algorithms (DPGA). In this study, the authors are trying to improve performance for running Virtual_Ms, maximise utilisation of resources and reduce energy consumption in servers. Teyeb et al. [27] proposed a new formulation to solve the problem of Virtual_Ms placement in datacentres on cloud computing based on multi-commodity flow and adopt variable aggregating methods. In this study, the authors aim to detect the optimal Virtual_Ms placement by minimising the total running time and computational resources.
Fu et al. [28] proposed a new technique to find optimal Virtual_Ms in datacentre based on dynamic consolidation of Virtual_Ms. The proposed technique focuses on minimising the cost spending in each plan for hosting Virtual_Ms in multiple cloud providers and the response time of each cloud provider is monitored periodically, in such a way to minimise delay in providing the resources to the users. In this study, the authors use dynamic consolidation to minimise energy consumption, response time, and improve physical resource utilisation. Camati et al. [12] proposed a new method to solve the problem of Virtual_Ms placement using the multiple multidimensional knapsack problem (MKP). In this study, the authors are trying to solve the Virtual_Ms placement problem by expediting task scheduling and minimising energy consumption in servers.
Chaurasia et al. [29] proposed a novel method to choose optimal Virtual_Ms placement for migration leading to server consolidation based on Pareto Optimal solution and the Fuzzy technique for order of preference by similarity to ideal solution (TOPSIS). In this paper, the authors are trying to choose the best Virtual_Ms placement by minimising the response time and the power consumption in servers while maximising resources utilisation. Parikh et al. [17] introduced a new strategy to find the best Virtual_Ms allocation in cloud computing based on the Hungarian algorithm. In this study, the authors are trying to find the best load balancing of services in the cloud through the scheduling of Virtual_Ms in the datacentre and use the CloudSim tool to verify the results. Zhao et al. [13] introduced a new method to select the best Virtual_Ms placement of live Virtual_Ms based on improved particle swarm optimisation (PSO), simulated annealing, probability theory, and mathematical statistics. In this study, the authors are trying to improve the total energy consumption in servers, protect the quality of Virtual_Ms running, and maximise resource utilisation using the CloudSim platform.
Vidhya et al. [30] introduced a new method for reducing data redundancy in heterogeneous cloud storage based on the PPSO algorithm and Monte Carlo sampling. In this study, the authors are trying to reduce the computation time of the algorithm and assign data blocks according to their online availability, resulting in reduced storage and communication costs. Garino [31] proposed a two-level scheduler of Virtual_Ms on the cloud environment based on PSO. In this study, the authors compare the PSO with round-robin (RR) and GA to detect the best Virtual_Ms placement using the CloudSim package as a simulation tool. Thiruvenkadam et al. [32] proposed a novel framework to find the best Virtual_Ms placement in the datacentre based on a queuing algorithm, traffic and load aware scheduling algorithms, and the ant colony optimisation algorithm. In this study, the authors are trying to improve Virtual_Ms placement to maximise resources utilisation and reduce response time, power usage, load imbalance rate, and migration rate. Seddigh et al. [33] introduced a virtual machine dynamic prediction scheduling method via ant colony optimisation (VMDPS-ACO) to evaluate the scheduling of Virtual_Ms in a datacentre based on the ant colony optimisation (ACO) algorithm and VM dynamic forecast scheduling (VM_DFS). This study seeks to predict the placement of Virtual_Ms in the datacentre to save power consumption using the CloudSim package as a simulation tool.
Dashti et al. [34] introduced a hierarchical architecture to satisfy the requirements of both providers and consumers in cloud computing technologies. They developed a new service in the platform as a service (PaaS) layer for managing consumer tasks and lower energy efficiency by modifying particle swarm optimisation to reallocate migrated Virtual_Ms in overloaded hosts and to create the under-loaded hosts which allow power-saving dynamically. Parmar et al. [35] proposed a Virtual_Ms allocation load balancing algorithm based on the Assignment Problem’s solution method concept for cloud environments to improve the execution time and utilise resources. Moorthy et al. [36] proposed an ant colony optimisation allocation Virtual_Ms to minimise the cost of managing Virtual_Ms hosting and the delay in delivering the resources to the users in a multiple cloud environment. The proposed algorithm is simulated in Eclipse integrated development environment (IDE) Hanen et al. [37] introduced a new mobile medical web service system by implementing a medical cloud multi-agent system (MCMAS) solution, using Google’s Android operating system and using the CloudSim simulator. Table 1 below summarises the previous related works with information on the task domain, methods, and results.

Table 1.
Related work summary.
Compared to some of the state-of-the-art algorithms from the literature, the proposed solution is improved in terms of the execution time of medical requests, see below Section 5. The findings indicate that the enhancement proportion regarding the state-of-the-art methods in the literature is in the range of 13% to 67%. This enhancement can be noted in Figure A1 see Appendix A for more details.
3. The Proposed Intelligent Model
This section shows the proposed intelligent model of cloud computing for medical applications. It is composed of five subsections, as follows:
- Stakeholders’ Devices
- Stakeholders’ Queries (Tasks)
- Cloud Broker
- Network Administrator
- Healthcare Services
Figure 1 explains the subsections of the intelligent model as follows:
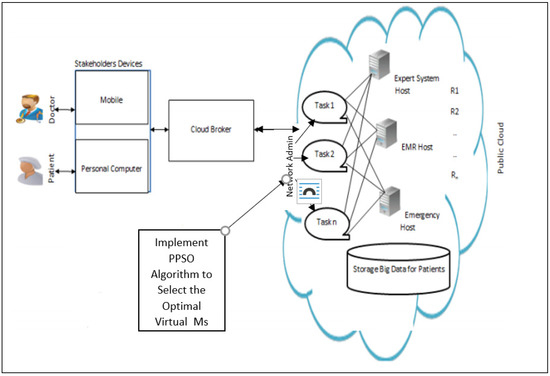
Figure 1.
The proposed intelligent model of cloud computing for medical applications.
- Stakeholder uses intelligent devices to transmit many medicinal queries efficiently via the cloud environment to gain many medicinal responses, such as disease diagnosis services and management of electronic medical records (EMR).
- The cloud broker is responsible for sending and receiving queries from the cloud service.
- The network administrator is responsible for the management of the connections between the hosts inside the network in the cloud.
- The network administrator is implementing an intelligent algorithm (PPSO algorithm) that it uses to obtain the best choice of Virtual_Ms in the cloud to minimise the execution time of stakeholders’ queries and maximise resources utilisation.
- Medical cloud introduces many healthcare services, such as diagnosis of diseases, telemedicine, EMR, and emergency medical data.
4. The Proposed Genetic Algorithm and Parallel Particle Swarm Optimisation in the Cloud
This section shows the genetic algorithm (GA) and parallel particle swarm optimisation (PPSO) algorithm for cloud computing to compute total execution time of stakeholders’ medical queries. The cost function is used to define the best choice of Virtual_Ms on the cloud environment via three factors, which are waiting time, CPU utilisation, and turnaround time. These factors are composed of three parameters, as follows:
- Arrival Time (AT): time at which the task arrives in the ready queue.
- Burst Time (BT): the time required by a task for CPU execution. BT is calculated as follows:where:BT = Clock Time to Burst/Burst RatioBurst ratio = Burst Threshold/Burst Limit
- Completion Time (CT): time at which task completes its execution.
Table 2 shows the three parameters which are needed to compute the total implementation time of medical queries from stakeholders.

Table 2.
Factors of optimal selection of Virtual Machines.
The three factors mentioned in Table 2 represent the cost function used in this study. It helps stakeholders in medical applications to reduce the implementation time of medical queries by using GA or PPSO to find optimal Virtual_Ms in the cloud environment.
4.1. The Proposed Genetic Algorithm in Cloud Environment
In this subsection, we extensively explain the proposed genetic algorithm (GA) that is utilised to execute our proposed model. The significant chromosomes’ size, mutation, and crossover prospects are producing new offspring that assists in obtaining novel solutions.
Suppose that there are F (GA) chromosomes population (Virtual_Ms) = 1000 and a set of iteration = 100. Each Virtual_Ms in the cloud environment is represented as a chromosome which considers a possibility solution (Virtual_Ms) that can be assigned for implementing the stakeholder’s requests. Calculate cost function (optimally chosen of Virtual_Ms) by using CPU Utilisation (U), Turnaround Time (TT), and Waiting Time (WT). If the stakeholder’s request is concluded, find the optimal implementation request time and optimally chosen Virtual_Ms, otherwise, execute selection, crossover, mutation, process, and produce new chromosomes, as shown below in Algorithm 1.
The selection process assists in holding the best chromosomes (Virtual_Ms) and electing a proper pair from each chromosome (Virtual_Ms). It relies on the division of the 2 chromosomes (two Virtual_Ms on the cloud environment) randomly and compares between them to select the best one. So, execute the 2-points crossover process between two chromosomes (two Virtual_Ms) and obtain two different offspring. The crossover process is computed by using two Equations (3) and (4) as follows:
where:
Offspring A = H × P1 + (1 − H) × P2
Offspring B = (1 − H) × P1 + H × P2
- H = random number (elected before each crossover process)
- P = parent (Virtual_Ms)
The purpose of the mutation process is to hold small changes in chromosomes. So, it utilises a flip bit mutation method for that purpose. In chromosomes (Virtual_Ms), the mutation process changes one or more gene values from its initial state. Mutation = 0.5. Algorithm 1 shows scientific steps to apply GA on the cloud environment, as follows.
- α = population,
- β = rate of Elitism,
- Y = rate of Mutation,
- σ = number of Iterations
| Algorithm 1. Genetic Algorithm (GA) Steps for Selecting Virtual_Ms on Cloud Environment. | |
| 1. | Input: Size α of population, |
| 2. | Rate β of Elitism, |
| 3. | Rate Y of Mutation, |
| 4. | Number σ of Iterations |
| 5. | Output: H ← (Optimal Chromosomes (Virtual_Ms), Optimal Exec Time) |
| 6. | Stakeholders Tasks = ST |
| 7. | Count I = 0 |
| 8. | Pk = Produce random σ solutions |
| 9. | Calculate fitness function (i) for each I Ɛ Pk |
| 10. | While (ST ≠ 0) |
| 11. | For I = 0 to σ do |
| 12. | Select chromosomes (Virtual_Ms) for tournament |
| 13. | Find chromosomes (Virtual_Ms) with the lowest fitness |
| 14. | Remove chromosomes (Virtual_Ms) with the lowest fitness |
| 15. | Two-points crossover process (create new chromosomes) |
| 16. | Evaluate new chromosomes (Virtual_Ms) |
| 17. | End for |
| 18. | BitFlip Mutation |
| 19. | Evaluate (mutated chromosomes (Virtual_Ms)) |
| 20. | Calculate fitness function (i) for each I Ɛ Pk |
| 21. | End while |
| 22. | H = fittest values from Pk |
| 23. | Return H |
Initially, the system contains many chromosomes (Virtual_Ms). The GA aims to calculate the fitness function (optimal selection of Virtual_Ms) by using U, TT, and WT for each chromosome (Virtual_Ms) to select the optimal selection of Virtual_Ms through the shortest execution time for each chromosome (Virtual_Ms) on a cloud environment. Suppose the stakeholder’s medical task is finished execution. We can find the optimal execution time and optimal priority scheduling of Virtual_Ms. Otherwise, we should apply the selection process, and nominate the optimal two chromosomes (two Virtual_Ms) from the population through their fitness value. Randomly choose two different chromosomes (Virtual_Ms) from the population. Then, apply the crossover process and determine the swap point: the parent swap is a part of a series of binary numbers separating swap points. Randomly choose two different previously unselected chromosomes from the population. Then, implement the mutation process on those offspring just interchanging the bit positions. Finally, implement an elitist process to ensure the continuity of good chromosomes (Virtual_Ms) and generate a new population to calculate fitness function and repeat these steps to find optimal Virtual_Ms on the cloud environment, as shown in Figure 2.
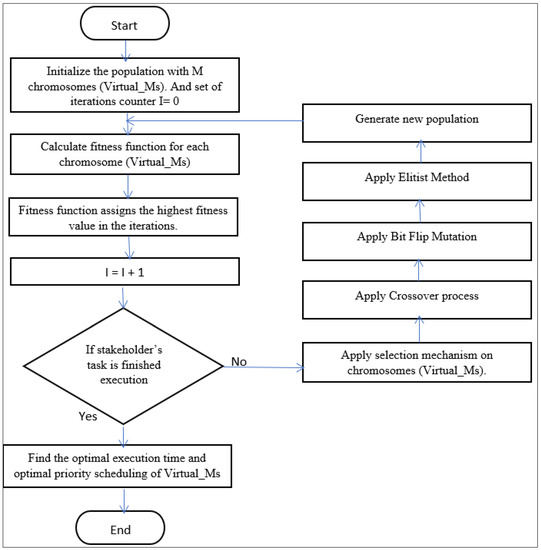
Figure 2.
The proposed GA for cloud computing.
Finally, the purpose of GA is to compute the cost function (the best selection of Virtual_Ms) by using U, TT, and WT for each chromosome (Virtual_Ms) to select the best selection of Virtual_Ms through the lowest implementation of the final time (make span) for each chromosome (Virtual_Ms) on a cloud environment.
4.2. The Proposed Parallel Particle Swarm Optimisation in Cloud Environment
Suppose there are F particles (Virtual_Ms) = 1000, C1 = 2, C2 = 2, and set of iterations = 100. In the particle swarm optimisation (PSO), inertia weight parameter is significant because it impacts the concourse, exploration, and exploitation trade-off in PSO operation. Each Virtual_Ms in the cloud environment is represented as a particle which considers a possibility solution (Virtual_Ms) that can be assigned for implementing the stakeholder’s requests. Calculate cost function (optimal choice of Virtual_Ms) by using U, TT, and WT. After computing the cost function, we compared each particle (Virtual_Ms) with its local best (pbesti). f the existing value is better than pbest, then set the existing position as pbest position. Moreover, if the existing value is better than global best (gbest), then put gbest to the existing index in particle array. Allocate the best particle (Virtual_Ms) as gbest. Update each particle velocity and position according to Equations (5) and (6).
The velocity value is computed by Equation (5):
where:
VI (t + 1) = VI (t) + U1C1 × (Pp-best − Xi (t)) + U2C2 × (Pg-best − Xi (t))
- VI (t + 1) represents the new velocity of a particle and VI (t) represents its current velocity.
- U1 and U2 are two random variables in the range [0, 1].
- The constants C1 and C2 represent the learning factors.
- The X-vector records the current position of the particle in the search space.
- Pp-best is the best particle agent I.
- Pg-best is the best particle in search space.
The position value is computed by Equation (6):
where:
Xi (t + 1) = Xi (t) + VI (t + 1)
- Xi (t + 1) represents the new position of a particle.
- Xi (t) represents its current position.
If a stakeholder’s request is concluded, the algorithm obtains the best implementation on the final time (make span) and the best selection of Virtual_Ms; otherwise, it computes the cost function (the best chosen of Virtual_Ms) for each particle (Virtual_Ms). Finally, the purpose of parallel PSO is to compute the cost function (the best selection of Virtual_Ms) by using U, TT, and WT for each particle (Virtual_Ms) to select the best selection of Virtual_Ms through the lowest on the final time (make span) for each particle (Virtual_Ms) on a cloud environment, as shown in Algorithm 2.
| Algorithm 2. PSO Steps for Selecting Virtual_Ms on Cloud Environment | |
| 1. | Input: Size α of population, |
| 2. | Set β of Pg-best, |
| 3. | Set σ of Pp-best, |
| 4. | Number Y of Iterations |
| 5. | Output: Pg-best ← (Optimal Particles (Virtual_Ms), Optimal Exec Time) |
| 6. | Stakeholders Tasks = X |
| 7. | Count I = 0 |
| 8. | For I = 0 to α do |
| 9. | Pvelocity ← Random velocity () |
| 10. | Pposition ← Random position (α) |
| 11. | σ ← Pposition |
| 12. | If (cost(σ) <= cost(β)) |
| 13. | β = σ |
| 14. | End if |
| 15. | End for |
| 16. | While (X ≠ 0) |
| 17. | For I = 0 to Y do |
| 18. | Calculate fitness function |
| 19. | Update velocity (Pvelocity, β, σ) |
| 20. | Update position (Pvelocity, Pposition) |
| 21. | Pvelocity ← Update velocity |
| 22. | Pposition← Update position |
| 23. | If (cost (Pposition) <= cost(σ)) |
| 24. | σ = Pposition |
| 25. | If (cost(σ) <= cost (β)) |
| 26. | β = σ |
| 27. | If (X is finished = true) |
| 28. | X = X − 1 |
| 29. | Save β |
| 30. | Else |
| 31. | Calculate fitness function for each particle (Virtual_Ms) |
| 32. | End if |
| 33. | End if |
| 34. | End if |
| 35. | I = I + 1 |
| 36. | End for |
| 37. | End while |
| 38. | Return β |
One of the swarm optimisation algorithms is PPSO which is an adjusted form of PSO. It is an iterative approach, which locates the best particle (Virtual_Ms) in iterative steps. Initially, the system contains many particles (Virtual_Ms) and locates the best particle (Virtual_Ms) by updating position and velocity. Here, each particle (Virtual_Ms) is updated with two best values. The first one is the local best (pbest), it contests with its neighbour, and the second one is the global best (gbest), the particle contests with its space population. The proposed algorithm aims to reduce the time of medical requests by selecting the optimal Virtual_Ms on the cloud environment, as shown in Figure 3.
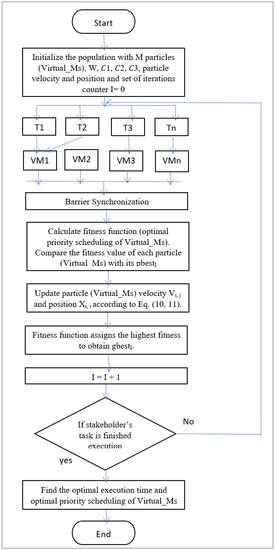
Figure 3.
The proposed parallel particle swarm optimisation algorithm for cloud computing.
In parallel PSO (PPSO), the purpose of parallel processing is to generate the same outputs of the traditional PSO by using several processors jointly to minimise the runtime. For the application of the PPSO, the same procedures cleared in PSO will be applied with some changes, as listed below.
PPSO will identify the number of processors that are requested for the cost function (the best priority scheduling of Virtual_Ms) to be implemented because it can be prepared to be 2N sets.
The barrier synchronisation aims to stop the algorithm from the move to the next step until the cost function (the best chosen of Virtual_Ms) has been notified, which is necessary to preserve algorithmic coherence. Assure that all the particles’ (Virtual_Ms) fitness estimations have been accomplished and results notified before the velocity and position computations can be implemented.
Update particle velocity, according to Equation (7):
where:
VI, j (t) = W VI, j (t − 1) +
C1 R1 (Pi, j (t − 1) − Xi, j (t − 1)) +
C2 R2 (PS, j (t − 1) − Xi, j (t − 1)) +
C3 R3 (Pg, j (t − 1) − Xi, j (t − 1))
C1 R1 (Pi, j (t − 1) − Xi, j (t − 1)) +
C2 R2 (PS, j (t − 1) − Xi, j (t − 1)) +
C3 R3 (Pg, j (t − 1) − Xi, j (t − 1))
- Xi, j = the position of ith particle in jth swarm,
- VI, j = the velocity of ith particle in jth swarm,
- Pi, j = the pbest of ith particle in jth swarm,
- PS, j = the swarm best of jth swarm,
- Pg, j = the global best among all the sub swarms,
- W = inertia weight,
- C1, C2, C3 = acceleration parameters,
- R1, R2, R3 = the random variables.
Update particle position according to Equation (8):
where:
Xi, j (t) = Xi, j (t − 1) + VI, j (t)
- Xi, j (t) = the current position of ith particle in jth swarm,
- Xi, j (t − 1) = the new position of ith particle in jth swarm,
- VI, j (t) = the current velocity of ith particle in jth swarm.
5. The Proposed Intelligent Model
This section shows the experimental results of our proposed model on the cloud environment by using the two proposed algorithms (GA and PPSO). These two algorithms are executed using two different tools which are the MATLAB [38] tool and the CloudSim package.
After comparing these algorithms, the optimal algorithm is selected in terms of implementation time, speed of processing live data, and system efficiency to apply it to cloud computing. The experiments are conducted based on the performance metrics, which consists of speedup and efficiency. The speedup is utilised to compute the attribution of the average execution time on one processor A [t1] and the average execution times on several processors A [tk]. The speedup is shown in Equation (9):
SK = A [t1]/A [tk]
Assume the k parameter is 8. The execution times of GA and PPSO are clarified in Table 3 and Table 4. Thus, the speedup of PPSO is 3.02 times faster than GA. The efficiency is shown as the proportion of speedup by k processors. It is shown in Equation (10):
Ek = (SK/K) × 100%

Table 3.
GA inputs.

Table 4.
GA outputs.
The required inputs to execute GA are shown in Table 3.
By executing GA using the values of the parameters reported in Table 3, the outputs in Table 4 are obtained. The values of the parameters were obtained through a preliminary tuning phase, in which different combinations of the parameters were tested. From this tuning phase, we concluded that 100 iterations guarantee the convergence of the algorithm also for a population size of 100. Concerning the crossover and mutation probability, the selected configuration is the one that produced the best performance across the different combinations considered. We highlight the importance of having a high value of the mutation probability because values that are commonly used in the GA literature (i.e., with a mutation rate usually smaller than 0.1) would result in poor performance. Table 4 displays several trials, populations, and final implementation time in each trial with a different population. The implementation time is correlated with the increasing population volumes due to the need to search in a great amount of potential solution. That is why the value of implementation time has risen with the increasing number of trials.
Figure A2, see Appendix A, displays the positive relation between the set of populations and the final execution time of each trial. Also, the mutation operation causes a random hop in the location of the produced solutions that can depict the cause of the curved decreasing in trials number 11, 14, and 18.
The quality of PSO can be enhanced by using parallel processors. Dependently, the PPSO will define the set of processors needed for the cost function to be executed. Our model can be utilised in environments with big-scale resources and requests. Therefore, Gustafson law is used in this study to deal with some parallel processing requests. The efficiency of the PPSO can be evaluated by using Gustafson’s Law in Equation (11):
where:
SP ≤ P − α × (P − 1)
- SP = speed up.
- α = the portion of non-parallelised tasks, where the parallel work per processor is fixed.
- P = set of processors.
Assume α = 0.5 and set of processors: 2, 5, 10, 20, 40, 80, 160, 320, 640, and 1280. Table 5 shows the number of processors and their corresponding value of speedup.

Table 5.
The efficiency of the parallel processing method.
- If α = 0.5 and P = 2:S2 ≤ 2 − 0.5 × (2 − 1) = 1.5
Raising the number of processors can impact the execution time of stakeholders’ tasks. Figure A3, see Appendix A, displays the relation between the utilised set of processors and the speedup of time.
The required inputs to execute PPSO are shown in Table 6.

Table 6.
PPSO inputs.
By executing PPSO using the values of the parameters reported in Table 6, the outputs in Table 7 are obtained. Just like the experiments performed with GA, the values of the parameters were selected using a tuning phase. In this case, we want to remark on the importance of the parameters C1 and C2 whose values are critical for achieving a satisfactory performance. Table 7 displays several trials, number of particles, and final implementation time in each trial with different particles. The execution time of PPSO is dramatically better than the corresponding execution time of GA. Also, the execution time is correlated with the increasing number of particles in each trial. The affirmative relation between execution time and the number of particles in PPSO is shown in Figure A4, see Appendix A.

Table 7.
PPSO outputs.
From these experiments, we can conclude that the PPSO algorithm outperforms GA in terms of efficiency. The PPSO algorithm is 37.7% more efficient than the GA for stakeholders to minimise the execution time of medical requests (medical tasks (T)). Figure 4 shows that the PPSO algorithm is much better than the GA in terms of execution time and efficiency.
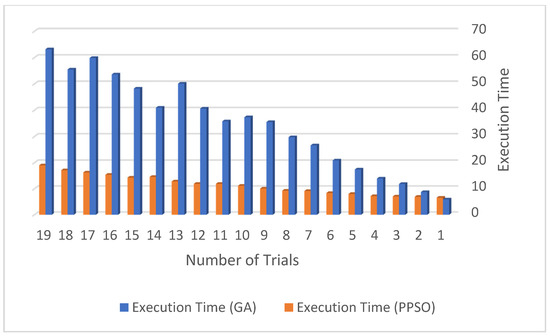
Figure 4.
The comparison between GA and PPSO.
A set of experiments were implemented on CloudSim to find the best choice of Virtual_Ms to prove that the matchmaking of our proposed PPSO algorithm on the cloud environment is correct. The first trial utilises the default CloudSim where the first cloudlet (medical task) picks the first Virtual_Ms, and the second cloudlet picks the second Virtual_Ms, etc. Finally, the total time to build a successful cloudlet is 3 s, as shown in Table 8.

Table 8.
Outputs of default CloudSim, first trial.
In the second trial by using the GA, the first cloudlet (medical task) picks the first Virtual_Ms, and the second cloudlet also picks the first Virtual_Ms, etc. Finally, the total time to build a successful cloudlet by using GA is 4 s, as shown in Table 9.

Table 9.
Outputs of default CloudSim, second trial.
In the second trial by using the PPSO algorithm, the first cloudlet (medical task) picks the first Virtual_Ms, and the second cloudlet also picks the first Virtual_Ms, etc. Finally, the total time to build a successful cloudlet by using the PPSO algorithm is 1 s, as shown in Table 10.

Table 10.
Outputs of PPSO algorithm on CloudSim.
In the cloud computing environment, PPSO outperforms on default CloudSim in terms of TT, WT, CPU utilisation, and make span, as shown in Table 11.

Table 11.
Turnaround Time (TT), Waiting Time (WT), and CPU outputs of the PPSO algorithm on CloudSim.
Figure A2 and Figure A3 (Appendix A), and Figure 5 and Figure 6 display the results of the PPSO algorithm on the CloudSim package in terms of turnaround time, waiting time, CPU utilisation, and final time (make span) of the medical task. There is an inverse relationship between the time and number of processors. For example, in turnaround time, it decreased based on many reasons, such as the numbers of medical requests and the number of processors in each trial on the CloudSim package, as shown in Figure 5.
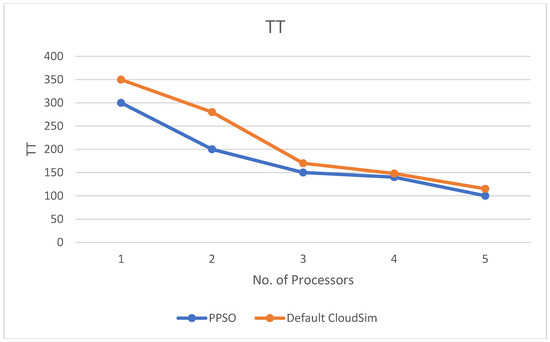
Figure 5.
The relation between TT and number of processors.
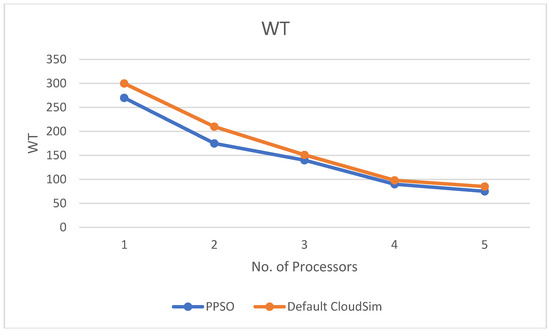
Figure 6.
The relation between WT and number of processors.
Figure 6, Figure 7 and Figure 8 show the inverse relationship between the number of processors and WT, U, and the final time (make span), respectively.
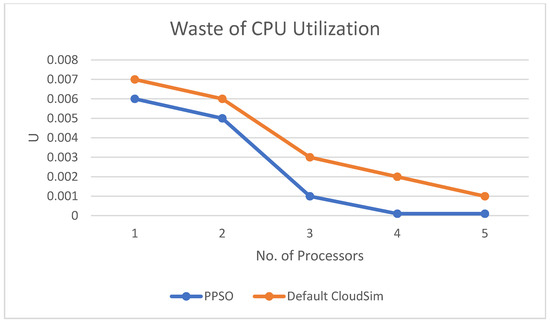
Figure 7.
The relation between U and number of processors.
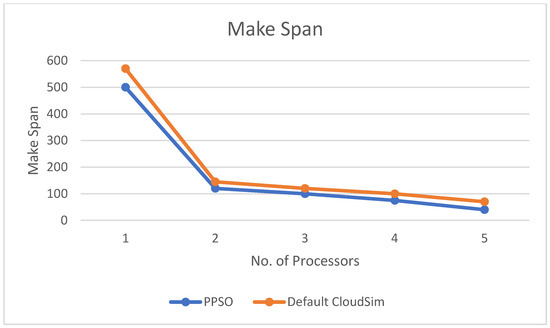
Figure 8.
The relation between make span and number of processors.
Compared to some of the state-of-the-art methods which are mentioned in the literature review, Table 12 presents the total running time of our proposed model. The results show that the enhancement proportion regarding the state-of-the-art methods in the literature review is in the range of 13% to 67%. This enhancement can be noted, as shown in Figure A1, see Appendix A.

Table 12.
Sample of execution time of recent methods in the Literature Review and the proposed model.
It is important to determine the number of populations in GA, particles in PPSO, and execution time of each of them to select the optimal algorithm in terms of speed and time efficiency to reduce the total execution time of medical requests on a cloud environment. The proposed algorithms were applied on the CloudSim package. We have concluded that the PPSO outperforms the GA and the state-of-the-art methods in terms of the total execution time of requests, as shown in Table 12.
The proposed model is clear regarding the speedup and efficiency of PPSO that outperformed both GA and the state-of-the-art methods, and it succeeded to choose the best Virtual_Ms on a cloud environment. The proposed model helps stakeholders in medical applications to reduce the execution time of medical requests and maximise utilisation of medical resources on the cloud computing environment.
6. Conclusions
The stakeholders in the health sector are facing many problems when deploying medical applications in cloud environments. One of the most important problems facing this sector is the delay of medical requests and the limited medical resources available on the cloud environment. By identifying the best Virtual_Ms on the cloud environment, we will be able to minimise the execution time of these medical requests and maximise usage of cloud computing resources. This paper proposes a novel model for medical applications on cloud computing using PPSO to define the optimal choice of Virtual_Ms. Also, the three factors used as a cost function are turnaround time, waiting time, and CPU utilisation for determining the optimal Virtual_Ms selection in a cloud environment. The results displayed that the PPSO algorithm gives accurate outcomes better than the GA in terms of the execution time of medical queries, efficiency, and standard error, by 3.02, 37.7% and 3.13, respectively.
Furthermore, the PPSO algorithm was implemented on the CloudSim package. The results displayed that PPSO algorithm gives accurate outcomes better than default CloudSim in terms of final implementation time of medicinal queries by 33.3%. Finally, the proposed model outperformed the state-of-the-art methods in the literature review by a range from 13% to 67%. The future work aims to execute novel optimisation algorithms such as whale optimisation and lion optimisation to find the optimal Virtual_Ms on the cloud environment as well as executing our model in different applications.
Author Contributions
Conceptualization, M.A.; Data curation, A.A.; Methodology, A.A.; Supervision, M.C.; Writing—original draft, M.A.; Writing—review & editing, M.A. and M.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by FCT, Portugal, through projects GADgET (DSAIPA/DS/0022/2018) and AICE (DSAIPA/DS/0113/2019), and by the financial support from the Slovenian Research Agency (research core funding No. P5-0410).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
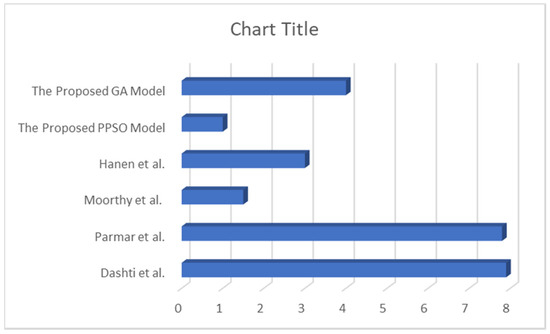
Figure A1.
The execution time of the proposed model compared to state-of-the-art methods.
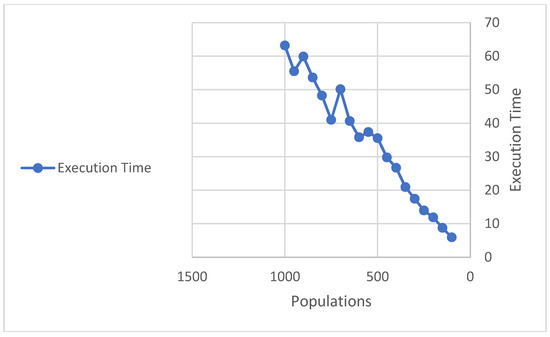
Figure A2.
The relation between populations and execution time in the GA.
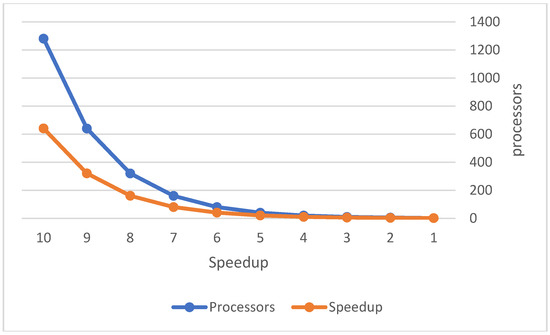
Figure A3.
The relation between processors and speedup in parallel processing.
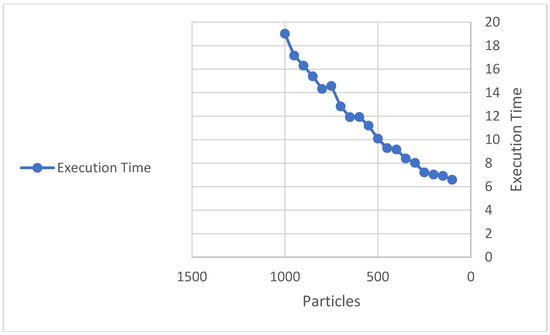
Figure A4.
The relation between particles and execution time in PPSO.
References
- Singh, N.A.; Hemalatha, M. Cluster based bee algorithm for virtual machine placement in cloud data centre. J. Theor. Appl. Inf. Technol. 2013, 57, 1–10. [Google Scholar]
- Abdelaziz, A.; Elhoseny, M.; Salama, A.S.; Riad, A. A machine learning model for improving healthcare services on cloud computing environment. Meas. J. Int. Meas. Confed. 2018, 119, 117–128. [Google Scholar] [CrossRef]
- Sharma, S. Cervical Cancer Stage Prediction using Decision Tree Approach of Machine Learning. Int. J. Adv. Res. Comput. Sci. Commun. Eng. 2016, 5, 345–348. [Google Scholar] [CrossRef]
- Arjun, C.; Anto, S. Diagnosis of Diabetes Using Support Vector Machine and Ensemble Learning Approach. Int. J. Eng. Appl. Sci. 2015, 2, 68–72. [Google Scholar]
- Kumar, K.D.M.N.; Koushik, K.V.S. Prediction of Heart Diseases Using Data Mining and Machine Learning Algorithms and Techniques. Int. J. Sci. Res. Comput. Sci. Eng. Inf. Technol. 2018, 3, 887–898. [Google Scholar] [CrossRef]
- Lutimath, N.M.; Chethan, C.; Pol, B.S. Prediction of heart disease using machine learning. Int. J. Recent Technol. Eng. 2019, 8, 474–477. [Google Scholar] [CrossRef]
- Kumar, C.B.; Kumar, M.V.; Gayathri, T.; Kumar, S.R. Data Analysis and Prediction of Hepatitis Using Support Vector Machine (SVM). Int. J. Comput. Sci. Inf. Technol. 2014, 5, 2235–2237. [Google Scholar]
- Ahmed, M.; Hossain, M.A. Cloud Computing and Security Issues in the Cloud. Int. J. Netw. Secur. Its Appl. 2014, 6, 25–36. [Google Scholar] [CrossRef]
- Selvaraj, A.; Patan, R.; Gandomi, A.H.; Deverajan, G.G.; Pushparaj, M. Optimal virtual machine selection for anomaly detection using a swarm intelligence approach. Appl. Soft Comput. 2019, 84, 105686. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, J.; Cai, L.; Li, R.; He, T.; Meng, T. MTAD: A Multitarget Heuristic Algorithm for Virtual Machine Placement. Int. J. Distrib. Sens. Netw. 2015, 11, 679170. [Google Scholar] [CrossRef]
- Alouane, M.; El Bakkali, H. Virtualization in Cloud Computing: Existing solutions and new approach. In Proceedings of the 2nd International Conference on Cloud Computing Technologies and Applications (CloudTech), Marrakech, Morocco, 24–26 May 2016; pp. 116–123. [Google Scholar]
- Camati, L.L.R.S.; Calsavara, A. Solving the Virtual Machine Placement Problem as a Multiple Multidimensional Knapsack Problem. Int. Conf. Netw. 2014, 2014, 264. [Google Scholar]
- Zhao, J.; Hu, L.; Ding, Y.; Xu, G.; Hu, M. A Heuristic Placement Selection of Live Virtual Machine Migration for Energy-Saving in Cloud Computing Environment. PLoS ONE 2014, 9, e108275. [Google Scholar] [CrossRef] [PubMed]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H.; Talatahari, S. Bat algorithm for constrained optimization tasks. Neural Comput. Appl. 2013, 22, 1239–1255. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 17–35. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yang, X.-S. Chaotic bat algorithm. J. Comput. Sci. 2014, 5, 224–232. [Google Scholar] [CrossRef]
- Zaidi, T.; Rampratap, R. Virtual Machine Allocation Policy in Cloud Computing Environment using CloudSim. Int. J. Electr. Comput. Eng. (IJECE) 2018, 8, 344–354. [Google Scholar] [CrossRef]
- Sawant, S. A Genetic Algorithm Scheduling Approach for Virtual Machine Resources in a Cloud Computing Environment. Master’s Thesis, San Jose State University, San Jose, CA, USA, 2011; pp. 1–36. [Google Scholar]
- Sadeghi, J.; Sadeghi, S.; Niaki, S.T.A. Optimizing a hybrid vendor-managed inventory and transportation problem with fuzzy demand: An improved particle swarm optimization algorithm. Inf. Sci. 2014, 272, 126–144. [Google Scholar] [CrossRef]
- Obitko, M. Introduction to Genetic Algorithms; Czech Technical University: Prague, Czech, 1998; Available online: http://www.obitko.com/tutorials/genetic-algorithms/index.php (accessed on 27 April 2020).
- Abdelaziz, A.; Elhoseny, M.; Salama, A.S.; Riad, A.M.; Hassanien, A.E. Intelligent algorithms for optimal selection of virtual machine in cloud environment, towards enhance healthcare services. In Advances in Intelligent Systems and Computing; Springer: Cham, Switzerland, 2018; Volume 639, pp. 289–298. [Google Scholar] [CrossRef]
- Almezeini, N.; Hafez, A. Task Scheduling in Cloud Computing Using Lion Optimization Algorithm. Int. J. Adv. Comput. Sci. Appl. 2017, 8, 77–83. [Google Scholar] [CrossRef]
- Barlaskar, E.; Singh, Y.J.; Issac, B. Energy-efficient virtual machine placement using enhanced firefly algorithm. Multiagent Grid Syst. 2016, 12, 167–198. [Google Scholar] [CrossRef]
- Liu, X.-F.; Zhan, Z.-H.; Deng, J.D.; Li, Y.; Gu, T.; Zhang, J. An Energy Efficient Ant Colony System for Virtual Machine Placement in Cloud Computing. IEEE Trans. Evol. Comput. 2018, 22, 113–128. [Google Scholar] [CrossRef]
- Shabeera, T.; Kumar, S.M.; Salam, S.M.; Krishnan, K.M. Optimizing VM allocation and data placement for data-intensive applications in cloud using ACO metaheuristic algorithm. Eng. Sci. Technol. Int. J. 2017, 20, 616–628. [Google Scholar] [CrossRef]
- Dong, Y.-S.; Xu, G.-C.; Fu, X.-D. A Distributed Parallel Genetic Algorithm of Placement Strategy for Virtual Machines Deployment on Cloud Platform. Sci. World J. 2014, 2014, 259139. [Google Scholar] [CrossRef] [PubMed]
- Teyeb, H.; Balma, A.; Alouane, N.B.H.; Tata, S. Optimal virtual machine placement in large-scale cloud systems. In Proceedings of the IEEE 7th International Conference on Cloud Computing, Anchorage, AK, USA, 27 June–2 July 2014; pp. 424–431. [Google Scholar] [CrossRef]
- Fu, X.; Zhou, C. Virtual machine selection and placement for dynamic consolidation in Cloud computing environment. Front. Comput. Sci. 2015, 9, 322–330. [Google Scholar] [CrossRef]
- Chaurasia, N.; Tapaswi, S.; Dhar, J. A Pareto Optimal Approach for Optimal Selection of Virtual Machine for Migration in Cloud. Int. J. Comput. Sci. Inf. Secur. 2016, 14, 117. [Google Scholar]
- Vidhya, M.; Sadhasivam, N. Parallel Particle Swarm Optimisation for Reducing Data Redundancy in Heterogeneous Cloud Storage. Int. J. Transp. Eng. Technol. 2015, 3, 73–78. [Google Scholar]
- Pacini, E.; Mateos, C.; Garino, C.G. Dynamic Scheduling based on Particle Swarm Optimization for Cloud-based Scientific Experiments. CLEI Electron. J. 2014, 17, 2:1–2:14. [Google Scholar] [CrossRef]
- Thiruvenkadam, T.; Kamalakkannan, P. Virtual Machine Placement and Load Rebalancing Algorithms in Cloud Computing Systems. Int. J. Eng. Sci. Res. Technol. 2016, 5, 346–359. [Google Scholar]
- Seddigh, M.; Taheri, H.; Sharifian, S. Dynamic prediction scheduling for virtual machine placement via ant colony optimisation. In Proceedings of the Signal Processing and Intelligent Systems Conference (SPIS), Tehran, Iran, 16–17 December 2015; pp. 104–108. [Google Scholar] [CrossRef]
- Dashti, S.E.; Rahmani, A.M. Dynamic VMs placement for energy efficiency by PSO in cloud computing. J. Exp. Theor. Artif. Intell. 2015, 28, 97–112. [Google Scholar] [CrossRef]
- Parmar, A.T.; Mehta, R. An Approach for VM Allocation in Cloud Environment. Int. J. Comput. Appl. 2015, 131, 1–5. [Google Scholar] [CrossRef]
- Moorthy, R.S.; Fareentaj, U.; Divya, T. An Effective Mechanism for Virtual Machine Placement Using Aco in IAAS Cloud. IOP Conf. Ser. Mater. Sci. Eng. 2017, 225, 12227. [Google Scholar] [CrossRef]
- Hanen, J.; Kechaou, Z.; Ben Ayed, M. An enhanced healthcare system in mobile cloud computing environment. Vietnam J. Comput. Sci. 2016, 3, 267–277. [Google Scholar] [CrossRef]
- The MathWorks. “MATLAB”. Available online: https://www.mathworks.com/products/matlab.html (accessed on 26 August 2020).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).