Kinematic Conceptual Design of In-Line Four-Cylinder Variable Compression Ratio Engine Mechanisms Considering Vertical Second Harmonic Acceleration

Abstract

In the in-line four-cylinder engine, it is well known that the shaking force is due to the vertical second harmonic acceleration components of the pistons. This paper proposes a kinematic conceptual design method to determine the kinematic structure of a feasible in-line four-cylinder variable compression ratio (VCR) engine and its dimensions that would yield a lower vertical second harmonic acceleration at joints. Through type and dimensional synthesis, candidate VCR engine mechanisms are chosen and their dimensions satisfying design specifications are determined. Based on the analysis of the vertical second harmonic acceleration components at the joints, a feasible mechanism for an in-line four-cylinder VCR engine is selected. Then, the method finds the dimensions that yield a nearly minimized sum of the vertical second harmonic acceleration at each joint by adjusting the link lengths within specified tolerances. For validation, the result is compared with that of a constrained optimization using MATLAB. The proposed method would be useful at the conceptual design stage of multi-link multi-cylinder VCR and variable-stroke engine mechanisms where the second harmonic acceleration is an important design factor in the automotive industrial applications.

1. Introduction

The general performance and thermal efficiency of the internal combustion engine have been improved by various technologies such as turbochargers, fuel injection systems, and variable valve actuation systems [1]. In addition to the above, the variable compression ratio (VCR) engine technology has been considered as a method for improving fuel efficiency and reducing pollutants [2,3,4,5]. Various approaches have been suggested for the variation of the compression ratio, which include moving the crankshaft axis or the cylinder head, varying the combustion chamber volume or the piston deck height, and modifying the connecting rod geometry [6,7,8,9,10]. Numerous VCR engine mechanisms have been proposed [11,12,13], and their kinematic structures have been identified [14].

In general, as the VCR engine mechanism has more links than the conventional fixed compression ratio engine, the design of a VCR engine mechanism could be a quite complicated problem: the kinematic structure and dimensions of the mechanism that fits within the internal space of the engine must be determined, and then the dynamic characteristics and the balancing of shaking force and shaking moment need to be considered. The latter problem on the balancing of the conventional engine has been studied extensively [15,16,17]. The vertical second harmonic acceleration components of the pistons cause the shaking moments in the in-line three-cylinder, in-line five-cylinder, and V six-cylinder engines; the shaking forces in the in-line four-cylinder engine. In order to balance the shaking forces, an extra device, such as a balancer, which rotates at double engine speed, is used to balance the shaking force [18,19]. From this point of view, even though the complete dynamic analysis of a VCR engine under development is not possible until the mass properties of the parts are determined, considering the vertical second harmonic acceleration components would provide a good starting point at the conceptual design stage of a new VCR engine mechanism.

In the case of the fixed compression ratio engine, the crank can be shortened to decrease the magnitude of the second harmonic acceleration of the piston, but shortening the crank length causes a change in the stroke. For the VCR engine mechanism, since more links can be used to connect the piston and the crank, the second harmonic acceleration can be reduced by adjusting the link lengths without scarifying a desired stroke and top dead center (TDC) position.

In this paper, a kinematic conceptual design process of in-line four-cylinder VCR engine mechanisms considering the vertical second harmonic acceleration component at each joint is proposed. The proposed method includes the type and dimensional synthesis of candidate VCR engine mechanisms, harmonic acceleration analysis, selection of a feasible mechanism, and the minimization of the vertical second harmonic acceleration sum in the selected mechanism. For the type synthesis, the atlas of kinematic chains is used to choose appropriate candidates. The displacement equations of candidate mechanisms are derived and used to determine the initial dimensions of links that satisfy prescribed design specifications. Then, the Fourier series expression for the displacement of each joint is determined numerically and differentiated to obtain the vertical harmonic acceleration components. Among the candidates, a feasible mechanism is selected based on the vertical second harmonic acceleration analysis when they are used in the in-line four-cylinder engine, and then by varying the link lengths of the initially designed mechanism within prescribed tolerances, the final dimensions of the mechanism that yields a nearly minimized sum of the second harmonic acceleration are determined. The result is compared with that of a constrained optimization for the validation of the proposed method.

2. Understanding of Harmonic Acceleration in the In-Line Four-Cylinder Engine

A slider-crank mechanism used in the conventional fixed compression ratio internal combustion engine is shown in Figure 1. The displacement of the piston pin, s, can be derived as

$$s=r\left\{\sin \theta +\frac{l}{r}\sqrt{1-{\left(\frac{e-r\cos \theta }{l}\right)}^2}\right\},$$

(1)

where θ is the crank angle, r is the crank length, l is the connecting rod length, and e is the piston offset.

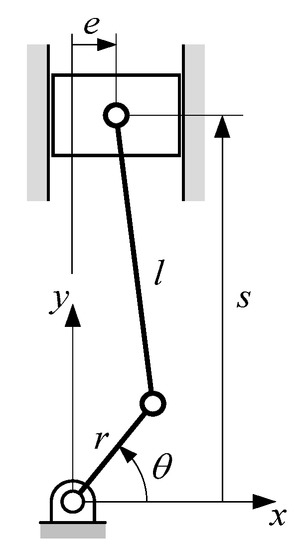
Figure 1. Slider-crank mechanism.

Equation (1) and its time derivatives can be directly used to determine the motion of the piston, however, in order to find the effects of changes in the design variables r and l on the acceleration thus on the inertia forces, an approximate form of Equation (1) is used [17,18,19]. When e = 0, for example, the binomial series expansion of the square root term in Equation (1) yields

$$\sqrt{1-{\left(\frac{r}{l}\right)}^2{\cos }^2\theta }=1-\frac{1}{2}{\left(\frac{r}{l}\right)}^2{\cos }^2\theta -\frac{1}{8}{\left(\frac{r}{l}\right)}^4{\cos }^4\theta -\frac{1}{16}{\left(\frac{r}{l}\right)}^6{\cos }^6\theta -\cdots .$$

(2)

In most engines, since the crank-connecting rod ratio r/l is less than 1/3, Equation (2) can be estimated quite closely by the first two terms. Hence, Equation (1) can now be approximated as

$$s\cong r\left\{\sin \theta +\frac{l}{r}-\frac{1}{2}\left(\frac{r}{l}\right){\cos }^2\theta \right\}.$$

(3)

Substituting the trigonometric identity ${\cos }^2\theta =\left(1+\cos 2\theta \right)/2$ into Equation (3) gives the displacement of the piston pin as

$$s\cong r\left\{\sin \theta +\frac{l}{r}-\frac{1}{4}\left(\frac{r}{l}\right)\left(1+\cos 2\theta \right)\right\}.$$

(4)

Since the position of the piston pin is a periodic function of the crank angle, the Fourier series approximation of Equation (1) would yield the same as Equation (4).

Assuming the angular velocity of the crank, ω is constant, the second time derivative of Equation (4) gives the acceleration of the piston pin as

$$\ddot{s}\cong r{\omega }^2\left(-\sin \theta +\frac{r}{l}\cos 2\theta \right),$$

(5)

which consists of the harmonics of the crank angle $\theta =\omega t$ where t is the time.

Let m_eq be the equivalent concentrated mass of the piston and connecting rod at the piston pin, then the inertia force at the piston pin, $F=m_{eq}\ddot{s}$, has its primary force component $-m_{eq}r{\omega }^2\sin \theta$ due to the first harmonic acceleration and the secondary force component $m_{eq}{\omega }^2\left(r^2/l\right)\cos 2\theta$ induced by the second harmonic acceleration.

When the slider-crank mechanism is used in an in-line four-cylinder engine with crank throws at 90°, 270°, 270°, and 90° phase angles, the harmonic acceleration components up to the fourth harmonic at the piston pins in cylinder 1 and cylinder 2 are calculated as shown in Figure 2. The nth harmonic acceleration components expressed in terms of cos(nθ) and sin(nθ) in cylinders 1 and 4 appear as cos{n(θ + π)} and sin{n(θ + π)} in cylinders 2 and 3, each of which becomes −cos(nθ) and −sin(nθ) for odd n; cos(nθ) and sin(nθ) for even n. Hence, the inertia forces due to the odd harmonic acceleration components in cylinders 1 and 2, and in cylinders 3 and 4 would cancel out and sum to zero, however those induced by the even harmonic acceleration components do not cancel out but add up and result in unwanted vibration. Hence, the minimization of the second harmonic acceleration is a good guideline for the kinematic conceptual design of a new in-line four-cylinder VCR engine.

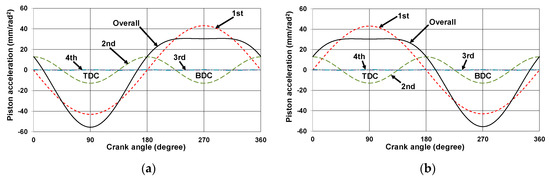
Figure 2. Harmonic acceleration components at the piston pin of slider-crank mechanism: (a) Cylinder 1 and (b) Cylinder 2.

3. Kinematic Conceptual Design Process

In this section, the general kinematic conceptual design process of a conventional engine mechanism was outlined, and a procedure for a VCR engine mechanism was proposed.

3.1. Kinematic Conceptual Design Process of Conventional Engine Mechanisms

The kinematic design of mechanisms requires type synthesis, dimensional synthesis, and analysis. Regarding the kinematic design of the driving system for a conventional engine mechanism, since its kinematic structure is the slider-crank mechanism, the conceptual kinematic design is subject to the determination of the lengths of the crank and connecting rod, the piston offset, and the compression height of the piston to achieve a target performance, and then is subject to kinematic and dynamic analysis. The guidelines for the main dimensions [1,19] and the balancing of the shaking force and shaking moment for engine mechanisms are well established [15,16,17,18,19].

3.2. Kinematic Conceptual Design Process of In-Line Four-Cylinder VCR Engine Mechanisms Considering Vertical Second Harmonic Acceleration

In general, since a VCR engine mechanism requires more links and joints than the conventional engine to vary the compression ratio, there can be many types of candidate mechanisms. Hence, the first step of the conceptual design process of a VCR engine is the type synthesis. For this, graph theory can be applied to enumerate feasible kinematic structures [20], or appropriate VCR engine mechanisms can be chosen from the atlas of kinematic chains [14,20,21]. Considering the number of graphs to be enumerated and the complexity of the dimensional synthesis of two-degree of freedom variable mechanisms, it would be enough to enumerate or choose basic one-degree of freedom candidate mechanisms excluding their control function [22]: the variable action can be achieved by moving one of the ground pivots.

After selecting candidate mechanisms, the next step is the dimensional synthesis to determine the joint positions and link lengths that satisfy desired specifications such as the TDC position and stroke. For this, the displacement equations of the selected mechanisms can be used to determine the dimensions.

The next step of the design process would be the kinematic and dynamic analysis of the initially designed candidate mechanisms. For the dynamic analysis, however, the mass properties of links and gas pressure are required, which are not available at the conceptual design stage. Instead, the harmonic acceleration analysis of candidates is the proper next step, since the distributed mass of a link can be substituted by dynamically equivalent point masses located at neighboring joints [23] and the shaking forces in the in-line four-cylinder engine depend upon the second harmonic acceleration. For illustration purpose, only the vertical harmonic acceleration of each joint will be considered in this paper. The same procedure can be applied to the horizontal acceleration. The vertical displacement of the ith joint of a candidate VCR engine mechanism, $f_{P_{iy}}\left(\theta \right)$, which is a periodic function of period 2π of crank angle θ, can be represented by a Fourier series as

$$f_{P_{iy}}(\theta )=a_0+{\displaystyle \sum _{n=1}^{\infty }\left(a_n\cos n\theta +b_n\sin n\theta \right)},$$

(6)

where

$$\begin{array}{l}{a}_0=\frac{1}{2\pi }{\displaystyle {\int }_{-\pi }^{\pi }{f}_{P_{iy}}(\theta )d\theta ,}\\ a_n=\frac{1}{\pi }{\displaystyle {\int }_{-\pi }^{\pi }{f}_{P_{iy}}(\theta )\cos n\theta d\theta },n=1,2,\cdots ,\\ b_n=\frac{1}{\pi }{\displaystyle {\int }_{-\pi }^{\pi }{f}_{P_{iy}}(\theta )\sin n\theta d\theta },n=1,2,\cdots .\end{array}$$

(7)

Differentiating Equation (6) with respect to θ twice gives the Fourier series expression of the vertical acceleration (length/rad²) of the ith joint.

The next step of the design process is the selection of feasible VCR engine mechanisms among candidates on the basis of the second harmonic acceleration analysis when they are used in the in-line four-cylinder engine. Then, for the selected feasible mechanism, evaluate the influence of the change in each link length on the sum of the vertical second harmonic acceleration at each joint and the stroke within prescribed tolerances, and adjust the link lengths to reduce the vertical second harmonic acceleration. With the adjusted link lengths, re-evaluate the influence of the link length changes and adjust the lengths of links, which are effective in reducing the vertical second harmonic acceleration sum and in satisfying the desired stroke.

4. Kinematic Conceptual Design of a Six-Link VCR Engine Mechanism

In this section, the proposed process is applied to the kinematic conceptual design of a six-link VCR engine mechanism excluding the control function.

4.1. Type Synthesis

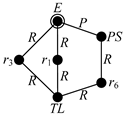
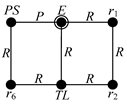
Limiting the search of candidate VCR engine mechanisms to planar one-degree of freedom six-link mechanisms with revolute (R) joints and one prismatic (P) joint, there are two types of kinematic chains: Stephenson and Watt chains [20,22] whose unlabeled kinematic graphs are shown in Table 1 in which the vertices represent the links and the edges represent the joints of the corresponding kinematic chain.

Table 1. Candidate variable compression ratio (VCR) engine mechanisms.

	Stephenson Chain	Watt Chain
Unlabeled Graph
	Stephenson III Mechanism	Watt II Mechanism
Labeled Graph
Skeleton diagram

◉: ground link, E: engine block, PS: piston, r₁: crank, r₆: connecting rod, TL: ternary link, R: revolute joint, P: prismatic joint, P_i: position of joint i.

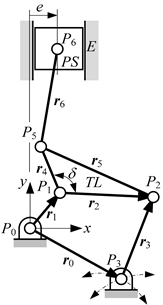
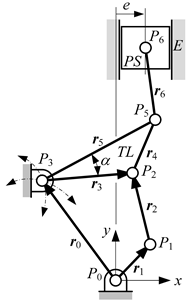
If the control link to alter the compression ratio needs to be connected to the ground link (engine block) as in most machinery, the engine block must be a ternary link, which is connected to three other links: the piston by a P joint, the crank, and control link by R joints. By assigning appropriate links and joints to the vertices and edges of the unlabeled graphs, the labeled graphs and skeleton diagrams of the candidates, the Stephenson III and Watt II mechanisms, are obtained as shown in Table 1. Notice that the vertex with a concentric circle in the labeled graph corresponds to the ground link of the mechanism. The compression ratio can be altered by moving the ground pivot, P₃, along the line with arrows shown in the skeleton diagrams of Table 1.

4.2. Dimensional Synthesis Using Displacement Equations

For the dimensional syntheses of the Stephenson III and Watt II mechanisms, the displacement equations are derived. For this, the four-bar linkage in both mechanisms with links r₀, r₁, r₂, and r₃ shown in the skeleton diagram of Table 1 is analyzed as follows [24].

The vector loop-closure equation of the four-bar linkage can be written as

$${\mathit{r}}_1+{\mathit{r}}_2={\mathit{r}}_0+{\mathit{r}}_3,$$

(8)

or, equivalently as

$${\mathit{r}}_2={\mathit{r}}_0+{\mathit{r}}_3-{\mathit{r}}_1.$$

(9)

The x and y components of Equation (9) can be written respectively as

$$r_2\cos {\theta }_2=r_0\cos {\theta }_0+r_3\cos {\theta }_3-r_1\cos {\theta }_1,$$

(10)

$$r_2\sin {\theta }_2=r_0\sin {\theta }_0+r_3\sin {\theta }_3-r_1\sin {\theta }_1,$$

(11)

where r_i is the length of r_i and θ_i is the angle of r_i measured from the positive x axis.

Square Equations (10) and (11), and sum to obtain

$$\begin{array}{cc}\hfill r_2^2=& r_0^2+r_1^2+r_3^2+2r_0{r}_3\left(\cos {\theta }_0\cos {\theta }_3+\sin {\theta }_0\sin {\theta }_3\right)\hfill \\ & -2r_0{r}_1\left(\cos {\theta }_0\cos {\theta }_1+\sin {\theta }_0\sin {\theta }_1\right)-2r_1{r}_3\left(\cos {\theta }_1\cos {\theta }_3+\sin {\theta }_1\sin {\theta }_3\right).\hfill \end{array}$$

(12)

Equation (12) can be written in terms of cosθ₃ and sinθ₃ as

$$A\cos {\theta }_3+B\sin {\theta }_3+C=0,$$

(13)

where

$$\begin{array}{l}A=2r_0{r}_3\cos {\theta }_0-2r_1{r}_3\cos {\theta }_1,\\ B=2r_0{r}_3\sin {\theta }_0-2r_1{r}_3\sin {\theta }_1,\\ C=r_0^2+r_1^2+r_3^2-r_2^2-2r_0{r}_1\left(\cos {\theta }_0\cos {\theta }_1+\sin {\theta }_0\sin {\theta }_1\right).\end{array}$$

(14)

Substitute the tangent half-angle identities into Equation (13) and solve the resulting equation to obtain

$${\theta }_3=2{\tan }^{-1}\left(\frac{-B\pm \sqrt{B^2-C^2+A^2}}{C-A}\right),-\pi \le {\theta }_3\le \pi .$$

(15)

Equation (15) states that there are two θ₃ values for a given angle θ₁, which correspond to two assembly modes. Dividing Equation (11) by Equation (10) gives the coupler angle θ₂ as

$${\theta }_2={\tan }^{-1}\left(\frac{r_0\sin {\theta }_0+r_3\sin {\theta }_3-r_1\sin {\theta }_1}{r_0\cos {\theta }_0+r_3\cos {\theta }_3-r_1\cos {\theta }_1}\right).$$

(16)

Now, the position of joint P₂ can be written as

$${\mathit{P}}_2=\left[\begin{array}{l}{P}_{2x}\\ P_{2y}\end{array}\right]=\left[\begin{array}{l}{r}_{0x}\\ r_{0y}\end{array}\right]+\left[\begin{array}{l}{r}_3\cos {\theta }_3\\ r_3\sin {\theta }_3\end{array}\right].$$

(17)

For the candidate mechanisms in Table 1 to be used in a VCR engine, there must be a crank connected to the ground link by an R joint in the four-bar linkage. In this research, it is assumed that the four bar is a crank and rocker. By Grashof criteria [25], the crank must be the shortest link and the following relation must hold for a crank-rocker four-bar linkage.

$$L+S<I2,$$

(18)

where L is the length of the longest link, S is the length of the shortest link, and I2 is the sum of the remaining two link lengths.

The positions of the other joints in the each mechanism in Table 1 can be determined as follows.

4.2.1. Stephenson III Mechanism

The position of joint P₅ is

$${\mathit{P}}_5=\left[\begin{array}{l}{P}_{5x}\\ P_{5y}\end{array}\right]=\left[\begin{array}{l}{r}_1\cos {\theta }_1\\ r_1\sin {\theta }_1\end{array}\right]+\left[\begin{array}{l}{r}_4\cos \left({\theta }_2+\delta \right)\\ r_4\sin \left({\theta }_2+\delta \right)\end{array}\right],$$

(19)

where δ is the angle between links r₂ and r₄, which can be obtained by the law of cosines as

$$\delta ={\cos }^{-1}\left(\frac{r_2{}^2+r_4{}^2-r_5{}^2}{2r_2{r}_4}\right),$$

(20)

and the position of P₆ is

$${\mathit{P}}_6=\left[\begin{array}{l}{P}_{6x}\\ P_{6y}\end{array}\right]=\left[\begin{array}{c}e\\ P_{5y}+\sqrt{r_6^2-{\left(e-P_{5x}\right)}^2}\end{array}\right],$$

(21)

and e is the piston offset.

4.2.2. Watt II Mechanism

The positions of joints P₅ and P₆ are found respectively by

$${\mathit{P}}_5=\left[\begin{array}{l}{P}_{5x}\\ P_{5y}\end{array}\right]=\left[\begin{array}{l}{r}_{0x}\\ r_{0y}\end{array}\right]+\left[\begin{array}{l}{r}_5\cos ({\theta }_3+\alpha )\\ r_5\sin ({\theta }_3+\alpha )\end{array}\right],$$

(22)

$${\mathit{P}}_6=\left[\begin{array}{l}{P}_{6x}\\ P_{6y}\end{array}\right]=\left[\begin{array}{c}e\\ P_{5y}+\sqrt{r_6^2-{\left(e-P_{5x}\right)}^2}\end{array}\right],$$

(23)

where α is the angle between r₃ and r₅, which can be determined by the law of cosines as

$$\alpha ={\cos }^{-1}\left(\frac{r_3{}^2+r_5{}^2-r_4{}^2}{2r_3{r}_5}\right),$$

(24)

and e is the piston offset.

4.2.3. Initial Design of Candidate VCR Engine Mechanisms

For the design specifications for the VCR engine mechanism given in Table 2, the dimensions of the two candidates are determined using Equations (8)–(24) as shown in Figure 3 and Table 3.

Table 2. Design specifications for VCR engine mechanism.

Engine Type	In-Line Four-Cylinder
Crank throw phase angle	90°, 270°, 270°, 90°
Bore	86 mm
Stroke	86 ± 0.025 mm
TDC position	220 ± 10 mm (Piston pin: 190 ± 10 mm)
Displacement	2 L
Piston offset	0 mm
Radius of engine block internal space	82.5 mm (measured form crank center)

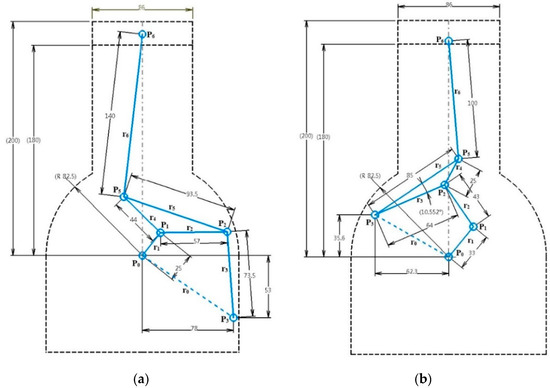
Figure 3. Initial design of VCR engine mechanisms: (a) Stephenson III and (b) Watt II.

Table 3. Dimensions of the initially designed VCR engine mechanisms.

Link	Link Length and Pivot Position (Unit: mm)
	Stephenson III Mechanism	Watt II Mechanism
r1	25.000	33.000
r2	57.000	43.000
r3	73.500	64.000
r4	44.000	25.000
r5	93.500	85.000
r6	140.000	100.000
r0x	78.000	−62.300
r0y	−53.000	35.600

The initially designed mechanisms satisfy the desired stroke and piston pin position at TDC as shown in Table 4, and there is no interference between the moving parts and the engine block.

Table 4. Analysis results of the initially designed mechanisms.

	Stephenson III	Watt II	Design Specifications
Stroke (mm)	85.993	86.008	86 ± 0.025
Piston pin position at TDC (mm)	197.391	199.191	190 ± 10

4.3. Harmonic Acceleration Analysis and Selection of the Final Mechanism Type

For the harmonic acceleration analysis of the initially designed mechanisms, the vertical displacement of each joint was expanded numerically to determine the Fourier series expression, and then differentiated twice with respect to crank angle θ₁. For the verification of the numerical results, the vertical harmonic acceleration components of the piston pin (P₆) of the initially designed Stephenson III mechanism in a single cylinder engine were evaluated as shown in Figure 4, and the result agreed well with the previous research [11].

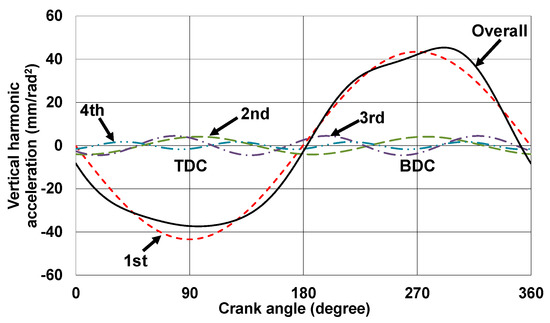
Figure 4. Vertical harmonic acceleration components at piston pin (P₆) of the initially designed Stephenson III mechanism in a single cylinder.

Figure 5 shows the vertical harmonic acceleration components at joints P₂ and P₅ in cylinder 1 and cylinder 2 when the initially designed Stephenson III mechanism was used in an in-line four-cylinder engine with crank throws at 90°, 270°, 270°, and 90° phase angles. As in the case of the slider-crank mechanism in the in-line four-cylinder engine in Section 2, the vertical inertia forces due to the odd harmonic acceleration components in cylinders 1 and 2, and cylinders 3 and 4 would cancel out, and those induced by the even harmonic acceleration components added up. The same canceling out of the vertical inertia forces due to the odd harmonic acceleration components occurred when the Watt II mechanism was used in the same in-line four-cylinder engine.

Figure 5. Vertical harmonic acceleration components at joints P₂ and P₅ of the initially designed Stephenson III mechanism: (a) Joint P₂ in Cylinder 1; (b) Joint P₂ in Cylinder 2; (c) Joint P₅ in Cylinder 1; and (d) Joint P₅ in Cylinder 2.

In order to determine the feasibility of the two candidate mechanisms when used in the in-line four-cylinder engine, the vertical second harmonic acceleration at each joint are plotted in Figure 6.

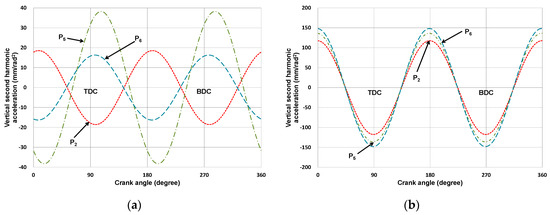
Figure 6. Vertical second harmonic acceleration at each joint in candidate mechanisms in the in-line four-cylinder engine: (a) initially designed Stephenson III and (b) initially designed Watt II.

As can be seen in Figure 6, the vertical second harmonic acceleration components at the joints in the Watt II linkage were much higher than those of the Stephenson III mechanism and they were in phase, hence the vertical inertia forces might add up to a high value. In the case of the Stephenson III mechanism, the vertical second harmonic acceleration at joint P₂ and those at joints P₅ and P₆ were out of phase, and some vertical inertia forces would cancel out. For these reasons, between the two candidates, the Stephenson III mechanism was selected as a feasible mechanism for a VCR engine.

4.4. Minimization of Vertical Second Harmonic Acceleration

Since the mass properties of links are not available at the initial phase of the conceptual design process, it is assumed that the concentrated mass at each joint is the same and the vertical harmonic acceleration of each joint contributes to the vertical inertia force proportional to its magnitude. In this paper, the following steps are proposed to find the optimum dimensions that yield a nearly minimized sum of the vertical second harmonic acceleration at each joint by varying the initial link lengths within prescribed tolerances on the stroke and link lengths.

S1

Within the prescribed tolerances on the link lengths and stroke, evaluate the influence of the change in the length of each link on the maximum sum of the vertical second harmonic acceleration components and the stroke.

S2

Find links that are more effective in reducing the maximum sum of the vertical second harmonic acceleration components when their link lengths are changed. Then, adjust their lengths to reduce the second harmonic acceleration sum.

S3

Repeat Step S1 for the links that are not adjusted in Step S2. As Step S2 may cause the deviation from the desired stroke, find links that are effective in both adjusting the stroke and reduce the maximum sum of the vertical second harmonic acceleration components. Then, adjust their lengths to reduce the second harmonic acceleration sum and to satisfy the desired stroke.

The above steps are applied to the initial design of the Stephenson III mechanism as follows. Step 1 is carried out and the result is plotted in Figure 7 by varying each link length by 0.1 mm sequentially within the prescribed tolerances on the link lengths and stroke given in Table 5.

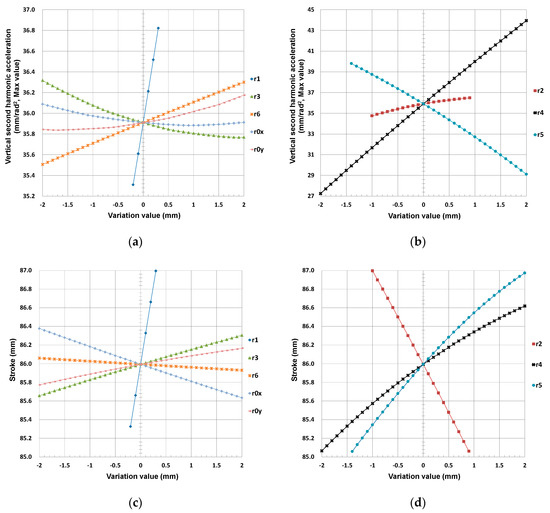
Figure 7. Influence on the maximum of vertical second harmonic acceleration sum of length change in: (a) r₁, r₃, r₆, r_0x, and r_0y and (b) r₂, r₄, and r₅ of the ternary link; influence on the stroke of length change in: (c) r₁, r₃, r₆, r_0x, and r_0y and (d) r₂, r₄, and r₅ in the in-line four-cylinder engine.

Table 5. Prescribed tolerances.

Link Lengths	ri ± 2 mm
Stroke	86 ± 1 mm

As can be seen from Figure 7a,b, since the lengths of r₄ and r₅ of the ternary link are more sensitive to the sum of the vertical second harmonic acceleration components, they are selected to adjust their lengths in Step 2: the length of link r₄ is taken to its minimum and r₅ is adjusted to its maximum within the prescribed tolerance on the link lengths given in Table 5. As Step S3, with the adjusted lengths of r₄ and r₅ in Step S2, the influences of the change in the length of each link except r₄ and r₅ are plotted in Figure 8. Figure 8c,d show that the stroke of the Stephenson III mechanism with the adjusted link lengths of r₄ and r₅ is 85.510 mm, which does not satisfy the design specification 86 ± 0.025 mm given in Table 2.

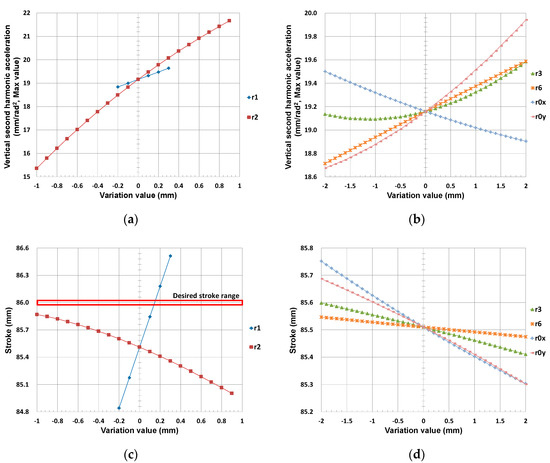
Figure 8. With the minimum length of r₄ and the maximum r₅, influence on the maximum of vertical second harmonic acceleration sum of length change in: (a) r₁ and r₂ and (b) r₃, r₆, r_0x, and r_0y; influence on the stroke of length change in: (c) r₁ and r₂ and (d) r₃, r₆, r_0x, and r_0y in the in-line four-cylinder engine.

From Figure 8c, it seems that the length of r₁ could be increased to meet the desired stroke range. However, since lengthening r₁ also increased the maximum sum of the vertical second harmonic accelerations as shown in Figure 8a, link r₁ was excluded from the adjustment. Examining Figure 8a,c, r₂ can be shortened to its minimum length to increase the stroke and to decrease the second harmonic acceleration sum, but another link needs to be adjusted to meet the desired stroke. Hence, with the minimum length of r₂, the other three link lengths were decreased by 0.1 mm in sequence within the tolerances as shown in Table 6 and Figure 9.

Table 6. Link length variation cases for Step S3.

Case		Variation Number	Link Length
			r2	r3	r4	r5	r6	r0y
1	Decrease r3 with min. r2, r4, and max. r5	1	56	73.5	42	95.5	140	−53
		:	56	:	42	95.5	140	−53
		21	56	71.5	42	95.5	140	−53
2	Decrease r6 with min. r2, r4, and max. r5	1	56	73.5	42	95.5	138	−53
		:	56	73.5	42	95.5	:	−53
		21	56	73.5	42	95.5	140	−53
3	Decrease r0y with min. r2, r4, and max. r5	1	56	73.5	42	95.5	140	−53
		:	56	73.5	42	95.5	140	:
		21	56	73.5	42	95.5	140	−55

The “:” in the table means the variation range as “-“. For example, the “1 : 21” and “73.5 : 71.5” for r3 in Case 1 mean that the variation Number “1, 2, 3, …, 21” correspond “73.5, 73.4, 73.3, …, 71.5” of r3.

Figure 9. Adjusted stroke and maximum value of vertical second harmonic acceleration sum in each case: (a) adjusted stroke and (b) maximum vertical second harmonic acceleration sum in the in-line four-cylinder engine.

In Figure 9a, the cases that satisfy the specified stroke range given in Table 2 are marked with a box. As shown in Figure 9b, Case 3 of variation number 10 has the lowest maximum sum of vertical second harmonic acceleration components. Hence, the final dimensions were selected from this case. In Table 7, the dimensions, stroke, piston pin position at TDC, and the maximum sums of the second and fourth harmonic acceleration components in the in-line four-cylinder engine are shown and compared with those of the initial design. The maximum of the vertical second and fourth harmonic acceleration sums were decreased by 58.333% and 34.882%, respectively.

Table 7. Comparison of the initial and final mechanism.

		Unit	Initial Design	Final Design	Effect (%)
Link	r1	mm	25.000	25.000
	r2	mm	57.000	56.000
	r3	mm	73.500	73.500
	r4	mm	44.000	42.000
	r5	mm	93.500	95.500
	r6	mm	140.000	140.000
	r0x	mm	78.000	78.000
	r0y	mm	−53.000	−53.900
Result	Stroke	mm	85.994	86.018
	Piston pin position at TDC	mm	197.391	185.124
	Max. of 2nd harmonic acceleration sum	mm/rad2	35.911	14.963	−58.333
	Max. of 4th harmonic acceleration sum	mm/rad2	10.714	6.977	−34.882

The link geometry of the initially designed Stephenson III mechanism was compared with the final design with minimized vertical second harmonic acceleration in Figure 10.

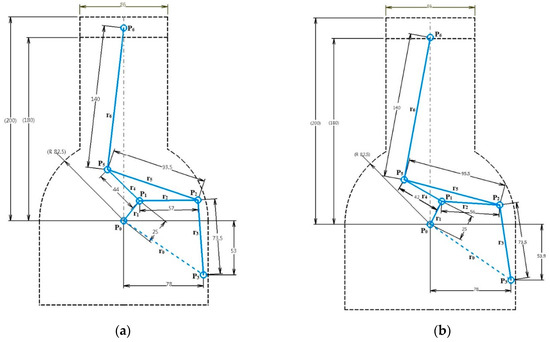
Figure 10. Stephenson III VCR engine mechanism: (a) initial design and (b) final design.

In Figure 11, the vertical harmonic acceleration components at the piston pin in the finally designed single-cylinder Stephenson III mechanism were compared with those of a conventional slider-crank mechanism whose crank length was 43 mm, offset was 0 mm, stroke was 86 mm, and piston pin position at TDC was 190 mm. The maximum vertical second harmonic acceleration at the piston pin in the final design of the Stephenson III mechanism was considerably lower than that of the slider-crank mechanism, each of which was calculated as 0.596 mm/rad² and 12.859 mm/rad². Even though the third and fourth acceleration components in the Stephenson III mechanism were calculated as 5.541 mm/rad² and 1.157 mm/rad², respectively, the vertical third harmonic acceleration would be cancelled out in the in-line four-cylinder engine and the vertical fourth harmonic acceleration was considerably lower than the second harmonic acceleration of the slider-crank mechanism.

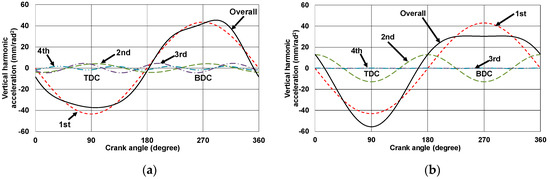
Figure 11. Vertical harmonic acceleration components at piston pin in single cylinder engine: (a) final design of the Stephenson III mechanism and (b) the slider-crank mechanism.

In Figure 12, the vertical second harmonic acceleration at each joint in the final design of the Stephenson III mechanism was compared with those of the slider-crank mechanism in the in-line four-cylinder engine configuration. In the case of the slider-crank mechanism, the peak value of the sum of the vertical second harmonic acceleration was 51.435 mm/rad², while the peak value of the overall or sum of the vertical second harmonic acceleration components of the Stephenson III mechanism was 14.963 mm/rad², which was about 29.091% of that for the slider-crank mechanism.

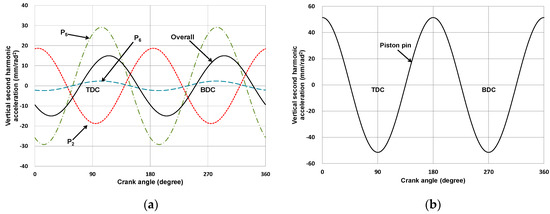
Figure 12. Vertical second harmonic acceleration components at each joint in four-cylinder engine: (a) final design of the Stephenson III mechanism and (b) the slider-crank mechanism.

5. Discussion

The conceptual design of a new VCR engine may depend on trial and error to find the feasible kinematic structure. The purpose of this research was to propose a simple method to determine a feasible mechanism and its dimensions that would yield a nearly minimized sum of the vertical second harmonic acceleration at joints without going through an optimization procedure. For the validation of the proposed method, a constrained nonlinear optimization was carried out using ‘fmincon’ solver of MATLAB optimization tool box to minimize the maximum sum of the second harmonic acceleration at each joint with the design specification given in Table 2 and the Grashof criteria for the crank-rocker four bar as the constraints. The computational time of the optimization was 9.6 s using a computer (Intel® i7 Quad CPU 1.8 GHz, 8 GB RAM) with Windows 10 (64 bit) operating system. The results of the optimization were compared with that of the proposed method in Table 8 and Figure 13. As shown in Table 8, the dimensions determined by the proposed method and the optimization were slightly different, because the selected variables in the proposed procedure were the link lengths except r₁ and r_0x, while the optimization considered all the link lengths as variables.

Table 8. Comparison of the results of the proposed method and the constrained optimization.

		Unit	Initial Design	Result of Proposed Method	Result of Optimization	Effect (%)
Link	r1	mm	25.000	25.000	24.95798	-
	r2	mm	57.000	56.000	56.00000	-
	r3	mm	73.500	73.500	73.44895	-
	r4	mm	44.000	42.000	42.00000	-
	r5	mm	93.500	95.500	95.49999	-
	r6	mm	140.000	140.000	138.0000	-
	r0x	mm	78.000	78.000	80.00000	-
	r0y	mm	−53.000	−53.900	−55.00000	-
Result	Stroke	mm	85.994	86.018	85.975	-
	Piston pin position	mm	197.391	185.124	184.424	-
	Max. 2nd harmonic acceleration sum	mm/rad2	35.911	14.963	13.773	−7.940
	Max. 4th harmonic acceleration sum	mm/rad2	10.714	6.977	7.114	+1.997

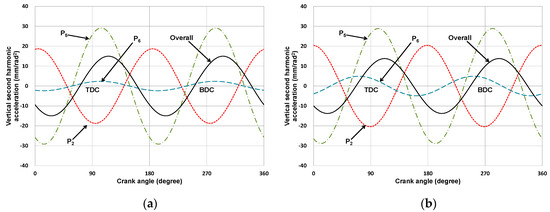
Figure 13. Vertical second harmonic acceleration components at joints of the Stephenson III mechanism in the four-cylinder engine: (a) proposed method and (b) optimization using commercial software.

Even though the optimization method yielded optimum dimensions when a mechanism to be optimized was selected, it did not provide information that could be used to select a feasible mechanism among many candidates. The proposed method, on the other hand, can be applied at the kinematic conceptual design stage to determine a feasible mechanism and its dimensions simply by plotting the vertical second harmonic acceleration component at each joint and the influence of link length changes. The influence of link length changes on the second harmonic acceleration can be utilized at the final layout design stage for a minute adjustment of link lengths and optimization as well.

For the completion of the kinematic design of a VCR engine, the control function needs to be considered. The proposed procedure can be initially applied to determine the dimensions of the mechanism for a specific compression ratio at which the vertical second harmonic acceleration needs to be taken into account more seriously. In order to vary the compression ratio, the ground pivot, P₃, in Figure 10b needs to be moved to a new position. For a new position of P₃, examine the vertical second harmonic acceleration components at the joints in the mechanism with the same dimensions except for the position of P₃(r_0x, r_0y). If the acceleration is not within an allowable range, the above procedure can be reapplied to find dimensions that compromise between the compression ratios.

The four-bar linkage in the Stephenson III mechanism may take the form of a crank-rocker or double-crank type. In this paper, the Stephenson III mechanism with a crank-rocker four bar is considered for the VCR engine, which is known to have lower levels of vertical and horizontal excitation forces and can achieve the same level of booming noise performance as conventional engines without a balance shaft [26]. The Stephenson III VCR engine mechanism with a double-crank four bar shown in Figure 14 is proposed by Komatsubara and Kuribayashi [12]: the domain of motion of this type is small compared to that of the Stephenson III crank-rocker version, and the second order of piston acceleration at the engine speed of 300 rpm in the single cylinder engine is lower than that of the slider-crank engine mechanism at compression ratios 8 and 9.3, but higher at compression ratio 16.5. For comparison, the vertical second harmonic acceleration components in the final design of the Stephenson III mechanism with a crank-rocker four bar shown Figure 10b were computed at low and high compression ratios by altering the position of the ground pivot, P₃. As shown in Table 9, the vertical second harmonic acceleration components in unit of m/sec² at 300 rpm in a single cylinder engine were lower than those of the slider-crank engine mechanism at both low and high compression ratios.

Figure 14. Stephenson III VCR engine mechanisms with double-crank type four-bar linkage.

Table 9. Vertical second harmonic acceleration components in the finally designed single-cylinder Stephenson III with crank-rocker four bar at low and high compression ratios.

Mechanism	Unit	Stephenson III (Crank-Rocker)		Slider Crank
Compression ratio	-	8	16.5	-
r0x	mm	72.100	78.000	-
r0y	mm	−46.900	−53.900	-
Stroke	mm	85.502	86.018	86.000
2nd harmonic acceleration at piston pin	m/s2	3.701	0.588	12.691
Max. 2nd harmonic acceleration sum	m/s2	5.542	3.692	12.691

6. Conclusions

This paper proposed a kinematic conceptual design process of VCR engine mechanisms considering the vertical second harmonic acceleration. From the graphs of six-link kinematic chains, Watt II and Stephenson III linkages were selected as candidate VCR engine mechanisms, and their initial dimensions satisfying the prescribed design specifications were determined. Fourier series analysis on the acceleration at each joint of the above two initially designed VCR engine mechanisms shows that the vertical second harmonic acceleration components of the Watt II linkage was much higher when they were used in the in-line four-cylinder engine, hence the Stephenson III mechanism was selected as the feasible VCR engine mechanism.

Assuming that the concentrated mass at each joint in the Stephenson III mechanism was the same, the effects of link length changes on the maximum sum of vertical second harmonic acceleration components and the stroke were examined, and then links whose lengths would be altered to reduce the second harmonic acceleration and the other links to satisfy the stroke and to reduce acceleration were selected. By adjusting the link lengths from those of the initial design, the overall vertical second harmonic acceleration of the finally designed Stephenson III mechanism was reduced by 58.333% compared to that of the initial design and by 70.909% compared to the slider-crank mechanism.

The proposed method can be applied to determine feasible mechanisms, their dimensions, and ideal mass distribution of the links in the automotive industrial applications, such as multi-link VCR and variable stroke engines of various multi-cylinder configurations, where the second harmonic acceleration needs to be considered at the kinematic conceptual design stage.