Single Image Super-Resolution: Depthwise Separable Convolution Super-Resolution Generative Adversarial Network

Abstract

The super-resolution generative adversarial network (SRGAN) is a seminal work that is capable of generating realistic textures during single image super-resolution. However, the hallucinated details are often accompanied by unpleasant artifacts. To further enhance the visual quality, we propose a deep learning method for single image super-resolution (SR). Our method directly learns an end-to-end mapping between the low/high-resolution images. The method is based on depthwise separable convolution super-resolution generative adversarial network (DSCSRGAN). A new depthwise separable convolution dense block (DSC Dense Block) was designed for the generator network, which improved the ability to represent and extract image features, while greatly reducing the total amount of parameters. For the discriminator network, the batch normalization (BN) layer was discarded, and the problem of artifacts was reduced. A frequency energy similarity loss function was designed to constrain the generator network to generate better super-resolution images. Experiments on several different datasets showed that the peak signal-to-noise ratio (PSNR) was improved by more than 3 dB, structural similarity index (SSIM) was increased by 16%, and the total parameter was reduced to 42.8% compared with the original model. Combining various objective indicators and subjective visual evaluation, the algorithm was shown to generate richer image details, clearer texture, and lower complexity.

1. Introduction

Single image super-resolution (SISR) reconstruction is the development of high-resolution (HR) images with richer details and clearer texture from low-resolution (LR) images or degraded images and has wide applications in the field of image processing [1,2,3,4,5]. At present, reconstruction techniques are divided into three main categories: interpolation-based, reconstruction-based, and learning-based methods. The interpolation reconstruction method proposed here includes nearest interpolation, bilinear interpolation, and bicubic interpolation. Further proposed reconstruction-based methods are iterative back projection (IBP) [6], projection onto convex sets (POCS) [7], and maximum a posteriori (MAP) [8]. Some learning-based methods have been proposed, including the early collar neighbor embedding (NE) [9] algorithm and the sparse representation-based classification algorithm [10]. Deep resolution reconstruction methods based on deep learning are gaining more attention. The super-resolution convolutional neural network (SRCNN) [11] algorithm introduced deep learning methods to SISR for the first time. In order to improve the network convergence speed of SRCNN, accelerating the super-resolution convolutional neural network (FSRCNN) [12] was developed. Efficient sub-pixel convolutional neural network (ESPCNN) [13] was also proposed to further improve the efficiency of computation. In order to further recover the high-frequency detail of images, Yang [14] et al. proposed a deep learning method called data-driven external compensation guided deep networks for image super­resolution. Traditional deep learning methods can optimize image quality by making the network structure deeper, to obtain more image features. The introduction of generative adversarial networks (GAN) [15] is a new direction for SISR.

Super-resolution generative adversarial network (SRGAN) [16] applied GAN to SISR for the first time. The images generated by SRGAN are clearer and more detailed than those produced using similar reconstruction methods. However, there are also shortcomings, such as edge blurring, image artifacts, excessive numbers of network parameters, and difficulty in achieving convergence of the neural network. The Wasserstein GAN [17] uses a gradient penalty to try to solve the problems of neural network training. In this paper, we propose a GAN based on depthwise separable convolution dense blocks, which can improve computational efficiency by greatly reducing the number of parameters. It also reduces algorithm complexity, reduces reliance on hardware resources, and extends the range of applications. For the better restoration of image edges and improvement of the quality of super-resolution images, we introduce a new loss function for generative networks: the frequency energy similarity loss function. This new loss function is used to constrain the generator network so that the image quality is better and the edges are clearer. In image super-resolution reconstruction experiments using the benchmark datasets Set5 and Set14, the performance of the depthwise separable convolution super-resolution generative adversarial network (DSCSRGAN) algorithm according to the objective indicators peak signal-to-noise ratio (PSNR), structural similarity index (SSIM), and mean square error (MSE), was better than that of similar algorithms. In terms of subjective visual evaluation, the super-resolution algorithm made the image edges clearer, the details richer, and according to comprehensive subjective and objective evaluation, the reconstruction algorithm described in this paper achieved good results. We describe the DSCSRGAN architecture, energy similarity loss function, and the DSC Dense Block in Section 3. The visual illustrations are provided in Section 4. The paper concludes with a discussion in Section 5.

In summary, we would like to make the following technical contributions:

• We propose DSCSRGAN. This is the first time that depthwise separable convolution has been used for SISR. A depthwise separable convolution dense block for learning the feature representation of the image;
• The frequency energy similarity loss function was proposed. This new loss function is more stable and effective than previous approaches in the experiments we conducted.

2. Related Work

2.1. Generative Adversarial Networks

Generative adversarial networks were proposed by Goodfellow et al. [15], based on game theory. They include generator networks and discriminator networks and reach Nash equilibrium through games between the two networks. For super-resolution using a generative adversarial network, the real sample data $S_r$ are generated by feature extraction of the real sample data by a generator network $G$, so that the generated sample data $S_g$ are as close to the $S_r$ as possible, as follows:

$$\underset{G}{min}\underset{D}{max}V\left(D,G\right)=E_{x~P_{data\left(x\right)}}\left[\log D\left(x\right)\right]+E_{Z~P_{z\left(z\right)}}\left[\log (1-D\left(G\left(Z\right)\right)\right)].$$

(1)

A low-resolution image $I^{LR}$ is input to a generator network to generate the super-resolution image $I^{SR}$, while a discriminator network takes the high-resolution images $I^{HR}$ and $I^{SR}$ as input, to determine which is the real image and which is the super-resolution image, as follows:

$$\underset{G}{\min }\underset{D}{\max }{E}_{I^{HR}~P_{data(I^{HR})}}[\log D(x)]+E_{I^{LR}~P_G(I^{LR})}[\log (1-D(G((I^{LR}))))].$$

(2)

2.2. Depthwise Separable Convolution

Depthwise separable convolution was proposed by Chollet [18]. The difference from traditional convolution is that it divides the convolution process into different channels, and uses pointwise convolution to change the number of channels of the output. The convolution process is shown in Figure 1.

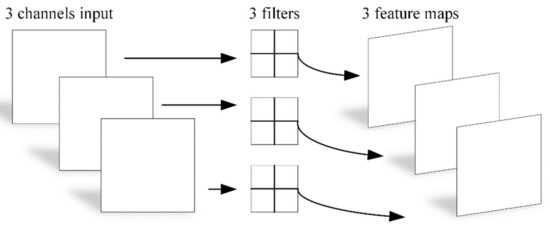
Figure 1. Overview of depthwise separable convolution.

The main differences produced by depthwise separable convolution are that the total number of parameters is greatly reduced, and the channel and region are processed separately.

3. Depthwise Separable Convolution Super-Resolution Generative Adversarial Network

3.1. DSCSRGAN Architecture

DSCSRGAN is an improved neural network based on SRGAN, including a generator network and a discriminator network. The architecture is shown in Figure 2. The generator network consists of two types of dense block. The DSC Dense Block structure is described in Section 3.2. In Block II, the structure is as follows: convolutional layer Pixelshuffler ×2 and activation function PReLU layer. In Block III, the structure is as follows: a convolutional layer and an activation function, the Leaky ReLU layer. Skip connection is used so that the primary features are not lost, but are extended and passed to the deep structure for further extraction and learning. The main design goals of DSCSRGAN are as follows: to improve the feature representation and learning ability of the generator network, to reduce the complexity of the algorithm, and to accelerate the convergence of the neural network. The main innovation in the algorithm is in the dense block of the generator and the dense block of the discriminator. A new loss function is also proposed to better constrain the generator network, to generate a super-resolution image closer to the high-resolution image. A new DSC Dense Block can reduce the number of network parameters and improve the learning ability of the neural network for image feature representation, which aids with network training and speeds up convergence. The algorithm further reduces the dependence on hardware resources, extending the applicability of the algorithm. For the discriminator dense block, the BN layer is removed. Experiments showed that unpleasant artifacts in the super-resolution image are improved after the batch normalization layer is removed. For the loss function, a frequency energy similarity loss function is proposed, which converts from the spatial domain to the frequency domain. Similarity comparison of the frequency domain energy is then carried out to constrain the generator network further so that the super-resolution images generated by it are richer in detail and closer to high-resolution images.

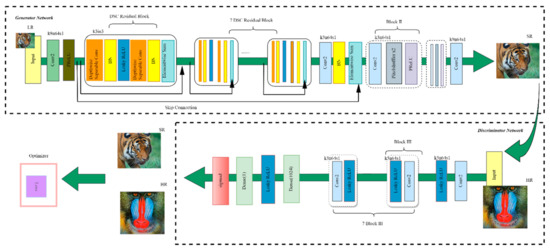
Figure 2. An overview of our DSCSRGAN. Kernel size(k), number of maps(n), in_channels(in), and stride(s) are indicated for each convolutional layer. The same color represents the same structure. (Best viewed in color).

3.2. Depthwise Separable Convolution Dense Block

Kaiming He [19] et al. first proposed the dense block structure, and solved some of the problems caused by deep neural networks by introducing a skip connection structure. Here ${\mathit{x}}_l$ is the input feature of the lth residual unit. ${\mathcal{W}}_l=\left\{{\mathcal{W}}_{l,k\left(1\le k\le K\right)}\right\}$ is a set of weights (and biases) associated with the lth residual unit, and $K$ is the number of layers in a residual unit. $\mathcal{F}$ denotes the residual function. The function $h$ is set as an identity mapping: $h\left({\mathit{x}}_l\right)={\lambda }_l{\mathit{x}}_l$. The main idea is shown in Equation (3):

$${\mathit{x}}_{l+1}={\lambda }_l{\mathit{x}}_l+\mathcal{F}\left({\mathit{x}}_l,{\mathcal{W}}_l\right).$$

(3)

This paper proposes the DSC Dense Block, a dense block based on depthwise separable convolution. It is used for generator network learning and extraction of image features and includes the following structures: a depthwise separable convolution layer, a batch normalization layer, a leaky ReLU layer, and an element-wise sum layer. The architecture is shown in Figure 2. The ${\mathit{x}}_l$ are passed through the identity map $h\left({\mathit{x}}_l\right)$ and then extracted from the dense block multiple layer as a layer $l+1$ input. $f({\mathit{x}}_l)$ represents the process, as shown in Equation (4):

$${\mathit{x}}_{l+1}=f({\mathit{x}}_l)+h\left({\mathit{x}}_l\right).$$

(4)

Since $h\left({\mathit{x}}_l\right)$ is an identity map, Equation (5) can be derived:

$${\mathit{x}}_{l+1}=f({\mathit{x}}_l)+{\mathit{x}}_l.$$

(5)

After extraction and learning through multiple module connections, the $L$ layer output is as in Equation (6):

$${\mathit{x}}_L={{\displaystyle \sum }}_{i=1}^{L-1}f({\mathit{x}}_i)+{\mathit{x}}_l.$$

(6)

From the chain rule, the DSC Dense Block backpropagation feature ensures that the gradient does not disappear when the weight is arbitrarily small and not zero, as shown in Equation (7), where $\epsilon$ is the loss function:

$$\frac{\partial \epsilon }{\partial x_l}=\frac{\partial \epsilon }{\partial x_L}\frac{\partial x_L}{\partial x_l}=\frac{\partial \epsilon }{\partial x_L}\left[1+\frac{\partial }{\partial x_l}{{\displaystyle \sum }}_{i=1}^{L-1}f(x_i)\right].$$

(7)

Experiments showed that after using DSC Dense Block, the characteristics and learning ability of the generator network improved, generating more realistic super-resolution images. The use of DSC Dense Block also significantly reduced the number of network parameters. When the number of input image channels is $C_{in}$, the convolution kernel is $f_p*f_p$. The number of output image channels is $C_{out}$ when the bias is 1. The traditional convolution parameter total calculation method is shown in Equation (8):

$$P_n=\left({\mathsf{\Pi }}_{i=1}^2{f}_p^i\right)C_{in}{C}_{out}+C_{out}.$$

(8)

After using the depthwise separable convolution method, the total number of parameters is calculated as shown in Equation (9):

$$P_d=\left({\mathsf{\Pi }}_{i=1}^2{f}_p^i\right)C_{in}+C_{out}*\left(C_{in}+1\right).$$

(9)

Taking the number of input channels as eight, the number of output channels as 16, and the convolution kernel as 3 × 3 as an example, the total number of convolution parameters is 1168, which is reduced to 216 by the depthwise separable convolution method. For the activation function, the DSCSRGAN algorithm selects four common functions: PReLU, LeakyReLU, Tanhshrink, and Softsign to test. The experimental results showed that the LeakyReLU function performed best. Detailed experimental results are shown in Section 4.1.

3.3. Frequency Energy Similarity Loss Function

In order to make the super-resolution image $I^{SR}$ generated by the generator network, closer to the high-resolution image $I^{HR}$, the loss function that best reflects the similarity between $I^{SR}$ and $I^{HR}$ is important. By optimizing the loss function, the quality of the image is better. The training process involves minimizing the loss function. The traditional loss function aims to reduce the mean squared error. $I^{SR}$ and $I^{HR}$ have their own characteristics as two-dimensional discrete signals, so this paper proposes a frequency energy similarity loss function. First, a fast Fourier transform (FFT) is used to convert between the frequency domain and the time domain. The FFT can be used to quickly convert the image from the time domain to the frequency domain (DFT). The traditional DFT is shown in Equation (10) in which $x\left(n\right)$ is an analog signal, $X\left(k\right)$ is the result of $x\left(n\right)$ after DFT, and $N$ is the length of signal samples:

$$X\left(k\right)={{\displaystyle \sum }}_{n=0}^{N-1}x\left(n\right)W_N^{kn},k=0,\mathrm{1...}N-1,W_N=e^{-j\frac{2\pi }{N}},$$

(10)

since the frequency domain does not take time into account. For example, there are two different signals about time $t$, $f_1\left(t\right)$, and $f_2\left(t\right)$, where $f_2\left(t\right)$ is the signal from $f_1\left(t\right)$ which is delayed for some time $\Delta t$, as shown in Equation (11):

$$\begin{array}{c}{f}_1\left(t\right)=cos(2\pi t),\\ f_2\left(t\right)=cos[2\pi \left(t+\Delta t\right)].\end{array}$$

(11)

Obviously, they have different magnitudes at the same time. However, the result of the Fourier transform is the same, and there is an error in directly using the result as a clue of signal similarity. As shown in Equation (12):

$$FFT \left[f_1\left(t\right)\left]=FFT \right[f_2\left(t\right)\right].$$

(12)

The processing of instantaneous local information in the $f\left(t\right)$ is consistent and does not reflect the local characteristics of the signal. Therefore, it is proposed to use the FFT to implement the frequency domain conversion, and then separately calculate the energy corresponding to the two signals $I^{SR}$ and $I^{HR}$, and compare the energy as a cosine. The FFT is shown in Equations (13) and (14):

$${\mathit{I}}_{FFT}^{SR}=FFT\left(I^{SR}\right).$$

(13)

$${\mathit{I}}_{FFT}^{HR}=FFT\left(I^{HR}\right).$$

(14)

Then it is necessary to further define the frequency energy similarity to compare $I^{SR}$ and $I^{HR}$, that is, the result after the fast Fourier transforms: ${\mathit{I}}_{FFT}^{SR}$ and ${\mathit{I}}_{FFT}^{HR}$. Inspired by Pascal’s theorem [20], the energy $I_{E_{ij}}^{SR}$ of the ${\mathit{I}}_{FFT}^{SR}$-frequency component is calculated, and the energy $I_{E_{ij}}^{HR}$ of the ${\mathit{I}}_{FFT}^{HR}$-frequency component, cosine similarity. As shown in Equation (15), ${\mathit{X}}_{n\times m}$ and ${\mathit{Y}}_{n\times m}$ are matrix vectors whose dimensions are $n\times m$:

$${cos}_{sim}(\mathit{X},\mathit{Y})=\frac{\mathit{X}\cdot \mathit{Y}}{\Vert \mathit{X}\Vert .\Vert \mathit{Y}\Vert }.$$

(15)

The $I^{SR}$ frequency-domain energy is ${\mathit{I}}_E^{SR}$, the $I^{HR}$ frequency domain energy is ${\mathit{I}}_E^{HR}$, and the results are substituted into $co{s}_{sim}$, as shown in Equation (16):

$$F_{sim}\left({\mathit{I}}_E^{SR},{\mathit{I}}_E^{HR}\right)=\frac{{\mathit{I}}_E^{SR}\cdot {\mathit{I}}_E^{HR}}{\Vert {\mathit{I}}_E^{SR}\Vert .\Vert {\mathit{I}}_E^{HR}\Vert }.$$

(16)

The generator loss function of SRGAN and WGAN includes content loss and adversarial loss. The generator loss function of DSCSRGAN is shown in Equation (17):

$$l^{SR}=l_X^{SR}+\lambda l_{Gen}^{SR}+\mu F_{sim}\left({\mathit{I}}_E^{SR},{\mathit{I}}_E^{HR}\right).$$

(17)

The experimental results show that the overall visual effect of the super-resolution image generated by the generator network was improved by introducing a frequency energy similarity loss function. Image quality problems, including edge blur, image artifact, and texture deficiency, were improved.

4. Experiments

4.1. Data and Similarity Measures

The algorithm in this paper was implemented on a Windows 10 system, using the programming language Python version 3.6, and the neural network framework was built using the Pytorch framework. The hardware configuration was Intel^® Xeon^® CPU E5-2680 v4 @ 2.40GHz, 128G RAM, and NVIDIA TITAN X (Pascal). The DIV2K dataset, which includes 800 training images and 2K resolution, was selected as the training data. Two test datasets, Set5 and Set14, were used for the image reconstruction test. The convolution layer parameter settings are shown in Figure 2. The generator was trained using the loss function presented in Equation (15) with λ = 0.001 and μ = −0.001. The evaluation index used PSNR and structural similarity, SSIM, to evaluate the super-resolution image. PSNR evaluates the image quality based on the error between images. The smaller the mean squared error between corresponding pixels, the larger the PSNR and the better the image quality. SSIM has three aspects: brightness, contrast, and structure. The value of the image quality has a range of $[0,1]$. The larger the value, the better the image quality; the relevant formula is as shown in Equation (18). MSE is the mean square error between the original image and the processed image. $n$ is the $n_{th}$ pixel value of the original image. ${\mu }_x$ and ${\mu }_y$ represent the mean values of images $x$ and $y$, respectively, and ${\sigma }_x$ and ${\sigma }_y$ represent the standard deviations of images. ${\sigma }_{xy}$ represents the covariance of the images $x$ and $y$. $c_1$ and $c_2$ are specified numbers:

$$\begin{array}{c}PSNR=10{\log }_{10}(\frac{{(2^n-1)}^2}{MSE}),\\ SSIM(x,y)=\frac{(2{\mu }_x{\mu }_y+c_1)({\sigma }_{xy}+c_2)}{({\mu }_x^2+{\mu }_y^2+c_1)({\sigma }_x^2+{\sigma }_y^2+c_2)}.\end{array}$$

(18)

4.2. Performance of the Final Networks

The DSC Dense Block performs feature extraction and representation in the generator network. The activation function affects the convergence speed, stability, and quality of the generated image. Therefore, different activation functions can be chosen to build the DSCSRGAN to train and test on the DIV2K dataset, including PReLU, LeakyReLU, Tanhshrink, and Softsign. Experimental results showed that a network model using LeakyReLU as the activation function had faster convergence and better network stability in the early stage. The results are shown in Figure 3.

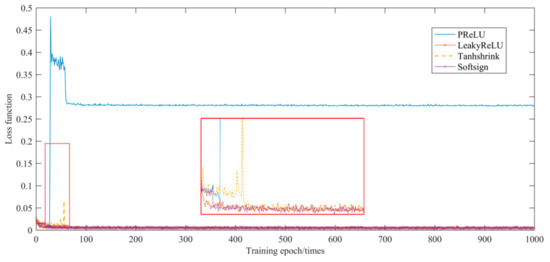
Figure 3. Changes of loss function with the number of iterations.

The number of algorithm parameters generated in the network reported in this paper was reduced by 557064 compared with SRGAN, a drop of 58.2% (Table 1). This reduction in the number of parameters helps to reduce the complexity of the algorithm, improve its robustness, and enhance the real-time performance of the algorithm.

Table 1. Parameters of different network models.

Network Model	DSCSRGAN	SRGAN	WSRGAN	SRCNN	FSRCNN	ESPCNN
Parameters	399367	956431	956431	148608	13697	61680

Five reconstruction algorithms based on learning and DSCSRGAN were selected to perform image reconstruction tests on the Set5 and Set14 datasets. The objective evaluation index average PSNR and average SSIM were calculated. The objective indices were better than those generated by the other algorithms. In Set5, PSNR and SSIM enhancements reached 3.3 dB and 15.97%, respectively. For the Set14 dataset, the PSNR increased by 3.1 dB, and the SSIM increased by 16.46%, as shown in Table 2.

Table 2. Comparison of the quantitative evaluation results of six methods with the Set5 and Set14 datasets.

Dataset	PSNR/dB		SSIM
Model	Set5	Set14	Set5	Set14
DSCSRGAN	30.1438	27.1176	0.9224	0.8217
WSRGAN	28.2423	25.0850	0.8779	0.7396
SRGAN	28.7594	25.1159	0.9074	0.7766
SRCNN	26.8796	23.9469	0.7627	0.6571
FSRCNN	27.9020	24.6097	0.8057	0.6991
ESPCNN	28.1569	24.7584	0.8001	0.6962

Figure 4 shows the reconstruction effects of the different algorithms. In the experiments, each picture of the image data set to be trained was first cut into a 128 × 128 sized picture, and then the 64 pieces were sent as a batch to the DSCSRGAN to train the generator and the discriminator, with the learning rate set to 10⁻⁵. The number of iterations was 1000, and the Adam algorithm was used for optimization. The up-sampling factor was $\times 4$. The generator was pre-trained to avoid falling into a local optimum. At the end of each training batch, the average PSNR and SSIM of the image generated by the batch were recorded. The subjective visual effects of images super-resolution using DSCSRGAN were clearer, and details such as faces, hats, textures, text, and shadows were well restored.

Figure 4. Super-resolution image reconstruction effect comparison schematic diagram. From left to right: DSCSRGAN, SRGAN, WSRGAN, SRCNN, FSRCNN, ESPCNN. Corresponding PSNR, SSIM, and MSE are shown below the figure. (4× upscaling) (Best viewed in color).

5. Discussion and Future Work

The algorithm in this paper is based on generative adversarial networks to achieve super-resolution reconstruction of low-quality images. Using deep learning, neural networks can learn a mapping between low-resolution and high-resolution images. Depthwise separable convolution combined with dense blocks is also introduced, and the DSC Dense Block suitable for super-resolution reconstruction was redesigned, greatly reducing the total number of network parameters and the complexity of the algorithm. A frequency energy similarity loss function is also proposed, based on the frequency domain, which better constrains the generator network, making the edges of the generated image sharper, richer in detail, and more natural. The reconstruction of some degraded images with missing details, insufficient illumination, and noise pollution still needs to be improved. By further improving the network structure and optimizing the loss function, the algorithms can be used in the fields of infrared image restoration and medical image reconstruction. We will explore intrinsic parallelism of convolutional neural network (CNN) [21] and consider for future studies the use of another framework in SISR. This single image super-resolution reconstruction algorithm is an improvement over previous work, and still has the potential for further refinement.