Abstract
Environmental problems associated with emergency emissions, indoor air pollution with harmful particles, and the spread of viruses and bacteria make the topic of cleaning indoor air from small particles of pollution relevant. In the event of a dangerous situation associated with the presence of small particles in the air, especially those smaller than 10 μm, methods for quickly cleaning the air from such pollutants are required. One of these new methods is the efficient spraying of fine aerosol using the ultrasound technique. Fine aerosol with a droplet size of about 30–50 μm interacts more effectively with pollutant particles compared to larger aerosols. In this paper, the process of interaction of droplets with a characteristic size of 30–50 μm with airborne pollutant particles sized 0.1–10 μm is theoretically studied. Particular attention is paid to particles sized 0.1–2 μm, which are the most difficult to remove from the air. The work will serve as a theoretical basis for the development of methods for cleaning indoor air of pollutant particles using fine aerosol.
1. Introduction
The issue of interaction between aerosol particles and air pollutants and methods of air purification from these pollutants remains relevant, as evidenced by a number of publications in recent years. The work in reference [1] provides a modern review of the global problem of indoor air quality. Review [2] describes in detail the impact of indoor air pollution on human health, systematizes the sources of these pollutants, and highlights some of the non-obvious consequences. Recent studies have discovered new, previously unconsidered effects of pollutants on human health. For example, reference [3] studies the effect of PM2.5 aerosol particles on the spread of the influenza virus in the body. It was found that the association of the virus with solid particles facilitates its delivery to the lower respiratory tract and further spread.
Works [4,5] consider and discuss air purification methods, including physicochemical technologies (e.g., filtration, adsorption, UV photocatalytic oxidation, ultraviolet disinfection, and ionization) and biological technologies (e.g., plant-based purification methods and microalgae-based methods). The works devoted to the purification of indoor air from pollutants do not mention the method of spraying water mist (or other liquid aerosol) to absorb and remove contaminants from the air. Such a method, however, would be useful, especially in disinfection and purification of air in hospitals or for the elimination of the consequences of emergency emissions in industrial premises.
In addition to droplet–particle interactions, recent studies have highlighted the importance of particle–particle and particle–surface interactions in both open and confined environments. For instance, Adeniran et al. (2021) [6] emphasized the health risks of PM2.5 pollution and discussed the significance of particle agglomeration and deposition processes. Chlebnikovas et al. (2022) [7] analyzed indoor particle behavior in closed spaces, stressing the role of ventilation and surface deposition in shaping exposure levels. Similarly, Sanada et al. (2023) [8] investigated particle transport dynamics in building environments, pointing out the interplay between airborne motion, surface interactions, and removal strategies. These findings complement the present study by showing that the efficiency of aerosol-based air purification is also influenced by background particle dynamics and environmental boundaries.
The interaction of specially sprayed aerosol with radioactive aerosol generated by leaks or accidents at nuclear power plants has been studied the most [9]. Many researchers have studied the characteristics of the aerosol removal process using a spray system. The mechanisms of removal of harmful aerosols were described in the classical works of Fuchs (1965) [10]. An improved model of particle removal from the air as a result of droplet interception is given in the work of Lee (1980) [11]. The mechanism of particle removal due to Brownian diffusion was studied by Postma (Postma et al., 1975) [12] and Jung (Jung and Lee, 1998) [13]—taking into account the circulation of liquid inside the droplet. A combination of mechanisms of particle removal from the air was studied in the work of Lee and Liu (1980) [14]. These classical models of single-droplet behavior allowed us to consider the efficiency of aerosol removal by spraying a special aerosol (multiple droplets). One of the first and relatively simple models of particle removal from air by spraying an aerosol was developed by Postma (Postma et al., 1978) [15]. Later, such models began to take into account the agglomeration of droplets during interaction with pollutant particles, for example, the work of Powers (Powers and Burson, 1993) [16]. The work in [17] discusses in detail the effect of droplet agglomeration on the removal of radioactive aerosol formed as a result of the accident. In particular, it was found that the effect of droplet agglomeration on the efficiency of aerosol removal is not linear. It depends on the specific droplet size distribution. It was found that droplet agglomeration has the greatest effect on the removal of finely dispersed contaminant aerosols, especially with a particle diameter of less than 1.5 μm. The effect of electrostatic charging of droplets of the capturing aerosol, as well as the wettability of contaminant particles on the efficiency of capturing, is investigated in [18]. It was found that charged droplets of sprayed aerosol provide almost complete removal of all particles due to the electrostatic effect, regardless of wettability/size, even for particles with a diameter of less than 10 μm. In this case, the wettability of particles is important when removing them with neutral sprays (hydrophilic particles are captured better than hydrophobic ones). An interesting result of this work was the finding that dynamic agglomeration of particles during the capturing process did not have a noticeable effect on the result of contaminant removal, but the initial size of the droplets of the sprayed aerosol is very important.
The mechanisms of contaminant removal by neutrally charged aerosol spraying are primarily inertial collision, interception, and Brownian diffusion (Ardon-Dryer et al., 2015) [19], with diffusiophoresis and thermophoresis (Santachiara et al., 2013) [20] also considered. The particle size of the contaminant is a key parameter determining its kinetic behavior. For particles larger than 10 μm, gravitational sedimentation plays a significant role, while smaller particles can remain in the air for a long time, and therefore are the most difficult to remove. For the removal of aerosol particles smaller than 0.1 μm, the main mechanism is Brownian diffusion, while for aerosol particles larger than 1 μm, the most effective removal method is inertial sedimentation. However, in the transition range for particles with a diameter of 0.1 to 1 µm (Greenfield, 1957) [21], these mechanisms demonstrate significantly lower efficiency.
It is known that particles with sizes less than 10 µm, especially less than 2.5 µm, are the most dangerous for human health, regardless of their chemical composition [22]. Therefore, it is necessary to study the behavior of contaminant particles with sizes less than 10 µm and the possibility of precisely removing such particles from the air using a specially sprayed aerosol.
One of the main conditions for the efficiency of contaminant removal using aerosol droplets is high aerosol dispersion. Such droplets do not settle for a long time and remain in the air, collecting harmful substances, and they have a large specific surface area, increasing the efficiency of interaction with substances in the air. On the other hand, aerosol generation should occur with a sufficiently high productivity. The development of methods for cleaning indoor air from contaminants using a specially sprayed aerosol has so far been limited by the shortcomings of the means for creating such an aerosol. Recently, methods of highly productive spraying of fine aerosol based on the use of ultrasound have appeared [23]. They make it possible to create an aerosol with a characteristic droplet size of about 30–40 μm, which remains in the air for a long time, collecting pollutants. The behavior of these droplets and their interaction with contaminants has its own characteristics and differences from, for example, the behavior of droplets with characteristic sizes significantly exceeding the size of contaminant particles (100 μm and more), which were usually considered by researchers before. The dominant mechanisms of interaction between fine droplets and contaminant particles differ from those characteristic of larger droplets. These mechanisms and differences, as well as the efficiency of contaminant capture by fine aerosol droplets (less than 50 μm in diameter), have not yet been studied.
Previous studies have primarily focused on aerosol droplets larger than 50–100 μm, which are typically formed in nozzle spraying and are applied to the mitigation of radioactive aerosol releases or industrial emissions [9,10,11,12,13,14,15,16,17]. These droplets demonstrate different dominant capture mechanisms, where inertial impaction and gravitational settling prevail, and their efficiency is well documented. In contrast, significantly fewer works have addressed fine droplets in the 30–50 μm range, which remain airborne longer and interact differently with submicron particles due to enhanced Brownian diffusion and interception. The novelty of the present work lies in bridging this knowledge gap: we analyze in detail the capture dynamics of submicron- and micron-sized contaminants in droplets smaller than 50 μm and quantify the efficiency in the Greenfield gap, which has not been adequately characterized in the earlier literature.
Unlike previous studies, which mainly examined capture through coarse droplets (>50 μm) where inertial impaction dominates, the present work integrates multiple mechanisms—diffusion, interception, and electrostatic effects—into a single framework for the less-explored range of fine droplets (30–50 μm). A distinctive contribution of this study is the introduction of the “characteristic capture time,” which provides a practical and quantifiable measure of purification efficiency and enables direct comparison across different particle sizes and droplet concentrations.
The aim of the work is to conduct a theoretical study of the mechanisms of interaction of aerosol droplets with a characteristic size of 30–50 μm with contaminants in the air, as well as the efficiency of trapping fine particles of contaminants with aerosol droplets. It is necessary to identify the leading mechanisms of interaction and determine the conditions for maximum efficiency of air purification from harmful particles.
Thus, the specific aim of this study is not to provide a universal description of all possible aerosol–particle interactions, but rather to focus on the critical size range of contaminant particles (0.5–2 μm) where capture efficiency is minimal (the so-called Greenfield gap). In particular, we investigate how fine droplets with diameters of 30–50 μm, generated by ultrasonic spraying, can mitigate this efficiency gap through diffusion, interception, and electrostatic mechanisms. By narrowing the scope to this most problematic size interval, the present work contributes a targeted theoretical basis for optimizing fine aerosol spraying as an indoor purification method.
2. Mathematical Description of the Interaction of Aerosol Droplets and Contaminant Particles
2.1. Statement of the Problem
We will consider an aerosol with a characteristic droplet diameter (modal diameter) dd ~ 30–50 μm, specially sprayed in a room volume where there is already an aerosol of pollutant particles with a modal diameter dp from 100 nm to 10 μm. The pollutant can be represented by various phase compositions, can have an electric charge (which is typical, for example, for bacteria), and can be characterized as hydrophobic or hydrophilic.
Below, when speaking about specially sprayed aerosol droplets, we will refer to them as “droplets,” and when speaking about particles that need to be removed from the air, we will refer to them as “particles”, “contaminant particles”, or “pollutant particles.”
The behavior of aerosol droplets with a characteristic size of 30–50 µm is fundamentally different from the behavior of droplets with a diameter of about 100 µm or more, for example, sprayed by a nozzle. Such spraying is used to precipitate radioactive particles and has been well studied, both theoretically and experimentally. What is the difference between an aerosol with droplets of 30–50 μm and larger ones?
- Such droplets quickly (<1 s) slow down in the air at a short distance (<10 cm) from the spray nozzle. Then, the droplets spread in space as a result of convective diffusion [24].
- The relative velocity of droplets and particles is determined not by the velocity of the droplet leaving the spray nozzle (as for droplets larger than 100 μm), but primarily by the difference in the velocity of gravitational settling [25].
- Droplets with a diameter of 30–50 µm settle under the action of gravity much more slowly than larger ones (with a diameter of 100 µm or more)—the settling velocity is proportional to the square of the particle diameter. The velocity of gravitational settling in air for a droplet with a diameter of 40 µm will be approximately 0.05 m/s, while for a droplet with a diameter of 100 µm, it is 6 times greater, 0.3 m/s. Therefore, smaller droplets remain in the air for a relatively long time and interact with contaminant particles all this time [25].
- Droplets with a diameter of 40 μm have a relatively large specific surface area, compared to larger droplets (e.g., 100 μm)—proportional to the ratio of the droplet diameters. Thus, the specific surface area of droplets with a diameter of 40 μm is 2.5 times greater than for droplets with a diameter of 100 μm (and will be 150,000 m−1). Also, with the same mass of sprayed aerosol, the numerical concentration of smaller droplets will be significantly higher. It is the numerical concentration of droplets and their total surface area that determines the efficiency of capturing contaminant particles as a result of coagulation and adsorption [25].
2.2. Mechanisms of Capture of Contaminant Particles by Aerosol Droplets Depending on the Size of Droplets and Particles
In the problem of interaction between droplets and small contaminant particles, the following mechanisms are usually considered:
- Inertial collision (large particles deviate from the streamlines and collide with the droplet). Relatively large aerosol particles (e.g., droplets > 30 μm in diameter) settle under the action of gravity and collide with smaller contaminant particles, capturing them along the way.
- Diffusion deposition (small particles, such as viruses, move due to Brownian or convective diffusion). Both types of particles (aerosol droplets and contaminants) are subject to chaotic thermal motions, which increases the probability of collisions.
- Interception (particles follow the streamlines and “graze” the droplet if they are close enough). When a contaminant particle moves along the air flow line and gets close enough to an aerosol droplet, it can be “captured” by adhesion on the droplet surface. This occurs if the streamline is at a distance less than or equal to the particle radius (dp/2) from the droplet surface.
- Electrostatic attraction (if the particles are charged). Viral envelopes (e.g., capsids or lipid membranes) and bacterial cell walls are often negatively charged due to the presence of ionized groups (e.g., carboxyl or phosphate) on their surface. The magnitude of the charge depends on the pH of the environment, but under typical air conditions (pH neutral or slightly acidic), the charge remains negative. For example, for viruses such as SARS-CoV-2, the surface charge is estimated to be in the range of −10 to −50 mV (ζ potential). Aerosol droplets are usually neutral in the absence of external influences (such as an electric field or ionization). However, a neutral particle can become polarized in the presence of a charged particle, which creates an attraction. An induced electrostatic interaction occurs between the negatively charged particle (virus/bacteria) and the neutral droplet. This occurs due to the polarization of the droplet: the negative charge of the contaminant repels the electrons in the droplet, creating a local positive charge on its surface near the particle.
The capture efficiency is defined as the ratio of the number of particles actually captured by the droplet to the number of particles that could theoretically collide with it if they moved in a straight line in the projection of its cross-section. The key parameters for the listed capture mechanisms are as follows.
2.2.1. Inertial Capture
The efficiency is determined by the Stokes number Stk:
where ρp is the density of the contaminant particle, dp is the diameter of the contaminant particle, U is the relative velocity between the droplet and the particle, ρd is the droplet density, g is the acceleration of gravity, μ is the viscosity of air, and dd is the droplet diameter.
The dependence of the capture efficiency for three ranges of the Stokes number is expressed as follows [16,26,27]:
2.2.2. Diffusion Capture
The capture efficiency depends on the Peclet number Pe [28]:
where is the diffusion coefficient of the particle, kb (m3/s) is the Boltzmann constant, and T is the temperature.
ηdif ~ 4 Pe−2/3,
Pe = U dd/kD,
This formula is suitable for cases with low droplet velocities and very low Reynolds number values, and this is the case we are considering.
2.2.3. Interception
The interception efficiency depends on the ratio of the particle and droplet sizes R = dp/dd [10,28]: ηinter ≈ 3/2 R2.
This approximate formula does not take into account the viscosity of the droplets or their volume concentration, but is suitable for a relatively low volume concentration of droplets and in the case when the viscosity of the liquid is much greater than the viscosity of the gas medium (which is true for water droplets in air).
2.2.4. Electrostatic Capture [24,29]
For a charged particle with charge q and a neutral drop, the attractive force in the approximation of a point charge and a polarizable sphere is given by
where r is the distance between the center of the drop and the particle, ε0 is the electric constant, ε is the dielectric constant of the droplet (for water, ε ≈ 80), and (ε − 1)/(ε + 2) is the polarization factor (for water, close to 1).
This force decreases as 1/r4, which makes it significant only at short distances. The electrostatic contribution to the capture efficiency depends on the dimensionless parameter NE, which characterizes the ratio of the electrostatic force to the resistance of the medium:
Viruses and bacteria can carry an electric charge due to the ionization of surface chemical groups (e.g., amino acids in viral capsid proteins or peptide glycan in bacterial cell walls) or adsorption of ions from the environment (e.g., in a humid environment). The charge of such a particle can be proportional to the diameter (if it is distributed volumetrically) or to the surface area (for a surface charge). Most often, the charge depends on the surface area of the particle, ~dp2 (surface charge) [30,31], so we will adopt this dependence in the calculations. Then, ηelec ~ NE = q0dp2, where q0 is the proportionality coefficient. According to experimental data, the charge of a virus with a diameter of 20–200 nm is q = 10–100 e (where e is the electron charge) [30]. For bacteria with a diameter of 0.5–10 μm, the charge is q = 104–106 e [31]. From this, the parameter q0 can be estimated.
The efficiency of particle capture by a droplet is described by the capture coefficient η, which depends on the interaction mechanism. For the droplet–contaminant system, the overall capture coefficient can be written as a combination of different mechanisms, taking into account their independence:
η = 1 − (1 − ηiner)(1 − ηdif )(1 − ηinter)(1 − ηelec)
2.3. Dynamics of the Decrease in the Mass of Contaminant Particles When They Are Captured by Aerosol Droplets
When assessing the efficiency of contaminant removal using aerosol droplets, an important issue is the reduction in the mass of contaminant particles in the air. How long will it take to clean the air of harmful particles? How completely can particles be removed from the air using an aerosol?
The capture efficiency η determines the fraction of particles that collide with a droplet from the flow passing through its cross-section. For a single droplet with a diameter dd, the effective capture area is proportional to the cross-sectional area of the droplet: Particle flow captured by a droplet can be expressed as follows:
where np is the concentration of contaminant particles.
We will assume that with a constant uniform supply (spraying in the room) of aerosol, a quasi-stationary concentration of droplets, nd, will be established in the volume of the room, determined by the arrival of droplets as a result of spraying and the loss as a result of settling on the walls, gravitational settling, and evaporation. Smaller particles of the contaminant in the air will settle much more slowly and will not undergo evaporation (for solid particles). Then, the decrease in their number will occur precisely as a result of the capture of aerosol by droplets. The rate of change in the concentration of particles is proportional to the concentration of droplets and the flow of particles captured by the droplet:
The capture constant will be denoted as
Then, the change in the number of contaminant particles in the air will be expressed as follows:
It is necessary to determine the mass of contaminant particles captured by the aerosol. The relative mass of captured contaminant particles depending on time will be expressed as follows:
We will also express the capture constant through the mass concentration of droplets, md:
All contaminant particles will be completely removed from the air, as time In the problem, we can determine the characteristic time (time constant) of the particle capture process—tcapt = 1/kcapt. This is the time during which the mass of contaminant particles in the air will decrease by e times. This value can be used to judge how quickly aerosol droplets will collect particles from the air under these conditions.
2.4. Correction for Small Particles
For relatively large (compared to the free path of molecules) particles and droplets, the continuous medium approximation is valid, and the Stokes equations for the resistance and motion of particles are valid. The possibility of using this approximation is determined by the Knudsen number, where λ is the mean free path of air molecules (~68 nm under normal conditions).
For particles whose diameter is much larger than λ, the condition Kn << 1 is satisfied. But for particles of 10–100 nm (e.g., viruses), Kn~1, and larger, the continuous medium approximation begins to break down. Then, the diffusion coefficient for such small particles is determined with the Cunningham correction, where The particle sedimentation velocity will also be determined with this correction, and then the relative sedimentation velocity can be expressed as follows:
Although the proposed model is based on well-established theoretical frameworks for diffusion, interception, and inertial capture, the novelty lies in adapting and combining these models for the specific case of small droplets (30–50 μm) interacting with contaminants in the 0.1–10 μm range. Importantly, the integration of electrostatic effects and the use of the characteristic capture time as a new metric provide a more practical perspective on the removal efficiency. Thus, the methodology is not a simple recalculation but an extension and contextualization of existing models for a less studied droplet size regime.
3. Results and Discussion
3.1. Comparison with Experiment
The paper [32] presents experimental data on the deposition of submicron zinc oxide particles by aerosol droplets of various diameters. The Sauter diameter of the aerosol droplets used in the work is 162 μm (the modal diameter is 80 μm). Although we consider droplets of a smaller size, we performed a calculation for droplets with a diameter of 80 μm according to the presented model for the capture time of various fractions of submicron particles in order to compare with the results of the paper [32]. The capture time for particles of a given size fraction was obtained from the Supplementary Materials of Ref. [32], where the time corresponding to a decrease in the particle number by a factor of e was taken as the capture time. The comparison results are shown in Figure 1. A mass concentration of droplets of 0.15 g/m3 was adopted in the calculation. The experimental points shown in Figure 1 were taken from the Supplementary Materials of Ref. [32], digitized, and re-processed by us to allow direct comparison with the present theoretical calculations. These experiments involved water droplets generated by ultrasonic spraying interacting with submicron airborne particles.
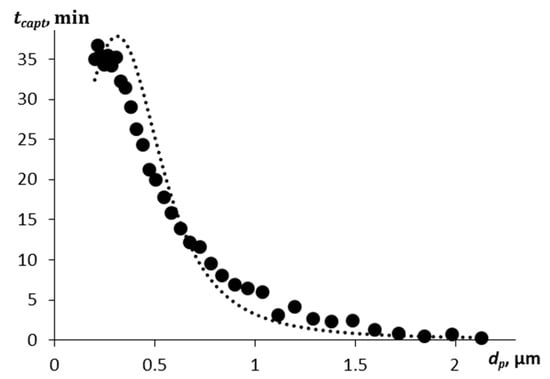
Figure 1.
Comparison of calculated capture efficiency (solid line) with experimental data taken from the Supplementary Materials of Ref. [32], digitized and re-processed by the authors. Experimental data correspond to water droplets generated by ultrasonic spraying.
As can be seen from the graph, the calculation based on the given model describes the experimental results well. The most difficult-to-capture particles are in the range from 0.1 to 1.5 μm. But particles with a diameter of more than 2 μm are captured by aerosol droplets in a few seconds, given a sufficient droplet concentration. In this calculation, the particle density is much higher than for soot (ρp = 5680 kg/m3), the aerosol droplets are larger, and the droplet concentration is higher than in the above model calculations. Therefore, the relative velocity of the particles is also higher, and the inertial component of the capture efficiency is significant even for small particles with a diameter of up to 3 μm.
3.2. Model Calculations
We perform calculations for various contaminants and various conditions, according to the model proposed above. In all calculations, the aerosol droplets were assumed to be composed of water, which is the most common and practical working fluid for indoor aerosol purification. The following physical properties of water at room temperature were used: density ρ = 1000 kg/m3, dynamic viscosity μ = 0.001 Pa·s, and surface tension σ = 0.072 N/m. As contaminant particles, we will take soot particles with a density of ρp = 2000 kg/m3. First, we will consider how the contaminant particle size for different droplet sizes affects the components of the particle capture efficiency by droplets (Figure 2).
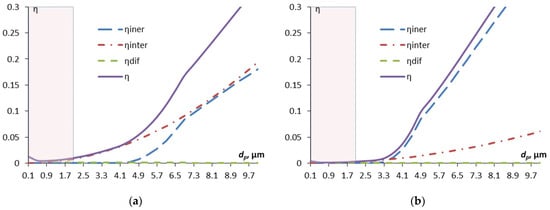
Figure 2.
Dependence of the components of the efficiency of capturing contaminant particles by aerosol droplets on the particle diameter: dd = 30 µm (a); dd = 50 µm (b). The shaded area corresponds to the Greenfield gap.
The efficiency of capture due to diffusion is only noticeable for the smallest particles, with a diameter of less than 0.5 μm; with increasing particle size, the contribution of the interception mechanism becomes increasingly significant, and then, starting from approximately 4 μm and more, the inertial capture mechanism “comes in”. Inertial capture is more significant for larger droplets, which is understandable—their cross-sectional area is larger. A small kink in the curve of the inertial capture efficiency is associated with the transition from empirical formulas for different ranges of particle diameters.
Figure 3 shows the curves for the capture time calculated for different droplet sizes, depending on the size of the contaminant particles (the mass concentration of droplets in the calculations is 0.1 g/m3).
Figure 3.
Dependence of the characteristic time of capture of contaminant particles by aerosol droplets of different diameters (from 30 to 50 µm) on the diameter of the particles. The mass concentration of droplets in the calculations is 0.1 g/m3. The shaded area corresponds to the Greenfield gap.
The curves in Figure 2 have an extremum associated with the Greenfield gap. Small particles (less than 0.5 μm in diameter), for which the diffusion capture mechanism is significant, are quickly absorbed by aerosol droplets. Relatively large particles (more than 2–3 μm in diameter) are quickly captured by aerosol droplets due to inertia and, in part, the interception mechanism. In the range from 0.5 to 2.5 μm, the capture efficiency due to diffusion is already low, and due to inertia, it is still low, so the capture time is maximum here. At the same time, the maximum capture time in this gap is less for droplets of smaller diameter; for example, for droplets of 30 μm in diameter, the maximum time will be 32 min, while for droplets of 50 μm, it will be 54 min (Table 1).

Table 1.
Characteristic time of capture of contaminant particles tcapt (min) by aerosol droplets of different droplet diameters dd (µm).
We now consider how droplet size for different particle sizes affects the components of droplet capture efficiency (Figure 4).
Figure 4.
Dependence of the components of the efficiency of capturing contaminant particles by aerosol droplets on the droplet diameter: dp = 0.1 μm (a), dp = 0.9 μm (b), dp = 2.4 μm (c), dp = 5 μm (d).
As can be seen from Figure 4a, for small particles, the capture is determined exclusively by diffusion; for particles larger than 2.4 μm, diffusion plays almost no role, but the interception mechanism plays an important role (Figure 4c). For particles of about 5 μm and larger, the inertial capture by droplets increasingly plays the main role, and the capture efficiency becomes increasingly higher. Inertial capture is most important for larger droplets compared to smaller ones (Figure 4d). In the most problematic region of particle diameters of about 0.5–1 μm, inertial capture does not play a role, and the efficiency of diffusion capture is also already low. The interception mechanism begins to have an effect, but the total efficiency due to interception and diffusion turns out to be minimal (and the capture time is maximum).
Figure 5 shows the dependence of the capture time on the droplet diameter for different particle diameters.
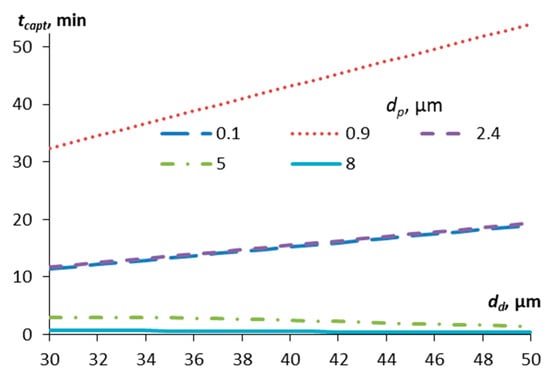
Figure 5.
Dependence of the characteristic time of capture of contaminant particles of different diameters by aerosol droplets on the diameter of the droplets.
For small particles, with a diameter of less than 2.4 μm, in this calculation, the dependence of the capture time on the droplet diameter is linear—it increases with the droplet size. For large particles (here, with a diameter of more than 5 μm), a slight decrease in the capture time is observed in the calculation. For particles of 0.1 and 2.4 μm, the capture time is practically the same in the entire range of droplet sizes. These are the sizes that limit the Greenfield gap. The particle diameter of 0.9 μm corresponds to the maximum capture time for all droplet sizes, but with an increase in the droplet diameter, this time also increases linearly. This suggests that for the most difficult-to-capture particles from the Greenfield gap zone, the smaller the size of the aerosol droplets, the sooner they will be captured. But this is not true for larger particles—for them, larger aerosol droplets give a slightly better result (the capture time is slightly lower, as in curves 5 and 8 in Figure 5).
The calculations above did not take into account the possible charge of the particles. However, if the particles are viruses or bacteria, or have a triboelectric charge, then this capture mechanism must also be taken into account for small particles.
Now, we will consider the effect of the contaminant particle size for different droplet sizes on the components of the particle capture efficiency by droplets, including the electrostatic mechanism (Figure 6). In the calculation, q0 = 0.0001 C/m2 is assumed.
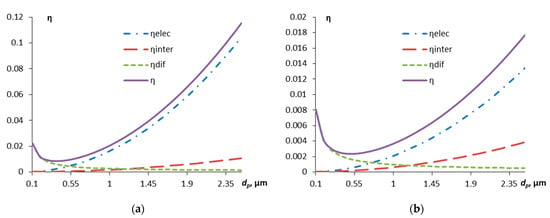
Figure 6.
Dependence of the components of the efficiency of capturing contaminant particles by aerosol droplets on the particle diameter: dd = 30 µm (a); dd = 50 µm (b).
Figure 6 does not show the inertial component of capture, since it is negligibly small for such small particles. On the other hand, it is the electrostatic component of the capture efficiency that plays a major role, starting with particle sizes of about 0.5–0.7 µm, where the diffusion component (the intersection of the blue and green curves on the graphs) begins to yield to this component. The component associated with interception makes an insignificant contribution.
Figure 7 shows the curves for the capture time calculated for different droplet sizes, depending on the contaminant particle size, taking into account the electrostatic component and the Cunningham correction.
Figure 7.
Dependence of the characteristic time of capture of contaminant particles by aerosol droplets of different diameters (from 30 to 50 µm) on the diameter of the particles, taking into account the charge of the particles. The shaded area corresponds to the Greenfield gap.
The capture time of contaminated particles is shorter than that of uncharged particles (Figure 3), while the maximum of the curves corresponding to the most problematic particle sizes is shifted to the left (towards smaller particles) compared to the case of no charge. The dependence on the droplet size is more pronounced—the smaller the droplets, the faster the particle capture occurs, especially in the problematic area. Thus, spraying finer aerosol droplets is an advantage in removing small particles, especially those with an electrostatic charge—such as viruses and bacteria.
The capture time is inversely proportional to the mass concentration of aerosol droplets, so the higher the droplet concentration, the shorter the time for removing contaminant particles. The effect of particle density on the capture time is shown in Figure 8. It shows the results of calculating the capture time for particles of different sizes and densities by water aerosol droplets with a diameter of 40 μm.
Figure 8.
Particle capture time depending on their diameter for particles of different densities: water aerosol with a droplet diameter of 40 µm. The shaded area corresponds to the Greenfield gap.
All other things being equal, the density of particles affects the time of their capture by droplets only in the transition region (the transition from the dominant mechanism of diffusion capture for small particles to the dominance of the inertial capture mechanism). The transition to inertial capture begins for heavier particles at 2 µm, and for lighter particles, at 3–5 µm. In this size range, heavy particles are removed faster than lighter ones. But for particle sizes over 5 µm, there is practically no difference in the capture time. Therefore, the effect of particle density on the process of their removal can be considered insignificant.
In the present work, soot was selected as a representative contaminant because of its environmental relevance, well-characterized physical properties, and frequent use as a model aerosol in air purification studies. Although particle density may vary with size, our calculations (see Figure 8) show that these variations have only a minor effect on capture efficiency compared to particle size and droplet parameters. Therefore, soot can be used as a convenient and representative example for the theoretical framework developed here.
To support the theoretical predictions, we compared our results with available experimental observations reported in [32]. Although systematic datasets for droplets smaller than 100 μm are scarce, the observed trends—such as enhanced capture with increasing droplet concentration and the persistence of the efficiency minimum in the 0.5–2 μm range—are consistent with experimental findings. Nevertheless, dedicated experimental studies will be essential to validate the quantitative aspects of the proposed model.
The scope of emergency conditions mentioned in the introduction was intentionally broad in order to emphasize the relevance of indoor aerosol purification across diverse scenarios. However, in this study, we have limited the modeling to a generic class of contaminant particles with sizes of 0.1–10 μm, including viruses, bacteria, and fine dust. While the implications of the results extend to a variety of practical cases—from medical disinfection to mitigation of industrial leaks—the presented calculations are not scenario-specific. Future studies may refine the modeling by considering emission source terms, chemical composition of pollutants, and environmental conditions (humidity, ventilation), which were beyond the scope of this paper.
4. Conclusions
The paper considers the problem of removing finely dispersed contaminant particles with a characteristic size from 100 nm to 10 μm from indoor air using a fine aerosol sprayed in the air (droplet diameter 30–50 μm). Precisely removing such finely dispersed particles from the air, including viruses, bacteria, and PM2.5 and PM10 particles, is very difficult. Aerosol spraying for removing finely dispersed radioactive particles is used in practice, but mainly with coarser aerosols. The emergence of new aerosol spraying methods that combine high productivity and high droplet dispersion opens up new possibilities for using this method of removing particles in a wider technological range. While the interaction of relatively large droplets (more than 100 μm in diameter) with contaminant particles has been studied theoretically and experimentally, the interaction of droplets 30–50 μm in diameter with finely dispersed particles, which have their own characteristics, has not yet been studied. We have considered in detail the mechanisms of such interaction, including diffusion, inertial, interception, and electrostatic forces (for charged particles). A mathematical description of capture corresponding to the case under consideration is proposed. The model is verified by comparison with experiments (the results are given in [32]).
As a measure of the capture efficiency, in addition to the efficiency coefficient, we propose to use the characteristic capture time, when the mass of particles in the air decreases by e times compared to the initial one. It was found that in the Greenfield gap, that is, in the range of particle diameters where no capture mechanism is sufficiently effective and the capture time is maximum, the best result is shown by aerosol droplets of the minimum size (in our calculations, these are droplets with a diameter of 30 μm). The capture time of charged particles (i.e., viruses and bacteria) is especially reduced by droplets with a diameter of 30 μm compared to larger droplets (with a diameter of 100 µm or more). The higher the aerosol dispersion, the more effective the removal of highly dispersed contaminant particles from the air in the most difficult range of sizes of these particles. The effect of particle density on the capture efficiency in the problem under consideration turned out to be insignificant. It is shown that the capture time is inversely proportional to the mass concentration of aerosol droplets. This means that the higher the mass concentration and the higher the dispersion of the sprayed aerosol, the higher the rate of removal of contaminant particles. The calculations performed and the results obtained create the prerequisites for the development and widespread use of a method for removing highly dispersed contaminant particles, including viruses and bacteria, from indoor air by spraying fine aerosol droplets.
In practical terms, the results obtained suggest several directions for optimizing aerosol spraying to mitigate the reduced capture efficiency in the 0.5–2 μm range. First, the concentration of sprayed droplets plays a decisive role: increasing the number of fine droplets per unit volume shortens the characteristic capture time in the Greenfield gap almost proportionally. Second, the configuration of the spray system can be adjusted to achieve a more homogeneous distribution and longer airborne residence time of droplets, thus maximizing interaction with contaminant particles. Additionally, the use of auxiliary external fields, such as electrostatic charging of droplets or mild airflow circulation, could enhance particle–droplet collision probability and help overcome the efficiency drop in this critical particle size range.
While water was used as the working liquid in this study due to its availability, low cost, and well-characterized properties, alternative liquids and emulsions may also be applied. For example, aqueous solutions with surfactants or glycols can reduce surface tension and increase droplet spreading and capture efficiency. Salt solutions may enhance the hygroscopic growth of airborne particles, facilitating their removal. Oil-based or polymer-stabilized emulsions, though more expensive, could offer improved stability or stronger adhesion to specific contaminants. The choice of liquid thus provides an additional parameter space for optimizing aerosol-assisted purification systems.
Potential applications of the method are realistically linked to hospital disinfection, indoor air purification, and the mitigation of fine dust and bioaerosols. Broader scenarios have been removed to maintain focus on the actual scope of the modeling. At the same time, some limitations should be recognized: achieving stable and high droplet concentrations requires sufficiently powerful ultrasonic spraying systems, and scaling up to very large volumes may be technically challenging. Furthermore, maintaining uniform aerosol distribution in complex geometries remains a non-trivial engineering task. Future work should therefore combine theoretical modeling with pilot-scale demonstrations to assess the balance between efficiency, energy consumption, and operational feasibility.
The present work has limitations inherent to its theoretical nature. Factors such as the role of humidity, droplet evaporation, particle chemical composition, and complex indoor airflow dynamics were not considered and should be addressed in future studies. Furthermore, systematic experimental validation of fine-droplet capture efficiency remains an open task. Future research should therefore combine controlled laboratory experiments with extended modeling to confirm and refine the theoretical predictions presented here.
While many factors may influence aerosol–contaminant interactions in real environments, the present study deliberately narrows its scope to the analysis of fine droplets (30–50 μm) and their interaction with particles in the 0.5–2 μm range, where capture is least efficient. This focus allows for a deeper understanding of the interplay between diffusion, interception, and electrostatics in overcoming the Greenfield gap. The results provide not only general trends but also specific insights into how droplet size and concentration affect the characteristic capture time in this critical interval. Such narrowing of the research perspective strengthens the applicability of the findings for designing fine aerosol-based indoor purification systems.
Author Contributions
Conceptualization, O.K. and A.S.; methodology, O.K.; software, N.T.; validation, N.T. and A.S.; formal analysis, O.K.; investigation, A.S.; resources, V.K.; data curation, A.S.; writing—original draft preparation, O.K.; writing—review and editing, A.S.; visualization, N.T.; supervision, V.K.; project administration, V.K.; funding acquisition, V.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Russian Science Foundation, grant number 23-19-00875, https://rscf.ru/project/23-19-00875/ (accessed on 23 September 2025).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| dd | µm | droplet diameter |
| dp | µm | diameter of the contaminant particle |
| Felectr | N | electrostatic attractive force |
| g | m/s2 | acceleration of gravity |
| Jd | m/s | particle flow captured by a droplet |
| kb | m3/s | Boltzmann constant |
| kcapt | 1/s | capture constant |
| kD | m2/s | diffusion coefficient of the particle |
| md | kg/m3 | mass concentration of droplets |
| np | 1/m3 | concentration of contaminant particles |
| q | C | electrostatic charge of a particle |
| r | m | distance between the center of the drop and the particle |
| Seff | m2 | cross-sectional area of the droplet |
| T | K | temperature |
| tcapt | s | characteristic time (time constant) of the particle capture |
| U | m/s | relative velocity between the droplet and the particle |
| ε | dimensionless | dielectric constant of the droplet |
| ε0 | F/m | the electric constant |
| η | dimensionless | Total capture efficiency |
| ηdif | dimensionless | diffusion capture efficiency |
| ηelec | dimensionless | electrostatic capture efficiency |
| ηiner | dimensionless | inertial capture efficiency |
| ηinter | dimensionless | interception capture efficiency |
| µ | Pa·s | viscosity of air |
| ρd | kg/m3 | droplet density |
| ρp | kg/m3 | density of the contaminant particle |
| CK | dimensionless | Cunningham correction coefficient |
| Kn | dimensionless | Knudsen number |
| NE | dimensionless | the ratio of the electrostatic force to the resistance of the medium |
| Pe | dimensionless | Peclet number |
| Stk | dimensionless | Stokes number |
References
- González-Martín, J.; Kraakman, N.J.R.; Pérez, C.; Lebrero, R.; Muñoz, R. A state–of–the-art review on indoor air pollution and strategies for indoor air pollution control. Chemosphere 2021, 262, 128376. [Google Scholar] [CrossRef] [PubMed]
- Rosário Filho, N.A.; Urrutia-Pereira, M.; D’Amato, G.; Cecchi, L.; Ansotegui, I.J.; Galán, C.; Peden, D.B.; Caraballo, L.; Rouadi, P.; Annesi-Maesano, I.; et al. Air pollution and indoor settings. World Allergy Organ. J. 2021, 14, 100499. [Google Scholar] [CrossRef]
- Dong, Z.; Ma, J.; Qiu, J.; Ren, Q.; Shan, Q.E.; Duan, X.; Liu, S.; Qi, Y.; Liu, J.; Li, G.; et al. Airborne fine particles drive H1N1 viruses deep into the lower respiratory tract and distant organs. Sci. Adv. 2023, 9, eadf2165. [Google Scholar] [CrossRef]
- Mata, T.M.; Martins, A.A.; Calheiros, C.S.; Villanueva, F.; Alonso-Cuevilla, N.P.; Gabriel, M.F.; Silva, G.V. Indoor air quality: A review of cleaning technologies. Environments 2022, 9, 118. [Google Scholar] [CrossRef]
- Singh, S.; Vishwakarma, P.; Gupta, T. Review of current and future indoor air purifying technologies. ACS EST Eng. 2024, 4, 2607–2630. [Google Scholar] [CrossRef]
- Adeniran, J.A.; Mohammed, I.A.; Muniru, O.I.; Oloyede, T.; Sonibare, O.O.; Yusuf, M.-N.O.; Abdulraheem, K.A.; Odediran, E.T.; Yusuf, R.O.; Sonibare, J.A. Indoor transmission dynamics of expired SARS-CoV-2 virus in a model African hospital ward. J. Env. Health Sci Eng. 2021, 19, 331–341. [Google Scholar] [CrossRef] [PubMed]
- Chlebnikovas, A.; Jasevičius, R. Air pollution with fine particles in closed parking and theoretical studies of the interaction of inhaled particles in respiratory tract. Buildings 2022, 12, 1696. [Google Scholar] [CrossRef]
- Sanada, S.J.; Mat, M.N.H.; Yinn, W.K.; Rosminahar, S.N. Minimizing pathogen transmission through indoor environment optimization using central composite design of experiment. Energy Build. 2023, 298, 113587. [Google Scholar] [CrossRef]
- Xu, R.; Sharma, A.K.; Kumar, R.; Ahmed, Z.; Yokoyama, R.; Miwa, S.; Suzuki, S.; Okamoto, K. Efficient radioactive aerosol removal with the development of water mist pre-injection methods and advanced spray charging system for safe Fukushima Daiichi decommissioning: Insights from recent experimental studies in UTARTS facility. J. Nucl. Sci. Technol. 2025, 1, 1–24. [Google Scholar] [CrossRef]
- Fuchs, N.A.; Daisley, R.E.; Fuchs, M.; Davies, C.N.; Straumanis, M.E. The mechanics of aerosols. Phys. Today 1965, 18, 73. [Google Scholar] [CrossRef]
- Lee, K.W.; Gieseke, J.A. Note on the approximation of interceptional collection efficiencies. J. Aerosol Sci. 1980, 11, 335–341. [Google Scholar] [CrossRef]
- Postma, A.K.; Ritzman, R.L.; Gieseke, J.A.; Schmidt, E.W. Models for Predicting the Removal of Airborne Contaminants by Reactor Containment Sprays; No. BNWL-B-417; Battelle Pacific Northwest Labs: Richland, WA, USA, 1975. [Google Scholar]
- Jung, C.H.; Lee, K.W. Filtration of fine particles by multiple liquid droplet and gas bubble systems. Aerosol Sci. Technol. 1998, 29, 389–401. [Google Scholar] [CrossRef]
- Lee, K.W.; Liu, B.Y.H. On the minimum efficiency and the most penetrating particle size for fibrous filters. J. Air Pollut. Control Assoc. 1980, 30, 377–381. [Google Scholar] [CrossRef]
- Postma, A.K.; Sherry, R.R.; Tam, P.S. Technological Bases for Models of Spray Washout of Airborne Contaminants in Containment Vessels; No. NUREG/CR-0009; Benton City Technology: Benton City, WA, USA, 1978. [Google Scholar]
- Powers, D.A.; Burson, S.B. A Simplified Model of Aerosol Removal by Containment Sprays; (No. NUREG/CR-5966; SAND-92-2689); Nuclear Regulatory Commission: Washington, DC, USA; Div. of Safety Issue Resolution, Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 1993. [Google Scholar]
- Yu, H.; Gu, H.; Sun, Z.; Zhou, Y.; Sun, C.; Chen, J.; Li, Y. Study on the influence of droplet agglomeration on the removal of aerosol by spray system. Prog. Nucl. Energy 2021, 140, 103903. [Google Scholar] [CrossRef]
- Ahmed, Z.; Kumar, R.; Sharma, A.K.; Xu, R.; Miwa, S.; Okamoto, K.; Suzuki, S. Effect of wettability and particle size on aerosol removal efficiency in charged and neutral water spray systems. J. Environ. Chem. Eng. 2025, 13, 115822. [Google Scholar] [CrossRef]
- Ardon-Dryer, K.; Huang, Y.W.; Cziczo, D.J. Laboratory studies of collection efficiency of sub-micrometer aerosol particles by cloud droplets on a single-droplet basis. Atmos. Chem. Phys. 2015, 15, 9159–9171. [Google Scholar] [CrossRef]
- Santachiara, G.; Prodi, F.; Belosi, F. Atmospheric aerosol scavenging processes and the role of thermo-and diffusio-phoretic forces. Atmos. Res. 2013, 128, 46–56. [Google Scholar] [CrossRef]
- Greenfield, S.M. Rain scavenging of radioactive particulate matter from the atmosphere. J. Atmos. Sci. 1957, 14, 115–125. [Google Scholar] [CrossRef]
- Gao, Y. Research on the harm degree of PM2. 5 atmospheric particulate pollution to human health. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 692, p. 032014. [Google Scholar]
- Shalunov, A.; Kudryashova, O.; Khmelev, V.; Genne, D.; Terentiev, S.; Nesterov, V. Innovative ultrasonic spray methods for indoor disinfection. Appl. Syst. Innov. 2024, 7, 126. [Google Scholar] [CrossRef]
- Hinds, W.C.; Zhu, Y. Aerosol Technology: Properties, Behavior, and Measurement of Airborne Particles; John Wiley & Sons: Hoboken, NJ, USA, 2022. [Google Scholar]
- Kudryashova, O.; Sokolov, S.; Vorozhtsov, A. Mathematical model of propagation of an aerosol created by an impulse method in space. Materials 2023, 16, 5701. [Google Scholar] [CrossRef]
- Slinn, W.G.N. Precipitation scavenging of aerosol particles. Geophys. Res. Lett. 1976, 3, 21–22. [Google Scholar] [CrossRef]
- Friedlander, S.K. Smoke, Dust, and Haze: Fundamentals of Aerosol Dynamics, 2nd ed.; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Seinfeld, J.H.; Pandis, S.N. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Pilat, M.J.; Jaasund, S.A.; Sparks, L.E. Collection of aerosol particles by electrostatic droplet spray scrubbers. Environ. Sci. Technol. 1974, 8, 360–362. [Google Scholar] [CrossRef]
- Wang, C.C.; Prather, K.A.; Sznitman, J.; Jimenez, J.L.; Lakdawala, S.S.; Tufekci, Z.; Marr, L.C. Airborne transmission of respiratory viruses. Science 2021, 373, eabd9149. [Google Scholar] [CrossRef] [PubMed]
- Ohshima, H. Electrophoretic mobility of soft particles. J. Colloid Interface Sci. 1994, 163, 474–483. [Google Scholar] [CrossRef]
- Xu, R.C.; Sharma, A.K.; Ozdemir, E.; Miwa, S.; Suzuki, S. Experimental investigation on effective aerosol scavenging using different spray configurations with pre-injection of water mist for Fukushima Daiichi decommissioning. Nucl. Sci. Tech. 2024, 35, 42. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).