Abstract
The identification of the most rockfall-prone areas is the first step of the risk assessment procedure. In the case of land and urban planning, hazard and risk analyses involve large portions of territory, and thus, preliminary methods are preferred to define specific zones where more detailed computations are needed. To reach this goal, the QGIS-based plugin QPROTO was developed, able to quantitatively compute rockfall time-independent hazard over a three-dimensional topography on the basis of the Cone Method. This is obtained by combining kinetic energy, passing frequency and detachment propensity of each rockfall source. QPROTO requires the definition of few angles (i.e., the energy angle and the lateral angle ) that should take into account all the phenomena occurring during the complex block movement along the slope. The outputs of the plugin are a series of raster maps reporting the invasion zones and the quantification of both the susceptibility and the hazard. In this paper, a method to relate these angles to some characteristics of the block (volume and shape) and the slope (inclination, forest density) is proposed, to provide QPROTO users with a tool for estimating the input parameters. The results are validated on a series of case studies belonging to the north-western Italian Alps.
1. Introduction
The assessment of susceptibility and hazard are the most challenging issues in the field of rockfall risk estimation [1]. In particular, the study of the hazard level requires three main steps [2]: (i) the spatial identification of the involved areas; (ii) the computation of the rockfall intensity (measurable via the estimation of the kinetic energy of the falling blocks); (iii) the definition of the temporal occurrence of the phenomenon.
Referring to the first two items, several methodologies allow to identify the spatial evolution of the rockfall phenomenon. First, rigorous 3D analytical models permit to take into account the inertia of the rock block, achieving a reliable knowledge of the involved energy. More simplified models reduce the volume of the block to a dimensionless point (neglecting the effect of block shape and size) within a 2D or 3D framework. These models are generally used on large scales (i.e., site-specific) and local scales, following the recommendations of Corominas et al. (2014) [3] for detailed risk analyses or to design protection works. Even more simplified models are used on small scales for territorial planning and preliminary study purposes [2,3,4]. Necessarily, in these cases, the runout model should be both simple and reliable in order to overcome the limited availability of data and their epistemic uncertainties. Among a large set of methodologies, one of the most used is the Energy Angle Method (EAM), which was theorized by Onofri and Candian (1979) [5] on the basis of the previous Fahrböscung approach, firstly proposed by Heim (1932) [6]. The EAM is a simple frictional model in which the entire rockfall process is thought of as an equivalent sliding motion of a rigid block along a straight line (i.e., the “energy line”) connecting the rockfall source with the farthest outlying block at the foot of the slope. The inclination of the energy line is usually defined by the “energy angle” [5,7], called the “shadow angle” [8,9,10] when the source point is located at the apex of the talus slope. Besides rockfall, the model is widely adopted even in the case of other slope instability phenomena, such as snow avalanches [7,11,12,13] and shallow landslides [14,15].
During the last decades, the EAM was implemented in several computer programs, even in the framework of GIS environment. First, Jaboyedoff and Labiouse (2011) [16] developed the CONEFALL tool, which is able to estimate the potential rockfall area only starting from a DTM and a grid file of the rockfall sources. In order to detect whether the DTM cell is located below the energy line (i.e., the topographical point is within the propagation area), CONEFALL introduces a series of cones having their apexes in the rockfall source points. The intersection of these cones with the surface of the slope gives the propagation area (Figure 1). Then, a simple energy balance provides the kinetic energy within the computed area. This 3D variation of the EAM is usually addressed as Cone Method (CM). The CM was further implemented in QPROTO [17], a cross-platform open-source plugin developed for the QGIS 3 environment. Starting from some rockfall source points, the tool performs a viewshed analysis via the application of the GRASS GIS function r.viewshed [18]. Such an analysis is limited to a visibility cone, described in space by three angles: (i) the dip direction θ, which defines the orientation of the cone with respect to the north; (ii) the energy angle , which defines the cone in the vertical plane; (iii) the lateral spreading angle , which encloses the cone in the horizontal plane.
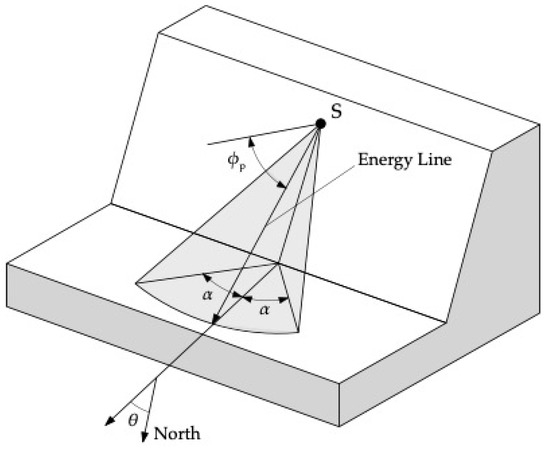
Figure 1.
Spatial definition of the visibility cone as it is defined in QPROTO: = energy angle in the vertical plane, lateral angle in the horizontal plane and θ = dip direction (modified from [16]).
At this point, a reasonable question might arise about the values to be used to characterize these angles (hereafter “cone angles”) within preliminary hazard analyses. Many authors have suggested a statistical solution to estimate as a function of the percentage of the stopping points [16,19]. For instance, Onofri and Candian (1979) [5], on the basis of on-site observations, noted that the 100% of the observed blocks stopped for > 28.5°, while the 50% for > 32°. Otherwise, a statistical analysis of the Principality of Andorra case study returned the value 41.3°, 39.5° and 36.9° for the 90, 99 and 99.9 percentiles, respectively [20,21]. Lied (1977) [8] found that all the blocks stopped with angles in a range between 28° and 30°. Other authors proposed a maximum value for the angles, by means of different case studies. Evans and Hungr (1993) [10] set a maximum shadow angle of 27.5° and a of 24°, while Wieczorek et al. (1998) [9] suggested a lower value for , equal to 22°. Such a wide variability and the strong site-dependence of these studies lead us to the conclusion that a reliable representation of rockfall phenomena through the energy line should take into account the influence of block characteristics (e.g., shape, volume, resistance) and slope conditions (e.g., inclination, length, roughness, vegetation). Some studies have been carried out in the last years to highlight the role of some of these factors on the energy line. For example, Rickli et al. (1994) [22] introduced a classification of the angles taking into account the resistance and the size of the block by referring to German mountain real cases: (i) = 33° for small rocks if the resistance is low and the underground smooth or the blocks are larger, resistance is high and the slope is rough; (ii) = 35° for medium-sized blocks; and (iii) = 37° for small blocks with high resistance and very rough slope. More recently, Volkwein et al. (2018) [23] presented the first results of an extensive in situ rockfall testing aimed at gaining very detailed information on the trajectories of falling blocks on a grass slope, that can be very useful to calibrate both numerical trajectory simulations and simplified analyses based on the energy line. These examples demonstrate that, for a proper use of the Cone Method, the need exists to analyze the dependence of the energy line to all the factors that influence rockfall trajectories.
With regards to the lateral angle , a few indications can be obtained from the literature. In general, the lateral dispersion of rockfall phenomena depends on three factors [24]: macro-topographic (slope morphology, steepness, presence of channels, longitudinal and transversal ridges etc.), micro-topographic (roughness of the slope surface), and dynamic (interaction between block and slope, trees, protection works etc.) factors. Starting from numerical models, Azzoni et al. (1995) stated that lateral dispersion usually amounts to 20% of the slope length, decreasing for short and steep slopes, but can be much larger for irregular or channeled slopes [25]. A higher value, equal to 34% of slope length, was found by Agliardi and Crosta (2003) [26]. Crosta and Agliardi (2004), adopting an original rockfall 3D simulation program, carried out a series of analyses on simulated slopes with different steepness, roughness and pixel size [24]. They found that lateral dispersion did not vary considerably with reference to slope steepness, with maximum values generally lower than 10%. Otherwise, the higher was the slope roughness, the larger was the lateral dispersion.
This wide variety of the results leads us to conclude that, except some very rough indication, at present, it is not possible to correlate the cone angles with the characteristics of the rockfall scenario under study through literature data, and more detailed analyses are needed. Thus, in this paper a new method to estimate the influence of slope and block features on the QPROTO input parameters ( and ) is proposed with the aim of providing the users of a set of reliable input parameters potentially tailored to different slope typologies. In particular, the role of the slope inclination, forest coverage, size and shape of the block are investigated. A series of trajectory analyses were carried out to this aim on artificially created slopes (called “synthetic slopes” hereafter) adopting the probabilistic process-based software Rockyfor3D [27]. Finally, the findings are validated and exemplified with reference to some real case studies belonging to the north-western Italian Alps.
2. The QPROTO Plugin
The QPROTO plugin (QGIS Predictive ROckfall TOol) [17] was created for implementing the Cone Method [16] in the QGIS environment, a user-friendly open-source geographic software, created and supported by the Open Source Geospatial Foundation (OSGeo). The plugin is based on the GRASS GIS 7 module r.viewshed [18], which allows to evaluate the visibility of the neighboring zones starting from a given set of viewpoints. Each of these points is the apex of a visibility cone covering a certain portion of the slope. As described in Section 1, the geometry of the cone is determined by three different angles: the dip direction θ, the energy angle and the lateral angle (Figure 1). A further visibility distance introduces the maximum distance to which the analysis can be extended. The basic assumption is the correspondence between the viewpoint and the source of rockfall event: the whole viewed zone of the slope can potentially be reached by the boulder paths starting from the considered source.
When diffused source points are considered, the plugin allows to define the rockfall subjected zones generated by the overlapping of the produced visibility cones. In this way, a frequency map can be obtained: the zones characterized by higher frequencies refer to more visible points, i.e., areas that can be easily reached by fallen blocks coming from different source points and that can be interpreted as the most prone to be affected by this type of phenomenon.
Through the Cone Method (Figure 2), it is also possible to quantitatively evaluate the velocity v(x,y) of the fallen block in each point P(x,y) of the topographic surface by using the following relation (Equation (1)):
where g is the gravity acceleration, x0 and y0 are the coordinates of the source point S, H(x0,y0) the elevation of the source point, hp(x,y) the elevation of the topographic surface at point P(x,y) and ϕp the energy angle. In Figure 2, the heights defined at the location of point P(x,y) are linked to the energy balance of the falling block. H(x0,y0) represents the total energy content of the block which is defined by the energy conservation principle as the sum of potential hp(x,y), kinetic hk(x,y) and friction or dissipative contributions ().
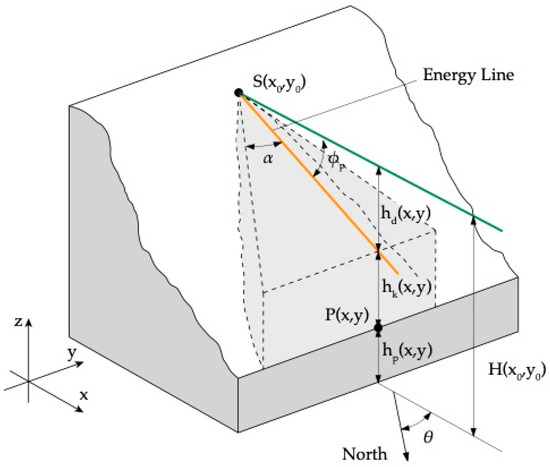
Figure 2.
3D sketch of the cone generation within the QPROTO plugin. The cone originates from the S(x0,y0) point and is sectioned by a vertical plane passing through the generic topographic point P(x,y). The light grey shows the volume of the cone, which is limited by the topographic surface and the plane defined by the energy line (orange line). The horizontal dark green line refers to the total energy of the block.
Thus, it is possible to obtain the kinetic energy Ek(x,y) at each point of the cone adopting the following relationship (Equation (2)):
where m is the mass of the block and v(x,y) its velocity at the point P(x,y).
It has to be considered that the calculated energy does not take into account the combination of free flight, bouncing, rolling and sliding phenomena that actually occur during the propagation phase: all these phenomena are simulated through an equivalent sliding motion along the above-mentioned plan with inclination equal to . Velocity and energy values obtained in this way need to be interpreted with great caution, especially by comparing them with the result of more accurate propagation analyses. Anyway, energy estimation through the Cone Method can lead to a preliminary estimation of the hazard, useful to highlight the most critical zones of a wide area in terms of process intensity as well as susceptibility.
To include the characteristics of the rockfall sources in the hazard estimation, the QPROTO plugin allows to assign a different propensity to detachment index (DI) to each source point. DI can be seen as a weight highlighting the most likely source zones to trigger rockfall events and can be defined as a function of the available information related to the study area (i.e., historical data, fracture density maps, inclination of the slope in the source zones) combined with the results of rapid on-site survey [28,29]. DI allows to calculate a weighted frequency map (i.e., a susceptibility map) and time-independent hazard maps (spatial hazard maps). The susceptibility map is a raster file describing how the rockfall phenomenon is distributed over the invasion area, highlighting the most affected zones through a very simplified and not temporal probability to be reached. The time-independent hazard maps combine the information about the detachment propensity of each source point with the estimated kinetic energy in a given cell of the invasion zone. Thus, each cell of these hazard maps corresponds with weighted energy values. It has to be noted that, with reference to the definition of the index DI, the hazard maps can be called as “time-independent” because of the difficulty in collecting information concerning rockfall temporal occurrence at a small and medium scale. However, in case a temporal probability of occurrence is available (e.g., an estimation of the return period), the QPROTO plugin allows to calculate a time based rockfall hazard map by substituting (or including) this information to the propensity to detachment index. However, these aspects of the hazard analysis are not relevant in this paper and thus we will not go more in detail. Further information on the hazard calculation can be found at https://plugins.qgis.org/plugins/qproto/ (accessed on 17 January 2021) [17].
For the proper execution of QPROTO, in addition to the QGIS algorithms, GRASS 7 and SAGA GIS open-source modules are required to create and manage vector and raster files and perform the viewshed analysis. A set of source points, each of them representing a single block, is created by the user within defined source areas. At each source point, the attributes listed in Table 1 have to be associated. Some of them can be easily inferred from the analysis of the DTM, such as point elevation and aspect; others have to be estimated on the basis of the available information about the slope geometry and condition, such as the energy angle , the lateral angle and the detachment propensity DI. Finally, boulder mass can be related to a specific scenario, characterized by a reference block volume.

Table 1.
List of attributes needed to perform a propagation analysis using the QPROTO plugin.
The main results of the QPROTO analysis are 10 raster files, listed in Table 2. The first raster (count) refers, for each cell belonging to the runout area, to the unweighted passage frequency, i.e., the number of source points viewing the cell. The second raster (susceptibility) shows the weighted passage frequency (i.e., the sum of all the detachment index DI of the source points viewing the considered cell). The following three raster maps (v_min, v_mean and v_max) concern the minimum, mean and maximum velocity, respectively, evaluated in each cell by using Equation (1). Based on these last three rasters, the corresponding energy raster maps (e_min, e_mean and e_max) are obtained adopting Equation (2). Furthermore, the two time-independent hazard maps (w_en and w_tot_en) are provided by multiplying the detachment index DI and the kinetic energy in each cell of the runout area. In addition to these outputs, the Finalpoints vector shapefile and the _log.txt logfile containing the report of the analysis are generated separately.

Table 2.
List of the QPROTO output files provided at the end of the analysis.
After the computation, the outputs are automatically loaded within the QGIS environment. Velocity and energy rasters are expressed in (m/s) and (J), respectively. Although the susceptibility and hazard files are expressed in (J), a classification on a five-level scale (i.e., very low, low, medium, high and very high) is adopted.
3. Estimation of the QPROTO Input Parameters: The Proposed Methodology
The application of the Cone Method through the QPROTO plugin requires the definition of a small number of parameters (the cone angles) that represent the reference scenario in terms of slope condition (geometry, forest coverage, etc.) and block characteristics (shape, volume). Indeed, such characteristics strongly influence the rockfall runout [30,31], and, thus, any hazard assessment methodology, although simplified, has to take them into account to obtain reliable as well as conservative results. To relate the cone angles to both block and slope features, a fully computational methodology was developed, based on simplified parametric analyses, able to provide some indications to QPROTO users for estimating the most reliable input parameters. The main steps of the proposed method are the following:
- Creation of simplified synthetic slopes and definition of their geometrical and physical characteristics;
- Execution of a statistically representative number of detailed 3D rockfall numerical simulations on the synthetic slopes in different conditions (presence of forest, block volume and shape etc.), on the basis of the parametric variation of some variables;
- Statistical interpretation of the results in terms of energy angle and lateral angle;
- Correlation of the cone angles with the considered variables;
- Interpolation of the results and definition of charts for the estimation of the cone angles;
- Validation of the results through their application to real study cases.
Among the available 3D rockfall simulation software, the Rockyfor3D model was used [27] for carrying out the parametric analyses because of its numerous advantages. In particular, it provides results in statistical terms and allows to consider the three-dimensional character of the falling block and the possibility of simulating impact with trees. This latter aspect assumes a crucial importance because of the dissipative capacity that trunks can offer and the protective role of forests against rockfall.
However, it is important to highlight that Rockyfor3D is not a fully three-dimensional model because it uses equivalent spherical shapes to compute block position, rebound on the slope surface and impacts against trees. In particular, the smallest sphere is adopted to calculate whether the block impacts a tree, while a larger one is used when block-soil interactions are involved. The shape changes operated by Rockyfor3D can influence the energy angles, especially in cases when the slenderness of the block cannot be neglected. Therefore, in this work, only isometric (cubic and spherical) shapes were taken into account, and the role of the slenderness was disregarded. This will be further investigated through different methods.
Because of the quick nature of the plugin QPROTO and the numerical basis of the methodology, many simplifying hypotheses were introduced in the analyses, which involved both slope and block characteristics. Of course, these hypotheses influence the applicability of the obtained results to real rockfall cases. In view of the foregoing, the present work assumes a double significance: first, the results of the analyses could be used within QPROTO or other small-scale methods to perform quantitative preliminary analyses of rockfall hazard. Second, the proposed method can be tailored to other types of slope and block features to include in the results any rockfall scenario not yet included. In the following sub-sections, a complete description of the methodology and the simplifying hypotheses is provided.
3.1. Synthetic Slopes
The first step of the proposed methodology consists of the creation of several synthetic slopes where the propagation analyses will be carried out. These slopes are numerically created with an automatic and specifically developed Matlab code. Following some examples from the literature [24], in this work, the synthetic slopes are composed of three consecutive ramps (or zones), as can be seen in Figure 3. Each zone has a specific role in the rockfall simulation and its own different inclinations, geometrical and physical properties. These properties have to reproduce some typical conditions (height, inclination, forest coverage, soil types, roughness etc.) of real mountain slopes subjected to rockfall phenomena. “Zone 1,” or the “detachment zone”, with a constant inclination with respect to the horizontal plane, represents the rock face from which the falling block detaches. For the sake of simplicity, only a single point within this area can originate the rockfall phenomenon. This point is the same for all the analyses and is located at the elevation of 270 m. “Zone 2,” or the “transit zone,” represents the propagation zone in which the falling block gradually loses its potential energy. To simulate a range of real slopes as wide as possible, the inclination of zone 2 can assume three different values: 30°, 45°, and 60°. Within this zone, the possible variation in forest coverage was also considered, as it will be better described in the following. Finally, “Zone 3,” or the “stopping zone,” is composed by a pseudo-horizontal plane () in which the falling blocks stop after the complete dissipation of their kinetic energy. No variation of the difference in height between the source and the foot of the slope is considered: in all the analyses, it is constant at 270 m. Such a height can be representative of many real rockfall events, but uncertainty increases when the source is located at different heights. This aspect is of great importance in the trajectory path of rockfall, and further investigation are needed to include the elevation of the rockfall source among the variables influencing the QPROTO parameters.
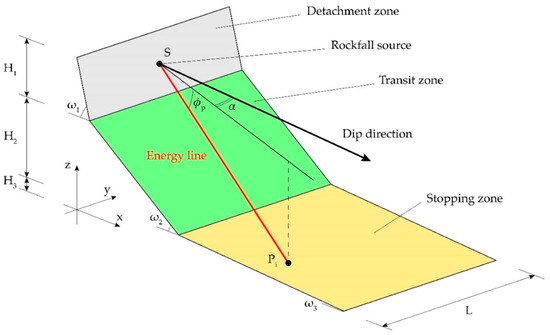
Figure 3.
Sketch of the synthetic slope adopted in the present work with indication of the main zones and dimensions. The energy line connects the source point S to the i-th stopping point Pi. The energy angle is defined in the vertical plane as the angle enclosing between the horizontal plane (black lines) and the energy line. The lateral angle is defined by the projection of the energy line on the horizontal plane and the dip direction of the source point.
Further information about the synthetic slopes is needed to properly perform the rockfall simulations. Therefore, some physical properties concerning the three above-mentioned zones were introduced. These properties were defined according to the specific requirements needed by Rockyfor3D. First, the “soil type” describes the elastic behavior of the soil coverage. For both zones 1 and 2, we adopted soil types “compact soil with large rock fragments” (i.e., soil 4), with normal restitution coefficient in the range (0.34, 0.42). For zone 3, we adopted the more plastic “fine soil material” (i.e., soil 1), able to faster dissipate the kinetic energy of the block. Normal restitution coefficient in the range (0.21, 0.25) are associated by Rockyfor3D to this soil type. The above-mentioned soil types can be considered as roughly representative of most of the slopes in the Alpine environment and were taken constant in all our analyses. Especially in zone 2, as elastic as possible soil properties were considered in order to take into account the worst energy dissipation condition during the block–slope interaction and to obtain precautionary results.
The presence of the forest was considered only in zone 2. In particular, a conifer forest was assumed because of the lower resistance of this type of trees [32,33,34], with a diameter at breast height (DBH) of the trunk equal to 35 ± 1 cm, which corresponds to a medium resistance capacity. Of course, the results are to be referred to real slopes characterized by forests of similar characteristics. For generalizing these results, a sensitivity study of these parameters will be carried out in the future. With regards to forest density and with the aim of fixing upper and lower limits to the range of variation of the results, two cases were considered: absence of trees (0% forest density) and dense forest coverage (100% forest density). A forest density of 100% can be assumed as 1 tree per cell of the DTM [35], which means 400 trees/ha if a 5 m DTM is used, as in this case.
A brief recap of the geometrical and physical characteristics of the synthetic slopes adopted in this work is provided in Table 3. To carry out the trajectory analyses, all geometrical and physical characteristics of the synthetic slopes were saved within raster files with a cell size resolution of 5 m.

Table 3.
Geometrical and physical characteristics of the synthetic slopes. See also Figure 3 for the meaning of symbols. Soil 4 refers to a compact soil with large rock fragment; soil 1 refers to a fine soil material [27].
3.2. Parametric Analyses
On the basis of the synthetic slopes described in the previous Section 3.1, several parametric analyses were performed by combining both slope and block features. Inclination and forest coverage density of zone 2 were varied among the values listed in Table 3. With reference to the block characteristics, a density of about 2500 kg/m3 was introduced and the following five classes of volume were assumed for the parametrical study: 0.1, 0.5, 1.0, 5.0 and 10.0 m3. Finally, both spherical and cubic shapes were taken into account in the Rockyfor3D simulations. In Table 4, a recap of the main characteristics of the blocks adopted in this work is reported. Finally, the probabilistic nature of Rockyfor 3D [27] allowed to perform 20,000 launches for each analysis in order to acquire a statistically representative number of simulations, necessary for a reliable statistical interpretation of the results.

Table 4.
Characteristics of the blocks adopted in the parametric analyses.
3.3. Statistical Interpretation of the Results
The outputs of the trajectory analyses provided by Rockyfor3D are many raster files showing the distribution on the slope of block velocity, energy, stopping points, etc. Here, the interest is focused on stopping points, whose position allows to estimate both the cone angles and . In Figure 3, an example of the definition of and is shown, with reference to the rockfall source point S and the i-th stopping point . Thus, 20,000 values for both the angles can be computed as follows (Equation (3)):
where and are the coordinates of the rockfall source S and the i-th stopping point respectively.
The goal of this paper is to produce a tool for the definition of a couple of values representative of the analyzed scenario in terms of block and slope characteristics, to be associated to the rockfall source points by the QPROTO users. To reach this goal, a single representative value has to be selected among the 20,000 results obtained through Equation (3). Thus, starting from the population of and computed values, the cumulative distribution functions (CDFs, hereafter) were defined (Figure 4a,b). Since representative angles should be conservative, i.e., should be related to the maximum possible extension of the invasion zone, the 2nd percentile () was selected as representative of the energy angle CDF. On the contrary, the 98th percentile () was adopted for the lateral angle CDF, in order to consider the maximum lateral dispersion of the trajectories. It is worth noting that these two angles are not related to each other. In other words, the trajectories that provide angle are not the same ones that provide . This can be easily observed if the cone angles are plotted into a bivariate plane. In Figure 5a the three-dimensional histogram of the cone angles analyzed in Figure 4 is reported: it can be seen that the majority of the results (high occurrence frequency) are related to lateral angles lower than 2° and energy angles around 25° (Figure 5b). This is due to the simple geometry and the peculiar symmetry characterizing the synthetic slopes adopted in this work. To obtain more general results that can be used in real cases, more conservative percentile values need to be considered.
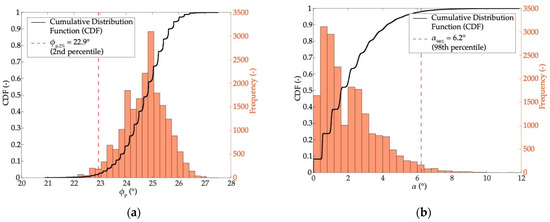
Figure 4.
Examples of the typical histograms and cumulative distribution functions (CDFs) of (a) the energy angle and (b) the lateral angle obtained in the case of 5 m3 spherical block, 0 trees/ha, and .
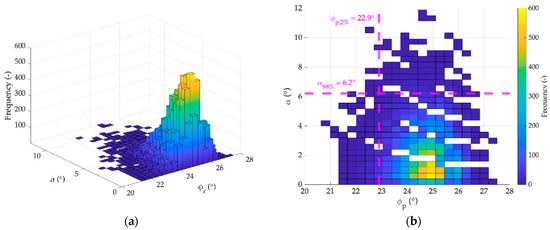
Figure 5.
Example of the frequency distribution obtained for the set of 20,000 launches described in Figure 4: (a) three-dimensional histogram; (b) two-dimensional view of the same histogram. The magenta vertical and horizontal lines highlight the value of and , respectively.
The result of this simple statistical data processing is a couple of values (; ) associated to different slope and block characteristics, useful to highlight the influence of each characteristic and to estimate the parameters in susceptibility and hazard analysis with QPROTO. These findings will be presented and discussed in the following Section 4.
4. Results
The results of the parametric analyses are presented on the following, organized in different charts with reference to both the energy angle and the lateral angle . Each chart refers to the correlation between the angles and the different variables considered in the simulations, in order to analyze the effect of each variable.
4.1. Influence of the Slope Characteristics
In order to consider the pure effect of the slope characteristics on the evolution of rockfall trajectories, the first results (Figure 6, Figure 7 and Figure 8) are related to a spherical block with unitary volume (0.625 m radius). Here, the main slope characteristics considered in the parametric analyses are slope inclination and forest coverage.
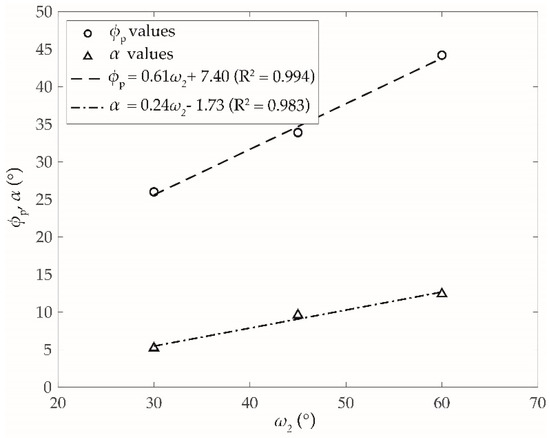
Figure 6.
Linear variation of angles and as a function of slope inclination . Spherical blocks of unitary volume and absence of forest are considered here.
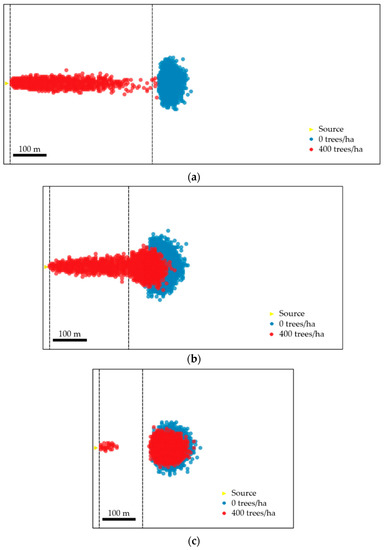
Figure 7.
Maps of deposited blocks in the case of a spherical block with a unitary volume. Upper and lower limits of the transit zone (zone 2) are indicated in black dashed lines. The blue area refers to the scenario with 0 trees/ha, while the red one refers to the scenario with 400 trees/ha. Slope inclination : (a) 30°, (b) 45° and (c) 60°.
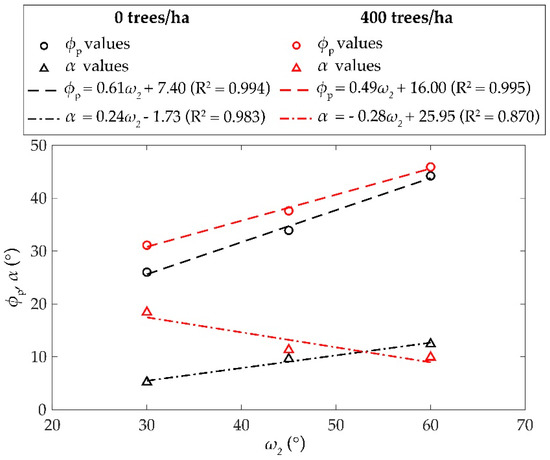
Figure 8.
Effect of forest on the variation of angles and as a function of slope inclination . Spherical blocks of unitary volume are considered here.
4.1.1. Slope Inclination
In absence of trees on the transit zone (Figure 7, in blue), all the blocks reach the foot of the slope and stop in the stopping zone, for all the geometrical configurations analyzed. The energy angle is 26° for 30°, 33.9° for 45° and 44.2° for 60°. The distribution of deposited blocks has very similar extension and the lateral angle is 5.2° for 30°, 9.6° for 45° and 12.4° for 60°. As shown in Figure 6, a linear variation can be assumed with very high R2 value in both cases.
4.1.2. Forest Coverage
The rockfall invasion area changes considerably if trees are introduced in the simulation with a maximum forest density of 400 trees/ha. It depends on the capacity of trees to stop or decelerate blocks within the runout zone. By comparing the results in terms of raster distribution of accumulated blocks (Figure 7), it is possible to highlight the difference between the two scenarios (with or without forest) as a function of the slope inclination angle :
- Figure 7a shows the results on a 30° inclined slope, where most of the simulated blocks are distributed on the transit zone in the presence of dense forest, according to the mitigation effect of trees. The energy angle increases from 26° without trees to 31.1° in presence of trees, while the lateral angle increases from 5.2° to 18.4°. Such values are a consequence of the large number of blocks deposited just below the source and will be discussed later (Section 5);
- Figure 7b shows the scenario with a 45° inclined slope, where the effect of trees is minor and blocks are distributed on the whole slope (transit and accumulation zone) in the presence of dense forest; the energy angle increases from 33.9° to 37.6°, while the lateral angle α98% increases from 9.6° to 11.3°. A lower number of blocks have accumulated just below the source and their effect on the statistical result is lower;
- Figure 7c shows the scenario with a 60° inclined slope, where the effect of trees is at a minimum. Due to the steep inclination of the slope, the majority of blocks reaches the foot, and the extension of the accumulation zone is similar to that obtained without trees; the energy angle increases from 44.2° to 46°, while the lateral angle α98% decreases from 12.4° to 9.9°.
As shown in Figure 8, a linear law can again be assumed to describe the variation of , very similar to that obtained without the forest. On the contrary, the overestimation of the lateral spreading in the presence of trees affects the linear variation of angle , which cannot be considered as reliable and needs further studies. For this reason, in the following, reference is made to only the energy angle . In Section 5, this problem will be better described and discussed.
4.2. Influence of Block Characteristics
A trajectographic study of rockfall events cannot ignore the influence of volume and shape of the block in the evolution of the phenomenon. In this section, spherical and cubic blocks of different volumes were considered (see Table 4) and their trend on the 30°, 45° and 60° inclined slopes was analyzed within both the scenarios related to forest coverage.
4.2.1. Block Volume
As resulting from our study, the runout distance is strongly influenced by block volume: smaller volumes run for smaller distances on the slope. First, the parametric analyses were carried out with reference to spherical blocks in absence of trees and the following items were observed (Figure 9, black solid lines):
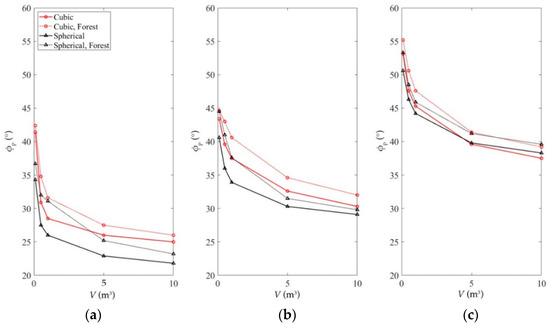
Figure 9.
Results of the parametrical simulations for (a) = 30°, (b) 45° and (c) 60° slopes. Energy angle values are given as a function of block volumes and forest coverage.
- For 30° (Figure 9a), only blocks of 0.1 m3 volume stop above the foot of the slope, while larger volumes reach the stopping zone. Energy angles are in the range [34.3°, 21.8°] with increasing block volume;
- For 45° (Figure 9b), all volumes reach the foot of the slope and are deposited in the stopping zone. Energy angles are in the range [40.6°, 29.1°] with increasing block volume;
- For 60° (Figure 9c), the map of deposits has the same configurations of the 45° slope. Energy angles are in the range [50.6°, 38.3°] with increasing block volume.
The same analyses were repeated after including 400 trees/ha forest density on the transit zone (Figure 9, black dotted lines). The general tendency is that trees can influence the path of smaller blocks, reducing the extension of the invasion zone, while for volumes bigger than 5 m3, the effect of trees seems less important. The influence of trees can also be observed as a function of the slope inclination angle. From Figure 9, it is possible to notice that:
- For 30°, energy angles are in the range of [36.7°, 23.2°]. The increment with respect to the previous scenario (without forest) is a function of the block volume and decreases with increasing volume;
- For a 45°, energy angles are in the range of [44.5°, 29.8°] with the same increment with respect to the previous scenario (without forest);
- For a 60°, energy angles are in the range of [53.3°, 39.6°] with a constant increment of 2° with respect to the previous scenario (without forest).
No further statistical analyses were carried out with reference to the lateral angle, due to the overestimation of the runout area induced by blocks accumulated just below the source point.
4.2.2. Block Shape
In order to evaluate the effect of block shape, all the simulations were repeated with reference to cubic blocks of different volumes. In general terms, the influence of the considered variables on the rockfall trajectories is the same as the spherical block. Smaller volumes are the most affected by the presence of a forest and run bigger distances with increasing slope inclination. However, under the same conditions, cubic blocks reach smaller distances than spherical ones. With reference to cubic blocks, as shown in Figure 9 (red lines):
- For 30°, energy angles are in the range [41.4°, 25°] with increasing block volume in the absence of trees; in the presence of trees, they vary in the range of [42.4°, 26°]
- For 45°, energy angle are in the range [43.4°, 30.3°] with increasing block volume in the absence of trees, in the presence of trees, they vary in the range of [44.6°, 32°]
- For 60° energy angle are in the range [53.1°, 37.5°] with increasing block volume in the absence of trees, in the presence of trees, they vary in the range of [55.2°, 39.2°].
From the analysis of Figure 9, it is possible to observe that the main effect is due to the presence of forest rather than block shape. The curves related to cubic and spherical blocks allow to highlight envelopes which upper boundary if referred to cubic blocks and lower ones to spherical blocks, consistently with the adopted numerical model. Other isometric shapes are supposed to obtain intermediate results, though the software Rockyfor3D does not allow us to investigate this. Considering the difficulties in characterizing the block shape in detail when preparing a preliminary rockfall analysis, a mean value of the energy angles can be computed between cubic and spherical blocks, which can be considered representative of a generic isometric block. In this way, the charts of Figure 9 can be simplified, as shown in Figure 10.
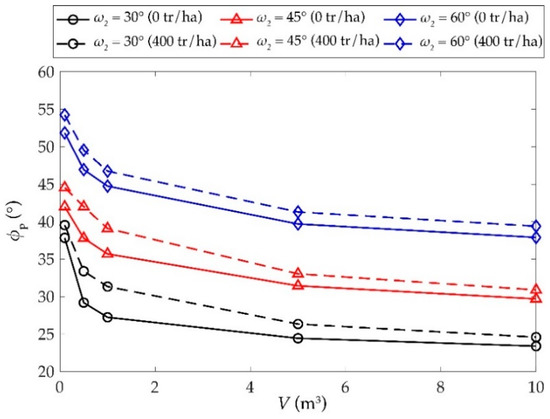
Figure 10.
Mean values of the energy angle on account of isometric cubic/spherical blocks, as a function of block volume, forest coverage and slope inclination.
Only isometric shapes are considered in this study, due to the difficulty in interpreting the results of Rockyfor3D simulations when block dimensions are characterized by slenderness. Thus, the problem of a block shape should be the object of further investigations focused on the effects of slenderness. However, the findings presented in this study can be considered as preliminary and refer to block shapes with unitary slenderness.
5. Discussion
On the basis of the proposed methodology, some conservative values were provided for the energy angle in the case of isometric blocks, as a function of slope inclination, forest coverage and block volume. Such values can be considered as conservative because they refer to the second percentile of the CDF: in 98% of cases, these angles could be exceeded and, consequently, blocks could run shorter paths along the slope. Therefore, the dataset can be easily adopted as a starting point for preliminary and quick analyses within the QPROTO environment, as will be shown in Section 6.
To organize the findings of the parametric analyses and to extend their validity to values of the variables not directly included in the analyses, an interpolation of all the data was performed, resulting in the charts of Figure 11. The kriging regression technique was adopted in order to obtain the best linear prediction of the intermediate values. The curves represented in Figure 11 allow to estimate the energy angles for any slope inclination ranging between 30° and 60° referring to isometric shapes and block volume between 0.1 and 10 m3 scenarios. Figure 11a refers to slopes without trees while Figure 11b is related to dense forest simulations. Intermediate forest density can be associated to interpolated values between the two sets of curves.
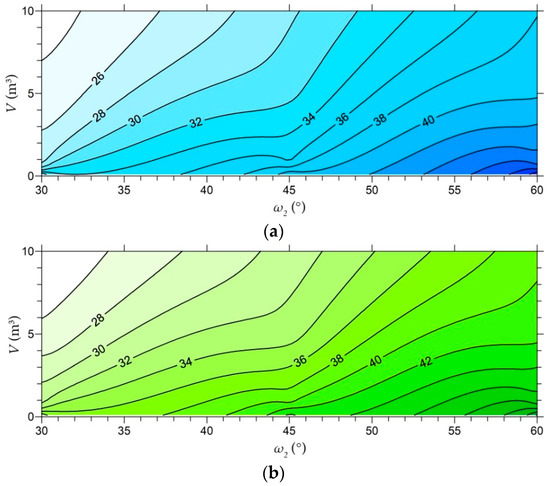
Figure 11.
Resulting chart for the estimation of the energy angle as a function of slope inclination and block volume. Contour black lines refer to the same energy angle conditions: (a) non-forested slope; (b) forested slope (400 trees/ha).
Here, it can be useful to summarize the main results of this work. In particular:
- Computed energy angles can reproduce the mitigation effect of dense forests located on the transit zone of the slope;
- The growth of a block volume causes the reduction of the energy angle and provide larger invasion areas;
- The growth of slope angle causes the increase of the energy angle and the reduction of the invasion area.
On the basis of the above-described observations, our findings are consistent with several literature works, real case observations and experimental activities [10,30,36,37,38,39].
With reference to the lateral angle , the 98th percentile of the CDF was considered as a reference value in order to maximize the lateral dispersion of the trajectories. Unfortunately, in many cases of our analyses, the lateral angles were affected by the presence of blocks stopped just below the rockfall source point. These deposited blocks were typically characterized by high values of the lateral angle, which are considerably larger than those obtained for the blocks that reached the foot of the slope. Such values strongly overestimate the maximum lateral spreading of blocks. To better understand this issue, it is possible to refer to the simulations performed with a spherical unitary block reported in Figure 7a in the forested scenario, where blocks are distributed over the transit zone. Assuming = 18.4° in the Cone Method, this can result in a considerable overestimation of the runout area, since the elongated shape of the stopping points can barely be represented by a cone, with the apex at the source point and the maximum width at the foot of the slope (Figure 12). Thus, in this case, the statistical data do not seem to be adequate to reproduce the rockfall invasion zone and more reliable methods are necessary. In the following improvements of the research, some qualitative considerations will be adopted and tested with reference to some real case studies in order to get more realistic results.
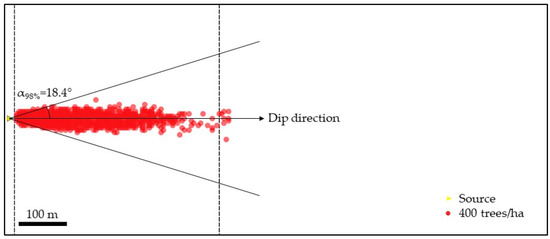
Figure 12.
Overestimated runout zone assuming for the cone in the case a significant number of blocks stops just below the source. Reference is made to the scenario described in Figure 7a.
6. Validation and Examples
The results achieved in this work were applied to two different study cases belonging to the Susa Valley, in the north-western Italian Alps. First, the results were validated with reference to the rockfall event that occurred in 2011 in the Cels-Morlière hamlet. A second validation was done for the rockfall event that occurred in 2010 in the Melezet hamlet. Finally, the results were applied to a larger portion of the slope to perform a forecasting rockfall analysis for the site of Melezet. The location of the two sites is reported in Figure 13.
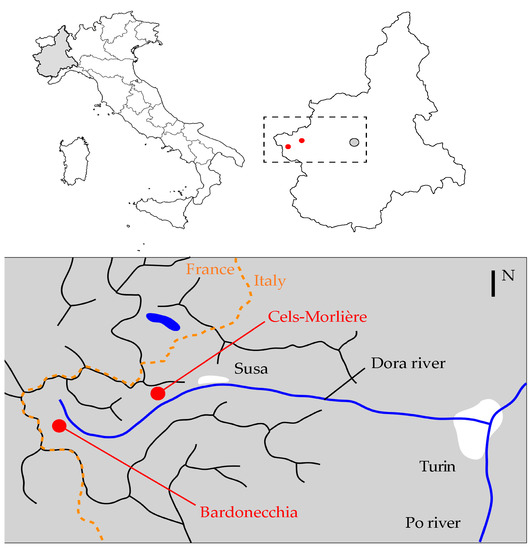
Figure 13.
Geographic framework of the two study cases.
The Cels-Morlière hamlet (UTM: 4996137 337399 32T) is located in the municipality of Exilles, on the left hydrographical bank of the Dora Riparia river. The site has an elevation of 850 m a.s.l. and is overlooked by a largely fractured rock face, with its peak at 1400 m a.s.l. Cels-Morlière has historically been subjected to high-intensity rockfall events that often reached and damaged several buildings. The most recent event occurred in 2011, when a cluster of three blocks (each of them with a volume of about 5 m3) destroyed a flexible net barrier whose capacity is estimated around 800 kJ and hit three buildings. On average, the slope involved in this event is inclined of about 45°. A back-analysis of the event was first conducted by means of Rockyfor3D. A pre-event DTM with a resolution of 5 m was used, and 5 m3 blocks with a rock matrix density of about 2600 kg/m3 were simulated from the detachment niches, defined on the basis of event reports and the available digital cartography.
A broad-leaf forest with a density of 400 trees/ha was assumed to cover the slope, on the basis of qualitative observation of the orthophoto and the available forest inventories provided by the Piedmont Region. A flexible net barrier of 800 kJ capacity and 4.5 m height was also considered. The result of the back analysis is given in Figure 14a in terms of mean kinetic energy. It is possible to observe that blocks keep descending beyond the existing protection works and arrive at the building’s location (Blds. 1 to 3) with the mean energy ranging between 500 kJ and 1500 kJ. These values seem slightly overestimated if compared to the observed damages (for Blds. 2 and 3, the estimated energies are in the range between 500 kJ and 1000 kJ), but they are acceptable, since the trajectory analysis has to be precautionary [2].
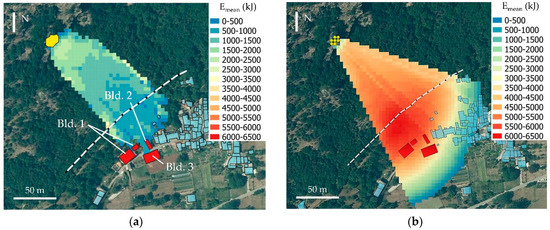
Figure 14.
Results of the back analyses for the 2011 rockfall event in Cels-Morlière hamlet (rockfall sources in yellow, barrier in dashed white line, impacted buildings in red). (a) Rockyfor3D mean kinetic energy; (b) QPROTO mean kinetic energy.
To validate the proposed methodology for the estimation of the QPROTO parameters, a back-analysis of the 2011 event was conducted by means of QPROTO as well.
The main inputs of the QPROTO back analysis are the average slope inclination of 45°, a block volume of 5 m3 and a dense forest coverage (400 trees/ha). The energy angle = 34° can be extracted from Figure 11b. A value of = 10° was finally assumed to completely define the visibility cones. Seven points were selected inside the source area and the attributes listed in Table 1 are associated to each of them. Finally, since it is a simulation of a real event, a constant propensity index DI = 1 was assumed. The result of the analysis is shown in Figure 14b, again in terms of the mean kinetic energy. The comparison between Figure 14a,b shows that QPROTO results are overestimated both in terms of invasion area and mean energy, involving a portion of the hamlet on the right side of the damaged buildings. It is worth noting that the analysis with Rockyfor3D considers the flexible net barrier of 800 kJ capacity, which played a role in the rockfall event, decelerating blocks and reducing their kinetic energy. However, this role seems weak, as shown in Figure 14a, since the capacity of the barrier is low with respect to the kinetic energy of the blocks. At the current state of the work, it is not possible to consider how the presence of protective works on the slope can influence the energy line, and thus, its angle. Therefore, the preliminary QPROTO analysis does not consider this effect, and therefore, leads to a conservative result. On the basis of these observations, it is possible to conclude that the results obtained are acceptable and encouraging for future implementations.
The second study case is referred to the site of Melezet. The investigated area (UTM: 4994268 319183 32T) is located 2 km south-west of Bardonecchia at elevation around 1400 m a.s.l. It develops along the provincial road no. 216, connecting the Italian Susa Valley to the French Vallée de la Clarée. During the last four decades, the slope has been affected by intense and extremely damaging rockfall phenomena that involved both the Melezet hamlet and the provincial road. The last documented event dates back to May 2010, when a rock face approximately 30 m high and 25 m wide collapsed, involving a volume of about 2000 m3. The fallen blocks partially hit and damaged the existing embankment located along the provincial road, and some boulders arrived on the provincial road, reaching the foot of the slope (Figure 15). Such blocks damaged the provincial road, destroyed two isolated buildings and compromised the safety of inhabitants (Figure 16b).
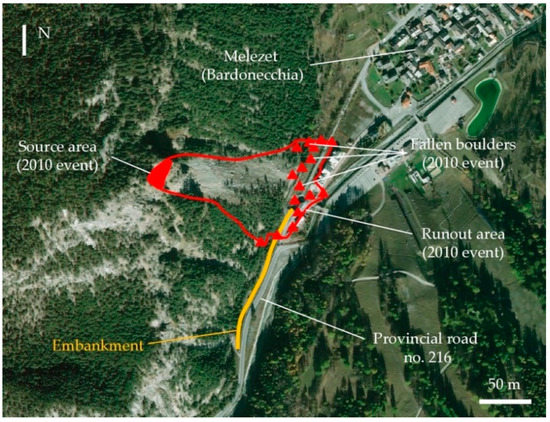
Figure 15.
Map of the 2010 event. The red line highlights the runout area of the phenomenon and the red triangles define the location of the observed fallen blocks. The embankment (yellow line), located along the provincial road, was impacted by a cluster of boulders in the southern part of the runout zone.
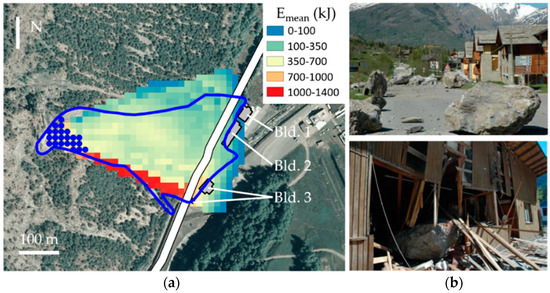
Figure 16.
(a) Back analysis of the 2010 event; results in terms of mean energy (kJ). Runout area is shown with a blue line, source points with blue dots, provincial road no. 216 in white and impacted buildings in grey. Orthophoto 2010 Regione Piemonte. (b) Effects of the May 2010 event on the Melezet site: at the top, blocks that stopped along the provincial road no. 216 (no direct damage to the buildings); at the bottom, a wood building that was seriously damaged (Bld.3 in Figure 16a).
First, a back analysis of this event was performed, as an additional validation of the method. The adopted DTM with a resolution of 10 m is representative of the slope condition before the event. The back analysis was carried out by generating a set of rockfall source points within the collapsed portion of the rock face during the 2010 event. The attributes required by QPROTO were associated to each of the source points (Table 5). The average inclination of the slope is equal to 35° and a dense forest coverage was assumed. Again, since it is a real event, a constant propensity index DI = 1 was considered. The reference block volume for the studied scenario is equal to 1 m3, which was the average observed volume at the foot of the slope according to the event report prepared by ARPA Piemonte [40].

Table 5.
Attributes associated to each source point.
On the basis of these data, the energy angle = 34° can be extracted from Figure 11b. Since the analysis on the lateral angle seems to need some additional refinement, in this case, a parametric study was performed, looking for the value that best simulated the observed runout area: the best results were obtained assuming a lateral angle The mean kinetic energy map resulting from the analysis is provided in Figure 16a. The maximum values (about 1300 kJ) are reached at the mid-part of the slope, on the southern side of the runout zone, while lower ones (from few tens up to 700 kJ) are registered at the slope foot where the provincial road is located. In the zones where the two isolated buildings are located (Bld. 3), destroyed by a block impact on May 2010, the mean energy reaches 900 kJ, which is compatible with the observed damages (Figure 16b). The presence of the embankment was not directly taken into account because of the limited effects that this protection work induced in the kinematics of the studied event.
Following this additional validation of the method, a new forecasting analysis on a more extended portion of land was carried out, to preliminarily analyze the slope in the neighbors and to estimate the susceptibility of the valley bottom.
The set of source points was obtained starting from 11 homogeneous areas (Figure 17) established on the basis of reports produced by local technicians. The homogeneous areas were defined as portions of the rock face having uniform characteristics, such as slope orientation, elevation and structural characteristics. Within each homogeneous area, a set of source points was generated by referring to a DTM with resolution 5 m, representative of the condition of the slope after the event of May 2010. The points were randomly selected at the center of the 50% of the grid cells with an inclination larger than 45°. The result is a shapefile composed by 1687 points. Then, the attributes listed in Table 5 were associated to each point. They were extracted either from the analysis of the DTM (elevation and aspect), or through the proposed method. A block volume of 1 m3 and a block mass of 2600 kg were assumed as representative of the phenomenon with reference to all the homogeneous areas because not enough data were available to obtain a more detailed characterization. Since the aim of the analysis is to test the methodology for the estimation of the QPROTO parameters, the detachment propensity DI was set equal to 1 within each homogeneous area. This means that all the computed parameters have the same probability of occurrence within any point of the propagation area, and the maps “count” and “susceptibility” are equal. In other words, the susceptibility within the invasion zone only depends on the number of source points and on the cone parameters and
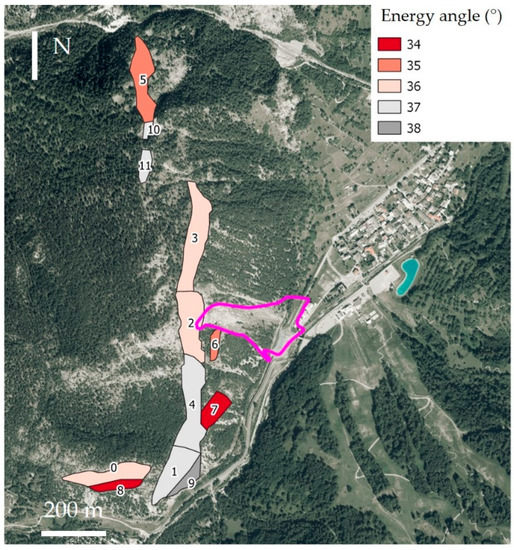
Figure 17.
Homogeneous source areas with indication of the energy angle associated to each one. Runout area of 2010 event in magenta. Orthophoto AGEA 2018.
For the definition of the energy angles, a simple study of the slope morphology below each homogeneous area was carried out, with particular reference to the average slope inclination. A dense forest coverage was finally assumed, according to the observation of some recent orthophotos. In Table 6, the mean orientation of the slope and the corresponding energy angle as resulting from the use of chart of Figure 11b are listed for each homogeneous area. In Figure 17, the distribution of the chosen energy angle values among the homogeneous areas is shown. Finally, on the basis of the results of the back analysis, a constant value of the lateral angle = ± 12° was assumed.

Table 6.
Mean slope orientation and energy angle for each homogeneous area, obtained from the chart in Figure 11b, with the assumption of a dense forest coverage and boulder volume V = 1 m3.
The results obtained by the QPROTO analysis are shown in Figure 18a in terms of the mean kinetic energy (kJ), and in Figure 18b in terms of the susceptibility. In general, it is possible to observe that the local viability, modified after the May 2010 event, seems highly affected by the considered scenario of rockfall events. About 1 km of the new provincial road no. 216 was involved, as well as the local viability and two bridges over the Dora Riparia river. However, the two inhabited areas seem only marginally reached by the rockfall scenario. The most affected zone in terms of susceptibility (frequency) is located below areas 2 and 3, due to the orientation of the slope and the large extension of the homogeneous source areas (high number of source points). Additionally, the zones of the slope where the mean energy is higher are located below areas 2 and 3. Here, the mean energy values are around 1500 kJ just below the sources and around 800 kJ at the slope foot where the roads are located. This area was interested by the rockfall event of May 2010 and the results obtained here are consistent with those of the back analysis (Figure 16a). The pre-existing embankment (Figure 15) located below areas 2, 4, 6 and 7 cannot be considered in the QPROTO analysis. Thus, the results shown in Figure 18 could be overestimated in that zone. The mean kinetic energy at the embankment location is estimated in the range between 500 kJ and 900 kJ, but more detailed analyses are needed to evaluate the efficiency of the embankment in stopping block trajectories.
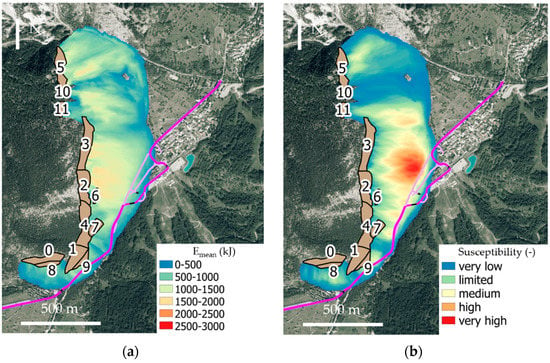
Figure 18.
QPROTO results for the site of Melezet. Source areas are shown in light brown, local viability in pink, provincial road no. 216 in magenta, bridges in black. (a) Mean energy in kJ, (b) susceptibility. Orthophoto AGEA 2018.
It is worth noting that the difference in height between source points and the foot of the slope is not uniform among the homogeneous areas. In the case of areas 6, 8 and 9, such a difference is less than 100 m; areas 0, 1 and 4 are located at a height ranging between 100 and 200 m; areas 2 and 3 are at a height ranging between 200 and 300 m; areas 5, 10 and 11 (northern part of the site) are at a height ranging between 400 and 500 m. Since this aspect of slope geometry was not taken into account in the parametrical analyses, the results could be further refined in the future development of the research.
The proposed methodology allowed to estimate the parameters to be used in the susceptibility analysis in a very simple way, i.e., only on the basis of the DTM, the available cartography and some observation of the slope conditions. The results seem very encouraging for further development of the research, aimed at providing the QPROTO users with a reliable tool to calibrate their analyses to the site under study.
7. Conclusions
In this paper, a methodology for the quick estimation of the parameters needed to perform preliminary rockfall susceptibility and hazard analyses using the QPROTO plugin is presented. The plugin is based on the Cone Method and simplifies the complex path of a block along the slope with an equivalent pure sliding motion on a plane. The inclination of this plane with respect to the horizontal plane (i.e., the energy angle ) is the main parameter of the method, because it represents all the dissipative phenomena that occur during motion. The 3D implementation of the method includes the definition of a second angle that represents the lateral spreading of the phenomenon (i.e., the lateral angle ). Both the energy angle and lateral angle contribute to define a cone in the space. On the basis of this cone, QPROTO performs a viewshed analysis starting from some source points: all the zones of the slope that can be viewed by an observer located in the source point can be reached by a boulder detached from that point. To perform a susceptibility/hazard analysis with the QPROTO plugin, energy and lateral angles are the only equivalent parameters to be estimated, which should represent all the factors actually influencing the rockfall phenomena.
To provide QPROTO users with a tool able to calibrate the parameters that characterize the rockfall scenario under investigation, several parametric analyses deepening the influence of both slope and block features on the cone angles were performed. Each analysis consists of: (i) detailed rockfall simulations on synthetic simplified slopes and (ii) the statistical processing of the results to designate representative values of the angles. The main variables whose influence was parametrically evaluated are: slope inclination, forest coverage, block volume and shape. Other characteristics, such as elevation of the source point, length of the slope, soil type, roughness and slenderness of the block, were kept constant in this research and their effect will be further investigated in the future.
In the light of the findings of the parametric analyses, described in Section 4, the following observations can be drawn:
- For unitary blocks, a linear variation of both energy and lateral angles can be assumed as a function of slope inclination if non-forested slopes are considered and all the simulated blocks reach the stopping zone (i.e., the foot of the slope);
- The effect of trees consists of reducing the extension of the runout area and, thus, in increasing the energy angle: a linear equation can be assumed as a function of the slope inclination in the case of . In the presence of trees, unitary blocks, in many cases, do not reach the foot of the slope and stop at the transit zone. Therefore, an overestimation of the lateral spreading can be observed as a consequence of the statistical processing of the data. Here, some preliminary results concerning the estimation of the lateral angle are reported, and more detailed analyses will be carried out in future works;
- The influence of trees is also a function of the slope inclination: it is higher for less steep slopes and gradually decreases when the slope inclination increases. The linear variation of the energy angle with slope inclination is, therefore, less pronounced in the case of densely forested slopes;
- Runout distance is strongly influenced by block volume: smaller volumes reach the closest distances on the slope, while larger blocks run farther. The variation of the energy angle with reference to block volume is not linear because it depends on the possibility that blocks reach the foot of the slope or stop in the transit zone;
- Trees can influence the path of smaller blocks, reducing the extension of the runout area. This effect reduces when block volume increases;
- Spherical and cubic blocks show similar behaviors. Considering the quick nature of the plugin QPROTO, a mean value of the energy angles can be considered as representative of generic isometric blocks.
The main output of the proposed methodology is a chart that interpolates all the obtained results and can be used to estimate the energy angle for different slope configurations and block volume scenarios. The chart was validated on the basis of some back analyses of real events that occurred in the Alpine environment. In this paper, the chart was finally used to provide the input variables required by the plugin QPROTO with reference to a preliminary susceptibility analysis carried out at medium and large scales. The example shows that the methodology, although very simplified, provides conservative and realistic results that are encouraging for further developments.
Several improvements arise from the work described here. With reference to the variables influencing the rockfall runout, the following items should be deepened:
- The elevation of the source point with respect to the foot of the slope (and consequently the length of the transit zone) was kept constant in all the parametric analyses. Since it affects the length of boulder paths, it is supposed to strongly influence the results of the analyses and the cone angles. Further investigations on this topic will be carried out in the future in order to extend the parametric analyses to different elevation classes of the source points;
- Block slenderness has not yet been taken into account because of the difficulty in interpreting the results provided by Rockyfor3D. This software is based on a hybrid model and simulates the block impacts (with the soil or with a tree) using equivalent spheres, whose dimensions are a function of the three initial dimensions of the block (height, width and thickness). This could affect the results in terms of runout area, and many uncertainties can be related to these changes of shape. To simulate the real behavior of blocks of elongated or slab shape, the use of a fully 3D rigid body model could be helpful and will be evaluated in the future;
- The forest coverage adopted in this work, and described in Section 3, has medium protective capacity against rockfall. To generalize the obtained results, in the future, a real sensitivity study will be carried out in order to consider different tree diameters, forest density, types of trees etc. Some interesting suggestions can be derived from previous studies on the protective role of forests, such as the one performed in the framework of the RockTheAlps project [41];
- In this work, a very smooth slope and elastic geomaterials were adopted in order to produce precautionary results. In case of small scales and preliminary rockfall analyses, very rough information concerning soil characteristics are usually available and using precautionary values could be the better solution;
- The entire work is based on trajectographic analyses carried out on artificially created simplified slopes, to control the input variable with high levels of detail. The obtained results are in good agreement both with real cases and literature data but can be unrealistic if the slope is characterized by strong orientation gradient, which can deviate blocks from the original dip direction. Currently, the problem can be faced only through a high number of source points, in order to obtain a wider invasion area by the overlapping of differently oriented cones. A GIS study of slope morphometric features (concavity, convexity, curvature etc.) using well-documented real cases could help in introducing this aspect in the evaluation of the orientation and the lateral aperture of the cone. This will be investigated in the future development of the research. Moreover, some laboratory experiments carried out with scaled slopes could be useful to further validate the obtained results.
Finally, with reference to the QPROTO plugin, some improvements may concern the effect of protection works on the slope (e.g., flexible barriers). Currently, they cannot be taken into account in the viewshed analysis, causing an overestimation of the results. However, considering their protection role against rockfall events, it could be important to refine the results to overcome this unrealistic ovestimation. The influence of pre-existing protective works on rockfall runout is, however, the function of a number of factors, such as their geometry (length, height), their resistance, their position on the slope, their efficiency and their degree of conservation, which is mainly a function of time. A deep investigation of such factors seems to be still needed before extending the proposed methodology to consider their effects on the QPROTO parameters.
Author Contributions
Conceptualization, M.C., G.T. and G.V.; methodology, M.C., G.T. and G.V.; software, G.T.; validation, M.C., G.T. and G.V.; writing—original draft preparation, M.C., G.T. and G.V.; writing—review and editing, M.C., G.T. and G.V.; supervision, M.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data described in this work are available on request to the correponding author.
Acknowledgments
The authors gratefully address their thanks to S. Campus (Regione Piemonte) and L. Lanteri (ARPA Piemonte) for the concession of the data relative to the study case.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fell, R.; Corominas, J.; Bonnard, C.; Cascini, L.; Leroi, E.; Savage, W.Z. Guidelines for landslide susceptibility, hazard and risk zoning for land-use planning. Eng. Geol. 2008, 102, 99–111. [Google Scholar] [CrossRef]
- Scavia, C.; Barbero, M.; Castelli, M.; Marchelli, M.; Peila, D.; Torsello, G.; Vallero, G. Evaluating rockfall risk: Some critical aspects. Geosciences 2020, 10, 98. [Google Scholar] [CrossRef]
- Corominas, J.; van Westen, C.; Frattini, P.; Cascini, L.; Malet, J.P.; Fotopoulou, S.; Catani, F.; Van Den Eeckhaut, M.; Mavrouli, O.; Agliardi, F. Recommendations for the quantitative analysis of landslide risk. Bull. Eng. Geol. Environ. 2014, 73, 209–263. [Google Scholar] [CrossRef]
- Ferlisi, S.; Gullà, G.; Nicodemo, G.; Peduto, D. A multi-scale methodological approach for slow-moving landslide risk mitigation in urban areas, southern Italy. EuroMediterr. J. Environ. Integr. 2019, 4, 1–15. [Google Scholar] [CrossRef]
- Onofri, R.; Candian, C. Indagine Sui Limiti di Massima Invasione dei Blocchi Rocciosi Franati Durante il Sisma del Friuli del 1976; CLUET: Regione Autonoma Friuli-Venezia-Giulia, Italy, 1979; p. 42. [Google Scholar]
- Heim, H. Bergsturz und Menschenleben; Fretz & Wasmuth: Zwrich, Switzerland, 1932; p. 20. [Google Scholar]
- Toppe, R. Terrain Models: A Tool for Natural Hazard Mapping. In Avalanche Formation, Movement and Effects, Proceedings of the Davos Symposium, Davos, Switzerland, 14–19 September 1986; IAHS Publication: Wallingford, CT, USA; Oxfordshire, UK, 1987; p. 162. [Google Scholar]
- Lied, K. Rockfall Problems in Norway; ISMES Publication: Bergamo, Italy, 1977; Volume 90, pp. 51–53. [Google Scholar]
- Wieczorek, G.F.; Morrissey, M.M.; Iovine, G.; Godt, J.W. Rock-Fall Hazards in the Yosemite Valley, California; USGS: Reston, VA, USA, 1998.
- Evans, S.G.; Hungr, O. The assessment of rockfall hazard at the base of talus slopes. Can. Geotech. J. 1993, 30, 620–636. [Google Scholar] [CrossRef]
- McClung, D.; Schaerer, P.A. The Avalanche Handbook; The Mountaineers Books: Seattle, WA, USA, 2006. [Google Scholar]
- Liévois, J. Guide Méthodologique des Plans de Preéention des Risques D’avalanches; La Documentation Française: Paris, France, 2006; p. 310. [Google Scholar]
- Barbolini, M.; Pagliardi, M.; Ferro, F.; Corradeghini, P. Avalanche hazard mapping over large undocumented areas. Nat. Hazards 2011, 56, 451–464. [Google Scholar] [CrossRef]
- Corominas, J. The angle of reach as a mobility index for small and large landslides. Can. Geotech. J. 1996, 33, 260–271. [Google Scholar] [CrossRef]
- Corominas, J.; Copons, R.; Vilaplana, J.M.; Altimir, J.; Amigó, J. Integrated landslide susceptibility analysis and hazard assessment in the principality of Andorra. Nat. Hazards 2003, 30, 421–435. [Google Scholar] [CrossRef]
- Jaboyedoff, M.; Labiouse, V. Technical note: Preliminary estimation of rockfall runout zones. Nat. Hazards Earth Syst. Sci. 2011, 11, 819–828. [Google Scholar] [CrossRef]
- QGIS Python Plugins. Available online: https://plugins.qgis.org/plugins/qproto/ (accessed on 14 January 2021).
- Toma, L.; Zhuang, Y.; Richard, W.; Metz, M. GRASS GIS Manual. Available online: https://grass.osgeo.org/grass78/manuals/r.viewshed.html (accessed on 14 January 2021).
- Kappes, M.S.; Gruber, K.; Frigerio, S.; Bell, R.; Keiler, M.; Glade, T. The MultiRISK platform: The technical concept and application of a regional-scale multihazard exposure analysis tool. Geomorphology 2012, 151–152, 139–155. [Google Scholar] [CrossRef]
- Copons, R.; Vilaplana, J.M. Rockfall susceptibility zoning at a large scale: From geomorphological inventory to preliminary land use planning. Eng. Geol. 2008, 102, 142–151. [Google Scholar] [CrossRef]
- Copons, R.; Vilaplana, J.M.; Linares, R. Rockfall travel distance analysis by using empirical models (Solà d’Andorra la Vella, Central Pyrenees). Nat. Hazards Earth Syst. Sci. 2009, 9, 2107–2118. [Google Scholar] [CrossRef]
- Rickli, C.; Böll, A.; Gerber, W. Ganzheitliche Gefahrenbeurteilung, Kursunterlagen FAN-Kurs; FAN: Bern, Switzerland, 1994. [Google Scholar]
- Volkwein, A.; Brügger, L.; Gees, F.; Gerber, W.; Krummenacher, B.; Kummer, P.; Lardon, J.; Sutter, T. Repetitive rockfall trajectory testing. Geosciences 2018, 8, 88. [Google Scholar] [CrossRef]
- Crosta, G.B.; Agliardi, F. Parametric evaluation of 3D dispersion of rockfall trajectories. Nat. Hazards Earth Syst. Sci. 2004, 4, 583–598. [Google Scholar] [CrossRef]
- Azzoni, A.; La Barbera, G.; Zaninetti, A. Analysis and prediction of rockfalls using a mathematical model. Int. J. Rock Mech. Min. Sci. 1995, 32, 709–724. [Google Scholar] [CrossRef]
- Agliardi, F.; Crosta, G.B. High resolution three-dimensional numerical modelling of rockfalls. Int. J. Rock Mech. Min. Sci. 2003, 40, 455–471. [Google Scholar] [CrossRef]
- Dorren, L.K.A. Rockyfor3D (v 5.2) Revealed. Transparent Description of the Complete 3D Rockfall Model. EcorisQ Paper; EcorisQ: Geneva, Switzerland, 2015; Available online: http://www.ecorisq.org/ (accessed on 14 January 2021).
- Pierson, L.A.; Van Vickle, R. Rockfall hazard rating system. Transp. Res. Rec. 1991, 1343, 6–13. [Google Scholar]
- Mignelli, C.; Peila, D.; Ratto, S.M.; Navillod, E.; Armand, M.; Cauduro, M.; Chabod, A. A New Susceptibility Index for Rockfall Risk Assessment on Road Networks. Eng. Geol. Soc. Territ. 2015, 2, 1949–1955. [Google Scholar]
- Leine, R.I.; Schweizer, A.; Christen, M.; Glover, J.; Bartelt, P.; Gerber, W. Simulation of rockfall trajectories with consideration of rock shape. Multibody Syst. Dyn. 2014, 32, 241–271. [Google Scholar] [CrossRef]
- Wegner, K.; Haas, F.; Heckmann, T.; Mangeney, A.; Durand, V.; Villeneuve, N.; Kowalski, P.; Peltier, A.; Becht, M. Assessing the effect of lithological setting, block characteristic and slope topography on the runout length of rockfalls in the Alps and on the La Réunion island. Nat. Hazards Earth Syst. Sci. Discuss. 2020, 1–27. [Google Scholar] [CrossRef]
- Dorren, L.K.A.; Berger, F.; Putters, U.S. Real-size experiments and 3-D simulation of rockfall on forested and non-forested slopes. Nat. Hazards Earth Syst. Sci. 2006, 6, 145–153. [Google Scholar] [CrossRef]
- Stokes, A. Mechanical resistance of different tree species to rockfall in the French Alps. Plant Soil 2008, 278, 107–117. [Google Scholar] [CrossRef]
- Dorren, L.K.A.; Berger, F. Stem breakage of trees and energy dissipation during rockfall impacts. Tree Physiol. 2006, 26, 63–71. [Google Scholar] [CrossRef]
- Netti, T.; Castelli, M.; De Biagi, V. Effect of the Number of Simulations on the Accuracy of a Rockfall Analysis. Procedia Eng. 2016, 158, 464–469. [Google Scholar] [CrossRef][Green Version]
- Nagendran, S.K.; Ismail, M.A.M. Analysis of Rockfall Hazards Based on the Effect of Rock Size and Shape. Int. J. Civ. Eng. 2016, 17, 1919–1929. [Google Scholar] [CrossRef]
- Okura, Y.; Kitahara, H.; Sammori, T.; Kawanami, A. Effects of rockfall volume on runout distance. Eng. Geol. 2000, 58, 109–124. [Google Scholar] [CrossRef]
- Glover, J. Rock-Shape and Its Role in Rockfall Dynamics. Ph.D. Thesis, Durham University, Durham, UK, 2015. [Google Scholar]
- Huang, S.; Lyu, Y.; Peng, Y.; Huang, M. Analysis of Factors Influencing Rockfall Runout Distance and Prediction Model Based on an Improved KNN Algorithm. IEEE Access 2019, 7, 66739–66752. [Google Scholar] [CrossRef]
- ARPA Piemonte. SIFRAP—Sistema Informativo Fenomeni Franosi in Piemonte Codice Frana: 001-76293-00; Comune di Bardonecchia: Rocce del Rouas, Italy, 2018. [Google Scholar]
- Dupire, S.; Toe, D.; Barré, J.B.; Bourrier, F.; Berger, F. Harmonized mapping of forests with a protection function against rockfalls over European Alpine countries. Appl. Geogr. 2020, 120, 102221. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).