Abstract
Green roofs improve building energy performance and constitute an alternative to sustainable buildings. A green roof model is dynamically coupled with a building thermal model to assess its energy performance that takes into account the indoor air temperature dynamic changes. Under the climate conditions in Antananarivo, we compared green and conventional roofs. The present study shows that green roofs protect the roof structure under extreme temperature and large temperature fluctuations. For the case of Antananarivo, the amplitude of the temperature fluctuations at the top face of the support is reduced by 28 °C when using green roof. The impact of the green roof on indoor air temperature and energy demand is investigated. The vegetation decreases the maximum indoor air temperature and improves the building thermal comfort during summer days. It has no effect on the minimum indoor air temperature, but additional soil thickness can increase it. In addition, a global sensitivity analysis, which is carried out on the proposed model without considering any specific weather data, allows us to identify the most influential parameters on the energy demand. It has been found that green roofs have almost insignificant thermal impact in insulated buildings; however, their potential prevails over the building envelope and weather characteristics in the case of non-insulated building.
1. Introduction
Rooftop greening is a practice that has been used since ancient civilizations. Historical structures, such as Babylon’s hanging gardens, provide us an example of green roofing used by early civilizations. However, its utilization had been rare for centuries, until the Swiss architect Le Corbusier included them in his “Five Points of a New Architecture” in the twentieth century [1,2].
This technique is considered to be an effective solution to improve the internal and external environments at the building and urban levels. Compared to conventional roofs, green roofs improve storm water management [3,4] and reduce air [5,6] and noise [7] pollution. They increase both plant and animal biodiversities in the cities [8,9] and reduce a city’s carbon footprint by converting carbon dioxide to oxygen through photosynthesis [6,10]. They also improve the thermal insulation of a building so that solar heat gain and heat loss are reduced by approximately 70%–90% in the summer and 10%–30% in the winter, respectively [11].
Rooftop greening is a valuable strategy in order to make buildings more sustainable [12,13,14]. Two types of green roofs are generally identified: extensive (with soil thickness less than 10–15 cm) and intensive (with soil thickness more than 15–20 cm) [4,10]. Extensive green roofs are suitable for retrofitting a building and do not require any additional strengthening [15]. The choice of their characteristics depends on the weather conditions and plant species [16]. In order to address this problem, the Roof Solutions for Natural Cooling (ROOFSOL) research project [17] focused on both the theoretical and experimental analyses of different roof solutions for cooling in the Mediterranean region, which are mainly based on evaporative and irradiative cooling principles. In the case of Greece, the work of Niachou et al. [18] as well as the study by Spala et al. [19] on the analysis of the green roof thermal properties and energy performance can be considered. Green roof technology is also able to help reduce energy consumption and improve internal comfort during the spring and summer seasons in areas where the climate is characterized by high temperature and irradiance values during the day [4]. There is growing literature data regarding green roof energy balance. An important work that has been performed resorts to both experimental and computational methods [20,21,22]. Few studies have investigated cases in the Southern hemisphere where green roof potential as a natural cooling technology is unknown or poorly known. Wong et al. [23,24] explored the thermal benefits of a green roof in Singapore through an experimental test done before and after the construction of a rooftop garden. William et al. [25] in their work compared climates, plants and substrate from Australia with those from European countries.
Madagascar is located in a tropical zone where the climate is usually both warm and humid, so the main advantage of using green roofs is the reduction of indoor daily temperature fluctuations [26], which depend on the growth substrate (soil) depths and the maximum indoor air temperature. However, as Madagascar is the fourth largest island in the world (587,041 km2 of area), there are many microclimates in its different regions. In the coastal areas, tropical weather conditions dominate, whereas in the central highlands, like Antananarivo (Figure 1), the weather is cooler and rainy during the wet season, between October 15 and April 15. As can be seen from Figure 2, which shows the 2007 heating and cooling degree days (HDD and CDD) of Antananarivo city, energy consumption related to building heating is much larger than that related to cooling.

Figure 1.
Location of Madagascar (inset) and Antananarivo City.
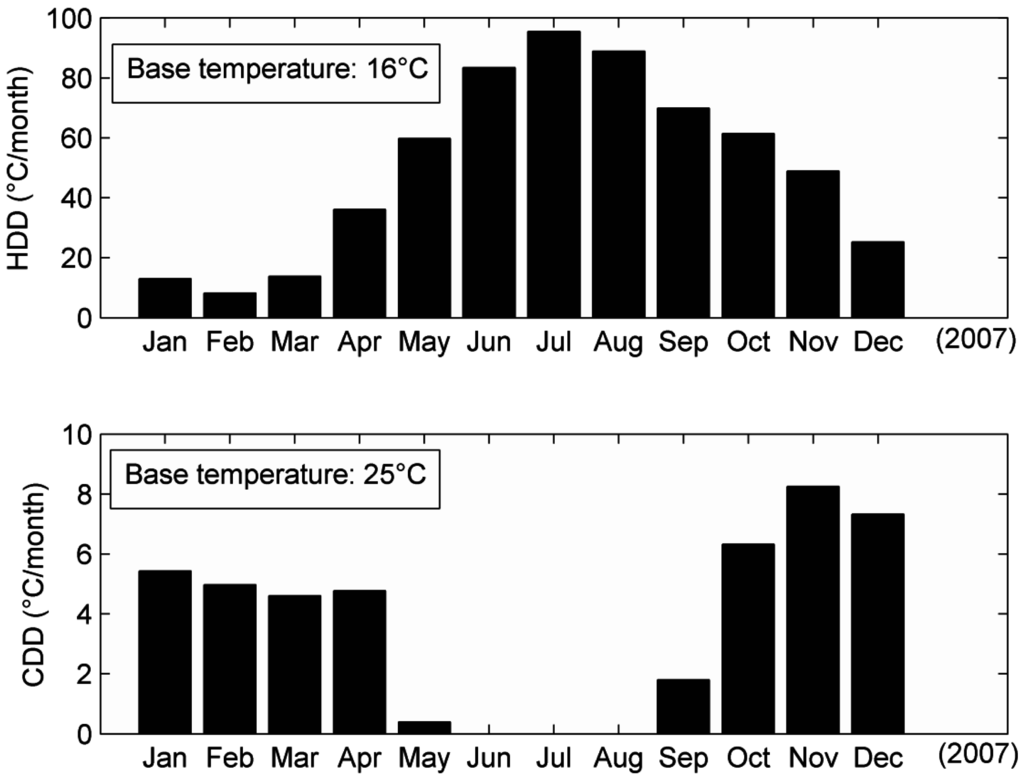
Figure 2.
Monthly heating and cooling degree days (HDD and CDD) in Antananarivo.
Like many works about modeling and performance analysis of the green roof reported in the literature [10,27,28,29,30], a comprehensive analysis of the impacts of green roofs on the thermal performance of building is presented in this study, including modeling and the energy demand impact of green roof for a specific region of Madagascar. We first present the coupled green roofed building model and carry out a performance analysis of this type of roof using weather data from the city of Antananarivo. Then, in order to identify the most influential parameters on the energy demand in the room underneath the green roof, a global sensitivity analysis is performed on the proposed model without considering any specific weather data.
2. Method
2.1. Description of the Studied Roofs
The model considers the green roof as a system composed of four elements: the canopy, the soil or the growth substrate layer, the drainage layer and the support (Figure 3a and Figure 4), whereas the conventional roof (Figure 3b) is only composed of the support.
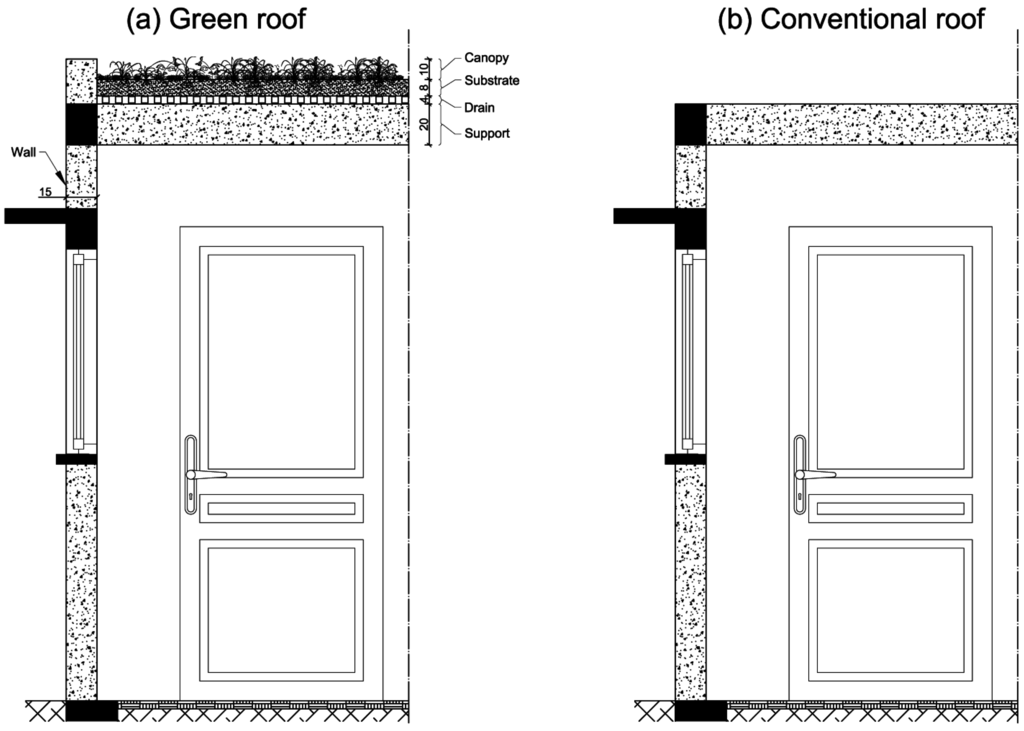
Figure 3.
Sketches of both considered types of roof: (a) green roof and (b) conventional roof.
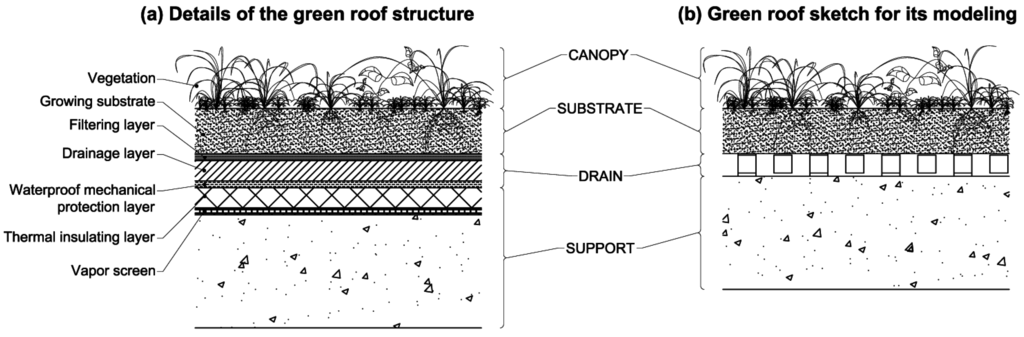
Figure 4.
Structures of a green roof: (a) details for its construction and (b) sketch for its modeling.
2.2. Green Roof Model
The model is developed under the following assumptions:
- (i)
- The plants, the soil and the drain are supposed to be horizontally homogeneous and the problem is one-dimensional;
- (ii)
- The temperatures of the canopy foliage and canopy air are considered uniform;
- (iii)
- The moisture contents of the soil substrate and drainage layers are time dependent, but constant in space;
- (iv)
- The soil and canopy layers are mulch free;
- (v)
- The plants are healthy and there is growth over time;
- (vi)
- The heat transfer by conduction in the plants is negligible.
Nomenclatures are given in Appendix. The equations governing the thermal and mass transfers per ground area unit in the green roof are based on the works of Del Barrio [21,29], Alexandri [31] and Djejig [32], and can be summarized as follow [33].
2.2.1. Thermal Balance
At the canopy foliage node: (subscript a is canopy air, g is soil, and p is canopy leaves except for cp)
On the canopy air node: (subscript m denotes outdoor ambient air)
On the soil nodes:
On the drain nodes: (subscript d denotes drain)
On the support nodes: (subscript in denotes indoor air, and s is support)
2.2.2. Mass Balance
On the canopy air node:
On the soil node:
2.3. Conventional Roof Model
The equations governing the thermal transfer in the conventional roof are:
2.4. Building Thermal Model
2.4.1. Hypotheses
In this section, we develop a model of the building thermal behavior. We are interested in the real variation of the indoor air temperature and make a comparison between the results obtained from both types of roof considered.
The building surveyed in this model is composed of the walls, or the envelopes (roof, floor, and the vertical walls), and the indoor air volume, or the thermal zone. The mathematical model is formulated using the following assumptions:
- (i)
- The layers are in good contact; hence the interface resistance is negligible;
- (ii)
- There is no heat source;
- (iii)
- The variation of thermal properties is negligible;
- (iv)
- The thickness of the composite elements is small compared to the other dimensions. Hence, a one-dimensional temperature variation is assumed.
Under these assumptions, the problem reduces to the set of equations that allow us to evaluate the time dependent evolution of the indoor air temperature of the room. To show that, it is necessary to write:
- -
- the heat balance of the indoor air volume; and
- -
- the assessments of internal and external surfaces of each wall.
The coupling of the green roof model with the dynamic building thermal one is based on solving the heat balance equation of the indoor air volume with the heat and mass transfer equations through the building envelope.
2.4.2. Indoor Air Volume Heat Balance Equation
Initially, the enthalpy balance of the indoor air volume is determined. This assessment can be divided into two parts: sensible and latent. However, we are only interested in the change of the temperature; thus we will consider the sensible balance.
The sensible enthalpy variation of a thermal zone i is equal to the sum of the incoming flow.
2.4.3. Walls Thermal Balance Equations
As illustrated in Figure 5, the section of a composite wall consists of a number of layers with different thicknesses and physical properties. The outside surface is exposed to solar radiation, convection heat transfer and radiation exchange with the outside environment. The inside surface is subject to combined convection and radiation heat transfers.
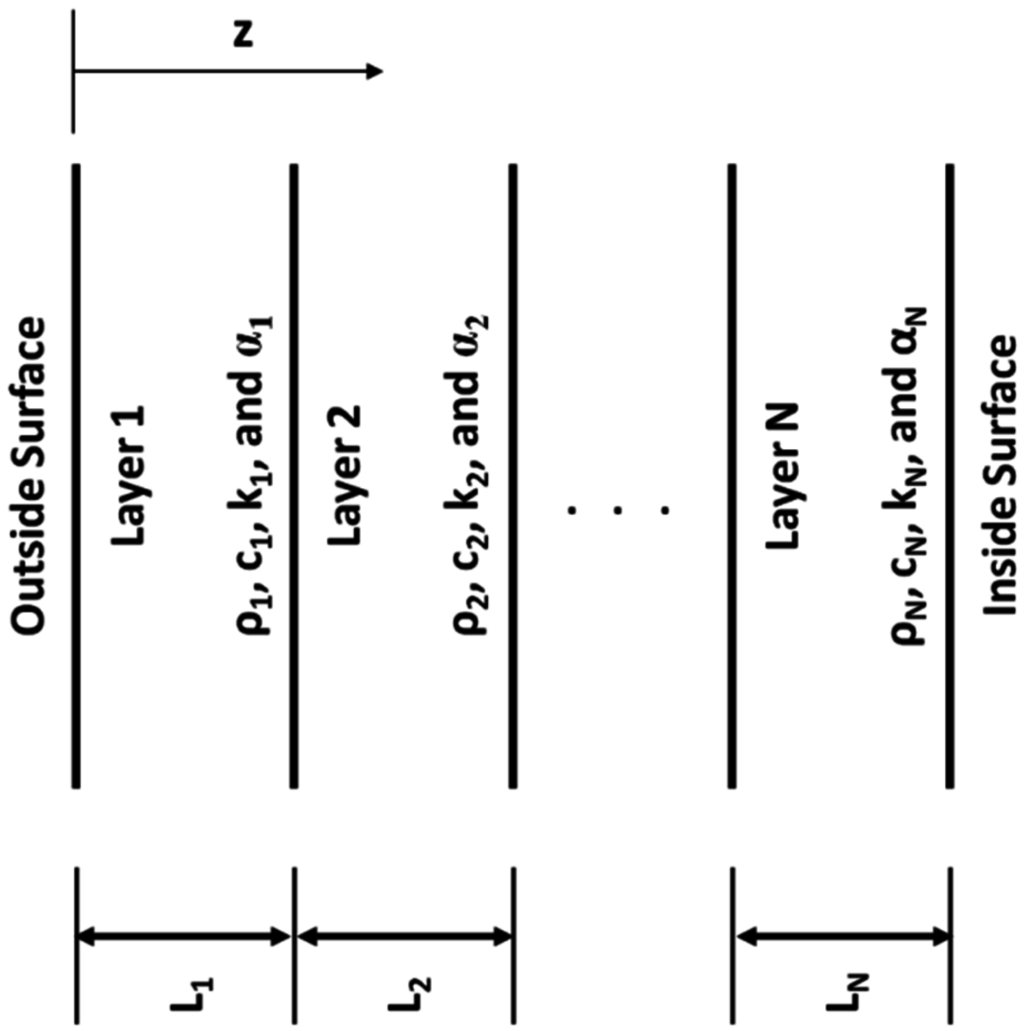
Figure 5.
Schematic showing a typical composite walls structure.
The walls were divided in several nodes classified in three types such as: the surface (inner and outer) nodes, the internal nodes and the interface nodes (between the layers).
The temperatures of the internal nodes are governed by the following law of conduction:
For the surface nodes, temperatures will be governed by the relations describing the boundary conditions on the outside and inside surfaces of the considered wall:
- (i)
- Boundary conditions at the inside surface i (x = 0):
- To simplify the model (avoiding the factor form calculation), we will not consider the exchange of long wave radiation (GLO) between the inside surfaces of the local. Thus, we have the following relation:
- The inside-surface heat transfer coefficient hCI,i is expressed as a function of the inclination pi (rd) of the wall [34]:
- (ii)
- Boundary conditions at the outside surface (x = L):
- The outside-surface heat transfer coefficient hCE,i is expressed as a function of wind speed v (m.s−1) [24]
- The expressions of the radiation exchanges are given by:with
2.5. Numerical Solutions
The solution of the present nonlinear problem is obtained by the finite-difference method using the implicit formulation. A Matlab [35] computing code was developed to solve the proposed model equations.
To solve the equations of heat balance of the canopy and the substrate surface, we need to linearize the terms of power 4. According to Deardorff [36], we can write for Tp (still valid for Tg), at iterations n:
The other nonlinear terms are linearized by using their Taylor expansion in the vicinity of their value in the previous time step.
The set of the finite-difference equations can be expressed as follows:
It is solved iteratively by using backslash operator in Matlab:
The convergence is achieved when the difference between the new and old values is smaller than a given tolerance. The solution is carried through a number of cycles until a periodic steady state is achieved.
3. Case Study: Building Located in Antananarivo
3.1. Roof and Wall Structure and Thermal Properties
Simulation was run by considering a cubic room of side length 3 m (Figure 6). We have two windows with dimensions 1 m × 1 m. They are made of glass with 0.01 m of thickness and centered on the west and east vertical walls.
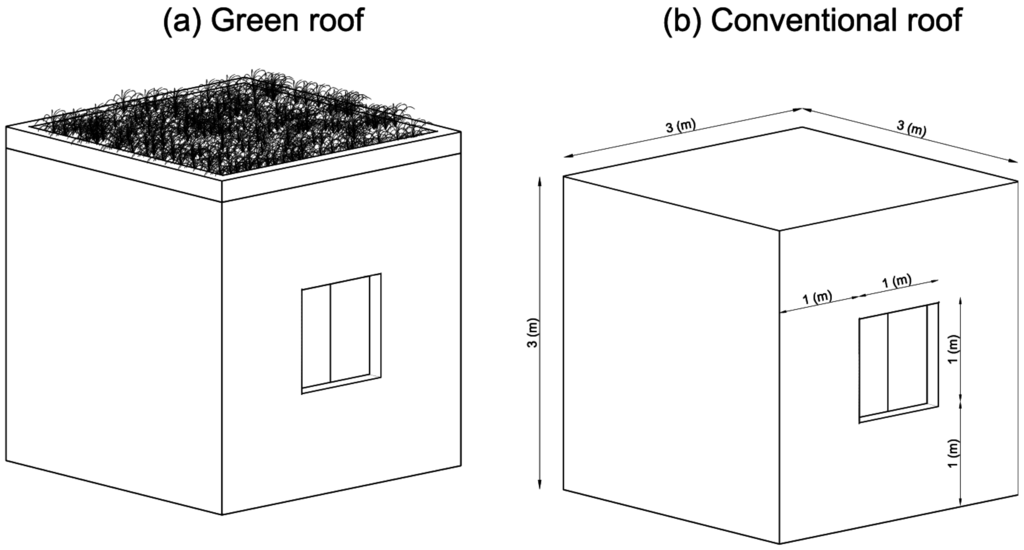
Figure 6.
Sketch of studied building: (a) green roof and (b) conventional roof.
Values of the structural and thermal properties of the materials initially used are listed in Table 1.

Table 1.
Structure and thermal properties of the building materials.
| Canopy | Substrate | Drain | Support (concrete) | Walls and floor |
|---|---|---|---|---|
| LAI = 3 | ρg = 1250 kg·m−3 | ρd = 1150 kg·m−3 | ρ = 2243 kg·m−3 | Concrete layer |
| σf = 80% | wg = 40% | Ld = 0.04 m | cp = 920 J·kg−1·K−1 | ρ = 2243 kg·m−3 |
| df = 0.001 m | Lg = 0.08 m | λ = 1.73 W·m−1·K−1 | cp = 920 J·kg−1·K−1 | |
| f =1.1 | L = 0.20 m | λ = 1.73 W·m−1·K−1 | ||
| k1 = 0.8 | L = 0.15 m | |||
| ρ∞ = 0.2 | Insulating layer | |||
| τ1 = 0.2 | ρ = 300 kg·m−3 | |||
| Lc = 0.1 m | cp = 837 J·kg−1·K−1 | |||
| λ = 0.08 W·m−1·K−1 | ||||
| L = 0.04 m |
3.2. Weather Data
The weather data in 2007 of Antananarivo, the capital city of Madagascar, which were provided by the public managed weather station of Antananarivo, were used for simulations. The months of July and March are chosen to represent, respectively, the typical winter and summer climate conditions. For the winter season, the day with the minimum temperature (25 July) and the day with the maximum solar radiation (20 July) are considered. For the summer season, the day with maximum temperature is considered (16 March).
The ambient temperature (Text), relative humidity (hr), wind speed (u), beam and diffuse global radiations (Rdirh and Rdifh, respectively), and the sky vault temperature (Tsky), related to the city of Antananarivo are the weather data inputs of the model.
We mainly focus on the results that highlight and compare the thermal performance of the green roofs. The heating set-point temperature is equal to 19 °C for the winter period. For the summer period, two cases are presented for the cooling demand, such as without cooling and with cooling, where the set-point temperature is equal to 28 °C.
For both conventional and green roofs we compare the following parameters:
- -
- top face temperature of the roof support Tst;
- -
- indoor air temperature Tin; and
- -
- energy demand.
This work shows the sensitivity of the variation of the indoor air temperature with respect to the following parameters: the leaf area index (LAI), the vegetation coverage ratio (σf), and the substrate thickness (Lg).
4. Results and Discussion
The main simulation results are presented in the following.
4.1. Comparison between Green and Conventional Roof Results
Figure 7 shows the variation of the temperature at the top face of the support of both conventional (Tst*) and green (Tst) roofs during three typical days in Antananarivo. The range of variation of Tst is lower than that of Tst* during each day. Particularly, in the sunny winter, a large fluctuation amplitude (FA) of Tst* is observed; in that day, Tst* varies between 9 °C and 41 °C (that is FA = 32 °C), but Tst remains between 19 °C and 23 °C (that is FA = 4 °C). The fluctuation amplitude of this temperature is reduced by 28 °C due to the green roof. So, green roofs protect the roof structure from extreme temperature and large temperature fluctuations.
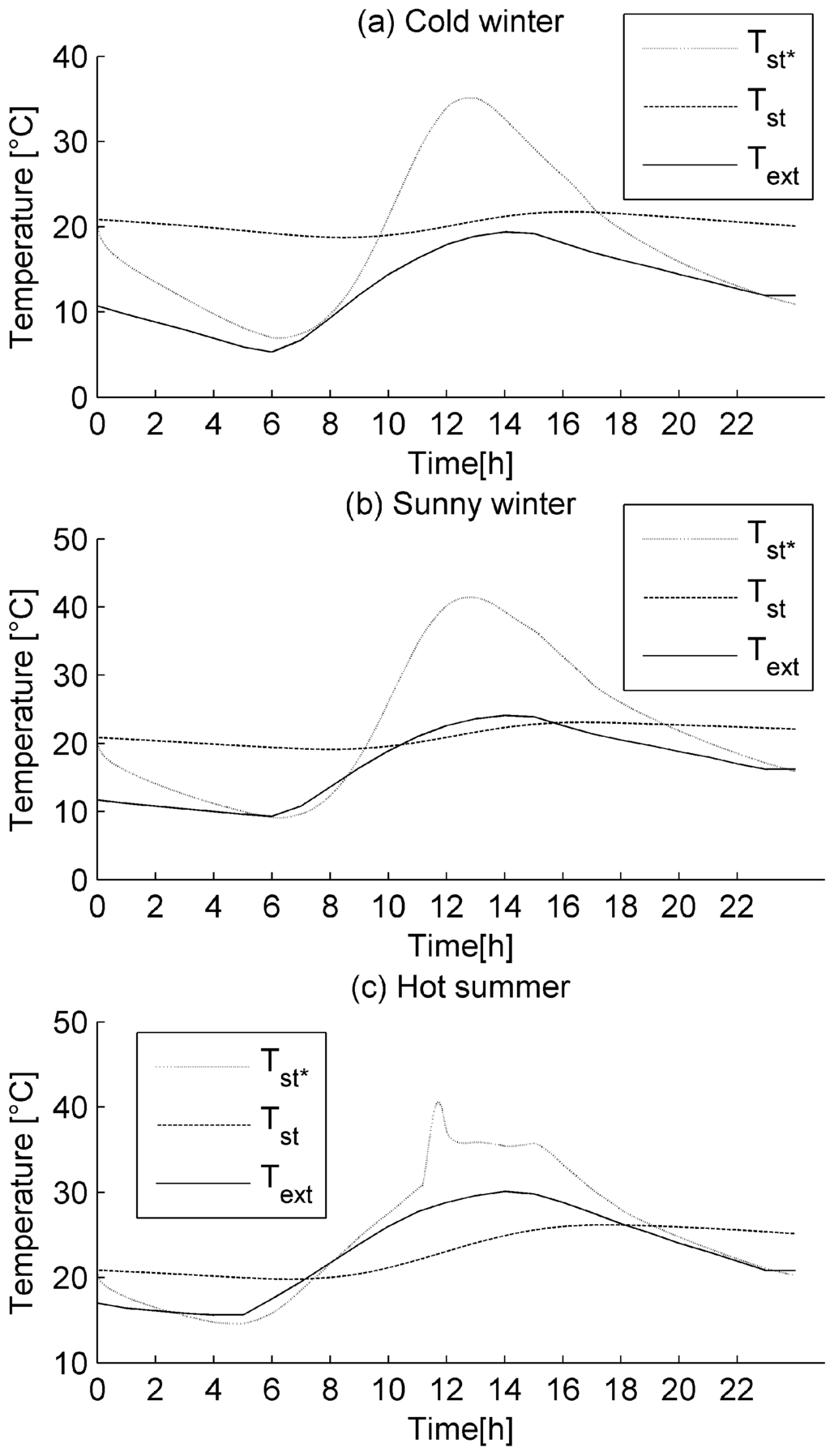
Figure 7.
Temperature at the top face support of both conventional (Tst*) and green roofs (Tst) during three typical days in Antananarivo: (a) cold winter; (b) sunny winter; and (c) hot summer.
The variation of the indoor air temperature of the chosen house with both conventional (Tin*) and green roofs (Tin) is presented in Figure 8 in which can be seen two horizontal lines denoted by SPC and SPH representing 28 °C and 19 °C, respectively. These lines delimit the thermal comfort zone. The fluctuation amplitude of the indoor air temperature is clearly lower for the case of the green roof during each day. Indeed, the green roof decreases heat loss in the building through the roof during the night. It prevents the building from heat gain through the roof during the day. During winter days, before noon, the indoor air temperature curve is largely outside the thermal comfort zone for the conventional roof. Particularly, during the sunny winter day, the thermal comfort duration is longer for the green roof. During the hot summer day, the indoor air temperature is completely within the thermal comfort zone for the green roof. This suggests that the green roof plays a role in the building thermal comfort during both winter and summer days in Antananarivo.
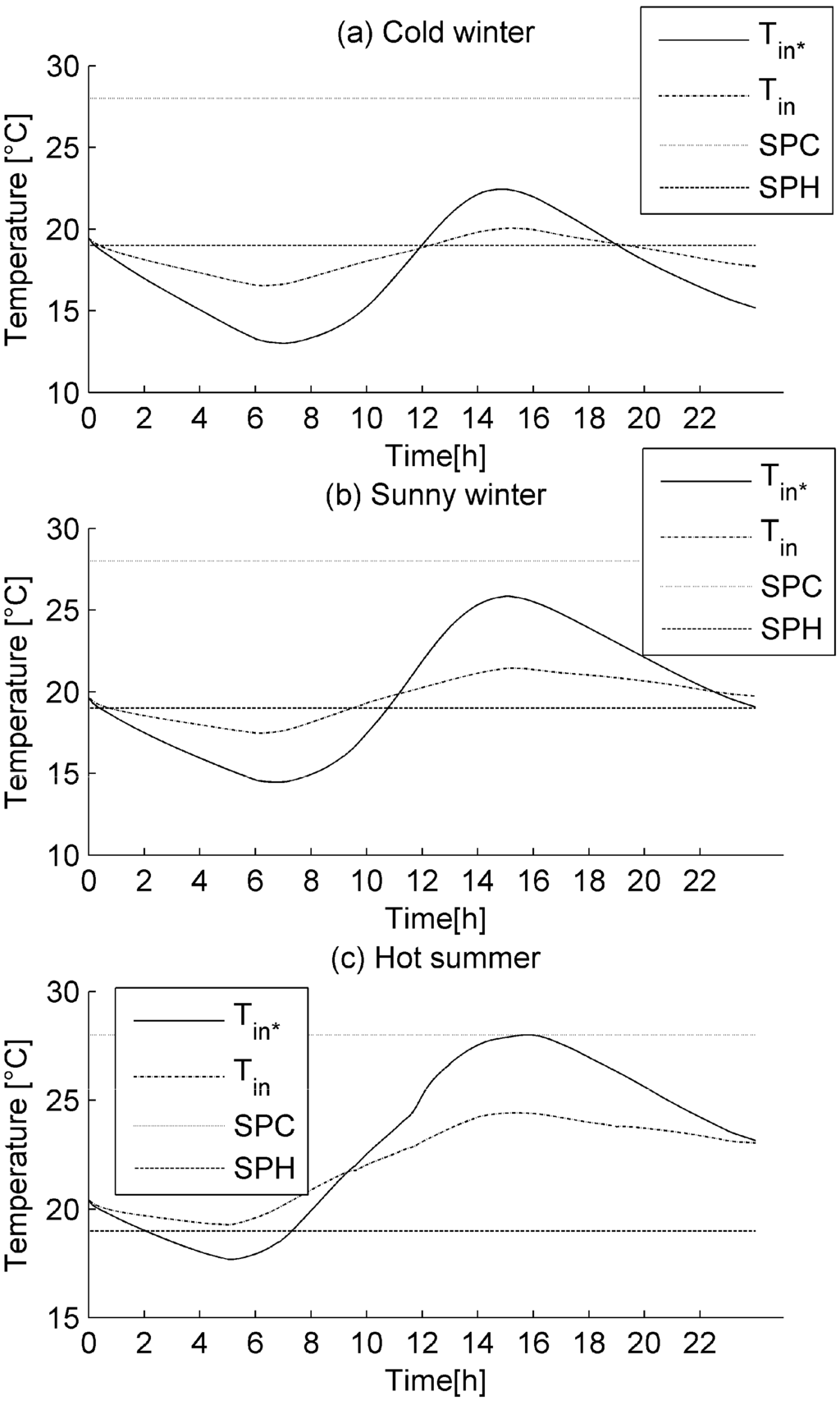
Figure 8.
Variation of the Indoor air temperatures observed for both conventional (Tin*) and green roofs (Tin) during three typical days in Antananarivo: (a) cold winter; (b) sunny winter; and (c) hot summer.
The indoor air conditions and the underneath room energy demand are directly related. We need energy to maintain the indoor air temperature within the thermal comfort zone. The comparison between the minimum energy required by the building with both conventional roof (CR) and green roof (GR) is shown in Figure 9. During each day, the energy demand is slightly lower for the green roof. Particularly, in the hot summer, there is no energy required by its passive effect. Therefore green roof effectively improves the building energy performance during summer and winter periods in Antananarivo.
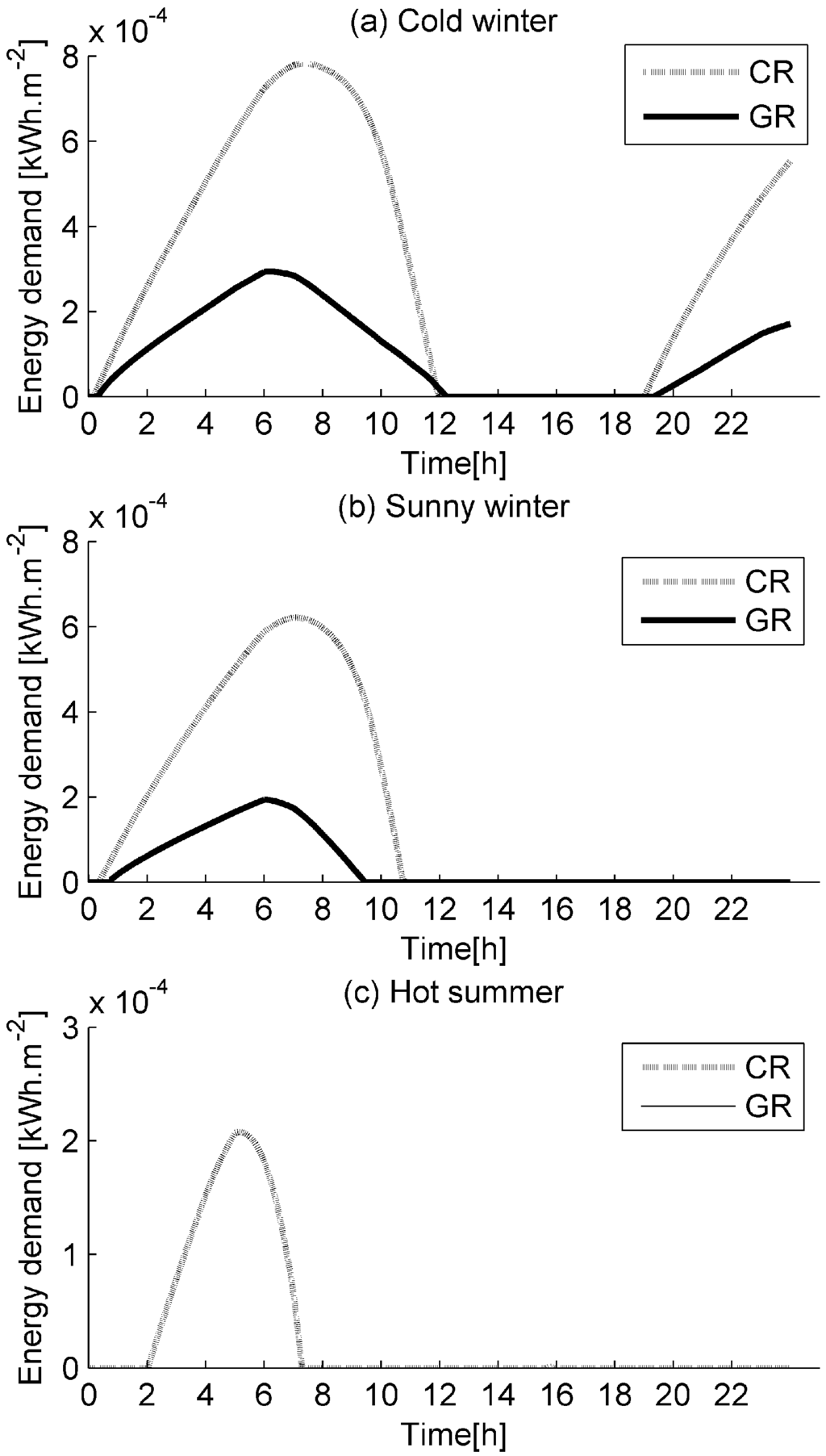
Figure 9.
Minimum energy demand for conventional (CR) and green (GR) roofs in Antananarivo: (a) cold winter; (b) sunny winter; and (c) hot summer.
4.2. Influences of Parameters on the Indoor Air Temperature of the Building
4.2.1. Influence of the Leaf Area Index (LAI)
The energy demand was estimated for different values of leaf area index (LAI), which are 1, 3 and 5 (Figure 10) and different values of the vegetation coverage ratio (σf) (Figure 11). These two figures show that increasing the LAI or σf reduces the maximum indoor air temperature due to solar shading and evapotranspiration by the foliage. The fact that these two parameters depend on the type of the chosen plants helps decrease the high temperature during summer day and thus the cooling demand. Therefore, the choice of plants to grow on the roof can help to significantly improve the thermal comfort and the energy performance of the building during summer day.
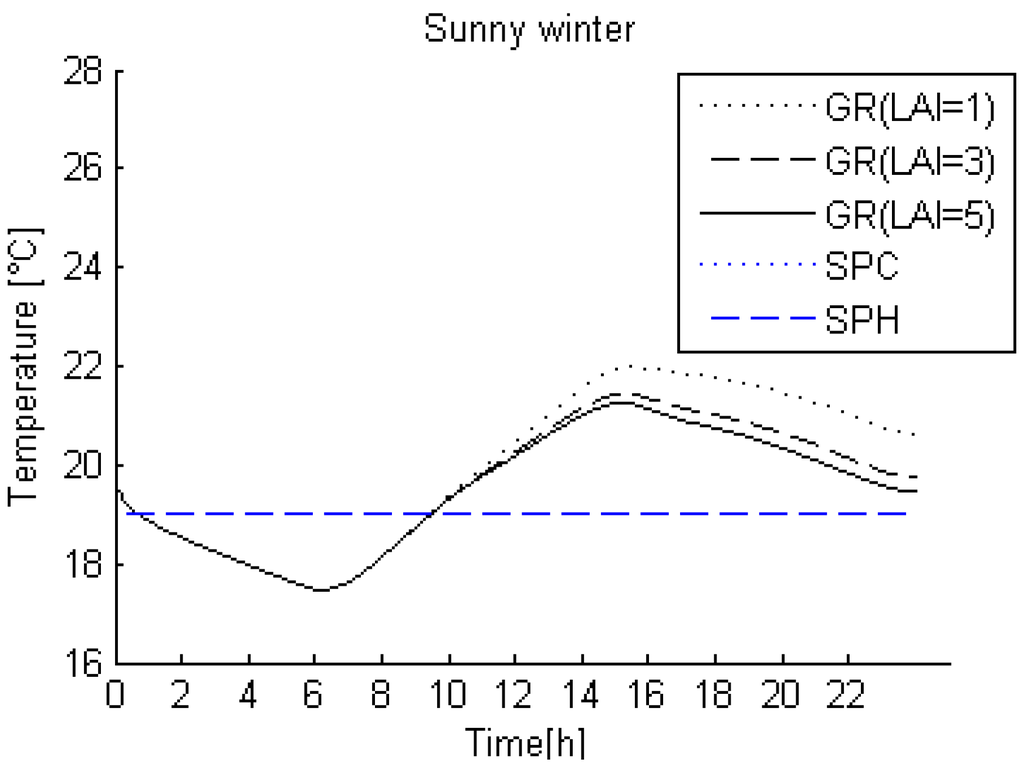
Figure 10.
Variation of the indoor air temperature (Tin) with different values of leaf area index (LAI).

Figure 11.
Variation of the Tin with different values of vegetation coverage ratio (σf).
4.2.2. Influence of the Substrate Thickness (Lg)
The indoor air temperature under sunny winter conditions was evaluated for different substrate depths (Figure 12). The additional substrate thickness reduces the maximum and minimum indoor air temperatures due to additional thermal resistance of the green roof. However, for thicknesses greater than 4 cm, the effect of the additional substrate on the indoor air temperature is negligible.
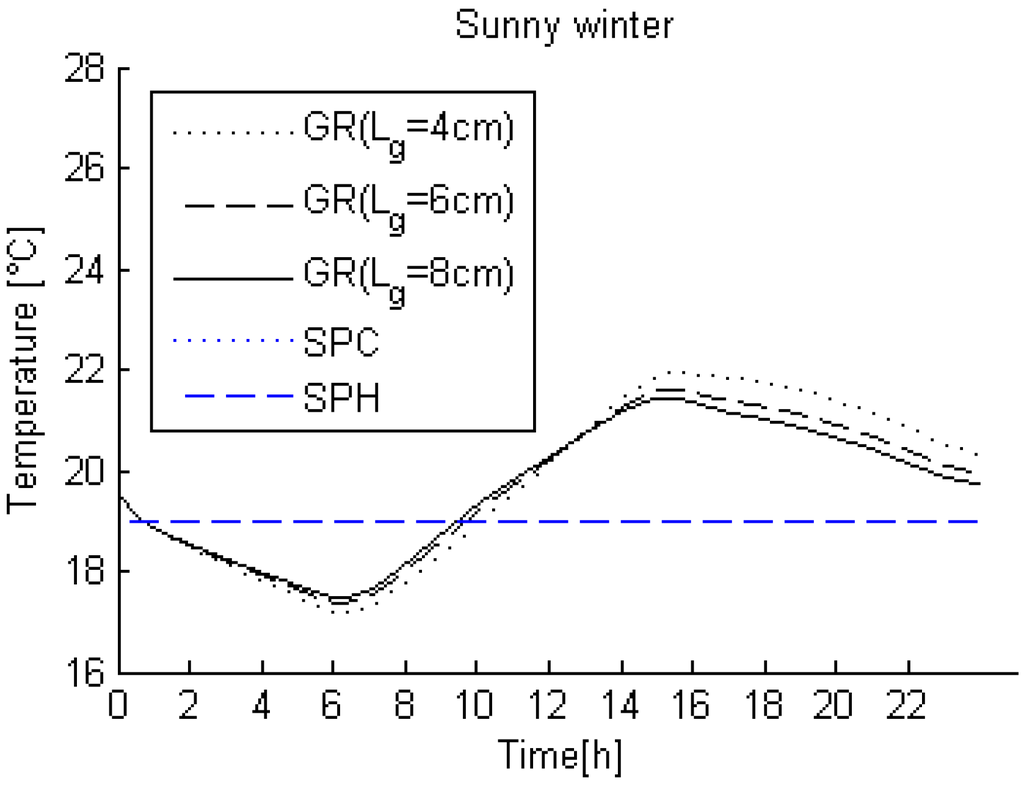
Figure 12.
Variation of the Tin with different values of the substrate thickness (Lg).
4.3. Results of the Global Sensitivity Analysis of the Surveyed Model
The energy demand in the room underneath the roof is our observed model output. Using a global sensitivity analysis tool called GoSAT [37], 2457 simulations have been performed for each of the following two cases: an insulated green roofed building (45 model parameters), and the case of non-insulated green roofed building (39 model parameters). It should be noted that these simulations were run without considering any specific weather data.
To interpret the horizontal bar charts presented in the following subsections, it is worth noting that a positive effect of any parameter on the model output parameter means that an increase in the value of this parameter would also increase that of the model output parameter. The opposite would occur in the case of a negative effect.
4.3.1. Global Sensitivity Analysis of an Insulated Green Roofed Building Model
Figure 13 shows the decreasing order of dominance of the most influential parameters of the insulated green roofed building model for diurnal period. As can be seen from this figure, only 12 of the 45 initially considered model parameters have significant influence on the energy demand in the room beneath the green roof, namely: (1) the outdoor air temperature (K); (2) the density of the insulating layer (kg·m−3); (3) the shading coefficient of glazing Sc ( ); (4) the diffuse solar radiation received per unit area of horizontal surface (W·m−2); (5) the floor insulating layer thickness Lfloorc2 (m); (6) the thermal conductivity of the insulating layer (W·m−1·K−1); (7) the wind speed u (m·s−1); (8) the sky vault temperature (K); (9) the beam solar radiation received per unit area of horizontal surface (W·m−2); (10) the heat capacity of the insulating layer (J·kg−1·K−1); (11) the side (m) of the square room; and (12) is the height (m) of the room. The impact of green roof is only indicated by the fact that the influence of diffuse radiation is higher than that of the beam radiation , as it forms a shading rooftop layer.
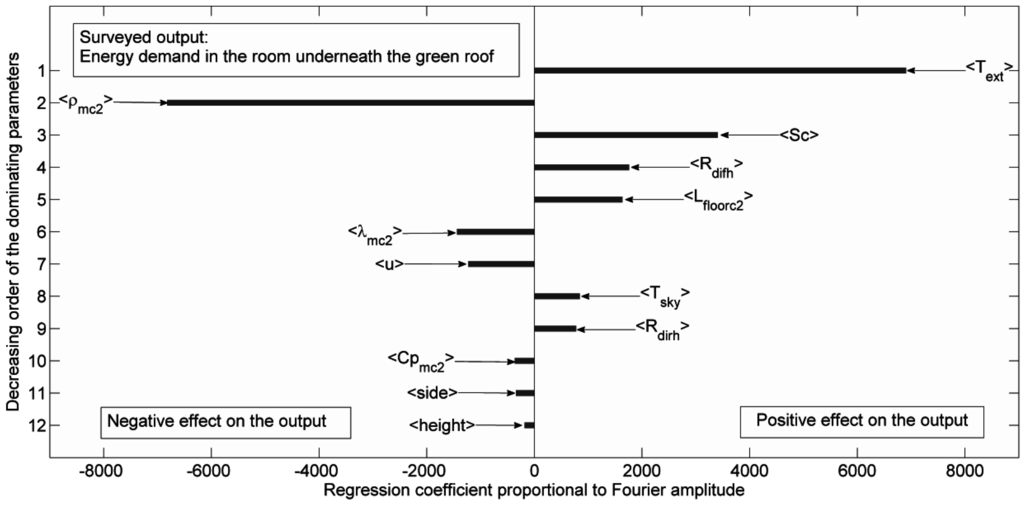
Figure 13.
Decreasing order of dominance of the most influential parameters of the insulated green roofed building model for diurnal period.
Apart from the weather parameters, such as , , u, and Tsky, which cannot be controlled, it is mainly the building envelope characteristics that prevail, namely the room size (side and height) and the physical properties of the insulating material (, , , and Lfloorc2) as well as the shading coefficient of glazing Sc. Here, it is worth pointing out that the green roof factors are not among the dominant parameters. Therefore, one can conclude that the green roofs have less impact in insulated buildings.
Furthermore, according to the meaning of the sign (positive or negative) of any parameter effects, the energy demand can be decreased either by using glazing with lower shading coefficient, choosing insulating material with higher density, heat capacity and thermal conductivity, and enlarging the volume of the considered room. In addition, heat conduction through the floor also plays a significant role in reducing the energy demand. It would be beneficial to diminish the thickness of the floor-insulating layer. If the considered room volume should be increased, it would be more advantageous to increase its side rather than increasing its height. However, the apparent inconsistency with the choice of “an insulating material with a higher thermal conductivity” requires the need to carry out an ulterior, multi-objective, optimization study and carefully choose the type of materials to use.
4.3.2. Global Sensitivity Analysis of a Non-Insulated Green Roofed Building
As can be seen from Figure 14, which shows the decreasing order of dominance of the most influential parameters of the non-insulated green roofed building model for diurnal period, green roof impacts are noticeable. The most influential parameter of the model on the energy demand in the underneath room is the vegetation coverage ratio whose positive effect on our model output means that energy demand is mainly due to heating. Indeed, an increase of the value of reduces the maximum indoor air temperature (as seen in Section 4.2.1.) and therefore increases the energy demand. The second most influential parameter is the growth substrate thickness , which is a green roof parameter. The shading coefficient of glazing Sc only ranks third in terms of importance. Then two other green roof parameters, the leaf area index LAI and the canopy thickness , are, respectively, in the fourth and fifth ranks in terms of degree of influence on the model output. Hence, these four green roof parameters prevail over weather characteristics, such as the diffuse solar radiation , the outdoor air temperature , and the wind speed , whose influences on our model output do not appear as main effects, but rather as interaction effects of order one (Figure 15). It can be noticed that the beam solar radiation and the sky vault temperature are completely missing from Figure 14 and Figure 15.
The results suggest that green roofs have significant impacts in non-insulated buildings. In order to get better energy performances of non-insulated green roofed buildings using a model that is very sensitive to the green roof characteristics, rooftop greening design/construction should be based on the results of multi-objective optimization studies that aim at determining the optimal values of the controllable influential parameters identified in our investigation.
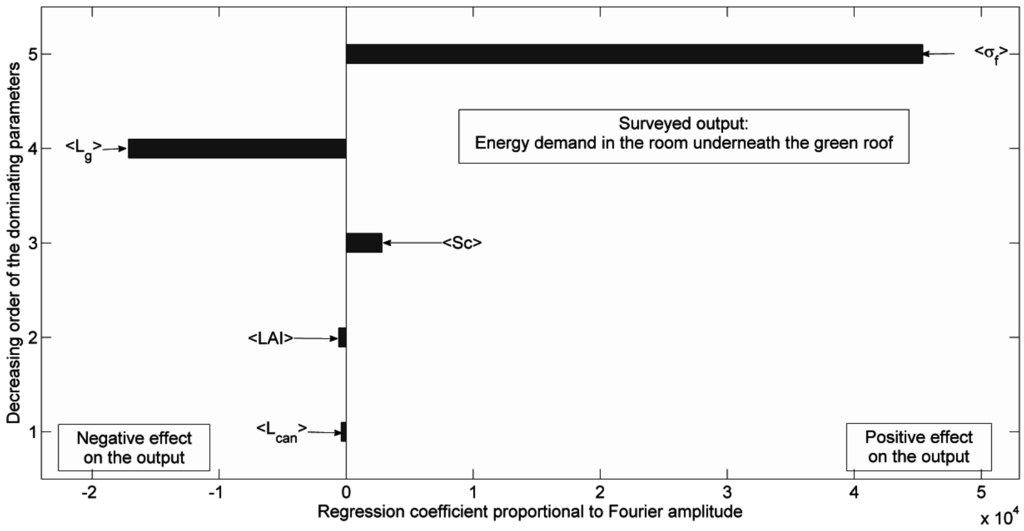
Figure 14.
Decreasing order of dominance of the most influential parameters of the non-insulated green roofed building model for diurnal period.
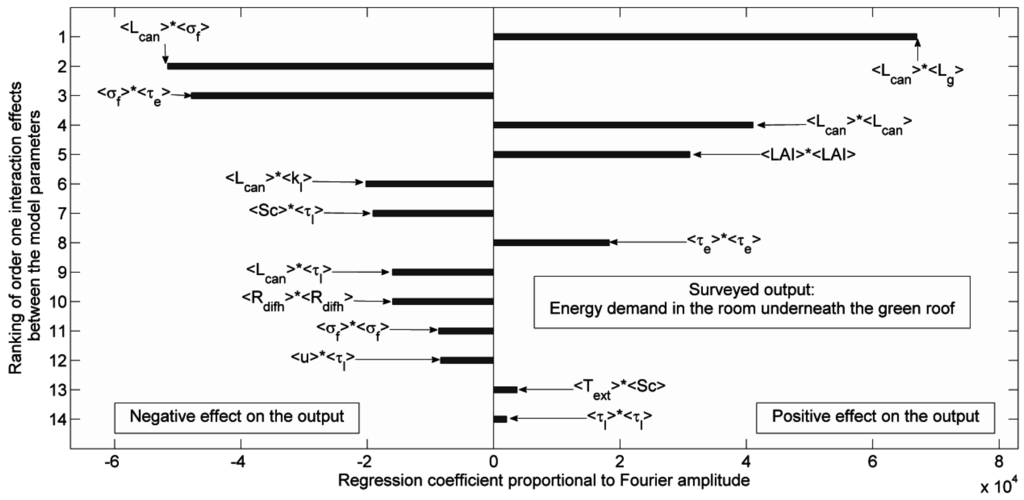
Figure 15.
Order one interaction effects of parameters of the non-insulated green roofed building model for diurnal period.
5. Conclusions
Although the large island of Madagascar is crossed by the Tropic of Capricorn, the capital Antananarivo has rather a cool and humid microclimate. Indeed, while comparing CDD and HDD of this city region, energy needed for heating buildings is much higher than that required for cooling.
Coupling a hygrothermal green roof model with a thermal model of building has been developed to dynamically evaluate the impact of the green roof on energy performance and thermal comfort of the building. Our main conclusion is that, considering energy savings and thermal comfort during summer and winter days, green roofs are suitable. The fluctuation range of the top face temperature of the roof support is reduced by 28 °C under Antananarivo climate conditions with the use of a green roof. The impact of the choice of plants with greater values of LAI and σf significantly improves the thermal comfort and the energy performance of the building during summer days. A moderate additional substrate thickness can help decrease the heating demand.
No specific weather data was considered when we carried out the global sensitivity analysis of the proposed green roofed building model. Such sensitivity analysis allowed us to identify the most influential model parameters on the energy demand in the room underneath. In addition, the results of this sensitivity analysis depend on whether the building is insulated. Green roof has almost a negligible thermal impact in insulated buildings, whereas in the case of non-insulated ones their impacts are significant. These results are in good agreement with those obtained by Jaffal et al. [38] and Kotsiris et al. [39].
It is recommended that future studies should include coupling the green roof with green wall while taking into account standards, such as the utilization of insulating layers in building envelope. The output should also be expanded to environmental aspects but not limited to indoor thermal comfort only. It would also be interesting to carry out a multi-objective optimization study to determine the optimal values of the humanly controllable influential parameters identified in this analysis. In situ building experimental validation of the proposed model and application of rooftop greening to larger and taller buildings would be an interesting follow-up project.
Author Contributions
The co-authors contributed actively to the discussion of this research and in reviewing the article.
Nomenclature
| A | coefficient matrix |
| Ar | watering (kg·m−2·s−1) |
| B | column vector containing the right sides of equations |
| Cair | air specific heat (J·kg−1·K−1) |
| cj | specific heat of the wall layer j (j = 1, 2, …, N) (J·kg−1·K−1) |
| cp | specific heat (J·kg−1·K−1) |
| CDD | cooling degree days (°C·month−1) |
| CR | conventional roof |
| (ρcp)i | specific heat capacity of the subcomponent i (J·m−3·K−1) |
| df | average leaves thickness (m) |
| Dr | drainage (kg·m−2·s−1) |
| ECLO,i | interior face shortwave radiation intensity after multiple reflections (W·m−2) |
| ECLOE,i | exterior face shortwave radiation intensity after multiple reflections (W·m−2) |
| (ei-ea) | partial vapor pressure deficit between the subcomponent i and the canopy air (Pa) |
| FA | temperature fluctuation amplitude (°C) |
| GR | green roof |
| hCIj | convective exchange coefficient of the inside face of the element j (W·m−2·K−1) |
| HDD | cooling degree days (°C·month−1) |
| hg | convective coefficient between the soil top face and the canopy air (W·m−2·K−1) |
| hin | convective coefficient between the support bottom face and the indoor air (W·m−2·K−1) |
| hout | convective coefficient between the support top face and the outdoor air (W·m−2·K−1) |
| kj | thermal conductivity of the wall layer j (j = 1, 2, …, N) |
| kl | foliage extinction coefficient for longwave radiation (-) |
| L | building material thickness (m) |
| LAI | leaf area index ( ) |
| Li | thickness of the subcomponent i (m) |
| N | total number of zone and (N+1) denoting the exterior |
| NTP(i) | total number of interior walls at zone i |
| Pc | convective power dissipated at the zone i by the internal thermal loads (W·m−2) |
| pi | inclination of the wall i (rd) |
| Pr | precipitation (kg·m−2·s−1) |
| Qmass(i,n) | mass flow from the zone i to the zone n |
| Rdirh | beam solar radiation received per unit area of horizontal surface (W·m−2) |
| Rdifh | diffuse solar radiation received per unit area of horizontal surface (W·m−2) |
| re | canopy external resistance (s·m−1) |
| rs | bulk stomatal resistance(s·m−1) |
| Sc | shading coefficient of glazing (-) |
| Sj | surface of the element j (roof, walls or floor) (m2) |
| t | time variable (s) |
| Text | ambient air temperature (K) |
| Ti | temperature of the subcomponent i (K) |
| T(i) | temperatures of the air in the zone i (K) |
| Tin | nude indoor air temperature of the building with green roof (K) |
| Tin* | nude indoor air temperature of the building with conventional roof (K) |
| Tin(i) | indoor air temperature or the temperature of the zone i (K) |
| T(n) | temperatures of the air in the zone n (K) |
| Tsb* | nude support bottom face temperature (K) |
| TSI,j | inside face temperature of the element j (roof, walls or floor) (K) |
| Tst* | nude support top face temperature (K) |
| u | wind speed (m·s−1) |
| Vair(i) | indoor air volume of the zone i (m3) |
| wg | volumetric moisture content of the green roof soil or the growing substrate (m3·m−3) |
| X | column vector of the unknown variables to be determined |
| z | spatial variable (m) |
Greek letters
| αCLOE,i | shortwave radiation absorptivity of the outside face (-) |
| αCLO,i | shortwave radiation absorptivity of the inside face (-) |
| αGLOE,i | longwave radiation absorptivity of the outside face (-) |
| αj | absorptivity of the wall layer j (j = 1, 2, …, N) |
| γ | thermodynamic psychrometric constant (Pa·K−1) |
| εi | emissivity of the subcomponent i (-) |
| εst | emissivity of the support top face (-) |
| λ | thermal conductivity (W·m−1·K−1) |
| λi | thermal conductivity of the subcomponent i (i = p,g,s) (W·m−1·K−1) |
| λSE,i | thermal conductivity of the nearest layer of the outside surface (W·m−1·K−1) |
| λSI,i | thermal conductivity of the nearest layer of the inside surface (W·m−1·K−1) |
| Λ(Ti) | latent heat of vaporization at the temperature Ti (J·kg−1) |
| ρ | density (kg·m−3) |
| ρa | air density (kg·m−3) |
| ρg | reflectance of the soil (-) |
| ρi | density of subcomponent i (kg·m−3) |
| ρ∞ | reflectance of a dense canopy (-) |
| τe | air change rates within the canopy (s−1) |
| τl | transmittance of the leaf tissue (-) |
| τs | canopy shortwave transmittance (-) |
| σ | Stefan-Boltzmann Constant (5.67 × 10−8 W·m−2·K−4) |
| σf | vegetation coverage ratio (%) |
| φCLOE,i | shortwave radiation exchanged with the outside face (W·m−2) |
| φCLOI,i | shortwave radiation exchanged with the inside face (W·m−2) |
| φGLOE,i | longwave radiation exchanged with the outside face (W·m−2) |
| φs | solar shortwave irradiance at the top of the canopy (W·m−2) |
Subscripts
| a | canopy air |
| c, can | canopy |
| d | drain (dt for its top face) |
| g | green roof soil (gt for its top face) |
| in | indoor air |
| i | index related to the green roof subcomponents such that i = g, p, s, d |
| j | index of layers such that j = 1, 2, …, N |
| m | outdoor ambient air |
| mc2 | insulating layer material |
| p | canopy leaves |
| s | support (sb for its bottom face and st for its top face) |
| sky | sky vault |
Conflicts of Interest
The authors declare no conflict of interest.
References
- Eisenman, T. Raising the bar on green roof design. Landsc. Archit. 2006, 96, 22–29. [Google Scholar]
- Berardi, U.; GhaffarianHoseini, A.; GhaffarianHoseini, A. State-of-the-art analysis of the environmental benefits of green roofs. Appl. Energy 2014, 115, 411–428. [Google Scholar] [CrossRef]
- Mentens, J.; Raes, D.; Hermy, M. Green roofs as a tool for solving the rainwater runoff problem in the urbanized 21st century? Landsc. Urban Plan. 2006, 77, 217–226. [Google Scholar] [CrossRef]
- Fioretti, R.; Palla, A.; Lanza, L.G.; Principi, P. Green roof energy and water related performance in the Mediterranean climate. Build. Environ. 2010, 45, 1890–1904. [Google Scholar] [CrossRef]
- Yang, J.; Yu, Q.; Gong, P. Quantifying air pollution removal by green roofs in Chicago. Atmos. Environ. 2008, 42, 7266–7273. [Google Scholar] [CrossRef]
- Li, J.F.; Wai, O.W.H.; Li, Y.S.; Zhan, J.M.; Ho, Y.A.; Li, J.; Lam, E. Effect of green roof on ambient CO2 concentration. Build. Environ. 2010, 45, 2644–2651. [Google Scholar] [CrossRef]
- Van Renterghem, T.; Botteldooren, D. In-situ measurements of sound propagating over extensive green roofs. Build. Environ. 2011, 46, 729–738. [Google Scholar]
- Schrader, S.; Böning, M. Soil formation on green roofs and its contribution to urban biodiversity with emphasis on Collembolans. Pedobiologia 2006, 50, 347–356. [Google Scholar] [CrossRef]
- Brenneisen, S. Space for urban wildlife: Designing green roofs as Habitats in Switzerland. Urban Habitat. 2006, 4, 27–36. [Google Scholar]
- Feng, C.; Meng, Q.; Zhang, Y. Theoretical and experimental analysis of the energy balance of extensive green roofs. Energy Build. 2010, 42, 959–965. [Google Scholar] [CrossRef]
- Liu, K.; Minor, J. Performance Evaluation of an Extensive Green Roof. In Proceedings of Green Rooftops for Sustainable Communities, Washington, DC, USA, 5–6 May 2005; pp. 1–11.
- Ghaffarian Hoseini, A.; Dahlan, N.D.; Berardi, U.; Ghaffarian Hoseini, A.; Makaremi, N.; Ghaffarian Hoseini, M. Sustainable energy performances of green buildings: A review of current theories, implementations and challenges. Renew. Sustain. Energy Rev. 2013, 25, 1–17. [Google Scholar] [CrossRef]
- Coutts, A.; Daly, E.; Beringer, J.; Tapper, N.J. Assessing practical measures to reduce urban heat: Green and cool roofs. Build. Environ. 2013, 70, 266–276. [Google Scholar] [CrossRef]
- Alexandri, E.; Jones, P. Temperature decreases in an urban canyon due to green walls and green roofs in diverse climates. Build. Environ. 2008, 43, 480–493. [Google Scholar] [CrossRef]
- Castleton, H.F.; Stovin, V.; Beck, S.B.M.; Davison, J.B. Green roofs; building energy savings and the potential for retrofit. Energy Build. 2010, 42, 1582–1591. [Google Scholar] [CrossRef]
- Getter, K.L.; Rowe, D.B.; Cregg, B.M. Solar radiation intensity influences extensive green roof plant communities. Urban For. Urban Green. 2009, 8, 269–281. [Google Scholar] [CrossRef]
- ROOFSOL. Building in ROOFSOL: Roof Solutions for Natural Cooling; Contract No. JOR3CT960074; Commission of the European Communities, DG XII, Science, Research and Development: Brussels, Belgium, 1998. [Google Scholar]
- Niachou, A.; Papakonstantinou, K.; Santamouris, M.; Tsangrassoulis, A.; Mihalakakou, G. Analysis of the green roof thermal properties and investigation of its energy performance. Energy Build. 2001, 33, 719–729. [Google Scholar] [CrossRef]
- Spala, A.; Bagiorgas, H.S.; Assimakopoulos, M.N.; Kalavrouziotis, J.; Matthopoulos, D.; Mihalakakou, G. On the green roof system. Selection, state of art and energy potential investigation of a system installed in an office building in Athens, Greece. Renew. Energy 2008, 33, 173–177. [Google Scholar] [CrossRef]
- Cappelli, M.; Cianfrini, C.; Corcicone, M. Effects of vegetation roof on indoor temperatures. Heat Environ. 1998, 16, 85–90. [Google Scholar]
- Del Barrio, E.P. Roof components models simplification via statistical linearization and model reduction techniques. Energy Build. 1999, 29, 259–281. [Google Scholar] [CrossRef]
- Good, W. Factors in planted roof design. Constr. Specif. 1990, 43, 132. [Google Scholar]
- Wong, N.H.; Cheong, D.K.W.; Yan, H.; Soh, J.; Ong, C.L.; Sia, A. The effect of rooftop gardens on energy consumption of a commercial building in Singapore. Energy Build. 2003, 35, 353–364. [Google Scholar] [CrossRef]
- Wong, N.H.; Chen, Y.; Ong, C.L.; Sia, A. Investigation of thermal benefits of rooftop garden in the tropical environment. Build. Environ. 2003, 38, 261–270. [Google Scholar] [CrossRef]
- Williams, N.S.G.; Rayner, J.P.; Raynor, K.J. Green roofs for a wide brown land: Opportunities and barriers for rooftop greening in Australia. Urban For. Urban Green. 2010, 9, 245–251. [Google Scholar] [CrossRef]
- La Roche, P.; Berardi, U. Comfort and energy savings with active green roofs. Energy Build. 2014, 82, 492–504. [Google Scholar] [CrossRef]
- Lazzarin, R.M.; Castellotti, F.; Busato, F. Experimental measurements and numerical modelling of a green roof. Energy Build. 2005, 37, 1260–1267. [Google Scholar] [CrossRef]
- Sailor, D.J.; Elley, T.B.; Gibson, M. Exploring the building energy impacts of greenroof design decisions—A modeling study of buildings in four distinct climates. J. Build. Phys. 2011, 35, 372–391. [Google Scholar] [CrossRef]
- Del Barrio, E.P. Analysis of the green roofs cooling potential in buildings. Energy Build. 1998, 27, 179–193. [Google Scholar] [CrossRef]
- Sailor, D.J. A green roof model for building energy simulation programs. Energy Build. 2008, 40, 1466–1478. [Google Scholar] [CrossRef]
- Alexandri, E.; Jones, P. Developing a one-dimensional heat and mass transfer algorithm for describing the effect of green roof on the built environment: Comparison with experimental results. Build. Environ. 2007, 42, 2835–2849. [Google Scholar] [CrossRef]
- Djedjig, R.; Ouldboukhitine, S.; Bélarbi, R.; Bozonnet, E. Development and validation of a coupled heat and mass transfer model for green roofs. Int. Commun. Heat Mass Transf. 2012, 39, 752–761. [Google Scholar] [CrossRef]
- Morau, D.; Rakotondramiarana, H.T.; Ranaivoarisoa, T.F.; Andriamamonjy, A.L. Thermal behavior of green roof in Reunion Island: Contribution towards a net zero building. Energy Proced. 2014, 57, 1908–1921. [Google Scholar] [CrossRef]
- Rakotondramiarana, H.T. Etude théorique du séchage thermique et de la digestion anaérobie des boues des stations d'épuration-Mise au point des dispositifs pilotes de laboratoires pour la caractérisation expérimentale liée au séchage et à la méthanisation des boues. In PhD Dissertation; University of Antananarivo: Antananarivo, Madagascar, January 2004. Available online: http://theses.recherches.gov.mg/pdfs/rakotondramiaranaherytiana_pc_doc3_04.pdf (accessed on 7 January 2015). [Google Scholar]
- Matlab R2010a. High-performance Numerical Computation and Visualization Software, The Mathworks, Inc.: Natick, MA, USA, 2010.
- Deardorff, J.W. Efficient prediction of ground surface temperature and moisture, with inclusion of a layer of vegetation. J. Geophys. Res. 1978, 83, 1889–1903. [Google Scholar] [CrossRef]
- Rakotondramiarana, H.T.; Andriamamonjy, A.L. Matlab automation algorithm for performing global sensitivity analysis of complex system models with a derived FAST method. J. Comput. Model. 2013, 3, 17–56. [Google Scholar]
- Jaffal, I.; Ouldboukhitine, S.; Belarbi, R. A comprehensive study of the impact of green roofs on building energy performance. Renew. Energy 2012, 43, 157–164. [Google Scholar] [CrossRef]
- Kotsiris, G.; Androutsopoulos, A.; Polychroni, E.; Nektarios, P.A. Dynamic U-value estimation and energy simulation for green roofs. Energy Build. 2012, 45, 240–249. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).