Analysis of Construction Process and Configuration Automatic Monitoring for the Spoke-Type Single-Layer Cable Net Structure

Abstract

As a full tension structural system, the spoke-type single-layer cable net structure has a light graceful shape and superior mechanical properties. During construction, the structure will gradually be tensioned from the flexible unstressed state to the formed state with stiffness, and the structural configuration changes greatly, making construction difficult. This study focused on the spoke-type single-layer cable net structure of the Linyi Olympic Sports Center Stadium. The structural finite element model was established in ANSYS, and the construction scheme was selected and simulated using the nonlinear dynamic finite element method (NDFEM). Most of the existing structural automatic measuring systems are suitable for measuring points with gentle deformation. However, there is the lack of a stable and reliable automatic configuration monitoring system for the construction of single-layer cable net structures. Based on the Lecia TS16 robotic total station (RTS), the configuration automatic monitoring system (CAMS) was developed to obtain the coordinate data of key nodes on the ring cable and compression ring during the construction process. The original finite element model of clamps was refined to obtain the corresponding data in ANSYS. The results indicate that the selected construction scheme has a rational mechanical response according to the finite element simulation. The radial cable force when anchoring the traction cables is smaller than or equal to that in the formed state, which proves that the construction method of anchoring in batches is safe. The results of the ANSYS simulation is basically consistent with those obtained by CAMS, proving that the simulation method is credible. CAMS has good stability and measurement accuracy and can achieve the automatic monitoring of large structural deformation. The research findings provide valuable guidance for practical construction and other similar projects.

1. Introduction

The spoke-type single-layer cable structure is similar to a bicycle wheel, consisting of inner tension rings, an outer compression ring, and radial cables [1,2]. As a full tension structural system [3,4], the spoke-type single-layer cable net structure has the characteristic of a beautiful and varied architectural appearance and can make full use of the material strength because a high-strength cable is used as the tension member. When using few compression members, this structural system can avoid structural instability problems and is known as one of the most efficient structural forms [5]. However, its structural characteristics have higher requirements not only in terms of the structural design and analysis, but also in construction forming technology.

The structure will appear to have large deformation during the construction process, which presents a strong geometric nonlinearity [6]. However, it is difficult to carry out structural form-finding. Therefore, it is significant to choose the appropriate construction scheme, an accurate analytical method of the cable structure’s construction process, and advanced construction technologies to guide the construction project [7,8,9]. The analysis of the cable structure’s construction process refers to constructing the finite element model according to the mechanical analysis method. The structural configuration and internal force under different construction conditions can be obtained to judge the feasibility of the construction scheme. Many methods have also been proposed for the form-finding problem during the construction process such as the dynamic relaxation method, force density method, and nonlinear finite element method [7,10,11,12,13,14,15]. Both Yu et al. [16] and Zhongling et al. [17] respectively used the dynamic relaxation method to analyze the construction process of the cable dome. Guerra Riaño and Várkonyi et al. [18], Li et al. [19], and Tang et al. [20] applied the force density method to carry out form-finding of cable structure. Based on morphological analysis theory, Luo and Xue et al. [21,22] used the nonlinear finite element method to determine the initial geometric configuration of the cable dome structure in construction. Ma et al. [23] proposed unbalanced force iteration, which removed the unbalanced forces using the equilibrium and stiffness equations and was used in the analysis of cable domes. Luo [24] came up with the nonlinear dynamic finite element method (NDFEM) to determine the energy balance state of the cable-rod system. The NDFEM makes the dynamic equilibrium state gradually converge to the static equilibrium by updating the finite element model iteratively. The analytical efficiency and accuracy of NDFEM have been proven by a large number of engineering construction studies [24,25,26,27,28], and was applied in the target engineering in this paper.

In order to ensure the safety of the cable net structure during the construction and achievement of the intended formed geometry, configuration monitoring can be used to obtain the real-time data of the key point coordinates to determine whether the deformation is moderate or not [29]. These measured values from configuration monitoring can be compared and analyzed with theoretical values from the finite element model of the construction process to judge the structural state and ensure the safety and stability. Formerly, manual measurement methods were usually used to obtain the key point coordinates of the cable structure during construction. However, there are many deficiencies such as not being in real-time, low efficiency, and large errors though manual measurement [30]. Therefore, if a robotic total station (RTS) is developed to build a set of automatic configuration monitoring systems that can capture, save, verify, and output the real-time data with acceptable accuracy, the construction efficiency will be significantly improved [31]. The robotic total station (RTS), which is also called a measuring robot, is a high-performance measurement platform integrating target recognition, target tracking, automatic aligning, automatic measurement, and data recording [31,32]. It can use fewer human resources to gain relatively accurate measurement data, which can help engineering technicians grasp the situation of the structural configuration and guide the construction. Based on a Lecia Nova TM50 robotic total station and the polar coordinate method, Zhou et al. [33] monitored the deformation of two dams continuously, which showed a satisfactory accuracy. Based on the TCA2003 surveying robot, Yao et al. [34] developed a landslide deformation monitoring system to monitor the landside deformation of Fuchunjinag Dam, which could realize automatic multiple observations and the generation of field data sheets. Based on a RTS, Stathis C. Stiros et al. [35] monitored the displacement characteristics including pattern, amplitude, and frequency of Gorgopotamos Bridge, which showed that the RTS is appropriate for monitoring stiff structures accurately under small deformation. Luo et al. [36] measured the tunnel displacement by a total station with the 3D coordinate measurement and the remote distance measurement that demonstrated excellent performance, especially in the tunnels with weak surrounding rock. RTSs have been applied in the construction of tunnels, dams, bridges foundation pits, and other fields. However, the automatic measuring of the above RTSs are only appropriate for fixed measuring points; once the measuring point moves a large distance, robot cannot easily find the target object.

The object engineering of this paper was the Linyi Olympic Sport Center Stadium, which has a spoke-type single-layer cable net roof. During the construction process, this structure will appear as a large deformation at the early stage of construction, and its internal force will change drastically at the late stage of development. Therefore, it is difficult to simulate its construction process accurately. Furthermore, the automatic monitoring system above cannot satisfy the requirement of the construction configuration monitoring for this roof structure. In order to ensure safety during its construction, it is necessary to apply the appropriate RTS to establish a set of automatic monitoring systems, which can be used in the situation of large deformation.

In this paper, a spoke-type single-layer cable net of the target engineering was modeled in the finite element software ANSYS 2019R1. The nonlinear dynamic finite element method (NDFEM) was applied to analyze the process of the selected construction scheme and verify its rationality. The configuration automatic monitoring system (CAMS) was established on the Visual Studio 2022 platform to obtain the measured configuration response, which was compared with the simulated theoretical responses. The results show that the measured configuration response was close to the simulated theoretical ones under each construction condition. It was also proven that the CAMS is effective, while the construction process is safe and reliable.

2. Engineering Background

The roof of the Linyi Olympic Sport Center Stadium is a spoke-type single-layer cable net structure (Figure 1 and Figure 2) that is saddle shaped. Its plane is approximately circular. The central opening is 146.2 m wide in the long axis direction, 171.2 m long in the short axis direction, and the overhanging length of the membrane surface is about 50 m.

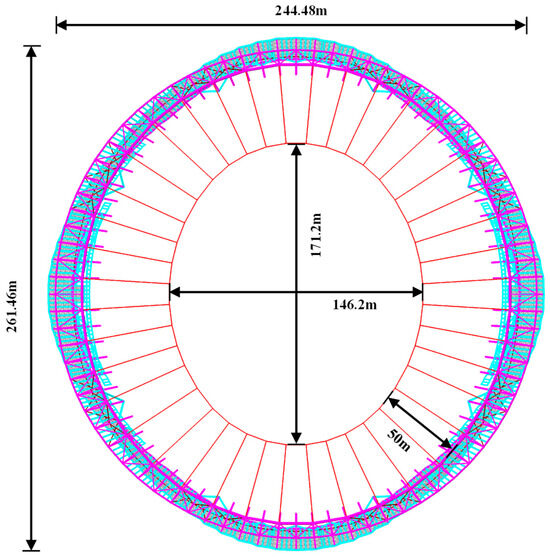
Figure 1. Plan diagram of the roof of the Linyi Olympic Sport Center Stadium.

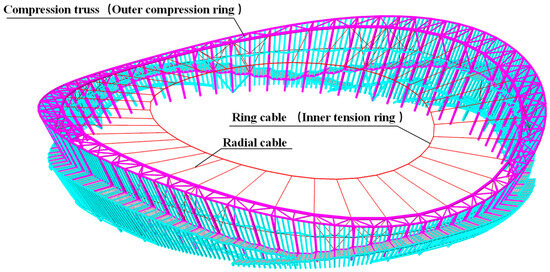
Figure 2. Spoke-type single-layer cable net structure of the Linyi Olympic Sport Center Stadium.

The cable net structure consists of 40 radial cables, each of which are double cables. An outer compression truss is used as the support member of the roof and the outer compression ring of the cable net. The inner tension ring is composed of 10 ring cables, and the diagram of the cables and cable clamp is shown in Figure 3. A Galfan full lock coil strand cable was used for both radial cables and ring cables, and their specifications and material properties are shown in Table 1. The numbering and layout of the cable is shown in Figure 4.

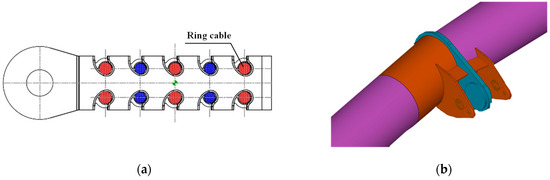
Figure 3. Diagram of the cables and cable clamp. (a) Clamp of the ring cable. (b) Pin-connected plate of the outer compression truss.

Table 1. Specification and material property of the steel and cables.

Name	Specification	Material	Elasticity Modulus (MPa)	Density (kg/mm3)	Thermal Expansivity	Strength (MPa)	Minimum Breaking Force (kN)
Compression truss	-	Q355	206,000	7.8503 × 10−6	1.2 × 10−5	310	-
Radial cable	2 × D100	Galfan full lock coil strand cable	165,000	8.0002 × 10−6	1.38 × 10−5	1570	2 × 10,100
	2 × D110					1570	2 × 12,200
Ring cable	10 × D115					1570	10 × 13,400

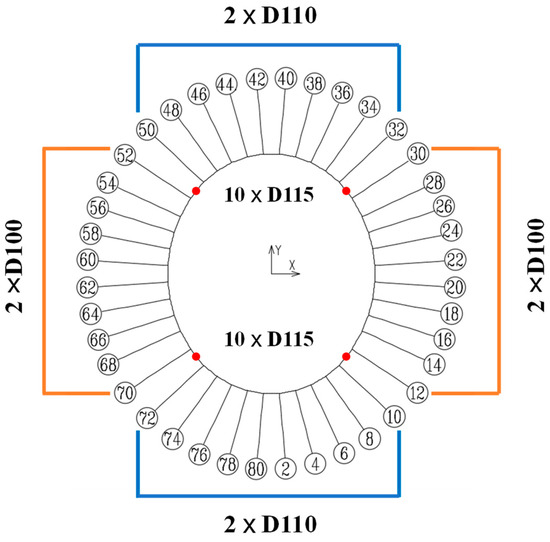
Figure 4. The numbering and layout of cables.

3. Construction Process Analysis

3.1. Selection of Construction Scheme

As a typical flexible structure [37], the stiffness of the spoke-type single-layer cable net structure is generated by tensioning the cables. Generally, the temporary supports are built to lift the rigid tension ring. However, the inner tension ring of this structure is composed of light ring cables, so it is uneconomical and inefficient to build temporary supports. Single-layer cable-net structures with flexible tension rings are often hoisted entirely by traction cables.

After considering the characteristics of the target engineering comprehensively, it was decided to adopt the construction scheme of “assembling on the ground with free stress, hoisting entirely using traction cables, and tensioning/anchoring in batches”. The radial cables were divided into three groups: A, B, and C (shown as Figure 5). Firstly, the radial and ring cables were assembled on the ground, and the traction devices were used in the outer compression truss to hoist three areas simultaneously. Then, area A was hoisted to the precalculated position, and the radial cables of area A were anchored to the pin-connected plate. Tension was continued on the cables of area B and C, then they were anchored chronologically. The construction scheme of the cables is shown in Figure 6.

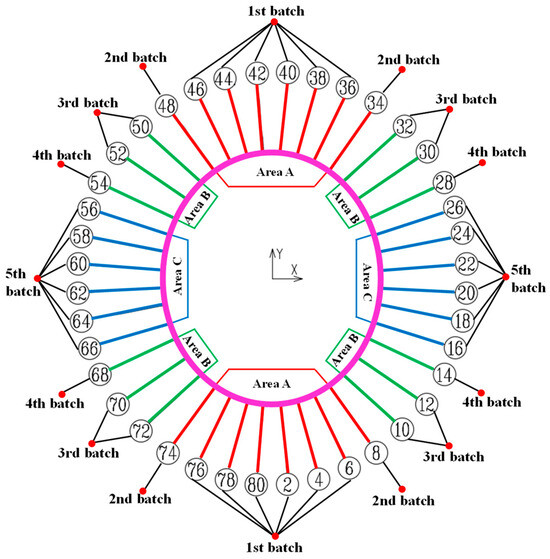
Figure 5. Cable net area and tension batch.

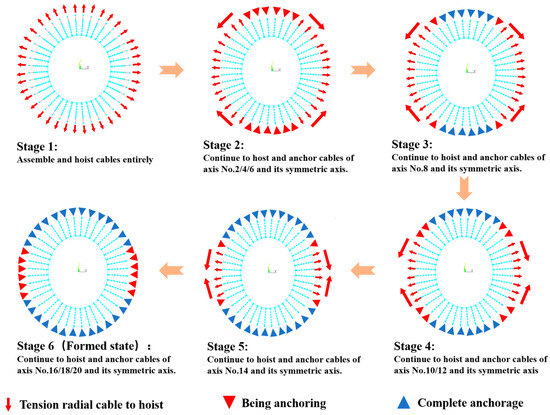
Figure 6. Flow diagram of cable construction.

After confirming the construction scheme of the cable net structure, the entire structure adopted the following construction scheme:

(1) Assembling of the outer diagonal column and compression truss;

(2) Assembling of the radial cables, ring cables, and cable clamps on the stands or stadium;

(3) Taking the outer compression truss as the fulcrum and using the traction cables to tension the radial cables to hoist the cable net structure;

(4) Anchoring the radial cables to the outer compression truss in batches (areas A–C) until the cable structure was formed.

3.2. Finite Element Modeling

The finite element model of the structure was established in ANSYS 2019R1 according to the information from the structure designer, and the finite element analysis of the construction process was carried out. The finite element model in ANSYS included the outer steel compression truss, radial cables, ring cables, and clamps, as shown in Figure 7a. In ANSYS, traction cables were modeled, and rigid arms were established to simulate the pin-connected plate that connected the radial cables to the outer compression truss, as shown in Figure 7b.

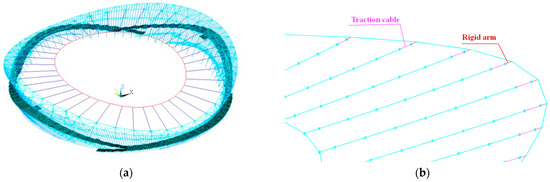
Figure 7. Finite element model in ANSYS. (a) Overall model. (b) Traction cables (pink) and rigid arms (red).

According to the connection form and force characteristics of different components, the appropriate element type and set element conditions were selected, as shown in Table 2. For this single-layer cable structure, most of the steel structure (BEAM or LINK element) was divided into one unit, and the longer element was divided into 3~5 elements. In order to accurately simulate the cable structure (LINK180 element), each ring cable was divided into ten elements, and each radial cable was divided into eight elements.

Table 2. Type and condition of the elements.

Components	Element Type	Element Condition
Cable	LINK180	Both ends hinged
Clamp	MASS21	Mass element
Membrane	SURF154	Surface effect element
Steel structure	BEAM188 or BEAM44	Both ends fixed and part beam hinged
	LINK180	Both ends hinged

The loading conditions were 1.0 times the structural self-weight and 1.0 times the cable prestress. The acceleration of gravity was 9.806 m/s², and the self-weight was automatically calculated by ANSYS. Each clamp of the inner ring cable weighed 5.2 tons and each clamp of the radial cable weighed 0.2 tons, both of which were modeled by the MASS21 element. The surface load of the PTFE membrane surface was 0.15 kN/m². The prestress (P) was applied to the cable by means of the equivalent temperature difference ${∆T}_0$ given by Formula (1).

$$\Delta T_0=-{\displaystyle \frac{P}{EA\times \alpha }}$$

(1)

where E is the elastic modulus, A is the section area, and $\alpha$ is the coefficient of linear expansion.

3.3. Nonlinear Dynamic Finite Element Method (NDFEM)

Before the nonlinear dynamic analysis, the structural self-vibration mode of the engineering project was studied. Assuming that the undamped free vibration of the multi-degree-of-freedom structure system was simple harmonic motion, the following formula can be obtained:

$$\left([K]-{\omega }^2[M]\right)\left\{u\left(t\right)\right\}=\left\{0\right\}$$

(2)

where $\left[K\right]$, $\left[M\right]$, $\left\{u\left(t\right)\right\}$, and $\omega$ are the stiffness matrix, mass matrix, displacement component, and natural circle frequency of the structure, respectively. By solving Equation (2), the natural frequencies of each order of the structure can be obtained. In ANSYS, considering the stress hardening effect, the mode of modal analysis adopted a 1.0 dead weight and prestress. The natural frequency of each order is shown in Table 3. The first four modes were mainly vertical vibration of the cable network, and the local torsion in the cable network plane began from the 5th mode.

Table 3. The first 20 order natural vibration period and frequency statistics table.

Order of Mode	Frequency (Hz)	Natural Period (s)	Order of Mode	Frequency (Hz)	Natural Period (s)
1	0.430	2.326	11	1.030	0.971
2	0.434	2.306	12	1.067	0.937
3	0.457	2.189	13	1.068	0.936
4	0.477	2.098	14	1.072	0.932
5	0.643	1.555	15	1.092	0.916
6	0.649	1.540	16	1.092	0.916
7	0.838	1.194	17	1.120	0.893
8	0.844	1.185	18	1.123	0.890
9	0.984	1.016	19	1.124	0.890
10	0.987	1.013	20	1.136	0.880

The above results show that the basic frequency of the structure was 0.430 Hz, the basic period was 2.236 s, and the vibration frequency distribution was relatively dense. The early mode was vertical vibration, and the local in-plane torsion appeared in the later stage.

The construction process analysis of the single-layer structure net was based on the nonlinear dynamic finite element method (NDFEM) proposed by Luo [24]. Based on the theory of nonlinear dynamics, this method added the virtual inertial force and viscous damping force to establish the nonlinear motion equation of the whole structure, transforming the static problem into a dynamic problem. The NDFEM makes the dynamic equilibrium state gradually converge to the static equilibrium by iteratively updating the configuration of the finite element model. The cable net structure was in a static unbalanced state before the analysis and in the static balanced state during the analysis. Whether the structure is in static equilibrium or not will be determined according to the peak kinetic energy and time stagnation point obtained in the virtual dynamic process. When the finite element model converged, the nonlinear static analysis was carried out to check the static equilibrium state. The detailed flowchart of the NDFEM is shown in Figure 8.

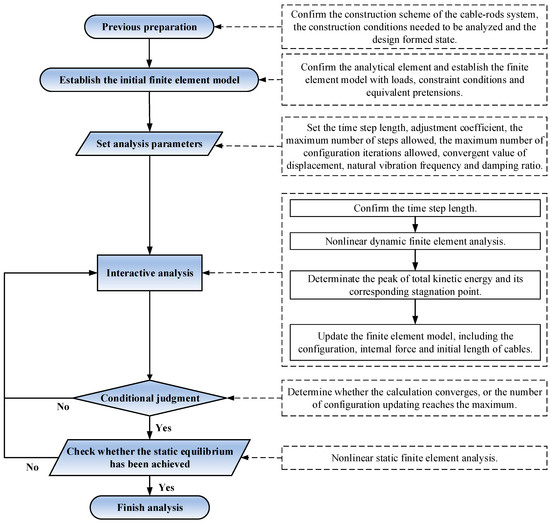
Figure 8. Analytical procedure of the NDFEM.

Setting the time step length, the determination of the peak of total kinetic energy, and its corresponding stagnation point are the significant technical measures of the NDFEM.

1. Setting and adjusting the time step length

Time step length, $\Delta T_s$, is one of the key factors that determine the convergence speed and efficiency of NDFEM. A lower $\Delta T_s$ can make the iteration of the dynamic equilibrium easier to converge as well as lead to the increase in the total time steps $\Sigma N_{\mathrm{ts}}$ required to achieve static equilibrium and the decrease in calculation efficiency. An acceptable time step should ensure that the total kinetic energy reaches its peak in less time steps under the premise of the convergence of dynamic analysis. The NDFEM can be divided into three stages, as shown in Table 4.

Table 4. Stages of the NDFEM form-finding analysis.

No.	Stage	The Length of Time Step	Explanation
1	Initial stage	Relatively small	The cable net moves intensely as a relatively small time step is required to facilitate the dynamic balance to converge iteratively.
2	Middle stage	Relatively large	The main displacement direction of the cable net is clear and gradually tends to the configuration of static equilibrium. A relatively larger time step should be set to make the structure close to the static equilibrium state in less $\Sigma N_{\mathrm{ts}}$.
3	Final stage	Larger	The cable net will vibrate near the static equilibrium state. A larger time step should be set to accelerate the convergence of the configuration iteration so that the structure can reach the static equilibrium state more easily.

Considering that the time step has an important influence on the dynamic balance iteration and analysis efficiency, the time step adjustment coefficient $C_{ts}$ was used to automatically adjust the time step of each dynamic analysis in the analysis process, and the adjustment strategy is as follows:

(1) The initial time step length $\Delta T_{s(1)}$ is used in the first iteration.

(2) If the time step $N_{\mathrm{ts}(m-1)}=N_{ts(m)}$ arises and the total kinetic energy does not decrease when conducting the (m − 1)th times dynamic analysis, the time step length of the (m)th times dynamic analysis will be adjusted to $\Delta T_{s(m)}=\Delta T_{s(m-1)}\times C_{\mathrm{ts}}$ automatically.

(3) If the (m − 1)th times dynamic analysis does not converge, then $\Delta T_{s(m)}=\Delta T_{s(m-1)}/C_{\mathrm{ts}}$.

2. The peak of total kinetic energy ($E_{(p)}$) and its corresponding stagnation point $T_{(p)}$

The calculation of the kth time step total kinetic energy in the dynamic analysis is as follows:

$$E_{(k)}={\displaystyle \frac{1}{2}}{\left\{\dot{U}\right\}}_{(k)}^T[M]{\left\{\dot{U}\right\}}_{(k)}$$

(3)

The deterministic strategy of the peak of total kinetic energy ($E_{(p)}$) and its corresponding stagnation point $T_{(p)}$ are as follows:

(1) Adjust $E_{(0)}=0$;

(2) When the kth time step converges iteratively, if $k<\left[N_{\mathrm{ts}}\right]$, $E_k>E_{(k-1)}$, the total kinetic energy does not reach its peak, so continue the dynamic analysis and enter the (k + 1)th time step. If $k\le \left[N_{\mathrm{ts}}\right]$, $E_k\le E_{(k-1)}$, make the total kinetic energy of the three continuous time steps $E_{(k)},E_{(k-1)},E_{(k-2)}$ fit with a quadratic parabola curve and calculate the peak value of the total kinetic energy and its corresponding time stagnation point. If $k=\left[N_{\mathrm{ts}}\right]$, $E_k\ge E_{(k-1)}$, then $E_{(p)}=E_{(k)}$, $T_{(p)}=T_{(k)}$.

(3) When the kth time step does not converge iteratively, if k = 1, adjust the time step and enter the next dynamic analysis. If 1 < k $\le \Sigma N_{\mathrm{ts}}$, $E_{(p)}=E_{(k-1)}$,$T_{(p)}=T_{(k-1)}$.

The NDFEM method can greatly improve the operation efficiency by using appropriate time steps, and the analytical results are stable and accurate. Up to now, the NDFEM method has been applied in the construction simulation analysis of some cable structures and guided their construction successfully. Single-layer cable and double-layer cable structures have been included in Suzhou Industrial Park Stadium [27], Suzhou Swimming Stadium, Sanya Stadium, Leshan Olympic Sport Center Stadium, Linyi Sport Center Stadium, and Desheng Sport Center Stadium.

3.4. Analysis, Results, and Discussion: Finite Element Simulation of Construction Process

The cable net will be anchored from area A to area C during construction. The value of cable forces is small in the early stage, so the length change of the traction cables can be fast. Subsequently, the cable forces become bigger, so the length change of the traction cables should be slower to control the cable force and configuration accurately. According to the above, the construction process analysis was divided into 11 construction conditions, as shown in Table 5.

Table 5. Analysis conditions of the whole process of construction.

Construction Condition	Construction Procedure	Length of Traction Cables (m)
		Axis No. 2/4/6 and Symmetry	Axis No. 8 and Symmetry	Axis No. 10/12 and Symmetry	Axis No. 14 and Symmetry	Axis No. 16/18/20 and Symmetry
GK-1	Assemble cables on the ground and begin to tension the cable net.	14.5	17.5	23.5	24	28
GK-2	Hoist cables entirely off the ground.	11.5	12	13	13.5	14.5
GK-3	Hoist cables entirely to mid-air.	5.5	6	7	7.5	8.5
GK-4	Continue to tension and anchor the cables of axis no. 2/4/6 and its symmetric axis.	0	0.5	1.5	2	3
GK-5	Continue to tension and anchor the cables of axis no. 8 and its symmetric axis.	0	0	1	1.5	2.5
GK-6	Continue to tension and anchor the cables of axis no. 10/12 and its symmetric axis.	0	0	0	0.5	1.5
GK-7	Continue to tension and anchor the cables of axis no. 14 and its symmetric axis.	0	0	0	0	1
GK-8	Continue to tension until the length of the cables in area C is 0.5 m.	0	0	0	0	0.5
GK-9	Continue to tension until the length of the cables in area C is 0.2 m.	0	0	0	0	0.2
GK-10	Continue to tension until the length of the cables in area C is 0.1 m.	0	0	0	0	0.1
GK-11	Continue to tension and anchor the cables of axis no. 16/18/20 and its symmetric axis. The structural cable net is formed.	0	0	0	0	0

In order to check the convergence performance of the nonlinear iteration of the NDFEM, the inverse process of cable net hoisting in two stages, GK6 and GK7-GK11, was tested. That is, the cable network was lowered to the specified position by lengthening the traction cable. The iterative process is shown in Figure 9. The convergence standard of the maximum adjustment of cable structure coordinates was set to 1 mm. With the progress of iteration, the peak kinetic energy of the cable net steadily decreased until it was close to 0 mm. The maximum value of cable structure coordinate adjustment oscillated in the early stage, gradually decreasing steadily in the later stage. Finally, the iteration was completed when it was less than 1 mm, and the structural nonlinear calculation converged.

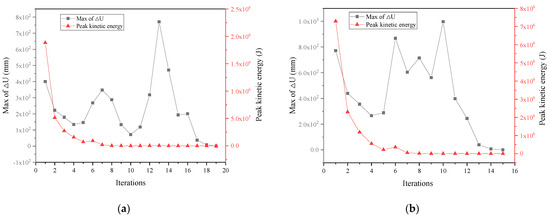
Figure 9. Convergence check of iterative process using the NDFEM method. (a) GK6. (b) GK7–GK11.

The NDFEM was applied to simulate the construction process of the cable structure in ANSYS. According to the results from ANSYS, we extracted the vertical displacement of the clamps and radial displacement of the outer compression truss, as shown in Figure 10. The maximum value of the traction cables is shown in Figure 11. From GK-1 to GK-4, it shows that the length change of the traction cables was relatively large and the elevation of the structure net rose rapidly, but the traction force varied little. In the meantime, the cable force transferred to the outer compression truss gradually, and the radial displacement of truss changed slowly. Starting with GK-4, there were 12 radial cables anchored, and the structure was close to being formed. The length of the traction cables changed less, and the cable net needed to be hoisted slowly because the traction cable force and radial displacement of the truss increased rapidly. It has been proven that the cable force of the single-layer cable net is very sensitive to the change in configuration when the structure approaches formation. It is also a characteristic of this full-tension structure. When the cable net accomplished tension (GK-11), the biggest value of cable force reached was 4504 kN, which is much less than the minimum breaking force of 24,200 kN. Furthermore, the forces of the traction cables in areas B and C were much less than those in the formed state.

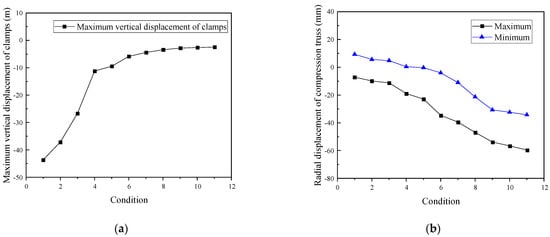
Figure 10. The change in structural displacement under 11 construction conditions. (a) Maximum vertical displacement of clamps. (b) Radial displacement of the compression truss.

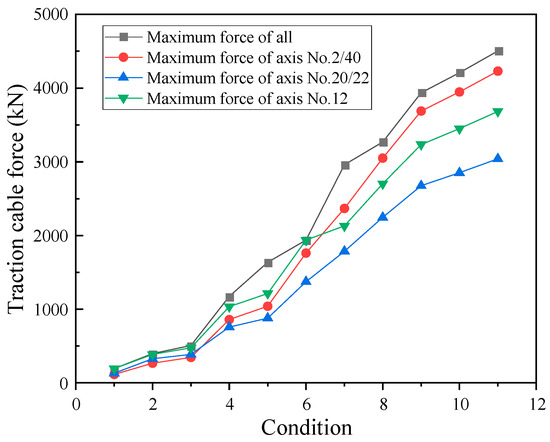
Figure 11. The change in maximum traction forces under 11 construction conditions.

This engineering project is a quarter symmetrical structure, so the traction cable force in the symmetrical position is equal. After the axis number merged, the traction cable forces during construction were as shown in Table 6, where the bold and underlined value indicates the cable force under the current condition. It shows that the forces of the traction cables in area B/C were 1000 kN lower than those in area A when the structure formed. Because the cables in area B/C were anchored first, the traction forces when anchored were much smaller than those when formed in axis no. 2–12, as shown in Figure 12. Tensioning and anchoring in batches, compared to that synchronously, can decrease the traction forces and ensure the safety of cable construction. Furthermore, tensioning and anchoring in batches can reduce the labor cost of construction. All of these results prove the advantages of the method “tensioning and anchoring in batches”.

Table 6. Traction cable forces under 11 construction conditions.

Construction Condition	Traction Cable Forces (kN)
	Axis No. 2/40/42/80	Axis No. 4/38/44/78	Axis No. 6/36/46/76	Axis No. 8/34/48/74	Axis No. 10/32/50/72	Axis No. 12/30/52/70	Axis No. 14/28/54/68	Axis No. 16/26/56/66	Axis No. 18/24/58/64	Axis No. 20/22/60/62
GK-1	115	122	139	155	149	193	158	119	126	130
GK-2	266	286	366	398	297	386	387	230	312	327
GK-3	345	365	473	506	339	476	475	247	366	386
GK-4	859	881	1129	1173	640	1034	1027	369	726	757
GK-5	1040	1060	1104	1637	740	1213	1208	410	847	879
GK-6	1762	1787	1838	1915	1926	1937	1931	581	1334	1372
GK-7	2367	2397	2458	2551	2539	2129	2960	745	1742	1785
GK-8	3050	3085	3157	3268	3237	2702	3105	1574	2218	2246
GK-9	3689	3727	3809	3936	3888	3234	3249	2348	2658	2676
GK-10	3948	3989	4075	4208	4152	3449	3303	2668	2837	2851
GK-11	4231	4274	4364	4504	4441	3684	3355	3023	3034	3041

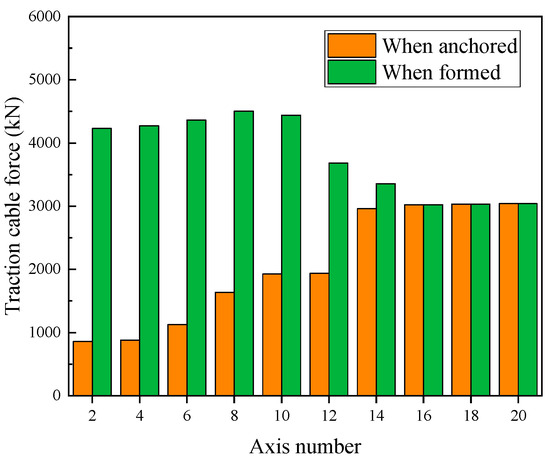
Figure 12. Comparison of cable forces between the anchored and formed state.

Equivalent stress of the outer compression truss was obtained to ensure that the stress of the steel did not exceed the limits when the structure net was hoisted. The maximum equivalent stress of the outer compression truss in each construction condition is shown in Table 7. From GK-1 to GK-11, the equivalent stress of the outer compression truss increased, and the maximum value was 102.1 MPa, which was much lower than the design strength. It can thus be seen that the cable net and outer steel were safe.

Table 7. The maximum equivalent stress of the outer compression truss.

Construction Condition	Maximum Equivalent Stress (MPa)	Construction Condition	Maximum Equivalent Stress (MPa)
GK-1	8.94	GK-7	62.9
GK-2	15.8	GK-8	77.0
GK-3	17.8	GK-9	90.6
GK-4	30.0	GK-10	96.1
GK-5	33.9	GK-11	102.1
GK-6	49.5

To sum up, based on the NDFEM to analyze the construction process in ANSYS, the value and change in the cable net displacement, cable forces, and steel equivalent stress were obtained. The results showed that there was a large security redundancy and the construction method had a considerable advantage.

4. Data Acquisition and Comparison of Configuration Automatic Monitoring System (CAMS)

4.1. Establishment and Data Acquisition of CAMS

4.1.1. Establishment of System

During the hoisting of the cable net, there were numerous monitoring points that were displaced drastically, so the manual measurement could not collect and process the data swiftly, timely, and accurately. Therefore, it was necessary to establish a configuration automatic monitoring system (CAMS) for cable structure construction that could realize continuous and rapid observation of the cable net monitoring points. Aiming at this requirement, C# was used as the programming language, USR-W610 was used as the communication module, and a CAMS was established on the Visual Studio 2022 platform to realize the function of automatic measurement. The selected hardware and their advantages are shown in Table 8. The system realized the functions of the remote control of the TS16 robotic total station, multi-point continuous measure, result output, data discrimination, replacing the search strategy, and so on. It was proven that the system can satisfy the cable monitoring requirement of real-time, automation, continuity, and stability.

Table 8. Hardware foundation of the CAMS.

Hardware	Version	Advantages
Robotic total station	The Leica TS16	Excellent prism automatic identification mode, measurement accuracy, convenient data interaction, and secondary development interface.
External control interface	GeoCOM secondary development interface, ASCII line communication protocol	Good compatibility, strong scalability, small memory space required, fast data transmission speed, being easy to process, and convert data.
Wireless transmission module	USR-W610	No wiring, no fixed position, transmitting long- distance data swiftly, setting encryption technology to ensure data security, needing no cable, and environment friendly.
Platform for secondary development	Microsoft Visual Studio (VS)	Powerful, efficient, and of high quality. It supports a variety of programming languages, has a wealth of tools and components such as code editor, debugger, designer, version control, and deployment tools.
Program language	C#	Object-oriented, type-safe, high-performance, and versatile programming language with a rich standard library and toolset, supporting cross-platform.

The software system framework of the CAMS is shown in Figure 13. The system consisted of three modules: communication setting, data acquisition, and data output. As the premise of normal operation of the system, the communication setting module ensures stable data communication between the computer and the RTS. As the core function of the system, the data acquisition module is divided into single measurement and timing measurement sub-modules according to the different number of measurement objects, and the search strategy and data determination sub-module are respectively the most important functions of the two measurement modules. The operation flow of the single measurement and timing measurement is shown in Figure 14. The data output module is divided into two sub-modules, which is convenient to operate.

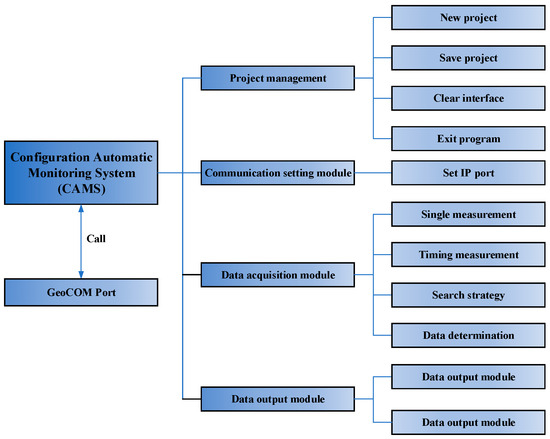
Figure 13. Functional framework of the CAMS.

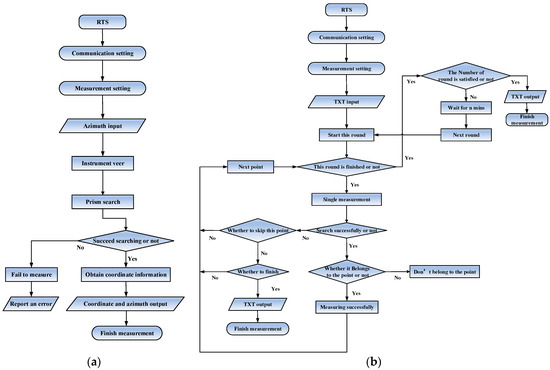
Figure 14. Flowchart of the measurement operation. (a) Single measurement. (b) Timing measurement.

4.1.2. Data Acquisition of CAMS

During the configuration monitoring of the cable net structure in the Linyi Olympic Sport Center Stadium, the CAMS was used to test the performance of the system and obtain the coordinates of the monitoring points.

The monitoring scheme adopted the method of rear-view point to set up the measuring station. The center of the stadium was selected as the monitoring station numbered as LY-CZ. Two rear-view points were the reference points, the location of which should be arranged in a place that is easy to store for a long time, is not disturbed by the external environment, and has good visibility conditions. In order to set three points equidistantly, the two rear-view points, numbered as LY-HA and LY-HB, were arranged on the column of stand, as shown in Figure 15. During the monitoring, the azimuth angle between the measuring station and the monitoring point remained unchanged, and the height and position of the RTS were fixed. The measuring site is shown in Figure 16.

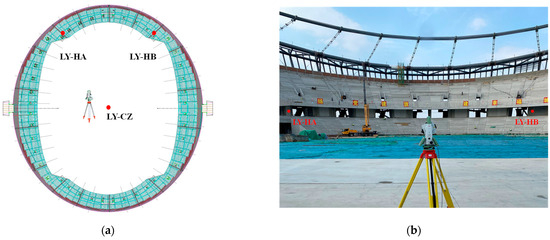
Figure 15. Arrangement of the measuring station and monitoring point. (a) Diagram of the measuring station and rear-view points. (b) Authentic image of measuring station and rear-view points.

Figure 16. Authentic image of the monitoring site.

According to the characteristics of this type of engineering and monitoring points, there were 48 monitoring points arranged in the stadium, where 40 points were on the clamp of the inner ring cable and 8 points on the outer compression truss, as shown in Figure 17a. Forty monitoring points (A-2~A-80) were located near the center of the inner ring of the cable clamps, and were attached to the side of the cable clamp by an aluminum alloy adapter, as shown in Figure 17b. These 40 monitoring points were arranged to measure the configuration of the cable net to obtain the deformation data, which were used to compare with the simulated theoretical value from ANSYS, judge the safety of the structure, and adjust the configuration of the cable structure in mid-air. Another eight monitoring points were arranged on the outer compression truss to measure the radial deformation of the outer steel structure to ensure safety.

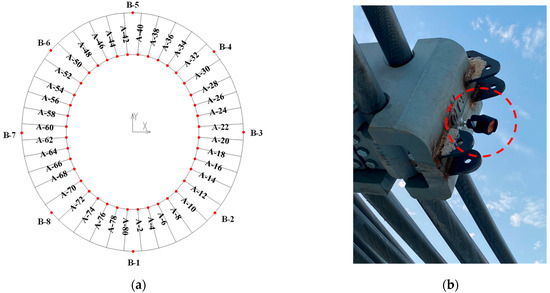
Figure 17. Monitoring points. (a) Layout of the monitoring points. (b) A monitoring point of the ring cable clamp.

The CAMS for the cable structure was carried out for 5 days on the construction site of the Linyi Olympic Sport Center Stadium. According to the actual situation, we chose seven process conditions, numbered from GC-1 to GC-7. The length of the traction cable of each axis is shown in Table 9. GC-1 indicates the start of monitoring, during which condition the construction of the outer steel structure was completed and was deformed due to its own weight. We then obtained the coordinate values of these 48 points.

Table 9. The length of the traction cables under different conditions (mm).

Axis Number	Conditions
	GC-1	GC-2	GC-3	GC-4	GC-5	GC-6	GC-7
2	2718	0	0	0	0	0	0
4	3861	0	0	0	0	0	0
6	2647	0	0	0	0	0	0
8	4698	1506	0	0	0	0	0
10	6284	2900	815	0	0	0	0
12	6763	3634	1237	0	0	0	0
14	7045	4066	2432	1626	0	0	0
16	7068	4504	3152	2068	360	0	0
18	7045	4624	3600	2916	1000	200	0
20	6794	4523	3567	3040	2484	900	0
22	6958	4391	3516	2910	2734	900	0
24	7037	4586	3500	2735	2044	0	0
26	6952	4558	3500	1693	668	0	0
28	6532	4073	3542	688	0	0	0
30	6134	3771	1419	0	0	0	0
32	5768	2757	682	0	0	0	0
34	4696	1398	0	0	0	0	0
36	2594	0	0	0	0	0	0
38	2680	0	0	0	0	0	0
40	2622	0	0	0	0	0	0
42	2693	0	0	0	0	0	0
44	2662	0	0	0	0	0	0
46	2681	0	0	0	0	0	0
48	4654	1703	0	0	0	0	0
50	5878	2676	498	0	0	0	0
52	5966	3386	1616	0	0	0	0
54	6606	4143	3224	2166	477	0	0
56	7101	4557	3359	3041	1591	0	0
58	7137	4610	3657	2959	1622	0	0
60	7077	4460	3649	2880	2874	200	0
62	7007	4233	3564	2892	2890	200	0
64	7223	4588	3638	2769	1981	0	0
66	7019	4582	3348	2802	1326	0	0
68	6703	4100	3201	1175	0	0	0
70	5917	4102	2484	0	0	0	0
72	5569	2919	776	0	0	0	0
74	4091	1374	0	0	0	0	0
76	2689	0	0	0	0	0	0
78	2604	0	0	0	0	0	0
80	2538	0	0	0	0	0	0

4.2. Simulation Theoretical Values Obtained from ANSYS

Considering that the monitoring points of ring cable clamp were attached to the ring cable clamp facing the center of the side of the field, the incline angle of the ring cables changed when the cable net was hoisted. Therefore, it was necessary to refine the original finite element model to obtain the coordinates of the monitoring points in ANSYS. According to the CAD solid model shown in Figure 18a, the finite element of the ring cable in ANSYS was subdivided into 10 loops to be as consistent as possible with the project. Monitoring points in ANSYS are shown separately, as shown in Figure 18b. The clamps of the ring cable were modeled in the element of BEAM 188 and the material stiffness was consistent with that of the rigid arm. The center point of the ring cable clamp was set as the main key point and the other point as the slave key point, then the rigid zone was established. The material type, member connection condition, loading condition, and construction condition were the same as the original analysis. The coordinates of the monitoring points were obtained from GC-1 to GC-7, as detailed in Section 4.1.2.

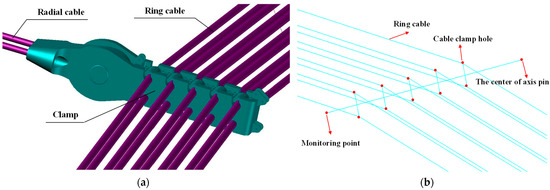
Figure 18. Clamp model of the ring cable. (a) CAD solid model. (b) Finite element model in ANSYS.

4.3. Comparison, Analysis and Discussion: The Theoretical and Measured Displacement

4.3.1. Comparison of Clamps’ Vertical Displacement

A-80, the lowest clamp, was taken as the datum point to obtain the theoretical and measured relative elevation, as shown in Figure 17a, that is, the elevation difference between the target point and the datum point, ΔZ₁ and ΔZ₂, respectively. The relative difference in elevation ΔZ = ΔZ₁ − ΔZ₂ was obtained, and the ΔZ from GC1 to GC7 was plotted, as shown in Figure 19.

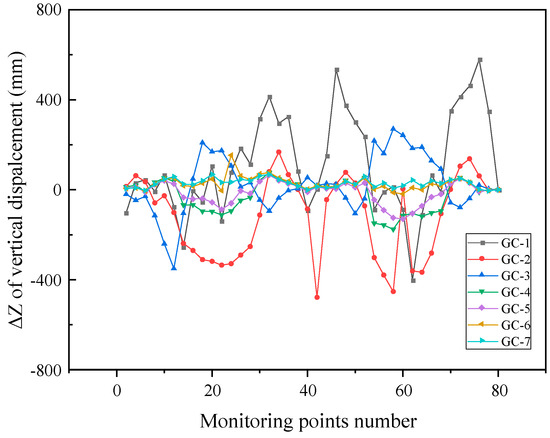
Figure 19. The relative difference in the elevation of the ring cable clamp between the theoretical and monitored values.

The biggest ΔZ appeared in GC-1, because the traction cables were long and the radial cables were relaxed. The cable forces were low, so that it would not be efficient to control the configuration of the cable net. Therefore, the discreteness of the measured values and the error were relatively large. Gradually, as the length of the traction cables decreased and the cable forces increased, the ΔZ decreased until the minimum was 68 m in GC-7, which appeared on the monitoring points of A20 and A32. It was proven that the greater the cable force, the less discreteness and ΔZ. As Figure 18 shows, taking axis no. 40 of the horizontal coordinates as the symmetry axis, ΔZ was basically symmetric. With the continuous reduction in the length of the traction cable, the symmetry phenomenon was more obvious, which is consistent with the symmetry of the engineering structure. Meanwhile, the change in cable force was more sensitive when the cable net structure was close to being formed, as shown by the simulations in ANSYS.

It can be concluded that the theoretical displacement is basically consistent with the measured displacement, and the displacement change in the ring cable is basically consistent with the theoretical analysis during construction. Therefore, construction can be carried out safely, and it was proven that the CAMS has considerable precision in vertical deformation monitoring.

4.3.2. Comparison of the Outer Compression Truss’s Radial Deformation

As Figure 20a shows, the radial deformation of eight measuring points decreased as the length of the traction cable decreased. The value of radial deformation developed from 0 mm in the initial state to 50 mm in the formed state compared to GC-1. Because the length of the traction cables decreased, the cable force increased and the outer compression truss was tensioned to move closer to the center of the field gradually. Therefore, the radial deformation increased.

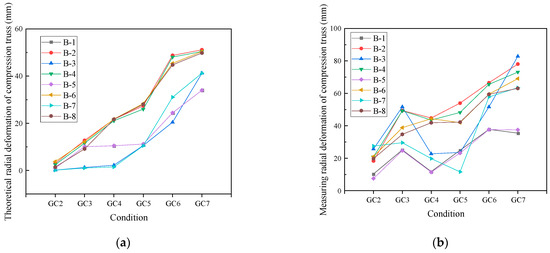
Figure 20. Deformation of the outer compression truss (compared to GC-1). (a) Theoretical deformation. (b) Measuring deformation.

Due to gravity in the initial state, the measuring radial deformation of truss was not 0 mm, and the configuration was not the design zero state. There was an error between the measured value and the theoretical value. The measuring trend of general deformation was consistent with the theoretical analysis shown in Figure 20b. However, there was an anomaly, where the deformation of the latter condition was smaller than that of the previous condition, because the outer compression truss monitoring points of B-3 between GC2 and GC3, B-1 between GC3 and GC4, and B-3 between GC6 and GC7 were disturbed by accidental human intervention. Although it was corrected in time, its coordinates still showed a certain deviation. Considering the above factors, there were some errors in the radial deformation measured.

The difference between the theoretic and measured deformation is shown in Figure 21. The difference ranged from −50.43 to −1.01 mm. Compared with the initial state (GC-1), the maximum measured deformation (GC-7) was 82.9 mm, and the maximum theoretical deformation was 50.5 mm, with a difference of about 30 mm. Although there was a relative difference, considering the large scale of the structure and different construction seasons, the relative difference is acceptable. Construction was carried out safely, and the automatic measurement system can be recognized as having considerable accuracy.

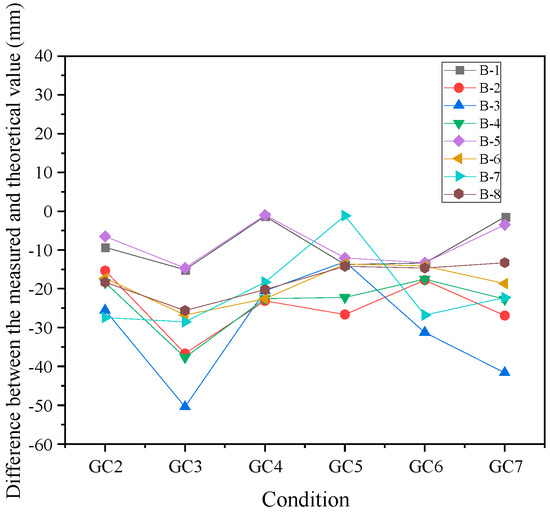
Figure 21. The difference between the measured value and theoretical value.

To sum up, the vertical and radial deformation between the measured value and the theoretical value were compared. It was proven that the CAMS in the Linyi Olympic Sport Center Stadium could complete the measurement task. The system had considerable accuracy and stability with acceptable error, which can provide some reference values for the construction of other similar engineering projects.

5. Conclusions

This paper took Linyi Olympic Sports Center Stadium as the engineering background and researched the key technologies of its spoke-type single-layer cable net structure. Based on the NDFEM method, the finite element simulation analysis of the whole construction process was carried out, and the CAMS was developed to monitor the structural configuration during the construction process. The study yielded the following conclusions:

(1) Based on the characteristics of the spoke-type single-layer cable structure used at the Linyi Olympic Sport Center Stadium, the method of “assembling in low-altitude with free stress, hoisting entirely using traction cables, tensioning, and anchoring in batches” was selected, the nonlinear dynamic finite element method (NDFEM) was applied to analyze the construction process in ANSYS, and key responses in ANSYS were obtained. The results showed that the maximum cable force was 4504 kN, the maximum equivalent stress was 102.1 MPa, structural deformation was within an acceptable range, and the structure was safe during construction. Furthermore, tensioning and anchoring in batches could decrease the traction forces, which proved the advantages of the selected construction method.

(2) The CAMS was established to realize the function of automatic measurement for the cable structure, which has large deformation during construction. The system consists of three modules: communication setting, data acquisition, and data output. These modules can realize the functions of the remote control of the TS16 robotic total station, multi-point continuous measure, result output, data discrimination, replacing search strategy, and so on. It was proven that the system could satisfy the monitoring requirement of real-time, automation, continuity, accuracy, and stability.

(3) The original finite element model of the clamps was refined to obtain the coordinates of the monitoring points and the theoretical deformation in ANSYS according to different conditions. The CAMS was applied to the cable structure construction to obtain the measuring coordinates. It was proven that the system had considerable accuracy and stability with acceptable error. It could also be seen that the configuration of the cable net was in a safe and controllable state during construction. Comparative results showed that the application of the CAMS could provide some reference values for the construction of other similar engineering projects.

(4) This study simulated the construction process from the macro level but did not focus on the further study of the component and node levels. In this project, ten ring cable clamps were connected with two radial cables, which was the most important node of the cable network structure. Considering the mechanical properties of the cast steel joints and welds, it is necessary to study the ultimate bearing capacity of the cable clamps. Furthermore, machine learning, deep learning, and artificial intelligence methodologies are expected to forecast the structural response [38,39]. At the same time, the CAMS can be further upgraded to enhance its visualization, and it is expected that the digital model of the construction process of the cable network structure can be quickly established based on the measured coordinates of the monitoring points.