A Comprehensive Evaluation Method for Assessing the Seismic Resilience of Building Sites Based on the TOPSIS Model and the Entropy Method

Abstract

The seismic design philosophy based on resilience represents the latest development in structural seismic design theory and is currently the most advanced concept in the field of seismic design research. A building site serves as the foundation and environment for structures, and evaluating its seismic resilience is a crucial aspect of designing and assessing buildings’ seismic resilience. To meet the needs of evaluating building seismic resilience, the concept of seismic resilience for building sites is introduced in this paper. This evaluation is approached from three dimensions: seismic action, site seismic capacity, and site recovery capability. An indicator system for evaluating the seismic resilience of building sites is constructed using 23 key indicators that reflect the site’s seismic resilience. A seismic resilience evaluation model for building sites is established based on the TOPSIS model and the entropy method. The feasibility and rationality of the proposed evaluation method are demonstrated through application examples. The research findings in this paper provide a valuable reference for advancing the evaluation of both building seismic resilience and site seismic resilience.

1. Introduction

Throughout the long history of human society, cities have suffered greatly from the devastation of earthquakes. Many cities have been destroyed by seismic disasters, resulting in significant loss of life and extensive property damage. As a result, earthquake resistance and disaster prevention have become enduring concerns for human civilization. An important part of these losses is attributed to the severe damages incurred to buildings, infrastructure, and structures of the production sector [1].

The building site plays a pivotal role in the seismic damage sustained by structures, acting as both the foundation and the surrounding environment. Its importance is related to a range of critical factors, including geological conditions, topographical features, soil composition, and hydrological characteristics, all of which significantly influence a building’s seismic performance. In various seismic design codes, site classification serves as the foundation for seismic design, with specific seismic requirements established accordingly for different types of sites [2,3,4,5]. The current standards primarily classify sites based on indicators such as lithology, overlying soil thickness, soil shear wave velocity, standard penetration test (SPT) blow count, and undrained shear strength. These classifications are then used to determine seismic design coefficients, which represent the intensity of strong ground motion. The impact of the site on buildings during an earthquake includes not only strong ground motion but also hazards such as sand liquefaction, soft soil settlement, landslides, surface rupture, and tsunamis [6,7,8,9,10]. Studies on the 2011 Tōhoku and Christchurch earthquakes have shown that the reconstruction of buildings was delayed considerably due to site damage. This led to prolonged recovery times and affected practical driving performance [11,12,13,14,15]; therefore, it is essential to assess the suitability of building sites comprehensively.

Seismic resilience is the further refinement and development of performance-based seismic design, offering a newer and more comprehensive approach to urban and building seismic planning and design. The urgent need for urban and building seismic safety provides a vast space and great motivation for research in the field of seismic resilience. As early as 2009, the San Francisco Planning and Urban Research Association (SPUR) proposed a seismic resilience evaluation system for cities [16]. FEMA-P58 (Federal Emergency Management Agency) [2] is a seismic performance evaluation method for buildings proposed by FEMA, which uses indicators such as casualties, repair costs, and repair time to assess the seismic performance of structures. In 2013, ARUP Group developed the Resilience-based Earthquake Design Initiative for the Next Generation of Building (REDi™) framework, a rating system for building seismic resilience [17]. NIST released seismic resilience guidelines that establish performance objectives for buildings and infrastructure, promoting collaboration among stakeholders for enhanced resilience [18,19]. Furthermore, in 2020, United Nations Human Settlements Programme (UN-Habitat) launched the “Resilient Cities” initiative, advocating for sustainable urban development and disaster risk reduction strategies on a global scale [20]. Researchers have followed the concepts of robustness, redundancy, resourcefulness, and rapidity to devise evaluation indicators for subsystems such as building structures [21,22,23,24], medical systems [25,26,27,28], and lifeline systems [29,30,31]. Several seismic resilience standards have also been subsequently established. Researchers have established evaluation frameworks and resilience assessment methods, driving the rapid development of seismic resilience research. It must be emphasized that both building structures and infrastructure are situated on sites, making site resilience a crucial component of overall resilience; however, current seismic resilience indicators and evaluation systems lack site resilience assessments, rendering the seismic resilience evaluation framework incomplete.

Building on the introduction of the concepts of site resilience and seismic resilience of building sites [32], an indicator system for evaluating site seismic resilience is systematically established in this paper. This system is based on the seismic response characteristics of building sites and the functional requirements that buildings impose on these sites. By integrating the entropy weight method and the TOPSIS method, a model for evaluating site seismic resilience is developed. Using this indicator system, the seismic resilience of 60 building sites in Beijing, China, is analyzed, with resilience values and classifications provided for each site. The findings of this study offer significant theoretical insights for advancing the evaluation of urban and building seismic resilience and provide valuable reference points for further exploration of site seismic resilience assessment.

2. The Concept and System of Seismic Resilience for Sites

2.1. Concept of Seismic Resilience for Sites

A site is a complex geological system composed of rock, soil, geological structures, groundwater, and other elements. An urban construction site refers to an area within a city’s boundaries. A site is defined as the location of an engineering group characterized by similar response spectrum features. The area of such a site is equivalent to that of industrial parks, residential areas, or natural villages, or it covers a planar area greater than 1.0 km² [5].

The seismic performance of a site is controlled by site conditions, which significantly impact seismic motion [33,34,35]. Site conditions typically include topography, geomorphology, soil composition, geological structures, hydrogeological conditions, and physical geological phenomena [36]. From a seismic perspective, when selecting a site for engineering construction, it is essential to choose sites or locations favorable for seismic resistance and to avoid unfavorable sites or locations. The impact of site conditions on seismic motion is the core content of site seismic performance evaluation.

It is crucial to emphasize that site seismic performance is an important aspect of evaluating site stability. In addition to seismic action, site stability is also affected by other geological processes, their evolution, and human engineering activities. Different engineering projects have different requirements for site stability based on their usage functions, leading to different demands for on-site seismic performance.

Resilience can be defined as the ability of a system to resist, absorb, recover from, and adapt to various disturbances. These disturbances can be natural or human-made, with varying implications across different academic disciplines [37]. In civil engineering, resilience primarily refers to the ability to maintain and restore original functions under various disturbances, including the ability to resist wind, explosions, floods, and earthquakes, as well as to restore these functions after such disturbances.

The original functions include wind resistance, explosion resistance, flood resistance, seismic performance, basic functions, and comprehensive functions. Basic functions refer to the necessary performance required to ensure the normal use, structural safety, and proper operation of equipment in civil engineering projects. Comprehensive functions refer to the ability to maintain basic functions while keeping the appearance and interior intact. The design requirements for these functions are based on the needs of the project. Recovery refers to the restoration of these functions after repairs.

According to the “Standard for Seismic Resilience Assessment of Buildings” (GB/T38591-2020) published by the Standards Press of China in 2020 [38], it defines the seismic resilience of buildings as the ability of a building to maintain and restore its original functions after a specified level of seismic action. This standard uses post-earthquake repair costs, repair time, and casualties caused by the earthquake as indicators to evaluate the seismic resilience of buildings; however, the standard only specifies seismic input and does not address the role of building sites in evaluating seismic resilience. Nevertheless, the seismic resilience of buildings is closely related to the seismic resilience of building sites, with the latter being an essential component of the former; therefore, evaluating the seismic resilience of buildings should begin with evaluating the seismic resilience of building sites.

Based on the above discussion, the seismic resilience of building sites is defined in this paper as the ability of a site to resist seismic damage and maintain and restore its original functions and environmental conditions after a specified level of seismic action. According to Bo et al. [32], site resilience can be defined as the ability of a site to maintain and restore its original functions and environmental conditions after being subjected to a certain intensity of geological processes and human engineering activities. Site resilience is an important indicator of the resilience of cities and engineering structures.

Since seismic resilience of sites primarily considers the ability to maintain and restore original functions and environmental conditions under seismic action, it is a critical indicator of site resilience. The site is both the supporting body for buildings and the medium through which seismic waves propagate. When subjected to a certain level of seismic action, the geotechnical body of the site may change, sometimes altering its original functions. Strong earthquakes may cause seismic geohazards, such as soil liquefaction, soft soil settlement, surface rupture, and slope instability, leading to foundation failure and the loss of original functions, ultimately resulting in severe damage to the superstructure. Additionally, earthquakes can trigger landslides, collapses, rockfalls, tsunamis, and lake surges, altering the original environment and functions of the site and damaging buildings; therefore, seismic performance is a critical factor in determining site resilience.

The original environment and functions of the site refer to the environmental conditions and site performance necessary to ensure the safety, stability, and proper operation of the building project, as required during site planning and design. Seismic action on the site can be understood as the dynamic action produced by seismic motion within the site, which is related not only to the characteristics of the seismic motion itself but also to the dynamic characteristics of the site. Considering the need for seismic resilience evaluation of buildings, the seismic action level adopted in this paper corresponds to a rare earthquake, i.e., an earthquake with a 2% probability of exceedance in 50 years.

Based on the above discussion, it is proposed in this paper that the evaluation of seismic resilience of building sites can be achieved by assessing the stability of the site under seismic action within a certain range and the recovery of the site’s original functions after the earthquake. The seismic resilience of building sites is influenced by multiple factors, with multiple indicators reflecting different aspects of site resilience; therefore, the evaluation of the seismic resilience of building sites can be approached as a multi-criteria comprehensive evaluation problem. There are many multi-criteria comprehensive evaluation methods [39,40,41]. In this paper, we explore the evaluation of seismic resilience of building sites using an integrated approach combining the TOPSIS model and entropy method.

2.2. Evaluation Indicator System

In mathematical terms, a multi-indicator comprehensive evaluation method requires determining the evaluation object and evaluation indicators and establishing an evaluation indicator system. The evaluation object (or goal) in this study is the seismic resilience of building sites. The evaluation indicators, in principle, include all the factors affecting the seismic resilience of building sites. The entire set of evaluation indicators across different hierarchical levels constitutes the evaluation indicator system. This system is an organic whole composed of multiple interrelated and interacting evaluation indicators structured in a certain hierarchy. The selection of evaluation indicators needs to focus on key factors and critical indicators, adhering to the principles of simplicity, independence, representativeness, and feasibility.

Following the requirements of the multi-indicator comprehensive evaluation method and based on the definition and connotation of seismic resilience of building sites, an evaluation indicator system is constructed consisting of three levels: the goal level, dimension level, and indicator level. As shown in Figure 1, the goal level is the seismic resilience of building sites (denoted as A). The dimension level includes seismic action (denoted as A₁), seismic capacity of the site (denoted as A₂), and recovery capability of the site (denoted as A₃); therefore, in this study, we evaluate the seismic resilience of building sites from three dimensions: the potential seismic action the site may experience, the seismic capacity (seismic stability) under a certain level of seismic action, and the recovery capability of the site after experiencing seismic action.

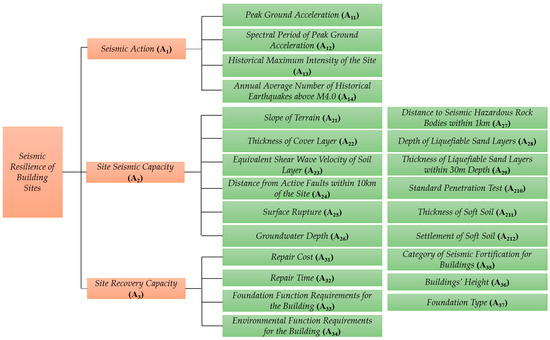
Figure 1. Building site seismic resilience indicator system.

Based on the characteristics and attributes of each dimension, as well as the principles for selecting evaluation indicators, several indicators are used to describe each dimension, forming the indicator level. As shown in Table 1, 23 indicators have been selected to represent these dimensions.

Table 1. Seismic resilience indicator system and value requirements for building sites.

Overall Goal Layer	Criteria Layer	Indicator Layer	Attributes
Seismic Resilience of Building Sites (A)	Seismic Action (A1)	Peak Ground Acceleration with a 2% Probability of Exceedance in 50 Years (A11): This value is provided based on results of the site seismic safety assessment or seismic parameter zoning maps, with units in gal. A higher value indicates a greater likelihood of damage to the site, thus reflecting lower site resilience.	Negative
		Spectral Period of Peak Ground Acceleration with a 2% Probability of Exceedance in 50 Years (A12): This value is provided based on the results of site seismic safety assessment or seismic parameter zoning maps, with units in seconds (s).	Negative
		Historical Maximum Intensity of the Site (A13): This is based on historical records of actual intensity levels with no units.	Negative
		Annual Average Number of Historical Earthquakes above M4.0 in the Area (A14): Dimensionless.	Negative
	Site Seismic Capacity (A2)	Slope of Terrain (A21): This is based on the actual terrain slope of the site, measured in degrees.	Negative
		Thickness of Cover Layer (A22): This refers to the thickness of soil or rocks with a shear wave velocity greater than 500 m/s. The unit is meters (m).	Negative
		Equivalent Shear Wave Velocity of Soil Layer (A23): This is based on actual test results, with the unit in meters per second (m/s). For bedrock sites, the value is 800 m/s.	Positive
		Distance from Active Faults within 10 km of the Site (A24): Given as the shortest distance from the site to active faults, measured in kilometers (km). If there is an active fault within the site, the value is 1; if there are no active faults within 10 km, the value is 10 km.	Positive
		Surface Rupture (A25): Dimensionless. A value of 1 is assigned if surface rupture is likely to occur; a value of 2 is assigned if surface rupture is unlikely to occur.	Positive
		Groundwater Depth (A26): Given according to the stable water table, measured in meters (m).	Positive
		Distance to Seismic Hazardous Rock Bodies within 1000 m (A27): Given according to the measured distance in meters (m). If no seismic hazardous rock bodies are within 1000 m, the value is 1000 m.	Positive
		Depth of Liquefiable Sand Layers (A28): Given according to actual survey results, in meters (m). If the depth is greater than 30 m or if no liquefiable sand layers are present, the value is 30 m.	Positive
		Thickness of Liquefiable Sand Layers within 30 m Depth (A29): Given according to actual survey results, in meters (m). If the thickness is 30 m or if no liquefiable sand layers are present, the value is 0 m.	Negative
		Standard Penetration Test (SPT) Blow Count of Liquefiable Sand Layers (A210): Given according to actual survey results, in blows (b).	Positive
		Thickness of Soft Soil (A211): Given according to actual survey results, in meters (m).	Negative
		Settlement of Soft Soil (A212): Calculated according to the industry standard [42] in centimeters (cm).	Negative
	Site Recovery Capability (A3)	Repair Cost (A31): Dimensionless, where – If the cost of repairing the foundation exceeds the original construction cost, the value is 1; – If it is equal to the original construction cost, the value is 2; – If it is less than the original construction cost, the value is 3.	Positive
		Repair Time (A32): Dimensionless. – A value of 3 indicates a repair time of less than 7 days; – A value of 2 indicates a repair time between 7 and 30 days; – A value of 1 indicates a repair time greater than 30 days.	Positive
		Foundation Function Requirements for the Building (A33): Dimensionless. – A value of 1 indicates that the foundation must be stable with no allowed changes in the foundation soil and rock; – A value of 2 indicates that the foundation must be stable, allowing minor changes in the foundation soil and rock; – A value of 3 indicates that the foundation must be stable, allowing minor damage to the foundation.	Positive
		Environmental Function Requirements for the Building (A34): Dimensionless. – A value of 1 indicates that the site must be free of adverse geological phenomena; – A value of 2 indicates that adverse geological phenomena may be present but do not threaten the safety of the engineering structure; – A value of 3 indicates that adverse geological phenomena are present but, after treatment, do not affect the structural safety.	Positive
		Category of Seismic Fortification for Buildings (A35): Dimensionless.	Positive
		Buildings’ Height (A36), in meters (m).	Negative
		Foundation Type (A37). – Pile and box mixed foundation, the value is 1; – Pile foundation, the value is 2; – Shallow foundation, the value is 3.	Positive

(A_ij in parentheses is the indicator code).

In this study, three indicators—Peak Ground Acceleration (PGA), Response Spectrum Characteristic Period (Tg), and Site Intensity—are employed to represent the effects of seismic motion on a site under the dimension of seismic action. The risk levels of these indicators can be set at exceedance probabilities of 2%, 10%, and 63% over 50 years. To align with the national standard GB/T38591-2020, this study adopts the PGA and Tg values corresponding to a 2% exceedance probability over 50 years. Research [33,34,35,36] has shown that the seismic resistance of a site is primarily governed by its seismic engineering geological conditions, including topography and geomorphology, soil and rock properties, active tectonics, groundwater, and seismic, geological hazards; therefore, in this study, we select the following 15 indicators to evaluate the site’s seismic resistance dimension: slope, elevation difference within 1000 m, soil and rock type, overburden thickness, equivalent shear wave velocity, site classification, distance from the active fault to the site, surface rupture, groundwater depth, distance from seismic hazardous rock masses within 1000 m to the site, depth of liquefiable sand layers, thickness of liquefiable sand layers within 30 m, standard penetration resistance of liquefiable sand layers, soft soil thickness, and soft soil settlement.

The evaluation of site recovery capability is more complex and involves a high degree of subjectivity. To simplify the problem, only four evaluation indicators are considered in this study: repair costs, repair time, building requirements for foundation functions, and building requirements for environmental functions.

The system of indicators and the corresponding criteria for evaluating the seismic resilience of building sites are presented in Table 1. All of these indicators can be obtained from site seismic safety evaluation reports and geotechnical engineering investigation reports.

3. Methods and Data

3.1. Methods

The resilience of a building site reflects its ability to resist and absorb stress and maintain and recover its original functions and site environment after being disturbed. In engineering practice, this ability needs to be evaluated so that it can be applied in urban and building resilience evaluation. There are many comprehensive evaluation methods used locally and internationally, and each method has its scope of application and advantages and disadvantages [43]. From the perspective of weight determination, the evaluation method mainly consists of two types: the weight that can be determined directly, including the Analytic Hierarchy Process, entropy method, and Rough Set Multi-Attribute Decision Making, and the weight that is determined indirectly, including the Fuzzy Comprehensive Evaluation, Grey Correlation Analysis, Material Element Analysis, TOPSIS model, and Catastrophe Progression Method. A single method or a combination of several methods is often used in the study of urban construction and disaster resilience evaluation [44,45,46,47,48]. The determination of indicator weights is key in resilience index system evaluation, and different weights for each indicator will lead to completely different evaluation results. The entropy method belongs to the objective weighting method, a commonly used method for determining weights, which can effectively eliminate subjective factor interference in determining the indicator weights and objectively reflect the evaluation object information. The advantage of the TOPSIS model is that it has no strict restrictions on the sample, and it can make fuller use of these original data. In this paper, a resilience evaluation model for building site seismic resilience is proposed by integrating the TOPSIS model and entropy value method, and the building site’s seismic resilience is evaluated through the model to obtain its seismic resilience grade.

3.1.1. TOPSIS Model

The TOPSIS model, proposed by Hwang. C.L and Yoon. K. in 1981 [49] has since been continuously improved by researchers to become a widely used multi-criteria (or attribute) decision-making analysis model for limited alternatives [50,51,52,53]. The idea comes from the discriminant problem in multivariate statistical analysis, and its basic principle is to assume the existence of an optimal solution among multiple solutions, which is called the ideal solution or optimal solution. Using multiple evaluation indicators for each solution, the distance between each solution and the ideal solution (optimal solution) is calculated, and its proximity to the ideal solution (optimal solution) is given based on this distance. The higher the proximity, the closer the solution is to the optimal solution. The proximity is used to rank or classify the solutions [54], providing a basis for solution selection. The seismic resilience of building sites reflects the ability to withstand seismic interference, which is affected by many indicators. If each site is taken as an evaluation object and several evaluation indicators are given for each site, the site’s resilience is defined in the range of [0,1], where 1 is an ideal solution theoretically; the closer the site is to the ideal solution, the higher the resilience is. Consequently, the proximity degree derived from the TOPSIS model can be utilized to evaluate the seismic resilience of building sites.

The primary computational steps of the TOPSIS model are outlined as follows:

Step 1.

Creating the initial matrix X

If m sites are evaluated and each site has n evaluation indicators, the distribution of the site set and indicator set of the TOPSIS model is M(M₁, M₂,…, Mm); N(N₁, N₂,…, N_n). If the value of the site M_i($i=1, 2,\dots ,m$) under the indicator N_j($j=1, 2,\dots ,n$) is $x_{ij}$, the initial matrix of multiple sites is $X={(x_{ij})}_{m\times n}.$

$$X={(x_{ij})}_{m\times n}=\left(\begin{array}{cccc}{x}_{11}& x_{12}& \cdots & x_{1n}\\ x_{21}& x_{22}& \dots & x_{2n}\\ ⋮& ⋮& x_{ij}& ⋮\\ x_{m1}& x_{m2}& \cdots & x_{mn}\end{array}\right)$$

(1)

Step 2.

Data standardization processing, establishing the standard discriminant matrix Y

Due to the different dimensions and sizes of the indicators, in order to reflect the commonness of each indicator in the comprehensive evaluation, the extreme value method is used to obtain dimensionless and normalized indicators, and the standard discriminant matrix Y is given as follows:

$$Y={(y_{ij})}_{m\times n}$$

(2)

For positive indicators

$$y_{ij}={\displaystyle \frac{x_{ij}-\mathit{min}(x_j)}{\mathit{max}(x_j)-\mathit{min}(x_j)}}$$

(3)

For negative indicators

$$y_{ij}={\displaystyle \frac{{\mathit{max}(x_j)-x}_{ij}}{\mathit{max}(x_j)-\mathit{min}(x_j)}}$$

(4)

$\mathit{max}(x_j) and \mathit{min}(x_j$) are, respectively, the maximum and minimum values of the jth indicator. After removing dimensions and normalizing, $y_{ij}\in \left(0, 1\right).$

Step 3.

Constructing the weighted decision matrix Z

Because there are differences between indicators for the seismic resilience of sites, a weighted decision matrix considering the weights of indicators is constructed on the basis of the standard discrimination matrix Y:

$$Z={{(z_{ij})}_{m\times n}=w}_j{\times (y_{ij})}_{m\times n}$$

(5)

where $w_j$ is the weight of the jth indicator, $w_j\in \left(0, 1\right)$. After research and comparison, the entropy weighting method, which highlights local differences, is used to determine the weights of each indicator.

Step 4.

Determining the positive ideal solution $S_j^{+}$ and the negative ideal solution $S_j^{-}$ for the jth indicator

In the TOPSIS model, the positive ideal solution and negative ideal solution are defined. The positive ideal solution, which is a set of data composed of the most advantageous indicators for evaluation results, is given by Equation (6). The negative ideal solution, which is a set of data composed of the most disadvantageous indicators for evaluation results, is given by Equation (7).

$$S_j^{+}=\left\{(\underset{i}{max(z_{ij})}|j\in J),(\underset{i}{min(z_{ij})}|j\in J^{\prime })\right\}=\left\{S_1^{+},S_2^{+},\dots ,S_n^{+}\right\}$$

(6)

$$S_j^{-}=\left\{(\underset{i}{min(z_{ij})}|j\in J),(\underset{i}{max(z_{ij})}|j\in J^{\mathrm{’}})\right\}=\left\{S_1^{-},S_2^{-},\dots ,S_n^{-}\right\}$$

(7)

$J$ and $J^{\prime }$ represent the subscript of the positive indicator and the subscript of the negative indicator, respectively.

Step 5.

Determining the distance $D_i^{+}$ and $D_i^{-}$ to positive and negative ideal solutions on indicators of each site, and giving the proximity degree $C_i$ to positive ideal solutions

In the seismic resilience of building sites, a set of indicators is given for each site according to the indicator evaluation system. In actual evaluation, there is a distance that is expected to be close to the positive one between the set and the positive and negative ideal solutions. In this paper, the Euclidean distance is calculated, the distance to the positive ideal solution is determined with Equation (8), and the distance to the negative ideal solution is determined with Equation (9).

$$D_i^{+}={(\sum _{j=1}^n(z_{ij}-s_j^{+}{)}^2) }^{{\displaystyle \frac{1}{2}}} , i=1, 2,\dots ,m$$

(8)

$${ D}_i^{-}={(\sum _{j=1}^n(z_{ij}-s_j^{-}{)}^2) }^{{\displaystyle \frac{1}{2}}} , i=1, 2,\dots ,m$$

(9)

By using $D_i^{+}$ and $D_i^{-}$, the proximity degree between the indicator set of each site and the positive ideal solution set can be calculated using Equations (1)–(9), which is defined as the proximity degree of building sites.

$$C_i={\displaystyle \frac{D_i^{-}}{ D_i^{-}+D_i^{+}}}, i=1, 2,\dots ,m$$

(10)

Step 6.

Evaluating the seismic resilience and rank division of building sites by the proximity degree

The proximity degree represents the close degree between the indicator set and the positive ideal solution set; the value range is (0, 1), which means the larger the value, the closer the indicator set is to the positive ideal solution set, and the higher the seismic resilience, and vice versa. It should be emphasized that seismic resilience, such as seismic intensity, is not a measurable physical quantity but a relative standard to measure the seismic performance of the site; therefore, the site proximity degree is used to evaluate the seismic resilience of building sites. In order to be consistent with the national standard GB/T38591-2020, the seismic resilience of building sites is divided into three parts, shown in Table 2.

Table 2. Seismic resilience division of building sites.

Proximity Degree C	0 < C ≤ 0.35	0.35 < C ≤ 0.65	0.65 < C ≤ 1.00
Rank Division	low	middle	high

3.1.2. Entropy Method

The TOPSIS model needs to give the weight of each indicator. After research and comparison, the entropy weighting method, which highlights local differences, is adopted to determine the weight of each indicator. Entropy is a thermodynamic and statistical physical concept. In the 1940s, C.E. Shannon, an American mathematician, electrical engineer, and founder of information theory, introduced the concept of entropy into communication engineering and proposed the concept of information entropy. Information entropy is a measure of information. Entropy reflects the amount of information on different signals in the system, also reflecting the importance of different signals. In multi-indicator synthesis, the concept of entropy is used to reflect the importance of different indicators in evaluation, and the entropy weighting method is formed. It is an objective weighting method with no interference from human factors, objectively reflecting the importance of each indicator in the comprehensive evaluation system. The steps for calculating indicator weights by the entropy method are as follows:

Step 1.

Creating the initial matrix

The initial matrix is constructed according to Equation (1).

Step 2.

Data standardization processing

Initial matrix data are processed according to Equations (3) and (4), and Equation (2) is obtained.

Step 3.

Calculating the proportion $P_{ij}$ of the jth indicator in the ith site

$$P_{ij}=Y_{ij}/(\sum _{i=1}^m{Y}_{ij})$$

(11)

Step 4.

Calculating the information entropy $E_j$ of the jth indicator

$$E_j=(-\sum _{i=1}^m{P}_{ij}\mathit{ln}{P}_{ij})/\mathit{ln}(m)$$

(12)

$E_j\ge 0$, according to Equation (11); when $Y_{ij}=0$, $P_{ij}=0$, it does not meet the mathematical requirements of Equation (12). In this situation, coordinate translation can be used to process these data to meet the mathematical requirements [55,56,57]. When $Y_{ij}=0$, $E_j=0$.

Step 5.

Calculating the weight $w_j$ of the jth indicator

$$w_j=(1-E_j)/\sum _{j=1}^m(1-E_j)$$

(13)

3.2. Data

In order to investigate the applicability and feasibility of the proposed method, 60 building sites in the Beijing area are selected as examples for analysis. It should be noted that because soft soil does not exist in Beijing, and there is no dangerous rock mass within 1 km, the A₂₇, A₂₁₁, and A₂₁₂ are excluded from the actual calculation.

3.2.1. Basic Information of Sites

We selected 60 representative building sites as evaluation subjects, with their locations shown in Figure 1. The information for these sites was obtained from seismic safety evaluation reports and geotechnical investigation reports. As an example, we provide the seismic resilience indicator values for five of these sites, as shown in Table 3. Figure 2 shows the distribution of sites. Building sites in Beijing are mainly of type II and type III (Figure 3). Type II sites are mostly concentrated in the western part of Beijing, such as Xicheng District, Shijingshan District, Fengtai District, and the eastern part of Mentougou District, while type III sites are mostly concentrated in the eastern part of Beijing, such as Chaoyang District, Dongcheng District, Tongzhou District, and the northern part of Daxing District.

Table 3. Basic information for five building sites.

Site ID	Building Name	Site Location	Geomorphic Type	Description of Geotechnical Characteristics for Sites	Site Category [5]
S1	Beijing Hospital of Traditional Chinese Medicine University Dongzhimen Hospital renovation and expansion project	Dongchen District	The middle of the Yongding River alluvial plain	Mainly composed of silty clay, clay silt, sandy silt, sand, and pebble layer	III
S2	HIJ block construction project, Xidian Village, Sunhe Township	Chaoyang District	Yongding River alluvial plain	Mainly composed of silty clay, sand, and pebble layer	III
S3	Dongfeng Home five district project 4#-1 land commodity housing project	Chaoyang District	The middle of the Yongding River alluvial plain	Mainly composed of clay, sand, and pebble layer	III
S4	Yinhe Business District K block C2 commercial finance project	Shijingshan District	The top of the Yongding River alluvial plain	Mainly composed of silty clay, residual soil, and tuff	II
…	…	…	…	…	…
S60	Chinese Academy of Arts Wanquan Temple residential area	Fengtai District	The top and middle of the Yongding River alluvial plain	Mainly composed of clay, silty clay, fine sand, and pebble layer	II

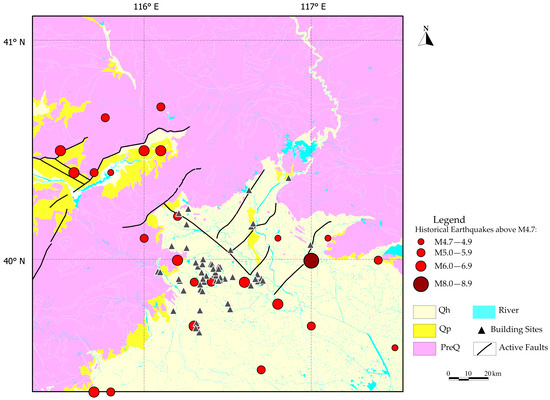
Figure 2. Maps of 60 building sites.

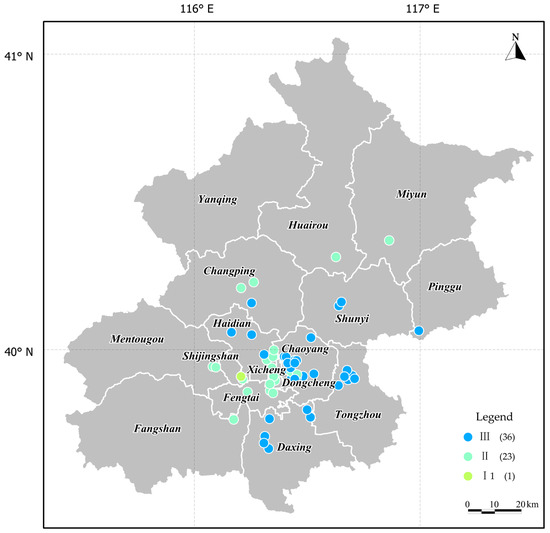
Figure 3. Category distribution map of 60 building sites in Beijing (The numbers in parentheses represent the number of building sites).

3.2.2. Creating the Initial Matrix

According to the seismic resilience evaluation system for building sites (Table 1), indicator data are extracted, and the initial matrix $X={(x_{ij})}_{60\times 20}$ is established; some site data extracted are listed in Table 4. Equations (3) and (4) are used to standardize data from the 60 building sites listed in Table 4, and the standard discrimination matrix $Y={(y_{ij})}_{m\times n}$ is given. Using the entropy method, the weights of each indicator are given by Equations (11)–(13), detailed in the Supplementary Materials. The results are listed in Table 4.

Table 4. Site initial matrix data and indicator weights.

Criteria Layer	Indicators	Site ID
		S1	S2	S3	S4	S5	…	S60	Indicator Weight	Sorting	Criteria Layer Weight
Seismic Action (A1)	A11	425	380	400	420	395	…	430	0.0578	1	0.2266
	A12	0.8	0.9	0.9	0.7	0.65	…	0.5	0.0557	7
	A13	8	9	9	8	8	…	8	0.0576	2
	A14	0.4778	0.4778	0.4234	0.1198	0.1318	…	0.4384	0.0555	8
Site Seismic Capacity (A2)	A21	0.057	0.057	0.057	0.115	0.115	…	0.057	0.0470	16	0.4303
	A22	52	83	90	23	34	…	29	0.0479	13
	A23	210	180	214	217	233	…	321	0.0570	3
	A24	8	1.25	4.8	10	10	…	10	0.0477	15
	A25	2	2	2	2	3	…	2	0.0562	5
	A26	16.9	25.01	24.56	21.23	12.19	…	12.06	0.0521	10
	A28	30	6.35	30	30	30	…	30	0.0478	14
	A29	0	3.5	0	0	0	…	0	0.0182	20
	A210	12	16	12	12	12	…	10	0.0564	4
Site Recovery Capability (A3)	A31	2	2	3	2	1	…	3	0.0524	9	0.3431
	A32	2	2	1	2	3	…	1	0.0502	11
	A33	1	2	1	1	1	…	2	0.0462	18
	A34	1	2	3	3	3	…	2	0.0489	12
	A35	2	2	2	2	2	…	3	0.0562	6
	A36	42	35	80	100	98	…	84.2	0.0425	19
	A37	1	2	1	1	1	…	1	0.0467	17

3.2.3. Calculating the Proximity Degree of Sites

According to data provided in Table 4 and the weight of indicators, the TOPSIS model can be used to calculate the proximity degree between the indicator set and the positive ideal solution set of 60 sites from Equations (3)–(10). Specifically, the site proximity degree is defined. The results are listed in Table 5. The seismic resilience of sites is ranked by the site proximity degree, and the resilience levels of sites are divided according to the division standards in Table 2. The results are listed in Table 5, and the proximity distribution of sites is shown in Figure 3.

Table 5. Proximity degree and resilience rank of building sites.

Sort	Proximity Degree	Site Type	Site ID	Rank	Sort	Proximity Degree	Site Type	Site ID	Rank	Sort	Proximity Degree	Site Type	Site ID	Rank
1	0.9407	II	32	high	21	0.5658	III	7	middle	41	0.4706	III	26	middle
2	0.9339	III	12	high	22	0.5558	III	47	middle	42	0.4657	III	54	middle
3	0.9297	I1	52	high	23	0.5480	III	14	middle	43	0.4653	II	42	middle
4	0.6532	II	5	high	24	0.5478	III	33	middle	44	0.4477	III	16	middle
5	0.6370	III	29	middle	25	0.5425	III	28	middle	45	0.4420	III	44	middle
6	0.6273	III	49	middle	26	0.5393	III	57	middle	46	0.4160	III	1	middle
7	0.6238	II	9	middle	27	0.5362	II	10	middle	47	0.4111	II	22	middle
8	0.6178	II	45	middle	28	0.5352	III	48	middle	48	0.4080	III	24	middle
9	0.6130	III	19	middle	29	0.5329	III	27	middle	49	0.4001	III	2	middle
10	0.6126	II	59	middle	30	0.5295	II	8	middle	50	0.3925	II	4	middle
11	0.6047	II	31	middle	31	0.5264	III	37	middle	51	0.3758	II	36	middle
12	0.6004	II	51	middle	32	0.5250	II	38	middle	52	0.3719	III	23	middle
13	0.5986	III	39	middle	33	0.5147	III	46	middle	53	0.3669	II	43	middle
14	0.5907	II	53	middle	34	0.5133	II	55	middle	54	0.3587	II	60	middle
15	0.5892	III	11	middle	35	0.5004	II	50	middle	55	0.3544	III	41	middle
16	0.5762	III	58	middle	36	0.4883	III	13	middle	56	0.3472	III	3	low
17	0.5727	III	34	middle	37	0.4867	II	30	middle	57	0.3436	III	40	low
18	0.5722	II	18	middle	38	0.4852	III	17	middle	58	0.3279	III	56	low
19	0.5718	II	35	middle	39	0.4844	III	15	middle	59	0.3253	III	20	low
20	0.5693	II	25	middle	40	0.4720	III	6	middle	60	0.3225	III	21	low

4. Discussion

Based on the analysis of Table 4, it can be seen that, in the criteria layer, the seismic capacity of sites has the greatest weight, indicating that the seismic capacity of sites has the greatest influence on the sites’ seismic resilience. In the 20 indicators, the Peak Ground Acceleration, the highest intensity of influence on the site, and equivalent shear wave velocity of the soil layer have the greater influence on building sites. SPT, surface rupture, category of seismic fortification for buildings, spectral period, and average annual occurrence times of earthquakes above M4.0 are the second. The foundation function requirements for buildings, height, and thickness of liquefiable sand layers within 30 m depth are the least. The above results are basically consistent with the common understanding within the engineering field at present, indicating that the method proposed in this paper can be applied to the evaluation of seismic resilience of building sites and is practically applicable to the Beijing area.

It can also be seen from Table 5 that the four sites with high resilience are characterized by no geological disasters such as sand liquefaction, shallow thickness of cover layer, weak fault activity, and little influence of groundwater; therefore, the resilience value is higher. The five sites with low resilience are characterized by severe sand liquefaction, deep thickness of cover layer, and high historical seismic intensity. In general, the site with low resilience has strong seismic activity, poor site conditions, and serious seismic geological disasters. After an earthquake, the basic functions of the site are restored slowly. The results align with the definition of the seismic resilience of building sites in this paper.

As can be seen from Figure 4, the sites with high resilience are in Shijingshan District, the southern part of Haidian District, and the eastern part of Chaoyang District, while the sites with low resilience are located at the border of Chaoyang District and Dongcheng District, which is closely related to site conditions. According to the analysis in Table 5, although the level of site resilience does not exactly correspond to the site category, the trend is that the sites with low resilience are all type III, which is consistent with the usual recognition. The reason why the resilience of the site is not completely consistent with the site category is that the resilience of the building site is determined by more than 20 indicators, including seismic action, site seismic capacity, and recovery capability, while the category of the site is determined by the double indicators including the thickness of the site covering layer and equivalent shear wave velocity of the soil layer. The selection of evaluation indicators needs further exploration, especially the site recovery ability after the earthquake, which has many influencing factors. The entropy method is objective with no interference from human factors, and can objectively reflect the importance of each indicator in the comprehensive evaluation system; however, the determination of the weight of each indicator by using the entropy method is affected by the number and type of sites, so it is necessary to explore further the number and type of sites that must be satisfied by the stable weight of each indicator. In summary, the study of the seismic resilience evaluation of building sites is still in the initial stage, and some problems need to be further explored. It can be predicted that the study of site seismic resilience will become a rich field in geotechnical engineering seismic research in the future. This paper is only a preliminary exploration of this aspect.

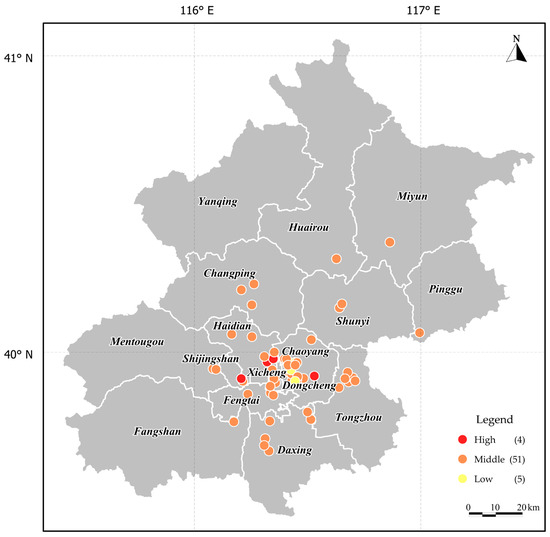
Figure 4. Resilience distribution map of 60 building sites in Beijing (The numbers in parentheses represent the number of building sites).

5. Conclusions

The seismic resilience of sites is an important part of the seismic resilience of buildings. The seismic resilience of building sites and their evaluation is a brand new concept and, thus, an important research direction in the seismic field of geotechnical engineering. The purpose of evaluating the seismic resilience of sites is to facilitate the assessment of the seismic resilience of buildings and compensate for the deficiencies in the evaluation of the seismic resilience of buildings regarding the influence of the site; it further enhances the evaluation criteria for assessing the seismic resilience of buildings. In this paper, the seismic resilience of building sites mainly refers to the ability of the site to withstand earthquake damage and recover after an earthquake. Therefore, 23 indicators are used to evaluate the seismic resilience of the building sites from three dimensions: the possible seismic action, the site seismic capacity, and the site recovery capability. The selection of evaluation indicators is a problem that needs further in-depth research, especially the ability of the site to recover after experiencing seismic action, which is affected by many factors.

The entropy method is an objective weighting method unaffected by human factors, which can objectively reflect the importance of each evaluation indicator in the comprehensive evaluation system. However, determining the weights of each evaluation indicator in the site using the entropy method is influenced by the number and type of sites, and further exploration is needed to determine the number and type of sites required for each evaluation index to have a stable weight.

In addition to the determination of weights, the choice of evaluation method is also very important. In subsequent research, the suitability and rationality of various mathematical methods for application to the evaluation of site resilience will be further argued and verified. Based on the characteristics of site seismic resilience evaluation, new comprehensive mathematical evaluation methods will be explored. With the increase in engineering site investigation reports and seismic safety evaluation reports, statistical data on seismic resilience evaluation of building sites in Beijing will be enriched in the future, providing more scientific and comprehensive seismic resilience evaluation for building sites in Beijing.

In summary, the research on the seismic resilience evaluation of building sites is still in its infancy, and there are still some issues that need further discussion. It can be predicted that, in the future, this will become a rich field of research in seismic engineering. This paper is only a preliminary exploration in this regard.