Wind-Induced Dynamic Critical Response in Buildings Using Machine Learning Techniques
Abstract
1. Introduction
2. Background
2.1. Dynamic Analysis of a Building Under Wind Action
2.2. Machine Learning Models
2.2.1. k-Nearest Neighbors
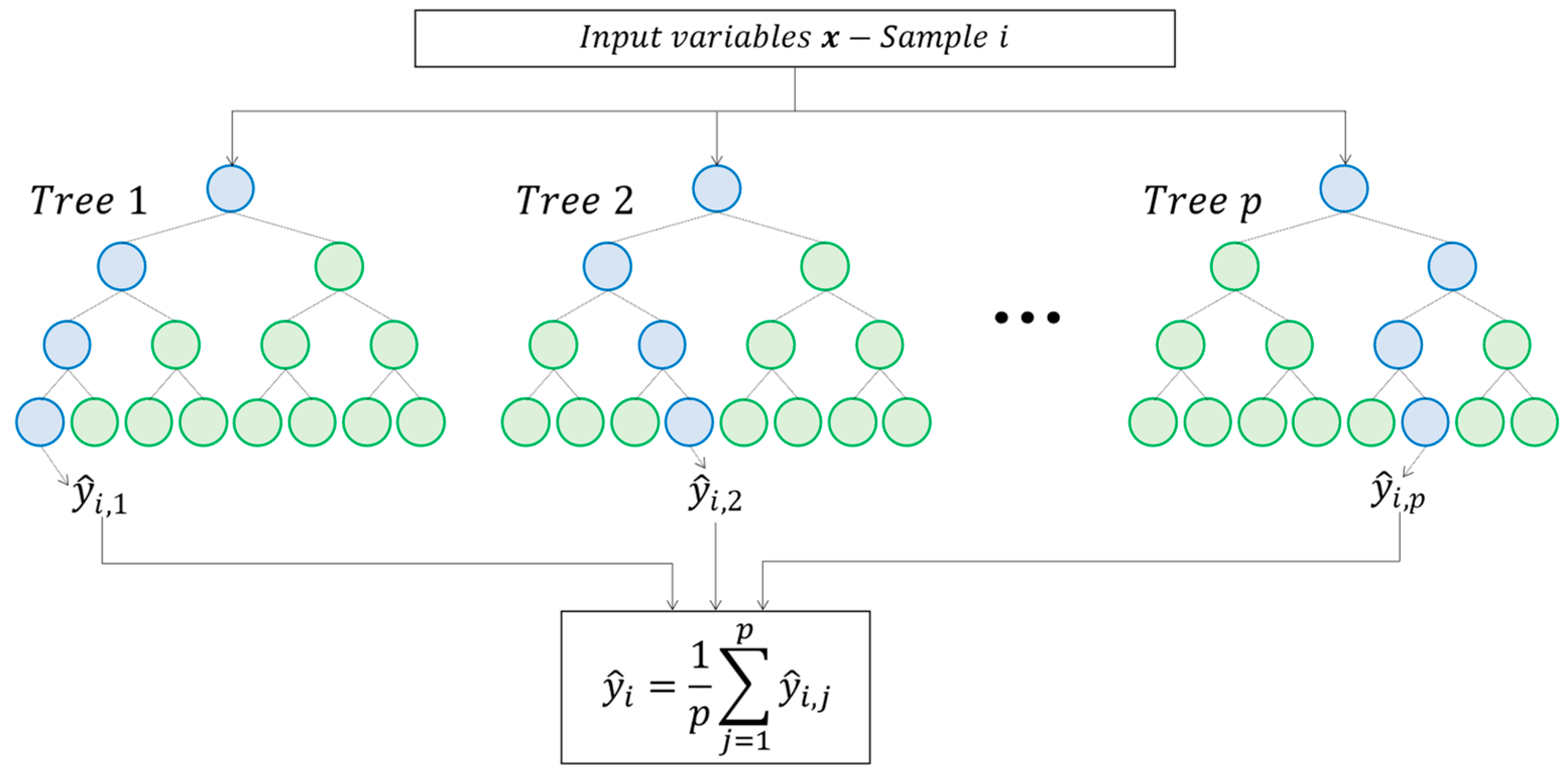
2.2.2. Random Forest
2.2.3. Support Vector Regression
2.2.4. Gaussian Process Regression
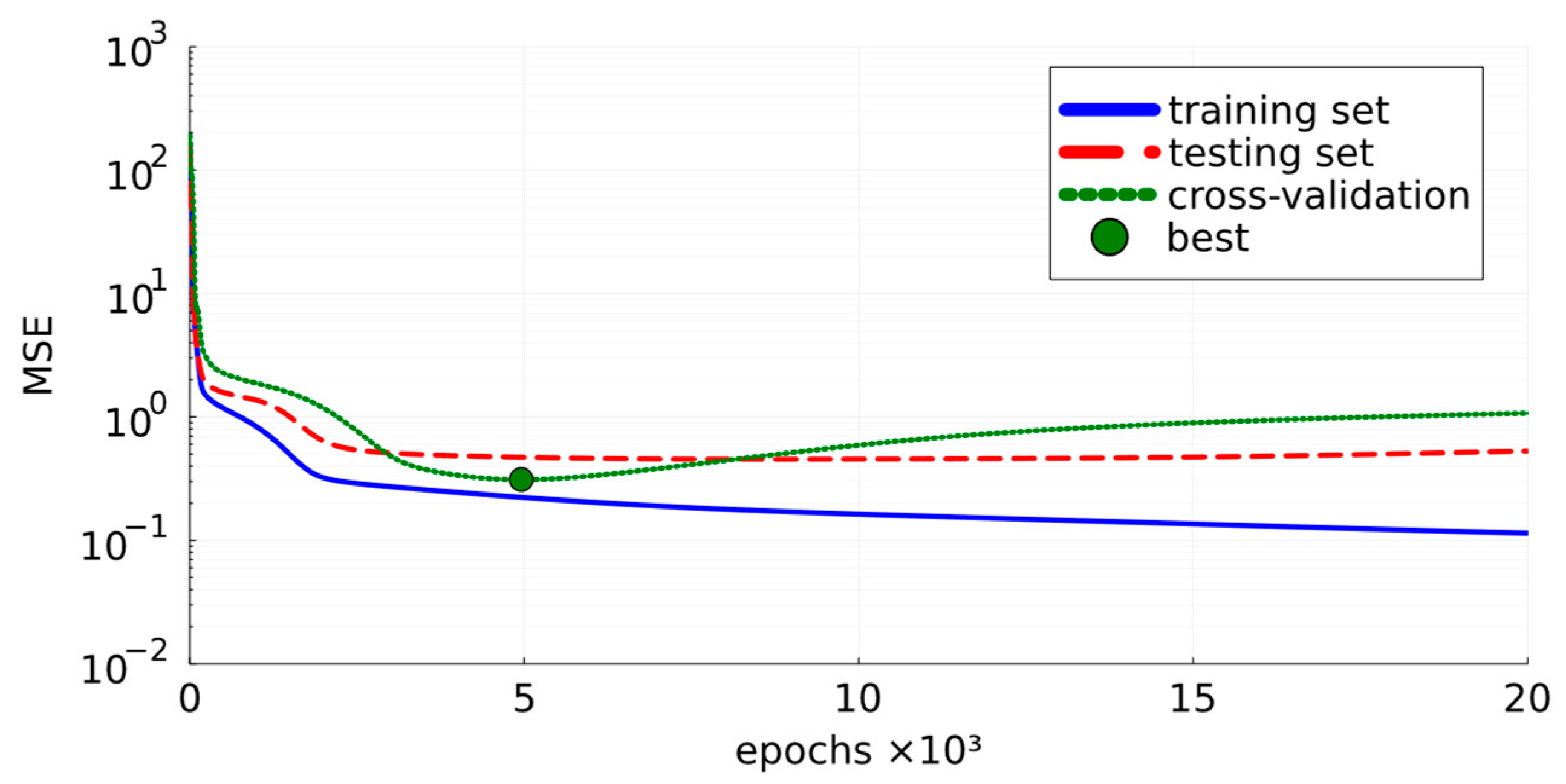
2.2.5. Artificial Neural Network
2.2.6. Performance Measurements of Machine Learning Models
3. Methodology
3.1. Presentation of the Problem
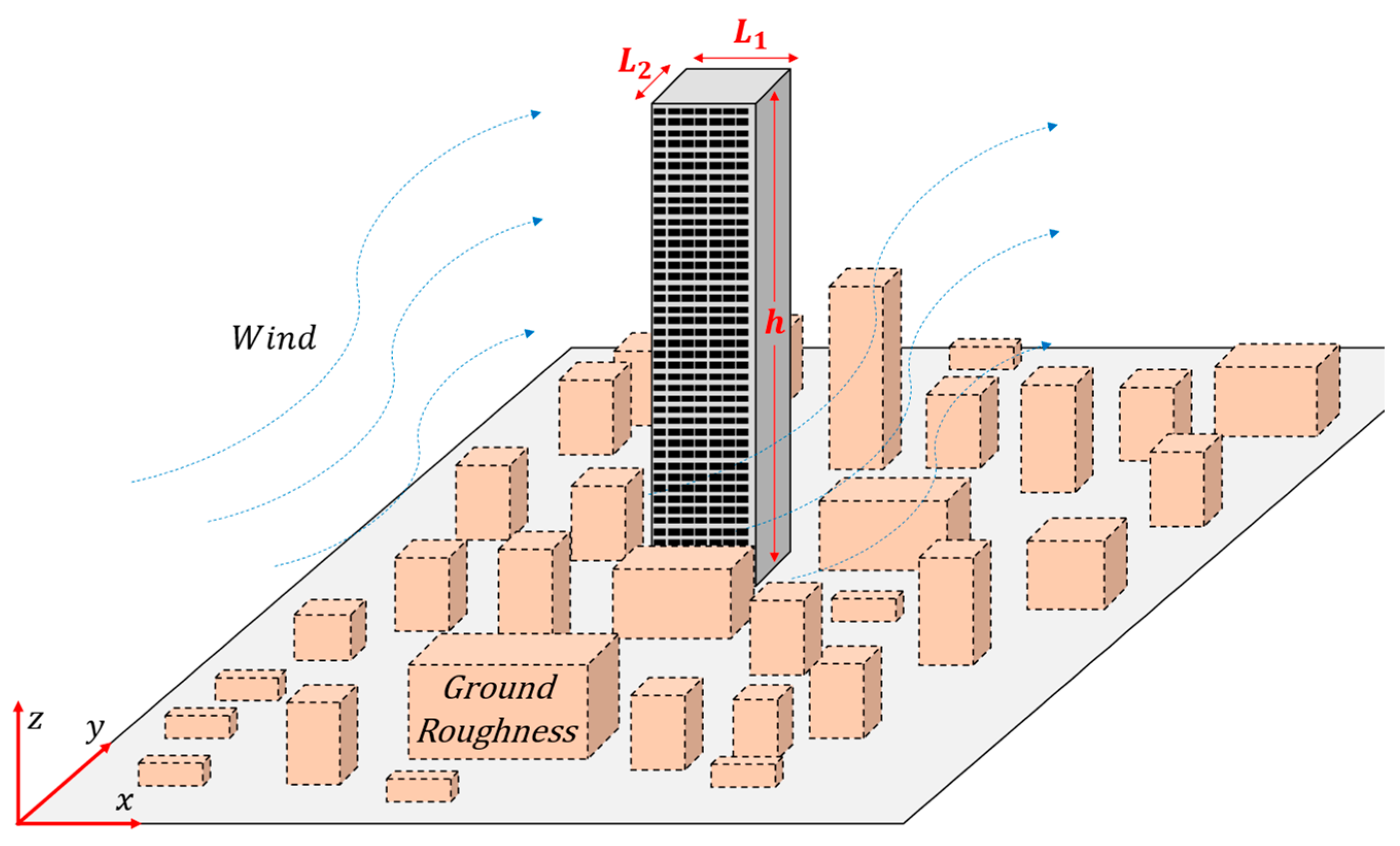
- Height (h)—dimension measured from the ground level to the top of the building. It influences the area obstructing the passage of wind (), aerodynamics (), and the natural vibration frequency of the building (), and consequently also the dynamic amplification of wind action.
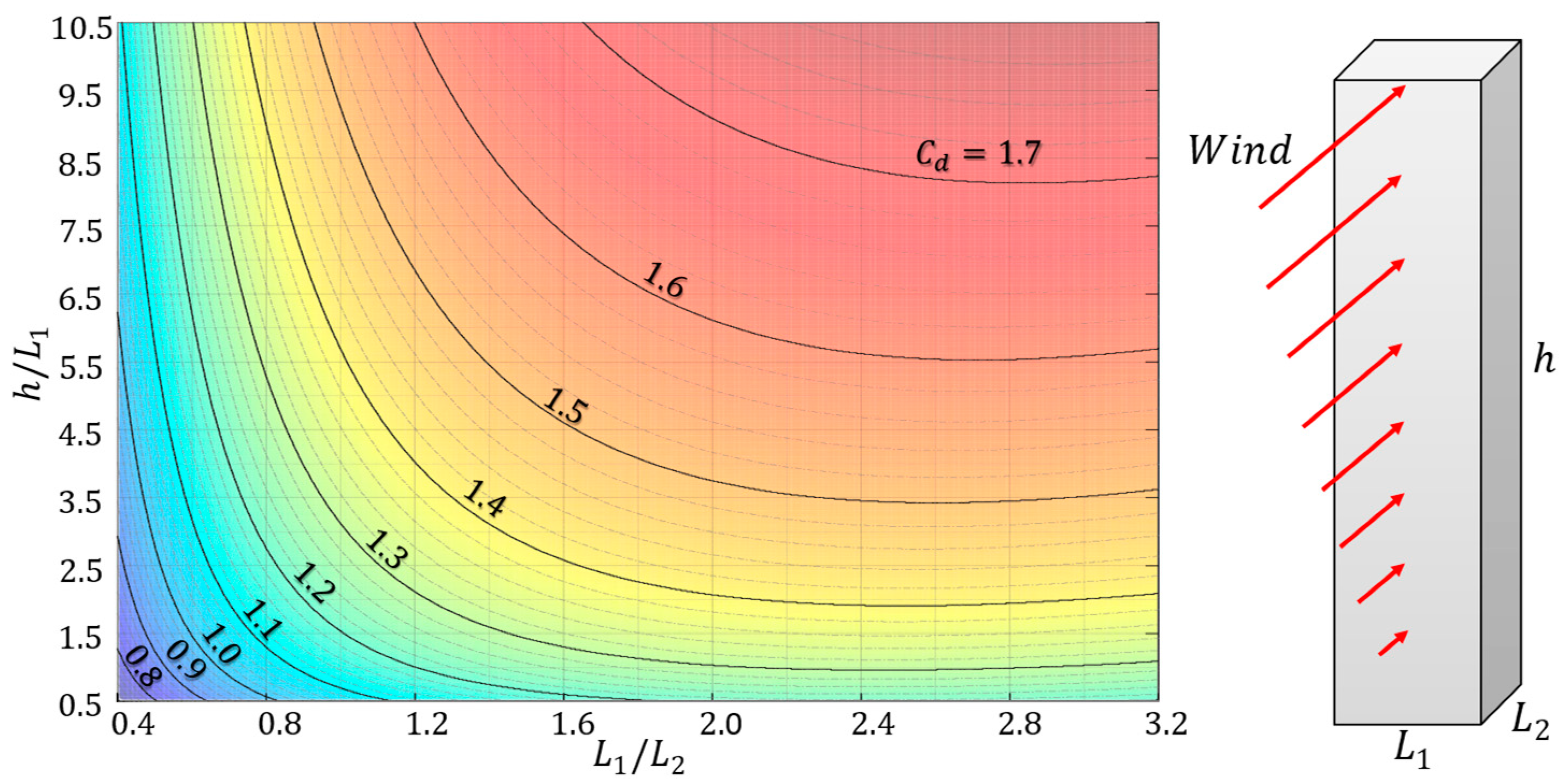
- Width ()—horizontal dimension of the building perpendicular to the wind direction. It influences the area obstructing the passage of wind (), aerodynamics (), and the mass of the structure ().
- Length ()—horizontal dimension of the building parallel to the wind direction. It influences the aerodynamics () and mass of the structure ().
- Average density of the building ()—influences the mass of the structure and, indirectly, the stiffness of the structure () given the correlation between mass and stiffness through frequency ().
- Building damping ratio ()—influences the dynamic response of the structure, mitigating displacement amplitudes.
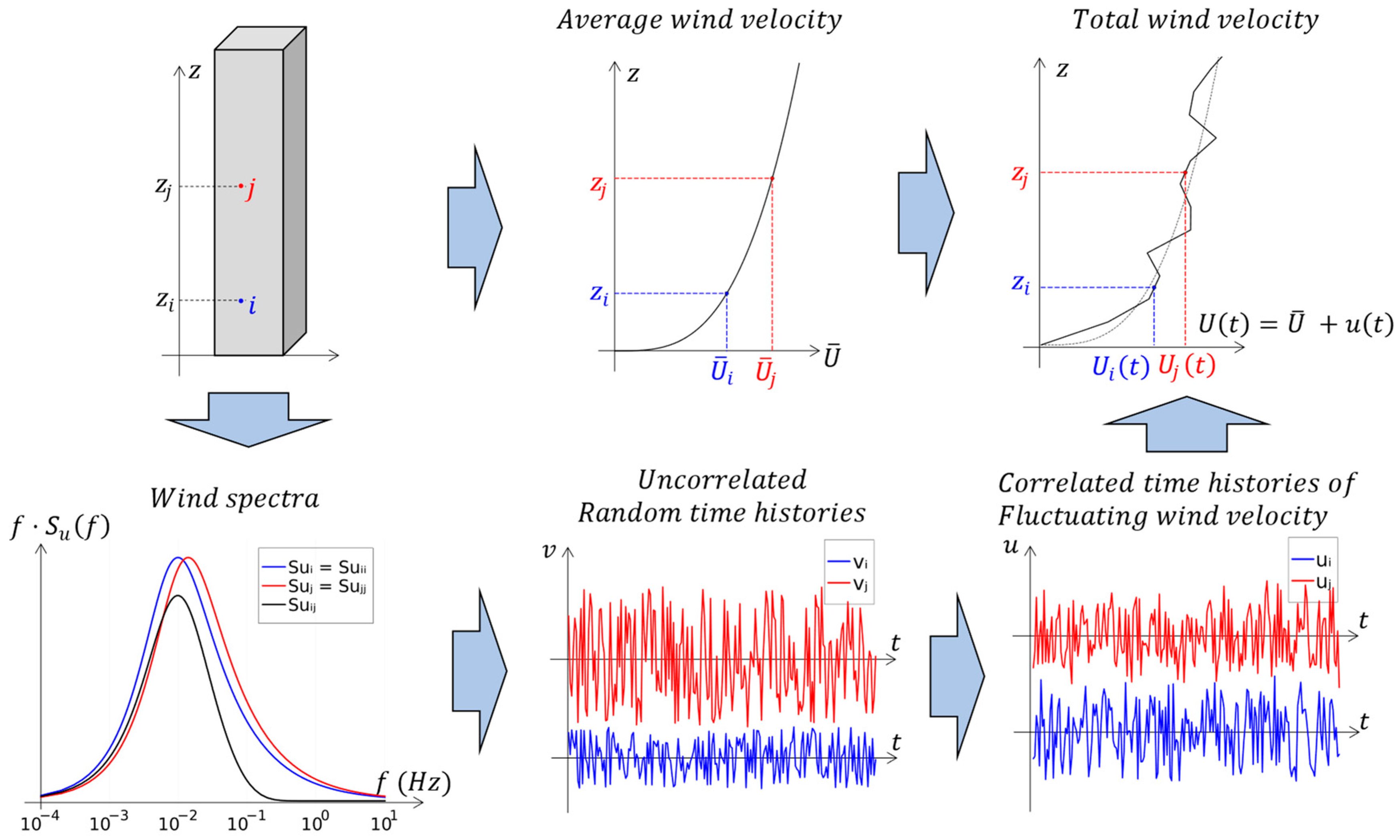
- Basic wind velocity ()—directly related to the average velocity and indirectly influences the intensity of flow turbulence, according to Equations (6) and (9).
- Ground surface roughness (GR)—represents the obstacles present around the building and is directly correlated to the intensity of flow turbulence. The standards EN 1991-1-4 [56] and NBR 6123 [55] present 5 categories, the first referring to large smooth surfaces and the last referring to the case of terrain covered by numerous, large, high, and closely spaced obstacles. The other categories represent intermediate conditions.
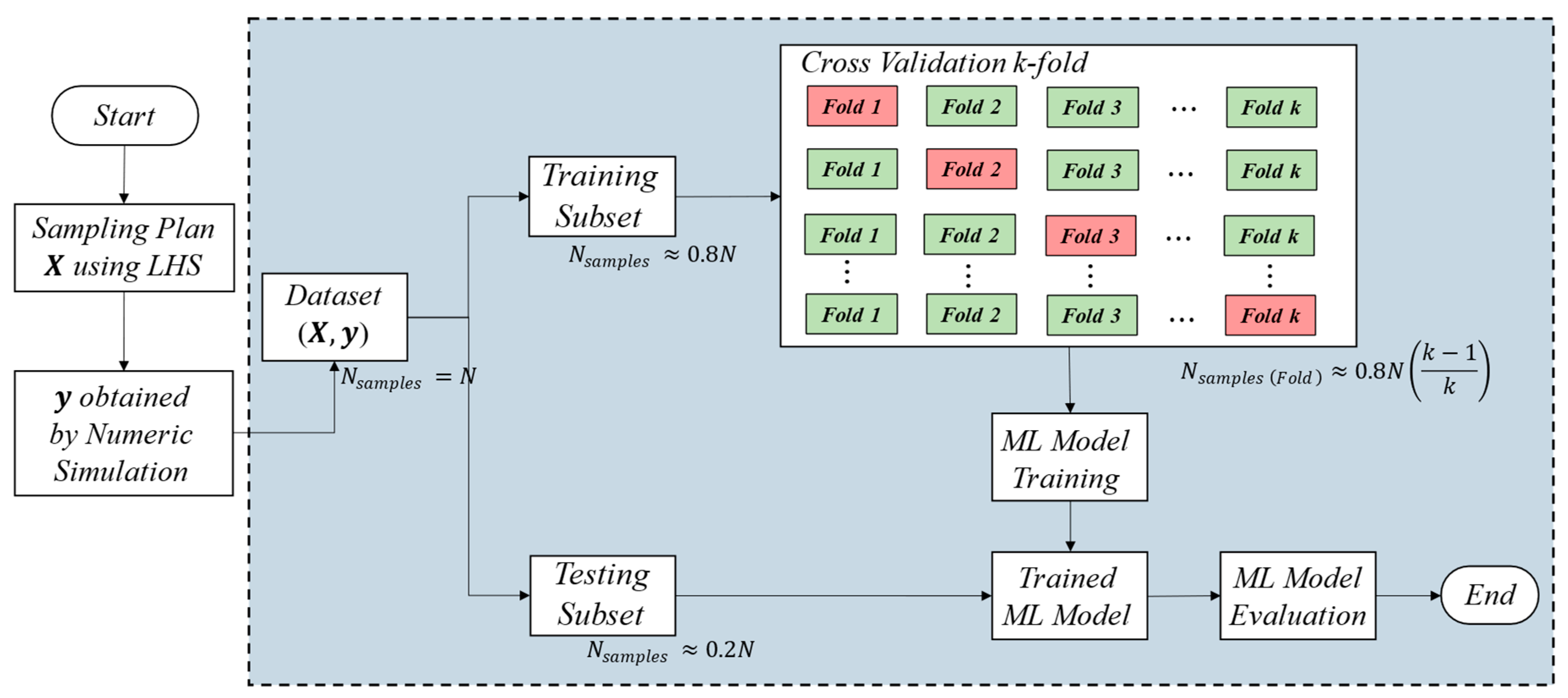
3.2. Sampling and Determination of the Target Variable Values
3.3. Machine Learning Models
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- CTBUH. Tall buildings in 2019: Another record year for supertall completions. CTBUH J. 2020, 1, 42–51. [Google Scholar]
- Iancovici, M.; Ionică, G.; Pavel, F.; Mota, F.; Nica, G.B. Nonlinear dynamic response analysis of buildings for wind loads. A new frontier in the structural wind engineering. J. Build. Eng. 2022, 47, 103708. [Google Scholar] [CrossRef]
- Hegyi, D.; Armuth, M.; Halmos, B.; Marotzy, K. The effect of wind on historical timber towers analyzed by plastic limit analysis in the focus of a collapse. Eng. Fail. Anal. 2022, 134, 105852. [Google Scholar] [CrossRef]
- Hareendran, S.P.; Alipour, A.; Shafei, B.; Sarkar, P. Characterizing wind-structure interaction for performance-based wind design of tall buildings. Eng. Struct. 2023, 289, 115812. [Google Scholar] [CrossRef]
- Avini, R.; Kumar, P.; Hughes, S.J. Wind loading on high-rise buildings and the comfort effects on the occupants. Sustain. Cities Soc. 2019, 45, 378–394. [Google Scholar] [CrossRef]
- Roncallo, L.; Solari, G.; Muscolino, G.; Tubino, F. Maximum dynamic response of linear elastic SDOF systems based on an evolutionary spectral model for thunderstorm outflows. J. Wind Eng. Ind. Aerodyn. 2022, 224, 104978. [Google Scholar] [CrossRef]
- Yaghmaei-Sabegh, S.; Daneshgari, S. Residual displacement ratios of highly damped SDOF systems by considering soft soil conditions. Soil Dyn. Earthq. Eng. 2023, 165, 107741. [Google Scholar] [CrossRef]
- Navarro-Quiles, A.; Laudani, R.; Falsone, G. Effect of uncertain damping coefficient on the response of a SDOF system. Probabilistic Eng. Mech. 2022, 68, 103238. [Google Scholar] [CrossRef]
- Clough, R.W.; Penzien, J. Dynamics of Structures, 3rd ed.; Computers and Structures: Berkeley, CA, USA, 2003. [Google Scholar]
- Jain, A.; Surana, M. Floor displacement-based torsional amplification factors for seismic design of acceleration-sensitive non-structural components in torsionally irregular RC buildings. Eng. Struct. 2022, 254, 113871. [Google Scholar] [CrossRef]
- Vicencio, F.; Alexander, N.A. Seismic Structure-Soil-Structure Interaction between a pair of buildings with consideration of rotational ground motions effects. Soil Dyn. Earthq. Eng. 2022, 163, 107494. [Google Scholar] [CrossRef]
- Surana, M.; Singh, Y.; Lang, D.H. Effect of structural characteristics on damping modification factors for floor response spectra in RC buildings. Eng. Struct. 2021, 242, 112514. [Google Scholar] [CrossRef]
- Wan, J.W.; Li, Q.S.; Han, X.L.; Xu, K. Investigation of structural responses and dynamic characteristics of a supertall building during Typhoon Kompasu. J. Wind Eng. Ind. Aerodyn. 2022, 230, 105209. [Google Scholar] [CrossRef]
- Huang, J.; Chen, X. Uncertainty analysis of inelastic response of high-rise buildings to wind using a reduced-order building model. Eng. Struct. 2023, 288, 116224. [Google Scholar] [CrossRef]
- Cruz, C.; Miranda, E. Evaluation of the Rayleigh damping model for buildings. Eng. Struct. 2017, 138, 324–336. [Google Scholar] [CrossRef]
- Dai, K.; Lu, D.; Zhang, S.; Shi, Y.; Meng, J.; Huang, Z. Study on the damping ratios of reinforced concrete structures from seismic response records. Eng. Struct. 2020, 223, 111143. [Google Scholar] [CrossRef]
- Lago, A.; Trabucco, D.; Wood, A. Damping Technologies for Tall Buildings: Theory, Design Guidance, and Case Studies, 1st ed.; Butterworth-Heinemann: Oxford, UK, 2019. [Google Scholar]
- Ellis, B.R. An assessment of the accuracy of predicting the fundamental natural frequencies of buildings and the implications concerning the dynamic analysis of structures. Proc. Inst. Civ. Eng. 1980, 69, 763–776. [Google Scholar]
- Reynolds, T.; Feldmann, A.; Ramage, M.; Chang, W.; Harris, R.; Dietsch, P. Design parameters for lateral vibration of multi-storey timber buildings. In Proceedings of the International Network on Timber Engineering Research Proceedings, Graz, Austria, 16–19 August 2016. [Google Scholar]
- Tamura, Y.; Suda, K.; Sasaki, A. Damping in buildings for wind resistant design. In Proceedings of the First International Symposium on Wind and Structures, Cheju, Republic of Korea, 26–28 January 2000. [Google Scholar]
- Doddipatla, L.S.; Kopp, G.A. Wind loads on roof-mounted equipment on low-rise buildings with low-slope roofs. J. Wind Eng. Ind. Aerodyn. 2011, 211, 104552. [Google Scholar] [CrossRef]
- Estephan, J.; Chowdhury, A.G.; Irwin, P. A new experimental-numerical approach to estimate peak wind loads on roof-mounted photovoltaic systems by incorporating inflow turbulence and dynamic effects. Eng. Struct. 2022, 252, 113739. [Google Scholar] [CrossRef]
- Alawode, K.J.; Vutukuru, K.S.; Elawady, A.; Chowdhury, A.G. Review of wind loading on roof to wall connections in low-rise light wood-frame residential buildings. J. Wind Eng. Ind. Aerodyn. 2023, 236, 105360. [Google Scholar] [CrossRef]
- Vital, W.; Silva, R.; Morais, M.V.; Sobrinho, B.E.; Pereira, R.; Evangelista Jr, F. Application of bridge information modelling using laser scanning for static and dynamic analysis with concrete damage plasticity. Alex. Eng. J. 2023, 79, 608–628. [Google Scholar] [CrossRef]
- Cluni, F.; Gioffrè, M.; Gusella, V. Dynamic response of tall buildings to wind loads by reduced order equivalent shear-beam models. J. Wind Eng. Ind. Aerodyn. 2013, 123, 339–348. [Google Scholar] [CrossRef]
- Nagase, T. Earthquake records were observed in tall buildings with tuned pendulum mass damper. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000. [Google Scholar]
- Martinez-Vazquez, P. Wind-induced vibrations of structures using design spectra. Int. J. Adv. Struct. Eng. 2016, 8, 379–389. [Google Scholar] [CrossRef]
- Braun, A.L.; Awruch, A.M. Aerodynamic and aeroelastic analyses on the CAARC standard tall building model using numerical simulation. Comput. Struct. 2009, 87, 564–581. [Google Scholar] [CrossRef]
- Pietrosanti, D.; De Angelis, M.; Basili, M. A generalized 2-DOF model for optimal design of MDOF structures controlled by Tuned Mass Damper Inerter (TMDI). Int. J. Mech. Sci. 2020, 185, 105849. [Google Scholar] [CrossRef]
- Ma, J.; Zou, W.; Bai, G. Analysis of random wind-induced response of isolation structure with viscoelastic damper and TMD. J. Wind Eng. Ind. Aerodyn. 2022, 230, 105178. [Google Scholar] [CrossRef]
- Lei, Z.; Liu, G.; Yang, Q.; Law, S.S.; Li, Y.; Cui, T. Experimental investigation on vibration suppression of a new prestressed TMD for wind turbine towers. Thin-Walled Struct. 2024, 202, 112080. [Google Scholar] [CrossRef]
- Xiang, Y.; Tan, P.; He, H.; Yao, H.; Zheng, X. Pendulum tuned mass damper (PTMD) with geometric nonlinear dampers for seismic response control. J. Sound Vib. 2024, 570, 118023. [Google Scholar] [CrossRef]
- Farsijani, D.; Gholam, S.; Karampour, H.; Talebian, N. The impact of the frequency content of far-field earthquakes on the optimum parameters and performance of tuned mass damper inerter. Structures 2024, 60, 105925. [Google Scholar] [CrossRef]
- Marrazzo, P.R.; Montuori, R.; Nastri, E.; Benzoni, G. Advanced seismic retrofitting with high-mass-ratio Tuned Mass Dampers. Soil Dyn. Earthq. Eng. 2024, 179, 108544. [Google Scholar] [CrossRef]
- Li, C.; Pan, H.; Cao, L. Pendulum-type tuned tandem mass dampers-inerters for crosswind response control of super-tall buildings. J. Wind Eng. Ind. Aerodyn. 2024, 247, 105706. [Google Scholar] [CrossRef]
- Fan, M.Y.; Li, W.J.; Luo, X.L.; Shui, Q.X.; Jing, L.Z.; Gu, Z.L.; Yu, C.W. Parameterised drag model for the underlying surface roughness of buildings in urban wind environment simulation. Build. Environ. 2022, 209, 108651. [Google Scholar] [CrossRef]
- LI, B.; Jiang, C.; Wang, L.; Liu, J. Wind tunnel study on influences of morphological parameters on drag coefficient of horizontal non-uniform buildings. Build. Environ. 2022, 207, 108412. [Google Scholar] [CrossRef]
- Evangelista, F., Jr.; Almeida, I.F. Machine learning RBF-based surrogate models for uncertainty quantification of age and time-dependent fracture mechanics. Eng. Fract. Mech. 2021, 258, 108037. [Google Scholar] [CrossRef]
- Evangelista, F., Jr.; García, N.A. A polynomial chaos expansion approach to the analysis of uncertainty in viscoelastic structural elements. DYNA: Revista de la Facultad de Minas. Universidad Nacional de Colombia. Sede Medellín 2016, 83, 172–182. [Google Scholar] [CrossRef]
- Silva, V.P.; Carvalho, R.D.A.; Rêgo, J.H.D.S.; Evangelista Jr, F. Machine Learning-Based Prediction of the Compressive Strength of Brazilian Concretes: A Dual-Dataset Study. Materials 2023, 16, 4977. [Google Scholar] [CrossRef]
- Lima, J.P.S.; Evangelista Jr, F.; Soares, C.G. Hyperparameter-optimized multi-fidelity deep neural network model associated with subset simulation for structural reliability analysis. Reliab. Eng. Syst. Saf. 2023, 239, 109492. [Google Scholar] [CrossRef]
- Wang, X.; Li, Z.; Shafieezadeh, A. Seismic response prediction and variable importance analysis of extended pile-shaft-supported bridges against lateral spreading: Exploring optimized machine learning models. Eng. Struct. 2021, 236, 112142. [Google Scholar] [CrossRef]
- Demertzis, K.; Kostinakis, K.; Morfidis, K.; Iliadis, L. An interpretable machine learning method for the prediction of R/C buildings’ seismic response. J. Build. Eng. 2023, 63, 105493. [Google Scholar] [CrossRef]
- Lin, P.; Hu, G.; Li, C.; Li, L.; Xiao, Y.; Tse, K.T.; Kwok, K.C. Machine learning-based prediction of crosswind vibrations of rectangular cylinders. J. Wind Eng. Ind. Aerodyn. 2021, 211, 104549. [Google Scholar] [CrossRef]
- Bright, I.; Lin, G.; Kutz, J.N. Compressive sensing based machine-learning strategy for characterizing the flow around a cylinder with limited pressure measurements. Phys. Fluids 2013, 25, 127102. [Google Scholar] [CrossRef]
- Weng, Y.; Paal, S.G. Machine learning-based wind pressure prediction of low-rise non-isolated buildings. Eng. Struct. 2022, 258, 114148. [Google Scholar] [CrossRef]
- Lin, P.; Ding, F.; Hu, G.; Li, C.; Xiao, Y.; Tse, K.T.; Kwok, K.C.S.; Kareem, A. Machine learning-enabled estimation of crosswind load effect on tall buildings. J. Wind Eng. Ind. Aerodyn. 2022, 220, 104860. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.; Yang, Y. Prediction of along-wind loading on tall building based on two-dimensional aerodynamic admittance. J. Wind Eng. Ind. Aerodyn. 2023, 238, 105439. [Google Scholar] [CrossRef]
- Li, S.; Li, X.; Yang, Q.; Zou, Y.; Hui, Y.; Wang, Y.; Su, Y.; Zeng, J.; Liao, Z. Modeling the along-wind loading on a high-rise building considering the turbulence scale effects in the wind tunnel tests. J. Build. Eng. 2024, 88, 109063. [Google Scholar] [CrossRef]
- Xu, L.; Spence, S.M.J. Collapse reliability of wind-excited reinforced concrete structures by stratified sampling and nonlinear dynamic analysis. Reliab. Eng. Syst. Saf. 2024, 250, 110244. [Google Scholar] [CrossRef]
- Choi, S.W.; Seo, J.H.; Lee, H.M.; Kim, Y.; Park, H.S. Wind-induced response control model for high-rise buildings based on resizing method. J. Civ. Eng. Manag. 2015, 21, 239–247. [Google Scholar] [CrossRef]
- Zeng, J.; Zhang, Z.; Li, M.; Li, S. Across-wind fluctuating aerodynamic force acting on large aspect-ratio rectangular prisms 2023. J. Fluids Struct. 2023, 121, 103935. [Google Scholar] [CrossRef]
- Li, Z.; Huang, G.; Chen, X.; Zhou, Y.; Yang, Q. Wind-resistant design and equivalent static wind load of base-isolated tall building: A case study. Eng. Struct. 2020, 212, 110533. [Google Scholar] [CrossRef]
- Gu, D.; Kareem, A.; Lu, X.; Cheng, Q. A computational framework for the simulation of wind effects on buildings in a cityscape. J. Wind Eng. Ind. Aerodyn. 2023, 234, 105347. [Google Scholar] [CrossRef]
- Associação Brasileira de Normas Técnicas (ABNT). Forças Devidas ao Vento em Edificações; NBR 6123—Wind Loads on Buildings; Brazilian Association for Technical Codes: Rio de Janeiro, Brazil, 2023. (In Portuguese) [Google Scholar]
- EN 1991-1-4:2005; Eurocode1: Actions on Structures—Part 1–4: General Actions—Wind Actions. CEN: Brussels, Belgium, 2005.
- ASCE. Minimum Design Loads for Buildings and Other Structures; ASCE Standard; ASCE: New York, NY, USA, 2016; pp. 7–16. [Google Scholar]
- Yan, B.; Shen, R.; Li, K.; Wang, Z.; Yang, Q.; Zhou, X.; Zhang, L. Spatio-temporal correlation for simultaneous ultra-short-term wind speed prediction at multiple locations. Energy 2023, 284, 128418. [Google Scholar] [CrossRef]
- Buchholdt, H.A. An Introduction to Cable Roof Structures, 2nd ed.; Thomas Telford: London, UK, 1999. [Google Scholar]
- Blessmann, J. O Vento Na Engenharia Estrutural, 2nd ed.; Editora da UFRGS: Porto Alegre, Brazil, 2013. [Google Scholar]
- Simiu, E.; Scanlan, R.H. Wind Effects on Structures: Fundamentals and Applications to Design, 3rd ed.; John Wiley: New York, NY, USA, 1996. [Google Scholar]
- Davenport, A.G. The application of statistical concepts to the wind loading of structures. Proc. Inst. Civ. Eng. 1961, 19, 449–472. [Google Scholar] [CrossRef]
- Géron, A. Hands-On Machine Learning with Scikit-Learn, Keras, and TensorFlow, 2nd ed.; O’Reilly Media: Sebastopol, CA, USA, 2019. [Google Scholar]
- Seghier, M.E.A.B.; Plevris, V.; Solorzano, G. Random forest-based algorithms for accurate evaluation of ultimate bending capacity of steel tubes. Structures 2022, 44, 261–273. [Google Scholar] [CrossRef]
- Tanga, A.T.; Araújo, G.L.S.; Evangelista, F., Jr. A comparison between geomembrane-sand tests and machine learning predictions. Geosynth. Int. 2024, 1–14. [Google Scholar] [CrossRef]
- Abellán-García, J.; Guzmán-Guzmán, J.S. Random forest-based optimization of UHPFRC under ductility requirements for seismic retrofitting applications. Constr. Build. Mater. 2021, 285, 122869. [Google Scholar] [CrossRef]
- Li, J.; Zhu, D.; Li, C. Comparative analysis of BPNN, SVR, LSTM, Random Forest, and LSTM-SVR for conditional simulation of non-Gaussian measured fluctuating wind pressures. Mech. Syst. Signal Process. 2022, 178, 109285. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Pourkamali-Anaraki, F. Support vector machine-based reliability analysis of concrete dams. Soil Dyn. Earthq. Eng. 2018, 104, 276–295. [Google Scholar] [CrossRef]
- Roy, A.; Manna, R.; Chakraborty, S. Support vector regression based metamodeling for structural reliability analysis. Probabilistic Eng. Mech. 2019, 55, 78–89. [Google Scholar] [CrossRef]
- Chocat, R.; Beaucaire, P.; Debeugny, L.; Lefebvre, J.P.; Sainvitu, C.; Breitkopf, P.; Wyart, E. Damage tolerance reliability analysis combining Kriging regression and support vector machine classification. Eng. Fract. Mech. 2019, 216, 106514. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, B.; Shiyuan, E. Adaptive relevance vector machine combined with Markov-chain-based importance sampling for reliability analysis. Reliab. Eng. Syst. Saf. 2022, 220, 108287. [Google Scholar] [CrossRef]
- Lima, J.P.S.; Evangelista Jr, F.; Soares, C.G. Bi-fidelity Kriging model for reliability analysis of the ultimate strength of stiffened panels. Mar. Struct. 2023, 91, 103464. [Google Scholar] [CrossRef]
- Hebbal, A.; Brevalt, L.; Balesdent, M.; Talbi, E.; Melab, N. Multi-fidelity modeling with different input domain definitions using Deep Gaussian Processes. Struct. Multidiscip. Optim. 2021, 63, 2267–2288. [Google Scholar] [CrossRef]
- Blevins, R.D. Formulas for Natural Frequency and Mode Shape, 1st ed.; Van Nostrand Reinhold Company: New York, NY, USA, 1979. [Google Scholar]
- Holmes, J.D. Wind Loading of Structures, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]



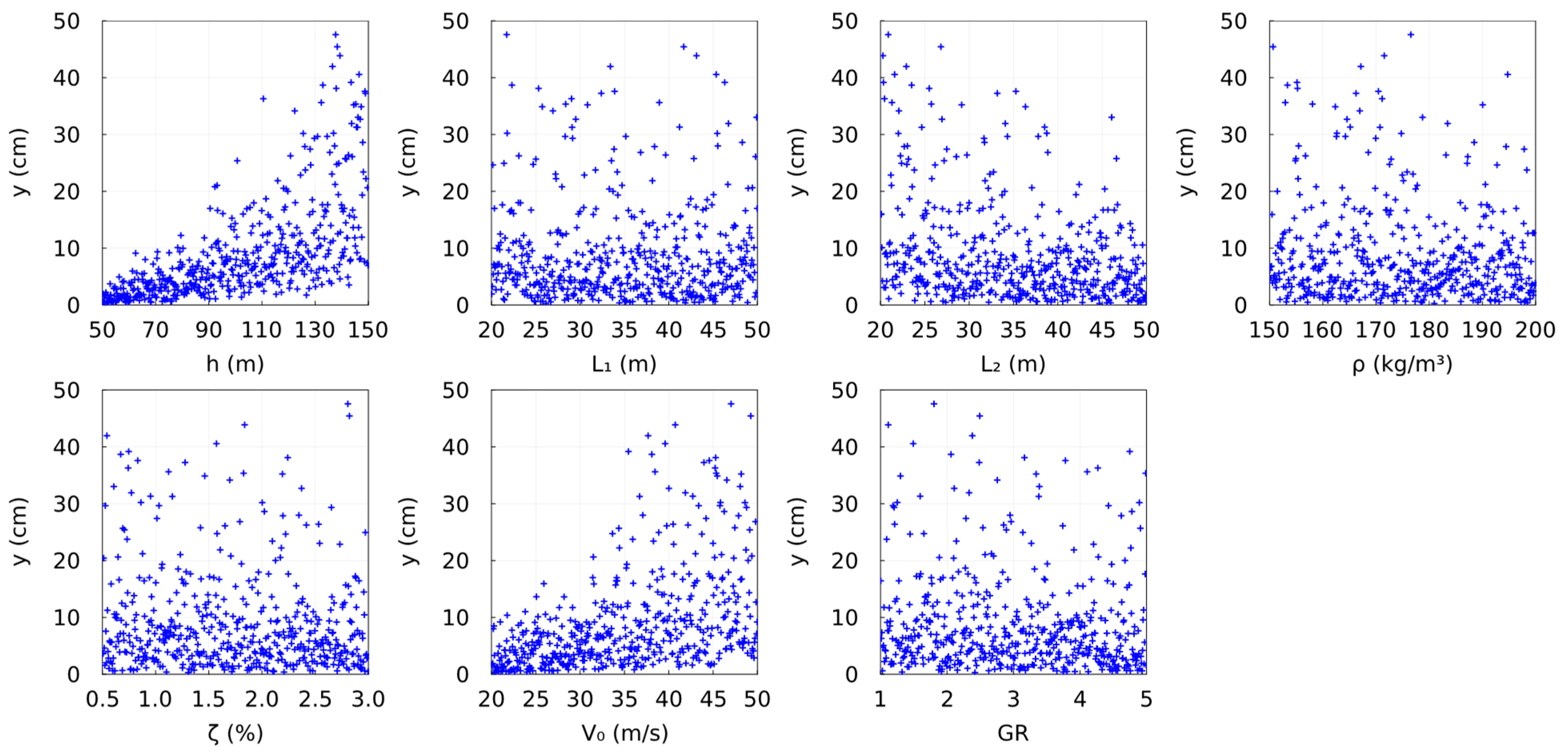
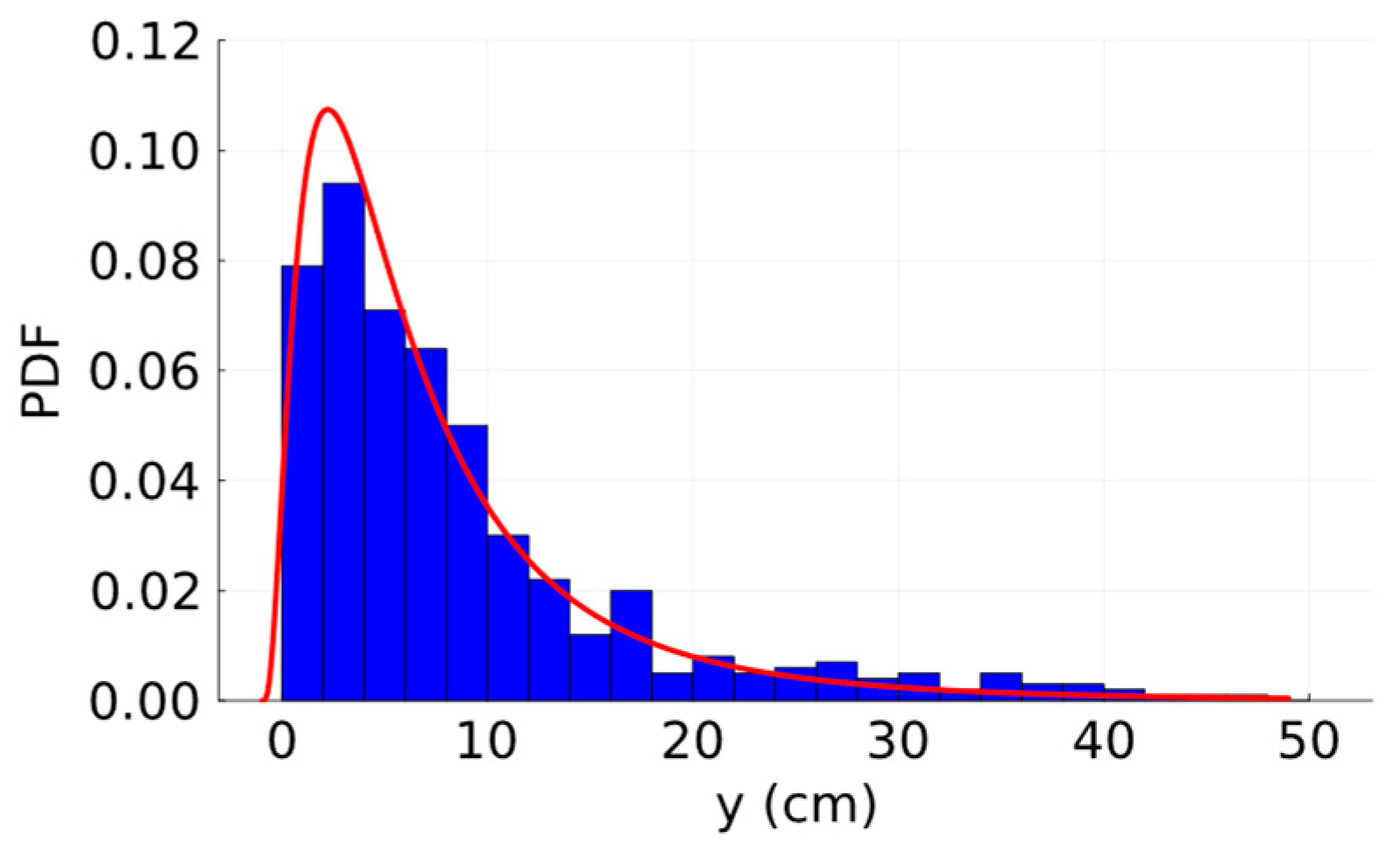
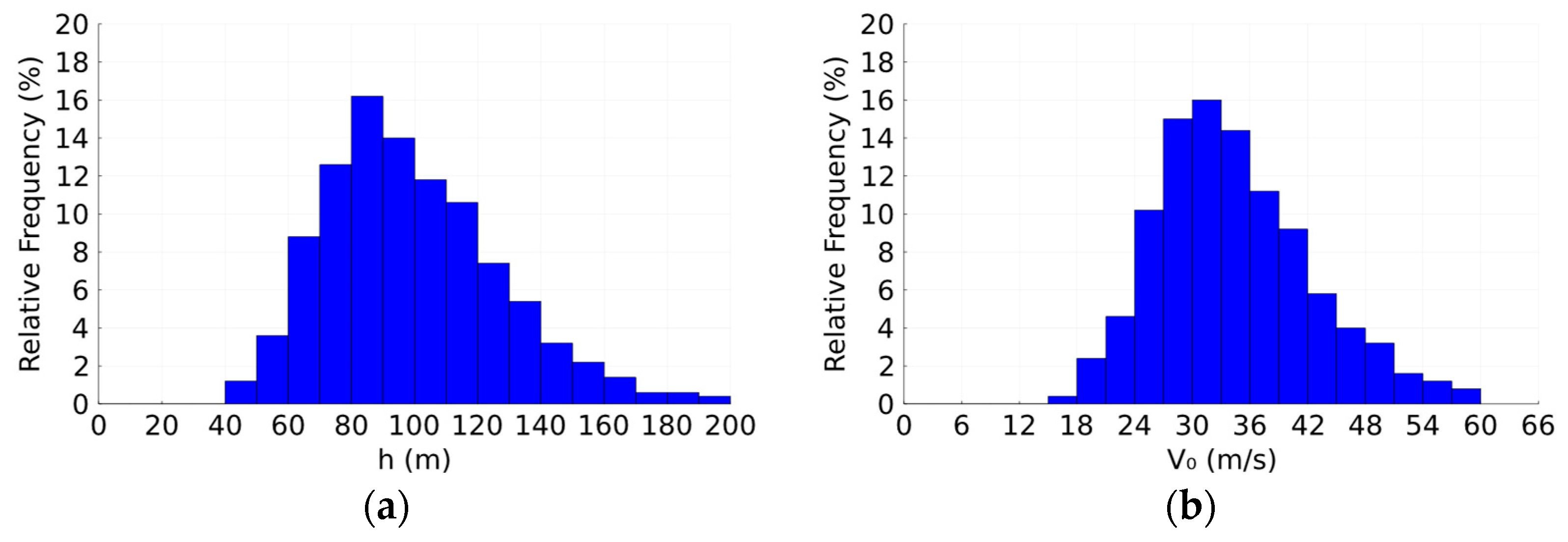




| Parameter | Ground Roughness Category | ||||
|---|---|---|---|---|---|
| I | II | III | IV | V | |
| p | 0.095 | 0.015 | 0.185 | 0.23 | 0.31 |
| b | 1.23 | 1.00 | 0.86 | 0.71 | 0.50 |
| × 103 | 2.8 | 6.5 | 10.5 | 22.6 | 52.7 |
| Variables | Abbreviation | Unit | Mean | Std | Min | Max |
|---|---|---|---|---|---|---|
| Building’s height | h | m | 99.960 | 28.836 | 50 | 150 |
| Building’s width | L1 | m | 35.000 | 8.669 | 20 | 50 |
| Building’s length | L2 | m | 35.018 | 8.667 | 20 | 50 |
| Building’s average density | kg/m3 | 175.030 | 14.440 | 150 | 200 | |
| Building’s damping ratio | % | 1.750 | 0.722 | 0.5 | 3.0 | |
| Basic wind velocity | m/s | 34.976 | 8.656 | 20 | 50 | |
| Ground roughness category | ---- | 3.000 | 1.156 | 1 | 5 | |
| Maximum displacement | cm | 8.877 | 8.720 | 0.274 | 47.566 |
| h | L1 | L2 | ρ | V0 | SR | ||
|---|---|---|---|---|---|---|---|
| 0.639 | −0.009 | −0.295 | −0.105 | −0.099 | 0.455 | −0.092 |
| Hyperparameter | Min | Max | Optimal |
|---|---|---|---|
| k | 1 | 5 | 3 |
| hweight | 0.000 | 5.000 | 5.0000 |
| L1weight | 0.000 | 5.000 | 0.3510 |
| L2weight | 0.000 | 5.000 | 1.9961 |
| weight | 0.000 | 5.000 | 0.7894 |
| weight | 0.000 | 5.000 | 1.0058 |
| V0weight | 0.000 | 5.000 | 3.7689 |
| GRweight | 0.000 | 5.000 | 0.4514 |
| Hyperparameter | Min | Max | Optimal |
|---|---|---|---|
| 1 | 7 | 7 | |
| 2 | 10 | 2 | |
| 2 | 10 | 3 | |
| 10 | 1000 | 500 |
| Hyperparameter | Min | Max | Optimal |
|---|---|---|---|
| ϵ | 0.0001 | 1 | 0.001 |
| γ | 0.0001 | 3 | 0.183 |
| c | 1 | 10,000 | 2000 |
| Hyperparameter | Min | Max | Optimal |
|---|---|---|---|
| Hidden layers | 1 | 6 | 2 |
| Neurons in hidden layers | 5 | 200 | 50 |
| Learning rate | 0.00001 | 0.1 | 0.001 |
| Epochs | 10 | 20,000 | 5000 |
| Activation Function | Optimizer | ||||||
|---|---|---|---|---|---|---|---|
| Descent | Momentum | Nesterov | RMSprop | AdaMax | AMSGrad | Adabelief | |
| ReLU | 1.414 | 1.090 | 1.227 | 1.174 | 1.359 | 1.265 | 1.190 |
| CELU | 2.124 | 1.181 | 1.204 | 5.446 | 2.021 | 1.547 | 1.000 |
| ELU | 2.114 | 0.944 | 1.304 | 2.119 | 2.012 | 1.667 | 1.919 |
| GELU | 1.809 | 0.931 | 0.890 | 1.877 | 1.646 | 1.788 | 1.426 |
| Leaky ReLU | 1.776 | 0.721 | 1.175 | 1.373 | 1.521 | 1.390 | 1.118 |
| LiSHT | 1.807 | 0.932 | 0.849 | 1.304 | 1.186 | 0.854 | 1.181 |
| Logcosh | 2.158 | 0.787 | 0.944 | 1.214 | 1.400 | 1.046 | 0.804 |
| Mish | 1.955 | 0.844 | 1.225 | 1.818 | 1.767 | 1.516 | 0.948 |
| RReLU | 1.981 | 1.252 | 1.413 | 1.660 | 2.156 | 1.886 | 1.404 |
| SELU | 3.117 | 1.126 | 2.014 | 2.486 | 2.459 | 1.841 | 1.074 |
| Softplus | 1.985 | 0.950 | 1.818 | 7.385 | 2.708 | 1.777 | 0.872 |
| Swish | 1.883 | 0.785 | 1.517 | 1.861 | 1.839 | 1.886 | 0.873 |
| Kernel Function | MSE | Kernel Function | MSE |
|---|---|---|---|
| Linear ARD | 25.734 | Matern Iso 5/2 | 2.145 |
| Matern ARD 1/2 | 2.861 | Polynomial | 24.577 |
| Matern Iso 1/2 | 4.855 | Rational Quadratic ARD | 0.673 |
| Matern ARD 3/2 | 0.972 | Rational Quadratic Iso | 0.969 |
| Matern Iso 3/2 | 2.312 | Squared exponential ARD | 0.717 |
| Matern ARD 5/2 | 0.701 | Squared exponential Iso | 1.658 |
| Mean Function | Kernel Function | |||
|---|---|---|---|---|
| Rational Quadratic ARD | Matern ARD 5/2 | Squared Exponential ARD | Matern ARD 3/2 | |
| Zero | 0.673 | 0.701 | 0.717 | 0.972 |
| Constant | 0.673 | 0.700 | 0.703 | 0.972 |
| Linear | 0.681 | 0.709 | 0.715 | 0.968 |
| Polynomial | 0.681 | 0.709 | 0.715 | 0.968 |
| Machine Learning Model | Training | Testing | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R2 | MBE (cm) | MAE (cm) | MSE (cm2) | MPE (%) | MAPE (%) | R2 | MBE (cm) | MAE (cm) | MSE (cm²) | MPE (%) | MAPE (%) | |
| kNN | 1.000 | −0.003 | 0.052 | 0.007 | −0.147 | 0.676 | 0.955 | −0.518 | 1.203 | 3.271 | 1.088 | 15.028 |
| RF | 0.981 | −0.078 | 0.790 | 1.932 | −5.762 | 11.060 | 0.933 | −0.673 | 1.536 | 5.690 | −3.734 | 20.901 |
| GPR | 0.999 | 0.000 | 0.149 | 0.045 | −0.038 | 2.661 | 0.995 | 0.111 | 0.416 | 0.379 | −0.993 | 8.145 |
| SVR | 0.994 | −0.069 | 0.290 | 0.542 | 1.064 | 4.027 | 0.990 | 0.024 | 0.472 | 0.633 | −0.322 | 8.767 |
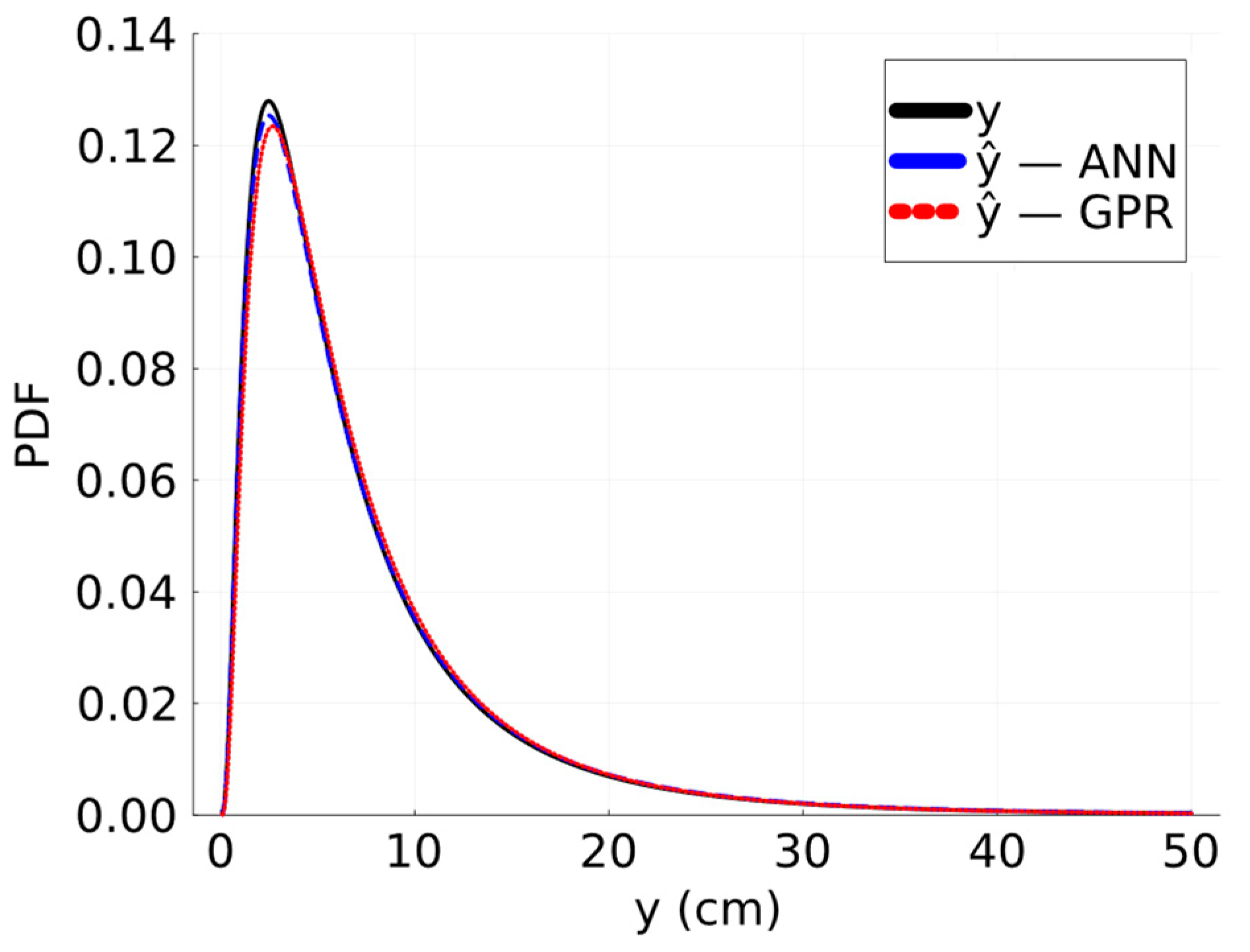
| ANN | 0.999 | 0.001 | 0.150 | 0.046 | −0.140 | 2.995 | 0.990 | −0.004 | 0.463 | 0.653 | −1.947 | 5.941 |
| Machine Learning Model | R2 | MBE (cm) | MAE (cm) | MSE (cm2) | MPE (%) | MAPE (%) |
|---|---|---|---|---|---|---|
| GPR | 0.984 | 0.196 | 0.414 | 0.894 | −4.744 | 6.868 |
| ANN | 0.991 | 0.103 | 0.325 | 0.455 | −2.138 | 4.561 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Conceição, R.S.; Evangelista Junior, F. Wind-Induced Dynamic Critical Response in Buildings Using Machine Learning Techniques. Buildings 2024, 14, 3286. https://doi.org/10.3390/buildings14103286
Conceição RS, Evangelista Junior F. Wind-Induced Dynamic Critical Response in Buildings Using Machine Learning Techniques. Buildings. 2024; 14(10):3286. https://doi.org/10.3390/buildings14103286
Chicago/Turabian StyleConceição, Rodolfo S., and Francisco Evangelista Junior. 2024. "Wind-Induced Dynamic Critical Response in Buildings Using Machine Learning Techniques" Buildings 14, no. 10: 3286. https://doi.org/10.3390/buildings14103286
APA StyleConceição, R. S., & Evangelista Junior, F. (2024). Wind-Induced Dynamic Critical Response in Buildings Using Machine Learning Techniques. Buildings, 14(10), 3286. https://doi.org/10.3390/buildings14103286





