Abstract
Based on a practical engineering case of seismic strengthening, this paper used the enlarging cross-section method and an external self-centering substructure to improve the seismic performance and seismic resilience of existing frame structures. Among them, the external self-centering substructure included setting a self-centering precast beam and diagonal braces. Utilizing the OpenSees finite element platform, a seismic fragility analysis was carried out to compare the improvements in seismic performance and seismic resilience before and after strengthening. The analysis results show that the proposed modelling method could be simulated satisfactorily. The maximum inter-story drift and the residual inter-story drift of the strengthened frame structures decreased significantly under the same peak ground acceleration. The peak ground acceleration of the strengthened frame structures significantly increased under different performance levels. Additionally, the exceedance probability of the strengthened frame structures was obviously reduced, which reflected that the seismic performance and seismic resilience of the strengthened frame structures were significantly improved.
1. Introduction
As economic development enters a new phase, the growth rate of infrastructure construction is gradually slowing down. Besides, the number of new buildings is also decreasing year by year due to limited urban land and space. A large number of early RC frame structures exist in cities. Although they have not reached the end of their design service life, there are still some potential problems. Firstly, it is difficult for early RC multi-story frame structures to meet the requirements of the current Code for the Seismic Design of Buildings (GB 50011-2010) [1] due to the rapid development of seismic technology. Secondly, the function of the existing frame structures may be changed during their service life. For example, some frame columns may be removed in order to open up large amounts of space; this means the lateral stiffness of frame structures is greatly reduced, which then presents a difficult problem for strengthening existing frame structures. Thirdly, early and existing frame structures are demolished, and new frame structures are built, which incurs high costs and other problems. In summary, the seismic strengthening of existing frame structures has gradually become a prominent issue in research.
There are various strengthening methods [2,3,4], and a simple and common method is the enlarging cross-section method. Existing frame structures can be strengthened by increasing the size of the concrete cross-section and the amount of steel bars to improve the lateral stiffness and bearing capacity. Additionally, the enlarging cross-section method could effectively improve the seismic performance and collapse resistance of existing frame structures under strong earthquakes [5,6]. However, the enlarging cross-section method has limited effects on reducing residual deformation. According to a performance-based seismic design method, prestress was applied to steel strands so that its residual deformation was reduced and its seismic resilience was increased, which was easy to repair after earthquakes [7]. In addition, the two ends of the steel strand were anchored to the cast-in-place concrete, and the performance of the co-working was good. Priestley et al. [8,9] studied the precast seismic structural systems (PRESSS) program and proposed a precast concrete frame structure system with dry prestressed hybrid connection joints. Lu et al. [10,11] conducted seismic performance tests on self-centering RC frame structures with beam–column joints and column–base joints. It was found that the frame structures were almost undamaged under extreme earthquake action, and the seismic performance and self-centering capacity were excellent. Kurosawa et al. [12] used precast prestressed concrete frames to retrofit existing RC frame structures, and found that precast frames had well-controlled cracking and minimized residual deformation compared to integral RC frames. Eldin et al. [13] used post-tensioned prestressed technology to retrofit existing frame structures, and the results showed that the maximum inter-story drift and residual inter-story drift of strengthened frame structures were significantly reduced. It could be seen that the use of prestressed steel strands effectively enhanced the seismic performance and seismic resilience of the frame structures.
In order to scientifically and reasonably evaluate the seismic performance and seismic resilience of frame structures before and after strengthening, the seismic fragility analysis has been developed [14]. The seismic fragility analysis, which quantitatively describes the dynamic relationship between the peak ground acceleration and exceedance probability of frame structures, plays an important role in global seismic risk assessment [15]. In addition, the seismic fragility analysis is relatively easy to perform, and the results are relatively intuitive. More and more scholars have adopted the seismic fragility analysis to assess the seismic performance and seismic resilience of structures in recent years. Ji et al. [16] proposed a simple lumped-parameter model for the seismic fragility assessment of existing high-rise buildings. Sarno et al. [17,18] conducted a seismic fragility analysis considering the influence of reinforcement corrosion on existing RC frame structures. Kumar et al. [19,20] considered the uncertainty in aleatory and epistemic sources, and evaluated the seismic fragility of existing low-, medium-, and high-rise RC frame structures. Pitilakis et al. [21] proposed a modular approach for a large-scale seismic fragility assessment of existing RC frame structures, including soil–structure interactions and site amplification effects. Gautam et al. [22] conducted a seismic fragility analysis of RC frame structures with structural and non-structural components, and found that the global fragility function could be used for overall loss estimation, but the component level fragility functions could be used to identify weak links in frame structures. Palagala et al. [23] proposed a quick seismic fragility assessment technique for existing RC frame structures, providing qualitative and quantitative assessments in a more engineered way. Dalal et al. [24] proposed a performance-based plastic design method for a seismic fragility analysis of RC frame structures, and found that the designed frame structure met three performance levels, namely immediate occupancy, life safety and collapse prevention. Cao et al. [25] proposed a new strengthening method for existing frames by using external substructures, and conducted incremental dynamic analysis (IDA) and seismic fragility analysis. The results illustrated that the strengthened RC frames had a higher bearing capacity and lower structural damage. It could be seen that the seismic fragility analysis was a relatively effective method for evaluating RC frame structures, and also contributed to achieving performance-based seismic design goals.
In brief, the finite element analysis was used to simulate the strengthened existing frame structures. On this basis, the dynamic increment analysis and seismic fragility analysis were conducted to evaluate its seismic performance and seismic resilience on a pilot project. The analysis results could be used for performance-based design, and could provide certain design recommendations.
2. Basic Information of RC Frame Structures
The basic information of the RC frame structures was introduced before and after seismic strengthening, including geometric dimensions, reinforcement layout, and load layout, etc.
2.1. Frame KJ1
The pilot project of seismic strengthening was a four-storey RC frame structure (namely frame KJ1), as shown in Figure 1. The total area of the frame KJ1 was approximately 1900 m2. The length was 25.5 m in the east–west direction, and the width was 18.0 m in the north–south direction. The total height of the frame KJ1 was 14.8 m, and the storey heights from the ground floor to the top floor were 4.11 m, 3.30 m, 3.30 m and 4.09 m, respectively. The RC frame structure was located in a seismic precautionary intensity of 8 degrees. The site class was Class II. The design earthquake group was Group II. Additionally, the characteristic period value was 0.4 s.

Figure 1.
Scene photos of frame KJ1.
The structural plan layout of frame KJ1 and the cross-sectional dimensions of beams and columns are depicted in Figure 2.
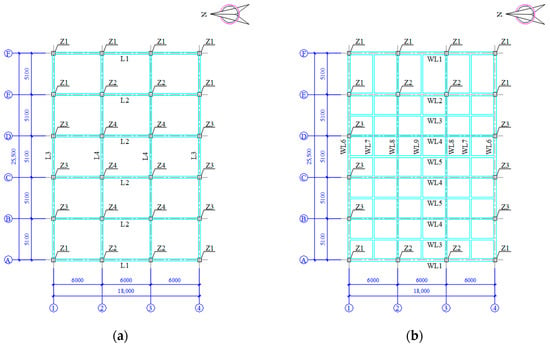
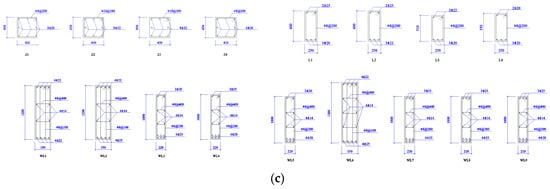
Figure 2.
Structural plan layout of frame KJ1. (a) Plan layout of the first to the third storey; (b) Plan layout of the fourth storey; (c) Cross-sectional dimensions of beams and columns.
The plan layout of the line load on the beam, the floor dead load and the floor live load is presented in Figure 3. The floor uniform load was marked at the center of the floor. Among them, the number outside the brackets indicated the floor dead load, and the number inside the brackets indicated the floor live load.
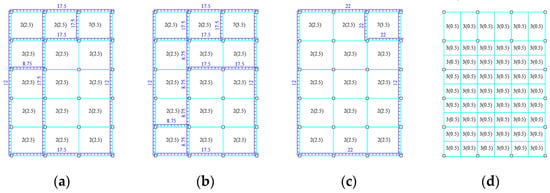
Figure 3.
Load plan layout of frame KJ1. (a) First storey; (b) Second storey; (c) Third storey; (d) Fourth storey.
2.2. Frame KJ2
According to the requirements of first party, it was planned to remove the four frame columns from the first to the third storey. The interior of the frame KJ1 was changed to a large space, which resulted in a significant reduction in the lateral stiffness. The bearing capacity and deformation capacity of the frame structure did not meet the code requirements. According to the performance-based seismic design method, the original frame structure was strengthened by the enlarging cross-section method and the external self-centering substructure to improve the seismic resilience, namely frame KJ2. The self-centering precast beams were set up on the north–south exterior facades, and the diagonal braces were set up on the west–east exterior facades. Additionally, the diameter of the diagonal braces was taken as 50 mm. The structural plan layout of frame KJ2 and the cross-sectional dimensions of the beams and columns are plotted in Figure 4.
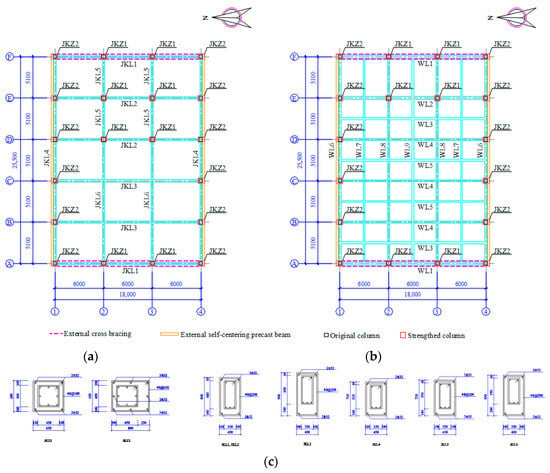
Figure 4.
Structural plan layout of frame KJ2. (a) Plan layout of the first to the third storey; (b) Plan layout of the fourth storey; (c) Cross-sectional dimensions of beams and columns.
After strengthening the frame KJ1 by the enlarging cross-section method, the floor dead load increased, while the line load on beam and the floor live load remained unchanged. The load plan layout of frame KJ2 is depicted in Figure 5.
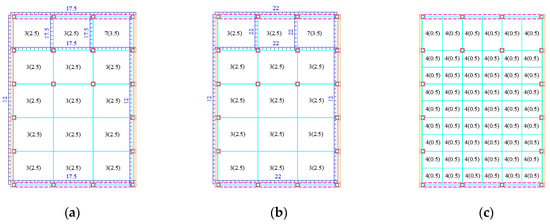
Figure 5.
Load plan layout of frame KJ2. (a) First to second storey; (b) Third storey; (c) Fourth storey.
3. Establishment and Verification of Finite Element Models
OpenSees (Open System for Earthquake Engineering Simulation) (University of California, Berkeley, CA, USA) is an open-source seismic engineering numerical simulation platform with a high computational efficiency and sustainable development rate. Firstly, the simulated hysteresis curve of one-story one-span frame structures were compared with quasi-static test results using the OpenSees version 2.5.0 as the numerical simulation platform. Secondly, the whole finite element models of the frame structures were established, and the incremental dynamic analysis and the seismic fragility analysis were carried out.
3.1. Finite Element Modelling Methods
The fiber model of OpenSees was chosen to establish the finite element model. Additionally, the frame beams and columns were simulated by beam–column elements. Concrete02 material was used to simulate the concrete in the frame structure and precast beams, taking into account the tensile strength and changes in loading and unloading stiffness of the concrete. The constitutive relationship of the core concrete adopted the Mander model [26] considering the constraint effect of stirrups. The Steel02 material was used for simulating the normal steel bars, energy-dissipating bars and steel strands in the frame structures. The steel strand adopted the Truss element to achieve an unbonded effect with concrete. In addition, it should be noted that the steel02 material can be prestressed, and the prestress of 250 MPa and 450 MPa was applied to steel strands in the self-centering precast beam and diagonal braces, respectively.
The connection part between the precast beam and the frame structure was a challenging part of the numerical simulation. The precast beams could be rotated in their plane. Additionally, the connection of the precast beam and the frame structure relied on steel strands and energy-dissipating bars. The ZeroLengthSection was set at the connection and given the ENT (Elastic-No Tension) material. Moreover, energy-dissipating bars were placed in the ZeroLengthSection. Considering the deformation compatibility between the precast beam and the frame structure during the loading process, the multi-point constraint (equalDOF) command was used to constrain the degrees of freedom for the nodes. Three nodes were constrained to the same position. Node 3 was the frame joint, and Node 2 was the end of the steel strand. The degrees of freedom for Node 2 and Node 3 were exactly the same. Node 1 was the end of the self-centering precast beam, and could rotate in the plane. The specific modelling method of self-centering precast beams is shown in Figure 6.
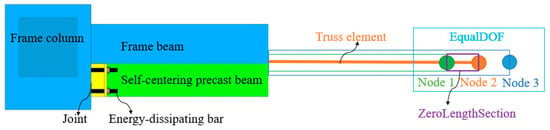
Figure 6.
Modelling methods of self-centering precast beams.
3.2. One-Story One-Span Frame Structures
In order to verify the finite element modeling method, the quasi-static test results of one-story, one-span frame structures were compared with the finite element simulation results.
3.2.1. Test Overview
The schematic diagrams and cross-section reinforcement of one-story, one-span frame structures are plotted in Figure 7, and detailed information refers to references [27,28]. K1 and K2 represented two frame structures of different beam spans strengthened with diagonal braces and self-centering precast beams, respectively. The final number 1 indicated the original frame structure, and number 2 indicated the strengthened frame structure. The column height was 2400 mm, and the cross-sectional dimensions of columns for K1-1 and K2-1 were 270 × 270 mm. The beam spans of K1-1 and K2-1 were 3600 mm and 3060 mm, respectively. The beam heights of K1-1 and K2-1 were 360 mm and 306 mm, respectively. Additionally, the beam widths of K1-1 and K2-1 were 150 mm. Compared with K1-1, K1-2 was strengthened by the enlarging cross-section method and setting the diagonal braces, and the cross-sectional dimensions of columns for K1-2 were 390 × 390 mm. Compared with K2-1, K2-2 was strengthened by the enlarging cross-section method and setting the self-centering precast beam. The cross-sectional dimensions of columns for K2-2 were 390 × 480 mm. The beam heights of K1-2 and K2-2 were 480 mm, and the beam widths of K1-2 and K2-2 were 270 mm.
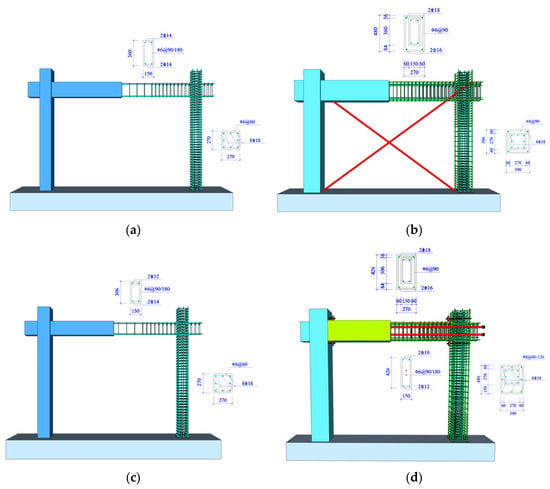
Figure 7.
Schematic diagram and cross-section reinforcement of one-story one-span frame structures. (a) K1-1; (b) K1-2; (c) K2-1; (d) K2-2.
For K1-2, the bottom of steel strands was the fixed end, and the top of steel strands was the tensioned end. Among them, the tensioned end used wedge-type anchorage, and the fixed end used extruding anchorage, as displayed in Figure 8a. For K2-2, both ends of steel strands were simultaneously tensioned before the test, as depicted in Figure 8b. The energy-dissipating bars were tapped and then fixed with nuts.

Figure 8.
Scene photos of anchorage for steel strands. (a) K1-2; (b) K2-2.
The origin concrete strength grade of K1-1 and K2-1 was C20, and the post-cast concrete strength grade of enlarging cross-section was C40. The mechanical performance index of concrete is presented in Table 1, and the mechanical performance index of steel is listed in Table 2.

Table 1.
Mechanical performance index of concrete.

Table 2.
Mechanical performance index of steel.
3.2.2. Model Establishment of One-Story One-Span Frame Structures
Based on the quasi-static test, the above modelling method was adopted. According to the actual cross-sectional size and reinforcement information, finite element models of one-story one-span frame structures were established, as illustrated in Figure 9.
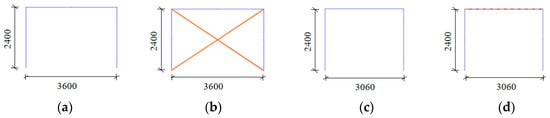
Figure 9.
Finite element models of one-story one-span frame structures. (a) K1-1 (b) K1-2 (c) K2-1 (d) K2-2.
3.2.3. Model Verification of One-Story One-Span Frame Structures
The hysteresis curves of the test and simulation are plotted in Figure 10. It could be seen that the test results were generally in good agreement with the finite element simulation results. All errors were within 20%, confirming the rationality and reliability of the modelling method.
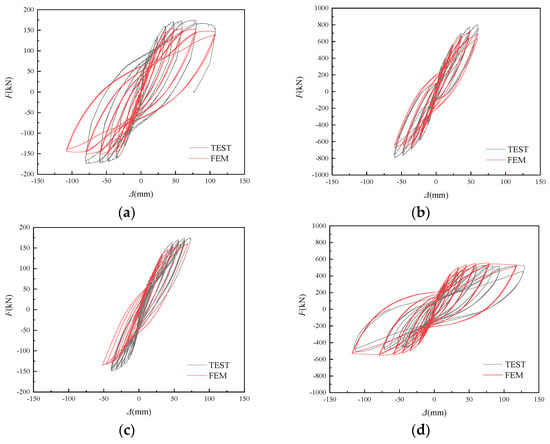
Figure 10.
Comparisons of test and simulation results for one-story one-span frame structures. (a) K1-1; (b) K1-2; (c) K2-1; (d) K2-2.
3.3. RC Frame Structures
According to finite element simulation of one-story, one-span frame structures, the finite element models of four-storey frame structures were established, and the correctness of the finite element models was verified.
3.3.1. Model Establishment of RC Frame Structures
According to the actual size and load plan layout of RC frame structures, finite element models were established, as displayed in Figure 11.
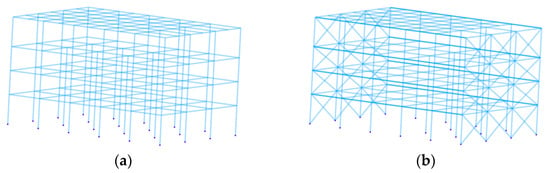
Figure 11.
Finite element models of RC frame structures. (a) KJ1; (b) KJ2.
3.3.2. Verification of RC Frame Structures
The finite element models of the RC frame structures were established by YJK and OpenSees, respectively. The modal analysis of the RC frame structures was conducted to compare the natural vibration periods of the first three modes to verify the rationality of the finite element modelling method. The comparison of the natural vibration periods is exhibited in Table 3. The results showed that the natural vibration periods of the first three modes were basically similar. The errors were less than 20%, which indicated that the model’s establishment of the frame structures was reasonable within this paper.

Table 3.
Comparison of natural vibration periods.
4. Earthquake Ground Motion Input
Twenty earthquake ground motion records were selected according to the natural vibration period, damping ratio, site characteristic period, site class and design earthquake groups, etc. Detailed information of earthquake ground motion records is summarized in Table 4. The response spectrum analysis of earthquake ground motion records was conducted as plotted in Figure 12. Additionally, the average response spectrum was compared with the standard response spectrum of a seismic precautionary intensity of 8 degrees. The error between each earthquake response spectrum and the standard response spectrum was within 20% near the first period of frame structures.

Table 4.
Earthquake ground motion records.
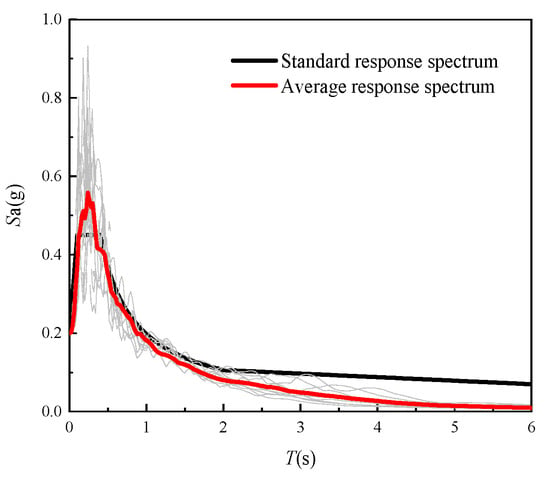
Figure 12.
Response spectrum analysis of earthquake ground motion records.
5. Incremental Dynamic Analysis of RC Frame Structures
Incremental dynamic analysis (IDA) [29] is a parameter analysis method that comprehensively evaluates the performance level of frame structures under earthquake action. Besides, the IDA curve better reflects the evolution process of the structures from intact to failure. The specific operation process is that several earthquake ground motion records are applied to the structure model, and then each earthquake ground motion record is scaled to several intensity levels, finally obtaining a series of response curves. The peak ground acceleration (aPG) was selected as the intensity measure (IM), and the maximum inter-story drift (θmax) was selected as the damage measure (DM). The peak ground acceleration underwent a total of 34 amplitude modulations during the IDA. The amplitude modulation increments of 0.1~1.0 g were 0.1 g; the amplitude modulation increments of 1.2~5.0 g were 0.2 g; and the amplitude modulation increments of 5.5~7.0 g were 0.5 g. In order to reduce the computational complexity and reflect various performance points on the IDA curves based on different seismic demand parameters, the ultimate state of IDA analysis was the point where the structure reached dynamic instability, the nonlinear time history analysis did not converge, the maximum inter-story drift reached 10%, or the slope reached the initial slope of 20% in the IDA curve. Additionally, the point with the smallest value was selected as the ultimate state of collapse.
Taking the No. 1 earthquake ground motion record as an example, the maximum inter-story drift, the residual inter-story drift, and IDA were carried out. Then, twenty earthquake ground motion records were input, and IDA curves and fractile curves were obtained through statistical analysis. The calculation results and analyses were as follows.
5.1. Distribution Diagram of Maximum Inter-Story Drifts
FEMA 356 [30] defines three performance points of the maximum inter-story drift (θmax). Under different performance states, the reference value CΔ of the maximum inter-story drift is exhibited in Table 5.

Table 5.
Reference value CΔ of θmax under different performance states.
The distribution diagrams of the maximum inter-story drift are obtained by amplitude modulation, as shown in Figure 13. The frame numbers of x and y represent earthquakes in the x and y direction, respectively. The maximum inter-story drift of each storey increased with increasing the peak ground acceleration. The maximum inter-story drift of frame KJ1 decreased as the storeys increased. Additionally, the maximum inter-story drift occurred in the first storey under different peak ground accelerations, which applied to the soft storey of the frame structures. Frame KJ2 adopted the enlarging cross-section method and set cross braces in the x direction; the maximum inter-story drift moved upwards, and the soft storey was transferred to the second or the third storey. However, the soft storey was still the first storey in the y direction. The maximum inter-story drift of frame KJ1 satisfied the IO state at 0.2 g; the LS state at 0.4 g; and the CP state near 0.8 g. The maximum inter-story drift of frame KJ2 satisfied the IO state at 0.4 g; the LS state near 0.8 g; and the CP state near 1.8 g. Besides, compared to frame KJ1, the maximum inter-story drift of frame KJ2 was significantly reduced under the same the peak ground acceleration. Additionally, the effect of the enlarging cross-section method and setting the cross braces was more significant.
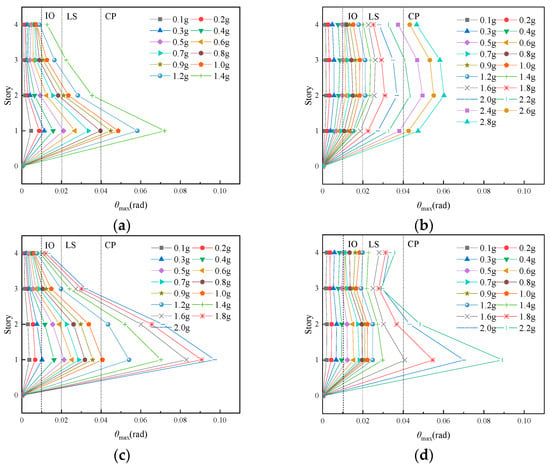
Figure 13.
Distribution diagram of maximum inter-story drifts. (a) KJ1-x; (b) KJ2-x; (c) KJ1-y; (d) KJ2-y.
5.2. Distribution Diagram of Residual Inter-Story Drifts
FEMA 356 [30] defines four performance points for the residual inter-story drift (θR) and gives the reference value CΔ for θR in different performance states. In this paper, three performance points were selected for analysis, as shown in Table 6. Among them, DS1 corresponded to the minor repair state; DS2 corresponded to the major repair state; and DS3 corresponded to the collapse state.

Table 6.
Reference value CΔ of θR under different performance states.
The distribution diagrams of the residual inter-story drift are obtained via amplitude modulation, as plotted in Figure 14. The residual inter-story drift of the frame structures decreased with the increase in storeys, and the maximum residual inter-story drift occurred on the first storey under different peak ground accelerations. The residual inter-story drift of the frame structures increased with the increase in the peak ground acceleration. Frame KJ1 reached the DS1 state at 0.4–0.5 g, DS2 state at 0.5–0.7 g, and DS3 state at 0.7–0.9 g; Additionally, frame KJ2 reached the DS1 state at 1.8 g under the x-direction earthquake; however, frame KJ2 reached the DS1 state at 1.0 g, DS2 state at 1.6 g, and DS3 state at 1.8 g under the influence of the y direction earthquake. Compared with frame KJ1, the residual inter-story drift of frame KJ2 was significantly reduced, and the seismic performance and seismic resilience were significantly improved under the same peak ground acceleration.
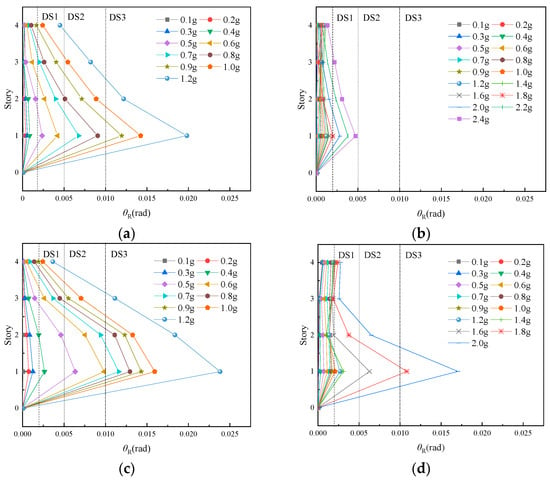
Figure 14.
Distribution diagram of residual inter-story drifts. (a) KJ1-x; (b) KJ2-x; (c) KJ1-y; (d) KJ2-y.
5.3. Incremental Dynamic Analysis
Under the action of the No. 1 earthquake ground motion record, the incremental dynamic analysis of the frame structures was carried out before and after strengthening, as illustrated in Figure 15. When aPG was small, the initial stage of the IDA curve showed approximately linear growth, indicating that the structures were in an elastic state. As aPG increased, the slope of the IDA curve gradually decreased, indicating that the structures were in an elastic–plastic state.
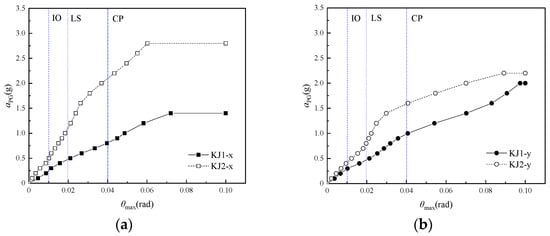
Figure 15.
IDA curve diagram of the No. 1 earthquake ground motion record. (a) x-direction earthquakes (b) y-direction earthquakes.
IDA curves and their summary fractile curves are depicted in Figure 16 under the action of twenty earthquake ground motion records. Statistical analysis was conducted according to θmax, and the median and logarithmic standard deviation of θmax were calculated. Thus, fractile curves of 16%, 50%, and 84% were obtained. It could be seen that (1) the shape of IDA curves was different. The curves had characteristics of “excessive softening”, “excessive hardening”, and “fluctuation”. The IDA curve could comprehensively reflect the possible seismic responses of frame structures under different intensity levels. (2) Under the same earthquake direction, the difference between the mean values of θmax was significant for frames KJ1 and KJ2. The IDA curve of frame KJ2 showed overall data points moving to the left, which indicated that the seismic performance of the existing frame structure could be significantly improved by the enlarging cross-section method and the external self-centering substructure.
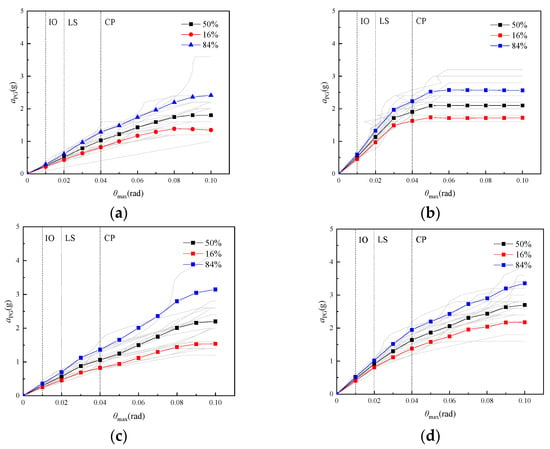
Figure 16.
IDA curves and fractile curves. (a) KJ1-x; (b) KJ2-x; (c) KJ1-y; (d) KJ2-y.
6. Seismic Fragility Analysis of RC Frame Structures
6.1. Probabilistic Seismic Demand Models
The median value of the seismic demand capacity and the peak ground acceleration aPG follow an exponential relationship [31], as shown in Equation (1):
Both sides of the equation take the natural logarithm at the same time. Linear regression was conducted using mathematical software. Additionally, the probabilistic seismic demand model curve of frame structures was obtained (as displayed in Figure 17), as given in Equation (2):
where lnα and β are the coefficient of statistical regression after a large number of incremental dynamic analyses.
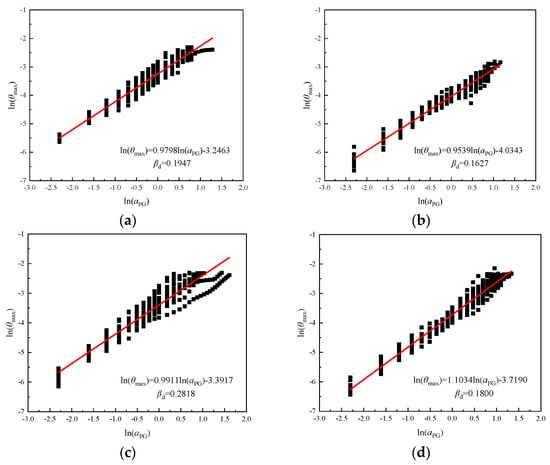
Figure 17.
Regression curve of probabilistic seismic demand models. (a) KJ1-x; (b) KJ2-x; (c) KJ1-y; (d) KJ2-y.
The standard deviation βd of the logarithmic normal distribution function for the seismic demand capacity is presented in Equation (3):
where N is the number of data points for the regression analysis, and Di is the result of the time history analysis (i = 1, 2, …, N).
It could be seen from Figure 17 that the curve of the probabilistic seismic demand model was approximately linear, the logarithmic standard deviation of the seismic demand parameter βd was approximately 0.2, and the fitting effect was good.
6.2. Seismic Fragility Curve of Frame Structures
After obtaining the probabilistic seismic demand model, the total probability method is used to calculate the exceedance probability of the frame structures under each performance state. The formula is given in Equation (4) [32]:
where βc is the logarithmic standard deviation of the seismic capacity of the frame structures, and the uncertainty was not considered.
The seismic fragility curves of the frame structures are plotted in Figure 18. It is apparent from Figure 18 that the exceedance probability of each performance level truly reflects the seismic performance level of frame structures under different peak ground accelerations. (1) The development law of the seismic fragility curve is similar, and the overall curve is S-shaped; (2) when the peak ground acceleration is relatively low, the frame structure is approximately intact, or undergoes slight damage, and the fragility curves basically overlap under different performance states; (3) as the peak ground acceleration increases, the elastic–plastic deformation of the frame structures fully develops, and the slope of the curve firstly increases and then decreases. The performance level of the frame structures gradually develops from immediate occupancy to collapse; (4) compared with frame KJ1, the exceedance probability of frame KJ2 decreases significantly at various performance levels under the same peak ground acceleration, especially under the action of the earthquake in the x direction. The exceedance probability of frame KJ2 in the IO state and LS state is even lower than that of frame KJ1 in the LS state and CP state.
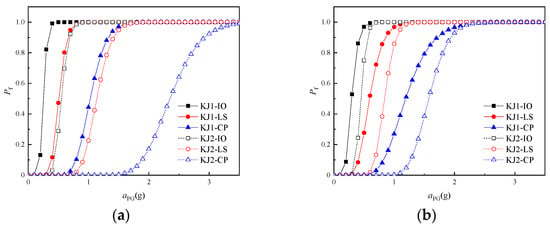
Figure 18.
Seismic fragility curve. (a) x-direction earthquakes; (b) y-direction earthquakes.
A comparison of failure states is illustrated in Figure 19. As an example of the analysis, the failure state of the frame structures is compared under the action of the earthquake in the x direction. Comparing Figure 19a,b, it can be seen that when aPG is 0.2 g, the exceedance probability of the IO state for frame KJ2 increases from 86.9% to 100.0%. When aPG is 0.4 g, the exceedance probability of the IO state increases from 0.9% to 96.9%. When aPG is 0.6 g, the exceedance probability of the IO state increases from 0.0% to 30.4%; the exceedance probability of the LS state increases from 19.8% to 69.6%; and the exceedance probability of the CP state decreases from 79.9% to 0.0%. When aPG is 1.0 g, the exceedance probability of the LS state increases from 0.0% to 77.4%; the exceedance probability of the CP state decreases from 55.6% to 22.6%; and the exceedance probability of the collapse state decreases from 44.4% to 0.0%. When aPG is 2.0 g, the exceedance probability of the CP state increases from 0.0% to 82.8%, and the exceedance probability of the collapse state decreases from 100.0% to 17.2%. It is evident that the exceedance probability of the frame structures is significantly reduced, and the safety margin is greatly increased.
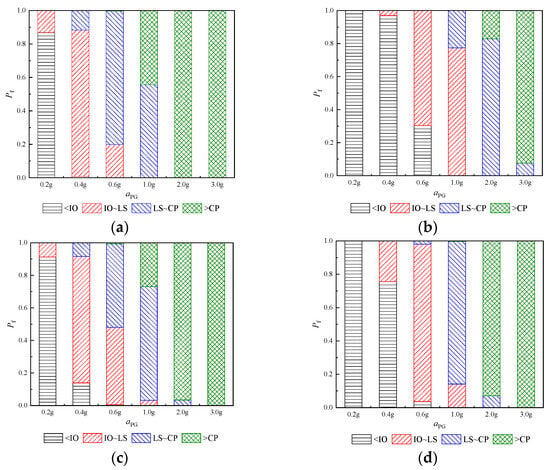
Figure 19.
Comparison of failure states. (a) KJ1-x; (b) KJ2-x; (c) KJ1-y; (d) KJ2-y.
7. Conclusions
Finite element models of one-story one-span frame structures and four-storey frame structures were established using OpenSees finite element platform. The seismic response laws of the frame structures were analyzed under twenty earthquake ground motion records. Additionally, the seismic fragility analysis of the frame structures was conducted. The main conclusions are as follows:
- (1)
- The proposed modeling method was reasonable, and the error between the experiment results and finite element simulation results was small;
- (2)
- Under the same peak ground acceleration, the maximum inter-story drift of frame KJ1 decreased with the increase in storeys. However, the maximum inter-story drift of frame KJ2 moved upwards, and was significantly reduced;
- (3)
- When the peak ground acceleration was small, the IDA curves showed a linear increase. As the peak ground acceleration increased, the slope of the IDA curves gradually decreased;
- (4)
- Based on the results of IDA, the probabilistic seismic demand model curve was fitted, and the fitting effect was good;
- (5)
- When the same peak ground acceleration was applied to the frame structures, the exceedance probability of frame KJ2 was significantly lower than that of frame KJ1 at various performance levels.
Author Contributions
Methodology, H.L., M.H.; software, F.W., J.L.; writing—original draft preparation, W.L.; writing—review and editing, J.Z.; supervision, J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by [the National Natural Science Foundation of China] grant number [52178448].
Data Availability Statement
The data that has been used is confidential.
Conflicts of Interest
The authors declare no conflict of interest.
References
- GB 50011-2010; Code for Seismic Design of Buildings. China Architecture and Building Press: Beijing, China, 2016. (In Chinese)
- Heydari, P.; Mostofinejad, D.; Mostafaei, H.; Ahmadi, H. Strengthening of deep RC coupling beams with FRP composites: A numerical study. Structures 2023, 51, 435–454. [Google Scholar] [CrossRef]
- Ortiz, J.D.; Khedmatgozar Dolati, S.S.; Malla, P.; Nanni, A.; Mehrabi, A. FRP-reinforced/strengthened concrete: State-of-the-art review on durability and mechanical effects. Materials 2023, 16, 1990. [Google Scholar] [CrossRef]
- Zhou, C.Y.; Wang, L.N.; Wang, Y.; Fang, Z. Experimental study on the flexural strengthening of one-way RC slabs with end-buckled and/or externally bonded CFRP sheets. Eng. Struct. 2023, 282, 115832. [Google Scholar] [CrossRef]
- Li, J.B.; Gong, J.X.; Wang, L.H. Experimental study on seismic behavior of corroded reinforced concrete columns strengthened with concrete jacket and CFRP. China Civ. Eng. J. 2009, 42, 17–26. (In Chinese) [Google Scholar] [CrossRef]
- Huang, J.F.; Zhu, C.M.; Gong, Z.G.; Zhang, F.W. Experimental study on seismic behavior of earthquake-damaged RC frame strengthened by enlarging cross-section. China Civ. Eng. J. 2012, 45, 9–17. (In Chinese) [Google Scholar]
- Song, L.L.; Guo, T.; Gu, Y.; Cao, Z.-L. Experimental study of a self-centering prestressed concrete frame subassembly. Eng. Struct. 2015, 88, 176–188. [Google Scholar] [CrossRef]
- Priestley, M.H.N. Overview of PRESSS research program. PCI J. 1991, 36, 50–67. [Google Scholar] [CrossRef]
- Priestley, M.H.N. The PRESSS program current status and proposed plans for phase III. PCI J. 1996, 41, 22–40. [Google Scholar] [CrossRef]
- Lu, X.L.; Cui, Y.; Liu, J.J.; Gao, W. Shaking table test and numerical simulation of a 1/2-scale self-centering reinforced concrete frame. Earthq. Eng. Struct. Dyn. 2015, 44, 1899–1917. [Google Scholar] [CrossRef]
- Cui, Y.; Lu, X.L.; Jiang, C. Experimental investigation of tri-axial self-centering reinforced concrete frame structures through shaking table tests. Eng. Struct. 2017, 132, 684–694. [Google Scholar] [CrossRef]
- Kurosawa, R.; Sakata, H.; Qu, Z.; Suyama, T. Precast prestressed concrete frames for seismically retrofitting existing RC frames. Eng. Struct. 2019, 184, 345–354. [Google Scholar] [CrossRef]
- Eldin, M.N.; Dereje, A.J.; Kim, J. Seismic retrofit of framed buildings using self-centering PC frames. J. Struct. Eng. 2020, 146, 04020208. [Google Scholar] [CrossRef]
- Huang, Z.H.; Cai, L.P.; Pandey, Y.; Tao, Y.; Telone, W. Hysteresis effect on earthquake risk assessment of moment resisting frame structures. Eng. Struct. 2021, 242, 112532. [Google Scholar] [CrossRef]
- Ge, F.W.; Tong, M.N.; Zhao, Y.G. A structural demand model for seismic fragility analysis based on three-parameter lognormal distribution. Soil Dyn. Earthq. Eng. 2021, 147, 106770. [Google Scholar] [CrossRef]
- Ji, J.; Elnashai, A.S.; Kuchma, D.A. An analytical framework for seismic fragility analysis of RC high-rise buildings. Eng. Struct. 2007, 29, 3197–3209. [Google Scholar] [CrossRef]
- Sarno, L.D.; Pugliese, F. Seismic fragility of existing RC buildings with corroded bars under earthquake sequences. Soil Dyn. Earthq. Eng. 2020, 134, 106169. [Google Scholar] [CrossRef]
- Sarno, L.D.; Pugliese, F. Effects of mainshock-aftershock sequences on fragility analysis of RC buildings with ageing. Eng. Struct. 2021, 232, 111837. [Google Scholar] [CrossRef]
- Kumar, P.; Samanta, A. Seismic fragility assessment of existing reinforced concrete buildings in Patna, India. Structures 2020, 27, 54–69. [Google Scholar] [CrossRef]
- Choudhury, T.; Kaushik, H.B. Treatment of uncertainties in seismic fragility assessment of RC frames with masonry infill walls. Soil Dyn. Earthq. Eng. 2019, 126, 105771. [Google Scholar] [CrossRef]
- Pitilakis, D.; Petridis, C. Fragility curves for existing reinforced concrete buildings, including soil-structure interaction and site amplification effects. Eng. Struct. 2022, 269, 114733. [Google Scholar] [CrossRef]
- Gautam, D.; Adhikari, R.; Rupakhety, R. Seismic fragility of structural and non-structural elements of Nepali RC buildings. Eng. Struct. 2021, 232, 111879. [Google Scholar] [CrossRef]
- Palagala, V.Y.; Singhal, V. Structural score to quantify the vulnerability for quick seismic assessment of RC framed buildings in India. Eng. Struct. 2021, 243, 112659. [Google Scholar] [CrossRef]
- Dalal, S.P.; Dalal, P. Strength, deformation and fragility assessment of reinforced concrete moment resisting frame designed by force based design and the performance based plastic design method for seismic loads. Structures 2021, 29, 1154–1164. [Google Scholar] [CrossRef]
- Cao, X.Y.; Feng, D.C.; Wu, G. Seismic performance upgrade of RC frame buildings using precast bolt-connected steel-plate reinforced concrete frame-braces. Eng. Struct. 2019, 195, 382–399. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley MJ, N.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Liu, H.; Zeng, Y.X.; Han, M.J.; Fan, Y.L.; Zhang, G.W.; Qin, C.A. Experimental research of seismic behavior of existing RC frame strengthened with attached diagonal cable brace. Build. Struct. 2023. (In Chinese) [Google Scholar] [CrossRef]
- Fan, Y.L.; Liu, H.; Han, M.J.; Zeng, Y.X.; Zhang, G.W.; Qin, C.A. Study on seismic performance of self-centering member reinforced frame based on finite element. Archit. Technol. 2023, 54, 1174–1177. (In Chinese) [Google Scholar]
- Vamvatsikos, D.; Cornell, C.A. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- American Society of Civil Engineers; Federal Emergency Management Agency. Prestandard and Commentary for the Seismic Rehabilitation of Buildings; Federal Emergency Management Agency: Washington, DC, USA, 2000.
- Cornell, C.A.; Jalayer, F.; Hamburger, R.O.; Foutch, D.A. Probabilistic basis for 2000 SAC Federal Emergency Management Agency steel moment frame guidelines. J. Struct. Eng. 2002, 128, 526–533. [Google Scholar] [CrossRef]
- Yu, X.H. Probabilistic Seismic Fragility and Risk Analysis of Reinforced Concrete Frame Structures; Harbin Institute of Technology: Harbin, China, 2012. (In Chinese) [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).