Multi-Objective Optimization Design of Corrugated Steel Sandwich Panel for Impact Resistance

Abstract

The application of corrugated steel sandwich panels on ships requires excellent structural performance in impact resistance, which is often achieved by increasing the weight without giving full play to the characteristics of the structure. Considering the mechanical properties of sandwich panels under static and impact loading, a multi-objective optimal method based on a back-propagation (BP) neural network and a genetic algorithm developed in MATLAB is proposed herein. The evaluation criteria for this method included structural mass, static and dynamic stress, static and dynamic deformation, and energy absorption. Before optimization, representative sample points were obtained through numerical simulation calculations. Then, the functional relationship between the design and output variables was generated using the BP neural network. Finally, a standard genetic algorithm (SGA) and an adaptive genetic algorithm (AGA) were used for multi-objective optimization analysis with the established function to obtain the best result. Through this study, a new design concept with high efficiency and reliability was developed to determine the structural parameters that provide the best impact resistance using limited sample points.

1. Introduction

With the advancement of science and technology, the shipping industry has achieved increasing prosperity in recent decades. However, modern airborne anti-ship weapons and collision accidents during navigation pose a considerable threat to ships [1,2,3]. A hull structure with excellent impact resistance is vital for improving the structural strength of ships. As a new type of structure with two face sheets and a cell core, corrugated sandwich panels have often been used to replace traditional metal components to reduce weight. Corrugated sandwich panels offer many advantages, such as lightness, low construction cost, high specific strength, effective sound insulation, high energy absorption efficiency, and strong impact resistance [4,5,6,7,8,9]. Hence, corrugated steel sandwich panels are being used in ship construction, for example, in the Visby class corvettes built by the Swedish Navy [10], in the European research project SANDWICH [11], and in the smooth components of ships [12]. Gajewski [13,14,15,16] conducted extensive research on the static mechanical properties of panels with a corrugated core. These studies present analytical methods for estimating the static top-to-bottom compressive strength of simple corrugated packaging and corrugated cardboard boxes with various openings. In addition, the formula for the torsional and transverse stiffness of orthotropic sandwich panels was defined. The low-velocity impact responses of steel sandwich panels [17] and circular corrugated sandwich cylindrical panels [18] have been studied. The results have shown that metal sandwich panels with a corrugated core possess a higher impact resistance than monolithic solid plates do and that the impact response is particularly dependent on the impact position. Wadley [19] analyzed the impact resistance of aluminum sandwich panels and proposed a method to control the spatial extent of the hybrid panel damage. However, these studies lack an in-depth analysis of the geometric parameters of sandwich panels. Conventional structural optimization improves the mechanical properties by increasing the weight of the structure, which increases the cost of fabrication. To address the contradiction between the structural weight and impact resistance, a new optimization method should be developed.

The genetic algorithm (GA) is a randomized search-and-optimization technique guided by the principles of evolution and natural genetics and possesses a large amount of implicit parallelism [20,21]. The GA performs searches in complex, large, and multimodal landscapes, providing near-optimal solutions for the objective or fitness functions of an optimization problem. In the field of ship-structure optimization, Sekulski [22,23,24] analyzed and optimized the least-weight distribution and size of high-speed vehicle–passenger catamaran structures with a GA, successfully solving the multi-variable optimization problem. Because slight changes in the control parameters may lead to different optimal results in the optimization process, it is necessary to ensure the accuracy of the data as much as possible. Additionally, it is necessary to conduct investigations based on the background of the specific application. Because of the risk of collision encountered by conventional tankers, it is undoubtedly important to improve the crashworthiness of the hull. Hence, Klanac et al. [25] coupled multi-objective structural optimization and crashworthiness analysis and optimized the traditional tanker structure to make it more crashworthy, while considering changes in hull quality; thereby they effectively improved the structural safety. A conclusion about the optimal design of tanker structures showed that the GA was superior to traditional optimization. Researchers have also improved the GA by referring to the gradient algorithm [26]. The improved GA not only improves the convergence speed and shows a strong local search ability, but also avoids premature phenomena.

Artificial neural networks, which can find various input and output mapping functions via learning and training and by adjusting the threshold and weight values, are used to simulate biological neural networks and process information [27]. Any continuous function can establish a mapping relationship with a three-layer neural network [28]. Based on this principle, the neural network has often been used to predict the trajectory of ships in the water zone and improve the safety of navigation [29,30]. This shows that high-precision neural network models can replace simulation calculations in some studies. The back propagation (BP) neural network (including the input, hidden, and output layers) can achieve nonlinear mapping between any output and input and is a multilayer feedforward neural network [31,32]. It is also the most widely applied artificial neural network [33]. BP neural networks generally have no restriction in terms of input samples, can handle highly nonlinear problems, and can be combined suitably with other modern optimization algorithms. Owing to these advantages, the new optimization method of combining artificial neural networks and GAs has been increasingly applied in the field of ship-structure optimization design [34,35,36].

In this study, a BP neural network and two GAs were combined to optimize the impact resistance of metal sandwich panels when applied to superstructures. Before optimization, the design variables in the sample points were selected through an orthogonal experimental design, and a numerical simulation method proved feasible by the author through experiment [37] was used to obtain the output variables of the sample points. Then, the multi-objective function, which can fully reflect the impact resistance of the structure, was mapped through a BP neural network. Finally, a GA was used to obtain the optimal sandwich panel structure design plan to provide full play to the impact resistance of the panel. Based on this study, the ideal geometric parameters of the sandwich panel can be obtained by optimizing the limited sample points, which improves the efficiency and reduces costs.

2. Optimization Method

The orthogonal experiment can segregate representative points from a comprehensive test and is often used for the sample training of neural networks to improve efficiency and to ensure generalization ability [38,39]. Because the optimized samples used in this study were obtained through simulation calculations, an orthogonal experiment was first used to screen out the representative sample points. Second, the BP neural network and GA were coupled into the optimizing program to realize data transmission based on MATLAB software. Third, the sample points were input into the BP neural network for training to create a multi-objective function that can realize the mapping relationship between the design and output variables. Finally, the multi-objective function was input into the GA to calculate the optimal solution after selection, crossover, and mutation, as shown in Figure 1. Once the result in the BP neural network or GA did not meet the requirements, the program was re-optimized until the optimal solution was obtained.

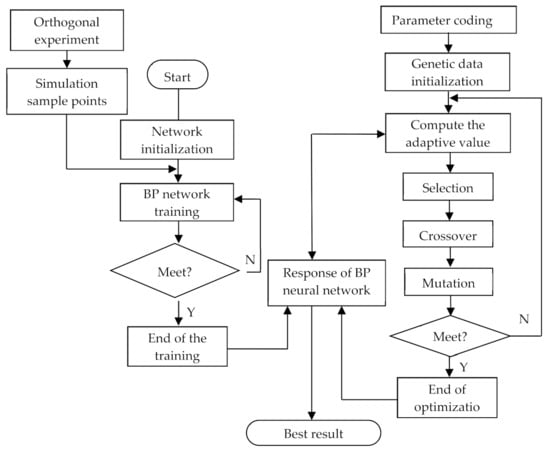
Figure 1. Optimized flow diagram between BP neural network and GA.

2.1. Mathematical Model

The optimal design of a target structure requires a suitable mathematical model to reflect the characteristics. The mathematical model to optimize the impact resistance of corrugated sandwich panels can be summarized as follows:

$$\left\{\begin{array}{l}\min F(X), X\in {\mathrm{R}}^n\\ \begin{array}{lll}\mathrm{s}.\mathrm{t}.& g_j(X)\le 0,& j=1,2,\cdots ,J\\ & l_k(X)=0,& k=1,2,\cdots ,K\end{array}\end{array}\right.$$

(1)

and when J or K is not zero, it is called a constrained optimal problem.

Because impact loading causes significant damage to the superstructure and threatens the safety of personnel and equipment, it is important to develop a reasonable objective function. After comprehensive consideration, the structural mass m, static deformation $v_0$, static stress under static loading $S_0$, dynamic deformation $v_1$, dynamic stress $S_1$, and energy absorption under impact loading $\eta$ were selected to form a multi-objective function.

$$f(x)=\alpha ·f_m+\beta ·f_{v_0}+\gamma ·f_{S_0}+\lambda ·f_{v_1}+\mu ·f_{S_1}+\xi f_{\eta }$$

(2)

where $f(x)$ is the multi-objective function, and $f_m$, $f_{v_0}$, $f_{S_0}$, $f_{v_1}$, $f_{S_1}$, and $f_{\eta }$ are the sub-objective functions of mass, static deformation, static stress, dynamic deformation, dynamic stress, and energy absorption, respectively. Because the six sub-objectives have different degrees of importance in reflecting the impact performance of sandwich panels, $\alpha$, $\beta$, $\gamma$, $\mu$, and $\zeta$ are used to refer to the weight coefficients. These weight coefficients indicate the importance of each sub-objective in the impact resistance evaluation, and the sum of these weight coefficients must be 1.

In the analysis, the MinMax method was used to process the calculation samples, which can be expressed as

$$f{(x)}^{*}=\frac{f(x)-f{(x)}_{\min }}{f{(x)}_{\max }-f{(x)}_{\min }}$$

(3)

2.2. Back-Propagation Neural Network

The BP neural network is a multi-layer feedforward network trained using an error back propagation algorithm. Two aspects are involved: the forward propagation of the signal and the backward propagation of the error. When the actual output is calculated, it is performed in the direction from input to output. In contrast, the correction of the weight and threshold is performed in the direction from output to input. The mapping relationship of the BP neural network is as follows:

$$\begin{array}{cc}F:R^m\to R^L,& Y=F(X)\end{array}$$

(4)

where X and Y are the sample input and output sets, respectively. After completing the data mapping, the error criterion function in the output layer can be expressed as

$$\left\{\begin{array}{l}{E}_p=\frac{1}{2}{\displaystyle \sum _{i=1}^n}{(T_i-z_i)}^2\\ E=\frac{1}{2}{\displaystyle \sum _{p=1}^P}{\displaystyle \sum _{i=1}^n}{(T_i-z_i)}^2\end{array}\right.$$

(5)

where z_i is the calculated output value, T_i is the initial value of the objective variable, and p is used to represent a single sample. E_p is the quadratic error criterion function for each sample p, and E is the total error criterion function of the system for all the training samples.

In this study, the Levenberg–Marquardt algorithm was used to determine the network weights and ensure that the error function can reach a minimum value within a limited number of iterations. Although the error curve is always complex and has some local minima, the adjustment of weights always aligns toward the descending direction of the error function to ensure the accuracy of the mapping function.

2.3. Standard Genetic Algorithm

2.3.1. Theory of Calculation

The theoretical basis for the effectiveness of standard genetic algorithms (SGAs) comprises the pattern and building block hypotheses. Generally, mode H includes four parameters: the original code length l, pattern length δ (H), order O (H), and dimension D (H), where l is the length of the string, δ (H) is the distance between the first and last fixed bits, O (H) is the number of fixed bits in the pattern, and D (H) represents the number of strings contained in the pattern. For the SGA, the number of patterns H can be estimated as

$$m(H,t+1)\ge m(H,t)(\frac{\overline{f}(H)}{{\overline{f}}_t})\left[1-P_c\frac{\delta (H)}{l-1}-O(H)P_m\right]$$

(6)

where $m(H,t+1)$ is the number of populations containing a specific pattern H at time t + 1, $\overline{f}=(\sum f_i)/n$ is the average fitness of the entire population, and $\overline{f}(H)$ is the average fitness of the string of pattern H at time t. P_c and P_m are the crossover probability and mutation probability of the entire population, respectively.

A pattern with low order, short length, and high adaptability is called a building block. By combining the building blocks with each other under the action of genetic operations, the ability of continuous optimization can be achieved, which is considered to be the main driving force of the search ability of the GA.

2.3.2. Penalty Function

The SGA is more suitable for optimization and is easy to implement using hardware when only the requirement of global searching is considered. First, the required precision is not high. Second, if binary encoding is adopted, the results can be directly reflected in the digital storage. Third, the arithmetic operation is simple, which is favorable for hardware implementation. To improve efficiency, the following formula is selected as the basis of judgment for the objective function:

$$Fit\left(O\left(x\right)\right)=\left\{\begin{array}{ll}{c}_{\max }-O\left(x\right),& O\left(x\right)<c_{\max }\\ 0,& \mathrm{other}\end{array}\right.$$

(7)

where $c_{\max }$ is the maximum estimate of $O(x)$. The default is 1.

Because the SGA can only deal directly with unconstrained optimization problems, it requires the transformation of the constraint problem into an unconstrained problem via the penalty function [10], as shown in Equation (8).

$$\left\{\begin{array}{l}Fit(O(x))=fit(O(x))+rP(O(x))\\ P(O(x))=\left\{\begin{array}{ll}=0,& x\in X\\ >0,& x\notin X\end{array}\right.\end{array}\right.$$

(8)

where r is the scale coefficient, and X is the feasible region of the problem solution.

2.4. Method Verification

To verify the accuracy of the optimization method, a single beam with length l = 3.75 m, elastic modulus E = 200 GPa, density of 7850 kg/m³, yield limit ${\sigma }_y$ = 235 MPa, and uniformly distributed load q = 20 N/mm was optimized in this study. The optimization results were then compared with the theoretical solution. A single beam is shown in Figure 2.

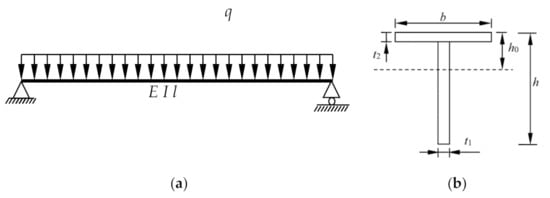
Figure 2. Schematic of the single beam. (a) Model of single beam, and (b) shape of beam section.

The optimization problem can be expressed as follows:

$$\begin{gathered} \min m(t_1,h,t_2,b)=t_1·(h-t_2)+t_2·b \\ \mathrm{s}.\mathrm{t}. 10 \mathrm{mm}\le t_1\le 18 \mathrm{m}\mathrm{m} \\ 300 \mathrm{mm}\le h\le 360 \mathrm{mm} \\ 20 \mathrm{mm}\le t_2\le 26 \mathrm{mm} \\ 180 \mathrm{mm}\le b\le 240 \mathrm{mm} \\ {\sigma }_{\max }\le {\sigma }_y/2=117.5\mathrm{MPa} \end{gathered}$$

The multi-objective function f(x) can be expressed as

$$f(t_1,h,t_2,b)=\alpha ·f_m+\beta ·f_{v_{\max }}+\gamma ·f_{{\sigma }_{bot\max }}+\lambda ·f_{{\sigma }_{top\max }}+\eta ·f_{\theta }$$

(9)

where $f_m$, $f_{v_{\max }}$, $f_{{\sigma }_{top\max }}$, $f_{{\sigma }_{bot\max }}$, and $f_{\theta }$ are the sub-objective function of mass (m), maximum deflection (v_max), maximum stress (σ_topmax) of the face plate, maximum stress (σ_botmax) of the web plate, and rotating angle (θ) of the boundary, respectively. In the function, changing the mass may inevitably have an influence on other sub-objectives, and the mass is directly related to the fabricating cost. Therefore, it is of practical significance to set the proportion of mass to the maximum. Secondly, maximum deflection can intuitively reflect the bending strength of the single beam structure, and the importance should be second only to mass. Compared with the face plate, the web plate can provide stronger bending strength under the uniformly distributed load, which means the importance of the σ_topmax is greater than σ_botmax. In the sub-objectives, the rotating angle is not the focus of attention, and the weight coefficient should be the lowest. Finally, we assume $\alpha =0.55$, $\beta =0.25$, $\gamma =0.15$, $\lambda =0.04$, and $\eta =0.01$.

For a single beam, the formula used in the theoretical calculation can be expressed as

$$v_{\max }=v(\frac{l}{2})=\frac{5}{384}\frac{q{l}^4}{EI}$$

(10)

$$\theta =\frac{1}{24}\frac{q{l}^3}{EI}$$

(11)

$${\sigma }_{\max }=\frac{y·M(l/2)}{I}=\frac{yq{l}^2}{8I}$$

(12)

The calculation results obtained using the theoretical formula are listed in Table 1. The test results met the requirements in terms of the stress and deformation constraints.

Table 1. Orthogonal design of single beam and calculation.

Number	t1 /mm	h /mm	t2 /mm	b /mm	vmax /mm	m /kg	σtopmax /MPa	σbotmax /MPa	θ /°	f
1	10	320	24	200	3.053	228.435	33.681	109.714	0.149	0.4371
2	14	360	20	200	1.906	257.873	30.174	68.732	0.093	0.3074
3	12	360	24	220	1.914	274.122	25.721	74.652	0.094	0.3707
4	18	320	20	220	2.121	288.488	30.809	67.661	0.104	0.4403
5	10	340	20	240	2.644	235.500	30.549	99.395	0.129	0.3847
6	14	300	24	240	2.696	283.307	29.559	89.688	0.132	0.5370
7	12	300	20	180	3.518	204.885	43.225	110.464	0.172	0.4287
8	18	340	24	180	1.8	294.611	29.17	60.289	0.088	0.4042
9	10	300	26	220	3.428	249.041	32.334	120.26	0.168	0.5757
10	14	340	22	220	2.065	273.533	28.41	73.672	0.101	0.3895
11	12	340	26	200	2.217	263.996	28.285	82.486	0.108	0.3930
12	18	300	22	200	2.487	276.830	33.863	75.488	0.122	0.4657
13	10	360	22	180	2.388	216.071	33.239	91.303	0.117	0.2725
14	14	320	26	180	2.407	258.932	32.072	81.613	0.118	0.4030
15	12	320	22	240	2.628	260.699	29.779	92.924	0.129	0.4564
16	18	360	26	240	1.364	360.668	20.735	51.163	0.067	0.5500

According to the samples in Table 1, the single-objective optimal solutions obtained by the optimization method are listed in Table 2.

Table 2. Optimized results of mass in single beam.

Type	t1 /mm	h /mm	t2 /mm	b /mm	vmax /mm	m /kg	σtopmax /MPa	σbotmax /MPa	θ /°	f
Theory	10.0	360	22	180	2.388	216.07	33.24	91.3	0.117	0.2725
Optimization	10.1	346.7	22	180	2.39	214.53	34.22	94.36	0.126	0.2765

It can be observed from Table 2 that the optimization method proposed in this paper has high credibility and can be used for subsequent optimization analysis.

3. Numerical Simulation Optimization

3.1. Description of Problem

The application of corrugated steel sandwich panels in a superstructure is illustrated in Figure 3. The superstructure was originally composed of a stiffened plate frame structure before it was replaced by sandwich panels. As a lightweight structure, the metal sandwich panel should not only meet the strength and functional requirements, but also exert its own lightweight characteristics to achieve weight reduction when performing alternative applications. Additionally, the weight has a significant influence on ship performance and construction cost, and if the sandwich panel can satisfy the performance requirements as part of the weight reduction premise, the application value of the sandwich panel will be further improved. Steel corrugated sandwich panels have been applied to ship structures to achieve light weight, and the weight savings were estimated to be as much as 50% compared with the structure before replacement [11]. However, if 50% weight savings is to be achieved in this article, the thickness of the sandwich panel will be too thin to be produced. To meet the processing conditions, the mass of the sandwich panel was designed to meet the constraint of a 20% weight savings after the comprehensive assessment. Since the original structural mass in the area of 2500 × 2300 mm² on the side wall of the superstructure is 306.5 kg, the mass of the sandwich panel should not be greater than 245.2 kg.

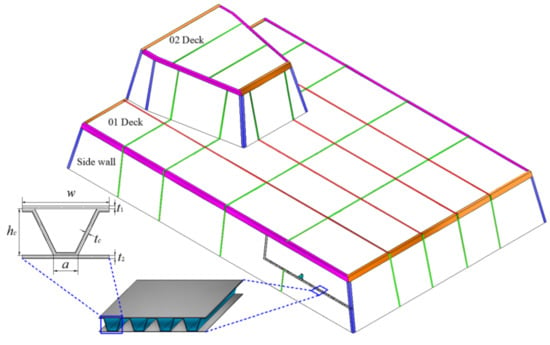
Figure 3. Basic structure of traditional superstructure and alternative area.

During the optimization of the target structure, the corrugated sandwich panel used in alternative designs has several unit cells, which are characterized by six geometric parameters: core height h_c, attachment width a, cell core length w, thickness of the face sheets t₁ and t₂, and thickness of the core, t_c. To reduce the difficulty of processing and optimization, the attachment width a was set to 20 mm. Therefore, the other five parameters were used as design variables during optimization. Under the constraint of the mass (m ≤ 245.2 kg), the ranges of values of these variables are as follows:

$$\begin{gathered} 60 \mathrm{mm}\le h_c\le 100 \mathrm{mm} \\ 100 \mathrm{mm}\le w\le 125 \mathrm{mm} \\ 1.5 \mathrm{mm}\le t_1, t_2\le 2 \mathrm{mm} \\ 1 \mathrm{mm}\le t_c\le 2 \mathrm{mm} \end{gathered}$$

Combined with Equation (2), the multi-objective function f(x) can be expressed as:

$$f(h_c, w, t_1, t_c, t_2)=\alpha ·f_m+\beta ·f_{v_0}+\gamma ·f_{S_0}+\lambda ·f_{v_1}+\mu ·f_{S_1}+\xi f_{\eta }$$

(13)

Making the change of h_c, w, t₁, t_c, and t₂ can directly affect the mass and the response of the structure. To establish the functional relationship between the left and right sides of the Equation (13), the BP neural network is used for network training to move the five geometric parameters into each sub-objective function. In Equation (9), the weight coefficient can effectively reflect the importance of the sub-objective and has a decisive influence on the optimization result. Compared with the single beam, changing the mass of the panel may also inevitably influence other sub-objectives, and the mass is also directly related to the fabricating cost. Thus, the value of the weight coefficient of mass should be the largest among the sub-objectives. Secondly, the dynamic deformation (v₁) can intuitively reflect the safety of the structure and easy to measure, meaning the importance should be second only to mass. Thirdly, the better the energy absorption (η) under impact loading, the weaker the effect caused by the impact. It can be second only to dynamic deformation. Then, the importance of dynamic stress is often not high because of the difficulty of measurement. Finally, while the impact of static loading is considered when evaluating the impact resistance of sandwich panels, the priority of dynamic loading is still higher. Thus, the proportion of the static deformation (v₀) and static stress (S₀) should be the smallest, and the proportion of v₀ is greater than S₀. Hence, the values of the weight coefficients must satisfy $\alpha >\lambda >\zeta \ge \mu \ge \beta \ge \gamma$. After comprehensively considering the importance of each objective function, a reasonable combination of weighting factors for each weight coefficient based on the size relationship is provided in Table 3.

Table 3. Combination of weight coefficients.

Weight Coefficient	$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\gamma }$	$\mathit{\lambda }$	$\mathit{\mu }$	$\mathit{\xi }$
Case 1	0.5	0.05	0.05	0.2	0.1	0.1
Case 2	0.5	0.05	0.05	0.2	0.05	0.15
Case 3	0.45	0.1	0.1	0.15	0.1	0.1
Case 4	0.45	0.1	0.05	0.2	0.1	0.1
Case 5	0.45	0.05	0.1	0.2	0.1	0.1
Case 6	0.4	0.05	0.05	0.2	0.15	0.15
Case 7	0.4	0.1	0.05	0.2	0.1	0.15
Case 8	0.4	0.05	0.05	0.25	0.1	0.15
Case 9	0.3	0.05	0.05	0.3	0.15	0.15

3.2. Simulation Calculation

Numerical simulations were conducted using the ABAQUS finite element software program. In the published article [37], relevant experiment has been carried out to prove that the required sample points can be obtained through the numerical simulation method. Figure 4 shows the comparison result of experiment and simulation. Since the initial area of 2500 × 2300 mm² on the sidewall of the superstructure is too large to make the experiment, the size used in the test is 1000 × 1000 mm². The result suggests that the structural deformation and failure mode are accurately captured by the numerical model [37]. Therefore, it is feasible to use numerical simulation to obtain the sample points needed for optimization in this paper.

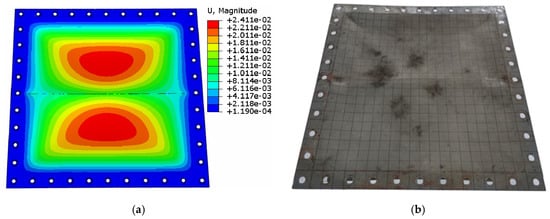
Figure 4. Comparison of plastic deformation for stiffened panel in simulation and test, reproduced from [37], with permission from Elsevier, 2021: (a) panel deformation from numerical simulation, and (b) panel deformation from test.

Figure 5 shows a schematic of the sandwich panel with four-node shell elements (S4R) with reduced integration points. Mesh sizes of 10, 15, 20, 50, and 100 mm (system default) were used for the entire model for mesh sensitivity analysis. A plane impact loading of 500 kPa was selected. The maximum deformation of the sandwich panel with h_c = 100 mm, w = 125 mm, t₁ = t₂ = 1.5 mm, and t_c = 1 mm is shown in Figure 6. The results indicate that a mesh size of 20 mm is suitable for the calculation models. After considering the influence of the material strain rate sensitivity, the Cowper–Symonds constitutive model was adopted as the material model. For high-strength steel, the values of the parameters were D = 3200 and P = 5 [40]. The density of the mild steel was 7850 kg/m³, the elastic modulus was 210 GPa, and the Poisson’s ratio was 0.3. In addition, the boundary condition was a fixed constraint.

Figure 5. Schematic of the corrugated sandwich panel. (a) Finite element model with fixed constraint, and (b) meshing of the model.

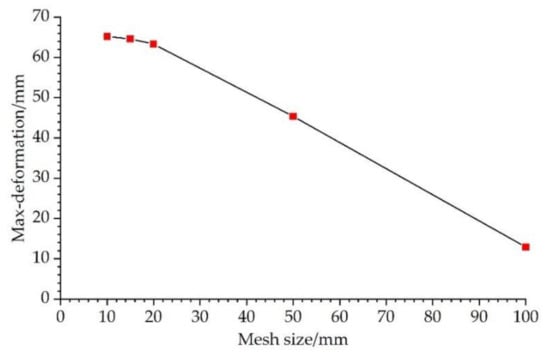
Figure 6. Maximum deformation of the sandwich panel with different mesh sizes.

After being screened by the orthogonal experiment, 20 sample points were finally determined within a mass of 245.2 kg. To facilitate the calculation, types A–F were used to number the sample points. Additionally, the sandwich panel type was mainly defined by the core height and cell core length. In the simulation calculation, a static loading of 5 kPa and a plane impact loading of 500 kPa were adopted for the samples that were selected by the orthogonal experiment. The calculation results are presented in Table 4.

Table 4. Results of simulation calculation under static and impact loading.

Type		Unit (mm)					m /kg	v0 /mm	S0 /MPa	v1 /mm	S1 /MPa	η /J
		hc	w	t1	tc	t2
A	1	60	100	1.5	1	1.5	214.0	0.89	15.89	111.42	560.21	134,210
	2	60	100	1.5	1	2	236.6	0.79	15.90	96.12	428.90	116,362
	3	60	100	2	1	1.5	236.6	0.78	15.76	92.91	414.79	111,519
	4	60	100	1.5	1.5	1.5	253.3	0.77	13.56	93.73	412.03	103,799
B	1	60	125	1.5	1	1.5	203.0	1.00	19.64	121.04	369.30	149,035
	2	60	125	1.5	1	2	225.5	0.90	21.09	106.64	408.79	131,635
	3	60	125	2	1	1.5	225.5	0.87	14.8	96.58	454.64	124,883
	4	60	125	1.5	1.5	1.5	236.7	0.86	22.11	99.55	446.12	117,425
	5	60	125	2	1	2	248.1	0.74	12.34	84.76	417.44	109,713
C	1	80	100	1.5	1	1.5	230.6	0.56	13.49	80.08	462.77	99,087
	2	80	100	1.5	1	2	253.2	0.51	12.77	69.33	480.16	81,676
	3	80	100	2	1	1.5	253.2	0.49	12.25	64.45	354.80	80,400
D	1	80	125	1.5	1	1.5	215.3	0.58	11.57	92.32	529.67	120,061
	2	80	125	1.5	1	2	237.9	0.61	16.37	78.37	396.02	101,116
	3	80	125	2	1	1.5	237.9	0.54	11.56	76.86	397.12	99,087
	4	80	125	1.5	1.5	1.5	255.2	0.58	11.57	64.95	466.86	77,806
E	1	100	100	1.5	1	1.5	247.7	0.43	10.18	50.82	393.04	62,604
F	1	100	125	1.5	1	1.5	228.3	0.47	12.57	63.29	336.44	84,736
	2	100	125	1.5	1	2	250.9	0.42	15.46	48.40	396.53	65,915
	3	100	125	2	1	1.5	250.9	0.36	11.69	48.16	408.53	68,834

Based on the normalization method and weight coefficient table, the objective functions of these sandwich panels are listed in Table 5.

Table 5. Objective functions of the corrugated steel sandwich panels.

Type		Multi-Objective Function
		Case 1	Case 2	Case 3	Case 4	Case 5	Case 6	Case 7	Case 8	Case 9
A	1	0.5271	0.5186	0.5386	0.5580	0.5405	0.5975	0.5889	0.5909	0.6632
	2	0.6145	0.6250	0.6070	0.6159	0.6063	0.6019	0.6149	0.6142	0.6034
	3	0.5925	0.6032	0.5858	0.5931	0.5837	0.5739	0.5892	0.5871	0.5709
	4	0.7345	0.7414	0.7012	0.7183	0.7005	0.6789	0.6940	0.6932	0.6450
B	1	0.4043	0.4470	0.4440	0.4543	0.4440	0.4617	0.5043	0.5043	0.5617
	2	0.5761	0.5999	0.6024	0.5967	0.6003	0.5891	0.6151	0.6131	0.6262
	3	0.5325	0.5421	0.5369	0.5508	0.5303	0.5518	0.5652	0.5586	0.5751
	4	0.6653	0.6725	0.6869	0.6721	0.6830	0.6570	0.6715	0.6677	0.6629
	5	0.6619	0.6710	0.6323	0.6484	0.6277	0.6208	0.6324	0.6278	0.5846
C	1	0.4801	0.4730	0.4613	0.4693	0.4676	0.4766	0.4640	0.4703	0.4675
	2	0.6478	0.6267	0.6078	0.6114	0.6106	0.5948	0.5744	0.5772	0.5277
	3	0.5732	0.5794	0.5327	0.5352	0.5338	0.4914	0.4975	0.4985	0.4176
D	1	0.4148	0.4049	0.3958	0.4203	0.4089	0.4677	0.4417	0.4548	0.5047
	2	0.5339	0.5428	0.5252	0.5200	0.5264	0.5026	0.5088	0.5100	0.4772
	3	0.5022	0.5098	0.4690	0.4829	0.4746	0.4700	0.4705	0.4762	0.4426
	4	0.6450	0.6246	0.6065	0.6121	0.6008	0.5829	0.5709	0.5653	0.5059
E	1	0.4662	0.4536	0.4271	0.4289	0.4234	0.3932	0.3861	0.3824	0.3113
F	1	0.3281	0.3409	0.3121	0.3124	0.3139	0.2924	0.3010	0.3028	0.2647
	2	0.5170	0.5055	0.4977	0.4758	0.4932	0.4406	0.4318	0.4273	0.3491
	3	0.5046	0.4921	0.4650	0.4587	0.4650	0.4325	0.4164	0.4164	0.3408

It can be observed from Table 5 that under impact loading of 500 kPa, panel F1 has the smallest objective function among those of the nine weight coefficient combinations. Hence, panel F1 is considered to have the best impact resistance. Among the 20 samples, the mass of the F1 was not the smallest nor the largest, which further showed that simply increasing the mass could not make the structure obtain the optimal impact resistance. However, both the core height (h_c) and the cell core length (w) are the maximum values. The thickness of the core (t_c) is the minimum, and the thickness (t₁ and t₂) of the two face sheets are equal. It can be indicated that there are there are three ways to improve the impact resistance of the sandwich panel, such as increasing the values of the core height and the cell core length, reducing the thickness of the core, and keeping the thickness of face sheets consistent.

4. Algorithm Optimization

To obtain the best impact resistance of the steel sandwich panel, the optimization program combined with the BP neural network and GA was selected for optimization analysis using case 7. In the optimization process, the training error of the BP neural network was selected as 1 × 10⁻³, and the number of training steps was 300. The maximum genetic frequency in the GA was 1000, the default initial population was 60, the number of chromosomes was 9, the crossover probability P_c was 0.7, and the mutation probability P_m was 0.01. Figure 7 shows the optimization results of the coupling algorithm under a multi-objective analysis.

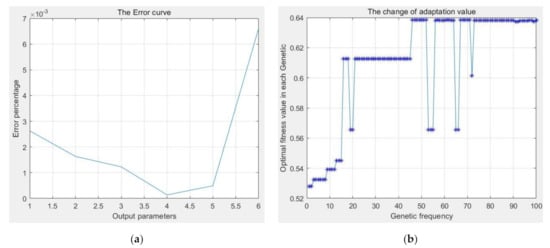
Figure 7. Coupling algorithm optimization based on BP neural network and genetic algorithm. (a) Training error map of BP network, and (b) fitness curve of the genetic algorithm.

Because the GA is mainly optimized through selection, crossover, and mutation, it makes sense to change the calculation principles of these three methods to obtain different results for the accuracy of optimization. An algorithm that can automatically adjust the crossover probability P_c and mutation probability P_m by the change in fitness is called an adaptive genetic algorithm (AGA). The calculation formula for the probability of crossover and mutation is expressed as follows [41]:

$$P_c=\left\{\begin{array}{ll}\frac{k_1(f_{\max }-f^{\prime })}{f_{\max }-f_{avg}},& f^{\prime }\ge f_{avg}\\ k_2,& f^{\prime }<f_{avg}\end{array}\right.$$

(14)

$$P_m=\left\{\begin{array}{ll}\frac{k_3(f_{\max }-f)}{f_{\max }-f_{avg}},& f\ge f_{avg}\\ k_4,& f<f_{avg}\end{array}\right.$$

(15)

where k₁, k₂, k₃, and k₄ are parameters with values between 0 and 1, $f_{\max }$ is the largest fitness function value in the population, $f_{avg}$ is the average fitness function value of each generation group, $f^{\prime }$ is the larger fitness function value of the two individuals to be crossed, and $f$ is the fitness function value of the individual to be mutated.

Table 6 lists the program optimization results and simulation calculation results for comparison.

Table 6. Comparison of optimization algorithm and simulation calculation results.

Type	Unit (mm)					m kg	v0 mm	S0 MPa	v1 mm	S1 MPa	η kJ	f
	hc	w	t1	tc	t2
F1	100	125	1.5	1	1.5	228.3	0.5	12.6	63.3	336.4	84.7	0.301
GSGA	97.7	124.9	1.5	1	1.5	225.7	0.5	10.9	61.8	323.8	83.9	0.273
GAGA	75.4	108.2	1.7	1.4	1.5	219.5	0.5	10.3	83.1	517.6	107.9	0.403

Compared with the F1 panel, the result of the optimal multi-objective function obtained from the coupling algorithm BP neural network and the SGA was reduced by 9.3%, showing that the structural parameters of the sandwich panel listed in Table 3 can be improved by optimizing the coupling algorithm. The resolution obtained by the BP network and the AGA was not dominant compared to the simulation results. However, the core height (h_c = 97.7 mm) and cell core length (w = 124.9 mm) obtained by SGA were not integers, which were difficult to be processed ideally in the presence of processing accuracy. The value of two parameters should be adjusted based on the principle of convenient processing to meet the processing requirements. Hence, a new geometric parameter was selected, and the objective function was also calculated, as presented in Table 7.

Table 7. Error between the optimal algorithm and simulation.

Type	Unit (mm)					m kg	v0 mm	S0 MPa	v1 mm	S1 MPa	η kJ	f
	hc	w	t1	tc	t2
G1	95	125	1.5	1	1.5	225.0	0.2	8.1	63.5	283.2	87.1	0.253
GSGA	97.7	124.9	1.5	1	1.5	225.7	0.5	10.9	61.8	323.8	83.9	0.273
Error (%)	2.76	-	-	-	-	0.31	60	25.69	2.75	12.54	3.81	7.33

As can be observed in Table 7, the G1 board not only meets the actual production requirements, but also has the smallest multi-objective function. Except for the deformation v₀ under static loading, the error of the other dependent variables between G1 and G_SGA was small. Within the allowable error range, the results obtained using the coupling algorithm were real and effective. Thus, the impact resistance performance is relatively optimal. Therefore, the corrugated steel sandwich panel with h_c = 95 mm, w = 125 mm, a = 10 mm, t₁ = 1.5 mm, t_c = 1 mm, and t₂ = 1.5 mm shows an excellent impact resistance. This further demonstrates that the coupling algorithm used in this study can optimize the impact resistance of corrugated steel sandwich panels for a superstructure.

5. Conclusions

The optimization of the impact resistance of a sandwich panel was divided into three main steps. First, a multi-objective function was established. Second, the relationship between the target and design variables was obtained using a BP neural network. Finally, a GA was used to optimize the multi-objective function and obtain the optimal solution. A comparison with the simulation results showed that the multi-objective analysis of the sandwich panel obtained using the orthogonal design under the premise of meeting the mass requirement could not yield the best design parameters. The coupling algorithm proposed herein thus must be optimized further.

Based on the static mechanical properties and impact resistance of sandwich panels, this study introduced a multi-objective function comprising structural weight, deformation, stress, and energy using a mathematical model. For the multi-objective function, the combination of the BP neural network with the SGA was more effective than combining it with the AGA for achieving the optimal design of impact resistance. The calculation showed that this method can provide better parameters for the sandwich structure, thus demonstrating its superiority.

The main results of the optimal design (e.g., structural weight and plastic displacement) were verified via a numerical simulation, the results of which demonstrated high precision. The optimization of the coupling algorithm showed that the core height is the main optimization influencing factor among the five design variables, which can provide a reference for the design and manufacture of sandwich panels.