Abstract
Cosmic Explorer is a concept for a new laser interferometric observatory in the United States to extend ground-based gravitational-wave astrophysics into the coming decades. Aiming to begin operation in the 2030s, Cosmic Explorer will extend current and future detector technologies to a 40 km interferometric baseline—ten times larger than the LIGO observatories. Operating as part of a global gravitational-wave observatory network, Cosmic Explorer will have a cosmological reach, detecting black holes and neutron stars back to the times of earliest star formation. It will observe nearby binary collisions with enough precision to reveal details of the dynamics of the ultradense matter in neutron stars and to test the general-relativistic model of black holes.
1. Introduction
By the latter half of the 2030s, the field of gravitational-wave astronomy will be very different from what it is today. Space-based interferometers will collect millihertz signals from merging black holes with thousands to millions of solar masses [1,2]. Pulsar timing arrays will observe a nanohertz background of signals from black hole binaries with billions of solar masses [3]. Polarimetry of the cosmic microwave background may capture the imprint of gravitational waves from the early universe [4]. New experimental efforts will look for mega- and gigahertz gravitational waves arising from physics beyond the Standard Model [5], and for decihertz gravitational waves from astrophysical sources [6,7,8,9]. This multibanded array of observations will enhance a catalog of observations in the audio band (roughly ten hertz to several kilohertz) from the global network of ground-based, laser-interferometric gravitational-wave observatories—Advanced LIGO, Advanced Virgo, KAGRA, and GEO600—which should reach full sensitivity in this decade [10,11,12,13,14].
Given this wide spectrum of expected gravitational-wave data, what is the role of continued observation in the audio band? As will be argued in this review, even with a fulsome catalog of data from the current generation of audio-band gravitational-wave detectors, including from the incremental upgrades LIGO A+ and AdVirgo+ [15,16], many questions about stellar-mass binary systems or other phenomena in the gravitational-wave universe will remain unanswered until a network of more sensitive observatories comes online that can collect signals with higher fidelity and from further back in cosmic history. Other than switching to a radically different detection strategy, there are two ways to realize greater sensitivity across the audio band. The first way is to pursue technology improvements to realize a less noisy detector with a similar length as today’s detectors, in an existing or potentially new observatory facility. The Voyager concept proposes shifting to a cryogenic test mass material and a longer laser wavelength, among other changes; if installed in the 4 km LIGO facilities, it would give a two- to threefold improvement in amplitude sensitivity over LIGO A+ [17]. This technology can also enable a kilohertz-focused gravitational-wave detector, which leads to the NEMO concept for a 4 km observatory in Australia [18,19]. The second way to realize greater sensitivity is to increase the detector length, since the strength of the gravitational-wave-induced optical signal grows linearly with the detector length, while most noises in the detector grow sublinearly. (This scaling holds so long as the travel time of the laser light down the detector arms is smaller than the period of the gravitational wave).
If technology improvements are coupled with a longer detector arm length, it seems possible to achieve a broadband tenfold improvement in amplitude sensitivity over today’s detectors, and to push the lower end of the observation band to well below 10 Hz. In Europe, this idea has developed into the Einstein Telescope project, which aims to construct an underground observatory comprising six interferometers with 10 km arm length [20]. In the United States, the Cosmic Explorer project aims to construct a surface facility hosting a single 40 km interferometer, with current plans additionally calling for a second facility, widely separated from the first, hosting a single 20 km interferometer. The Einstein Telescope and Cosmic Explorer are both referred to as next-generation gravitational-wave observatories, since they represent a significant increase in sensitivity from the current generation of observatories.1
Broadly speaking, the ethos of Cosmic Explorer is to “just scale up” a LIGO facility and install a single interferometer with the best technology available. The germ of this idea goes back to at least 2013, when a noise analysis of a 40 km facility with the Advanced LIGO technology set was presented at the Advanced Detector Workshop in Elba [21]. Dwyer et al. [22] elaborated this analysis, demonstrating that such a detector could achieve cosmological reach (redshift ) over a wide mass range of binary stellar remnants. An analysis of the noise scalings of such a detector, along with the scalings of a detector using the Voyager technology set, followed thereafter [23]. From 2018 to 2021, the US National Science Foundation funded a horizon study that set out Cosmic Explorer’s science case, choice of technology, instrument design, community relationship, project realization, and cost estimate [24]; in parallel, a Cosmic Explorer consortium was established to organize the growing community of interested researchers. Cosmic Explorer intends to come online in the mid-2030s and operate as part of a global next-generation network with Einstein Telescope and potentially other observatories [25,26].
2. Science Program
Cosmic Explorer’s leap in sensitivity will deliver a catalog of observations that is fundamentally different from the catalog delivered by the current generation of observatories. Whereas today’s observatories can detect mergers of binary stellar remnants from redshifts less than 3, Cosmic Explorer will be able to detect them out to cosmological redshifts greater than 10—in other words, from the entire stellar history of the universe (Figure 1 and Figure 2). This also means that the rate of binary merger detections will likely exceed 100,000 per year, enabling detailed inferences about stellar remnant populations. Individual merger signals, especially those in the local universe, will be detected with greatly enhanced signal-to-noise ratio, sometimes exceeding 1000 in amplitude, enabling precision observation of the dynamics at play in these systems.
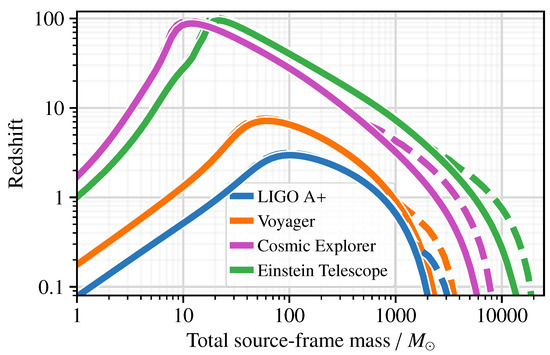
Figure 1.
Detection capability of selected current and next-generation gravitational-wave interferometers. Each curve indicates the highest cosmological redshift at which an equal-mass, non-spinning compact binary coalescence could be detected with amplitude signal-to-noise ratio of 8, if the system is optimally oriented on the sky. Solid lines indicate detection using the gravitational radiation from the angular mode of the system only; dashed lines show the inclusion of higher-order angular modes using the simulated waveform family IMRPhenomXHM [36].
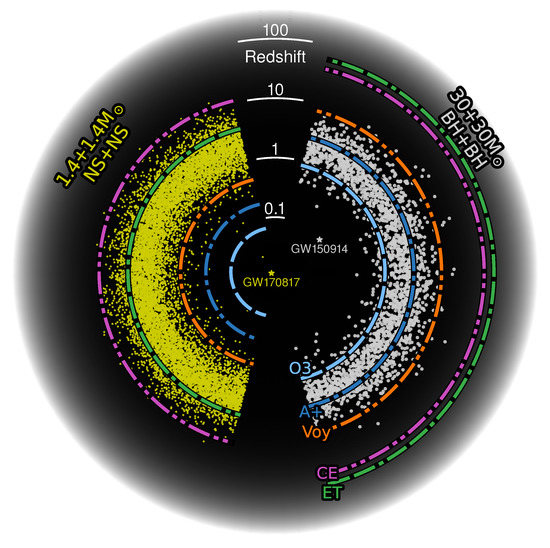
Figure 2.
The cosmic history of binary stellar remnant mergers, with 1.4 + 1.4 neutron star mergers on the left and 30 + 30 black hole mergers on the right; the radial coordinate is cosmological redshift z. The distribution of mergers as a function of redshift assumes the Madau–Dickinson star formation rate and that the typical time from binary formation to merger is 100 million years [37,38]; under these assumptions, most of these binaries merge at . The first gravitational-wave detections of a binary black hole merger (GW150914) and a binary neutron star merger (GW170817) are indicated [39,40]. The colored bands then show the detection capabilities of selected gravitational-wave observatories from Figure 1, as well as the capability of Advanced LIGO during the third LIGO–Virgo observing run.
Cosmic Explorer’s broad scientific program has been arranged around four themes. The first is black holes and neutron stars throughout cosmic time (Section 2.1); the second is the dynamics of dense matter (Section 2.2); and the third is extreme gravity and fundamental physics (Section 2.3). A fourth theme, discovery potential (Section 2.4), covers other phenomena and emphasizes the possibility of finding something completely unexpected. Many of these topics overlap with the science case of the Einstein Telescope [27], and the scientific output of both observatories will be enhanced if they operate jointly as part of a worldwide network, particularly due to the improved ability to measure the distance, inclination, and sky location of the systems [28,29,30,31,32,33,34,35].
2.1. Black Holes and Neutron Stars throughout Cosmic Time
2.1.1. Remnants of the First Stars
The stellar history of the universe extends from the present day back to a redshift higher than 10, beyond which the matter in the universe was predominantly neutral hydrogen. Even the oldest stars that astronomers have observed today, belonging to the so-called Population II, have a metal content that is too high to be explained by direct formation from this neutral hydrogen, leading to a hypothesized cohort of stars (Population III) that would have produced the first phase of stellar nucleosynthesis in the universe [41]. No such Population III star has been observed, but simulations suggest these stars were typically larger than 100 . If they were sufficiently massive, they would have collapsed into black holes [42,43], implying rich observational prospects for high-redshift gravitational-wave astronomy. Cosmic Explorer will be able to search for the remnant black holes of binary Population III systems at redshift beyond 10 over two decades in mass, about 3–300 ; see Figure 1 and Figure 2).
2.1.2. Seeds of Galaxy Formation
Most galaxies contain at their center a black hole with a mass of millions to billions of solar masses. The formation mechanism of such supermassive black holes has not been conclusively determined, but multiple scenarios rely on seeding from so-called intermediate-mass black holes, with masses ranging from hundreds to hundreds of thousands of solar masses. These intermediate-mass black holes could have formed from accretion onto the black hole remnants of Population III stars, from the collapse of clouds of neutral hydrogen, or from the gravitational collapse of globular clusters [44].
Whatever the mechanism, the formation process must have been underway before , given the observation of high-redshift active galactic nuclei likely powered by supermassive black holes (see, for example, Banados et al. [45]). Cosmic Explorer, ideally operating in a network with the Einstein Telescope, will be able to track the growth of high-redshift black holes up to a thousand solar masses, providing key information about the early stages of assembly of intermediate-mass and supermassive black holes [46].
2.1.3. Formation and Evolution of Compact Binaries
The question of how binary systems form, especially with orbits compact enough to coalesce via gravitational-wave emission, is still an open area of research. In regions of high stellar density, such as globular clusters, tightly bound binaries can form from dynamical encounters of stars or stellar remnants; alternatively, an isolated binary can become compact if one star ejects enough gas to form a common envelope around both stars, inducing a drag that tightens the orbit [47]. These formation mechanisms lead to varying predictions about the masses, spins, eccentricities, and other properties of the population of compact binaries, which can be inferred from gravitational-wave observations of the coalescence [48,49].
The existing catalog of gravitational-wave observations already gives hints that multiple formation mechanisms are at work [50]. Next-generation observatories such as Cosmic Explorer will densely sample the compact binary population out to high redshift, and the resulting catalog of observations will be able to not only differentiate between formation channels operating in the present day, but to track the operation of these channels throughout the stellar history of the universe [51].
2.2. Dynamics of Dense Matter
2.2.1. Structure and Composition of Neutron Stars
Neutron stars are known to be cold and ultradense, but the exact behavior of the matter inside them is not known. Particularly in the core, the high pressure and density could cause a phase transition from hadrons to deconfined quarks [52]. This subatomic behavior of the matter determines the equation of state relating pressure, density, and temperature. In neutron stars, the equation of state controls the relation between a star’s mass, radius, and deformability in a tidal gravitational field, which are observable in the gravitational waveform of a merging binary neutron star system [53]. Cosmic Explorer will be able to measure hundreds of neutron star radii to within 1% each year, providing a catalog of precise observations of tidal signatures that can be used to distinguish between different models of the neutron star equation of state.
The behavior of cold, dense matter can also be understood through observations of neutron stars in isolation, which could produce gravitational waves through solid body oscillations or through an elliptical mass distribution that rotates with the star [54]. Cosmic Explorer will be able to search for spinning neutron stars with ellipticities on the order of 10−9, testing the initial conclusion from electromagnetic observations that these stars have a minimum ellipticity [55].
2.2.2. New Phases in Quantum Chromodynamics
In the aftermath of a neutron star merger, the cold progenitor stars give way to a hot, dense postmerger remnant, which provides an avenue to probe the behavior of ultradense matter at a finite temperature. Here again the hadronic matter could, given the elevated temperature and density of the postmerger environment, transition to deconfined quarks, and this transition would be imprinted onto the portion of the gravitational waveform resulting from the postmerger oscillations of the remnant [56,57]. Additionally, the postmerger waveform reveals the fate of the remnant: whether it collapses promptly to a black hole, lingers momentarily as a hypermassive neutron star, or survives as a stable neutron star [58,59].
Postmerger oscillations are expected to occur somewhere between 2–4 kHz, which motivates the development of more sensitive gravitational-wave detectors in this frequency range and a careful consideration of their optical configuration [60]. Reliably detecting these postmerger oscillations at least once per year requires a next-generation detector such as the Einstein Telescope or Cosmic Explorer [61], or a dedicated high-frequency detector such as NEMO.
Core-collapse supernovae offer another avenue for witnessing the behavior of matter at extreme temperatures and densities. These supernovae are expected only a few times per century in our galaxy and there is considerable modeling uncertainty in the strength and morphology of their gravitational-wave emission. The detection prospects with the current generation of gravitational-wave observatories is thus uncertain, but a next-generation observatory such as Cosmic Explorer would boost the optimal signal-to-noise ratio by tenfold, vastly increasing the chance of detection [62]. Even so, the rate of detectable core-collapse supernovae is likely to remain low even for the next-generation observatories unless further broadband sensitivity improvements of 100 in amplitude are achieved [63].
2.2.3. Chemical Evolution of the Universe
The observation of a neutron star collision jointly by gravitational-wave and electromagnetic observatories in 2017 (GW170817 [64]) confirmed that these collisions are responsible for the synthesis of many of the heavy elements in the universe [65]. This initial observation anticipates a new set of questions, such as how the properties of the binary affect the rates of nucleosynthesis and the abundances of the products, and whether other systems (especially supernovae and collisions of a neutron star with a black hole) have a significant role in producing these heavy elements. A number of theoretical uncertainties, particularly in the modeling of the optical–infrared afterglow (kilonova), make these questions difficult to answer without a larger sample of joint gravitational-wave and electromagnetic observations of these systems [66]. In concert with next-generation electromagnetic telescopes, Cosmic Explorer will deliver just such a catalog of observations out to .
2.2.4. The Engine Powering Short -ray Bursts
The observation of a short -ray burst nearly simultaneously with GW170817 provided evidence that such bursts originate in neutron star collisions [67], but mysteries linger. Atypical features in the burst lead to questions about whether it was a canonical burst observed at an unusual angle, or whether some fundamental process differentiates it from the catalog of canonical short -ray burst observations [68]. In any case, the central engine driving short -ray bursts is still uncertain, and could be accreting black holes or (hyper)massive neutron stars; consequently, these bursts may or may not be observed in the collision of a neutron star with a black hole, in addition to the collision of two neutron stars [68]. Cosmic Explorer will deliver a large catalog of signals from neutron star collisions at a wide variety of observing angles, especially at redshifts where systems are accessible with electromagnetic telescopes, enabling an elucidation of the burst mechanism and the engine that drives it [24].
2.3. Extreme Gravity and Fundamental Physics
2.3.1. Testing General Relativity
Gravitational radiation is a powerful tool to test general relativity, particularly in the strong-field regime [69]. Today’s gravitational-wave detectors have already begun some of these tests [70,71], and next-generation observatories will continue these tests with greater sensitivity, and enable new kinds of tests not possible today. These observatories will be able to observe mergers with amplitude signal-to-noise ratios in excess of 1000, enabling them to probe theory-agnostic modifications to general relativity with several more orders of magnitude of constraining power than what is possible today [72]. Among the new kinds of tests that will be enabled, Cosmic Explorer and other next-generation detectors will be able to reliably resolve the higher-order multipole moments as a black hole rings down after merger, and they will do so with enough precision to compare the observed signal with the prediction from general relativity that the spectral content is uniquely determined by the mass, spin, and charge of the black hole (the “no hair theorem”) [73,74,75].
2.3.2. Rare and Novel Compact Objects
Cosmic Explorer will detect most of the stellar-mass compact binary coalescences in the low-redshift universe, amounting to hundreds of thousands of events per year. Among these coalescences will be black hole or neutron star systems with rare properties, which could be missed by current observatories. Moreover, Cosmic Explorer may discover that some of the compact objects in its catalog are neither black holes nor neutron stars. A variety of theoretical objects, such as boson stars or gravastars, may superficially mimic the behavior of black holes, but the precise observations enabled by Cosmic Explorer could reveal the absence of a true spacetime horizon; alternatively, observations could reveal new physics associated with black holes [76].
2.3.3. Dark Matter and Dark Energy
The possible gravitational-wave signatures of dark matter are manifold, and essentially every category of astrophysical source targeted by gravitational-wave observatories can be pressed into service to search for dark matter; we will only mention a few here and refer the reader to Bertone et al. [77] for a comprehensive review. By searching for sub-solar-mass binary coalescences, Cosmic Explorer will more tightly constrain the fraction of dark matter that could exist as primordial black holes in the range 10–100 [78]. Cosmic Explorer can also probe ultralight scalar-field dark matter models in the mass range 0.1–10 peV by searching for a stochastic background of oscillatory gravitational-wave signals from these fields in the vicinity of spinning black holes [79]. Like other interferometers, Cosmic Explorer can be used to directly detect terrestrial dark matter, especially if it couples to Standard Model particles. In particular, it can provide improved constraints on the photon coupling of dark matter for masses below 0.1 peV [80].
Cosmic Explorer will also make contributions to dark energy and cosmology. Joint observation by Cosmic Explorer and the Rubin observatory will yield a sub-percent measurement of the Hubble constant, independent of the traditional cosmic distance ladder. These observations will additionally yield measurements of the local dark matter density and the local dark energy equation of state to within 20% [81].
2.4. Discovery Potential
Cosmic Explorer’s leap in sensitivity may deliver observations not enumerated in the above three science themes. Ultimately, it is impossible to give an exhaustive account of what we might see—perhaps an observational consequence of the unification of quantum mechanics and general relativity, or a new elementary particle, or new physics at work in the early history of the universe. Many potential phenomena in this latter category could appear as a stochastic gravitational-wave background lying beneath the background of merging binary systems; Cosmic Explorer could reveal these phenomena as part of a next-generation network [82,83,84,85,86]. Cosmic Explorer may even reveal phenomena that we cannot yet conceive of: history shows that new, more sensitive astronomical instruments often deliver signals from the Universe that are totally unexpected [87].
3. Observatory
Cosmic Explorer’s science goals are premised on achieving a detector with a typical sensitivity of order 10−25/ in the audio band. Achieving such a sensitivity in the 2030s seems possible with further research and development on laser Michelson interferometers, which already can achieve sensitivity better than 10−23/ and with a tenfold increase in the interferometer arm length. Thus, Cosmic Explorer, like the Einstein Telescope, assumes a Michelson interferometer topology, using Fabry–Perot arm cavities along with optical recycling techniques to increase circulating power and achieve broadband operation.
The Cosmic Explorer concept as presented in the 2021 Horizon Study takes as a baseline design the construction of two widely separated facilities on the Earth’s surface, one hosting a 40 km detector and the other hosting a 20 km detector, although it considers alternate scenarios in which Cosmic Explorer consists of a single 40 km facility, two 40 km facilities, or two 20 km facilities [24]. In any case, the choice of one detector per facility is different from the Einstein Telescope, which plans for three pairs of interferometric detectors located in a single underground triangular 10 km facility. The trade-off for having only one detector per facility is that each facility then is only sensitive to one gravitational-wave polarization and will not be able to form a null (gravitational-wave-free) diagnostic channel.
There is also the question of what the Cosmic Explorer detector(s) should use as a technology set. Although there is no requirement that the technology set stay fixed over the lifetime of the observatory, the horizon study assumes that Cosmic Explorer will extend the LIGO A+ set, meaning room-temperature fused silica test masses and suspensions, active vibration isolation, and a 1064 nm laser, as well as a new mirror coating technology that is currently still under development and slated for deployment in the next few years. It is also conceivable that a different technology set, such as the cryogenic silicon concept for LIGO Voyager, could be scaled up to Cosmic Explorer, and several previous works have explored that possibility [23,88]. However, the LIGO A+ technology set is more mature, having already been demonstrated on kilometer-scale instruments.
This section presents the expected sensitivity of a 40 km Cosmic Explorer (Section 3.1), and then discusses the detector design (Section 3.2), the vacuum system (Section 3.3), the observatory location (Section 3.4), and the possibility of a 20 km detector (Section 3.5).
3.1. Sensitivity
Figure 3 shows the noise of current and next-generation detectors, including a 40 km Cosmic Explorer, expressed as an equivalent spacetime strain noise. This has by now become the standard way to characterize the sensitivities of gravitational-wave interferometers, and for the current observatories, the construction of these curves is simple: the amplitude spectral density of the observatory strain noise is found by taking the amplitude spectral density of the detector’s displacement noise and dividing by the arm length L. However, the situation for next-generation observatories is more complicated, firstly because Cosmic Explorer is of comparable size to the wavelengths of kilohertz gravitational waves, and secondly, because the Einstein Telescope comprises multiple interferometers with a 60° opening angle.
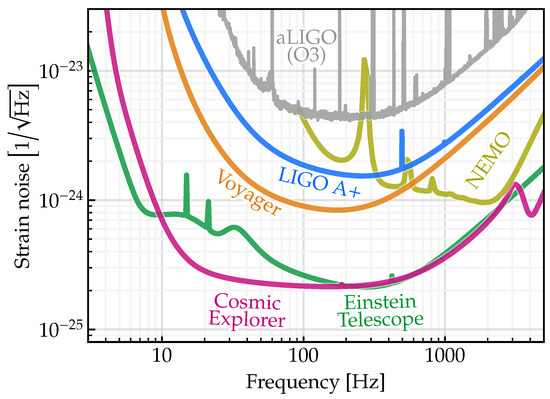
Figure 3.
Strain curves for selected current and next-generation detectors, including a 40 km Cosmic Explorer. The curves indicate the sensitivity for an optimally oriented and polarized monochromatic source. Several subtleties of these curves for the next-generation detectors are discussed in Section 3.1.
Each next-generation curve in Figure 3 represents the strain noise of the observatory as a whole corresponding to an optimally oriented and polarized source on the sky at each Fourier frequency. Computing this optimum requires recourse to the antenna response functions (for + polarized waves) and (for × polarized waves) of each detector in the observatory, keeping in mind both the source location on the sky and the angular frequency of the arriving waves [89]. In the case of the Einstein Telescope, arriving at the total observatory strain noise requires summing the power collected by each of the three detectors (in other words, treating the Einstein Telescope as a network of three colocated, but rotated, detectors). For Cosmic Explorer, especially, the stipulation of computing the sensitivity separately at each Fourier frequency is important because the optimal sky location and polarization varies significantly with frequency: for a single L-shaped detector such as Cosmic Explorer, the optimum sky location for a zero-frequency source is directly at the detector’s zenith or nadir; however, for a source with (the free spectral range), the detector is completely insensitive to a source arriving at the zenith or nadir, and the maximum response instead occurs for sources arriving at other angles [90,91]. Figure 4 compares the normalized observatory sensitivities as the gravitational-wave frequency approaches the free spectral range, showing that the antenna pattern of an L-shaped detector is reduced, but not identically zero, at the free spectral range. It also evinces a lack of nulls in the total antenna pattern of the three-detector triangle geometry employed by the Einstein Telescope [20].
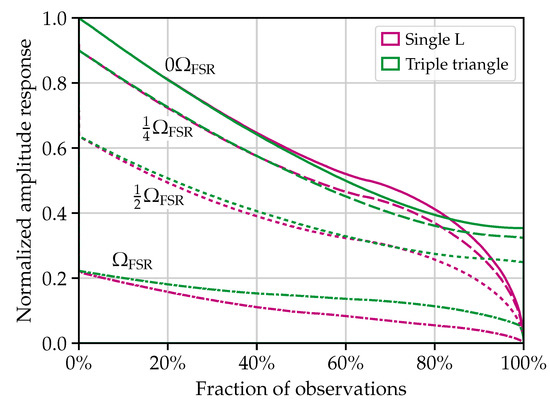
Figure 4.
Histogram of normalized, polarization-averaged antenna patterns for a single L-shaped interferometer (such as Cosmic Explorer) and a three-detector triangle (such as the Einstein Telescope), assuming sources distributed isotropically on the sky. Curves are shown for gravitational waves at frequencies 0, , and 1 times the detector free spectral range . Note that .
3.2. Detector
This subsection focuses on the design of a 40 km Cosmic Explorer instrument using an extension of LIGO A+ technology. The fundamental noises in such a detector are shown in Figure 5 (We will return to a 20 km instrument in Section 3.5).
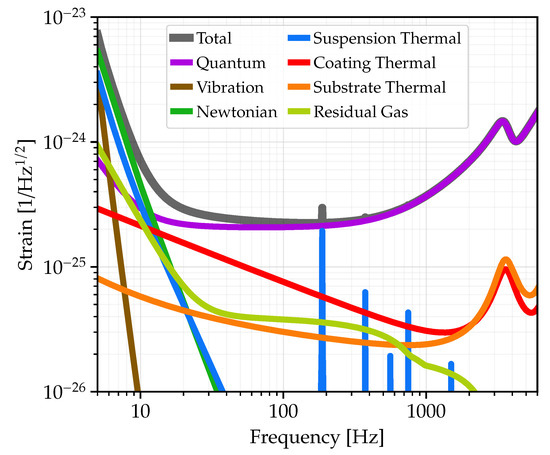
Figure 5.
Fundamental noise contributions to the overall strain sensitivity of a 40 km Cosmic Explorer detector, discussed in Section 3.2. The fundamental noises are modeled in pygwinc [92], and the noise here is referred to a source arriving from 15° off the detector’s zenith.
3.2.1. Optical Configuration
The choice of optical cavity lengths and mirror transmissivities influences many of the noise sources in the detector, particularly the noise arising from quantum mechanical fluctuations of the optical field. In terms of equivalent spacetime strain, most noise sources in the detector decrease with increasing arm length [23,24]; in particular, the amplitude spectral density of quantum shot noise scales as if the detector bandwidth is held fixed. On the other hand, the free spectral range limits the maximum bandwidth of the instrument; thus, to achieve the science goals relating to postmerger neutron star physics (Section 2.2.2), the detector cannot be longer than several tens of kilometers. The choice of 40 km represents a trade-off, yielding a free spectral range of 3.7 kHz while still offering a clear improvement in the shot-noise-limited performance compared to a detector with a shorter baseline. Further consideration of arm length choice is found in Section 3.5.
The optical power circulating in the Cosmic Explorer arm cavities is assumed to be , which is twice the nominal value for Advanced LIGO; it is not established whether this represents a true upper limit for the detector. Aside from affecting the level of shot noise in the detector, the choice of arm power has several optomechanical implications. First, the quantum backaction (radiation pressure noise) must be counteracted by increasingly heavy test masses; Cosmic Explorer assumes they are each 320 , which will already require a scaling up of current fabrication technologies. Second, radiation pressure modifies the angular susceptibility of the suspended masses, and could necessitate feedback control schemes that degrade the sensitivity by injecting servo control noise; however, since Cosmic Explorer plans to use heavier test masses and a near-confocal rather than near-concentric arm cavity resonator geometry, these modifications to the suspension dynamics are weaker than in LIGO A+, even with twice the circulating power [93,94]. Third, high power results in more elastic modes in the test masses being driven into parametric instability by interaction with optical modes [95], although a detailed analysis for Cosmic Explorer is yet to be given. Aside from optomechanical effects, elastic deformation and refractive index changes in the mirrors due to heat absorption in the substrates or coatings can degrade the quantum noise performance of the detector or complicate the feedback control of the mirrors’ length or angular degrees of freedom; a quantitative accounting requires fairly detailed models of the detector’s optical configuration and sensing and control systems, which have not yet been developed.
The choice of the signal extraction parameters and the transmissivities of the input test mass mirrors depend on the desired quantum-limited bandwidth and peak sensitivity, and on power handling considerations. As in current detectors, the desire to lower the optical power traveling through the beamsplitter and input test mass substrates favors a high arm finesse . On the other hand, the desire to reduce the effect of noise in the signal extraction cavity favors lower finesse, since losses in this cavity contribute to the quantum noise with a power spectral density [96]. Cosmic Explorer assumes the Advanced LIGO finesse of 450. In contrast to the current detectors, Cosmic Explorer’s long arm length means that stronger signal extraction is needed to expand the interferometer bandwidth to several hundred hertz; it also means that for any realistic choice of signal extraction cavity length, dispersion in the cavity noticeably alters the level of quantum shot noise. Cosmic Explorer’s nominal design assumes a signal extraction cavity length of 20 , with a 2% transmissive signal extraction mirror, but other length and transmissivity values can be chosen to tune the detector for low-frequency- or high-frequency-focused operation [60]. Cosmic Explorer assumes that the loss in the signal extraction cavity is 500 ppm, including loss due the mismatch of transverse optical modes; this is roughly ten times less than the current value in the LIGO detectors [97].
The quantum noise will be reduced using squeezed vacuum injected into the interferometer’s signal port; the goal is 10 dB of quantum noise reduction across the entire sensitive band. Cosmic Explorer proposes to use a 4 km filter cavity with 80 ppm round-trip loss to achieve the simultaneous reduction of radiation pressure and shot noise. Given injection losses of slightly less than 10% and output losses of a few percent, this requires 15–20 dB of squeezed light generation, with the relative path-length fluctuation between the squeezed field and the signal field stabilized to 10 mrad rms.
3.2.2. Test Masses
Cosmic Explorer will need fused silica test masses larger by roughly a factor of two in every linear dimension compared to Advanced LIGO. This is driven first by the need for a large inertia to lessen the effect of radiation pressure fluctuations, to decrease the mechanical susceptibility of the suspension system (Section 3.2.4), and to reduce position fluctuations from gas damping. A mass of 320 is enough to keep radiation pressure noise, suspension noise, and gas noise below the geophysical background below 10 Hz. Second, because the radius of the optical mode at each test mass can be no smaller than due to diffraction [93], the test mass diameter D must be large enough to avoid a significant round-trip power loss due to the finite aperture of the test mass.2 For Cosmic Explorer’s planned operating wavelength of μm, a test mass diameter of about 70 cm is needed to maintain a sub-part-per-million optical loss while allowing for optical mode sizes slightly larger than the extremal value. If Cosmic Explorer were instead operated with Voyager technology (cryogenic silicon masses and 2 μm laser wavelength), a test mass diameter of more than 80 km would be needed to maintain similar optical loss, which requires scaling up the current largest monocrystalline silicon ingot size of 45 cm [17].
With larger beam sizes than current detectors, Cosmic Explorer must have test masses that are polished on spatial scales up to tens of centimeters to reduce scattering out of the optical mode of the arm. The most stringent requirements will likely come from the need to control noise arising from scattered light reflecting from a moving surface and then recombining with the optical mode. This is a challenging modeling task, since it requires cataloging and then simulating multiple scattering surfaces in a three-dimensional geometry—notably the baffling in the beam tubes (see Section 3.3).
3.2.3. Mirror Coatings
Cosmic Explorer will use the future state-of-the-art in thin-film mirror coatings, which is likely to be different from the coatings that are used today, which employ fused silica as the low-index material and titania-doped tantala as the high-index material [100]. The Cosmic Explorer model currently adopts the same target as LIGO A+, which is to use a coating whose effective mechanical loss (taking into account coating thickness and elastic parameters) is fourfold less than the LIGO silica–tantala coatings, while still maintaining sub-part-per-million optical absorption and an acceptable level of optical scatter.
Because of the interest from LIGO A+ and AdVirgo+, there is already significant coating development underway. Strategies include retaining fused silica as the low-index material while replacing the high-index material with titania-doped germania, some other metal oxide, or silicon nitride [101,102]. Other strategies include crystalline material pairs such as gallium arsenide and aluminum-doped gallium arsenide [103]. The chief development for Cosmic Explorer will be to scale up the area of the coating to the larger test mass size. The coatings will require low contamination to avoid thermal deformations that degrade the buildup of power in the arm cavities [104,105].
3.2.4. Test Mass Suspensions
Cosmic Explorer will adapt the quadruple pendulum suspension design used for Advanced LIGO [106], giving a amplitude suppression of horizontal vibrations for frequencies above the normal modes of the suspension. Cosmic Explorer will retain the monolithic design, in which the test mass, penultimate mass, and the suspension fibers between them are all fabricated from fused silica; the upper components are steel.
The chief adaptations for the Cosmic Explorer suspensions focus on decreasing their mechanical susceptibility (the amount of test mass displacement in response to applied forces) at frequencies within the gravitational-wave band. This serves to increase the amount of vibrational isolation. Consistent with the fluctuation–dissipation theorem, this also reduces the thermodynamic fluctuations perturbing the test masses in this band, since these fluctuations are proportional to the imaginary portion of the susceptibility [107]. The susceptibility should also be engineered so that the frequencies of the normal modes associated with motions of the suspension masses lie below the sensitive band of the interferometer (5 Hz), since this prevents resonant enhancement of seismic or thermal noise within the band and allows for more flexible feedback damping of the modes. The frequencies of these modes can be lowered by increasing the length of the pendulum stages. A total length of is sufficient for the longitudinal modes, although it may not by itself provide sufficient reduction in the mode frequencies of the suspension’s vertical motion; due to the Earth’s finite radius , these modes appear in the gravitational-wave readout with a typical amplitude coupling factor . These vertical frequencies could be lowered even further by attaching the fibers to compliant silica cantilevers (“blade springs”) or by decreasing the cross-sectional area of the fibers. In either case, the main limitation is the strength of the fused silica. It is believed that the current tensile stress of in the LIGO fibers can be increased to at least in Cosmic Explorer [88,108].
3.2.5. Active Vibration Isolation
The Cosmic Explorer test mass suspensions will be attached to actively controlled platforms that provide improved vibration isolation compared to the analogous system in Advanced LIGO [109]. The improvement will come mainly through the use of inertial sensors that have lower self-noise and can measure in six degrees of freedom [110,111]. Cosmic Explorer aims to achieve a residual platform motion of about 30 fm/ at 10 Hz, which is ten times better than the LIGO performance and directly impacts the test mass motion within the sensitive frequency band. Additional inertial sensing improvements at 1 Hz and below, including improved tilt sensing, will enhance the instrument performance by lowering the amount of noise in other feedback control loops [88].
3.2.6. Local Gravity Fluctuations
Local fluctuations of the Earth’s gravity present an emerging challenge that will soon limit the low-frequency performance of the current generation of observatories [112,113]. For Cosmic Explorer, which aims to achieve roughly ten times less displacement noise at 10 Hz compared to Advanced LIGO, the challenge will be even more acute and will require a concerted effort to account for fluctuations from both seismic and atmospheric fluctuations. Because Cosmic Explorer will be located on the Earth’s surface, it is unlikely that the ambient seismicity will be dramatically lower than that of existing observatories.
To reach the sensitivity shown in Figure 5, it is assumed that the effect of local gravity fluctuations due to the seismic field can be mitigated, either by estimating the fluctuations and subtracting them from the observatory’s time series data, or by altering the seismic field in the immediate vicinity of the test masses. Current proposals for subtraction techniques involve an array of seismometers or tiltmeters to measure the ground motion and thereby estimate the fluctuation at each test mass [114]. Altering the seismic field could involve displacing soil underneath the test mass to increase the distance from the mass to the source of the gravitational perturbation, or the installation of metamaterials [115]. Regardless of the method, the level of required mitigation to reach the sensitivity goal is 20 dB for the Rayleigh wave field and 10 dB for the body wave field, given ambient noise levels of 1 ()
in Rayleigh waves and (/s2)/ in body waves.
The gravity fluctuation limit shown in Figure 5 is dominated not by the residual seismic contributions, but rather the infrasonic background from the atmosphere. Other than burying the test masses hundreds of meters underground, mitigation strategies for atmospherically induced gravity fluctuations are uncertain [116] and so no infrasound mitigation has been assumed for Cosmic Explorer. Figure 5 assumes that the typical level of the ambient infrasound is 1 mPa/, based on long-term global monitoring [117].
3.2.7. Laser System
Cosmic Explorer will use a 1064 nm laser system. The optical design for the instrument (Section 3.2.1) assumes MW of power in each arm, along with = 40 ppm of loss per round-trip pass in each arm. If the power recycling mirror were critically matched to the arms, this would require an input power of ; however, to allow for a slightly overcoupled power recycling cavity, the laser power at the interferometer input is assumed to be 140 . This requirement is only modestly larger than the requirement for Advanced LIGO. The maximum power produced by the laser system will need to be higher than this value to account for propagation through the input optics system, which will prepare the light in a frequency-, intensity-, and pointing-stabilized Gaussian mode.
For Cosmic Explorer, the frequency stabilization requirements are somewhat more stringent than those of Advanced LIGO. In Advanced LIGO, the apparent displacement noise in the gravitational-wave readout channel due to laser frequency noise is dominated by coupling of higher-order transverse optical modes, with a typical value 1 fm/Hz; if the coupling in Cosmic Explorer is similar, then the requirement on the laser frequency noise at the interferometer input is 0.7 μHz/
[118]. In contrast to Advanced LIGO, it is unlikely that the laser can be frequency-locked to the Cosmic Explorer interferometer with sufficient bandwidth due to the low free spectral range of 3.7 kHz. Cahillane et al. [118] propose instead to use two suspended, triangular mode-cleaning cavities, rather than the one cavity of Advanced LIGO.
3.2.8. Calibration
The calibration requirements for the Cosmic Explorer data will need to be drawn from the multiple components of its science program, although some initial bounds can already be given. If Cosmic Explorer (along with electromagnetic observatories) is to deliver Hubble constant measurements to better than 0.2% [81], then the systematic error on the amplitude of the gravitational-wave response must be smaller than this value. For measurements of tidal effects in nearby binary neutron star mergers, which could be observed with total amplitude signal-to-noise ratios in the thousands, calibration errors should be about 1% or better [119]. For signals (such as compact binary mergers) that can be precisely modeled a priori, detector calibration requirements are likely to be informed by the level of improvement that can be achieved in the accuracy of gravitational waveform families [120].
Cosmic Explorer could use several calibration techniques. The main calibration apparatus for today’s detectors uses a metrologically traceable photon radiation pressure drive, which in the case of LIGO is currently able to deliver a calibrated test mass displacement with a 0.4% uncertainty [121]; anticipated improvements in optical power metrology may be able deliver an uncertainty better than 0.15% [122]. Separately, spinning source masses in the vicinity of the interferometer test masses can be used to apply a known gravitational force. Prototypes employed in current detectors achieved uncertainty smaller than 1% [123,124], and future apparatus could achieve better than 0.2% uncertainty [125].
3.3. Vacuum System
The vacuum system for Cosmic Explorer, particularly the beam tubes that envelop the 40 km arms, is an active area of research and development. The noise requirements on the vacuum system are not too different from those of LIGO, and the thrust of the research is instead focused on reducing construction cost, developing better diagnostic capabilities, and improving robustness. These activities are crucial so that the observatory is not hamstrung by excessive cost during construction or by infrastructure failures during operation.
Gas-induced optical scattering of the laser light in the arms sets upper limits on the partial pressures of various molecular species in the beam tubes. Two especially important species, hydrogen and water, have partial pressure requirements and , which are only slightly more stringent than the goals for the LIGO system. In LIGO, the pressure requirements were met through a series of heat treatments (“baking”), first to deplete hydrogen from the raw 304L stainless steel stock, and then to desorb water from the inner surface of the tubes after installation [126]. Cosmic Explorer may be able to reduce costs by using carbon (mild) steel, which already has a low hydrogen content, by coating the interior of the tubes to reduce water adsorption, or by using novel (e.g., double-walled) tube geometries [126]. Stochastic momentum transfer from residual gas to the test masses additionally sets a requirement on the pressure in the vacuum chambers containing the masses. For meter-scale chambers, the pressure requirement is less stringent than the above requirements for the pressures in the arms [88]; however, they must be able to repeatedly attain this pressure after periodic exposure to atmosphere due to detector maintenance activities.
The diameter of the tube, along with the geometry of the interior baffles, must be chosen to pass the beam through the arm without truncation, especially as such truncation can impress the ground-driven motion of the baffles onto the phase and amplitude of the main optical mode. Although Cosmic Explorer’s anticipated beam size (11 cm with 1 μm light) is nearly twice that of Advanced LIGO, it appears that a tube of the same diameter as LIGO () with a interior clear aperture (set by the inner radius of the annular baffles) is sufficient to avoid problematic truncation of the beam or baffle-induced noise as the light propagates down the arms [127].3
As described in Section 3.2.2, the beam tubes and baffles can also mediate the scattering of stray light back into the main optical mode. In the most common scenario considered, light is scattered out of the main optical mode due to the surface figure error of the test mass and then is reflected from the baffles back toward the same test mass. Bai [128] examined this scenario using a power budgeting calculation, and determined that current polishing techniques, if extended to slightly larger spatial scales, could give acceptable noise performance if the Cosmic Explorer beam tube and baffling system is similar to that of LIGO. However, this power budgeting needs to be confirmed by phase-sensitive calculations (e.g., using Fourier optics [129]) before the polishing requirements of the test masses can be finalized.
3.4. Observatory Location
Aside from the overall shape of the observatory, the main contrast between the Einstein Telescope facility [130] and the Cosmic Explorer facility is that the former is planned to be underground, while the latter is planned to be on the Earth’s surface. Cosmic Explorer’s choice of surface construction is motivated primarily by the expectation that tunneling would be more expensive than surface construction, especially as tunneling projects are typically more expensive per unit length in the Americas than in Europe [131].
If a 40 km facility is laid out on a perfectly spherical earth (with radius km), one must deal with the m difference in ground height between the center and the ends of the arms. This requires that the soil (or rock) is redistributed along the length of the arm to provide a flat grade on which to build the arms’ vacuum pipe; the width of this grade must be at least a few meters to accommodate the infrastructure around the pipe, and the slope on either side of the finished grade cannot be steeper than the soil’s angle of repose, typically less than 45°. Additionally, the layout should be chosen so that the deviation of the local gravity from vertical at each test mass is not significantly worse than the deviation expected from a perfectly spherical earth, since this will couple vertical motion of the test mass into the detector degree of freedom that is sensitive to gravitational waves. To redistribute soil in this fashion for two 40 km arms on the spherical Earth, roughly 107 m3 of redistribution is required. Local topography, however, can alter the amount of soil redistribution, and several groups have undertaken algorithmic searches using publicly available topography and land-use data to find locations with a reduced volume of redistributed soil. These searches revealed that sites with favorable topographic profiles, yielding total redistributed volumes of order 106 m3 or better, are not uncommon in the United States and around the world, particularly if the requirements on the detector length and opening angle are allowed to deviate slightly from their nominal values of 40 km and 90°, respectively [132].
Long-term seismic and infrasonic studies will be needed to estimate the impact of ambient geophysical noise on the detector performance, with attention paid to a full characterization of the seismic field (e.g., the types of seismic waves and their isotropy) and of the ground (e.g., its homogeneity and isotropy) to evaluate reduction strategies for local gravity fluctuations. Above a few hertz, where ground acceleration directly impacts the detector sensitivity, the ambient seismic field is generated mostly by nearby anthropogenic sources and different sites can display several orders of magnitude difference in their ground acceleration spectra [88,133,134]. Aside from the ambient noise conditions at the initial site, the facility infrastructure also plays an important role: Nguyen et al. [135] showed that the ground acceleration at the LIGO facilities is largely sourced from local elements such as air handler systems, meaning that Cosmic Explorer can likely make modest improvements to the ground noise spectrum by paying attention to civil engineering and other facility design considerations. Below a few hertz, where ground acceleration affects the controllability of the detector, the ambient seismic field is usually dominated by natural processes [133], such as the secondary microseism at decihertz frequencies sourced by storms in the open ocean [136]. At lower frequencies, ground tilt sourced by local atmospheric pressure fluctuations (e.g., wind) induces significant variability in ground motion and introduces a confusion noise in horizontal seismometer measurements [134,137]. Many of the sources responsible for the ambient seismic background also contribute to the ambient infrasonic background. At frequencies above the microbarom (the atmospheric counterpart of the microseism), wind and eddies are the dominant natural contributors to the infrasonic spectrum [117], with anthropogenic sources including local observatory equipment likely playing an important role as well.
Potential observatory sites will also need to be vetted for suitability in other ways. A geotechnical survey must be carried out to establish a realistic cost estimate for the construction of the facility. Environmental impacts must also be identified, along with strategies for avoiding or remediating these impacts. A plan for the eventual decommissioning of the site must be developed. Separately from topographical and geotechnical considerations, the social implications of the observatory location must also be integrated into the planning. Cosmic Explorer must build a mutually beneficial relationship with the local community. This requires taking community input into account from the beginning of the process and integrating it into the trajectory of the project. This includes engagement with local Indigenous communities, focused on ongoing consent for the project [24,138,139].
3.5. A 20 km Cosmic Explorer?
The 2021 horizon study calls for a 20 km Cosmic Explorer facility in addition to a 40 km facility. While two widely separated facilities will improve the estimation of extrinsic parameters for all types of astrophysical systems, a 20 km facility in particular is motivated by the dense matter portion of Cosmic Explorer’s scientific program (Section 2.2). This portion of the program relies heavily on measuring gravitational waves at 2–4 kHz, where the optical response of a 40 km detector is reduced due to the travel time of the light down the arms (Section 3.1). The choice of 20 km for the arm length arose from the desire to choose the length of the detector’s arms and signal extraction cavity and the transmissivities of the signal extraction mirror to result in “tuned” operation, where the quantum noise is reduced in the 2–4 kHz band at the expense of higher quantum noise elsewhere.4
Importantly, this tuning is limited by optical losses in both the arms and the signal extraction cavity, which noticeably reduces the effectiveness of tuning when realistic loss values (on the order of 0.1%) are included (Section 3.2.1). Martynov et al. [140] studied how to optimize the parameters of a high-frequency-focused detector, including arm length, to best tune to signals in the 2–4 kHz band. The study found that the optimal detector had an arm length slightly less than 20 km and yielded a 30% improvement in average signal-to-noise ratio in the 2–4 kHz band compared to a 40 km detector. Srivastava et al. [60] examined the performance of a 20 km detector versus a 40 km detector against the whole of the Cosmic Explorer science program, finding that while the 20 km detector offers a modest improvement in the detection of post-merger signals, most science themes are better addressed by a 40 km detector; this is because the 40 km detector has superior noise performance outside the 2–4 kHz frequency range (Figure 6).
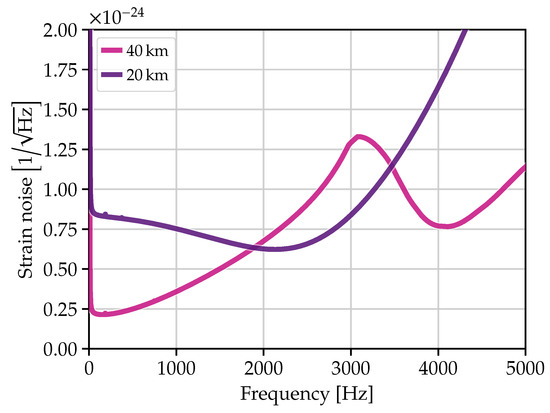
Figure 6.
Comparison of a broadband 40 km Cosmic Explorer observatory and a 20 km kilohertz-optimized observatory (Section 3.5).
4. Project and Realization
A key component of the Horizon Study process was the development of an initial cost estimate for Cosmic Explorer. This cost estimate involved extrapolation of detector and facility costs from LIGO, along with the input of civil and vacuum engineers. Based on this process, the cost for the observatory reaches the billion-dollar scale, split in similar proportions between civil engineering, the vacuum system, and the detector, with a smaller portion from management. The anticipated yearly operating cost for two observatories is not significantly larger than LIGO’s operating costs [24].
The scale of the Cosmic Explorer effort places it within the category of scientific megaproject. Although the process (and funding source) for realizing Cosmic Explorer is still under discussion, inspiration for the technical aspects of the project trajectory has been taken from the Research Infrastructure Guide from the US National Science Foundation [141]. Under the timeline laid out in the Horizon Study, much of the effort in the 2020s would involve developing a design for the observatory, leading to construction beginning near the end of the decade; installation of the detector would occur in the early 2030s, leading to the first stable operation of the detector (i.e., the first lock) around 2035. The 2020 US Astronomy and Astrophysics Decadal Survey endorsed technology development for Cosmic Explorer as part of the effort in this decade to ensure the advancement of ground-based gravitational-wave astronomy [25,26,142], and Cosmic Explorer is also represented in the 2021 Snowmass Process [9,143,144,145].
5. Outlook
As part of a global next-generation observatory network, Cosmic Explorer will reach back much further in cosmic time and probe sources with far greater sensitivity than is possible with today’s detectors. This promises to revolutionize our understanding of the gravitational-wave universe on multiple fronts: the evolution of black holes and neutron stars throughout cosmic time, the behavior of matter at densities that cannot be probed terrestrially, and the fundamental nature of gravitation and cosmology. This promise can be realized with a research and development program that extends today’s gravitational-wave detector technology to a longer baseline, with improvements that include more optical power, larger test masses, and better environmental isolation. To become reality, Cosmic Explorer needs a broad base of support from the gravitational-wave community, the broader astrophysical community, and the local communities where the observatories will be built.
Funding
The author is supported by the MathWorks, Inc. (Apple Hill Drive Natick, MA, USA).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The author thanks Kevin Kuns, Matthew Evans, Joshua Smith, Philippe Landry, B. S. Sathaprakash, Paul Lasky, and David Shoemaker for comments on the manuscript.
Conflicts of Interest
The author declares no conflict of interest.
Notes
| 1 | Elsewhere, Einstein Telescope and Cosmic Explorer are referred to as third-generation observatories, with the current observatories and their incremental upgrades referred to as second generation; the initial detectors in the LIGO and Virgo observatories were first generation. |
| 2 | An initial estimate of the round-trip power loss can be found from the clipping loss of a Gaussian mode with spot radius w impinging on a test mass with diameter D [22]. However, the Eigenfunction of a finite-aperture cavity is not Gaussian, and accurately computing its round-trip loss requires numerical simulation with Eigenvalue or Fourier-transform methods [93,98,99]. |
| 3 | For 2 μm light, the transverse motion of the baffles could introduce significant noise due to the larger beam size (16 cm) [127]. |
| 4 | This tuning of the macroscopic cavity lengths is distinct from “detuned” operation, in which resonant enhancement at kilohertz frequencies is instead achieved by adjusting the microscopic length of the signal extraction cavity. |
References
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D.; et al. Laser Interferometer Space Antenna. arXiv 2017, arXiv:1702.00786. [Google Scholar]
- Mei, J.; Bai, Y.Z.; Bao, J.; Barausse, E.; Cai, L.; Canuto, E.; Cao, B.; Chen, W.M.; Chen, Y.; Ding, Y.W.; et al. The TianQin project: Current progress on science and technology. Prog. Theor. Exp. Phys. 2021, 2021, 05A107. [Google Scholar] [CrossRef]
- Verbiest, J.P.W.; Oslowski, S.; Burke-Spolaor, S. Pulsar Timing Array Experiments. arXiv 2021, arXiv:2101.10081. [Google Scholar]
- Kamionkowski, M.; Kovetz, E.D. The Quest for B Modes from Inflationary Gravitational Waves. Ann. Rev. Astron. Astrophys. 2016, 54, 227–269. [Google Scholar] [CrossRef]
- Aggarwal, N.; Aguiar, O.D.; Bauswein, A.; Cella, G.; Clesse, S.; Cruise, A.M.; Domcke, V.; Figueroa, D.G.; Geraci, A.; Goryachev, M.; et al. Challenges and opportunities of gravitational-wave searches at MHz to GHz frequencies. Living Rev. Rel. 2021, 24, 4. [Google Scholar] [CrossRef]
- Kawamura, S.; Ando, M.; Seto, N.; Sato, S.; Musha, M.; Kawano, I.; Yokoyama, J.; Tanaka, T.; Ioka, K.; Akutsu, T.; et al. Current status of space gravitational wave antenna DECIGO and B-DECIGO. Prog. Theor. Exp. Phys. 2021, 2021, 05A105. [Google Scholar] [CrossRef]
- Geiger, R. Future Gravitational Wave Detectors Based on Atom Interferometry; World Scientific: Singapore, 2017; p. 285. [Google Scholar] [CrossRef]
- Harms, J.; Ambrosino, F.; Angelini, L.; Braito, V.; Branchesi, M.; Brocato, E.; Cappellaro, E.; Coccia, E.; Coughlin, M.; Della Ceca, R.; et al. Lunar Gravitational-wave Antenna. Astrophys. J. 2021, 910, 1. [Google Scholar] [CrossRef]
- Ballmer, S.W.; Adhikari, R.; Badurina, L.; Brown, D.A.; Chattopadhyay, S.; Evans, M.; Fritschel, P.; Hall, E.; Hogan, J.M.; Jani, K.; et al. Snowmass2021 Cosmic Frontier White Paper: Future Gravitational-Wave Detector Facilities. In Proceedings of the 2022 Snowmass Summer Study, Settle, WA, USA, 17–26 July 2022. [Google Scholar]
- Aasi, J.; Abbott, B.; Abbott, R.; Abbott, T.; Abernathy, M.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; et al. Advanced LIGO. Class. Quant. Grav. 2015, 32, 074001. [Google Scholar] [CrossRef]
- Acernese, F.; Agathos, M.; Agatsuma, K.; Aisa, D.; Allemandou, N.; Allocca, A.; Amarni, J.; Astone, P.; Balestri, G.; Ballardin, G.; et al. Advanced Virgo: A second-generation interferometric gravitational wave detector. Class. Quant. Grav. 2015, 32, 024001. [Google Scholar] [CrossRef]
- Akutsu, T.; Ando, M.; Arai, K.; Arai, Y.; Araki, S.; Araya, A.; Aritomi, N.; Asada, H.; Aso, Y.; Atsuta, S.; et al. KAGRA: 2.5 Generation Interferometric Gravitational Wave Detector. Nat. Astron. 2019, 3, 35–40. [Google Scholar] [CrossRef]
- Dooley, K.L. Status of GEO 600. J. Phys. Conf. Ser. 2015, 610, 012015. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adya, V.; Affeldt, C.; Agathos, M.; et al. Prospects for observing and localizing gravitational-wave transients with Advanced LIGO, Advanced Virgo and KAGRA. Living Rev. Rel. 2018, 21, 3. [Google Scholar] [CrossRef] [PubMed]
- Barsotti, L.; McCuller, L.; Evans, M.; Fritschel, P. The A+ Design Curve. Technical Report T1800042; LIGO. 2018. Available online: https://dcc.ligo.org/public/0149/T1800042/004/T1800042-v4.pdf (accessed on 14 April 2022).
- Bersanetti, D.; Patricelli, B.; Piccinni, O.J.; Piergiovanni, F.; Salemi, F.; Sequino, V. Advanced Virgo: Status of the Detector, Latest Results and Future Prospects. Universe 2021, 7, 322. [Google Scholar] [CrossRef]
- Adhikari, R.; Arai, K.; Brooks, A.; Wipf, C.; Aguiar, O.; Altin, P.; Barr, B.; Barsotti, L.; Bassiri, R.; Bell, A.; et al. A cryogenic silicon interferometer for gravitational-wave detection. Class. Quant. Grav. 2020, 37, 165003. [Google Scholar] [CrossRef]
- Ackley, K.; Adya, V.; Agrawal, P.; Altin, P.; Ashton, G.; Bailes, M.; Baltinas, E.; Barbuio, A.; Beniwal, D.; Blair, C.; et al. Neutron Star Extreme Matter Observatory: A kilohertz-band gravitational-wave detector in the global network. Publ. Astron. Soc. Austral. 2020, 37, e047. [Google Scholar] [CrossRef]
- Eichholz, J.; Holland, N.A.; Adya, V.B.; van Heijningen, J.V.; Ward, R.L.; Slagmolen, B.J.J.; McClelland, D.E.; Ottaway, D.J. Practical test mass and suspension configuration for a cryogenic kilohertz gravitational wave detector. Phys. Rev. D 2020, 102, 122003. [Google Scholar] [CrossRef]
- Einstein Telescope Steering Committee. Einstein Telescope: Science Case, Design Study and Feasibility Report. Technical Report ET–0028A–20; Einstein Telescope. 2020. Available online: http://www.et-gw.eu/index.php/relevant-et-documents (accessed on 14 April 2022).
- Barsotti, L.; Evans, M.; Mavalvala, N.; Ballmer, S. Long Uncomplicated Next-Generation Gravitational-Wave Observatory. In Proceedings of the Gravitational-Wave Advanced Detector Workshop 2013, Elba, Italy, 19–25 May 2013. [Google Scholar]
- Dwyer, S.; Sigg, D.; Ballmer, S.W.; Barsotti, L.; Mavalvala, N.; Evans, M. Gravitational wave detector with cosmological reach. Phys. Rev. D 2015, 91, 082001. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Ackley, K.; Adams, C.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; et al. Exploring the Sensitivity of Next Generation Gravitational Wave Detectors. Class. Quant. Grav. 2017, 34, 044001. [Google Scholar] [CrossRef]
- Evans, M.; Adhikari, R.X.; Afle, C.; Ballmer, S.W.; Biscoveanu, S.; Borhanian, S.; Brown, D.A.; Chen, Y.; Eisenstein, R.; Gruson, A.; et al. A Horizon Study for Cosmic Explorer: Science, Observatories, and Community. arXiv 2021, arXiv:2109.09882. [Google Scholar]
- Reitze, D.; Abbott, R.; Adams, C.; Adhikari, R.; Aggarwal, N.; Anand, S.; Ananyeva, A.; Anderson, S.; Appert, S.; Arai, K.; et al. The US Program in Ground-Based Gravitational Wave Science: Contribution from the LIGO Laboratory. arXiv 2019, arXiv:1903.04615. [Google Scholar]
- Reitze, D.; Adhikari, R.X.; Ballmer, S.; Barish, B.; Barsotti, L.; Billingsley, G.; Brown, D.A.; Chen, Y.; Coyne, D.; Eisenstein, R.; et al. Cosmic Explorer: The U.S. Contribution to Gravitational-Wave Astronomy beyond LIGO. arXiv 2019, arXiv:1907.04833. [Google Scholar]
- Maggiore, M.; Van Den Broeck, C.; Bartolo, N.; Belgacem, E.; Bertacca, D.; Bizouard, M.A.; Branchesi, M.; Clesse, S.; Foffa, S.; García-Bellido, J.; et al. Science Case for the Einstein Telescope. JCAP 2020, 03, 050. [Google Scholar] [CrossRef]
- Raffai, P.; Gondán, L.; Heng, I.S.; Kelecsényi, N.; Logue, J.; Márka, Z.; Márka, S. Optimal Networks of Future Gravitational-Wave Telescopes. Class. Quant. Grav. 2013, 30, 155004. [Google Scholar] [CrossRef]
- Hu, Y.M.; Raffai, P.; Gondán, L.; Heng, I.S.; Kelecsényi, N.; Hendry, M.; Márka, Z.; Márka, S. Global optimization for future gravitational wave detector sites. Class. Quant. Grav. 2015, 32, 105010. [Google Scholar] [CrossRef]
- Vitale, S.; Evans, M. Parameter estimation for binary black holes with networks of third generation gravitational-wave detectors. Phys. Rev. D 2017, 95, 064052. [Google Scholar] [CrossRef]
- Hall, E.D.; Evans, M. Metrics for next-generation gravitational-wave detectors. Class. Quant. Grav. 2019, 36, 225002. [Google Scholar] [CrossRef]
- Nitz, A.H.; Dal Canton, T. Pre-merger Localization of Compact-binary Mergers with Third-generation Observatories. Astrophys. J. Lett. 2021, 917, L27. [Google Scholar] [CrossRef]
- Li, Y.; Heng, I.S.; Chan, M.L.; Messenger, C.; Fan, X. Exploring the sky localization and early warning capabilities of third generation gravitational wave detectors in three-detector network configurations. Phys. Rev. D 2022, 105, 043010. [Google Scholar] [CrossRef]
- Gossan, S.E.; Hall, E.D.; Nissanke, S.M. Optimizing the Third Generation of Gravitational-wave Observatories for Galactic Astrophysics. Astrophys. J. 2022, 926, 231. [Google Scholar] [CrossRef]
- Borhanian, S.; Sathyaprakash, B.S. Listening to the Universe with Next Generation Ground-Based Gravitational-Wave Detectors. arXiv 2022, arXiv:2202.11048. [Google Scholar]
- García-Quirós, C.; Colleoni, M.; Husa, S.; Estellés, H.; Pratten, G.; Ramos-Buades, A.; Mateu-Lucena, M.; Jaume, R. Multimode frequency-domain model for the gravitational wave signal from nonprecessing black-hole binaries. Phys. Rev. D 2020, 102, 064002. [Google Scholar] [CrossRef]
- Madau, P.; Dickinson, M. Cosmic Star Formation History. Ann. Rev. Astron. Astrophys. 2014, 52, 415–486. [Google Scholar] [CrossRef]
- Vitale, S.; Farr, W.M.; Ng, K.; Rodriguez, C.L. Measuring the star formation rate with gravitational waves from binary black holes. Astrophys. J. Lett. 2019, 886, L1. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Abernathy, M.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; et al. GW150914: First results from the search for binary black hole coalescence with Advanced LIGO. Phys. Rev. D 2016, 93, 122003. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Salaris, M.; Cassisi, S. Evolution of Stars and Stellar Populations; Wiley: Chichester, UK, 2005. [Google Scholar]
- Bromm, V.; Larson, R.B. The First stars. Ann. Rev. Astron. Astrophys. 2004, 42, 79–118. [Google Scholar] [CrossRef]
- Madau, P.; Rees, M.J. Massive black holes as Population III remnants. Astrophys. J. Lett. 2001, 551, L27–L30. [Google Scholar] [CrossRef]
- Greene, J.E.; Strader, J.; Ho, L.C. Intermediate-Mass Black Holes. Ann. Rev. Astron. Astrophys. 2020, 58, 257–312. [Google Scholar] [CrossRef]
- Banados, E.; Venemans, B.P.; Mazzucchelli, C.; Farina, E.P.; Walter, F.; Wang, F.; Decarli, R.; Stern, D.; Fan, X.; Davies, F.; et al. An 800-million-solar-mass black hole in a significantly neutral Universe at redshift 7.5. Nature 2018, 553, 473–476. [Google Scholar] [CrossRef]
- Chen, H.Y.; Ricarte, A.; Pacucci, F. Prospects to Explore High-redshift Black Hole Formation with Multi-band Gravitational Waves Observatories. arXiv 2022, arXiv:2202.04764. [Google Scholar]
- Mapelli, M. Binary Black Hole Mergers: Formation and Populations. Front. Astron. Space Sci. 2020, 7, 38. [Google Scholar] [CrossRef]
- Rodriguez, C.L.; Amaro-Seoane, P.; Chatterjee, S.; Rasio, F.A. Post-Newtonian Dynamics in Dense Star Clusters: Highly-Eccentric, Highly-Spinning, and Repeated Binary Black Hole Mergers. Phys. Rev. Lett. 2018, 120, 151101. [Google Scholar] [CrossRef] [PubMed]
- Zevin, M.; Romero-Shaw, I.M.; Kremer, K.; Thrane, E.; Lasky, P.D. Implications of Eccentric Observations on Binary Black Hole Formation Channels. Astrophys. J. Lett. 2021, 921, L43. [Google Scholar] [CrossRef]
- Zevin, M.; Bavera, S.S.; Berry, C.P.L.; Kalogera, V.; Fragos, T.; Marchant, P.; Rodriguez, C.L.; Antonini, F.; Holz, D.E.; Pankow, C. One Channel to Rule Them All? Constraining the Origins of Binary Black Holes Using Multiple Formation Pathways. Astrophys. J. 2021, 910, 152. [Google Scholar] [CrossRef]
- Ng, K.K.Y.; Vitale, S.; Farr, W.M.; Rodriguez, C.L. Probing multiple populations of compact binaries with third-generation gravitational-wave detectors. Astrophys. J. Lett. 2021, 913, L5. [Google Scholar] [CrossRef]
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. Rept. Prog. Phys. 2018, 81, 056902. [Google Scholar] [CrossRef]
- Chatziioannou, K. Neutron star tidal deformability and equation of state constraints. Gen. Rel. Grav. 2020, 52, 109. [Google Scholar] [CrossRef]
- Haskell, B.; Schwenzer, K. Isolated Neutron Stars. In Handbook of Gravitational Wave Astronomy; Springer: Singapore, 2021. [Google Scholar] [CrossRef]
- Woan, G.; Pitkin, M.D.; Haskell, B.; Jones, D.I.; Lasky, P.D. Evidence for a Minimum Ellipticity in Millisecond Pulsars. Astrophys. J. Lett. 2018, 863, L40. [Google Scholar] [CrossRef]
- Most, E.R.; Papenfort, L.J.; Dexheimer, V.; Hanauske, M.; Schramm, S.; Stöcker, H.; Rezzolla, L. Signatures of quark-hadron phase transitions in general-relativistic neutron-star mergers. Phys. Rev. Lett. 2019, 122, 061101. [Google Scholar] [CrossRef]
- Prakash, A.; Radice, D.; Logoteta, D.; Perego, A.; Nedora, V.; Bombaci, I.; Kashyap, R.; Bernuzzi, S.; Endrizzi, A. Signatures of deconfined quark phases in binary neutron star mergers. Phys. Rev. D 2021, 104, 083029. [Google Scholar] [CrossRef]
- Sarin, N.; Lasky, P.D. The evolution of binary neutron star post-merger remnants: A review. Gen. Rel. Grav. 2021, 53, 59. [Google Scholar] [CrossRef]
- Kashyap, R.; Das, A.; Radice, D.; Padamata, S.; Prakash, A.; Logoteta, D.; Perego, A.; Godzieba, D.A.; Bernuzzi, S.; Bombaci, I.; et al. Numerical relativity simulations of prompt collapse mergers: Threshold mass and phenomenological constraints on neutron star properties after GW170817. arXiv 2021, arXiv:2111.05183. [Google Scholar] [CrossRef]
- Srivastava, V.; Davis, D.; Kuns, K.; Landry, P.; Ballmer, S.; Evans, M.; Hall, E.; Read, J.; Sathyaprakash, B.S. Science-Driven Tunable Design of Cosmic Explorer Detectors. arXiv 2022, arXiv:2201.10668. [Google Scholar] [CrossRef]
- Clark, J.A.; Bauswein, A.; Stergioulas, N.; Shoemaker, D. Observing Gravitational Waves From The Post-Merger Phase Of Binary Neutron Star Coalescence. Class. Quant. Grav. 2016, 33, 085003. [Google Scholar] [CrossRef]
- Abdikamalov, E.; Pagliaroli, G.; Radice, D. Gravitational Waves from Core-Collapse Supernovae. arXiv 2020, arXiv:2010.04356. [Google Scholar]
- Srivastava, V.; Ballmer, S.; Brown, D.A.; Afle, C.; Burrows, A.; Radice, D.; Vartanyan, D. Detection Prospects of Core-Collapse Supernovae with Supernova-Optimized Third-Generation Gravitational-wave Detectors. Phys. Rev. D 2019, 100, 043026. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Kasen, D.; Metzger, B.; Barnes, J.; Quataert, E.; Ramirez-Ruiz, E. Origin of the heavy elements in binary neutron-star mergers from a gravitational wave event. Nature 2017, 551, 80. [Google Scholar] [CrossRef]
- Barnes, J. The Physics of Kilonovae. Front. Phys. 2020, 8, 355. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. Gravitational Waves and Gamma-rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Ciolfi, R. Short gamma-ray burst central engines. Int. J. Mod. Phys. D 2018, 27, 1842004. [Google Scholar] [CrossRef]
- Will, C.M. The Confrontation between General Relativity and Experiment. Living Rev. Rel. 2014, 17, 4. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.; Adya, V.; Affeldt, C.; et al. Tests of General Relativity with the Binary Black Hole Signals from the LIGO-Virgo Catalog GWTC-1. Phys. Rev. D 2019, 100, 104036. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, A.; Adams, C.; Adhikari, R.; Adya, V.; Affeldt, C.; et al. Tests of general relativity with binary black holes from the second LIGO-Virgo gravitational-wave transient catalog. Phys. Rev. D 2021, 103, 122002. [Google Scholar] [CrossRef]
- Perkins, S.E.; Yunes, N.; Berti, E. Probing Fundamental Physics with Gravitational Waves: The Next Generation. Phys. Rev. D 2021, 103, 044024. [Google Scholar] [CrossRef]
- Gossan, S.; Veitch, J.; Sathyaprakash, B.S. Bayesian model selection for testing the no-hair theorem with black hole ringdowns. Phys. Rev. D 2012, 85, 124056. [Google Scholar] [CrossRef]
- Meidam, J.; Agathos, M.; Van Den Broeck, C.; Veitch, J.; Sathyaprakash, B.S. Testing the no-hair theorem with black hole ringdowns using TIGER. Phys. Rev. D 2014, 90, 064009. [Google Scholar] [CrossRef]
- Berti, E.; Sesana, A.; Barausse, E.; Cardoso, V.; Belczynski, K. Spectroscopy of Kerr black holes with Earth- and space-based interferometers. Phys. Rev. Lett. 2016, 117, 101102. [Google Scholar] [CrossRef]
- Cardoso, V.; Pani, P. Testing the nature of dark compact objects: A status report. Living Rev. Rel. 2019, 22, 4. [Google Scholar] [CrossRef]
- Bertone, G.; Croon, D.; Amin, M.A.; Boddy, K.K.; Kavanagh, B.J.; Mack, K.J.; Natarajan, P.; Opferkuch, T.; Schutz, K.; Takhistov, V.; et al. Gravitational wave probes of dark matter: Challenges and opportunities. SciPost Phys. Core 2020, 3, 007. [Google Scholar] [CrossRef]
- Chen, Z.C.; Huang, Q.G. Distinguishing Primordial Black Holes from Astrophysical Black Holes by Einstein Telescope and Cosmic Explorer. JCAP 2020, 08, 039. [Google Scholar] [CrossRef]
- Yuan, C.; Brito, R.; Cardoso, V. Probing ultralight dark matter with future ground-based gravitational-wave detectors. Phys. Rev. D 2021, 104, 044011. [Google Scholar] [CrossRef]
- Nagano, K.; Nakatsuka, H.; Morisaki, S.; Fujita, T.; Michimura, Y.; Obata, I. Axion dark matter search using arm cavity transmitted beams of gravitational wave detectors. Phys. Rev. D 2021, 104, 062008. [Google Scholar] [CrossRef]
- Chen, H.Y.; Cowperthwaite, P.S.; Metzger, B.D.; Berger, E. A Program for Multimessenger Standard Siren Cosmology in the Era of LIGO A+, Rubin Observatory, and Beyond. Astrophys. J. Lett. 2021, 908, L4. [Google Scholar] [CrossRef]
- Wu, C.; Mandic, V.; Regimbau, T. Accessibility of the Gravitational-Wave Background due to Binary Coalescences to Second and Third Generation Gravitational-Wave Detectors. Phys. Rev. D 2012, 85, 104024. [Google Scholar] [CrossRef]
- Regimbau, T.; Evans, M.; Christensen, N.; Katsavounidis, E.; Sathyaprakash, B.; Vitale, S. Digging deeper: Observing primordial gravitational waves below the binary black hole produced stochastic background. Phys. Rev. Lett. 2017, 118, 151105. [Google Scholar] [CrossRef] [PubMed]
- Sharma, A.; Harms, J. Searching for cosmological gravitational-wave backgrounds with third-generation detectors in the presence of an astrophysical foreground. Phys. Rev. D 2020, 102, 063009. [Google Scholar] [CrossRef]
- Sachdev, S.; Regimbau, T.; Sathyaprakash, B.S. Subtracting compact binary foreground sources to reveal primordial gravitational-wave backgrounds. Phys. Rev. D 2020, 102, 024051. [Google Scholar] [CrossRef]
- Biscoveanu, S.; Talbot, C.; Thrane, E.; Smith, R. Measuring the primordial gravitational-wave background in the presence of astrophysical foregrounds. Phys. Rev. Lett. 2020, 125, 241101. [Google Scholar] [CrossRef]
- Lang, K.R. Serendipitous Astronomy. Science 2010, 327, 39–40. [Google Scholar] [CrossRef]
- Hall, E.D.; Kuns, K.; Smith, J.R.; Bai, Y.; Wipf, C.; Biscans, S.; Adhikari, R.X.; Arai, K.; Ballmer, S.; Barsotti, L.; et al. Gravitational-wave physics with Cosmic Explorer: Limits to low-frequency sensitivity. Phys. Rev. D 2021, 103, 122004. [Google Scholar] [CrossRef]
- Schutz, B.F. Networks of gravitational wave detectors and three figures of merit. Class. Quant. Grav. 2011, 28, 125023. [Google Scholar] [CrossRef]
- Rakhmanov, M.; Romano, J.D.; Whelan, J.T. High-frequency corrections to the detector response and their effect on searches for gravitational waves. Class. Quant. Grav. 2008, 25, 184017. [Google Scholar] [CrossRef]
- Essick, R.; Vitale, S.; Evans, M. Frequency-dependent responses in third generation gravitational-wave detectors. Phys. Rev. D 2017, 96, 084004. [Google Scholar] [CrossRef]
- Rollins, J.G.; Hall, E.; Wipf, C.; McCuller, L. pygwinc: Gravitational Wave Interferometer Noise Calculator. 2020. Available online: https://ascl.net/2007.020 (accessed on 14 April 2022).
- Kogelnik, H.; Li, T. Laser Beams and Resonators. Appl. Opt. 1966, 5, 1550–1567. [Google Scholar] [CrossRef] [PubMed]
- Sidles, J.A.; Sigg, D. Optical torques in suspended Fabry–Perot interferometers. Phys. Lett. A 2006, 354, 167–172. [Google Scholar] [CrossRef]
- Evans, M.; Gras, S.; Fritschel, P.; Miller, J.; Barsotti, L.; Martynov, D.; Brooks, A.; Coyne, D.; Abbott, R.; Adhikari, R.; et al. Observation of Parametric Instability in Advanced LIGO. Phys. Rev. Lett. 2015, 114, 161102. [Google Scholar] [CrossRef]
- Miao, H.; Smith, N.D.; Evans, M. Quantum limit for laser interferometric gravitational wave detectors from optical dissipation. Phys. Rev. X 2019, 9, 011053. [Google Scholar] [CrossRef]
- McCuller, L.; Dwyer, S.; Green, A.; Yu, H.; Barsotti, L.; Blair, C.; Brown, D.; Effler, A.; Evans, M.; Fernandez-Galiana, A.; et al. LIGO’s quantum response to squeezed states. Phys. Rev. D 2021, 104, 062006. [Google Scholar] [CrossRef]
- Siegman, A.E. Lasers; University Science Books: Sausalito, CA, USA, 1986. [Google Scholar]
- Barriga, P.; Bhawal, B.; Ju, L.; Blair, D.G. Numerical calculations of diffraction losses in advanced interferometric gravitational wave detectors. J. Opt. Soc. Am. A 2007, 24, 1731–1741. [Google Scholar] [CrossRef]
- Granata, M.; Amato, A.; Balzarini, L.; Canepa, M.; Degallaix, J.; Forest, D.; Dolique, V.; Mereni, L.; Michel, C.; Pinard, L.; et al. Amorphous optical coatings of present gravitational-wave interferometers. Class. Quant. Grav. 2020, 37, 095004. [Google Scholar] [CrossRef]
- Vajente, G.; Yang, L.; Davenport, A.; Fazio, M.; Ananyeva, A.; Zhang, L.; Billingsley, G.; Prasai, K.; Markosyan, A.; Bassiri, R.; et al. Low Mechanical Loss TiO2:GeO2 Coatings for Reduced Thermal Noise in Gravitational Wave Interferometers. Phys. Rev. Lett. 2021, 127, 071101. [Google Scholar] [CrossRef] [PubMed]
- Granata, M.; Amato, A.; Cagnoli, G.; Coulon, M.; Degallaix, J.; Forest, D.; Mereni, L.; Michel, C.; Pinard, L.; Sassolas, B.; et al. Progress in the measurement and reduction of thermal noise in optical coatings for gravitational-wave detectors. Appl. Opt. 2020, 59, A229–A235. [Google Scholar] [CrossRef] [PubMed]
- Penn, S.D.; Kinley-Hanlon, M.M.; MacMillan, I.A.O.; Heu, P.; Follman, D.; Deutsch, C.; Cole, G.D.; Harry, G.M. Mechanical Ringdown Studies of Large-Area Substrate-Transferred GaAs/AlGaAs Crystalline Coatings. J. Opt. Soc. Am. B 2019, 36, C15–C21. [Google Scholar] [CrossRef]
- Brooks, A.; Vajente, G.; Yamamoto, H.; Abbott, R.; Adams, C.; Adhikari, R.; Ananyeva, A.; Appert, S.; Arai, K.; Areeda, J.; et al. Point absorbers in Advanced LIGO. Appl. Opt. 2021, 60, 4047. [Google Scholar] [CrossRef]
- Jia, W.; Yamamoto, H.; Kuns, K.; Effler, A.; Evans, M.; Fritschel, P.; Abbott, R.; Adams, C.; Adhikari, R.; Ananyeva, A.; et al. Point Absorber Limits to Future Gravitational-Wave Detectors. Phys. Rev. Lett. 2021, 127, 241102. [Google Scholar] [CrossRef]
- Aston, S.; Barton, M.; Bell, A.; Beveridge, N.; Bland, B.; Brummitt, A.; Cagnoli, G.; Cantley, C.; Carbone, L.; Cumming, A.; et al. Update on quadruple suspension design for Advanced LIGO. Class. Quant. Grav. 2012, 29, 235004. [Google Scholar] [CrossRef]
- Saulson, P.R. Thermal noise in mechanical experiments. Phys. Rev. D 1990, 42, 2437–2445. [Google Scholar] [CrossRef]
- Cumming, A.V.; Jones, R.; Hammond, G.D.; Hough, J.; Martin, I.W.; Rowan, S. Large-scale Monolithic Fused-Silica Mirror Suspension for Third-Generation Gravitational-Wave Detectors. Phys. Rev. Appl. 2022, 17, 024044. [Google Scholar] [CrossRef]
- Matichard, F.; Lantz, B.; Mittleman, R.; Mason, K.; Kissel, J.; Abbott, B.; Biscans, S.; McIver, J.; Abbott, R.; Abbott, S.; et al. Seismic isolation of Advanced LIGO: Review of strategy, instrumentation and performance. Class. Quant. Grav. 2015, 32, 185003. [Google Scholar] [CrossRef]
- Mow-Lowry, C.M.; Martynov, D. A 6D interferometric inertial isolation system. Class. Quant. Grav. 2019, 36, 245006. [Google Scholar] [CrossRef]
- van Heijningen, J.V.; Bertolini, A.; van den Brand, J.F.J. A novel interferometrically read out inertial sensor for future gravitational wave detectors. In Proceedings of the 2018 IEEE Sensors Applications Symposium (SAS), Seoul, Korea, 12–14 March 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Harms, J. Terrestrial gravity fluctuations. Living Rev. Rel. 2019, 22, 6. [Google Scholar] [CrossRef]
- Coughlin, M.W.; Harms, J.; Driggers, J.; McManus, D.J.; Mukund, N.; Ross, M.P.; Slagmolen, B.J.J.; Venkateswara, K. Implications of dedicated seismometer measurements on Newtonian-noise cancellation for Advanced LIGO. Phys. Rev. Lett. 2018, 121, 221104. [Google Scholar] [CrossRef] [PubMed]
- Driggers, J.C.; Harms, J.; Adhikari, R.X. Subtraction of Newtonian Noise Using Optimized Sensor Arrays. Phys. Rev. D 2012, 86, 102001. [Google Scholar] [CrossRef]
- Gan, W.S. Seismic Metamaterials. In New Acoustics Based on Metamaterials; Springer: Singapore, 2018; pp. 277–288. [Google Scholar] [CrossRef]
- Fiorucci, D.; Harms, J.; Barsuglia, M.; Fiori, I.; Paoletti, F. Impact of infrasound atmospheric noise on gravity detectors used for astrophysical and geophysical applications. Phys. Rev. D 2018, 97, 062003. [Google Scholar] [CrossRef]
- Bowman, J.R.; Baker, G.E.; Bahavar, M. Ambient infrasound noise. Geophys. Res. Lett. 2005, 32, L09803. [Google Scholar] [CrossRef]
- Cahillane, C.; Mansell, G.; Sigg, D. Laser Frequency Noise in Next Generation Gravitational-Wave Detectors. Opt. Express 2021, 29, 42144–42161. [Google Scholar] [CrossRef]
- Essick, R. Calibration uncertainty’s impact on gravitational-wave observations. Phys. Rev. D 2022, 105, 082002. [Google Scholar] [CrossRef]
- Pürrer, M.; Haster, C.J. Gravitational waveform accuracy requirements for future ground-based detectors. Phys. Rev. Res. 2020, 2, 023151. [Google Scholar] [CrossRef]
- Bhattacharjee, D.; Lecoeuche, Y.; Karki, S.; Betzwieser, J.; Bossilkov, V.; Kandhasamy, S.; Payne, E.; Savage, R.L. Fiducial displacements with improved accuracy for the global network of gravitational wave detectors. Class. Quant. Grav. 2021, 38, 015009. [Google Scholar] [CrossRef]
- Spidell, M.; Lehman, J.; López, M.; Lecher, H.; Kück, S.; Bhattacharjee, D.; Lecoeuche, Y.; Savage, R. A bilateral comparison of NIST and PTB laser power standards for scale realization confidence by gravitational wave observatories. Metrologia 2021, 58, 055011. [Google Scholar] [CrossRef]
- Ross, M.P.; Mistry, T.; Datrier, L.; Kissel, J.; Venkateswara, K.; Weller, C.; Kumar, K.; Hagedorn, C.; Adelberger, E.; Lee, J.; et al. Initial results from the LIGO Newtonian calibrator. Phys. Rev. D 2021, 104, 082006. [Google Scholar] [CrossRef]
- Estevez, D.; Mours, B.; Pradier, T. Newtonian calibrator tests during the Virgo O3 data taking. Class. Quant. Grav. 2021, 38, 075012. [Google Scholar] [CrossRef]
- Inoue, Y.; Haino, S.; Kanda, N.; Ogawa, Y.; Suzuki, T.; Tomaru, T.; Yamanmoto, T.; Yokozawa, T. Improving the absolute accuracy of the gravitational wave detectors by combining the photon pressure and gravity field calibrators. Phys. Rev. D 2018, 98, 022005. [Google Scholar] [CrossRef]
- Dylla, F.; Weiss, R.; Zucker, M.E. Proceedings of the NSF Workshop on Large Ultrahigh-Vacuum Systems for Frontier Scientific Research, Livingston, LA, USA, 28–31 January 2019; Available online: https://dcc.ligo.org/LIGO-P1900072/public (accessed on 14 April 2022).
- Vajente, G. Noise from Clipping on Cosmic Explorer Beam Tube Baffles; Technical Report CE–T2100011; Cosmic Explorer; 2021; Available online: https://arxiv.org/pdf/2109.09882.pdf (accessed on 14 April 2022).
- Bai, Y. Cosmic Explorer: Back-scatter Noise and Design Recommendations; Technical Report T1900854–v1; LIGO; 2019; Available online: https://dcc.ligo.org/public/ (accessed on 14 April 2022).
- Day, R. FFT Simulation Using FOG; Technical Report G1300532; LIGO; 2013; Available online: https://dcc.ligo.org/LIGO-G1300532/public (accessed on 14 April 2022).
- Amann, F.; Bonsignorio, F.; Bulik, T.; Bulten, H.J.; Cuccuru, S.; Dassargues, A.; DeSalvo, R.; Fenyvesi, E.; Fidecaro, F.; Fiori, I.; et al. Site-selection criteria for the Einstein Telescope. Rev. Sci. Instrum. 2020, 91, 9. [Google Scholar] [CrossRef]
- Efron, N.; Read, M. Analysing International Tunnel Costs; Technical Report; Worcester Polytechnic Institute: Worcester, MA, USA, 2012. [Google Scholar]
- Kuns, K.; Massachusetts Institute of Technology, Cambridge, MA, USA; Schiettekatte, F.; University of Montreal, Montréal, QC, Canada; Slagmolen, B.J.J.; Australian National University, Canberra ACT, Australia; Töyra, D.; Australian National University, Canberra ACT, Australia. Personal communication, 2020.
- Bonnefoy-Claudet, S.; Cotton, F.; Bard, P.Y. The nature of noise wavefield and its applications for site effects studies: A literature review. Earth-Sci. Rev. 2006, 79, 205–227. [Google Scholar] [CrossRef]
- Peterson, J.R. Observations and Modeling of Seismic Background Noise; Technical Report; US Geological Survey: Albuquerque, NM, USA, 1993. [CrossRef]
- Nguyen, P.; Schofield, R.M.; Effler, A.; Austin, C.; Adya, V.; Ball, M.; Banagiri, S.; Banowetz, K.; Billman, C.; Blair, C.D.; et al. Environmental noise in advanced LIGO detectors. Class. Quant. Grav. 2021, 38, 145001. [Google Scholar] [CrossRef]
- Physics of Ambient Noise Generation by Ocean Waves. In Seismic Ambient Noise; Cambridge University Press: Cambridge, UK, 2019; pp. 69–108. [CrossRef]
- De Angelis, S.; Bodin, P. Watching the Wind: Seismic Data Contamination at Long Periods due to Atmospheric Pressure-Field-Induced Tilting. Bull. Seismol. Soc. Am. 2012, 102, 1255–1265. [Google Scholar] [CrossRef]
- Kahanamoku, S.; Alegado, R.A.; Kagawa-Viviani, A.; Kamelamela, K.L.; Kamai, B.; Walkowicz, L.M.; Prescod-Weinstein, C.; de los Reyes, M.A.; Neilson, H. A Native Hawaiian-Led Summary of the Current Impact of Constructing the Thirty Meter Telescope on Maunakea. arXiv 2020, arXiv:2001.00970. [Google Scholar]
- Barbu, B. Where science meets the sacred. Symmetry Magazine, 2021. [Google Scholar]
- Martynov, D.; Miao, H.; Yang, H.; Vivanco, F.H.; Thrane, E.; Smith, R.; Lasky, P.; East, W.E.; Adhikari, R.; Bauswein, A.; et al. Exploring the sensitivity of gravitational wave detectors to neutron star physics. Phys. Rev. D 2019, 99, 102004. [Google Scholar] [CrossRef]
- NSF Large Facilities Office. Research Infrastructure Guide; Technical Report NSF 21–107; National Science Foundation: Washington, DC, USA, 2021.
- Harrison, F.A.; Kennicutt, R.C., Jr. (Eds.) Pathways to Discovery in Astronomy and Astrophysics for the 2020s; National Academies of Science, Engineering, and Medicine: Washington, DC, USA, 2021. [Google Scholar] [CrossRef]
- Foucart, F.; Laguna, P.; Lovelace, G.; Radice, D.; Witek, H. Snowmass 2021 Cosmic Frontier White Paper: Numerical relativity for next-generation gravitational-wave probes of fundamental physics. arXiv 2022, arXiv:2203.08139. [Google Scholar]
- Chakrabarti, S.; Drlica-Wagner, A.; Li, T.S.; Sehgal, N.; Simon, J.D.; Birrer, S.; Brown, D.A.; Bernstein, R.; Bolatto, A.D.; Chang, P.; et al. Snowmass2021 Cosmic Frontier White Paper: Observational Facilities to Study Dark Matter. In Proceedings of the 2022 Snowmass Summer Study, Settle, WA, USA, 17–26 July 2022. [Google Scholar]
- Engel, K.; Lewis, T.; Muzio, M.S.; Venters, T.M. Advancing the Landscape of Multimessenger Science in the Next Decade. In Proceedings of the 2022 Snowmass Summer Study, Settle, WA, USA, 17–26 July 2022. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).