Abstract
Future automation systems are likely to include devices with a varying degree of autonomy, as well as advanced algorithms for perception and control. Human operators will be expected to work side by side with both collaborative robots performing assembly tasks and roaming robots that handle material transport. To maintain the flexibility provided by human operators when introducing such robots, these autonomous robots need to be intelligently coordinated, i.e., they need to be supported by an intelligent automation system. One challenge in developing intelligent automation systems is handling the large amount of possible error situations that can arise due to the volatile and sometimes unpredictable nature of the environment. Sequence Planner is a control framework that supports the development of intelligent automation systems. This paper describes Sequence Planner and tests its ability to handle errors that arise during execution of an intelligent automation system. An automation system, developed using Sequence Planner, is subjected to a number of scenarios where errors occur. The error scenarios and experimental results are presented along with a discussion of the experience gained in trying to achieve robust intelligent automation.
1. Introduction
Introduction of collaborative robotics [1], together with other intelligent [2] and autonomous machines [3], is an ongoing trend in production. Fully benefiting from introducing collaboration between human operators without compromising on flexibility requires that the machines and human operators can take decisions together. This means that the automation system needs to be able to adapt to unexpected events [4], for example as a result of decisions taken by operators—it needs to be more intelligent than traditional automation systems. This intelligence comes from complex software solutions for tasks such as perception, motion planning, resource allocation, etc. In an automation context, these intelligent sub-systems need to be coordinated by a control system that also takes into account human operators. While a high quality automation system should strive for high reliability, the fact that many perception and motion algorithms are not 100% reliable (e.g., [5,6,7]), combined with the volatile nature of the environment this kind of system, means there are always sources of errors.
Flexibility and robustness are difficult to achieve in an efficient manner already for traditional automation systems, particularly to restart production once an unanticipated error has occurred. For traditional automation systems, several approaches to enabling efficient restart exist in the literature of discrete event systems. One strategy is to precompute a set of control system states that are known to be safe to restart from [8,9,10,11], another is to adapt the control system on-line [12]. When errors are anticipated, recovery actions can be included in the models of the automation system [13,14] to ensure safe restart.
In this new class of intelligent automation systems, where automation systems include autonomous machines, long-term robustness without sacrificing flexibility will be a challenging task. If the semi-autonomous robots of an industrial automation system can ask for help in intuitive ways [15], the existence of the human operators in the system becomes an enabler for intelligent automation systems, as they can intervene when something goes wrong [16]. This means that not only robustness is required, but also that it needs to be possible for an operator to influence the automation system to a large degree. To meet the challenges posed by these additional requirements, new ways of developing control systems will be needed.
One way to scale development is to apply model-based approaches. Using model-based control system development allows for applying formal verification techniques and enables flexible control strategies to be used that can change without manual programming. Sequence Planner (SP) [17] is a model-based framework for control of intelligent automation systems. To ease modeling and control, SP uses formal models together with on-line planning to reach the current goal of the automation system. SP has support for Robot Operating System (ROS) [18] to enable quick prototyping and composition of ROS resources. SP has previously been used to model and control an intelligent automation system for collaborative final assembly [17,19,20,21]. SP implements a strategy to recover from unexpected errors based on automated planning and learning which resources and operations are currently unavailable, combined with allowing special “human intervention” actions to be defined. In contrast to previous work on restart of automation systems [8,9,10,11], SP requires no off-line computation. As in [13,14], recovery actions can be added but are not necessarily used, depending on the error situation.
Intelligent automation systems require low-level control of continuous dynamics (e.g., [22]), as well as path (e.g., [23]) and task planning (e.g., [24]). In the ROS ecosystem, an abundance of drivers, controllers, and control frameworks exist. Examples of task composition and planning frameworks are ROSPlan [25] that uses PDDL-based models for automated task planning and dispatching, SkiROS [26] that simplifies the planning with the use of a skill-based ontology, and CoSTAR [27] that uses Behavior Trees (BTs) [28] to define complex tasks, combined with a novel way of defining computer perception pipelines.
However, these frameworks are mainly robot-oriented and focuses relatively little on error handling for the automation system as a whole. While ROSPlan and SkiROS can indeed replan as well as retry failed steps in a plan, there exists little user support for controlling when and how errors should be handled. On the other hand, BTs work very well for defining how to deal with anticipated errors. The downside of BTs is that they easily deadlock when unanticipated errors occur.
1.1. A Motivating Example: Collaborative Final Assembly
The collaborative final assembly application involves conversion of an existing manual assembly station from a truck engine final assembly line, shown in Figure 1a, into an intelligent and collaborative robot assembly station, shown in Figure 1b. The aim of the conversion work is to include a robot working together with an operator in order to jointly perform the assembly of an engine side by side, sharing tools hanging by wires from the ceiling. A dedicated camera system keeps track of operators, ensuring safe coexistence with machines. It is desired to let a human operator be human and not simply used as an additional cog in the machine.

Figure 1.
Transformation of a manual assembly station into a collaborative one: (a) the original manual assembly station; and (b) the collaborative robot assembly station controlled by a network of ROS2 nodes. A video clip from the demonstrator can be found at: https://youtu.be/TK1Mb38xiQ8 (accessed 11 March 2021).
Diesel engines are transported from station to station in a predetermined time slot on Automated Guided Vehicles (AGVs). Material to be mounted on a specific engine is loaded by an operator from kitting facades located adjacent to the line. An autonomous mobile platform (MiR100) carries the kitted material to be mounted on the engine, to the collaborative robot assembly station.
In the station, a robot and an operator work together to mount parts on the engine by using different tools suspended from the ceiling. For example, they lift a heavy ladder frame on to the engine and either the operator or the robot can use the tools to tighten bolts and oil-filter which should be mounted.
1.2. Handling Error Situations
In this paper, we are interested to see how well the automated error handling in SP works on a practical example. A few examples of errors that we are interested in evaluating are listed below.
- Unresponsiveness: A resource does not respond in time, for example communication failure or equipment malfunction (e.g., a sensor that does not give the expected result).
- Task failure: A resource fails to perform its current task. This may be both expected and unexpected failures.
- Unexpected events: The state unexpectedly changes. For example, consider the case of a product slipping away from the grip of a robotic gripper.
- Specification errors: The automation system breaks safety specifications or cannot make progress. This can occur due to mistakes in programming, or as a consequence of previous errors.
Handling of these different types of errors using SP is evaluated using a number of different scenarios implemented on the use case.
1.3. Contribution
This paper presents SP, a framework for control of intelligent automation systems. Previous work in control and coordination of automation systems in the ROS ecosystem lacks the focus on error handling which is required to deal with many real-world situations. This paper aims to close this gap by presenting a novel framework within SP for defining how errors can and should be handled. Additionally, the paper demonstrates the ability of SP to handle errors on an application from final assembly which features collaborative robots and computer vision systems. The error scenarios in the application together with experimental results are presented along with a discussion of the experience gained in striving to achieve an intelligent automation control solution.
1.4. Outline
The paper is organized as follows. Section 2 gives some background to what makes error recovery difficult, both in the traditional sense and what is different in intelligent automation. Section 3 describes SP and Section 4 shows how SP handles solving complex situations that can arise after errors. Section 6 describes the experimental setups and a number of error handling scenarios related to the intelligent automation system. In Section 7, the results are discussed and the paper is ended with some concluding remarks.
2. Difficulties with Error Handling
In this section, we briefly introduce the fundamental challenges of robust and flexible automation system design with a focus on recovering after errors. We give examples of how sequence based control and combinatorial control can be used. Additionally, the modeling language of Sequence Planner is introduced.
2.1. Sequence Based Control
A common way to reduce complexity when developing automation software is to structure execution as sequences of operations, e.g., a set of actions that should happen one after the other, or in parallel, maybe with additional constraints. Sequences are easy to understand and reduce the complexity that needs to be dealt with at a single point in time. However, this comes at the cost of flexibility. It may be difficult to “switch tasks” mid-sequence, and extra effort needs to be spent on making sure that a sequence can be properly stopped. Another difficulty is that the sequence needs a well defined initial state. Consider the case of a robot with a gripper that should move a product from buffer A to buffer B. A sequence for performing this is illustrated as a state machine in Figure 2.
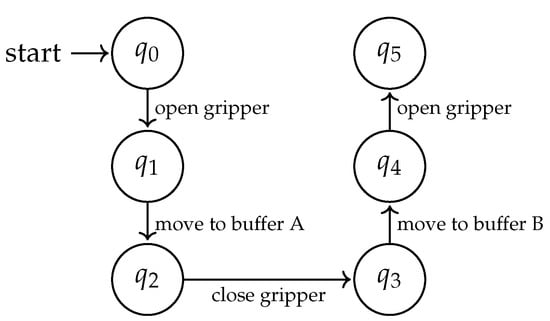
Figure 2.
Sequence control for moving a part between two buffers.
A sequence such as the one in Figure 2 can be tricky to recover from if an error has occurred mid-sequence. Even if the state of the resources and buffers is measurable, the sequence in itself does not give any clues as how the sequence relates to the physical world. To restart, the part must be placed in buffer A and the robot and gripper returned to their initial states. The simplicity of the sequence is deceptive—it effectively hides important states required to know where execution can continue.
2.2. Combinatorial Control
Another way to design the system is applying a combinatoric approach, where, at all points in time, the next action to be taken is computed as a function of the current state. However, due to the fundamental difficulty of reasoning about combinatoric systems (due to the state growth), programs often end up performing very narrowly defined tasks to keep the solution space small.
Consider again moving the product as in Figure 2. The sequence can be programmed as follows:
if something in buffer A and nothing in gripper and gripper closed
-> then open gripper
if something in buffer A and nothing in gripper and gripper opened and robot not at buffer A
-> then move robot to buffer A
if something in buffer A and nothing in gripper and gripper opened and robot at buffer A
-> then close gripper
if something in gripper and robot at buffer A
-> move to buffer B
if something in gripper and robot at buffer B
-> open gripper
At a first glance, a control policy such as the above will be able to continue its execution at any point of the “sequence” (if we consider closing and opening the gripper as atomic actions and the state of the buffers can be measured).
However, consider that, later, an additional operation needs to be added to move the product in the opposite direction, i.e., from buffer B to buffer A. Consider the original policy: if something in gripper and robot at buffer A -> then move to buffer B. This will conflict with the new operation, as the correct action in this state when the new operation is active is to open the gripper to release the product in buffer A. To handle this situation, a new state variable needs to be introduced to keep track of in which direction the product is being moved. In practice, then, the newly introduced state encodes the same thing as the sequence counter in the previous version. If the system has stopped executing for whatever reason, the state of the involved resources (which can ideally be measured) is no longer enough knowledge to resume execution, and now the additional state describing the direction also needs to be appropriately set.
2.3. Automated Planning
An alternative to the aforementioned approaches is to leverage an automated planner. When implementing a control solution that applies automated planning, the extra memory variable (or sequence counter/state machine location) introduced above does not need to be part of the program. The resulting sequence (the computed plan) is instead a result of the currently active goal.
This makes it easier to recover after errors, as there is no additional state that needs to be changed or double-checked before resuming. It is enough that the goals are in order. It also means that, ideally, program execution can continue from any point of the program, as long as a new plan can be computed. Additionally, complexity in the programs can be reduced. If we think about the combinatorial approach described in Section 2.2, to be able to move to a buffer B or C, the number of policies will need to increase to cover the different cases.
Several problems remain; planning is computationally very intensive and is as such not suitable where real-time performance is needed. Even if complexity can be reduced with respect to programming, a good understanding of the state space is still needed—it is easy to be fooled by the planner into accepting a plan that does not have the desired properties.
A fundamental prerequisite for producing correct plans is that the control system needs to be in synchrony with the actual state of resources and products, and it needs to be in a valid state (i.e., not in violation of any safety specifications).
3. Sequence Planner
SP tries to combine the three control approaches described in Section 2 by keeping a purely combinatorial control model at the bottom. Sequences are modeled as constraints, which are adhered to by an online planning system. This section intends to give an overview of SP. Details on how to model in the framework are described in [29].
SP is based on models of resources in terms of their state, with non-deterministic guarded actions (transitions) that can transition the system between these states. Transitions exist in three kinds: controllable, automatic, and effect. Controllable and automatic transitions are taken by SP, while effect transitions are used to model the environment. The resource models are composed and constrained by formal specifications which automatically undesired states. Figure 3 presents an overview of how an automation system in SP is structured. SP is based on planning in two levels: first with the operation planner to determine which operations should be run and then with the transition planner to determine exactly how resources should perform the operations.
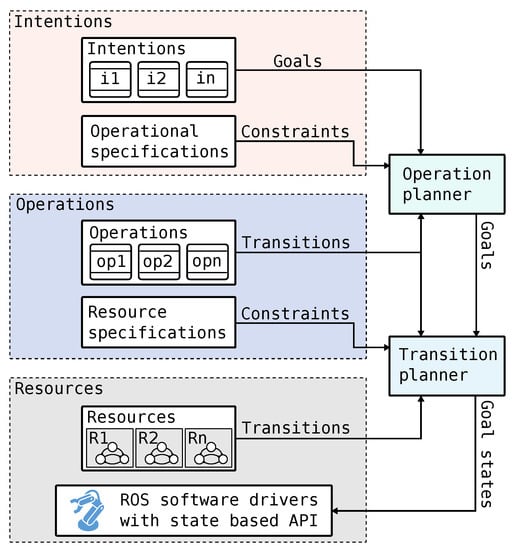
Figure 3.
Overview of the SP control framework.
SP uses a state based control design, where resources continuously receive goal states from SP and continuously update measured states, which are inputs to SP. For example, consider a simple indicator light; it may have a goal state and a measured state with the same domain. Contrary, a robot may have a complex goal state that includes a frame to reach in space, perhaps with additional active constraints such as speed or joint limits.
Given a set of resources, the system is initially allowed to take any actions. Resource specifications are defined as invariants over the system state, constraining the system to avoid unsafe regions during execution. Operations define goal states in terms of decision variables. Goal states are predicates over the resource variables.
SP models the resources using a formalism with finite domain variables, states that are unique valuations of the variables, and transitions between states. Some definitions to clarify this are presented below.
Definition 1.
A transition system (TS) is a tuple , where S is a set of states, is the transition relation, and is the nonempty set of initial states.
Definition 2.
A state is a unique valuation of each variable in the system. For example, .
Variables have finite discrete domains, i.e., Boolean or enumeration types.
The transition relation → can be created from transitions that modify the system state:
Definition 3.
A transition t has a guard g, which is a Boolean function over a state, , and a set of action functions A where , which updates the assignments to the state variables in a state. We often write a transition as to save space.
SP uses reusable models of the behavior of the resources. These are simple transition systems that the operations navigate using planning to reach their goals.
Definition 4.
A resource i is defined as where is a set of measured state variables, is a set of goal state variables, and is a set of estimated state variables. Variables are of finite domain. The set defines all state variables of a resource. The sets and define controlled and automatic transitions, respectively. is a set of effect transitions describing the possible consequences to of being in certain states.
, , and have the same formal semantics but are separated due to their different uses:
Controlled transitions are taken when their guard condition evaluates to true, only if they are also activated by the planning system.
Automatic transitions are always taken when their guard condition evaluates to true, regardless of if there are any plans active or not. All automatic transitions are taken before any controlled transitions can be taken. This ensures that automatic transitions can never be delayed by the planner.
Effect transitions define how the measured state is updated, and as such they are not used during control like the control transitions and . They are important to keep track of however, as they are needed for online planning and formal verification algorithms. They are also used to know if the plan is correctly followed—if expected effects do not occur it can be due to an error.
Resources in SP are connected via constraints. The constraints are simple invariant formulas over the system state. The negation of invariant formulas (e.g., forbidden states) are extended into larger sets of states using symbolic backwards reachability analysis to properly deal with the uncontrollability of automatic and effect transitions. This allows resources to be self-contained, as the interaction between resources can be defined via specification instead of programming. The method used is described in [19].
In addition to the variables defined by the resources, another set of variables exist: decision variables. These are estimated variables that define the state of the system in abstract terms to plan which operations to execute. For example, a decision variable could be the abstract state of a particular resource or the state of a product in the system. Decision variables can sometimes be directly measured by resources, in which case these measurements are copied into the decision variables, in some cases after undergoing some form of transformation (e.g., discretization).
Definition 5.
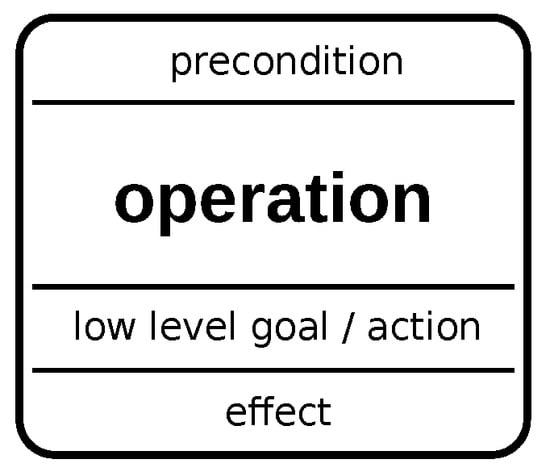
An operation j is defined as , where is a guard predicate over the decision variables defining when the operation can start, a set of effect of completing the operation, which are actions defined on the decision variables, as well as a goal predicate defined over the resource variables. is a set of actions for synchronizing the operation with the resource state. Finally, the operation has an associated state variable . Throughout the paper, operations are graphically depicted as in Figure 4.

Figure 4.
We use this graphical notation to visualize operations. For the operation j, the precondition is , the effect is , the low level goal is , and the set of low level actions is .
When the precondition of an operation is satisfied, the operation can start. The effect actions are then evaluated against the current state, and the difference between the current state and the next state is converted into a predicate. This predicate becomes the post-condition of the operation. For example, if the effect of the operation is and when the operation starts, then the post-condition (and thus its planning goal) becomes . If the operation needs to update the resource state, can additionally include actions from a transition in the resource layer, in which case is also conjuncted with the guard of the transition to be synchronized.
Definition 6.
The intention k is defined as , where is a predicate over (all) the variables in the system, defining when the intention starts (automatically), is a goal predicate defined over the decision variables, is an optional LTL formula (see Section 4.2) over the decision variables, is the set of actions that can update (all) variables in the system and that are applied when the intention finishes, and is the state of the intention.
The goals defined by the intentions over the decision variables is the way the system is driven forward. The decision variables are meant to be allowed to be changed at any time from the outside. It can be that they can be changed to a high level state from which the goal cannot be reached, in which case replanning occurs automatically. Not only does the planner allow SP to be agnostic about the current resource state, it also allows for interrupting or canceling currently running operations in a safe way—by simply changing the goal state, the planning system will find the correct way to instead reach the new goal.
4. Error Handling in SP
The operations and the decision variables naturally define a hierarchy, where the operations define an abstraction of how the products can move around and change state in the system, ignoring the state of the resources and low-level constraints. In SP, this is done by having two planners: one that plans when operations should be executed and one that manages the detailed goals of the resources in the system. The state of the system as well as the planners are managed by the transition runner. Figure 5 gives an overview of how planning in SP works. In this paper, we are mostly interested in the boxes that deal with error handling. These are highlighted in pink.
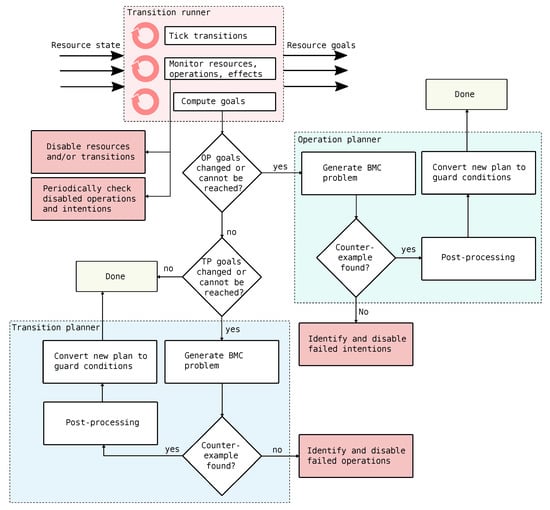
Figure 5.
Overview of the planning system in SP. Pink boxes indicate error handling tasks.
4.1. Transition Runner
The transition runner, (top part in Figure 5) keeps track of the current state of all resource states, decision variables, operations, and intentions. It continuously applies transitions (controlled and automatic) which updates the system state, reacting to any changes to incoming state from the ROS nodes on the network.
When the guard expression of a transition is evaluated to true in the current state, the transition is taken and the state is updated by the transition’s action functions. The state variables relating to resource goals are continuously published to the appropriate ROS2 topics.
Controlled transitions get additional guard expressions every time a new plan is computed which defines the execution order and what external state changes that need waiting for. Intentions and operations are active based on their state. This state can safely be changed arbitrarily in order to cancel running operations or active intentions, as the planner will not allow any forbidden states to be reached.
Because the system is modeled with effect transitions, it is possible for the transition runner to continuously monitor if an effect does not occur within some time bound or the “wrong” effect occurs. When an effect does not occur within a (user specified) timeout period, the effect is disabled in the generated planning problem. For example, there may exist an effect which transitions between a “request” state and a “response” state for a particular resource. Keeping track of the duration an effect has been enabled provides a general way to specify behavior for timeouts. If the system leaves the state where an effect is active, the timestamp for that effect is reset.
A special case of effects not occurring in time is if a resource fails to communicate with SP, for example due to a network, hardware, or software error. This leads to the resource being marked as unavailable, which disables all transitions related to it.
The transition runner also keeps track of which operations that are in an error state, and keeps this information updated based on continuously checking if the operation can be completed from the current state. This is done by periodically executing a one-off planning request in the background. If an operation can be completed, the error state is automatically removed. This allows the system to continue automatically when errors have been cleared.
4.2. Operation Planner
Given a set of active intentions, the operation planner (to the right in Figure 5) computes sequences of operations that allow the intentions to reach their goal states.
SP uses the model checker nuXmv [30], for both the operation planner and the transition planner. In model checking [31], temporal properties are verified by means of state space exploration based on a set of initial states and a set of transitions. The temporal properties are specified in extensions to propositional logic such as Computation Tree Logic (CTL) or Linear Temporal Logic (LTL) [32]. nuXmv supports bounded model checking (BMC) [33] of LTL specifications. In BMC, the model checking problem is reduced to a Boolean satisfiablity problem with a bounded length in the number of discrete “timesteps” from the initial states. One advantage of BMC in this setting is that it produces counterexamples of minimal length, i.e., the plans will never be longer than necessary.
By turning the problem around, and having the model checker proving that a desired future state is not reachable, one can use the counterexample as a plan, which, if followed, will reach a state defined by the formula. In contrast to a more simplistic forward search, using model checking allows SP to restrict the plans by providing additional temporal specifications that need to hold. In SP, the goals of the currently active intentions, as well as their LTL formulas, are used for formulate LTL specifications using the LTL “until” operator. That is, for the intention k, the operational specification should hold until the goal of the operation is reached.
Based on the current goals and information about which operations are available from the transition runner, a BMC problem is generated and solved. One downside to using a BMC solver to perform the planning is that the counterexample trace is a totally ordered plan. In contrast to a partial order plan, totally ordered plans have a fixed sequential execution order [34]. The partial order plan can thus execute some steps in parallel, where the ordering of actions do not matter. This is important in automation as different resources may be able to perform tasks independently. Therefore, the counterexample traces are analyzed and ordering is removed where possible as a post-processing step, enabling operations that are independent to be started in parallel. Two operations are considered independent if their set of used variables (i.e., the set of all variables used in the preconditions, goal predicates, and effect actions) are disjoint. The sets of variables compared is additionally extended to account for operational specifications.
If a counter-example cannot be found, the operation planner tries to identify which intention is the cause of the error and disables it. This is done by attempting to solve the problem for each intention’s goal individually.
4.3. Transition Planner
The transition planner tries to reach the goals of all currently executing operations. If the goals of the operation planner are predicted to be reachable, a simulation is run using the current transition plan to see if the goals of the transition planner is reachable. If the goals cannot be reached, or if the goals have changed since the plan was last calculated, a new transition plan needs to be computed. The bottom of Figure 5 presents an overview of the transition planner.
All automatic, controlled, and effect transitions are encoded as a BMC problem which includes the state of resources, any estimated states, and the decision variables. The BMC problem is constrained by the (global) expanded invariant formulas described in Section 3. The operations and the decision variables naturally define a hierarchy, where the operations define an abstraction of how products and important abstract information about resource state can change in the system. To produce correct plans this abstraction needs to be ordered monotonic [35], which means that the transition planner must make sure not to change any other decision variables than the ones in the current goal. To ensure this, the goal states of all operations that are not currently executing are removed in the same way as the invariants are handled. This effectively forbids the low-level planner from completing operations that are not currently executing. While this may seem limiting, it makes the plans more predicable for the user—they either succeed in an expected way or fail due to not being able to reach the goal.
The BMC problem is solved in order to find a counter-example. If a counter-example is found, the trace is post-processed and converted into guard conditions on the controllable transitions. If a counter-example cannot be found, the same strategy as for the intentions is used to identifying which operations cannot be reached. In the next cycle of the transition runner, the operation planner will replan without these newly disabled operations.
4.4. Short Example
Figure 6 shows an example of how an error can propagate in the hierarchy (this particular example is expanded upon in Section 6.3). The figure shows one intention which has a goal that all “bolts” in the system should be tightened. The bolts can be tightened by a robot holding a tool built for this purpose. An operation plan has been computed which reaches the goal that all bolts should be tightened. The plan includes locating the proper tool using a 3D camera, attaching the tool to the robot, and then using the tool to tighten the bolts.
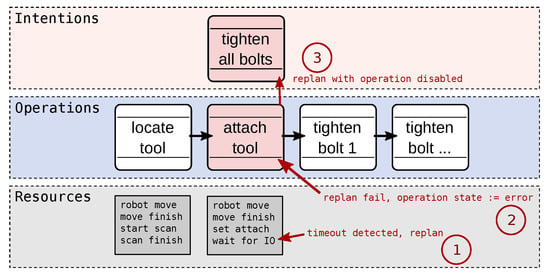
Figure 6.
Propagating errors in the hierarchy.
During execution, a low level effect fails to occur (1). This disables the problematic effect transition, which triggers a replan with the transition planner. If this replan fails (2), the operation that posted the goal is identified and is put into its error state (pink color). Thus, the system learns which operations are currently not possible to complete. It may or may not be able to continue execution with this new knowledge. A new operation plan is computed, (3) in Figure 6, with the operation disabled. In this case, no plan was found, and the intention is also disabled.
4.5. Maintenance Transitions (MTs)
In the case that execution cannot continue, the exact cause of the problem needs to be possible for an operator to pin-point. The planner can be used to aid the operator by suggesting a solution to the problem. This is done with the help of maintenance transitions (MTs).
MTs are controlled transitions that are only active when checking if the disabled operations can be restarted. Their purpose is to give the planning system more freedom to operate in, by encoding specific actions that the operator can take (in the physical world) to solve problems.
For example, clearing an error state off a resource can be modeled as an MT if clearing the error cannot or should not be done automatically by the control system. It is common that resources include a ’reset’ maintenance transition, which sets the state of the resource to some predefined (safe) state.
By letting the planning system correct errors via MTs, safety is ensured—either the goals can be reached without violating any safety constraints or they cannot be reached at all.
4.6. Forbidden States
Sometimes the system cannot make progress due to being in a forbidden state, i.e., a state which violates one or more safety constraints. To handle this situation, the offending specifications can (must) be temporarily removed in order to find a plan. With the offending specification removed, the transition planner tries to find a way (including the MTs) to reach a state where all specifications hold, including the violated ones, i.e., the goal is , rather than the goal currently decided by the active operations. As we are in an unsafe state, this plan must be executed with caution, i.e., an operator needs to approve the involved steps.
5. Description of the Test System
The application used for the experiments in Section 6 is an intelligent automation system where robots and operators work together to mount parts on a diesel engine using various tools suspended from the ceiling. A dedicated camera system keeps track of operators, ensuring safe coexistence with machines.
An autonomous robot (MiR100), as seen to the left in Figure 1b, brings kitting material that a Universal Robots (UR10) robot, r1, and an operator collaboratively use to perform assembly tasks. The tasks include lifting a heavy ladder frame on to the engine in a coactive fashion. After placing the ladder frame on the engine, an operator informs the control system with a button press on a smartwatch or with a gesture, after which r1 switches tools; the lifting end-effector is replaced with a nutrunner for tightening bolts. During this tool change, the operator starts to insert 24 bolts that the r1 will tighten.
The tools required for the assembly tasks are hanging with wires from the ceiling, these are local to the assembly station. The tools can be operated by both the robots and a human operator. The robots are mounted on pallets that can be manually moved when necessary.
A second robot, r2, moves between two assembly stations and is sometimes available for use. When r2 is available, r2 should have priority for performing tighten bolt operations. Having r2 available sometimes also adds redundancy in the case r1 is not available. Both robots are equipped with small 3D cameras that are used to localize both tools and products.
During the tightening of the bolts by any of the robots, the operator can mount three oil filters. When the operator is done, the robot attaches a new end-effector for oil filter tightening. During that time, the operator attaches two oil transport pipes on the engine and uses the same nutrunner previously used by the robot to tighten plates that hold the pipes to the engine. After executing these operations, the AGV with the assembled engine and the empty MiR100 leave the collaborative robot assembly station.
6. Error Handling Scenarios
In this section, several different experiments performed on the assembly station depicted in Figure 1 are detailed. The aim is to get an understanding for which errors can be automatically handled, which needs manual intervention, and which need extra error handling constraints. Table 1 shows a summary of the findings. The section remainder of the section examines the different error situations in more detail, grouped by the determined error types. While replanning is the core mechanism for error recovery, the “Recovery type” column of Table 1 describes what steps needed to be taken to arrive at the plan. In this column, “TP” means a replan of the transition planner, “OP” means a replan with the operation planner, “TP w/RTO” means replanning with one or more resources in its time-out state, “TP w/MT” means replanning of the transition planner with maintenance transitions enabled, and “OP w/DO” means replanning using the operation planner with one or more operations unavailable. A new operation plan may lead to a new transition plan and in that case it is also included in the table. In the column “Planning time”, the time, in milliseconds, needed for each replanning task is shown. In the cases where there are several planning actions needed to recover from the current situation, the times should be summed up to find how long it took for the system to be able to recover.

Table 1.
Experiments with error situations.
The experiments do not include the autonomous robot or the lifting tool, which leaves the following seven resources: r1, r2, the connector interfaces on each robot (which attaches to the tools), the cameras on each robot, and the nutrunning tool. Thirty operations are defined which use these resources. Combined with the state of the products (bolts and oil filters), this translates into planning problems for the transition planner that have 72 transitions and 87 Boolean variables (with enumerations flattened).
6.1. Unresponsive Resource (E5–E7)
Resources are continually sending out their current state. This is monitored by SP, which allows detecting if for some reason a resource has stopped responding (see Section 4).
In Experiments E5–E7, the driver software of r2 is forcefully terminated. As a result of this, r2 suddenly stops responding in the middle of its assembly tasks. Since all transitions of a resource are guarded on whether the resource is available, the current goal can no longer be reached and a new plan is computed automatically. However, it is unlikely that the system will simply find a new plan that can complete the current goals, which are most likely related to the missing robot. There may also exist interdependencies between the now disabled r2 and other resources that make it impossible for the system to continue execution. For example, r2 may be physically blocking the path for r1 to complete its tasks, which happens in E6. In E7, the situation becomes even more complex when r2 is also holding the smart tool (orange) necessary to complete assembly, as illustrated in Figure 7.
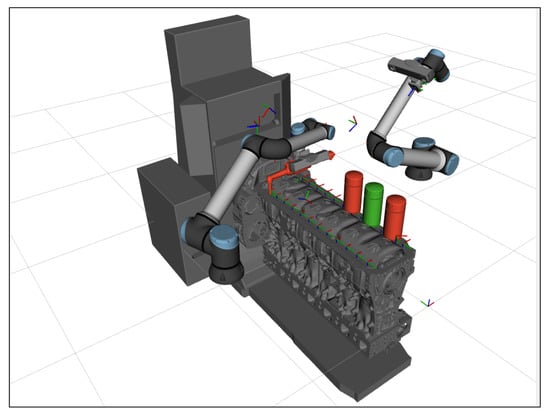
Figure 7.
Simulation showing experiment E7. In this experiment, the robot to the left, r2, has stopped responding for an unknown reason. However, it is still attached to the smart tool (orange), which is needed to complete assembly. Additionally, r2 is physically blocking the space around the bolts.
In E5, r2 fails without being in the way of r1, which eventually leads to a new high level plan that uses only r1 to complete the assembly task. However, as can be seen in Table 1, it requires failing with the transition planner first, which in turn disables the operation for attaching the nutrunning tool. With this operation disabled, the operation planner finds a new plan using only r1.
In E6, r2 is at a the “scan tool” location, above the engine when being disconnected, but it is not yet holding any tool. The operation planner finds a new plan with r2 timed out, where only r1 is used (similar as to Figure 6). This plan seems to work, until r1 should attach its tool. Because r2 cannot be moved, it is not possible to find a transition plan where r1 ends up in the correct position. This is due to safety specifications that forbid the robots from entering shared zones. As in Figure 6, the operation is disabled, which leads to the intention also being disabled. With all intentions disabled, maintenance transitions are enabled and the disabled operations are tried again to see if a solution can be found. If so, the operator is asked to perform the maintenance task after which will re-enable the disabled operation. In the case of E6, r2 must be moved to its home state, from where it is safe to continue execution. To solve the situation in E7, r2 must be manually moved out of the way as well as the tool being put back for r1 to take.
6.2. Expected Task Failures (E8 and E9)
Some tasks are expected to fail occasionally. In SP, these errors are handled by replanning in the same way as handling other errors. For example in E9, the hanging tool is not localized properly by the 3S camera on the robot, something which may be expected to happen occasionally.
The default behavior in SP is to replan once the current goal can not be reached. In the case of E8 and E9, a new plan can be found by replanning which tries the same actions again. However, if the problem is not intermittent, this strategy will fail as it will always retry with the same plan, leading to the same plan being tried over and over. A simple strategy to overcome this is to add counters which makes goals unreachable after a number of (re-)tries to avoid such situations. This forces an error state as the plan can not be reached after having failed n times, and the error can be handled in the same way as for any other error.
In E8, computing a new plan simply involves activating the 3D camera scanner again, while, in E9, both the robot (which needs to move up again before being able to move down with the spinner tool) and the tool get new commands.
6.3. Unexpected Task Failures (E3, E4, and E8)
In E3, the tool change mechanism of robot r2 (to the right in Figure 7) is (physically) broken. As such, it fails to register the proper effect (an input goes high when proper contact is made). When effects fail to happen within a timeout period, they are removed from the planning problem. This is the example depicted in Figure 6. With the effect missing from the planning problem (TP w/ETO), the planner cannot find a way to reach the goal, which in turn disables the operation that posted the goal (OP w/DO). Since the r2 resource is still operational, it can be moved away by the planner and the other, r1, can complete the tasks instead.
In Experiment E4, the failure happens upon releasing the tool. As per the error handling strategy, the following sequence of actions now happen: first, the detach effect transition is removed and the transition planner fails to find a new plan (TP w/ETO), and then a new operation plan is computed with the detach operation disabled (OP w/DO). This also fails as there is no way for the tool to be put back for the other robot to attach to. The intention is put into its error state, maintenance transitions are enabled, and a plan which solves the disabled operation is computed, where a maintenance transition for resetting the tool into its hanging state is included.
6.4. Unexpected Events (E1 and E2)
Consider a localization system that keeps track of the position of the products, which discretizes the position into one of a few known, desired, locations, as well as an unknown position. These data are streamed as measured states, and it may happen that a product is suddenly moved unexpectedly (i.e., without an active effect transition which predicts the move).
Such a sudden change can have large consequences for the other products in the system, for example as a result of sequencing constraints being violated. Products may then need to move “backwards” in the system.
In E2, an oil filter is detected to be mounted before the bolts have been tightened. The oil filters in the system must be mounted only after the ladder frame is moved onto the engine and bolted down. Consider Figure 7 again. This time the two robots are functional, but in this example the problem is that an eager operator has placed the oil filters while the tightening of the bolts is in progress. This violates a sequencing constraint which leads to the system ending up in a forbidden state.
When the system is in a forbidden state, MTs are enabled for the planner and the goal is changed to simply leaving the forbidden state. In this case, there is no way for the robots to remove the oil filter, but there is a MT which removes them.
In E1, the state of an already tightened bolt is undone by an operator, perhaps as a manual intervention. In this case, no specifications were violated and a simple replan is sufficient to solve the problem.
7. Discussion and Conclusions
This paper describes how unforeseen errors can be handled by the Sequence Planner control framework. We show that the system could continue functioning after errors have occurred even though no manual modeling of error situations was done, with the exception of adding a “reset” maintenance transition for each resource and product in the system. Even though the operator needed to be called in four out of nine situations, he or she was given specific tasks to perform in order to help the system continue on its own. Table 1 shows that the situations tried are all solved in under 3 s. This time is negligible compared to the expected rate of errors as well as compared to the time it takes for an operator to intervene, which leads us to believe that the approach could scale to larger systems. Future work will involve studying how the proposed approach scales with more resources as well as for other types of systems.
There are also considerations that need to be taken about the failures that can be handled automatically: Is it always desirable? Consider E5—the current task can be completed by r1 instead of r2 without operator intervention. However, it will be done in a manner that operators may not be familiar with, which leads to safety considerations. Sometimes it may be preferable to simply halt the system until the error has been rectified.
Another problematic topic is when to try a failed action again. If a task has failed n times and is put into an error state, when should we reset the counter? Conversely, what if an effect has timed out? Should these things be performed manually or automatically after a certain time? What about when we detect a state change that relates to the resource in question? This depends very much on the specific situation and is difficult to generalize. What we can do is to make it easy to safely configure such details on a high level.
Author Contributions
Conceptualization, M.D., K.B., and P.F.; methodology, M.D., K.B., and P.F.; software, M.D. and K.B.; writing—original draft preparation, M.D.; writing—review and editing, K.B. and P.F.; and supervision, K.B. and P.F. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been supported by UNIFICATION, Vinnova, Produktion 2030.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bauer, A.; Wollherr, D.; Buss, M. Human-Robot Collaboration: A Survey. Int. J. Humanoid Robot. 2008, 05, 47–66. [Google Scholar] [CrossRef]
- Alterovitz, R.; Koenig, S.; Likhachev, M. Robot Planning in the Real World: Research Challenges and Opportunities. AI Mag. 2016, 37, 76–84. [Google Scholar] [CrossRef]
- Perez, L.; Rodriguez, E.; Rodriguez, N.; Usamentiaga, R.; Garcia, D.F. Robot Guidance Using Machine Vision Techniques in Industrial Environments: A Comparative Review. Sensors 2016, 16, 335. [Google Scholar] [CrossRef] [PubMed]
- Wally, B.; Vyskočil, J.; Novák, P.; Huemer, C.; Šindelář, R.; Kadera, P.; Mazak-Huemer, A.; Wimmer, M. Leveraging Iterative Plan Refinement for Reactive Smart Manufacturing Systems. IEEE Trans. Autom. Sci. Eng. 2020, 18, 230–243. [Google Scholar] [CrossRef]
- Solowjow, E.; Ugalde, I.; Shahapurkar, Y.; Aparicio, J.; Mahler, J.; Satish, V.; Goldberg, K.; Claussen, H. Industrial Robot Grasping with Deep Learning using a Programmable Logic Controller (PLC). arXiv 2020, arXiv:2004.10251. [Google Scholar]
- Morrison, D.; Corke, P.; Leitner, J. Learning robust, real-time, reactive robotic grasping. Int. J. Robot. Res. 2020, 39, 183–201. [Google Scholar] [CrossRef]
- James, S.; Wohlhart, P.; Kalakrishnan, M.; Kalashnikov, D.; Irpan, A.; Ibarz, J.; Levine, S.; Hadsell, R.; Bousmalis, K. Sim-to-real via sim-to-sim: Data-efficient robotic grasping via randomized-to-canonical adaptation networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 12627–12637. [Google Scholar]
- Tittus, M.; Andreasson, S.A.; Adlemo, A.; Frey, J. Fast restart of manufacturing cells using restart points. In Proceedings of the 4th World Automation Congress, Wailea, HI, USA, 11–16 June 2000. [Google Scholar]
- Andersson, K.; Lennartson, B.; Fabian, M. Restarting manufacturing systems; Restart states and restartability. IEEE Trans. Autom. Sci. Eng. 2009, 7, 486–499. [Google Scholar] [CrossRef]
- Bergagård, P.; Fabian, M. Calculating restart states for systems modeled by operations using supervisory control theory. Machines 2013, 1, 116–141. [Google Scholar] [CrossRef]
- Bergagård, P.; Falkman, P.; Fabian, M. Modeling and automatic calculation of restart states for an industrial windscreen mounting station. IFAC-PapersOnLine 2015, 48, 1030–1036. [Google Scholar] [CrossRef]
- Yalcin, A. Supervisory control of automated manufacturing cells with resource failures. Robot. -Comput.-Integr. Manuf. 2004, 20, 111–119. [Google Scholar] [CrossRef]
- Shu, S. Recoverability of discrete-event systems with faults. IEEE Trans. Autom. Sci. Eng. 2014, 11, 930–935. [Google Scholar] [CrossRef]
- Alves, L.V.; Pena, P.N. Secure Recovery Procedure for Manufacturing Systems using Synchronizing Automata and Supervisory Control Theory. IEEE Trans. Autom. Sci. Eng. 2020. [Google Scholar] [CrossRef]
- Knepper, R.A.; Tellex, S.; Li, A.; Roy, N.; Rus, D. Recovering from failure by asking for help. Auton. Robot. 2015, 39, 347–362. [Google Scholar] [CrossRef]
- Sankaran, B.; Pitzer, B.; Osentoski, S. Failure recovery with shared autonomy. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Algarve, Portugal, 7–12 October 2012; pp. 349–355. [Google Scholar]
- Erős, E.; Dahl, M.; Hanna, A.; Götvall, P.L.; Falkman, P.; Bengtsson, K. Development of an Industry 4.0 Demonstrator Using Sequence Planner and ROS2. In Robot Operating System (ROS); Springer: Berlin, Germany, 2020; pp. 3–29. [Google Scholar]
- Quigley, M.; Faust, J.; Foote, T.; Leibs, J. ROS: An open-source Robot Operating System. In Proceedings of the ICRA Workshop on Open Source Software, Kobe, Japan, 12–17 May 2009; Volume 3. [Google Scholar]
- Dahl, M.; Bengtsson, K.; Fabian, M.; Falkman, P. Guard extraction for modeling and control of a collaborative assembly station. In Proceedings of the IFAC Workshop on Discrete Event Systems, WODES, Virtual Conference, 11–13 November 2020. [Google Scholar]
- Dahl, M.; Erős, E.; Hanna, A.; Bengtsson, K.; Fabian, M.; Falkman, P. Control components for Collaborative and Intelligent Automation Systems. In Proceedings of the 2019 24th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Zaragoza, Spain, 10–13 September 2019; pp. 378–384. [Google Scholar] [CrossRef]
- Erős, E.; Dahl, M.; Hanna, A.; Albo, A.; Falkman, P.; Bengtsson, K. Integrated virtual commissioning of a ROS2-based collaborative and intelligent automation system. In Proceedings of the 2019 24th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Zaragoza, Spain, 10–13 September 2019; pp. 407–413. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, S.; Wang, J.; Xu, K.; Lei, T.; Zhang, H.; Wang, X.; Liu, D.; Si, J. Control strategy of stable walking for a hexapod wheel-legged robot. ISA Trans. 2021, 108, 367–380. [Google Scholar] [CrossRef]
- Rösmann, C.; Makarow, A.; Bertram, T. Online Motion Planning Based on Nonlinear Model Predictive Control with Non-Euclidean Rotation Groups. arXiv 2020, arXiv:2006.03534. [Google Scholar]
- Testa, A.; Camisa, A.; Notarstefano, G. ChoiRbot: A ROS 2 Toolbox for Cooperative Robotics. arXiv 2020, arXiv:2010.13431. [Google Scholar]
- Cashmore, M.; Fox, M.; Long, D.; Magazzeni, D.; Ridder, B.; Carreraa, A.; Palomeras, N.; Hurtós, N.; Carrerasa, M. ROSPlan: Planning in the Robot Operating System. In Proceedings of the Twenty-Fifth International Conference on International Conference on Automated Planning and Scheduling, ICAPS’15, Jerusalem, Israel, 7–11 June 2015; pp. 333–341. [Google Scholar]
- Rovida, F.; Crosby, M.; Holz, D.; Polydoros, A.S.; Großmann, B.; Petrick, R.P.A.; Krüger, V. SkiROS—A Skill-Based Robot Control Platform on Top of ROS. In Robot Operating System (ROS): The Complete Reference (Volume 2); Springer International Publishing: Cham, Switzerland, 2017; pp. 121–160. [Google Scholar] [CrossRef]
- Paxton, C.; Hundt, A.; Jonathan, F.; Guerin, K.; Hager, G.D. CoSTAR: Instructing collaborative robots with behavior trees and vision. In Proceedings of the 2017 IEEE International Conference on Robotics and Automation (ICRA), Singapore, 29 May–3 June 2017; pp. 564–571. [Google Scholar] [CrossRef]
- Colledanchise, M.; Ögren, P. Behavior Trees in Robotics and AI: An Introduction; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Dahl, M. Preparation and Control of Intelligent Automation Systems; Doktorsavhandlingar vid Chalmers tekniska högskola. Ny serie, no: 4913; Institutionen för elektroteknik, Chalmers tekniska högskola: Gothenburg, Sweden, 2021. [Google Scholar]
- Cavada, R.; Cimatti, A.; Dorigatti, M.; Griggio, A.; Mariotti, A.; Micheli, A.; Mover, S.; Roveri, M.; Tonetta, S. The nuXmv Symbolic Model Checker. In Proceedings of the 26th International Conference on Computer Aided Verification (CAV), Vienna, Austria, 18–22 July 2014; pp. 334–342. [Google Scholar]
- Clarke, E.M., Jr.; Grumberg, O.; Kroening, D.; Peled, D.; Veith, H. Model Checking, 2nd ed.; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Pnueli, A. The temporal logic of programs. In Proceedings of the 18th Annual Symposium on Foundations of Computer Science (SFCS), Providence, RI, USA, 31 October–2 November 1977; pp. 46–57. [Google Scholar]
- Biere, A.; Cimatti, A.; Clarke, E.; Zhu, Y. Symbolic model checking without BDDs. In Proceedings of the International Conference on Tools and Algorithms for the Construction and Analysis of Systems, Amsterdam, The Netherlands, 22–28 March 1999; pp. 193–207. [Google Scholar]
- Weld, D.S. An introduction to least commitment planning. AI Mag. 1994, 15, 27. [Google Scholar]
- Knoblock, C.A.; Tenenberg, J.D.; Yang, Q. Characterizing Abstraction Hierarchies for Planning. In Proceedings of the 9th National Conference on Artificial Intelligence, Anaheim, CA, USA, 14–19 July 1991; pp. 692–697. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).