Abstract
Electric cars are typically subject to highly variable operational conditions, especially when they drive in urban environments. Consequently, the efficiency of the electric motors may degrade significantly, possibly leading to lower autonomy and higher running costs. Latest advances in power electronics and motion control have paved the way to the development of novel architectures of full electric power transmissions. In this paper, a dual-motor solution is proposed where two smaller motors are coupled via a planetary gear, in contrast to the standard configuration that uses one larger motor directly connected to the drive wheels with a fixed ratio reducer. The dual-motor architecture guarantees that both motors operate in the vicinity of their optimal working range, resulting in a higher overall energy efficiency. The technical requirements and the control strategy of the dual-motor system are selected through a parametric optimization process. Results included were obtained from extensive simulations performed over different standard driving cycles, showing that the dual-motor power transmission generally outperforms the single-motor counterpart with an average efficiency improvement of about 9% that is reached in both the power delivery and regeneration stage.
1. Introduction
Full-electric vehicles (EVs) are increasingly attracting attention as they promise to offer advantages over traditional internal combustion engine vehicles in terms of environmental impact and improved efficiency [1]. However, some issues need to be addressed before a widespread diffusion of EVs can be achieved. One of the main challenges refers to the limited autonomy that can be obtained through the development of efficient transmission systems and their integration with existing EV powertrains. Electric motors can be directly connected to the drive wheels of EVs, or a transmission system can be placed between the motor and the wheels to optimize the vehicle performance [2]. Currently, manufacturers tend to adopt single-speed transmission systems, as they ensure minimization of the cost, volume, energy loss, and drivetrain mass. However, with a fixed ratio transmission system, EV powertrain performance significantly depends on the performance of the traction motor, which is not equally efficient in all speed ranges [3,4,5]. The further an electric motor moves from the nominal operating point, the higher the efficiency drop. This results in a significant energy consumption during cycles with highly changing conditions (e.g., urban driving cycles [6]).
Recent advances in power electronics for drive motors have made available new motion controllers that allow more complex algorithms and architectures to be adopted in the pursuit of improved energy efficiency for electric vehicles [7]. In previous research [8,9], the energy efficiency over a given standard driving cycle was characterized against a few representative points, and the design optimization was performed with respect to these points. Similarly, in [10], a procedure was proposed to evaluate the most effective design areas by means of a series of representative points taken from the map of a permanent-magnet-assisted synchronous reluctance motor, which have been considered for the global optimization.
Propulsion systems that use a series of gearless electrical continuously variable transmissions (E-CVT) were presented in [11]. A differential evolution algorithm was used in conjunction with the finite element method to gain optimal torque and energy efficiency, and to reduce, at the same time, the torque ripples of the E-CVT.
Other optimization approaches can be found in [12], where the design of an induction motor was studied by applying a genetic algorithm. An evolutionary optimization procedure was proposed in [13] for drive motors of electric vehicles that adopts an adaptive differential evolution algorithm involving dynamic variation of the mutation factor that is combined with finite-element (FE) and circuit models.
Various attempts have been discussed to introduce novel architectures of power transmissions that allow the working range of an electric motor to be kept in the vicinity of its point of best efficiency [14], including the use of continuous variable transmission [15] also in combination with a series spring system [16]. A system with an infinitely variable transmission has been also proposed in [17] to maximize the efficiency of an electric motor.
With the goal of maximizing the energy stored by a wind system, a planetary gear solution was proposed in [18], by investigating the analytical relationship that maps the torque with the speed of the wind turbine. The use of a planetary gear also allows the power of two motors to be combined to reduce transmission nonlinearities [19]. Finally, in [20], a strategy was developed to adaptively split the load between two sources for an electric vehicle adopting a hybrid energy storage system that can effectively reduce the battery power stress.
In this paper, we propose a powertrain solution for EVs that includes two electric motors and a planetary gear, which allows the load to be distributed between the two motors. The aim is to increase the energy efficiency of the vehicle, by optimizing the combined speeds of two motors. Such a solution is possible thanks to the additional degree of freedom provided by the planetary combiner. The control strategy for the power distribution of energy between the motors is a decisive factor in the minimization of power losses of the propulsion system. The proposed power split control strategy has the capacity to achieve vehicle speeds either working only with one electric motor (relying on a brake system) and working with two electric motors at the same speed, or working with two electric motors at different speeds. Figure 1 shows a comparison between the functional scheme of the standard single-motor, single-speed powertrain (Figure 1a) and the proposed dual-motor multispeed alternative (Figure 1b). In the standard configuration, the speed of the single motor is tightly connected with the speed of the car. Therefore, when the vehicle drives at low speed, the traction motor operates at low efficiency. In contrast, in the proposed dual-motor configuration, the speed range of the two smaller drive motors can be uncoupled from that of the vehicle, ensuring the best efficiency for both motors for any load condition.

Figure 1.
Functional schemes of the standard single-motor, single-speed powertrain (a) and the proposed dual-motor multispeed system (b).
The main contributions of this research are: (i) evaluation of the increase in the energy efficiency of the proposed powertrain over different standard drive cycles; (ii) definition of the optimal nominal requirements of the planetary gear and electric motors; (iii) a control strategy to set the operating condition of the two electric motors in order to maximize the efficiency of the powertrain. While the idea of a dual-motor multispeed powertrain was preliminarily introduced in [21], this paper represents a substantial extension that introduces a discussion on: (a) system operations during regeneration stages; (b) the adoption of two different configurations of planetary gear that use a single-planet and a double-planet set; (c) the mechanical efficiency of the planetary gear that is explicitly modeled; (d) the performance evaluation of the powertrain for different standard driving cycles; (e) the optimal control strategy for the dual-motor planetary coupling based on a genetic algorithm.
As a final remark, it should be noted that today many hybrid vehicles use a planetary gear transmission. For example, in the Toyota Prius, the combustion engine is connected to the carrier while one generator is connected to the sun gear. Finally, the ring gear is coupled to the final drive, as is a second electric motor [22]. During normal operations, the ring gear velocity is determined by the vehicle speed, while the first motor speed can be controlled with the aim to keep the combustion engine in its best efficiency window. Other recent applications can be found in robotics, where the use of multiple motors for a single revolute joint is evaluated in [23], whereas a customized planetary gear train for human limb assistance and replication is discussed in [24]. Here, we investigate the use of a planetary gear for the power transmission of full electric vehicles with the aim to uncouple the speed range of two electric motors from that of the car and keep both electric machines in their optimal efficiency window.
2. Powertrain Modeling
In the proposed dual-motor configuration, the planetary gear plays a critical role as it allows the speed range of the car to be uncoupled from that of the two drive motors. With reference to Figure 2, a typical planetary gearbox comprises a sun gear that is attached to the first motor, a ring gear that is connected to the second motor, and a carrier that is attached to the external load. Two different configurations of epicyclic gear can be considered that use a single or a double planet set, as shown, respectively, on the left and right of Figure 2.
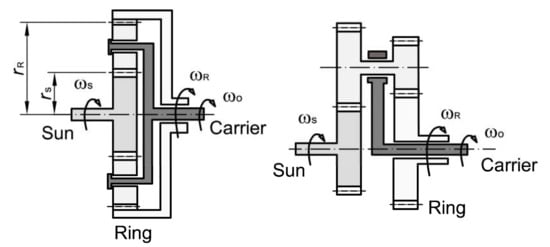
Figure 2.
Planetary gears can adopt a single-planet set (left) or a double-planet set (right).
First, the basic kinematic relationships of the planetary gear train are recalled, [25], as follows
where ωS, ωR, ωo are the velocities, respectively, of the sun, the ring, and the carrier of the planetary gear, ρ = rR/rS the ratio between the primitive radius of ring and sun, and i = ωR/ωS. Given ρ that defines the planetary gear geometry, the speed of the carrier ωo results as the weighted sum of the velocities of the sun and the ring, ωS and ωR; according to Equation (3) that is the only kinematic constraint of the system. Therefore, once the carrier velocity ωo is set by the required vehicle velocity, there is one remaining degree of freedom, i, that defines the relationship between the sun and the ring speed according to Equations (1) and (2), and that is the variable used in the parametric optimization process described later.
Looking at the energy balance of the system, the following relationship holds
where TS and TR refer, respectively, to the sun and ring torque, To is the torque request, and ηpd is the efficiency of the planetary gear. Equation (4) holds true for steady-state conditions. However, it can be considered a good approximation during transients as well if the motor inertia is small enough.
The efficiency of the planetary gear can be defined following [26] as
where refers to the efficiency of the equivalent ordinary gear train.
One important aspect of this study refers to the definition of the efficiency of the dual-motor powertrain, . With reference to Figure 3, can be expressed during positive power supply as
where PmeR/S is the mechanical power delivered by the ring/sun motor, and PelR/S and the corresponding electrical power and single motor efficiency, respectively. Note that in this analysis the loss in the power converters is not explicitly considered.
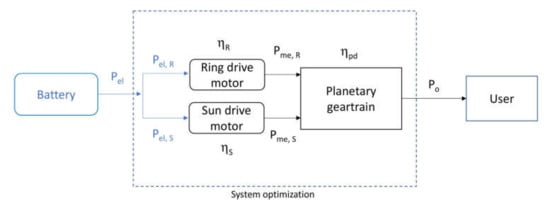
Figure 3.
Block diagram describing the power flow of the dual-motor powertrain.
During the regenerative stage, the powertrain efficiency can be defined instead as
where is the ring/sun regenerative motor efficiency.
3. Electric Motor and Load Modeling
The electric motor map needs to be defined. Without loss of generality, a normalized efficiency map can be obtained for a standard induction motor [27], as shown in Figure 4, under the assumption of relatively limited variation in the rated power. This map can be used for both the power delivery and regeneration stages without losing much accuracy.
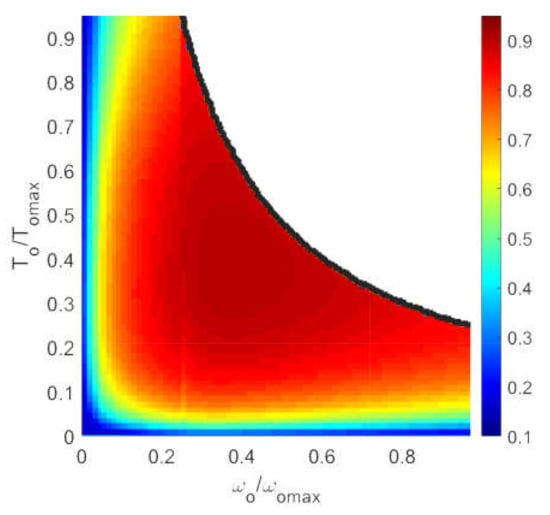
Figure 4.
Efficiency map of a standard induction electric motor normalized with respect to maximum angular speed and torque.
Load profiles for electric vehicles are described by various standard drive cycles (DC); for example, the Artemis urban cycle that is shown in Figure 5 in terms of velocity, torque, and power requirement. The Artemis DC develops for about 4.8 km during a 993 s-time window with an average 17.6 km/h velocity.
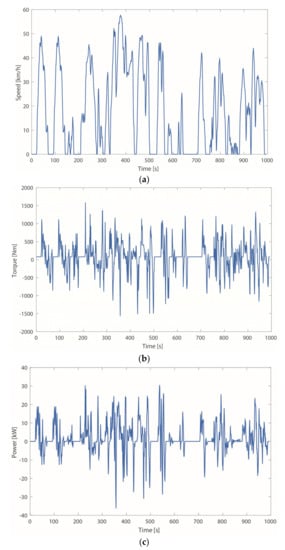
Figure 5.
Load profile prescribed by the Artemis urban cycle: (a) speed demand; (b) corresponding torque; and (c) power demand.
The power and torque demand, respectively, Po and To, can be obtained under the assumption of planar driving as:
where M is the vehicle apparent mass, and R the angular velocity and radius of the tires, and fv the rolling resistance, whereas define the aerodynamic resistance. The values of the vehicle parameters used in this research are collected in Table 1. The maximum vehicle speed is assumed as 115 km/h.

Table 1.
Vehicle parameters.
The load profile of the Artemis DC, expressed in terms of the operating pair (), is overlaid over the normalized efficiency map of the single-motor architecture in Figure 6, respectively, for the power supply (Figure 6a) and regeneration (Figure 6b) phase. It is interesting to note that when the vehicle is required to drive at low speed and high torque, the efficiency of the single-motor powertrain tends to degrade, as is apparent from the associated color map.
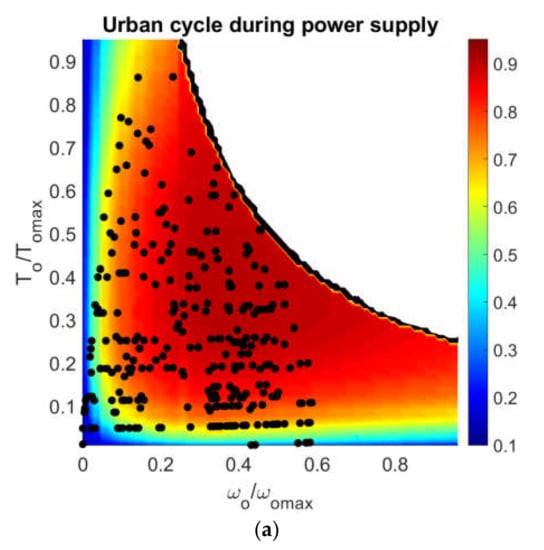
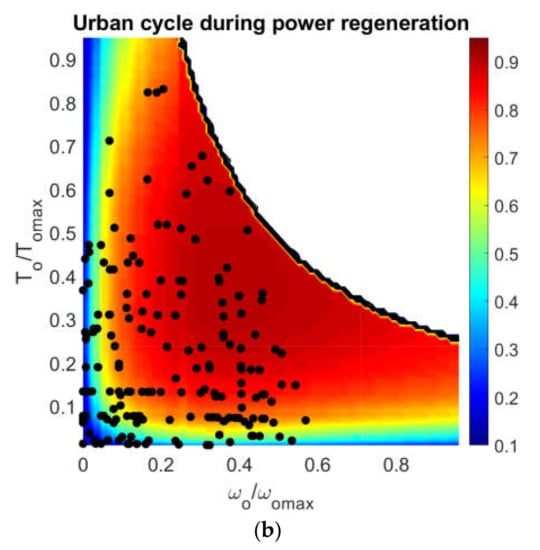
Figure 6.
Working points of the Artemis drive cycle (DC) overlaid over the efficiency map during: (a) power supply; and (b) power regeneration.
4. Controller and Design Optimization
In this research, two powertrains are contrasted: (a) one electric motor that is directly connected to the wheels providing the user-required power; and (b) two electric motors integrated with a planetary gear train that provide equal power to the single-motor powertrain.
The idea is that by uncoupling the load velocity profile of the vehicle with that of the two electric motors via the planetary gear, the powertrain efficiency can be improved. The control strategy and the technical requirements of the dual-motor powertrain can be defined through a two-step optimization process.
First, the strategy to set the best speed of the two motors for any given operating point is defined. Then, the geometrical constraint of the planetary gear and the power rates of the electrical motors are selected to provide optimal results over a standard drive cycle. In more detail, the two optimization stages are:
- Optimization of the ratio i that maximizes the efficiency ηtot for each operating pair (ωo, To), given [ρ ωR,max ωS,max].
- Optimization of the parameter set [ρ, ωR,max, ωS,max] to obtain the highest average efficiency over an urban cycle, ηcyc.
4.1. Dual-Motor System Control
Given the current load demand, the combination of motor speeds that is the ratio i between them needs to be chosen to ensure the best efficiency for a fixed value of the planetary gear ratio, ρ, and a maximum speed of the ring and sun motor. The functions to be maximized for the power delivery and regeneration stage are, respectively:
subject to the constraints expressed by Equations (2) and (4). In order to find the best solution, a genetic algorithm (GA) is adopted that is one type of global, derivative-free, and stochastic approach widely used to solve optimization problems in the design of electric vehicles [24]. The GA algorithm keeps a random population of N individuals (here 25), each defining a speed ratio i in the range of interest [0, 100]. For a given individual, the decoding procedure results in a powertrain efficiency that is evaluated according to Equation (5). The selection stage is performed using selection and crossover.
Standard tournament selection is applied with a given tournament size (typically 3–5) and a tournament probability of pt (around 0.6–0.8), whereas single-point crossover with a probability of pcross (around 0.8–0.9) is adopted. Once two new individuals are formed, mutation is enforced with probability of pmut (about 0.06–0.1) with either creep mutation (probability of 0.5 and creep rate of 10% of the full range) or full-range mutation (probability of 0.5). In addition, to avoid the best speed ratio found so far being lost in the pursuit of the next generation, this speed ratio is passed to the next generation according to the concept of elitism.
Results obtained from the first GA-based step of the optimization are shown in Figure 7, where the efficiency of the optimized dual-motor powertrain, ηtot (bottom plot), is compared against that of the single-motor, η0 (upper plot). As expected, the largest discrepancy can be observed for low speed and high torque. The highest difference of about 0.24 (0.27 for regeneration) is found for a torque and a speed ranging, respectively, between 55% and 96% of the maximum torque and between 5% and 22% of the maximum speed.
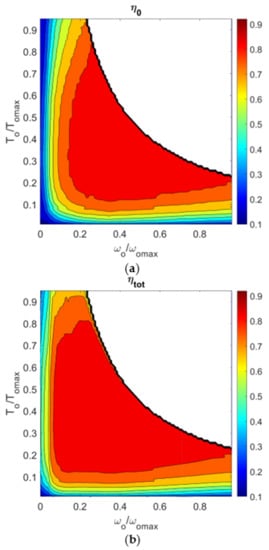
Figure 7.
Comparison of the efficiency map provided by the single-motor (a) and dual-motor (b) powertrains (ρ = 3.5, ωR,max = 0.8 ωomax and ωS,max = 1.7 ωomax).
A direct comparison of the dual-motor powertrain with the single-motor configuration is shown in Figure 8 in terms of relative energy efficiency improvement obtained over the Artemis DC. It is apparent that the better performance is from the dual-motor system that ensures better energy management with an increase in the efficiency that ranges from 0.4% up to 8.4%.
Figure 8.
Relative percentage improvement in efficiency obtained by the dual-motor powertrain compared with the single-motor powertrain over the Artemis driving cycle (ρ = 3.5, ωR,max = 0.8 ωo,max, and ωS,max = 1.7 ωomax).
4.2. Powertrain Design
The previous optimization step can be iterated by varying the planetary gear ratio and the maximum velocity of the ring and sun motor. The best value for the parameter set [ρ, ωR,max, ωS,max] can then be selected as the one that maximizes the average efficiency, ηcyc, over the entire Artemis DC. ηcyc is introduced as the ratio between the overall mechanical energy delivered during the urban cycle and the corresponding electric energy drawn by the motors:
In detail, the planetary gear ratio ρ has been changed from 2 to 4.6 for the single-planet epicyclical combiner (Figure 2a), whereas the [−4.5, −2] range has been inspected for the double-planet set configuration (Figure 2b). The maximum velocity of the ring motor (ωmaxR) has been progressively incremented in the window [ωo/2, ωo·(ρ + 1)/ρ]. The upper limit corresponds to the maximum speed of the ring motor when the power of the sun motor is null. It is worth noting that, when the maximum velocity of the ring is set, in turn, the highest speed of the sun (ωmaxS) is also determined since the power of the sun and the ring motors must be equal to the user-required power.
Results obtained from the powertrain design optimization are shown in Figure 9. While the DC average efficiency is little affected by ρ and ωmaxR when the single planet gear set is adopted (Figure 9a), a larger impact is observed for the double-planet gear. Table 2 collects the optimized values of ωmaxR, ωmaxS, TmaxR, TmaxS and ρ, for both planetary gear types, showing that the dual-motor powertrain generally outperforms the single-motor counterpart, ηo,avg, with an improvement in the overall efficiency estimated by Equation (11), ηcyc,opt, of about 8.8% (8.9% during regeneration) for the single-planet and of about 8.7% (8.6% during regeneration) for the double-planet in the power delivery stage.
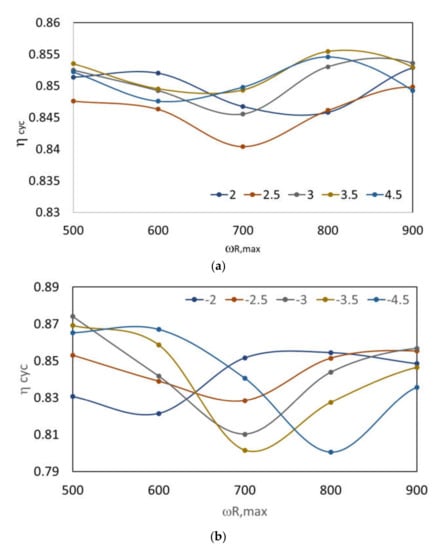
Figure 9.
Average efficiency over the Artemis DC by varying ρ and ωmaxR: (a) single-planet gear; (b) double-planet gear.

Table 2.
Powertrain optimal design.
Note also that the optimal powertrain design is achieved when the two drive motors have a nominal power equal to 38% (22%) and 62% (78%) of the maximum power required by the vehicle, respectively, for the drive and sun motor, when the single- (double) planet combiner is adopted.
4.3. Optimization Results
Since the time in which the motor remains in each efficiency region is a key parameter to ensure the best efficiency of the motor, the percentage driving cycle time is shown in Figure 10 for ten discrete values of the efficiency range. Following the proposed approach, the transmission system operates with an efficiency greater than 0.8 for more than 70% of the time, which is a clear improvement compared to the standard single-motor system that ensures the same efficiency range for 42% of the driving cycle.
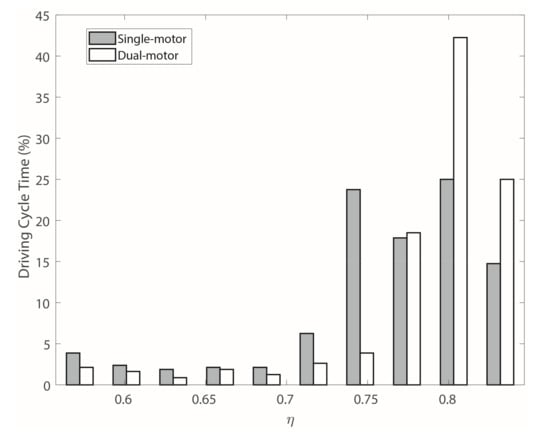
Figure 10.
Distribution of the driving cycle time as a function of the efficiency for the single- and dual-motor power transmissions.
Moreover, Figure 11 shows the velocity profile of the ring and sun motor (normalized with respect to the corresponding maximum value) that minimizes the energy consumption over the Artemis DC with reference to the optimized single-planet powertrain.
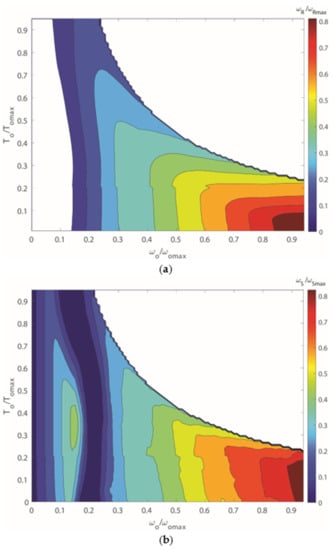
Figure 11.
Optimal speed profiles that ensure efficiency maximization for the power supply stage over the Artemis DC: (a) ring motor; and (b) sun motor.
As seen from this figure, the sun motor is the only one that operates at low vehicle speed (i.e., ωo < 0.15 ωo,max), whereas the ring motor is blocked. In this working condition, the planetary gear works as a fixed-ratio reducer. At high vehicle velocity (i.e., ωo > 0.7 ωo,max), power is supplied simultaneously by both motors, as expected due to the design constraint that imposes that the maximum power demand must be balanced by the sum of the power delivered by the two motors. A similar behavior can be observed as well for the regeneration stage.
Finally, the power distribution between the sun and ring motor is shown in Figure 12 for the first 100 s of the Artemis DC. During the positive power stages, the sun motor is the only one active when low power and high torque demand is required. Conversely, for high speed and low torque (constant high speed), the ring motor is the only one delivering power. Both motors operate simultaneously when about 85% of the maximum power is required.
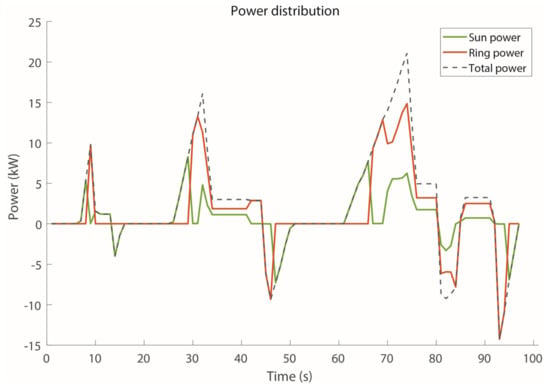
Figure 12.
Power split between sun and ring motors in the Artemis DC (first 100 s).
4.4. Performance over Different Driving Cycles
For a general evaluation of the optimized dual-motor powertrain, its performance is now estimated for various standard driving cycles, namely the urban driving cycle ECE-15, the Artemis rural road cycle, and the Artemis motorway cycle [28]. For each cycle, the relative percentage efficiency improvement obtained from the dual-motor powertrain with respect to the single-motor configuration is calculated considering both operating conditions of power delivery and regeneration. In addition, the two possible embodiments of the dual-motor transmission using single- and double-planet set are evaluated. Results are collected in Table 3, showing that the proposed dual-motor architecture consistently outperforms the standard power transmission with an average increment of, respectively, 6.5% (11.3% for regeneration) and 7.4% (12.3% for regeneration) when the single-planet and the double-planet set are adopted. The largest efficiency gain is recorded for the ECE-15 urban DC using the double-planet set with a 10.9% improvement.

Table 3.
Percentage efficiency gain obtained from the proposed dual-motor powertrain compared with standard single-motor transmission for various cycles.
5. Conclusions
A novel architecture for full-electric vehicles was proposed that combines two motors through a planetary gear, allowing both motors to operate in their high efficiency range. This solution fits very well city cars that are characterized by a highly variable operating range. An optimization process allowed the controller and the system design to be set. The proposed dual-motor multispeed powertrain was compared with a standard single-motor, single-speed transmission, showing better efficiency in various driving cycles. As an example, for the Artemis urban cycle, an average improvement of about 9% was found for both the power supply and regeneration phase, ensuring the same maximum velocity, mechanical torque, and power. Similar results were obtained from other driving cycles. As expected, the largest improvements were observed at low speeds and large torques, attesting to the feasibility of the system for urban electric vehicles and, in general, for vehicles that operate at different speeds in diverse driving conditions.
Two types of planetary gears were investigated that feature a single-planet and double-planet set. They provided comparable results with a slight improvement obtained with the double-planet gear.
The dual-motor powertrain and the associated optimization framework can be potentially used to improve efficiency performance and thus autonomy of full-electric vehicles.
Future developments of this research will be devoted to validate experimentally the dual-motor powertrain in a laboratory test bench and on a vehicle test bed.
Author Contributions
Both authors equally contributed to the conceptualization, methodology, and writing of the paper. All authors have read and agreed to the published version of the manuscript.
Funding
The research leading to these results has received funding from the Horizon 2020 European Commission under grant agreement n. 821988 ADE.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| rR | ring gear radius |
| rS | sun gear radius |
| rP | carrier radius |
| ωR | ring motor angular velocity |
| ωS | sun motor angular velocity |
| ωo | angular speed required by the user (speed of the carrier) |
| i | ratio between the angular velocity of the ring and the sun (ωR/ωS) |
| TR | ring motor torque |
| TS | sun motor torque |
| To | torque required by the user (torque on the carrier) |
| ρ | planetary gear ratio |
| ωmaxS | sun motor maximum angular velocity |
| TmaxS | sun motor maximum torque |
| PmaxS | sun motor maximum power |
| ωmaxR | ring motor maximum angular velocity |
| TmaxR | ring motor maximum torque |
| PmaxR | ring motor maximum power |
| Tomax | maximum torque of the carrier |
| ωomax | carrier maximum angular speed |
| ηS | sun motor efficiency (power delivery) |
| ηR | ring motor efficiency (power delivery) |
| ηpd | planetary gear mechanical efficiency |
| ηtot | efficiency of the dual-motor transmission for a given working point (power delivery) |
| ηtot, opt | optimized efficiency of the dual-motor transmission for a given working point (power delivery) |
| η0 | efficiency of the single-motor transmission for a given working point (power delivery) |
| ηcyc | average efficiency of the optimized dual-motor transmission over a driving cycle (power delivery) |
| ηcyc, max | average efficiency of the optimized dual-motor transmission over a driving cycle, given the best values of ρ, ωmaxS, ωmaxR |
| ηS, reg | sun motor efficiency (power regeneration) |
| ηR, reg | ring motor efficiency (power regeneration) |
| η0,reg | efficiency of the single-motor transmission for a given working point (power regeneration) |
| ηcyc, reg | average efficiency of the optimized dual-motor transmission over a driving cycle (power regeneration) |
| ηcyc, max, reg | average efficiency of the optimized dual-motor transmission over a driving cycle (power regeneration), given the best values of ρ, ωmaxS, ωmaxR |
References
- Chu, W.; Zhu, Z.; Zhang, J.; Liu, X.; Stone, D.; Foster, M. Investigation on Operational Envelops and Efficiency Maps of Electrically Excited Machines for Electrical Vehicle Applications. IEEE Trans. Magn. 2015, 51, 1–10. [Google Scholar] [CrossRef]
- Wang, H.; Song, X.; Saltsman, B.; Hu, H. Comparative Studies of Drivetrain Systems for Electric Vehicles; SAE Technical Paper 2013-01-2467; 2013. Available online: https://www.sae.org/publications/technical-papers/content/2013-01-2467/ (accessed on 11 March 2021).
- Derammelaere, S.; Dereyne, S.; Defreyne, P.; Algoet, E.; Verbelen, F.; Stockman, K. Energy efficiency measurement procedure for gearboxes in their entire operating range. In Proceedings of the IEEE Industry Application Society Annual Meeting, Vancouver, BC, Canada, 5–9 October 2014. [Google Scholar]
- Verstraten, T.; Furnémont, R.; López-García, P.; Rodriguez-Cianca, D.; Cao, H.; Vanderborght, B.; Lefeber, D. Modeling and design of an energy-efficient dual-motor actuation unit with a planetary differential and holding brakes. Mechatronics 2018, 49, 134–148. [Google Scholar] [CrossRef]
- De Pinto, S.; Chatzikomis, C.; Sorniotti, A.; Mantriota, G. Comparison of Traction Controllers for Electric Vehicles with On-Board Drivetrains. IEEE Trans. Veh. Technol. 2017, 66, 6715–6727. [Google Scholar] [CrossRef]
- Stockman, K.; Dereyne, S.; Defreyne, P.; Algoet, E.; Derammelaere, S. Efficiency Measurement Campaign on Gearboxes. In Proceedings of the Energy Efficiency in Motor Driven Systems, Henslink, Denmark, 15–17 September 2015. [Google Scholar]
- De Santiago, J.; Bernhoff, H.; Ekergård, B.; Eriksson, S.; Ferhatovic, S.; Waters, R.; Leijon, M. Electrical motor drivelines in commercial all-electric vehicles: A review. IEEE Trans. Veh. Technol. 2012, 61, 475–484. [Google Scholar] [CrossRef]
- Chen, L.; Wang, J.; Lazari, P.; Chen, X. Optimizations of a permanent magnet machine targeting different driving cycles for electric vehicles. In Proceedings of the 2013 International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013; pp. 1–6. [Google Scholar]
- Lazari, P.; Wang, J.; Chen, L. A Computationally Efficient Design Technique for Electric-Vehicle Traction Machines. IEEE Trans. Ind. Appl. 2014, 50, 3203–3213. [Google Scholar] [CrossRef]
- Carraro, E.; Morandin, M.; Bianchi, N. Traction PMASR Motor Optimization According to a Given Driving Cycle. IEEE Trans. Ind. Appl. 2016, 52, 209–216. [Google Scholar] [CrossRef]
- Mao, Y.; Niu, S.; Yang, Y. Differential Evolution-Based Multiobjective Optimization of the Electrical Continuously Variable Transmission System. IEEE Trans. Ind. Electron. 2018, 65, 2080–2089. [Google Scholar] [CrossRef]
- Mallik, S.; Mallik, K.; Barman, A.; Maiti, D.; Biswas, S.; Deb, N.; Basu, S. Efficiency and Cost Optimized Design of an Induction Motor Using Genetic Algorithm. IEEE Trans. Ind. Electron. 2016, 64, 9854–9863. [Google Scholar] [CrossRef]
- Sarigiannidis, A.; Beniakar, M.; Kladas, A. Fast Adaptive Evolutionary PM Traction Motor Optimization Based on Electric Vehicle Drive Cycle. IEEE Trans. Veh. Technol. 2017, 66, 5762–5774. [Google Scholar] [CrossRef]
- Ramelan, L.; Firmansyah, E.; Liu, T.; Tseng, S.; Hsu, J. An improved maximum efficiency control for dual-motor drive systems. In Proceedings of the 2014 6th International Conference on Information Technology and Electrical Engineering (ICITEE), Yogyakarta, Indonesia, 7–8 October 2014. [Google Scholar]
- Ruan, J.; Walker, P.D.; Wu, J.; Zhang, N.; Zhang, B. Development of Continuously Variable Transmission and Multi-Speed Dual-Clutch Transmission for Pure Electric Vehicle. Adv. Mech. Eng. 2018, 10, 1–15. [Google Scholar] [CrossRef]
- Mooney, L.; Herr, H. Continuously-variable series-elastic actuator. In Proceedings of the IEEE 13th International Conference on Rehabilitation Robotics (ICORR), Seattle, WA, USA, 24–26 June 2013; pp. 1–6. [Google Scholar]
- Bottiglione, F.; De Pinto, S.; Mantriota, G.; Sorniotti, A. Energy Consumption of a Battery Electric Vehicle with Infinitely Variable Transmission. Energies 2014, 7, 8317–8337. [Google Scholar] [CrossRef]
- Mantriota, G. Power split transmissions for wind energy systems. Mech. Mach. Theory 2017, 117, 160–174. [Google Scholar] [CrossRef]
- Ontañón-Ruiz, J.; Daniel, R.; McǍree, P. On the use of differential drives for overcoming transmission nonlinearities. J. Robot. Syst. 1998, 15, 641–660. [Google Scholar] [CrossRef]
- Sun, L.; Feng, K.; Chapman, C.; Zhang, N. An Adaptive Power-Split Strategy for Battery–Supercapacitor Powertrain—Design, Simulation, and Experiment. IEEE Trans. Power Electron. 2017, 32, 9364–9375. [Google Scholar] [CrossRef]
- Mantriota, G.; Reina, G. Efficient Power-Split Powertrain for Full Electric Vehicles. In Advances in Italian Mechanism Science; Mechanisms and Machine Science; Niola, V., Gasparetto, A., Eds.; Springer: Cham, Switzerland, 2021; Volume 91. [Google Scholar]
- Mi, C.; Masrur, M.A. Hybrid Electric Vehicles; Wiley & Sons Ltd.: New York, NY, USA, 2018. [Google Scholar]
- Verstraten, T.; Furnémont, R.; López-García, P.; Rodriguez-Cianca, D.; Vanderborght, B.; Lefeber, D. Kinematically redundant actuators, a solution for conflicting torque–speed requirements. Int. J. Robot. Res. 2019, 38, 612–629. [Google Scholar] [CrossRef]
- Crispel, S.; López-García, P.; Verstraten, T.; Saerens, E.; Lefeber, D. Introduction of a redundant actuator using planetary gear trains for human centred robotics. MATEC Web Conf. 2020, 317, 01003. [Google Scholar] [CrossRef]
- De Carlo, M.; Mantriota, G. Electric vehicles with two motors combined via planetary gear train. Mech. Mach. Theory 2020, 148, 103789. [Google Scholar] [CrossRef]
- Mantriota, G.; Pennestrì, E. Theoretical and experimental efficiency analysis of multi-degrees-of-freedom epicyclic gear trains. Multibody Syst. Dyn. 2003, 9, 389–408. [Google Scholar] [CrossRef]
- Li, K.; Cui, S.; Bouscayrol, A.; Hecquet, M. Analytical Derivation of Efficiency Map of an Induction Machine for Electric Vehicle Applications. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 27–30 August 2018. [Google Scholar]
- Nicola, R. The Different Driving Cycles. Available online: https://www.car-engineer.com/the-different-driving-cycles/ (accessed on 24 October 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).