Design and Optimization of a Centrifugal Pump for Slurry Transport Using the Response Surface Method
Abstract
1. Introduction
2. Initial Design of Pump and Pump Optimization
2.1. Pump and Volute Casing Design
2.1.1. Hydraulic Efficiency (
2.1.2. Volumetric Efficiency
2.1.3. Mechanical Efficiency
2.1.4. Pump Efficiency
2.1.5. Calculation of Leading Blade Angles
2.1.6. Calculations of Tip Diameter
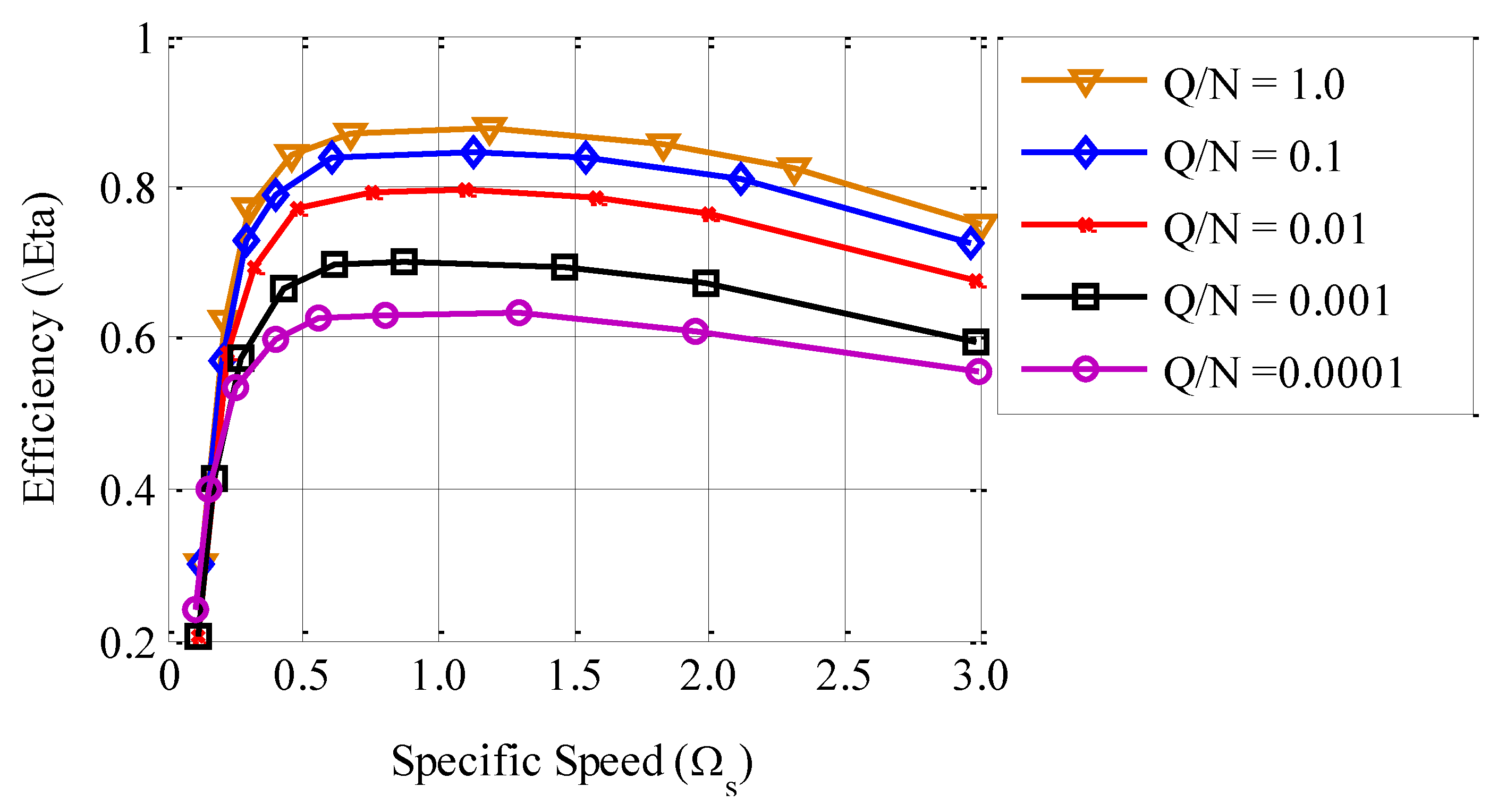
2.1.7. Specific Velocity
3. Pump Impeller Optimization
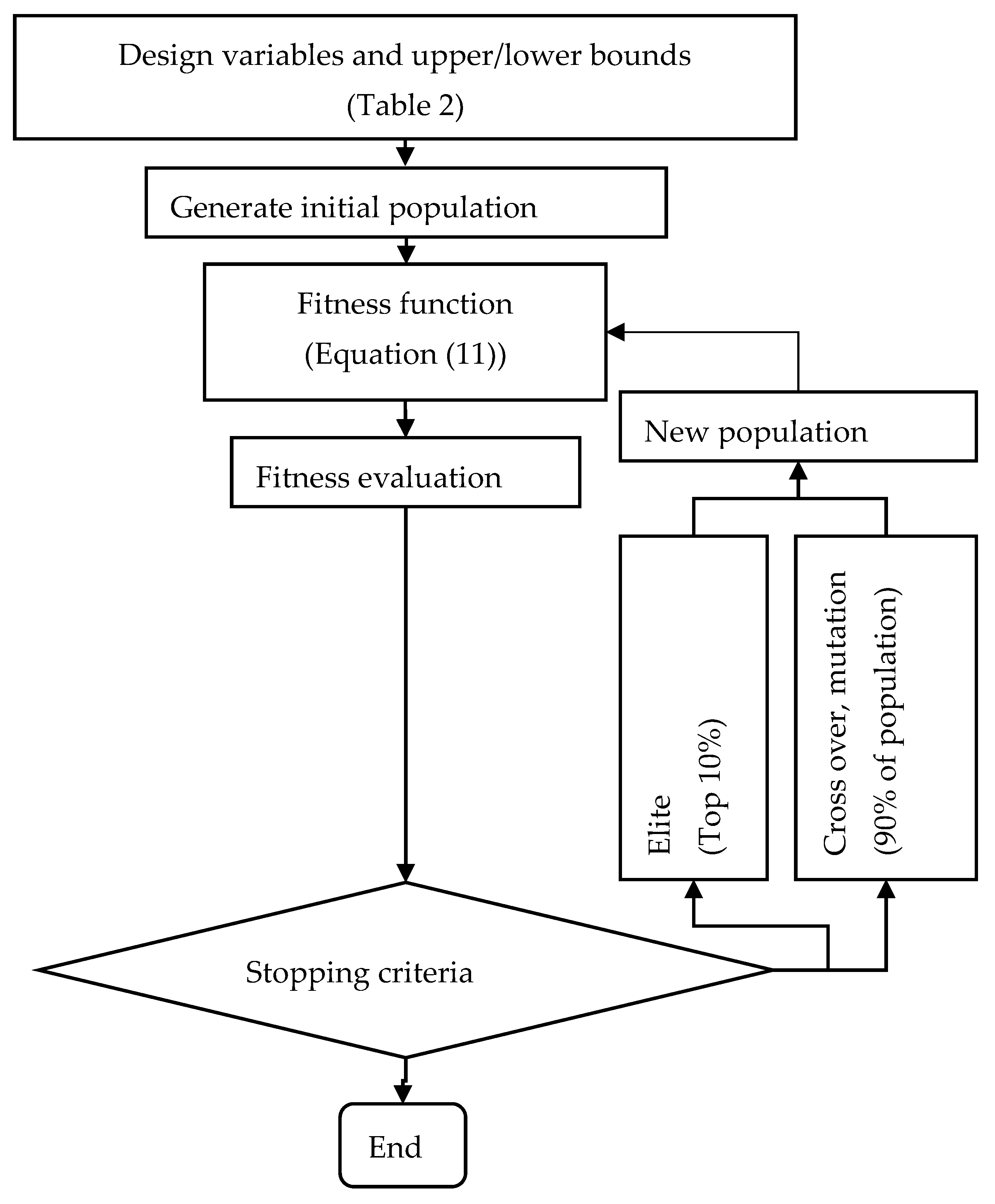
Multi-Objective Genetic Algorithm
4. 3-D Computational Model
4.1. Governing Equations
4.2. Erosion Model
4.3. Computational Domain and Boundary Conditions
4.4. Mesh Generation
5. Validation of the Computational Model
6. Computational Results
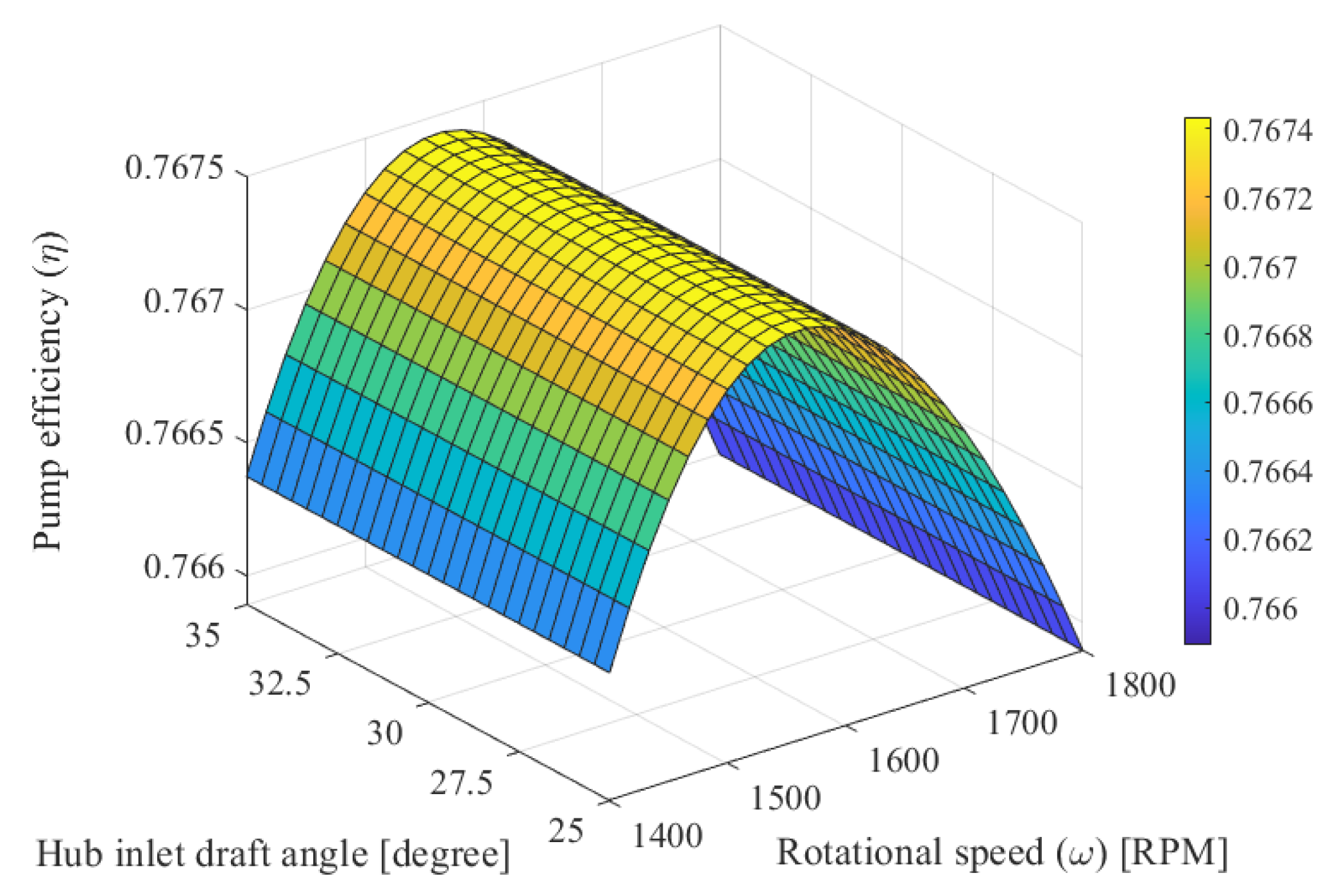
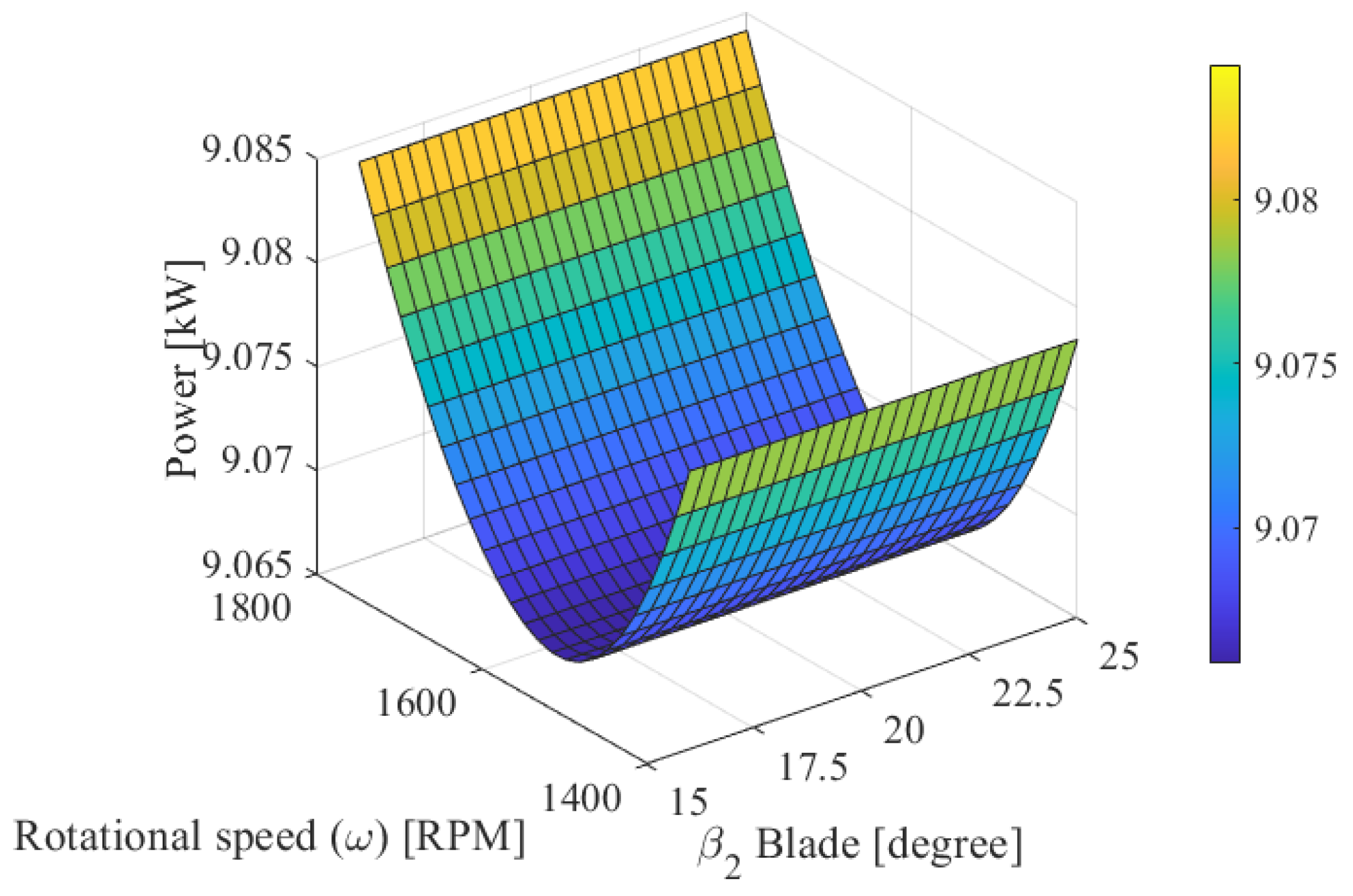
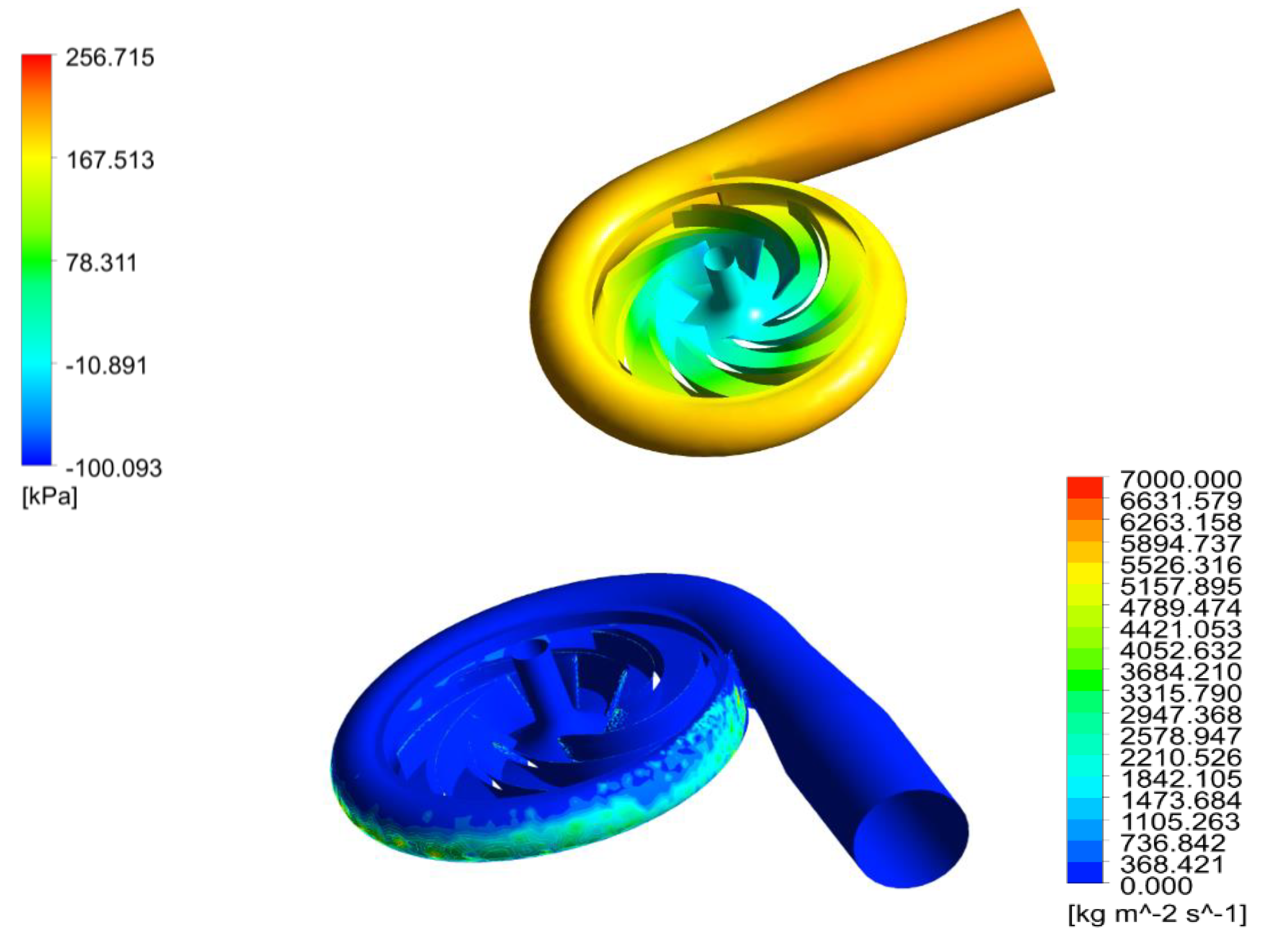
6.1. Characteristic Maps of the Optimized Pump Geometry
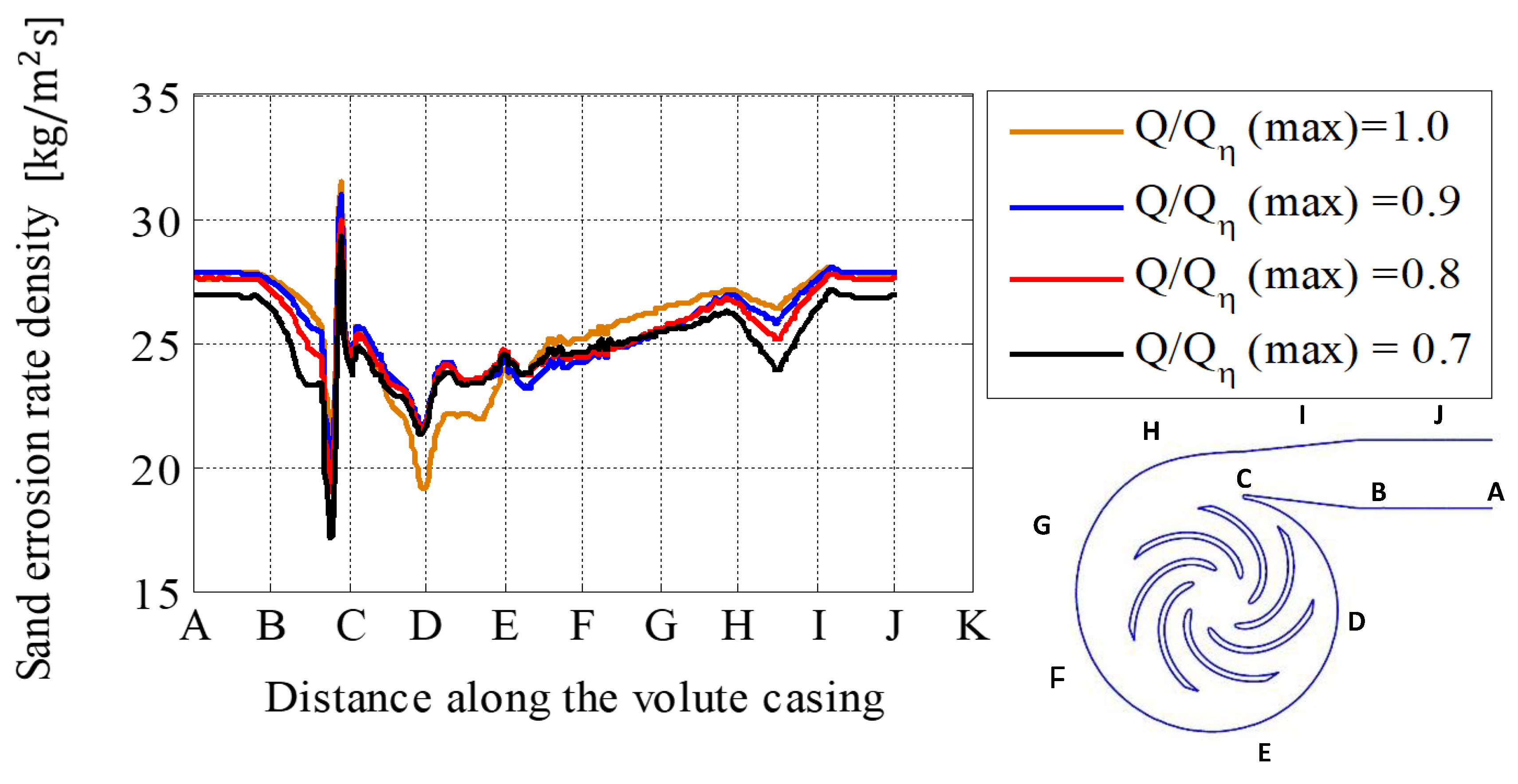
6.2. Effect of Flow Rate on Erosion Rate Density
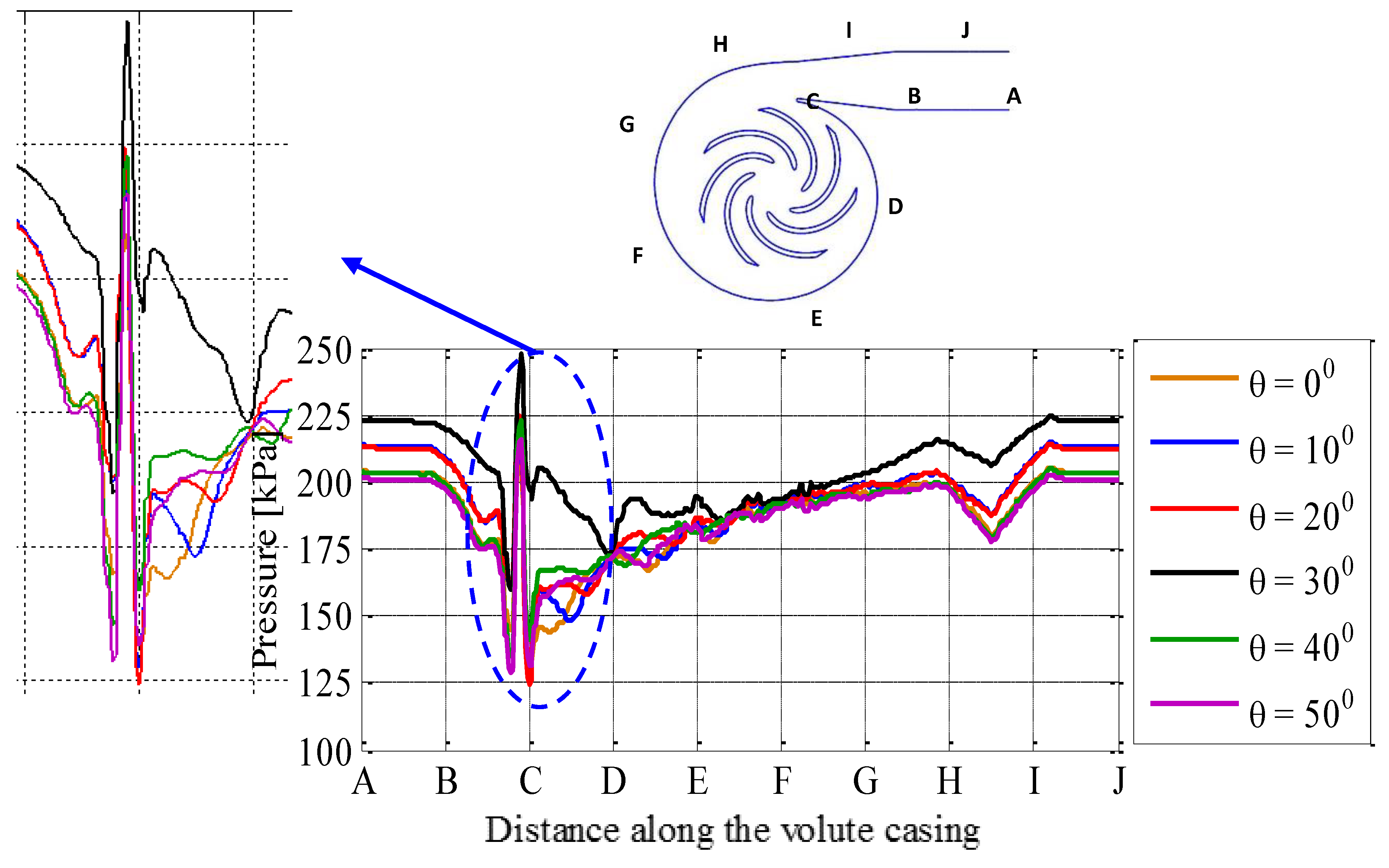
6.3. Transient Behavior of the Pump under a Slurry Flow Condition
7. Conclusions
- Response surface optimization has proven to be an effective method for the optimization process in the ANSYS workbench environment, where it could be coupled with another meshing software and the Navier–Stokes solver.
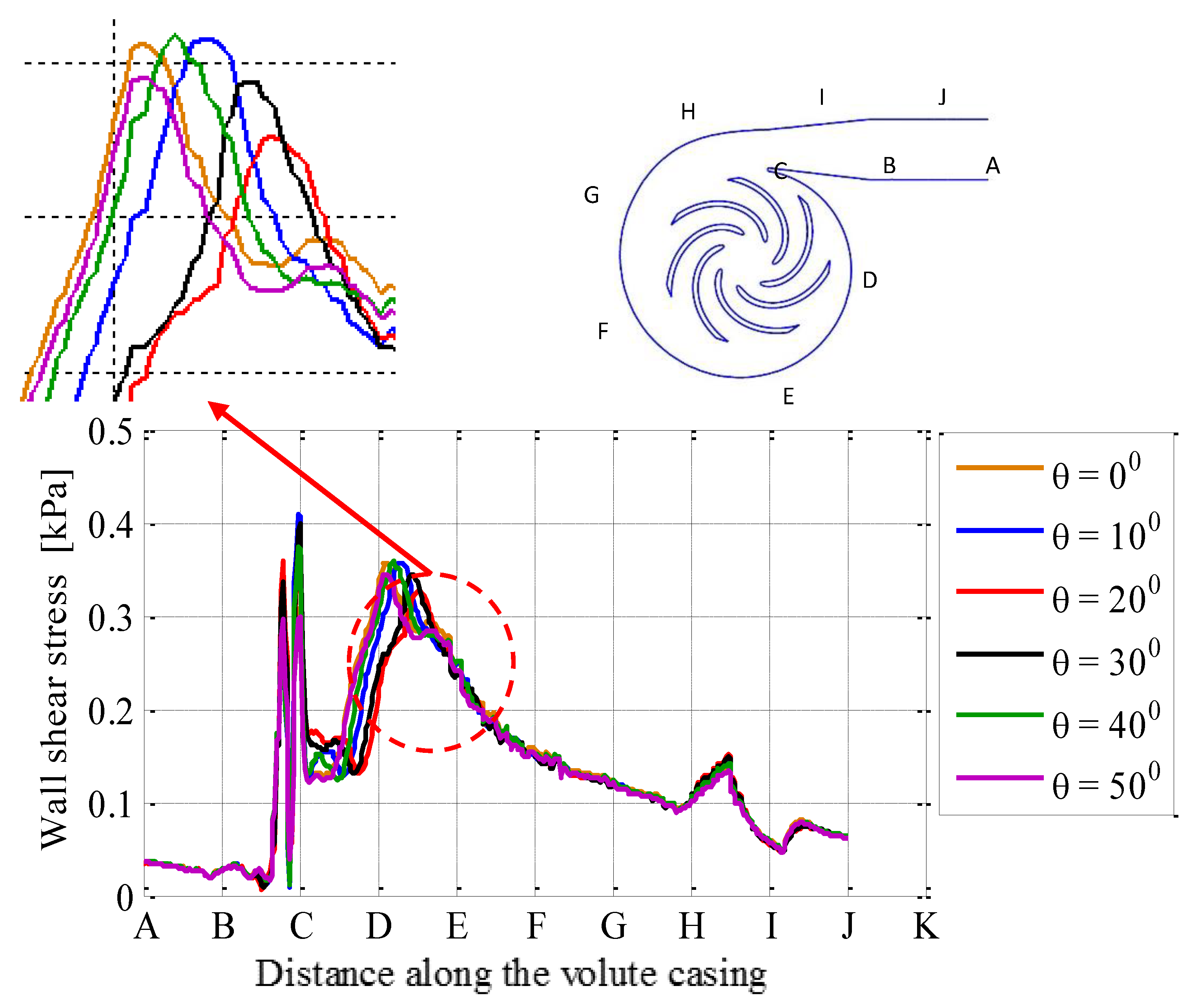
- Pressure varies slightly, but shear stresses on the wall vary significantly with flow rate variations.
- Maximum pressure at the casing exits at phase angle θ = 0° − 30° and also increases at some other locations, and then it starts decreasing as the phase angle further increases from θ = 30° − 50°
- Fluctuating pressure was recorded at the pump’s exit with a fluctuating frequency equal to the number of impeller blades of the pump. The magnitude of fluctuation for the current design was observed as 9.46%. Its dependence on other parameters requires further investigation.
Author Contributions
Funding
Conflicts of Interest
References
- Wilson, K.C.; Addie, G.R.; Sellgren, A.; Clift, R. Slurry Transport Using Centrifugal Pumps; Gardners Books; Elsevier Applied Science: London, UK, 1992; ISBN 9781441935915. [Google Scholar]
- Shah, S.R.; Jain, S.V.; Patel, R.N.; Lakhera, V.J. CFD for centrifugal pumps: A review of the state-of-the-art. Procedia Eng. 2013, 51, 715–720. [Google Scholar] [CrossRef]
- George, A.; Muthu, D.P. CFD Analysis of Performance Characteristics of Centrifugal Pump Impeller to Minimizing Cavitation. In Proceedings of the International Conference on Current Research in Engineering Science and Technology (ICCREST-2016), Trichy, Tamilnadu, India, 4 May 2016; pp. 24–30. [Google Scholar]
- Asuaje, M.; Bakir, F.; Kouidri, S.; Rey, R. Inverse Design Method for Centrifugal Impellers and Comparison with Numerical Simulation Tools. Int. J. Comut. Fluid Dyn. 2004, 18, 101–110. [Google Scholar] [CrossRef]
- Shojaeefard, M.H.; Tahani, M.; Ehghaghi, M.B.; Fallahian, M.A.; Beglari, M. Numerical study of the effects of some geometric characteristics of a centrifugal pump impeller that pumps a viscous fluid. Comput. Fluids 2012, 60, 61–70. [Google Scholar] [CrossRef]
- Kim, J.H.; Oh, K.T.; Pyun, K.B.; Kim, C.K.; Choi, Y.S.; Yoon, J.Y. Design optimization of a centrifugal pump impeller and volute using computational fluid dynamics. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 032025. [Google Scholar] [CrossRef]
- Nourbakhsh, A.; Safikhani, H.; Derakhshan, S. The comparison of multi-objective particle swarm optimization and NSGA II algorithm: Applications in centrifugal pumps. Eng. Optim. 2011, 43, 1095–1113. [Google Scholar] [CrossRef]
- Derakhshan, S.; Pourmahdavi, M.; Abdolahnejad, E.; Reihani, A.; Ojaghi, A. Numerical shape optimization of a centrifugal pump impeller using artificial bee colony algorithm. Comput. Fluids 2013, 81, 145–151. [Google Scholar] [CrossRef]
- ANSYS 16.0 Vista RTD; Ansys Inc.: Canonsburg, PA, USA, 2016; Available online: https://www.ansys.com/products/fluids/ansys-vistatf (accessed on 26 June 2018).
- ANSYS 16, Response Surface Optimization User Manual; Ansys Inc.: Canonsburg, PA, USA, 2016; Available online: https://www.ansys.com/products/platform/ansys-designxplorer (accessed on 12 August 2019).
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley Publishing Company, Inc.: Menlo Park, CA, USA, 1989; ISBN 0201157675. [Google Scholar]
- Saeed, M.; Kim, M. Analysis of a recompression supercritical carbon dioxide power cycle with an integrated turbine design/optimization algorithm. Energy 2018, 165, 93–111. [Google Scholar] [CrossRef]
- Saeed, M.; Kim, M.-H. Thermal-hydraulic analysis of sinusoidal fin-based printed circuit heat exchangers for supercritical CO2 Brayton cycle. Energy Convers. Manag. 2019, 193, 124–139. [Google Scholar] [CrossRef]
- Saeed, M.; Khatoon, S.; Kim, M.-H. Design optimization and performance analysis of a supercritical carbon dioxide recompression Brayton cycle based on the detailed models of the cycle components. Energy Convers. Manag. 2019, 196, 242–260. [Google Scholar] [CrossRef]
- Salim, M.S.; Saeed, M.; Kim, M.-H. Performance Analysis of the Supercritical Carbon Dioxide Re-compression Brayton Cycle. Appl. Sci. 2020, 10, 1129. [Google Scholar] [CrossRef]
- Wang, K.; He, Y.-L. Thermodynamic analysis and optimization of a molten salt solar power tower integrated with a recompression supercritical CO2 Brayton cycle based on integrated modeling. Energy Convers. Manag. 2017, 135, 336–350. [Google Scholar] [CrossRef]
- Li, H.; Su, W.; Cao, L.; Chang, F.; Xia, W.; Dai, Y. Preliminary conceptual design and thermodynamic comparative study on vapor absorption refrigeration cycles integrated with a supercritical CO2 power cycle. Energy Convers. Manag. 2018, 161, 162–171. [Google Scholar] [CrossRef]
- Bahamonde Noriega, J.S. Design Method for s-CO2 Gas Turbine Power Plants Integration of Thermodynamic Analysis and Components Design for Advanced Applications, Report: P&E-2530; Delft University of Technology: Delft, The Netherlands, 2012. [Google Scholar]
- Zhang, X.; Sun, X.; Christensen, R.N.; Anderson, M.; Carlson, M. Optimization of S-Shaped Fin Channels in a Printed Circuit Heat Exchanger for Supercritical CO2 Test Loop. In Proceedings of the 5th International Supercritical CO2 Power Cycles Symposium, San Antonio, TX, USA, 28–31 March 2016. [Google Scholar]
- Shen, X.; Yang, H.; Chen, J.; Zhu, X.; Du, Z. Aerodynamic shape optimization of non-straight small wind turbine blades. Energy Convers. Manag. 2016, 119, 266–278. [Google Scholar] [CrossRef]
- Ha, S.T.; Ngo, L.C.; Saeed, M.; Jeon, B.J.; Choi, H. A comparative study between partitioned and monolithic methods for the problems with 3D fluid-structure interaction of blood vessels. J. Mech. Sci. Technol. 2017, 31, 281–287. [Google Scholar] [CrossRef]
- Venkata Rao, R.; Patel, V. Multi-objective optimization of combined Brayton and inverse Brayton cycles using advanced optimization algorithms. Eng. Optim. 2012, 44, 965–983. [Google Scholar] [CrossRef]
- Xiao, D.; do Prado, J.C.; Qiao, W. Optimal joint demand and virtual bidding for a strategic retailer in the short-term electricity market. Electr. Power Syst. Res. 2021, 190, 106855. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, J.; Xiao, D.; Qiao, W. Security-Constrained Optimal Power Flow Solved with a Dynamic Multichain Particle Swarm Optimizer. In Proceedings of the 51st North American Power Symposium, NAPS 2019, Wichita, KS, USA, 13–15 October 2019. [Google Scholar]
- Jiang, S.; Chen, X.; Cao, G.; Tan, Y.; Xiao, X.; Zhou, Y.; Liu, S.; Tong, Z.; Wu, Y. Optimization of fresh concrete pumping pressure loss with CFD-DEM approach. Constr. Build. Mater. 2021, 276, 122204. [Google Scholar] [CrossRef]
- Ping, X.; Yang, F.; Zhang, H.; Zhang, J.; Zhang, W.; Song, G. Introducing machine learning and hybrid algorithm for prediction and optimization of multistage centrifugal pump in an ORC system. Energy 2021, 222, 120007. [Google Scholar] [CrossRef]
- Xiao, W.; Tan, L. Design method of controllable velocity moment and optimization of pressure fluctuation suppression for a multiphase pump. Ocean Eng. 2021, 220, 108402. [Google Scholar] [CrossRef]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics—The Finite Volume Method. In Fluid Flow Handbook; McGraw-Hill: Essex, UK, 1995; p. 267. [Google Scholar]
- Pagalthivarthi, K.V.; Gupta, P.K.; Tyagi, V.; Ravi, M.R. CFD Predictions of Dense Slurry Flow in Centrifugal Pump Casings. World Acad. Sci. Eng. Technol. Int. J. Mech. Aerosp. Ind. Mechatron. Manuf. Eng. 2011, 5, 538–550. [Google Scholar]
- Menter, F.R. Zonal two equation kappa-omega turbulence models for aerodynamic flows. In Proceedings of the 24th Fluid Dynamics Conference, Orlando, FL, USA, 6–9 July 1993. [Google Scholar]
- Siddiqui, M.S.; Latif, S.T.M.; Saeed, M.; Rahman, M.; Badar, A.W.; Hasan, S.M. Reduced order model of offshore wind turbine wake by proper orthogonal decomposition. Int. J. Heat Fluid Flow 2020, 82, 108554. [Google Scholar] [CrossRef]
- Saeed, M.; Berrouk, A.S.; Salman Siddiqui, M.; Ali Awais, A. Numerical investigation of thermal and hydraulic characteristics of sCO2-water printed circuit heat exchangers with zigzag channels. Energy Convers. Manag. 2020, 224, 113375. [Google Scholar] [CrossRef]
- Cai, X.; Gu, R.; Pan, P.; Zhu, J. Unsteady aerodynamics simulation of a full-scale horizontal axis wind turbine using CFD methodology. Energy Convers. Manag. 2016, 112, 146–156. [Google Scholar] [CrossRef]
- Sayed, M.A.; Kandil, H.A.; Shaltot, A. Aerodynamic analysis of different wind-turbine-blade profiles using finite-volume method. Energy Convers. Manag. 2012, 64, 541–550. [Google Scholar] [CrossRef]
- Sörensen, N.N.; Michelsen, J.A.; Schreck, S. Navier-Stokes predictions of the NREL phase VI rotor in the NASA Ames 80 ft × 120 ft wind tunnel. Wind Energy 2002, 5, 151–169. [Google Scholar] [CrossRef]
- Saeed, M.; Kim, M.-H. Thermal and hydraulic performance of SCO2 PCHE with different fin configurations. Appl. Therm. Eng. 2017, 127, 975–985. [Google Scholar] [CrossRef]
- Saeed, M.; Kim, M.-H. Aerodynamic performance analysis of an airborne wind turbine system with NREL Phase IV rotor. Energy Convers. Manag. 2017, 134, 278–289. [Google Scholar] [CrossRef]
- Saeed, M.; Kim, M.-H. Airborne wind turbine shell behavior prediction under various wind conditions using strongly coupled fluid structure interaction formulation. Energy Convers. Manag. 2016, 120, 217–228. [Google Scholar] [CrossRef]
- Hutchings, I. Mechanical and metallurgical aspects of the erosion of metals. Wear 1979, 393–427. [Google Scholar]
- Finnie, I. Some observations on the erosion of ductile metals. Wear 1972, 19, 81–90. [Google Scholar] [CrossRef]
- Aslam Noon, A.; Kim, M.H. Erosion wear on Francis turbine components due to sediment flow. Wear 2017, 378–379, 126–135. [Google Scholar] [CrossRef]
- Noon, A.A.; Kim, M.H. Erosion wear on centrifugal pump casing due to slurry flow. Wear 2016, 364–365, 103–111. [Google Scholar] [CrossRef]
- ANSYS CFX CFX-Pre User’s Guide Release 16.0. 2015. Available online: https://www.ansys.com/products/fluids/ansys-cfx (accessed on 25 November 2019).
- Roco, C.; Addie, G.R. Analytical Model and Experimental studies on Slurry flow and erosion in pump casings. Slurry Transp. 1983, 8, 263–275. [Google Scholar]
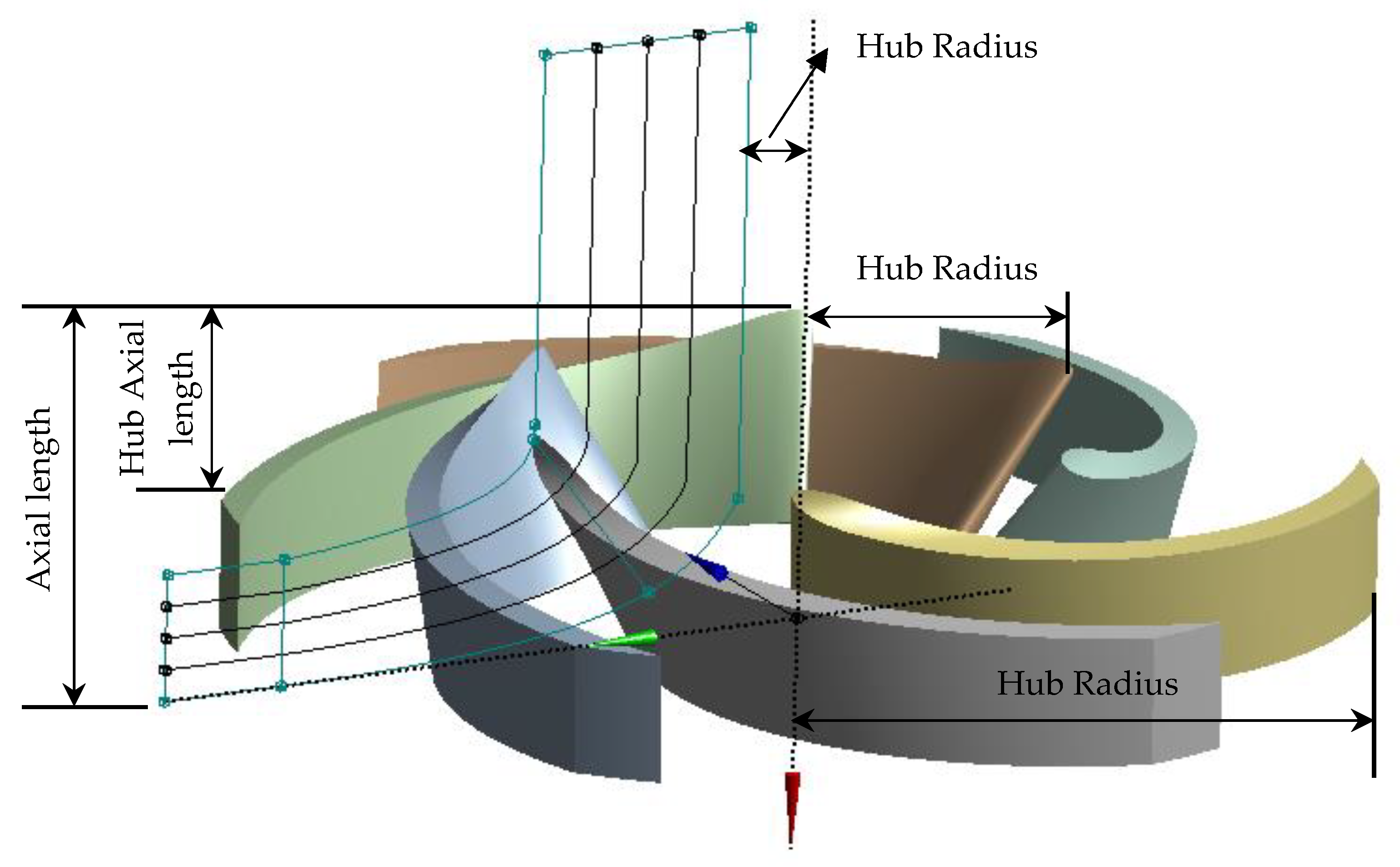
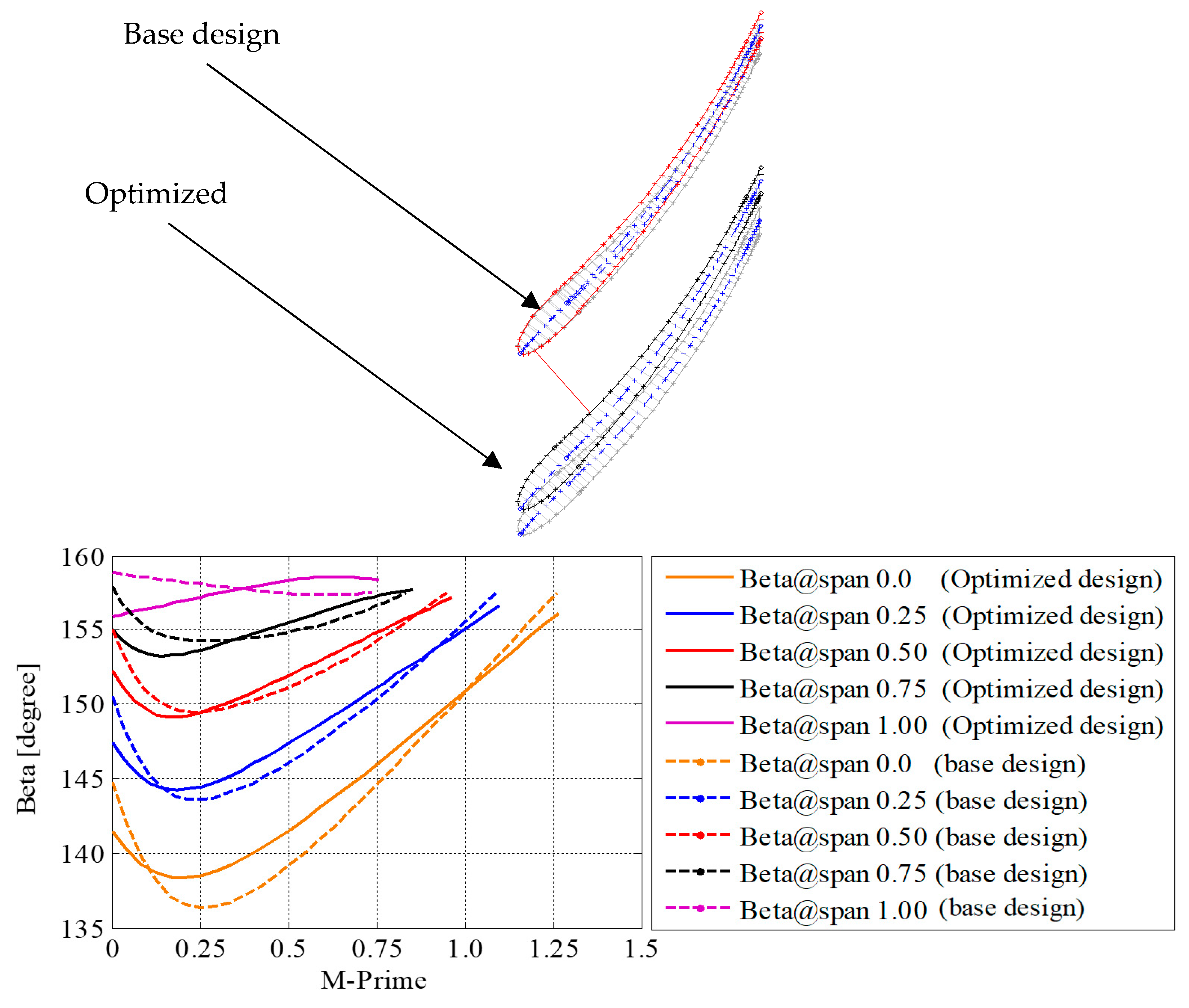

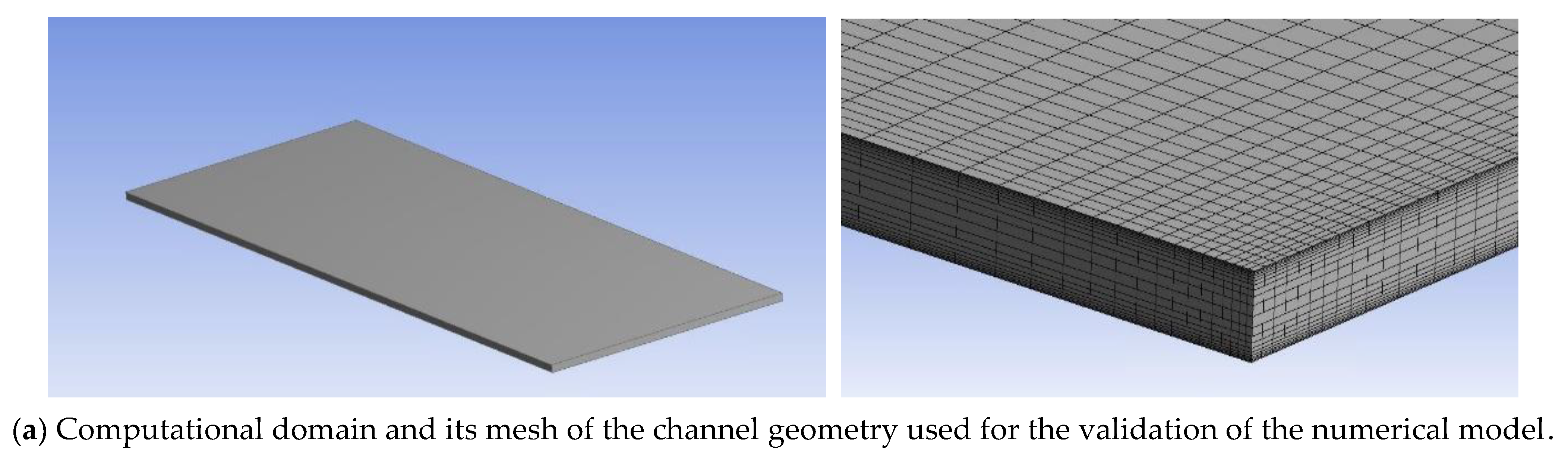
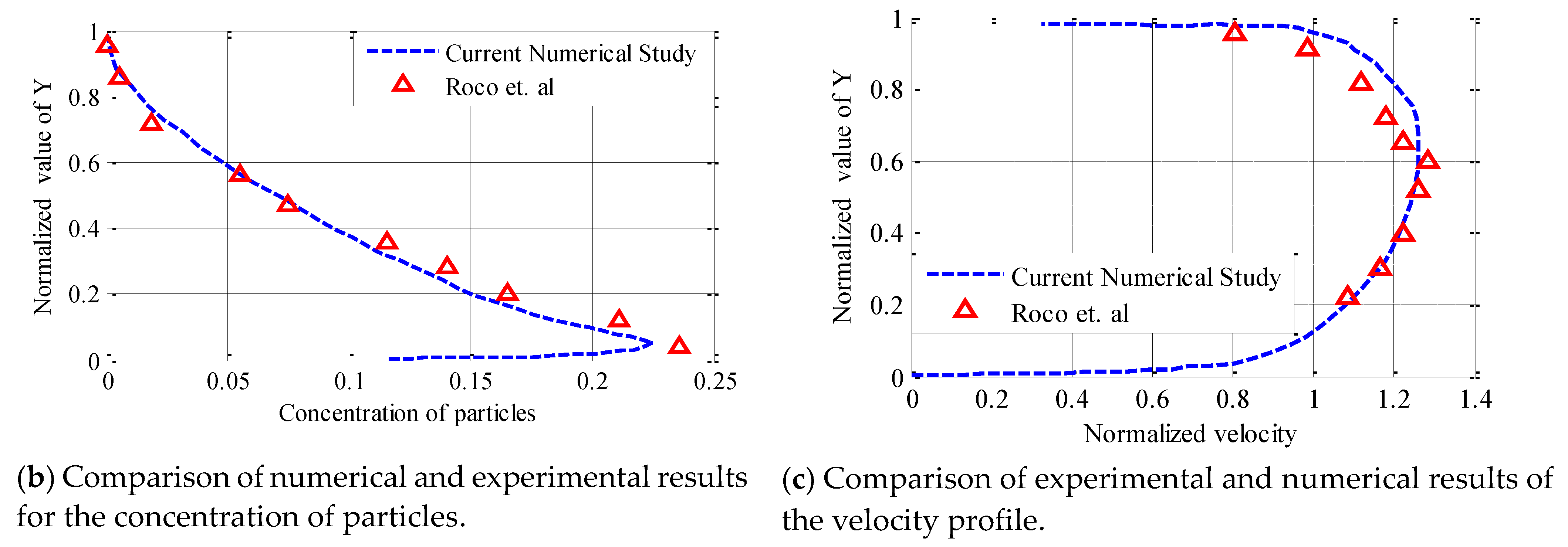



| Input Parameter | Symbol | Value |
| Volume flow rate | ||
| Rotational speed | ||
| Head rise | ||
| Inlet flow angle | ||
| Hydraulic Efficiency | ||
| Volumetric Efficiency | ||
| Mechanical Efficiency | ||
| Pump Efficiency | ||
| Assumptions | Symbol | Value |
| Shaft min diameter factor | ||
| Hub to shaft diameter ratio | ||
| Blade inlet angle at hub | ||
| Blade angle mean | ||
| Tip diameter | ||
| Blade angle at exit |
| Input Design Variable for the Optimization Procedure | Lower Bound | Upper Bound | |
|---|---|---|---|
| Number of vanes (N) | 8 | ||
| Inlet beta shroud ( | +5 | ||
| Exit blade angle | |||
| Hub inlet draft | |||
| Rotation speed (rpm) | 1716 | ||
| Rake angle |
| Response Variables | Constraints |
|---|---|
| Shaft power | Minimize |
| Maximize | |
| Maximize | |
| Maximize |
| S. No. | Inlet Beta Shroud | Hub Inlet Draft (degree) | ||||
|---|---|---|---|---|---|---|
| 1 | 7 | 0.0 | 20.5 | 30.0 | 0.0 | 1600 |
| 2 | 5 | 0.0 | 20.5 | 30.0 | 0.0 | 1600 |
| 3 | 8 | 0.0 | 20.5 | 30.0 | 0.0 | 1600 |
| 4 | 7 | −5.0 | 20.5 | 30.0 | 0.0 | 1600 |
| 5 | 7 | 5.0 | 20.5 | 30.0 | 0.0 | 1600 |
| 6 | 7 | 0.0 | 16.0 | 30.0 | 0.0 | 1600 |
| 7 | 7 | 0.0 | 25.0 | 30.0 | 0.0 | 1600 |
| 8 | 7 | 0.0 | 20.5 | 25.0 | 0.0 | 1600 |
| 9 | 7 | 0.0 | 20.5 | 35.0 | 0.0 | 1600 |
| 10 | 7 | 0.0 | 20.5 | 30.0 | −5.0 | 1600 |
| 11 | 7 | 0.0 | 20.5 | 30.0 | 5.0 | 1600 |
| 12 | 7 | 0.0 | 20.5 | 30.0 | 0.0 | 1400 |
| 13 | 7 | 0.0 | 20.5 | 30.0 | 0.0 | 1800 |
| 14 | 6 | −2.9 | 17.9 | 27.1 | −2.9 | 1484 |
| 15 | 7 | −2.9 | 17.9 | 27.1 | −2.9 | 1716 |
| 16 | 6 | 2.9 | 17.9 | 27.1 | −2.9 | 1716 |
| 17 | 7 | 2.9 | 17.9 | 27.1 | −2.9 | 1484 |
| 18 | 6 | −2.9 | 23.1 | 27.1 | −2.9 | 1716 |
| 19 | 7 | −2.9 | 23.1 | 27.1 | −2.9 | 1484 |
| 20 | 6 | 2.9 | 23.1 | 27.1 | −2.9 | 1484 |
| 21 | 7 | 2.9 | 23.1 | 27.1 | −2.9 | 1716 |
| 22 | 6 | −2.9 | 17.9 | 32.9 | −2.9 | 1716 |
| 23 | 7 | −2.9 | 17.9 | 32.9 | −2.9 | 1484 |
| 24 | 6 | 2.9 | 17.9 | 32.9 | −2.9 | 1484 |
| 25 | 7 | 2.9 | 17.9 | 32.9 | −2.9 | 1716 |
| 26 | 6 | −2.9 | 23.1 | 32.9 | −2.9 | 1484 |
| 27 | 7 | −2.9 | 23.1 | 32.9 | −2.9 | 1716 |
| 28 | 6 | 2.9 | 23.1 | 32.9 | −2.9 | 1716 |
| 29 | 7 | 2.9 | 23.1 | 32.9 | −2.9 | 1484 |
| 30 | 6 | −2.9 | 17.9 | 27.1 | 2.9 | 1716 |
| 31 | 7 | −2.9 | 17.9 | 27.1 | 2.9 | 1484 |
| 32 | 6 | 2.9 | 17.9 | 27.1 | 2.9 | 1484 |
| 33 | 7 | 2.9 | 17.9 | 27.1 | 2.9 | 1716 |
| 34 | 6 | −2.9 | 23.1 | 27.1 | 2.9 | 1484 |
| 35 | 7 | −2.9 | 23.1 | 27.1 | 2.9 | 1716 |
| 36 | 6 | 2.9 | 23.1 | 27.1 | 2.9 | 1716 |
| 37 | 7 | 2.9 | 23.1 | 27.1 | 2.9 | 1484 |
| 38 | 6 | −2.9 | 17.9 | 32.9 | 2.9 | 1484 |
| 39 | 7 | −2.9 | 17.9 | 32.9 | 2.9 | 1716 |
| 40 | 6 | 2.9 | 17.9 | 32.9 | 2.9 | 1716 |
| 41 | 7 | 2.9 | 17.9 | 32.9 | 2.9 | 1484 |
| 42 | 6 | −2.9 | 23.1 | 32.9 | 2.9 | 1716 |
| 43 | 7 | −2.9 | 23.1 | 32.9 | 2.9 | 1484 |
| 44 | 6 | 2.9 | 23.1 | 32.9 | 2.9 | 1484 |
| 45 | 7 | 2.9 | 23.1 | 32.9 | 2.9 | 1716 |
| Input Parameters | Objective Functions | ||
|---|---|---|---|
| Range | Parameters | Constraints | |
| Number of vanes (N) | 5–8 | Shaft power | Minimize |
| Inlet beta shroud ( | −5–+5 | Maximize | |
| Maximize | |||
| Hub inlet blade angle | Maximize | ||
| Rotation speed (rpm) | 1200–1800 | ||
| Hub inlet draft (degree) | |||
| Input Parameters | Objective Functions | ||
|---|---|---|---|
| Parameter | Value | Parameters | Value |
| Number of vanes (N) | 7 | Shaft power | 9.06 |
| Inlet beta shroud ( | 1.7° | 97.5 | |
| 22° | 89.3 | ||
| Hub inlet blade angle | 27° | 96.3 | |
| Rotation speed (rpm) | 1533 | ||
| Hub inlet draft (degree) | 32° | ||
| Simulation Sets | Flow Rate | Analysis Type | Particle Distribution [micro] | |||
| Min | Max | Ave | Std. dev. | |||
| 1 | 0.7 | Steady state | 50 | 150 | 80 | 70 |
| 2 | 0.8 | 50 | 150 | 80 | 70 | |
| 3 | 0.9 | 50 | 150 | 80 | 70 | |
| 4 | 1.0 | 50 | 150 | 80 | 70 | |
| 5 | 1.0 | Unsteady Time step 0.001 s Simulation time 1.0 s Total number of time steps = 1000 | 50 | 150 | 80 | 70 |
| Simulations to create characteristic curves | ||||||
| Simulations corresponding to various values of | Particle Distribution [micro] | |||||
| Min | Max | Ave | Std. dev. | |||
| 6 | 9 simulations | 50 | 150 | 80 | 70 | |
| 7 | 9 simulations | 50 | 150 | 80 | 70 | |
| 8 | 9 simulations | 50 | 150 | 80 | 70 | |
| 9 | 9 simulations | 50 | 150 | 80 | 70 | |
| 10 | 0.0001 | 9 simulations | 50 | 150 | 80 | 70 |
| Impeller Domain | Casing Domain | Number of Nodes | Memory Allocate [MB] | Computation Time for Ten Iteration | Computed Pump Power [kW] | ||||
|---|---|---|---|---|---|---|---|---|---|
| Mesh | Number of Nodes in the Spanwise Direction | Number of Nodes in the O-Grid Region | Number of Nodes in the Tip Clearance Region | Number of Nodes in the Inlet Domain | Element Size in the Stationary Domain | ||||
| M1 | 35 | 10 | 5 | 15 | 0.003 | 1,025,341 | 11,325 | 57 | 11.2 |
| M2 | 45 | 20 | 7 | 20 | 0.002 | 1,523,452 | 18,256 | 97 | 10.7 |
| M3 | 60 | 30 | 11 | 25 | 0.0015 | 2,742,863 | 35,261 | 195 | 9.26 |
| M4 | 70 | 40 | 15 | 30 | 0.001 | 3,929,536 | 47,325 | 310 | 9.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alawadhi, K.; Alzuwayer, B.; Mohammad, T.A.; Buhemdi, M.H. Design and Optimization of a Centrifugal Pump for Slurry Transport Using the Response Surface Method. Machines 2021, 9, 60. https://doi.org/10.3390/machines9030060
Alawadhi K, Alzuwayer B, Mohammad TA, Buhemdi MH. Design and Optimization of a Centrifugal Pump for Slurry Transport Using the Response Surface Method. Machines. 2021; 9(3):60. https://doi.org/10.3390/machines9030060
Chicago/Turabian StyleAlawadhi, Khaled, Bashar Alzuwayer, Tareq Ali Mohammad, and Mohammad H. Buhemdi. 2021. "Design and Optimization of a Centrifugal Pump for Slurry Transport Using the Response Surface Method" Machines 9, no. 3: 60. https://doi.org/10.3390/machines9030060
APA StyleAlawadhi, K., Alzuwayer, B., Mohammad, T. A., & Buhemdi, M. H. (2021). Design and Optimization of a Centrifugal Pump for Slurry Transport Using the Response Surface Method. Machines, 9(3), 60. https://doi.org/10.3390/machines9030060





