Abstract
The latest development trend in rolling industry is the combination of various technological operations in continuous production lines. In the production of long products, the combination of rolling and drawing processes looks promising. A wire drawing mill developed by the team of authors of this work belongs to the conceptually new, integrated lines. The creation of new integrated rolling mills requires a research phase, where relevant concepts are scrutinized using the methods of mathematical modeling. This requires the development of digital (Digital Twin) models that reliably describe the technological processes. It seems efficient to create a Digital Twin for individual units, with their subsequent integration into a complex digital model. This approach was applied in the development of models of electrical systems for the new line. Such models should take into account a wide range of real-life physical relationships. At the same time, a three-high continuous train of stands with an idle inter-stand is the least studied technological unit of the new mill. The absence of an electric drive of the middle stand determines the particulars of deformation processes and the stands’ interconnections through the processed metal. To date, a comprehensive study of such objects has not been carried out. Therefore, the task of studying this technological unit is of immediate interest. The presented publication is devoted to the development of digital models of deformation zones of drive stands and idle stands, as well as of their relationship through the processed metal. The task is solved using the example of an operating pilot production line that implements rolling technology with an idle stand. The authors describe individual Digital Twins and present the structure of the complex model of the studied unit. The most important purpose of the model is to use it in the development of a control method for electric drives of stands to ensure the stability of the rolling process. The developed method should provide a reduction in energy consumption due to the use of friction force reserves present in the idle stand. The authors also substantiate the control principle based on continuous monitoring and alignment of critical angles in the deformation zones of the drive stands. The paper describes a structure of the control system and explains the technical implementation of this principle. The results of mathematical modeling and oscillograms of typical transient processes are presented. The advantages provided by implementing the proposed control method are shown. The work provides an indirect confirmation of the adequacy of the model to the physical object. Recommendations are given on the use of the developed Digital Twin in the study of rolling processes on sheet and sectional mills.
1. Introduction
The creation of Digital Twins of technological processes and equipment for pressure-based metal treatment (metalworking processes) is a prerequisite for the implementation of the development of rolling production in digital dimension. The scientific publication [1] provides a simple and at the same time concise definition of the Digital Twin (DT) concept as “a virtual replica of a physical asset that can track the state thereof”. It is noted that “at present, this concept is gradually acquiring the features of a real technology that can have a global impact on the market”. This definition is fully applicable to metalworking processes, too.
Academic works [2,3,4] provide literature reviews that give insight into DT applications in industry and business. A significant number of publications is devoted to the development of DT in the metallurgical industry. For example, in [5,6,7,8,9], the authors considered DT development for the implementation of the concept of “digital” or intelligent metallurgical enterprises.
It is obvious that the use of Digital Twins looks promising for the development and improvement of rolling mills, which are the most complex units of metallurgical production. Attention is paid to DT creation both for technological lines and for solving the problems of industrial engineering. An illustrative example is the publication [10] on the development of DTs for optimization of roll changes in a wire rod mill. Equally important is the conceptual direction of using DT in the development of new technological units and electromechanical systems for rolling mills. Digital modeling ensures minimization of costs for the development of automated electric drives and process control systems for pressure-based metal treatment. This helps to reduce the launch time for technological lines and decreases the likelihood of emergencies during their commissioning. The developments discussed in the article are an example of the implementation of this conceptual approach.
Monographs [11,12,13] are devoted to developing models and designing the technological lines of rolling mills. In [14,15], the authors carried out dynamic modeling and analysis of rolling parameters on a hot rolling tandem mill. Publications [16,17,18] are devoted to the modeling of processes in cold rolling mills, taking into account the connection of stands through the processed metal. The article in [19] provides an overview of the processes for individual production of rolled products, as well as modeling methods that provide for designing or optimization of these processes. The article in [20] presents a developed system for modeling the rolling of rectangular, round or square workpieces in various symmetric or asymmetric shapes during continuous, reversed or combined rolling. Therefore, it can be conventionally accepted as universal.
The disadvantage of the reviewed publications lies in the lack of information about the development or improvement of electrical profiles (automated electric drives and control systems) of the rolling units under study. Such profiles play a key role in supporting the rolling technology, product quality and optimization of energy requirement for production. This article is intended to fill this gap. Improvement of electrical profiles is carried out for a fundamentally new rolling–drawing unit with a block containing a non-driven rolling stand.
Considerable attention in the literature is paid to the creation of models and digital modeling of processes in the deformation zone [21,22,23,24]. One of the first publications in this direction, devoted to the development of grid models, is found in [25]. There, the authors developed a numerical model describing the flow of metal, heat transfer and the evolution of the microstructure during the hot deformation process. They provided a program of generalized plane deformation, adapted to modeling the strip rolling process.
The disadvantage of these, as well as other publications, is the lack of studies of wire-rolling processes in the deformation zones. The main focus is on the processes of deformation of a flat sheet or workpieces (rectangular-shaped, square-shaped, etc.). There is insufficient research on forming of a round workpiece in the production of wire. With that, the wire deformation in the deformation zones of the non-driven rolling stands has not been studied at all. This information gap is filled with the submitted work. The authors developed digital models to study the wire-rolling deformation processes in drive and idle stands. Based on the research results, a comparative analysis of these processes is given. This provides means for calculation of the energy parameters for wire-rolling in the designed unit with idle inter-stand. The ultimate goal of this research is the technical implementation of automated electric drives of the designed rolling–drawing unit.
General directions for the development of Digital Twins of section mills, which include wire mills, are justified in the publication [26] by Primetals Technologies (a joint venture of Mitsubishi Heavy Industries (MHI) and partners). The company is developing new technological programs and packages to improve product quality, production flexibility, mill efficiency and productivity. It is argued that the development of “digitalization” of plants has led to a revolution in sectioned rolling production.
Clearly, the use of digital models is most effective in the development of promising technologies for metalworking and new technological lines. A promising direction in the development of wire production is the creation of units that ensure the combination of continuous rolling and drawing processes. Resulting technology combines the advantages of rolling mills (low deformation costs) and drawing mills (high accuracy of the geometry of the produced wire).
According to experts, the use of the integrated rolling and drawing technology provides the following advantages [27,28].
- Higher productivity due to:
- increasing the speed of rolling–drawing up to 30–45 m/s (conventional straight-through drawing mills run at 10–13 m/s); and
- increasing the operating efficiency (efficiency of the production process) from 0.5 to 0.9–0.95 by reducing the wire breakage and shortening the time for auxiliary operations (feeding the mill, replacing the coils of the winding machines, etc.).
- Reduction of energy consumption for wire production by 30–40%, mainly due to the use of the reserve of frictional forces during rolling and reduction of friction losses during drawing.
- Improving the product quality by combining the advantages of rolling (uniform drafting, etc.) and drawing: high-quality lengthwise surface and sectional “geometry”.
- Expansion of the assortment and increasing the flexibility of production due to the use of a rolling section, which provides the option of quick readjustment to the required drafting and, accordingly, to a new thickness of the rolling stock.
- An option for producing wire from difficult-to-form steel grades by installing two or more rolling sections in the technological line.
Analyzing these factors, it can be argued that the integration of processes provides a synergistic effect via utilization of hidden potential of individual technological operations. Theoretical research and the creation of experimental integrated rolling–drawing units were intensively carried out over 1990–2010. The greatest success in this direction was achieved by the academic schools of the Institute of Ferrous Metallurgy of the National Academy of Sciences of Ukraine (Dnipropetrovsk) under the guidance of Professor S.M. Zhuchkov [29,30,31,32] and the Siberian State Technical University (Novokuznetsk, Russia) [33,34,35] under the guidance of Professor A.R. Fastykovsky. According to Professor A.R. Fastykovsky, “the integration implies, in addition to the main functions, the implementation of additional functions through the use of hidden potential”. For example, due to better use of friction forces in the deformation zone, the integrated methods for metalworking process perform additional operations, such as deformation in the idle stand, longitudinal separation with a non-powered splitting tool and matrix-based deformation, ensuring the operation of the “deformation zone–roll fittings” system.
However, the solutions of the specialists of the said academic schools refer to technological lines for the production of bar reinforcement and to the study of extrolling process. Therefore, they cannot be directly applied to creation of rolling–drawing lines.
Despite the fact that replacing wire drawing with wire rolling provides the above advantages, this technology has not gained widespread acceptance. This is due to the complexity of the rolling mill equipment and high capital and operating costs. However, by using idle stands as part of a continuous mill, it is possible to significantly simplify the composition of the equipment used and reduce costs. The energy required for deformation of the metal in such a stand is supplied by back pressure (negative tension) of the processed metal from the side of the previous stand and tension from the side of the next one. Such a solution ensures the use of friction force reserves in the deformation zones of the drive stands, reduces the capital costs for the mill construction and increases the efficiency of the rolling process by 10–15% [28,36].
A promising development is an integrated rolling–drawing unit that has passed industrial tests at the Beloretsk Metallurgical Plant (Beloretsk, Russia). The technology for wire manufacturing [37], as discussed in [38,39], has passed the pre-developed stage. The line contains a three-stand rolling section (rolling train) with a distinctive feature—absence of electric drive in the second stand. Below is information on the development of digital models and the results of the study of dynamic processes during rolling in this block.
2. Problem Formulation
Continuous rolling is a complex process of deformation zones interacting through metal. Therefore, Digital Twins for metalworking processes should be developed taking into account a set of internal and external factors. The fundamental difference of this approach lies in the fact that deformation in pressure-based metal treatment is considered taking into account the forming factors in the focal area and external impact of, primarily, tension. Rolling stands, automated electric drives, pressure devices (if any) and other devices are separate systems with natural cross-link connections. The main one is the force connection through the metal. The physical essence of the force connection is the tension or back pressure of the feed (intermediate product) in the inter-stand space.
The method for implementing this approach provides for the creation of independent DTs describing the impact of individual factors, with their subsequent integration into a complex digital model with due consideration for the diversity of DT connections. Below, we consider digital models developed for the rolling block of the wire mill being created, taking into account the colligation of the electromechanical complexes of the technological line through the metal.
2.1. Description of the Research Object
Figure 1 shows a diagram of the technological line of the studied unit [37]. It consists of a rolling section, which includes two drive stands, an idle inter-stand and a drawing section, conventionally shown in the form of two dies and two elongating reels. The drawing section is essentially a continuous, straight-through drawing mill with adjustable back tension. The mill is also equipped with a decoiler and a coiler.
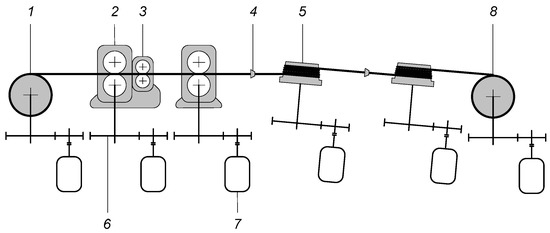
Figure 1.
Technological line of the integrated rolling–drawing mill: 1, decoiler; 2, drive stand; 3, idle stand; 4, die block; 5, drum of the drawing block; 6, gearbox; 7, electric actuator; 8, coiler.
A research prototype of the unit is built on the basis of a 3 × 2/160 wire flattening precision mill and a UDZWGT 40/21 drawing mill (Germany). The wire flattening mill was reconstructed in an industrial environment; its stands were used to create a three-stand rolling section, which is a mechatronic system. The arrangement of the system’s equipment and the kinematic diagram are shown in Figure 2.
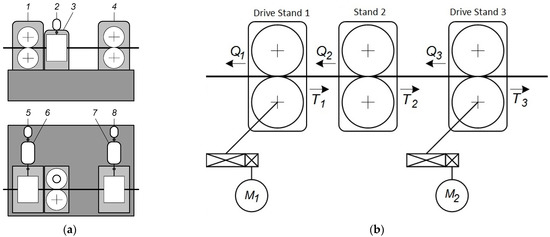
Figure 2.
Equipment arrangement (a) and kinematic diagram (b) of a continuous three-stand rolling section (block): 1 and 4, drive stands; 3, idle stand; 6 and 7, electric motors; 2, 5, and 8, velocity generators.
Analysis of the physical processes occurring in the system provides for its separation into the following parts: electromechanical converters (electric motors and power section of frequency converters), stands (including gearboxes), deformation zones and inter-stand spaces. In this case, electromechanical converters and stands are different technological units, with easily identifiable physical boundaries. The boundaries between deformation zones and inter-stand spaces are established on the inner surfaces (sections) of the zone where all surface points have velocities equal to the metal’s entry or exit speeds from the stand. This division is convenient for developing a mathematical description.
The structure of the created model should have entry actions in the form of control voltages at the input of the frequency converters, one output coordinate (the wire speed at the exit from the last stand) and two disturbance effects (the rear tension in the first deformation zone and the front tension in the last deformation zone). Models of logically related parts must have entry and exit coordinates that are consistent with each other in terms of quantity and time.
2.2. Structure of the Digital Model of the Rolling–Drawing Mill
An enlarged block diagram of the unit model is shown in Figure 3. The mathematical interpretation of the functional blocks is similar to the corresponding units of the continuous rolling and straight-through drawing mills considered in [27,40]. Exceptions are the mathematical models of the deformation zone of the idle stand and the inter-stand space before it [41].
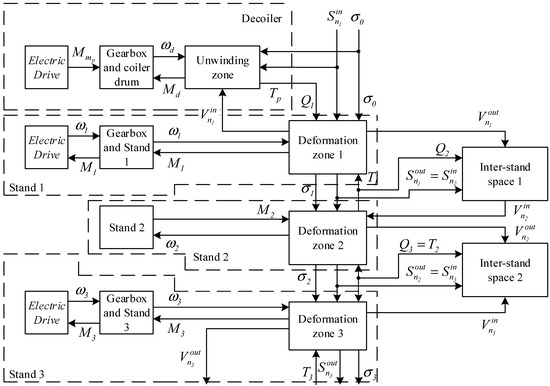
Figure 3.
Simplified block diagram of a three-stand rolling section as a controlled object.
To implement models presented in the form of complex multi-connected structures, the most effective option is to use of the Simulink graphical programming environment, which is part of the Matlab software suite. This software is widely used in modeling the automated electric drives and control systems for rolling mills. Such models were used by the authors of [42,43,44,45] and many other researchers. This suite is a convenient tool for implementing the developed model.
2.3. List of Active Tasks
The presence of the idle stand is the key difference of the continuous train of the unit under study. Essentially, in this stand, the rolling process is replaced by drawing and pressing processes. Accordingly, the occurring deformation of the metal has particular features that must be taken into account when constructing a model of the deformation zone. The development of the deformation zone model taking into account these features is the first active task.
The forming process in the idle stand differs somewhat, as rolling is ensured only by the forces of tension and back pressure created by the electric drives of the next and previous stands. As a result, there are certain particulars in the relationship between the drive stands and the idle stand. Therefore, rolling-block models should be designed with this difference in mind. This is the second task covered in this publication.
The absence of an electric drive for the second stand renders impossible the direct use of the known control systems for electric drives of continuous train of rolling mill stands. A particular feature of rolling in the studied section is the opportunity to use the reserve of friction forces to improve energy conditions and optimize the power parameters of rolling. This would provide an answer to the third task: developing control systems for electric actuators of the drive stands of the block, taking into account this technological feature. The solution to the tasks is considered below.
3. Materials and Methods
3.1. Assumptions Made in the Development of Digital Models of a Continuous Rolling Mill
For any technological unit, the complex of digital models is a set of mathematical relationships that describe its behavior in dynamic modes. These relationships link input and output variables, process parameters and time. The input variables are control and disturbance actions. The output variables are controlled and uncontrolled coordinates.
When developing the digital models, the following assumptions were made.
- In the intervals between the deformation zones, the unwinding and winding sections:
- The weight of the wire is insignificant and has no impact on its deformation.
- The physical and mechanical properties of the material are uniform.
- The workpiece and wire have a constant area and cross-sectional shape.
- The forces in the workpiece and the processed wire outside the deformation zones do not exceed the yield point of the material, i.e., the deformation is extremely elastic.
- Elastic deformation is uniformly distributed over the entire section of the workpiece, and the wave processes associated with the distribution of deformation along the length are negligible and neglected.
- In the deformation zones:
- Mill rolls and stands are considered as absolutely rigid mechanical systems.
- The roughness of the tool surface is uniform throughout the deformation zone.
- The properties of the technological lubricant, and, consequently, the friction coefficient, are constant within the deformation zone.
- The boundaries of the deformation zone are determined by the “rigid ends” theory and coincide with the inlet and outlet sections of the milled metal.
- In the mechanical units of the mill:
- The elastic properties of the connecting shafts and gearboxes do not affect the operating modes of electric motors and the process of forming tension (back pressure) in rhe workpiece.
- There is neither roll slipping nor wire slipping along the drum of the drawing block.
3.2. Digital Model of the Deformation Zone of the Drive Stand
The mathematical model of the deformation zone was developed on the basis of the energy conservation law (its simplified formula for the rolling process was substantiated by Prof. Vydrin V.N.) [46]:
where Nв is the power provided to the deformation zone from the side of the electric drive; NQ is the power provided to the deformation zone by back pressure Q (“−” sign) or by tensile force (“+” sign) through the rear end of the feed; NT is the power provided to the deformation zone by tensile force T (“+” sign) or by back pressure (“−” sign) through the front end of the feed; Nf is the power spent for metal forming; Nm is the power of slipping friction forces on the “feed/rolls” contact surface; and i is the serial number of the stand (1 or 2).
This expression does not take into account the power spent for the elastic deformation of the feed, the power for creating additional deformations (shears) due to the shape of the deformation zone or other types of powers (for changing the kinetic energy of the metal, etc.), which account for less than 2–3% of the power balance [24].
The powers provided by the front tension (or back pressure) and rear back pressure (or tension) are determined by the dependencies
where and are the feed speed at the entry and exit of the deformation zone; is the draw-down during rolling; and , , and are, respectively, the sections and lengths of the feed at the entry and exit of the deformation zone.
The power supplied to the deformation zone from the actuating unit is defined as the product of elementary friction forces τ, the direction of which coincides with the trajectory of movement of the points of the contact surface, by the peripheral speed of the rolls Vв, summed over the surface S of metal contact with the rolls:
Considering the assumption of a rectilinear law of variation of the width b and the yield point of the metal along the deformation zone
and the absence of elastic deformation of the rolls
Expression (3) takes the form
where Rr is the radius of the rolls of the stand and α is the current value of the angle in the deformation zone (in the range from 0 to α0, see Figure 4).
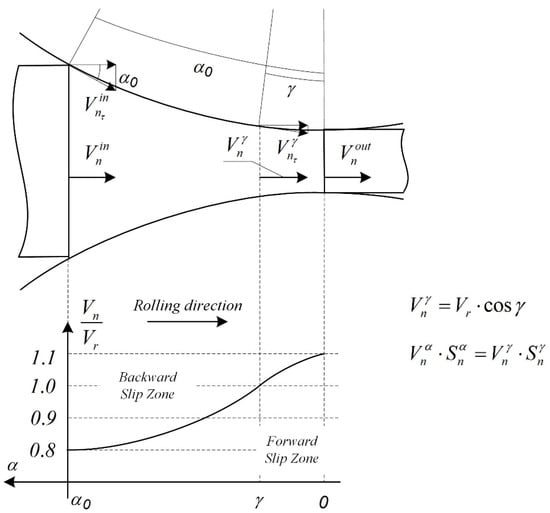
Figure 4.
Slip on the feed surface in the uniform deformation zone.
The direction of the longitudinal friction force τ in the deformation zone changes. According to the “rigid ends” theory proposed by I.M. Pavlov [47], the velocities of particles of the inlet section, as well as the velocities of particles of the outlet section of the deformation zone, are equal to each other. Here, the condition holds true.
Obviously, in this case, there are two areas in the deformation zone, as shown in Figure 4. In the first, the backward slip zone, the speed of the metal is lower than the circumferential speed of the rolls, so energy is transferred from the roll to the metal. In the second, the forward slip zone, on the contrary, the speed of the metal is higher than the circumferential speed of the rolls, so energy is transferred in the opposite direction, from the metal to the rolls. There is a certain central angle, which defines a line on the surface of the rolls where the speeds of the metal and the roll are equal. This angle, similar to the indicated line, is usually called the “critical” angle. The given pattern is constructed for the “classic” case of rolling, with front tension and back pressure arising from backward slip of the metal. At the same time, the calculations presented below are valid for the case of the reverse distribution of tensile (back pressure) forces. Differences between tension and back pressure modes should be taken into account in the final model by introducing appropriate signs in the relationships between blocks.
In the backward and forward slip zones, the longitudinal friction forces and have opposite direction; therefore, Expression (6) for two rolls should be rewritten as
provided that
Expression (7) takes the form
where α0 is the entering angle; σ is the deformation resistance; and f is the friction coefficient.
The power of the forming force can be obtained by differentiating the Fink’s dependence [46]:
where Af is the action for forming the roll; θ is the metal volume; and θvd is the volume displaced in deformation.
In the interval ∆t, through the deformation zone passes a volume of metal equal to the area of its critical surface (the surface inside the deformation zone where all points have the velocity equal to the circumferential speed of the rolls) multiplied by the forward velocity of the particles of this surface, corresponding to the forward velocity of the rolls at the critical section point :
The area under the given rectilinear law of width variation (Figure 5) is determined by the dependence
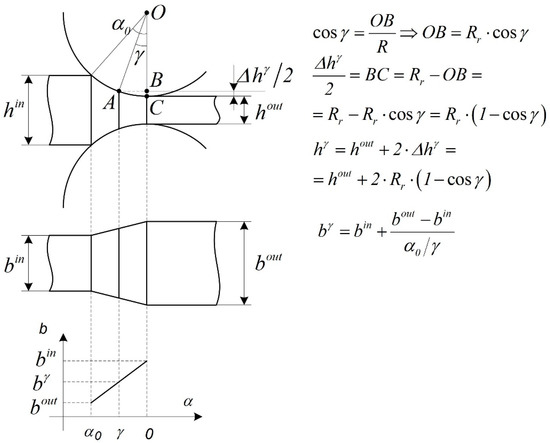
Figure 5.
Determination of the critical surface area.
The indicated volume, determined by the dimensions ( ), enters the deformation zone, undergoes there a final deformation lnµ and leaves with new dimensions (; ). Thus, the displaced volume in time ∆t will be determined as
, or, provided that ,
After substituting (12) into (10), an expression is obtained to determine the power of the forming force during the rolling:
The power of the force Nm of slipping friction on the contact surface should also be determined taking into account the backward and forward slip zones. In the general case, for two rolls, the slipping friction value can be found from the expression:
or, taking into account (4), (5) and (8),
The slipping speed of the metal relative to the rolls is determined by the dependences.
- For backward slip zone:
- For forward slip zone:
and are the contact surface area and translational speed of the rolls at the point corresponding to the current value of the angle α.
Substituting (15) and (16) into (14), we obtain expressions for the powers of sliding friction force.
- For backward slip zone:
- For forward slip zone:
- For full power of friction:
Provided that the angular velocity of the rolls is constant throughout the entire deformation zone, taking into account the ratio of torque and power, , Expressions (1), (2), (13) and (17) for the ith stand can be represented as
Here, the area in an arbitrary section, including the neutral section, is found from Expression (11), without taking into account the spreading effect:
where and are the cross-sectional areas of the strip at the entry and exit of the ith deformation zone.
The angle of the neutral section can be determined from the dependence (9):
The metal speed at the exit from the stand is determined by the angular speed of rotation of the rolls and depends on the value of the critical angle
The speed of the metal at the entrance to the stand
Changes in the section of the processed metal and its deformation resistance are determined by the expressions
Figure 6 shows a diagram of the mathematical model of the deformation zone compiled according to Equations (18)–(30). Functional converters FC1–FC3 implement the dependences (22), (21) and (25), respectively. The presented digital model most accurately determines the relationship between the input and output coordinates of the structure shown in Figure 3.
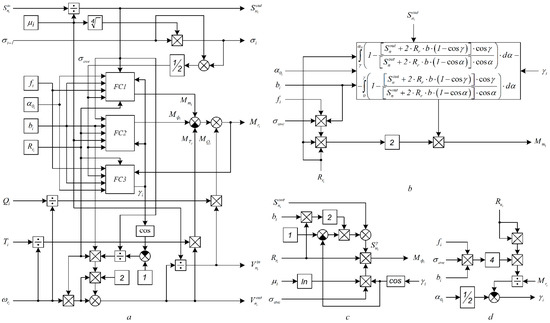
Figure 6.
Functional layout of the mathematical model of the rolling stand deformation zone: (a) general diagram; and (b–d) diagrams of functional converters FC1, FC2 and FC3, respectively.
3.3. Mathematical Description of Idle Stand Deformation Zone
The energy conservation law for the idle stand has the form
where is the idle moment required to overcome the rolling frictional forces in bearings.
The system of equations describing the idle stand deformation zone (provided that ) is composed of Expressions (31), (19)–(22) and (25)–(30) and has the form
If this inequation is not fulfilled, the applied forces are insufficient and the speed of the metal at the entry and exit from the rolls (and the speed of the rolls themselves) is equal to zero.
The diagram of the mathematical model of the idle stand deformation zone is shown in Figure 7. Functional converters FC1–FC3 implement the dependencies (22), (21) and (25); their block diagrams are shown in Figure 6b–d, respectively.
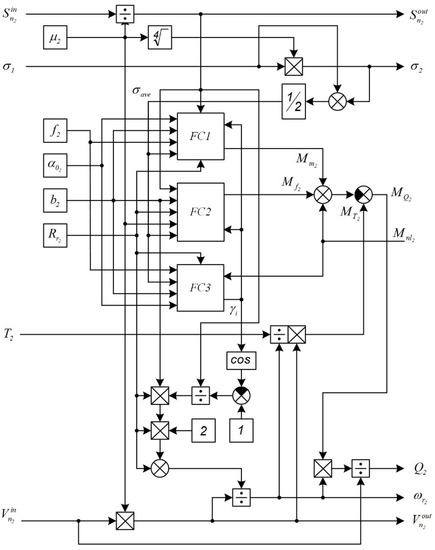
Figure 7.
Block diagram of the mathematical model of the idle stand deformation zone.
3.4. Digital Model of the Inter-Stand Space
The processed metal experiences tensile force (or back pressure) in the sections between the deformation zones (Figure 8), due to the discrepancy between the instantaneous values of the velocities of the exit from the previous stand and the entry into the next stand. Under the impact of these forces, the metal feed is elastically deformed: under tensile force, it becomes longer and thinner, while, under back pressure, it becomes shorter and broader. In this case, the magnitude of the forces can be described by integral equations:
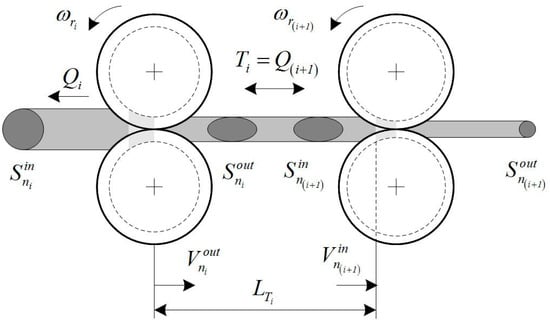
Figure 8.
Inter-stand space, design diagram.
After simple transformations, they take the form
According to these expressions,
When rolling with tensile force, , and, with back pressure, .
Figure 9 shows the block diagram of the dynamic mathematical model of the inter-stand space of the rolling block. The diagram is based on Equations (35) and (36). Thus, the DT of the inter-stand space determines the relationship between the three input and two output coordinates shown in the diagram.
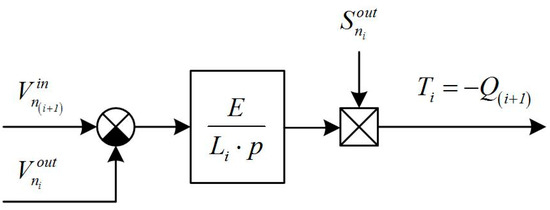
Figure 9.
Structural diagram of the Digital Twin of the inter-stand space.
According to Figure 3, the mathematical model of the inter-stand space in front of the idle stand must have three input coordinates: the speed and value of the cross-sectional area of the strip at the exit from Stand 1; the tensile force in the feed between Stand 1 and idle stand; and one output coordinate, namely the strip speed at the entry to the idle stand. The elastic deformation of the metal in the inter-stand space is described by the integral equation
from which, after differentiation, we obtain
Figure 10 shows a block diagram of the inter-stand space in front of the idle stand. To exclude the differentiating link (Figure 10a), this diagram is transformed to the form shown in Figure 10b.
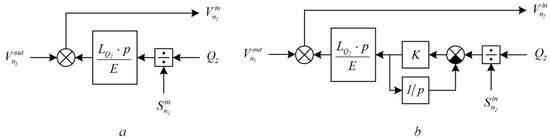
Figure 10.
Block diagram of the mathematical model of the inter-stand space in front of the idle stand: (a) with the differentiating link; (b) without the differentiating link.
3.5. Purpose of the Developed Digital Models
In accordance with the actual tasks, the following areas of application of the developed DT were validated.
- Development of an integrated model of multi-connected mechatronic systems of a rolling mill. The purpose of the model is to study the interaction of such systems through metal.
- Study of the impact of external factors on the metal forming in the deformation zone.
- Analysis of load modes of electric drives during adoption of new assortments and profiles of rolled products and calculation of the strength characteristics of mechanical equipment.
- Study of dynamic loads and transient processes of electromechanical systems under disturbances arising during rolling and optimization of dynamic modes.
- Development of new control algorithms in digital control systems of various levels.
Obviously, the solution of these challenges falls outside of the scope of a single publication. Below, we consider the application of models in the design of a control system for electric drives of a rolling block with an idle stand.
4. Development of a Method for Controlling Electric Drives of a Rolling Block
Experience of designing and operating the rolling mills shows that the technological process of rolling is carried out with an underutilization of the equipment potential regarding supplying the energy to the deformation zone. The reason for this is a large number of technological limitations and, as a consequence, large values of critical angles. A detailed description of this issue is given in [48,49].
4.1. Using the Frictional Force Reserve during Rolling
Both Russian and foreign scientists have repeatedly made attempts to intensify the process of metal deformation, including through the use of the so-called reserve of pulling friction forces in the deformation zone. However, during these attempts, there were difficulties associated with ensuring the process stability when rolling with large drafting or with dimensional stability along the length of the strip when rolling with high tensile force [50]. These factors meant that such technologies were not applied in practice.
Below is an analysis of energy efficiency during the rolling process with the idle stand in the production line.
In the absence of tension or back pressure, the efficiency factor for the steady rolling mode is determined by the ratio of the forming work to full work on the roll barrel
For a comparative assessment of the use of the reserve of friction forces, this coefficient is taken as the base ().
Change in the process efficiency during varied load of the deformation zone of the idle rolls, as determined by the ratio , is found from the dependence
This expression was obtained under the condition that rolling in the “drive stand–idle stand” system is carried out at a constant total draw-down ratio of the processed metal () and a constant speed at the exit from the deformation zone. Joint solution of Equation (41) with Equations (9), (13) and (17) provides the curves shown in Figure 11. These explain the proposed principle of controlling electric drives of the rolling block using friction forces in deformation zones.
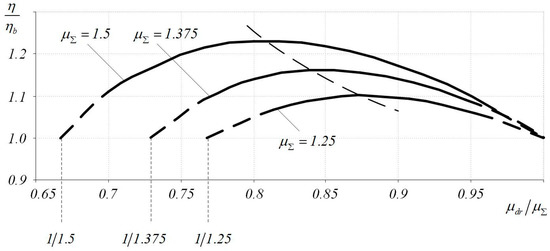
Figure 11.
Curves of rolling process efficiency factored on the load of the idle rolls.
An electric drive with control of the critical angle values which implements this principle is discussed below.
4.2. Regulation Principle and Electric Drive Control System
Efficient use of electric drives of the rolling section stands requires highly developed system of indirect control and alignment of critical angles in deformation zones. Such control ensures the implementation of the principle of using the reserves of friction force in the deformation zones. The functional layout of the system is shown in Figure 12 [51].
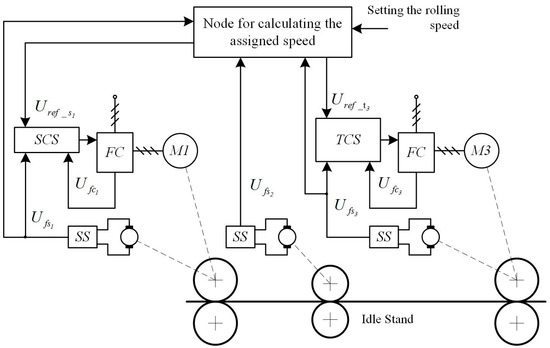
Figure 12.
Functional layout of the control system with control of the friction force reserve in the deformation zones: node for calculating the assigned speed; setting the rolling speed; SCS, automatic control system for speed/pressure position; idle stand; SS, speed sensor.
Electric drives of Stand 1 and Stand 3 are made on the basis of asynchronous motors with squirrel-cage rotors M1 and M3, which receive power from frequency converters (FC). Electric drive control systems are built on the principle of the coordinate axis orientation in the direction of the resulting vector of the rotor flux linkage [52]. The vector control system uses proportional-integral (PI) rotation speed controllers. Their use is justified, as the processes in continuous lines are relatively “slow”. Therefore, disturbance effects have no impact on the stability of speed control systems. Scalar control systems with proportional (P) controllers can be used in other technological lines, where shock load is applied during the roll bite. In this case, additional research is required, since such systems have a known disadvantage, a static speed control error. This will lead to the need for its elimination by the automatic tension control system and, accordingly, to a decrease in the tension control accuracy. Therefore, this method of speed control is not recommended for the studied electric drives.
The structure includes a counter-tension control system (CTCS), a speed control system or a tension control system (TCS). According to the definition, counter-tension is a longitudinal force applied to the metal entering the deformation zone, directed opposite to its motion [53]. When rolling in the section under study, this force is caused by the back pressure that occurs in the second inter-stand space due to the difference in the speeds of adjacent stands.
An additional control loop for adjusting the critical angle included into the unit for calculating the speed and assigned tension is not shown. Its functional layout is discussed below. It either controls the critical angle in Stand 1 by preventing its reduction below a predetermined value or ensures the alignment of critical angles in the deformation zones of the drive stands. If the reserve of friction forces is completely exhausted when compensating for the disturbance effects in one of the drive stands, then the value of the critical angle will approach zero. This would automatically correct the assigned speed for Stand 1. As a result, the tension in the second and back pressure in the first inter-stand spaces will change. The energy input into the idle zone from the side of the stand that has exhausted the reserve of friction forces will not increase any further. The increase in energy will occur thanks to the stand with a larger critical angle.
The controlling principle that ensures the alignment of critical angles is explained as follows. According to the law of energy conservation, written in the form of a power balance (1), any disturbance effect leads to a change in the conditions of deformation. This causes a change in dependencies between the powers of forming, elastic deformation, friction and other parameters. Moreover, as noted above, the energy balance is regulated by the critical angle separating the backward and forward slip zones in the deformation zone (see Figure 4). The greater is the value of the critical angle, the longer is the forward slip zone and the higher is the speed of the metal at the exit from the stand (provided that the rotation speed of the rolls is constant). Hence, it follows that the critical angles can be controlled indirectly. For this, only control of the rotation speed of the rolls, that is, the actuating units, is required.
This is explained mathematically as follows. The speeds of the metal at the stand’s entry and exit are determined by the dependencies
In this case, critical angles are calculated by the expressions
It follows from the above that the node for calculating the assigned speed must be implemented in accordance with the system of equations:
Figure 13 shows a diagram of a functional block that implements these dependencies. The use of the integral critical angle controller (CAC) is substantiated.
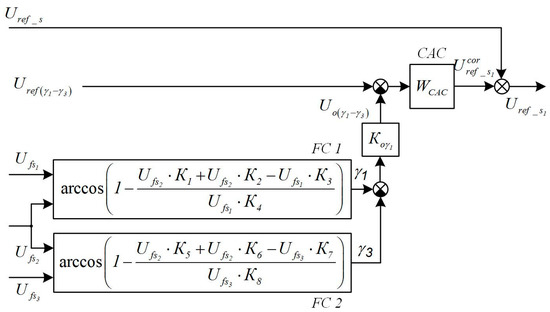
Figure 13.
Functional diagram of the block for calculating the assigned speed CAC (critical angle controller).
This block is included in the node for calculating the assigned speed, as shown in the diagram in Figure 12. It is implemented as a control algorithm in the automated control system of the technological process of the rolling–drawing unit.
5. Result
Based on the structure shown in Figure 3 of the developed models of deformation zones, inter-stand spaces (Figure 6 and Figure 7) and functional layouts of the developed electric drive (Figure 12 and Figure 13), the authors designed a complex mathematical model of interconnected electromechanical systems of a rolling section with an idle stand. It is implemented in the Matlab’s Simulink environment. The model proposes a new algorithm for controlling electric drives. When developing the model, the authors used the characteristics of the experimental integrated rolling–drawing mill shown in Figure 1 and Figure 2. The parameters of the rolling section are presented in Table 1.

Table 1.
Constructive and technological parameters of the rolling section of the integrated rolling–drawing mill.
The work shows runtime assessment of a rolling cycle during implementation of the developed method. Selected results of modeling and experimental studies are presented below.
5.1. Results of Mathematical Modeling
To illustrate the proposed control method, Figure 14a shows the transient processes of the main controlled coordinates when the block accelerates to the steady rolling speed. The time dependencies ωm3 of the angular speed of the Stand 3 drive, the tensile force T2 and the back pressure Q2 in the second interval and the critical angles γ1 and γ3 in the deformation zones of Stand 1 and Stand 3 are shown. Figure 14b shows similar processes in the mode of tension change during rolling, over the same interval.
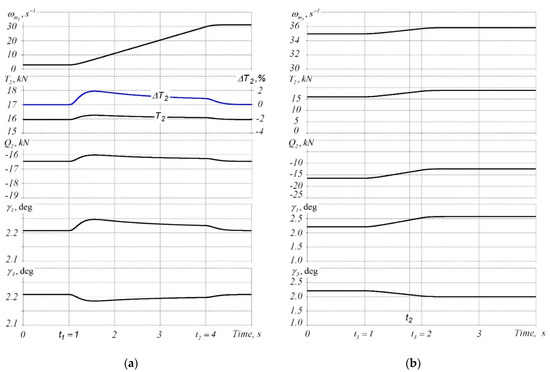
Figure 14.
Results of modeling the acceleration processes for the rolling block (a) and changes in tension in the second inter-stand space (b).
Figure 14a shows supplying the signal for assigned acceleration at the time t1 = 1 s. Within the interval t1 − t2 = 3 s, the mill is accelerated to operating speed. The initial rolling conditions are taken at the angular drive speed of 0.5 s−1 and steady-state values of tension and back pressure equal 15.9 and 16.5 kN, respectively.
The maximum tensile deviation ΔT2 does not exceed 2% of the steady-state value. Analysis of similar time dependences obtained under different initial conditions showed that the absence of control of critical angles in the acceleration mode leads to significant deviations of inter-stand tensions and back pressure. Thus, the tensile deviation in the known direct tension control system exceeds 12% [27]. In the developed system, similar values do not exceed 5%. The higher accuracy of tension control is explained by the fact that the critical angle control loop continuously corrects the speed setting of the stand.
Figure 14b depicts the changed assignment for the difference in critical angles (from 0 to 0.6 degrees) at the moment of time t1 = 1 s, at the input of the speed control system of Stand 3. This leads to 5 kN increase in tension, and the transient time is about 1 s. This speed of the system is sufficient to work out transients caused by changes in tension during rolling, without excessive corrections and fluctuations.
The modeling results confirm the efficiency of the proposed control algorithm for electric drives of the rolling section. In the steady state, the rolling speed control error does not exceed 0.2 m/s, which meets the technological requirements. The tension control error in all modes per rolling cycle (acceleration, deceleration and seam rolling) is also less than the allowable error (as a rule, ±5%).
5.2. Results of Experimental Studies
Figure 15 depicts the oscillograms of the coordinates of electric drives obtained at the industrial installation shown in Figure 2. The installation implements the new algorithm for controlling electric drives using the reserve of friction forces in the deformation zones (see Figure 12). The authors analyzed modes similar to those shown in Figure 14: acceleration of electric drives (Figure 15a) and disturbance attack in the form of the difference in critical angles of deformation zones (Figure 15b). The oscillograms show the coordinates: and are angular velocities of the first and third drives; is the speed of the rolls of the idle stand; and and are drive currents.
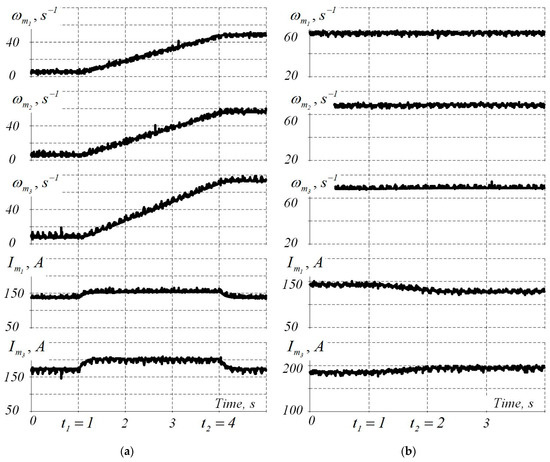
Figure 15.
Results of experimental studies during acceleration (a) and when changing the setting of critical angles in the first and third deformation centers (b).
Notably, the presented oscillograms are completely identical with the results of mathematical modeling discussed above. This confirms the correspondence of the experimental data to the calculated results, also prompting a conclusion about the adequacy of the developed digital model to the object under study.
In general, the conducted runtime assessment of electric drives of the rolling block confirms the operability of the proposed control systems, the reliability of theoretical conclusions and the correctness of the choice of principles for constructing the control systems. The considered principle of controlling the electric drives, as well as the proposed transfer functions of the regulators, ensures the control of the rolling speed with <2% maximum error and tension control with <5% error. Consequently, the specified technological requirements are met in all operating modes.
6. Discussion of the Results
The presented publication provides the results of developing a digital model and studying a rolling block with an idle inter-stand. Concurrently, the authors develop mathematical models of the drawing section of the integrated rolling–drawing unit. These include models of the deformation zone during drawing, models for the inter-drum space interdependence and decoiler and coiler models. However, since this work is devoted to the study of electromechanical systems of the rolling section, these models are not considered. The model of the deformation zone during drawing is based on the energy conservation equation similar to (1). Therefore, its structure follows the patterns presented in Figure 6 and Figure 7. The model of the inter-drum space of the drawing section is based on the integral equations of the drawing and tension forces shown in Expressions (33) and (34). Similar expressions are used for models of change in power parameters for the intervals “decoiler–stand” and “drawing drum–coiler” (see Figure 1).
Obviously, it is impossible to consider all the models of the unit under study within the framework of one publication. Models of drawing mills can be assessed in [41,54] and models of coiling–decoiling devices are presented in [55,56].
The developed digital models of the rolling stand deformation zone and the model of the interconnection of the stands through the metal are recommended for use in researching processes in multivariable systems of continuous train of sheet-rolling and section mills. Currently, these were used to develop a mathematical model of a three-stand continuous train of a wide-strip hot-rolling mill. [24]. It is applied in the research of the developed systems for limiting the dynamic loads [57,58,59] and systems for automatic control of zero tension [60,61]. The results are presented in [62,63]. In addition, the considered principle of modeling the interconnection of stands is used in the study of processes in the electromechanical systems of the stands of a wire mill with multi-roll grooves [64,65].
Along with the application on wire mills, the obtained results are recommended for practical implementation in three-stand continuous trains of wide-strip hot-rolling mills. These include the mills “2000” of the Magnitogorsk Iron and Steel Works, PJSC Severstal (Cherepovets, Russia), “2286” (France), “2250” (Japan), “2300” (Germany) and others. Relevant information is presented in [66,67,68].
In all cases, the overall goals are:
- Improve the quality of rolled products by increasing the accuracy of control of process conditions.
- Reduce energy consumption by optimizing load modes and redistributing loads between the stands.
- Increase equipment durability by optimizing rolling forces and reducing dynamic loads.
7. Conclusions
- Functional dependencies of technological variables of a continuous rolling section with an idle inter-stand of an integrated rolling–drawing mill are determined. These include rolling forces, drive torques, drive or roll speeds and inter-stand tensions. The assumptions made during the development of models of deformation zones and inter-stand spaces are substantiated.
- Digital models of deformation zones of stands and inter-stand spaces of a three-stand train are developed, with due consideration of the relationship between the driven and idle stands through the metal. They provide ground for analyzing the processes in the deformation and tension zones when changing the process conditions of rolling and the mechanical properties of the processed metal.
- On the basis of local digital models, a block diagram of a rolling section model with an idle inter-stand is developed. The development takes into account the relative elastic elongation of the wire in the inter-stand spaces and the conditions for its deformation in the driven and idle stands.
- A complex mathematical model is developed, providing for analysis of the steady-state and dynamic rolling modes by methods of structural modeling. The model is implemented in the form of software modules in the Simulink programming environment as part of the Matlab 7.0 suite.
- The control principle for electric drives of a three-stand rolling section with control of critical angles in the deformation zones of the drive stands is substantiated. The implementation of the method provides for the use of the energy of frictional forces for controlled rolling of the feed metal in an idle stand.
- As a result of mathematical modeling and experimental studies, it was found that the absence of the critical angle control in the acceleration mode leads to deviations of the inter-stand tension, up to 12%. Implementation of the developed control method results in fall of the maximum tensile deviations even below the permissible level of ±5%. This is achieved due to the rapid response time of the critical angle control system, which ensures the equalization of the speeds of the electric drives in successive stands. As a result, the precision of tension regulation in the inter-stand spaces is increased. The research results confirm a 2.5-fold decrease in regulation error, from 12% to 5%.
- The conducted runtime assessment of electric drives of the rolling section confirmed the adequacy of the developed model to the physical object. The legitimacy of the theoretical premises and assumptions used in the development of a control system for electric drives was confirmed indirectly.
- The developed digital models are recommended for use in research of dynamic modes and power interconnection of electromechanical systems of continuous sheet and section rolling mills. The proposed method for controlling electric drives can be used in the development of control algorithms that limit the power connection of the stands through the metal.
Author Contributions
Methodology, A.A.R.; software, V.R.G.; validation A.S.K.; and formal analysis, B.M.L. All authors have read and agreed to the published version of the manuscript.
Funding
The work was carried out with the financial support of the Ministry of Science and Higher Education of the Russian Federation within the framework of a subsidy for financial support for the fulfillment of a state task (fundamental scientific research), contract No. FENU-2020-0020 (2020071GZ).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brook, P.A. Digital twins based on the simulation of multiphysics processes. Des. Autom. 2019, 1–2, 74–76. [Google Scholar]
- Oztemel, E.; Gursev, S. Literature review of Industry 4.0 and related technologies. J. Intell. Manuf. 2020, 31, 127–182. [Google Scholar] [CrossRef]
- Lim, K.Y.H.; Zheng, P.; Chen, C.H. A state-of-the-art survey of Digital Twin: Techniques, engineering product lifecycle management and business innovation perspectives. J. Intell. Manuf. 2020, 31, 1313–1337. [Google Scholar] [CrossRef]
- Kunath, M.; Winkler, H. Integrating the Digital Twin of the manufacturing system into a decision support system for improving the order management process. Procedia Cirp 2018, 72, 225–231. [Google Scholar] [CrossRef]
- Park, C.Y.; Kim, J.W.; Kim, B.; Lee, J. Prediction for Manufacturing Factors in a Steel Plate Rolling Smart Factory Using Data Clustering-Based Machine Learning. IEEE Access 2020, 8, 60890–60905. [Google Scholar] [CrossRef]
- Qu, Y.J.; Ming, X.G.; Liu, Z.W. Smart manufacturing systems: State of the art and future trends. Int. J. Adv. Manuf. Technol. 2019, 103, 3751–3768. [Google Scholar] [CrossRef]
- Ansaldo Sistemi Industriali. Automation Systems in Flat Products White Paper. Available online: https://www.nidec.com/~/media/nidec-com/product/catalog/pdf/asi/Automation_Systems_in_Flat_Products.pdf (accessed on 1 January 2021).
- Zhang, F.; Wang, X.; Zong, S.; Xiang, X. Research and application of computer control system for aluminium single-stand 4-high cold rolling mill. J. Eng. 2016, 2016, 415–422. [Google Scholar] [CrossRef]
- Ohlert, J.; Sprock, A.; Sudau, P. Digitalization in Hot and Cold Rolling Mills. Mater. Sci. Forum 2016, 854, 215–224. [Google Scholar] [CrossRef]
- Junquera, A.M.V.; González, J.G.; Balsera, J.M.V.; Montequín, V.R. A Wire Rod Rolling Mill Digital Twin for the Simulation of the Rolls Replacement Process. Proceedings 2020, 63, 13. [Google Scholar] [CrossRef]
- Sadovoi, O.; Nazarova, O.; Bondarenko, V.; Pirozhok, A.; Hutsol, T.; Nurek, T.; Glowacki, S. Modeling and Research of Electromechanical Systems of Cold Rolling Mills; Monograph: Krakow, Poland, 2020; Available online: http://188.190.33.55:7980/jspui/handle/123456789/7350pdf (accessed on 1 January 2021).
- Kharitonov, V.A.; Radionova, L.V. Designing of Resource Saving Technologies of High Tensile Carbon Steel Wire Production Based on Modelling; MSTU: Magnitogorsk, Russia, 2008. [Google Scholar]
- Pedersen, L.M. Modeling and Control of Plate Mill Processes. Department of Automatic Control, Lund Institute of Technology. Available online: https://portal.research.lu.se/portal/en/publications/modeling-and-control-of-plate-mill-processes(99cfc9e1-ce09-4e9d-b5e7-92033a4a31b0).html (accessed on 1 January 2021).
- Yin, F.; Zhang, D.; Zhang, Y. Dynamic modelling and rolling data analysis of the tandem hot rolling process. Trans. Soc. Model. Simul. Int. 2017, 93, 307–321. [Google Scholar] [CrossRef]
- Karandaev, A.S.; Baskov, S.N.; Gasiyarova, O.A.; Loginov, B.M.; Khramshin, V.R. Calculating Simulation Model Parameters for Electromechanical System of Rolling Mill Stand. Int. Ural Conf. Electr. Power Eng. 2020, 469–474. [Google Scholar] [CrossRef]
- Alves, P.G.; Castro, J.A.; Moreira, L.P.; Hemerly, E.M. Modeling, simulation and identification for control of tandem cold metal rolling. Mater. Res. 2012, 15, 928–936. [Google Scholar] [CrossRef]
- Alves, P.G.; Hemerly, E.M. Modeling and numerical simulation of the deformation for calculations of set-up parameters in processes of cold rolling. In Proceedings of the 44th Rolling Seminar—Processes, Rolled and Coated Products. 2007. Available online: https://www.scielo.br/scielo.php?script=sci_nlinks&ref=000176&pid=S1516-1439201200060001500018&lng=en (accessed on 1 January 2021).
- Kozhevnikov, A.V.; Kozhevnikova, I.A.; Bolobanova, N.L. Simulation of cold-rolling process in dynamic conditions. Metallurgist 2017, 61, 519–522. [Google Scholar] [CrossRef]
- Hirt, G.; Senge, S. Selected processes and modelling techniques for rolled products. Procedia Eng. 2014, 81, 18–27. [Google Scholar] [CrossRef]
- Hanoglu, U.; Šarler, B. Hot Rolling Simulation System for Steel Based on Advanced Meshless Solution. Metals 2019, 9, 788. [Google Scholar] [CrossRef]
- Sorochan, E.; Artiukh, V.; Melnikov, B.; Raimberdiyev, T. Mathematical Model of Plates and Strips Rolling for Calculation of Energy Power Parameters and Dynamic Loads. Matec Web Conf. 2016, 73, 04009. [Google Scholar] [CrossRef]
- Sun, J.; Peng, Y.; Liu, H. Dynamic characteristics of cold rolling mill and strip based on flatness and thickness control in rolling process. J. Cent. South Univ. 2014, 21, 567–576. [Google Scholar] [CrossRef]
- Kozhevnikov, A.V.; Kozhevnikova, I.A.; Bolobanova, N.L. Development of the model of cold rolling process in dynamic conditions. J. Chem. Technol. Metall. 2018, 53, 366–372. [Google Scholar]
- Radionov, A.A.; Karandaev, A.S.; Evdokimov, A.S.; Andryushin, I.Y.; Gostev, A.N.; Shubin, A.G. Mathematical modelling of interconnected electromechanical systems of a continuous subgroup of rolling mill stands. Part 1. Development of a mathematical model. Bull. South Ural State Univ. Ser. Energy Ind. 2015, 15, 59–73. [Google Scholar] [CrossRef]
- Glowacki, M.; Kedzierski, Z.; Kusiak, H.; Madej, W.; Pietrzyk, M. Simulation of metal flow, heat transfer and structure evolution during hot rolling in square-oval-square series. J. Mater. Process. Technol. 1992, 34, 509–516. [Google Scholar] [CrossRef]
- Riches, P. Rolling into the Future, Long Rolling Control System Utilizing the Changing Trends in Technology and Digitalization. Technical Contribution to the 21 Seminário de Automação e TI, Part of the ABM Week. SP, Brazil. 2017. Available online: https://abmproceedings.com.br/en/article/rolling-into-the-future-long-rolling-control-system-utilizing-the-changing-trends-in-technology-and-digitalization (accessed on 1 January 2021).
- Radionov, A.A. Automated Electric Drive for Steel Wire Production: A Monograph; GOU VPO “MSTU”: Magnitogorsk, Russia, 2007. [Google Scholar]
- Radionova, L.V.; Radionov, A.A. Current state and development prospects of steel wire drawing process. Mech. Eng. Netw. Electron. Sci. J. 2013, 1, 3–11. [Google Scholar] [CrossRef]
- Zhuchkov, S.M.; Gorbanev, A.A.; Kolosov, B.N. New technology and equipment for improving the quality of wire rod. Nauka Innov. 2007, 3, 43–49. [Google Scholar] [CrossRef]
- Zhuchkov, S.M.; Gorbanev, A.A.; Tokmakov, P.V.; Kolosov, B.N. Terms of using of three-focused rolling module in the process of bar rolling. Foundry Prod. Metall. 2005, 46–50. [Google Scholar]
- Radionov, A.A.; Radionova, L.V.; Kharitonov, V.A.; Malakhov, O.S. On the possibility of reducing the power spent on the process of wire rolling on a combined rolling-drawing mill. Electrotech. Syst. Complexes. 2005, 10, 63–70. [Google Scholar]
- Zhuchkov, S.M.; Kulakov, L.V.; Lokhmatov, A.P. Efficiency of continuous section rolling with undriven stands. Met. Cast. Ukr. 2004, 8–10, 50–52. [Google Scholar]
- Fastykovsky, A.R. Longitudinal stability of the strip during the operation of the ‘rolling stand—Idle tool’ system. Izvestiya vuzov. Chernaya Metall. 2013, 12, 21–24. [Google Scholar]
- Fastykovsky, A.R.; Nikitin, A.G.; Belyaev, S.V.; Dobriansky, A.V. Particular features of mastering the technology of rolling and separation on the operating continuous small-section mill. Izvestiya. Ferr. Metall. 2020, 63, 5, 313–317. [Google Scholar] [CrossRef]
- Fastykovskii, A.R. Region for Extrolling Feasibility and Effective Deformation Modes. Russ. J. Non Ferr. Met. 2011, 52, 230–233. [Google Scholar] [CrossRef]
- Lokhmatov, A.P.; Zhuchkov, S.M.; Kulakovm, L.V. Continuous Rolling of Sectional Steel Using Operational Idle Stands: Monograph; Naukova Dumka: Kiev, Ukraine, 1998. [Google Scholar]
- Nikiforov, B.A.; Dubrovsky, B.A.; Radionova, L.V.; Radionov, A.A.; Kharitonovm, V.A. Wire Manufacturing Method. RU Patent 2,319,559, March 2008. [Google Scholar]
- Radionov, A.A. Analysis of construction methods for electric drives of straight-through wire drawing machines. Proc. Univ. Electromec. 2006, 4, 55–59. [Google Scholar]
- Zyuzin, V.I.; Radionova, L.V.; Radionov, A.A. Resource Saving in the Steel Industry; MSTU: Magnitogorsk, Russia, 2001. [Google Scholar]
- Ulyanov, D.V.; Gasiyarov, V.R. Analysis of Advantages and Disadvantages on Control Systems for Straight-Through Drawing Machine Electric Drives. Russ. Internet J. Ind. Eng. 2014, 1, 16–27. [Google Scholar]
- Linkov, S.A.; Radionov, A.A. Mathematical model of multiple straight-through drawing machine as a controlled facility. Electr. Syst. Complexes Interuniv. Collect. Sci. Pap. 2006, 11, 50–56. [Google Scholar]
- Shokhin, V.V.; Permyakova, O.V. The study of continuous rolling mill inter-stand tension inferential control systems. Procedia Eng. 2015, 129, 231–238. [Google Scholar] [CrossRef]
- Zilkova, J.; Timko, J.; Girovský, P. Modelling and control of tinning line entry section using neural networks. Int. J. Simul. Model. 2012, 11, 97–109. [Google Scholar] [CrossRef]
- Schreiner, R.T. Mathematical Modeling AC Electric Drives with Semiconductor Frequency Converters; Ural Department of Russian Academy of Sciences: Ekaterinburg, Russia, 2000. [Google Scholar]
- Chernykh, I.V. Modelling Electric Devices in MATLAB, SimPowerSystem and Simulink; DMK Press: Moscow, Russia, 2008. [Google Scholar]
- Vydrin, V.N. Dynamics of Rolling Mills; Metallurgy: Sverdlovsk, Russia, 1960. [Google Scholar]
- Pavlov, I.M. Rolling Theory; Metallurgizdat: Moscow, Russia, 1950. [Google Scholar]
- Hensel, A.; Spittel, T.; Spittel, M. Optimisation of Energy Consumption in Deformation Processes; Metallurgy: Moscow, Russia, 1985. [Google Scholar]
- Klimenko, V.M.; Pogorzhelsky, V.I.; Gorelik, B.C.; Konovalov, L.V. Technological and Power Reserves of Rolling Mills; Metallurgy: Moscow, Russia, 1976. [Google Scholar]
- Lokhmatov, A.P.; Zhuchkov, S.M.; Kulakov, L.V. Using the reserve of the pulling frictional forces in deformation zones of the working stands during continuous sectional rolling. Steel 1996, 5, 27–32. [Google Scholar]
- Radionov, A.A.; Malakhov, O.S.; Radionova, L.V. Device for Automatic Control of the Rotation Speed of the Roll Stands of a Continuous Rolling Mill. RU Patent 58,396, April 2006. [Google Scholar]
- Terekhov, V.M.; Osipov, O.I. Control Systems for Electric Drives; Publishing House “Academy”: Moscow, Russia, 2005. [Google Scholar]
- Perlin, I.L.; Yermanok, M.Z. Drawing Theory; Metallurgy: Moscow, Russia, 1971. [Google Scholar]
- Radionov, A.A.; Ulyanov, D.V. Advantages and disadvantages analysis of the known methods of the straight-through drawing machine electric drives making. Electr. Syst. Complexes Interuniv. Collect. Sci. Pap. 2011, 19, 163–171. [Google Scholar]
- Radionov, A.A.; Karandaev, A.S. On the optimal law of tension change in the process of metal wire winding. Izv. Vuzov. Mech. Eng. 2008, 10, 43–58. [Google Scholar]
- Radionov, A.A. Control system for the electric drive of a two-reel winding apparatus. Russ. Electromech. 2009, 1, 32–37. [Google Scholar]
- Radionov, A.A.; Karandaev, A.S.; Khramshin, V.R.; Andryushin, I.Y.; Gostev, A.N. Speed and Load Modes of Rolling Hollow Billet at the Wide-Strip Rolling Mill. In Proceedings of the 2014 International Conference on Mechanical Engineering, Automation and Control Systems (MEACS), Tomsk, Russian Federation, 16–18 October 2014. [Google Scholar] [CrossRef]
- Khramshin, V.R.; Karandaev, A.S.; Evdokimov, S.A.; Andryushin, I.Y.; Shubin, A.G.; Gostev, A.N. Reduction of the Dynamic Loads in the Universal Stands of a Rolling Mill. Metallurgist 2015, 59, 315–323. [Google Scholar] [CrossRef]
- Radionov, A.A.; Karandaev, A.S.; Evdokimov, A.S.; Andryushin, I.Y.; Gostev, A.N.; Shubin, A.G.; Gasiyarov, V.R. Mathematical modelling of interconnected electromechanical systems of a continuous subgroup of rolling mill stands. Part 2. Research of dynamic loads in universal stands. Bull. South Ural State Univ. Ser. Energy Ind. 2015, 15, 67–76. [Google Scholar] [CrossRef]
- Andryushin, I.Y.; Galkin, V.V.; Gostev, A.N.; Kazakov, I.V.; Evdokimov, S.A.; Karandaev, A.S.; Khramshin, V.R.; Khramshin, R.R. Method for Automatic Coil Tension Control in the Roughing Train of Continuous Rolling Mill Stands. RU Patent 2,494,828, June 2013. [Google Scholar]
- Khramshin, V.R.; Karandaev, A.S.; Khramshin, R.R.; Andryushin, I.Y.; Gostev, A.N. Device for Automatic Tension Control of Metal in Two Inter-Stand Spaces of Roughing Train of Hot Rolling Mill. RU Patent 147,042, December 2014. [Google Scholar]
- Khramshin, V.R.; Evdokimov, S.A.; Karandaev, A.S.; Andryushin, I.Y.; Shubin, A.G. Algorithm of No-Pull Control in the Continuous Mill Train. In Proceedings of the 2015 International Siberian Conference on Control and Communications (SIBCON–2015), Omsk, Russian Federation, 23–25 May 2015. [Google Scholar] [CrossRef]
- Andryushin, Y.; Shubin, A.G.; Gostev, A.N.; Radionov, A.A.; Karandaev, A.S.; Gasiyarov, V.R.; Khramshin, V.R. Automatic Tension Control in the Continuous Roughing Train of a Wide-Strip Hot-Rolling Mill. Metallurgist 2017, 61, 366–374. [Google Scholar] [CrossRef]
- Karandaev, A.S.; Yakimov, I.A.; Petukhova, O.I.; Antropova, L.I.; Khramshina, E.A. Power Parameters of Electric Drives of Five-Stand Wire Rod Mill with Four-Roll Pasess. In Proceedings of the IEEE NW Russia Young Researchers in Electrical and Electronic Engineering Conference (EIConRus), St. Petersburg, Russia, 1–3 February 2017; pp. 1524–1528. [Google Scholar] [CrossRef]
- Samodurova, M.N.; Karandaeva, O.I.; Khramshin, V.R.; Liubimov, I.V. Calculating Power Parameters of Rolling Mill Based on Model of Deformation Zone with Four-Roll Passes. Machines 2020, 8, 73. [Google Scholar] [CrossRef]
- Salganik, V.M.; Gun, I.G.; Karandayev, A.S.; Radionov, A.A. Thin-Slab Casting and Rolling Units for Production of Steel Bars: Study Guide; Bauman MSTU: Moscow, Russia, 2003; 506p. [Google Scholar]
- Fomin, G.G.; Dubeykovsky, A.V.; Grinchuk, P.S. Mechanisation and Automation of Wide-Strip Hot-Rolling Mills; Metallurgy: Moscow, Russia, 1982; 128p. [Google Scholar]
- Voskan’yants, A.A. Avtomatizirovannoe upravlenie protsessami prokatki: Ucheb. In Posobie Automated Control for Rolling Processes: Study Guide; MGTU im. N.E. Baumana: Moscow, Russia, 2010; p. 85. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).