Valve Deadzone/Backlash Compensation for Lifting Motion Control of Hydraulic Manipulators
Abstract
1. Introduction
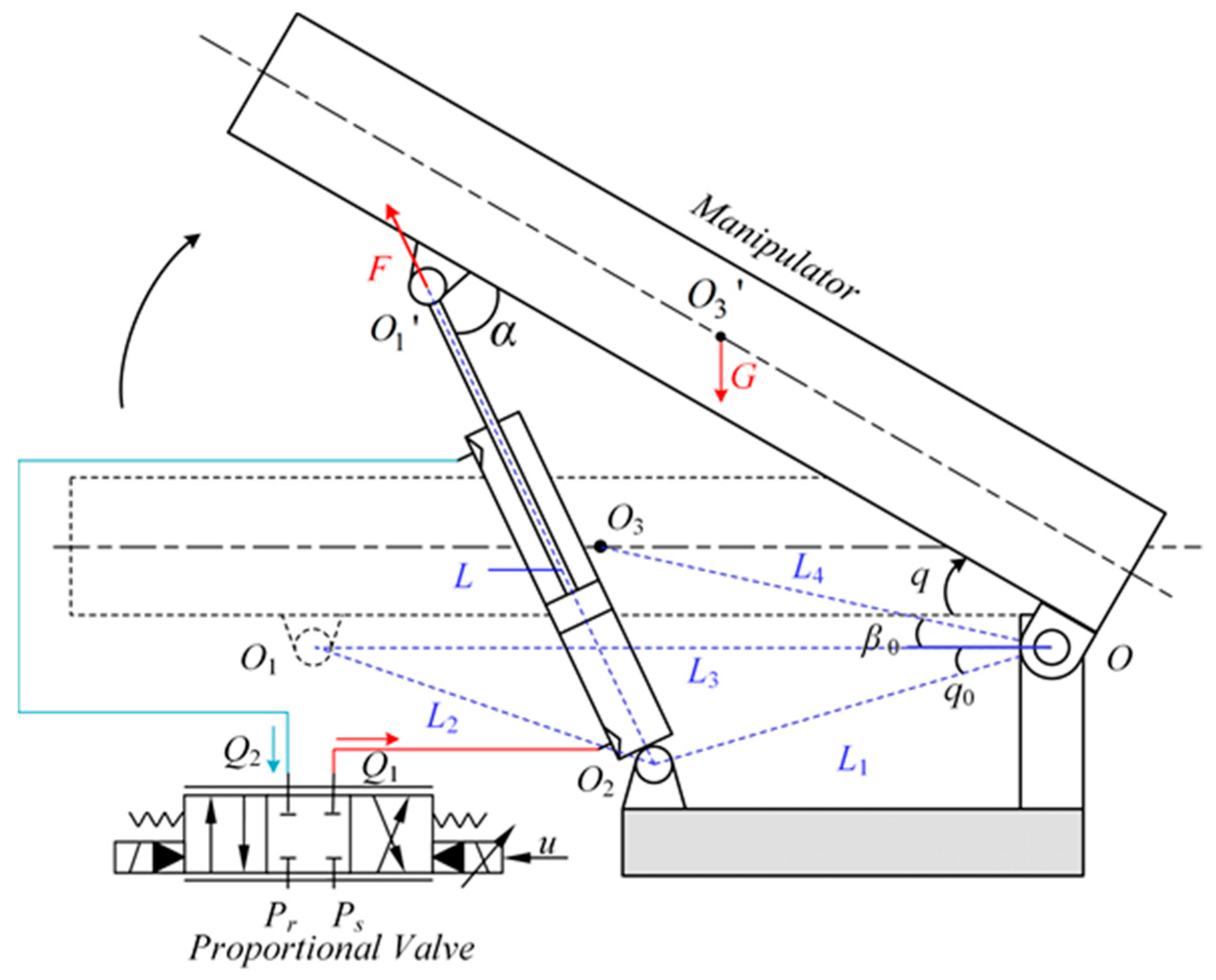
2. Dynamic Model and Problem Formulation
2.1. Manipulator Dynamics
2.2. Friction Dynamics
2.3. Pressure Dynamics
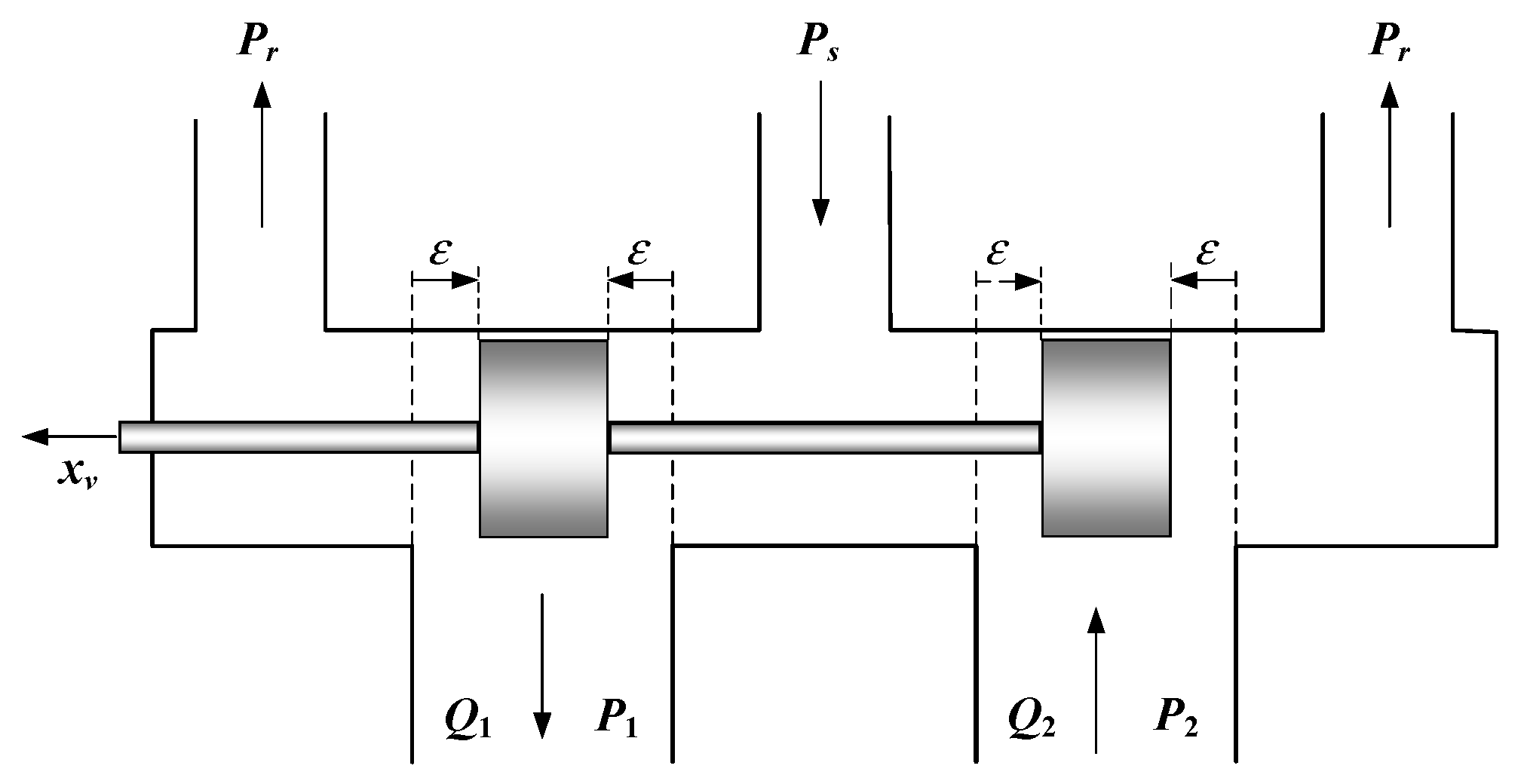
2.4. Flow Characteristics
3. Nonlinear Adaptive Robust Controller Design
3.1. Design Model and Issues to Be Addressed
3.2. Projection Mapping and Parameter Adaptation
3.3. Controller Design
3.4. Main Results
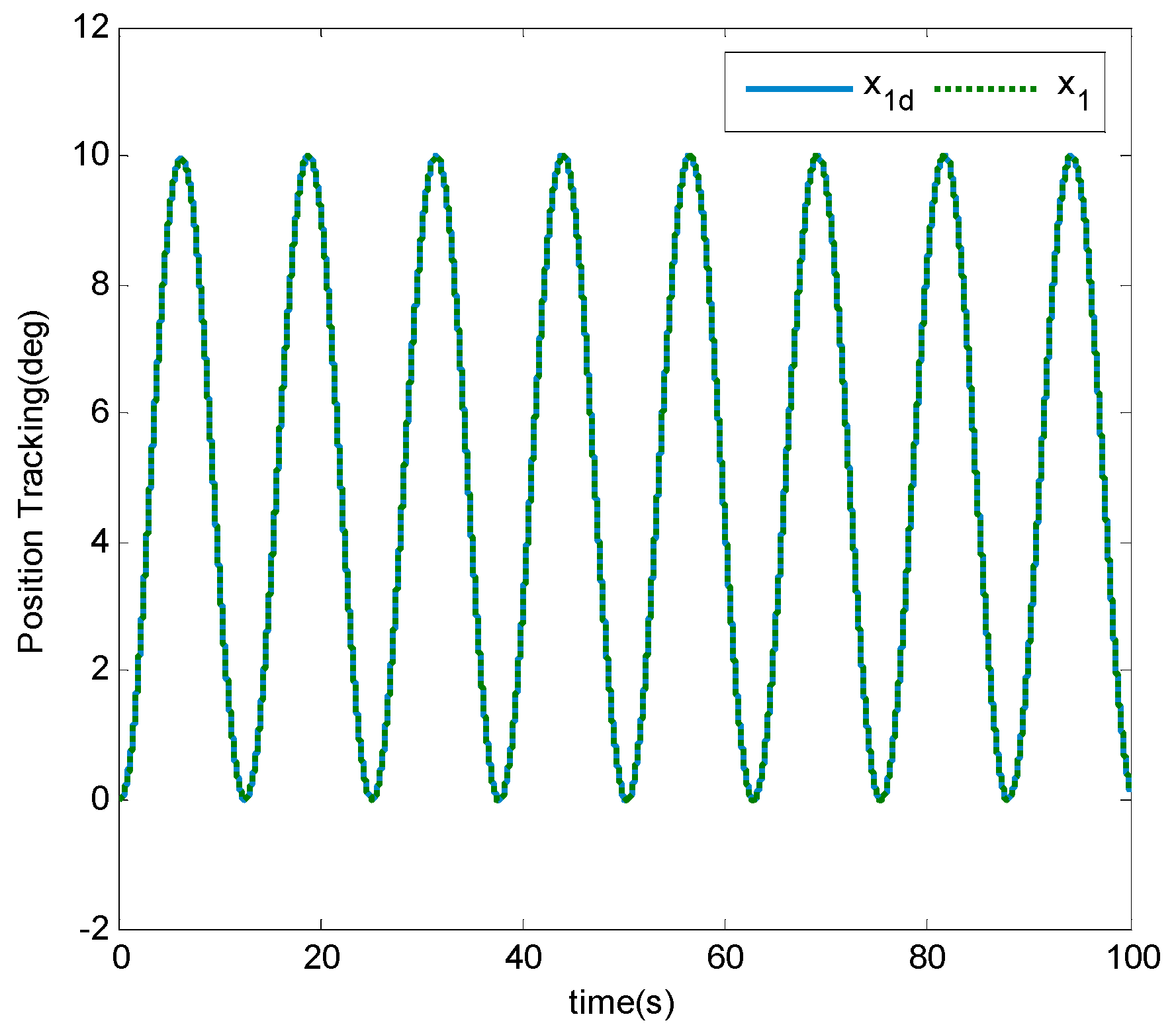
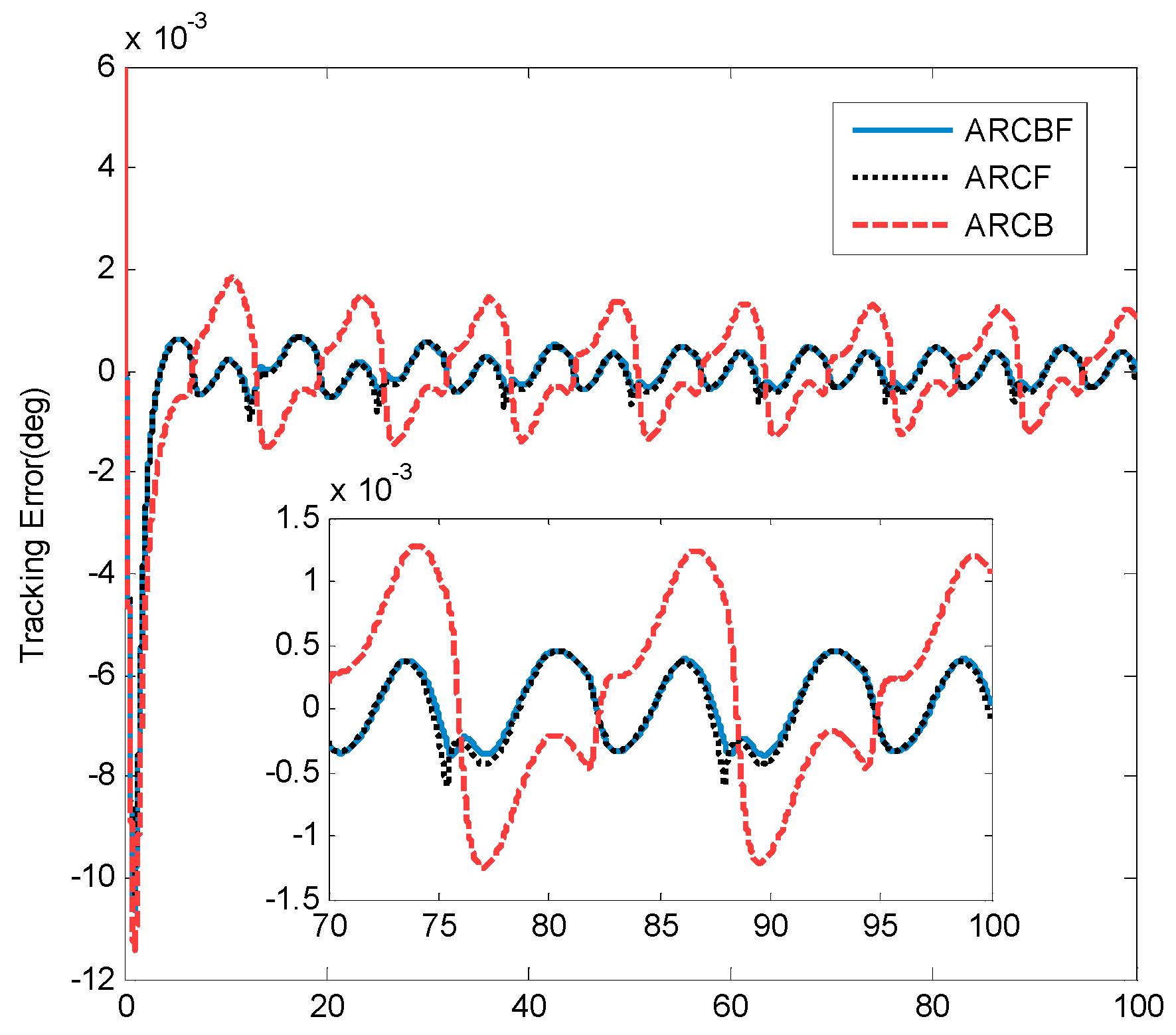
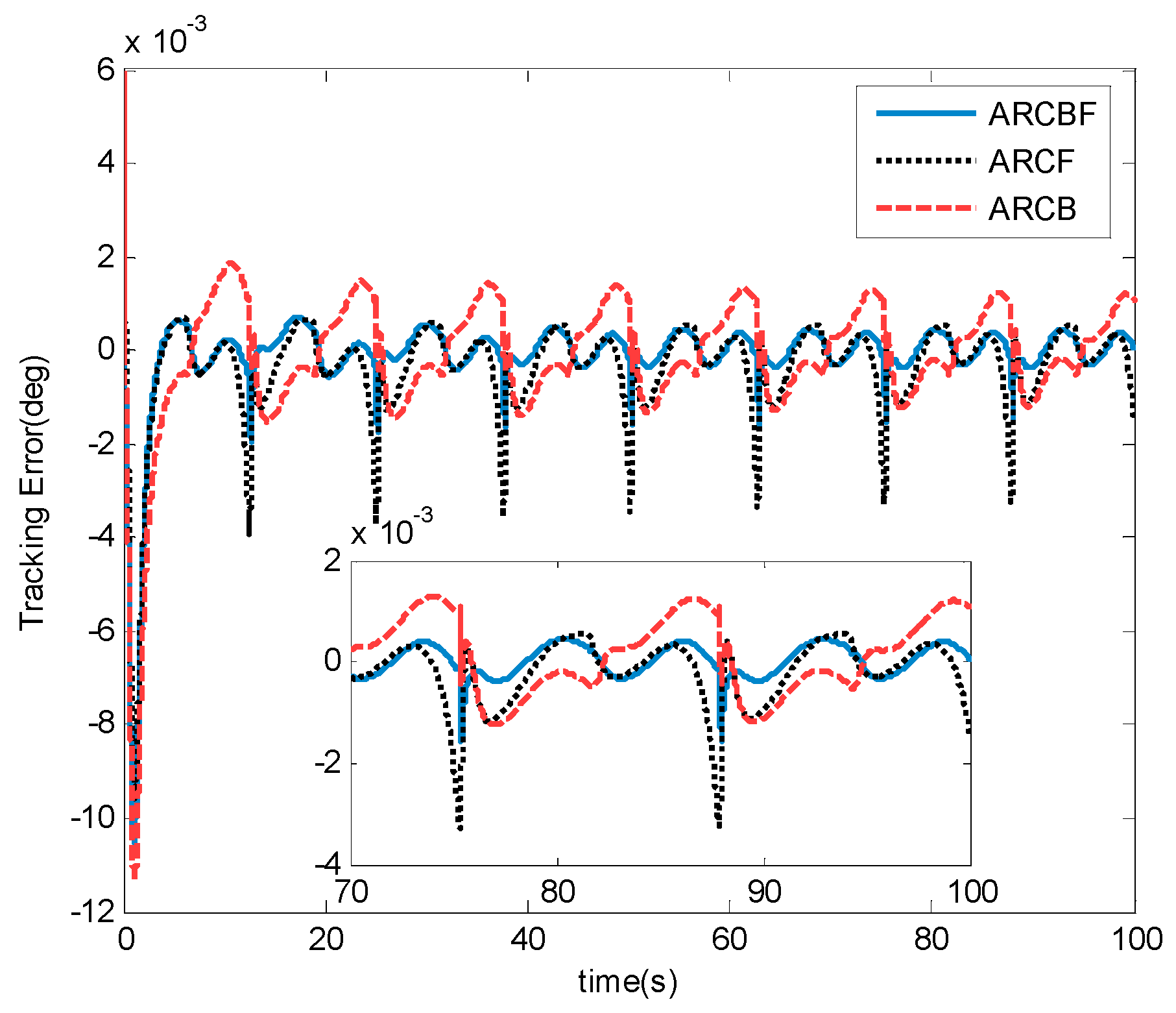
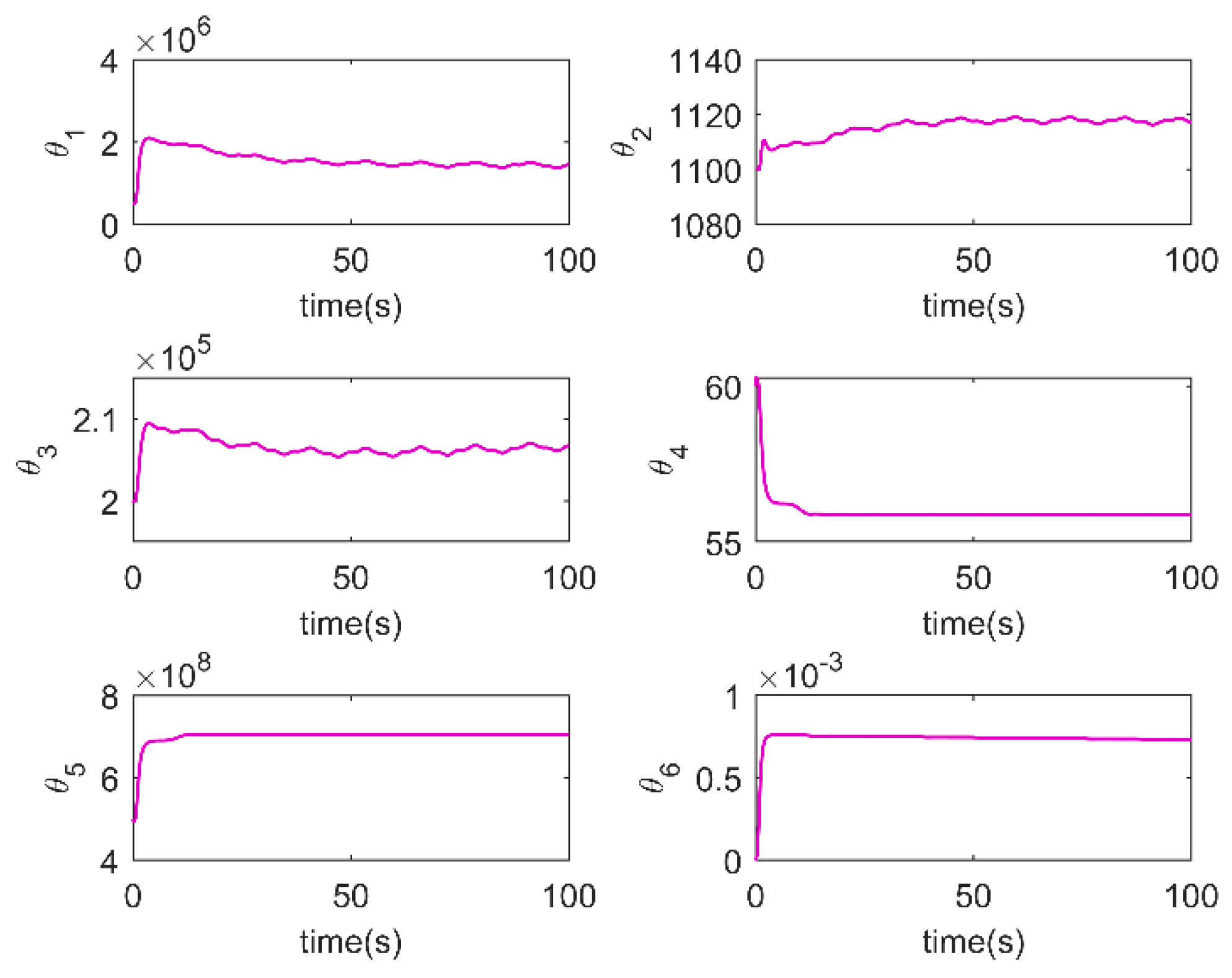
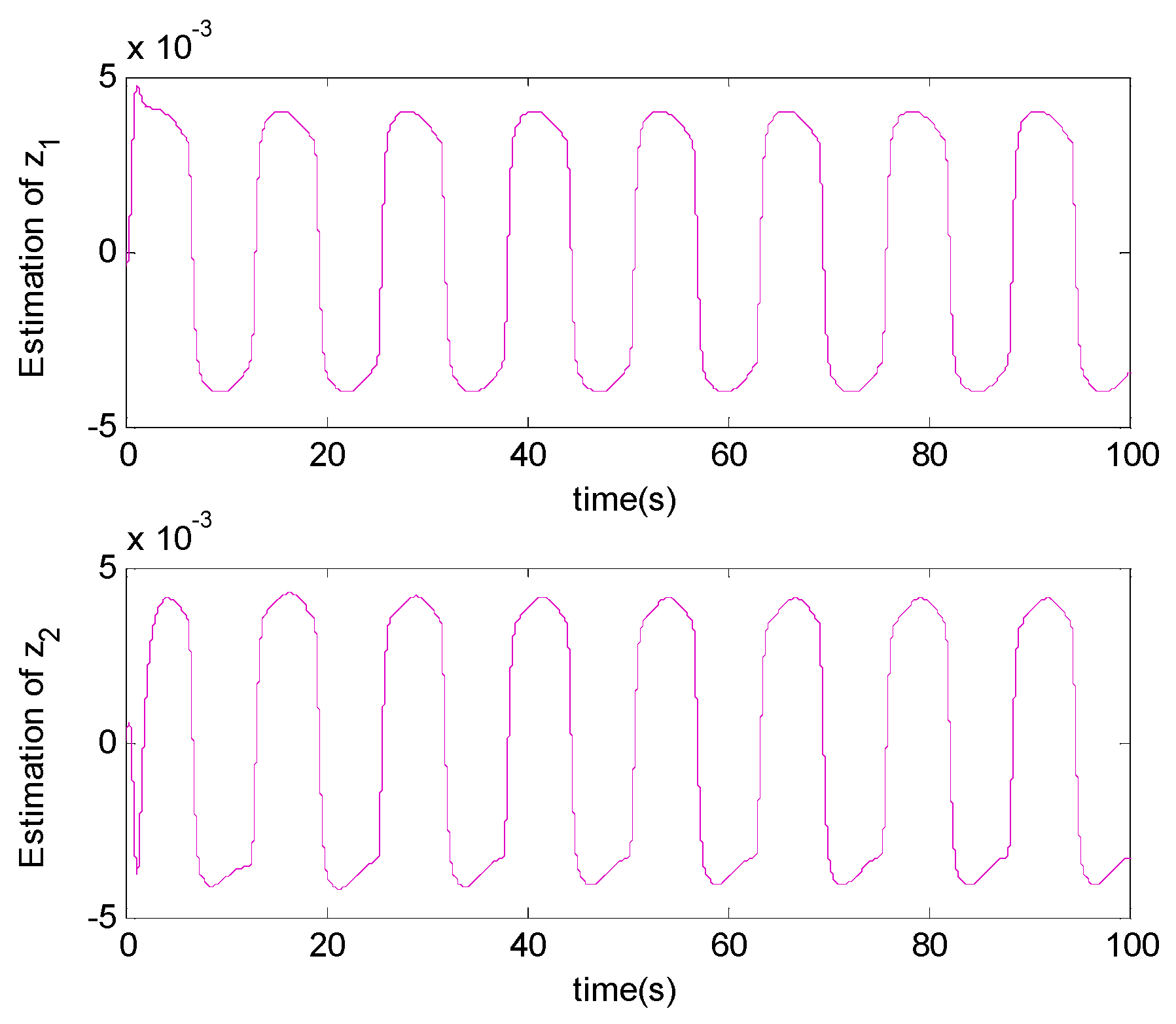
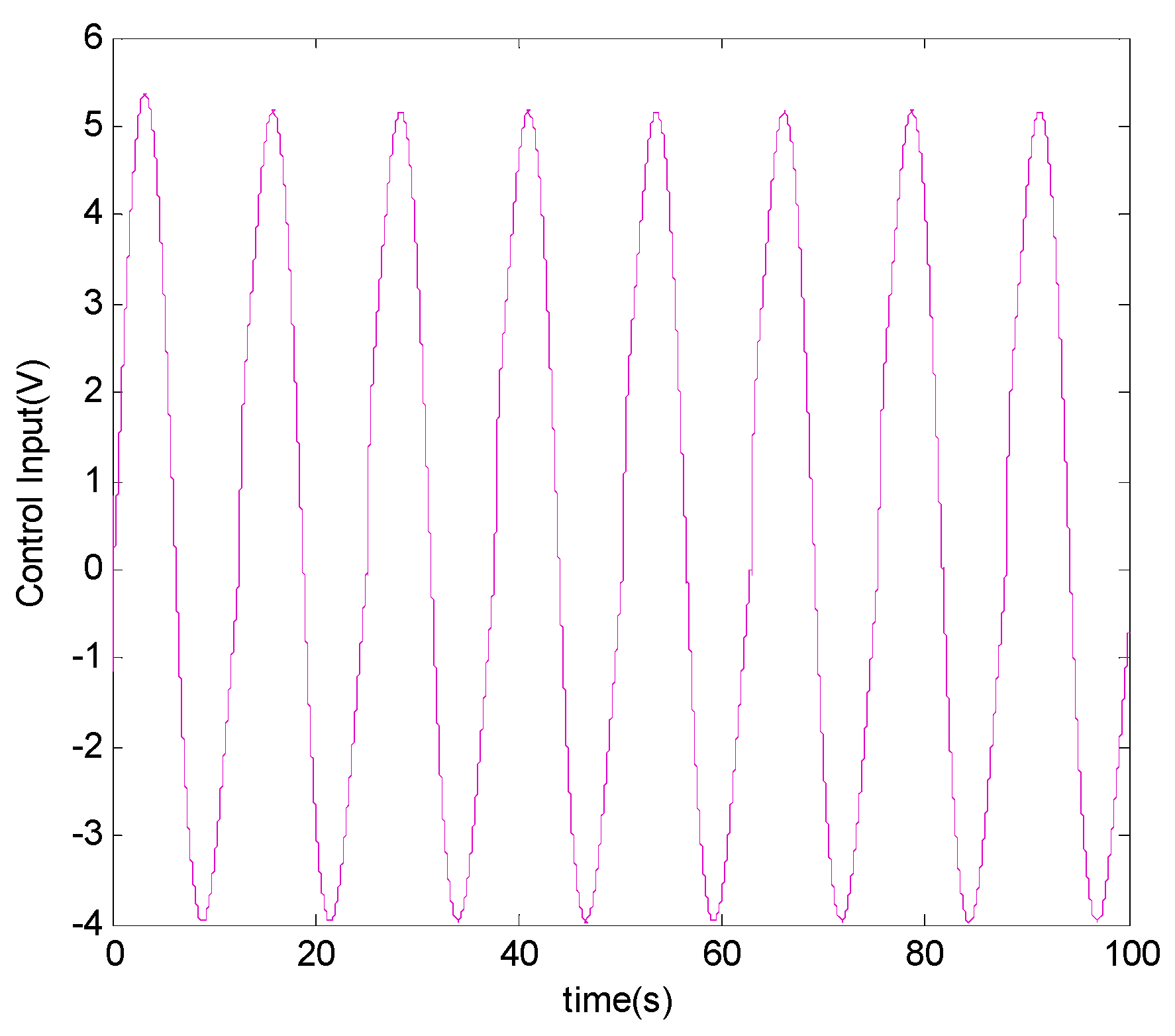
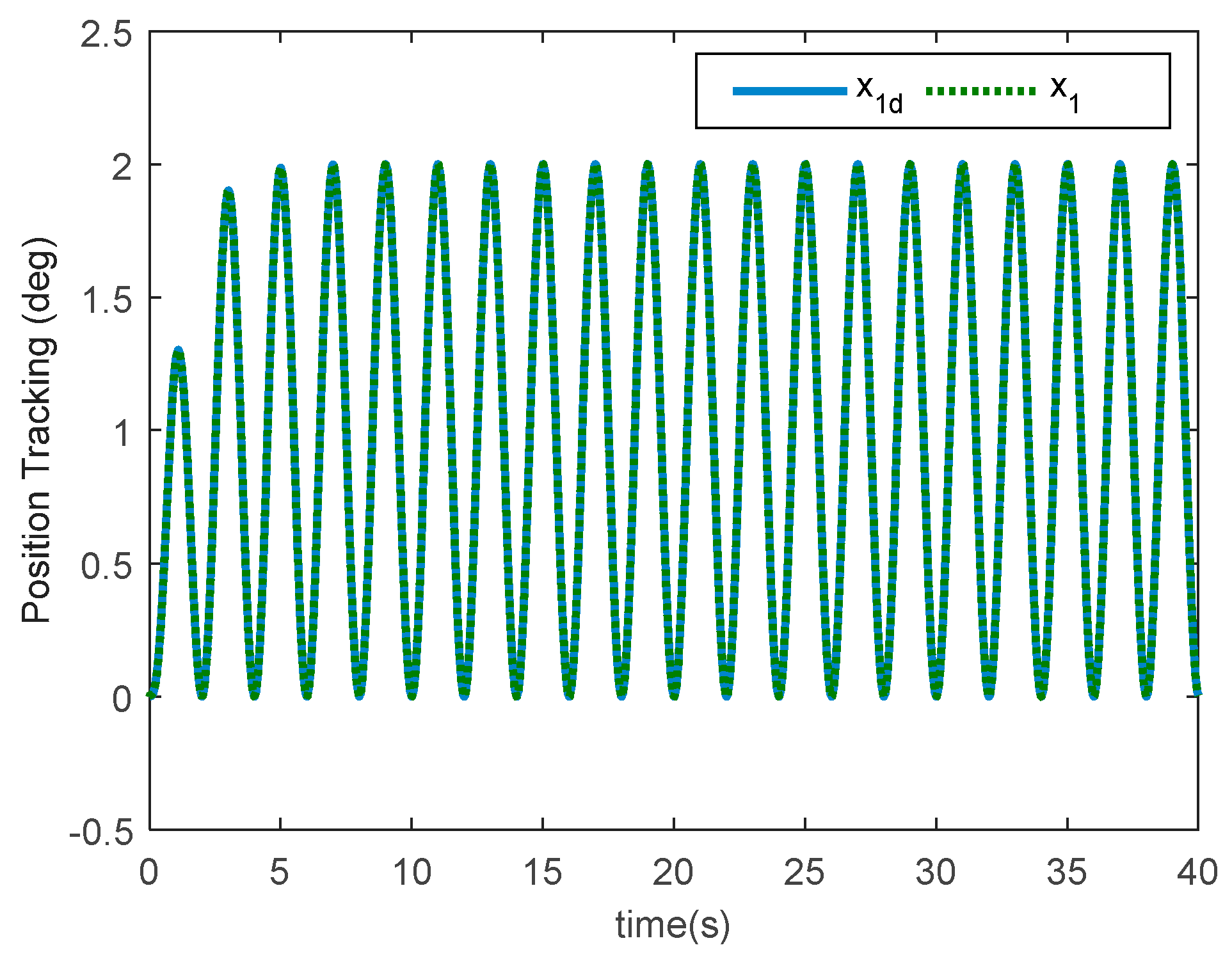
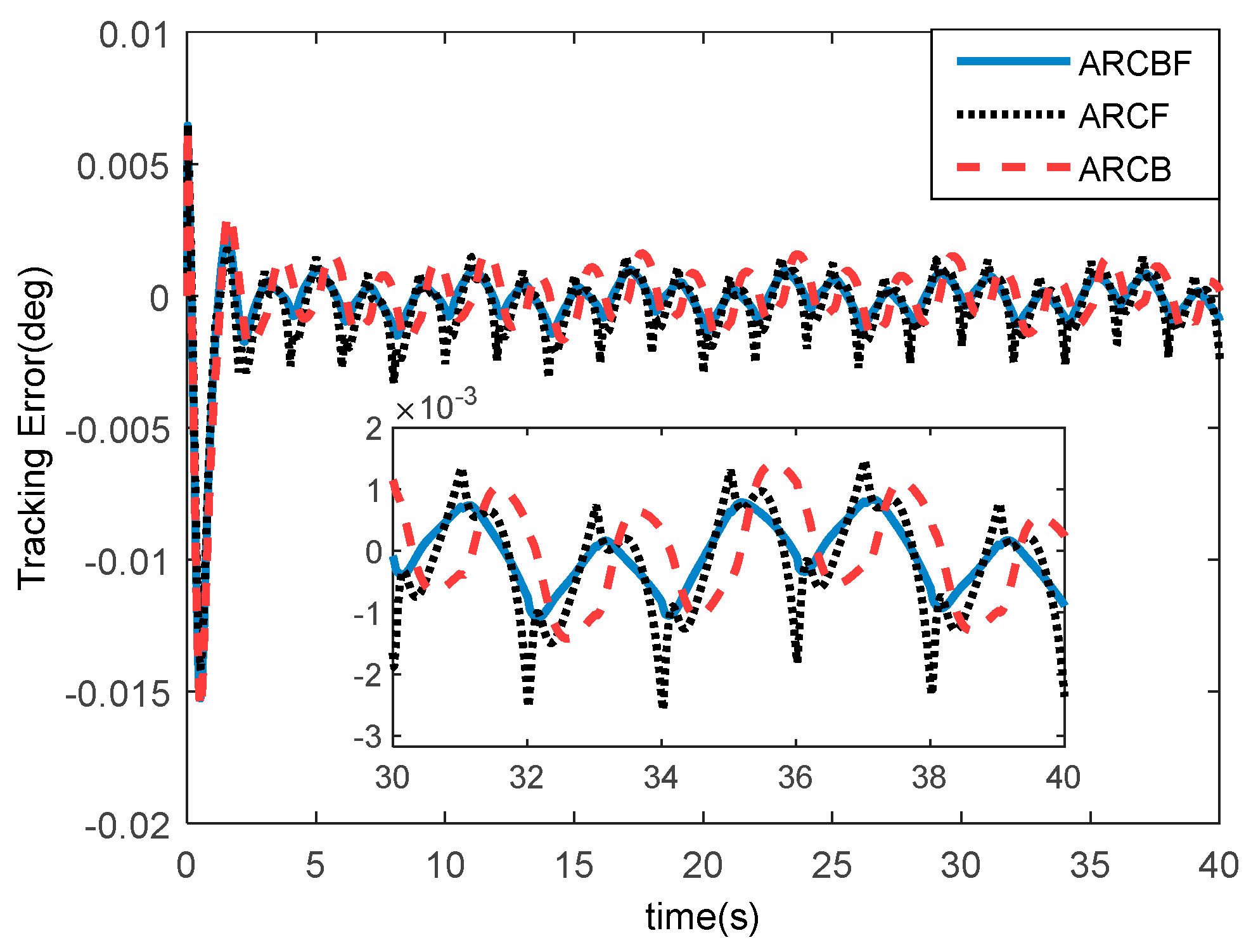
4. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Lu, L.; Yao, B. Energy-Saving Adaptive Robust Control of a Hydraulic Manipulator Using Five Cartridge Valves with an Accumulator. IEEE Trans. Ind. Electron. 2014, 61, 7046–7054. [Google Scholar] [CrossRef]
- Seron, J.; Martinez, J.L.; Mandow, A.; Reina, A.J.; Morales, J.; Garcia-Cerezo, A.J. Automation of the Arm-Aided Climbing Maneuver for Tracked Mobile Manipulators. IEEE Trans. Ind. Electron. 2013, 61, 3638–3647. [Google Scholar] [CrossRef]
- Lane, D.M.; Dunnigan, M.W.; Clegg, A.C.; Dauchez, P.; Cellier, L. A comparison between robust and adaptive hybrid position/force control schemes for hydraulic underwater manipulators. Trans. Inst. Meas. Control 1997, 19, 107–116. [Google Scholar] [CrossRef]
- Koivumaki, J.; Mattila, J. Stability-Guaranteed Force-Sensorless Contact Force/Motion Control of Heavy-Duty Hydraulic Manipulators. IEEE Trans. Robot. 2015, 31, 918–935. [Google Scholar] [CrossRef]
- Yao, J.; Yang, G.; Jiao, Z. High dynamic feedback linearization control of hydraulic actuators with backstepping. Proc. Inst. Mech. Eng. Part. I J. Syst. Control Eng. 2015, 229, 728–737. [Google Scholar] [CrossRef]
- Kim, W.; Won, D.; Tomizuka, M. Flatness-Based Nonlinear Control for Position Tracking of Electrohydraulic Systems. IEEE/ASME Trans. Mechatron. 2014, 20, 197–206. [Google Scholar] [CrossRef]
- Choi, Y.-S.; Choi, H.H.; Jung, J.-W. Feedback Linearization Direct Torque Control With Reduced Torque and Flux Ripples for IPMSM Drives. IEEE Trans. Power Electron. 2016, 31, 3728–3737. [Google Scholar] [CrossRef]
- Al Aela, A.M.; Kenne, J.-P.; Mintsa, H.A. A Novel Adaptive and Nonlinear Electrohydraulic Active Suspension Control System with Zero Dynamic Tire Liftoff. Machines 2020, 8, 38. [Google Scholar] [CrossRef]
- Lin, Y.-T.; Tseng, C.-Y.; Kuang, J.-H.; Hwang, Y.-M. A Design Method for a Variable Combined Brake System for Motorcycles Applying the Adaptive Control Method. Machines 2021, 9, 31. [Google Scholar] [CrossRef]
- Noghredani, N.; Pariz, N. Robust adaptive control for a class of nonlinear switched systems using state-dependent switching. SN Appl. Sci. 2021, 3, 290. [Google Scholar] [CrossRef]
- Homayounzade, M. Adaptive robust output-feedback boundary control of an unstable parabolic PDE subjected to unknown input disturbance. Int. J. Syst. Sci. 2021, 1–14. [Google Scholar] [CrossRef]
- Kissai, M.; Monsuez, B.; Mouton, X.; Martinez, D.; Tapus, A. Adaptive Robust Vehicle Motion Control for Future Over-Actuated Vehicles. Machines 2019, 7, 26. [Google Scholar] [CrossRef]
- Zhao, D.; Wang, Y.; Xu, L.; Wu, H. Adaptive Robust Control for a Class of Uncertain Neutral Systems with Time Delays and Nonlinear Uncertainties. Int. J. Control Autom. Syst. 2021, 1–13. [Google Scholar] [CrossRef]
- Hu, C.; Yao, B.; Wang, Q. Performance-Oriented Adaptive Robust Control of a Class of Nonlinear Systems Preceded by Unknown Dead Zone with Comparative Experimental Results. IEEE/ASME Trans. Mechatron. 2011, 18, 178–189. [Google Scholar] [CrossRef]
- Jia, X.; Xu, S.; Qi, Z.; Zhang, Z.; Chu, Y. Adaptive output feedback tracking of nonlinear systems with uncertain nonsymmetric dead-zone input. ISA Trans. 2019, 95, 35–44. [Google Scholar] [CrossRef] [PubMed]
- Jia, X.; Xu, S.; Zhang, Z.; Cui, G. Output feedback robust stabilization for uncertain nonlinear systems with dead-zone input. IET Control Theory Appl. 2020, 14, 1828–1836. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, S.; Zhang, B. Asymptotic Tracking Control of Uncertain Nonlinear Systems with Unknown Actuator Nonlinearity. IEEE Trans. Autom. Control. 2014, 59, 1336–1341. [Google Scholar] [CrossRef]
- Ma, Z.; Ma, H. Decentralized adaptive NN output-feedback fault compensation control of nonlinear switched large-scale systems with actuator dead-zones. IEEE Trans. Syst. Man Cybern. Syst. 2018, 1–13. [Google Scholar] [CrossRef]
- Mohanty, A.; Yao, B. Integrated Direct/Indirect Adaptive Robust Control of Hydraulic Manipulators with Valve Deadband. IEEE/ASME Trans. Mechatron. 2010, 16, 707–715. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, C.; Zhang, Y. Adaptive Output Control of Nonlinear Systems with Uncertain Dead-Zone Nonlinearity. IEEE Trans. Autom. Control 2006, 51, 504–511. [Google Scholar] [CrossRef]
- Deng, W.; Yao, J.; Ma, D. Robust adaptive precision motion control of hydraulic actuators with valve dead-zone compensation. ISA Trans. 2017, 70, 269–278. [Google Scholar] [CrossRef] [PubMed]
- Lewis, F.; Tim, W.K.; Wang, L.-Z.; Li, Z. Deadzone compensation in motion control systems using adaptive fuzzy logic control. IEEE Trans. Control Syst. Technol. 1999, 7, 731–742. [Google Scholar] [CrossRef]
- Yao, J.; Deng, W.; Jiao, Z. Adaptive Control of Hydraulic Actuators with LuGre Model-Based Friction Compensation. IEEE Trans. Ind. Electron. 2015, 62, 6469–6477. [Google Scholar] [CrossRef]
- Yao, B.; Tomizuka, M. Adaptive robust control of SISO nonlinear systems in a semi-strict feedback form. Automatica 1997, 33, 893–900. [Google Scholar] [CrossRef]
- Makkar, C.; Dixon, W.; Sawyer, W.; Hu, G. A new continuously differentiable friction model for control systems design. In Proceedings of the 2005 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Monterey, CA, USA, 24–28 July 2005; IEEE: New York, NY, USA, 2006; pp. 600–605. [Google Scholar]
- Eryilmaz, B.; Wilson, B.H. Unified modeling and analysis of a proportional valve. J. Frankl. Inst. 2006, 343, 48–68. [Google Scholar] [CrossRef]
- Manring, N.D. Hydraulic Control Systems; John Wiley & Sons: Hoboken, NJ, USA, 2005; pp. 224–228. [Google Scholar]
- Krstic, M.; Kanellakopoulos, I.; Kokotovic, P. Nonlinear and Adaptive Control Design; Wiley: New York, NY, USA, 1995. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Lin, Z.; Jiang, Y.; Yu, C.; Yao, J. Valve Deadzone/Backlash Compensation for Lifting Motion Control of Hydraulic Manipulators. Machines 2021, 9, 57. https://doi.org/10.3390/machines9030057
Li L, Lin Z, Jiang Y, Yu C, Yao J. Valve Deadzone/Backlash Compensation for Lifting Motion Control of Hydraulic Manipulators. Machines. 2021; 9(3):57. https://doi.org/10.3390/machines9030057
Chicago/Turabian StyleLi, Lan, Ziying Lin, Yi Jiang, Cungui Yu, and Jianyong Yao. 2021. "Valve Deadzone/Backlash Compensation for Lifting Motion Control of Hydraulic Manipulators" Machines 9, no. 3: 57. https://doi.org/10.3390/machines9030057
APA StyleLi, L., Lin, Z., Jiang, Y., Yu, C., & Yao, J. (2021). Valve Deadzone/Backlash Compensation for Lifting Motion Control of Hydraulic Manipulators. Machines, 9(3), 57. https://doi.org/10.3390/machines9030057





