Abstract
This research focuses on the minimum process of classifying three upper arm movements (elbow extension, shoulder extension, combined shoulder and elbow extension) of humans with three electromyography (EMG) signals, to control a 2-degrees of freedom (DoF) robotic arm. The proposed minimum process consists of four parts: time divisions of data, Teager–Kaiser energy operator (TKEO), the conventional EMG feature extraction (i.e., the mean absolute value (MAV), zero crossings (ZC), slope-sign changes (SSC), and waveform length (WL)), and eight major machine learning models (i.e., decision tree (medium), decision tree (fine), k-Nearest Neighbor (KNN) (weighted KNN, KNN (fine), Support Vector Machine (SVM) (cubic and fine Gaussian SVM), Ensemble (bagged trees and subspace KNN). Then, we compare and investigate 48 classification models (i.e., 47 models are proposed, and 1 model is the conventional) based on five healthy subjects. The results showed that all the classification models achieved accuracies ranging between 74–98%, and the processing speed is below 40 ms and indicated acceptable controller delay for robotic arm control. Moreover, we confirmed that the classification model with no time division, with TKEO, and with ensemble (subspace KNN) had the best performance in accuracy rates at 96.67, recall rates at 99.66, and precision rates at 96.99. In short, the combination of the proposed TKEO and ensemble (subspace KNN) plays an important role to achieve the EMG classification.
1. Introduction
Electromyography (EMG) has been considered an important area for study, especially as biological signal control to promote quality of life and self-reliance. There are several areas of applications of EMG, such as disease diagnosis, rehabilitation evaluation, and control strategy for the assistive device. EMG provides rich information obtained by muscle contractions [1,2,3,4,5,6,7,8,9]. Recent research developments in the field of robots have led to robotic arm control with very complex mechanical capabilities, sensor technology, and control algorithms that do not necessarily make it easier for users to intuitively control robots [2,3,4,10]. Hand gesture recognition (HGR) is an important part of human–robot interaction that studies to recognize commands from humans by the development of robot technology. HGR models are human–computer systems that predict what motions or gestures were conducted and when a human conducted the gesture [3,4,5,7,8,10]. Human–robot interactions (HRI) are a wide research field. Currently, those systems are used in many applications and researches such as robot control systems [11,12,13,14,15,16,17,18,19,20,21,22,23], medical recognitions and rehabilitations [24,25,26,27], and intelligence assistive devices [5,12,15,28,29,30,31,32,33,34].
There are several issues related to the process of controlling the robotic arm using the EMG signal. Noise, motion artifact, and crosstalk have an impact on the prediction intention. The high variability of EMG signal amplitude estimation is a challenge in developing the control system [3,23,35,36,37,38]. Ideally, an assistive upper limb robotic arm system should fulfill several criteria such as an intuitive interface for the user; robust system; adaptive to the user; minimal number of sensors and not sensitive to the precise muscle placement; short and easy training/calibration (possibly without training); provide feedback (closed-loop control); low cost and simple computational; and produce good estimation with perceivable delays (real-time) [4,8,14,25,29,39]. Laksono et al. [9] proposed a model mapping for three EMG channels from three different muscles to control the robotic arm to predict three movements of the upper arm. This simple model can discriminate against three upper arm movements by considering the influence of the targeted muscle position when doing the movement; the characteristics of the muscles that perform the activity will play an important role in carrying out the movement. Even though the model was capable of performing motion mapping, the overall reported accuracy in 76.64% was still not optimal. The existing research on the classification of hand movements based on EMG signals still faces many challenges such as weak robustness, the minimum number of sensors, short training data, low computational process, and good prediction with perceivable time delay [2,4,10,34,39,40,41,42,43]. To address these challenges, we propose models for classifying upper arm movements that conducted 1- and 2-degrees of freedom (DoF) motions using machine learning. The HGRs include three movements (elbow extension, shoulder extension, combined shoulder and elbow extension), and a case with no movement (default condition). Simultaneous and independent control of multi degrees of freedom (DoF), such as elbow and shoulder joints, is the main target of the machine learning-based model for controlling robotic arm using electromyography (EMG) signal [44]. This research also focused on the positioning of the EMG sensor on the target muscles that are directly involved in the movement of the upper arm. In this research, we introduce machine-learning models for controlling the robot arm that EMG signals are obtained from three muscles as a multi-channel (three channels of input). This three-motion produced four class predictions consist of motion 1, motion 2, motion 3, and no motion.
Machine learning has been used extensively in HGR and other EMG-related studies targeting different functionalities. Several kinds of research focusing particularly on elbow and shoulder movements have been reported in Triwiyanto et al. [13], Antuvan et al. [14], Martinez et al. [16], Hassan, Abou-Loukh, and Ibraheem [19], Young et al. [45], Jiang et al. [46], and Tsai et al. [47], classification of upper limb motion using extreme learning machines by Antuvan et al. [39], using Support Vector Machine (SVM) [6,8,19,48], investigation of shoulder muscle activation pattern recognition using machine learning by Jiang et al. [46], and detection movements using EMG signal for upper limb exoskeletons in reaching tasks by Trigili et al. [49]. These papers verify the suitability of EMG signals for biopotential intelligent robot control.
The key to any EMG control is the measurement system in use. As expected, accurate EMG signal recording increases the performance of the pattern recognizing model. In this paper, the experiment was conducted systematically to investigate the impact of using Teager–Kaiser energy operator (TKEO) and variable segmentation levels of EMG signal input. To get better classification performance and try to tackle the challenges, we propose the following framework to classify EMG signals for controlling a robotic arm. The use of multi-channels for data retrieval has aided in recognition as it covers more muscle areas. Hence, in this research the focus of EMG data collection is in three positions, namely brachioradialis, biceps brachii, and deltoid to move the robotic arm. EMG processes such as data segmentation had similarly been shown to better the results of discriminative models [34]. We performed three levels of data segmentation. On the first level, no segmentation was performed. On the second and third level, the EMG signal was split into two or three segments of data and treated as distinct input to feature extraction process. To overcome muscle activation signals, TKEO was used for onset detection [47,50,51]. TKEO method has been mainly used to enhance the magnitude and frequency of time-domain signals without requiring the conversion of those signals to the frequency domain [41]. The other preprocessing processes, such as normalization, rectification, and smoothing signals using moving average, are commonly used by many researchers [47,52,53,54].
Feature extractions take an important role in machine learning. Features were extracted from the different EMG signal sources. The feature of EMG signals commonly includes time-domain (TD) and frequency-domain (FD) feature. Feature extraction proposed in this paper was multi-feature TD, which includes the mean absolute value (MAV), zero crossings (ZC), slope-sign changes (SSC), and waveform length (WL) [47,52,53,54,55]. A calibration phase was utilized to acquire training phase data. From this, we evaluated the features as well as extent of the sampled data. In total, four classes (motion 1, motion 2, motion 3, and no motion) were classified. Machine learning model classifiers were used as a feasible decoder to predict the four movements. The results obtained in this study were applied online for real-time implementation. The performance shown includes a fairly accurate and consistent prediction accuracy. Three metric performances; accuracy, recall, and precision were evaluated for evaluation of performance. In real-time processing, there were various optimal controller delays in the literature review that reported below 500 ms which is still feasible for real-time robotic control [4,8].
In this paper, we deployed a teleoperation HRI cooperating between surface EMG and an upper-arm robotic, to fast-detect the user’s hand gesture intention. We implemented an offline supervised machine-learning algorithm, using a set of five subject-independents. The proposed system established various scenarios consisting of three-level variables of segmentation signal, using TKEO, and classification types of the machine-learning model, such as decision tree, k-Nearest Neighbor (KNN), SVM, and Ensemble. All machine-learning algorithms are provided in the classification learner application in Matlab®. The significant contribution of this study is to provide the results of investigations regarding the optimal performance of the supervised machine-learning model using limited data training to classify upper arm motions based on three EMG signal channel inputs from three different target muscles and to control the robotic arm in teleoperation HRI simultaneous.
2. Materials and Methodology
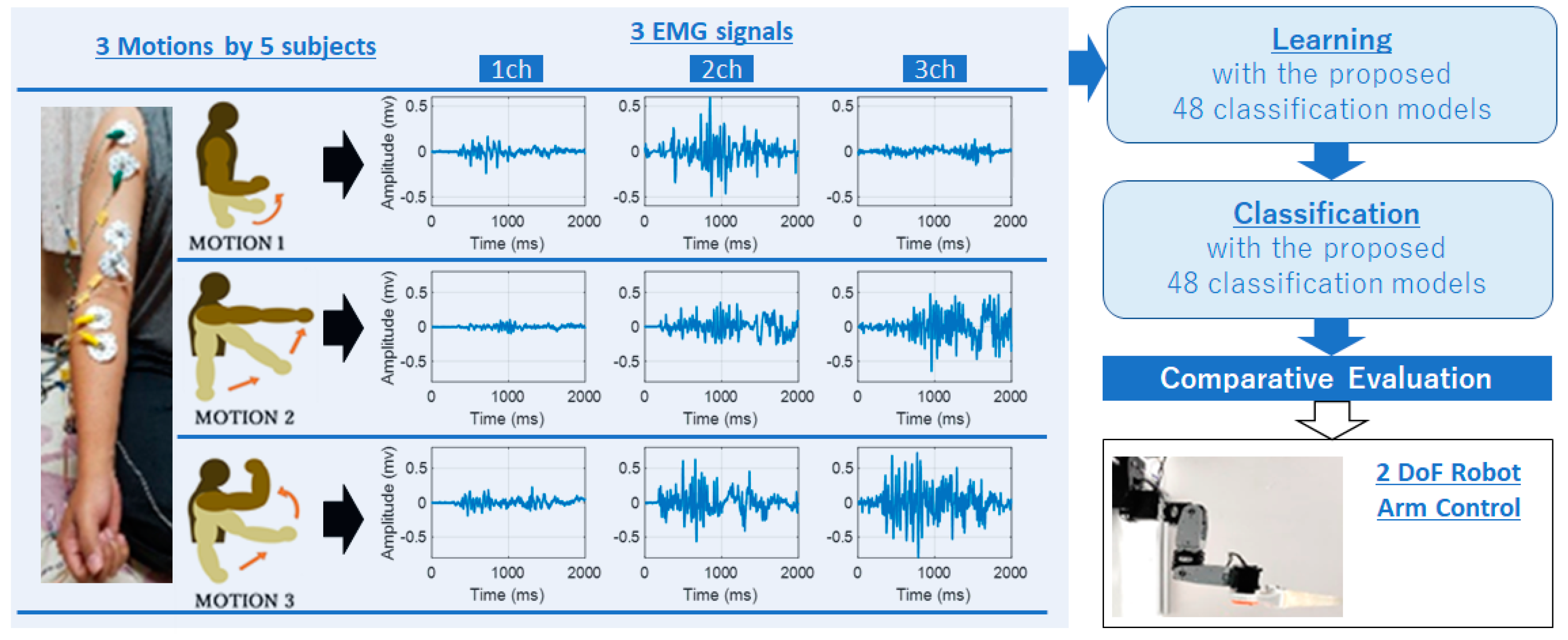
Five healthy subjects participated as volunteers for the experiment. All of the participants provided written informed consent letters following approval procedures (number 27–226) issued by the Gifu University ethics committee and complying with the Helsinki declaration. This experiment explored machine-learning approaches that can be useful in the prediction of elbow and shoulder joint movements classification as an alternative to the modeled equation for robotic controlling. The proposed experiment system used to describe the process of controlling the robotic arm using EMG signal classification is illustrated in Figure 1. The subjects conducted upper limb motion which was similar to our previous research. The experimental setup that included EMG measurements system, muscle position, data acquisition, data analysis, and robotic control is described by Laksono et al. [9].
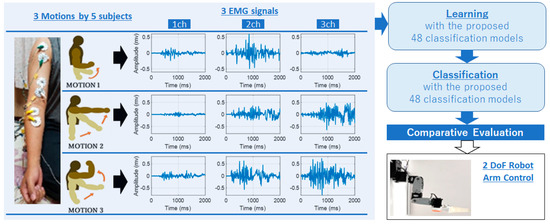
Figure 1.
The proposed system for electromyography (EMG) controlled robotic arm.
2.1. Feature Extraction Stage
EMG signals are easily corrupted by the environment in the data acquisition process. Motions artifacts, crosstalk, baseline offset, and power line frequency may lead to distortion in the process classification [41,48,52,54,56,57]. We used an isolator to reduce the powerline frequency noise. Three EMG sensors were used to capture EMG signals and then they were used as inputs for the learning process. Teager–Kaiser energy operator (TKEO) was used for enhancing the amplitude and frequency of TD EMG signals without converting those signals to the FD [41,42,43]. TKEO was performed to enhance muscle activation detection. The TKEO is denoted in Equation (1):
Then, the conventional EMG feature extraction methods were employed to extract meaningful information for EMG signal classification. Each of them is explained below.
Mean absolute value (MAV) was used as an onset index to detect muscle activity. MAV is the average absolute value of EMG signal amplitude. MAV is a popular feature used in EMG hand movement recognition applications [55]. It is defined as
Waveform length (WL): WL is the cumulative length of the waveform overtime segment. WL is similar to waveform amplitude, frequency, and time [55]. The WL can be formulated as
Zero crossing (ZC) is the number of times that the amplitude values of EMG signal cross zero in the x-axis. In the EMG feature, the threshold condition is used to avoid background noise. ZC provides an approximate estimation of frequency domain properties [55]. The calculation is defined as
Slope-sign change (SSC): SSC is related to ZC. It is another method to represent the frequency domain properties of EMG signal calculated in the time domain. The number of changes between positive and negative slope among three sequential segments is performed with threshold function for avoiding background noise in EMG signal [55]. It is given by
2.2. Machine Learning (ML) Stage
The classification started with preparing data for the learning process. Data was generated from three EMG channels recorded at a sampling rate of 2000 Hz with recording times varying between 1.5–3 s per motion stored in the workspace. In total, five subjects performed three motions. The data were segmented as follows; 60% for training and 40% for performance validation.
As mentioned, 40% of the data was reserved for testing/inferencing. The machine learning models operate as shown in Figure 2. In this case, the learning algorithm is fed with a pair of training data, which conventionally includes a response signal and a corresponding correct signal, which acts as a teacher. After the learning phase, inferencing can be made with the generated model. This output prediction based on weightings of the learned model for accurate inferencing; the data supplied should be novel to the model and hence the separation into testing data employed in the model.
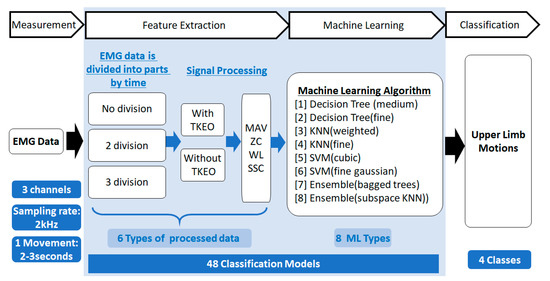
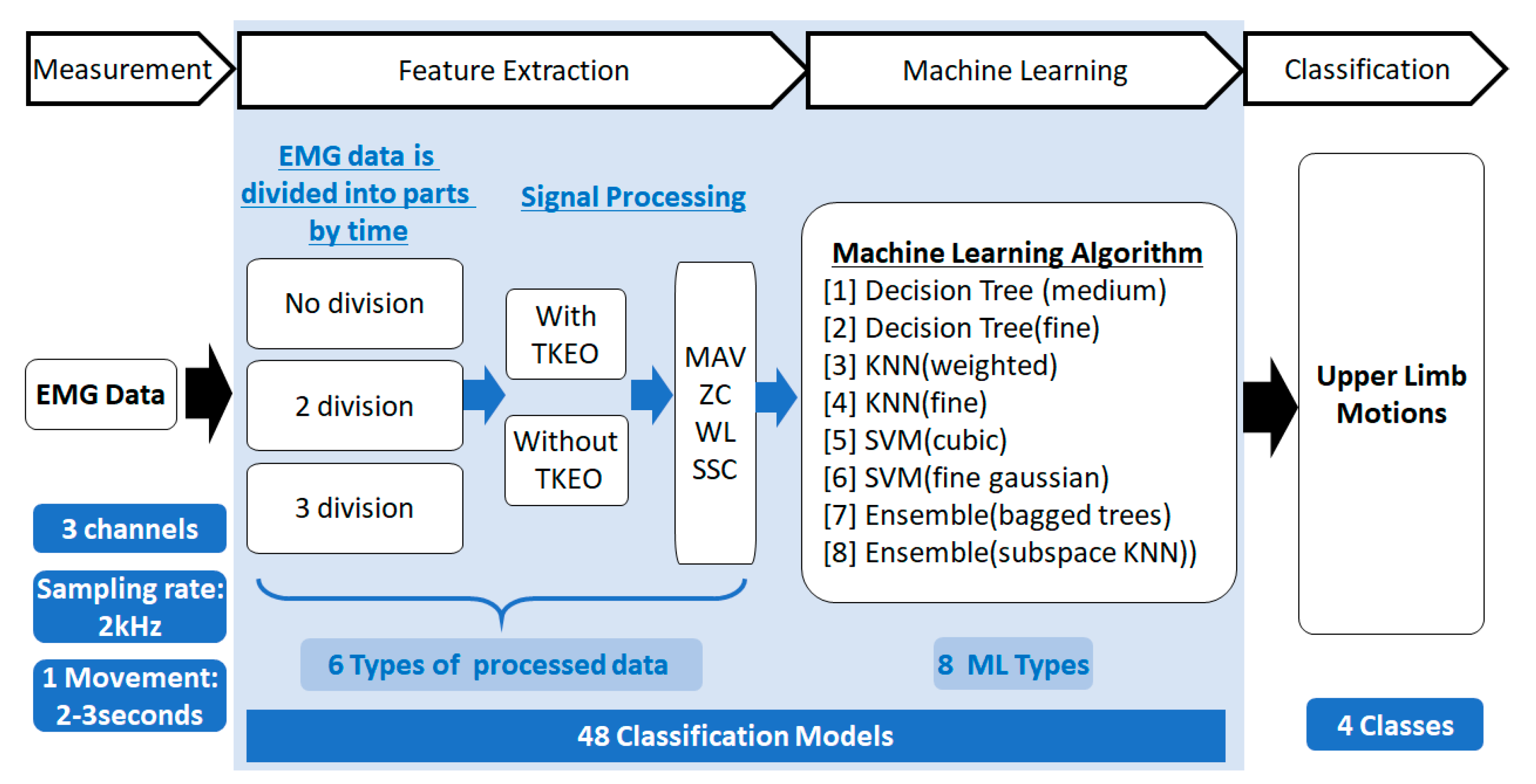
Figure 2.
Classification models for comparative evaluation.
Figure 2 shows the proposed machine learning model subdivision (six scenario models) utilized in the systematic investigation of optimal controller. The data is subdivided into two groups; processed with TKEO and without TKEO dataset. For each of the datasets, three variations of data are applied with the variation of dividing the signal into no segment, two segments, and three segments as inputs for training. Feature extraction is performed on each of the models to arrive at a trained model. A total of 48 types of trained models were investigated.
We used four features (MAV, WL, ZC, and SSC as multi-features from each channel) for training in one segment as an input. As such, 13 predictor signals (features) and one correct “teacher” signal were fed to the training model. For the second data input (using two segments input for each channel), we used similar features resulting in 25 predictors. Then, three segments were input in 37 predictors. It is worth noting that the same data was fed to the two distinct groups for comparison purposes. In both cases, we used five-fold cross-validation for accuracy estimation and to avoid overfitting.
A Matlab classification learner application that performs multiclass error-correcting output code with the different learner models was employed. In this case, eight types of machine learning learner models were employed; decision tree (medium), decision tree (fine), KNN (weighted and fine), SVM (cubic and fine Gaussian SVM), Ensemble (bagged trees and subspace KNN) were used. The hyperparameters for each classifier were initialized with the default setting. All ML methods performed training data properly. Based on the prediction performance (see Table 1), KNN (fine) and ensemble (subspace KNN) algorithms had the best accuracy for the method using TKEO and the method without using TKEO, respectively. These models were used for further analysis, shown in the next section.

Table 1.
Accuracy of machine learning training model prediction performance.
Ensemble classifier is a system made by combining different classifiers to produce more safe and stable predictions [58]. The system is built with the N classifier that can be single or multiple, while the classification is appropriate to the feature vector, for each feature vector 1, each classifier yields the output value (the resulting output value is counted). Then, the output of the ensemble classifier is determined by the number of votes. If the number of classifiers is, in fact, the average value of the classifier’s decision, it is rounded off, and the ensemble classifier decision is determined. All feature vectors are applied by this process [59]. We used the ensemble (subspace KNN) method using six dimensions subspace and learner nearest neighbors using 30 learners.
One of the classifications of machine learning methods with advisory learning is KNN. Under the structure from the training dataset, the classification is carried out according to the nearest distance to points in a training data set. In this study, we used model type fine KNN with k = 1 selected, and Euclidean distance calculation formulas were used.
2.3. Performance Analysis
The performance of six trained models was compared based on classification accuracy. The performance of the ML for each model is shown in Table 1 below. From the table, accuracy ranged between 80.5–98%. The highest accuracy was selected as the target model for evaluation. As such, Ensemble (subspace KNN) was chosen for model 1, 2, 3, and 6 while KNN (fine) was chosen for model 4 and 5.
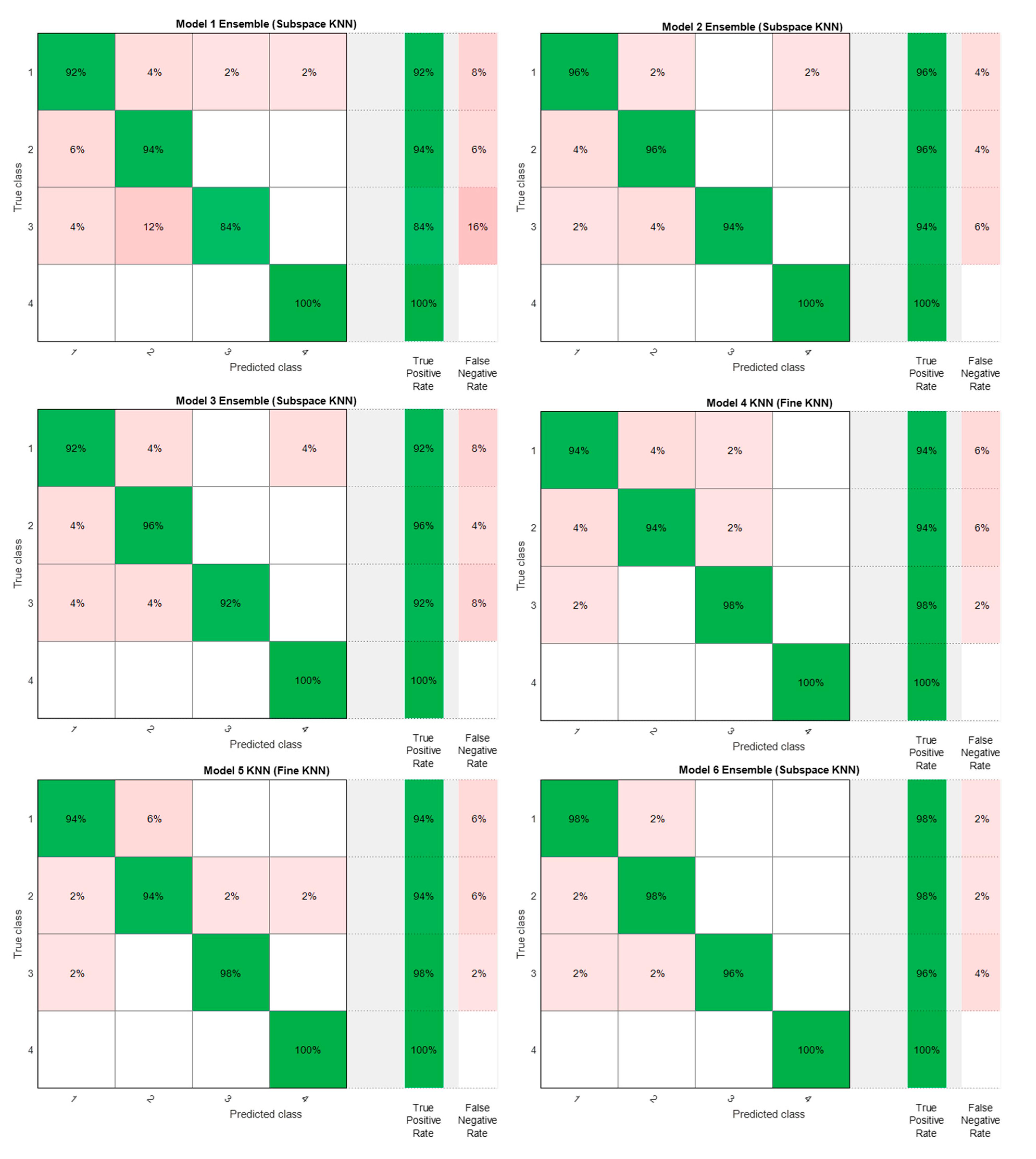
The confusion matrix for five subjects is plotted in Figure 3. From the figure, all models achieved significant performance with regard to accuracy. Motion prediction comparison shows that the rank of accuracy class 2 (motion 2) is higher than the others, and class 3 (motion 3) is the lowest rank. The best accuracy is having a bigger number of true-positive rates (TPR) than others and a smaller number of false-negative rates (FNR). Mostly all training models have the value of TPR about 74–96.5% and the value of FNR about 0–16%. Compared with 65 primary studies reviewed by Jaramillo-Yanez et al. regarding the use of ML on HGR using the EMG signal, the accuracy of the classification model resulted in a range of 70–100% [8]. We showed that all ML training models are working and predicting properly.
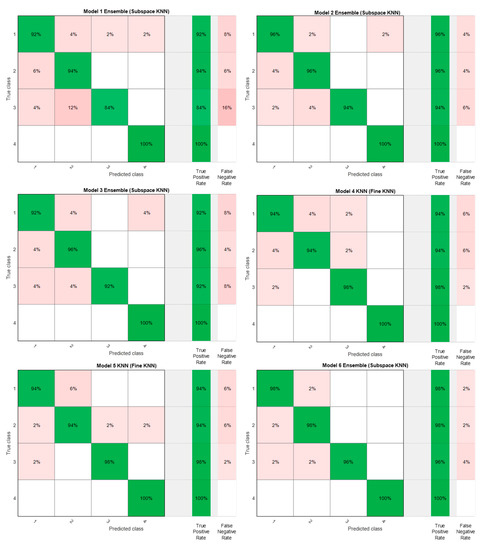
Figure 3.
Confusion matrix of six scenario models.
The prediction performances in every motion were computationally analyzed using three performance metrics: accuracy, recall, and precision. The classification accuracy metric (see Equation (6)) is the ratio of motions perceived correctly among all of the test data. The classification recall metric (Equation (7)) is the fraction of motions predicted correctly for a class among the test data of this class. The precision metric (Equation (8)) is the ratio of motion realized correctly from a class among the motions recognized by the ML model as this class [8].
where ni,j,k is the number of motions conducted by the subject i, which were recognized by the model as j, but they were k. iєI = i1, i2, ..., iu is the set of test subjects, jєJ = j1, j2, ..., jg is the set of predicted classes, kєK = k1, k2, ..., kg is the set of actual classes, u is the total number of test subjects, and g is the number of classes.
3. Results and Discussion
Identifying multiple hand motions using a few EMG sensors and muscles is one of the challenges for improving high levels of usability in controlling robotic hands, which we are attempting to solve. The experiment was conducted systematically, and the results are shown below.
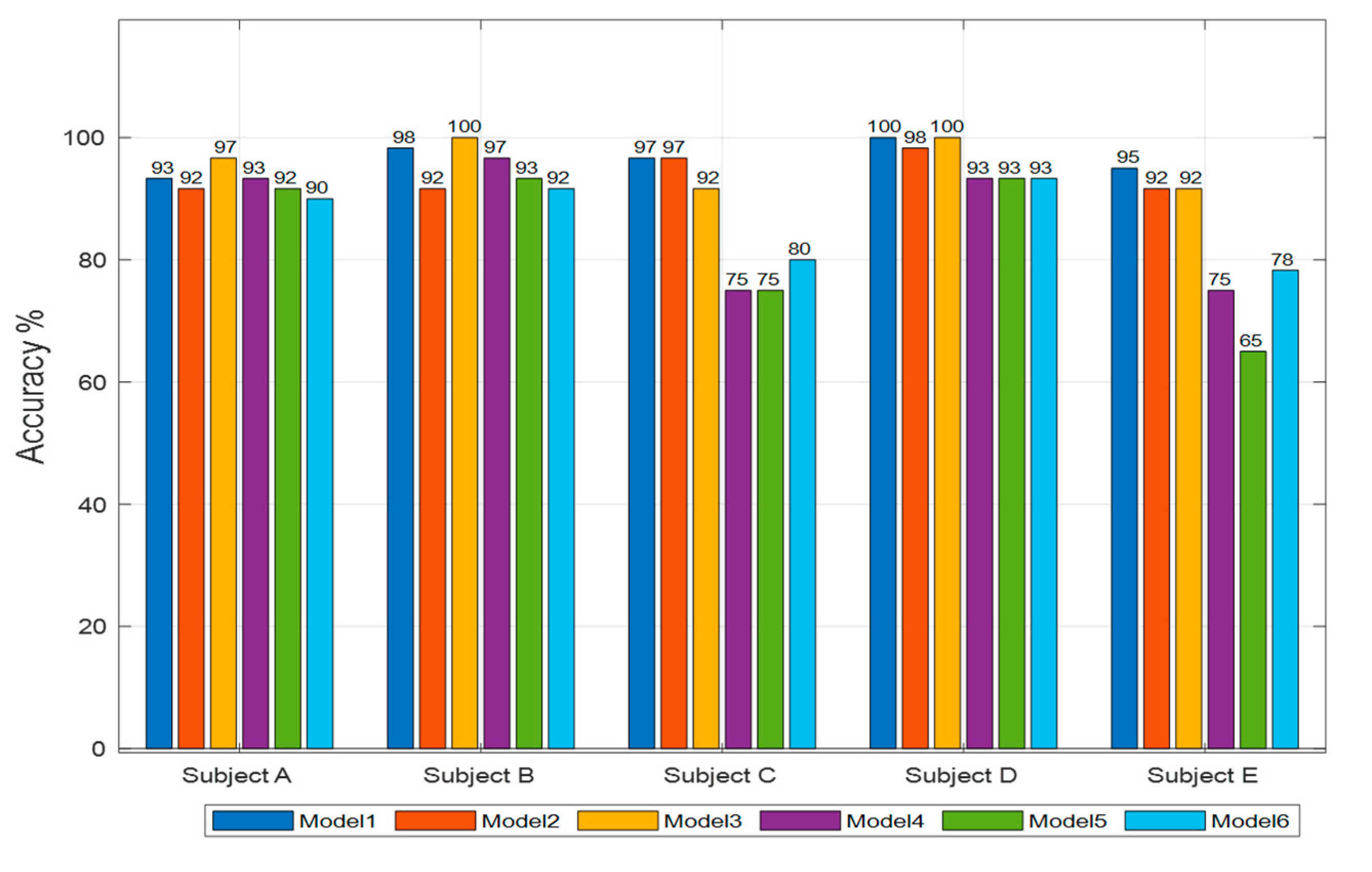
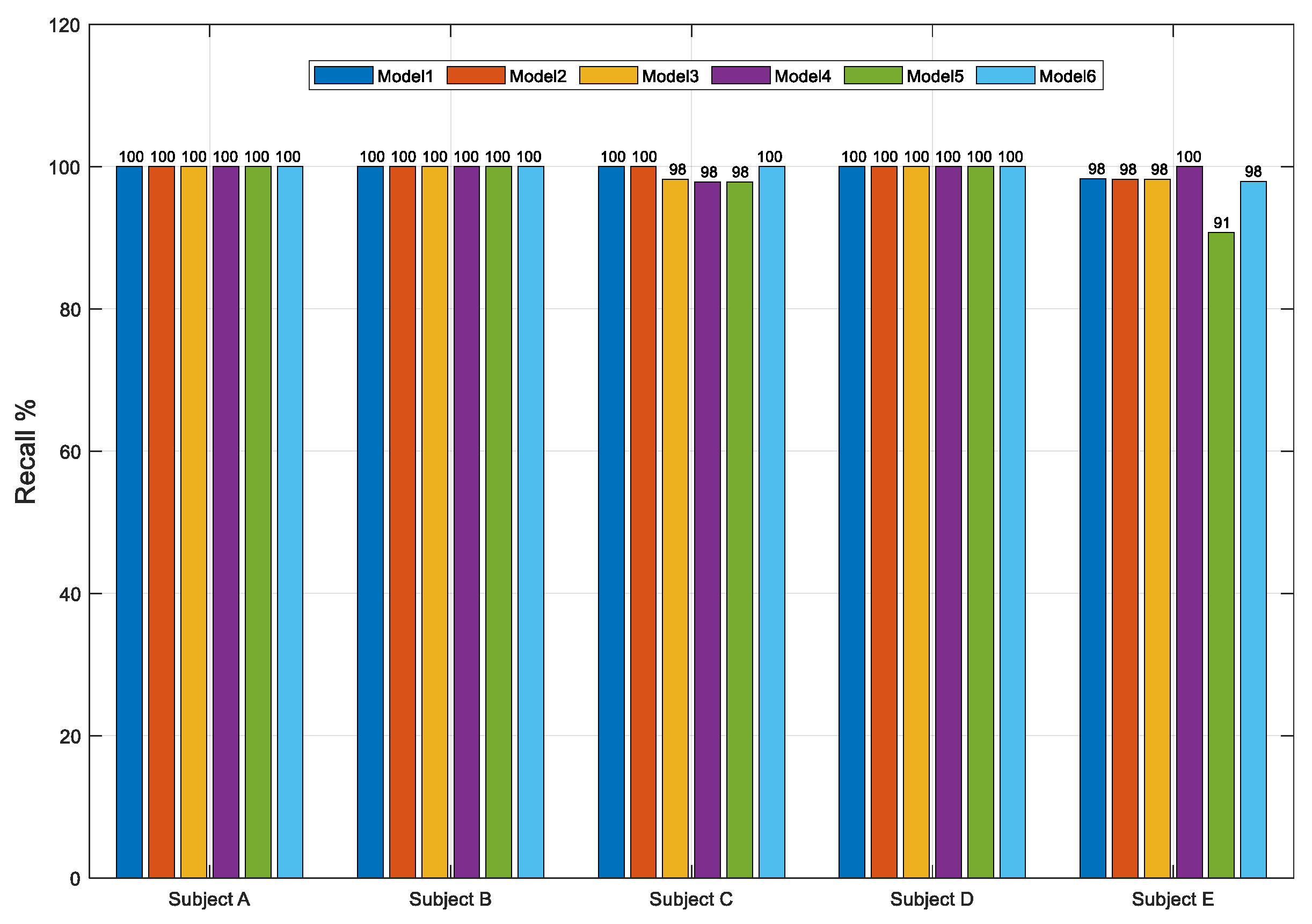
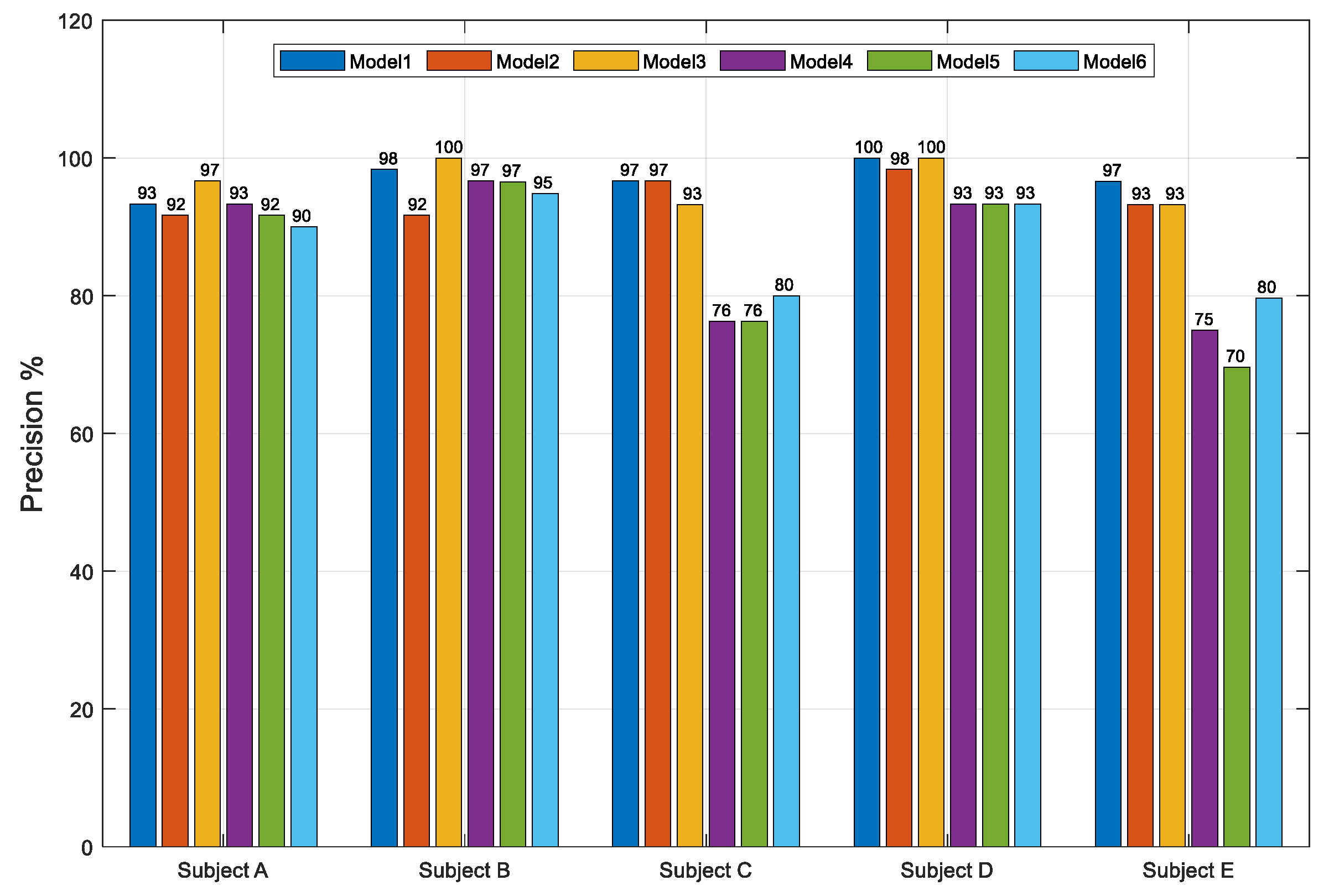
The overall performance comparison for five subjects shows that the users could achieve the acceptable percentage of performances, including accuracy (Figure 4), recall (Figure 5), and precision rates (Figure 6). The development of a machine learning model that is used to discriminate EMG signals from three sensor inputs of three muscles for three kinds of movements shows promising results. Scenarios of six models were used based on the level of the frequency cut-out factor in the segmentation, whether or not using TKEO is used, and the model classification. The results of the classifications performance percentage of the five subjects are, for the accuracy rate, in the range of 65–100%, for the recall rate, in the range 91–100%, while for the precision rate, in the range of 70–100%.
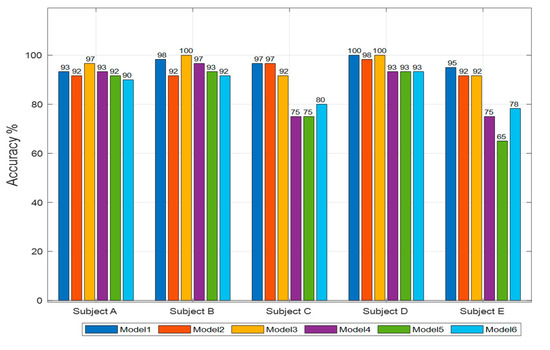
Figure 4.
Average classification accuracy percentages over five subjects with six models.
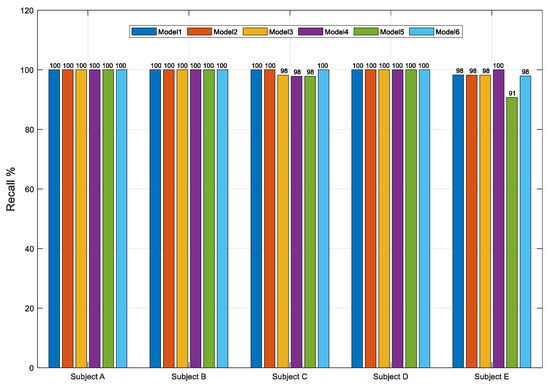
Figure 5.
Average classification recall percentages over five subjects with six models.
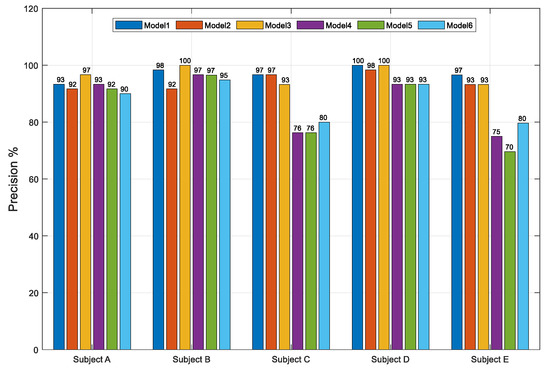
Figure 6.
Average precision percentages over five subjects with six models.
Subject D reports the highest consistent accuracy results than the others, model 1 achieved the highest average percentages of accuracy at 97.67%, while model 6 obtained the lowest at 86.33%(see Table 2). At least all the subjects reported consistent results for recall rate, ranging from 96.97% to 99.67%. Subject A had the most consistent precision with model 1 which reported an average precision of 96.99%. The reasons why the performances are varied are because of motion artifacts and inconsistent motion issues.

Table 2.
Total performance index.
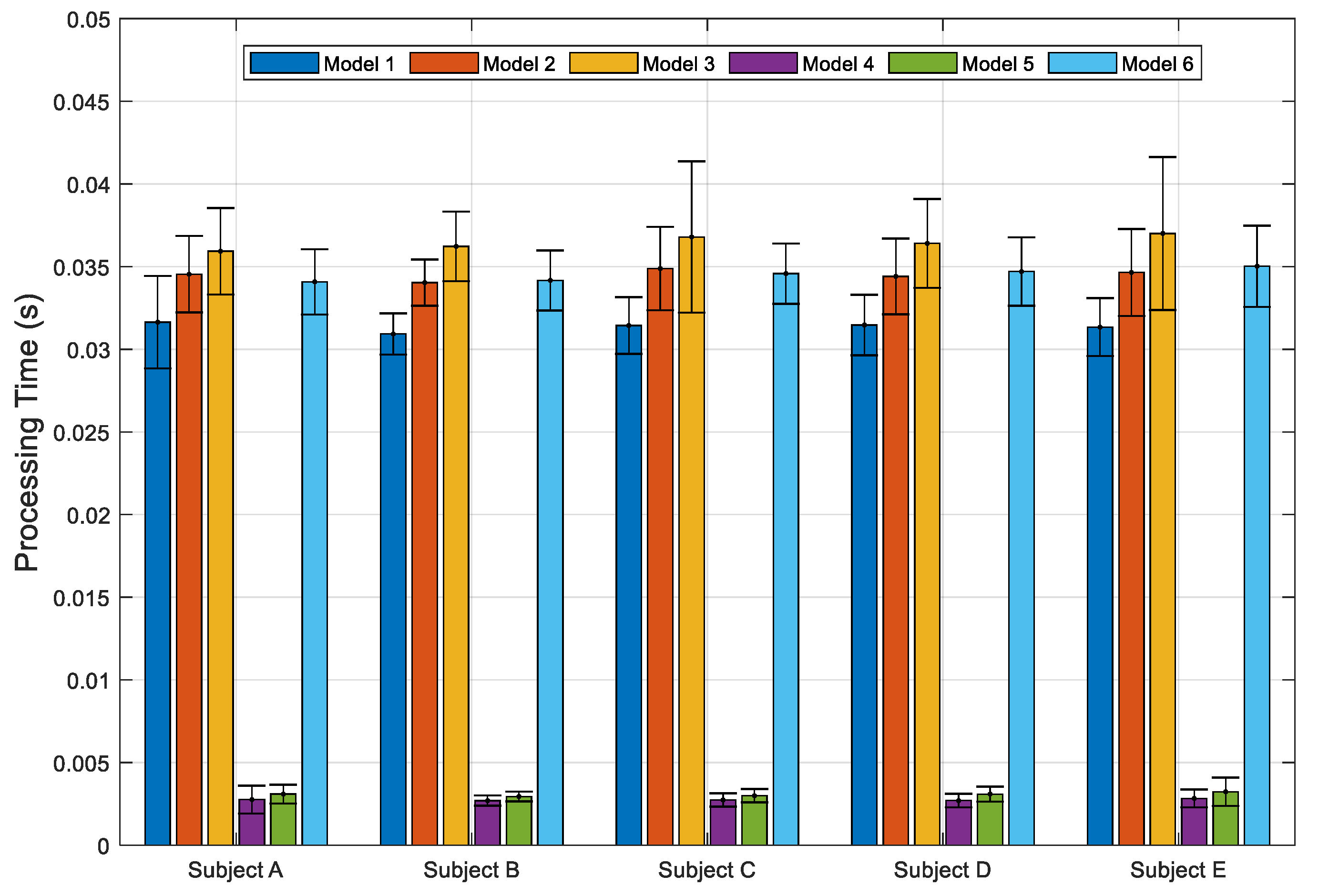
Table 3 shows the processing time required for the different ML model classification. The measured delay controller for the HGR model must reach optimal timing. Overall, all the models that are used by the five subjects require less than 40 ms for processing speeds of time data analysis (see Figure 7). The fastest average processing time is obtained by model 4 at 2.7 ms, while the longest time is acquired by model 3 at 36.5 ms (see Table 3). If the data collection time is less than 200 ms and the data analysis time is added, the embedded system should be quite relevant to categorize as the real-time system [4,8,60,61].

Table 3.
Average processing speed time of six models.
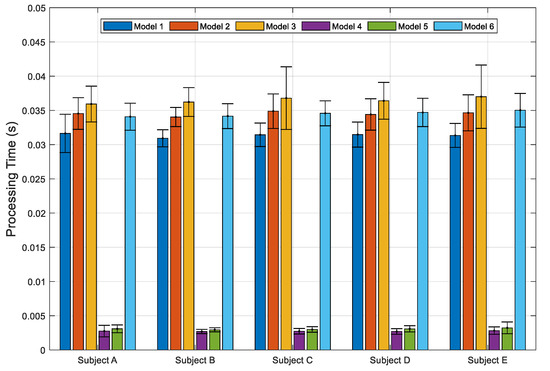
Figure 7.
Average processing speed time over five subjects with six models.
Based on the performance accuracy rates, recall rates, precision rates, and processing time, model 1 (TKEO processing with no division inputs per channel using ensemble subspace KNN) classification achieved the best performance. Model 1 hit accuracy rates in 96.67%, recall rates 99.66%, and precision rates 96.99%, while model 5 (without using TKEO, two segments input per channel, and four features with ensemble (subspace KNN) classifier)) had the worst performance. Model 5 had performance accuracy rates, recall rates, and precision rates of 86.33%, 96.97%, and 89.31%. Subject D showed more consistent performance than others. Based on this study, using TKEO achieved better performance results. However, inconsistent motions and motion artifacts are the main issue. Improving experiment setup for participants, such as giving a proper explanation and monitoring of participants, can be done to decrease inconsistency.
4. Conclusions
We designed 48 classification models for discriminating three EMG signals at three upper limb motions and compared and evaluated the minimum parameters of feature extractions and machine learning models with five healthy subjects’ data. The results showed that all the proposed models achieved accuracy rates in the range of 74–98% and the processing speed was below 40 ms, which is an acceptable delay for controlling a robotic arm. Then, the best classification model was discriminated with 12-parameter-ensemble (subspace KNN) accuracy rates of 96.67, recall rates of 99.66, and precision rates of 96.99. The difference between the best model and the conventional model was TKEO. It seemed that TKEO functioned to make the results of MAV, ZC, SSC, and WL stand out. Further research will deal with classifying more than three upper motions with three EMG sensors.
Author Contributions
P.W.L., M.S. and K.M. made the conception and design of the study. P.W.L., M.S.A.b.S., T.K. and J.M. conducted experiments and analyzed data. P.W.L., T.K., M.S. and J.M. wrote and edited this paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
The study was conducted according to the guidelines of the Declaration of Helsinki, and approved by the Gifu University ethics (approval procedures number 27–226) issued by Gifu University ethics committee).
Informed Consent Statement
Written informed consent has been obtained from the patients (confidential; not for publishing).
Data Availability Statement
Not applicable.
Conflicts of Interest
This paper has no conflicts of interest.
References
- Sasaki, M.; Matsushita, K.; Rusydi, M.I.; Laksono, P.W.; Muguro, J.; Bin Suhaimi, M.S.A.; Njeri, P.W. Robot control systems using bio-potential signals Robot Control Systems Using Bio-Potential Signals. AIP Conf. Proc. 2020, 2217, 020008. [Google Scholar] [CrossRef]
- Farina, D.; Jiang, N.; Rehbaum, H.; Holobar, A.; Graimann, B.; Dietl, H.; Aszmann, O.C. The Extraction of Neural Information from the Surface EMG for the Control of Upper-Limb Prostheses: Emerging Avenues and Challenges. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 797–809. [Google Scholar] [CrossRef]
- Bi, L.; Feleke, A.; Guan, C. A review on EMG-based motor intention prediction of continuous human upper limb motion for human-robot collaboration. Biomed. Signal Process. Control 2019, 51, 113–127. [Google Scholar] [CrossRef]
- Parajuli, N.; Sreenivasan, N.; Bifulco, P.; Cesarelli, M.; Savino, S.; Niola, V.; Esposito, D.; Hamilton, T.J.; Naik, G.R.; Gunawardana, U.; et al. Real-Time EMG Based Pattern Recognition Control for Hand Prostheses: A Review on Existing Methods, Challenges and Future Implementation. Sensors 2019, 19, 4596. [Google Scholar] [CrossRef]
- Meattini, R.; Benatti, S.; Scarcia, U.; De Gregorio, D.; Benini, L.; Melchiorri, C. An sEMG-Based Human–Robot Interface for Robotic Hands Using Machine Learning and Synergies. IEEE Trans. Compon. Packag. Manuf. Technol. 2018. [Google Scholar] [CrossRef]
- Toledo-Pérez, D.C.; Rodríguez-Reséndiz, J.; Gómez-Loenzo, R.A.; Jauregui-Correa, J.C. Support Vector Machine-Based EMG Signal Classification Techniques: A Review. Appl. Sci. 2019, 9, 4402. [Google Scholar] [CrossRef]
- Jia, G.; Lam, H.-K.; Liao, J.; Wang, R. Classification of electromyographic hand gesture signals using machine learning techniques. Neurocomputing 2020, 401, 236–248. [Google Scholar] [CrossRef]
- Jaramillo-Yánez, A.; Benalcázar, M.E.; Mena-Maldonado, E. Real-Time Hand Gesture Recognition Using Surface Electromyography and Machine Learning: A Systematic Literature Review. Sensors 2020, 20, 2467. [Google Scholar] [CrossRef]
- Laksono, P.W.; Matsushita, K.; Bin Suhaimi, M.S.A.; Kitamura, T.; Njeri, W.; Muguro, J.; Sasaki, M. Mapping Three Electromyography Signals Generated by Human Elbow and Shoulder Movements to Two Degree of Freedom Upper-Limb Robot Control. Robotics 2020, 9, 83. [Google Scholar] [CrossRef]
- Simao, M.; Mendes, N.; Gibaru, O.; Neto, P. A Review on Electromyography Decoding and Pattern Recognition for Human-Machine Interaction. IEEE Access 2019, 7, 39564–39582. [Google Scholar] [CrossRef]
- Rubio, J.D.J.; Ochoa, G.; Mujica-Vargas, D.; Garcia, E.; Balcazar, R.; Elias, I.; Cruz, D.R.; Juarez, C.F.; Aguilar, A.; Novoa, J.F. Structure Regulator for the Perturbations Attenuation in a Quadrotor. IEEE Access 2019, 7, 138244–138252. [Google Scholar] [CrossRef]
- Tavakoli, M.; Benussi, C.; Lourenco, J.L. Single channel surface EMG control of advanced prosthetic hands: A simple, low cost and efficient approach. Expert Syst. Appl. 2017, 79, 322–332. [Google Scholar] [CrossRef]
- Triwiyanto, T.; Rahmawati, T.; Yulianto, E.; Mak’Ruf, M.R.; Nugraha, P.C. Dynamic feature for an effective elbow-joint angle estimation based on electromyography signals. Indones. J. Electr. Eng. Comput. Sci. 2020, 19, 178–187. [Google Scholar] [CrossRef]
- Antuvan, C.W.; Ison, M.; Artemiadis, P. Embedded Human Control of Robots Using Myoelectric Interfaces. IEEE Trans. Neural Syst. Rehabil. Eng. 2014, 22, 820–827. [Google Scholar] [CrossRef]
- Fukuda, O.; Tsuji, T.; Kaneko, M.; Otsuka, A. A human-assisting manipulator teleoperated by EMG signals and arm motions. IEEE Trans. Robot. Autom. 2003. [Google Scholar] [CrossRef]
- Martinez, D.I.; De Rubio, J.J.; Vargas, T.M.; Garcia, V.; Ochoa, G.; Balcazar, R.; Cruz, D.R.; Aguilar, A.; Novoa, J.F.; Aguilar-Ibanez, C. Stabilization of Robots With a Regulator Containing the Sigmoid Mapping. IEEE Access 2020, 8, 89479–89488. [Google Scholar] [CrossRef]
- Bin Suhaimi, M.S.A.; Matsushita, K.; Sasaki, M.; Njeri, W. 24-Gaze-Point Calibration Method for Improving the Precision of AC-EOG Gaze Estimation. Sensors 2019, 19, 3650. [Google Scholar] [CrossRef]
- Sánchez-Velasco, L.E.; Arias-Montiel, M.; Guzmán-Ramírez, E.; Lugo-González, E. A Low-Cost EMG-Controlled Anthropomorphic Robotic Hand for Power and Precision Grasp. Biocybern. Biomed. Eng. 2020, 40, 221–237. [Google Scholar] [CrossRef]
- Hassan, H.F.; Abou-Loukh, S.J.; Ibraheem, I.K. Teleoperated robotic arm movement using electromyography signal with wearable Myo armband. J. King Saud Univ. Eng. Sci. 2019. [Google Scholar] [CrossRef]
- Aguilar-Ibanez, C.; Suarez-Castanon, M.S. A Trajectory Planning Based Controller to Regulate an Uncertain 3D Overhead Crane System. Int. J. Appl. Math. Comput. Sci. 2020, 29, 693–702. [Google Scholar] [CrossRef]
- Rusydi, M.I.; Sasaki, M.; Ito, S. Affine Transform to Reform Pixel Coordinates of EOG Signals for Controlling Robot Manipulators Using Gaze Motions. Sensors 2014, 14, 10107–10123. [Google Scholar] [CrossRef]
- García-Sánchez, J.R.; Tavera-Mosqueda, S.; Silva-Ortigoza, R.; Hernández-Guzmán, V.M.; Sandoval-Gutiérrez, J.; Marcelino-Aranda, M.; Taud, H.; Marciano-Melchor, M. Robust Switched Tracking Control for Wheeled Mobile Robots Considering the Actuators and Drivers. Sensors 2018, 18, 4316. [Google Scholar] [CrossRef] [PubMed]
- Wang, N.; Lao, K.; Zhang, X. Design and Myoelectric Control of an Anthropomorphic Prosthetic Hand. J. Bionic Eng. 2017, 14, 47–59. [Google Scholar] [CrossRef]
- Nascimento, L.M.S.D.; Bonfati, L.V.; Freitas, M.L.B.; Junior, J.J.A.M.; Siqueira, H.V.; Stevan, J.S.L. Sensors and Systems for Physical Rehabilitation and Health Monitoring—A Review. Sensors 2020, 20, 4063. [Google Scholar] [CrossRef] [PubMed]
- Fang, C.; He, B.; Wang, Y.; Cao, J.; Gao, S. EMG-Centered Multisensory Based Technologies for Pattern Recognition in Rehabilitation: State of the Art and Challenges. Biosensors 2020, 10, 85. [Google Scholar] [CrossRef] [PubMed]
- Qidwai, U.; Ajimsha, M.; Shakir, M. The role of EEG and EMG combined virtual reality gaming system in facial palsy rehabilitation—A case report. J. Bodyw. Mov. Ther. 2019, 23, 425–431. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, A.; Raza, H.; Meena, Y.K.; Dutta, A.; Prasad, G. An EEG-EMG correlation-based brain-computer interface for hand orthosis supported neuro-rehabilitation. J. Neurosci. Methods 2019, 312, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Vujaklija, I.; Farina, D.; Aszmann, O.C. New developments in prosthetic arm systems. Orthop. Res. Rev. 2016, 8, 31–39. [Google Scholar] [CrossRef]
- Ramírez-Martínez, D.; Alfaro-Ponce, M.; Pogrebnyak, O.; Aldape-Pérez, M.; Argüelles-Cruz, A.-J. Hand Movement Classification Using Burg Reflection Coefficients. Sensors 2019, 19, 475. [Google Scholar] [CrossRef] [PubMed]
- Campeau-Lecours, A.; Cote-Allard, U.; Vu, D.-S.; Routhier, F.; Gosselin, B.; Gosselin, C. Intuitive Adaptive Orientation Control for Enhanced Human–Robot Interaction. IEEE Trans. Robot. 2019, 35, 509–520. [Google Scholar] [CrossRef]
- Rahman, S. Machine Learning-Based Cognitive Position and Force Controls for Power-Assisted Human–Robot Collaborative Manipulation. Machines 2021, 9, 28. [Google Scholar] [CrossRef]
- Zhou, S.; Yin, K.; Fei, F.; Zhang, K. Surface electromyography–based hand movement recognition using the Gaussian mixture model, multilayer perceptron, and AdaBoost method. Int. J. Distrib. Sens. Netw. 2019, 15. [Google Scholar] [CrossRef]
- Khushaba, R.N.; Kodagoda, S.; Takruri, M.; Dissanayake, G. Toward improved control of prosthetic fingers using surface electromyogram (EMG) signals. Expert Syst. Appl. 2012, 39, 10731–10738. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.K.; Samui, S. An experimental study on upper limb position invariant EMG signal classification based on deep neural network. Biomed. Signal Process. Control 2020, 55, 101669. [Google Scholar] [CrossRef]
- Ko, A.J.; Latoza, T.D.; Burnett, M.M. A practical guide to controlled experiments of software engineering tools with human participants. Empir. Softw. Eng. 2013, 20, 110–141. [Google Scholar] [CrossRef]
- Faber, M.; Bützler, J.; Schlick, C.M. Human-robot Cooperation in Future Production Systems: Analysis of Requirements for Designing an Ergonomic Work System. Procedia Manuf. 2015, 3, 510–517. [Google Scholar] [CrossRef]
- Huang, Y.; Chen, K.; Zhang, X.; Wang, K.; Ota, J. Joint torque estimation for the human arm from sEMG using backpropagation neural networks and autoencoders. Biomed. Signal Process. Control 2020, 62, 102051. [Google Scholar] [CrossRef]
- Márquez-Figueroa, S.; Shmaliy, Y.S.; Ibarra-Manzano, O. Optimal extraction of EMG signal envelope and artifacts removal assuming colored measurement noise. Biomed. Signal Process. Control 2020, 57, 101679. [Google Scholar] [CrossRef]
- Antuvan, C.W.; Bisio, F.; Marini, F.; Yen, S.-C.; Cambria, E.; Masia, L. Role of Muscle Synergies in Real-Time Classification of Upper Limb Motions using Extreme Learning Machines. J. Neuroeng. Rehabil. 2016, 13, 1–15. [Google Scholar] [CrossRef]
- Englehart, K.K.; Hudgins, B. A Robust, Real-Time Control Scheme for Multifunction Myoelectric Control. IEEE Trans. Biomed. Eng. 2003, 50, 848–854. [Google Scholar] [CrossRef] [PubMed]
- Samuel, O.W.; Asogbon, M.G.; Geng, Y.; Al-Timemy, A.H.; Pirbhulal, S.; Ji, N.; Chen, S.; Fang, P.; Li, G. Intelligent EMG Pattern Recognition Control Method for Upper-Limb Multifunctional Prostheses: Advances, Current Challenges, and Future Prospects. IEEE Access 2019, 7, 10150–10165. [Google Scholar] [CrossRef]
- Nougarou, F.; Campeau-Lecours, A.; Massicotte, D.; Boukadoum, M.; Gosselin, C.; Gosselin, B. Pattern recognition based on HD-sEMG spatial features extraction for an efficient proportional control of a robotic arm. Biomed. Signal Process. Control 2019, 53, 101550. [Google Scholar] [CrossRef]
- Rabin, N.; Kahlon, M.; Malayev, S.; Ratnovsky, A. Classification of human hand movements based on EMG signals using nonlinear dimensionality reduction and data fusion techniques. Expert Syst. Appl. 2020, 149, 113281. [Google Scholar] [CrossRef]
- Krasoulis, A.; Nazarpour, K. Myoelectric digit action decoding with multi-label, multi-class classification: An offline analysis. Sci. Rep. 2020, 1–10. [Google Scholar] [CrossRef]
- Young, A.J.; Smith, L.H.; Rouse, E.J.; Hargrove, L.J. A comparison of the real-time controllability of pattern recognition to conventional myoelectric control for discrete and simultaneous movements. J. Neuroeng. Rehabil. 2014, 11, 1–10. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, C.; Zhang, X.; Chen, C.; Zhou, Y.; Ni, G.; Muh, S.; Lemos, S. Shoulder muscle activation pattern recognition based on sEMG and machine learning algorithms. Comput. Methods Programs Biomed. 2020, 197. [Google Scholar] [CrossRef]
- Tsai, A.-C.; Hsieh, T.-H.; Luh, J.-J.; Lin, T.-T. A comparison of upper-limb motion pattern recognition using EMG signals during dynamic and isometric muscle contractions. Biomed. Signal Process. Control 2014, 11, 17–26. [Google Scholar] [CrossRef]
- Cai, S.; Chen, Y.; Huang, S.; Wu, Y.; Zheng, H.; Li, X.; Xie, L. SVM-Based Classification of sEMG Signals for Upper-Limb Self-Rehabilitation Training. Front. Neurorobotics 2019, 13, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Trigili, E.; Grazi, L.; Crea, S.; Accogli, A.; Carpaneto, J.; Micera, S.; Vitiello, N.; Panarese, A. Detection of movement onset using EMG signals for upper-limb exoskeletons in reaching tasks. J. Neuroeng. Rehabil. 2019, 16, 1–16. [Google Scholar] [CrossRef]
- Kaiser, J.F. Some useful properties of Teager’s energy operators. In Proceedings of the 1993 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP 1993), Minneapolis, MN, USA, 27–30 April 1993; volume 3, pp. 149–152. [Google Scholar]
- Li, X.; Zhou, P.; Aruin, A.S. Teager–Kaiser Energy Operation of Surface EMG Improves Muscle Activity Onset Detection. Ann. Biomed. Eng. 2007, 35, 1532–1538. [Google Scholar] [CrossRef]
- Phinyomark, A.; Khushaba, R.N.; Scheme, E. Feature Extraction and Selection for Myoelectric Control Based on Wearable EMG Sensors. Sensors 2018, 18, 1615. [Google Scholar] [CrossRef]
- Karabulut, D.; Ortes, F.; Arslan, Y.Z.; Adli, M.A. Comparative evaluation of EMG signal features for myoelectric controlled human arm prosthetics. Biocybern. Biomed. Eng. 2017, 37, 326–335. [Google Scholar] [CrossRef]
- Chowdhury, R.H.; Reaz, M.B.I.; Ali, M.A.B.M.; Bakar, A.A.A.; Chellappan, K.; Chang, T.G. Surface Electromyography Signal Processing and Classification Techniques. Sensors 2013, 13, 12431–12466. [Google Scholar] [CrossRef]
- Phinyomark, A.; Phukpattaranont, P.; Limsakul, C. Feature reduction and selection for EMG signal classification. Expert Syst. Appl. 2012. [Google Scholar] [CrossRef]
- Gopura, R.A.R.C.; Bandara, D.S.V.; Gunasekara, J.M.P.; Jayawardane, T.S.S. Recent Trends in EMG-Based Control Methods for Assistive Robots. In Electrodiagnosis in New Frontiers of Clinical Research; IntechOpen: London, UK, 2013; pp. 237–268. [Google Scholar]
- Soedirdjo, S.D.H.; Merletti, R. Comparison of different digital filtering techniques for surface EMG envelope recorded from skeletal muscle. In Proceedings of the 20th Congress of the International Society of Electrophysiology and Kinesiology (ISEK 2014), Rome, Italy, 15–18 July 2014. [Google Scholar]
- Rokach, L.; Schclar, A.; Itach, E. Ensemble methods for multi-label classification. Expert Syst. Appl. 2014, 41, 7507–7523. [Google Scholar] [CrossRef]
- Noor, A.; Uçar, M.K.; Polat, K.; Assiri, A.; Nour, R. A Novel Approach to Ensemble Classifiers: FsBoost-Based Subspace Method. Math. Probl. Eng. 2020, 2020. [Google Scholar] [CrossRef]
- Rasool, G.; Iqbal, K.; Bouaynaya, N.; White, G. Real-Time Task Discrimination for Myoelectric Control Employing Task-Specific Muscle Synergies. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 98–108. [Google Scholar] [CrossRef] [PubMed]
- Smith, L.H.; Hargrove, L.J.; Lock, B.A.; Kuiken, T.A. Classification Error and Controller Delay. IEEE Trans. Neural Syst. Rehabil. Eng. 2011, 19, 186–192. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).