A Module Configuration Design Approach for Complex Equipment of Port Shipping Based on Heterogeneous Customer Requirements and Product Operational Data

Abstract

Modularization fails to adequately meet the diverse customer requirements and the product operational data for complex equipment of port shipping (CEPS). To address this challenge, we propose a module configuration design approach (MCDA) that incorporates module parameter planning (MPP) and service module customization (SMC). Initially, the design ranges and weights of functional requirements are established using fuzzy information derived from customer requirements, facilitated by fuzzy quality function deployment. Subsequently, a multi-objective model of MPP is developed, incorporating the cost utility, information content, and delivery time of module and product based on a probabilistic assessment of module instances from operational data. The non-dominated sorting genetic algorithm II (NSGA-II) is employed to derive the solution set for MPP. The personalized configuration of the Pareto solution set for SMC is derived based on each objective function pair. Finally, we illustrate the effectiveness of the proposed approach through a case study involving a wheel loader and method comparison.

1. Introduction

Modularization is an effective methodology to make positive promotions to the product life cycle [1]. To implement the modularization strategy, primary parameters of partitioned modules should be identified, and module parameters would have many values, which may be discrete or continuous; all the module parameters constitute module parameter planning (MPP) [2]. Some parametric modules and customized modules with uncertain valued parameters are designed to achieve the function requirements (FRs), which are mapped from customer requirements (CRs) [3,4]. However, the fuzziness of CRs leads to the inaccuracy of FRs, where service module customization (SMC) is not considered. As well, a specific parametric module in MPP will be difficult to pick over with the increase in the number of modules, and then the result of MPP cannot be applied in engineering design directly. Thus, a module configuration design approach (MCDA) that incorporates MPP and SMC specifically for complex equipment of port and shipping (CEPS) must be carefully established, planned, and managed. It would be dramatically significant to establish the MCDA framework for MPP and SMC based on heterogeneous data of CRs and product operations.

With the development and confluence of big data, artificial intelligence, and the internet of things, a multitude of profound changes and emerging trends in the design field have been witnessed [5,6,7]. These works primarily offer high-level, directional discussions about the digital transformation in design, yet they lack detailed implementation pathways for applying these technologies to specific domains, such as CEPS. Thereinto, modularization, as the foundation of module partition, is an effective strategy to reduce the cost of product research and development [8,9,10]. While these studies confirm the value of modularization, they often focus on traditional, function-and-physics-based partitioning, without fully exploring how to leverage operational data to dynamically guide and optimize module configuration planning. Over the last decade, many approaches of modularization have been introduced based on product function [11], manufacturing and assembly [12,13], and product design [14,15], as well as innovation design methods [16,17], where these studies rely on function-driven or data-driven approaches to improve product performance. So far, few studies have addressed the issue of MPP and SMC based on heterogeneous information, especially for CEPS based on heterogeneous CR data and product operational data. Fortunately, all these issues can be viewed as combinational optimization problems to achieve an optimal combination of discrete model parameters or attribute levels [18,19]. The limitation of these approaches is that their optimization objectives often rely on static and subjective evaluations and lack the integration of real-time operational data from the product lifecycle, leading to solutions that may diverge from actual operational performance. Then, they obtain the best alternative scheme.

The MCDA incorporating MPP and SMC should be presented to derive the FRs of the product and achieve the personalization value of the module parameter. Among these presented MPP approaches, the part-worth model and the information axiom are effective methods to calculate the cost utility of the parametric module and the information content of FRs, respectively. The quality function deployment (QFD) [20] and Kano model [21] are effective ways to measure the CRs and their satisfaction. The conjoint analysis [22] is another widely adopted method to explore the configuration scheme in product design. The product configuration approach has turned out to be one of the most popular preference-based techniques for presenting new product concepts or product-service systems [23]. However, MPP should be established to achieve the FRs as much as possible and obtain a near-optimal product concept, which the product operational data and SMC do not have. Thus, personalization configuration of parametric modules and customized modules for MPP and SMC should be established and managed to improve the satisfaction of customers.

In this article, an integrated MCDA approach for CEPS is presented to derive MPP and SMC based on heterogeneous CR data and product operational data. The rest of this article is organized as follows. Section 2 presents the literature review of this study. Section 3 introduces the basic concepts of FRs and module configuration, and the proposed approach for the MCDA is introduced. Section 4 presents a real-world case study of a wheel loader to demonstrate the effectiveness of the proposed approach. Finally, the conclusions as well as future work of this study are summarized in Section 5.

2. Literature Review

MPP and SMC technologies have focused on the assembly process of products that require high development costs and technology contents, along with a long lead time for application [24]. This section reviews the related works for CRs and MPP as well as SMC, which are the major issues of the MCDA for CEPS.

2.1. CRs for Complex Equipment

The trend of diversity and personalization of CRs posed great challenges in design and development. CEPS, such as cranes, excavators, and loaders, are widely used in ports and shipping, including the handling of goods, loading and unloading, etc. In CR modeling, Li et al. [1] built an integer programming model based on CRs to plan the combination of modules of complex equipment products. This provides a mathematical method for obtaining optimal module combinations. However, the model heavily relies on precise, static customer data and does not incorporate product operational data. Chiu et al. [25] developed a smart product service system that leverages unsupervised NLP and deep learning to transform customers into active data producers for personalized recommendations and value cocreation. Ji et al. [26] proposed a two-layer optimization model for joint decision-making in technical systems and material reuse modularization based on a constrained genetic algorithm. Nevertheless, the approach remains static and rigid in handling CRs, lacking consideration for operational feedback. Zeng et al. [27] studied the inclusive relationship between parametric models based on the Apriori algorithm by comparing the confidence of frequent itemsets and taking product data as the object. Hu et al. [28] proposed Kano-based engineering feature mapping and artificial immune system-based product design models to comprehensively meet CRs for product characteristics and obtained product design solutions. Cheng et al. [29] proposed a coupling analysis method based on axiomatic design and a module association matrix for the product family design coupling problem and analyzed the corresponding association relationships among product family CRs, FRs, design parameters, and modules. This helps reduce management complexity in product family design. The relationships are established based on static expert judgment or historical data, without leveraging operational data for validation and dynamic updates. Ma et al. [30] proposed a framework to identify and redesign key functional modules based on performance degradation analysis by considering causal associations of functional failures. Dou et al. [31] established an evolutionary game-based CR response model for the customer-side multi-energy load coupling problem. Qu et al. [32] provided a systematic method to capture the smart manufacturing systems requirements list and explain the complex relationship between the smart manufacturing systems and their multi-stakeholders. The perspective is macro- and system-level, offering only indirect guidance for module configuration at the product level.

Based on the above analysis, customer or market requirements were derived through various methods, including market research, customer evaluations, questionnaires, online data sources [33], and product operation data [34]. Consequently, this information was incorporated into the developed cost–benefit or satisfaction function model to identify the optimal combination of module parameters. However, those approaches are hindered by a reliance on subjective and one-dimensional evaluation information, a limited modeling perspective, and a lack of consideration for post-production services. As a result, they fail to meet the diverse expectations of different customers and the subsequent SMC. Therefore, there is a pressing need for multi-objective planning that integrates heterogeneous data from CRs and product operational data to enhance MPP for CEPS.

2.2. Methods of MPP and SMC

Traditional MPP and SMC problems primarily rely on the subjective evaluations of designers, which can directly impact project schedules. Customers possess diverse requirements for products, necessitating that they be suitable for their intended applications, cost-effective, and supported by robust product services. Modular design is recognized as an effective approach to address these MPP and SMC challenges. Within a modularization strategy, a product is decomposed into modules, each characterized by a set of instances defined by continuous or discrete parameters, resulting in a combinatorial optimization problem known as NP-hard. Researchers have investigated various design methodologies for MPP and SMC tailored to complex equipment, as outlined below.

Wang et al. [34] presented an optimization design method of a wheel loader gearbox considering product operational big data based on the non-dominated sorting genetic algorithm II (NSGA-II) and multi-objective particle swarm optimization (MOPSO) algorithm. Oliva and Opabola [35] presented a framework that integrates hazard characterization, facility-specific exposure assessment, fragility model selection, damage simulation, and fault tree analysis to estimate the probability of operational disruption under given hazard intensity measures. Li et al. [36] introduced a novel modularization method of the complex product, which incorporates the modularity and the scope of design change propagation. This helps design module architectures that are stable with minimal change propagation. However, it focuses on managing changes during design and does not explore using operational data to guide initial MPP. Hou et al. [37] proposed an innovation evolution method for product families to address the shortcomings of research on dynamic evolution mechanisms and systematic innovation methods. This provides a methodology for the long-term evolution of product families. It focuses on macro-level technical evolution rather than supporting real-time module configuration for individual custom orders. To enhance worker experience, Ulmer et al. [13] introduced an adaptive manufacturing assistance system based on hardware modularization and gamified instructions tailored to individual workers. Given the high coupling and heterogeneity characteristics among complex equipment component modules, Li et al. [38] proposed a module division method based on a weighted complex network. To address complex product modularization, Liu et al. [10] introduced a network-based method that employs stable overlapping community detection and genetic algorithm optimization for superior module partition. Zhang and Du [39] established a mixed integer nonlinear two-layer programming model with product family configuration design as the main focus and remanufacturer selection decision as the secondary focus to optimize remanufactured product family configurations. This optimizes the configuration of remanufactured product families. The model is tailored for the remanufacturing context and faces challenges in handling uncertainty and dynamic data. Li et al. [40] introduced the concept of a digital twin to the multidisciplinary collaborative design of complex mechanical products. This provides a vision for interaction and iteration between the design and physical spaces. It is a conceptual framework that lacks detailed models and algorithms for its specific implementation in configuration design. Yang et al. [6] established a technology association-based project organization and task dependency network model by identifying functional associations and organizing execution associations between tasks. Macherki et al. [41] formulated the self-reconfiguration of manufacturing systems as a constraint satisfaction problem solved using Satisfiability Modulo Theories (SMTs), providing a formal logic-based approach for dynamic module and layout reconfiguration. Lai et al. [42] determined module redesign priorities by the ratio of a green performance evaluation value to a proposed functional commonality index value based on a product family hierarchy model. Forti et al. [43] presented the integration process of two modularization methods. Wang et al. [44] proposed a novel precooling strategy based on multi-modules, in which the precooler is divided into multiple identical modules, and the number of modules cooled by different fuels could be regulated. This study provides a flexible engineering design adaptable to different working conditions. It is a highly specific solution where modularization refers to physical replication of parts, differing from the parametric customization of functional modules in product family design.

From the preceding discussion, it is evident that the design methodologies for MPP and SMC of complex equipment primarily emphasize modularization strategies. However, the previously mentioned excessive reliance on modularization strategies is associated with limitations, such as a singular modeling perspective and a lack of diverse solution approaches, as well as insufficient attention to the personalization of parametric modules and customized modules for MPP and SMC. Consequently, these approaches fail to adequately address the varying expectations of different CRs. Therefore, it is essential to integrate heterogeneous data from CRs and the engineering data of CEPS to develop a framework of the MCDA that incorporates MPP and SMC.

To sum up, this study is structured around addressing the following three research questions (RQs):

RQ1: How can a heterogeneous data-driven framework be constructed to effectively integrate CRs and product operational data for the module configuration of CEPS?

RQ2: How can a multi-objective optimization model for MPP be formulated and solved to balance the trade-offs among cost utility, information content, and delivery time?

RQ3: How can a linkage mechanism between MPP and SMC be established to enable adaptive personalization based on optimal module configuration schemes?

2.3. Research Gap and Contribution

As a classic modular design challenge, MPP and SMC of complex equipment cannot be effectively resolved through a singular approach. The identified research gaps are summarized as follows.

(1) Limited data-driven personalization configuration. Existing modularization strategies for complex equipment predominantly emphasize functional standardization, lacking robust methodologies to integrate heterogeneous data, such as usage scenarios and operational preferences with product operational data [10]. In contrast to these standardized approaches, our work leverages both CRs and operational data for personalized configuration. The traditional QFD method for deriving FRs relies on static and homogeneous customer feedback, thereby failing to capture dynamic and multi-source operational data (e.g., sensor logs, product operational data, and failure risk information) that significantly influence long-term product performance [14,20]. This study addresses this gap by employing fuzzy QFD to process imprecise CRs and incorporating operational data into the process of requirement mapping.

(2) Lack of integrated service customization. Most studies treat module configuration and module customization as distinct processes, thereby missing opportunities for synergistic optimization in the product lifecycle management [45,46]. Unlike these decoupled approaches, the proposed MCDA integrates MPP and SMC within a unified framework. Additionally, current MPP methodologies often prioritize singular objectives (e.g., cost minimization, time reduction, or value maximization), neglecting to balance trade-offs among part-worth utility, information entropy, and delivery time. This oversight can result in module configurations that do not align with real-world operational constraints [22]. Our research tackles this limitation by formulating a multi-objective optimization model that simultaneously considers these three critical factors.

Motivated by the above discussion, this study proposes an integrated framework for the MCDA aimed at deriving MPP and SMC for CEPS based on heterogeneous data from CRs and product operational data. The main contributions of this study are summarized as follows.

(1) The fuzzy QFD (FQFD) was utilized to map CRs to FRs and to delineate the design range, with the weights of FRs calculated using triangular fuzzy numbers. This approach, unlike the traditional QFD, effectively handles the fuzziness in CRs. A multi-objective model for MPP was constructed, incorporating the cost utility, information content, and delivery time of the module and product based on product operational data. This model provides a more comprehensive and balanced solution compared to single-objective models prevalent in the literature.

(2) This study introduced a heterogeneous data-driven MCDA framework that integrates CR information and product operational data for CEPS specifically. This directly addresses the data integration gap identified in existing modularization strategies. A multi-objective optimization model based on the NSGA-II with an elite strategy was developed to address the Pareto optimal problem.

(3) A mechanism linking MPP and SMC was presented to Pareto optimal product configurations, facilitating adaptive post-sale services that included predictive maintenance and spare part recommendations. This linkage is a novel contribution, overcoming the process isolation issue noted in prior research. The superiority of this approach is demonstrated through a case study of a wheel loader, which reveals enhanced customer satisfaction and reduced lifecycle costs compared to conventional design methodologies of modular configuration.

3. Preliminaries

3.1. Acquisition of FRs

Each divided module will encompass several module instances, each characterized by continuous or discrete parameter values, thereby forming module combination planning schemes to address various CRs. Prior to planning the parameter values, it is essential to select the relevant CRs. These CRs are gathered based on company orders and subsequently integrated and ranked by weighting their significance. The weighted CRs are then mapped to FRs using FQFD [45], which is illustrated in Figure 1.

Figure 1. Mapping relationships on CRs, FRs, and design parameters.

The range of design parameters and weights of FRs is determined according to the values of FRs. The mapping relationship transformation of FQFD and determination of FR weights are performed using triangular fuzzy numbers as follows:

$$\left\{\begin{array}{c}{\ddot{R}}_{gj}={\displaystyle \frac{{\sum }_{t=1}^J({\check{R}}_{gj}\times {\check{r}}_{tj})}{{\sum }_{j=1}^J{\sum }_{t=1}^J(R_{gj}\times {\check{r}}_{tj})}}\\ {\ddot{w}}_j={\displaystyle \sum _{g=1}^G}\left(e_g\times {\ddot{R}}_{gj}\right)\end{array}\right.$$

(1)

where ${\check{R}}_{gj}$ is the correlation between the gth CR and jth FR after normalization, ${\check{r}}_{tj}$ is the correlation between the tth FR and jth FR after normalization (expressed as a triangular fuzzy number), and $e_g$ and ${\ddot{w}}_j$ are the respective weights of CRs and FRs.

3.2. Conceptual Description of Module Configuration

The proposed MCDA of CEPS can be divided into two stages (as shown in Figure 2), including phase (1) MPP and phase (2) SMC. Some concepts and descriptions are defined as follows.

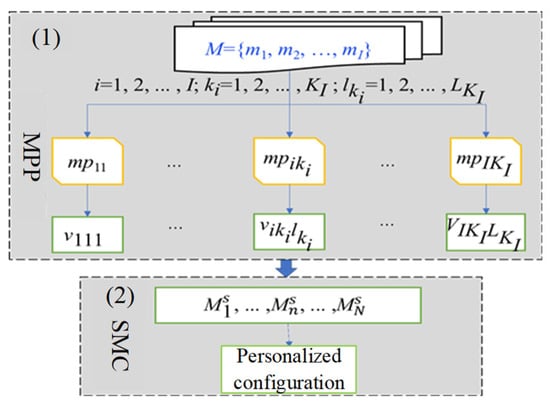
Figure 2. Two stages of the MCDA.

Definition 1. 

The set of functional modules of MPP is represented as $M=\left\{m_i|i=1,2,\dots ,I\right\}$; the set of module instances contained in each module is $M{P}_i=\left\{{mp}_{i{k}_i}|i=1,2,\dots ,I;k_i=1,2,\dots ,K_I\right\}$; and the list of parameter values for each module instance is $V_{i{k}_i}=\left\{v_{i{k}_i{l}_{k_i}}|i=1,2,\dots ,I;k_i=1,2,\dots ,K_I;l_{k_i}=1,2,\dots ,L_{K_I}\right\}$.

Definition 2. 

The set of functional modules of SMC is represented as $M^s=\left\{M_n^s|n=1,2,\dots ,N\right\}$, where the results obtained from MPP have an association relationship f with SMC, and the weighting matrix is obtained by integrating the scheme service evaluation matrix to obtain the service module ranking, i.e., the more the configuration scheme is associated with a service module, the more it satisfies personalization requirements.

Definition 3. 

If the ith module instance is capable of generating an acceptable utility $U_{ij}=\left\{i=1,2,\dots ,I;j=1,2,\dots ,J\right\}$ to the jth functional requirement FR, then the ith module should be capable of reuse to reduce the load of redesign. According to the part-worth utility model [1], the utility of the ith module to the jth FR is assumed to be the part-worth utility preference function for the parameter values of module m_i as follows:

$$u_{ij}=\sum _{k_i=1}^{K_I}\sum _{l_{k_i}=1}^{L_{K_I}}\left(w_{i{k}_i}{x}_{i{k}_i{l}_{k_i}}{u}_{j{k}_i{l}_{k_i}}\right)+{\epsilon }_{ij}$$

(2)

$$x_{i{k}_i{l}_{k_i}}=\left\{\begin{array}{cc}1,\hfill & \hfill \mathrm{if}{m}_i\mathrm{contributes}\mathrm{to}\mathrm{a}FR\\ 0,\hfill & \hfill \mathrm{otherwise}\end{array}\right.$$

(3)

where $w_{i{k}_i}$ is the utility weight of parameter ${mp}_{i{k}_i}$ of module m_i; $u_{j{k}_i{l}_{k_i}}$ is the part-worth utility of FR_j to the $l_{k_i}$ value of parameter ${mp}_{i{k}_i}$; ${\epsilon }_{ij}$ is the error trend of each FR module pair; and $x_{i{k}_i{l}_{k_i}}$ is a binary variable.

Definition 4. 

If module m_i is assembled from integral parts of type f₁ and parts of type f₂, then its engineering cost EC_i (i = 1, 2, …, I) can be expressed as

$${EC}_i=w_i\sum _{f_1=1}^{d_1}{n}_{f_1}^{in}{c}_{f_1}^{in}+w_i\sum _{f_2=1}^{d_2}{n}_{f_2}^{in}{c}_{f_2}^{in}+r_a{t}_a$$

(4)

where $c_{f_2}^{in}$ is the cost of module m_i with type f₂ input parts; $n_{f_2}^{in}$ is the quantity requirement; $r_a$ and $t_a$ are the cost rate and working time, respectively, of the module m_i assembly operation; $c_{f_1}^{in}$ is the cost of using integral parts of type f₁ by module m_i; and $n_{f_1}^{in}$ is the quantity requirement. Since the input part of module m_i is the output of the relevant manufacturing process, the cost $c_{f_1}^{in}$ of module m_i using integral parts of type f₁ can be calculated as follows:

$$c_{f_1}^{in}=c_{f_1}^{raw}+c_{f_1}^a=c_{f_1}^{raw}+r_{w}t$$

(5)

where $c_{f_{1w}}^{out}$ is the manufacturing cost of a part of type f₁ at manufacturing center w, $c_{f_1}^{raw}$ is the raw material cost, $c_{f_{1w}}^{in}$ is the input material cost, $r_w$ is the cost rate (¥/h) for setting up operation w (CNY/h), and t is the manufacturing time.

Definition 5. 

According to the information axiom [21] that a good engineering product concept should satisfy functional independence while containing the least possible information, the amount of information that satisfies FR_j with probability of success p_j (j = 1, 2, …, J) is as follows:

$${IC}_j=-{log}_2{p}_j$$

(6)

If FR is a fuzzy variable, then its success probability p_j (determined by the desired design range and system range given by the customer) can be expressed as follows:

$$p_j={\displaystyle \frac{\mathrm{Common}\mathrm{range}}{\mathrm{System}\mathrm{range}}}$$

(7)

where the common range is the overlap area between the design and system ranges on a uniform probability distribution curve, the design range is defined by the designer to satisfy the FR, and the system range is the range within which the system can be delivered to the customer. If the FR_j is a continuous random variable, then the probability of success in satisfying FR_j within the design range can be expressed as follows:

$$p_j={\int }_{d{r}^l}^{d{r}^u}p\left({FR}_j\right)d{FR}_j,$$

(8)

where $p({FR}_j)$ is the systematic probability density function of FR_j and $d{r}^l$ and $d{r}^u$ are the lower and upper bounds, respectively, of the design range.

Definition 6. 

The configuration delivery time of each module parameter is another important factor considered by the customer. After submitting an order, the customer wants to obtain the product as soon as possible. Let the time evaluation of the product module parameter be C_ij. Then, the product delivery time is

$$P_T=\sum _{i=1}^I\sum _{j=1}^J(y_i{C}_{ij})$$

(9)

3.3. Model Construction of the MCDA

(1) Model construction of MPP. A comprehensive product performance can be described by three objective values: module cost utility $P_{E/U}$ (ratio of engineering cost to acceptable utility; the smaller the better), module information content $P_{IC}$, and product delivery time $P_T$ (meet the timeliness of service customization; the smaller the better). Then, MPP can be described as a multi-objective model of integer planning as follows:

$$\mathit{Minimize}{P}_{E/U}=\sum _{i=1}^I\sum _{j=1}^J(y_i{\displaystyle \frac{{EC}_i}{U_{ij}}})$$

(10)

$$\mathit{Minimize}{P}_{IC}=-{\sum }_{i=1}^I{\sum }_{j=1}^J\left(y_i{log}_2{p}_j\right)$$

(11)

$$\mathit{Minimize}{P}_T=\sum _{i=1}^I\sum _{j=1}^J(y_i{C}_{ij})$$

(12)

$$s.t.y_i=\left\{\begin{array}{rr}1,& \mathrm{if}{V}_{i{k}_i}\mathrm{contributes}\mathrm{to}\mathrm{a}FR\\ 0,& \mathrm{otherwise}\end{array}\right.$$

(13)

Joining Equations (1)–(13), the multi-objective model for MPP is constructed as follows:

$$\mathit{Minimize}{P}_{E/U}=\sum _{i=1}^I\sum _{j=1}^J(y_i{\displaystyle \frac{w_i\sum _{f_1=1}^{d_1}{n}_{f_1}^{in}\left(c_{f_1}^{raw}+r_{w}t\right)+w_i\sum _{f_2=1}^{d_2}{n}_{f_2}^{in}{c}_{f_2}^{in}+r_a{t}_a}{\sum _{k_i=1}^{K_I}\sum _{l_{k_i}=1}^{L_{K_I}}\left[(x_{i{k}_i{l}_{k_i}}{w}_{i{k}_i}{u}_{j{k}_i{l}_{k_i}})+{\epsilon }_{ij}\right]}})$$

(14)

$$\mathit{Minimize}{P}_{IC}=-\sum _{i=1}^I\sum _{j=1}^J(y_i{log}_2\left({\int }_{d{r}^l}^{d{r}^u}p\left({FR}_j\right)d{FR}_j\right))$$

(15)

$$\mathit{Minimize}{P}_T=\sum _{i=1}^I\sum _{j=1}^J\left(y_i{C}_{ij}\right)$$

(16)

$$s.t.\left\{\begin{array}{c}{\displaystyle \sum _{l_{k_i}=1}^{L_{K_I}}}{x}_{i{k}_i{l}_{k_i}}=1\left(i=1,2,\dots ,I;j=1,2,\dots ,J;k=1,2,\dots ,K;k_i=1,2,\dots ,K_I;l_{k_i}=1,2,\dots ,L_{K_I}\right)\\ x_{i{k}_i{l}_{k_i}}=\left\{\begin{array}{rr}1,& \mathrm{if}{m}_i\mathrm{contributes}\mathrm{to}\mathrm{a}FR\\ 0,& \mathrm{otherwise}\end{array}\right.\\ y_i=\left\{\begin{array}{rr}1,& \mathrm{if}{V}_{i{k}_i}\mathrm{contributes}\mathrm{to}\mathrm{a}FR\\ 0,& \mathrm{otherwise}\end{array}\right.\end{array}\right.$$

(17)

where $x_{i{k}_i{l}_{k_i}}$ and $y_i$ are binary decision variables. The input is a known module instance parameter and the output is a set of module parameter combinations satisfying minimum cost utility, information content, and delivery time. The combinatorial optimization problem (Equations (14)–(17)) is an NP problem that can be solved with the help of a heuristic algorithm. The three-dimensional solution set distribution is obtained based on the NSGA-II and MOPSO algorithm [34].

(2) Model construction of SMC. To obtain SMC, the Pareto solution set of MPP under each objective function pair (a two-objective optimization function) is computed to obtain different module combination schemes Q_i (i = 1, 2, 3) as follows:

$$\left\{\begin{array}{c}{Q}_1\leftrightarrow {\mathsf{\cup }(P}_{E/U},P_{IC})\\ Q_2\leftrightarrow {\mathsf{\cup }(P}_{E/U},P_T)\\ Q_3\leftrightarrow \mathsf{\cup }(P_{IC},P_T)\end{array}\right.$$

(18)

The values of SMC are calculated according to the obtained MPP scheme. The manufacturer provides service modules, such as technical consulting, equipment maintenance, performance monitoring, fault diagnosis, part replacement, and recycling services (expressed by service statistics $M_n^s$), which are subject to different MPP schemes. According to the obtained $Q_i$ with target values of MPP, SMC can be customized based on $M_n^s$. The configuration relationship f between the combination scheme and the service module can be obtained through the weighted integration of the scheme service evaluation matrix. The more a configuration scheme is associated with a service module, the more it satisfies the personalization requirements of customers. Then, the scheme $Q_i^{*}$ of SMC within the MCDA can be constructed as follows:

$$\left\{\begin{array}{c}{Q}_i={\displaystyle \prod _{k=1}^t}{\left(M_n^s\right)}^{{\lambda }_k}\\ Q_i^{*}\leftrightarrow f(Q_i,M_n^s)\end{array}\right.$$

(19)

3.4. Problem-Solving Procedures of the Proposed MCDA

The problem-solving procedures of the proposed MCDA are shown in Figure 3, and the detailed steps are described as follows.

Figure 3. The problem-solving procedures of the proposed MCDA.

Step 1: Obtain CRs based on the order data of the enterprise and obtain weights of FRs based on FQFD.

Step 2: Construct a multi-objective model of MPP based on the information content, delivery time, and cost utility of module and product and obtain the Pareto solution set under each objective function pair.

Step 3: The NSGA-II is selected to obtain the Pareto solution sets of the MPP schemes. And then, SMC is presented based on the configuration relationship between the combination scheme MPP and the service modules with different customer usage scenarios.

Step 4: Compare and analyze the results of the case study based on the proposed MCDA framework.

4. Case Study

4.1. Background Illustration and FR Calculation

A mechanical company located in Xiamen specializes in the integration of design and development, manufacturing, and sales services, with a focus on CEPS such as cranes, excavators, and loaders. To meet the diverse requirements of its customers, the company aims to implement personalized customization designs for its product family of wheel loaders, which constitutes a significant aspect of product redesign. The wheel loader (as depicted in Figure 4) features a modular system structure composed of front, rear, and middle components, each containing several functional module layers. Only a selection of representative software functions and hardware functions, as well as service modules, are included as case studies. Table 1 provides descriptions of the selected modules and parameters associated with the wheel loader.

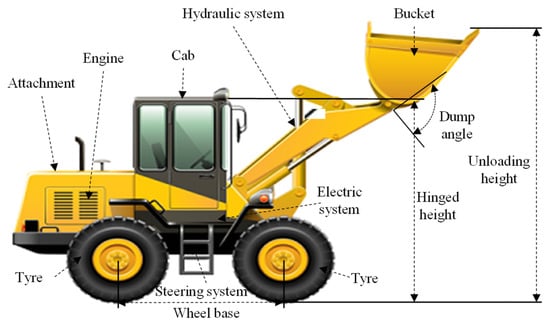
Figure 4. Modular system structure of a wheel loader.

Table 1. List of module instances and module parameters for a wheel loader.

Section	Functional Module M	Module Instance	Module Parameter	Note
MPP	m1 bucket	mp11 bucket capacity	v111: 2.2	m3
			v112: 3.8	m3
			v113: 4.5	m3
		mp12 hydraulic system	v121: quantitative	type
			v122: variable	type
			v123: mixed	type
		mp13 equipped with load	v131: 3	t
			v132: 3.2	t
			v133: 5	t
		mp14 unloading height	v141: 2800	mm
			v142: 2965	mm
			v143: 3167	mm
	m2 engine	mp21 brand	v211: Yuchai	for 3 t
			v212: Shangchai	for 5 t
		mp22 rated power	v221: 92	kW
			v222: 175	kW
	m3 turning radius	mp31 outer side of bucket	v311: 5860	mm
			v312: 6550	mm
			v313: 7470	mm
		mp32 outer side of wheel	v321: 5500	mm
			v322: 5560	mm
			v323: 6650	mm
	m4 vehicle configuration	mp41 intelligence level	v411: low	type
			v412: middle	type
			v413: high	type
		mp42 tire type	v421: Delta	68 days
			v422: Aeolus	75 days
			v423: Michelin	90 days
SMC	service module $M_n^s$	$M_1^s$ technical consulting		cost index
		$M_2^s$ equipment maintenance		cost index
		$M_3^s$ performance monitoring		cost index
		$M_4^s$ fault diagnosis		cost index
		$M_5^s$ part replacement		cost index
		$M_6^s$ recycling services		cost index

The descriptions of CRs and FRs are presented in Table 2, based on the customer order data and the enterprise’s product database. The CRs were subjected to statistical analysis utilizing the Kano model, resulting in integrated weights of CRs as follows: 0.14, 0.16, 0.15, 0.12, 0.13, 0.13, 0.08, and 0.09. These weights were subsequently mapped to the FRs using FQFD in conjunction with triangular fuzzy numbers to establish the range of design parameters. The weights of the FRs were computed using Equation (1), and the resulting data are summarized in Table 3.

Table 2. Description of CRs and FRs.

Initial CRs	Integrated CRs	FRs and Their Design Range
CR1, high-temperature environment	CR1, environmental requirements	FR1, working environment. The working environment of the loader is harsh, and customer purchase orders require high-temperature and alpine working environments. Its requirement range is [−50 °C, 50 °C].
CR2, alpine environment
CR3, high power for mountain rock transport	CR2, power size	FR2, power performance. The loader rated power size varies by working condition, and it is mainly equipped with different engines; the requirement range is [90 kW, 200 kW].
CR4, small power for bridge and road repair
CR5, low fuel consumption	CR3, cost requirement	FR3, economic performance. The economic performance of the loader includes the purchase cost, daily fuel consumption, and maintenance cost of the whole machine or accessories, and its functional requirement range is [50 W, 80 W] RMB.
CR6, long life cycle of parts
CR7, site size restrictions	CR4, range of activities	FR4 has a turning radius in the range [5860 mm, 7470 mm]. The rated load of the FR5 bucket consists of a hydraulic system and bucket together, in the range [3 t, 5 t]. FR6, bucket capacity, is in the range [2.2 m3, 4.5 m3].
CR8, overall vehicle weight	CR5, weight range
CR9, bucket size	CR6, shovel requirement
CR10, difficulty of operation	CR7, driving requirement	FR7, human–computer interaction, is medium and above, expressed as H or above by a triangular fuzzy number.
CR11, driving comfort
CR12, exhaust emissions	CR8, environmental requirement	FR8, environmental performance, meets the national minimum emission standards, expressed as greater than or equal to M by a triangular fuzzy number.
CR13, noise level

Table 3. Mapping the relationship and weights of FRs.

Weight of CRs		FR1	FR2	FR3	FR4	FR5	FR6	FR7	FR8
0.14	CR1	0	0.2548	0.1042	0.1937	0.0747	0.1936	0.0747	0.1042
0.16	CR2	0.1103	0	0.1104	0.1559	0.2051	0.2278	0.1066	0.0838
0.15	CR3	0.1448	0.1026	0	0.1449	0.1026	0.1026	0.1906	0.2118
0.12	CR4	0.1464	0.2140	0.1464	0	0.1464	0.1002	0.1002	0.1464
0.13	CR5	0.1094	0.2105	0.2105	0.1094	0	0.2105	0.0403	0.1094
0.13	CR6	0.1266	0.1851	0.2435	0.0866	0.2435	0	0.0466	0.0681
0.08	CR7	0.2244	0.1050	0.2953	0.1535	0.0565	0.0565	0	0.1087
0.09	CR8	0.1845	0.0679	0.1845	0.0679	0.1844	0.0679	0.2429	0
Weights of FRs		0.1222	0.1427	0.1491	0.1177	0.1290	0.1289	0.1013	0.1091

4.2. Calculation of Parameter Values

Utilizing the customer orders and the module utility weights from the company’s database, the cost utility for each module parameter corresponding to the FRs was computed using Equation (2). The results of this analysis are presented in Table 4.

Table 4. The cost utility of module parameters.

Module Parameter	FR1	FR2	FR3	FR4	FR5	FR6	FR7	FR8
v111: 2.2	0.078	0.143	0.056	0.013	0.093	0.039	0.090	0.029
v112: 3.8	0.109	0.111	0.093	0.039	0.066	0.066	0.047	0.053
v113: 4.5	0.047	0.079	0.131	0.066	0.040	0.118	0.025	0.078
v121: quantitative	0.047	0.111	0.168	0.066	0.093	0.118	0.047	0.078
v122: variable	0.078	0.079	0.131	0.039	0.066	0.092	0.069	0.053
v123: mixed	0.109	0.048	0.093	0.013	0.040	0.039	0.090	0.029
v131: 3	0.109	0.079	0.056	0.013	0.093	0.118	0.069	0.053
v132: 3.2	0.078	0.111	0.093	0.039	0.066	0.092	0.047	0.053
v133: 5	0.047	0.143	0.131	0.066	0.040	0.066	0.025	0.078
v141: 2800	0.078	0.048	0.019	0.066	0.093	0.118	0.069	0.078
v142: 2965	0.109	0.079	0.056	0.092	0.066	0.092	0.018	0.078
v143: 3167	0.141	0.111	0.093	0.118	0.040	0.066	0.069	0.053
v211: Yuchai	0.047	0.079	0.131	0.013	0.093	0.092	0.047	0.078
v212: Shangchai	0.078	0.111	0.093	0.039	0.066	0.118	0.069	0.053
v221: 92	0.078	0.111	0.056	0.039	0.066	0.118	0.069	0.103
v222: 175	0.109	0.143	0.093	0.092	0.093	0.092	0.090	0.053
v311: 5860	0.016	0.048	0.093	0.039	0.093	0.118	0.047	0.078
v312: 6550	0.047	0.079	0.131	0.066	0.066	0.092	0.069	0.053
v313: 7470	0.078	0.111	0.168	0.092	0.040	0.066	0.047	0.029
v321: 5500	0.047	0.079	0.056	0.013	0.093	0.118	0.047	0.078
v322: 5560	0.078	0.111	0.093	0.039	0.066	0.092	0.069	0.078
v323: 6650	0.109	0.143	0.131	0.066	0.040	0.066	0.047	0.053
v411: low	0.141	0.079	0.056	0.092	0.120	0.118	0.025	0.078
v412: middle	0.109	0.111	0.093	0.066	0.093	0.092	0.047	0.053
v413: high	0.078	0.143	0.131	0.039	0.040	0.039	0.069	0.029
v421: Delta	0.078	0.048	0.131	0.118	0.040	0.039	0.025	0.053
v422: Aeolus	0.109	0.079	0.093	0.092	0.093	0.066	0.047	0.078
v423: Michelin	0.141	0.111	0.056	0.066	0.120	0.092	0.069	0.103

Based on the data from the production department and the associated costs of manufacturing, assembly, and engineering within the company, the costs for the modules are calculated using Equation (4). The results of these calculations are presented in Table 5.

Table 5. Engineering cost of module parameters (CNY/min).

Value	ECi	f1	rw	ta	f2	ra	Process Time
v111	3200		120	10	800	60	Average, 0.5
v112	3600		120	10	1200	60	Fair, 0.7
v113	3800		120	10	1400	60	Good, 0.9
v121	4000	4000					Good, 0.9
v122	5000	5000					Fair, 0.7
v123	6000	6000					Average, 0.5
v131	3400		120	10	1000	60	Average, 0.5
v132	3400		120	10	1000	60	Fair, 0.7
v133	3700		120	10	1300	60	Good, 0.9
v141	3600		120	10	1200	60	Average, 0.5
v142	3600		120	10	1200	60	Fair, 0.7
v143	3800		120	10	1400	60	Good, 0.9
v211	27,200	23,000	150	20		60	Fair, 0.7
v212	29,200	25,000	150	20		60	Good, 0.9
v221	4200		150	20		60	Good, 0.9
v222	4200		150	20		60	Fair, 0.7
v311	3300		150	14		60	Good, 0.9
v312	3300		150	14		60	Fair, 0.7
v313	3600		150	16		60	Average, 0.5
v321	3000		150	12		60	Good, 0.9
v322	3000		150	12		60	Fair, 0.7
v323	3450		150	15		60	Average, 0.5
v411	32,000						Average, 0.5
v412	42,000						Fair, 0.7
v413	52,000						Good, 0.9
v421	4600	1800	120	10	400	60	Average, 0.5
v422	5000	2100	120	10	500	60	Fair, 0.7
v423	5600	2600	120	10	600	60	Good, 0.9

In accordance with the design range of FRs presented in Table 2, the company’s designers established the system range for module parameters based on customer orders. The results of this determination are illustrated in Table 6.

Table 6. The system range of module parameters.

Value	FR1	FR2	FR3	FR4	FR5	FR6	FR7	FR8
	[−50, 50]	[90, 200]	[50, 80]	[5860, 7470]	[3, 5]	[2.2, 4.5]	[H, VH]	[M, H]
v111	[−20, 50]	[74, 116]	[55, 60]	[5500, 5860]	[3, 3.5]	[1.8, 2.6]	VH	L
v112	[−30, 60]	[147, 196]	[65, 75]	[5860, 6650]	[3, 4]	[2.6, 4]	M	M
v113	[−10, 40]	[92, 126]	[60, 70]	[6550, 6650]	[2.6, 3.2]	[1.8, 2.2]	L	H
v121	[−40, 80]	[147, 200]	[75, 80]	[6650, 7470]	[4.5, 6]	[3.8, 4.5]	M	H
v122	[−40, 70]	[90, 147]	[60, 65]	[6550, 6650]	[3.5, 5.5]	[2.6, 3.8]	H	M
v123	[−20, 50]	[74, 110]	[50, 55]	[5500, 5860]	[2.2, 3.6]	[1.8, 2.2]	VH	L
v131	[−40, 80]	[165, 220]	[75, 85]	[5560, 5860]	[5, 6.5]	[4.5, 5.5]	H	M
…	…	…	…	…	…	…	…	…
v323	[−40, 70]	[92, 126]	[65, 75]	[5500, 6550]	[3.2, 4.5]	[3.8, 4.5]	M	M
v411	[−30, 50]	[74, 116]	[65, 70]	[5560, 6550]	[3, 3.6]	[2.6, 3.8]	L	H
v412	[−40, 60]	[74, 126]	[70, 80]	[6650, 7470]	[3, 3.2]	[4.5, 5.5]	M	M
v413	[−20, 50]	[74, 96]	[50, 60]	[6550, 6650]	[3.6, 5]	[1.8, 2.6]	H	L
v421	[−30, 60]	[74, 126]	[60, 70]	[5500, 7470]	[4.5, 5]	[2.6, 3.8]	L	M
v422	[−40, 70]	[92, 186]	[65, 75]	[5500, 5860]	[3, 3.6]	[2.2, 3.2]	M	H
v423	[−40, 60]	[74, 126]	[70, 80]	[6650, 7470]	[3, 3.2]	[4.5, 5.5]	H	VH

Since the FRs are random and fuzzy variables, the probability of information content P_ij for the module parameters under each FR can be calculated according to Equations (6)–(8), as shown in Table 7.

Table 7. Probability of information content for module parameters.

Value	FR1	FR2	FR3	FR4	FR5	FR6	FR7	FR8
v111	0.64	0.38	0.17	0.22	0.25	0.35	0.50	0.50
v112	0.82	0.45	0.33	0.49	0.50	0.61	0.50	0.50
v113	0.45	0.31	0.33	0.06	0.30	0.17	0.25	0.25
v121	1.00	0.48	0.17	0.51	0.75	0.30	0.25	0.40
v122	1.00	0.52	0.17	0.06	1.00	0.52	0.50	0.50
v123	0.64	0.33	0.17	0.22	0.70	0.17	0.25	0.40
v131	1.00	0.50	0.33	0.19	0.75	0.43	0.50	0.50
v132	1.00	0.55	0.17	1.00	0.25	0.35	0.50	0.35
v133	0.64	0.42	0.33	0.49	0.15	0.39	0.25	0.25
v141	0.82	0.25	0.17	0.19	0.50	0.35	0.35	0.40
v142	0.55	0.16	0.33	0.49	0.25	0.17	0.50	0.50
v143	0.73	0.66	0.17	0.19	0.25	0.30	0.40	0.50
v211	1.00	0.50	0.17	0.51	0.75	0.35	0.50	0.25
v212	0.45	0.31	0.17	0.06	0.50	0.35	0.25	0.25
v221	1.00	0.45	0.17	0.61	0.10	0.30	0.50	0.15
v222	0.73	0.47	0.17	0.49	0.65	0.52	0.50	0.50
v311	1.00	0.66	0.33	0.65	0.75	0.43	0.50	0.25
v312	0.91	0.47	0.17	1.00	0.75	0.17	0.25	0.15
v313	1.00	0.38	0.17	0.19	0.50	0.65	0.35	0.25
v321	0.91	0.38	0.17	0.65	0.30	0.22	0.40	0.40
v322	0.45	0.16	0.33	1.00	0.70	0.35	0.25	0.60
v323	1.00	0.31	0.33	0.65	0.65	0.30	0.35	0.50
v411	0.73	0.38	0.17	0.61	0.30	0.52	0.25	0.50
v412	0.91	0.47	0.33	0.51	0.10	0.43	0.35	0.25
v413	0.64	0.20	0.33	0.06	0.70	0.35	0.25	0.50
v421	0.82	0.47	0.33	1.00	0.25	0.52	0.50	0.50
v422	1.00	0.85	0.33	0.22	0.30	0.43	0.50	0.25
v423	0.91	0.47	0.33	0.51	0.10	0.43	0.35	0.25

4.3. Calculation of the MCDA Based on the NSGA-II

The NSGA-II with an elite strategy is selected for the coding process; the workflow is illustrated in Figure 5. The parameters of the NSGA-II were configured with a population size, solution set size, the maximum iterations set to 100, a crossover probability of 0.8, and a mutation probability of 0.3. We selected three of the most representative and coupled core parameters of the NSGA-II: maximum number of iterations, crossover rate, and mutation rate. Each parameter was set at three levels, forming an L9(34) orthogonal array. Using Taguchi orthogonal experimental design, the hypervolume (HV) indicator, which can simultaneously characterize population convergence, diversity, and distribution, was used as the response variable. The signal-to-noise ratio (S/N) and mean were used as evaluation indicators [46]. Through nine sets of orthogonal experiments, we analyzed the impact of parameters on algorithm performance. Finally, the optimal parameter combination for the NSGA-II was determined as (maximum number of iterations, crossover probability, mutation probability) = (100, 0.8, 0.3) (as shown in Figure 6). Based on the data presented in Table 6 and Table 7, as well as Equations (10)–(17), the solution set of MPP obtained through MATLAB 2022a is shown in Figure 7.

Figure 5. Workflow of the NSGA-II.

Figure 6. Parameter settings of the NSGA-II.

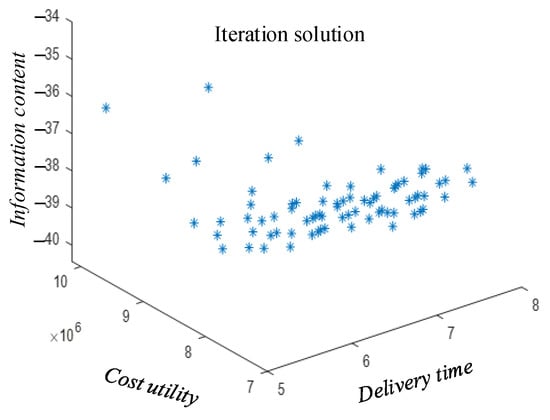
Figure 7. Iteration solution of MPP based on the NSGA-II.

As illustrated in Figure 7, a total of 75 feasible solutions corresponding to the module parameter value are identified across the three objective functions, necessitating further selection to satisfy the specified SMC. This abundance of alternatives underscores a core principle of multi-objective optimization: there exists no single best solution, but rather a set of compelling trade-offs, from which a final choice must be made according to higher-level priorities. To identify the Pareto solution set Q_i under different objective functions, a two-objective optimization function was constructed based on Equation (18); the results are shown in Figure 8.

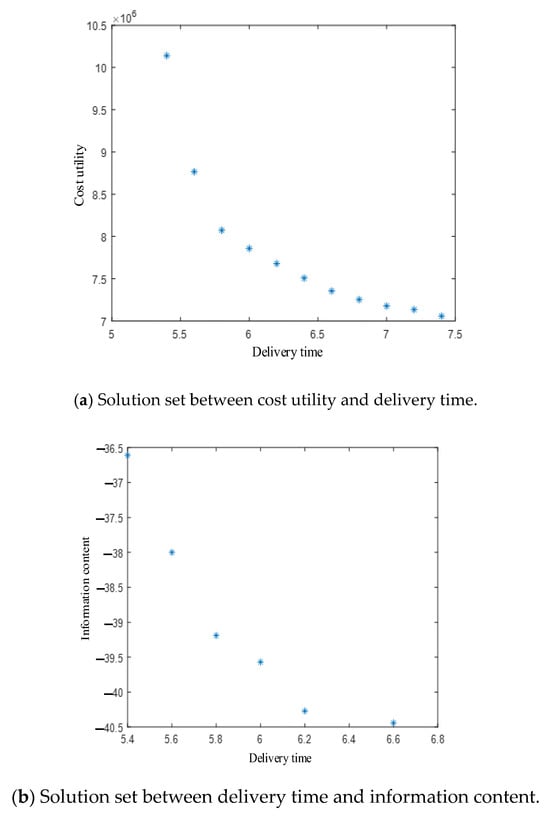
Figure 8. Pareto solution set under each objective function pair.

For clarity, only the three MPP schemes located at the extremes and the midpoint of the obtained target solution set are presented for SMC analysis. These specific schemes were selected to represent the spectrum of design priorities. One extreme prioritizes one objective, the other extreme prioritizes the competing objective, and the midpoint offers a balanced compromise between them. The corresponding results are detailed in Table 8.

Table 8. The extremes and the midpoint of the Pareto solution set.

Combinatorial Function	Function Value	MPP Scheme
(Delivery time, cost utility) Q1	(5.4, 10,140,964)	1, 2, 1, 1, 2, 2, 3, 3, 1, 1
	(6.4, 7,507,569)	2, 1, 2, 1, 2, 2, 2, 2, 1, 2
	(7.4, 7,058,061)	2, 2, 1, 1, 2, 2, 3, 3, 1, 2
(Delivery time, information content) Q2	(5.4, −36.61)	1, 3, 1, 1, 1, 2, 3, 3, 2, 1
	(6.0, −39.57)	2, 2, 1, 1, 1, 2, 2, 3, 2, 2
	(6.6, −40.44)	2, 2, 1, 3, 2, 2, 1, 3, 1, 3
(Cost utility, information content) Q3	(7,058,061, −36.85)	2, 1, 2, 3, 2, 2, 2, 2, 2, 2
	(8,509,198, −38.79)	2, 2, 1, 3, 1, 2, 1, 3, 1, 1
	(9,236,679, −40.44)	2, 1, 2, 3, 2, 2, 2, 3, 3, 3

In combination with Definition 2, individualized modules were configured from the service statistics matrix $M_n^s$ based on the obtained MPP schemes $Q_i$ in Table 8. Q₁ was evaluated under the criteria of delivery time and cost utility, wherein five decision-makers were invited to perform a five-point scaling (0.1, 0.3, 0.5, 0.7, 0.9) of service statistics for SMC across six service criteria. $M_n^s$ represents technical consulting, equipment maintenance, performance monitoring, fault diagnosis, parts replacement, and recycling services. The scheme service evaluation matrix of Q₁ is presented in Table 9.

Table 9. Scheme service evaluation matrix of Q₁.

Decision-Maker	Scheme of SMC	${\mathbf{M}}_1^{\mathbf{s}}$	${\mathbf{M}}_2^{\mathbf{s}}$	${\mathbf{M}}_3^{\mathbf{s}}$	${\mathbf{M}}_4^{\mathbf{s}}$	${\mathbf{M}}_5^{\mathbf{s}}$	${\mathbf{M}}_6^{\mathbf{s}}$
e1	q11	0.7	0.1	0.9	0.5	0.1	0.9
	q12	0.5	0.3	0.5	0.5	0.3	0.7
	q13	0.3	0.5	0.5	0.3	0.5	0.5
e2	q11	0.7	0.5	0.7	0.7	0.3	0.7
	q12	0.5	0.7	0.5	0.7	0.3	0.7
	q13	0.9	0.3	0.7	0.7	0.3	0.5
e3	q11	0.5	0.7	0.5	0.7	0.1	0.7
	q12	0.5	0.9	0.3	0.5	0.5	0.5
	q13	0.5	0.5	0.7	0.3	0.5	0.3
e4	q11	0.7	0.5	0.5	0.5	0.3	0.7
	q12	0.3	0.7	0.5	0.3	0.5	0.7
	q13	0.7	0.3	0.7	0.3	0.3	0.5
e5	q11	0.3	0.5	0.7	0.3	0.5	0.7
	q12	0.5	0.5	0.7	0.1	0.7	0.5
	q13	0.1	0.1	0.9	0.1	0.9	0.5

Here, each decision-maker was assigned a weight of 0.2. The decision matrix $Q_i^{*}$ for SMC was derived by integrating the geometric weighting operators corresponding to the weights as outlined in Equation (19). The decision matrix $Q_1^{*}$ for SMC is presented in Table 10.

Table 10. Decision matrix $Q_1^{*}.$

	Scheme of SMC	${\mathbf{M}}_1^{\mathbf{s}}$	${\mathbf{M}}_2^{\mathbf{s}}$	${\mathbf{M}}_3^{\mathbf{s}}$	${\mathbf{M}}_4^{\mathbf{s}}$	${\mathbf{M}}_5^{\mathbf{s}}$	${\mathbf{M}}_6^{\mathbf{s}}$
$Q_1^{*}$	q11	0.643	0.267	0.688	0.516	0.214	0.736
	q12	0.516	0.483	0.572	0.350	0.436	0.612
	q13	0.368	0.643	0.483	0.285	0.458	0.451

From Table 10, the first scheme of SMC q₁₁ under the objective function of delivery time and cost utility focuses on the service modules, which are ranked as recycling services > performance monitoring > technical consultation > fault diagnosis > equipment maintenance > part replacement. Since q₁₁ has the largest cost utility (delivery time has the smallest), the hope is not to add additional costs for part replacement and equipment maintenance. For recycling services and performance monitoring, there is a focus on the cost to receive benefit returns. The software and hardware configuration modules of q₁₁ are as follows: 2.2 m³ bucket capacity, variable hydraulic configuration, 3 t load, 2800 mm unloading height, Shangchai brand engine, 175 kW rated power, 7470 mm outer bucket radius, 6650 mm inner wheel radius, low smart system, and Delta tires. Hence, q₁₁ has low intelligence and does not have a good human–machine interaction function. It, therefore, needs performance monitoring and technical consulting. Accordingly, the comparison of decision values between $Q_1^{*}$ (q₁₁, q₁₂, and q₁₃) is shown in Figure 9.

Figure 9. Comparison of decision values between $Q_1^{*}$.

Similarly, the decision matrix $Q_2^{*}$ under the delivery time and information content function is shown in Table 11, and the decision matrix $Q_3^{*}$ under information content and cost utility function is shown in Table 12. And, the comparison of decision values between $Q_2^{*}$ is shown in Figure 10, and the comparison between $Q_3^{*}$ is shown in Figure 11.

Table 11. Decision matrix $Q_2^{*}$.

	Scheme of SMC	${\mathbf{M}}_1^{\mathbf{s}}$	${\mathbf{M}}_2^{\mathbf{s}}$	${\mathbf{M}}_3^{\mathbf{s}}$	${\mathbf{M}}_4^{\mathbf{s}}$	${\mathbf{M}}_5^{\mathbf{s}}$	${\mathbf{M}}_6^{\mathbf{s}}$
$Q_2^{*}$	q21	0.643	0.394	0.483	0.516	0.374	0.214
	q22	0.436	0.408	0.394	0.394	0.368	0.316
	q23	0.394	0.451	0.316	0.267	0.483	0.350

Table 12. Decision matrix $Q_3^{*}.$

	Scheme of SMC	${\mathbf{M}}_1^{\mathbf{s}}$	${\mathbf{M}}_2^{\mathbf{s}}$	${\mathbf{M}}_3^{\mathbf{s}}$	${\mathbf{M}}_4^{\mathbf{s}}$	${\mathbf{M}}_5^{\mathbf{s}}$	${\mathbf{M}}_6^{\mathbf{s}}$
$Q_3^{*}$	q31	0.500	0.466	0.535	0.552	0.612	0.408
	q32	0.612	0.451	0.516	0.483	0.408	0.368
	q33	0.368	0.572	0.394	0.500	0.332	0.516

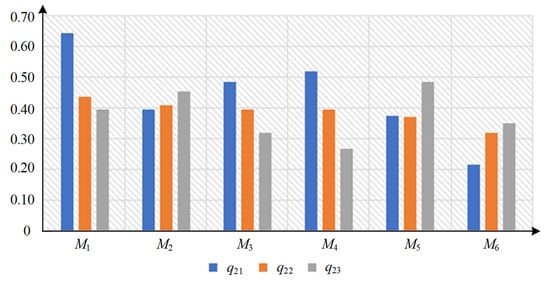
Figure 10. Comparison of decision values between $Q_2^{*}.$

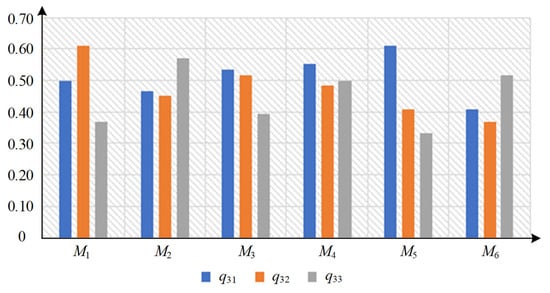
Figure 11. Comparison of decision values between $Q_3^{*}.$

4.4. Method Comparison and Result Analysis

The MOPSO algorithm [34] (as illustrated in Figure 12) was employed to encode the proposed MPP model. To validate the stability of the results obtained from the MCDA, the parameters for the MOPSO algorithm were configured as follows [46]: population and solution set sizes were set to 100, the maximum number of iterations was limited to 50, individual and global learning coefficients were both set to 1, and the maximum transfer speed weight was established at 0.8. And, the solution set of MPP based on the MOPSO algorithm is shown in Figure 13.

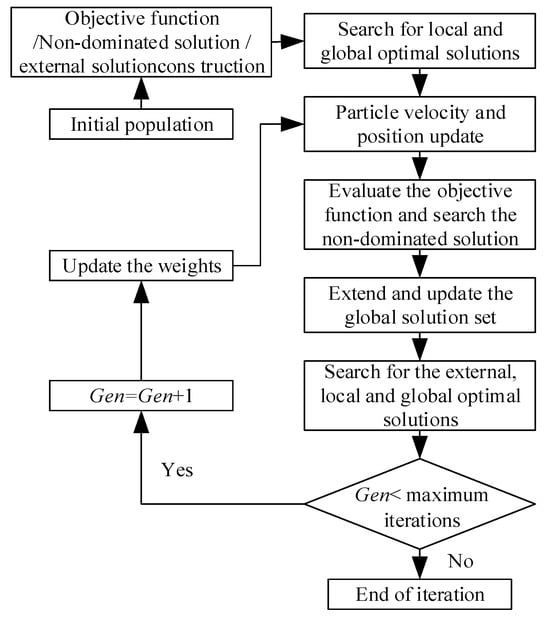
Figure 12. Flowchart of the MOPSO algorithm.

Figure 13. Solution set of MPP based on the MOPSO algorithm.

There were 24 feasible solutions corresponding to the parameter value of the module across the three objective functions; further selection was necessary to identify a configuration scheme that aligns with CRs. This necessity stems from the inherent trade-offs in multi-objective optimization, where no single solution can simultaneously optimize all conflicting goals, thus requiring a decision-making process to select the most preferable compromise. Two-objective optimization functions were developed based on Figure 13 to identify the Pareto optimal solution set Q_i under each objective function pair. For the purpose of clarity, only the extremes and the midpoint of each objective solution set are presented, with the results summarized in Table 13. These representative schemes effectively capture the spectrum of design philosophies. One extreme prioritizes one objective (e.g., minimal delivery time), the other extreme prioritizes the competing objective (e.g., minimal cost utility), and the midpoint offers a balanced compromise between the two. The decision values indicate that the objective function values and combination schemes obtained from the two algorithms are largely consistent (with the exception of q₁₁), suggesting that the constructed model and schemes of the proposed MCDA are both stable and effective. This convergence in results, despite the different search mechanisms of the NSGA-II and MOPSO, indicates that the identified Pareto front is a robust property of the underlying problem formulation rather than an artifact of a specific algorithm. The minor discrepancy in q₁₁ highlights the presence of near-optimal solutions in the search space, which different algorithms may approximate slightly differently, without undermining the overall validity of the model.

Table 13. Solution set based on the MOPSO algorithm.

Combinatorial Function	Function Value	MPP Scheme
(Delivery time, cost utility) Q1	(5.6, 8,766,561)	1, 1, 1, 1, 1, 2, 2, 2, 1, 1
	(6.4, 7,507,569)	2, 1, 2, 1, 2, 2, 2, 2, 1, 2
	(7.4, 7,058,061)	2, 2, 1, 1, 2, 2, 3, 3, 1, 2
(Delivery time, information content) Q2	(5.4, −36.61)	1, 3, 1, 1, 1, 2, 3, 3, 2, 1
	(5.8, −39.19)	2, 2, 1, 1, 1, 2, 2, 3, 2, 2
	(6.2, −40.27)	2, 2, 1, 3, 2, 2, 1, 3, 1, 3
(Cost utility, information content) Q3	(7,058,061, −36.85)	2, 1, 2, 3, 2, 2, 2, 2, 2, 2
	(8,509,198, −38.79)	2, 2, 1, 3, 1, 2, 1, 3, 1, 1
	(9,236,679, −40.44)	2, 1, 2, 3, 2, 2, 2, 3, 3, 3

The robustness of the MCDA corresponding to the combination scheme was analyzed. Since the evaluation values of the service modules focused on the combination scheme are mainly provided by decision-makers, whose weights in the process of decision matrix integration directly affect the final configuration results, the changes of the service modules can be observed by the changes of the decision-maker weights. To reduce the number of weight perturbations, the weight change range of each decision-maker was [0.1, 0.3]. The scheme of SMC perturbation results $Q_1^{*}$, $Q_2^{*}$, and $Q_3^{*}$ after six uniform perturbations are shown in Table 14. The comparison results between $Q_1^{*}$, $Q_2^{*}$, and $Q_3^{*}$ after perturbation is shown in Figure 14. The observed stability in the SMC rankings under weight perturbations underscores the robustness of the proposed decision-making mechanism within the MCDA framework.

Table 14. Weight perturbation and the decision matrix of $Q_1^{*}$, $Q_2^{*}$, and $Q_3^{*}.$

Times of Weight Perturbation (Weights of Decision-Maker)	Scheme of SMC	${\mathbf{M}}_1^{\mathbf{s}}$	${\mathbf{M}}_2^{\mathbf{s}}$	${\mathbf{M}}_3^{\mathbf{s}}$	${\mathbf{M}}_4^{\mathbf{s}}$	${\mathbf{M}}_5^{\mathbf{s}}$	${\mathbf{M}}_6^{\mathbf{s}}$
1 (0.1 0.2 0.3 0.1 0.3)	q11	0.682	0.283	0.694	0.508	0.225	0.718
	q12	0.475	0.526	0.592	0.314	0.475	0.572
	q13	0.387	0.660	0.475	0.256	0.512	0.429
2 (0.1 0.1 0.3 0.3 0.2)	q11	0.660	0.313	0.649	0.516	0.214	0.718
	q12	0.516	0.526	0.553	0.322	0.483	0.592
	q13	0.368	0.682	0.459	0.262	0.458	0.429
3 (0.2 0.2 0.2 0.2 0.2)	q11	0.643	0.267	0.688	0.516	0.214	0.736
	q12	0.516	0.483	0.572	0.350	0.436	0.612
	q13	0.368	0.643	0.483	0.285	0.458	0.451
4 (0.2 0.1 0.1 0.3 0.3)	q11	0.627	0.281	0.665	0.459	0.252	0.736
	q12	0.491	0.467	0.572	0.274	0.475	0.612
	q13	0.332	0.607	0.526	0.235	0.486	0.475
5 (0.3 0.3 0.1 0.2 0.1)	q11	0.607	0.239	0.706	0.544	0.203	0.755
	q12	0.562	0.444	0.572	0.425	0.381	0.654
	q13	0.368	0.627	0.491	0.347	0.411	0.475
6 (0.3 0.3 0.2 0.1 0.1)	q11	0.643	0.227	0.730	0.562	0.182	0.755
	q12	0.544	0.459	0.572	0.447	0.381	0.633
	q13	0.387	0.643	0.467	0.347	0.432	0.451

Figure 14. Comparison results between $Q_1^{*}$, $Q_2^{*}$, and $Q_3^{*}.$

The results of the ranking for $Q_1^{*}$, $Q_2^{*}$, and $Q_3^{*}$ indicate that the values of the SMC under the objective function Q_i vary with the weights assigned by decision-makers. This variation is expected, as different weight assignments naturally alter the aggregated evaluation scores. However, the ranking order exhibits a tendency towards stability. This stability suggests a strong inherent correlation between the optimal module configuration derived from MPP and its most suitable service modules, which is not easily overturned by minor changes in subjective judgment. This observation underscores the robustness of the results obtained from the proposed MCDA framework.

5. Conclusions

This study proposes an MCDA framework, which investigates CR information and product operational data to address the module configuration problem for CEPS. The research has successfully addressed the three questions posed at the outset (1) by developing a heterogeneous data-driven framework that integrates MPP and SMC; (2) by formulating and solving a multi-objective MPP model; and (3) by establishing a linkage mechanism for personalized service customization. In the proposed MCDA, an MPP model was constructed considering cost utility, information content, and delivery time, followed by the SMC model to meet the customization design for a wheel loader. The principal contributions of this research are summarized as follows.

(1) The FQFD was employed to map CRs to FRs and to establish the design range of modules based on CR data. The weights of the FRs were determined using triangular fuzzy numbers. A multi-objective model of MPP was developed, incorporating the cost utility, information content, and delivery time based on product operational data.

(2) The NSGA-II and MOPSO algorithms were utilized to derive the Pareto solution sets for the MPP schemes, and then the SMC scheme was formulated for the customization design. The application and analysis of CEPS demonstrated the effectiveness of the proposed MCDA framework.

A case study on the configuration design of a wheel loader illustrated the efficacy of the proposed MCDA framework, which has been successfully implemented in a corporate project. Nevertheless, the CR information, cost utility, information content, and delivery time of the module and product often exhibit imprecision when establishing the MPP problem, and the identification of SMC still lacks robust supporting tools and theoretical foundations. This study has certain limitations that point to future research directions. It is acknowledged that the framework’s validation is primarily based on a case study of a wheel loader, and the comparative analysis of multi-objective algorithms could be expanded beyond the NSGA-II and MOPSO to further generalize the findings. Future work will focus on analyzing and mining heterogeneous data related to CR information and product operations data to identify potential FRs based on usage scenarios, facilitating the redesign and optimization of key functional components of CEPS.