Abstract
Solar energy can mitigate the power supply shortage in remote regions for portable irrigation systems. The accurate prediction of solar irradiance is crucial for determining the power capacity of photovoltaic power generation (PVPG) systems for mobile sprinkler machines. In this study, a prediction method is proposed to estimate the solar irradiance of typical irrigation areas. The relation between meteorological parameters and solar irradiance is studied, and four different parameter combinations are formed and considered as inputs to the prediction model. Based on meteorological data provided by ten typical radiation stations uniformly distributed nationwide, an Extreme Gradient Boosting (XGBoost) model optimized using the Whale Optimization Algorithm (WOA) is developed to predict solar radiation. The prediction accuracy and stability of the proposed method are then evaluated for different input parameters through training and testing. The differences between the prediction performances of models trained based on single-station data and mixed data from multiple stations are also compared. The obtained results show that the proposed model achieves the highest prediction accuracy when the maximum temperature, minimum temperature, sunshine hours ratio, relative humidity, wind speed, and extraterrestrial radiation are used as input parameters. In the model testing, the RMSE and MAE of WOA-XGBoost are 2.142 MJ·m−2·d−1 and 1.531 MJ·m−2·d−1, respectively, while those of XGBoost are 2.298 MJ·m−2·d−1 and 1.598 MJ·m−2·d−1. The prediction effectiveness is also verified based on measured data. The WOA-XGBoost model has higher prediction accuracy than the XGBoost model. The model developed in this study can be applied to forecast solar irradiance in different regions. By inputting the meteorological parameter data specific to a given area, this model can effectively produce accurate solar irradiance predictions for that region. This study provides a foundation for the optimization of the configuration of PVPG systems for mobile sprinkler machines.
1. Introduction
A mobile sprinkler machine is a motor-driven irrigation device whose operation relies on grid power. However, in remote areas suffering from electricity shortage or during peak demand periods, ensuring a stable power supply is often challenging, which results in delaying the timely irrigation of crops [1,2]. At present, photovoltaic (PV) power is mainly adopted to maintain the power supply for mobile sprinkler machines in regions exhibiting electricity shortage [3,4]. Due to the randomness and instability of solar power generation, it is crucial to properly configure the components of the PV power generation (PVPG) system. A decent configuration allows for increasing the adaptability of the machine, reducing the setup costs, and improving the efficiency. Solar irradiance is the key factor affecting the configuration of PV systems [5]. Figure 1 shows a schematic diagram of a PV power supply system for a mobile sprinkler irrigation machine. However, acquiring these data is challenging in remote regions due to the lack of weather stations. Therefore, the accurate prediction of solar irradiance is crucial to optimize the configuration of the PVPG system for mobile sprinkler machines.
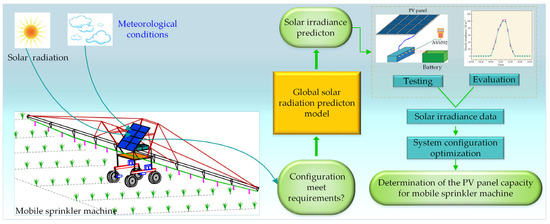
Figure 1.
A schematic diagram of a PV power supply system for a mobile sprinkler irrigation machine.
Daily global solar radiation observations are highly restricted due to the high cost of the monitoring equipment. In particular, in developing countries, obtaining daily global solar radiation data is not as straightforward as acquiring conventional meteorological data such as the sunshine hours and temperature [6,7,8]. In China, out of 752 national meteorological stations, only 122 are equipped to measure solar radiation, which leads to a sparse and uneven distribution of these monitoring stations [9]. Even the available solar irradiance data often suffer from incomplete time series and frequent gaps [10]. Therefore, the development of a daily global solar radiation prediction model is crucial to acquire precise solar irradiance data.
The estimation of daily global solar radiation using empirical formulas is the most widely used approach, providing high simulation accuracy [11,12]. Although it is limited by insufficient sunshine data, the Angstrom–Prescott method based on sunshine hours is widely applied. Jemaa et al. [13] addressed this limitation by adopting three simple sunshine-based models to estimate daily global solar radiation and monthly average radiation. Their results showed that the linear model outperforms quadratic and cubic models. Khorasanizadeh et al. [14] compared several sunshine-based empirical formula models for solar radiation. Their results demonstrated that the third-degree model is the optimal one. Mahima et al. [15] proposed a model for daily global solar radiation prediction based on meteorological parameters (e.g., temperature, relative humidity, and wind speed). In complex weather conditions, empirical formulas cannot deal with the complex nonlinear relationship between independent and dependent variables. Consequently, intelligent algorithms, such as Artificial Neural Networks (ANNs), Support Vector Machines (SVMs), and Adaptive Neuro-Fuzzy Inference Systems (ANFISs), have been widely used to estimate solar radiation [16]. For instance, Chen et al. [17] compared the performances of SVM models and sunshine-based empirical models in predicting solar radiation. Their results showed that the former have higher estimation accuracy than the latter. Ramli et al. [18] studied the accuracy of SVM and ANN models in predicting solar radiation. Their results showed that the former have higher prediction accuracy and computational speed compared with the latter.
Most of the models based on the aforementioned intelligent algorithms are complex, and thus they require significant computational resources during the training phase. In recent years, ensemble methods based on decision trees have been widely studied. These algorithms are straightforward and have high robustness [19]. For instance, Hassan et al. [20] studied the application of decision tree-based ensemble methods for simulating solar radiation, reaching high reliability and accuracy. Fan et al. [21] compared the accuracies of an SVM, Extreme Gradient Boosting (XGBoost), and four empirical formula models in estimating solar radiation in subtropical regions of China. Their results showed that the SVM and XGBoost outperform the empirical models. Benali et al. [22] compared the efficiencies of ANN and RF models in estimating solar radiation. Their results showed that the latter are more effective than the former. XGBoost merges gradient boosting with decision trees, and employs second-order derivative expansion to improve the accuracy in optimizing target error functions. Its key advantage is the use of parallel computing on multi-core CPUs, greatly boosting computational speed. The WOA overcomes the limitations of other population-based optimization algorithms that often become stuck in local optima, resulting in global optimization through a thorough search process. This study integrates these two methods to achieve solar irradiance prediction.
However, in the application of solar irradiance forecasting for PV systems, most of the existing studies rely on the development of prediction models based on meteorological data from a single station. Moreover, these studies rarely focus on the accuracy of solar irradiance forecasting under different combinations of meteorological input parameters. Few general models trained by mixed data from multiple representative stations exist, and those validated based on actual measurements are even fewer [23,24]. In this study, when optimizing the configuration of a mobile irrigation system powered by a PV system based on predicted solar irradiance, the model should exhibit high universality.
The objectives of this study are to (i) select the optimal combination of input parameters for the prediction model to ensure high accuracy and strong stability in solar irradiance forecasting, (ii) develop a predictive method for forecasting solar irradiance in typical irrigation areas, and (iii) compare the prediction effects based on mixed data from multiple stations versus single-station data. The research results can provide technical support for optimizing decision-making regarding the configuration of PVPG systems for mobile sprinkler machines.
2. Materials and Methods
2.1. PV Power Generation System for Sprinkler Machine
The structure of the mobile sprinkler machine is shown in Figure 2. Its locomotion system mainly comprises four identical drive wheels, a set of PV panels (CS5M32-260, with a peak power of 260 W, peak voltage of 49.71 V, and peak current of 5.25 A, supplied by Golden Electronics Co., Limited, Taizhou, China), a set of batteries (6-QA-200, rated capacity of 200 Ah, rated voltage of 12 V, supplied by Wind Sail Co., Ltd., Baoding, China), four DC stepper motors (3404HS60-F, Hamderburg Motors Co., Ltd., Shenzhen, China), four reducers, and a controller. The stepper motors are a crucial component of the drive system.

Figure 2.
Structure and composition of mobile sprinkler machine, where 1–5 represent PV panel, battery, controller, stepper motor, and reducer, respectively.
Table 1 presents the main technical parameters of the mobile sprinkler machine. The solar PV components of the unit convert the solar energy into electricity. During operation, electricity is partially converted into mechanical energy by the stepper motor to drive the wheels and partially transformed into pressure utilized by the water pump to lift water. Any remaining electricity is subsequently directed into the battery for storage. All the stepper motors are equipped with drive controllers to regulate the motor speed and allow the irrigation system to move.

Table 1.
Main performance parameters of sprinkler.
To appropriately use the mobile sprinkler machine, it should be ensured that the power demand for locomotion matches the power generated by the PV system. The daily global solar radiation is the sum of the direct and diffuse solar radiation received on a horizontal surface at a specific observation point on the Earth’s surface in a day. The required configuration of PV components for the mobile sprinkler machine varies depending on its application area. This is mainly due to the different levels of daily global solar radiation in different regions, which leads to varying irradiance levels on an hourly basis. This results in differences in PVPG, that is, the capacity of the PV system to generate electricity. In remote irrigation areas where monitoring daily global solar radiation is challenging, forecasting methods should be adopted to obtain daily global solar radiation.
2.2. Development of Solar Radiation Prediction Model
2.2.1. Meteorological Data for Prediction Model Construction
In this study, data from ten national evenly distributed typical radiation stations between the years 1960 to 2020 were considered to estimate, validate, and construct a solar radiation dataset. The meteorological data were obtained from the National Meteorological Information Center (NMIC) of the China Meteorological Administration (CMA). The station codes, geographical location information, and climatic characteristics of these stations are shown in Table 2, and their geographical distribution is illustrated in Figure 3.

Table 2.
Spatiotemporal distribution of ten weather stations.
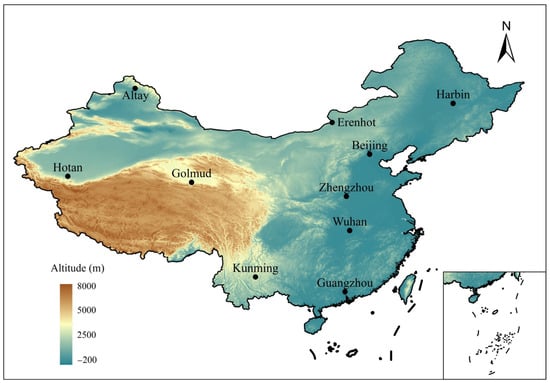
Figure 3.
The geographical locations of the ten weather stations.
Based on the quality control protocol proposed by Liu et al. [25], the meteorological data were processed as follows: if one or more data points are missing from the daily meteorological data, the data of the entire day are excluded; if the daily global solar radiation exceeds the extraterrestrial total radiation on a given day, all the data of this day are removed.
2.2.2. Selection of Input Parameters for Prediction Model
The spatial and temporal distributions of daily global solar radiation are affected by various factors. The latter include astronomical factors, such as the solar altitude, Earth–Sun distance, and geographical latitude, which are considered direct influencing factors, as well as meteorological factors, which are considered indirect influencing factors. Under the combined influence of these factors, the global radiation exhibits significant spatial and temporal variations. The accurate calculation of the amount of global radiation is essential for the analysis and effective utilization of the solar radiation. Among the numerous factors, temperature can significantly influence radiation transfer processes, while water vapor exhibits an absorptive effect on certain wavelengths of light. Higher wind speeds may induce a cooling effect that impacts the radiation of surfaces. The sunshine hour ratio directly affects the land surface’s energy absorption efficiency, and extraterrestrial radiation serves as a fundamental parameter in solar radiation prediction. Numerous previous studies have demonstrated effective predictive outcomes utilizing these parameters. For instance, in daily solar radiation predictions, meteorological observation data included sunshine duration, minimum temperature, maximum temperature, average relative humidity, average air temperature, wind speed, and actual values of solar radiation [26]. The astronomical factor of extraterrestrial radiation, along with climatic variables such as sunshine duration, maximum temperature, minimum temperature, and cloud cover were employed as input attributes in estimating daily global solar radiation [27].
Therefore, based on a previous study, this paper uses partial or complete sets of six factors (maximum temperature (Tmax), minimum temperature (Tmin), relative humidity (RH), wind speed (u2), sunshine hour ratio (n/N) (i.e., ratio of the sunshine duration to the maximum possible sunshine hours), and extraterrestrial radiation (Ra)) as input parameters to analyze the predictive effects of the daily global solar radiation for different combinations of input parameters. The Ra is mainly affected by astronomical factors, such as the solar altitude angle, Earth–Sun distance, and geographical latitude. It is calculated as follows [28,29]:
where dr is the Earth–Sun distance factor; Isc is the solar constant (1367 W·m−2); J is the day of the year; and φ, δ, and ωs are, respectively, the latitude, declination angle, and sunset hour angle (rad).
Note that the unit of Ra is MJ·m−2·d−1.
The sunshine hour ratio is that of the actual sunshine duration to the maximum possible sunshine hours. The maximum possible sunshine duration is computed as follows [28]:
Four different sets of input parameters to the model were established to accurately estimate the daily global solar radiation, in order to evaluate the effect of various meteorological factors on solar radiation. As presented in Table 3, these combinations are denoted by A1, A2, A3, and A4, respectively.

Table 3.
Combinations of input meteorological factors.
2.2.3. Development of Prediction Models
The daily global solar radiation has complex nonlinear relationships with meteorological factors, such as temperature, humidity, and wind speed. Machine learning models are well suited for addressing the complex nonlinear relationships between dependent and independent variables. This study adopts the XGBoost machine leaning model to accurately estimate the total surface solar radiation. It also uses the Whale Optimization Algorithm (WOA) to optimize the parameters of the XGBoost model.
- (1)
- The WOA
The WOA simulates whales hunting for prey. It uses random search agents to mimic the hunting behavior and perform global search. This process involves surrounding, attacking, and searching for the optimal prey [30].
- (i)
- Surrounding prey
In the WOA, the assumed best candidate position for prey is either the hunting target or a location near the optimal search agent. The other individuals will constantly adjust their positions relative to the optimal agent in real-time, which can be mathematically expressed as follows:
where t is the current iteration number, X(t) is the position vector of the current search agent, X* (t) is the position vector of the current best search agent, and A and C are coefficient matrices given by the following:
where r1 and r2 are random vectors of components in the range 0~1.
Note that m linearly decreases at [0, 2].
- (ii)
- Attacking prey
The bubble-net feeding behavior of humpback whales consists of two mechanisms: contraction and spiral position updating. These two behaviors simultaneously occur, while the whale randomly chooses to either contract in a loop or move along a spiral path, with equal probability for its choices. The position of the whale is updated accordingly in real-time:
where is the distance between the positions of the current search agent and the best one, b is a constant determining the shape of the spiral path, l is a random number in the range −1~1, and P is the probability.
- (iii)
- Searching for the optimal prey
In contrast to the development phase, during each iteration, the remaining search agents update their positions in real-time based on the randomly selected search agent, rather than the current best search agent. The iteration process is expressed as follows:
where Xrand (t) represents the position vector of the randomly chosen search agent.
The WOA avoids the pitfalls of other population-based optimization algorithms that often become trapped in local optima by balancing and enhancing the development and search abilities, which results in global optimization through a searching process.
- (2)
- The XGBoost model
XGBoost is an advanced machine learning model built on gradient boosting and decision trees. Its key strength lies in leveraging parallel computing on multi-core CPUs, which allows for increasing the computational speed compared with the traditional models. Moreover, it employs second-order derivative expansion, which increases the accuracy when optimizing target error functions. When predicting the PV power using XGBoost, the model is essentially a collection of K decision trees. Each decision tree, denoted by fk, operates on the input vector set D = {(xi, yi)}. By combining these K decision trees, the model generates predictions for the PV power of individual samples [31]:
where j = φ (xi) is the leaf node in the k-th tree and ε is the score vector of the leaves.
The errors of all the samples are aggregated to calculate the sum (S) as follows:
where is the loss function, γ and λ are hyperparameters, Z is the amount of leaf nodes, and Ω(f) is a regular term.
Based on Equation (13), the loss function obtained after the superposition of the k-th decision tree is expressed as follows:
where Q is a constant.
Equation (15) is then expanded using a Taylor series:
- (3)
- Implementation of WOA-XGBoost
This study uses three key hyperparameters (max_depth, learning_rate, and L2 reg_lambda) in the WOA optimization forecasting model. The process can be divided into the following steps: (1) normalizing and splitting the experimental data into training and testing sets; (2) initializing the WOA by setting search parameters; (3) defining the parameter ranges for XGBoost and creating an initial whale population; (4) computing the fitness for each whale position; (5) ranking the fitness, selecting the best agent, and updating the corresponding positions; (6) iteratively updating the positions using Equations (6)–(11); (7) repeating steps (2)–(6) using the mean squared error as the fitness function until the termination criteria are met; (8) applying the optimized parameters to the XGBoost model. Note that after optimization, the maximum decision tree depth, learning rate, and L2 regularization coefficient were 7, 0.033, and 0.05, respectively.
Figure 4 shows the calculation process of the daily global solar radiation estimation model. Based on the collected data, such as solar radiation, temperature, and sunshine duration, 70% of the data are used as training samples and the remaining 30% are used as testing samples.
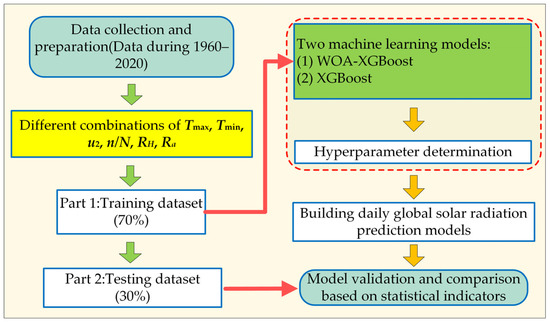
Figure 4.
Flowchart of proposed methodology.
The daily global solar radiation is considered as the dependent variable, while other variables, including the maximum temperature, minimum temperature, sunshine hour ratio, relative humidity, wind speed, and extraterrestrial radiation, are taken as independent variables. The machine learning models are employed to develop the daily global solar radiation prediction model. Finally, statistical metrics are used to evaluate the estimation accuracy of the models. Note that all the models are implemented in Python 3.6.
2.2.4. Indicators for the Evaluation of the Prediction Accuracy
The Coefficient of Determination (R2), Root Mean Squared Error (RMSE), and Mean Absolute Error (MAE) are employed to evaluate the accuracy of the proposed model. These metrics are presented in Equations (19)–(22). R2 is utilized to evaluate the adequacy of the model’s fit to the data. Higher R2 values indicate a stronger correspondence between the observed data and the model output. RMSE reflects the degree of difference between actual measurements and those predicted by the model. MAE quantifies the average size of errors in a model, focusing solely on their magnitude and ignoring their signs. The optimal outcomes for RMSE and MAE are both zero, while an R2 value of one signifies a perfect fit. Consequently, model performance improves as RMSE and MAE values approach zero and the R2 value approaches one.
where Ei represents the estimated value, Mi represents the measured value, represents the mean of the estimated values, represents the mean of the measured values, and n is the number of samples.
2.3. Calculation of Hourly Solar Irradiance
In order to evaluate the hourly solar irradiance conditions per unit area, the daily global solar radiation is converted into hourly solar irradiance. The adopted calculation steps are based on the method of Picazo et al. [32]. The ratio (rt) of hourly total to daily total radiation is expressed as follows:
where ω represents the hour angle between the sunrise and sunset (rad).
The hourly solar irradiance (IT (t)) is calculated as follows:
where Rs is the daily global solar radiation (MJ·m−2·d−1).
3. Results
3.1. Prediction Accuracy of WOA-XGBoost Model and XGBoost Model (Single-Station Data)
The proposed WOA-XGBoost model was used to predict the daily global solar radiation at ten typical stations. Table 4 shows the results obtained during the training and testing phases for each station. It can be clearly seen that the input parameters affect the prediction accuracy of the model, which is highlighted by the variations in the statistical metrics.

Table 4.
Statistical metrics for the evaluation of daily global solar radiation estimation obtained by the WOA-XGBoost model.
Considering the Harbin station as an example, during the training and testing phases, the highest R2 value as well as the lowest RMSE and MAE were obtained by the proposed model for the A1 input parameter combination, which denotes the highest accuracy. On the contrary, for the A3 input parameter combination, the model yields the lowest R2 value and the highest RMSE and MAE values, which denotes the lowest accuracy. It can be observed that the maximum, minimum temperature, wind speed, sunshine duration ratio, relative humidity, and extraterrestrial radiation affect the daily global solar radiation. The sunshine duration ratio has the most significant impact on the daily global solar radiation.
The optimal input parameter combinations and the results obtained by the machine learning model for the Altay, Golmud, Beijing, Erenhot, Kunming, Zhengzhou, Wuhan, Guangzhou, and Hotan stations are consistent with those of the Harbin station.
The effectiveness of the WOA-XGBoost model is then compared with that of the XGBoost model without parameter optimization. Figure 5 shows the relationship between the measured values during the testing phase at each station and the predicted values calculated by these two models for the A1 parameter combination, including the maximum, minimum temperature, wind speed, sunshine hours ratio, relative humidity, and extraterrestrial radiation. It can be seen that at all the stations, the WOA-XGBoost model generates scatter plots of daily global solar radiation closer to the 1:1 line compared with the XGBoost model. This demonstrates that the WOA-XGBoost model exhibits reduced error between the predicted and measured daily global solar radiation.
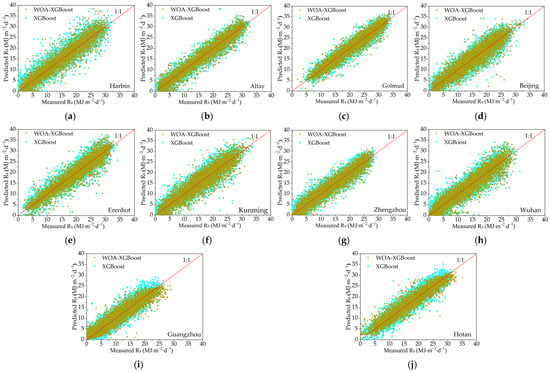
Figure 5.
Scatter plots of the predicted daily global solar radiation versus the corresponding measured values for the testing phase at the (a) Harbin, (b) Altay, (c) Golmud, (d) Beijing, (e) Erenhot, (f) Kunming, (g) Zhengzhou, (h) Wuhan, (i) Guangzhou, and (j) Hotan stations. Note that the straight lines represent the 1:1 line.
3.2. Prediction Stabilitiy of WOA-XGBoost Model and XGBoost Model (Single-Station Data)
The prediction stability of WOA-XGBoost and XGBoost was evaluated by measuring the percentage increase in RMSE on the testing set compared with the training set ((RMSEtesting − RMSEtraining)/RMSEtesting). The average RMSE values during the training and testing phases were calculated for the same input parameter combinations (A1) at ten stations. The average percentage increase in RMSE for each station was then calculated for the input parameter combinations. The obtained results are shown in Figure 6. It can be observed that the ranges of average percentage increase in RMSE for the WOA-XGBoost and XGBoost models are 2.86–11.16% and 4.29–13.06%, respectively. The WOA-XGBoost model has a smaller average percentage increase in RMSE, which denotes a higher predictive stability compared with the XGBoost model.
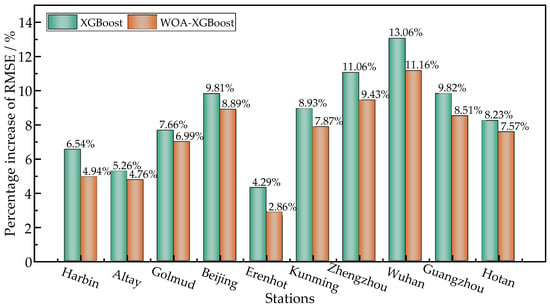
Figure 6.
Percentage increase in testing RMSE over training RMSE for WOA-XGBoost and XGBoost models.
3.3. Prediction of the WOA-XGBoost and XGBoost Models (Mixed Data of Multiple Stations)
This study also involves the development of daily global solar radiation prediction models using mixed data from ten meteorological stations. A total of 70% of the data are used for model training, and the remaining 30% are used for testing. The prediction accuracies of the WOA-XGBoost and XGBoost models, trained on mixed data from all the stations, are compared. The results obtained during training and testing are shown in Table 5. From Table 5, it can be seen that in the testing, the model built on mixed data from multiple stations, WOA-XGBoost, has RMSE and MAE values that are lower than those of XGBoost by 0.156 MJ·m−2·d−1 and 0.067 MJ·m−2·d−1, respectively. For the A1 input combination, including the maximum, minimum temperature, relative humidity, wind speed, sunshine duration ratio, and extraterrestrial radiation, the WOA-XGBoost model has higher prediction accuracy than the XGBoost model. Thus, it can be used to forecast daily global solar radiation in various regions nationwide. Although its prediction accuracy may be slightly lower than those of models built solely on data from individual meteorological stations, this model can still be applied to forecast the daily global solar radiation in various regions across the country, showcasing its broader range of applications.

Table 5.
Statistical indices calculated on the results obtained by the WOA-XGBoost and XGBoost models during training and testing phases.
3.4. Experimental Verification for Prediction Results
3.4.1. Verification Experiment for Prediction Method
Hourly solar irradiance data were collected by the China Institute of Water-Saving Agriculture in the Northwest A&F University in Yangling, Shaanxi (34°18′ N, 108°24′ E; 521 m a.s.l.). The experimental setup includes monocrystalline PV panels of the CS5M32-260 model (the same PV panels as the mobile sprinkler machine), with a peak power, voltage, and current of 260 W, 49.71 V, and 5.25 A, respectively (Figure 7). The solar irradiance was monitored using an AV6592 portable PV tester (environmental temperature testing: accuracy ±1 °C; testing range −30–100 °C; PV panel temperature detection: accuracy ±1 °C; irradiance detection: accuracy ±3%; testing range 0–1800 W·m−2; PV power generation testing: testing range 0.1–500 W). Data were collected every ten minutes, transmitted via Bluetooth and serial interface, displayed, and stored on a personal computer. Meteorological data were automatically collected (once per hour) and recorded by a weather station located 400 m south of the PV panels, including the temperature, humidity, and wind speed, etc.

Figure 7.
Experimental platform: (a) mobile sprinkler machine, and (b) PVPG testing system.
3.4.2. Experimental Results
We utilized data from four days (15 March 2021, 28 June 2021, 29 September 2021, and 15 December 2021) in the Yangling region for experimental verification. The objective of this experiment was to evaluate the consistency between the predicted hourly irradiance values generated by the WOA-XGBoost model and the measured hourly irradiance values.
On 15 March 2021, the meteorological parameters were a maximum temperature of 20 °C, a minimum temperature of 7 °C, a relative humidity of 33%, a wind speed of 3.4 m·s−1, a sunshine hourly ratio of 0.72, and an extraterrestrial radiation of 31.437 MJ·m−2·d−1. The initially computed daily global solar radiation is 18.345 MJ·m−2·d−1. Afterwards, hourly irradiance calculations were made from 1 to 24 h. The resulting hourly irradiance calculation is presented in Figure 8a. It can be observed from Figure 8a that the measured and predicted hourly irradiance values are consistent. The maximum absolute error between the predicted and measured values is 10 W·m−2. The RMSE and MAE are 5.295 W·m−2, and 3.375 W·m−2, respectively.
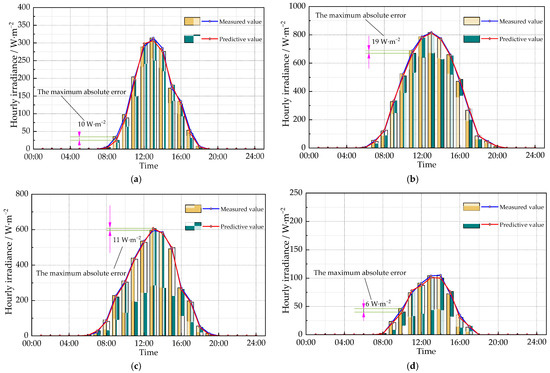
Figure 8.
A comparison of predicted hourly irradiance values generated by the WOA-XGBoost model and measured hourly irradiance values are presented for (a) 15 March 2021, (b) 28 June 2021, (c) 29 September 2021, and (d) 15 December 2021.
On 28 June 2021, the meteorological parameters were a maximum temperature of 34 °C, a minimum temperature of 21 °C, a relative humidity of 58%, a wind speed of 2.5 m·s−1, a sunshine hourly ratio of 0.78, and an extraterrestrial radiation of 44.343 MJ·m−2·d−1. The initially computed daily global solar radiation was 29.512 MJ·m−2·d−1. Afterwards, hourly irradiance calculations were made from 1 to 24 h. It can be observed from Figure 8b that the maximum absolute error between the predicted and measured values is 19 W·m−2. The RMSE and MAE are 7.121 W·m−2, and 4.792 W·m−2, respectively. This shows that the proposed method has a high prediction accuracy.
On 29 September 2021, the meteorological parameters were a maximum temperature of 26 °C, a minimum temperature of 14 °C, a relative humidity of 46%, a wind speed of 1.5 m·s−1, a sunshine hourly ratio of 0.74, and an extraterrestrial radiation of 38.258 MJ·m−2·d−1. The initially computed daily global solar radiation was 24.113 MJ·m−2·d−1. Afterwards, hourly irradiance calculations were made from 1 to 24 h. Figure 8c also demonstrates that the measured and predicted hourly irradiance values are consistent with each other. The maximum absolute error between the predicted and measured values is 11 W·m−2. The RMSE and MAE are 5.323 W·m−2 and 3.833 W·m−2, respectively.
On 15 December 2021, the meteorological parameters included a maximum temperature of 6 °C, a minimum temperature of 0 °C, a relative humidity of 62%, a wind speed of 1.5 m·s−1, a sunshine hourly ratio of 0.70, and an extraterrestrial radiation of 23.462 MJ·m−2·d−1. The initially computed daily global solar radiation is 12.565 MJ·m−2·d−1. Afterwards, hourly irradiance calculations were made from 1 to 24 h. The resulting hourly irradiance calculation is presented in Figure 8d. It can be seen from Figure 8d that the predicted and measured hourly irradiance values are highly consistent. The maximum absolute error between the predicted and measured values is 6 W·m−2 with an RMSE and MAE of 2.508 W·m−2 and 1.458 W·m−2, respectively. This demonstrates that the proposed method has a high prediction accuracy.
4. Discussion
This study addressed the prediction of solar irradiance for optimizing the configuration of a portable solar-powered irrigation system in remote areas. The solar irradiance can be calculated once the daily global solar radiation is obtained. The WOA-XGBoost model was employed to develop a daily global solar radiation prediction model using meteorological data from ten typical locations nationwide having different input parameter combinations. The obtained results demonstrate that the predictive accuracy of the proposed method is higher than that of the XGBoost model. By taking the factors affecting the ground total radiation into consideration, the influencing parameters were categorized into different combinations for optimal parameter selection. In addition, the WOA was adopted to solve the problem of excessive hyperparameters in XGBoost. The data from the ten stations were combined for model training and prediction to obtain a universal daily global solar radiation prediction model. Many studies have been conducted on solar irradiance forecasting. For instance, Chakchak and Cetin [33] evaluated daily global solar radiation prediction models for different weather conditions using Nonlinear Autoregressive models with External Input neural networks, feedforward neural networks, and generalized regression neural network models. The models that utilize actual sunshine duration, cloud cover, air temperature, relative humidity, wind speed, wind direction, air pressure, global solar radiation during cloudless skies, and extraterrestrial solar radiation as climatic input variables. Given the consideration of different types of cloud cover, these models cannot be developed at a regional scale. These studies place significant emphasis on algorithm accuracy [34] and short-term solar irradiance predictions of a certain region [35]. Additionally, current research has paid less attention to the effect of mixed data from multiple meteorological stations on the accuracy of solar irradiance predictions.
There are some challenges involved in combining data from multiple meteorological stations. First, the use of different equipment and measurement standards across stations can result in inconsistencies and inaccuracies within the data. Additionally, meteorological conditions, such as temperature, humidity, and wind speed, can vary significantly between locations, leading to spatial heterogeneity. Furthermore, data from multiple stations may contain redundant information, making dimensionality reduction or feature selection necessary to prevent model overfitting. Addressing these challenges entails extensive data preprocessing, which is crucial for enhancing the accuracy and reliability of solar irradiance prediction models.
XGBoost has significant advantages in weather data management, but optimizing its hyperparameters can be challenging [36]. The WOA-XGBoost model outperforms the XGBoost model, since the former can automatically search for the optimal prediction parameters [37], while the latter manually determines them [38]. WOA is highly effective in solving the problem of excessive hyperparameters in XGBoost. The WOA-XGBoost model solves the overfitting problems encountered by the XGBoost model, which allows for an increase in data fitting and prediction accuracy.
The daily global solar radiation can only reflect the overall radiation situation throughout the day, while it cannot reflect the hourly radiation per unit area within a specific region. On the other hand, the hourly solar irradiance denotes the hourly radiation energy reaching the Earth’s surface per unit area after the solar radiation undergoes absorption, scattering, reflection, and other effects in the atmosphere. It is a crucial parameter for quantitatively describing the solar radiation. A quantitative conversion relationship exists between the daily global solar radiation and hourly irradiance [32]. However, in real applications, the hourly irradiance holds broader application value [39]. Thus, in this paper, the daily global solar radiation was converted into hourly irradiance for evaluation.
However, this study has some limitations, such as the use of data from typical areas for prediction, which results in a limited sample size. In future work, efforts will be made to increase the sample size. Additionally, we intend to develop a hybrid predictive system that utilizes models such as Recurrent Neural Networks (RNNs), Convolutional Neural Networks (CNNs), and Long Short-Term Memory (LSTM) Neural Networks. This approach seeks to integrate the strengths of these diverse predictive models to enhance the overall accuracy of solar irradiance predictions.
5. Conclusions
This paper addressed the solar irradiance prediction problem for a solar-powered system in a shifting irrigation machine. A daily global solar radiation prediction model was developed using the WOA-XGBoost machine learning model. Performing predictions using this model allowed us to obtain gradual irradiance for ten typical meteorological stations nationwide. The prediction accuracy and stability were then analyzed. The model reached its highest precision when the input parameters were the maximum, minimum temperature, sunshine duration ratio, relative humidity, wind speed, and extraterrestrial radiation. The rates of average percentage increase in RMSE for the WOA-XGBoost and XGBoost models were in the ranges 2.86–11.16% and 4.29–13.06%, respectively. The WOA-XGBoost model had a lower percentage increase in RMSE between the training and testing sets compared with the XGBoost model, which demonstrated its higher stability. The WOA-XGBoost model has better parameter initialization and search capabilities compared to the XGBoost model, further enhancing prediction performance. In the testing of the model built on mixed data from multiple stations, WOA-XGBoost had RMSE and MAE values that were lower than those of XGBoost by 0.156 MJ·m−2·d−1 and 0.067 MJ·m−2·d−1, respectively. The model using mixed data from multiple stations, compared to the model using single station data, exhibited good universality, and can be applied to predict solar irradiance in different regions. Overall, the experimental validation showed that the proposed method has high accuracy, meeting the requirements of solar irradiance prediction.
Author Contributions
Conceptualization, D.L. and J.Q.; methodology, D.L.; software, D.L. and Z.Q.; validation, D.L.; formal analysis, D.L., J.Q. and D.Z.; investigation, D.Z. and Z.Q.; resources, D.Z. and Z.Q.; data curation, J.Q.; writing—original draft preparation, D.L.; writing—review and editing, D.L. and J.Q.; visualization, D.L.; supervision, D.Z. and J.Q.; project administration, D.L.; funding acquisition, D.L. and J.Q. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Jiangsu Higher Education Institutions (grant numbers 22KJD510012 and 23KJD510013), the Jiangsu Provincial Natural Science Foundation (grant number BK20210823), the Lvyangjinfeng Talent Project of Yangzhou (grant number YZLYJFJH2021YXBS055), and the Yangzhou City Zero-carbon Smart Manufacturing Engineering Technology Research Center.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors express their sincere appreciation to the editor and referees for their valuable time and efforts towards our manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Ahmed, H.F.; Helgason, W. Reliability model for designing solar-powered center-pivot irrigation systems. Trans. ASABE 2015, 58, 947–958. [Google Scholar] [CrossRef]
- Li, D.; Zhu, D.; Ge, M.; Wu, S.; Wang, R.; Wang, B.; Wu, Y.; Yang, Y. Optimal configuration and field experiments for photovoltaic generation system of solar-powered hose-drawn traveler. Trans. ASABE 2019, 62, 1789–1801. [Google Scholar] [CrossRef]
- Campana, P.E.; Leduc, S.; Kim, M.; Olssond, A.; Zhang, J.; Liu, J.; Kraxnerb, F.; McCallum, I.; Li, H.; Yan, J. Suitable and optimal locations for implementing photovoltaic water pumping systems for grassland irrigation in China. Appl. Energy 2017, 185, 1879–1889. [Google Scholar] [CrossRef]
- Chandel, S.S.; Naik, M.N.; Chandel, R. Review of performance studies of direct coupled photovoltaic water pumping systems and case study. Renew. Sustain. Energy Rev. 2017, 76, 163–175. [Google Scholar] [CrossRef]
- Krishna, R.K.D.V.S.; Premalatha, M.; Naveen, C. Analysis of different combinations of meteorological parameters in predicting the horizontal global solar radiation with ANN approach: A case study. Renew. Sustain. Energy Rev. 2018, 91, 248–258. [Google Scholar] [CrossRef]
- Ramedani, Z.; Omid, M.; Keyhani, A. Modeling solar energy potential in a tehran province using artificial neural networks. Int. J. Green. Energy 2013, 10, 427–441. [Google Scholar] [CrossRef]
- Şahin, M. Comparison of modelling ANN and ELM to estimate solar radiation over Turkey using NOAA satellite data. Int. J. Remote Sens. 2013, 34, 7508–7533. [Google Scholar] [CrossRef]
- Quej, V.H.; Almorox, J.; Ibrakhimov, M.; Saito, L. Estimating daily global solar radiation by day of the year in six cities located in the Yucat? N Peninsula, Mexico. J. Clean. Prod. 2017, 141, 75–82. [Google Scholar] [CrossRef]
- Zang, H.; Xu, Q.; Bian, H. Generation of typical solar radiation data for different climates of China. Energy 2012, 38, 236–248. [Google Scholar] [CrossRef]
- Alia, A.; Norb, N.M.; Ibrahimc, T.; Romlied, M.F. Sizing and placement of solar photovoltaic plants by using time-series historical weather data. J. Renew. Sustain. Energy 2018, 10, 023702. [Google Scholar] [CrossRef]
- Kong, X.; Du, X.; Xue, G.; Xu, Z. Multi-step short-term solar radiation prediction based on empirical mode decomposition and gated recurrent unit optimized via an attention mechanism. Energy 2023, 282, 128825. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Chen, Y.; Gong, D.; Hu, X. Development of data-driven models for prediction of daily global horizontal irradiance in Northwest China. J. Clean. Prod. 2019, 223, 136–146. [Google Scholar] [CrossRef]
- Jemaa, A.B.; Rafa, S.; Essounbouli, N.; Hamzaoui, A.; Hnaien, F.; Yalaoui, F. Estimation of global solar radiation using three simple methods. Energy Procedia 2013, 42, 406–415. [Google Scholar] [CrossRef]
- Khorasanizadeh, H.; Mohammadi, K. Introducing the best model for predicting the monthly mean global solar radiation over six major cities of Iran. Energy 2013, 51, 257–266. [Google Scholar] [CrossRef]
- Mahima; Karakoti, I.; Nandan, H.; Pathak, P.P. An empirical technique to predict monthly mean global solar radiation for PV applications in Indian context. Environ. Prog. Sustain. 2023, 43, e14277. [Google Scholar] [CrossRef]
- Wu, W.; Liu, H.B. Assessment of monthly solar radiation estimates using support vector machines and air temperatures. Int. J. Climatol. 2012, 32, 274–285. [Google Scholar] [CrossRef]
- Chen, J.; Li, G.; Wu, S. Assessing the potential of support vector machine for estimating daily solar radiation using sunshine duration. Energy Convers. Manag. 2013, 75, 311–318. [Google Scholar] [CrossRef]
- Ramli, M.A.M.; Twaha, S.; Al-Turki, Y.A. Investigating the performance of support vector machine and artificial neural networks in predicting solar radiation on a tilted surface: Saudi Arabia case study. Energy Convers. Manag. 2015, 105, 442–452. [Google Scholar] [CrossRef]
- Olatomiwa, L.; Mekhilef, S.; Shamshirband, S.; Petković, D. Adaptive neuro-fuzzy approach for solar radiation prediction in Nigeria. Renew. Sustain. Energy Rev. 2015, 51, 1784–1791. [Google Scholar] [CrossRef]
- Hassan, M.A.; Khalil, A.; Kaseb, S.; Kassem, M.A. Exploring the potential of tree-based ensemble methods in solar radiation modeling. Appl. Energy 2017, 203, 897–916. [Google Scholar] [CrossRef]
- Fan, J.; Wang, X.; Wu, L.; Zhou, H.; Zhang, F.; Yu, X.; Lu, X.; Xiang, Y. Comparison of Support Vector Machine and Extreme Gradient Boosting for predicting daily global solar radiation using temperature and precipitation in humid subtropical climates: A case study in China. Energy Convers. Manag. 2018, 164, 102–111. [Google Scholar] [CrossRef]
- Benali, L.; Notton, G.; Fouilloy, A.; Voyant, C.; Dizene, R. Solar radiation forecasting using Aartificial Neural Network and Random Forest methods: Application to normal beam, horizontal diffuse and global components. Renew. Energy 2019, 132, 871–884. [Google Scholar] [CrossRef]
- Khan, M.J.; Yadav, A.K.; Mathew, L. Techno economic feasibility analysis of different combinations of PV-wind-diesel-battery hybrid system for telecommunication applications in different cities of Punjab, India. Renew. Sust. Energy Rev. 2017, 76, 577–607. [Google Scholar] [CrossRef]
- Malvoni, M.; Giorgi, M.G.D.; Congedo, P.M. Photovoltaic forecast based on hybrid PCA-LSSVM using dimensionality eeducted data. Neurocomputing 2016, 211, 72–83. [Google Scholar] [CrossRef]
- Liu, X.; Mei, X.; Li, Y.; Wang, Q.; Jensen, J.R.; Zhang, Y.; Porter, J.R. Evaluation of temperature- based global solar radiation models in China. Agric. For. Meteorol. 2009, 149, 1433–1446. [Google Scholar] [CrossRef]
- Xing, L.; Cui, N.; Guo, L.; Gong, D.; Wen, S.; Zhang, Y.; Fan, M. Predicting daily solar radiation using a novel hybrid long short-term memory network across four climate regions of China. Comput. Electron. Agric. 2023, 212, 108139. [Google Scholar] [CrossRef]
- Kaba, K.; Sarıgül, M.; Avcı, M.; Kandırmaz, H.M. Estimation of daily global solar radiation using deep learning model. Energy 2018, 162, 126–135. [Google Scholar] [CrossRef]
- Wang, Z. Irrigation and Drainage Engineering; China Agriculture Press: Beijing, China, 2010; pp. 117–228. (In Chinese) [Google Scholar]
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; John Wiley and Sons: Madison, WI, USA, 2013; pp. 24–27. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Zhang, L.; Guo, Z.; Tao, Q.; Xiong, Z.; Ye, J. XGBoost-based short-term prediction method for power system inertia and its interpretability. Energy Rep. 2023, 9, 1458–1469. [Google Scholar] [CrossRef]
- Picazo, M.Á.P.; Juárez, J.M.; García-Márquez, D. Consumption Optimization in irrigation networks supplied by a standalone direct pumping photovoltaic system. Sustainability 2018, 110, 4203. [Google Scholar] [CrossRef]
- Chakchak, J.; Cetin, N.S. Investigating the impact of weather parameters selection on the prediction of solar radiation under different genera of cloud cover: A case-study in a subtropical location. Measurement 2021, 176, 109159. [Google Scholar] [CrossRef]
- Wen, H.; Du, Y.; Chen, X.; Lim, E.G.; Wen, H.; Yan, K. A regional solar forecasting approach using generative adversarial networks with solar irradiance maps. Renew. Energy 2023, 216, 119043. [Google Scholar] [CrossRef]
- Molu, R.J.J.; Tripathi, B.; Mbasso, W.F.; Naoussi, S.R.D.; Bajaj, M.; Wira, P.; Blazek, V.; Prokop, L.; Misak, S. Advancing short-term solar irradiance forecasting accuracy through a hybrid deep learning approach with Bayesian optimization. Results Eng. 2024, 23, 102461. [Google Scholar] [CrossRef]
- Hachimi, C.E.; Belaqziz, S.; Khabba, S.; Sebbar, B.; Dhiba, D.; Chehbouni, A. Smart Weather Data Management Based on Artificial Intelligence and Big Data Analytics for Precision Agriculture. Agriculture 2023, 13, 95. [Google Scholar] [CrossRef]
- Wang, F.; Mi, Z.; Su, S.; Zhao, H. Short-term solar irradiance forecasting model based on Artificial Neural Network using statistical feature parameters. Energies 2012, 5, 1355–1370. [Google Scholar] [CrossRef]
- Eseye, T.A.; Zhang, J.; Zheng, D. Short-term photovoltaic solar power forecasting using a hybrid Wavelet-PSO-SVM model based on SCADA and Meteorological information. Renew. Energy 2018, 118, 357–367. [Google Scholar] [CrossRef]
- Kumari, P.; Toshniwal, D. Extreme gradient boosting and deep neural network based ensemble learning approach to forecast hourly solar irradiance. J. Clean. Prod. 2021, 279, 123285. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).