A Note on Distance-Based Entropy of Dendrimers

Abstract

This paper introduces a variant of entropy measures based on vertex eccentricity and applies it to all graphs representing the isomers of octane. Taking into account the vertex degree as well (degree-ecc-entropy), we find a good correlation with the acentric factor of octane isomers. In particular, we compute the degree-ecc-entropy for three classes of dendrimer graphs.

1. Introduction

This paper introduces a new measure of graph entropy that takes into account the vertex degree and eccentricity. Each vertex is assigned a probability based on its degree and eccentricity. This assignment defines a probability distribution over the vertices of a graph to which Shannon’s entropy function is applied. The result is a numerical value called the eccentricity-entropy of the graph. The main goal of this paper is to study the properties of so-called dendrimer graphs [1,2] by means of eccentricity entropy; the principal result reported here is a good correlation between eccentricity-entropy and an important physical property of dendrimers.

In [1,2], we derived some topological information content of fullerenes. Since fullerenes are three regular graphs, the degree-ecc-entropy and the ecc-entropy explore the same topological information content of a graph. However, dendrimers are completely different. They are hyper-branched macromolecules, and thus, the degree of vertices is important in computing the degree-ecc-entropy. Since the degree-ecc-entropies are based on both the degree and eccentricity of vertices, we chose dendrimers. Here, we first obtain concrete expressions for the graph entropy measures on the defined classes of dendrimers. These results can be useful when applying the measures on the dendrimers for practical applications. Second, we generated numerical results to examine the correlations between the ecc-entropy and the acentric factor of octane isomers. We show that degree-ecc-entropy is highly correlated on dendrimers.

2. Definition and Examples

Let $G=(V,E)$ be a graph where V and E denote the sets of vertices and edges, respectively. The distance between two vertices u, v in G, denoted by $d(u,v)$, is defined as the length of a minimum path connecting them. The eccentricity of a vertex v, denoted by $\sigma \left(v\right)$, is given by $max\left\{d\right(u,v):u\in V(G\left)\right\};$ see [3,4].

A number of measures using Shannon’s entropy function have been introduced and investigated since the 1950s; see [5,6,7,8,9,10,11,12,13,14,15]. The discrete form of this well-known function is defined for a probability vector $p=(p_1,p_2,\dots ,p_n)$ and has the form ${\displaystyle I\left(p\right)=-\sum _{i=1}^n{p}_{i}log\left(p_i\right)}$; see [16]. Note that the logarithms used in this paper are all base two.

Measures such as the one introduced here typically define probability distributions over subsets of graph elements. In the present case, the subsets consist of single vertices. A precise definition of eccentricity entropy is as follows. For a given graph $G=(V,E)$, let $v_i\in V$ and $\mu \left(v_i\right)=c_i\sigma \left(v_i\right)$, where $c_i>0$ and $1\le i\le n$. The entropy $I{f}_{\sigma }\left(G\right)$ is called the ecc-entropy based on $\mu$ where:

$${\displaystyle I{f}_{\sigma }\left(G\right)=-{\displaystyle \frac{1}{T}}\sum _{i=1}^n{c}_i\sigma \left(v_i\right)log\left(c_i\sigma \left(v_i\right)\right)+log\left(T\right),}$$

(1)

and $T={\sum }_{j=1}^n{c}_j\sigma \left(v_j\right)$. If we put $c_i=deg{v}_i$, then we can reformulate Equation (1) as the following equation:

$${\displaystyle I{f}_{d\sigma }\left(G\right)=-{\displaystyle \frac{1}{T}}\sum _{i=1}^{n}deg{v}_i\sigma \left(v_i\right)log(deg{v}_i\sigma \left(v_i\right))+log\left(T\right).}$$

(2)

Example 1.

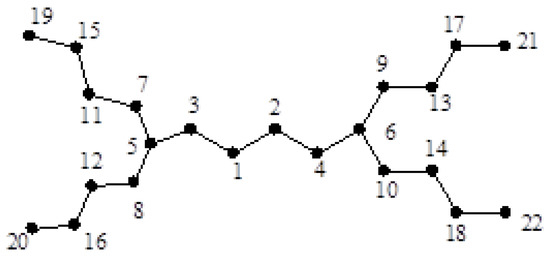
Consider the dendrimer graph $G\left[1\right]$ shown in Figure 1. It is easy to see that:

$$\begin{array}{ccc}\sigma \left(1\right)\hfill & =& \sigma \left(2\right)=7,\sigma \left(3\right)=\sigma \left(4\right)=8,\sigma \left(5\right)=\sigma \left(6\right)=9,\hfill \\ \sigma \left(7\right)\hfill & =& \sigma \left(8\right)=\sigma \left(9\right)=\sigma \left(10\right)=10,\hfill \\ \sigma \left(11\right)\hfill & =& \sigma \left(12\right)=\sigma \left(13\right)=\sigma \left(14\right)=11,\hfill \\ \sigma \left(15\right)\hfill & =& \sigma \left(16\right)=\sigma \left(17\right)=\sigma \left(18\right)=12,\hfill \\ \sigma \left(19\right)\hfill & =& \sigma \left(20\right)=\sigma \left(21\right)=\sigma \left(22\right)=13.\hfill \end{array}$$

Figure 1. The dendrimer graph $G\left[1\right]$.

Furthermore, $deg\left(5\right)=deg\left(6\right)=3$, $deg\left(19\right)=deg\left(20\right)=deg\left(20\right)=deg\left(22\right)=1$, and the degree of other vertices is two. Hence,

$$\begin{array}{cc}{\displaystyle \sum _{i=1}^{22}deg\left(v_i\right)\sigma \left(v_i\right)}& =7\times 2\times 2+8\times 2\times 2+9\times 2\times 3+10\times 4\times 2+11\times 4\times 2\\ & +12\times 4\times 2+13\times 4=430\end{array}$$

and thus:

$$\begin{array}{cc}I{f}_{d\sigma }\left(G\left[1\right]\right)& =log430-(28log14+32log16+54log27+80log20+88log22\\ & +96log24+52log13)/430=4.417650155.\end{array}$$

Consider now two dendrimer graphs $G\left[2\right]$ and $G\left[3\right]$ depicted in Figure 2 and Figure 3. Similar to the last example, by computing their eccentricities, one can see that:

$$\begin{array}{cc}I{f}_{d\sigma }\left(G\left[2\right]\right)& =log1814-(44log22+48log24+78log39+112log28+120log30\\ & +128log32+204log51+288log36+304log38+320log40\\ & +168log21)/1814=5.710176689.\end{array}$$

and:

$$\begin{array}{cc}I{f}_{d\sigma }\left(G\left[3\right]\right)\hfill & =log5694-(60log30+64log32+102log51+144log36+152log38\hfill \\ & +160log40+252log63+352log44+368log46+384log48+600log75\hfill \\ & +832log52+846log54+896log56+464log29)/5694=6.837410219.\hfill \end{array}$$

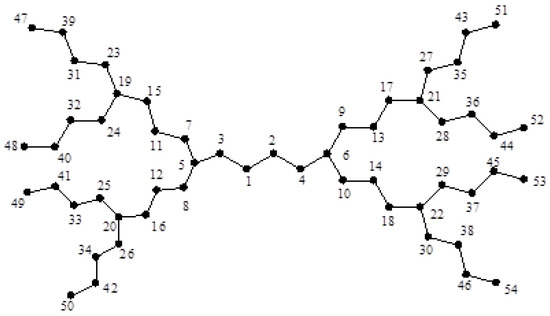
Figure 2. The dendrimer graph $G\left[2\right]$.

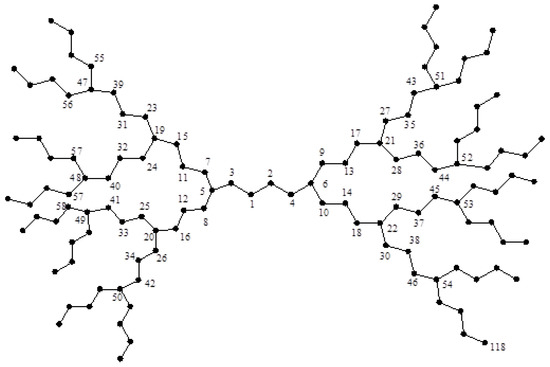
Figure 3. The dendrimer graph $G\left[3\right]$.

Example 2.

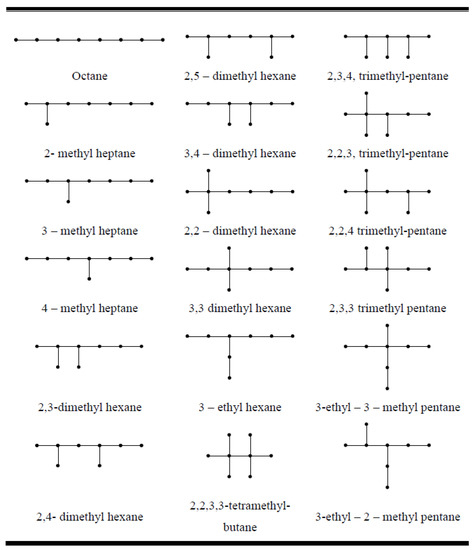
Consider all isomers of octane as shown in Figure 4. The acentric factor and the entropy of the octane isomers are given in Table 1. The ecc-entropy of these isomers can be directly derived from the definition of eccentricity and Equation (1). These values are reported in Table 1. By comparing the values of Table 1, one can see easily that there is a correlation $R^2\approx -0.348$ between ecc-entropy and the acentric factor of octane isomers and a correlation $R^2\approx -0.36$ between ecc-entropy and S. However, by putting $c_i=deg{v}_i$, we achieve a new version of entropy, namely degree-ecc-entropy, in which the correlation between degree-ecc-entropy and the acentric factor of octane isomers increases sharply to $R^2\approx 0.8$. This shows that important physical properties of these molecules can be determined by computing degree-ecc-entropy. Degree-ecc-entropy is a very specialized measure, and of course, other entropy measures might capture other properties of these molecules.

Figure 4. All octane isomers.

Table 1. AcenFac, S, ecc-entropy, anddeg-ecc-entropy of the octane isomers.

Molecule	AcentFac	S	ecc-ent	deg-ecc-ent
octane	0.397898	111	2.969845	2.969175
2-methyl 1-heptane	0.377916	109.84	2.9648	2.916803
3-methyl-heptane	0.371002	111.26	2.968892	2.936056
4-methyl-heptane	0.371504	109.32	2.96638	2.947337
3-ethyl-hexane	0.362472	109.43	2.973525	2.961035
2,2-dimethyl-hexane	0.339426	103.42	2.971335	2.852746
2,3-dimethyl-hexane	0.348247	108.02	2.977217	2.905118
2,4-dimethyl-hexane	0.344223	106.98	2.973525	3.433438
2,5-dimethyl-hexane	0.35683	105.72	2.971335	2.887762
3,3-dimethyl-hexane	0.322596	104.74	2.977217	2.897582
3,4-dimethyl-hexane	0.340 345	106.59	2.977217	2.925864
2-methyl-3-ethyl-pentane	0.332433	106.06	2.967307	2.936529
3-methyl-3-ethyl-pentane	0.306 899	101.48	2.968919	2.935986
2,2,3-trimethyl-pentane	0.300816	101.31	2.967307	2.84966
2,2,4-trimethyl-pentane	0.30537	104.09	2.96772	2.7696979
2,3,3-trimethyl-pentane	0.293177	102.06	2.968919	2.88075
2,3,4-trimethyl-pentane	0.317422	102.39	2.967307	2.883862
2,2,3,3-tetramethylbutane	0.255294	93.06	2.980826	2.8366

3. General Results on the Ecc-Entropy of Dendrimers

Two vertices of a graph are said to be similar if one can be mapped into the other by an automorphism. This is important here since it is well known that similar vertices have the same eccentricity. Hence, in a vertex-transitive graph, for all sequences $c_1\ge c_2\ge \dots \ge c_n$, we have:

$$\begin{array}{c}{\displaystyle I{f}_{\sigma }\left(G\right)=log\left({\displaystyle \sum _{i=1}^n{c}_i}\right)-\sum _{i=1}^n\frac{c_i}{{\displaystyle \sum _{j=1}^n{c}_j}}log\left(c_i\right).}\hfill \end{array}$$

(3)

As a special case, if $c_i=c_j$ for all $i\ne j$, then $I{f}_{\sigma }\left(G\right)=log\left(n\right).$

Proposition 1

([9]). Suppose G is a graph and $V_1,V_2,\cdots ,V_k$ are all orbits of $Aut\left(G\right)$ on $V\left(G\right)$. Then:

$$\begin{array}{c}{\displaystyle I{f}_{\sigma }\left(G\right)=log\left({\displaystyle \sum _{i=1}^k\sigma \left(x_i\right)\sum _{i=1}^{|V_i|}{c}_j}\right)-\sum _{i=1}^k\sigma \left(x_i\right)\sum _{j=1}^{|V_i|}\frac{c_j}{{\displaystyle \sum _{t=1}^k\sigma \left(x_t\right)\sum _{l=1}^{|V_i|}{c}_l}}log\left(c_j\sigma \left(x_i\right)\right).}\hfill \end{array}$$

(4)

In addition, if $c_1=c_2=\dots =c_n$, then:

$${\displaystyle log\left(\Theta \left(G\right)\right)-{\displaystyle \frac{1}{\Theta \left(G\right)}}\sum _{i=1}^k\left|V_i\right|\sigma \left(x_i\right)log\left(\sigma \left(x_i\right)\right),}$$

(5)

where ${\displaystyle \Theta \left(G\right)=\sum _{u\in V}\sigma \left(u\right).}$

Dendrimers constructed by hyper-branched macromolecules can be arranged in either convergent or divergent form. A dendrimer graph is a molecular graph associated with a dendrimer molecule. The aim of this section is to determine the ecc-entropy of three classes of dendrimers. The first class consists of connected, acyclic graphs, namely trees.

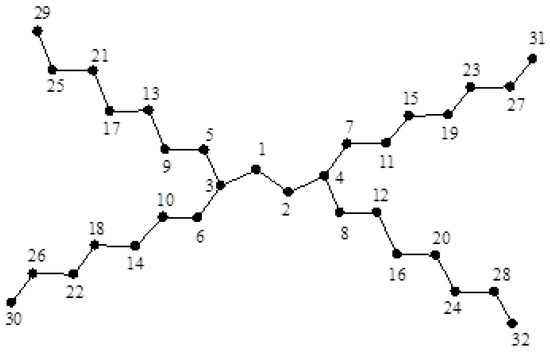
Let $G\left[n\right]$ be the dendrimer graph shown in Figure 5 with ${\displaystyle 6+\sum _{i=1}^n{2}^{i+3}}$ vertices. Note that $G\left[0\right]$ is isomorphic to the path $P_6$. Clearly,

$$\begin{array}{c}\left|V\left(G\left[n\right]\right)\right|=8\sum _{i=1}^n{2}^i+6=8(2^{n+1}-1-1)+6=2^{n+4}-10.\hfill \end{array}$$

(6)

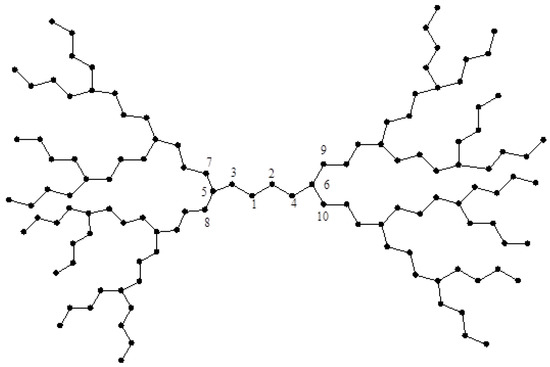
Figure 5. The dendrimer graph $G\left[n\right]$.

Hence, we have the following theorem.

Theorem 1.

For graph $G\left[n\right]$, if $c_i=c_j$ for $i\ne j$ then,

$$\begin{array}{cc}I{f}_{\sigma }\left(G\left[n\right]\right)\hfill & =log\left(m\right)-2(\sigma log\sigma +(\sigma +1)log(\sigma +1)+(\sigma +2)log(\sigma +2)\hfill \\ & +\sum _{i=1}^n{2}^i\sum _{j=3}^6(\sigma +4(i-1)+j)log(\sigma +4(i-1)+j))/m\hfill \end{array}$$

where $\sigma =4n+3$ and $m=6\sigma +6+2{\sum }_{i=1}^n{2}^i(4\sigma +16i+2).$ If in addition $c_i=deg{v}_i$, then:

$$\begin{array}{cc}I{f}_{d\sigma }\left(G\left[n\right]\right)\hfill & =log\left(m\right)-\left(4\right(\sigma log2\sigma +(\sigma +1)log2(\sigma +1))+6(\sigma +2)log3(\sigma +2)\hfill \\ & +4\sum _{i=1}^n{2}^i\sum _{j=3}^5(\sigma +4(i-1)+j)log2(\sigma +4(i-1)+j)\hfill \\ & +6\sum _{k=1}^{n-1}{2}^k(\sigma +4k+2)log3(\sigma +4k+2)\hfill \\ & +2^{n+1}(\sigma +4n+2)log(\sigma +4n+2))/m\hfill \end{array}$$

where:

$$\begin{array}{cc}\sigma =4n+3,m\hfill & =14\sigma +16+4\sum _{i=1}^n{2}^i(3\sigma +12i)+6\sum _{j=1}^{n-1}{2}^j(\sigma +4j+2)\hfill \\ & +2^{n+1}(\sigma +4n+2).\hfill \end{array}$$

Proof. 

Applying our method for graph $G\left[1\right],G\left[2\right]$ and $G\left[3\right]$ in Example 1, we obtain the eccentricity values of vertices in Table 2. It is easy to see that every vertex of $G\left[n\right]$ has degree 1, 2, or 3. Since $G\left[n\right]$ has n orbits, there are n types of vertices in $G\left[n\right]$ and $\sigma =4n+3$. Computing the eccentricity of each vertex as reported in Table 2, the assertion follows. □

Table 2. Eccentricity of every vertex of $G\left[n\right]$ in general.

Step	Vertex	No.	$\mathit{d}\left(\mathit{u}\right)$	$\mathit{\sigma }\left(\mathit{u}\right)$
1	$v_1$	2	2	$\sigma$
	$v_3$	2	2	$\sigma +1$
	$v_5$	2	3	$\sigma +2$
	$v_7$	4	2	$\sigma +3$
	$v_{11}$	4	2	$\sigma +4$
	$v_{15}$	4	2	$\sigma +5$
	$v_{19}$	4	3	$\sigma +6$
2	$v_1$	8	2	$\sigma +7$
	$v_9$	8	2	$\sigma +8$
	$v_{17}$	8	2	$\sigma +9$
	$v_{25}$	8	3	$\sigma +10$
⋮
i	$v_1$	$2^{i+1}$	2	$\sigma +4(i-1)+3$
	$v_{2^{i+1}+1}$	$2^{i+1}$	2	$\sigma +4(i-1)+4$
	$v_{2\times 2^{i+1}+1}$	$2^{i+1}$	2	$\sigma +4(i-1)+5$
	$v_{3\times 2^{i+1}+1}$	$2^{i+1}$	3	$\sigma +4(i-1)+6$
⋮
n	$v_1$	$2^{n+1}$	2	$\sigma +4(n-1)+3$
	$v_{2^{n+1}+1}$	$2^{n+1}$	2	$\sigma +4(n-1)+4$
	$v_{2\times 2^{n+1}+1}$	$2^{n+1}$	2	$\sigma +4(n-1)+5$
	$v_{3\times 2^{n+1}+1}$	$2^{n+1}$	1	$\sigma +4(n-1)+6$

Example 3.

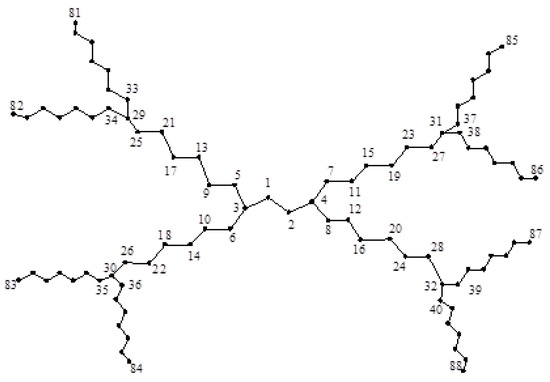
Consider the dendrimer graph $H\left[1\right]$ as depicted in Figure 6. It is easy to see that:

$$\begin{array}{ccc}\sigma \left(1\right)\hfill & =& \sigma \left(2\right)=9,\sigma \left(3\right)=\sigma \left(4\right)=10,\sigma \left(5\right)=\sigma \left(6\right)=\sigma \left(7\right)=\sigma \left(8\right)=11,\hfill \\ \sigma \left(9\right)\hfill & =& \sigma \left(10\right)=\sigma \left(11\right)=\sigma \left(12\right)=12,\sigma \left(13\right)=\sigma \left(14\right)=\sigma \left(15\right)=\sigma \left(16\right)=13,\hfill \\ \sigma \left(17\right)\hfill & =& \sigma \left(18\right)=\sigma \left(19\right)=\sigma \left(20\right)=14,\sigma \left(21\right)=\sigma \left(22\right)=\sigma \left(23\right)=\sigma \left(24\right)=15,\hfill \\ \sigma \left(25\right)\hfill & =& \sigma \left(26\right)=\sigma \left(27\right)=\sigma \left(28\right)=16,\sigma \left(29\right)=\sigma \left(30\right)=\sigma \left(31\right)=\sigma \left(32\right)=17.\hfill \end{array}$$

Figure 6. The dendrimer graph $H\left[1\right]$.

Furthermore, $deg\left(3\right)=deg\left(4\right)=3$, $deg\left(29\right)=deg\left(30\right)=deg\left(31\right)=deg\left(32\right)=1$, and the degree of other vertices is two. Hence,

$$\begin{array}{cc}{\displaystyle \sum _{i=1}^{32}deg\left(v_i\right)\sigma \left(v_i\right)}\hfill & =2\times 2\times 9+2\times 3\times 10+8(11+12+13+14+15+16)\hfill \\ & +4\times 17=812.\hfill \end{array}$$

and thus:

$$\begin{array}{cc}I{f}_{d\sigma }\left(H\left[1\right]\right)\hfill & =log812-\frac{1}{812}\left(36log18+60log30+8\sum _{i=11}^{16}ilog2i+4\times 17\right)\hfill \\ & =4.971787954.\hfill \end{array}$$

Furthermore, for $n=2,3$, $H\left[2\right]$ and $H\left[3\right]$ are depicted in Figure 7 and Figure 8, and we obtain:

$$\begin{array}{cc}I{f}_{d\sigma }\left(H\left[2\right]\right)\hfill & =log4326-{\displaystyle \frac{1}{4326}}(64log32+102log34+8\sum _{i=18}^{23}ilog2i\hfill \\ & +4\times 3\times 24log72+16\sum _{j=25}^{30}log2j+8\times 31log31)\hfill \\ & =6.426696727.\hfill \end{array}$$

$$\begin{array}{cc}I{f}_{d\sigma }\left(H\left[3\right]\right)\hfill & =log14840-{\displaystyle \frac{1}{14840}}(52log46+144log48+8\sum _{i=25}^{30}ilog2i\hfill \\ & +4\times 3\times 31log93+16\sum _{j=32}^{37}jlog2j+8\times 3\times 38log114\hfill \\ & +32\sum _{k=39}^{44}klog2k+16\times 45log45)=7.605173937.\hfill \end{array}$$

Figure 7. The dendrimer graph $H\left[2\right]$.

Figure 8. The dendrimer graph $H\left[3\right]$.

In general, the number of vertices of $H\left[n\right]$ is:

$$\begin{array}{ccc}\left|V\right(H\left[n\right]\left)\right|\hfill & =& {\displaystyle 4+4\times 7+8\times 7+\cdots +2^{n+1}\times 7=4+7\sum _{i=1}^n{2}^{i+1}}\hfill \\ & =& 4+14(2^{n+1}-1-1)=7\times 2^{n+2}-24.\hfill \end{array}$$

Hence, we conclude the following theorem.

Theorem 2.

Let $H\left[n\right]$ be a dendrimer graph as shown in Figure 7 and Figure 8. If $c_i=c_j$ for $i\ne j$, then:

$$\begin{array}{cc}I{f}_{\sigma }\left(H\left[n\right]\right)\hfill & =log\left(m\right)-2\left(\sigma log\sigma +(\sigma +1)log(\sigma +1)+\sum _{i=1}^n{2}^i\sum _{j=2}^8\left(\alpha \right)log\left(\alpha \right)\right)/m\hfill \end{array}$$

where $\sigma =7n+2$, $m=4\sigma +2+14{\sum }_{i=1}^n{2}^i(\sigma +7i-2)$ and $\alpha =\sigma +7(i-1)+j.$ If $c_i=d_i$, then:

$$\begin{array}{cc}I{f}_{d\sigma }\left(H\left[n\right]\right)\hfill & =log\left(m\right)-(4\sigma log2\sigma +6(\sigma +1)log3(\sigma +1)\hfill \\ & +4\sum _{i=1}^n{2}^i\sum _{j=2}^7(\sigma +7(i-1)+j)log(\sigma +7(i-1)+j)\hfill \\ & +6\sum _{k=1}^{n-1}{2}^k(\sigma +7k+1)log3(\sigma +7k+1)\hfill \\ & +2^{n+1}(\sigma +7n+1)log(\sigma +7n+1))/m\hfill \end{array}$$

where $\sigma =7n+2$ and $m=10\sigma +6+12{\sum }_{i=1}^n{2}^i(2\sigma +14i-5)+6{\sum }_{j=1}^{n-1}{2}^j(\sigma +7j+1)+2^{n+1}(\sigma +7n+1).$

Proof. 

As in the proof of Theorem 1, since there are n orbits for this graph, we can divide the vertices of the graph into n distinct types. Using Table 3, the proof is straightforward. □

Table 3. Eccentricity of every vertex of $H\left[n\right]$ where $\sigma =7n+2$.

Step	Vertex	No.	$\mathit{d}\left(\mathit{u}\right)$	$\mathit{\sigma }\left(\mathit{u}\right)$
1	$v_1$	2	2	$\sigma$
	$v_3$	2	3	$\sigma +1$
	$v_5$	4	2	$\sigma +2$
	$v_9$	4	2	$\sigma +3$
	⋮	⋮	⋮	⋮
	$v_{25}$	4	2	$\sigma +7$
	$v_{29}$	4	3	$\sigma +8$
2	$v_1$	8	2	$\sigma +9$
	$v_9$	8	2	$\sigma +10$
	⋮	⋮	⋮	⋮
	$v_{41}$	8	2	$\sigma +14$
	$v_{49}$	8	3	$\sigma +15$
⋮
i	$v_1$	$2^{i+1}$	2	$\sigma +7(i-1)+2$
	$v_{2^{i+1}+1}$	$2^{i+1}$	2	$\sigma +7(i-1)+3$
	$v_{2\times 2^{i+1}+1}$	$2^{i+1}$	2	$\sigma +7(i-1)+4$
	⋮	⋮	⋮	⋮
	$v_{6\times 2^{i+1}+1}$	$2^{i+1}$	3	$\sigma +7(i-1)+8$
⋮
n	$v_1$	$2^{n+1}$	2	$\sigma +7(n-1)+2$
	$v_{2^{n+1}+1}$	$2^{n+1}$	2	$\sigma +7(n-1)+3$
	$v_{2\times 2^{n+1}+1}$	$2^{n+1}$	2	$\sigma +7(n-1)+4$
	⋮	⋮	⋮	⋮
	$v_{6\times 2^{n+1}+1}$	$2^{n+1}$	1	$\sigma +7(n-1)+8$

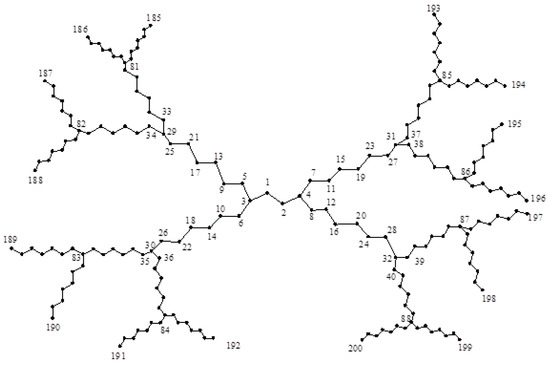
Finally, we are ready to compute the entropy of dendrimer graph $K\left[n\right]$ shown in Figure 9, Figure 10 and Figure 11. First, we assume $n=1$; see Figure 9. It is not difficult to see that:

$$\begin{array}{ccc}\sigma \left(1\right)\hfill & =& \sigma \left(2\right)=14,\sigma \left(3\right)=\sigma \left(4\right)=\sigma \left(25\right)=\sigma \left(28\right)=13,\hfill \\ \sigma \left(5\right)\hfill & =& \sigma \left(6\right)=\sigma \left(7\right)=\sigma \left(8\right)=\sigma \left(26\right)=\sigma \left(27\right)=12,\hfill \\ \sigma \left(9\right)\hfill & =& \sigma \left(10\right)=\sigma \left(11\right)=\sigma \left(12\right)=\sigma \left(22\right)=\sigma \left(23\right)=11,\hfill \\ \sigma \left(13\right)\hfill & =& \sigma \left(14\right)=\sigma \left(15\right)=\sigma \left(16\right)=\sigma \left(18\right)=\sigma \left(19\right)=10,\hfill \\ \sigma \left(17\right)\hfill & =& \sigma \left(18\right)=\sigma \left(19\right)=\sigma \left(20\right)=14,\sigma \left(21\right)=\sigma \left(22\right)=\sigma \left(23\right)=\sigma \left(24\right)=15,\hfill \\ \sigma \left(29\right)\hfill & =& \sigma \left(30\right)=15,\sigma \left(31\right)=\sigma \left(32\right)=16,\sigma \left(33\right)=\sigma \left(34\right)=\sigma \left(35\right)=\sigma \left(36\right)=17,\hfill \\ \sigma \left(37\right)\hfill & =& \sigma \left(38\right)=15,\sigma \left(39\right)=\sigma \left(40\right)=18,\hfill \\ \sigma \left(41\right)\hfill & =& \sigma \left(42\right)=\sigma \left(43\right)=\sigma \left(44\right)=\sigma \left(45\right)=\sigma \left(46\right)=19.\hfill \end{array}$$

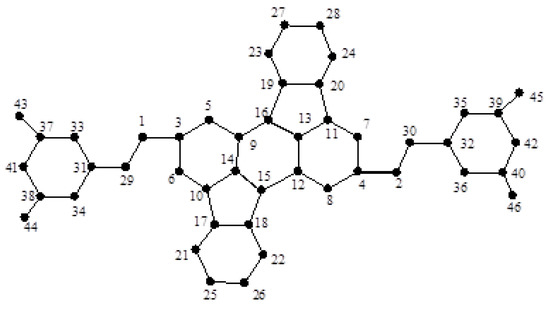
Figure 9. The dendrimer graph $K\left[1\right]$.

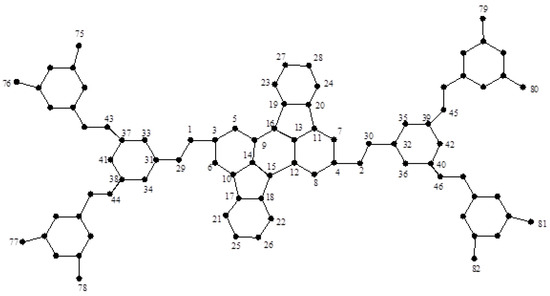
Figure 10. The dendrimer graph $K\left[2\right]$.

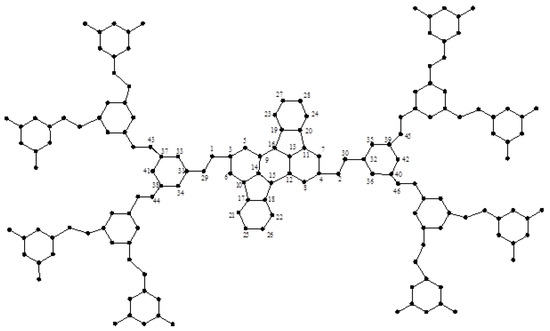
Figure 11. The dendrimer graph $K\left[n\right]$.

Furthermore, $deg\left(3\right)=deg\left(4\right)=deg\left(9\right)=\dots =deg\left(20\right)=deg\left(31\right)=deg\left(32\right)=deg\left(37\right)=\dots =deg\left(40\right)=3$, $deg\left(43\right)=deg\left(44\right)=deg\left(45\right)=deg\left(46\right)=1$, and the degree of the other vertices is two. Hence,

$$\begin{array}{cc}{\displaystyle \sum _{i=1}^{46}deg\left(v_i\right)\sigma \left(v_i\right)}\hfill & =6\times 3\times 10+2\times 2\times 11+6\times 3\times 11+8\times 2\times 12+2\times 2\times 13\hfill \\ & +2\times 3\times 13+2\times 2\times 14+2\times 2\times 15+2\times 3\times 16+4\times 2\times 17\hfill \\ & +4\times 3\times 18+2\times 2\times 19+4\times 1\times 19=1460\hfill \end{array}$$

and thus:

$$\begin{array}{cc}I{f}_{d\sigma }\left(K\left[1\right]\right)\hfill & =log1460-(180log30+198log33+44log22+192log24+52log24\hfill \\ & +156log39+56log28+60log30+96log48+136log34+216log54\hfill \\ & +76log38+76log19)/1460=5.466783542.\hfill \end{array}$$

Similarly, we can compute these values for the cases $n=2$ in graph $K\left[n\right]$, which is depicted in Figure 10. A direct computation shows that:

$$\begin{array}{cc}I{f}_{d\sigma }\left(K\left[2\right]\right)\hfill & =log4284-(270log45+288log48+64log32+272log34+72log36\hfill \\ & +216log54+76log38+80log40+126log63+176log44+276log69\hfill \\ & +288log48+200log50+312log78+432log54+672log84\hfill \\ & +232log58+232log29)/4284=6.094766741.\hfill \end{array}$$

Now, consider Table 4 and Figure 11. As found in the previous theorems, there are n types of vertices in graph $K\left[n\right]$, and their eccentricities are reported in Table 4. In general, the number of vertices of $K\left[n\right]$ is:

$$\begin{array}{ccc}\left|V\right(H\left[n\right]\left)\right|\hfill & =& {\displaystyle 28+2\times 9+4\times 9+\dots +2^n\times 9=28+9\sum _{i=1}^n{2}^i}\hfill \\ & =& 28+9(2^{n+1}-1-1)=9\times 2^{n+1}+10.\hfill \end{array}$$

Table 4. Eccentricity of every vertex of $K\left[n\right]$ in the total case.

Step	Vertex	No.	$\mathit{d}\left(\mathit{u}\right)$	$\mathit{\sigma }\left(\mathit{u}\right)$
1	$v_1$	2	2	$\sigma$
	$v_3$	2	3	$\sigma -1$
	$v_{25}$	2	2	$\sigma -1$
	$v_5$	8	2	$\sigma -2$
	$v_{22}$	2	2	$\sigma -3$
	$v_9$	6	3	$\sigma -3$
	$v_{13}$	6	3	$\sigma -4$
	$v_{29}$	2	2	$\sigma +1$
	$v_{31}$	2	3	$\sigma +2$
	⋮	⋮	⋮	⋮
	$v_{41}$	2	2	$\sigma +5$
	$v_{43}$	4	2	$\sigma +5$
2	$v_1$	4	2	$\sigma +6$
	$v_{29}$	4	3	$\sigma +7$
	$v_{29}$	8	2	$\sigma +8$
	$v_1$	8	3	$\sigma +9$
	$v_9$	4	2	$\sigma +10$
	$v_9$	8	2	$\sigma +10$
⋮
i	$v_1$	$2^i$	2	$\sigma +5(i-1)+1$
	$v_{2^i+1}$	$2^i$	3	$\sigma +5(i-1)+2$
	$v_{2^{i+1}+1}$	$2^{i+1}$	2	$\sigma +5(i-1)+3$
	$v_{2^{i+2}+1}$	$2^{i+1}$	3	$\sigma +5(i-1)+4$
	$v_{3\times 2^{i+1}+1}$	$2^i$	2	$\sigma +5(i-1)+5$
	$v_{7\times 2^i+1}$	$2^{i+1}$	2	$\sigma +5(i-1)+5$
⋮
n	$v_1$	$2^n$	2	$\sigma +5(n-1)+1$
	$v_{2^n+1}$	$2^n$	3	$\sigma +5(n-1)+2$
	$v_{2^{n+1}+1}$	$2^{n+1}$	2	$\sigma +5(n-1)+3$
	$v_{2^{n+2}+1}$	$2^{n+1}$	3	$\sigma +5(n-1)+4$
	$v_{3\times 2^{n+1}+1}$	$2^n$	2	$\sigma +5(n-1)+5$
	$v_{7\times 2^{n+1}}$	$2^{n+1}$	1	$\sigma +5(n-1)+5$

Hence, we have the following theorem:

Theorem 3.

Let $K\left[n\right]$ be the dendrimer graph shown in Figure 11. If $c_i=c_j$ for $i\ne j$, then:

$$\begin{array}{cc}I{f}_{\sigma }\left(K\left[n\right]\right)\hfill & =log\left(m\right)-(2\sigma log\sigma +4(\sigma -1)log(\sigma -1)+8(\sigma -2)log(\sigma -2)\hfill \\ & +8(\sigma -3)log(\sigma -3)+6(\sigma -4)log(\sigma -4)\hfill \\ & +\sum _{i=1}^n{2}^i(\sigma +5i-4)log(\sigma +5i-4)+\sum _{j=1}^n{2}^j(\sigma +5j-3)log(\sigma +5j-3)\hfill \\ & +\sum _{k=1}^n{2}^{k+1}(\sigma +5k-2)log(\sigma +5k-2)\hfill \\ & +\sum _{l=1}^n{2}^{l+1}(\sigma +5l-1)log(\sigma +5l-1)+3\sum _{t=1}^n{2}^t(\sigma +5t)log(\sigma +5t))/m\hfill \end{array}$$

where $\sigma =5n+9$, $m=28\sigma -68+{\sum }_{i=1}^n{2}^i(9\sigma +45i-13).$ If $c_i=d_i$, then:

$$\begin{array}{cc}I{f}_{d\sigma }\left(K\left[n\right]\right)\hfill & =log\left(m\right)-\left(18\right(\sigma -4)log3(\sigma -4)+4(\sigma -3)log2(\sigma -3)\hfill \\ & +18(\sigma -3)log3(\sigma -3)+16(\sigma -2)log2(\sigma -2)+6(\sigma -1)log3(\sigma -1)\hfill \\ & +4(\sigma -1)log2(\sigma -1)+\sigma log2\sigma +2\sum _{i=1}^n{2}^i(\sigma +5i-4)log2(\sigma +5i-4)\hfill \\ & +3\sum _{j=1}^n{2}^j(\sigma +5j-3)log3(\sigma +5j-3)\hfill \\ & +4\sum _{k=1}^n{2}^{k+1}(\sigma +5k-2)log2(\sigma +5k-2)\hfill \\ & +6\sum _{l=1}^n{2}^l(\sigma +5l-1)log3(\sigma +5l-1)+2\sum _{t=1}^n{2}^t(\sigma +5t)log2(\sigma +5t)\hfill \\ & +4\sum _{r=1}^{n-1}{2}^r(\sigma +5r)log2(\sigma +5r)+2^{n+1}(\sigma +5n)log(\sigma +5n))/m\hfill \end{array}$$

where $\sigma =5n+9$ and

$m=350n+450+{\sum }_{i=1}^n{2}^i(85n+85i+122)+4{\sum }_{j=1}^{n-1}{2}^j(5n+5j+9)+2^n(20n+18).$

4. Numerical Results

One method to estimate the complexity of a network is to measure the entropy of network invariants, such as eccentricity or degree sequences; see [17]. On the other hand, the main application of the Shannon entropy is the information content of graphs. In [18], it was shown how the entropy of different graph properties can produce divergent values of entropy for exactly the same graph.

The findings presented in this section show that the correlation between ecc and degree-ecc-entropy measures of three dendrimers is approximately $R^2\approx 0.999$, see Figure 12, Figure 13 and Figure 14. This means that the ecc and degree-ecc-entropy measures might be interesting for further investigations in predicting the physico-chemical properties of molecules [12,14,18,19,20,21,22,23,24]. The reasons for choosing these molecular descriptors is that the dendrimers are hyper-branched molecules the degree and eccentricity of vertices of which are important.

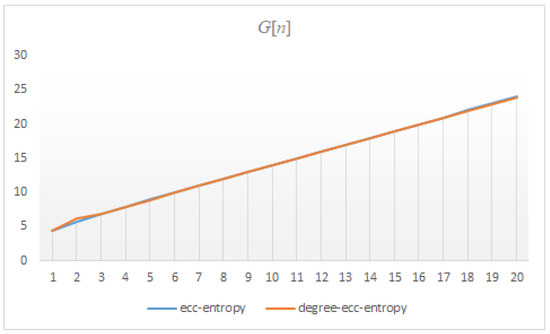
Figure 12. The correlation $R^2\approx 0.999858$ between the ecc and degree-ecc-entropies of $G\left[n\right]$.

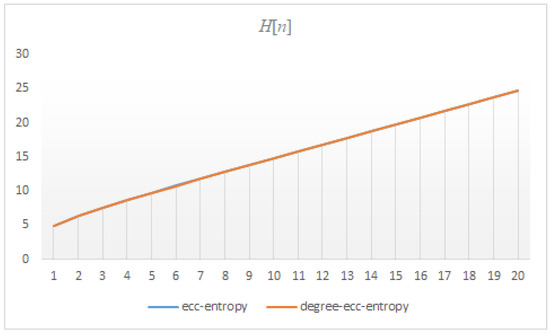
Figure 13. The correlation $R^2\approx 0.999858$ between the ecc and degree-ecc-entropies of $H\left[n\right]$.

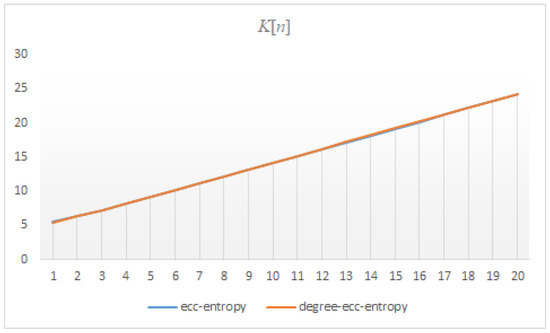
Figure 14. The correlation $R^2\approx 0.999858$ between the ecc and degree-ecc-entropies of $K\left[n\right]$.

5. Conclusions

In this paper, we studied the mathematical description of chemical structures using information- entropy-based structural descriptors. In other words, the present paper established important correlations between ecc and degree-ecc-entropies of three dendrimers $G\left[n\right]$, $H\left[n\right]$, and $K\left[n\right]$. In [1], the authors focused on fullerenes and computed some results on these structures. Since fullerenes are regular graphs and the degree-ecc-entropies are based on both the degree and eccentricity of vertices, we chose dendrimers, which are highly branched molecules. In future work, we plan to apply our methods to other classes of molecular graphs.