Abstract
In recent years, the numerical solution of differential problems, possessing constants of motion, has been attacked by imposing the vanishing of a corresponding line integral. The resulting methods have been, therefore, collectively named (discrete) line integral methods, where it is taken into account that a suitable numerical quadrature is used. The methods, at first devised for the numerical solution of Hamiltonian problems, have been later generalized along several directions and, actually, the research is still very active. In this paper we collect the main facts about line integral methods, also sketching various research trends, and provide a comprehensive set of references.
1. Introduction
The numerical solution of differential problems in the form
is needed in a variety of applications. In many relevant instances, the solution has important geometric properties and the name geometric integrator has been coined to denote a numerical method able to preserve them (see, e.g., the monographs [1,2,3,4]). Often, the geometric properties of the vector field are summarized by the presence of constants of motion, namely functions of the state vector which are conserved along the solution trajectory of (1). For this reason, in such a case one speaks about a conservative problem. For sake of simplicity, let us assume, for a while, that there exists only one constant of motion, say
along the solution of (1). Hereafter, we shall assume that both and are suitably smooth (e.g., analytical). In order for the conservation property (2) to hold, one requires that
Consequently, one obtains the equivalent condition
However, the conservation property (2) can be equivalently restated through the vanishing of a line integral:
In fact, since y satisfies (1), one obtains that the integrand is given by
because of (3). On the other hand, if one is interested in obtaining an approximation to y, ruled by a discrete-time dynamics with time-step h, one can look for any path joining to , i.e.,
and such that
Definition 1.
Obviously, the process is then repeated on the interval , starting from , and so on. We observe that the path now provides the vanishing of the line integral in (6) without requiring the integrand be identically zero. This, in turn, allows much more freedom during the derivation of such methods. In addition to this, it is important to observe that one cannot, in general, directly impose the vanishing of the integral in (6) since, in most cases, the integrand function does not admit a closed form antiderivative. Consequently, in order to obtain a ready to use numerical method, the use of a suitable quadrature rule is mandatory.
Since we shall deal with polynomial paths , it is natural to look for an interpolatory quadrature rule defined by the abscissae and weights , . In order to maximize the order of the quadrature, i.e., , we place the abscissae at the zeros of the kth shifted and scaled Legendre polynomial (i.e., , ). Such polynomials provide an orthonormal basis for functions in :
with denoting the Kronecker delta. Consequently, (6) becomes
Definition 2.
As is clear, if C is such that the quadrature in (8) is exact, then the method reduces to the line integral method satisfying (5) and (6), exactly conserving the invariant. In the next sections we shall make the above statements more precise and operative.
Line integral methods were at first studied to derive energy-conserving methods for Hamiltonian problems: a coarse idea of the methods can be found in [5,6]; the first instances of such methods were then studied in [7,8,9]; later on, the approach has been refined in [10,11,12,13] and developed in [14,15,16,17,18]. Further generalizations, along several directions, have been considered in [19,20,21,22,23,24,25,26,27,28]: in particular, in [19] Hamiltonian boundary value problems have been considered, which are not covered in this review. The main reference on line integral methods is given by the monograph [1].
With these premises, the paper is organized as follows: in Section 2 we shall deal with the numerical solution of Hamiltonian problems; Poisson problems are then considered in Section 3; constrained Hamiltonian problems are studied in Section 4; Hamiltonian partial differential equations (PDEs) are considered in Section 5; highly oscillatory problems are briefly discussed in Section 6; at last, Section 7 contains some concluding remarks.
2. Hamiltonian Problems
A canonical Hamiltonian problem is in the form
with H the Hamiltonian function and, in general, hereafter denoting the identity matrix of dimension r. Because of the skew-symmetry of J, one readily verifies that H is a constant of motion for (9):
For isolated mechanical systems, H has the physical meaning of the total energy, so that it is often referred to as the energy. When solving (9) numerically, it is quite clear that this conservation property becomes paramount to get a correct simulation of the underlying phenomenon. The first successful approach in the numerical solution of Hamiltonian problems has been the use of symplectic integrators. The characterization of a symplectic Runge-Kutta method
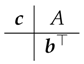 is based on the following algebraic property of its Butcher tableau [29,30] (see also [31])
which is tantamount to the conservation of any quadratic invariant of the continuous problem.
is based on the following algebraic property of its Butcher tableau [29,30] (see also [31])
which is tantamount to the conservation of any quadratic invariant of the continuous problem.
Under appropriate assumptions, symplectic integrators provide a bounded Hamiltonian error over long time intervals [2], whereas generic numerical methods usually exhibit a drift in the numerical Hamiltonian. Alternatively, one can look for energy conserving methods (see, e.g., [32,33,34,35,36,37,38,39]). We here sketch the line integral solution to the problem. According to (5) and (6) with , let us set
where the coefficients are at the moment unknown. Integrating term by term, and imposing the initial condition, yields the following polynomial of degree s:
By defining the approximation to as
where we have taken into account the orthonormality conditions (7), so that , one then obtains that the conditions (5) are fulfilled. In order to fulfil also (6) with , one then requires, by taking into account (11)
This latter equation is evidently satisfied, due to the skew-symmetry of J, by setting
Consequently, (12) becomes
which, according to ([12], Definition 1), is the master functional equation defining . Consequently, the conservation of the Hamiltonian is assured. Next, we discuss the order of accuracy of the obtained approximation, namely the difference : this will be done in the next section, by using the approach defined in [18].
2.1. Local Fourier Expansion
By introducing the notation
one has that (9) can be written, on the interval , as
with defined according to (16), by formally replacing with y. Similarly,
with the polynomial in (15) satisfying, by virtue of (11) and (14), the differential equation:
The following result can be proved (see [18], Lemma 1).
Lemma 1.
Let , with V a vector space, admit a Taylor expansion at 0. Then, for all
Moreover, let us denote by the solution of the ODE-IVPs
and by the fundamental matrix solution of the variational problem associated to it. We recall that
We are now in the position to prove the result concerning the accuracy of the approximation (13).
Theorem 1.
(in other words, the polynomial σ defines an approximation procedure of order 2s).
2.2. Hamiltonian Boundary Value Methods
Quoting Dahlquist and Björk [40], p. 521, as is well known, even many relatively simple integrals cannot be expressed in finite terms of elementary functions, and thus must be evaluated by numerical methods. In our framework, this obvious statement means that, in order to obtain a numerical method from (15), we need to approximate the integrals appearing in that formula by means of a suitable quadrature procedure. In particular, as anticipated above, we shall use the Gauss-Legendre quadrature of order , whose abscissae and weights will be denoted by (i.e., , ). Hereafter, we shall obviously assume . In so doing, in place of (15), one obtains a (possibly different) polynomial,
where (see (16)):
with the quadrature error. Considering that the quadrature is exact for polynomial integrands of degree , one has:
As a consequence, if H is a polynomial of degree . In such a case, , i.e., the energy is exactly conserved. Differently, one has, by virtue of (22) and Lemma 1:
The result of Theorem 1 continues to hold for u. In fact, by using arguments similar to those used in the proof of that theorem, one has, by taking into account (22) and that :
Definition 3.
The polynomial u defined at (21) defines a Hamiltonian Boundary Value Method (HBVM) with parameters k and s, in short HBVM.
Actually, by observing that in (21) only the values of u at the abscissae are needed, one obtains, by setting , and rearranging the terms:
with the new approximation given by
Consequently, we are speaking about the k-stage Runge-Kutta method with Butcher tableau given by:
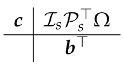 with
and
with
and
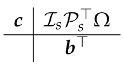
The next result summarizes the properties of HBVMs sketched above, where we also take into account that the abscissae are symmetrically distributed in the interval [0, 1] (we refer to [1,18] for full details).
Theorem 2.
For all , a HBVM method:
- is symmetric and ;
- when it becomes the s-stage Gauss collocation Runge-Kutta method;
- it is energy conserving when the Hamiltonian H is a polynomial of degree not larger than ;
- conversely, one has .
We conclude this section by showing that, for HBVM, whichever is the value considered, the discrete problem to be solved has dimension s, independently of k. This fact is of paramount importance, in view of the use of relatively large values of k, which are needed, in order to gain a (at least practical) energy conservation. In fact, even for non polynomial Hamiltonians, one obtains a practical energy conservation, once the Hamiltonian error falls, by choosing k large enough, within the round-off error level.
By taking into account the stage Equation (24), and considering that , one has that the stage vector can be written as
where
and
is the block vector (of dimension s) with the coefficients (22) of the polynomial u in (21). By combining (29) and (31), one then obtains the discrete problem, equivalent to (24),
having (block) dimension s, independently of k. Once this has been solved, one verifies that the new approximation (25) turns out to be given by (compare also with (13)):
Next section will concern the efficient numerical solution of the discrete problem
generated by the application of a HBVM method. In fact, a straightforward fixed-point iteration,
may impose severe stepsize limitations. On the other hand, the application of the simplified Newton iteration for solving (34) reads, by considering that (see (27) and (28))
and setting the Jacobian of f evaluated at :
This latter iteration, in turn, needs to factor a matrix whose size is s times larger than that of the continuous problem. This can represent an issue, when large-size problems are to be solved and/or large values of s are considered.
2.3. Blended Implementation of HBVMs
We here sketch the main facts concerning the so called blended implementation of HBVMs, a Newton-like iteration alternative to (36), which only requires to factor a matrix having the same size as that of the continuous problem, thus resulting into a much more efficient implementation of the methods [1,16]. This technique derives from the definition of blended implicit methods, which have been at first considered in [41,42], and then developed in [43,44,45]. Suitable blended implicit methods have been implemented in the Fortran codes BIM [46], solving stiff ODE-IVPs, and BIMD [47], also solving linearly implicit DAEs up to index 3. The latter code is also available on the Test Set for IVP Solvers [48] (see also [49]), and turns out to be among the most reliable and efficient codes currently available for solving stiff ODE-IVPs and linearly implicit DAEs. It is worth mentioning that, more recently, the blended implementation of RKN-type methods has been also considered [50].
Let us then consider the iteration (36), which requires the solution of linear systems in the form
By observing that matrix defined at (35) is nonsingular, we can consider the equivalent linear system
where is a positive parameter to be determined. For this purpose, let
be the Jordan canonical form of . For simplicity, we shall assume that is diagonal, and let be any of its diagonal entries. Consequently, the two linear systems (37) and (38), projected in the invariant subspace corresponding to that entry, respectively become
again being equivalent to each other (i.e., having the same solution ). We observe that the coefficient matrix of the former system is , when , whereas that of the latter one is , when . Consequently, one would like to solve the former system, when , and the latter one, when . This can be done automatically by considering a weighting function such that
then considering the blending of the two equivalent systems (39) with weights and , respectively:
In particular, (40) can be accomplished by choosing
Consequently, one obtains that
As a result, one can consider the following splitting for solving the problem:
The choice of the scalar parameter is then made in order to optimize the convergence properties of the corresponding iteration. According to the analysis in [42], we consider
where, as is usual, denotes the spectrum of matrix . A few values of are listed in Table 1.

Table 1.
A few values of the parameter defined at (43).
Coming back to the original iteration (36), one has that the weighting function (42) now becomes
which requires to factor only the matrix
having the same size as that of the continuous problem, thus obtaining the following blended iteration for HBVMs:
It is worth mentioning that:
- in the special case of separable Hamiltonian problems, the blended implementation of the methods can be made even more efficient, since the discrete problem can be cast in terms of the generalized coordinates only (see [16] or ([1], Chapter 4));
- the coding of the blended iteration becomes very high-performance by considering a matrix formulation of (45) (see, e.g., ([1], Chapter 4.2.2) or [51]). As matter of fact, it has been actually implemented in the Matlab code hbvm, which is freely available on the internet at the url [52].
In order to give evidence of the usefulness of energy conservation, let us consider the solution of the well-known pendulum problem, with Hamiltonian
When considering the trajectory starting at [1,53]
one obtains a periodic solution of period . In Table 2 we list the obtained results when solving the problem over 10 periods, by using a stepsize , with HBVM(6,3) and HBVM(3,3) (i.e., the symplectic 3-stage Gauss collocation method), for increasing values of n. As one may see, even though both methods are 6th order accurate, nevertheless, HBVM(6,3) becomes (practically) energy-conserving as soon as , whereas HBVM(3,3) does not. One clearly sees that, for the problem at hand, the energy-conserving method is pretty more accurate than the non conserving one.
2.4. Energy and QUadratic Invariants Preserving (EQUIP) Methods
According to Theorem 2, when , HBVM reduces to the s-stage Gauss method. For such a method, one has, with reference to (26)–(28) and (35) with ,
so that the Butcher matrix in (26) becomes the W-transformation [54] of the s-stage Gauss method, i.e., the Butcher matrix is . Moreover, since , the method is easily verified to be symplectic, because of (10). In fact, by setting in general the ith unit vector, and with reference to the vector defined in (30) with , one has:
We would arrive at the very same conclusion if we replace by
In particular, if the parameter is small enough, matrix will act as a perturbation of the underlying Gauss formula and the question is whether it is possible to choose , at each integration step, such that the resulting integrator may be energy conserving. In order for , we need to assume, hereafter, . In particular, by choosing
it is possible to show [26] that the scalar parameter can be chosen, at each integration step, such that, when solving the Hamiltonian problem (9) with a sufficiently small stepsize h:
- ,
- the method retains the order of the original s-stage Gauss method,
- .
This fact is theoretically intriguing, since this means that we have a kind of state-dependent Runge-Kutta method, defined by the Butcher tableau
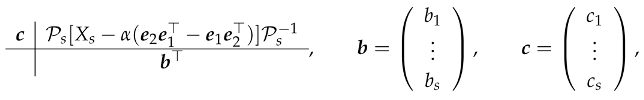 which is energy conserving and is defined, at each integration step, by a symplectic map, given by a small perturbation of that of the underlying s-stage Gauss method. Consequently, EQUIP methods do not infringe the well-known result about the nonexistence of energy conserving symplectic numerical methods [55,56]. Since the symplecticity condition (10) is equivalent to the conservation of all quadratic invariants of the problem, these methods have been named Energy and QUadratic Invariants Preserving (EQUIP) methods [26,57]. It would be interesting to study the extent to which the solutions generated by an EQUIP method inherit the good long time behavior of the associated Gauss integrator with reference to the nearly conservation property of further non-quadratic first integrals. This investigation would likely involve a backward error analysis approach, similar to that done in [2], and up to now remains an open question.
which is energy conserving and is defined, at each integration step, by a symplectic map, given by a small perturbation of that of the underlying s-stage Gauss method. Consequently, EQUIP methods do not infringe the well-known result about the nonexistence of energy conserving symplectic numerical methods [55,56]. Since the symplecticity condition (10) is equivalent to the conservation of all quadratic invariants of the problem, these methods have been named Energy and QUadratic Invariants Preserving (EQUIP) methods [26,57]. It would be interesting to study the extent to which the solutions generated by an EQUIP method inherit the good long time behavior of the associated Gauss integrator with reference to the nearly conservation property of further non-quadratic first integrals. This investigation would likely involve a backward error analysis approach, similar to that done in [2], and up to now remains an open question.
For a thorough analysis of such methods we refer to [26,53]. In the next section, we sketch their line-integral implementation when solving Poisson problems, a wider class than that of Hamiltonian problems.
3. Poisson Problems
Poisson problems are in the form
When as defined in (9), then one retrieves canonical Hamiltonian problems. As in that case, since is skew-symmetric, then H, still referred to as the Hamiltonian, is conserved:
Moreover, any scalar function such that is also conserved, since:
C is called a Casimir function for (50). Consequently, all possible Casimirs and the Hamiltonian H are conserved quantities for (50). In the sequel, we show that EQUIP methods can be conveniently used for solving such problems. As before, the scalar parameter in (49) is selected in such a way that the Hamiltonian H is conserved. Moreover, since the Butcher matrix in (49) satisfies (10), then all quadratic Casimirs turn out to be conserved as well. The conservation of all quadratic invariants, in turn, is an important property as it has been observed in [58].
Let us then sketch the choice of the parameter to gain energy conservation (we refer to [53] for full details). By setting
one has that the Butcher matrix in (49) can be written as
Consequently, by denoting , and setting , , the stages of the method, one obtains that the polynomial is given by
with the (block) vectors formally defined as in (22) with . In vector form, one has then (compare with (31)):
We observe that, from (51), one also obtains:
Nevertheless, the new approximation, still given by
now differs from
Consequently, in order to define a path joining to , to be used for imposing energy-conservation by zeroing a corresponding line-integral, we can consider the polynomial path made up by u plus
In more details, by defining the vectors
and resorting to the usual line integral argument, it is possible to prove the following result ([53], Theorem 2).
Theorem 3.
(57) holds true, provided that
As in the case of HBVMs, however, we shall obtain a practical numerical method only provided that the integrals in (58) are suitably approximated by means of a quadrature which, as usual, we shall choose as the Gauss-Legendre formula of order . In so doing, one obtains an EQUIP method. The following result can be proved ([53], Theorem 8).
Theorem 4.
Under suitable regularity assumptions on both and , one has that for all , the EQUIP method has order , conserves all quadratic invariants and, moreover,
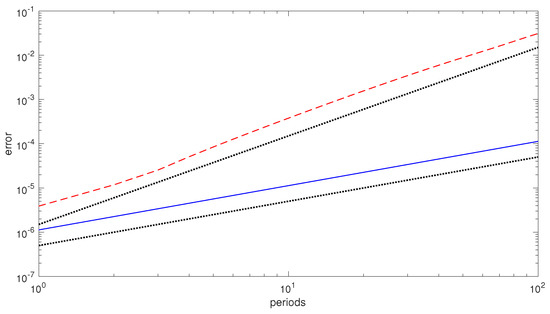
We observe that, for EQUIP, even a not exact conservation of the energy may result in a much better error growth, as the next example shows. We consider the Lotka-Volterra problem [53], which is in the form (50) with
By choosing the following parameters and initial values,
one obtains a periodic solution of period . If we solve the problems (60) and (61) with the EQUIP(6,3) and the 3-stage Gauss methods with stepsize over 100 periods, we obtain the error growths, in the numerical solution, depicted in Figure 1. As one may see, the EQUIP(6,3) method (which only approximately conserves the Hamiltonian), exhibits a linear error growth; on the contrary, the 3-stage Gauss method (which exhibits a drift in the numerical Hamiltonian) has a quadratic error growth. Consequently, there is numerical evidence that EQUIP methods can be conveniently used for numerically solving Poisson problems (a further example can be found in [53]).
4. Constrained Hamiltonian Problems
In this section, we report about some recent achievements concerning the line integral solution of constrained Hamiltonian problems with holonomic contraints [23]. This research is at a very early stage and, therefore, it is foreseeable that new results will follow in the future.
To begin with, let us consider the separable problem defined by the Hamiltonian
with M a symmetric and positive definite matrix, subject to the holonomic constraints
We shall assume that the points are regular for the constraints, so that has full column rank and, therefore, the matrix is nonsingular. By introducing the vector of the Lagrange multipliers , problems (62) and (63) can be equivalently cast in Hamiltonian form by defining the augmented Hamiltonian
thus obtaining the equivalent constrained problem:
subject to the initial conditions
We observe that the first requirement () obviously derives from the given constraints. The second, in turn, derives from
which has to be satisfied by the solution of (65). These latter constraints are sometimes referred to as the hidden constraints. A formal expression of the vector of the Lagrange multipliers can be obtained by further differentiating the previous expression, thus giving
which is well defined, because of the assumption that is nonsingular. Consequently,
where the notation means that the vector is a function of q and p. It is easily seen that both the two Hamiltonians (62) and (64) are conserved along the solution of the problems (65) and (66), and assume the same value. For numerically solving the problem, we shall consider a discrete mesh with time-step h, i.e., , , looking for approximations
such that, starting from , one arrives at by choosing in order for:
Consequently, the new approximation conserves the Hamiltonan and exactly satisfies the constraints, but only approximately the hidden contraints. In particular, we shall consider a piecewise constant approximation of the vector of the Lagrange multipliers , i.e., is assumed to be constant on the interval . In other words, we consider the sequence of problems (compare with (65)), for :
where the constant vector is chosen in order to satisfy the constraints at . That is, such that the new approximations, defined as
satisfy (68). The reason for choosing as a constant vector stems from the following result, which concerns the augmented Hamiltonian (64).
Proof.
In fact, denoting by the gradient of with respect to the q variables, and similarly for , the usual line integral argument provides:
☐
Consequently, one obtains that
i.e., energy conservation is equivalent to satisfy the constraints.
In order to fulfil the constraints, we shall again resort to a line integral argument. For this purpose, we need to define the Fourier coefficients (along the Legendre basis (7)) of the functions appearing at the right-hand sides in (69):
so that, in particular,
We also need the following result.
Lemma 2.
With reference to matrix defined in (35), one has, for all :
Proof.
See, e.g., ([23], Lemma 2). ☐
We are now in the position of deriving a formal expression for the constant approximation to the vector of the Lagrange multipliers through the usual line integral approach:
Because of Lemma 2, one then obtains that (see (35)),
The following result can be proved [23].
Theorem 6.
The Equation (73) is consistent with (67) and is well defined for all sufficiently small . The sequence generated by (69)–(73) satisfies, for all :
Moreover, in the case where , for all , then , , .
At this point, in order to obtain a numerical method, the following two steps need to be done:
- approximate the integrals in (71), for . As usual, we shall consider a Gauss-Legendre formula of order , with , thus obtaining corresponding approximations which we denote, for ,
In so doing, it can be seen that one retrieves the usual HBVM method defined in Section 2, applied for solving (69), coupled with the following equation for , representing the approximation of (73):
The following result can be proved [23].
Theorem 7.
For all sufficiently small stepsizes h, the HBVM method coupled with (74), used for solving (65) and (66) over a finite interval, is well defined and symmetric. It provides a sequence of approximations such that (see (67)):
Moreover, in the case where , for all , then
It is worth mentioning that, even in the case where the vector of the Lagrange multipliers is not constant, so that all HBVM are second-order accurate for all , the choice generally provides a much smaller solution error.
We refer to [23] for a number of examples of application of HBVMs to constrained Hamiltonian problems. We here only provide the application of HBVM(4,4) (together with (74) with ) for solving the so called conical pendulum problem. In more details, let us have a pendulum of unit mass connected to a fixed point (the origin) by a massless rod of unit length. The initial conditions are such that the motion is periodic of period T and takes place in the horizontal plane . Normalizing the acceleration of gravity, the augmented Hamiltonian is given by
where and is the ith unit vector. Choosing , , results in
Since the augmented Hamiltonian is quadratic and is constant, any HBVM method, coupled with (74), is energy and constraint conserving, and of order . If we apply the HBVM(4,4) method for solving the problem over 10 periods by using the stepsize , , it turns out the , , , and within the round-off error level, for all . On the other hand, the corresponding solution errors, after 10 periods, turn out to be given by 4.9944 × 10, 1.9676 × 10, 7.3944 × 10, thus confirming the order 8 of convergence of the resulting method.
5. Hamiltonian PDEs
Quoting [4], p. 187, the numerical solution of time dependent PDEs may often be conceived as consisting of two parts. First the spatial derivatives are discretized by finite differences, finite elements, spectral methods, etc. to obtain a system of ODEs, with t as the independent variable. Then this system of ODEs is integrated numerically. If the PDEs are of Hamiltonian type, one may insist that both stages preserve the Hamiltonian structure. Thus the space discretization should be carried out in such a way that the resulting system of ODEs is Hamiltonian (for a suitable Poisson bracket). This approach has been systematically used for solving a number of Hamiltonian PDEs by using HBVMs [1,20,22,59,60] and this research is still under development. We here sketch te main facts for the simplest possible example, provided by the semilinear wave equation,
with the derivative of f, coupled with the initial conditions
and periodic boundary conditions. We shall assume that f, , are regular enough (the last two functions, as periodic functions). By setting (hereafter, when not necessary, we shall avoid the arguments of the functions)
so that , , the problem can be cast into Hamiltonian form as
i.e.,
where is the vector of the functional derivatives [2,3,22] of the Hamiltonian functional
Because of the periodic boundary conditions, this latter functional turns out to be conserved. In fact, by considering that
one obtains:
because of the periodicity in space. Consequently,
Moreover, since is periodic for , we can expand it in space along the following slight variant of the Fourier basis,
so that, for all allowed :
In so doing, for suitable time dependent coefficients , one obtains the expansion:
having introduced the infinite vectors
By considering that
the identity operator, and introducing the infinite matrix (see (77))
so that and , one then obtains that (79) can be rewritten as the infinite system of ODEs:
subject to the initial conditions (see (76))
The following result is readily established.
Theorem 8.
Problem (87) is Hamiltonian, with Hamiltonian
Proof.
The first part of the proof is straightforward. Concerning the second part, one has, by virtue of (85):
Similarly, by considering that , one obtains:
☐
In order to obtain a computational procedure, one needs to truncate the infinite series in (83) to a finite sum, i.e.,
Clearly, such an approximation no longer satisfies the wave Equation (79). Nevertheless, in the spirit of Fourier–Galerkin methods [61], by requiring that the residual be orthogonal to the functional subspace
containing the approximation for all times , one obtains a finite dimensional ODE system, formally still given by (87) and (88), upon replacing the involved infinite vectors and matrices, previously defined in (84) and (86), with the following finite dimensional ones (of dimension ):
Moreover, the result of Theorem 8 continues formally to hold for the finite dimensional problem, with the sole exception that now the Hamiltonian (89) only yields an approximation to the continuous functional (80). Nevertheless, it is well known that, under suitable regularity assumptions on f and the initial data, this truncated version converges exponentially to the original functional (80), as (this phenomenon is usually referred to as spectral accuracy). Since problem (87) is Hamiltonian, one can use HBVM methods for solving it. It is worth mentioning that, in so doing, the blended implementation of the methods can be made extremely efficient, by considering that:
- an accurate approximation in space usually requires the use of large values of N;
- as a consequence, in most cases one hasin a suitable neighbourhood of the solution.
Consequently, the Jacobian matrix of (87) can be approximated by the linear part alone, i.e., as
This implies that matrix involved in the definition of in (44) becomes (all the involved matrices are diagonal and have dimension ):
where is the parameter defined in (43), and h is the used time-step. As a result, :
- is constant for all time steps, so that it has to be computed only once;
- it has a block diagonal structure (and, in particular, is positive definite).
The above features make the resulting blended iteration (45) inexpensive, thus allowing the use of large values of N and large time-steps h. As an example, let us solve the sine-Gordon equation [22],
with , whose solution is, by considering the value ,
In such a case, the value in (90) and (91) is sufficient to obtain an error in the spatial semi-discretization comparable with the round-off error level. Then, we solve in time the semi-discrete problem (87), of dimension , by using the HBVM methods. In Table 3 we list the obtained maximum errors in the computed solution, by using a time-step , along with the corresponding Hamiltonian errors and execution times, for various choices of (in particular, for , , we have the s-stage Gauss collocation methods, which are symplectic but not energy conserving) (all numerical tests have been performed on a laptop with a 2.2 GHz dual core i7 processor, 8 GB of memory, and running Matlab R2017b). From the listed results, one sees that HBVM methods become energy-conserving for and the error decreases until the round-off error level, for , with a computational time 10 times larger than that of the implicit mid-point rule (obtained for ) which, however, has a solution error times larger.
6. Highly Oscillatory Problems
The Hamiltonian system of ODEs (87) is a particular instance of problems in the form
where, without loss of generality, A is a symmetric and positive definite matrix and f is a scalar function such that
in a neighbourhood of the solution. Moreover, hereafter we consider the 2-norm, so that equals the largest eigenvalue of A (in general, any convenient upper bound would suffice). The problem is Hamiltonian, with Hamiltonian
Problems in the form (94) satisfying (95) are named (multi-frequency) highly oscillatory problems, since they are ruled by the linear part, possessing large (possibly different) complex conjugate eigenvalues. Such problems have been investigated since many years, starting from the seminal papers [62,63], and we refer to the monograph [64] for more recent findings. A common feature of the methods proposed so far, however, is that of requiring the use of time-steps h such that , either for stability and/or accuracy requirements. We here sketch the approach recently defined in [27], relying on the use of HBVMs, which will allow the use of stepsizes h without such a restriction.
To begin with, and for analysis purposes, let us recast problem (94) in first order form, by setting , as
with the skew-symmetric matrix defined in (77). As is usual in this context, one considers at first the linear part of (97),
The solution of (98), , on the interval is readily seen to be given, according to the local Fourier expansion described in Section 2.1, by:
However, when using a finite precision arithmetic with machine epsilon u, the best we can do is to approximate
where hereafter ≐ means “equal within round-off error level”, provided that
In fact, further terms in the infinite series in (99) would provide a negligible contribution, in the used finite precision arithmetic. By defining the function
with the Bessel functions of the first kind, it can be shown ([27], Criterion 1) that the requirement (101) is accomplished by requiring
In so doing, one implicitly defines a function , depending on the machine epsilon u, such that
The plot of such a function is depicted in Figure 2 for the double precision IEEE: as one may see, the function is well approximated by the line [27]
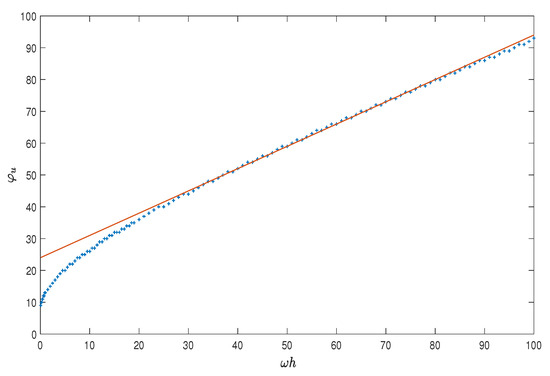
As observed before, when using a finite precision arithmetic with machine epsilon u, the best we can do is to approximate (106) with a polynomial:
provided that
Assuming the ansatz , for a suitable (essentially, one requires that is well approximated by a polynomial of degree ), the requirement (109) is accomplished by choosing ([27], Criterion 2)
where is the same function considered in (104). By taking into account that and that is an increasing funcion (see Figure 2), one then obtains that .
Next, one has to approximate the Fourier coefficients (see (107)) , , needed in (108): for this purpose, we consider the Gauss-Legendre quadrature formula of order . In order to gain full machine accuracy, when using the double precision IEEE, according to [27], we choose
In so doing, we arrive to a HBVM method. For such a method, the blended iteration (45) can be made extremely efficient by approximating the Jacobian of (97) with its linear part (this has been already done when solving Hamiltonian PDEs, see (92)), so that the matrix in (44) has to be computed only once. Moreover, since we are going to use relatively large stepsizes h, the initial guess for the vector in (45) is chosen, by considering the polynomial defined in (100) derived from the linear problem (98), as:
The name spectral HBVM with parameters has been coined in [27] to denote the resulting method, in short SHBVM. In order to show its effectiveness, we report here some numerical results obtained by solving the Duffing equation
with Hamiltonian
and exact solution
Here, is the elliptic Jacobi function, with elliptic modulus specified by the second argument. In particular, we choose the values
providing a problem in the form (94) to (95), with a corresponding Hamiltonian value . For solving it, we shall use the SHBVM method with parameters:
and a time-step , for various values of N, as specified in Table 4. In that table we also list the corresponding:

- maximum absolute error in the computed solution, ;
- the maximum relative error in the numerical Hamiltonian, ;
- the value of (which is always much greater than 1);
- the execution time (in sec).
As before, the numerical tests have been performed on a laptop with a 2.2 GHz dual core i7 processor, 8 GB of memory, and running Matlab R2017b.
As one may see, the method is always energy conserving and the error, as expected, is uniformly small. Also the execution times are all very small (of the order of 3.5 s). It must be emphasized that classical methods, such as the Gautschi or the Deuflhard method, would require the use of much smaller time-steps, and much larger execution times (we refer to [27] for some comparisons).
7. Conclusions
In this paper, we have reviewed the main facts concerning the numerical solution of conservative problems within the framework of (discrete) line integral methods. Relevant instances of line integral methods are provided by the energy-conserving Runge-Kutta methods named Hamiltonian Boundary Value Methods (HBVMs) and the Energy and QUadratic Invariants Preserving (EQUIP) methods, providing efficient geometric integrators for Hamiltonian problems. It is worth mentioning that HBVMs can be easily adapted to efficiently handle Hamiltonian BVPs [19], whereas EQUIP methods can be also used for numerically solving Poisson problems. In this paper, we have also reviewed some active research trends, concerning the application of HBVMs for numerically solving constrained Hamiltonian problems, Hamiltonian PDEs, and highly-oscillatory problems. The effectiveness of HBVMs is emphasized by the availability of an efficient nonlinear iteration for solving the generated discrete problems, relying on the so called blended implementation of the methods. Matlab software implementing HBVMs for Hamiltonian problems is available at the url [52].
Acknowledgments
The authors wish to thank Gianmarco Gurioli, Gianluca Frasca Caccia, Cecilia Magherini, and the three anonymous reviewers, for carefully reading the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brugnano, L.; Iavernaro, F. Line Integral Methods for Conservative Problems; Chapman et Hall/CRC: Boca Raton, FL, USA, 2016. [Google Scholar]
- Hairer, E.; Lubich, C.; Wanner, G. Geometric Numerical Integration, 2nd ed.; Springer: Berlin, Germany, 2006. [Google Scholar]
- Leimkuhler, B.; Reich, S. Simulating Hamiltonian Dynamics; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Sanz-Serna, J.M.; Calvo, M.P. Numerical Hamiltonian Problems; Chapman & Hall: London, UK, 1994. [Google Scholar]
- Iavernaro, F.; Trigiante, D. On some conservation properties of the trapezoidal method applied to Hamiltonian systems. In Proceedings of the International Conference on Numerical Analysis and Applied Mathematics (ICNAAM), Rhodes, Greece, Germany, 16–20 September 2005; Simos, T.E., Psihoyios, G., Tsitouras, Ch., Eds.; Wiley-Vch Verlag GmbH & Co.: Weinheim, Germany, 2005; pp. 254–257. [Google Scholar]
- Iavernaro, F.; Trigiante, D. Discrete Conservative Vector Fields Induced by the Trapezoidal Method. JNAIAM J. Numer. Anal. Ind. Appl. Math. 2006, 1, 113–130. [Google Scholar]
- Iavernaro, F.; Pace, B. s-stage trapezoidal methods for the conservation of Hamiltonian functions of polynomial type. AIP Conf. Proc. 2007, 936, 603–606. [Google Scholar]
- Iavernaro, F.; Pace, B. Conservative block-Boundary Value Methods for the solution of polynomial Hamiltonian systems. AIP Conf. Proc. 2008, 1048, 888–891. [Google Scholar]
- Iavernaro, F.; Trigiante, D. High-order Symmetric Schemes for the Energy Conservation of Polynomial Hamiltonian Problems. JNAIAM J. Numer. Anal. Ind. Appl. Math. 2009, 4, 87–101. [Google Scholar]
- Brugnano, L.; Iavernaro, F.; Susca, T. Numerical comparisons between Gauss-Legendre methods and Hamiltonian BVMs defined over Gauss points. Monogr. Real Acad. Cienc. Zaragoza 2010, 33, 95–112. [Google Scholar]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. Hamiltonian BVMs (HBVMs): A family of “drift-free” methods for integrating polynomial Hamiltonian systems. AIP Conf. Proc. 2009, 1168, 715–718. [Google Scholar]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. Hamiltonian Boundary Value Methods (Energy Preserving Discrete Line Integral Methods). JNAIAM J. Numer. Anal. Ind. Appl. Math. 2010, 5, 17–37. [Google Scholar]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. Analisys of Hamiltonian Boundary Value Methods (HBVMs): A class of energy-preserving Runge-Kutta methods for the numerical solution of polynomial Hamiltonian systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 20, 650–667. [Google Scholar] [CrossRef]
- Brugnano, L.; Frasca Caccia, G.; Iavernaro, F. Efficient implementation of Gauss collocation and Hamiltonian Boundary Value Methods. Numer. Algorithms 2014, 65, 633–650. [Google Scholar] [CrossRef]
- Brugnano, L.; Frasca Caccia, G.; Iavernaro, F. Hamiltonian Boundary Value Methods (HBVMs) and their efficient implementation. Math. Eng. Sci. Aerosp. 2014, 5, 343–411. [Google Scholar]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. A note on the efficient implementation of Hamiltonian BVMs. J. Comput. Appl. Math. 2011, 236, 375–383. [Google Scholar] [CrossRef]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. The lack of continuity and the role of Infinite and infinitesimal in numerical methods for ODEs: The case of symplecticity. Appl. Math. Comput. 2012, 218, 8053–8063. [Google Scholar] [CrossRef]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. A simple framework for the derivation and analysis of effective one-step methods for ODEs. Appl. Math. Comput. 2012, 218, 8475–8485. [Google Scholar] [CrossRef]
- Amodio, P.; Brugnano, L.; Iavernaro, F. Energy-conserving methods for Hamiltonian Boundary Value Problems and applications in astrodynamics. Adv. Comput. Math. 2015, 41, 881–905. [Google Scholar] [CrossRef]
- Barletti, L.; Brugnano, L.; Frasca Caccia, G.; Iavernaro, F. Energy-conserving methods for the nonlinear Schrödinger equation. Appl. Math. Comput. 2018, 318, 3–18. [Google Scholar] [CrossRef]
- Brugnano, L.; Calvo, M.; Montijano, J.I.; Ràndez, L. Energy preserving methods for Poisson systems. J. Comput. Appl. Math. 2012, 236, 3890–3904. [Google Scholar] [CrossRef]
- Brugnano, L.; Frasca Caccia, G.; Iavernaro, F. Energy conservation issues in the numerical solution of the semilinear wave equation. Appl. Math. Comput. 2015, 270, 842–870. [Google Scholar] [CrossRef]
- Brugnano, L.; Gurioli, G.; Iavernaro, F.; Weinmüller, E.B. Line integral solution of Hamiltonian systems with holonomic constraints. Appl. Numer. Math. 2018, 127, 56–77. [Google Scholar] [CrossRef]
- Brugnano, L.; Iavernaro, F. Line Integral Methods which preserve all invariants of conservative problems. J. Comput. Appl. Math. 2012, 236, 3905–3919. [Google Scholar] [CrossRef]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. A two-step, fourth-order method with energy preserving properties. Comput. Phys. Commun. 2012, 183, 1860–1868. [Google Scholar] [CrossRef]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. Energy and QUadratic Invariants Preserving integrators based upon Gauss collocation formulae. SIAM J. Numer. Anal. 2012, 50, 2897–2916. [Google Scholar] [CrossRef]
- Brugnano, L.; Montijano, J.I.; Rández, L. On the effectiveness of spectral methods for the numerical solution of multi-frequency highly-oscillatory Hamiltonian problems. Numer. Algorithms 2018. [Google Scholar] [CrossRef]
- Brugnano, L.; Sun, Y. Multiple invariants conserving Runge-Kutta type methods for Hamiltonian problems. Numer. Algorithms 2014, 65, 611–632. [Google Scholar] [CrossRef]
- Lasagni, F.M. Canonical Runge-Kutta methods. Z. Angew. Math. Phys. 1988, 39, 952–953. [Google Scholar] [CrossRef]
- Sanz-Serna, J.M. Runge-Kutta schemes for Hamiltonian systems. BIT Numer. Math. 1988, 28, 877–883. [Google Scholar] [CrossRef]
- Burrage, K.; Butcher, J.C. Stability criteria for implicit Runge-Kutta methods. SIAM J. Numer. Anal. 1979, 16, 46–57. [Google Scholar] [CrossRef]
- Betsch, P.; Steinmann, P. Inherently Energy Conserving Time Finite Elements for Classical Mechanics. J. Comput. Phys. 2000, 160, 88–116. [Google Scholar] [CrossRef]
- Betsch, P.; Steinmann, P. Conservation properties of a time FE method. I. Time-stepping schemes for N-body problems. Int. J. Numer. Methods Eng. 2000, 49, 599–638. [Google Scholar] [CrossRef]
- Bottasso, C.L. A new look at finite elements in time: A variational interpretation of Runge-Kutta methods. Appl. Numer. Math. 1997, 25, 355–368. [Google Scholar] [CrossRef]
- Celledoni, E.; McLachlan, R.I.; McLaren, D.I.; Owren, B.; Quispel, G.R.W.; Wright, W.M. Energy-preserving Runge-Kutta methods. M2AN Math. Model. Numer. Anal. 2009, 43, 645–649. [Google Scholar] [CrossRef]
- Hairer, E. Energy preserving variant of collocation methods. JNAIAM J. Numer. Anal. Ind. Appl. Math. 2010, 5, 73–84. [Google Scholar]
- McLachlan, R.I.; Quispel, G.R.W.; Robidoux, N. Geometric integration using discrete gradient. Philos. Trans. R. Soc. Lond. A 1999, 357, 1021–1045. [Google Scholar] [CrossRef]
- Quispel, G.R.W.; McLaren, D.I. A new class of energy-preserving numerical integration methods. J. Phys. A Math. Theor. 2008, 41, 045206. [Google Scholar] [CrossRef]
- Tang, Q.; Chen, C.M. Continuous finite element methods for Hamiltonian systems. Appl. Math. Mech. 2007, 28, 1071–1080. [Google Scholar] [CrossRef]
- Dahlquist, G.; Björk, Å. Numerical Methods in Scientific Computing; SIAM: Philadelphia, PA, USA, 2008. [Google Scholar]
- Brugnano, L. Blended Block BVMs (B3VMs): A Family of Economical Implicit Methods for ODEs. J. Comput. Appl. Math. 2000, 116, 41–62. [Google Scholar] [CrossRef]
- Brugnano, L.; Magherini, C. Blended Implementation of Block Implicit Methods for ODEs. Appl. Numer. Math. 2002, 42, 29–45. [Google Scholar] [CrossRef]
- Brugnano, L.; Magherini, C. Blended Implicit Methods for solving ODE and DAE problems, and their extension for second order problems. J. Comput. Appl. Math. 2007, 205, 777–790. [Google Scholar] [CrossRef]
- Brugnano, L.; Magherini, C. Recent advances in linear analysis of convergence for splittings for solving ODE problems. Appl. Numer. Math. 2009, 59, 542–557. [Google Scholar] [CrossRef]
- Brugnano, L.; Magherini, C. Blended General Linear Methods based on Boundary Value Methods in the Generalized BDF family. JNAIAM J. Numer. Anal. Ind. Appl. Math. 2009, 4, 23–40. [Google Scholar]
- Brugnano, L.; Magherini, C. The BiM code for the numerical solution of ODEs. J. Comput. Appl. Math. 2004, 164–165, 145–158. [Google Scholar] [CrossRef]
- Brugnano, L.; Magherini, C.; Mugnai, F. Blended Implicit Methods for the Numerical Solution of DAE Problems. J. Comput. Appl. Math. 2006, 189, 34–50. [Google Scholar] [CrossRef]
- Test Set for IVP Solvers. Available online: https://archimede.dm.uniba.it/ testset/testsetivpsolvers/ (accessed on 4 May 2018).
- The Codes BiM and BiMD Home Page. Available online: http://web.math.unifi.it/users/brugnano/BiM/index.html (accessed on 4 May 2018).
- Wang, B.; Meng, F.; Fang, Y. Efficient implementation of RKN-type Fourier collocation methods for second-order differential equations. Appl. Numer. Math. 2017, 119, 164–178. [Google Scholar] [CrossRef]
- Simoncini, V. Computational methods for linear matrix equations. SIAM Rev. 2016, 58, 377–441. [Google Scholar] [CrossRef]
- Line Integral Methods for Conservative Problems. Available online: http://web.math.unifi.it/users/brugnano/LIMbook/ (accessed on 4 May 2018).
- Brugnano, L.; Gurioli, G.; Iavernaro, F. Analysis of Energy and QUadratic Invariant Preserving (EQUIP) methods. J. Comput. Appl. Math. 2018, 335, 51–73. [Google Scholar] [CrossRef]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II. Stiff and Differential-Algebraic Problems, 2nd ed.; Springer: Berlin, Germany, 1996. [Google Scholar]
- Chartier, P.; Faou, E.; Murua, A. An algebraic approach to invariant preserving integrators: The case of quadratic and Hamiltonian invariants. Numer. Math. 2006, 103, 575–590. [Google Scholar] [CrossRef]
- Ge, Z.; Marsden, J.E. Lie-Poisson Hamilton-Jacobi theory and Lie-Poisson integrators. Phys. Lett. A 1988, 133, 134–139. [Google Scholar]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. Energy and Quadratic Invariants Preserving Integrators of Gaussian Type. AIP Conf. Proc. 2010, 1281, 227–230. [Google Scholar]
- Sanz-Serna, J.M. Symplectic Runge-Kutta schemes for adjoint equations, automatic differentiation, optimal control, and more. SIAM Rev. 2016, 58, 3–33. [Google Scholar] [CrossRef]
- Brugnano, L.; Gurioli, G.; Sun, Y. Energy-conserving Hamiltonian Boundary Value Methods for the numerical solution of the Korteweg-de Vries equation. J. Comput. Appl. Math. 2018, submitted. [Google Scholar]
- Brugnano, L.; Zhang, C.; Li, D. A class of energy-conserving Hamiltonian boundary value methods for nonlinear Schrödinger equation with wave operator. Commun. Nonlinear Sci. Numer. Simul. 2018, 60, 33–49. [Google Scholar] [CrossRef]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods, 2nd ed.; Dover Publications Inc.: Mineola, NY, USA, 2001. [Google Scholar]
- Deuflhard, P. A study of extrapolation methods based on multistep schemes without parasitic solutions. Z. Angew. Math. Phys. 1979, 30, 177–189. [Google Scholar] [CrossRef]
- Gautschi, W. Numerical integration of ordinary differential equations based on trigonometric polynomials. Numer. Math. 1961, 3, 381–397. [Google Scholar] [CrossRef]
- Wu, X.; Wang, B. Recent Developments in Structure-Preserving Algorithms for Oscillatory Differential Equations; Springer: Singapore, 2018. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).