Geometric Characteristics of Specific Classes Associated with q-Janowski Functions

Abstract

In this paper, we integrate the concepts of spiral-like functions and Janowski-type functions within the framework of q-calculus to define new subclasses in the open unit disk. Our primary focus is on analyzing convolution conditions that form the foundation for further theoretical developments. The main contributions include establishing sufficient conditions and applying Robertson’s theorem. Furthermore, motivated by a recent definition, we propose analogous neighborhood concepts for the above-mentioned classes, and we explore the corresponding neighborhood results.

1. Introduction

Geometric function theory is a branch of mathematics that investigates the properties of analytic and harmonic functions in the context of geometric and topological spaces. It encompasses the study of functions of a complex variable and their mappings onto geometric domains, with a focus on understanding the interplay between their algebraic, analytic, and geometric properties. This work examines the space of analytic functions $\mathcal{H}\left(\mathrm{\Delta }\right)$, which refers to the set of all functions analytic within the open unit disk $\mathrm{\Delta }=\left\{\eta \in \mathbb{C}:\left|\eta \right|<1\right\}$. A specific subset of these functions is denoted by $\mathcal{H}$, and an element $h\in \mathcal{H}\left(\mathrm{\Delta }\right)$ can be expressed as

$$h\left(\eta \right)=\eta +\sum _{k=2}^{\infty }{a}_k{\eta }^k.$$

(1)

Next, let $\widehat{\mathcal{S}}$ represent the set of all univalent functions within $\mathrm{\Delta }$ that belong to $\mathcal{H}$. The Hadamard product or convolution of two analytic functions h and g, both from $\mathcal{H}$, is defined as

$$(h\ast g)\left(\eta \right)=\eta +\sum _{k=2}^{\infty }{a}_k{b}_k{\eta }^k,\eta \in \mathrm{\Delta }.$$

For h given by Equation (1) and $g\left(\eta \right)=\eta +{\sum }_{k=2}^{\infty }{b}_k{\eta }^k$, those interested in the Hadamard product and its generalizations should refer to the works in [1].

Before introducing new classes of spiral-like and q-Janowski functions defined within $\mathrm{\Delta }$, it is essential to revisit the fundamental concepts and notations related to Janowski-type functions, $\alpha$-spiral-like functions, and quantum calculus (also referred to as q-calculus). In [2], Janowski introduced the class $\mathcal{P}[\mathcal{A},\mathcal{B}]$, defined for a function $p\in \mathcal{H}$ satisfying $p\left(0\right)=1$. A function p belongs to the class $\mathcal{P}[\mathcal{A},\mathcal{B}]$ if and only if

$$p\left(\eta \right)={\displaystyle \frac{1+\mathcal{A}w\left(\eta \right)}{1+\mathcal{B}w\left(\eta \right)}},$$

where $-1\le \mathcal{B}<\mathcal{A}\le 1$, and $w\left(\eta \right)\in \mathrm{\Omega }$. Here, $\mathrm{\Omega }$ denotes the class of Schwartz functions. defined by

$$\mathrm{\Omega }:=\left\{w\in \mathcal{H}:w\left(0\right)=0,\left|w\right(\eta \left)\right|<1,\eta \in \mathrm{\Delta }\right\}.$$

Janowski functions constitute a fascinating area within geometric function theory, offering a profound exploration of the behavior of analytic functions in the complex plane. These functions, named after the mathematician Janowski, represent a class of analytic functions defined within a specific domain of the complex plane, often the open unit disk. The function h is called $\alpha$-spiral-like if the real part of $\left\{e^{i\alpha }{\displaystyle \frac{\eta h^{\prime }\left(\eta \right)}{h\left(\eta \right)}}\right\}$ is positive, where $\alpha$ is a real number such that $\left|\alpha \right|<{\displaystyle \frac{\pi }{2}}$.

One area where q-calculus finds significant application is in the study of q-analytic functions. Understanding the properties of q-analytic functions provides insights into the geometry and topology of complex domains under q-deformation. In [3], Jackson introduced and studied the concept of the q-derivative operator, denoted by ${\partial }_{q}h\left(\eta \right)$, where $q\in (0,1)$. This operator is defined as follows:

$${\partial }_{q}h\left(\zeta \right)=\left\{\begin{array}{cc}{\displaystyle \frac{h\left(\eta \right)-h\left(q\eta \right)}{\eta (1-q)}},\hfill & \eta \ne 0,\\ h^{\prime }\left(0\right),\hfill & \eta =0.\end{array}\right.$$

(2)

Alternatively, as depicted in Equation (2), it takes the form

$${\partial }_{q}h\left(\eta \right)=1+\sum _{k=2}^{\infty }{\left[k\right]}_q{a}_k{\eta }^{k-1}\eta \ne 0,$$

where

$${\left[k\right]}_q={\displaystyle \frac{1-q^k}{1-q}}=1+q+...+q^{k-1}.$$

(3)

It is important to note that as $q\to 1^{-}$, ${\left[k\right]}_q$ approaches k. For the function $h\left(\eta \right)={\eta }^k$, we can observe that

$${\partial }_{q}h\left(\eta \right)={\partial }_q\left({\eta }^k\right)={\displaystyle \frac{1-q^k}{1-q}}{\eta }^{k-1}={\left[k\right]}_q{\eta }^{k-1}.$$

Then

$$\underset{q\to 1^{-}}{lim}{\partial }_{q}h\left(\eta \right)=\underset{q\to 1^{-}}{lim}{\left[k\right]}_q{\eta }^{k-1}=k{\eta }^{k-1}=h^{\prime }\left(\eta \right),$$

where $h^{\prime }\left(\eta \right)$ is the ordinary derivative.

The q-integral of a function h, introduced by Jackson [4], is defined as the right inverse of the q-derivative, under the assumption that

$${\int }_0^{\eta }h\left(\phi \right)d_q\phi =\eta (1-q)\sum _{k=0}^{\infty }{q}^{k}h\left(\eta q^k\right),$$

provided that the series ${\sum }_{k=0}^{\infty }{q}^{k}h\left(\eta q^k\right)$ converges.

The interconnection between the quantum calculus and geometric function theory arises from their shared investigation into analytic functions within complex domains, offering new perspectives on their behavior, properties, and applications. The initial link between these fields was established by Ismail et al. [5]. In recent years, quantum calculus has emerged as a powerful tool for investigating the geometric behavior of various subclasses of analytic functions. Several researchers have contributed to this growing area of study. For example, Naeem et al. [6] analyzed the class of q-convex functions, while Srivastava et al. [7] focused on subclasses of q-starlike functions. Alsarari and Alzahrani [8] explored convolution conditions for classes of q-Janowski symmetrical functions, and Ovindaraj and Sivasubramanian [9] introduced subclasses associated with q-conic domains. Furthermore, recent work has continued to explore a variety of analytic function subclasses defined through specialized q-calculus operators. For instance, Cotîrlă and Murugusundaramoorthy [10] investigated starlike functions using the Ruscheweyh q-differential operator within the Janowski domain, providing new geometric insights. Purohit et al. [11] introduced a unified class of spiral-like functions incorporating Kober fractional operators in the framework of quantum calculus, expanding the scope of fractional operator theory. Moreover, Breaz et al. [12] studied the geometric properties of a novel class of analytic functions defined through a certain operator, highlighting symmetry and other significant features. Khan et al. [13] employed the symmetric q-derivative operator, while Srivastava [14] provided an extensive survey and review, offering valuable insights for the research community.

Proposition 1. 

For any constants $v,u\in \mathbb{R}$ (or $\mathbb{C}$) and $\eta \in \mathrm{\Delta }$, we have

1.

${\partial }_q(nh\left(\eta \right)\pm ug\left(\eta \right))=v{\partial }_{q}h\left(\eta \right)\pm u{\partial }_{q}g\left(\eta \right)$,

2.

${\partial }_q\left(h\left(\eta \right)g\left(\eta \right)\right)=h\left(q\eta \right){\partial }_{q}g\left(\eta \right)+{\partial }_{q}h\left(\eta \right)g\left(\eta \right)=h\eta ){\partial }_{q}g\left(\eta \right)+{\partial }_{q}h\left(\eta \right)g\left(q\eta \right),$

3.

${\partial }_q\left({\displaystyle \frac{h\left(\eta \right)}{g\left(\eta \right)}}\right)={\displaystyle \frac{g\left(\eta \right){\partial }_{q}h\left(\eta \right)-h\left(\eta \right){\partial }_{q}g\left(\eta \right)}{g\left(q\eta \right)g\left(\eta \right)}}.$

We merge the concepts of $\alpha$-spiral-like, Janowski-type functions and the q-derivative to define the resulting classes.

Definition 1. 

For fixed constants $q,\alpha ,\mathcal{A},\mathcal{B}$, let ${\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$ be the family of functions $h\in \mathcal{H}$ that satisfy

$$e^{i\alpha }{\displaystyle \frac{w{\partial }_{q}h\left(\eta \right)}{h\left(\eta \right)}}\in \mathcal{P}[\mathcal{A},\mathcal{B}],forall\eta \in \mathrm{\Delta },$$

(4)

where $0<q<1,\left|\alpha \right|<{\displaystyle \frac{\pi }{2}},$ $-1\le \mathcal{B}<\mathcal{A}\le 1.$

For specific choices of the parameters $q,\alpha ,\mathcal{A},\mathcal{B}$, the class ${\widehat{\mathcal{S}}}_1^0(\mathcal{A},\mathcal{B})$ reduces to several well-known subclasses previously introduced in the literature. These include the following:

• ${\widehat{\mathcal{S}}}_1^{\alpha }(\mathcal{A},\mathcal{B}):=\widehat{\mathcal{S}}(\alpha ,\mathcal{A},\mathcal{B})$, studied by Polatoğlu et al. [15],
• ${\widehat{\mathcal{S}}}_q^0(1-2\kappa ,-1)={\widehat{\mathcal{S}}}_q\left(\kappa \right)$, investigated by Agrawal and Sahoo [16],
• ${\widehat{\mathcal{S}}}_q^0(1,-1)={\widehat{\mathcal{S}}}_q$, introduced by Ismail et al. [5],
• ${\widehat{\mathcal{S}}}_1^0(1-2\kappa ,-1)=\widehat{\mathcal{S}}\left(\kappa \right)$, considered by Robertson [17],
• ${\widehat{\mathcal{S}}}_1^0(1,-1)={\widehat{\mathcal{S}}}^{*}$, introduced by Nevanlinna [18].

We now define the class ${\widehat{\mathcal{K}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$ as a subclass of $\mathcal{H}$, consisting of all functions h that satisfy the condition

$$\eta {\partial }_{q}h\left(\eta \right)\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B}).$$

(5)

To further illustrate the behavior and geometric properties of the newly introduced class ${\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$, we have included several explicit examples of functions that belong to this class. These examples serve to highlight the variety of functions that satisfy the defining condition and help clarify the theoretical framework presented.

In particular, Example 2 has been graphically represented in the complex plane. The graphical visualization offers deeper insight into the image domain of the function and the effect of the parameters q, $\alpha$, $\mathcal{A}$, and $\mathcal{B}$. Such visual tools are especially valuable in understanding the distortion, rotation, and growth behavior of the functions within this class; see the following graph.

The inclusion of both analytical examples and their graphical representations enhances the comprehensiveness of the work and supports the theoretical results with concrete illustrations. Below are some illustrative examples of functions that belong to the class ${\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$ for appropriate choices of the parameters $q,\alpha ,\mathcal{A},\mathcal{B}$.

Example 1. 

Consider the function

$$h_1\left(\eta \right)={\displaystyle \frac{\eta }{1-\eta }}.$$

This function is known to be starlike in the unit disk Δ, and maps Δ onto the right half-plane. Its q-derivative is given by

$${\partial }_q{h}_1\left(\eta \right)={\displaystyle \frac{h_1\left(q\eta \right)-h_1\left(\eta \right)}{(q-1)\eta }}.$$

For small $q\in (0,1)$ and angle $\alpha \approx 0$, with parameters $\mathcal{A}=1$, $\mathcal{B}=-1$, the expression

$$\Re \left\{e^{i\alpha }{\displaystyle \frac{w{\partial }_q{h}_1\left(\eta \right)}{h_1\left(\eta \right)}}\right\}$$

belongs to $\mathcal{P}[\mathcal{A},\mathcal{B}]$. Therefore, $h_1\left(\eta \right)\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$.

Example 2. 

Let

$$h_2\left(\eta \right)=\eta e^{\eta }.$$

This function is entire and univalent in the unit disk Δ, and it is known to be convex. Using the definition of the q-derivative

$${\partial }_q{h}_2\left(\eta \right)={\displaystyle \frac{h_2\left(q\eta \right)-h_2\left(\eta \right)}{(q-1)\eta }},$$

one can verify that for suitable values of $q,\alpha ,\mathcal{A},\mathcal{B}$, the condition

$$\Re \left\{e^{i\alpha }{\displaystyle \frac{w{\partial }_q{h}_2\left(\eta \right)}{h_2\left(\eta \right)}}\right\}\in \mathcal{P}[\mathcal{A},\mathcal{B}]$$

is satisfied. Hence, $h_2\left(\eta \right)\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$.

Example 3. 

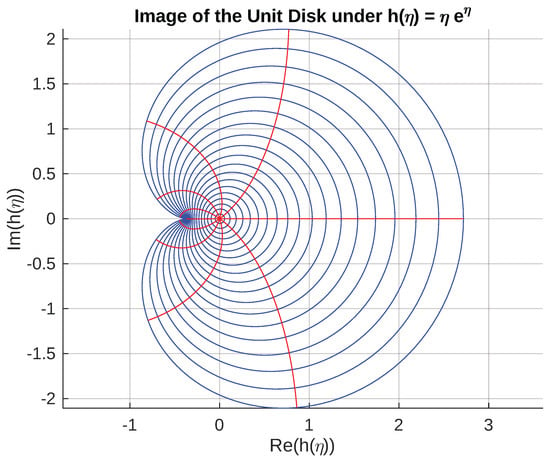
Let $p\left(\eta \right)\in \mathcal{P}[\mathcal{A},\mathcal{B}]$, and define

$$h_3\left(\eta \right)=exp\left({\int }_0^{\eta }{\displaystyle \frac{p\left(t\right)}{t}}dt\right).$$

Then

$$log{h}_3\left(\eta \right)={\int }_0^{\eta }{\displaystyle \frac{p\left(t\right)}{t}}dt.$$

Using the product and chain rules, the q-derivative becomes

$${\partial }_q{h}_3\left(\eta \right)=h_3\left(\eta \right)·{\partial }_q\left(log{h}_3\left(\eta \right)\right),$$

so that

$${\displaystyle \frac{w{\partial }_q{h}_3\left(\eta \right)}{h_3\left(\eta \right)}}=w·{\partial }_q\left(log{h}_3\left(\eta \right)\right).$$

If $p\left(\eta \right)\in \mathcal{P}[\mathcal{A},\mathcal{B}]$, then the real part of this expression belongs to the same class, and therefore $h_3\left(\eta \right)\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$. The geometric behavior of the function is shown in Figure 1.

Figure 1. Asymptotic analysis as $q\to 1^{-}$.

Recall the definition of the q-derivative for a function f:

$${\partial }_{q}f\left(\eta \right)={\displaystyle \frac{f\left(\eta \right)-f\left(q\eta \right)}{(1-q)\eta }},\eta \ne 0.$$

As $q\to 1^{-}$, the q-derivative converges to the classical derivative

$$\underset{q\to 1^{-}}{lim}{\partial }_{q}f\left(\eta \right)=f^{\prime }\left(\eta \right).$$

Similarly, the q-integer ${\left[k\right]}_q$ defined by

$${\left[k\right]}_q={\displaystyle \frac{1-q^k}{1-q}}$$

satisfies

$$\underset{q\to 1^{-}}{lim}{\left[k\right]}_q=k.$$

Moreover, generating functions and other expressions involving q approach their classical analogues. For example,

$${\displaystyle \frac{1}{(1-q\eta )(1-\eta )}}\underset{q\to 1^{-}}{\to }{\displaystyle \frac{1}{{(1-\eta )}^2}}.$$

Consequently, the classes ${\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$ and ${\widehat{\mathcal{K}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$ defined via q-calculus satisfy the following limits:

$$\underset{q\to 1^{-}}{lim}{\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})={\widehat{\mathcal{S}}}^{\alpha }(\mathcal{A},\mathcal{B}),$$

$$\underset{q\to 1^{-}}{lim}{\widehat{\mathcal{K}}}_q^{\alpha }(\mathcal{A},\mathcal{B})={\widehat{\mathcal{K}}}^{\alpha }(\mathcal{A},\mathcal{B}),$$

where the right-hand sides denote the classical spiral-like and Janowski-type function classes defined through ordinary derivatives and classical convolution.

Thus, the geometric properties of these q-based function classes asymptotically converge to those of the classical function classes as $q\to 1^{-}$.

This observation strengthens the theoretical connection between the q-analogue framework and classical geometric function theory.

We must revisit the following concept of neighborhoods, first introduced by Goodman [19]; this concept was later extended by Ruscheweyh [20].

Definition 2. 

For any $h\in \mathcal{H}$, ρ-neighborhood of function h can be defined as

$${\mathcal{N}}_{\rho }\left(h\right)=\left\{g\in \mathcal{H}:g\left(\eta \right)=\eta +\sum _{k=2}^{\infty }{b}_k{\eta }^k,\sum _{k=2}^{\infty }k|a_k-b_k|\le \rho \right\},(\rho \ge 0).$$

(6)

For $e\left(\eta \right)=\eta$, we can see that

$${\mathcal{N}}_{\rho }\left(e\right)=\left\{g\in \mathcal{H}:g\left(\eta \right)=\eta +\sum _{k=2}^{\infty }{b}_k{\eta }^{\eta },\sum _{k=2}^{\infty }k\left|b_k\right|\le \rho \right\},(\rho \ge 0).$$

(7)

Ruscheweyh [20] established, among other findings, that for all $\eta \in \mathbb{C}$ with $\left|\eta \right|<\rho$,

$${\displaystyle \frac{h\left(w\right)+\eta w}{1+\eta }}\in {\tilde{\mathcal{S}}}^{*}\Rightarrow {\mathcal{N}}_{\rho }\left(h\right)\subset {\tilde{\mathcal{S}}}^{*}.$$

Lemma 1 

([21]). If T is analytic in Δ with $T\left(0\right)=1$ and letting f be convex and g be starlike, then

$${\displaystyle \frac{f\ast Tg}{f\ast g}}\left(\mathrm{\Delta }\right)\subset \overline{CO}\left(T\left(\mathrm{\Delta }\right)\right),$$

where $\overline{CO}\left(T\left(\mathrm{\Delta }\right)\right)$ denotes the smallest closed convex set containing $T\left(\mathrm{\Delta }\right)$.

2. Main Results

Theorem 1. 

A function h belongs to ${\widehat{\mathcal{K}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$ if and only if

$${\displaystyle \frac{1}{\eta }}\left[h\ast \left({\displaystyle \frac{(\eta -q{\eta }^3)(1+\mathcal{B}{e}^{i\varphi })}{(1-q\eta )(1-\eta )(1-q^2\eta )}}-{\displaystyle \frac{(1+e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\})\eta }{(1-q\eta )(1-\eta )}}\right)\right]\ne 0,\left|\eta \right|<1,$$

where $0<q<1,$$0\le \varphi <2\pi ,-1\le \mathcal{B}<\mathcal{A}\le 1,$ and $\left|\alpha \right|<{\displaystyle \frac{\pi }{2}}$.

Proof. 

We have, $h\in {\widehat{\mathcal{K}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$ if and only if

$${\displaystyle \frac{e^{i\alpha }\frac{{\partial }_q\left(\eta {\partial }_{q}h\left(\eta \right)\right)}{{\partial }_{q}h\left(\eta \right)}-isin\left(\alpha \right)}{cos\left(\alpha \right)}}\ne {\displaystyle \frac{1+\mathcal{A}{e}^{i\varphi }}{1+\mathcal{B}{e}^{i\varphi }}},$$

which implies that

$${\partial }_q\left(\eta {\partial }_{q}h\left(\eta \right)\right)(1+\mathcal{B}{e}^{i\varphi })-{\partial }_{q}h\left(\eta \right)\{1+e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\}\}\ne 0.$$

(8)

Setting $h\left(\eta \right)=\eta +{\sum }_{k=2}^{\infty }{a}_k{\eta }^k$, we have

$${\partial }_{q}h=1+\sum _{k=2}^{\infty }{\left[k\right]}_q{a}_k{\eta }^{k-1},{\partial }_q\left(\eta {\partial }_{q}h\right)=1+\sum _{k=2}^{\infty }{\left[k\right]}_q^2{a}_k{\eta }^{k-1}={\partial }_{q}h\ast {\displaystyle \frac{1}{(1-\eta )(1-q\eta )}}.$$

The left-hand side of Equation (8) can be expressed as

$${\partial }_{q}h\ast \left({\displaystyle \frac{1+\mathcal{B}{e}^{i\varphi }}{(1-\eta )(1-q\eta )}}-{\displaystyle \frac{1+e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\}}{1-\eta }}\right),$$

(9)

Simplifying (9), we get

$${\displaystyle \frac{1}{\eta }}\left[\eta {\partial }_{q}h\ast \left({\displaystyle \frac{(1+\mathcal{B}{e}^{i\varphi })\eta }{(1-\eta )(1-q\eta )}}-{\displaystyle \frac{(e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\}+1)\eta }{1-\eta }}\right)\right]\ne 0,$$

(10)

Utilizing the identity $\eta {\partial }_{q}h\ast g=h\ast \eta {\partial }_{q}g$, Equation (10) can be rewritten as

$${\displaystyle \frac{1}{\eta }}\left[h\ast \left({\displaystyle \frac{(\eta -q{\eta }^3)(1+\mathcal{B}{e}^{i\varphi })}{(1-q\eta )(1-\eta )(1-q^2\eta )}}-{\displaystyle \frac{(1+e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\})\eta }{(1-q\eta )(1-\eta )}}\right)\right]\ne 0.$$

Remark 1. 

According to Ganesan et al. [22] and Silverman et al. [23], the following holds true as q approaches 1 the result is valid for various values of $\mathcal{A},\mathcal{B}$, and α.

Theorem 2. 

A function h belongs to ${\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$ if and only if

$${\displaystyle \frac{1}{\eta }}\left[h\ast \left({\displaystyle \frac{(1+\mathcal{B}{e}^{i\varphi })\eta }{(1-q\eta )}}-(1+e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\})\eta \right){\displaystyle \frac{1}{1-\eta }}\right]\ne 0,\left|\eta \right|<1,$$

where $0<q<1$, $0\le \varphi <2\pi ,-1\le \mathcal{B}<\mathcal{A}\le 1$, and $\left|\alpha \right|<{\displaystyle \frac{\pi }{2}}$.

Proof. 

Since $h\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$ if and only if $g\left(\eta \right)={\int }_0^{\eta }{\displaystyle \frac{h\left(\zeta \right)}{\zeta }}{d}_q\zeta \in {\widehat{\mathcal{K}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$, we have

$${\displaystyle \frac{1}{\eta }}\left[g\ast \left({\displaystyle \frac{(1+\mathcal{B}{e}^{i\varphi })(\eta -q{\eta }^3)}{(1-q\eta )(1-q^2\eta )(1-\eta )}}-{\displaystyle \frac{(1+\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\}{e}^{i(\varphi -\alpha )})}{(1-q\eta )(1-\eta )}}\right)\right]$$

$$={\displaystyle \frac{1}{\eta }}\left[h\ast \left({\displaystyle \frac{(\mathcal{B}{e}^{i\varphi }+1)\eta }{(1-q\eta )}}-(e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\}+1)\eta \right){\displaystyle \frac{1}{(1-\eta )}}\right].$$

Consequently, Theorem 2 is established. □

Leveraging Theorem 2, the subsequent corollary effortlessly determines the necessary property for the function.

Leveraging Theorem 2, we can explicitly characterize the membership of functions in the class ${\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$ via a convolution condition. The following corollary provides a practical and useful criterion involving an auxiliary function g in the class $\mathcal{H}$.

Corollary 1. 

$$h\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})\iff {\displaystyle \frac{(h\ast g)\left(\eta \right)}{\eta }}\ne 0,g\in \mathcal{H},\eta \in \mathrm{\Delta },$$

(11)

where $g\left(\eta \right)$ has the form

$$\begin{array}{cc}\hfill g\left(\eta \right)=\eta +\sum _{k=2}^{\infty }{t}_k{\eta }^k,& \\ \hfill t_k={\displaystyle \frac{({\left[k\right]}_q-1)+({\left[k\right]}_q\mathcal{B}-e^{i(-\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\})e^{i\varphi }}{(\mathcal{B}-e^{i(-\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\})e^{i\varphi }}}.\end{array}$$

(12)

Utilizing Theorem 2 and Corollary 1 as foundational principles, we proceed to illustrate their application in the subsequent example.

Example 4. 

Let $h\left(\eta \right)=\eta +\zeta {\eta }^k,k\ge 2$, then $h\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$ if and only if

$$\left|\zeta \right|\le {\displaystyle \frac{|\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\alpha +i\mathcal{B}sin\alpha \}|}{{\left[k\right]}_q-1+|{\left[k\right]}_q\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\alpha +i\mathcal{B}sin\alpha \}|}}.$$

(13)

Proof. 

Suppose that $h\left(\eta \right)=\eta +\zeta {\eta }^k,$ with satisfies inequality (13). Suppose g is defined as in Corollary 1, and

$$\left|{\displaystyle \frac{(g\ast h)\left(\eta \right)}{\eta }}\right|\ge 1-\sum _{k=2}^{\infty }\left|\zeta \right||t_k{\left|\right|\eta |}^{k-1}>1-\left|\eta \right|>0.$$

Applying Theorem 2, we get $h\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$. Conversely let $h\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$ and let

$$g\left(\eta \right)=\eta +\sum _{k=2}^{\infty }{\displaystyle \frac{{\left[k\right]}_q-1+|{\left[k\right]}_q\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\alpha +i\mathcal{B}sin\alpha \}|}{|\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\alpha +i\mathcal{B}sin\alpha \}|}}{\left|\eta \right|}^k.$$

Hence, from Theorem 2, we have

$${\displaystyle \frac{(g\ast h)\left(\eta \right)}{\eta }}=1+\zeta {\displaystyle \frac{{\left[k\right]}_q-1+|{\left[k\right]}_q\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\alpha +i\mathcal{B}sin\alpha \}|}{|\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\alpha +i\mathcal{B}sin\alpha \}|}}{\eta }^{k-1}\ne 0.$$

Let $\left|\zeta \right|>{\displaystyle \frac{|\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\}|}{{\left[k\right]}_q-1+|{\left[k\right]}_q\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\}|}}$, then some $x\in \mathrm{\Delta }$ exists such that

$${\displaystyle \frac{(g\ast h)\left(x\right)}{x}}=0,x\in \mathrm{\Delta },$$

resulting in a contradiction. Therefore, $\left|\zeta \right|\le {\displaystyle \frac{|\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\}|}{{\left[k\right]}_q-1+|{\left[k\right]}_q\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\}|}}.$ Building upon Corollary 1, we derive a sufficient condition theorem that elucidates the necessary conditions for the given mathematical construct. □

Next, we exploit the implications of Corollary 1 to establish a sufficient conditions theorem, thereby furnishing a pivotal result that undergirds our subsequent investigation.

Theorem 3. 

Let $h\left(\eta \right)=\eta +{\sum }_{k=2}^{\infty }{a}_k{\eta }^k,$ be analytic in Δ, for $-1\le \mathcal{B}<\mathcal{A}\le 1,\left|\alpha \right|<{\displaystyle \frac{\pi }{2}}$, and $0<q<1$, if

$$\sum _{k=2}^{\infty }\left\{{\displaystyle \frac{\left|e^{i(\varphi -\alpha )}\{\mathcal{A}cos\alpha +i\mathcal{B}sin\alpha \}-\mathcal{B}{\left[k\right]}_q\right|+{\left[k\right]}_q-1}{|e^{i(\varphi -\alpha )}\{\mathcal{A}cos\alpha +i\mathcal{B}sin\alpha \}-\mathcal{B}|}}\right\}\left|a_k\right|\le 1,$$

(14)

then, the function h belongs to ${\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$.

Proof. 

For the demonstration of Theorem 3, it is adequate to demonstrate that ${\displaystyle \frac{(h\ast g)\left(\eta \right)}{\eta }}\ne 0$, given that the function g is defined as in Equation (12). Let $g\left(\eta \right)=\eta +{\sum }_{k=2}^{\infty }{t}_k{\eta }^k$ and h is defined in (1). The convolution

$${\displaystyle \frac{(h\ast g)\left(\eta \right)}{\eta }}=1+\sum _{k=2}^{\infty }{t}_k{a}_k{\eta }^{k-1},\eta \in \mathrm{\Delta }.$$

From Theorem 2, we know that $h\left(\eta \right)\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$ if and only if ${\displaystyle \frac{(g\ast h)\left(\eta \right)}{\eta }}\ne 0$, where g is given by (12). By applying (12) and (14), we obtain

$$\left|{\displaystyle \frac{(f*g)\left(\eta \right)}{\eta }}\right|\ge 1-\sum _{k=2}^{\infty }{\displaystyle \frac{{|\left[k\right]}_q\mathcal{B}-e^{i(\varphi -\alpha )}{\{\mathcal{A}cos\alpha +i\mathcal{B}sin\alpha \}|+\left[k\right]}_q-1}{|\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\alpha +i\mathcal{B}sin\alpha \}|}}|a_k{\left|\right|\eta |}^{k-1}>0,\eta \in \mathrm{\Delta }.$$

Thus, $h\left(\eta \right)\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$. □

It is known that the convolution of a convex function and a starlike function is starlike. This result is often attributed to Robertson 1936 in [17]. We are using Corollary 1 to derive Robertson’s theorem for our class ${\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$.

Theorem 4. 

Suppose f is a convex function, and let $h\left(\eta \right)\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$ be a function that satisfies the inequality

$$\sum _{k=2}^{\infty }\left\{{\displaystyle \frac{({\left[k\right]}_q-1)+\left|e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\}-\mathcal{B}{\left[k\right]}_q\right|}{|e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\}-\mathcal{B}|}}\right\}\left|a_k\right|<1,$$

(15)

then $(h\ast f)\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$.

Proof. 

Let $f\left(\eta \right)=\eta +{\sum }_{k=2}^{\infty }{b}_k{\eta }^k$ is convex and $h\left(\eta \right)=\eta +{\sum }_{k=2}^{\infty }{a}_k{\eta }^k\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$ and satisfies inequality (15), and therefore

$$1-\sum _{k=2}^{\infty }{\displaystyle \frac{{\left[k\right]}_q-1+|{\left[k\right]}_q\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\alpha +i\mathcal{B}sin\alpha \}|}{|\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\alpha +i\mathcal{B}sin\alpha \}|}}\left|a_k\right|>0.$$

(16)

To prove that $(h\ast f)\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$ it suffices to demonstrate that ${\displaystyle \frac{(h\ast g\ast f)\left(\eta \right)}{\eta }}\ne 0$, where g is defined by (12). Consider

$$\left|{\displaystyle \frac{(g\ast f\ast h)\left(\eta \right)}{\eta }}\right|\ge 1-\sum _{k=2}^{\infty }|a_k\left|\right|b_k\left|\right|t_k{\left|\right|\eta |}^{k-1}.$$

Since $\eta \in \mathrm{\Delta }$ and g is convex, it follows that $|b_k|\le 1$. Applying Equation (16), we obtain

$$\left|{\displaystyle \frac{(h\ast f\ast g)\left(\eta \right)}{\eta }}\right|\ge 1-\sum _{k=2}^{\infty }{\displaystyle \frac{{\left[k\right]}_q-1+|{\left[k\right]}_q\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\}|}{|\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\}|}}\left|a_k\right|>0,\eta \in \mathrm{\Delta }.$$

Thus, $h\ast f\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B}).$ □

Example 5. 

Let $h\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$, satisfying inequality (15). Then

• ${\varphi }_1\left(\eta \right)={\sum }_1^{\infty }{\displaystyle \frac{1}{k}}{\eta }^k=log{(1-\eta )}^{-1}\mathit{is}\mathit{convex}\Rightarrow ({\varphi }_1\ast h)\left(\eta \right)={\int }_0^{\eta }{\displaystyle \frac{h\left(t\right)}{t}}dt\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B}).$
• ${\varphi }_2\left(\eta \right)={\sum }_0^{\infty }{\displaystyle \frac{1-z^k}{k(1-z)}}{\eta }^k={\displaystyle \frac{1}{1-z}}log\left({\displaystyle \frac{1-z\eta }{1-\eta }}\right),\mathit{is}\mathit{convex}\Rightarrow ({\varphi }_2\ast h)\left(\eta \right)={\int }_1^{\eta }{\displaystyle \frac{h\left(t\right)-h\left(zt\right)}{t-zt}}dt\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B}),\left|z\right|\le 1,z\ne 1.$
• ${\varphi }_3\left(\eta \right)={\sum }_1^{\infty }{\displaystyle \frac{2}{k+1}}{\eta }^k={\displaystyle \frac{-2[\eta +log(1-\eta \left)\right]}{\eta }}\mathit{is}\mathit{convex}\Rightarrow ({\varphi }_3\ast h)\left(\eta \right)={\displaystyle \frac{2}{\eta }}{\int }_1^{\eta }h\left(t\right)dt\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B}).$
• ${\varphi }_4\left(\eta \right)={\sum }_0^{\infty }{\displaystyle \frac{1+m}{k+m}}{\eta }^k,\Re \left\{m\right\}>0\mathit{is}\mathit{convex}\Rightarrow ({\varphi }_4\ast h)\left(\eta \right)={\displaystyle \frac{m+1}{m}}{\int }_0^{\eta }{t}^{m-1}h\left(t\right)dt\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B}).$

$(\rho ,q)$-Neighborhoods for Functions in the Classes ${\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$ and ${\widehat{\mathcal{K}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$

In this section, we try to expand our understanding of neighborhood properties within our classes. For the sake of clarity and to align with the established framework laid out in Definition 2, and with the aim of uncovering analogous local properties for the classes in question, we put forth the following definitions of neighborhood. These definitions are inspired by, and bear a resemblance to, the work of Ruscheweyh as documented in reference [20].

Definition 3. 

For any function $h\in \mathcal{H}$, the ρ-neighborhood of h is given by

$${\mathcal{N}}_{\mu ,\rho }\left(h\right)=\left\{g\in \mathcal{H}:g\left(\eta \right)=\eta +\sum _{k=2}^{\infty }{b}_k{\eta }^k,\sum _{k=2}^{\infty }{\mu }_k|a_k-b_k|\le \rho \right\},(\rho \ge 0).$$

(17)

For $e\left(\eta \right)=\eta$, we can see that

$${\mathcal{N}}_{\mu ,\rho }\left(e\right)=\left\{g\in \mathcal{H}:g\left(\eta \right)=\eta +\sum _{k=2}^{\infty }{b}_k{\eta }^k,\sum _{k=2}^{\infty }{\mu }_k\left|b_k\right|\le \rho \right\},(\rho \ge 0).$$

(18)

Remark 2. 

• For${\gamma }_k={\displaystyle \frac{({\left[k\right]}_q-1)+\left|e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\}-\mathcal{B}{\left[k\right]}_q\right|}{|e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\}-\mathcal{B}|}}$In Definition 3, the neighborhood corresponding to the classes is defined as ${\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$ and ${\widehat{\mathcal{K}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$ which is ${\mathcal{N}}_{q,\rho }(\mathcal{A},\mathcal{B};h)$.
• By setting ${\mu }_v=v$ in Definition 3, we recover the neighborhood concept originally introduced by Goodman [19] and subsequently generalized by Ruscheweyh [20].
• By setting ${\mu }_k={\left[k\right]}_q$ in Definition 3, we obtain the definition of the neighborhood associated with the q-derivative, denoted by ${\mathcal{N}}_{q,\rho }^{\mu }\left(h\right)$ and ${\mathcal{N}}_{q,\rho }^{\mu }\left(e\right)$, where ${\left[k\right]}_q$ is defined in Equation (3).

Theorem 5. 

Let $h\in \mathcal{H}$, and for every complex number λ such that $\left|\lambda \right|<\rho$, if

$${\displaystyle \frac{h\left(\eta \right)+\lambda \eta }{1+\lambda }}\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B}).$$

(19)

Then

$${\mathcal{N}}_{q,{\rho }_1}(\mathcal{A},\mathcal{B};h)\subset {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B}),$$

where ${\rho }_1={\displaystyle \frac{\rho |\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\}|}{1+\left|\mathcal{B}\right|}}$.

Proof. 

Let f be defined by $f\left(\eta \right)=\eta +{\sum }_{k=2}^{\infty }{b}_k{\eta }^k$. We want to show that f belongs to the class ${\mathcal{N}}_{q,{\rho }_1}(\mathcal{A},\mathcal{B};h)$. In order to establish the validity of this theorem, it suffices to demonstrate that $f\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$. To this end, we divide the proof into the following three steps, each addressing a critical aspect required to verify the membership of f in the specified class.

• Step 1.

From Theorem 2, we get

$$h\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})\iff {\displaystyle \frac{1}{\eta }}\left[(h\ast g\left(\eta \right))\right]\ne 0,$$

(20)

where

$$g\left(\eta \right)=\eta +\sum _{k=2}^{\infty }{\displaystyle \frac{({\left[k\right]}_q\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\})e^{i\varphi }+{\left[k\right]}_q-1}{(\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\})e^{i\varphi }}}.{\eta }^k$$

for $0\le \varphi <2\pi ,-1\le \mathcal{B}<\mathcal{A}\le 1,$ and $0\le \alpha <1$. Thus, we may represent it as $g\left(\eta \right)=\eta +{\sum }_{k=2}^{\infty }{t}_k{\eta }^k$, where $t_k$ is given by Equation (12); and thus, $|t_k|\le {\displaystyle \frac{{\left[k\right]}_q(1+|\mathcal{B}\left|\right)}{|\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\}|}}$.

• Step 2.

We find that (19) is equivalent to

$$\left|{\displaystyle \frac{h\left(\eta \right)\ast g\left(\eta \right)}{\eta }}\right|\ge \rho .$$

(21)

This is because, if $h\left(\eta \right)=\eta +{\sum }_{k=2}^{\infty }{a}_k{\eta }^k\in \mathcal{H}$ and satisfy (19), then (20) is equivalent to

$$g\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})\iff {\displaystyle \frac{1}{\eta }}\left[{\displaystyle \frac{h\left(\eta \right)\ast g\left(\eta \right)}{1+\lambda }}\right]\ne 0,\left|\lambda \right|<\rho .$$

• Step 3.

Letting $f\left(\eta \right)=\eta +{\sum }_{k=2}^{\infty }{b}_k{\eta }^k$, we notice that

$$\left|{\displaystyle \frac{f\left(\eta \right)\ast g\left(\eta \right)}{\eta }}\right|=\left|{\displaystyle \frac{h\left(\eta \right)\ast g\left(\eta \right)}{\eta }}+{\displaystyle \frac{\left(f\right(\eta )-h(\eta \left)\right)\ast g\left(\eta \right)}{\eta }}\right|$$

$$\ge \rho -\left|{\displaystyle \frac{\left(f\right(\eta )-h(\eta \left)\right)\ast g\left(\eta \right)}{\eta }}\right|(\mathrm{by}\mathrm{using}(21\left)\right)$$

$$=\rho -\left|\sum _{k=2}^{\infty }(b_k-a_k)t_k{\eta }^k\right|$$

$$\ge \rho -\left|\eta \right|\sum _{k=2}^{\infty }{\displaystyle \frac{{\left[k\right]}_q(1+|\mathcal{B}\left|\right)}{|\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\}|}}|b_k-a_k|$$

$$\ge \rho -\rho \left|\eta \right|>0$$

This proves that ${\displaystyle \frac{(f\ast g)\left(\eta \right)}{\eta }}\ne 0,\eta \in \mathrm{\Delta }.$ Based on our observations in (20), it follows that $f\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$. Therefore, we conclude the proof of the theorem. □

Theorem 6. 

Let $h\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$, and suppose that ${\rho }_1<c$. Then,

$${\mathcal{N}}_{q,{\rho }_1}(\mathcal{A},\mathcal{B};h)\subset {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B}),$$

where c is a non-zero real number satisfying $c\le \left|{\displaystyle \frac{(h\ast g)\left(\eta \right)}{\eta }}\right|$ for $\eta \in \mathrm{\Delta }$, with g given by Equation (12).

Proof. 

Let $f\left(\eta \right)=\eta +{\sum }_{k=2}^{\infty }{b}_k{\eta }^k$ belong to the class ${\mathcal{N}}_{q,{\rho }_1}^{x,y}(\mathcal{A},\mathcal{B};h)$. To establish Theorem 6, it is enough to demonstrate that

$${\displaystyle \frac{(f\ast g)\left(\eta \right)}{\eta }}\ne 0,$$

where the function g is given by Equation (12). Now, consider

$$\left|{\displaystyle \frac{f\left(\eta \right)\ast g\left(\eta \right)}{\eta }}\right|\ge \left|{\displaystyle \frac{h\left(\eta \right)\ast g\left(\eta \right)}{\eta }}\right|-\left|{\displaystyle \frac{\left(f\right(\eta )-h(\eta \left)\right)\ast g\left(\eta \right)}{\eta }}\right|.$$

(22)

Since $h\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$, and hence, invoking Theorem 3, we obtain

$$\left|{\displaystyle \frac{(h\ast g)\left(\eta \right)}{\eta }}\right|\ge c,$$

(23)

where c denotes a non-zero real constant, and $\eta$ ranges over $\mathrm{\Delta }$. We now proceed by

$$\begin{array}{c}\hfill \left|{\displaystyle \frac{\left(f\right(\eta )-h(\eta \left)\right)\ast g\left(\eta \right)}{\eta }}\right|=\left|\sum _{k=2}^{\infty }(b_k-a_k)t_k{\eta }^k\right|\\ \hfill \le \sum _{k=2}^{\infty }{\displaystyle \frac{\left|e^{i(\varphi -\alpha )}\{\mathcal{A}cos\alpha +i\mathcal{B}sin\alpha \}-\mathcal{B}{\left[k\right]}_q\right|+{\left[k\right]}_q-1}{|e^{i(\varphi -\alpha )}\{\mathcal{A}cos\alpha +i\mathcal{B}sin\alpha \}-\mathcal{B}|}}|b_k-a_k|\\ \hfill \le \sum _{k=2}^{\infty }{\displaystyle \frac{{\left[k\right]}_q(1+|\mathcal{B}\left|\right)}{|\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\}|}}|b_k-a_k|\\ \hfill \le {\displaystyle \frac{\rho |\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\}|}{{\left[k\right]}_q(1+|\mathcal{B}\left|\right)}}={\rho }_1,\end{array}$$

(24)

using (23) and (24) in (22), we obtain

$$\left|{\displaystyle \frac{f\left(\eta \right)\ast g\left(\eta \right)}{\eta }}\right|\ge c-{\rho }_1>0,$$

where ${\rho }_1<c$. Thus, the proof is now complete. □

Theorem 7. 

Let $h\in {\widehat{\mathcal{K}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$, and for any complex number δ, with $\left|\delta \right|<{\displaystyle \frac{1}{4}}$, we have

$$F_{\delta }\left(\eta \right)={\displaystyle \frac{h\left(\eta \right)+\delta \eta }{1+\delta }}\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B}).$$

(25)

Proof. 

Let $h\in {\widehat{\mathcal{K}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$, for ${\rho }_1<c$. Then

$$F_{\delta }\left(\eta \right)={\displaystyle \frac{h\left(\eta \right)+\delta \eta }{1+\delta }}$$

$$=\left(h\left(\eta \right)\ast \psi \left(\eta \right)\right),$$

where

$$\psi \left(\eta \right)={\displaystyle \frac{\eta -\frac{\delta }{1+\delta }{\eta }^2}{1-\eta }}.$$

Using the convolution principle, we derive

$$h\left(\eta \right)\ast \psi \left(\eta \right)=\eta {\partial }_{q}h\ast \left(\psi \left(\eta \right)\ast log\left({\displaystyle \frac{1}{1-\eta }}\right)\right),$$

Given that $h\in {\widehat{\mathcal{K}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$, $\eta {\partial }_{q}h\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$, For $\left|\delta \right|<{\displaystyle \frac{1}{4}}$, the function $\psi$ belongs to the class of starlike functions $\tilde{\mathcal{S}}$. By applying the convolution theorem, we obtain the following expression:

$$\psi \left(\eta \right)\ast log\left({\displaystyle \frac{1}{1-\eta }}\right)={\int }_0^{\eta }{\displaystyle \frac{\psi \left(w\right)}{w}}{d}_{q}w.$$

(26)

By applying the Alexander relation (26), we deduce that the convolution

$$\psi \left(\eta \right)\ast log\left({\displaystyle \frac{1}{1-\eta }}\right)$$

belongs to the class of convex functions $\tilde{\mathcal{K}}$. Utilizing Lemma 1, it can be further established that this convolution inherits important geometric properties, which play a crucial role in the subsequent analysis. In particular, these properties facilitate the derivation of coefficient bounds and inclusion relations necessary for proving the main results.

$\tilde{\mathcal{K}}\ast {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})\subset {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$. Hence

$$F_{\delta }\left(\eta \right)=w{\partial }_{q}h\ast \left(\psi \left(\eta \right)\ast log\left({\displaystyle \frac{1}{1-\eta }}\right)\right)\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B}),\left|\delta \right|<{\displaystyle \frac{1}{4}}.$$

Thus, the proof is now fully established. □

Theorem 8. 

Let $h\in {\widehat{\mathcal{K}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$. Then

$${\mathcal{N}}_{q,\rho }^{\alpha }(\mathcal{A},\mathcal{B};h)\subset {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B}),$$

where $\rho ={\displaystyle \frac{|\mathcal{B}-e^{i(\varphi -\alpha )}\{\mathcal{A}cos\left(\alpha \right)+i\mathcal{B}sin\left(\alpha \right)\}|}{4(1+|\mathcal{B}\left|\right)}}$.

Proof. 

Let $h\in {\widehat{\mathcal{K}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$, then by Theorem 7 $F_{\delta }\left(\eta \right)\in {\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B}),\left|\delta \right|<{\displaystyle \frac{1}{4}}.$ By selecting $\rho ={\displaystyle \frac{1}{4}}$ and applying Theorem 5, we arrive at the desired result. □

3. Conclusions

In this paper, we have introduced new subclasses of analytic functions by combining the concepts of spiral-like functions and Janowski-type functions within the framework of q-calculus. By investigating convolution conditions, we established sufficient criteria that guarantee membership in these classes. Additionally, we applied Robertson’s theorem to deepen the theoretical understanding of these function families.

Motivated by recent advances, we also defined neighborhood concepts associated with the classes ${\widehat{\mathcal{S}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$ and ${\widehat{\mathcal{K}}}_q^{\alpha }(\mathcal{A},\mathcal{B})$, and we derived relevant neighborhood results. These contributions enrich the geometric function theory in the q-calculus setting and open avenues for future research.