Parabolic and Linear Rotational Motions on Cones and Hyperboloids

Abstract

In this study, we consider the Lorentzian rotation about a lightlike axis. First, we introduce a geometric characterization for the rotation angle between two vectors that can overlap each other under a Lorentzian rotation about a lightlike axis. Then, we give a definition for the angle measurement between two spacelike vectors whose vector product is lightlike. Later, we generalize the Lorentzian rotation about a lightlike axis, and determine matrices of these transformations using the Cartan frame and the well-known Rodrigues formula, then using the Cayley map, and finally using the generalized split quaternions. We see that such transformations give parabolic rotational motions on general cones or general hyperboloids of one or two sheets, while they also give linear rotational motions on general hyperboloids of one sheet.

1. Introduction

As a ubiquitous phenomenon, Euclidean rotational motions serve as a bridge between theoretical abstraction and practical applications. They are linear transformations that can be expressed by the orthogonal matrices whose determinants are 1, forming a non-Abelian group denoted by SO(3). Rotation matrices have attracted the attention of many researchers, as they play an important role in many application areas in many fields such as robotics [1,2], and differential geometry [3]. Some well-known methods to obtain rotation matrices are the Rodrigues formula, the Cayley map, and quaternion multiplication.

Rotation transformations and their matrices can be defined for other scalar product spaces, and these new rotation transformations can create new fields of study. One of those spaces is the Minkowski 3-space [4,5,6], which is a geometric framework that is used to study the structure of spacetime in special relativity. Rotation transformations of Minkowski 3-space are a crucial component of the three-dimensional Lorentz group, and their mathematical properties and the simplified physical scenarios they govern make them a valuable tool for theoretical physicists and mathematicians to explore fundamental concepts in relativity, quantum mechanics, and field theory. On the other hand, rotation transformations of the Minkowski spacetime finds diverse applications, including analyzing lens optics or laser cavity kinematics [7], deriving robot manipulator equations of motion [8], facilitating motion interpolations [9], and modeling ideal fluid hydrodynamics [10]. There are many studies on generating or generalizing the rotation matrices of the Minkowski 3-space, which have spacelike, timelike, or lightlike axes of rotation [11,12,13,14]. The rotation matrices of the generalized Minkowski 3-space that have spacelike or timelike axes are given in [15,16]. However, the rotation matrices that have generalized lightlike axes are not given yet.

The main aim of our study is to give generalized Lorentzian rotation matrices with generalized lightlike axes, which provide parabolic motions on general cones or hyperboloids of one or two sheets, while they also give linear motions on hyperboloids of one sheet, using the well-known classical methods of the Rodrigues formula, the Cayley map, and quaternion multiplication. Here, we have established that the generalized Lorentz rotation formulas are identical to the standard Lorentz rotation formulas, with the exception of skew-symmetric matrices. In addition, we consider the angle of a Lorentzian rotation about a lightlike axis in the Minkowski 3-space, and we introduce a geometric characterization for it, using the region swept by the rotated vector as in the classical geometries. Moreover, we provide a definition not found in the literature for measuring the angle between two spacelike vectors whose vector product is lightlike. We also adapt this characterization to the generalized Minkowski 3-space.

This paper is organized as follows: First, we give a brief introduction to the generalized Minkowski 3-space and the related number system. Then, we consider the Lorentzian rotation about a lightlike axis, and introduce the geometric meaning for the rotation angles, giving a definition of angle between two spacelike vectors on the same pseudosphere, whose vector product is lightlike. Finally, we generate the generalized Lorentzian rotation matrices which determine parabolic and linear rotational motions in the space, using the Rodrigues formula, the Cayley map, and the generalized split quaternion methods in the generalized Minkowski 3-space.

2. Preliminaries

The generalized Minkowski 3-space ${\mathbb{R}}_{\Omega }^3$ derived by the standard Minkowski 3-space ${\mathbb{R}}_1^3$ of signature $(-,+,+)$, and its associated number system ${\mathbb{H}}_{\Omega }$, which is the generalized split quaternion, were introduced in [15]. Accordingly, ${\mathbb{R}}_{\Omega }^3$ is the real vector space ${\mathbb{R}}^3$ with the three-dimensional generalized Lorentzian scalar product or $\Omega$-scalar product defined by a real symmetric matrix

$$\Omega =\left[\begin{array}{ccc}A& D& E\\ D& B& F\\ E& F& C\end{array}\right]$$

(1)

with a negative determinant whose eigenvalues are not all of the same sign, which can be written as

$$\begin{array}{cc}\hfill {⟨\mathbf{x},\mathbf{y}⟩}_{\Omega }& ={\mathbf{x}}^T\Omega \mathbf{y}\hfill \\ \hfill & =A{x}_1{y}_1+B{x}_2{y}_2+C{x}_3{y}_3+D(x_1{y}_2+x_2{y}_1)+E(x_1{y}_3+x_3{y}_1)+F(x_2{y}_3+x_3{y}_2)\hfill \end{array}$$

(2)

for vectors $\mathbf{x}=(x_1,x_2,x_3)$, $\mathbf{y}=(y_1,y_2,y_3)\in {\mathbb{R}}^3$, while the standard Lorentzian scalar product is

$${⟨\mathbf{x},\mathbf{y}⟩}_L={\mathbf{x}}^T{I}^{\ast }\mathbf{y}$$

(3)

where $I^{\ast }=diag(-1,1,1)$. The matrix $\Omega$ is the associated matrix of the bilinear form, and

$$\Delta =\sqrt{\left|det\Omega \right|}=\sqrt{\left|ABC+2FDE-A{F}^2-C{D}^2-B{E}^2\right|}$$

(4)

is called the constant of the matrix $\Omega$. A nonzero vector $\mathbf{x}$ is called $\Omega$-spacelike, $\Omega$-timelike and $\Omega$-lightlike (or $\Omega$-null), if “$\mathbf{x}=\mathbf{0}$ or ${⟨\mathbf{x},\mathbf{x}⟩}_{\Omega }>0$”, ${⟨\mathbf{x},\mathbf{x}⟩}_{\Omega }<0$, and “$\mathbf{x}\ne \mathbf{0}$ and ${⟨\mathbf{x},\mathbf{x}⟩}_{\Omega }=0$”, respectively. The $\Omega$-norm of the vector $\mathbf{x}$ is given by

$${∥x∥}_{\Omega }=\sqrt{\left|{⟨\mathbf{x},\mathbf{x}⟩}_{\Omega }\right|}=\sqrt{\left|A{x}_1^2+B{x}_2^2+C{x}_3^2+2D{x}_1{x}_2+2E{x}_1{x}_3+2F{x}_2{x}_3\right|}.$$

(5)

For $r\in {\mathbb{R}}^{+}$, spheres of the generalized Minkowski 3-space or $\Omega$-spheres with a center at the origin and radius r are the sets

$${\mathcal{S}}_{\Omega }^2\left(r\right)=\left\{\mathbf{x}\in {\mathbb{R}}^3:{⟨\mathbf{x},\mathbf{x}⟩}_{\Omega }=r^2\right\}\mathrm{and}{\mathcal{H}}_{\Omega }^2\left(r\right)=\left\{\mathbf{x}\in {\mathbb{R}}^3:{⟨\mathbf{x},\mathbf{x}⟩}_{\Omega }=-r^2\right\}$$

(6)

which is called an $\Omega$-pseudosphere, which is a general hyperboloid of one sheet and an $\Omega$-hyperbolic sphere which is a general hyperboloid of two sheets. In addition, the $\Omega$-sphere with its center at the origin and radius 0 is

$${\mathcal{L}}_{\Omega }=\left\{\mathbf{x}\in {\mathbb{R}}^3:{⟨\mathbf{x},\mathbf{x}⟩}_{\Omega }=0\right\}$$

(7)

which is called $\Omega$-light cone, which is a general cone.

A $3\times 3$ matrix S is defined as $\Omega$-skew-symmetric if it satisfies the equation $S^T\Omega =-\Omega S$, and for a given vector $\mathbf{x}=(x_1,x_2,x_3)\in {\mathbb{R}}^3$, the $\Omega$-skew-symmetric matrix related to the vector $\mathbf{x}$ has the form of

$$S_{\mathbf{x}}=\left[\begin{array}{ccc}{\Lambda }_{5,6}& {\Lambda }_{3,5}^{\prime }& {\Lambda }_{6,3}^{″}\\ {\Lambda }_{4,2}& {\Lambda }_{6,4}^{\prime }& {\Lambda }_{2,6}^{″}\\ {\Lambda }_{1,4}& {\Lambda }_{5,1}^{\prime }& {\Lambda }_{4,5}^{″}\end{array}\right]$$

(8)

where ${\Lambda }_{i,j}={\Delta }_i{x}_2-{\Delta }_j{x}_3$, ${\Lambda }_{i,j}^{\prime }={\Delta }_i{x}_3-{\Delta }_j{x}_1$, ${\Lambda }_{i,j}^{″}={\Delta }_i{x}_1-{\Delta }_j{x}_2$ and ${\Delta }_1=(AB-D^2)/\Delta$, ${\Delta }_2=(AC-E^2)/\Delta$, ${\Delta }_3=(BC-F^2)/\Delta$, ${\Delta }_4=(DE-AF)/\Delta$, ${\Delta }_5=(DF-BE)/\Delta$ and ${\Delta }_6=(EF-CD)/\Delta$. Using this notion, the generalized Lorentzian vector product of vectors $\mathbf{x},\mathbf{y}\in {\mathbb{R}}^3$ is given as follows:

$$\mathbf{x}{\times }_{\Omega }\mathbf{y}=S_{\mathbf{x}}\mathbf{y}.$$

(9)

In addition, for vectors $\mathbf{x},\mathbf{y},\mathbf{z}\in {\mathbb{R}}^3$, the following equation is satisfied:

$$\mathbf{x}{\times }_{\Omega }\left(\mathbf{y}{\times }_{\Omega }\mathbf{z}\right)={⟨\mathbf{x},\mathbf{y}⟩}_{\Omega }\mathbf{z}-{⟨\mathbf{x},\mathbf{z}⟩}_{\Omega }\mathbf{y}.$$

(10)

The $\Omega$-measure $\theta$ of the angle between linearly independent $\Omega$-spacelike vectors $\mathbf{x}$ and $\mathbf{y}$ is defined as follows [16]:

(i)

If $\mathbf{x}{\times }_{\Omega }\mathbf{y}$ is $\Omega$-spacelike and ${⟨\mathbf{x},\mathbf{y}⟩}_{\Omega }>0$, which are equivalent to ${⟨\mathbf{x},\mathbf{y}⟩}_{\Omega }>{∥\mathbf{x}∥}_{\Omega }{∥\mathbf{y}∥}_{\Omega }$, then

$${⟨\mathbf{x},\mathbf{y}⟩}_{\Omega }={∥\mathbf{x}∥}_{\Omega }{∥\mathbf{y}∥}_{\Omega }cosh\theta .$$

(11)

(ii)

If $\mathbf{x}{\times }_{\Omega }\mathbf{y}$ is $\Omega$-timelike, which is equivalent to ${⟨\mathbf{x},\mathbf{y}⟩}_{\Omega }<{∥\mathbf{x}∥}_{\Omega }{∥\mathbf{y}∥}_{\Omega }$, then

$${⟨\mathbf{x},\mathbf{y}⟩}_{\Omega }={∥\mathbf{x}∥}_{\Omega }{∥\mathbf{y}∥}_{\Omega }cos\theta .$$

(12)

The $\Omega$-measure $\theta$ of the angle between linearly independent $\Omega$-timelike vectors $\mathbf{x}$ and $\mathbf{y}$ satisfying ${⟨\mathbf{x},\mathbf{y}⟩}_{\Omega }<0$ is defined as

$${⟨\mathbf{x},\mathbf{y}⟩}_{\Omega }=-{∥\mathbf{x}∥}_{\Omega }{∥\mathbf{y}∥}_{\Omega }cosh\theta .$$

(13)

Additionally, if ${⟨\mathbf{x},\mathbf{y}⟩}_{\Omega }=0$, then $\mathbf{x}$ and $\mathbf{y}$ are called $\Omega$-orthogonal; in addition, if the $\Omega$-norms of them are 1, then they are called $\Omega$-orthonormal.

On the other hand, for the real numbers A, B, C, D, E, F which are the entries of the matrix $\Omega$, and for the base elements $\mathbf{i},\mathbf{j},\mathbf{k}$ satisfying the following equalities

$$\begin{array}{ccc}\hfill {\mathbf{i}}^2& =& A,{\mathbf{j}}^2=B,{\mathbf{k}}^2=C\hfill \\ \hfill \mathbf{ij}& =& D-\mathbf{i}{\Delta }_5-\mathbf{j}{\Delta }_4-\mathbf{k}{\Delta }_1\hfill \\ \hfill \mathbf{ji}& =& D+\mathbf{i}{\Delta }_5+\mathbf{j}{\Delta }_4+\mathbf{k}{\Delta }_1\hfill \\ \hfill \mathbf{jk}& =& E-\mathbf{i}{\Delta }_3-\mathbf{j}{\Delta }_6-\mathbf{k}{\Delta }_5\hfill \\ \hfill \mathbf{kj}& =& E+\mathbf{i}{\Delta }_3+\mathbf{j}{\Delta }_6+\mathbf{k}{\Delta }_5\hfill \\ \hfill \mathbf{ki}& =& F-\mathbf{i}{\Delta }_6-\mathbf{j}{\Delta }_2-\mathbf{k}{\Delta }_4\hfill \\ \hfill \mathbf{ik}& =& F+\mathbf{i}{\Delta }_6+\mathbf{j}{\Delta }_2+\mathbf{k}{\Delta }_4,\hfill \end{array}$$

(14)

each element of the set

$${\mathbb{H}}_{\Omega }=\left\{q_0+q_1\mathbf{i}+q_2\mathbf{j}+q_3\mathbf{k}:q_0,q_1,q_2,q_3\in \mathbb{R}\right\}$$

(15)

is called a generalized split quaternion or an $\Omega$-split quaternion. The set ${\mathbb{H}}_{\Omega }$ with its sum and multiplication operations is a non-commutative, non-division, and associative ring. For an $\Omega$-split quaternion $\mathbf{q}=q_0+q_1\mathbf{i}+q_2\mathbf{j}+q_3\mathbf{k}=q_0+{\mathbf{v}}_q$, the real number $q_0$ and the vector ${\mathbf{v}}_q=q_1\mathbf{i}+q_2\mathbf{j}+q_3\mathbf{k}$ are called the scalar part and the vector part of $\mathbf{q}$, respectively. A pure $\Omega$-split quaternion is defined as an $\Omega$-split quaternion with a zero scalar part. So, the vectors of ${\mathbb{R}}^3$ can be thought of as pure $\Omega$-split quaternions. For any two $\Omega$-split quaternions $\mathbf{p}=p_0+{\mathbf{v}}_p$ and $\mathbf{q}=q_0+{\mathbf{v}}_q$, the multiplication of them is given by

$$\mathbf{pq}=p_0{q}_0+{⟨{\mathbf{v}}_p,{\mathbf{v}}_q⟩}_{\Omega }+p_0{\mathbf{v}}_q+q_0{\mathbf{v}}_p+{\mathbf{v}}_p{\times }_{\Omega }{\mathbf{v}}_q.$$

(16)

Then for two pure $\Omega$-split quaternions $\mathbf{p}$ and $\mathbf{q}$, the following equation is satisfied:

$$\mathbf{pq}={⟨\mathbf{p},\mathbf{q}⟩}_{\Omega }+\mathbf{p}{\times }_{\Omega }\mathbf{q}.$$

(17)

In addition, left and right multiplications of $\Omega$-split quaternions can be computed as follows:

$$L_{\mathbf{p}}\left(\mathbf{q}\right)=\mathbf{pq}=\left[\begin{array}{cccc}{p}_0& A{p}_1+D{p}_2+E{p}_3& D{p}_1+B{p}_2+F{p}_3& E{p}_1+F{p}_2+C{p}_3\\ p_1& p_0+p_2{\Delta }_5-p_3{\Delta }_6& p_3{\Delta }_3-p_1{\Delta }_5& p_1{\Delta }_6-p_2{\Delta }_3\\ p_2& p_2{\Delta }_4-p_3{\Delta }_2& p_0+p_3{\Delta }_6-p_1{\Delta }_4& p_1{\Delta }_2-p_2{\Delta }_6\\ p_3& p_2{\Delta }_1-p_3{\Delta }_4& p_3{\Delta }_5-p_1{\Delta }_1& p_0+p_1{\Delta }_4-p_2{\Delta }_5\end{array}\right]\left[\begin{array}{c}{q}_0\\ q_1\\ q_2\\ q_3\end{array}\right]$$

(18)

$$L_{\mathbf{p}}\left(\mathbf{q}\right)=\mathbf{qp}=\left[\begin{array}{cccc}{p}_0& A{p}_1+D{p}_2+E{p}_3& D{p}_1+B{p}_2+F{p}_3& E{p}_1+F{p}_2+C{p}_3\\ p_1& p_0+p_3{\Delta }_6-p_2{\Delta }_5& p_1{\Delta }_5-p_3{\Delta }_3& p_2{\Delta }_3-p_1{\Delta }_6\\ p_2& p_3{\Delta }_2-p_2{\Delta }_4& p_0+p_1{\Delta }_4-p_3{\Delta }_6& p_2{\Delta }_6-p_1{\Delta }_2\\ p_3& p_3{\Delta }_4-p_2{\Delta }_1& -p_1{\Delta }_1-p_3{\Delta }_5& p_0+p_2{\Delta }_5-p_1{\Delta }_4\end{array}\right]\left[\begin{array}{c}{q}_0\\ q_1\\ q_2\\ q_3\end{array}\right].$$

(19)

For an $\Omega$-split quaternion $\mathbf{q}=q_0+{\mathbf{v}}_q$, the conjugate, norm and inverse of $\mathbf{q}$ are defined as follows:

$$\begin{array}{ccc}\hfill \overline{\mathbf{q}}& =& q_0-{\mathbf{v}}_q\hfill \\ \hfill N_{\mathbf{q}}& =& \sqrt{\left|\overline{\mathbf{q}}\mathbf{q}\right|}=\sqrt{\left|\mathbf{q}\overline{\mathbf{q}}\right|}=\sqrt{\left|q_0^2-{⟨{\mathbf{v}}_q,{\mathbf{v}}_q⟩}_{\Omega }\right|}\hfill \\ \hfill {\mathbf{q}}^{-1}& =& {\displaystyle \frac{\overline{\mathbf{q}}}{I_q}},\mathrm{for}{I}_q\ne 0\mathrm{where}{I}_q=q_0^2-{⟨{\mathbf{v}}_q,{\mathbf{v}}_q⟩}_{\Omega }.\hfill \end{array}$$

(20)

If $N_{\mathbf{q}}=1$ then $\mathbf{q}$ is called a unit $\Omega$-split quaternion. Generalized split quaternions, like ordinary split quaternions, can be classified as follows: an $\Omega$-split quaternion is called spacelike, timelike and lightlike (or null), if $I_q<0,$$I_q>0$ and $I_q=0$, respectively.

3. On the Lorentzian Rotation About a Lightlike Axis

In [17], Sodsiri, using an elementary approach, determined the rotation matrices in the Minkowski 3-space ${\mathbb{R}}_1^3$ about the lightlike axis ${\mathsf{\ell }}^{\prime }=\left\{(s,s,0):s\in \mathbb{R}\right\}$ by the angle $\gamma \in \mathbb{R}$, as

$$R^{\prime }=\left[\begin{array}{ccc}{\displaystyle \frac{1}{2}}{n}^2{\gamma }^2+1& -{\displaystyle \frac{1}{2}}{n}^2{\gamma }^2& n\gamma \\ {\displaystyle \frac{1}{2}}{n}^2{\gamma }^2& 1-{\displaystyle \frac{1}{2}}{n}^2{\gamma }^2& n\gamma \\ n\gamma & -n\gamma & 1\end{array}\right]$$

(21)

for each $n\in \mathbb{R}-\left\{0\right\}$. It is easy to see that for each value of n, a different Lorentzian rotation matrix is obtained, which fixes the axis ℓ′ pointwise. Then, using the vectorial representation of the spherical rotations, the rotation about a general lightlike axis ℓ spanned by a lightlike vector $\mathbf{n}$ as a geodesic was given as

$${\alpha }_{\gamma }\left(\mathbf{x}\right)=\mathbf{x}+\gamma \mathbf{n}$$

(22)

for the unit vector $\mathbf{x}$, in [18]. Later, Nešović determined the rotation matrix R about a general axis ℓ spanned by a lightlike vector $\mathbf{n}$ by the angle $\gamma$ using Cartan’s frame [19].

Cartan’s frame in ${\mathbb{R}}_1^3$ is a pseudo-orthonormal frame $\left\{\mathbf{c},\mathbf{t},\mathbf{n}\right\}$ satisfying the following conditions:

$$\begin{array}{c}{⟨\mathbf{c},\mathbf{c}⟩}_L={⟨\mathbf{n},\mathbf{n}⟩}_L={⟨\mathbf{c},\mathbf{t}⟩}_L={⟨\mathbf{n},\mathbf{t}⟩}_L=0,\\ {⟨\mathbf{t},\mathbf{t}⟩}_L={⟨\mathbf{c},\mathbf{n}⟩}_L=1,\\ \mathbf{c}{\times }_L\mathbf{t}=\mathbf{c},\mathbf{t}{\times }_L\mathbf{n}=\mathbf{n},\mathbf{n}{\times }_L\mathbf{c}=\mathbf{t}.\end{array}$$

(23)

In this frame, $\mathbf{t}$ is on the pseudosphere with radius 1, and linearly independent lightlike vectors $\mathbf{c}$ and $\mathbf{n}$ are always on different naps of the light cone, since two lightlike linearly independent vectors lie in the same nap of the light cone if and only if their Lorentzian scalar product is less than 0 [20]. In addition, the frame is positively oriented, since the frame conditions give the result det$(\mathbf{c},\mathbf{t},\mathbf{n})=1>0$. In particular, if ${\mathbf{n}}^{\prime }=\left(n,n,0\right)$ and ${\mathbf{t}}^{\prime }=(t,t,1)$ for real numbers $n\ne 0$ and t in Cartan’s frame $\left\{{\mathbf{c}}^{\prime },{\mathbf{t}}^{\prime },{\mathbf{n}}^{\prime }\right\}$, then it is possible to see with some calculations that

$${\mathbf{c}}^{\prime }=\left(-\frac{t^2+1}{2n},-\frac{t^2-1}{2n},-\frac{t}{n}\right).$$

Hence, using the matrix (21) and the frame coordinates or using Equation (22), one can easily see the equation

$${⟨R^{\prime }\left({\mathbf{t}}^{\prime }\right),{\mathbf{c}}^{\prime }⟩}_L=\gamma ,$$

(24)

which determines the angle of the Lorentzian rotation matrix $R^{\prime }$. On the other hand, the most general form of this frame can be written as $\left\{\mathbf{c},\mathbf{t},\mathbf{n}\right\}$ where $\mathbf{n}=R_{\theta }\left({\mathbf{n}}^{\prime }\right),$$\mathbf{t}=R_{\theta }\left({\mathbf{t}}^{\prime }\right)$, $\mathbf{c}=R_{\theta }\left({\mathbf{c}}^{\prime }\right)$ for the following Euclidean rotation about the x-axis by the angle $\theta$

$$R_{\theta }=\left[\begin{array}{ccc}1& 0& 0\\ 0& cos\theta & -sin\theta \\ 0& sin\theta & cos\theta \end{array}\right],$$

(25)

which is also a Lorentzian rotation, and $R_{\theta }{R}^{\prime }{R}_{-\theta }$ is the Lorentzian rotation about the general lightlike axis ℓ spanned by the lightlike vector $\mathbf{n}$, since the multiplication of two Lorentzian rotations is also a Lorentzian rotation and

$$R_{\theta }{R}^{\prime }{R}_{-\theta }\left(\mathbf{n}\right)=R_{\theta }{R}^{\prime }\left({\mathbf{n}}^{\prime }\right)=R_{\theta }\left({\mathbf{n}}^{\prime }\right)=\mathbf{n}.$$

(26)

In addition, since the Lorentzian rotations preserve the Lorentzian scalar product, one gets

$${⟨R\left(\mathbf{t}\right),\mathbf{c}⟩}_L=\gamma .$$

(27)

So, the rotation angle of $R=R_{\theta }{R}^{\prime }{R}_{-\theta }$ is also $\gamma$.

Using this fact, Nešović determined the rotation matrix R about the axis ℓ spanned by the lightlike vector $\mathbf{n}=(n_1,n_2,n_3)$ by the angle $\gamma$ as

$$R=R_{\mathsf{\ell },\gamma }=I_3-\gamma S_{\mathbf{n}}+{\displaystyle \frac{{\gamma }^2}{2}}{S}_{\mathbf{n}}^2$$

(28)

where

$$S_{\mathbf{n}}=\left[\begin{array}{ccc}0& n_3& -n_2\\ n_3& 0& -n_1\\ -n_2& n_1& 0\end{array}\right]$$

(29)

which is the semi-skew-symmetric matrix with respect to $\mathbf{n}$. However, in these studies, the rotation angle $\gamma$ has no geometric meaning. In the next section, we introduce a geometric meaning for this value, and this meaning gives a new definition for the angle between two spacelike vectors on the same pseudosphere in ${\mathbb{R}}_1^3$, whose vector product is lightlike.

4. Geometric Meaning of the Angle for Rotations About a Lightlike Axis

In this section, we introduce a geometric characterization of the rotation angle $\gamma$ between two linearly independent vectors on the same three-dimensional Lorentzian sphere, such that one of the vectors is rotated on to the other one by the Lorentzian rotation matrix (28) about the lightlike axis with direction vector $\mathbf{n}$ by the angle $\gamma$. Since all structure is invariant under the transformation $R_{\theta }$, we only consider the vector $\mathbf{n}=\left(n,n,0\right)$ where $n\ne 0$. Notice that for two different linear dependent different lightlike vectors ${\mathbf{n}}_1$ and ${\mathbf{n}}_2$, the Lorentzian rotation matrices about the axis ℓ with direction vector ${\mathbf{n}}_1$ or ${\mathbf{n}}_2$ by the angle $\gamma$ are different. So, the representation $R_{\mathsf{\ell },\gamma }$ may be a cause of confusion. To avoid this confusion, $R_{\mathbf{n},\gamma }$ is a more suitable representation than $R_{\mathsf{\ell },\gamma }$ for the rotation transformation, and $\mathbf{n}$ is a more suitable representation than ℓ for the rotation axis. For this reason, from now on, we only use the $R_{\mathbf{n},\gamma }$ notation for the Lorentzian rotation around the axis $\mathbf{n}$ by the angle $\gamma$. But one can also prefer to call it the Lorentzian rotation about the axis ℓ with respect to the vector $\mathbf{n}$, by the angle $\gamma$.

It is known that any nonzero vector $\mathbf{x}\in {\mathbb{R}}_1^3$ and $R_{\mathbf{n},\gamma }\left(\mathbf{x}\right)$ are in the same casual character, and the endpoint of the rotated vector $R_{\mathbf{n},\gamma }\left(\mathbf{x}\right)$ is on the plane ${\mathsf{\Pi }}_{\mathbf{n},\mathbf{x}}$ which passes through the endpoint of $\mathbf{x}$ and Lorentzian orthogonal to $\mathbf{n}$. So, the trajectory of the motion of the endpoint of the vector $\mathbf{x}$ under the rotation $R_{\mathbf{n},\gamma }$ is either a line or a parabola since the intersection of the Lorentzian sphere and the plane ${\mathsf{\Pi }}_{\mathbf{n},\mathbf{x}}$ is either two parallel lines or a parabola. More clearly, the trajectory is a parabola when the endpoint of $\mathbf{x}$ is on a hyperbolic sphere or a light cone, while the trajectory is either a line or a parabola when the endpoint is on a pseudosphere; in particular, the trajectory is a line when the endpoint of $\mathbf{x}$ is on the plane ${\mathsf{\Pi }}_{\mathbf{n}}$ which passes through the origin and Lorentzian orthogonal to $\mathbf{n}$, and the trajectory is a parabola when the endpoint of $\mathbf{x}$ is not on the plane ${\mathsf{\Pi }}_{\mathbf{n}}$.

Let $\mathbf{x}$ be any nonzero vector linearly independent from $\mathbf{n}$. Then, either the vector $\mathbf{x}$ lies in the plane ${\mathsf{\Pi }}_{\mathbf{n}}$ or it does not; in other words, either ${⟨\mathbf{x},\mathbf{n}⟩}_L=0$, or ${⟨\mathbf{x},\mathbf{n}⟩}_L\ne 0$.

(1) First, let $\mathbf{x}$ lie in the plane ${\mathsf{\Pi }}_{\mathbf{n}}$. In this case, $\mathbf{x}$ is a spacelike vector that can be written in general form as $\mathbf{x}=(x,x,r)$, and its endpoint is on the Lorentz space circle ${∥\mathbf{x}∥}_L=\left|r\right|$, which consists of a pair of parallel lines. Then, one can see that

$$R_{\mathbf{n},\gamma }\left(\mathbf{x}\right)=\mathbf{x}+\gamma r\mathbf{n},$$

(30)

and so the rotation occurs in the plane ${\mathsf{\Pi }}_{\mathbf{n}}$, which is a tangent to the light cone along the line with direction vector $\mathbf{n}$. Moreover, if ${∥\mathbf{n}∥}_E=1$, then the directed area of the vector $\mathbf{x}$ swept under the rotation $R_{\mathbf{n},\gamma }$ is $\gamma r^2/2$ (see Figure 1). Therefore, in accordance with the classical geometries, the measurement $\gamma$ of the directed angle of the rotation with the axis $\mathbf{n}$ form $\mathbf{x}$ to $R_{\mathbf{n},\gamma }\left(\mathbf{x}\right)$ corresponds to the directed area $\gamma r^2/2$. In addition, if ${∥\mathbf{n}∥}_E\ne 1$, then the corresponding area increases ${∥\mathbf{n}∥}_E$-fold. Consequently, for two given vectors $\mathbf{x}=(x_1,x_1,r)$ and $\mathbf{y}=(y_1,y_1,r)$ such that $R_{\mathbf{n},\gamma }\left(\mathbf{x}\right)=\mathbf{y}$ where $\mathbf{n}=\left(n,n,0\right)$, the directed angle $\gamma$ of the rotation can be computed by

$$\gamma ={\displaystyle \frac{2S}{{∥\mathbf{x}∥}_L^2{∥\mathbf{n}∥}_E}}$$

(31)

where S is equal to the directed area of the triangle determined by the vectors $\mathbf{x}$ and $\mathbf{y}$.

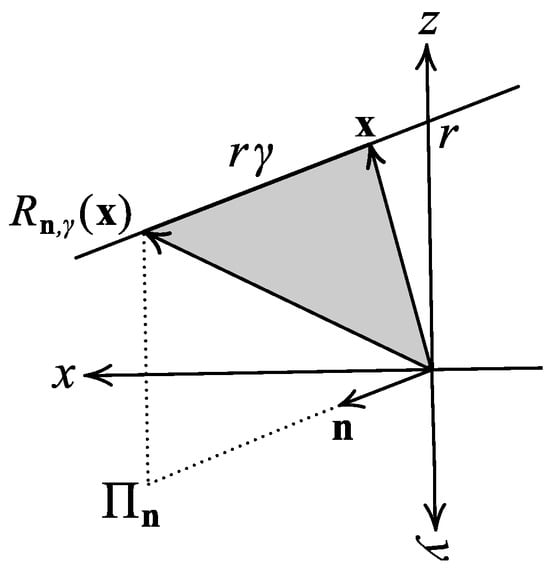
Figure 1. Area of the region swept by $\mathbf{x}$ under $R_{\mathbf{n},\gamma }$, where ${∥\mathbf{n}∥}_E=1$ and ${⟨\mathbf{x},\mathbf{n}⟩}_L=0$.

Notice that, since the Lorentzian vector product of $\mathbf{x}$ and $\mathbf{y}$ is in the same direction as $\mathbf{n}$ in this case, one can define the angle between them by the angle of the rotation with the standard lightlike axis $\mathbf{n}=(1,1,0)$, which transforms $\mathbf{x}$ to $\mathbf{y}$, as follows

$$\gamma ={\displaystyle \frac{\sqrt{2}S}{{∥\mathbf{x}∥}_L^2}}.$$

(32)

Clearly, this definition completes the angle definition between spacelike vectors given in the preliminary section.

(2) For the other cases, let us consider a nonzero vector $\mathbf{x}$ which does not lie in the plane ${\mathsf{\Pi }}_{\mathbf{n}}$. In this case, $\mathbf{x}$ can be a spacelike, timelike or lightlike vector, and the rotation occurs in the plane ${\mathsf{\Pi }}_{\mathbf{n},\mathbf{x}}$, which is parallel to ${\mathsf{\Pi }}_{\mathbf{n}}$. Then, one can see that the plane ${\mathsf{\Pi }}_{\mathbf{n},\mathbf{x}}$ can be written in general form as $-x+y+d\sqrt{2}=0$ for a nonzero real number d, such that $\left|d\right|$ is equal to the Euclidean distance from the origin to the plane ${\mathsf{\Pi }}_{\mathbf{n},\mathbf{x}}$. So, $\mathbf{x}$ can be written in general form as $\mathbf{x}=(x_1,x_1-d\sqrt{2},x_3)$ for $x_1,x_3\in \mathbb{R}$. Using the matrix of the Lorentzian rotation (21) about the axis $\mathbf{n}$ with ${∥\mathbf{n}∥}_E=1$ by the angle $\gamma$, one finds that the difference of the third component of the coordinates of $\mathbf{x}$ and $R_{\mathbf{n},\gamma }\left(\mathbf{x}\right)$ is $\gamma d$. In addition, the Euclidean length of the Euclidean orthogonal projection of the vector $\mathbf{x}$ to the plane ${\mathsf{\Pi }}_{\mathbf{n}}^E$, which passes through the origin and Euclidean orthogonal to $\mathbf{n}$, is $\left|d\right|$. Therefore, when $\mathbf{x}$ completes its movement under the transformation $R_{\mathbf{n},\gamma }$, the area of the Euclidean orthogonal projection of the triangle scanned by $\mathbf{x}$ onto the plane Euclidean orthogonal to $\mathbf{n}$ is $\gamma d^2/2$ (see Figure 2). Therefore, in accordance with the classical geometries again, the measurement $\gamma$ of the directed angle of the rotation with the axis $\mathbf{n}$ from $\mathbf{x}$ to $R_{\mathbf{n},\gamma }\left(\mathbf{x}\right)$ corresponds to the directed area $\gamma d^2/2$, where $\left|d\right|$, acting like a radius, is the Euclidean distance from the origin to the plane ${\mathsf{\Pi }}_{\mathbf{n},\mathbf{x}}$. In addition, if ${∥\mathbf{n}∥}_E\ne 1$, then the corresponding area and the difference of the third components increases ${∥\mathbf{n}∥}_E$-fold. Consequently, for two given vectors $\mathbf{x}=(x_1,x_2,x_3)$ and $\mathbf{y}=(y_1,y_2,y_3)$ such that $R_{\mathbf{n},\gamma }\left(\mathbf{x}\right)=\mathbf{y}$, the directed angle $\gamma$ can be computed by

$$\gamma ={\displaystyle \frac{2S}{d^2{∥\mathbf{n}∥}_E}},$$

(33)

where S is equal to the directed area of the Euclidean orthogonal projection of the triangle defined by vectors $\mathbf{x}$ and $\mathbf{y}$ onto the plane ${\mathsf{\Pi }}_{\mathbf{n}}^E$. Notice that in this case, the rotation angle from $\mathbf{x}$ to $R_{\mathbf{n},\gamma }\left(\mathbf{x}\right)$ cannot be equal to the angle between them, since their Lorentzian vector product cannot be in the same direction as $\mathbf{n}$.

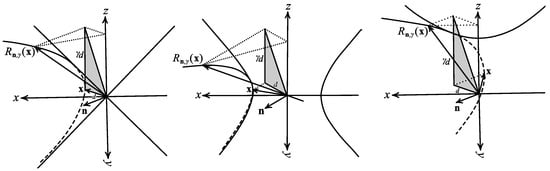
Figure 2. Area of the Euclidean orthogonal projection of the region swept by $\mathbf{x}$ under $R_{\mathbf{n},\gamma }$, where ${∥\mathbf{n}∥}_E=1$ and ${⟨\mathbf{x},\mathbf{n}⟩}_L\ne 0$.

Example 1.

Let us take two spacelike vectors $\mathbf{x}=\left(1,1,3\right)$ and $\mathbf{y}=\left(2,2,3\right)$ whose Lorentzian vector product is lightlike. Then one can obtain the angle between $\mathbf{x}$ and $\mathbf{y}$ as

$$\gamma ={\displaystyle \frac{\sqrt{2}S}{{∥\mathbf{x}∥}_L^2}}={\displaystyle \frac{\sqrt{2}\left(\frac{3\sqrt{2}}{2}\right)}{9}}={\displaystyle \frac{1}{3}}$$

where $S=3\sqrt{2}/2$ is the area of the triangle determined by the vectors $\mathbf{x}$ and $\mathbf{y}$. One can check that for the Lorentzian rotation $R_{\mathbf{n},\gamma }\left(\mathbf{x}\right)$ about the axis $\mathbf{n}=\left(1,1,0\right)$ by the angle $\gamma =1/3$,

$$R_{\left(1,1,0\right),{\displaystyle \frac{1}{3}}}\left(\mathbf{x}\right)=\left[\begin{array}{ccc}{\displaystyle \frac{19}{18}}& -{\displaystyle \frac{1}{18}}& {\displaystyle \frac{1}{3}}\\ {\displaystyle \frac{1}{18}}& {\displaystyle \frac{17}{18}}& {\displaystyle \frac{1}{3}}\\ {\displaystyle \frac{1}{3}}& -{\displaystyle \frac{1}{3}}& 1\end{array}\right]\left[\begin{array}{c}1\\ 1\\ 3\end{array}\right]=\mathbf{y}.$$

Notice that the trajectory in this example is a line. In addition to this example, the measurement of the angle of the rotation about another lightlike axis $\mathbf{n}=\left(2,2,0\right)$ from $\mathbf{x}$ to $\mathbf{y}$ can be computed as

$$\gamma ={\displaystyle \frac{2S}{{∥\mathbf{x}∥}_L^2{∥\mathbf{n}∥}_E}}={\displaystyle \frac{2\left(\frac{3\sqrt{2}}{2}\right)}{\left(9\right)\left(2\sqrt{2}\right)}}={\displaystyle \frac{1}{6}}.$$

It is easy to check that

$$R_{\left(2,2,0\right),{\displaystyle \frac{1}{6}}}\left(\mathbf{x}\right)=\left[\begin{array}{ccc}{\displaystyle \frac{19}{18}}& -{\displaystyle \frac{1}{18}}& {\displaystyle \frac{1}{3}}\\ {\displaystyle \frac{1}{18}}& {\displaystyle \frac{17}{18}}& {\displaystyle \frac{1}{3}}\\ {\displaystyle \frac{1}{3}}& -{\displaystyle \frac{1}{3}}& 1\end{array}\right]\left[\begin{array}{c}1\\ 1\\ 3\end{array}\right]=\mathbf{y}.$$

Example 2.

Let us take a timelike vector $\mathbf{x}=\left(3,0,1\right)$ to rotate by the Lorentzian rotation about the lightlike axis $\mathbf{n}=\left(2,\sqrt{2},\sqrt{2}\right)$ by the angle $\gamma =1$. Then the rotation matrix can be found as

$$R_{\left(2,\sqrt{2},\sqrt{2}\right),1}=\left[\begin{array}{ccc}3& -2\sqrt{2}& 0\\ 0& 0& 1\\ 2\sqrt{2}& -3& 0\end{array}\right]$$

and we get

$$R_{\left(1/2,1/2,0\right),2}\left(\mathbf{x}\right)=\left(9,1,6\sqrt{2}\right)=\mathbf{y}.$$

One can verify the rotation angle γ by the formula as

$$\gamma ={\displaystyle \frac{2S}{d^2{∥\mathbf{n}∥}_E}}={\displaystyle \frac{2\left(\frac{19}{4}\sqrt{2}-3\right)}{{\left(\frac{6-\sqrt{2}}{2\sqrt{2}}\right)}^2\left(2\sqrt{2}\right)}}=1$$

where $d={\displaystyle \frac{6-\sqrt{2}}{2\sqrt{2}}}$ is the Euclidean distance from the origin to the plane ${\mathsf{\Pi }}_{\mathbf{n},\mathbf{x}}:-2x+\sqrt{2}y+\sqrt{2}z-\sqrt{2}+6=0$, and S is equal to the area of the Euclidean orthogonal projection of the triangle defined by vectors $\mathbf{x}$ and $\mathbf{y}$ onto the plane ${\mathsf{\Pi }}_{\mathbf{n}}^E:2x+\sqrt{2}y+\sqrt{2}z=0$ which passes through the origin and Euclidean orthogonal to $\mathbf{n}$. Notice that the trajectory in this case is a parabola.

5. $\mathsf{\Omega }$-Rotation About an $\mathsf{\Omega }$-Lightlike Axis

It is known that any given general hyperboloid of one or two sheets or general cones, which are $\Omega$-spheres, can be transformed to their standard forms, which are Lorentzian spheres, by an affine transformation. So, if $q_L\left(\mathbf{v}\right)={\mathbf{v}}^T{I}^{\ast }\mathbf{v}$ and $q_{\Omega }\left(\mathbf{v}\right)={\mathbf{v}}^T\Omega \mathbf{v}$ are the quadratic forms associated with the Lorentzian and $\Omega$-scalar products, respectively, and A is a linear transformation that transforms the $\Omega$-spheres to the standard Lorentz spheres, then

$$q_L\left(\mathbf{v}\right)=q_{\Omega }\left(A\mathbf{v}\right)$$

(34)

for every vector $\mathbf{v}\in {\mathbb{R}}^3$, and one gets

$$A^T\Omega A=I^{\ast }\mathrm{or}\Omega ={\left(A{I}^{\ast }{A}^T\right)}^{-1}$$

(35)

and

$${⟨\mathbf{x},\mathbf{y}⟩}_L={⟨A\mathbf{x},A\mathbf{y}⟩}_{\Omega }.$$

(36)

Therefore, the geometric structure of the $\Omega$-space ${\mathbb{R}}_{\Omega }^3$ is the same as the standard Lorentzian space ${\mathbb{R}}_1^3$. In other words, orthogonality, parallelism, and tangency are preserved.

For example, if $\mathbf{n}$ is $\Omega$-lightlike vector, then the plane ${\mathsf{\Pi }}_{\mathbf{n}}^{\Omega }$ which passes through the origin and $\Omega$-orthogonal to $\mathbf{n}$ is the tangent plane to the $\Omega$-light cone along the line with direction vector $\mathbf{n}$; the intersection of the plane ${\mathsf{\Pi }}_{\mathbf{n}}^{\Omega }$ with the $\Omega$-pseudo spheres is two parallel lines. Likewise, Cartan’s $\Omega$-frame is a $\Omega$-pseudo-orthonormal positively oriented frame $\left\{\mathbf{c},\mathbf{t},\mathbf{n}\right\}$ formed by linearly independent $\Omega$-lightlike vectors $\mathbf{c}$ and $\mathbf{n}$ which are on the $\Omega$-light cone, and a unit $\Omega$-spacelike vector $\mathbf{t}$ which is on the $\Omega$-pseudosphere with radius 1, satisfying the following conditions:

$$\begin{array}{c}{⟨\mathbf{c},\mathbf{c}⟩}_{\Omega }={⟨\mathbf{n},\mathbf{n}⟩}_{\Omega }={⟨\mathbf{c},\mathbf{t}⟩}_{\Omega }={⟨\mathbf{n},\mathbf{t}⟩}_{\Omega }=0,\\ {⟨\mathbf{t},\mathbf{t}⟩}_{\Omega }={⟨\mathbf{c},\mathbf{n}⟩}_{\Omega }=1,\\ \mathbf{c}{\times }_{\Omega }\mathbf{t}=\mathbf{c},\mathbf{t}{\times }_{\Omega }\mathbf{n}=\mathbf{n},\mathbf{n}{\times }_{\Omega }\mathbf{c}=\mathbf{t}.\end{array}$$

(37)

A real matrix O is $\Omega$-orthogonal if and only if $O^T\Omega O=\Omega$, and the set of all $\Omega$-orthogonal matrices whose determinants are equal to 1 gives the generalized Lorentzian group consists of all $\Omega$-rotation matrices of ${\mathbb{R}}_{\Omega }^3$. For any vector $\mathbf{x}\in {\mathbb{R}}^3$, if R is an $\Omega$-rotation matrix, the endpoint of $R\left(\mathbf{x}\right)$ is on the plane ${\mathsf{\Pi }}_{\mathbf{n},\mathbf{x}}^{\Omega }$ which passes through the endpoint of $\mathbf{x}$ and $\Omega$-orthogonal to $\mathbf{n}$, since

$${⟨\mathbf{x}-R\left(\mathbf{x}\right),\mathbf{n}⟩}_{\Omega }={⟨\mathbf{x},\mathbf{n}⟩}_{\Omega }-{⟨R\left(\mathbf{x}\right),R\left(\mathbf{n}\right)⟩}_{\Omega }=0.$$

(38)

So, as in the standard Lorentzian case, the trajectory of motion of the endpoint of a vector under $\Omega$-rotation is either a line or a parabola since the intersection of the $\Omega$-Lorentzian spheres and such a plane whose $\Omega$-normal is $\Omega$-lightlike vector is either two parallel lines or a parabola. If R is an $\Omega$-rotation matrix, then one of the eigenvalues of R is 1, and the eigenvector $\mathbf{n}$ corresponding to 1 determines the axis of rotation. In addition, in analogy with the standard Lorentzian geometry, if $R_{\mathbf{n}}$ is an $\Omega$-rotation matrix about the axis $\mathbf{n}$, we define the angle $\gamma$ as the $\Omega$-measurement of the rotation angle if

$${⟨R_{\mathbf{n}}\left(\mathbf{t}\right),\mathbf{c}⟩}_{\Omega }=\gamma$$

(39)

is satisfied for Cartan’s $\Omega$-frame $\left\{\mathbf{c},\mathbf{t},\mathbf{n}\right\}$, and denoted as $R_{\mathbf{n}}$ with the angle $\gamma$ by $R_{\mathbf{n},\gamma }$.

However, the geometric meaning of $\Omega$-measurement of the angle $\gamma$ slightly changes, since one needs to use the generalization of the Euclidean norm by the same linear transformation A in the corresponding angle formula. One can obtain that

$${⟨\mathbf{x},\mathbf{y}⟩}_E={⟨A\mathbf{x},A\mathbf{y}⟩}_{{\Omega }_E}$$

(40)

for

$${\Omega }_E=\Omega \left(A{I}^{\ast }{A}^{-1}\right)$$

(41)

which gives the generalization of the Euclidean norm with respect to the linear transformation A. So, for two given vectors $\mathbf{x}$ and $\mathbf{y}$ such that $R_{\mathbf{n},\gamma }\left(\mathbf{x}\right)=\mathbf{y}$ where $R_{\mathbf{n},\gamma }$ is an $\Omega$-rotation matrix about the axis $\mathbf{n}$ by the angle $\gamma$, the directed angle $\gamma$ can be computed by the formula

$$\gamma ={\displaystyle \frac{2S_{{\Omega }_E}}{{∥\mathbf{x}∥}_{\Omega }^2{∥\mathbf{n}∥}_{{\Omega }_E}}}$$

(42)

if ${⟨\mathbf{x},\mathbf{n}⟩}_{\Omega }=0$ in which $\mathbf{x}$ can only be an $\Omega$-spacelike vector in the plane ${\mathsf{\Pi }}_{\mathbf{n}}^{\Omega }$, and by the formula

$$\gamma ={\displaystyle \frac{2S_{{\Omega }_E}}{d_{{\Omega }_E}^2{∥\mathbf{n}∥}_{{\Omega }_E}}}$$

(43)

if ${⟨\mathbf{x},\mathbf{n}⟩}_{\Omega }\ne 0$ in which $\mathbf{x}$ can be any vector not in the plane ${\mathsf{\Pi }}_{\mathbf{n}}^{\Omega }$, where $d_{{\Omega }_E}$ is the ${\Omega }_E$-distance from the origin to the plane ${\mathsf{\Pi }}_{\mathbf{n},\mathbf{x}}^{{\Omega }_E}$, and $S_{{\Omega }_E}$ is the directed ${\Omega }_E$-area of the ${\Omega }_E$-orthogonal projection of the triangle defined by vectors $\mathbf{x}$ and $\mathbf{y}$ onto the plane ${\mathsf{\Pi }}_{\mathbf{n}}^{{\Omega }_E}$.

Here, one can derive the matrix A using the Euclidean orthogonal diagonalization of the matrix $\Omega$ as follows: Let P be the Euclidean-normalized orthogonal matrix with the first column determined by the negative eigenvalue of the matrix $\Omega$, which has one negative and two positive eigenvalues. And let D be the diagonal matrix determined by the eigenvalues corresponding to the columns of P. Then we have $\Omega =PD{P}^T$ or $P^T\Omega P=D$. If $N^2=D{I}^{\ast }$ then $A=P{N}^{-1}{I}^{\ast }$ gives the linear transformation A, since

$$\begin{array}{ccc}\hfill {⟨A\mathbf{x},A\mathbf{y}⟩}_{\Omega }& =& {\mathbf{x}}^T{\left(P{N}^{-1}{I}^{\ast }\right)}^T\Omega \left(P{N}^{-1}{I}^{\ast }\right)\mathbf{y}\hfill \\ & =& {\mathbf{x}}^T{I}^{\ast }{N}^{-1}D{N}^{-1}{I}^{\ast }\mathbf{y}\hfill \\ & =& {\mathbf{x}}^T{I}^{\ast }{I}^{\ast }{I}^{\ast }\mathbf{y}={\mathbf{x}}^T{I}^{\ast }\mathbf{y}={⟨\mathbf{x},\mathbf{y}⟩}_L.\hfill \end{array}$$

In the next sections, we determine the matrix of $\Omega$-rotation about an $\Omega$-lightlike axis, and the rotation angle of a given $\Omega$-rotation matrix, using the Rodrigues and Cayley methods and $\Omega$-split quaternions, by the following five theorems. These theorems are actually well-known results for the standard Minkowski 3-space. We just use the $\Omega$-scalar product in the proofs instead of the standard Lorentzian scalar product, and we see that the generalized Lorentz rotation formulas are identical to the standard Lorentzian rotation formulas with the exception of skew-symmetric matrices.

6. $\mathsf{\Omega }$-Rotation Formula by the Rodrigues Formula

Here, we determine the matrix of the $\Omega$-rotation around an $\Omega$-lightlike vector $\mathbf{n}$ by an angle $\gamma$, using the Rodrigues formula and Cartan’s $\Omega$-frame. Note that the characteristic polynomial of $S_{\mathbf{n}}$ is

$$P\left(x\right)=x^3-{⟨\mathbf{n},\mathbf{n}⟩}_{\Omega }x,$$

(44)

and so one gets

$$S_{\mathbf{n}}^3=0$$

(45)

for the $\Omega$-lightlike vector $\mathbf{n}$.

Theorem 1.

Let us take an $\Omega$-lightlike vector $\mathbf{n}$, and angle $\gamma \in \mathbb{R}$. Then, for the $\Omega$-skew-symmetric matrix $S_{\mathbf{n}}$, the matrix exponential function

$$e^{-\gamma S_{\mathbf{n}}}=I_3-\gamma S_{\mathbf{n}}+\frac{{\gamma }^2}{2}{S}_{\mathbf{n}}^2$$

(46)

is the matrix $R_{\mathbf{n},\gamma }$ of the $\Omega$-rotation about the vector $\mathbf{n}$ by the angle γ. In addition, $R_{\mathbf{n},\gamma }$ can be written as follows:

$$R_{\mathbf{n},\gamma }=\left[\begin{array}{ccc}-{\displaystyle \frac{1}{2}}{\gamma }^2{\sigma }_{u_1}^{\prime }-\gamma {\Lambda }_{5,6}^{\prime }+1& -{\displaystyle \frac{1}{2}}{\gamma }^2{\sigma }_{u_1}^{″}-\gamma {\Lambda }_{3,5}^{″}& -{\displaystyle \frac{1}{2}}{\gamma }^2{\sigma }_{u_1}^{‴}-\gamma {\Lambda }_{6,3}^{‴}\\ -{\displaystyle \frac{1}{2}}{\gamma }^2{\sigma }_{u_2}^{\prime }-\gamma {\Lambda }_{4,2}^{\prime }& -{\displaystyle \frac{1}{2}}{\gamma }^2{\sigma }_{u_2}^{″}-\gamma {\Lambda }_{6,4}^{″}+1& -{\displaystyle \frac{1}{2}}{\gamma }^2{\sigma }_{u_2}^{‴}-\gamma {\Lambda }_{2,6}^{‴}\\ -{\displaystyle \frac{1}{2}}{\gamma }^2{\sigma }_{u_3}^{\prime }-\gamma {\Lambda }_{1,4}^{\prime }& -{\displaystyle \frac{1}{2}}{\gamma }^2{\sigma }_{u_3}^{″}-\gamma {\Lambda }_{5,1}^{″}& -{\displaystyle \frac{1}{2}}{\gamma }^2{\sigma }_{u_3}^{‴}-\gamma {\Lambda }_{4,5}^{‴}+1\end{array}\right]$$

(47)

where ${\sigma }_{n_i}^{\prime }=n_i\left(A{n}_1+D{n}_2+E{n}_3\right)$, ${\sigma }_{n_i}^{″}=n_i\left(D{n}_1+B{n}_2+F{n}_3\right)$, ${\sigma }_{n_i}^{‴}=n_i\left(E{n}_1+F{n}_2+C{n}_3\right)$, ${\Lambda }_{i,j}^{\prime }=\left({\Delta }_i{n}_2-{\Delta }_j{n}_3\right)$${\Lambda }_{i,j}^{″}=\left({\Delta }_i{n}_3-{\Delta }_j{n}_1\right)$ and ${\Lambda }_{i,j}^{‴}=\left({\Delta }_i{n}_1-{\Delta }_j{n}_2\right)$.

Proof. 

Let $R_{\mathbf{n},\gamma }\left(\mathbf{x}\right)={\mathbf{x}}^{\prime }$ for a nonzero vector $\mathbf{x}$. The vector $\mathbf{x}$ can be written in Cartan’s $\Omega$-frame $\left\{\mathbf{c},\mathbf{t},\mathbf{n}\right\}$ as $\mathbf{x}=x\mathbf{c}+y\mathbf{t}+z\mathbf{n}$ where $x,y,z\in \mathbb{R}$. Using the linearity, we get

$${\mathbf{x}}^{\prime }=x{R}_{\mathbf{n},\gamma }\left(\mathbf{c}\right)+y{R}_{\mathbf{n},\gamma }\left(\mathbf{t}\right)+z\mathbf{n}.$$

The vectors $R_{\mathbf{n},\gamma }\left(\mathbf{c}\right)$ and $R_{\mathbf{n},\gamma }\left(\mathbf{t}\right)$ can also be written in Cartan’s $\Omega$-frame as

$$\begin{array}{ccc}\hfill R_{\mathbf{n},\gamma }\left(\mathbf{c}\right)& =& x_1\mathbf{c}+y_1\mathbf{t}+z_1\mathbf{n}\hfill \\ \hfill R_{\mathbf{n},\gamma }\left(\mathbf{t}\right)& =& x_2\mathbf{c}+y_2\mathbf{t}+z_2\mathbf{n}\hfill \end{array}$$

where $x_1,x_2,y_1,y_2,z_1,z_2\in \mathbb{R}$. Then considering Cartan’s $\Omega$-frame conditions, one gets

$$\begin{array}{ccc}\hfill {⟨R_{\mathbf{n},\gamma }\left(\mathbf{c}\right),\mathbf{n}⟩}_{\Omega }& =& x_1\hfill \\ \hfill {⟨R_{\mathbf{n},\gamma }\left(\mathbf{t}\right),\mathbf{n}⟩}_{\Omega }& =& x_2.\hfill \end{array}$$

In addition, since we have

$$\begin{array}{ccc}\hfill {⟨R_{\mathbf{n},\gamma }\left(\mathbf{c}\right),\mathbf{n}⟩}_{\Omega }& =& {⟨\mathbf{c},\mathbf{n}⟩}_{\Omega }=1\hfill \\ \hfill {⟨R_{\mathbf{n},\gamma }\left(\mathbf{t}\right),\mathbf{n}⟩}_{\Omega }& =& {⟨\mathbf{t},\mathbf{n}⟩}_{\Omega }=0,\hfill \end{array}$$

we get $x_1=1$ and $x_2=0$. In addition, one can obtain the followings:

$$\begin{array}{ccc}\hfill 0& =& {⟨\mathbf{c},\mathbf{t}⟩}_{\Omega }={⟨R_{\mathbf{n},\gamma }\left(\mathbf{c}\right),R_{\mathbf{n},\gamma }\left(\mathbf{t}\right)⟩}_{\Omega }=z_2+y_1{y}_2\hfill \\ \hfill 0& =& {⟨\mathbf{c},\mathbf{c}⟩}_{\Omega }={⟨R_{\mathbf{n},\gamma }\left(\mathbf{c}\right),R_{\mathbf{n},\gamma }\left(\mathbf{c}\right)⟩}_{\Omega }=y_1^2+2z_1\hfill \\ \hfill 1& =& {⟨\mathbf{t},\mathbf{t}⟩}_{\Omega }={⟨R_{\mathbf{n},\gamma }\left(\mathbf{t}\right),R_{\mathbf{n},\gamma }\left(\mathbf{t}\right)⟩}_{\Omega }=y_2^2.\hfill \end{array}$$

Then, it follows that

$$\begin{array}{ccc}\hfill z_1& =& -{\displaystyle \frac{y_1^2}{2}}\hfill \\ \hfill y_2& =& 1\hfill \\ \hfill z_2& =& -y_1\hfill \end{array}$$

and so we get

$$\begin{array}{ccc}\hfill R_{\mathbf{n},\gamma }\left(\mathbf{c}\right)& =& \mathbf{c}+y_1\mathbf{t}-\frac{y_1^2}{2}\mathbf{n}\hfill \\ \hfill R_{\mathbf{n},\gamma }\left(\mathbf{t}\right)& =& \mathbf{t}-y_1\mathbf{n}.\hfill \end{array}$$

Moreover, since we have that

$${⟨R_{\mathbf{n},\gamma }\left(\mathbf{t}\right),c⟩}_{\Omega }=\gamma =-y_1$$

we get

$$\begin{array}{ccc}\hfill R_{\mathbf{n},\gamma }\left(\mathbf{c}\right)& =& \mathbf{c}+\gamma \mathbf{t}-\frac{{\gamma }^2}{2}\mathbf{n}\hfill \\ \hfill R_{\mathbf{n},\gamma }\left(\mathbf{t}\right)& =& \mathbf{t}+\gamma \mathbf{n}\hfill \end{array}$$

and so have

$${\mathbf{x}}^{\prime }=x\left(\mathbf{c}+\gamma \mathbf{t}-\frac{{\gamma }^2}{2}\mathbf{n}\right)+y\left(\mathbf{t}+\gamma \mathbf{n}\right)+z\mathbf{n}.$$

Differentiating this equation for the variable $\gamma$, we get

$${\displaystyle \frac{d{\mathbf{x}}^{\prime }}{d\gamma }}=-x{R}_{\mathbf{n},\gamma }\left(\mathbf{t}\right)+y\mathbf{n}.$$

On the other hand, considering again Cartan’s $\Omega$-frame conditions, we derive that

$$\begin{array}{ccc}\hfill \mathbf{n}{\times }_{\Omega }{\mathbf{x}}^{\prime }& =& x\left(\mathbf{n}{\times }_{\Omega }{R}_{\mathbf{n},\gamma }\left(\mathbf{c}\right)\right)+y\left(\mathbf{n}\times R_{\mathbf{n},\gamma }\left(\mathbf{t}\right)\right)\hfill \\ & =& x\left(\mathbf{n}{\times }_{\Omega }\left(\mathbf{c}+\gamma \mathbf{t}-\frac{{\gamma }^2}{2}\mathbf{n}\right)\right)+y\left(\mathbf{n}{\times }_{\Omega }\left(\mathbf{t}+\gamma \mathbf{n}\right)\right)\hfill \\ & =& x\left(\mathbf{t}-\gamma \mathbf{n}\right)-y\mathbf{n}=x{R}_{\mathbf{n},\gamma }\left(\mathbf{t}\right)-y\mathbf{n}\hfill \end{array}$$

and we obtain

$${\displaystyle \frac{d{\mathbf{x}}^{\prime }}{d\gamma }}=-S_{\mathbf{n}}{\mathbf{x}}^{\prime }.$$

Integrating this equation, we get

$${\mathbf{x}}^{\prime }=e^{-\gamma S_{\mathbf{n}}}\mathbf{x}$$

and

$$R_{\mathbf{n},\gamma }\left(\mathbf{x}\right)=e^{-\gamma S_{\mathbf{n}}}.$$

By using the Taylor power series expansion of $e^{-\gamma S_{\mathbf{n}}}$ and $S_{\mathbf{n}}^3=0$ (see [21,22] for the exponential of semi-skew matrices), we obtain the Rodrigues rotation formula as

$$R_{\mathbf{n},\gamma }=e^{-\gamma S_{\mathbf{n}}}=I_3-\gamma S_{\mathbf{n}}+\frac{{\gamma }^2}{2}{S}_{\mathbf{n}}^2.$$

Substituting the matrix (8) into this equation, one derives the matrix (47). One can see that the determinant of the matrix (47) is 1. In addition, using the $\Omega$-skew-symmetric matrix property, one gets the $\Omega$-orthogonality of $R_{\mathbf{n},\gamma }$ as follows:

$$\begin{array}{ccc}\hfill R_{\mathbf{n},\gamma }^T\Omega R_{\mathbf{n},\gamma }& =& {\left(I_3-\gamma S_{\mathbf{n}}+\frac{{\gamma }^2}{2}{S}_{\mathbf{n}}^2\right)}^T\Omega R_{\mathbf{n},\gamma }\hfill \\ & =& \left(I_3+\gamma \Omega S_{\mathbf{n}}{\Omega }^{-1}+\frac{{\gamma }^2}{2}\Omega S_{\mathbf{n}}^2{\Omega }^{-1}\right)\Omega R_{\mathbf{n},\gamma }\hfill \\ & =& \left(\Omega +\gamma \Omega S_{\mathbf{n}}+\frac{{\gamma }^2}{2}\Omega S_{\mathbf{n}}^2\right)\left(I_3-\gamma S_{\mathbf{n}}+\frac{{\gamma }^2}{2}{S}_{\mathbf{u}}^2\right)\hfill \\ & =& \Omega +\frac{{\gamma }^2}{2}\Omega S_{\mathbf{n}}^2-{\gamma }^2\Omega S_{\mathbf{n}}^2+\frac{{\gamma }^2}{2}\Omega S_{\mathbf{n}}^2=\Omega .\hfill \end{array}$$

Thus, $R_{\mathbf{n},\gamma }$ is the $\Omega$-rotation matrix about the $\Omega$-lightlike axis $\mathbf{n}$ by the angle $\gamma$. Notice that the matrix (47) has eigenvalues $x_1=x_2=x_3=1$. □

If R is an $\Omega$-rotation matrix whose axis and angle are unknown, then while its axis can be determined by the eigenvector corresponding to the eigenvalue 1, its angle can be found by the following theorem.

Theorem 2.

Let R be an $\Omega$-rotation matrix. If $\mathbf{n}$ is the axis of the $\Omega$-rotation R, then the angle γ can be computed by the formula

$$\gamma \Omega S_{\mathbf{n}}={\displaystyle \frac{1}{2}}\left(R^T\Omega -\Omega R\right).$$

(48)

Proof. 

By using Formula (46), and the $\Omega$-skew-symmetric matrix property $S_{\mathbf{n}}^T\Omega =-\Omega S_{\mathbf{n}}$, one obtains that

$$\begin{array}{ccc}\hfill R^T\Omega & =& \Omega -\gamma S_{\mathbf{n}}^T\Omega +\frac{{\gamma }^2}{2}{\left(S_{\mathbf{n}}^2\right)}^T\Omega \hfill \\ & =& \Omega +\gamma \Omega S_{\mathbf{n}}+\frac{{\gamma }^2}{2}\Omega S_{\mathbf{n}}^2\hfill \\ & =& \Omega R+2\gamma \Omega S_{\mathbf{n}}.\hfill \end{array}$$

which gives Equation (48). □

Example 3.

Given a general cone, two general hyperboloids with the equations

$$\begin{array}{ccc}\hfill x^2+3y^2+4zy& =& 0\hfill \\ \hfill x^2+3y^2+4zy& =& -4\hfill \\ \hfill x^2+3y^2+4zy& =& 4,\hfill \end{array}$$

which are the $\Omega$-light cone, the $\Omega$-hyperbolic sphere, and the $\Omega$-pseudosphere with centers at the origin, for the matrix

$$\Omega =\left[\begin{array}{ccc}1& 0& 0\\ 0& 3& 2\\ 0& 2& 0\end{array}\right],$$

respectively. Let us consider an $\Omega$-lightlike vector $\mathbf{n}=\left(-3/2,-1/2,3/2\right)$. Using the Equation (47), one can calculate $R_{\mathbf{n},\gamma }$ for the angle $\gamma =4$ as follows:

$$R_{\left(-3/2,-1/2,3/2\right),4}=\left[\begin{array}{ccc}-17& 30& -8\\ -8& 13& -4\\ 15& -27& 7\end{array}\right].$$

Consider an $\Omega$-lightlike vector ${\mathbf{x}}_1=\left(1,-1,1\right)$, $\Omega$-timelike vector ${\mathbf{x}}_2=\left(1,2,-3\right)$, and two $\Omega$-spacelike vectors ${\mathbf{x}}_3=\left(1,2,0\right)$ and ${\mathbf{x}}_4=\left(2,1,-3/2\right)$ such that ${⟨{\mathbf{x}}_4,\mathbf{n}⟩}_{\Omega }=0$, and rotate them about the vector $\mathbf{n}$ by the angle 4. One can derive the following results:

$$\begin{array}{ccc}\hfill R_{\left(-3/2,-1/2,3/2\right),4}\left({\mathbf{x}}_1\right)& =& (-55,-25,49)\hfill \\ \hfill R_{\left(-3/2,-1/2,3/2\right),4}\left({\mathbf{x}}_2\right)& =& (67,30,-60)\hfill \\ \hfill R_{\left(-3/2,-1/2,3/2\right),4}\left({\mathbf{x}}_3\right)& =& (43,18,-39)\hfill \\ \hfill R_{\left(-3/2,-1/2,3/2\right),4}\left({\mathbf{x}}_4\right)& =& (8,3,-15/2).\hfill \end{array}$$

Under the $\Omega$-rotation about $\mathbf{n}$, the trajectories of the endpoints of ${\mathbf{x}}_1,{\mathbf{x}}_2,{\mathbf{x}}_3$ are parabolas on the planes passing through the endpoint of ${\mathbf{x}}_1,{\mathbf{x}}_2,{\mathbf{x}}_3,$ and $\Omega$-orthogonal to the vector $\mathbf{n}$, which are the intersection of the $\Omega$-light cone with the plane ${\mathsf{\Pi }}_{\mathbf{n},{\mathbf{x}}_1}^{\Omega }:3x-3y+2z=8$, the $\Omega$-hyperbolic sphere with the plane ${\mathsf{\Pi }}_{\mathbf{n},{\mathbf{x}}_2}^{\Omega }:3x-3y+2z=-9$, and the $\Omega$-pseudosphere with the plane ${\mathsf{\Pi }}_{\mathbf{n},{\mathbf{x}}_3}^{\Omega }:3x-3y+2z=-3$, respectively. In addition, since ${\mathbf{x}}_4$ is on the plane ${\mathsf{\Pi }}_{\mathbf{n}}^{\Omega }:3x-3y+2z=0$, the trajectory of the endpoint of ${\mathbf{x}}_4$ is a line which is a part of the intersection of the $\Omega$-pseudosphere and ${\mathsf{\Pi }}_{\mathbf{n}}^{\Omega }$. Using the matrix ${\Omega }_E$ determined by the positive affine transformation A and $\Omega$, we can check the angle γ from Formula (31). For the matrix $\Omega$, one can obtain that

$$\Omega =PD{P}^T$$

where

$$P=\left[\begin{array}{ccc}0& 0& 1\\ -{\displaystyle \frac{1}{\sqrt{5}}}& {\displaystyle \frac{2}{\sqrt{5}}}& 0\\ {\displaystyle \frac{2}{\sqrt{5}}}& {\displaystyle \frac{1}{\sqrt{5}}}& 0\end{array}\right]andD=\left[\begin{array}{ccc}-1& 0& 0\\ 0& 4& 0\\ 0& 0& 1\end{array}\right].$$

Then one derives that

$$A=P{N}^{-1}{I}^{\ast }=\left[\begin{array}{ccc}0& 0& 1\\ {\displaystyle \frac{1}{\sqrt{5}}}& {\displaystyle \frac{1}{\sqrt{5}}}& 0\\ -{\displaystyle \frac{2}{\sqrt{5}}}& {\displaystyle \frac{1}{2\sqrt{5}}}& 0\end{array}\right]$$

where $N^2=D{I}^{\ast }$, and get

$${\Omega }_E=\Omega \left(A{I}^{\ast }{A}^{-1}\right)=\left[\begin{array}{ccc}1& 0& 0\\ 0& {\displaystyle \frac{17}{5}}& {\displaystyle \frac{6}{5}}\\ 0& {\displaystyle \frac{6}{5}}& {\displaystyle \frac{8}{5}}\end{array}\right].$$

One can check for ${\mathbf{x}}_4=\left(2,1,-3/2\right)$ and $R_{\left(-3/2,-1/2,3/2\right),4}\left({\mathbf{x}}_4\right)={\mathbf{y}}_4$ that

$$\gamma ={\displaystyle \frac{2S_{{\Omega }_E}}{{∥{\mathbf{x}}_4∥}_{\Omega }^2{∥\mathbf{n}∥}_{{\Omega }_E}}}=4$$

where ${∥{\mathbf{x}}_4∥}_{\Omega }^2=1$, ${∥\mathbf{n}∥}_{{\Omega }_E}={\displaystyle \frac{7}{\sqrt{10}}}$ and

$$S_{{\Omega }_E}={\displaystyle \frac{1}{2}}{\left({⟨{\mathbf{x}}_4,{\mathbf{x}}_4⟩}_{{\Omega }_E}{⟨{\mathbf{y}}_4,{\mathbf{y}}_4⟩}_{{\Omega }_E}-{⟨{\mathbf{x}}_4,{\mathbf{y}}_4⟩}_{{\Omega }_E}{⟨{\mathbf{x}}_4,{\mathbf{y}}_4⟩}_{{\Omega }_E}\right)}^{1/2}={\displaystyle \frac{7\sqrt{2}}{\sqrt{5}}}.$$

7. $\mathsf{\Omega }$-Rotation Formula by the Cayley Map

For the $\Omega$-skew-symmetric matrix $S_{\mathbf{n}}$ (8) where $\mathbf{n}$ is an $\Omega$-lightlike vector, one can derive by lengthy calculations that the determinant of $I_3+S_{\mathbf{n}}$ is equal to 1. So, $I_3+S_{\mathbf{n}}$ is an invertible matrix, and the well-known Cayley map can be given as

$$Cay\left(S_{\mathbf{n}}\right)=\left(I_3-S_{\mathbf{n}}\right){\left(I_3+S_{\mathbf{n}}\right)}^{-1}.$$

(49)

Then, it is not difficult to see that

$$\begin{array}{ccc}\hfill {\left(I_3+S_{\mathbf{n}}\right)}^T\Omega & =& \Omega \left(I_3-S_{\mathbf{n}}\right)\hfill \end{array}$$

(50)

$$\begin{array}{ccc}\hfill {\left(I_3-S_{\mathbf{n}}\right)}^T\Omega & =& \Omega \left(I_3+S_{\mathbf{n}}\right)\hfill \end{array}$$

(51)

using the fact that $S_{\mathbf{n}}^T\Omega =-\Omega S_{\mathbf{n}}$. Hence, one can obtain that

$$\begin{array}{ccc}\hfill Ca{y}^T\left(S_{\mathbf{n}}\right)\Omega Cay\left(S_{\mathbf{n}}\right)& =& {\left(\left(I_3-S_{\mathbf{n}}\right){\left(I_3+S_{\mathbf{n}}\right)}^{-1}\right)}^T\Omega \left(I_3-S_{\mathbf{n}}\right){\left(I_3+S_{\mathbf{n}}\right)}^{-1}\hfill \\ & =& {\left({\left(I_3+S_{\mathbf{n}}\right)}^T\right)}^{-1}{\left(I_3-S_{\mathbf{n}}\right)}^T\Omega {\left(I_3+S_{\mathbf{n}}\right)}^{-1}\left(I_3-S_{\mathbf{n}}\right)\hfill \\ & =& {\left({\left(I_3+S_{\mathbf{n}}\right)}^T\right)}^{-1}\Omega \left(I_3-S_{\mathbf{n}}\right)\hfill \\ & =& {\left({\left(I_3+S_{\mathbf{n}}\right)}^T\right)}^{-1}{\left(I_3+S_{\mathbf{n}}\right)}^T\Omega =\Omega .\hfill \end{array}$$

In addition, since we have $det{\left(I_3+S_{\mathbf{n}}\right)}^{-1}=det\left(I_3-S_{\mathbf{n}}\right)=1$, we get that $detCay\left(S_{\mathbf{n}}\right)=1$. Thus, $Cay\left(S_{\mathbf{n}}\right)$ is an $\Omega$-rotation matrix since it is $\Omega$-orthogonal and its determinant is equal to 1. By the following theorem, the $\Omega$-rotation matrix about the $\Omega$-lightlike axis $\mathbf{n}$ by the angle $\gamma$ can be obtained using the Cayley map:

Theorem 3.

Let $\mathbf{n}$ be an $\Omega$-lightlike vector, and $\gamma \in \mathbb{R}$. For the $\Omega$-skew-symmetric matrix $S_{\mathbf{n}}$, the matrix

$$Cay\left(\frac{\gamma }{2}{S}_{\mathbf{n}}\right)=\left(I_3-\frac{\gamma }{2}{S}_{\mathbf{n}}\right){\left(I_3+\frac{\gamma }{2}{S}_{\mathbf{n}}\right)}^{-1}$$

(52)

gives the $\Omega$-rotation about the axis $\mathbf{n}$ by the angle γ, that is $R_{\mathbf{u},\gamma }$.

Proof. 

Clearly, for all $k\in \mathbb{R}-\left\{0\right\}$, $k{S}_{\mathbf{n}}$ is an $\Omega$-skew-symmetric matrix. Therefore

$$Cay\left(k{S}_{\mathbf{n}}\right)=\left(I_3-k{S}_{\mathbf{n}}\right){\left(I_3+k{S}_{\mathbf{n}}\right)}^{-1}$$

is the matrix of an $\Omega$-rotation. If $Cay\left(k{S}_{\mathbf{n}}\right)=R_{\mathbf{u},\gamma }$, multiplying it by $\left(I_3+k{S}_{\mathbf{n}}\right)$ on the right, then one gets

$$R_{\mathbf{u},\gamma }\left(I_3+k{S}_{\mathbf{n}}\right)=I_3-k{S}_{\mathbf{n}}.$$

In addition, by Formula (46), one has

$$R_{\mathbf{u},\gamma }\left(I_3+k{S}_{\mathbf{n}}\right)=\left(I_3-\gamma S_{\mathbf{n}}+\frac{{\gamma }^2}{2}{S}_{\mathbf{n}}^2\right)\left(I_3+k{S}_{\mathbf{n}}\right).$$

So,

$$I_3+\left(k-\gamma \right)S_{\mathbf{n}}+\left(\frac{{\gamma }^2}{2}-\gamma k\right)S_{\mathbf{n}}^2=I_3-k{S}_{\mathbf{n}}.$$

This equation implies that

$$k-\gamma =-k\mathrm{and}\frac{{\gamma }^2}{2}-\gamma k=0$$

which results in $k={\displaystyle \frac{\gamma }{2}}$. Substituting this value into $Cay\left(k{S}_{\mathbf{n}}\right)$, one obtains

$$Cay\left(\frac{\gamma }{2}{S}_{\mathbf{n}}\right)=\left(I_3-\frac{\gamma }{2}{S}_{\mathbf{n}}\right){\left(I_3+\frac{\gamma }{2}{S}_{\mathbf{n}}\right)}^{-1}=R_{\mathbf{n},\gamma }.$$

□

Since one has

$$R=(I-S){(I+S)}^{-1}\Rightarrow R+RS=I-S\Rightarrow (I+R)S=I-R\Rightarrow S={(I+R)}^{-1}\left(I-R\right),$$

(53)

one can express Equation (52) as

$$Ca{y}^{-1}\left(R_{\mathbf{n},\gamma }\right)={\left(I_3+R_{\mathbf{n},\gamma }\right)}^{-1}\left(I_3-R_{\mathbf{n},\gamma }\right)=\frac{\gamma }{2}{S}_{\mathbf{n}}.$$

(54)

It is obvious that it is well defined for $\gamma \ne 0$, since we have

$$S_{\mathbf{n}}={\displaystyle \frac{1}{2\gamma }}{\Omega }^{-1}\left(R_{\mathbf{n},\gamma }^t\Omega -\Omega R_{\mathbf{n},\gamma }\right)$$

(55)

by Theorem 2. For a given $\Omega$-rotation matrix R, if the rotation axis is $\mathbf{n}$, then one can also find the rotation angle $\gamma$ with the help of the following theorem instead of Theorem 2.

Theorem 4.

Let R be an $\Omega$-rotation matrix. If $\mathbf{n}$ is the axis of the $\Omega$-rotation R, then the angle γ can be computed by the formula

$$\frac{\gamma }{2}{S}_{\mathbf{n}}={\left(I_3+R\right)}^{-1}\left(I_3-R\right).$$

(56)

Proof. 

By Theorem 3, we have

$$Cay\left(\frac{\gamma }{2}{S}_{\mathbf{n}}\right)=\left(I_3-\frac{\gamma }{2}{S}_{\mathbf{n}}\right){\left(I_3+\frac{\gamma }{2}{S}_{\mathbf{n}}\right)}^{-1}=R$$

for the $\Omega$-rotation matrix R. Considering the inverse of the Cayley function (54), we get

$$Ca{y}^{-1}\left(R\right)={\left(I_3+R\right)}^{-1}\left(I_3-R\right)=\frac{\gamma }{2}{S}_{\mathbf{n}}.$$

□

Example 4.

Let us take a general cone with the equation

$$2y^2+4z^2+2xy+4yz=0,$$

which is the $\Omega$-light cone for

$$\Omega =\left[\begin{array}{ccc}0& 1& 0\\ 1& 2& 2\\ 0& 2& 4\end{array}\right].$$

Let us consider an $\Omega$-lightlike vector as $\mathbf{n}=\left(1,0,0\right)$. The $\Omega$-skew-symmetric matrix with respect to $\mathbf{n}$ is

$$S_{\mathbf{n}}=\left[\begin{array}{ccc}0& -1& -2\\ 0& 0& 0\\ 0& {\displaystyle \frac{1}{2}}& 0\end{array}\right].$$

Thus, one can obtain the $\Omega$-rotation matrix for the $\Omega$-lightlike axis $\mathbf{n}$ and the angle γ as follows:

$$\begin{array}{ccc}\hfill R_{\mathbf{n},\gamma }& =& Cay\left(\frac{\gamma }{2}{S}_{\mathbf{n}}\right)\hfill \\ & =& \left(I_3-{\displaystyle \frac{\gamma }{2}}\left[\begin{array}{ccc}0& -1& -2\\ 0& 0& 0\\ 0& {\displaystyle \frac{1}{2}}& 0\end{array}\right]\right){\left(I_3+{\displaystyle \frac{\gamma }{2}}\left[\begin{array}{ccc}0& -1& -2\\ 0& 0& 0\\ 0& {\displaystyle \frac{1}{2}}& 0\end{array}\right]\right)}^{-1}\hfill \\ & =& \left[\begin{array}{ccc}1& \gamma -{\displaystyle \frac{1}{2}}{\gamma }^2& 2\gamma \\ 0& 1& 0\\ 0& -{\displaystyle \frac{1}{2}}\gamma & 1\end{array}\right].\hfill \end{array}$$

This matrix can be checked by the Rodrigues Formula (47) as follows:

$$\begin{array}{ccc}\hfill R_{\mathbf{n},\gamma }& =& \left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]-\gamma \left[\begin{array}{ccc}0& -1& -2\\ 0& 0& 0\\ 0& {\displaystyle \frac{1}{2}}& 0\end{array}\right]+{\displaystyle \frac{{\gamma }^2}{2}}{\left[\begin{array}{ccc}0& -1& -2\\ 0& 0& 0\\ 0& {\displaystyle \frac{1}{2}}& 0\end{array}\right]}^2\hfill \\ & =& \left[\begin{array}{ccc}1& \gamma -{\displaystyle \frac{1}{2}}{\gamma }^2& 2\gamma \\ 0& 1& 0\\ 0& -{\displaystyle \frac{1}{2}}\gamma & 1\end{array}\right].\hfill \end{array}$$

Example 5.

Consider an $\Omega$-rotation matrix

$$R=\left[\begin{array}{ccc}1& 0& 4\\ 0& 1& 0\\ 0& -1& 1\end{array}\right]$$

where

$$\Omega =\left[\begin{array}{ccc}0& 1& 0\\ 1& 2& 2\\ 0& 2& 4\end{array}\right].$$

Let us find the axis and the angle of the $\Omega$-rotation. The form of eigenvectors of R associated with the eigenvalue of 1 is $\mathbf{n}=k\left(1,0,0\right)$ for $k\in \mathbb{R}-\left\{0\right\}$, which are $\Omega$-lightlike vectors. If $\mathbf{n}=\left(1,0,0\right)$, then the $\Omega$-skew-symmetric matrix corresponding to $\mathbf{n}$ is derived as

$$S_{\mathbf{n}}=\left[\begin{array}{ccc}0& -1& -2\\ 0& 0& 0\\ 0& {\displaystyle \frac{1}{2}}& 0\end{array}\right].$$

Then, using Equation (48) or (56), one can obtain the angle as $\gamma =2$. We can verify that the matrix of the $\Omega$-rotation for $\gamma =2$ in the previous example gives the matrix R.

8. $\mathsf{\Omega }$-Rotation Formula by the $\mathsf{\Omega }$-Split Quaternions

Like the ordinary split quaternions, $\Omega$-split quaternions can be used to produce $\Omega$-rotations in ${\mathbb{R}}_{\Omega }^3$. In this section, we use the $\Omega$-split quaternions with their multiplication in the ${\mathbb{R}}_{\Omega }^3$ to generate an $\Omega$-rotation matrix about an $\Omega$-lightlike axis $\mathbf{n}$. One can see that for every $\Omega$-lightlike vector $\mathbf{n}$, $\mathbf{q}=1-\frac{\gamma }{2}\mathbf{n}$ is a unit timelike $\Omega$-split quaternion. For a unit timelike $\Omega$-split quaternion $\mathbf{q}=1-\frac{\gamma }{2}\mathbf{n}$, the $\Omega$-rotation operator $R^{\mathbf{q}}$ can be defined as

$$R^{\mathbf{q}}\left(\mathbf{v}\right)=\mathbf{qv}\overline{\mathbf{q}}$$

(57)

where $\mathbf{v}$ is a pure $\Omega$-split quaternion which can be considered a vector to be rotated. The following theorem shows that this operator $\Omega$-rotates $\mathbf{v}$ about the $\Omega$-lightlike axis $\mathbf{n}$ by the angle $\gamma$:

Theorem 5.

For a unit timelike $\Omega$-split quaternion

$$\mathbf{q}=1-\frac{\gamma }{2}\mathbf{n}$$

(58)

where $\mathbf{n}$ is a $\Omega$-lightlike vector and $\gamma \in \mathbb{R}$, and for any pure $\Omega$-split quaternion $\mathbf{v}$, the transformation

$$R^{\mathbf{q}}\left(\mathbf{v}\right)=\mathbf{qv}\overline{\mathbf{q}}$$

(59)

gives an $\Omega$-rotation about the $\Omega$-lightlike axis $\mathbf{n}$ by the angle γ.

Proof. 

Since $\mathbf{n}$ is $\Omega$-lightlike, one gets

$$\mathbf{n}{\times }_{\Omega }\left(\mathbf{v}{\times }_{\Omega }\mathbf{n}\right)=-{⟨\mathbf{n},\mathbf{v}⟩}_{\Omega }\mathbf{n}$$

by Equation (10). Then, using the relations (16) and (17), one obtains

$$\begin{array}{ccc}\hfill R^{\mathbf{q}}\left(\mathbf{v}\right)& =& \left(1-\frac{\gamma }{2}\mathbf{n}\right)\mathbf{v}\left(1+\frac{\gamma }{2}\mathbf{n}\right)\hfill \\ & =& \left(1-\frac{\gamma }{2}\mathbf{n}\right)\left(\mathbf{v}+\frac{\gamma }{2}{⟨\mathbf{v},\mathbf{n}⟩}_{\Omega }+\frac{\gamma }{2}\mathbf{v}{\times }_{\Omega }\mathbf{n}\right)\hfill \\ & =& \mathbf{v}+\frac{\gamma }{2}{⟨\mathbf{v},\mathbf{n}⟩}_{\Omega }+\frac{\gamma }{2}\mathbf{v}{\times }_{\Omega }\mathbf{n}-\frac{\gamma }{2}\mathbf{nv}-\frac{{\gamma }^2}{4}{⟨\mathbf{v},\mathbf{n}⟩}_{\Omega }\mathbf{n}-\frac{{\gamma }^2}{4}\mathbf{n}\left(\mathbf{v}{\times }_{\Omega }\mathbf{n}\right)\hfill \\ & =& \mathbf{v}+\frac{\gamma }{2}{⟨\mathbf{v},\mathbf{n}⟩}_{\Omega }+\frac{\gamma }{2}\mathbf{v}{\times }_{\Omega }\mathbf{n}-\frac{\gamma }{2}{⟨\mathbf{v},\mathbf{n}⟩}_{\Omega }-\frac{\gamma }{2}\mathbf{n}{\times }_{\Omega }\mathbf{v}-\frac{{\gamma }^2}{4}{⟨\mathbf{v},\mathbf{n}⟩}_{\Omega }\mathbf{n}\hfill \\ & & \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-\frac{{\gamma }^2}{4}{⟨\mathbf{n},\mathbf{v}{\times }_{\Omega }\mathbf{n}⟩}_{\Omega }-\frac{{\gamma }^2}{4}\mathbf{n}{\times }_{\Omega }\left(\mathbf{v}{\times }_{\Omega }\mathbf{n}\right)\hfill \\ & =& \mathbf{v}-\gamma \mathbf{n}{\times }_{\Omega }\mathbf{v}-\frac{{\gamma }^2}{2}{⟨\mathbf{v},\mathbf{n}⟩}_{\Omega }\mathbf{n}+\frac{{\gamma }^2}{4}{⟨\mathbf{n},\mathbf{n}⟩}_{\Omega }\mathbf{v}.\hfill \end{array}$$

In addition, since $\mathbf{n}{\times }_{\Omega }\mathbf{v}=S_{\mathbf{n}}\mathbf{v}$, one has

$$\begin{array}{ccc}\hfill R^{\mathbf{q}}\left(\mathbf{v}\right)& =& \mathbf{v}-\gamma \mathbf{n}{\times }_{\Omega }\mathbf{v}-\frac{{\gamma }^2}{2}{⟨\mathbf{v},\mathbf{n}⟩}_{\Omega }\mathbf{n}\hfill \\ & =& \mathbf{v}-\gamma S_{\mathbf{n}}\mathbf{v}+\frac{{\gamma }^2}{2}\mathbf{n}{\times }_{\Omega }\left(\mathbf{n}{\times }_{\Omega }\mathbf{v}\right)\hfill \\ & =& \mathbf{v}-\gamma S_{\mathbf{n}}\mathbf{v}+\frac{{\gamma }^2}{2}{S}_{\mathbf{n}}^2\mathbf{v}\hfill \\ & =& \left(I_3-\gamma S_{\mathbf{n}}+\frac{{\gamma }^2}{2}\right)\mathbf{v}\hfill \end{array}$$

which equals to $R_{\mathbf{n},\gamma }\left(\mathbf{v}\right)$ by Theorem 1. Then, $R^{\mathbf{q}}$ is an $\Omega$-rotation about the $\Omega$-lightlike axis $\mathbf{n}$ by the angle $\gamma$. □

Example 6.

Given a $\Omega$-lightlike vector $\mathbf{n}=\left(1,0,-{\displaystyle \frac{1}{2}}\right)$ for

$$\Omega =\left[\begin{array}{ccc}1& 0& 2\\ 0& 1& 1\\ 2& 1& 4\end{array}\right].$$

Let us $\Omega$-rotate the vector $\mathbf{v}=(1,3,2)\in {\mathbb{R}}^3$ about the vector $\mathbf{n}$ by the angle $\gamma =1$. Using the unit timelike $\Omega$-split quaternion

$$\mathbf{q}=1-\frac{\gamma }{2}\mathbf{n}=1-\frac{1}{2}\mathbf{i}+\frac{1}{4}\mathbf{k},$$

one obtains the $\Omega$-rotation operator

$$R^{\mathbf{q}}\left(\mathbf{v}\right)=\mathbf{qv}\overline{\mathbf{q}}$$

considering the vector $\mathbf{v}$ as a pure $\Omega$-split quaternion. Then, using the $\Omega$-split quaternion multiplication, we get

$$R^{\mathbf{q}}\left(\mathbf{v}\right)=-\frac{19}{4}\mathbf{i}+3\mathbf{j}+\frac{33}{8}\mathbf{k}$$

which can be considered as the rotated vector ${\mathbf{v}}^{\prime }=\left(-\frac{19}{4},3,\frac{33}{8}\right)$. One can easily check this result using Theorem 1, to generate the $\Omega$-rotation matrix $R_{\mathbf{n},\gamma }$ with the axis $\mathbf{n}=\left(1,0,-{\displaystyle \frac{1}{2}}\right)$ and the angle $\gamma =1$, as

$$R_{\mathbf{n},1}=\left[\begin{array}{ccc}0& -{\displaystyle \frac{1}{4}}& -2\\ 0& 1& 0\\ {\displaystyle \frac{1}{2}}& -{\displaystyle \frac{1}{8}}& 2\end{array}\right]\left[\begin{array}{c}1\\ 3\\ 2\end{array}\right]=\left[\begin{array}{c}-{\displaystyle \frac{19}{4}}\\ 3\\ {\displaystyle \frac{33}{8}}\end{array}\right].$$

9. Conclusions

In this study, we gave a geometric characterization with the notion of the area for the angle of Lorentzian rotations about a lightlike axis, and we gave a definition not found in the literature for the angle measurement between two spacelike vectors whose vector product is lightlike, in the Minkowski 3-space. Then, we established the affine relation between the standard and generalized Minkowski 3-spaces, and we generalized the Lorentzian rotations about a lightlike axis, determining them in the generalized Minkowski 3-space with the angle measurement characterized similarly, using the well-known Rodrigues and Cayley maps, and the generalized split quaternions. We showed that the generalized Lorentzian rotations about a generalized lightlike axis give parabolic and linear rotational motions on general hyperboloids of one or two sheets or cones, and their formulas are identical to the standard Lorentz rotation formulas with the exception of skew-symmetric matrices.