The Subdominant Eigenvalue of Möbius Monotone Transition Probability Matrix

Abstract

We establish a Perron–Frobenius-type theorem for the subdominant eigenvalue of Möbius monotone transition matrices defined on partially ordered state spaces. This result extends the classical work of Keilson and Kester, where they considered stochastically monotone transition matrices in a totally ordered setting. Furthermore, we show that this subdominant eigenvalue is the geometric ergodicity rate.

1. Introduction

A central problem in the theory of Markov chains concerns quantifying the convergence rate to the stationary distribution. This rate is determined by the spectral properties of the corresponding transition matrix, where the subdominant eigenvalue modulus plays a crucial role. Standard references on this topic include Chen [1] and Levin and Peres [2].

Consider an irreducible and aperiodic Markov chain ${\left\{X_n\right\}}_{n\ge 0}$ on a finite state space $\mathbb{E}$, with transition matrix P and stationary distribution $\pi$. For any square matrix A, we denote its spectrum by $\sigma \left(A\right)$. Using the Perron–Frobenius theorem for stochastic matrices—see, e.g., Seneta [3] (Theorem 1.1)—the eigenvalue 1 is simple and strictly dominant in $\sigma \left(P\right)$. Our analysis therefore focuses on $\sigma \left(P\right)\setminus \left\{1\right\}.$ Define the subdominant eigenvalue modulus of transition matrix P as follows:

$${\lambda }_{\ast }:=max\left\{\left|\lambda \right|:\lambda \in \sigma \left(P\right)\setminus \left\{1\right\}\right\}.$$

If ${\lambda }_{\ast }\in \sigma \left(P\right)$, we call ${\lambda }_{\ast }$ the subdominant eigenvalue.

Denote, using ${\delta }_i$, the Dirac measure concentrated on the state $i\in \mathbb{E}.$ According to Levin and Peres [2] (12.37), if ${\lambda }_{\ast }<1$, then the total variation distance to stationarity decays geometrically at the rate of ${\lambda }_{\ast }$:

$${\left(\underset{i\in \mathbb{E}}{max}{\parallel {\delta }_i{P}^n-\pi \parallel }_{\mathrm{TV}}\right)}^{1/n}\to {\lambda }_{\ast }\mathrm{as}n\to \infty .$$

This result naturally raises two fundamental questions about the subdominant eigenvalue modulus:

1.

Does the strict inequality ${\lambda }_{\ast }<1$ hold ?

2.

Is ${\lambda }_{\ast }$ itself an eigenvalue of the transition matrix P ?

When P corresponds to a time-reversible Markov chain, all its eigenvalues are real. Then, both questions can be answered affirmatively: ${\lambda }_{\ast }<1$ and ${\lambda }_{\ast }\in \sigma \left(P\right)$. However, when P is nonreversible, it is generally challenging to address both questions, as P may have complex eigenvalues. In the non-reversible case, guaranteeing the mentioned properties related to ${\lambda }_{\ast }$ commonly requires imposing some monotonicity assumptions on the chain. When $\mathbb{E}$ is a totally ordered state space, we say that P is stochastically monotone if, for any $i,j\in \mathbb{E}$ with $i<j$ and $k\in \mathbb{E}$,

$$\begin{array}{c}\hfill \sum _{n=k}^{\infty }P(i,n)\le \sum _{n=k}^{\infty }P(j,n).\end{array}$$

For stochastically monotone Markov chains in totally ordered state spaces, regarding the two mentioned questions, Keilson and Kester [4] established a Perron-Frobenius-type theorem for the subdominant eigenvalue, thus resolving both questions in a totally ordered setting.

While the theory of stochastically monotone chains on totally ordered spaces provides foundational insights, this framework has limitations in its ability to model complex systems with partially ordered state spaces. This motivated us to study partially ordered state spaces, where stochastic monotonicity generalizes to Möbius monotonicity (formally defined in the next section). The concept of Möbius monotonicity was first introduced by Kester [5] in his PhD thesis. Subsequently, Massy [6] established that Möbius monotonicity implies weak stochastic monotonicity. Lorek [7] further developed this theory, demonstrating its applicability to various systems, including queueing models and interacting particle systems [7,8,9,10].

The primary objective of this work is to establish a Perron–Frobenius-type theorem for the subdominant eigenvalue of Möbius monotone transition matrices. This result extends the Perron–Frobenius theorem developed by Keilson and Kester [4] and provides a systematic framework for analyzing the subdominant eigenvalue in partially ordered state spaces. Furthermore, we establish that the subdominant eigenvalue is the geometric ergodicity rate.

2. Main Results

In the following, we assume that $\mathbb{E}:=\{e_1,\dots ,e_M\}$ is a finite state space equipped with a partial order ⪯. We further assume the following:

• $e_1$ is the unique minimal element, and $e_M$ is the unique maximal element under ⪯.
• The enumeration of $\mathbb{E}$ is consistent with the partial order; that is, if $e_i⪯e_j$ for any $i,j\in \{1,\dots ,M\}$, then $i<j$.

Define the matrix $C\in {\{0,1\}}^{M\times M}$ as

$$\begin{array}{c}\hfill C(x,y)={\mathbf{1}}_{\{x⪯y\}}\mathrm{for}\mathrm{all}x,y\in \mathbb{E},\end{array}$$

(1)

where ${\mathbf{1}}_{\{·\}}$ denotes the indicator function. According to Rota [11] (Proposition 1), there exists an inverse matrix $C^{-1}$ of C such that, for any $x,y\in \mathbb{E}$

$$\sum _{x⪯z⪯y}C(x,z)C^{-1}(z,y)=\sum _{x⪯z⪯y}{C}^{-1}(x,z)C(z,y)=\sum _{x⪯z⪯y}{C}^{-1}(x,z)={\mathbf{1}}_{\{x=y\}},$$

(2)

and the following support restriction holds:

$$C^{-1}(x,y)=0\mathrm{if}x\cancel{⪯}y.$$

(3)

The matrix $C^{-1}$ admits explicit expression for some specific partially ordered sets $\mathbb{E}$. For example, let $\mathbb{E}={\{0,\dots ,m\}}^n$ be the lattice set. According to [11] (Proposition 5), we know for any $x=(x_1,\dots ,x_n),y=(y_1,\dots ,y_n)\in \mathbb{E},$$C^{-1}$ can be written as

$$\begin{array}{c}\hfill C^{-1}(x,y)=\left\{\begin{array}{cc}{(-1)}^{{\sum }_{i=1}^n(y_i-x_i)}\hfill & \mathrm{if}\mathrm{each}{y}_i-x_i=0or1;\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(4)

For the specific state space $\mathbb{E}=\left\{\right(0,0),(0,1),(1,0),(1,1\left)\right\}$, from (4), we can derive $C^{-1}$ as follows:

$$\begin{array}{c}\hfill C^{-1}=\left(\begin{array}{cccc}1& -1& -1& 1\\ 0& 1& 0& -1\\ 0& 0& 1& -1\\ 0& 0& 0& 1\end{array}\right)\end{array}$$

(5)

For any element $x\in \mathbb{E}$ and subset $A\subset \mathbb{E}$, define $P(x,A)={\sum }_{z\in A}P(x,z).$ Denote ${\left\{y\right\}}^{\uparrow }=\{z\in \mathbb{E}:z⪰y\}$ for any $y\in \mathbb{E}.$ The classical notion of stochastic monotonicity (defined for totally ordered sets such as natural numbers) can be extended to partially ordered sets.

Definition 1.

Let P be a transition matrix on $(\mathbb{E},⪯)$.

• We say P is Möbius monotone, if for any $x,y\in \mathbb{E}\setminus \left\{e_1\right\}$,

  $$\sum _{z⪯x}P(z,{\left\{y\right\}}^{\uparrow })C^{-1}(z,x)\ge 0.$$
• We say P is strictly Möbius monotone, if for any $x,y\in \mathbb{E}\setminus \left\{e_1\right\}$,

  $$\sum _{z⪯x}P(z,{\left\{y\right\}}^{\uparrow })C^{-1}(z,x)>0.$$

Remark 1.

Using the definition of C in (1) and the support restriction of $C^{-1}$ in (3), for any $x,y\in \mathbb{E}\setminus \left\{e_1\right\}$, we have

$$\begin{array}{ccc}\hfill {\left(C^{\top }\right)}^{-1}P{C}^{\top }(x,y)& =& \sum _z{C}^{-1}(z,x)\sum _{z^{\prime }}P(z,z^{\prime })C(y,z^{\prime })\hfill \\ \hfill & =& \sum _{z⪯x}{C}^{-1}(z,x)\sum _{z^{\prime }⪰y}P(z,z^{\prime })\hfill \\ \hfill & =& \sum _{z⪯x}{C}^{-1}(z,x)P(z,{\left\{y\right\}}^{\uparrow }).\hfill \end{array}$$

(6)

Then, we can conclude that ${\left(C^{\top }\right)}^{-1}P{C}^{\top }(x,y)\ge 0$ for all $x,y\in \mathbb{E}\setminus \left\{e_1\right\}$ if and only if P is Möbius monotone, while ${\left(C^{\top }\right)}^{-1}P{C}^{\top }(x,y)>0$ for all $x,y\in \mathbb{E}\setminus \left\{e_1\right\}$ if and only if P is strictly Möbius monotone.

When P is Möbius monotone, the matrix transformation (6) actually defines a new transition matrix

$$\tilde{P}:=C{P}^{\top }{C}^{-1}={\left({\left(C^{\top }\right)}^{-1}P{C}^{\top }\right)}^{\top },$$

known as the Siegmund dual of P. The concept of Siegmund duality was introduced by Siegmund [12], who established the equivalence between absorbing and reflecting barrier problems for stochastically monotone Markov processes. Following Siegmund’s seminal work, subsequent research has significantly expanded the applications of Siegmund duality across various domains of Markov process theory; see, e.g., [10,13,14].

Remark 2.

When the state space $\mathbb{E}=\{1,2,\dots ,M\}$ is totally ordered, from Equation (4), the matrix $C^{-1}$ admits the following explicit form:

$$\begin{array}{c}\hfill C^{-1}(x,y)=\left\{\begin{array}{ccc}1\hfill & & y=x;\hfill \\ -1\hfill & & y=x+1;\hfill \\ 0\hfill & & otherwise.\hfill \end{array}\right.\end{array}$$

Then, we have

$$\begin{array}{ccc}\hfill \sum _{z⪯x}P(z,{\left\{y\right\}}^{\uparrow })C^{-1}(z,x)& =& P(x,{\left\{y\right\}}^{\uparrow })C^{-1}(x,x)+P(x-1,{\left\{y\right\}}^{\uparrow })C^{-1}(x-1,x)\hfill \\ \hfill & =& P(x,{\left\{y\right\}}^{\uparrow })-P(x-1,{\left\{y\right\}}^{\uparrow })\hfill \\ \hfill & =& \sum _{k=y}^{M}P(x,k)-\sum _{k=y}^{M}P(x-1,k),\hfill \end{array}$$

from which we conclude that (strict) Möbius monotonicity reduces to (strict) stochastic monotonicity in totally ordered spaces.

Theorem 1.

Let P be an irreducible Möbius monotone transition matrix on $(\mathbb{E},⪯)$. Then, the subdominant eigenvalue modulus ${\lambda }_{\ast }$ belongs to $\sigma \left(P\right)$ and satisfies $0<{\lambda }_{\ast }<1$. If we further assume that P is strictly Möbius monotone, then ${\lambda }_{\ast }$ is a simple eigenvalue, and the strict inequality $\left|\lambda \right|<{\lambda }_{\ast }$ holds for all $\lambda \in \sigma \left(P\right)\setminus \{1,{\lambda }_{\ast }\}$.

Proof. 

Since similarity transformations preserve spectral properties, it suffices to analyze the matrix ${\left(C^{\top }\right)}^{-1}P{C}^{\top }$. We shall first prove that ${\lambda }_{\ast }$ is an eigenvalue of ${\left(C^{\top }\right)}^{-1}P{C}^{\top }$. Noting that $e_1$ is the minimal element in $\mathbb{E}$, for any $x\in \mathbb{E}$,

$${\left(C^{\top }\right)}^{-1}P{C}^{\top }(x,e_1)=\sum _{z⪯e_1}{C}^{-1}(z,x)P(z,{\left\{e_1\right\}}^{\uparrow })=C^{-1}(e_1,x)P(e_1,{\left\{e_1\right\}}^{\uparrow })={\mathbf{1}}_{\{x=e_1\}}.$$

Then, one can write the matrix ${\left(C^{\top }\right)}^{-1}P{C}^{\top }$ as

$$\begin{array}{c}\hfill {\left(C^{\top }\right)}^{-1}P{C}^{\top }=\left(\begin{array}{cc}1& a\\ \mathbf{0}& Q\end{array}\right),\end{array}$$

(7)

where $\mathbf{0}$ is a column vector of dimension $M-1$, $\mathbf{a}$ is a row vector of dimension $M-1$, and Q is a nonnegative $(M-1)\times (M-1)$ matrix.

Now, we claim that the spectrum of P consists of 1, together with the spectrum of $Q.$ To see this, observe that the characteristic polynomial of P can be written as

$$\begin{array}{c}\hfill det(P-\lambda I_M)=(1-\lambda )det(Q-\lambda I_{M-1}),\end{array}$$

where $I_n$ denotes the $n\times n$ identity matrix for $n\in \mathbb{N}$. Consequently,

$${\lambda }_{\ast }=max\left\{\left|\lambda \right|:\lambda \in \sigma \left(P\right)\setminus \left\{1\right\}\right\}=max\left\{\left|\lambda \right|:\lambda \in \sigma \left(Q\right)\right\}.$$

Since Q is nonnegative, using Perron–Frobenius theorem—see, e.g., Horn and John- son [15] (Theorem 8.3.1)—${\lambda }_{\ast }$ belongs to the spectrum of Q, and satisfies

$$\left|\lambda \right|\le {\lambda }_{\ast },\forall \lambda \in \sigma \left(Q\right)\setminus \left\{{\lambda }_{\ast }\right\}.$$

Furthermore, under the additional assumption of strict Möbius monotonicity for P, matrix Q becomes strictly positive. Thus, using another version of the Perron–Frobenius theorem—see, e.g., [15] (Theorem 8.2.8)—we know that ${\lambda }_{\ast }$ is indeed a simple eigenvalue, and the strict inequality $\left|\lambda \right|<{\lambda }_{\ast }$ holds for all $\lambda \in \sigma \left(Q\right)\setminus \left\{{\lambda }_{\ast }\right\}$.

To complete the proof, it remains to show that ${\lambda }_{\ast }<1$. We divide the arguments into two parts:

(i) We first prove that $Q^{\top }$ is a strictly substochastic matrix on the reduced space $\mathbb{E}\setminus \left\{e_1\right\}$. Using (2), we obtain the following:

$$\begin{array}{c}\hfill \sum _{x⪰e_1,x\ne e_1}{C}^{-1}(e_1,x)=\sum _{e_1⪯x⪯e_M}{C}^{-1}(e_1,x)-C^{-1}(e_1,e_1)={\mathbf{1}}_{\{e_1=e_M\}}-1=-1,\end{array}$$

(8)

and

$$\begin{array}{c}\hfill \sum _{x⪰z}{C}^{-1}(z,x)=\sum _{z⪯x⪯e_M}{C}^{-1}(z,x)={\mathbf{1}}_{\{z=e_M\}}.\end{array}$$

(9)

By (6), (7), (8) and (9), for any $y\ne e_1$,

$$\begin{array}{ccc}\hfill \sum _{x\ne e_1}{Q}^{\top }(y,x)& =& \sum _{x\ne e_1}{\left(C^{\top }\right)}^{-1}P{C}^{\top }(x,y)\hfill \\ \hfill & =& \sum _{x\ne e_1}\sum _{z⪯x}{C}^{-1}(z,x)P(z,{\left\{y\right\}}^{\uparrow })\hfill \\ \hfill & =& \sum _{x⪰e_1,x\ne e_1}P(e_1,{\left\{y\right\}}^{\uparrow })C^{-1}(e_1,x)+\sum _{z\ne e_1}\sum _{x⪰z}P(z,{\left\{y\right\}}^{\uparrow })C^{-1}(z,x)\hfill \\ \hfill & =& P(e_1,{\left\{y\right\}}^{\uparrow })\sum _{x⪰e_1,x\ne e_1}{C}^{-1}(e_1,x)+\sum _{z\ne e_1}P(z,{\left\{y\right\}}^{\uparrow })\sum _{x⪰z}{C}^{-1}(z,x)\hfill \\ \hfill & =& P(e_1,{\left\{y\right\}}^{\uparrow })·(-1)+\sum _{z\ne e_1}P(z,{\left\{y\right\}}^{\uparrow }){\mathbf{1}}_{\{z=e_M\}}\hfill \\ \hfill & =& -P(e_1,{\left\{y\right\}}^{\uparrow })+P(e_M,{\left\{y\right\}}^{\uparrow })\le 1,\hfill \end{array}$$

(10)

where, in the third equality, we interchange the order of summation between x and z. To establish the strict inequality in (10), we employ proof by contradiction. Assume the equality holds in (10). This implies

$$P(e_1,{\left\{y\right\}}^{\uparrow })=0\mathrm{and}P(e_M,{\left\{y\right\}}^{\uparrow })=1,\forall y\in \mathbb{E}\setminus \left\{e_1\right\},$$

which consequently forces $P(e_1,y)=0$ for all $y\in \mathbb{E}\setminus \left\{e_1\right\}.$ This contradicts the irreducibility of P. We therefore conclude that $Q^{\top }$ must be strictly substochastic.

(ii) Now, we are in a position to prove ${\lambda }_{\ast }<1.$ Using Perron–Frobenius theorem [15] (Theorem 8.3.1), a nonnegative nonzero eigenvector $[v\left(e_2\right),v\left(e_3\right),\dots ,$$v\left(e_M\right){]}^{\top }$ is observed, such that

$$\begin{array}{c}\hfill \sum _{y\in \mathbb{E}\setminus \left\{e_1\right\}}Q(x,y)v\left(y\right)={\lambda }_{\ast }v\left(x\right),\forall x\in \mathbb{E}\setminus \left\{e_1\right\}.\end{array}$$

Summing up both sides yields the following:

$$\begin{array}{c}\hfill \sum _{x\in \mathbb{E}\setminus \left\{e_1\right\}}\sum _{y\in \mathbb{E}\setminus \left\{e_1\right\}}Q(x,y)v\left(y\right)={\lambda }_{\ast }\sum _{x\in \mathbb{E}\setminus \left\{e_1\right\}}v\left(x\right).\end{array}$$

Interchanging the order of summation on the left-hand side gives

$$\begin{array}{c}\hfill \sum _{y\in \mathbb{E}\setminus \left\{e_1\right\}}v\left(y\right)\sum _{x\in \mathbb{E}\setminus \left\{e_1\right\}}Q(x,y)={\lambda }_{\ast }\sum _{x\in \mathbb{E}\setminus \left\{e_1\right\}}v\left(x\right).\end{array}$$

(11)

From the strictly substochastic property $Q^{\top }$ (established in (i)), there exists a $y_0\in \mathbb{E}\setminus \left\{e_1\right\}$, such that

$$\begin{array}{c}\hfill \sum _{x\in \mathbb{E}\setminus \left\{e_1\right\}}Q(x,y_0)=\sum _{x\in \mathbb{E}\setminus \left\{e_1\right\}}{Q}^{\top }(y_0,x)<1,\end{array}$$

while, for all other $y\ne y_0$,

$$\begin{array}{c}\hfill \sum _{x\in \mathbb{E}\setminus \left\{e_1\right\}}Q(x,y)=\sum _{x\in \mathbb{E}\setminus \left\{e_1\right\}}{Q}^{\top }(y,x)\le 1.\end{array}$$

Substituting these inequalities into (11) and noting the positivity of v, we derive

$$\begin{array}{c}\hfill \sum _{y\in \mathbb{E}\setminus \left\{e_1\right\}}v\left(y\right)>{\lambda }_{\ast }\sum _{x\in \mathbb{E}\setminus \left\{e_1\right\}}v\left(x\right),\end{array}$$

which immediately implies ${\lambda }_{\ast }<1.$ □

We emphasize that strict Möbius monotonicity is not a necessary condition for the simplicity of the subdominant eigenvalue. In fact, to apply the Perron–Frobenius theorem—see, e.g., Seneta [3] (Theorem 1.1)—one only needs Q to be irreducible and aperiodic; matrix Q is defined in (7). This condition is related to the strict monotonicity of the powers of Q, as follows.

Lemma 1.

Let P be a Möbius monotone transition matrix on $(\mathbb{E},⪯)$. There exists an integer $k>0$ such that $P^k$ is strictly Möbius monotone if and only if Q defined in (7) is irreducible and aperiodic.

Proof. 

From the block structure in (7), for any integer $n>0$, we have

$$\begin{array}{c}\hfill {\left(C^{\top }\right)}^{-1}{P}^n{C}^{\top }=\left(\begin{array}{cc}1& {\mathbf{a}}_n\\ \mathbf{0}& Q^n\end{array}\right),\end{array}$$

(12)

where ${\mathbf{a}}_n$ denotes a row vector of dimension $M-1$.

Assume Q is irreducible and aperiodic. Then, by [3] (Theorem 1.4), an integer $k>0$ exists such that $Q^k$ is strictly positive. Substituting this into (12), the strict positivity of $Q^k$ implies that $P^k$ is strictly Möbius monotone.

Conversely, suppose that $P^k$ is strictly Möbius monotone for some integer $k>0$. It follows from (12) that $Q^k$ is strictly positive. To show that $Q^{k+1}$ remains strictly positive, suppose, for contradiction, that there is an element in $Q^{k+1}$ equal to 0. This implies that at least one row of Q consists entirely of zeros, which contradicts the strict positivity of $Q^k$. Therefore, through induction, we can conclude that for any $l\ge k$, $Q^l$ is a strictly positive matrix. Consequently, Q must be irreducible and aperiodic. □

The next theorem slightly relaxes the condition for the second statement in Theorem 1.

Theorem 2.

Let P be a Möbius monotone transition matrix on $(\mathbb{E},⪯)$. Suppose that there exists an integer $k>0$ such that $P^k$ is strictly Möbius monotone, or equivalently, the matrix Q defined in (7) is irreducible and aperiodic. Then, ${\lambda }_{\ast }$ is a simple eigenvalue satisfying $0<{\lambda }_{\ast }<1$, and the strict inequality $\left|\lambda \right|<{\lambda }_{\ast }$ holds for all $\lambda \in \sigma \left(P\right)\setminus \{1,{\lambda }_{\ast }\}$.

Proof. 

Using Lemma 1, the strict Möbius monotonicity of $P^k$ is equivalent to the irreducibility and aperiodicity of Q. According to [3] (Theorem 1.4), Q is primitive; that is, there exists an integer $k>0$, such that $Q^k$ is a strictly positive matrix. Applying [3] (Theorem 1.1), we can see that ${\lambda }_{\ast }>0$ is a simple eigenvalue of Q, and the strict inequality $\left|\lambda \right|<{\lambda }_{\ast }$ holds for all $\lambda \in \sigma \left(P\right)\setminus \{1,{\lambda }_{\ast }\}$. The remainder of the proof for ${\lambda }_{\ast }<1$ is the same as that of Theorem 1. □

Recall that when the modulus ${\lambda }_{\ast }\in \sigma \left(P\right)$, we call ${\lambda }_{\ast }$ the subdominant eigenvalue. The following theorem establishes the immediate application of Theorems 1 and 2 by linking the subdominant eigenvalue to the geometric ergodicity rate. Although Levin and Peres [2] (12.37) noted this connection for nonreversible Markov chains, they did not provide a rigorous proof. For the reader’s convenience, we provide a complete proof here.

Theorem 3.

Let P be an aperiodic, irreducible, Möbius monotone transition matrix on $(\mathbb{E},⪯)$. Then, the corresponding Markov chain admits a unique stationary distribution, denoted by π, and

$${\left(\underset{i\in \mathbb{E}}{max}{\parallel {\delta }_i{P}^n-\pi \parallel }_{\mathrm{TV}}\right)}^{1/n}\to {\lambda }_{\ast }asn\to \infty ,$$

where ${\lambda }_{\ast }$ is the subdominant eigenvalue belonging to $(0,1).$

Proof. 

According to Seneta [3] (Theorem 1.1), 1 is the simple eigenvalue of P, with the left eigenvector being its stationary distribution. Define the matrix $\mathsf{\Pi }={\left({\mathsf{\Pi }}_{ij}\right)}_{i,j\in \mathbb{E}}$ by

$${\mathsf{\Pi }}_{ij}={\pi }_j,\mathrm{for}\mathrm{all}i,j\in \mathbb{E}.$$

Then, for any $n\in \mathbb{N}$, it can be verified that

$${\mathsf{\Pi }}^n=\mathsf{\Pi }\mathrm{and}{(P-\mathsf{\Pi })}^n=P^n-\mathsf{\Pi }.$$

Using these identities and the definition of total variation norm, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \underset{i\in \mathbb{E}}{max}{\parallel {\delta }_i{P}^n-\pi \parallel }_{\mathrm{TV}}& ={\displaystyle \frac{1}{2}}\underset{i\in \mathbb{E}}{max}\sum _{j\in \mathbb{E}}\left|P^n\left(ij\right)-{\pi }_j\right|\hfill \\ & ={\displaystyle \frac{1}{2}}{\parallel P^n-\mathsf{\Pi }\parallel }_{\infty }\hfill \\ & ={\displaystyle \frac{1}{2}}{∥{(P-\mathsf{\Pi })}^n∥}_{\infty },\hfill \end{array}\end{array}$$

(13)

where ${\parallel ·\parallel }_{\infty }$ denotes the maximum row sum matrix norm, given by

$${\parallel A\parallel }_{\infty }:=\underset{i\in \mathbb{E}}{max}\sum _{j\in \mathbb{E}}\left|a_{ij}\right|,\forall A\in {\mathbb{R}}^{\mathbb{E}\times \mathbb{E}}.$$

Let $\mathbf{e}$ be the all-ones column vector. Using Seneta [3] (Theorem 1.1) again, 1 is a simple eigenvalue with left eigenvector $\pi$ and right eigenvector $\mathbf{e}$. Through invariant subspace decomposition, any right eigenvector $\rho$ of P associated with an eigenvalue other than 1 satisfies $\pi \rho =0$. This implies that $P-\mathsf{\Pi }$ shares all the eigenvalues of P, except that 1 is replaced by 0. Therefore, according to Theorem 1,

$$\begin{array}{c}\hfill {\lambda }_{\ast }=max\left\{\left|\lambda \right|:\lambda \in \sigma \left(P\right)\setminus \left\{1\right\}\right\}=max\left\{\left|\lambda \right|:\lambda \in \sigma (P-\mathsf{\Pi })\right\}.\end{array}$$

From (13) and [15] (Corollary 5.6.14), it follows that

$${\left(\underset{i\in \mathbb{E}}{max}{\parallel {\delta }_i{P}^n-\pi \parallel }_{\mathrm{TV}}\right)}^{1/n}={\parallel {(P-\mathsf{\Pi })}^n\parallel }_{\infty }^{1/n}\to {\lambda }_{\ast },asn\to \infty .$$

□

3. An Example

In this section, we illustrate the main contributions of this work through a typi- cal example.

Example 1.

Consider the finite lattice space $\mathbb{E}=\left\{\right(0,0),(0,1),(1,0),(1,1\left)\right\}$. Suppose that the transition matrix P on $\mathbb{E}$ is given by

$$\begin{array}{c}\hfill P=\left(\begin{array}{cccc}0.9& 0.1& 0& 0\\ 0.8& 0& 0& 0.2\\ 0& 0.5& 0.5& 0\\ 0& 0& 0.1& 0.9\end{array}\right).\end{array}$$

This transition matrix is clearly irreducible. Following Remark 1, to establish Möbius monotonicity, it suffices to verify that ${\left(C^{\top }\right)}^{-1}P{C}^{\top }$ is a nonnegative matrix. From (1) and (5), we obtain the following:

$$\begin{array}{c}\hfill C^{\top }=\left(\begin{array}{cccc}1& 0& 0& 0\\ 1& 1& 0& 0\\ 1& 0& 1& 0\\ 1& 1& 1& 1\end{array}\right)\end{array}$$

and

$$\begin{array}{c}\hfill {\left(C^{\top }\right)}^{-1}=\left(\begin{array}{cccc}1& 0& 0& 0\\ -1& 1& 0& 0\\ -1& 0& 1& 0\\ 1& -1& -1& 1\end{array}\right).\end{array}$$

Direct computation yields

$$\begin{array}{c}\hfill {\left(C^{\top }\right)}^{-1}P{C}^{\top }=\left(\begin{array}{cccc}1& 0.1& 0& 0\\ 0& 0.1& 0.2& 0.2\\ 0& 0.4& 0.5& 0\\ 0& 0.3& 0.3& 0.7\end{array}\right)\ge 0.\end{array}$$

This confirms that the conditions for the first statement of Theorem 1 are satisfied. However, since ${\left(C^{\top }\right)}^{-1}P{C}^{\top }((1,0),(1,1))=0$, the matrix fails to be strictly Möbius monotone. Conversely, consider the submatrix

$$\begin{array}{c}\hfill Q=\left(\begin{array}{ccc}0.1& 0.2& 0.2\\ 0.4& 0.5& 0\\ 0.3& 0.3& 0.7\end{array}\right).\end{array}$$

As Q is irreducible and aperiodic, it satisfies the conditions required by Theorem 2.

The spectrum of P is given by

$$\sigma \left(P\right)=\left\{1,{\displaystyle \frac{9}{10}},{\displaystyle \frac{(2+\sqrt{7})}{10}},{\displaystyle \frac{(2-\sqrt{7})}{10}}\right\},$$

where ${\lambda }_{\ast }=0.9$ is the subdominant eigenvalue modulus of P. This verifies the first statement of Theorem 1: ${\lambda }_{\ast }=0.9$ belongs to $\sigma \left(P\right)$ with $0<{\lambda }_{\ast }<1$. Although P is not strictly Möbius monotone (so the second statement of Theorem 1 does not apply), ${\lambda }_{\ast }$ is nevertheless a simple eigenvalue and $\left|\lambda \right|<{\lambda }_{\ast }$ holds for all $\lambda \in \sigma \left(P\right)\setminus \{1,{\lambda }_{\ast }\}$. This confirms Theorem 2.

By solving the linear equation $\pi P=\pi$, we obtain the unique stationary distribution

$$\pi =\left({\displaystyle \frac{40}{57}},{\displaystyle \frac{5}{57}},{\displaystyle \frac{2}{57}},{\displaystyle \frac{10}{57}}\right).$$

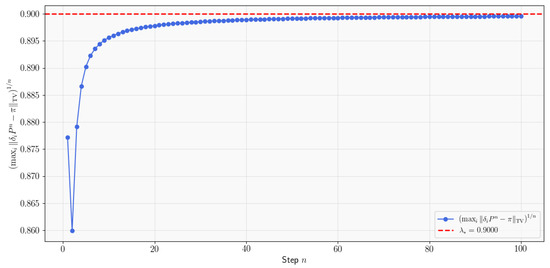
The following Figure 1 illustrates the geometric convergence rate

$${\left(\underset{i\in \mathbb{E}}{max}{\parallel {\delta }_i{P}^n-\pi \parallel }_{\mathrm{TV}}\right)}^{1/n}\to {\lambda }_{\ast }=0.9$$

established in Theorem 3.

Figure 1. ${\left({max}_{i\in \mathbb{E}}{\parallel {\delta }_i{P}^n-\pi \parallel }_{\mathrm{TV}}\right)}^{1/n}\to {\lambda }_{\ast }$.

4. Conclusions

This paper establishes a Perron–Frobenius-type theory for the subdominant eigenvalue of transition matrices on partially ordered state spaces, with the following key contributions:

• Spectral Framework for Möbius Monotonicity: While Möbius monotonicity was introduced in [5], we developed its first systematic application to spectral analysis. Our framework enables rigorous study of subdominant eigenvalues in partially ordered spaces where classical stochastic monotonicity is inapplicable.
• Generalized Perron–Frobenius Theory: For irreducible Möbius monotone chains, we proved that ${\lambda }_{\ast }\in \sigma \left(P\right)$ with $0<{\lambda }_{\ast }<1$ (Theorem 1), extending Keilson and Kester’s theory from totally ordered to partially ordered spaces. Furthermore, we established that ${\lambda }_{\ast }$ is a simple eigenvalue and strictly dominates all other eigenvalues except 1 when Q is strictly Möbius monotone. This condition is subsequently relaxed in Theorem 2 through novel submatrix analysis.
• Convergence Rate Characterization: We provided a complete proof establishing ${\lambda }_{\ast }$ as the geometric convergence rate for total variation distance (Theorem 3), confirming the fundamental link between spectral gap and ergodicity in non-reversible chains.

The developed theory facilitates convergence analysis in multi-dimensional queuing systems and lattice random walks. Future work includes continuous-state extensions and Siegmund duality applications.