Modified Heisenberg Commutation Relations, Free Schrödinger Equations, Tunnel Effect and Its Connections with the Black–Scholes Equation

Abstract

This paper explores the implications of modifying the canonical Heisenberg commutation relations over two simple systems, such as the free particle and the tunnel effect generated by a step-like potential. The modified commutation relations include position-dependent and momentum-dependent terms analyzed separately. For the position deformation case, the corresponding free wave functions are sinusoidal functions with a variable wave vector $k(x)$. In the momentum deformation case, the wave function has the usual sinusoidal behavior, but the energy spectrum becomes non-symmetric in terms of momentum. Tunneling probabilities depend on the deformation strength for both cases. Also, surprisingly, the quantum mechanical model generated by these modified commutation relations is related to the Black–Scholes model in finance. In fact, by taking a particular form of a linear position deformation, one can derive a Black–Scholes equation for the wave function when an external electromagnetic potential is acting on the particle. In this way, the Scholes model can be interpreted as a quantum-deformed model. Furthermore, by identifying the position coordinate x in quantum mechanics with the underlying asset S, which in finance satisfies stochastic dynamics, this analogy implies that the Black–Scholes equation becomes a quantum mechanical system defined over a random spatial geometry. If the spatial coordinate oscillates randomly about its mean value, the quantum particle’s mass would correspond to the inverse of the variance of this stochastic coordinate. Further, because this random geometry is nothing more than gravity at the microscopic level, the Black–Scholes equation becomes a possible simple model for understanding quantum gravity.

1. Introduction

The Heisenberg commutation relations are as follows:

$$\left[\widehat{x},{\widehat{p}}_x\right]=\widehat{x}{\widehat{p}}_x-{\widehat{p}}_x\widehat{x}=i\hslash \mathbb{I}.$$

(1)

where $\hslash ={\displaystyle \frac{h}{2\pi }}$ and $\mathbb{I}$ denote the identity operator and constitute the principal element for quantizing a physical system—that is, to determine its microscopic evolution from the information contained in a classical macroscopic Hamiltonian function.

In recent years, there has been a growing interest in studying possible modifications to the usual canonical commutation relations (1) in various contexts. For example, it is well known that quantum gravity effects—modeled by string theory, loop quantum gravity, or black hole physics—predict the existence of a Generalized Uncertainty Principle (GUP), which can change the usual canonical commutation relations [1,2,3,4,5,6,7] and their possible implications for entanglement, and the Hamilton–Jacobi equations are analyzed in [8,9,10,11,12]. In this case, the canonical commutation relations (1) are replaced by a more general one, of the type

$$[\widehat{x},{\widehat{p}}_x]=i\hslash \left(\mathbb{I}+F(\widehat{x},{\widehat{p}}_x)\right)$$

(2)

for some function $F(x,p_x)$ depending on the position and momentum. The form of the quantum algebra (2) guarantees that the system has a classical limit when ℏ goes to zero. To study the effects of an algebra of the form (2), one can expand the function $F\left(x,p_x\right)$ in a Taylor series so that algebra (2) becomes

$$\left[\widehat{x},{\widehat{p}}_x\right]=i\hslash \left(\mathbb{I}+{\alpha }_0\mathbb{I}+{\alpha }_1\widehat{x}+{\alpha }_2{\widehat{x}}^2+\cdots +{\beta }_1{\widehat{p}}_x+\cdots \right)$$

(3)

and explore first the effects of each one of its terms in a separate way. Thus, in this spirit, one can consider some special cases of (3) such as the case of a linear deformation

$$\left[\widehat{x},{\widehat{p}}_x\right]=i\hslash \left(\mathbb{I}+\alpha \widehat{x}\right)$$

or the case of a general $\widehat{x}$ power as

$$\left[\widehat{x},{\widehat{p}}_x\right]=i\hslash \left(\mathbb{I}+\alpha {\widehat{x}}^n\right)n=2,3,\cdots$$

Also, one can consider a linear momentum deformation

$$\left[\widehat{x},{\widehat{p}}_x\right]=i\hslash \left(\mathbb{I}+\beta {\widehat{p}}_x\right)$$

or the case of a momentum’s power

$$\left[\widehat{x},{\widehat{p}}_x\right]=i\hslash \left(\mathbb{I}+\beta {\widehat{p}}_x^n\right)n=2,3,\cdots$$

In this paper, we want to explore some implications of these modified commutation relations for some simple cases, such as the free particle, and also analyze its consequences on the tunnel effect generated over a step-like potential. Surprisingly, these modified commutation relations, especially in the case of linear deformation in position, are related to the modeling of financial derivatives through the Black–Scholes model. In fact, by taking a particular form of the linear position deformation, one can derive a Black–Scholes equation for the wave function when an external electromagnetic potential is incorporated into the particle. In this way, the Black–Scholes model can be interpreted as a quantum-deformed model.

The implications of these modified Heisenberg commutations relations over another simple one-dimensional system, specifically on the infinite square-well potential, can be found in [13,14,15,16,17,18,19,20,21].

The structure of the paper is as follows: Section 2 discusses the case of linear deformation in position. The Schrödinger equation for the free particle is determined, and its solutions are analyzed. Also, the tunnel effect is discussed and compared with the usual non-deformed case. In Section 3, the same analysis is performed on the position’s non-linear deformation case. Section 4 and Section 5 discuss these same issues for the linear and non-linear momentum deformation cases, respectively. Finally, Section 6 is dedicated to the Black–Scholes model and its interpretations as a quantum-deformed model. The conclusions of this work are resumed in Section 7.

2. The Linear $\widehat{\mathit{x}}$ Deformation Case

For the linear deformation case, the commutation relations are

$$\left[\widehat{x},{\widehat{p}}_x\right]=i\hslash (\mathbb{I}+\alpha \widehat{x})$$

(4)

for which $F(x,p)=\alpha x$. The $\alpha$ parameter essentially measures the deformation from the standard Heisenberg commutation relation. An operator representation of the above commutation relations is

$$\begin{array}{c}\widehat{x}=x\\ {\widehat{p}}_x=-i\hslash \left({\displaystyle \frac{\partial }{\partial x}}+\alpha x{\displaystyle \frac{\partial }{\partial x}}\right)=-i\hslash (1+\alpha x){\displaystyle \frac{\partial }{\partial x}}\end{array}$$

2.1. The Linear $\widehat{x}$ Deformation Case and the Free Particle

Consider now the simplest non-relativistic free particle classical Hamiltonian

$$H\left(x,p_x\right)={\displaystyle \frac{p_x^2}{2m}}$$

(5)

The quantization of this Hamiltonian by rule (4) implies the following Schrödinger equation:

$${\displaystyle \frac{{\widehat{p}}^2}{2m}}\Psi =i\hslash {\displaystyle \frac{\partial \Psi (x,t)}{\partial t}}$$

that is,

$${\displaystyle \frac{-{\hslash }^2}{2m}}(1+\alpha x){\displaystyle \frac{\partial }{\partial x}}\left[(1+\alpha x){\displaystyle \frac{\partial }{\partial x}}\right]\Psi (x,t)=i\hslash {\displaystyle \frac{\partial \Psi (x,t)}{\partial t}}$$

or

$${\displaystyle \frac{-{\hslash }^2}{2m}}\left[\alpha (1+\alpha x){\displaystyle \frac{\partial \Psi (x,t)}{\partial x}}+{(1+\alpha x)}^2{\displaystyle \frac{{\partial }^2\Psi (x,t)}{\partial x^2}}\right]=i\hslash {\displaystyle \frac{\partial \Psi (x,t)}{\partial t}}$$

By taking $\Psi (x,t)=\Psi (x)e^{-{\displaystyle \frac{i}{\hslash }}Et}$, the associated time-independent Schrödinger equation is

$${\displaystyle \frac{{\widehat{p}}^2}{2m}}\Psi (x)=E\Psi (x)$$

(6)

or

$${\displaystyle \frac{-{\hslash }^2}{2m}}\left[\alpha (1+\alpha x){\displaystyle \frac{d\Psi (x)}{dx}}+{(1+\alpha x)}^2{\displaystyle \frac{d^2\Psi (x)}{d{x}^2}}\right]=E\Psi (x)$$

(7)

where E is the particle energy. The above equation can be written as

$${\displaystyle \frac{d^2\Psi (x)}{d{x}^2}}+{\displaystyle \frac{\alpha }{1+\alpha x}}{\displaystyle \frac{d\Psi (x)}{dx}}+{\displaystyle \frac{k^2}{{(1+\alpha x)}^2}}\Psi (x)=0$$

(8)

with $k=\sqrt{{\displaystyle \frac{2mE}{{\hslash }^2}}}$. This second-order differential equation has a singular regular point in $x_0=-{\displaystyle \frac{1}{\alpha }}$. Thus, by the Frobenius theorem [22,23], there exists a solution of the form

$$\Psi (x)={\left(x-x_0\right)}^r\sum _{n=0}^{\infty }{c}_n{\left(x-x_0\right)}^n$$

(9)

The corresponding indicial equation is

$$r(r-1)+r+{\displaystyle \frac{{\alpha }^2}{k^2}}=0$$

so

$$r_{\pm }=\pm {\displaystyle \frac{\alpha }{k}}$$

In this case, the difference $r_{+}-r_{-}={\displaystyle \frac{2\alpha }{k}}$ is not an integer (we assume that E and $\alpha$ are such that they satisfy this requisite), so there exist two independent solutions of the form (9). However, instead of using the expansion in series, these solutions can be obtained from (6) by observing that the wave function must be a combination of eigenstates of the momentum operator. Let ${\Phi }_{p_x}$ be the corresponding eigenstate, so

$${\widehat{p}}_x{\Phi }_{p_x}(x)=p_x{\Phi }_{p_x}(x)$$

that is,

$$-i\hslash (1+\alpha x){\displaystyle \frac{\partial {\Phi }_{p_x}(x)}{\partial x}}=p_x{\Phi }_{p_x}(x)$$

so, integrating the above equation gives

$${\Phi }_{p_x}(x)=C{(1+\alpha x)}^{{\displaystyle \frac{i{p}_x}{\alpha \hslash }}}=C{e}^{{\displaystyle \frac{i{p}_x}{\hslash \alpha }}ln(1+\alpha x)}$$

Now, ${\Phi }_{p_x}(x)$ and ${\Phi }_{-p_x}(x)$ are two independent solutions of (6) with the same energy $E={\displaystyle \frac{p_x^2}{2m}}$, and if one defines $p_x=\hslash k$, the free particle wave function can be written as

$$\Psi (x)=A{e}^{i{\displaystyle \frac{k}{\alpha }}ln(1+\alpha x)}+B{e}^{-i{\displaystyle \frac{k}{\alpha }}ln(1+\alpha x)}$$

Now, consider $\alpha >0$; then, the above solution is valid for $1+\alpha x>0$—that is, $x>-{\displaystyle \frac{1}{\alpha }}$.

For $1+\alpha x<0$, one can write $1+\alpha x=|1+\alpha x|e^{i\pi }$, so the wave function is

$$\Psi (x)=A{e}^{i{\displaystyle \frac{k}{\alpha }}(ln|1+\alpha x|+i\pi )}+B{e}^{-i{\displaystyle \frac{k}{\alpha }}(ln|1+\alpha x|+i\pi )}$$

or

$$\Psi (x)=A{e}^{-{\displaystyle \frac{k\pi }{\alpha }}}{e}^{i{\displaystyle \frac{k}{\alpha }}ln|1+\alpha x|}+B{e}^{{\displaystyle \frac{k\pi }{\alpha }}}{e}^{-i{\displaystyle \frac{k}{\alpha }}ln|1+\alpha x|}$$

Thus, the free wave function becomes a function with two branches

$$\Psi (x)=\left\{\begin{array}{cc}A{e}^{i{\displaystyle \frac{k}{\alpha }}ln(1+\alpha x)}+B{e}^{-i{\displaystyle \frac{k}{\alpha }}ln(1+\alpha x)}\hfill & x>-{\displaystyle \frac{1}{\alpha }}\\ A{e}^{-{\displaystyle \frac{k\pi }{\alpha }}}{e}^{i{\displaystyle \frac{k}{\alpha }}ln|1+\alpha x|}+B{e}^{{\displaystyle \frac{k\pi }{\alpha }}}{e}^{-i{\displaystyle \frac{k}{\alpha }}ln|1+\alpha x|}\hfill & x<-{\displaystyle \frac{1}{\alpha }}\end{array}\right.$$

(10)

In the limit $\alpha \to 0^{+}$, one recovers the usual Heisenberg algebra (1) and, because $-{\displaystyle \frac{1}{\alpha }}\to -\infty$, the wave function becomes

$$\Psi (x)=A{e}^{i{\displaystyle \frac{k}{\alpha }}ln(1+\alpha x)}+B{e}^{-i{\displaystyle \frac{k}{\alpha }}ln(1+\alpha x)}\forall x$$

(11)

Also, when $\alpha \to 0^{+}$,

$$\underset{\alpha \to 0}{lim}{e}^{i{\displaystyle \frac{k}{\alpha }}ln(1+\alpha x)}=\underset{\alpha \to 0}{lim}{e}^{ikx[ln{(1+\alpha x)}^{\frac{1}{\alpha x}}]}=e^{ikxln(e)}=e^{ikx}$$

so the wave function converges to the standard imaginary exponential free behavior

$$\Psi (x)=A{e}^{ikx}+B{e}^{-ikx}\forall x$$

(12)

For $\alpha <0$ and $1+\alpha x>0$, one has that $x<-{\displaystyle \frac{1}{\alpha }}$, so the wave function in this case is

$$\Psi (x)=\left\{\begin{array}{ccc}A{e}^{i{\displaystyle \frac{k}{\alpha }}ln(1+\alpha x)}+B{e}^{-i{\displaystyle \frac{k}{\alpha }}ln(1+\alpha x)}\hfill & \mathrm{if}& x<-{\displaystyle \frac{1}{\alpha }}\\ A{e}^{-{\displaystyle \frac{k\pi }{\alpha }}}{e}^{i{\displaystyle \frac{k}{\alpha }}ln|1+\alpha x|}+B{e}^{{\displaystyle \frac{k\pi }{\alpha }}}{e}^{-i{\displaystyle \frac{k}{\alpha }}ln|1+\alpha x|}\hfill & \mathrm{if}& x>-{\displaystyle \frac{1}{\alpha }}\end{array}\right.$$

(13)

Now, in the limit, $\alpha \to 0^{-}$; then, $-{\displaystyle \frac{1}{\alpha }}\to +\infty$, and only the upper branch of (13) survives in the $\alpha \to 0^{-}$ deformation limit.

Note that the solution (10) can be written also in the form $(\alpha >0)$

$$\Psi (x)=\left\{\begin{array}{ccc}Ccos({\displaystyle \frac{k}{\alpha }}ln(1+\alpha x))+Dsin({\displaystyle \frac{k}{\alpha }}ln(1+\alpha x))\hfill & \mathrm{if}& x>-{\displaystyle \frac{1}{\alpha }}\\ Ecos({\displaystyle \frac{k}{\alpha }}ln|1+\alpha x|)+Fsin({\displaystyle \frac{k}{\alpha }}ln|1+\alpha x|)\hfill & \mathrm{if}& x<-{\displaystyle \frac{1}{\alpha }}\end{array}\right.$$

(14)

with $C=A+B$, $D=i(A-B)$, $E=A{e}^{{\displaystyle \frac{k\pi }{\alpha }}}+B{e}^{-{\displaystyle \frac{k\pi }{\alpha }}}$, and $F=i(A{e}^{{\displaystyle \frac{k\pi }{\alpha }}}-B{e}^{-{\displaystyle \frac{k\pi }{\alpha }}})$.

Figure 1 shows the free wave function (14) for $\alpha =1/10$ in the case where $D=0$ in the range $-{\displaystyle \frac{1}{\alpha }}<x<20$. Note that, for $x<-{\displaystyle \frac{1}{\alpha }}$, the wave function (14) becomes complex. It is interesting to see how the wavelength is shortened when the wave function is near the singular regular point $x_0=-{\displaystyle \frac{1}{\alpha }}$.

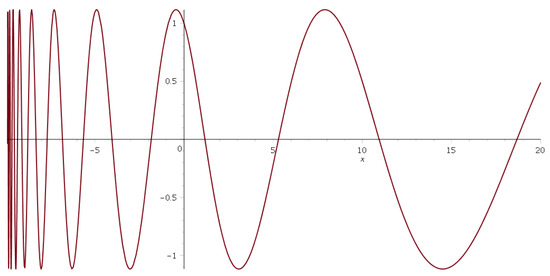
Figure 1. Free wave function for $\alpha =1/10$ in the range $-{\displaystyle \frac{1}{\alpha }}<x<20$ when $D=0$ and $C=1$.

2.2. The Linear $\widehat{x}$ Deformation Case and the Tunnel Effect

Consider the potential

$$U(x)=\left\{\begin{array}{ccc}\hfill 0& \mathrm{if}\hfill & x<0\hfill \\ \hfill U_0& \mathrm{if}\hfill & x\ge 0\hfill \end{array}\right.$$

(15)

shown in Figure 2.

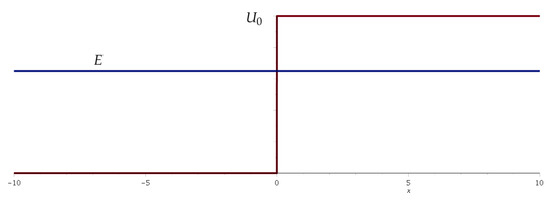
Figure 2. A step potential for the Schrödinger equation.

In this case, the time-independent Schrödinger equation is

$$\left\{\begin{array}{ccc}\hfill {\displaystyle \frac{-{\hslash }^2}{2m}}\left[\alpha (1+\alpha x){\displaystyle \frac{\partial \Psi (x)}{\partial x}}+{(1+\alpha x)}^2{\displaystyle \frac{{\partial }^2\Psi (x)}{\partial x^2}}\right]=E\Psi (x)& \mathrm{if}\hfill & x<0\hfill \\ & & \\ \hfill {\displaystyle \frac{-{\hslash }^2}{2m}}\left[\alpha (1+\alpha x){\displaystyle \frac{\partial \Psi (x)}{\partial x}}+{(1+\alpha x)}^2{\displaystyle \frac{{\partial }^2\Psi (x)}{\partial x^2}}\right]+U_0\Psi (x)=E\Psi (x)& \mathrm{if}\hfill & x\ge 0\hfill \end{array}\right.$$

or

$$\left\{\begin{array}{ccc}\hfill \left[\alpha (1+\alpha x){\displaystyle \frac{\partial \Psi (x)}{\partial x}}+{(1+\alpha x)}^2{\displaystyle \frac{{\partial }^2\Psi (x)}{\partial x^2}}\right]=k_0^2\Psi (x)& \mathrm{if}\hfill & x<0\hfill \\ & & \\ \hfill \left[\alpha (1+\alpha x){\displaystyle \frac{\partial \Psi (x)}{\partial x}}+{(1+\alpha x)}^2{\displaystyle \frac{{\partial }^2\Psi (x)}{\partial x^2}}\right]=k_1^2\Psi (x)& \mathrm{if}\hfill & x\ge 0\hfill \end{array}\right.$$

where $k_0=\sqrt{{\displaystyle \frac{2mE}{{\hslash }^2}}}$ and $k_1=\sqrt{{\displaystyle \frac{2m(E-U_0)}{{\hslash }^2}}}$. To analyze the tunnel effect, we consider $\alpha >0$ (so the singular regular point $x_0=-{\displaystyle \frac{1}{\alpha }}$ is at the left of the step potential), and we study the case $E<U_0$ for which $k_1$ becomes an imaginary number given by $k_1=ik=i\sqrt{{\displaystyle \frac{2m|E-U_0|}{{\hslash }^2}}}$.

For $x<0$, we search for a solution that is the superposition of a momentum eigenstate moving to the right (the incident wave) with another moving to the left (the reflected wave)—that is,

$${\Psi }^{-}(x)=A{\Phi }_{p_x}(x)+B{\Phi }_{-p_x}(x)=A{e}^{i{\displaystyle \frac{k_0}{\alpha }}ln(1+\alpha x)}+B{e}^{-i{\displaystyle \frac{k_0}{\alpha }}ln(1+\alpha x)}x<0$$

where $p_x=\hslash k_0$.

For $x\ge 0$, one has only a transmitted wave—that is, an eigenstate with positive momentum $p_x^{\prime }=\hslash k_1$

$${\Psi }^{+}(x)=C{\Phi }_{p_x^{\prime }}(x)=C{e}^{i{\displaystyle \frac{k_1}{\alpha }}ln(1+\alpha x)}=C{e}^{-{\displaystyle \frac{k}{\alpha }}ln(1+\alpha x)}={\displaystyle \frac{C}{{(1+\alpha x)}^{\frac{k}{\alpha }}}}x\ge 0$$

Continuity of the wave function and its derivative at $x=0$ implies the following equations:

$$\begin{array}{cc}A+B\hfill & =C\hfill \\ A-B\hfill & =Ci{\displaystyle \frac{k}{k_0}}\hfill \end{array}$$

so

$$\begin{array}{cc}A\hfill & ={\displaystyle \frac{C}{2}}(1+i{\displaystyle \frac{k}{k_0}})\hfill \\ B\hfill & ={\displaystyle \frac{C}{2}}(1-i{\displaystyle \frac{k}{k_0}})\hfill \end{array}$$

Then,

$${\Psi }^{-}(x)={\displaystyle \frac{C}{2}}(1+i{\displaystyle \frac{k}{k_0}})e^{i{\displaystyle \frac{k_0}{\alpha }}ln(1+\alpha x)}+(1-i{\displaystyle \frac{k}{k_0}})e^{-i{\displaystyle \frac{k_0}{\alpha }}ln(1+\alpha x)}x<0$$

If we write the complex number $(1+i{\displaystyle \frac{k}{k_0}})$ as $r{e}^{i\varphi }$, then $(1-i{\displaystyle \frac{k}{k_0}})$ is $r{e}^{-i\varphi }$, so

$${\Psi }^{-}(x)={\displaystyle \frac{Cr}{2}}\left(e^{i({\displaystyle \frac{k_0}{\alpha }}ln(1+\alpha x)+\varphi )}+e^{-i({\displaystyle \frac{k_0}{\alpha }}ln(1+\alpha x)+\varphi )}\right)x<0$$

or

$${\Psi }^{-}(x)=Crcos({\displaystyle \frac{k_0}{\alpha }}ln(1+\alpha x)+\varphi )x<0$$

where $r=\sqrt{1+{({\displaystyle \frac{k}{k_0}})}^2}$ and $\varphi =arctan({\displaystyle \frac{k}{k_0}})$.

Thus, the wave function is

$$\Psi (x)=\left\{\begin{array}{ccc}Crcos({\displaystyle \frac{k_0}{\alpha }}ln(1+\alpha x)+\varphi )\hfill & \mathrm{if}& x<0\\ {\displaystyle \frac{C}{{(1+\alpha x)}^{\frac{k}{\alpha }}}}\hfill & \mathrm{if}& x>0\end{array}\right.$$

(16)

Figure 3 shows the wave function $\Psi (x)$ in the range $-{\displaystyle \frac{1}{\alpha }}<x<20$ for $0<E<U_0$.

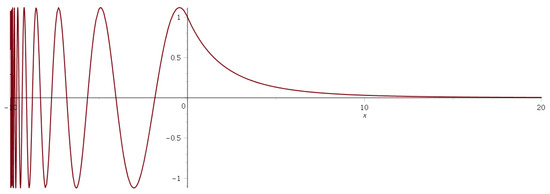
Figure 3. The red curve shows the wave function $\Psi (x)$ associated to the step-function potential with $E<U_0$ when $\alpha =1/10$, $k_0=1$, $k=1/2$, and $C=1$ in the range $-{\displaystyle \frac{1}{\alpha }}<x<20$.

One can see that Equation (8) is equivalent to the Sturm–Liouville problem [22]:

$${\displaystyle \frac{d}{dx}}\left(p(x){\displaystyle \frac{d\Psi (x)}{dx}}\right)+q(x)\Psi (x)=-\lambda \omega (x)\Psi (x)$$

with $p(x)=1+\alpha x$, $q(x)=0$, and $\lambda =k^2$, and the non-trivial weight function $\omega (x)$ is given by

$$\omega (x)={\displaystyle \frac{1}{(1+\alpha x)}}$$

which implies [22,24] that the inner product for two wave functions ${\Psi }_1$ and ${\Psi }_2$ in the Hilbert-Space is

$$<{\Psi }_1(x),{\Psi }_2(x)>={\int }_{-\infty }^{+\infty }\omega (x){\Psi }_1^{*}(x){\Psi }_2(x)dx={\int }_{-\infty }^{+\infty }{\displaystyle \frac{1}{\left(1+\alpha x\right)}}{\Psi }_1^{*}(x){\Psi }_2(x)dx$$

In this way, one can consider an effective wave function $\tilde{\Psi }(x)$ defined by

$$\tilde{\Psi }(x)={\displaystyle \frac{\Psi (x)}{\sqrt{1+\alpha x}}}$$

so, in terms of the $\tilde{\Psi }$, the inner product becomes the usual one

$$<{\tilde{\Psi }}_1(x),{\tilde{\Psi }}_2(x)>={\int }_{-\infty }^{+\infty }{\tilde{\Psi }}_1^{*}(x){\tilde{\Psi }}_2(x)dx$$

The probability density is then

$$\rho (x)=|\tilde{\Psi }{(x)|}^2={\displaystyle \frac{{|\Psi (x)|}^2}{(1+\alpha x)}}$$

representing the effective probability density generated by the non-trivial weight factor $\omega$.

Figure 4 compares, for $x>0$, the deformed solution

$${\Psi }^{+}(x)={\displaystyle \frac{C}{{(1+\alpha x)}^{\frac{k}{\alpha }}}}$$

and the effective deformed solution

$${\tilde{\Psi }}^{+}(x)={\displaystyle \frac{C}{{(1+\alpha x)}^{\frac{k}{\alpha }+\frac{1}{2}}}}$$

with the non-deformed one

$${\Psi }_0^{+}(x)=C{e}^{-kx}$$

(17)

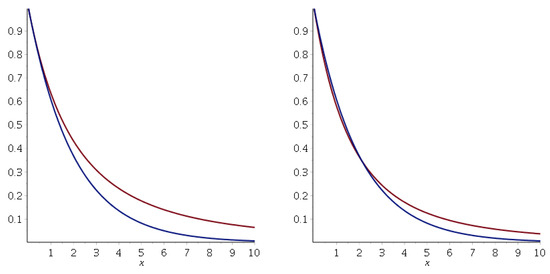
Figure 4. Left side: wave function ${\Psi }^{+}(x)$ in the range $x>0$ for the deformed case (red curve) and the non-deformed case ${\Psi }_0^{+}(x)$ (blue curve). Right side: effective wave function ${\tilde{\Psi }}^{+}(x)$ of the deformed case (red curve) and the non-deformed case ${\Psi }_0^{+}(x)$ (blue curve) for $x>0$. The parameter values are $\alpha =1/5$, $k_0=1$, $k=1/2$, and $C=1$.

It is important to note that the effective wave function $\tilde{\Psi }$ has more significant values in the classical prohibited region $x>3$ than the non-deformed one ${\Psi }_0^{+}(x)$. This leads to modified tunneling probabilities that are more likely than the non-deformed ones, with the outcome being influenced by the strength parameter $\alpha$. Therefore, the alteration of the Heisenberg commutation relation by gravity could result in a higher tunneling probability for certain physical processes. This suggests that near a black hole, the decay laws may differ from those we typically observe.

3. The Non-Linear $\widehat{\mathit{x}}$ Deformation Case

Consider now the following deformed Heisenberg algebra for $n>2$:

$$\left[\widehat{x},{\widehat{p}}_x\right]=i\hslash \left(\mathbb{I}+\alpha {\widehat{x}}^n\right)n=2,3,\cdots$$

(18)

This algebra has the following representation in terms of differential operators:

$$\begin{array}{c}\widehat{x}=x\\ {\widehat{p}}_x=-i\hslash \left(1+\alpha x^n\right){\displaystyle \frac{\partial }{\partial x}}\end{array}$$

3.1. The Non-Linear $\widehat{x}$ Deformation Case and the Free Particle

In this case, the quantization of the free particle by the rule (18) implies the Schrödinger equation:

$${\displaystyle \frac{-{\hslash }^2}{2m}}(1+\alpha x^n){\displaystyle \frac{\partial }{\partial x}}\left[(1+\alpha x^n){\displaystyle \frac{\partial }{\partial x}}\right]\Psi (x,t)=i\hslash {\displaystyle \frac{\partial \Psi (x,t)}{\partial t}}$$

or

$${\displaystyle \frac{-{\hslash }^2}{2m}}\left[\alpha n{x}^{n-1}(1+\alpha x^n){\displaystyle \frac{\partial \Psi (x,t)}{\partial x}}+{(1+\alpha x)}^2{\displaystyle \frac{{\partial }^2\Psi (x,t)}{\partial x^2}}\right]=i\hslash {\displaystyle \frac{\partial \Psi (x,t)}{\partial t}}$$

The corresponding time-independent Schrödinger equation can be written for the wave function $\Psi (x)$ as

$${\displaystyle \frac{d^2\Psi (x)}{d{x}^2}}+{\displaystyle \frac{\alpha n{x}^{n-1}}{1+\alpha x^n}}{\displaystyle \frac{d\Psi (x)}{dx}}+{\displaystyle \frac{k^2}{{(1+\alpha x^n)}^2}}\Psi (x)=0$$

(19)

where, again, $k=\sqrt{{\displaystyle \frac{2mE}{{\hslash }^2}}}$. Thus, $x_0={(-{\displaystyle \frac{1}{\alpha }})}^{{\displaystyle \frac{1}{n}}}$ is a singular regular point of Equation (19) for odd n. Instead, for even n, $x_0$ is imaginary, so the singularity is not on the real axis. The general solution of (19) can be found again by generating a superposition of two eigenstates ${\Phi }_{p_x}^n$ and ${\Phi }_{-p_x}^n$ of the momentum operator with opposite momentums. These eigenstates are defined by

$${\widehat{p}}_x{\Phi }_{p_x}^n=-i\hslash \left(1+\alpha x^n\right){\displaystyle \frac{\partial {\Phi }_{p_x}^n}{\partial x}}=p_x{\Phi }_{p_x}^n$$

so

$$ln\left({\Phi }_{p_x}^n\right)={\displaystyle \frac{i{p}_x}{\hslash }}\int {\displaystyle \frac{dx}{\left(1+\alpha x^n\right)}}+C_0$$

or

$${\Phi }_{p_x}^n(x)=A{e}^{{\displaystyle \frac{i{p}_x}{\hslash }}{\Theta }_n(x)}$$

(20)

where the phase ${\Theta }_n(x)$ is

$${\Theta }_n(x)=\int {\displaystyle \frac{dx}{\left(1+\alpha x^n\right)}}$$

whose solution is

$${\Theta }_n(x)=x\mathrm{hypergeom}\left(\left[1,{\displaystyle \frac{1}{n}}\right],\left[1+{\displaystyle \frac{1}{n}}\right],\mathrm{I}{x}^n\alpha {(-1)}^{{\displaystyle \frac{1}{2}}csgn(\mathrm{I}\alpha )+{\displaystyle \frac{1}{2}}csgn\left(\mathrm{I}{x}^n\right)-{\displaystyle \frac{1}{2}}csgn\left(\mathrm{I}{x}^n\right)csgn(\mathrm{I}\alpha )}\right)$$

The general solution of (19) is then

$${\Psi }_n(x)=A{e}^{{\displaystyle \frac{i{p}_x}{\hslash }}{\Theta }_n(x)}+B{e}^{{\displaystyle \frac{-i{p}_x}{\hslash }}{\Theta }_n(x)}n=2,3,4,...$$

or

$${\Psi }_n(x)=Acos(k{\Theta }_n(x))+Bsin(k{\Theta }_n(x))n=2,3,4,...$$

where $p_x=\hslash k$. For example, for $n=2$,

$${\Psi }_2(x)=Asin\left({\displaystyle \frac{karctan(\sqrt{\alpha }x)}{\sqrt{\alpha }}}\right)+Bcos\left({\displaystyle \frac{karctan(\sqrt{\alpha }x)}{\sqrt{\alpha }}}\right)$$

Figure 5 shows the free wave function for $n=2$ with $B=0$.

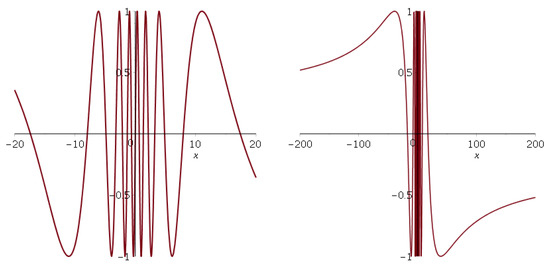
Figure 5. Left side: the free wave function ${\Psi }_2(x)$ in the range $-20<x<20$. The right side is the same wave function in the range $-200<x<200$. Note that ${\Psi }_2(x)$ is well defined in all real axes because the singular regular point $x_0$ lies on the imaginary axis. The parameter values are $\alpha =1/10$, $k=5$, $A=1$, and $B=0$.

For $n=3$,

$$\begin{array}{cc}{\Psi }_3(x)=\hfill & Asin\left({\displaystyle \frac{1}{6}}{\displaystyle \frac{k\left(-2\sqrt{3}arctan\left(\frac{1}{3}\frac{\sqrt{3}\left(-2x+{\left(\frac{1}{\alpha }\right)}^{1/3}\right)}{{\left(\frac{1}{\alpha }\right)}^{1/3}}\right)+2ln\left(x+{\left(\frac{1}{\alpha }\right)}^{1/3}\right)-ln\left(x^2-x{\left(\frac{1}{\alpha }\right)}^{1/3}+{\left(\frac{1}{\alpha }\right)}^{2/3}\right)\right)}{\alpha {\left(\frac{1}{\alpha }\right)}^{2/3}}}\right)+\hfill \\ & +Bcos\left({\displaystyle \frac{1}{6}}{\displaystyle \frac{k\left(-2\sqrt{3}arctan\left(\frac{1}{3}\frac{\sqrt{3}\left(-2x+{\left(\frac{1}{\alpha }\right)}^{1/3}\right)}{{\left(\frac{1}{\alpha }\right)}^{1/3}}\right)+2ln\left(x+{\left(\frac{1}{\alpha }\right)}^{1/3}\right)-ln\left(x^2-x{\left(\frac{1}{\alpha }\right)}^{1/3}+{\left(\frac{1}{\alpha }\right)}^{2/3}\right)\right)}{\alpha {\left(\frac{1}{\alpha }\right)}^{2/3}}}\right)\hfill \end{array}$$

Figure 6 shows the free wave function for $n=3$ with $B=0$. The singular point is at $x_0=-{\displaystyle \frac{1}{{\alpha }^{1/3}}}$.

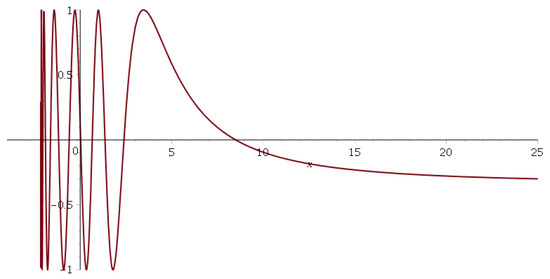
Figure 6. The free wave function ${\Psi }_3(x)$ in the range $x_0<x<20$. Note how the wave shortens its wavelength as it approaches the $x_0$ point. The parameter values are $\alpha =1/10$, $k=5$, $A=1$, and $B=0$. For $x<x_0$, the wave function becomes complex.

For $n=4$,

$$\begin{array}{cc}{\Psi }_4(x)=\hfill & Asin\left({\displaystyle \frac{1}{4}}k{\left({\displaystyle \frac{1}{\alpha }}\right)}^{1/4}\sqrt{2}arctan\left({\displaystyle \frac{-\sqrt{2}x+{\left(\frac{1}{\alpha }\right)}^{1/4}}{{\left(\frac{1}{\alpha }\right)}^{1/4}}}\right)-{\displaystyle \frac{1}{8}}k{\left({\displaystyle \frac{1}{\alpha }}\right)}^{1/4}\sqrt{2}ln\left({\displaystyle \frac{x^2+{\left(\frac{1}{\alpha }\right)}^{1/4}x\sqrt{2}+\sqrt{\frac{1}{\alpha }}}{x^2-{\left(\frac{1}{\alpha }\right)}^{1/4}x\sqrt{2}+\sqrt{\frac{1}{\alpha }}}}\right)\right.\hfill \\ & \left.-{\displaystyle \frac{1}{4}}k{\left({\displaystyle \frac{1}{\alpha }}\right)}^{1/4}\sqrt{2}arctan\left({\displaystyle \frac{\sqrt{2}x+{\left(\frac{1}{\alpha }\right)}^{1/4}}{{\left(\frac{1}{\alpha }\right)}^{1/4}}}\right)\right)+\hfill \\ & Bcos\left({\displaystyle \frac{1}{4}}k{\left({\displaystyle \frac{1}{\alpha }}\right)}^{1/4}\sqrt{2}arctan\left({\displaystyle \frac{-\sqrt{2}x+{\left(\frac{1}{\alpha }\right)}^{1/4}}{{\left(\frac{1}{\alpha }\right)}^{1/4}}}\right)\right.\hfill \\ & \left.-{\displaystyle \frac{1}{8}}k{\left({\displaystyle \frac{1}{\alpha }}\right)}^{1/4}\sqrt{2}ln\left({\displaystyle \frac{x^2+{\left(\frac{1}{\alpha }\right)}^{1/4}x\sqrt{2}+\sqrt{\frac{1}{\alpha }}}{x^2-{\left(\frac{1}{\alpha }\right)}^{1/4}x\sqrt{2}+\sqrt{\frac{1}{\alpha }}}}\right)-{\displaystyle \frac{1}{4}}k{\left({\displaystyle \frac{1}{\alpha }}\right)}^{1/4}\sqrt{2}arctan\left({\displaystyle \frac{\sqrt{2}x+{\left(\frac{1}{\alpha }\right)}^{1/4}}{{\left(\frac{1}{\alpha }\right)}^{1/4}}}\right)\right)\hfill \end{array}$$

Figure 7 shows the free wave function for $n=4$ with $B=0$.

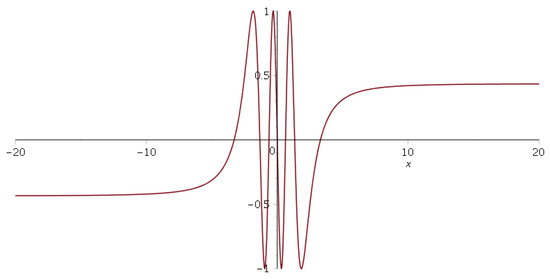
Figure 7. The free wave function ${\Psi }_4(x)$ in the range $-20<x<20$. Again, ${\Psi }_4(x)$ is well defined in all real axes because the singular regular point $x_0$ lies on the imaginary axis. The parameter values are $\alpha =1/10$, $k=5$, $A=1$, and $B=0$.

In the limit $\alpha \to 0$, all these deformed free wave functions converge to the usual sinusoidal free solution (12), and for the non-linear case, the weight factor is

$$\omega (x)={\displaystyle \frac{1}{(1+\alpha x^n)}}$$

so the effective deformed wave function is

$$\tilde{\Psi }(x)={\displaystyle \frac{\Psi (x)}{\sqrt{(1+\alpha x^n)}}}$$

3.2. The Non-Linear $\widehat{x}$ Deformation and the Tunnel Effect

To analyze the effect of the non-linear Heisenberg commutation relation (18) on the tunnel effect, one must consider only the transmitted wave (with positive momentum) for $x>0$, so

$${\Psi }_n^{+}(x)=C{e}^{{\displaystyle \frac{i{p}_x}{\hslash }}{\Theta }_n(x)}n=2,3,4,\cdots x>0$$

As $p_x=\hslash k_1=i\hslash k=i\sqrt{{\displaystyle \frac{2m|E-U_0|}{{\hslash }^2}}}$,

$${\Psi }_n^{+}(x)=C{e}^{-k{\Theta }_n(x)}n=2,3,4,\cdots x>0$$

For example, for $n=2$,

$${\Psi }_2^{+}(x)=C{\mathrm{e}}^{-{\displaystyle \frac{karctan(\sqrt{\alpha }x)}{\sqrt{\alpha }}}}x>0$$

Figure 8 compares the deformed wave function ${\Psi }_2$ and the effective wave function ${\tilde{\Psi }}_2$ with the non-deformed one (17) for $x>0$.

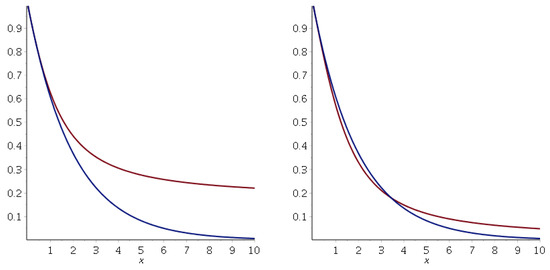
Figure 8. Left side: deformed wave function ${\Psi }_2^{+}(x)$ (red curve) and the non-deformed one (blue curve) in the range $0<x<10$. Right side: effective deformed wave function ${\tilde{\Psi }}_2^{+}(x)$ (red curve) and the non-deformed one (blue curve) in the same range. Note that ${\Psi }_2^{+}(x)$ becomes constant for $x\to \infty$, whereas ${\tilde{\Psi }}_2^{+}(x)$ goes to zero. The parameter values are $\alpha =1/5$, $k=1/2$.

For $n=3$,

$${\Psi }_3^{+}(x)=C{e}^{-k\left({\displaystyle \frac{1}{3}}{\displaystyle \frac{ln\left(x+{\left(\frac{1}{\alpha }\right)}^{1/3}\right)}{\alpha {\left(\frac{1}{\alpha }\right)}^{2/3}}}-{\displaystyle \frac{1}{6}}{\displaystyle \frac{ln\left(x^2-x{\left(\frac{1}{\alpha }\right)}^{1/3}+{\left(\frac{1}{\alpha }\right)}^{2/3}\right)}{\alpha {\left(\frac{1}{\alpha }\right)}^{2/3}}}+{\displaystyle \frac{1}{3}}{\displaystyle \frac{\sqrt{3}arctan\left(\frac{1}{3}\sqrt{3}\left(\frac{2x}{{\left(\frac{1}{\alpha }\right)}^{1/3}-1}\right)\right)}{\alpha {\left(\frac{1}{\alpha }\right)}^{2/3}}}\right)}x>0$$

Figure 9 compares the deformed wave function ${\Psi }_3$ and the effective wave function ${\tilde{\Psi }}_3$ with the non-deformed one (17) for $x>0$.

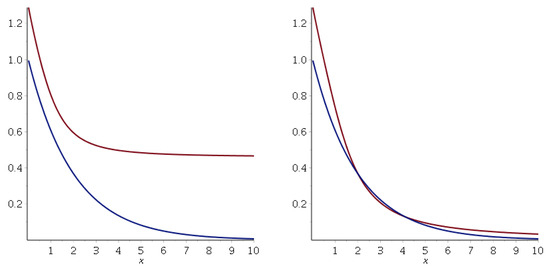
Figure 9. Left side: the deformed wave function ${\Psi }_3^{+}(x)$ (red curve) and the non-deformed one (blue curve) in the range $0<x<10$. Right side: effective deformed wave function ${\tilde{\Psi }}_3^{+}(x)$ (red curve) and the non-deformed one (blue curve) in the same range. The parameter values are those of Figure 8. Again, ${\Psi }_3^{+}(x)$ becomes constant for $x\to \infty$, whereas ${\tilde{\Psi }}_3^{+}(x)$ goes to zero.

Thus, the effective wave functions ${\tilde{\Psi }}_2^{+}$ and ${\tilde{\Psi }}_3^{+}$ have more significant values in the classical prohibited region $x>3$ than the non-deformed one ${\Psi }_{+}^0(x)$, generating more likely tunneling probabilities than the non-deformed ones, which also depend on $\alpha$.

4. The Linear $\widehat{\mathit{p}}$ Deformation Case

Consider now the dependency of the deformed Heisenberg algebra in terms of the particle momentum. We start with the linear case, so we assume a modified Heisenberg algebra of the form

$$\left[\widehat{x},{\widehat{p}}_x\right]=i\hslash \left(\mathbb{I}+\beta {\widehat{p}}_x\right)$$

A representation of these commutation relations in terms of differential operators is given by

$$\begin{array}{c}\widehat{x}=x\\ {\widehat{p}}_x={\displaystyle \frac{1}{\beta }}\left(e^{\beta {\widehat{p}}_0}-\mathbb{I}\right)\end{array}$$

where ${\widehat{p}}_0=-i\hslash {\displaystyle \frac{\partial }{\partial x}}$ is the standard momentum operator for $\beta =0$. The eigenfunctions of ${\widehat{p}}_0$,

$${\widehat{p}}_0{\Phi }_p=p{\Phi }_p$$

are of course

$${\Phi }_p=A{e}^{{\displaystyle \frac{ipx}{\hslash }}}$$

(21)

4.1. The Linear $\widehat{p}$ Deformation Case and the Free Particle

For the free particle classical Hamiltonian (5), the time-independent Schrödinger equation is

$${\displaystyle \frac{{\left(e^{\beta {\widehat{p}}_0}-\mathbb{I}\right)}^2}{2m{\beta }^2}}\Psi =E\Psi$$

(22)

Because the Hamiltonian operator is a function of ${\widehat{p}}_0$, the energy eigenstates must be combinations of the eigenstates of the ${\widehat{p}}_0$ operator. Thus, the general solution of (22) is the form

$$\Psi (x)=A{\Phi }_p+B{\Phi }_{-p}$$

or

$$\Psi (x)=A{e}^{{\displaystyle \frac{ipx}{\hslash }}}+B{e}^{{\displaystyle \frac{-ipx}{\hslash }}}$$

(23)

The deformed wave function, in this case, is just a non-deformed one, but the energy spectrum acquires a non-trivial dependence in the free momentum p. In fact, from (22), one has that

$$E=E(p)={\displaystyle \frac{{\left(e^{\beta p}-1\right)}^2}{2m{\beta }^2}}$$

which differs from the non-deformed one $E_0=E_0(p)={\displaystyle \frac{p^2}{2m}}$.

Figure 10 shows the energy as a function of the momentum for the deformed and non-deformed cases.

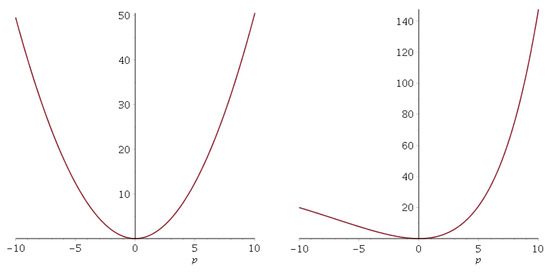
Figure 10. Left figure: energy spectrum $E_0(p)$ for the non-deformed case. Note that it is symmetric in terms of the momentum. Right figure: energy spectrum $E(p)$ for the deformed case. Here, the spectrum is not symmetric. The parameter values are $\beta =0.1$ and $m=1$.

The fact that the deformed energy spectrum is not symmetric has very interesting consequences. For example, free particles with positive momentum (moving to the right) have greater energy than free particles moving to the left (with negative momentum). This property generates a left–right asymmetry. If the particle energy can be thought of as an analogue of distance measure, this asymmetry could be related to what mathematicians call quasimetric spaces [25,26,27,28], i.e., spaces in which the distance measured when moving to the right differs from that measured when moving to the left. In this sense, the case of linear momentum deformation would represent these quasimetric spaces in the physical world. A more detailed analysis of the properties of the deformed spectrum $E(p)$ can be found in [21].

4.2. The Linear $\widehat{p}$ Deformation Case and Tunneling

For the step function potential (15), the time-independent Schrödinger in the $x>0$ region is

$${\displaystyle \frac{{\left(e^{\beta {\widehat{p}}_0}-\mathbb{I}\right)}^2}{2m{\beta }^2}}\Psi +U_0\Psi =E\Psi$$

(24)

The solution (associated with the transmitted wave moving to the right) is $\Psi ={\Psi }_{+}(x)=C{e}^{{\displaystyle \frac{i}{\hslash }}px}$; so, by replacing ${\Psi }_{+}(x)$ in (24), one has

$${\displaystyle \frac{{\left(e^{\beta p}-1\right)}^2}{2m{\beta }^2}}=E-U_0$$

from which

$$e^{\beta p_{\pm }}=1\pm \sqrt{2m{\beta }^2(E-U_0)}$$

or

$$p_{\pm }={\displaystyle \frac{1}{\beta }}ln\left(1\pm \sqrt{2m{\beta }^2(E-U_0)}\right)$$

Note that, for $U_0=0$, one must recover the wave with positive momentum (moving to the right), so the correct sign is plus. Thus,

$$p=p_{+}={\displaystyle \frac{1}{\beta }}ln\left(1+\sqrt{2m{\beta }^2(E-U_0)}\right)$$

Because we consider $U_0>E$,

$$p=p_{+}={\displaystyle \frac{1}{\beta }}ln\left(1+i\sqrt{2m{\beta }^2|E-U_0|}\right)$$

By writing the complex number $z=1+i\sqrt{2m{\beta }^2|E-U_0|}$ in the polar form $z=r{e}^{i\varphi }$,

$$p={\displaystyle \frac{1}{\beta }}ln\left(\sqrt{1+2m{\beta }^2|E-U_0|}\right)+i{\displaystyle \frac{1}{\beta }}arctan(\sqrt{2m{\beta }^2|E-U_0|})$$

The solution for $x>0$ is then

$$\begin{array}{cc}\hfill {\Psi }_{+}(x)=& C{e}^{{\displaystyle \frac{i}{\hslash }}px}=C{e}^{{\displaystyle \frac{ix}{\beta \hslash }}ln\left(\sqrt{1+2m{\beta }^2|E-U_0|}\right)-{\displaystyle \frac{x}{\beta \hslash }}arctan(\sqrt{2m{\beta }^2|E-U_0|})}\hfill \\ \hfill =& C{e}^{-{\displaystyle \frac{x}{\beta \hslash }}arctan(\beta \sqrt{2m|E-U_0|})}{e}^{{\displaystyle \frac{ix}{2\beta \hslash }}ln\left(1+2m{\beta }^2|E-U_0|\right)}\hfill \end{array}$$

Apart from the typical decay factor, the wave function acquires a complex oscillatory factor. Using $arctan(x)\approx x$ and $ln(1+x)\approx x$ for $x<<1$, one has that, for $\beta <<1$,

$$e^{-{\displaystyle \frac{x}{\beta \hslash }}arctan(\beta \sqrt{2m|E-U_0|})}\approx e^{-{\displaystyle \frac{x}{\beta \hslash }}(\beta \sqrt{2m|E-U_0|})}=e^{-{\displaystyle \frac{x}{\hslash }}\sqrt{2m|E-U_0|}}=e^{-kx}$$

and

$$e^{{\displaystyle \frac{ix}{2\beta \hslash }}ln\left(1+2m{\beta }^2|E-U_0|\right)}\approx e^{{\displaystyle \frac{ix}{2\beta \hslash }}\left(2m{\beta }^2|E-U_0|\right)}=e^{{\displaystyle \frac{ix}{\hslash }}\left(m\beta |E-U_0|\right)}\approx 1+{\displaystyle \frac{ixm\beta |E-U_0|}{\hslash }}$$

Thus, the oscillatory complex term goes to zero for $\beta =0$ and the decay term acquires its typical exponential form.

Figure 11 compares the deformed decay factor

$$e^{-{\displaystyle \frac{x}{\beta \hslash }}arctan(\beta \sqrt{2m|E-U_0|})}=e^{-{\displaystyle \frac{x}{\beta \hslash }}arctan(\beta \hslash \sqrt{{\displaystyle \frac{2m|E-U_0|}{{\hslash }^2}}})}=e^{-{\displaystyle \frac{x}{\beta \hslash }}arctan(\beta \hslash k)}$$

with the non-deformed one $e^{-kx}$, for $\beta \hslash =4,10,\mathrm{and}100$.

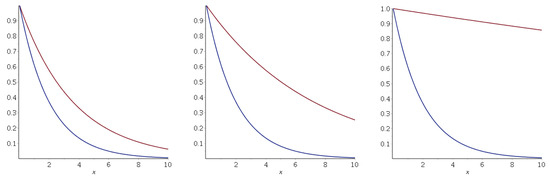
Figure 11. Comparison between the deformed (red curve) and non-deformed (blue curve) decay factors for $k=1/2$ in the linear momentum deformation case. Left plot: $\beta \hslash =4$; middle plot: $\beta \hslash =10$; right plot: $\beta \hslash =100$.

Thus, for higher $\beta$ deformation values, the free particle can reach greater distances in the classical forbidden zone.

5. The Non-Linear $\widehat{\mathit{p}}$ Deformation Case

Finally, we consider the non-linear momentum generalization

$$\left[\widehat{x},{\widehat{p}}_x\right]=i\hslash \left(\mathbb{I}+\beta {\widehat{p}}_x^n\right)n=1,2,3,\cdots$$

(25)

As is shown in [3], a deformed Heisenberg commutation relation of the form

$$\left[\widehat{x},{\widehat{p}}_x\right]=ig\left({\widehat{p}}_x\right)$$

for some function $g(p)$, can be represented by the differential operators

$$\begin{array}{c}\widehat{x}=x\\ {\widehat{p}}_x=h\left({\widehat{p}}_0\right)\end{array}$$

where the function $h(p)$ is the solution to the differential equation [3]

$${\displaystyle \frac{dh(p)}{dp}}=g(h(p))$$

(26)

Consider now the case $n=2$; the g function is

$$g(p)=1+\beta p^2$$

and Equation (26) becomes

$${\displaystyle \frac{dh(p)}{dp}}=1+\beta h{(p)}^2$$

(27)

with the solution

$$h(p)={\displaystyle \frac{tan(p\sqrt{\beta }+C_1)}{\sqrt{\beta }}}$$

Note that, for $0<\beta <<1$, one hopes to recover the non-deformed operator p. Because $tan(x)\approx x$ for $x<<1$, one has that if $0<\beta <<1$

$$h(p)={\displaystyle \frac{tan(p\sqrt{\beta }+C_1)}{\sqrt{\beta }}}\approx p+{\displaystyle \frac{C_1}{\sqrt{\beta }}}$$

Then, to recover the non-deformed case $h(p)=p$, the constant $C_1$ must be zero. Thus,

$$h(p)={\displaystyle \frac{tan(p\sqrt{\beta })}{\sqrt{\beta }}}$$

and as is indicated in [18], the Heisenberg algebra (25) can be represented by the differential operators

$$\begin{array}{c}\widehat{x}=x\\ {\widehat{p}}_x={\displaystyle \frac{tan\left(\sqrt{\beta }{\widehat{p}}_0\right)}{\sqrt{\beta }}}\end{array}$$

where ${\widehat{p}}_0=-i\hslash {\displaystyle \frac{\partial }{\partial x}}$ is the standard momentum operator for $\beta =0$.

5.1. The Non-Linear $\widehat{p}$ Deformation Case and the Free Particle

The Schrödinger equation for the free particle is

$${\displaystyle \frac{{tan}^2\left(\sqrt{\beta }{\widehat{p}}_0\right)}{2m\beta }}\Psi (x)=E\Psi (x)$$

Again, $\Psi$ must be a superposition eigenvector of the momentum ${\widehat{p}}_0$ operator, given by Equation (23), and its energy spectrum is, for $\beta >0$,

$$E(p)={\displaystyle \frac{{tan}^2(\sqrt{\beta }p)}{2m\beta }}\beta >0$$

Note that, in this case, the spectrum is symmetric and periodic in p.

For $\beta <0$, one has that

$$E(p)={\displaystyle \frac{{tan}^2(\sqrt{\beta }p)}{2m\beta }}=-{\displaystyle \frac{{tan}^2(i\sqrt{\left|\beta \right|}p)}{2m\left|\beta \right|}}={\displaystyle \frac{{tanh}^2(\sqrt{\left|\beta \right|}p)}{2m\left|\beta \right|}}\beta <0$$

In this case, the spectrum is not periodic. Figure 12 shows the deformed energy spectrum for $\beta =1$ and $\beta =-1$ as a function of momentum p.

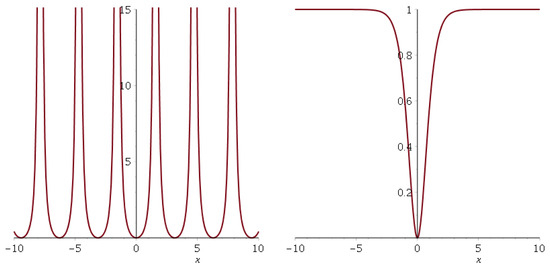
Figure 12. Deformed free particle energy spectrum as a function of the momentum p for $\beta =1$ (left side figure) and $\beta =-1$ (right side figure). The mass value is $m=1/2$.

For an arbitrary n value, the eigenstates of the free Hamiltonian (5) will always be eigenstates of the non-deformed momentum operator ${\widehat{p}}_0$, and the wave function will be of the form (23).

5.2. The Non-Linear $\widehat{p}$ Deformation Case and Tunneling

For the step-function potential (15), the Schrödinger equation for $x>0$ and $\beta >0$ is

$${\displaystyle \frac{{tan}^2\left(\sqrt{\beta }{\widehat{p}}_0\right)}{2m\beta }}\Psi (x)+U_0\Psi (x)=E\Psi (x)$$

(28)

Considering a free wave moving to the right,

$${\Psi }_{+}(x)=C{e}^{{\displaystyle \frac{ipx}{\hslash }}}$$

and replacing in (28) obtains

$${\displaystyle \frac{1}{2}}{\displaystyle \frac{tan{(\sqrt{\beta }p)}^2}{m\beta }}=E-U_0$$

Solving for the momentum p gives

$$p={\displaystyle \frac{arctan(\sqrt{2m\beta (E-U_0)})}{\sqrt{\beta }}}$$

and, because $E<U_0$, one has

$$p={\displaystyle \frac{arctan(i\sqrt{2m\beta |E-U_0|})}{\sqrt{\beta }}}={\displaystyle \frac{iarctanh(\sqrt{2m\beta |E-U_0|})}{\sqrt{\beta }}}$$

so the deformed wave ${\Psi }_{+}(x)$ is

$${\Psi }_{+}(x)=C{e}^{{\displaystyle \frac{ipx}{\hslash }}}=C{\mathrm{e}}^{-{\displaystyle \frac{xarctanh(\sqrt{2m\beta |E-U_0|})}{\hslash \sqrt{\beta }}}}=C{\mathrm{e}}^{-{\displaystyle \frac{xarctanh\left(\hslash \sqrt{\beta }\sqrt{\frac{2m|E-U_0|}{{\hslash }^2}}\right)}{\hslash \sqrt{\beta }}}}$$

or

$${\Psi }_{+}(x)=C{\mathrm{e}}^{-{\displaystyle \frac{xarctanh(\hslash \sqrt{\beta }k)}{\hslash \sqrt{\beta }}}}\beta >0$$

(29)

Figure 13 shows the deformed and non-deformed wave functions for $x>0$ and $\beta >0$ for cases $\sqrt{\beta }\hslash =2$ and $\sqrt{\beta }\hslash =2\sqrt{2}$.

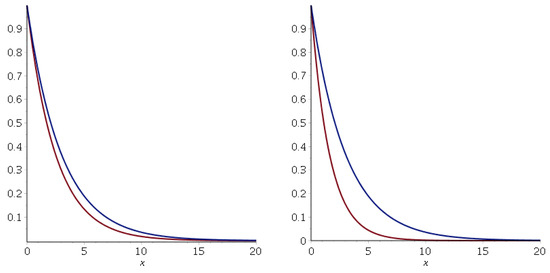
Figure 13. Comparison between the deformed (red curve) and non-deformed (blue curve) decay factors for $k=1/3$ and $C=1$. Left figure: $\sqrt{\beta }\hslash =2$; right figure: $\sqrt{\beta }\hslash =2\sqrt{2}$.

As the parameter $\beta >0$ increases, the deformed wave function becomes smaller and smaller than the undeformed one. Therefore, the deformed wave has a lower probability of crossing the potential barrier than the undeformed wave. Also, as $arctanh(x)$ is well defined only for $-1\le x\le 1$, the $\beta$ values are restricted to the region $0\le \beta \le {\displaystyle \frac{1}{{(\hslash k)}^2}}.$

When $\beta <0$, the wave function (29) becomes

$${\Psi }_{+}(x)=C{\mathrm{e}}^{-{\displaystyle \frac{xarctanh(i\hslash \sqrt{\left|\beta \right|}k)}{i\hslash \sqrt{\left|\beta \right|}}}}\beta <0$$

or

$${\Psi }_{+}(x)=C{\mathrm{e}}^{-{\displaystyle \frac{xarctan(\hslash \sqrt{\left|\beta \right|}k)}{\hslash \sqrt{\left|\beta \right|}}}}\beta <0$$

(30)

Figure 14 shows the deformed and non-deformed wave functions for $x>0$ and $\beta <0$ for cases $\sqrt{\left|\beta \right|}\hslash =2$ and $\sqrt{\left|\beta \right|}\hslash =2\sqrt{2}$.

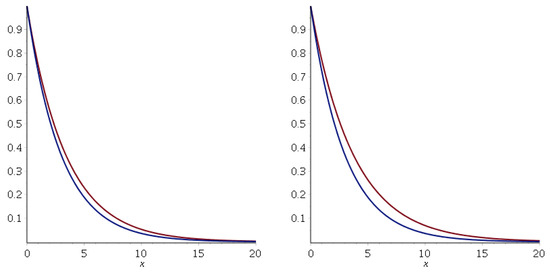
Figure 14. Comparison between the deformed (red curve) and non-deformed (blue curve) decay factors for $k=1/3$ and $C=1$. Left figure: $\sqrt{\left|\beta \right|}\hslash =2$; right figure: $\sqrt{\left|\beta \right|}\hslash =2\sqrt{2}$.

In this case, the deformed wave function for increasingly negative $\beta$ values is larger than the undeformed one. Therefore, the particle is more likely to cross the potential barrier. In summary, the tunneling probabilities for the momentum deformation case depend on the sign of the beta deformation parameter.

The following section will explore the intriguing relationship between quantum mechanics and finance. We will demonstrate that a specific form of linear deformation in the position of the Heisenberg commutation relations enables us to derive a Schrödinger equation that bears a striking resemblance to the Black–Scholes equation, a vital tool in determining the price of financial derivatives in the stock market. This Schrödinger equation is obtained by quantizing the Hamiltonian of a charged particle in an external electromagnetic field. In fact, for a particular choice of these electromagnetic potentials, the Schrödinger equation becomes identical to the Black–Scholes equation.

6. The Black–Scholes Model and Quantum Mechanics

Since the publication in the first years of the 1970s of the seminal articles by Black and Scholes [29] and Merton [30], the Black–Scholes model has become the main tool in financial engineering for modeling and pricing the value of a derivative on equity. Two decades after that, in the mid-1990s, the science of econophysics (so named by professor H. Eugene Stanley [31] at a conference in Calcutta) emerged, where physicists began to analyze, in a more systematic way, the problems of economics using the conceptual and mathematical methods from physics [32].

From the beginnings of econophysics, different authors have tried to relate the Black–Scholes equation with quantum mechanics [33,34,35,36,37]—with the Schrödinger equation in particular [38,39,40,41,42]—and its possible generalizations [43,44,45,46,47].

In [38], the Black–Scholes equation is mapped to the Schrödinger equation of a free particle through a series of coordinate transformations as follows: in the Black–Scholes equation,

$${\displaystyle \frac{\partial \pi }{\partial t}}+{\displaystyle \frac{1}{2}}{\sigma }^2{S}^2{\displaystyle \frac{{\partial }^2\pi }{\partial S^2}}+r\left(S{\displaystyle \frac{\partial \pi }{\partial S}}-\pi \right)=0$$

(31)

Note that the Black–Scholes equation has two free parameters—the volatility $\sigma$ and the interest rate r, which can be obtained from the empirical financial data.

Now, by taking the variable change $\xi =lnS$, one obtains

$${\displaystyle \frac{\partial \pi }{\partial t}}+{\displaystyle \frac{1}{2}}{\sigma }^2{\displaystyle \frac{{\partial }^2\pi }{\partial {\xi }^2}}+\left(r-{\displaystyle \frac{1}{2}}{\sigma }^2\right){\displaystyle \frac{\partial \pi }{\partial \xi }}-r\pi =0$$

If one makes a second (time-dependent) change of variables

$$x=\xi -\left(r-{\displaystyle \frac{1}{2}}{\sigma }^2\right)t$$

one arrives at

$${\displaystyle \frac{\partial \pi }{\partial t}}+{\displaystyle \frac{1}{2}}{\sigma }^2{\displaystyle \frac{{\partial }^2\pi }{\partial x^2}}-r\pi =0$$

By performing

$$\pi (x,t)={\mathrm{e}}^{-r(T-t)}\psi (x,t)$$

the $\psi$ dynamic is given by

$${\displaystyle \frac{\partial \psi (x,t)}{\partial t}}+{\displaystyle \frac{1}{2}}{\sigma }^2{\displaystyle \frac{{\partial }^2\psi (x,t)}{\partial x^2}}=0$$

Finally, a Wick rotation in time

$$t=-i\tau$$

(32)

maps the heat equation above into

$$i{\displaystyle \frac{\partial \psi }{\partial \tau }}=-{\displaystyle \frac{1}{2}}{\sigma }^2{\displaystyle \frac{{\partial }^2\psi }{\partial x^2}}.$$

(33)

This last equation is the Schrödinger equation of a free particle with $\hslash =1$ and mass $m={\displaystyle \frac{1}{{\sigma }^2}}$ in the $(x,\tau )$ space. It is assumed that in the final coordinate systems $(x,\tau )$, the position x and its related momentum $p_x$ can be quantized by the usual Heisenberg canonical commutation relations (1), which admits the representation as a differential operator acting on a function space or Hilbert space according to

$$\widehat{x}\to x,{\widehat{p}}_x\to -i\hslash {\displaystyle \frac{\partial }{\partial x}}$$

(34)

So, Equation (33) can be obtained from the non-relativistic Hamiltonian of a free particle

$$H(x,p_x)={\displaystyle \frac{p_x^2}{2m}}$$

(35)

From this perspective, the Black–Scholes model can be interpreted, from the point of view of quantum mechanics, as a dynamic model without interactions, i.e., a free quantum particle model. In [33], a discussion of the necessary conditions to embed the Black–Scholes option pricing model, in terms of the original space $(S,t)$ in a more general quantum physics setting, is presented. So, one may wonder, if it is not possible to obtain a Black–Scholes equation by directly quantizing the relevant variables in the $(S,\tau )$ space, to instead use coordinates changes.

For example, one could start with the Hamiltonian of a charged particle moving along the one-dimensional x axis, in the presence of a magnetic (Although there is no magnetic field in one dimension, we call $A_S$ the magnetic potential because of how it pairs with momentum. The Hamiltonian of a charged particle in three dimensions in the presence of an external electromagnetic field has the structure

$$H={\displaystyle \frac{{(\overrightarrow{p}-q\overrightarrow{A}(\overrightarrow{x},t))}^2}{2m}}+U(\overrightarrow{x},t)$$

which has quadratic terms in the momentum—a linear term in $\overrightarrow{p}$ that is multiplied by the magnetic potential vector, in the form

$$\overrightarrow{A}·\overrightarrow{p}$$

that, for the one-dimensional case, is simply $A_S{p}_S$. For this reason, we call $A_S$ the magnetic potential.) and electric potential according to

$$H(x,p_x)={\displaystyle \frac{{(p_x-qA(x))}^2}{2m}}+U(x).$$

(36)

By quantizing this classical Hamiltonian by the usual Heisenberg commutation relations (1) and left momentum quantization ordering, one obtains the Hamiltonian operator

$$\widehat{H}={\displaystyle \frac{{\widehat{p}}_x^2}{2m}}-{\displaystyle \frac{q}{2m}}A(x){\widehat{p}}_x-{\displaystyle \frac{q}{2m}}{\widehat{p}}_{x}A(x)+{\displaystyle \frac{q^2}{2m}}{A}^2+U(x)$$

(37)

so the corresponding time-dependent Schrödinger equation

$$\widehat{H}\Psi =i\hslash {\displaystyle \frac{\partial \Psi }{\partial \tau }}$$

using the representation (34) in terms of $\widehat{x}$ and ${\widehat{p}}_x$, is

$$-{\displaystyle \frac{{\hslash }^2}{2m}}{\displaystyle \frac{{\partial }^2\Psi }{\partial x^2}}+i{\displaystyle \frac{q\hslash }{2m}}A(x){\displaystyle \frac{\partial \Psi }{\partial x}}+i{\displaystyle \frac{q\hslash }{2m}}{\displaystyle \frac{\partial }{\partial x}}\left(A(x)\Psi \right)+\left({\displaystyle \frac{q^2}{2m}}{A}^2+U(x)\right)\Psi =i\hslash {\displaystyle \frac{\partial \Psi }{\partial \tau }}$$

or

$$-{\displaystyle \frac{\hslash }{2m}}{\displaystyle \frac{{\partial }^2\Psi }{\partial x^2}}+i{\displaystyle \frac{q}{m}}A(x){\displaystyle \frac{\partial \Psi }{\partial x}}+{\displaystyle \frac{1}{\hslash }}\left({\displaystyle \frac{q^2}{2m}}{A}^2+U(x)+i{\displaystyle \frac{q\hslash }{2m}}{\displaystyle \frac{\partial A(x)}{\partial x}}\right)\Psi =i{\displaystyle \frac{\partial \Psi }{\partial \tau }}$$

The Wick rotation (32) transforms this equation in

$$-{\displaystyle \frac{\hslash }{2m}}{\displaystyle \frac{{\partial }^2\Psi }{\partial x^2}}+i{\displaystyle \frac{q}{m}}A(x){\displaystyle \frac{\partial \Psi }{\partial x}}+{\displaystyle \frac{1}{\hslash }}\left({\displaystyle \frac{q^2}{2m}}{A}^2+U(x)+i{\displaystyle \frac{q\hslash }{2m}}{\displaystyle \frac{\partial A(x)}{\partial x}}\right)\Psi ={\displaystyle \frac{\partial \Psi }{\partial t}}$$

Thus, one could then choose $A(x)$, $U(x)$, and m such that

$$\begin{array}{ccc}-rx& =& i{\displaystyle \frac{q}{m}}A(x)\hfill \\ r& =& {\displaystyle \frac{1}{\hslash }}\left({\displaystyle \frac{q^2}{2m}}A{(x)}^2+U(x)+i{\displaystyle \frac{q\hslash }{2m}}{\displaystyle \frac{\partial A(x)}{\partial x}}\right)\hfill \\ {\sigma }^2& =& {\displaystyle \frac{\hslash }{m}}\hfill \end{array}$$

so the Schrödinger equation becomes

$${\displaystyle \frac{\partial \Psi }{\partial t}}+{\displaystyle \frac{1}{2}}{\sigma }^2{\displaystyle \frac{{\partial }^2\Psi }{\partial x^2}}+rx{\displaystyle \frac{\partial \Psi }{\partial x}}-r\Psi =0$$

The problem with this procedure is that if one identifies the coordinate x with the S variable of the Black–Scholes model (and also the wave function with the option price), the second-order derivative term in the above equation is incorrect because there is no $S^2$ present multiplying the volatility, see Equation (31). So, the usual Heisenberg commutation relations (1) do not permit obtaining the correct Black–Scholes equation directly in the $(S,t)$ space.

6.1. GUP and the Black–Scholes Equation

In this section, we explore the possibility of using the modifications of the Heisenberg algebra given in (2) to obtain the Black–Scholes equation in the $(x,t)$ space. In particular, one can consider the following GUP

$$[\widehat{x},{\widehat{p}}_x]=i\hslash \left(\mathbb{I}+F(\widehat{x})\right)$$

(38)

where $F(x)$ is some function of x. By expanding $F(x)$ in Taylor series in the form

$$F(x)={\beta }_0+{\beta }_{1}x+....$$

then

$$[\widehat{x},{\widehat{p}}_x]=i\hslash \left(\mathbb{I}+{\beta }_0\mathbb{I}+{\beta }_1\widehat{x}+...\right)$$

(39)

By keeping only the first two terms in the series (to explore the effect of the first contributions of $\widehat{x}$), the corresponding GUP can be written as

$$[\widehat{x},{\widehat{p}}_x]=i\hslash \left(\alpha \mathbb{I}+\beta \widehat{x}\right)$$

(40)

where we define $\alpha =1+{\beta }_0$ and $\beta ={\beta }_1$ to keep the notation simple. An operator representation of the above commutation relations is

$$\begin{array}{ccc}\widehat{x}& =& x\hfill \\ {\widehat{p}}_x& =& -i\hslash (\alpha +\beta x){\displaystyle \frac{\partial }{\partial x}}\hfill \end{array}$$

(41)

Consider now the usual non-relativist classical Hamiltonian

$$H(x,p_x)={\displaystyle \frac{p_x^2}{2m}}+U(x)$$

(42)

The quantization of this Hamiltonian function in the $(x,\tau )$ space by rule (40) gives the following Schrödinger equation for the wave function $\Psi (x,\tau )$

$${\displaystyle \frac{-{\hslash }^2}{2m}}(\alpha +\beta S){\displaystyle \frac{\partial }{\partial x}}\left[(\alpha +\beta x){\displaystyle \frac{\partial }{\partial x}}\right]\Psi +U(x)\Psi =i\hslash {\displaystyle \frac{\partial \Psi }{\partial \tau }}$$

(43)

or

$$-{\displaystyle \frac{{\hslash }^2}{2m}}{(\alpha +\beta x)}^2{\displaystyle \frac{{\partial }^2\Psi }{\partial x^2}}-{\displaystyle \frac{{\hslash }^2}{2m}}\beta (\alpha +\beta x){\displaystyle \frac{\partial \Psi }{\partial x}}+U(S)\Psi (x,t)=i\hslash {\displaystyle \frac{\partial \Psi }{\partial \tau }}$$

(44)

In the limit $\alpha <<\beta$ (or $\alpha \to 0)$, the Schrödinger equation in the space $(x,\tau )$ goes to

$$-{\displaystyle \frac{{\hslash }^2}{2m}}{\beta }^2{x}^2{\displaystyle \frac{{\partial }^2\Psi }{\partial x^2}}-{\displaystyle \frac{{\hslash }^2}{2m}}{\beta }^{2}x{\displaystyle \frac{\partial \Psi }{\partial x}}+U(x)\Psi (x,t)=i\hslash {\displaystyle \frac{\partial \Psi }{\partial \tau }}$$

(45)

By performing the Wick rotation (32), one obtains

$$-{\displaystyle \frac{\hslash {\beta }^2}{2m}}{x}^2{\displaystyle \frac{{\partial }^2\Psi }{\partial x^2}}-{\displaystyle \frac{\hslash {\beta }^2}{2m}}x{\displaystyle \frac{\partial \Psi }{\partial x}}+{\displaystyle \frac{1}{\hslash }}U(x)\Psi (x,t)={\displaystyle \frac{\partial \Psi }{\partial t}}$$

(46)

or

$${\displaystyle \frac{\partial \Psi }{\partial t}}+{\displaystyle \frac{\hslash {\beta }^2}{2m}}{x}^2{\displaystyle \frac{{\partial }^2\Psi }{\partial x^2}}+{\displaystyle \frac{\hslash {\beta }^2}{2m}}x{\displaystyle \frac{\partial \Psi }{\partial x}}-{\displaystyle \frac{1}{\hslash }}U(x)\Psi =0$$

(47)

Now, by choosing $\beta$, $\sigma$, and $U(x)$ such that

$$\begin{array}{ccc}{\displaystyle \frac{\hslash {\beta }^2}{m}}& =& {\sigma }^2\hfill \\ \\ {\displaystyle \frac{1}{2}}{\sigma }^2& =& r\hfill \\ \\ {\displaystyle \frac{1}{\hslash }}U(x)& =& r\hfill \end{array}$$

one ended with a Black–Scholes equation of the form

$${\displaystyle \frac{\partial \Psi }{\partial t}}+r{x}^2{\displaystyle \frac{{\partial }^2\Psi }{\partial x^2}}+rx{\displaystyle \frac{\partial \Psi }{\partial x}}-r\Psi =0$$

(48)

in which the volatility ${\sigma }^2$ is fixed and is equal to two times the interest rate r.

Note that, in the limit $\alpha \to 0$, the commutation relations (40) go to

$$[\widehat{x},{\widehat{p}}_x]=i\hslash \beta \widehat{x}$$

(49)

and its operator representation goes to

$$\begin{array}{ccc}\widehat{x}& =& x\hfill \\ {\widehat{p}}_x& =& -i\hslash \beta x{\displaystyle \frac{\partial }{\partial x}}\hfill \end{array}$$

(50)

Of course, the resulting Black–Scholes Equation (48) is very restrictive, because it has only one free parameter, which can be chosen as the interest rate r (volatility is completely determined by the interest rate according to $\sigma =\sqrt{r}$).

6.2. Adding a Magnetic Potential

If, instead of the Hamiltonian (42), one quantizes the Hamiltonian (36) with modified Heisenberg commutation relations (49), then the operator Hamiltonian (37) obtains the following Schrödinger equation:

$${\displaystyle \frac{-{\hslash }^2}{2m}}\beta x{\displaystyle \frac{\partial }{\partial x}}\left(\beta x{\displaystyle \frac{\partial }{\partial x}}\right)\Psi +i{\displaystyle \frac{q\hslash }{2m}}A(x)\beta x{\displaystyle \frac{\partial \Psi }{\partial x}}+i{\displaystyle \frac{q\hslash }{2m}}\beta x{\displaystyle \frac{\partial }{\partial x}}\left(A(x)\Psi \right)+\left({\displaystyle \frac{q^2}{2m}}{A}^2+U(x)\right)\Psi =i\hslash {\displaystyle \frac{\partial \Psi }{\partial \tau }}$$

or

$$-{\displaystyle \frac{{\hslash }^2{\beta }^2}{2m}}{x}^2{\displaystyle \frac{{\partial }^2\Psi }{\partial x^2}}-\left({\displaystyle \frac{{\hslash }^2{\beta }^2}{2m}}-i{\displaystyle \frac{2q\hslash \beta }{2m}}A(x)\right)x{\displaystyle \frac{\partial \Psi }{\partial x}}+\left({\displaystyle \frac{q^2}{2m}}{A}^2+U(x)+i{\displaystyle \frac{q\hslash \beta }{2m}}x{\displaystyle \frac{\partial A(x)}{\partial x}}\right)\Psi =i\hslash {\displaystyle \frac{\partial \Psi }{\partial \tau }}$$

Dividing by ℏ and performing a Wick rotation (32) gives

$${\displaystyle \frac{\partial \Psi }{\partial t}}+{\displaystyle \frac{\hslash {\beta }^2}{2m}}{x}^2{\displaystyle \frac{{\partial }^2\Psi }{\partial x^2}}+\left({\displaystyle \frac{\hslash {\beta }^2}{2m}}-i{\displaystyle \frac{q\beta }{m}}A(x)\right)x{\displaystyle \frac{\partial \Psi }{\partial x}}-\left({\displaystyle \frac{q^2}{2m\hslash }}{A}^2+{\displaystyle \frac{1}{\hslash }}U(x)+i{\displaystyle \frac{q\beta }{2m}}x{\displaystyle \frac{\partial A(x)}{\partial x}}\right)\Psi =0$$

(51)

In this way, if one sets

$$\begin{array}{ccc}{\sigma }^2& =& {\displaystyle \frac{\hslash {\beta }^2}{m}}\hfill \\ \\ r& =& {\displaystyle \frac{\hslash {\beta }^2}{2m}}-i{\displaystyle \frac{q\beta }{m}}A(x)\hfill \\ \\ r& =& {\displaystyle \frac{q^2}{2m\hslash }}{A}^2+{\displaystyle \frac{1}{\hslash }}U(x)+i{\displaystyle \frac{q\beta }{2m}}x{\displaystyle \frac{\partial A(x)}{\partial x}}\hfill \end{array}$$

then $\beta$ and the magnetic potential A are given, respectively, by

$$\beta =\sigma \sqrt{{\displaystyle \frac{m}{\hslash }}}$$

(52)

and

$$A(x)=i{\displaystyle \frac{m\left(r-\frac{1}{2}{\sigma }^2\right)}{q\beta }}=i{\displaystyle \frac{\left(r-\frac{1}{2}{\sigma }^2\right)}{q\sigma }}\sqrt{\hslash m}$$

Here, the magnetic potential is a constant imaginary number, so ${\displaystyle \frac{\partial A(x)}{\partial x}}=0$, which implies that the electric potential energy U is

$$U(x)=\hslash \left(r-{\displaystyle \frac{q^2}{2m\hslash }}{A}^2\right)=\hslash \left(r+{\displaystyle \frac{q^2}{2m\hslash }}{\displaystyle \frac{{\left(r-\frac{1}{2}{\sigma }^2\right)}^2}{q^2{\sigma }^2}}\hslash m\right)=\hslash \left(r+{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\left(r-\frac{1}{2}{\sigma }^2\right)}^2}{{\sigma }^2}}\right)$$

or

$$U(x)=\hslash \left({\displaystyle \frac{2r{\sigma }^2+{\left(r-\frac{1}{2}{\sigma }^2\right)}^2}{2{\sigma }^2}}\right)=\hslash {\displaystyle \frac{{\left(r+\frac{1}{2}{\sigma }^2\right)}^2}{2{\sigma }^2}}$$

which is also constant. The Schrödinger Equation (51) is then just the Black–Scholes equation:

$${\displaystyle \frac{\partial \Psi }{\partial t}}+{\displaystyle \frac{1}{2}}{\sigma }^2{x}^2{\displaystyle \frac{{\partial }^2\Psi }{\partial x^2}}+rx{\displaystyle \frac{\partial \Psi }{\partial x}}-r\Psi =0$$

The explicit modified Heisenberg commutation relation (49), after replacing the value of $\beta$ determined in (52), is

$$[\widehat{x},{\widehat{p}}_x]=i\sigma \sqrt{m\hslash }\widehat{x}$$

(53)

As both the magnetic potential A and the potential energy U are constant, the forces acting on the particle are null, so the above Black–Scholes equation corresponds, from a physicist’s point of view, again to a free quantum particle, such as Equation (33).

Thus, the Black–Scholes equation can be obtained by quantizing the classical Hamiltonian (36) by a deformed Heisenberg commutation relation directly in the $(S,\tau )$ space.

Note that we are not aiming to provide new solutions to the Black–Scholes equation. Instead, we want to emphasize the stronger-than-expected relationship between quantum mechanics and the Black–Scholes model. We also want to underscore the role of analogies between different knowledge areas, particularly finance and physics. The analogy we propose here is relevant and can interest the physicist’s community in the following sense: from the point of view of quantum mechanics, space-time at microscopic scales, i.e., at the Planck length scale, should be diffuse or stochastic. This is where the analogy with the Black–Scholes model of quantum mechanics comes in. In Black–Scholes, the option price is the wave function in quantum mechanics. Therefore, the underlying asset S on which the option takes values must be identified with the position x coordinate in quantum mechanics. The Black–Scholes model is equivalent to applying quantum mechanics on a stochastic or fuzzy space-time. However, since the Black–Scholes equation is obtained by quantization of deformed Heisenberg relations or the GUP, there must be a relation between this stochastic geometry and the deformed commutation relations. In particular, Ito lemma must have some role to play between these two approaches. Further, since this stochastic geometry is nothing more than gravity at the microscopic level, we see again that gravity is intrinsically related to the deformed commutation relations.

Furthermore, Equation (33) reveals that the particle’s mass in quantum mechanics is analogous to the inverse square of the volatility associated with the underlying asset. By relating the underlying asset’s price to a random spatial coordinate, the particle’s mass would result from the inverse of the square of the volatility of this stochastic geometry. This property could become very interesting and must be explored in both disciplines.

Unresolved questions about the precise relation and the derivation of modified commutation relations from stochastic geometry are crucial. Drawing on the analogy with the Black–Scholes model, this paper aims to shed light on these questions. The paper’s value is that it generates new ideas for analyzing gravity at the microscopic level through analogies with finance.

On the other hand, although there is no certainty about the possible relationships between the parameters of finance (such as expected return, risk-free rate, underlying asset price, derivative asset price, and payoff functions, among others) and the observables in quantum mechanics (such as kinetic energy, potential energy, position, linear momentum, angular momentum, and wave functions), the fact that the Black–Scholes arbitrage pricing model generates the same equations as those obtained with the modified Schrödinger model opens the possibility of advancing in the exploration of similarities that allow them to be used in both directions. For example, risk-neutral valuation (which follows from the Black–Scholes solution) allows the value of any derivative asset to be calculated by changing the probability measure. One wonders whether this argument can be used in quantum physics.

6.3. The Time-Dependent Case

In this subsection, we explore the case of time-dependent potentials A and U.

6.3.1. Arbitrage Models

It should be noted that the presence of time-dependent potentials in the Black–Scholes equation is related, from a financial point of view, to the breaking of the no-arbitrage hypothesis. Consider a portfolio $P(t)$ based on one option $\pi (S,t)$ and the underlying stock S, whose dynamics are given by

$$dS(t)=\alpha S(t)dt+\sigma S(t)dW(t)$$

(54)

where $W(t)$ is a Wiener process. If no bonds are included in the portfolio P and considering only non-dividend paying assets, as pointed out in [48], the breaking of the non-arbitrage hypothesis

$$\mathrm{d}P(t)=rP(t)\mathrm{d}t$$

(55)

can be written as

$$\mathrm{d}P(t)=rP(t)\mathrm{d}t+f(S,t)P(t)\mathrm{d}W(t)$$

(56)

where the function $f(S,t)$ is called an arbitrage bubble and measures the portfolio’s deviation from the equilibrium value given by the interest rate r. In this case, the associated non-equilibrium Black–Scholes equation for the option price $\pi$ is [38,48]

$${\displaystyle \frac{\partial \pi }{\partial t}}+{\displaystyle \frac{1}{2}}{\sigma }^2{S}^2{\displaystyle \frac{{\partial }^2\pi }{\partial S^2}}+\left(r+V(S,t)\right)\left(S{\displaystyle \frac{\partial \pi }{\partial S}}-\pi \right)=0$$

(57)

where the time-dependent potential $V(S,t)$ is related to the arbitrage bubble f according to

$$V(S,t)={\displaystyle \frac{\left(r-\alpha \right)f(S,t)}{\sigma -f(S,t)}}$$

(58)

Equation (56) summarizes several possible arbitrage models. In the literature, some efforts exist to generalize the Black–Scholes model that explicitly try to incorporate the notion of arbitrage. For example, refs. [49,50] introduces the idea of virtual arbitrage in derivative pricing. In this case, the usual non-arbitrage hypothesis (55) is changed to

$$dP(t)=\mathcal{R}\left(t,P\right)Pdt$$

where the arbitrage return $\mathcal{R}$ evolves according to the following equation:

$${\displaystyle \frac{\mathrm{d}\mathcal{R}}{\mathrm{d}t}}=-\lambda \mathcal{R}$$

with a decay parameter $\lambda$, which is characteristic for the market. A more natural way to introduce these same ideas is to assume that there exist market short-life arbitrage statistical fluctuations $x(t)$, which can be characterized by an Ornstein–Uhlenbeck process [50,51]

$${\displaystyle \frac{dx(t)}{dt}}=-\lambda x(t)+\eta (t)$$

with $\eta$ being a random noise $\eta (t)$. The statistical fluctuations imply that the portfolio returns behave as

$$dP(t)=rP(t)dt+x(t)P(t)dt=(r+x(t))P(t)dt$$

Another effort in this line is that of Panayides [52], who (following Panayides and Fedotov [53]) considers a market that consists of a stock S, a bond B, and a European option $\pi$. The market is assumed to be affected by two sources of uncertainty: the random fluctuations of the return from the stock S, whose dynamics are given in Equation (54), and a random arbitrage return from the bond B described by the equation

$${\displaystyle \frac{dB}{B}}=rdt+\xi (t)dt$$

where the random process $\xi (t)$ describes the fluctuations of the arbitrage return around the spot rate r. Panayides [52], following an approach suggested by Papanicolaou and Sircar [54], shows that the option price $\pi$ obeys the following PDE:

$${\displaystyle \frac{\partial \pi }{\partial \tau }}={\displaystyle \frac{{\sigma }^2{S}^2}{2}}{\displaystyle \frac{{\partial }^2\pi }{\partial S^2}}+rS{\displaystyle \frac{\partial \pi }{\partial S}}-r\pi +\xi \left({\displaystyle \frac{\tau }{\epsilon }}\right)\left(S{\displaystyle \frac{\partial \pi }{\partial S}}-\pi \right)$$

Finally, Contreras et al. [48], inspired by the ideas of Ilinski [50], proposed a generalization of the Black–Scholes model that incorporates market imperfections using arbitrage bubbles. In this case, portfolio return $dP$ is assumed to follow stochastic dynamics of the form (56), where the amplitude $f(S,t)$ of the Wiener process $dW$ is a given deterministic function and is called an arbitrage bubble (which is essentially the portfolio’s volatility). Equation (56) essentially mimics Equation (54), which determines the dynamics of the underlying asset price S. In addition, (56) is the minimal change that one can make to the no-arbitrage hypothesis without incorporating external structures (e.g., new independent Brownian motions). As shown in [48], Equation (56) implies the interacting Black–Scholes Equation (57).

Note that Equation (56) has the same form of equations obtained by Ilinski and Panayides and includes these models as special cases. Thus, a generic way to represent a non-risk-free portfolio is given by Equation (56), where the function $f(S,t)$ encapsulates all of the information about the market equilibrium’s deviations regardless of their causes. Then, in principle, any nonequilibrium option behavior can be modeled endogenously in the framework of Equation (57) by providing the appropriate bubble form $f(S,t)$, and f need not be thought of as a small perturbation. In fact, for $f\to \infty$, the potential $V(S,t)$ in (58) goes to a constant potential

$$V(S,t)=\alpha -r$$

and the interacting Black–Scholes equation in this limit becomes a non-interacting one, but with an interest rate given by $\alpha$:

$${\displaystyle \frac{\partial \pi }{\partial t}}+{\displaystyle \frac{1}{2}}{\sigma }^2{S}^2{\displaystyle \frac{{\partial }^2\pi }{\partial S^2}}+\alpha \left(S{\displaystyle \frac{\partial \pi }{\partial S}}-\pi \right)=0$$

(59)

This property is consistent with the fact that when all market participants engage in arbitrage, it must necessarily disappear, and the system must return to equilibrium, in this case, with a new interest rate given by $\alpha$. Thus, in (57) and (58), the bubble amplitude f does not need to be a small perturbation and can take any value.

Then, a natural question arises: is it possible to find solutions to the interacting Black–Scholes Equation (57) for an arbitrary bubble form $f(S,t)$?

For the case of a pure time-dependent bubble $f=f(t)$, the answer is given in [55]. The authors proved three theorems about the exact solutions of the generalized or interacting Black–Scholes Equation (57) that explicitly includes arbitrage bubbles. These arbitrage bubbles can be characterized by an arbitrage number $A_N$.

The first theorem states that if $A_N=0$, then the solution at maturity of the interacting equation is identical to the solution of the free Black–Scholes equation with the same initial interest rate of r—that is, the external potential has no net effect over the option’s price dynamics.

The second theorem states that if $A_N\ne 0$, then the interacting solution can be expressed in terms of all higher derivatives of the solutions to the free Black–Scholes equation with an initial interest rate of r. Here, the bubble potential changes the usual Black–Scholes free dynamic.

The third theorem states that for a given arbitrage number, the interacting solution is a solution to the free Black–Scholes equation but with a variable interest rate of

$$r(\tau )=r+(1/\tau )A_N(\tau ),$$

where $\tau =T-t$ and

$$A_N(\tau )={\int }_0^{\tau }V\left({\tau }^{\prime }\right)d{\tau }^{\prime }={\int }_0^{\tau }{\displaystyle \frac{(r-\alpha )f\left({\tau }^{\prime }\right)}{\sigma -f\left({\tau }^{\prime }\right)}}d{\tau }^{\prime }.$$

is the accumulative potential. Thus, no matter the bubble $f(t)$’s intensity, one can always obtain an exact solution for the option price $\pi (S,t)$.

In some sense, the bubbles with $A_N=0$ are analogues to neutrons whose dynamics are not altered by the nucleus, and bubbles with $A_N\ne 0$ are equivalent to charged particles, which are deviated by the electromagnetic nuclear potential. All details of this topic are developed in [55].

Note that, from a practitioner’s point of view, the calibration of the non-equilibrium model is an important topic. For the case of a pure time-dependent arbitrage bubble $f(t)$, it can be obtained directly from the empirical option’s price data. The idea is to use a procedure analogous to scattering theory in nuclear physics, from which one obtains information about the nuclear forces and their potential from the cross-sections experimentally measured in the laboratory. A study of this type and its corresponding methodology applied to the financial case can be found in [56], where the time-dependent bubble $f(t)$ is obtained from the empirical options prices.

After this digression on the arbitrage models, we return to our principal objective: to determine the magnetic and electric potentials $A_S$ and U for the time-dependent case.

6.3.2. Time Varying Potentials A and U

For time-dependent magnetic and electric potentials, in order for the Schrödinger Equation (51) (after identify x with S) to recover the non-equilibrium Black–Scholes Equation (57), one must choose A and U as

$$\begin{array}{ccc}r+V(x,t)& =& {\displaystyle \frac{\hslash {\beta }^2}{2m}}-i{\displaystyle \frac{q\beta }{m}}A(x,t)\hfill \\ \\ r+V(x,t)& =& {\displaystyle \frac{q^2}{2m\hslash }}{A}^2+{\displaystyle \frac{1}{\hslash }}U(x,t)+i{\displaystyle \frac{q\beta }{2m}}x{\displaystyle \frac{\partial A(x)}{\partial x}}\hfill \end{array}$$

so, the potentials are given by

$$A(x,t)=i{\displaystyle \frac{\sqrt{\hslash m}}{q\sigma }}\left(r-{\displaystyle \frac{{\sigma }^2}{2}}+V(x,t)\right)$$

and

$$U(x,t)={\displaystyle \frac{\hslash }{2{\sigma }^2}}{\left(r+{\displaystyle \frac{1}{2}}{\sigma }^2+V(x,t)\right)}^2+{\displaystyle \frac{\hslash }{2}}x{\displaystyle \frac{\partial V(x,t)}{\partial x}}$$

such that the Schrödinger equation becomes

$${\displaystyle \frac{\partial \Psi }{\partial t}}+{\displaystyle \frac{1}{2}}{\sigma }^2{x}^2{\displaystyle \frac{{\partial }^2\Psi }{\partial x^2}}+\left(r+V(x,t)\right)\left(x{\displaystyle \frac{\partial \Psi }{\partial x}}-\Psi \right)=0$$

(60)

which is the same Equation (57) after identification of $(x,\Psi )$ with $(S,\pi )$.

Thus, the magnetic and electric potentials are determined completely by the arbitrage bubble f through the potential $V={\displaystyle \frac{\left(r-\alpha \right)f}{\sigma -f}}$. Note that, in this case, there are non-trivial forces acting on the financial quantum particle.

Then, the quantization of the classical Hamiltonian (36) through the deformed Heisenberg commutation relations in the $(S,\tau )$ space allows us to recover the Black–Scholes equation, both in its equilibrium case (when the arbitrage bubble is zero) and for the non-equilibrium or interacting case ($f\ne$ 0) when the arbitrage hypothesis is no longer valid. This result highlights the profound relationship between the Black–Scholes model and quantum mechanics.

7. Conclusions

This article explores the implications of modifying the canonical Heisenberg commutation relations over two simple systems: the free particle and the tunnel effect generated by a step-like potential. The modified commutation relations include position-dependent and momentum-dependent terms of the form ${\widehat{x}}^n$ and ${\widehat{p}}^n$, respectively. The deformation strength is characterized by a parameter that can take values in real numbers. For the position deformation case, the corresponding free wave functions are sinusoidal functions with a variable wave vector $k_n(x)$ that depends on n. In the momentum deformation case, the free wave function has the usual sinusoidal behavior with a constant wave vector. The energy spectrum for the case $n=1$ becomes non-symmetric in terms of momentum; whereas, in the $n=2$ case, the spectrum is symmetric, but for $\beta >0$, it is periodic and non-periodic for $\beta <0$. Tunneling probabilities depend on the deformation strength for the position and momentum deformation cases. For the position deformation case, the particle is more likely to explore the right side of the step function potential than for the non-deformed case.

Also, surprisingly, the quantum mechanical model generated by these modified commutation relations is related to the Black–Scholes model in finance. In fact, by taking a particular form of a linear position deformation, one can derive a Black–Scholes equation for the wave function when an external electromagnetic potential is acting on the particle. Thus, this analysis permits interpreting the Black–Scholes model as a quantum mechanical system defined over a stochastic spatial geometry if one identifies the underlying asset S with the position coordinate x in quantum mechanics. Further, because this stochastic geometry is nothing more than gravity at the microscopic level, we see that the Black–Scholes equation becomes a possible simple model for understanding quantum gravity. Furthermore, because the Black–Scholes equation is obtained via a deformed Heisenberg algebra or GUP, there must be a relation between this stochastic geometry (gravity) and the deformed Heisenberg commutation relations. In particular, Ito lemma must play a role between these two approaches. This analogy can be interesting to the physicist community due to its relation with gravity at the quantum level. In fact, if the spatial coordinate oscillates randomly about its mean value, the mass of the quantum particle corresponds to the inverse of the variance of this stochastic coordinate. Significant unresolved questions remain about the precise relation and the derivation of modified commutation relations from stochastic geometry. This paper aims to address these questions by drawing on the analogy with the Black–Scholes model, thereby shedding light on these crucial issues.

In a subsequent paper, we explore the consequences of this analogy and how modified Heisenberg commutation relations are related to stochastic spatial geometry.