Fractal Differential Equations of 2α-Order

Abstract

In this research paper, we provide a concise overview of fractal calculus applied to fractal sets. We introduce and solve a $2\alpha$-order fractal differential equation with constant coefficients across different scenarios. We propose a uniqueness theorem for $2\alpha$-order fractal linear differential equations. We define the solution space as a vector space with non-integer orders. We establish precise conditions for $2\alpha$-order fractal linear differential equations and derive the corresponding fractal adjoint differential equation.

1. Introduction

Fractal patterns, although represented across various scales rather than infinitely, have been extensively modeled due to limitations related to time and space constraints. These models can simulate theoretical fractals or natural phenomena with fractal features, and the results derived from modeling processes can serve as benchmarks for fractal analysis. Fractal calculus, which emerged as a formulation extending ordinary calculus, procures a constructive and algorithmic approach toward the smooth differentiable-structured modeling of natural processes through fractals.

Benoit Mandelbrot is credited with pioneering the field of fractal geometry [1], which revolves around shapes possessing fractal dimensions that surpass their topological dimensions [2,3]. These intricate fractals exhibit self-similarity and frequently demonstrate non-integer and complex dimensions [4,5]. An eclectic survey of fractals has been organized into two parts, covering a diverse array of innovative applications. The first part has been designed to focus on the glossary of fractals, their mathematical description, and their aesthetic, artistic, and architectural applications, while the second part has been focused on engineering, industry, commercial, and futuristic applications of fractals [6]. The focus is on engineering, industrial, commercial, and futuristic fractal applications, with prior coverage of fractal fundamentals. Key applications include landscape modeling, antennas, and image compression, highlighting innovative, industry-oriented uses [7]. The fractal morphology of scale-invariant patterns has been surveyed, with emphasis on scale and conformal invariance, fractal non-uniformity, inhomogeneity, and anisotropy. Six adimensional indices have been identified to quantify these features, and distinctions between mathematical and real-world fractals have been highlighted [8].

Nevertheless, the analysis of fractals presents challenges, given that traditional geometric measures such as Hausdorff measure [9], length, surface area, and volume are typically applied to standard shapes [10]. As a result, applying these measures directly to fractal analysis becomes complex [11,12,13,14,15,16].

Researchers have tackled the challenge of fractal analysis through various methodologies, including harmonic analysis [17,18], measure theory [19,20,21,22,23,24], fractional space and nonstandard methods [25], probabilistic methods [26] fractional calculus [27,28,29,30,31], and non-standard methods [32].

Fractal calculus is a mathematical framework that extends traditional calculus, allowing for the treatment of equations whose solutions take the form of functions exhibiting fractal properties, such as fractal sets and curves [33,34]. What makes fractal calculus particularly appealing lies in its elegance and algorithmic methodologies, which contrast favorably with other techniques [35].

The generalization of $F^{\alpha }$-calculus (FC) has been successfully achieved by employing the gauge integral method. This generalization focuses on the integration of functions over a specific subset of the real number line that contains singularities found within fractal sets [35].

Various methods have consequently been employed to solve fractal differential equations, and their stability conditions have been determined accordingly [35].

The application of FC is demonstrated through the analysis of fractal interpolation functions and Weierstrass functions. These functions often display characteristics of non-differentiability and non-integrability when viewed through the lenses of traditional calculus [35].

Fractal calculus has been expanded to encompass the study of Cantor cubes and Cantor tartan [35], and within this framework, the Laplace equation has been formally defined [35].

Analyses based on non-local fractal calculus have been conducted for electrical circuits with arbitrary source terms, broadening the scope of examination to include circuits [36].

Numerical simulations explored the influence of parameters on noise performance. Increasing the orders of fractal-fractional reactive components generally improved noise performance across different circuits [37,38].

The utilization of non-local fractal derivatives to characterize fractional Brownian motion on thin Cantor-like sets was demonstrated. The proposal of the fractal Hurst exponent establishes its connection to the order of non-local fractal derivatives [35]. Furthermore, fractal stochastic differential equations have been defined and categorized for processes such as fractional Brownian motion and diffusion occurring within media with fractal structures [35]. Local vector calculus within fractional-dimensional spaces, on fractals, and in fractal continua has been developed. The proposition was put forth that within spaces characterized by non-integer dimensions, it was feasible to define two distinct del-operators, each operating on scalar and vector fields. Employing these del-operators, the foundational vector differential operators and Laplacian in fractional-dimensional space were formulated conventionally. Additionally, Laplacian and vector differential operators linked with $F^{\alpha }$-derivatives on fractals were established [39]. The concept of a fractal comb and its associated staircase function was introduced. Derivatives and integrals were defined for functions on these combs using the staircase function [40]. Fractal retarded, neutral, and renewal delay differential equations with constant coefficients were solved through the utilization of the method of steps and the Laplace transform [41]. Fractal integral and differential forms were defined using non-standard analysis [42]. The solution space for higher $\alpha$-order linear fractal differential equations was defined, showcasing its non-integer dimensionality [43].

Fractal time, recently suggested by physics researchers for its self-similar properties and fractional dimension, was investigated in the context of economic models utilizing both local and non-local fractal Caputo derivatives [35,44,45,46,47,48].

Along these lines of developments and implications, we have introduced $2\alpha$-order fractal linear differential equations and elucidated their corresponding solutions.

To this end, the current paper is structured as follows: in Section 2, we provide a concise review of fractal calculus. Moving on to Section 3, we define and solve the $2\alpha$-order fractal differential equation and present the uniqueness theorem associated with it. In Section 4, we extend the discussion to encompass the uniqueness theorem for $2\alpha$-order fractal linear differential equations. Section 5 addresses the comprehensive study of the exact $2\alpha$-order fractal differential equation. In Section 6, we delve into the solution and presentation of the nonhomogeneous $2\alpha$-order fractal differential equation. Finally, Section 7 provides the conclusion, discussion, and future directions.

2. Overview of Fractal Calculus on Fractal Sets

In this section, we present a concise overview of fractal calculus applied to fractal sets, as summarized in [33,34,35]. Moreover, in this section and more generally throughout the paper, we will indicate by F a fractal subset of a real line.

Definition 1. 

The flag function of a set F and a closed interval $I\subset [a,b]$ is defined as:

$$\rho (F,I)=\left\{\begin{array}{cc}1,\hfill & ifF\cap I\ne \varnothing ;\hfill \\ 0,\hfill & otherwise.\hfill \end{array}\right.$$

(1)

Definition 2. 

For a subdivision $P_{[a,b]}$ of $[a,b]$, and for a given $\delta >0$, the coarse-grained mass of $F\cap [a,b]$ is defined by

$${\gamma }_{\delta }^{\alpha }(F,a,b)=\underset{\left|P\right|\le \delta }{inf}\sum _{i=0}^{n-1}\mathsf{\Gamma }(\alpha +1){(t_{i+1}-t_i)}^{\alpha }\rho (F,[t_i,t_{i+1}]),$$

(2)

where $\left|P\right|={max}_{0\le i\le n-1}(t_{i+1}-t_i)$, and $0<\alpha \le 1$.

Definition 3. 

The mass function of F is defined as the limit of the coarse-grained mass as δ approaches zero:

$${\gamma }^{\alpha }(F,a,b)=\underset{\delta \to 0}{lim}{\gamma }_{\delta }^{\alpha }(F,a,b).$$

(3)

Definition 4. 

The γ-dimension of $F\cap [a,b]$ is defined as:

$$\begin{array}{cc}\hfill {dim}_{\gamma }(F\cap [a,b])& =inf\{\alpha :{\gamma }^{\alpha }(F,a,b)=0\}\hfill \\ & =sup\{\alpha :{\gamma }^{\alpha }(F,a,b)=\infty \}.\hfill \end{array}$$

(4)

Definition 5. 

The integral staircase function of order α for F is given by:

$$S_F^{\alpha }\left(x\right)=\left\{\begin{array}{cc}{\gamma }^{\alpha }(F,a_0,x),\hfill & \mathrm{if}x\ge a_0;\hfill \\ -{\gamma }^{\alpha }(F,x,a_0),\hfill & otherwise,\hfill \end{array}\right.$$

(5)

where $a_0$ is an arbitrary fixed real number.

Definition 6. 

Let $F\subset \mathbb{R}$, $f:\mathbb{R}\to \mathbb{R}$, and $x\in F$. A number l is called the limit of $f\left(y\right)$ for $y\to x$, if for any given $ϵ>0$, there exists $\delta >0$ such that:

$$y\in F,and|y-x|<\delta \Rightarrow \left|f\right(y)-l|<ϵ.$$

(6)

If such a number exists, then it is denoted by:

$$l=\underset{y\to x}{F_{-}lim}f\left(y\right).$$

(7)

Definition 7. 

Let $F\subset R$, $f:\mathbb{R}\to \mathbb{R}$ and $x\in F$. Whenever

$$\underset{y\to x}{F_{-}lim}f\left(y\right)=f\left(x\right),$$

we say that the function f is F-continuous at x. If f is F-continuous at each point of $\mathbb{R}$, we say that f is F-continuous in $\mathbb{R}.$

Remark 1. 

Let us observe that the continuity of a function f in interval $(a,b)\subset \mathbb{R}$ implies the F-continuity of f in $(a,b),$ however, the converse is not true (see [33,34,35]).

Definition 8. 

Let f be a real function defined in $(a,b).$ The $F^{\alpha }$-derivative of f is defined as follows:

$$D_{F,x}^{\alpha }f\left(x\right)=\left\{\begin{array}{cc}\underset{y\to x}{F_{-}lim}{\displaystyle \frac{f\left(y\right)-f\left(x\right)}{S_F^{\alpha }\left(y\right)-S_F^{\alpha }\left(x\right)}},\hfill & ifx\in F;\hfill \\ 0,\hfill & otherwise,\hfill \end{array}\right.$$

(8)

if $F_{-}lim$ exists [33]. Moreover, if f has the $F^{\alpha }$-derivative at each point of the fractal set $F,$ we say that f is $F^{\alpha }$-differentiable on $(a,b).$

Remark 2. 

Let us observe that if a function f is differentiable on $(a,b)$, f is also $F^{\alpha }$-differentiable on $(a,b)$. The converse is not true. Indeed, let us consider $f\left(x\right)={\chi }_F\left(x\right),\forall x\in (a,b)$. It is trivial to observe that $D_{F,x}^{\alpha }{\chi }_F\left(x\right)=0,\forall x\in (a,b).$ However, ${\chi }_F\left(x\right)$ is not differentiable on $(a,b)$ since it is not continuous on $(a,b).$

Theorem 1. 

Let f be a real function defined on $(a,b).$ If f is $F^{\alpha }$-differentiable on $(a,b),$ then the function f is F-continuous on $(a,b).$

Definition 9. 

Let f be a real function defined on $(a,b)$. If f is $F^{\alpha }$-differentiable on $(a,b),$ the second $F^{\alpha }$-derivative of f at the point x is defined as follows:

$$D_{F,x}^{2\alpha }f\left(x\right)=\left\{\begin{array}{cc}\underset{y\to x}{F_{-}lim}{\displaystyle \frac{D_{F,y}^{\alpha }f\left(y\right)-D_{F,x}^{\alpha }f\left(x\right)}{S_F^{\alpha }\left(y\right)-S_F^{\alpha }\left(x\right)}},\hfill & ifx\in F;\hfill \\ 0,\hfill & otherwise,\hfill \end{array}\right.$$

(9)

Moreover, if f has the second $F^{\alpha }$-derivative at each point of the fractal set F, we say that f is twice $F^{\alpha }$-differentiable on $(a,b)$.

Remark 3. 

Let us observe that if a function f is twice differentiable on $(a,b)$, f is also twice $F^{\alpha }$-differentiable on $(a,b)$. The converse is not true. Let us consider $f\left(x\right)=S_F^{\alpha }\left(x\right),\forall x\in (a,b)$. Since $D_{F,x}^{\alpha }{S}_F^{\alpha }\left(x\right)={\chi }_F\left(x\right),\forall x\in (a,b)$ (see [33,34]), it is trivial to observe that $D_{F,x}^{2\alpha }{S}_F^{\alpha }\left(x\right)=0$, $\forall x\in (a,b).$ However, as already observed in Remark 2, ${\chi }_F\left(x\right)$ is not differentiable on $(a,b)$.

Definition 10. 

Let $I=[a,b]$ such that $S_F^{\alpha }$ is finite on I. Let f be a bounded function defined on $(a,b)$ and let $x\in F\cap I$. The $F^{\alpha }$-integral of f on I is defined as:

$$\begin{array}{cc}\hfill {\int }_a^{b}f\left(x\right)d_F^{\alpha }x& =\underset{P_{[a,b]}}{sup}\sum _{i=0}^{n-1}\underset{x\in F\cap I}{inf}f\left(x\right)(S_F^{\alpha }\left(x_{i+1}\right)-S_F^{\alpha }\left(x_i\right))\hfill \\ & =\underset{P_{[a,b]}}{inf}\sum _{i=0}^{n-1}\underset{x\in F\cap I}{sup}f\left(x\right)(S_F^{\alpha }\left(x_{i+1}\right)-S_F^{\alpha }\left(x_i\right)).\hfill \end{array}$$

(10)

3. Preliminaries on the $\mathbf{2}\mathit{\alpha }$-Order Fractal Differential Equation

A relation of the form:

$$G(x,f\left(x\right),D_{F,x}^{\alpha }f\left(x\right),D_{F,x}^{2\alpha }f\left(x\right))=0,$$

(11)

where $f\left(x\right)$ is the unknown function and G is an assigned function of the 4 variables $x,f\left(x\right),D_{F,x}^{\alpha }f\left(x\right),D_{F,x}^{2\alpha }f\left(x\right)$, is called $2\alpha$-order ordinary fractal differential equation; here, 2th indicate the maximum order of the $F^{\alpha }$-derivative that appears in the equation while, as usual, $\alpha$ denotes the dimension of the fractal subset of the real line, $0<\alpha \le 1.$ If G is a first-degree polynomial of the variables $f\left(x\right),D_{F,x}^{\alpha }f\left(x\right),D_{F,x}^{2\alpha }f\left(x\right)$, the equation is said to be linear and its general form is:

$$a_0\left(x\right)D_{F,x}^{2\alpha }f\left(x\right)+a_1\left(x\right)D_{F,x}^{\alpha }f\left(x\right)+a_2\left(x\right)f\left(x\right)=g\left(x\right),$$

(12)

where the coefficients $a_i\left(x\right),$ for $i=0,1,\cdots ,n$ are F-continuous functions in $(a,b)$ as well as the function $g\left(x\right).$ Whenever $g\left(x\right)=0,$ Equation (12) is said to be homogeneous. An equation that is not of the form of Equation (12) is said to be a nonlinear $2\alpha$-order fractal differential equation.

Example 1. 

The following $2\alpha$-order fractal differential equation

$$2exp\left(S_F^{\alpha }\left(x\right)\right)D_{F,x}^{2\alpha }f\left(x\right)+3D_{F,x}^{\alpha }f\left(x\right)=S_F^{\alpha }{\left(x\right)}^4,$$

(13)

is linear.

Example 2. 

The following $2\alpha$-order fractal differential equation that represents the motion of an oscillating pendulum with fractal time

$$D_{F,t}^{2\alpha }\theta \left(t\right)+{\displaystyle \frac{g}{L}}sin\left(\theta \left(t\right)\right)=0,$$

(14)

where $\theta \left(t\right)$ is the unknown function that physically means an oscillating pendulum of length L with the vertical direction, is nonlinear because of the term $sin\left(\theta \right(t\left)\right)$.

Remark 4. 

Now, let us observe that, if in Equation (11) it is possible to explicate the 2th $F^{\alpha }$-derivative, the $2\alpha$-order fractal differential equation is said to be written in normal form and we have:

$$D_{F,x}^{2\alpha }f\left(x\right)=g(x,f\left(x\right),D_{F,x}^{\alpha }f\left(x\right)),\forall x\in F,$$

(15)

where g is an assigned function of the 3 variables:

$$x,f\left(x\right),D_{F,x}^{\alpha }f\left(x\right).$$

Definition 11. 

A solution of the $2\alpha$-order fractal differential equation is a function

$$\psi :(a,b)\to \mathbb{R},\psi \in C^{2\alpha }(a,b),$$

such that:

$$G(x,\psi \left(x\right),D_{F,x}^{\alpha }\psi \left(x\right),D_{F,x}^{2\alpha }\psi \left(x\right))=0,\forall x\in F.$$

Remark 5. 

It is trivial to observe that if (12) is written in a normal form, i.e., in the form of Equation (15), a solution of (15) is a function

$$\psi :(a,b)\to \mathbb{R},\psi \in C^{2\alpha }(a,b),$$

such that

$$D_{F,x}^{2\alpha }\psi \left(x\right)=g(x,\psi \left(x\right),D_{F,x}^{\alpha }\psi \left(x\right)),\forall x\in F.$$

(16)

we can conjecture that the set of all solutions of a $2\alpha$-order fractal differential equation is represented by a family of functions depending on 2 parameters.

$2\alpha$-Order Fractal Differential Equation with Constant Coefficient

Let us consider a homogeneous $2\alpha$-order fractal differential equation with constant coefficients

$$a{D}_x^{2\alpha }f\left(x\right)+b{D}_x^{\alpha }f\left(x\right)+cf\left(x\right)=0.$$

(17)

We are interested in the problem of finding all solutions of Equation (17). To do that, let us note that the linearity of the differential equation means that if ${\psi }_1\left(x\right)$ and ${\psi }_2\left(x\right)$ are any two solutions of Equation (17) and $c_1$ and $c_2$ are any two constants, then the function $\psi \left(x\right)=c_1{\psi }_1\left(x\right)+c_2{\psi }_2\left(x\right)$ is also a solution of Equation (17). Moreover, let us recall that if ${\displaystyle \frac{{\psi }_1\left(x\right)}{{\psi }_2\left(x\right)}}\ne k,\forall x\in (a,b)$ where k is a generic constant, the functions ${\psi }_1\left(x\right)$ and ${\psi }_2\left(x\right)$ are linearly independent on $(a,b).$ By a similarity with the $\alpha$-order fractal differential equation (see [49]), we assume that the function ${\psi }_1\left(x\right)=exp\left(r{S}_F^{\alpha }\left(x\right)\right)$ is a solution of Equation (17). Therefore, by substituting ${\psi }_1\left(x\right)$ into Equation (17), we have:

$$(a{r}^2+br+c)exp\left(r{S}_F^{\alpha }\left(x\right)\right)=0.$$

(18)

Since $exp\left(r{S}_F^{\alpha }\left(x\right)\right)$ is never zero, we can conclude:

$$(a{r}^2+br+c)=0.$$

(19)

This equation is known as the characteristic equation for Equation (17). We encounter three main cases:

1. Real Roots Case ($b^2-4ac>0$): In this scenario, let us assume that $r_1$ and $r_2$ are the two real distinct root solutions of Equation (19). Therefore, the functions ${\psi }_1\left(x\right)=exp\left(r_1{S}_F^{\alpha }\left(x\right)\right)$ and ${\psi }_2\left(x\right)=exp\left(r_2{S}_F^{\alpha }\left(x\right)\right)$ are two linear independent solutions of Equation (17). By this conjecture, we obtain that the general solution of Equation (17) is given by:

$$\psi \left(x\right)=c_1{\psi }_1\left(x\right)+c_2{\psi }_2\left(x\right)=c_{1}exp\left(r_1{S}_F^{\alpha }\left(x\right)\right)+c_{2}exp\left(r_1{S}_F^{\alpha }\left(x\right)\right).$$

(20)

2. Complex Roots Case ($b^2-4ac<0$): In this case, let us assume that $r_1=\lambda +i\nu$ and $r_2=\lambda -i\nu$, where $\lambda$ and $\nu$ are two real distinct root solutions of Equation (19). Therefore, the function

$${\psi }_1\left(x\right)=exp\left((\lambda +i\nu )S_F^{\alpha }\left(x\right)\right)=exp\left(\lambda S_F^{\alpha }\left(x\right)\right)\left(cos\nu S_F^{\alpha }\left(x\right)+isin\nu S_F^{\alpha }\left(x\right)\right),$$

and the function

$${\psi }_2\left(x\right)=exp\left((\lambda -i\nu )S_F^{\alpha }\left(x\right)\right)=exp\left(\lambda S_F^{\alpha }\left(x\right)\right)\left(cos\nu S_F^{\alpha }\left(x\right)-isin\nu S_F^{\alpha }\left(x\right)\right),$$

are two linear independent solutions of Equation (17). Since we are considering only real functions, by the elementary property of the complex numbers and by our conjecture about the set of all solutions of the $2\alpha$-order fractal differential equation, we obtain that the functions:

$${\displaystyle \frac{1}{2}}({\psi }_1\left(x\right)+{\psi }_2\left(x\right))=exp(\lambda S_F^{\alpha }\left(x\right)cos\left(\nu S_F^{\alpha }\left(x\right)\right),$$

(21)

and

$${\displaystyle \frac{1}{2i}}({\psi }_1\left(x\right)+{\psi }_2\left(x\right))=exp\left(\lambda S_F^{\alpha }\left(x\right)\right)sin\left(\nu S_F^{\alpha }\left(x\right)\right),$$

(22)

are still solutions of Equation (17). Therefore, we can represent the general solution of Equation (17) in terms of trigonometric functions:

$$\psi \left(x\right)=c_{1}exp\left(\lambda S_F^{\alpha }\left(x\right)\right)cos\left(\nu S_F^{\alpha }\left(x\right)\right)+c_{2}exp\left(\lambda S_F^{\alpha }\left(x\right)\right)sin\left(\nu S_F^{\alpha }\left(x\right)\right).$$

(23)

3. Repeated Roots Case ($b^2-4ac=0$): In this situation, we have $r_1=r_2=-b/2a$. Therefore, the general solution for Equation (17) takes the form:

$$\psi \left(x\right)=c_{1}exp\left(-{\displaystyle \frac{b{S}_F^{\alpha }\left(x\right)}{2a}}\right)+c_2{S}_F^{\alpha }\left(x\right)exp\left(-{\displaystyle \frac{b{S}_F^{\alpha }\left(x\right)}{2a}}\right).$$

(24)

Indeed, let us observe that if $v\left(x\right)$ is a real function on $(a,b)$ that is also twice $F^{\alpha }$-differentiable at $x\in F$, indicated by ${\psi }_2\left(x\right)=v\left(x\right)exp(-b{S}_F^{\alpha }\left(x\right)/2a)$, it follows that the function ${\psi }_1\left(x\right)=exp(-b{S}_F^{\alpha }\left(x\right)/2a)$ and the function ${\psi }_2\left(x\right)$ are linearly independent, since ${\displaystyle \frac{{\psi }_2\left(x\right)}{{\psi }_1\left(x\right)}}=v\left(x\right).$ So, by replacing ${\psi }_2\left(x\right)$ in Equation (17), we have:

$$D_x^{2\alpha }v\left(x\right)=0,$$

(25)

and by solving this equation for $v\left(x\right)$, we obtain:

$$v\left(x\right)=c_1+c_2{S}_F^{\alpha }\left(x\right).$$

(26)

This completes the solutions for the $2\alpha$-order fractal differential equation with constant coefficients under various cases.

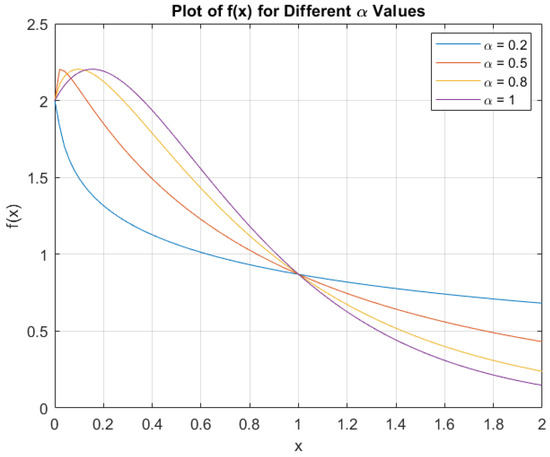
Example 3. 

Consider the $2\alpha$-order fractal differential equation:

$$D_x^{2\alpha }f\left(x\right)+D_x^{\alpha }f\left(x\right)+f\left(x\right)=0.$$

(27)

Its characteristic equation is given by:

$$r^2+r+1=0.$$

(28)

The roots of this characteristic equation are:

$$r_1=-{\displaystyle \frac{1}{2}}+i{\displaystyle \frac{\sqrt{3}}{2}}and{r}_2=-{\displaystyle \frac{1}{2}}-i{\displaystyle \frac{\sqrt{3}}{2}}.$$

(29)

Therefore, the general solution of Equation (27) is:

$$\begin{array}{cc}\hfill \psi \left(x\right)& =c_{1}exp\left(-{\displaystyle \frac{S_F^{\alpha }\left(x\right)}{2}}\right)cos\left({\displaystyle \frac{\sqrt{3}{S}_F^{\alpha }\left(x\right)}{2}}\right)+c_{2}exp\left(-{\displaystyle \frac{S_F^{\alpha }\left(x\right)}{2}}\right)sin\left({\displaystyle \frac{\sqrt{3}{S}_F^{\alpha }\left(x\right)}{2}}\right)\hfill \\ & \propto c_{1}exp\left(-{\displaystyle \frac{x^{\alpha }}{2}}\right)cos\left({\displaystyle \frac{\sqrt{3}{x}^{\alpha }}{2}}\right)+c_{2}exp\left(-{\displaystyle \frac{x^{\alpha }}{2}}\right)sin\left({\displaystyle \frac{\sqrt{3}{x}^{\alpha }}{2}}\right).\hfill \end{array}$$

(30)

In Figure 1, we illustrate Equation (30) for various values of α, highlighting how the fractal support influences the solutions.

Figure 1. Graph of Equation (30) for $c_1=1,c_2=1$.

4. Uniqueness Theorem for $\mathbf{2}\mathit{\alpha }$-Order Fractal Linear Differential Equations

In this section, we prove the existence and the uniqueness of the solution of a given $2\alpha$-order fractal differential equation with some fixed initial conditions.

Theorem 2. 

(Existence Theorem) Consider the following $2\alpha$-order fractal differential equation:

$$D_x^{2\alpha }f\left(x\right)+a_1{D}_x^{\alpha }f\left(x\right)+a_{2}f\left(x\right)=0,$$

(31)

with the initial conditions

$$f\left(x_0\right)=f_0,D_x^{\alpha }f\left(x\right){|}_{x=x_0}=D_x^{\alpha }{f}_0,$$

(32)

where $x_0\in (a,b)\cap F$ and $f_0$, $D_x^{\alpha }{f}_0$ are two predefined constants.

Let ${\psi }_1\left(x\right)$ and ${\psi }_2\left(x\right)$ be the two linear independent solutions of Equation (31) (as already found in the previous section); therefore, there exist two constants $c_1$ and $c_2$ such that $\psi \left(x\right)=c_1{\psi }_1\left(x\right)+c_2{\psi }_2\left(x\right)$ is a solution of the assigned $2\alpha$-order fractal differential equation given by Equation (31) with the initial conditions given by Equation (32).

Proof. 

So that $\psi \left(x\right)=c_1{\psi }_1\left(x\right)+c_2{\psi }_2\left(x\right)$ is a solution of the Equation (31) with the initial conditions given by Equation (32), the constants $c_1$ and $c_2$ should be the solutions of the following linear system:

$$\begin{array}{cc}\hfill c_1{\psi }_1\left(x_0\right)+c_2{\psi }_2\left(x_0\right)& =f_0\hfill \\ \hfill c_1{D}_x^{\alpha }{\psi }_1\left(x_0\right)+c_2{D}_x^{\alpha }{\psi }_2\left(x_0\right)& =D_x^{\alpha }{f}_0.\hfill \end{array}$$

(33)

It is well known that the system (33) admits one and only one solution if the determinant,

$$\begin{array}{c}\hfill W[{\psi }_1,{\psi }_2]=\left|\begin{array}{cc}{\psi }_1\left(x_0\right)& {\psi }_2\left(x_0\right)\\ D_x^{\alpha }{\psi }_1\left(x_0\right)& D_x^{\alpha }{\psi }_2\left(x_0\right)\end{array}\right|,\end{array}$$

(34)

called Wronskian, is nonzero. Since the functions ${\psi }_1\left(x\right)$ and ${\psi }_2\left(x\right)$ are linearly independent, the Wronskian condition (determinant of Wronskian different from zero) is satisfied in either case (see [50,51]). Therefore, $c_1,c_2$ are the unique constants satisfying Equation (31) with the initial conditions given by Equation (32). This shows that there is a unique linear combination of ${\psi }_1\left(x\right)$ and ${\psi }_2\left(x\right)$ which is a solution of the assigned $2\alpha$-order fractal differential equation.  □

Now, in order to prove the uniqueness theorem, we need to prove the following technical lemma.

Lemma 1. 

Let $\psi \left(x\right)$ be any solution on $(a,b)\cap F$ of the following fractal differential equation:

$$D_x^{2\alpha }f\left(x\right)+a_1{D}_x^{\alpha }f\left(x\right)+a_{2}f\left(x\right)=0.$$

(35)

Let $x_0\in (a,b)\cap F.$ Then, for all $x\in (a,b)\cap F$, we have

$$\begin{array}{cc}\hfill \parallel \psi \left(x_0\right)\parallel exp(-k|S_F^{\alpha }\left(x\right)& -S_F^{\alpha }\left(x_0\right)\left|\right)\le \parallel \psi \left(x\right)\parallel \le \hfill \\ & \parallel \psi \left(x_0\right)\parallel exp\left(k\right|S_F^{\alpha }\left(x\right)-S_F^{\alpha }\left(x_0\right)\left|\right),\hfill \end{array}$$

(36)

where

$$\parallel \psi \left(x\right)\parallel ={\left[\right|\psi \left(x\right)|}^2+|D_x^{\alpha }{\psi \left(x\right)|}^2{]}^{1/2},k=1+|a_1|+|a_2|.$$

(37)

Proof. 

Let $v\left(x\right)={\parallel \psi \left(x\right)\parallel }^2$. This implies that

$$\begin{array}{cc}\hfill v\left(x\right)& ={\left(\psi \left(x\right)\right)}^2+{\left(D_x^{\alpha }\psi \left(x\right)\right)}^2.\hfill \end{array}$$

(38)

Subsequently,

$$\begin{array}{cc}\hfill D_x^{\alpha }v\left(x\right)& =2\psi \left(x\right)D_x^{\alpha }\psi \left(x\right)+2D_x^{\alpha }\psi \left(x\right)D_x^{2\alpha }\psi \left(x\right),\hfill \end{array}$$

(39)

and

$$\left|D_x^{\alpha }v\left(x\right)\right|\le 2\left|\psi \left(x\right)\right|\left|D_x^{\alpha }\psi \left(x\right)\right|+2\left|D_x^{\alpha }\psi \left(x\right)\right|\left|D_x^{2\alpha }\psi \left(x\right)\right|.$$

(40)

By the hypothesis on $\psi \left(x\right)$, we have:

$$D_x^{2\alpha }\psi \left(x\right)=-a_1{D}_x^{\alpha }\psi \left(x\right)-a_2\psi \left(x\right),$$

(41)

and, consequently,

$$\left|D_x^{2\alpha }\psi \left(x\right)\right|\le |a_1|\left|D_x^{\alpha }\psi \left(x\right)\right|+|a_2\left|\right|\psi \left(x\right)|.$$

(42)

Now, by substituting (42) into (40), we obtain

$$\left|D_x^{\alpha }v\left(x\right)\right|\le 2(1+|a_2\left|\right)\left|\psi \left(x\right)\right|\left|D_x^{\alpha }\psi \left(x\right)\right|+2\left|a_1\right|{\left|D_x^{\alpha }\psi \left(x\right)\right|}^2,$$

(43)

and by the inequality

$$2\left|b\right|\left|c\right|\le {\left|b\right|}^2+{\left|c\right|}^2,$$

(44)

setting $b=\psi \left(x\right)$ and $c=D_x^{\alpha }\psi \left(x\right)$, we obtain

$$\begin{array}{cc}\hfill \left|D_x^{\alpha }v\left(x\right)\right|& \le (1+|a_2{\left|\right)\left|\psi \left(x\right)\right|}^2+(1+2|a_1|+|a_2\left|\right)\left|D_x^{\alpha }\psi \left(x\right)\right|\hfill \\ \hfill & \le 2(1+|a_1|+|a_2{\left|\right)\left[\right|\psi \left(x\right)|}^2+|{\psi }^{\alpha }\left(x\right){|}^2].\hfill \end{array}$$

(45)

Therefore, we obtain

$$\left|D_x^{\alpha }v\left(x\right)\right|\le 2kv\left(x\right).$$

(46)

Subsequently, we obtain

$$-2kv\left(x\right)\le v^{\alpha }\left(x\right)\le 2kv\left(x\right).$$

(47)

Now, to prove Equation (36), let us observe that the right inequality of Equation (47) can be expressed as

$$D_x^{\alpha }v\left(x\right)-2kv\left(x\right)\le 0.$$

(48)

Since $exp(-2k{S}_F^{\alpha }\left(x\right))\ge 0$ for all $x\in (a,b)\cap F$, we can multiply both members of Equation (48) by $exp(-2k{S}_F^{\alpha }\left(x\right)$, so we obtain that

$$D_x^{\alpha }v\left(x\right)exp(-2k{S}_F^{\alpha })\left(x\right)\le 0.$$

(49)

Now, let $x\in (a,b)\cap F.$ Let us start by considering $x>x_0$; therefore, the $F^{\alpha }$-integral from $x_0$ to x of $D_x^{\alpha }v\left(x\right)exp(-2k{S}_F^{\alpha })\left(x\right)$ results in

$$exp(-2k{S}_F^{\alpha }\left(x\right))v\left(x\right)-exp(-2k{S}_F^{\alpha }\left(x_0\right))v\left(x_0\right)\le 0.$$

(50)

This leads to the inequality

$$v\left(x\right)\le v\left(x_0\right)exp\left(2k(S_F^{\alpha }\left(x\right)-S_F^{\alpha }\left(x_0\right))\right),$$

(51)

which yields

$$\parallel \psi \left(x\right)\parallel \le \parallel \psi \left(x_0\right)\parallel exp\left(2k(S_F^{\alpha }\left(x\right)-S_F^{\alpha }\left(x_0\right))\right),(x>x_0).$$

(52)

The corresponding left inequality in Equation (47) implies

$$\parallel \psi \left(x_0\right)\parallel exp(-2k(S_F^{\alpha }\left(x\right)-S_F^{\alpha }\left(x_0\right)))\le \parallel \psi \left(x\right)\parallel ,(x>x_0),$$

(53)

which consequently leads to

$$\begin{array}{cc}\hfill \parallel \psi \left(x_0\right)\parallel exp(-2k(S_F^{\alpha }\left(x\right)& -S_F^{\alpha }\left(x_0\right)\left)\right)\le \parallel \psi \left(x\right)\parallel \le \hfill \\ & \parallel \psi \left(x_0\right)\parallel exp\left(2k(S_F^{\alpha }\left(x\right)-S_F^{\alpha }\left(x_0\right))\right).\hfill \end{array}$$

(54)

Now, considering Equation (47) for $x<x_0$ along with a fractal integration from x to $x_0$, we obtain

$$\begin{array}{cc}\hfill \parallel \psi \left(x_0\right)\parallel exp\left(2k\right(S_F^{\alpha }\left(x\right)& -S_F^{\alpha }\left(x_0\right)\left)\right)\le \parallel \psi \left(x\right)\parallel \le \hfill \\ & \parallel \psi \left(x_0\right)\parallel exp(-2k(S_F^{\alpha }\left(x\right)-S_F^{\alpha }\left(x_0\right))),\hfill \end{array}$$

(55)

which completes the proof.  □

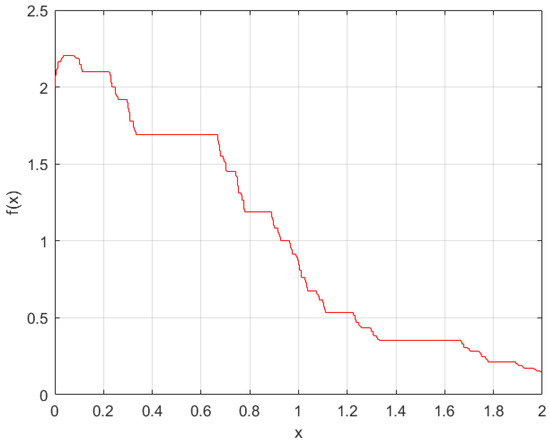
In Figure 2, it is evident that $\left|\psi \right(x\left)\right|$ consistently remains between the two curves $|\psi \left(x_0\right)|exp\left(2k(S_F^{\alpha }\left(x\right)-S_F^{\alpha }\left(x_0\right))\right)$ and $|\psi \left(x_0\right)|exp(-2k(S_F^{\alpha }\left(x\right)-S_F^{\alpha }\left(x_0\right)))$.

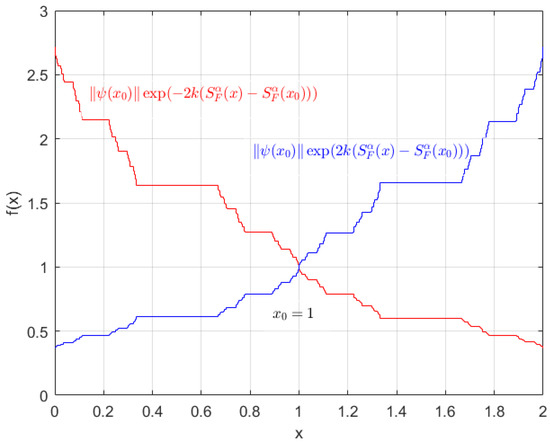
Figure 2. Graph of lower and upper bound of $\parallel \psi \left(x\right)\parallel$ given by Equation (55).

Theorem 3. 

(Uniqueness Theorem) Let $f_0$ and $D_x^{\alpha }{f}_0$ be any two constants and let $x_0$ be any point in the fractal set F. On any interval $I\subset (a,b)\cap F$ containing $x_0$, there exists at most one solution $\psi \left(x\right)$ of the initial value problem

$$a{D}_x^{2\alpha }f\left(x\right)+b{D}_x^{\alpha }f\left(x\right)+cf\left(x\right)=0f\left(x_0\right)=f_0,f^{\alpha }\left(x_0\right)=D_x^{\alpha }{f}_0.$$

(56)

Proof. 

Let us assume that there are two different solutions indicated by $\psi$ and $\varphi$ of the assigned initial value problem. Let $\chi =\psi -\varphi$. Then, we have that $\chi \left(x\right)$ satisfies the initial value problem with the initial conditions $f_0=D_x^{\alpha }{f}_0=0$. Thus, $\parallel \chi \left(x_0\right)\parallel =0$ and by applying the inequality Equation (55) of the previous Lemma to $\chi \left(x\right)$, we obtain $\parallel \chi \left(x\right)\parallel =0$ for all $x\in I\subset F\cap (a,b)$. Therefore, $\psi \left(x\right)-\varphi \left(x\right)=0$ for all $x\in I.$ Thus, there exists at most one solution to the initial value problem (56), establishing the uniqueness of the solution.  □

Example 4. 

Consider a $2\alpha$-order fractal differential equation as

$$D_x^{2\alpha }f\left(x\right)+5D_x^{\alpha }f\left(x\right)+6f\left(x\right)=0,x\in F,$$

(57)

with initial condition

$$f\left(0\right)=2,D_x^{\alpha }{f}_0=3.$$

(58)

By using Equations (20) and (58), we obtain the solution of Equation (57) as follows

$$\begin{array}{cc}\hfill \psi \left(x\right)& =9exp(-2S_F^{\alpha }\left(x\right))-7exp(-3S_F^{\alpha }\left(x\right))\hfill \\ \hfill & \propto 9exp(-2x^{\alpha })-7exp(-3x^{\alpha }).\hfill \end{array}$$

(59)

The exact and approximate solutions of Equation (57) can be observed in Figure 3 and Figure 4, respectively.

Figure 3. Solution of Equation (57) with initial condition Equation (58) for $\alpha =0.63$.

Figure 4. Approximate solution of Equation (57) with initial condition Equation (58) for different value of $\alpha$.

Remark 6. 

We observe that for $F\subset [a,b]$, the inequality $a{x}^{\alpha }<S_F^{\alpha }\left(x\right)<b{x}^{\alpha }$ holds [52].

Definition 12. 

We say that the fractal dimension of the solution space of the $2\alpha$-order fractal differential equation is $2\alpha$.

5. Exact $\mathbf{2}\mathit{\alpha }$-Order Fractal Differential Equation

In this section, we present the concept of a homogeneous fractal differential equation of order $2\alpha$ and outline the approach to determine its solution.

Definition 13. 

A $2\alpha$-order fractal differential equation:

$$P\left(x\right)D_x^{2\alpha }f\left(x\right)+Q\left(x\right)D_x^{\alpha }f\left(x\right)+R\left(x\right)f\left(x\right)=0,$$

(60)

is considered exact when it can be transformed into the following form:

$$D_x^{\alpha }\left(P\left(x\right)D_x^{\alpha }f\left(x\right)\right)+D_x^{\alpha }\left(g\left(x\right)f\left(x\right)\right)=0,$$

(61)

where the function $g\left(x\right)$ can be determined in terms of $P\left(x\right)$, $Q\left(x\right)$, and $R\left(x\right)$.

Theorem 4. 

The $2\alpha$-order fractal differential equation, as given by Equation (60):

$$P\left(x\right)D_x^{2\alpha }f\left(x\right)+Q\left(x\right)D_x^{\alpha }f\left(x\right)+R\left(x\right)f\left(x\right)=0,$$

(62)

is exact if

$$D_x^{2\alpha }P\left(x\right)-D_x^{\alpha }Q\left(x\right)+R\left(x\right)=0.$$

(63)

In other words, the equation is exact when the combination of the second $F^{\alpha }$-derivative of the coefficient function $P\left(x\right)$ and the $F^{\alpha }$-derivative of the coefficient function $Q\left(x\right)$, along with the term $R\left(x\right)$, equals zero.

Proof. 

To prove this theorem, we can equate the coefficients of Equations (61) and (62) and then eliminate $g\left(x\right)$, resulting in the equation:

$$D_x^{2\alpha }P\left(x\right)-D_x^{\alpha }Q\left(x\right)+R\left(x\right)=0.$$

(64)

□

Theorem 5. 

Consider a $2\alpha$-order fractal homogeneous equation given by:

$$P\left(x\right)D_x^{2\alpha }f\left(x\right)+Q\left(x\right)D_x^{\alpha }f\left(x\right)+R\left(x\right)=0.$$

(65)

If this equation is not exact, we can make it exact by multiplying it by a function $\mu \left(x\right)$, which is a solution of the following equation, often referred to as the adjoint equation associated with Equation (65):

$$\begin{array}{cc}\hfill & P\left(x\right)D_x^{2\alpha }\mu \left(x\right)+(2D_x^{\alpha }P\left(x\right)-Q\left(x\right))D_x^{\alpha }\mu \left(x\right)\hfill \\ \hfill & +(D_x^{2\alpha }P\left(x\right)-D_x^{\alpha }Q\left(x\right)+R\left(x\right))\mu \left(x\right)=0.\hfill \end{array}$$

(66)

Proof. 

Let us consider the equation obtained by multiplying the given $2\alpha$-order fractal linear homogeneous equation by $\mu \left(x\right)$:

$$\mu \left(x\right)P\left(x\right)D_x^{2\alpha }f\left(x\right)+\mu \left(x\right)Q\left(x\right)D_x^{\alpha }f\left(x\right)+\mu \left(x\right)R\left(x\right)=0.$$

(67)

We can express Equation (67) in the following form:

$$D_x^{\alpha }\left(\mu \left(x\right)P\left(x\right)D_x^{\alpha }f\left(x\right)\right)+D_x^{\alpha }\left(g\left(x\right)f\left(x\right)\right)=0.$$

(68)

By equating the coefficients of Equations (67) and (68), we can eliminate the function $g\left(x\right)$, revealing that the function $\mu \left(x\right)$ must satisfy the following equation:

$$\begin{array}{cc}\hfill & P\left(x\right)D_x^{2\alpha }\mu \left(x\right)+(2D_x^{\alpha }P\left(x\right)-Q\left(x\right))D_x^{\alpha }\mu \left(x\right)\hfill \\ \hfill & +(D_x^{2\alpha }P\left(x\right)-D_x^{\alpha }Q\left(x\right)+R\left(x\right))\mu \left(x\right)=0.\hfill \end{array}$$

(69)

□

Lemma 2. 

A $2\alpha$-order fractal homogeneous equation, represented as:

$$P\left(x\right)D_x^{2\alpha }f\left(x\right)+Q\left(x\right)D_x^{\alpha }f\left(x\right)+R\left(x\right)=0,$$

(70)

can be referred to as self-adjoint if it satisfies the condition:

$$D_x^{\alpha }P\left(x\right)=Q\left(x\right).$$

(71)

In simpler terms, the equation is considered self-adjoint when the α-derivative of the coefficient function $P\left(x\right)$ is equal to the function $Q\left(x\right)$.

Proof. 

The proof follows straightforwardly from Equation (66). □

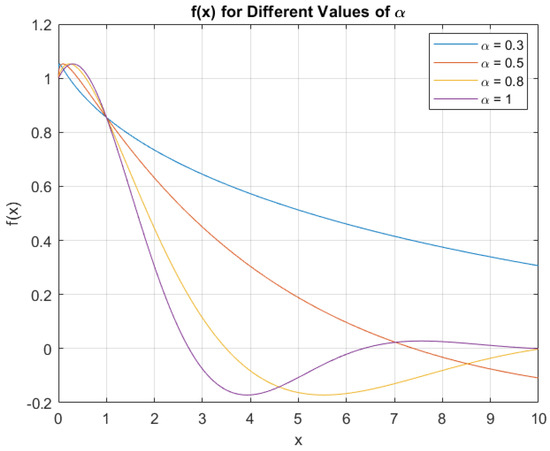
Example 5. 

Consider a $2\alpha$-order fractal differential equation given by:

$$16D_x^{2\alpha }f\left(x\right)-8D_x^{\alpha }f\left(x\right)+145f\left(x\right)=0,$$

(72)

with the following initial conditions:

$$f\left(0\right)=-2,D_x^{\alpha }{f\left(x\right)|}_{x=0}=1.$$

(73)

The solution to this equation is given by:

$$\begin{array}{cc}\hfill f\left(x\right)& =-2exp\left({\displaystyle \frac{S_F^{\alpha }\left(x\right)}{4}}\right)cos\left(3S_F^{\alpha }\left(x\right)\right)+{\displaystyle \frac{1}{2}}exp\left({\displaystyle \frac{S_F^{\alpha }\left(x\right)}{4}}\right)sin\left(3S_F^{\alpha }\left(x\right)\right)\hfill \\ & \propto -2exp\left({\displaystyle \frac{x^{\alpha }}{4}}\right)cos\left(3x^{\alpha }\right))+{\displaystyle \frac{1}{2}}exp\left({\displaystyle \frac{x^{\alpha }}{4}}\right)sin\left(3x^{\alpha }\right).\hfill \end{array}$$

(74)

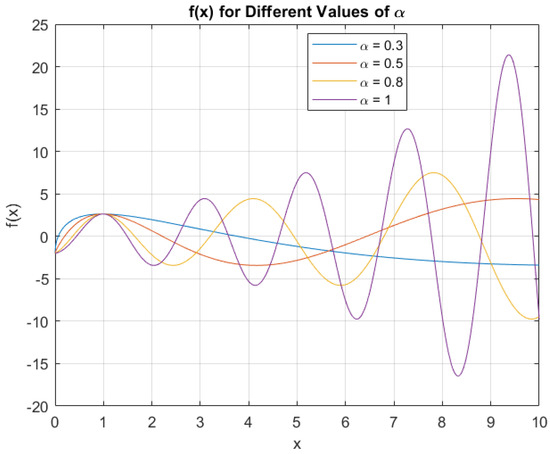
In Figure 5, we have graphed Equation (74), illustrating how varying dimensions influence the solution. In simpler terms, this example illustrates a $2\alpha$-order fractal differential equation with specific initial conditions and provides the corresponding solution expressed in terms of trigonometric and exponential functions.

Figure 5. Graph of Equation (74).

Theorem 6. 

Let us consider a solution, denoted as $f_1\left(x\right)$, to a $2\alpha$-order fractal differential equation given by:

$$D_x^{2\alpha }f\left(x\right)+p\left(x\right)D_x^{\alpha }f\left(x\right)+q\left(x\right)f\left(x\right)=0.$$

(75)

Now, the second solution, denoted as $f\left(x\right)$, can be expressed as:

$$f\left(x\right)=v\left(x\right)f_1\left(x\right),$$

(76)

which satisfies the following equation:

$$f_1\left(x\right)D_x^{2\alpha }v\left(x\right)+(2D_x^{\alpha }{f}_1\left(x\right)+p\left(x\right)f_1\left(x\right))D_x^{\alpha }v\left(x\right)=0.$$

(77)

In essence, this theorem explains how to find a second solution to a $2\alpha$-order fractal differential equation when we already have one solution, and it provides a differential equation for the function $v\left(x\right)$ that relates the two solutions.

Proof. 

To prove this theorem, we can find the $F^{\alpha }$-derivatives of $f\left(x\right)$ with respect to x as follows:

$$\begin{array}{cc}\hfill D_x^{\alpha }f\left(x\right)& =v\left(x\right)D_x^{\alpha }{f}_1\left(x\right)+D_x^{\alpha }v\left(x\right)f_1\left(x\right),\hfill \\ \hfill D_x^{2\alpha }f\left(x\right)& =v\left(x\right)D_x^{2\alpha }{f}_1\left(x\right)+2D_x^{\alpha }v\left(x\right)D_x^{\alpha }{f}_1\left(x\right)+D_x^{2\alpha }v\left(x\right)f_1\left(x\right).\hfill \end{array}$$

(78)

Now, we substitute Equation (78) back into Equation (75):

$$\begin{array}{cc}\hfill & f_1\left(x\right)D_x^{2\alpha }v\left(x\right)+(2D_x^{\alpha }{f}_1\left(x\right)+p\left(x\right)f_1\left(x\right))D_x^{\alpha }v\left(x\right)\hfill \\ & +(D_x^{2\alpha }{f}_1\left(x\right)+p\left(x\right)D_x^{\alpha }{f}_1\left(x\right)+q{f}_1\left(x\right))v\left(x\right)=0.\hfill \end{array}$$

(79)

Since $f_1\left(x\right)$ is a solution of Equation (75), then we have

$$f_1\left(x\right)D_x^{2\alpha }v\left(x\right)+(2D_x^{\alpha }{f}_1\left(x\right)+p\left(x\right)f_1\left(x\right))D_x^{\alpha }v\left(x\right)=0.$$

(80)

This completes the proof of the theorem. □

Example 6. 

Let us consider the equation:

$$2S_F^{\alpha }{\left(x\right)}^2{D}_x^{2\alpha }f\left(x\right)+3S_F^{\alpha }\left(x\right)D_x^{\alpha }f\left(x\right)-f\left(x\right)=0,$$

(81)

where $f_1\left(x\right)=S_F^{\alpha }{\left(x\right)}^{-1}$ is one of the solutions. To find a second fundamental solution, we propose $f\left(x\right)=v\left(x\right)S_F^{\alpha }{\left(x\right)}^{-1}$. By substituting this expression for $f\left(x\right)$, $D_x^{\alpha }f\left(x\right)$, and $D_x^{2\alpha }f\left(x\right)$ into Equation (81) and collecting terms, we obtain:

$$2S_F^{\alpha }\left(x\right)D_x^{2\alpha }v\left(x\right)-D_x^{\alpha }v\left(x\right)=0.$$

(82)

if we let $w\left(x\right)=D_x^{\alpha }v\left(x\right)$, we have a separable α-order differential equation. By solving it, we find:

$$w\left(x\right)=c{S}_F^{\alpha }{\left(x\right)}^{1/2}.$$

(83)

So, we can determine $v\left(x\right)$ as:

$$v\left(x\right)={\displaystyle \frac{2}{3}}c{S}_F^{\alpha }{\left(x\right)}^{3/2}+k,$$

(84)

and, consequently, the solution $f\left(x\right)$ becomes:

$$\begin{array}{cc}\hfill f\left(x\right)& ={\displaystyle \frac{2}{3}}c{S}_F^{\alpha }{\left(x\right)}^{1/2}+k{S}_F^{\alpha }{\left(x\right)}^{-1}\hfill \\ & \propto {\displaystyle \frac{2}{3}}c{x}^{\alpha /2}+k{x}^{-\alpha }.\hfill \end{array}$$

(85)

In Figure 6, we have depicted an approximation of Equation (85).

Figure 6. Graph of $f\left(x\right)\propto {\displaystyle \frac{2}{3}}c{x}^{\alpha /2}+k{x}^{-\alpha }$ for $c=k=1$.

In summary, this example demonstrates how to find a second solution to the given differential equation, building on the knowledge of the first solution $f_1\left(x\right)$.

6. Nonhomogeneous $\mathbf{2}\mathit{\alpha }$-Order Fractal Differential Equation

In this section, we introduce and discuss nonhomogeneous $2\alpha$-order fractal differential equations. These equations involve both the $2\alpha$-order derivative of a function and a nonhomogeneous term, typically denoted as $g\left(x\right)$. Nonhomogeneous equations are important in modeling real-world phenomena where external influences or sources contribute to the behavior of the system. We explore various aspects of these equations, including their solutions and properties.

Definition 14. 

Let us consider a nonhomogeneous $2\alpha$-order fractal differential equation as

$$L\left[f\right]=D_x^{2\alpha }f\left(x\right)+p\left(x\right)D_x^{\alpha }f\left(x\right)+q\left(x\right)f\left(x\right)=g\left(x\right),$$

(86)

where $p,q$, and g are given F-continuous on the $(a,b)$. If $g\left(x\right)=0$,

$$L\left[f\right]=D_x^{2\alpha }f\left(x\right)+p\left(x\right)D_x^{\alpha }f\left(x\right)+q\left(x\right)f\left(x\right)=0,$$

(87)

which is called the homogenous fractal differential equation.

Theorem 7. 

Consider a nonhomogeneous linear fractal differential equation given by Equation (86), where $F_1\left(x\right)$ and $F_2\left(x\right)$ are two solutions. Then, their difference $F_1-F_2$ is a solution of the corresponding homogeneous fractal differential equation, as given by Equation (87). Furthermore, if $f_1$ and $f_2$ form a fundamental set of solutions of the homogeneous fractal differential equation, then the difference $F_1-F_2$ can be expressed as:

$$F_1-F_2=c_1{f}_1+c_2{f}_2,$$

(88)

where $c_1$ and $c_2$ are constants.

Proof. 

To prove this theorem, we start by noting that for the nonhomogeneous linear fractal differential equation:

$$L\left[F_1\right]=g\left(x\right),L\left[F_2\right]=g\left(x\right),$$

(89)

where L represents the differential operator and $g\left(x\right)$ is the nonhomogeneous term, we have two solutions, $F_1\left(x\right)$ and $F_2\left(x\right)$. Now, by subtracting these Equation (89), we obtain:

$$L\left[F_1\right]-L\left[F_2\right]=L[F_1-F_2]=0.$$

(90)

Therefore, we can conclude that:

$$F_1-F_2=c_1{f}_1+c_2{f}_2,$$

(91)

where $c_1$ and $c_2$ are constants. □

Theorem 8. 

The general solution of the nonhomogeneous fractal differential equation given by (87) can be represented in the form:

$$f\left(x\right)=\psi \left(x\right)=c_1{f}_1\left(x\right)+c_2{f}_2\left(x\right)+F\left(x\right),$$

(92)

where $f_1$ and $f_2$ are fundamental solutions of the corresponding homogeneous Equation (87), $c_1$ and $c_2$ are arbitrary constants, and $F\left(x\right)$ is any solution of the nonhomogeneous Equation (86). This form allows us to describe the general solution of the nonhomogeneous equation in terms of both homogeneous solutions and a particular solution.

Proof. 

The proof of this theorem follows directly from Theorem 7. If we consider $F_1$ to be $\psi \left(x\right)$ and $F_2$ to be $F\left(x\right)$, then we immediately obtain Equation (92). This demonstrates that the general solution in the form stated in the theorem is indeed valid.  □

Example 7. 

Let us consider a nonhomogeneous fractal differential equation:

$$D_x^{2\alpha }f\left(x\right)-3D_x^{\alpha }f\left(x\right)-4f\left(x\right)=3exp\left(2S_F^{\alpha }\left(x\right)\right).$$

(93)

We are looking for a particular solution $F\left(x\right)$ that satisfies the following equation:

$$D_x^{2\alpha }F\left(x\right)-3D_x^{\alpha }F\left(x\right)-4F\left(x\right)=3exp\left(2S_F^{\alpha }\left(x\right)\right).$$

(94)

To find this particular solution $F\left(x\right)$, let us assume that the solution of Equation (94) can be written as $F\left(x\right)=Aexp\left(2S_F^{\alpha }\left(x\right)\right)$. By substituting this into Equation (94), we obtain:

$$(4A-6A-4A)exp\left(2S_F^{\alpha }\left(x\right)\right)=3exp\left(2S_F^{\alpha }\left(x\right)\right).$$

(95)

By solving for A, we find that $A=-1/2$. Therefore, the particular solution $F\left(x\right)$ is:

$$F\left(x\right)=-{\displaystyle \frac{1}{2}}exp\left(2S_F^{\alpha }\left(x\right)\right).$$

(96)

This provides a specific solution to the nonhomogeneous fractal differential Equation (93).

Theorem 9 

(Fractal Variation of Parameters). Let us consider a nonhomogeneous $2\alpha$-order linear fractal differential equation:

$$L\left[f\left(x\right)\right]=D_x^{2\alpha }f\left(x\right)+p\left(x\right)D_x^{\alpha }f\left(x\right)+q\left(x\right)f\left(x\right)=g\left(x\right).$$

(97)

Assuming that the functions $p\left(x\right)$, $q\left(x\right)$, and $g\left(x\right)$ are F-continuous on the open interval $(a,b)$, and that $f_1\left(x\right)$ and $f_2\left(x\right)$ form a fundamental set of solutions for the corresponding homogeneous fractal equation:

$$D_x^{2\alpha }f\left(x\right)+p\left(x\right)D_x^{\alpha }f\left(x\right)+q\left(x\right)f\left(x\right)=0.$$

(98)

Then, a particular solution of Equation (97) can be expressed as:

$$F\left(x\right)=-f_1{\int }_{x_0}^x{\displaystyle \frac{f_2\left(s\right)g\left(s\right)}{W[f_1,f_2]}}{d}_F^{\alpha }s+f_2{\int }_{x_0}^x{\displaystyle \frac{f_1\left(s\right)g\left(s\right)}{W[f_1,f_2]}}{d}_F^{\alpha }s,$$

(99)

where $x_0$ is any conveniently chosen point in the open interval $(a,b)$. The general solution of Equation (97) is then:

$$f\left(x\right)=c_1{f}_1\left(x\right)+c_2{f}_2\left(x\right)+F\left(x\right),$$

(100)

where $c_1$ and $c_2$ are constants. This theorem provides a method to find both particular and general solutions for nonhomogeneous $2\alpha$-order linear fractal differential equations under certain conditions on the functions involved.

Proof. 

To establish this theorem, we begin by considering a general solution for the nonhomogeneous equation:

$$F\left(x\right)=A\left(x\right)f_1\left(x\right)+B\left(x\right)f_2\left(x\right),$$

(101)

where $A\left(x\right)$ and $B\left(x\right)$ are unknown functions, and $f_1$ and $f_2$ are the solutions to the homogeneous Equation (98). Since this equation introduces two unknown functions, it is appropriate to impose an additional condition. We choose the following conditions:

$$D_x^{\alpha }A\left(x\right)f_1\left(x\right)+D_x^{\alpha }B\left(x\right)f_2\left(x\right)=0.$$

(102)

Now, let us compute the fractal derivatives of $F\left(x\right)$:

$$\begin{array}{cc}\hfill D_x^{\alpha }F\left(x\right)& =D_x^{\alpha }(A\left(x\right)f_1\left(x\right)+B\left(x\right)f_2\left(x\right)\hfill \\ & =A\left(x\right)D_x^{\alpha }{f}_1\left(x\right)+B\left(x\right)D_x^{\alpha }{f}_2\left(x\right).\hfill \end{array}$$

(103)

By differentiating once more:

$$\begin{array}{cc}\hfill D_x^{2\alpha }F\left(x\right)& =A\left(x\right)D_x^{2\alpha }{f}_1\left(x\right)+B\left(x\right)D_x^{2\alpha }{f}_2\left(x\right)\hfill \\ & +D_x^{\alpha }A\left(x\right)D_x^{\alpha }{f}_1\left(x\right)+D_x^{\alpha }B\left(x\right)D_x^{\alpha }{f}_2\left(x\right).\hfill \end{array}$$

(104)

Now, we can express the action of L on $F\left(x\right)$ as:

$$\begin{array}{cc}\hfill L\left[F\right(x\left)\right]& =A\left(x\right)L\left[f_1\left(x\right)\right]+B\left(x\right)L\left[f_2\left(x\right)\right]+D_x^{\alpha }A\left(x\right)D_x^{\alpha }{f}_1\left(x\right)\hfill \\ & +D_x^{\alpha }B\left(x\right)D_x^{\alpha }{f}_2\left(x\right).\hfill \end{array}$$

(105)

Since $f_1\left(x\right)$ and $f_2\left(x\right)$ are solutions to the homogeneous equation, we have:

$$L\left[F\left(x\right)\right]=D_x^{\alpha }A\left(x\right)D_x^{\alpha }{f}_1\left(x\right)+D_x^{\alpha }B\left(x\right)D_x^{\alpha }{f}_2\left(x\right).$$

(106)

This leads to the system of equations:

$$\left[\begin{array}{cc}{f}_1\left(x\right)& f_2\left(x\right)\\ D_x^{\alpha }{f}_1\left(x\right)& D_x^{\alpha }{f}_2\left(x\right)\end{array}\right]\left[\begin{array}{c}{D}_x^{\alpha }A\left(x\right)\\ D_x^{\alpha }B\left(x\right)\end{array}\right]=\left[\begin{array}{c}0\\ g\left(x\right)\end{array}\right].$$

(107)

To determine $A\left(x\right)$ and $B\left(x\right)$ from these conditions, we solve this system, resulting in:

$$\begin{array}{cc}\hfill A\left(x\right)& =-{\int }_{x_0}^x{\displaystyle \frac{f_2\left(s\right)g\left(s\right)}{W[f_1,f_2]}}{d}_F^{\alpha }s\hfill \\ \hfill B\left(x\right)& ={\int }_{x_0}^x{\displaystyle \frac{f_2\left(s\right)g\left(s\right)}{W[f_1,f_2]}}{d}_F^{\alpha }s.\hfill \end{array}$$

(108)

By substituting Equation (108) into Equation (101), we obtain the general solution for the nonhomogeneous equation. This concludes the proof. □

Remark 7. 

Although the statement of the theorems is similar to that known in the literature, it is worth proposing the proof for the sake of completeness, since the domain of action is a fractal subset of the real line and not the whole real line, and as already observed, a solution of a fractal differential equation of $2\alpha$-order is not necessarily a solution of a second-order differential equation which has as its domain a real and not fractal subset of the real line.

Example 8. 

Consider the equation describing the motion of an undamped forced oscillator:

$$m{D}_t^{2\alpha }f\left(t\right)+kf\left(t\right)=F_{0}cos\left(\omega S_F^{\alpha }\left(t\right)\right).$$

(109)

This equation represents the behavior of the oscillator, where $m,k,F_0,$ and ω are constants. The initial conditions for this oscillator are given as:

$$f\left(0\right)=0,D_t^{\alpha }f\left(t\right){|}_{t=0}=0.$$

(110)

To find the general solution for Equation (109), which describes the oscillator’s motion, we obtain the following expression:

$$f\left(t\right)=c_{1}cos\left({\omega }_0{S}_F^{\alpha }\left(t\right)\right)+c_{2}sin\left({\omega }_0{S}_F^{\alpha }\left(t\right)\right)+{\displaystyle \frac{F_0}{m({\omega }_0^2-{\omega }^2)}}cos\left(\omega S_F^{\alpha }\left(t\right)\right),$$

(111)

where ${\omega }_0=\sqrt{k/m}$ represents the natural frequency of the oscillator. By applying the initial conditions from Equation (110), we further simplify the solution to:

$$\begin{array}{cc}\hfill f\left(t\right)& ={\displaystyle \frac{F_0}{m({\omega }_0^2-{\omega }^2)}}(cos\left(\omega S_F^{\alpha }\left(t\right)\right)-cos\left({\omega }_0{S}_F^{\alpha }\left(t\right)\right))\hfill \\ & \propto {\displaystyle \frac{F_0}{m({\omega }_0^2-{\omega }^2)}}(cos\left(\omega t^{\alpha }\right)-cos\left({\omega }_0{t}^{\alpha }\right)).\hfill \end{array}$$

(112)

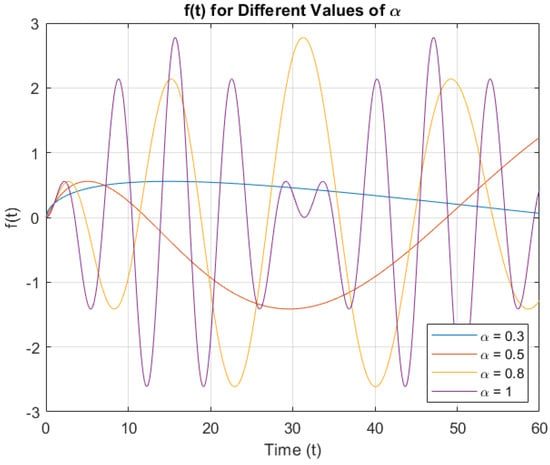
In the accompanying Figure 7, we have depicted the behavior described by Equation (112) for the given parameters: ${\omega }_0=1,\omega =0.8,$ and $F_0=1/2$.

Figure 7. Graph of $f\left(t\right)=2.778sin\left(0.1t^{\alpha }\right)sin\left(0.9\right)t^{\alpha }$.

7. Conclusions

In our paper, we have introduced the concept of second-order fractal differentials, denoted as $2\alpha$-order, along with a method for solving them. We have also defined a solution space for these differentials, which encompasses non-integer dimensions. Furthermore, we have presented a uniqueness theorem for $2\alpha$-order linear fractal differential equations, and we have provided an exact formulation for a second-order fractal differential equation. This equation is complemented by its adjoint equation, making it self-adjoint. In addition, we have defined and successfully solved nonhomogeneous $2\alpha$-order fractal differential equations. The models we have presented can be applied to processes occurring in fractal time and space.