Strong Convergence of a Two-Step Modified Newton Method for Weighted Complementarity Problems

Abstract

This paper focuses on the weighted complementarity problem (WCP), which is widely used in the fields of economics, sciences and engineering. Not least because of its local superlinear convergence rate, smoothing Newton methods have widespread application in solving various optimization problems. A two-step smoothing Newton method with strong convergence is proposed. With a smoothing complementary function, the WCP is reformulated as a smoothing set of equations and solved by the proposed two-step smoothing Newton method. In each iteration, the new method computes the Newton equation twice, but using the same Jacobian, which can avoid consuming a lot of time in the calculation. To ensure the global convergence, a derivative-free line search rule is inserted. At the same time, we develop a different term in the solution of the smoothing Newton equation, which guarantees the local strong convergence. Under appropriate conditions, the algorithm has at least quadratic or even cubic local convergence. Numerical experiments indicate the stability and effectiveness of the new method. Moreover, compared to the general smoothing Newton method, the two-step smoothing Newton method can significantly improve the computational efficiency without increasing the computational cost.

1. Introduction

The weighted complementarity problem (WCP for short) is

$$x\ge 0,s\ge 0,G(x,s,y)=0,xs=w,$$

(1)

in which $x,s\in R^n$, $y\in R^m$, $w\in R_{+}^n$ is a known weighted vector, $G(x,s,y):R^{2n+m}\to R^{n+m}$ is a nonlinear mapping and $xs$ represents the vector obtained by multiplying the components of x with s, respectively.

The concept of WCP was introduced first by Potra [1], is an extension of the complementarity problem (CP) [2,3], and is widely used in engineering, economics and science. As shown in [1], Fisher market equilibrium problems from economics can be transformed into WCPs, and quadratic programming and weighted centering problems can be equivalently converted to monotone WCPs. Not only that, the WCP has the potential to be developed into atmospheric chemistry [4,5] and multibody dynamics [6,7].

When $G(x,s,y):R^{2n+m}\to R^{n+m}$ is a linear mapping, the WCP (1) can be degenerated into the linear weighted complementarity problem (WLCP) as

$$x\ge 0,s\ge 0,Mx+Ns+Py=t,xs=w,$$

(2)

where $M,N\in R^{(m+n)\times n}$, $P\in R^{(m+n)\times m}$, $t\in R^{m+n}$. Many scholars have studied the WLCP and have put forward many effective algorithms. Potra [1] proposed two interior-point algorithms and discussed their computational complexity and convergence based on the methods by Mcshane [8] and Mizuno et al. [9]. Gowda [10] discussed a class of WLCP over Euclidean Jordan algebra. Chi et al. [11,12] proposed infeasible interior-point methods for WLCPs, which have good computational complexity. Asadi et al. [13] presented a modified interior-point method and obtained an iteration bound for the monotone WLCP.

On the other hand, recent years have witnessed a growing development of smoothing Newton methods for WCPs whose basic idea is to convert the problem to a smoothing set of nonlinear equations by employing a smoothing function, which is then solved by Newton methods [14,15,16,17,18,19]. Zhang [20] proposed a smoothing Newton method for the WLCP. For WCPs over Euclidean Jordan algebras, Tang et al. [21] presented a smoothing method and analyzed its convergence property under some weaker assumptions.

The two-step Newton method [22,23,24], which typically achieves third-order convergence when solving nonlinear equations $H\left(x\right)=0$, has a higher order of convergence than the classical Newton method. The two-step Newton algorithm computes not only a Newton step defined as

$$d_1^k=-H^{\prime }{\left(x^k\right)}^{-1}H\left(x^k\right),$$

but also an approximate Newton step as

$$d_2^k=-H^{\prime }{\left(x^k\right)}^{-1}H\left(y^k\right),$$

where $y^k=x^k+d_1^k$ and $H^{\prime }\left(x\right)$ represents the Jacobian matrix of $H\left(x\right)$. Compared with classical third-order methods such as Halley’s method [25] or super-Newton’s method [26], the two-step Newton algorithm does not need to compute the second-order Hessen matrix, and its computational cost is lower. Without adding additional derivatives and inverse operators, it is possible to raise the order of convergence from second to third order by evaluating the function only once.

In light of those considerations, we present here a two-step Newton algorithm possessing a high-order convergence rate for the WCP (1) on a smoothing complementarity function and an equivalent smoothing system of equations. The new algorithm has the following advantageous properties:

• The proposed method computes the Newton direction twice in each iteration. The first calculation yields a Newton direction, and the second yields an approximate Newton direction. Moreover, both calculations employ the same Jacobian matrix (see Section 3), which saves computing costs.
• The new algorithm utilizes a new term ${\zeta }_k=min\{\gamma ,{\epsilon }_k^{\varrho }\}$ where $\varrho \in [1,2]$ (see Section 3), when computing the Newton direction, unlike existing Newton algorithms for the WCP [20,21], which determine the local strong convergence. In particular, when $\varrho =2$, the algorithm has local cubic convergence properties.
• To obtain global convergence properties, we employ a derivative-free line search rule.

This paper is structured as follows. Section 2 presents a smoothing function and discusses its basic properties. Section 3 presents a derivative-free two-step smoothing Newton algorithm for the WCP, which is shown to be feasible. Section 4 deals with convergence properties. Section 5 shows some experiment results. Section 6 gives some concluding remarks.

2. Preliminaries

We define a smoothing function as

$${\theta }_{\epsilon }(u,v,r)=\sqrt{u^2+v^2+2r+2\epsilon }-(u+v),$$

(3)

where $\epsilon \in (0,1)$ and $r\ge 0$ is a given constant. It readily follows that ${\theta }_0(u,v,r)=0$ if and only if $u\ge 0,v\ge 0,uv=r.$

By simple reasoning and calculations, we can conclude the following.

Lemma 1. 

For any $0<\epsilon <1$, ${\theta }_{\epsilon }(u,v,r)$ is continuously differentiable, where

$$\begin{array}{cc}\hfill {\left({\theta }_{\epsilon }(u,v,r)\right)}_{\epsilon }^{\prime }& ={\displaystyle \frac{1}{\sqrt{u^2+v^2+2r+2\epsilon }}},\hfill \\ \hfill {\left({\theta }_{\epsilon }(u,v,r)\right)}_u^{\prime }& ={\displaystyle \frac{u}{\sqrt{u^2+v^2+2r+2\epsilon }}}-1,\hfill \\ \hfill {\left({\theta }_{\epsilon }(u,v,r)\right)}_v^{\prime }& ={\displaystyle \frac{v}{\sqrt{u^2+v^2+2r+2\epsilon }}}-1.\hfill \end{array}$$

In addition, ${\left({\theta }_{\epsilon }(u,v,r)\right)}_u^{\prime }<0$ and ${\left({\theta }_{\epsilon }(u,v,r)\right)}_v^{\prime }<0$.

Let $z=(\epsilon ,x,s,y)\in R\times R^{2n+m}$ and $w\in R_{+}^n$; we define $M\left(z\right)$ by

$$M\left(z\right)=\left(\begin{array}{c}\epsilon \\ {\theta }_{\epsilon }(x,s,w)\\ G(x,s,y)\end{array}\right),$$

(4)

where

$${\theta }_{\epsilon }(x,s,w)=\left(\begin{array}{c}{\theta }_{\epsilon }(x_1,s_1,w_1)\\ ⋮\\ {\theta }_{\epsilon }(x_n,s_n,w_n)\end{array}\right).$$

(5)

It follows that the WCP (1) can be transformed into an equivalent equation:

$$M\left(z\right)=0.$$

(6)

The following lemma states the continuous differentiability of $M\left(z\right)$.

Lemma 2. 

Define $M\left(z\right)$ and ${\theta }_{\epsilon }(x,s,w)$ by (4) and (5), respectively. For any $\epsilon >0$, $M\left(z\right)$ is continuously differentiable with

$$M^{\prime }\left(z\right)=\left(\begin{array}{cccc}1& 0& 0& 0\\ D_1& D_2& D_3& 0\\ 0& G_x^{\prime }& G_s^{\prime }& G_y^{\prime }\end{array}\right),$$

(7)

where

$$\begin{array}{cc}\hfill D_1& =\mathrm{vec}\left\{{\displaystyle \frac{1}{\sqrt{x_i^2+s_i^2+2w_i+2\epsilon }}}\right\},i=1,2,\dots ,n,\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill D_2& =\mathrm{diag}\left\{{\displaystyle \frac{x_i}{\sqrt{x_i^2+s_i^2+2w_i+2\epsilon }}}-1\right\},i=1,2,\dots ,n,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill D_3& =\mathrm{diag}\left\{{\displaystyle \frac{s_i}{\sqrt{x_i^2+s_i^2+2w_i+2\epsilon }}}-1\right\},i=1,2,\dots ,n.\hfill \end{array}$$

(10)

In order to discuss the nonsingularity of Jacobian matrix $M^{\prime }\left(z\right)$, it is necessary to make some assumption.

Assumption A1. 

Assuming that $G_y^{\prime }$ is column full rank, then it holds that any $(\Delta x, \Delta s, \Delta y)\in R^{2n+m}$ with

$$G_x^{\prime }\Delta x+G_s^{\prime }\Delta s+G_y^{\prime }\Delta y=0$$

yields $⟨\Delta x, \Delta s⟩\ge 0$.

For the WLCP (2), i.e., $G(x,s,y):R^{2n+m}\to R^{n+m}$ is a linear mapping, then Assumption 1 reduces to

$$M\Delta x+N\Delta s+P\Delta y=0,$$

which shows that $G(x,s,y)$ is monotone, and this case has been discussed for the feasibility of smoothing algorithms for the WLCP, see [1,20,27] and the reference therein.

Theorem 1. 

If Assumption 1 holds, then for any $\epsilon >0$, $M^{\prime }\left(z\right)$ is nonsingular.

Proof of Theorem 1. 

It only needs to verify that there exists $\Delta z=(\Delta \epsilon ,\Delta x,\Delta s,\Delta y)\in R^{2n+m+1}$ such that

$$M^{\prime }\left(z\right)\Delta z=0,$$

(11)

with $\Delta z=0$. Substituting (7) into (11) yields

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \Delta \epsilon & =0,\hfill \\ \hfill G_x^{\prime }\Delta x+G_s^{\prime }\Delta s+G_y^{\prime }\Delta y& =0,\hfill \\ \hfill D_1\Delta \epsilon +D_2\Delta x+D_3\Delta s& =0.\hfill \end{array}\end{array}$$

(12)

By Lemmas 1 and 2, we obtain that the diagonal matrices $D_2$ and $D_3$ are both negative definite. Upon (12), we get

$$\Delta x=-D_2^{-1}{D}_3\Delta s,$$

(13)

and then

$$⟨\Delta x,\Delta s⟩=-\Delta s^T{D}_3{D}_2^{-1}\Delta s\le 0.$$

(14)

Using Assumption 1 yields that $⟨\Delta x,\Delta s⟩\ge 0$, which, together with (14), implies

$$⟨\Delta x,\Delta s⟩=-\Delta s^T{D}_3{D}_2^{-1}\Delta s=0,$$

and then $\Delta s=0$. We conclude from (13) that $\Delta x=0$; hence, $\Delta y=0$ due to the second equation in (12). We complete the proof.    □

3. A Two-Step Newton Method

Now, we state the two-step smoothing Newton method. In order to understand Algorithm 1 more intuitively, we also give the flow chart of the new algorithm, as shown in Figure 1.

Algorithm 1 A Two-Step Newton Method.

Initial Step. Choose ${\epsilon }_0>0$ and $\gamma ,\eta \in (0,1)$. Choose $c\in (0,1)$, $l\in (0,1)$ and $\varrho \in [1,2]$. $\left\{{\xi }_k\right\}\subseteq R_{+}$ satisfies that ${\sum }_{k=0}^{\infty }{\xi }_k\le \xi <\infty$. Choose any $(x^0,s^0,y^0)\in R^{2n+m}$ as a starting point and let ${\mu }_0={({\epsilon }_0,0,0,0)}^T\in R\times R^{2n+m}$. Set $z^0=({\epsilon }_0,x^0,s^0,y^0)$ and $k=0$. Step 1. If $\parallel M\left(z^k\right)\parallel =0$, stop. Else, calculate $\Delta z_1^k$ by $$M^{\prime }\left(z^k\right)\Delta z_1^k=-M\left(z^k\right)+{\zeta }_k{\mu }_k,$$ (15) where ${\zeta }_k=min\{\gamma ,{\epsilon }_k^{\varrho }\}$ and ${\mu }_k={({\epsilon }_k,0,0,0)}^T$. Let ${\overline{z}}^k=z^k+\Delta z_1^k$. Step 2. Calculate $\Delta z_2^k$ by $$M^{\prime }\left(z^k\right)\Delta z_2^k=-M\left({\overline{z}}^k\right)+{\zeta }_k{\mu }_k.$$ (16) Step 3. If $$\parallel M(z^k+\Delta z_1^k+\Delta z_2^k)\parallel \le c·\parallel M\left(z^k\right)\parallel ,$$ (17) set ${\beta }_k=1$ and go to Step 5. Step 4. Set ${\beta }_k$ be the maximum of 1, l, $l^2$, … that satisfies the following inequality $$\parallel M(z^k+{\beta }_k\Delta z_1^k+{\beta }_k^2\Delta z_2^k){\parallel }^2\le (1+{\xi }_k)\parallel M\left(z^k\right){\parallel }^2-\eta {\beta }_k^2(\parallel \Delta z_1^k{\parallel }^2+\parallel \Delta z_2^k{\parallel }^2+\parallel M\left(z^k\right){\parallel }^2).$$ (18) Step 5. Set $z^{k+1}=z^k+{\beta }_k\Delta z_1^k+{\beta }_k^2\Delta z_2^k$, $k=k+1$ and return to Step 1.

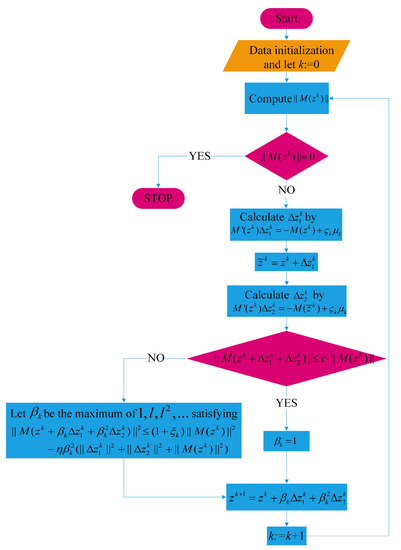
Figure 1. Flow chart of Algorithm 1.

Remark 1. 

1.

In each iteration, Algorithm 1 computes the Newton direction by the equations

$$M^{\prime }\left(z^k\right)\Delta z_1^k=-M\left(z^k\right)+{\zeta }_k{\mu }_k,$$

and

$$M^{\prime }\left(z^k\right)\Delta z_2^k=-M\left({\overline{z}}^k\right)+{\zeta }_k{\mu }_k,$$

using a new term ${\zeta }_k=min\{\gamma ,{\epsilon }_k^{\varrho }\}$, which is of significance for discussing the local strong convergence of Algorithm 1. Moreover, although Algorithm 1 computes the Newton direction twice, its computational cost is comparable to the classical Newton method.

2.

Algorithm 1 employs a derivative-free line search rule, a variant of that in [28]. As is shown in Theorem 2, the new derivative-free line search is feasible.

Theorem 2. 

If Assumption 1 holds, then Algorithm 1 is feasible. Moreover, we have

1.

${\epsilon }_k\ge 0$ for any $k\ge 0$.

2.

$\left\{{\epsilon }_k\right\}$ is non-increasing monotonically.

Proof of Theorem 2. 

With Theorem 1, we get that $M^{\prime }\left(z\right)$ is invertible. Then, both Step 1 and Step 2 are feasible. Next, we show the feasibility of Step 4. Supposing not, then for any ${\beta }_k\ge 0$,

$$\begin{array}{cc}\hfill & \parallel M(z^k+{\beta }_k\Delta z_1^k+{\beta }_k^2\Delta z_2^k){\parallel }^2\hfill \\ \hfill >& (1+{\xi }_k)\parallel M\left(z^k\right){\parallel }^2-\eta {\beta }_k^2(\parallel \Delta z_1^k{\parallel }^2+\parallel \Delta z_2^k{\parallel }^2+\parallel M\left(z^k\right){\parallel }^2)\hfill \\ \hfill \ge & \parallel M\left(z^k\right){\parallel }^2-\eta {\beta }_k^2(\parallel \Delta z_1^k{\parallel }^2+\parallel \Delta z_2^k{\parallel }^2+\parallel M\left(z^k\right){\parallel }^2).\hfill \end{array}$$

(19)

Hence,

$$\parallel M(z^k+{\beta }_k\Delta z_1^k+{\beta }_k^2\Delta z_2^k){\parallel }^2-\parallel M\left(z^k\right){\parallel }^2>\eta {\beta }_k^2(\parallel \Delta z_1^k{\parallel }^2+\parallel \Delta z_2^k{\parallel }^2+\parallel M\left(z^k\right){\parallel }^2)$$

(20)

Dividing (20) by ${\beta }_k$ and taking the limit as $k\to \infty$, we can conclude that

$$\underset{k\to \infty }{lim}{\displaystyle \frac{\parallel M(z^k+{\beta }_k\Delta z_1^k+{\beta }_k^2\Delta z_2^k){\parallel }^2-{\parallel M\left(z^k\right)\parallel }^2}{{\beta }_k}}\ge 0.$$

Therefore, we get

$$\begin{array}{cc}\hfill & \underset{k\to \infty }{lim}{\displaystyle \frac{\parallel M(z^k+{\beta }_k\Delta z_1^k+{\beta }_k^2\Delta z_2^k){\parallel }^2-{\parallel M\left(z^k\right)\parallel }^2}{{\beta }_k}}\hfill \\ \hfill =& 2M{\left(z^k\right)}^T(M^{\prime }\left(z^k\right)\Delta z_1^k)\hfill \\ \hfill \ge & 0.\hfill \end{array}$$

(21)

On the other hand, if $z^k$ is not the solution of (1), then it follows from Step 1 that

$$\begin{array}{cc}\hfill & M{\left(z^k\right)}^T(M^{\prime }\left(z^k\right)\Delta z_1^k)\hfill \\ \hfill =& M{\left(z^k\right)}^T(-M\left(z^k\right)+{\zeta }_k{\mu }_k)\hfill \\ \hfill \le & (\gamma -1)]\parallel M\left(z^k\right){\parallel }^2\hfill \\ \hfill <& 0,\hfill \end{array}$$

(22)

where the first equality comes from the fact that ${\zeta }_k=min\{\gamma ,{\epsilon }_k^{\varrho }\}\le \gamma \le 1$. This contradicts (21). Hence, Step 4 is feasible, and then Algorithm 1 is well-defined.

Then, we show ${\epsilon }_k\ge 0$ by induction. Suppose that ${\epsilon }_k\ge 0$ for some $k>0$, we obtain from (15) and (16) that

$$\Delta {\epsilon }_k^1=-{\epsilon }_k+{\zeta }_k{\epsilon }_k,$$

(23)

and

$$\Delta {\epsilon }_k^2=-{\epsilon }_k-\Delta {\epsilon }_k^1+{\zeta }_k{\epsilon }_k.$$

(24)

Then, it holds by Step 5 that

$$\begin{array}{cc}\hfill {\epsilon }_{k+1}& ={\epsilon }_k+{\beta }_k\Delta {\epsilon }_k^1+{\beta }_k^2\Delta {\epsilon }_k^2\hfill \\ \hfill & ={\epsilon }_k+{\beta }_k(-{\epsilon }_k+{\zeta }_k{\epsilon }_k)+{\beta }_k^2(-{\epsilon }_k-\Delta {\epsilon }_k^1+{\zeta }_k{\epsilon }_k)\hfill \\ \hfill & =(1-{\beta }_k){\epsilon }_k+{\beta }_k{\zeta }_k{\epsilon }_k\hfill \\ \hfill & =[1-{\beta }_k(1-{\zeta }_k)]{\epsilon }_k,\hfill \end{array}$$

(25)

which means that ${\epsilon }_{k+1}\ge 0$ due to the fact that ${\beta }_k\le 1$ and ${\zeta }_k\le 1$. Moreover, it follows that

$${\epsilon }_{k+1}=[1-{\beta }_k(1-{\zeta }_k)]{\epsilon }_k\le {\epsilon }_k,$$

i.e., $\left\{{\epsilon }_k\right\}$ is non-increasing monotonically. □

Lemma 3. 

If Assumption 1 holds, then $\{\parallel M\left(z^k\right)\parallel \}$ is convergent, and the sequence $\left\{z^k\right\}$ remains in the level set $L\left(z\right)$ of $\parallel M\left(z\right)\parallel$

$$L\left(z\right)=\{z\in R_{+}\times R^{2n+m}|\parallel M\left(z\right)\parallel \le e^{\frac{\xi }{2}}\parallel M\left(z^0\right)\parallel \}.$$

Proof of Lemma 3. 

According to (18), we have

$$\parallel M\left(z^{k+1}\right){\parallel }^2\le (1+{\xi }_k){\parallel M\left(z^k\right)\parallel }^2.$$

(26)

Since ${\sum }_{k=0}^{\infty }{\xi }_k\le \xi <\infty$, it follows from Lemma 3.3 in [29] that $\{\parallel M\left(z^k\right){\parallel }^2\}$ is convergent. Then, $\{\parallel M\left(z^k\right)\parallel \}$ is also convergent.

Moreover, we have

$$\begin{array}{cc}\hfill \parallel M\left(z^{k+1}\right)\parallel & \le \sqrt{1+{\xi }_k}\parallel M\left(z^k\right)\parallel \hfill \\ \hfill & \le \sqrt{1+{\xi }_k}·\sqrt{1+{\xi }_{k-1}}·\cdots ·\sqrt{1+{\xi }_0}\parallel M\left(z^0\right)\parallel \hfill \\ \hfill & =\prod _{j=0}^k\sqrt{1+{\xi }_j}\parallel M\left(z^0\right)\parallel \hfill \\ \hfill & \le {\left[\sum _{j=0}^k{\displaystyle \frac{1}{k+1}}(1+{\xi }_j)\right]}^{\frac{k+1}{2}}\parallel M\left(z^0\right)\parallel \hfill \\ \hfill & \le {\left(1+{\displaystyle \frac{\xi }{k+1}}\right)}^{\frac{k+1}{2}}\parallel M\left(z^0\right)\parallel \hfill \\ \hfill & \le e^{\frac{\xi }{2}}\parallel M\left(z^0\right)\parallel .\hfill \end{array}$$

(27)

□

4. Convergence Properties

4.1. Global Convergence

We first show a statement of great significance before analyzing the convergence properties of Algorithm 1.

Theorem 3. 

If Assumption 1 holds, then it holds that $\underset{k\to \infty }{lim}{\beta }_k\parallel M\left(z^k\right)\parallel =0.$

Proof of Theorem 3. 

Define $S\left(k\right)$ and $R\left(k\right)$ by

$$S\left(k\right)=\{j\le k|\left(17\right)is satisfied\}$$

and

$$R\left(k\right)=\{0,1,\dots ,k\}\setminus S\left(k\right).$$

Let $\left|S\right(k\left)\right|$ be the number of elements in $S\left(k\right)$.

If (17) holds for infinite k, then $\left|S\right(k\left)\right|\to \infty$ as $k\to \infty$. By (17), (18) and (27), we get

$$\begin{array}{cc}\hfill \parallel M\left(z^{k+1}\right){\parallel }^2& \le \prod _{i\in R\left(k\right)}(1+{\xi }_i)\prod _{i\in S\left(k\right)}{l}^2{\parallel M\left(z^0\right)\parallel }^2\hfill \\ \hfill & =\prod _{i\in R\left(k\right)}(1+{\xi }_i)l^{2\left|S\right(k\left)\right|}{\parallel M\left(z^0\right)\parallel }^2\hfill \\ \hfill & \le e^{\xi }{l}^{2\left|S\right(k\left)\right|}{\parallel M\left(z^0\right)\parallel }^2.\hfill \end{array}$$

As $k\to \infty$, $\parallel M\left(z^{k+1}\right){\parallel }^2\to 0$, i.e., $\parallel M\left(z^{k+1}\right)\parallel \to 0$, and then $\underset{k\to \infty }{lim}{\beta }_k\parallel M\left(z^k\right)\parallel =0$.

Assume that (17) holds for finite k. Then, we have from (18) that

$$\sum _{k=0}^{\infty }{\beta }_k^2\parallel M\left(z^k\right)\parallel =0,$$

which implies

$$\underset{k\to \infty }{lim}{\beta }_k\parallel M\left(z^k\right)\parallel =0.$$

The proof is completed. □

Theorem 4. 

If Assumption 1 holds, then $\left\{z^k\right\}$ converges to a solution of the WCP (1).

Proof of Theorem 4. 

According to Lemma 3, we know that $\{\parallel M\left(z^k\right)\parallel \}$ is convergent. Suppose, without loss of generality, that $\{z^k=({\epsilon }_k,x^k,s^k,y^k)\}$ converges to $z*=({\epsilon }_{*},x*,s*,y*)$ and $\underset{k\to \infty }{lim}\parallel M\left(z^k\right)\parallel =\parallel M(z*)\parallel \ge 0$. Next, we show $\parallel M(z*)\parallel =0$ by contradiction. Assume that $\parallel M(z*)\parallel >0$, then $\underset{k\to \infty }{lim}{\beta }_k=0$ due to Theorem 3.

Let $\widehat{\beta }={\displaystyle \frac{{\beta }_k}{l}}$, it follows from Step 4 that

$$\begin{array}{cc}\hfill \parallel M(z^k+\widehat{\beta }\Delta z_1^k+{\widehat{\beta }}^2\Delta z_2^k){\parallel }^2>& (1+{\xi }_k){\parallel M\left(z^k\right)\parallel }^2\hfill \\ \hfill & -\eta {\widehat{\beta }}^2(\parallel \Delta z_1^k{\parallel }^2+\parallel \Delta z_2^k{\parallel }^2+\parallel M\left(z^k\right){\parallel }^2),\hfill \end{array}$$

(28)

for sufficiently large k.

On the other hand, since

$$M(z^k+\widehat{\beta }(\Delta z_1^k+\widehat{\beta }\Delta z_2^k))=M\left(z^k\right)+\widehat{\beta }{M}^{\prime }\left(z^k\right)(\Delta z_1^k+\widehat{\beta }\Delta z_2^k)+o\left(\widehat{\beta }\right),$$

it follows that

$$\begin{array}{cc}\hfill & \parallel M(z^k+\widehat{\beta }(\Delta z_1^k+\widehat{\beta }\Delta z_2^k)){\parallel }^2\hfill \\ \hfill =& \parallel M\left(z^k\right)+\widehat{\beta }{M}^{\prime }\left(z^k\right)(\Delta z_1^k+\widehat{\beta }\Delta z_2^k){\parallel }^2+o\left(\widehat{\beta }\right)\hfill \\ \hfill =& \parallel M\left(z^k\right){\parallel }^2+2\widehat{\beta }M{\left(z^k\right)}^T\left(M^{\prime }\left(z^k\right)(\Delta z_1^k+\widehat{\beta }\Delta z_2^k)\right)+o\left(\widehat{\beta }\right).\hfill \end{array}$$

(29)

Combining (15) and (16) with (29), we obtain

$$\begin{array}{cc}\hfill \parallel M(z^k+\widehat{\beta }(\Delta z_1^k+\widehat{\beta }\Delta z_2^k)){\parallel }^2& =\parallel M\left(z^k\right){\parallel }^2+2\widehat{\beta }M{\left(z^k\right)}^T\left(-M\left(z^k\right)+{\zeta }_k{\mu }_k\right)+o\left(\widehat{\beta }\right)\hfill \\ \hfill & =(1-2\widehat{\beta }){\parallel M\left(z^k\right)\parallel }^2+2\widehat{\beta }{\zeta }_{k}M{\left(z^k\right)}^T{\mu }_k+o\left(\widehat{\beta }\right)\hfill \\ \hfill & \le [1-2\widehat{\beta }(1-\gamma )]{\parallel M\left(z^k\right)\parallel }^2+o\left(\widehat{\beta }\right).\hfill \end{array}$$

(30)

Then, from (28) and (30), we get

$$\begin{array}{cc}\hfill & [1-2\widehat{\beta }(1-\gamma )]{\parallel M\left(z^k\right)\parallel }^2+o\left(\widehat{\beta }\right)\hfill \\ \hfill >& (1+{\xi }_k)\parallel M\left(z^k\right){\parallel }^2-\eta {\widehat{\beta }}^2(\parallel \Delta z_1^k{\parallel }^2+\parallel \Delta z_2^k{\parallel }^2+\parallel M\left(z^k\right){\parallel }^2)\hfill \\ \hfill \ge & \parallel M\left(z^k\right){\parallel }^2-\eta {\widehat{\beta }}^2(\parallel \Delta z_1^k{\parallel }^2+\parallel \Delta z_2^k{\parallel }^2+\parallel M\left(z^k\right){\parallel }^2).\hfill \end{array}$$

It follows by simple calculation that

$$2(1-\gamma )\parallel M\left(z^k\right){\parallel }^2+{\displaystyle \frac{o\left(\widehat{\beta }\right)}{\widehat{\beta }}}<\eta \widehat{\beta }(\parallel \Delta z_1^k{\parallel }^2+\parallel \Delta z_2^k{\parallel }^2+\parallel M\left(z^k\right){\parallel }^2).$$

(31)

Passing to the limit in (31), then

$$2(\gamma -1)\parallel M(z*){\parallel }^2\ge 0.$$

As $\parallel M(z*)\parallel >0$, it follows that

$$\gamma >1,$$

a contradiction. Thus, $\parallel M(z*)\parallel =0$, which means that $\left\{z^k\right\}$ converges to a solution of the WCP (1). □

4.2. Local Convergence

We then discuss the local superquadratical convergence properties of Algorithm 1.

Theorem 5. 

If Assumption 1 holds, all $J\in \partial M(z*)$ are nonsingular. Suppose that $G^{\prime }(x,s,y)$ and $M^{\prime }(x,s,y)$ are both Lipschitz continuous on some neighborhood of $z*$, then

1.

${\beta }_k\equiv 1$ for any sufficiently large k.

2.

$\left\{z^k\right\}$ converges to $z^{*}$ locally superquadratically. In particular, $\left\{z^k\right\}$ converges to $z^{*}$ locally cubically if $\varrho =2$.

Proof of Theorem 5. 

Upon Theorem 4, we have that $\parallel M\left(z^{*}\right)\parallel =0$. All $J\in \partial M(z*)$ are nonsingular, so we have for any sufficiently large k that

$$\parallel M^{\prime }{\left(z^k\right)}^{-1}\parallel =O\left(1\right).$$

(32)

Since $G^{\prime }(x,s,y)$ is Lipschitz continuous on some neighborhood of $z*$, $M\left(z\right)$ is strongly semismooth and Lipschitz continuous on some neighborhood of $z*$, namely,

$$\parallel M\left(z^k\right)-M(z*)-M^{\prime }\left(z^k\right)(z^k-z*)\parallel =O(\parallel z^k-z*{\parallel }^2),$$

(33)

and

$$\parallel M\left(z^k\right)\parallel =\parallel M\left(z^k\right)-M(z*)\parallel =O(\parallel z^k-z*\parallel ),$$

(34)

for any sufficiently large k.

By the definition of ${\zeta }_k$ and ${\mu }_k$, it follows that

$$\parallel {\zeta }_k{\mu }_k\parallel \le {\epsilon }_k^{\varrho +1}\le {\parallel M\left(z^k\right)\parallel }^{\varrho +1}.$$

(35)

Then, combining (15) and (32)–(35) implies

$$\begin{array}{cc}\hfill \parallel z^k+\Delta z_1^k-z*\parallel & =\parallel z^k+M^{\prime }{\left(z^k\right)}^{-1}(-M\left(z^k\right)+{\zeta }_k{\mu }_k)-z*\parallel \hfill \\ \hfill & =O\left(\parallel M\left(z^k\right)-M\left(z^{*}\right)-M^{\prime }\left(x^k\right)(z^k-z^{*})+{\zeta }_k{\mu }_k\parallel \right)\hfill \\ \hfill & \le O(\parallel z^k-z*{\parallel }^2)+O(\parallel M\left(z^k\right){\parallel }^3)\hfill \\ \hfill & =O(\parallel z^k-z*{\parallel }^2),\hfill \end{array}$$

(36)

which means that $z^k+\Delta z_1^k$ is sufficiently close to $z*$ for sufficiently large k. Then, according to (34) and (36), we have that

$$\begin{array}{cc}\hfill \parallel M(z^k+\Delta z_1^k)\parallel & =\parallel M(z^k+\Delta z_1^k)-M(z*)\parallel \hfill \\ \hfill & =O(\parallel z^k+\Delta z_1^k-z*\parallel )\hfill \\ \hfill & =O(\parallel z^k-z*{\parallel }^2)=O(\parallel M\left(z^k\right){\parallel }^2)\hfill \end{array}$$

(37)

Hence, since $\varrho \ge 1$, it follows from (16), (32), (35) and (37) that

$$\begin{array}{cc}\hfill \parallel \Delta z_2^k\parallel & =∥M^{\prime }{\left(z^k\right)}^{-1}\left(-M(z^k+\Delta z_1^k)+{\zeta }_k{\mu }_k\right)∥\hfill \\ \hfill & \le O\left(\parallel M(z^k+\Delta z_1^k)\parallel +\parallel {\zeta }_k{\mu }_k\parallel \right)\hfill \\ \hfill & =O(\parallel M\left(z^k\right){\parallel }^2)+O(\parallel M\left(z^k\right){\parallel }^{\varrho +1})\hfill \\ \hfill & =O(\parallel M\left(z^k\right){\parallel }^2),\hfill \end{array}$$

(38)

combining with (34) and (36) yields

$$\begin{array}{cc}\hfill \parallel z^k+\Delta z_1^k+\Delta z_2^k-\Delta z*\parallel & \le \parallel z^k+\Delta z_1^k-z*\parallel +\parallel \Delta z_2^k\parallel \hfill \\ \hfill & =O(\parallel z^k-z*{\parallel }^2),\hfill \end{array}$$

(39)

for any sufficiently large k, which also means that $z^k+\Delta z_1^k+\Delta z_2^k$ is sufficiently close to $z*$ for a sufficiently large k, which, together with the Lipschitz continuity of $M\left(z\right)$ on some neighborhood of $z*$, implies

$$\parallel M(z^k+\Delta z_1^k+\Delta z_2^k)-M\left(z^k\right)-M^{\prime }\left(z^k\right)(\Delta z_1^k+\Delta z_2^k)\parallel =O(\parallel \Delta z_1^k+\Delta z_2^k{\parallel }^2).$$

(40)

Then, it holds that

$$\begin{array}{cc}\hfill & \parallel M(z^k+\Delta z_1^k+\Delta z_2^k)\parallel \hfill \\ \hfill \le & \parallel M\left(z^k\right)+M^{\prime }\left(z^k\right)(\Delta z_1^k+\Delta z_2^k)\parallel \hfill \\ \hfill & +\parallel M(z^k+\Delta z_1^k+\Delta z_2^k)-M\left(z^k\right)-M^{\prime }\left(z^k\right)(\Delta z_1^k+\Delta z_2^k)\parallel \hfill \\ \hfill =& \parallel M\left(z^k\right)+M^{\prime }\left(z^k\right)\Delta z_1^k\parallel +\parallel M\left({\overline{z}}^k\right)\parallel \hfill \\ \hfill & +\parallel M\left({\overline{z}}^k\right)+M^{\prime }\left(z^k\right)\Delta z_2^k\parallel +O(\parallel \Delta z_1^k+\Delta z_2^k{\parallel }^2).\hfill \end{array}$$

(41)

Now, we consider the term

$$\parallel M\left(z^k\right)+M^{\prime }\left(z^k\right)\Delta z_1^k\parallel +\parallel M\left({\overline{z}}^k\right)\parallel +\parallel M\left({\overline{z}}^k\right)+M^{\prime }\left(z^k\right)\Delta z_2^k\parallel +O(\parallel \Delta z_1^k+\Delta z_2^k{\parallel }^2).$$

By (15), (32) and (34), we obtain

$$\begin{array}{cc}\hfill \parallel \Delta z_1^k\parallel & =∥M^{\prime }{\left(z^k\right)}^{-1}\left(-M\left(z^k\right)+{\zeta }_k{\mu }_k\right)∥\hfill \\ \hfill & =O(\parallel M\left(z^k\right)\parallel ),\hfill \\ \hfill & =O(\parallel z^k-z*\parallel ).\hfill \end{array}$$

(42)

On the other hand, according to (15), (16) and (35), we obtain

$$\parallel M\left(z^k\right)+M^{\prime }\left(z^k\right)\Delta z_1^k\parallel =\parallel {\zeta }_k{\mu }_k\parallel =O(\parallel M\left(z^k\right){\parallel }^{\varrho +1}),$$

(43)

and

$$\parallel M\left({\overline{z}}^k\right)+M^{\prime }\left(z^k\right)\Delta z_2^k\parallel =\parallel {\zeta }_k{\mu }_k\parallel =O(\parallel M\left(z^k\right){\parallel }^{\varrho +1}).$$

(44)

So, combining (34), (38) and (41)–(44), we have

$$\begin{array}{cc}\hfill & \parallel M(z^k+\Delta z_1^k+\Delta z_2^k)\parallel \hfill \\ \hfill =& O(\parallel M\left(z^k\right){\parallel }^{\varrho +1})+O(\parallel z^k-z*{\parallel }^2)\hfill \\ \hfill =& o(\parallel M\left(z^k\right)\parallel )\hfill \\ \hfill =& {\rho }_k\parallel M\left(z^k\right)\parallel ,\hfill \end{array}$$

(45)

where ${\rho }_k\to 0$. This means that (17) makes sense for a sufficiently large k, which shows that ${\beta }_k\equiv 1$ when $z^k$ is sufficiently close to $z^{*}$, i.e.,

$$z^{k+1}=z^k+\Delta z_1^k+\Delta z_2^k.$$

(46)

By using (16), (32), (35), (46) and the Lipschitz continuity of $M^{\prime }\left(z\right)$ on some neighborhood of $z^{*}$, we get

$$\begin{array}{cc}\hfill & \parallel z^{k+1}-z*\parallel \hfill \\ \hfill =& \parallel {\overline{z}}^k-z*+M^{\prime }{\left(z^k\right)}^{-1}(-M\left({\overline{z}}^k\right)+{\zeta }_k{\mu }_k)\parallel \hfill \\ \hfill =& O\left(\parallel M\left({\overline{z}}^k\right)-M(z*)-M^{\prime }\left(z^k\right)({\overline{z}}^k-z*)\parallel +\parallel {\zeta }_k{\mu }_k\parallel \right)\hfill \\ \hfill =& O\left(\parallel M\left({\overline{z}}^k\right)-M(z*)-M^{\prime }\left({\overline{z}}^k\right)({\overline{z}}^k-z*)+(M^{\prime }\left({\overline{z}}^k\right)-M^{\prime }\left(z^k\right))({\overline{z}}^k-z*)\parallel +\parallel {\zeta }_k{\mu }_k\parallel \right)\hfill \\ \hfill =& O(\parallel {\overline{z}}^k-z*{\parallel }^2)+O(\parallel M\left(z^k\right){\parallel }^{\varrho +1})\hfill \\ \hfill =& O(\parallel z^k-z*{\parallel }^{\varrho +1}).\hfill \end{array}$$

(47)

Moreover, we have from (34) that

$$\parallel M\left(z^{k+1}\right)\parallel =O(\parallel z^{k+1}-z*\parallel )=O(\parallel z^k-z*{\parallel }^{\varrho +1})=O(\parallel M\left(z^k\right){\parallel }^{\varrho +1}),$$

which means that $\left\{z^k\right\}$ converges to $z^{*}$ locally and superquadratically since $\varrho \in [1,2]$. In particular, if $\varrho =2$, then

$$\parallel z^{k+1}-z^{*}\parallel =O(\parallel z^k-z^{*}{\parallel }^3)$$

and

$$\parallel M\left(z^{k+1}\right)\parallel =O(\parallel M\left(z^k\right){\parallel }^3),$$

which means that $\left\{z^k\right\}$ converges to $z^{*}$ locally cubically. □

5. Numerical Experiments

We implement Algorithm 1 in practice and use it to solve some numerical examples to verify the feasibility and effectiveness in this section. All programs are implemented on Matlab R2018b and a PC with 2.30 GHz CPU and 16.00 GB RAM. We also code the algorithm in [20], denoted as SNM_Z, and compare it with the new algorithm. To illustrate the performance of the new algorithm, we also code and compare the algorithm in [20], denoted as SNM_Z, with Algorithm 1. The stopping criterion is $\parallel M\left(z^k\right)\parallel \le {10}^{-6}$ and the parameters are set as

$$l=0.5,c=0.8,\gamma =0.01,{\epsilon }_0=0.1,\eta =0.001\mathrm{and}{\xi }_k=1/2^{k+2}.$$

For SNM_Z, the stopping criterion is the same as that in Algorithm 1, and the parameters are the same as [20].

Example 1. 

Consider an example of the WLCP (2) with

$$M=\left(\begin{array}{c}A\\ B\end{array}\right),N=\left(\begin{array}{c}0\\ -I\end{array}\right),P=\left(\begin{array}{c}0\\ -A^T\end{array}\right),t=\left(\begin{array}{c}Af\\ g\end{array}\right),$$

where $B\in R^{n\times n}$, $A\in R^{m\times n}$ whose elements are produced by the normal distribution on $[0,1]$, $f,g\in R^n$ are chosen uniformly from $[0,1]$ and $[-1,0]$, respectively. The weighted vector $w\in R^n$ is generated by $w=uv$ with $v=Bu-g$, where $u,v\in R^n$ are generated uniformly from $[0,1]$.

We test two kinds of problems using Algorithm 1 with different B, denoted by $B_1$ and $B_2$. $B_1$ is produced by setting $B_1=Q{Q}^T/\parallel Q{Q}^T\parallel$, where Q is generated uniformly from $[0,1]$. The diagonal matrix $B_2$ is generated randomly on $[0,1]$. The initial points $x^0$, $s^0$ and $y^0$ are chosen as ${(1,0,\dots ,0)}^T$ with relevant dimensions in every experiment.

First, in order to state the influence of $\varrho$ on the local convergence, we perform different $\varrho$ for each case on $B_1$. We perform three experiments for each problem and present the numerical results in Table 1. In what follows, (AIT)IT represents the (average) number of iterations, (ATime)Time is the (average) time taken for the algorithm to run in seconds, and (AERO)ERO represents the (average) value of $\parallel M\left(z^k\right)\parallel$ in the last iteration. As we can see in Table 1, Algorithm 1 has different local convergence rates with different values of $\varrho$. Moreover, Algorithm 1 has at least a local quadratic rate of convergence.

Table 1. Numerical results for a WLCP with $B_1$.

m	n	$\mathit{\varrho }=1$			$\mathit{\varrho }=1.5$			$\mathit{\varrho }=2$
		IT	Time	ERO	IT	Time	ERO	IT	Time	ERO
500	1000	5	2.0413	$1.7219\times {10}^{-10}$	4	1.9238	$5.4462\times {10}^{-7}$	4	1.8250	$5.8769\times {10}^{-12}$
		6	2.3358	$3.9422\times {10}^{-7}$	5	2.4771	$3.1306\times {10}^{-13}$	4	1.7943	$3.3544\times {10}^{-12}$
		6	2.3764	$1.3445\times {10}^{-11}$	5	2.4997	$3.1950\times {10}^{-13}$	4	1.7302	$3.5464\times {10}^{-12}$
1000	2000	6	14.0543	$1.7549\times {10}^{-12}$	5	11.9847	$5.9945\times {10}^{-7}$	4	12.4097	$1.8342\times {10}^{-12}$
		6	14.5208	$2.6955\times {10}^{-12}$	5	11.8457	$3.0670\times {10}^{-9}$	4	12.3936	$1.1576\times {10}^{-8}$
		6	14.2352	$1.3315\times {10}^{-9}$	5	12.5786	$2.7924\times {10}^{-10}$	4	12.4111	$1.8763\times {10}^{-12}$
1500	3000	5	39.7915	$5.0310\times {10}^{-7}$	5	38.5589	$3.0246\times {10}^{-12}$	4	36.4203	$6.2360\times {10}^{-12}$
		7	48.1246	$2.9957\times {10}^{-7}$	6	41.4926	$3.2203\times {10}^{-12}$	4	39.9579	$6.7978\times {10}^{-11}$
		7	46.4935	$1.3715\times {10}^{-9}$	6	41.8099	$3.4429\times {10}^{-10}$	4	46.6347	$2.0403\times {10}^{-11}$
2000	4000	6	110.1033	$5.6894\times {10}^{-10}$	5	81.3782	$5.9703\times {10}^{-7}$	4	100.4127	$2.7987\times {10}^{-11}$
		6	107.8945	$2.2694\times {10}^{-8}$	6	104.6634	$3.3573\times {10}^{-7}$	4	110.2353	$1.2117\times {10}^{-11}$
		7	128.1354	$2.6992\times {10}^{-11}$	7	136.8423	$5.7307\times {10}^{-12}$	4	103.2185	$2.2580\times {10}^{-10}$
2500	5000	6	178.1547	$3.4099\times {10}^{-10}$	5	176.0884	$6.7770\times {10}^{-7}$	4	100.4127	$2.7987\times {10}^{-11}$
		6	261.9206	$2.5631\times {10}^{-10}$	6	178.2723	$1.1975\times {10}^{-10}$	4	110.2353	$1.2117\times {10}^{-11}$
		6	286.3750	$6.7117\times {10}^{-12}$	6	209.1771	$6.7177\times {10}^{-12}$	4	130.8529	$8.7520\times {10}^{-12}$
3000	6000	6	371.0119	$4.0263\times {10}^{-10}$	6	356.2151	$1.8624\times {10}^{-8}$	4	316.1594	$4.5234\times {10}^{-11}$
		6	332.6154	$2.4767\times {10}^{-8}$	6	306.6382	$9.6163\times {10}^{-12}$	4	320.2794	$6.5542\times {10}^{-11}$
		6	352.4338	$1.7184\times {10}^{-10}$	6	369.1693	$8.3990\times {10}^{-8}$	4	320.2625	$1.8997\times {10}^{-11}$

Then, we test an example of $m=400$ and $n=800$ for $B_1$ to visually demonstrate the local convergence properties of Algorithm 1 and SNM_Z. In what follows, we set $\varrho =2$ in Algorithm 1. The results are shown in Table 2, which shows that Algorithm 1 has a local cubic convergence rate whose convergence rate is actually faster than SNM_Z, which possesses the local quadratic convergence rate.

Table 2. Variation of the value of $\parallel M\left(z^k\right)\parallel$ with the number of iterations for $B_1$.

k	Algorithm 1	SNM_Z
1	$3.5025\times {10}^0$	$9.0554\times {10}^0$
2	$1.4006\times {10}^{-1}$	$1.5244\times {10}^0$
3	$1.7885\times {10}^{-4}$	$1.3534\times {10}^{-1}$
4	$3.0450\times {10}^{-12}$	$4.6924\times {10}^{-3}$
5	∖	$1.2604\times {10}^{-5}$
6	∖	$1.5665\times {10}^{-10}$

Finally, we randomly performed 10 trials for each case. The tested results are shown in Table 3, which demonstrates that Algorithm 1 carries out fewer iterations than SNM_Z. In addition, although Algorithm 1 calculates the Newton direction twice in each iteration, it does not consume too much time compared with SNM_Z.

Table 3. Numerical comparison results for a WLCP.

B	m	n	Algorithm 1			SNM_Z
			AIT	ATime	AERO	AIT	ATime	AERO
$B_1$	500	1000	4.0	1.6388	$2.2736\times {10}^{-7}$	5.9	2.5001	$3.8463\times {10}^{-8}$
	1000	2000	4.0	15.8679	$3.5679\times {10}^{-11}$	5.6	17.8929	$7.1401\times {10}^{-8}$
	1500	3000	4.1	42.0557	$3.5400\times {10}^{-7}$	5.9	31.5197	$3.7355\times {10}^{-8}$
	2000	4000	4.1	90.4867	$5.3932\times {10}^{-7}$	5.5	80.4471	$5.7230\times {10}^{-8}$
	2500	5000	4.1	179.8909	$4.8241\times {10}^{-7}$	6.0	142.9854	$7.1523\times {10}^{-8}$
	3000	6000	4.1	300.2717	$5.7601\times {10}^{-7}$	6.8	215.0043	$2.5449\times {10}^{-8}$
$B_2$	500	1000	4.2	1.5968	$7.5550\times {10}^{-8}$	6.8	1.5040	$1.0939\times {10}^{-7}$
	1000	2000	4.2	9.5536	$2.7452\times {10}^{-7}$	7.0	9.4423	$9.6079\times {10}^{-8}$
	1500	3000	4.4	32.8206	$2.2022\times {10}^{-7}$	5.8	35.8170	$3.9237\times {10}^{-8}$
	2000	4000	4.5	80.3553	$1.9778\times {10}^{-9}$	7.1	73.1503	$1.2470\times {10}^{-7}$
	2500	5000	4.6	159.6309	$7.6437\times {10}^{-9}$	7.5	127.3718	$1.2020\times {10}^{-7}$
	3000	6000	4.8	270.6326	$5.9255\times {10}^{-8}$	7.3	204.2898	$1.1762\times {10}^{-7}$

Example 2. 

Consider an example of the WCP (1), where

$$G(x,s,y)=\left(\begin{array}{c}Bx+C^{T}y-s+d\\ C(x-t)\end{array}\right),$$

with $B=\mathrm{diag}\left(b\right)$ where $b\in R^n$ is generated uniformly from $[0,1]$, $C\in R^{m\times n}$ whose entries are produced from the standard normal distribution randomly. $d,t\in R^n$ and $w\in R^n$ are all generated randomly from $[0,1]$.

We also generated 10 trials for each case. The initial points $x^0$, $s^0$ and $y^0$ are all chosen as ${(1,0,\dots ,0)}^T$ with relevant dimensions. The test results are shown in Table 4, which also indicates that Algorithm 1 is more stable and efficient than SNM_Z.

Table 4. Numerical comparison results for a WCP.

m	n	Algorithm 1			SNM_Z
		AIT	ATime	AERO	AIT	ATime	AERO
500	1000	4.4	1.8729	$1.7379\times {10}^{-7}$	6.7	2.4799	$2.4252\times {10}^{-8}$
1000	2000	4.6	13.3430	$7.0375\times {10}^{-9}$	6.9	17.1639	$1.1370\times {10}^{-7}$
1500	3000	5.0	44.8153	$1.2673\times {10}^{-7}$	7.4	61.5095	$4.7525\times {10}^{-8}$
2000	4000	5.2	120.9742	$4.0044\times {10}^{-8}$	6.8	114.9068	$1.7140\times {10}^{-8}$
2500	5000	5.3	220.2452	$3.6690\times {10}^{-8}$	7.3	217.9106	$2.0620\times {10}^{-8}$
3000	6000	5.2	371.6272	$2.2190\times {10}^{-9}$	6.6	404.5870	$1.1662\times {10}^{-7}$

6. Conclusions

The two-step Newton method, known for its efficiency in solving nonlinear equations, is adopted to solve the WCP in this paper. A novel two-step Newton method designed specifically for solving the WCP is proposed. The best property of this method is its consistent Jacobian matrix in each iteration, resulting in an improved convergence rate without additional computational expenses. To guarantee the global convergence, a new derivative-free line search rule is introduced. With appropriate conditions and parameter selection, the algorithm achieves cubic local convergence. Numerical results show that the two-step Newton method significantly improves the computational efficiency without increasing the computational cost compared to the general smoothing Newton method.