A Study on Fixed-Point Techniques under the α-ϝ-Convex Contraction with an Application
Abstract
1. Introduction and Preliminaries
- (Γ1)
- , for all ;
- (Γ2)
- andimply, for all.
- and if and only if .
- , for all .
- , for all .
- (ϝ1)
- ϝ is strictly nondecreasing, i.e., for allsuch that;
- (ϝ2)
- For each sequence, ;
- (ϝ3)
- There existssuch that.
- (i)
- ;
- (ii)
- ;
- (iii)
- ;
- (iv)
- .
- (i)
- is the unique fixed point of Γ;
- (ii)
- For all, the sequenceis convergent to.
2. Main Results
- (i)
- There existsandsuch that for all,where
- (ii)
- Γ is α-admissible;
- (iii)
- There exists such that .
- (i)
- There existsandsuch that for all,where
- (ii)
- Γ is α-admissible;
- (iii)
- There existssuch that;
- (iv)
- Γ is continuous or orbitally continuous on Λ.
- (i)
- ,where;
- (ii)
- Γ is α-admissible;
- (iii)
- There existssuch that;
- (iv)
- Γ is continuous or orbitally continuous on Λ.
- (i)
- ,wheresuch that;
- (ii)
- Γ is α-admissible;
- (iii)
- There existssuch that;
- (iv)
- Γ is continuous or orbitally continuous on Λ.
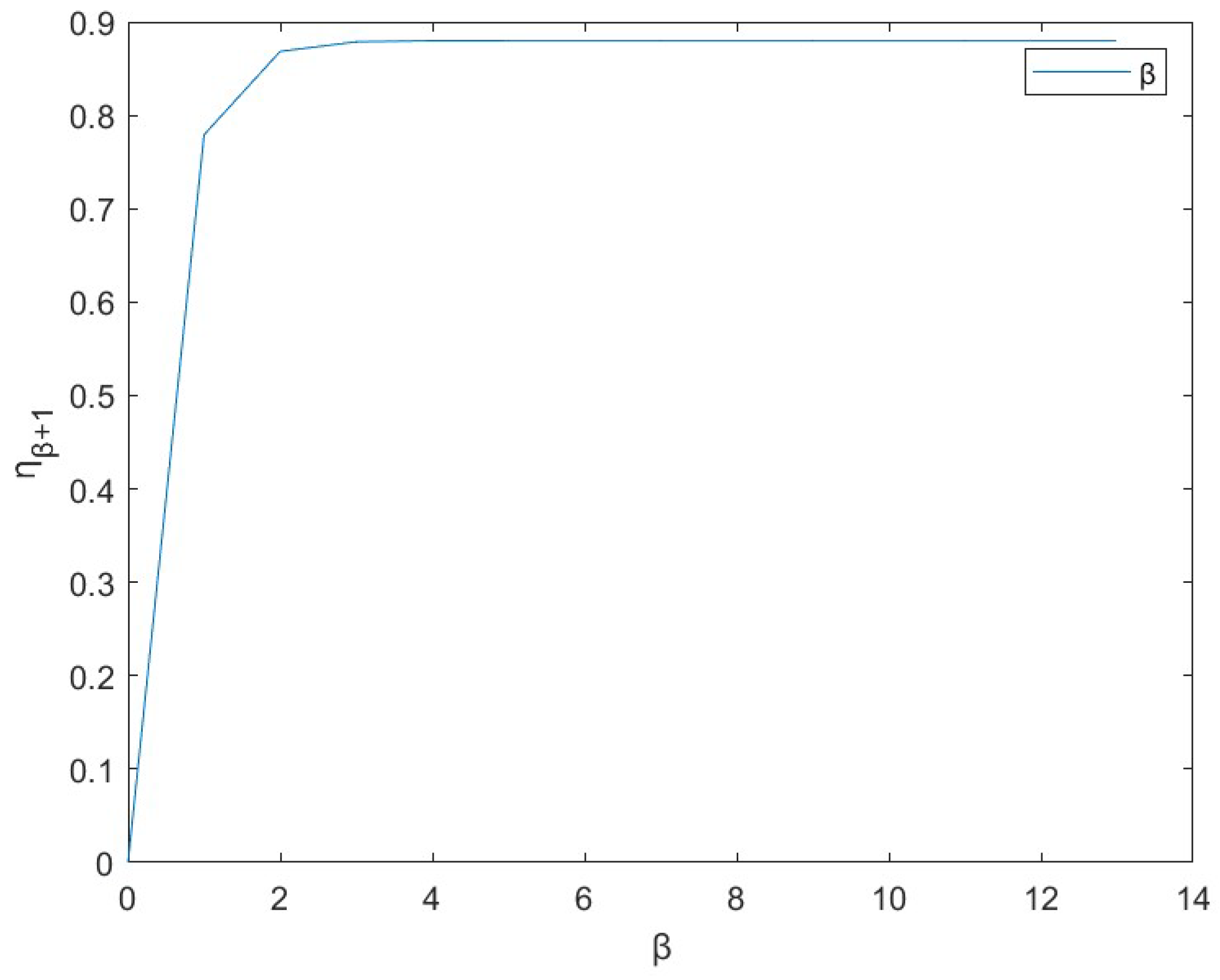
3. Application
- for all;
- For allwithandand using (18), we obtain
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Čirić, L.B. Generalized contractions and fixed point theorems. Publ. Inst. Math. 1971, 12, 19–26. [Google Scholar]
- Istrătescu, V.I. Some fixed point theorems for convex contraction mappings and convex non expansive mappings (I). Liberta Math. 1981, 1, 151–163. [Google Scholar]
- Alghamdi, M.A.; Alnafei, S.H.; Radenovic, S.; Shahzad, N. Fixed point theorems for convex contraction mappings on cone metric spaces. Math. Comput. Model. 2011, 54, 2020–2026. [Google Scholar] [CrossRef]
- Miculescu, R.; Mihail, A. A generalization of Istrătescu’s fixed point theorem for convex contractions. arXiv 2015. [Google Scholar] [CrossRef]
- Miculescu, R.; Mihail, A. A generalization of Matkowski’s fixed point theorem and Istrăţescu’s fixed point theorem concerning convex contractions. Fixed Point Theory Appl. 2017, 19, 1525–1533. [Google Scholar] [CrossRef]
- Latif, A.; Sintunavarat, W.; Ninsri, A. Approximate fixed point theorems for partial generalized convex contraction mappings in α-complete metric spaces. Taiwanese J. Math. 2015, 19, 315–333. [Google Scholar] [CrossRef]
- Latif, A.; Al Subaie, R.F.; Alansari, M.O. Fixed points of generalized multi-valued contractive mappings in metric type spaces. J. Nonlinear Var. Anal. 2022, 6, 123–138. [Google Scholar]
- Miandaragh, M.A.; Postolache, M.; Rezapour, S. Some approximate fixed point results for generalized α-contractive mapping. Politehn. Univ. Bucharest Sci. Bull. Ser. A Appl. Math. Phys. 2013, 75, 3–10. [Google Scholar]
- Miandaragh, M.A.; Postolache, M.; Rezapour, S. Approximate fixed points of generalized convex contractions. Fixed Point Theory Appl. 2013, 2013, 255. [Google Scholar] [CrossRef]
- Wardowski, D. Fixed points of a new type of contractive mappings in complete metric spaces. Fixed Point Theory Appl. 2012, 2012, 94. [Google Scholar] [CrossRef]
- Samet, B.; Vetro, C.; Vetro, P. Fixed point theorems for (α, ψ)-contractive type mappings. Nonlinear Anal. 2012, 75, 2154–2165. [Google Scholar] [CrossRef]
- Asem, V.; Singh, Y.M. On Meir-Keeler proximal contraction for non-self mappings. J. Adv. Math. Stud. 2022, 15, 250–261. [Google Scholar]
- Karapinar, E.; Kumam, P.; Salimi, P. On α-ψ- Meir-Keeler contractive mappings. Fixed Point Theory Appl. 2013, 2013, 94. [Google Scholar] [CrossRef]
- Karapinar, E. α-Geraghty contraction type mappings and some related fixed point results. Filomat 2014, 28, 37–48. [Google Scholar] [CrossRef]
- Khan, M.S.; Singh, Y.M.; Maniu, G.; Postolache, M. On (α, p)-convex contraction and asymptotic regularity. J. Math. Comput. Sci. 2018, 18, 132–145. [Google Scholar] [CrossRef]
- Yildirim, I. Fixed point results for F-Hardy-Rogers contractions via Mann’s iteration process in complete convex b-metric spaces. Sahand Commun. Math. Anal. 2022, 19, 15–32. [Google Scholar]
- Singh, Y.M.; Khan, M.S.; Kang, S.M. F-convex contraction via admissible mapping and related fixed point theorems with an application. Mathematics 2018, 6, 105. [Google Scholar] [CrossRef]
- Eke, K.S. Some approximate fixed point theorems for partial Chatterjea convex contractive maps in metric spaces. Int. J. Math. Sci. J. Optim. Theory Appl. 2022, 8, 1–8. [Google Scholar]
- Geleta, K.W.; Tola, K.K.; Teweldemedhin, S.G. Alpha-F-convex contraction mappings in b-metric space and a related fixed point theorem. J. Function Spaces 2021, 2021, 5720558. [Google Scholar] [CrossRef]
- Alecsa, C.D. Some fixed point results regarding convex contractions of Presi’c type. J. Fixed Point Theory Appl. 2018, 20, 7. [Google Scholar] [CrossRef]
- Chen, L.; Li, C.; Kaczmarek, R.; Zhao, Y. Several Fixed Point Theorems in Convex b-Metric Spaces and Applications. Mathematics 2020, 8, 2422. [Google Scholar] [CrossRef]
- Karaca, N.; Yildirim, I. Fixed point theorem for Reich contraction mapping in convex b-metric spaces. Aligarh Bull. Math. 2021, 40, 29–39. [Google Scholar]
- Arul Joseph, G.; Gunaseelan, M.; Lee, J.R.; Park, C. Solving a nonlinear integral equation via orthogonal metric space. AIMS Math. 2022, 7, 1198–1210. [Google Scholar]
- Arul Joseph, G.; Gunasekaran, N.; Absar, U.H.; Gunaseelan, M.; Imran, A.B.; Kamsing, N. Common Fixed-Points Technique for the Existence of a Solution to Fractional Integro-Differential Equations via Orthogonal Branciari Metric Spaces. Symmetry 2022, 14, 1859. [Google Scholar]
- Haokip, N. Convergence of an iteration scheme in convex metric spaces. Proyecciones J. Math. 2022, 41, 777–790. [Google Scholar] [CrossRef]
- Khan, M.S.; Menaka, M.; Jacob, G.K.; Marudai, M. Proximity points for cyclic 2-convex contraction mappings. Nonlinear Functional Anal. Appl. 2020, 25, 1–12. [Google Scholar]
- Gunasekaran, N.; Arul Joseph, G.; Gunaseelan, M.; Ozgur, E. Solving integral equations via admissible contraction mappings. Filomat 2022, 36, 4947–4961. [Google Scholar]
- Khantwala, D.; Anejab, S.; Gairolac, U. A fixed point theorem for (ϕ, ψ)-convex contraction in metric spaces. Adv. Theory Nonlinear Anal. Its Appl. 2021, 5, 240–245. [Google Scholar]
- Mitrovi’c, Z.D.; Aydi, H.; Mlaiki, N.; Gardaševi’c-Filipovi’c, M.; Kuki’c, K.; Radenovi’c, S.; De la Sen, M. Some new observations and results for convex contractions of Istrătescu’s type. Symmetry 2019, 11, 1457. [Google Scholar] [CrossRef]
- Faraji, H.; Radenovi’c, S. Some fixed point results for convex contraction mappings on F-metric spaces. Ser. Math. Inform. 2020, 35, 939–948. [Google Scholar] [CrossRef]
- Nallaselli, G.; Gnanaprakasam, A.J.; Mani, G.; Mitrović, Z.D.; Aloqaily, A.; Mlaiki, N. Integral equation via fixed point theorems on a new type of convex contraction in b-metric and 2-metric spaces. Mathematics 2023, 11, 344. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, Z.; Wen, C.F.; Yao, J.C.; Zeng, S. Existence of solutions for a class of noncoercive variational-hemivariational inequalities arising in contact problems. Appl. Math. Optim. 2021, 84, 2037–2059. [Google Scholar] [CrossRef]
- Liu, Y.; Migórski, S.; Nguyen, V.T.; Zeng, S. Existence and convergence results for an elastic frictional contact problem with nonmonotone subdifferential boundary conditions. Acta Math. Sci. 2021, 41, 1151–1168. [Google Scholar] [CrossRef]
- Zeng, S.; Migórski, S.; Khan, A.A. Nonlinear quasi-hemivariational inequalities: Existence and optimal control. SIAM J. Control Optim. 2021, 59, 1246–1274. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nallaselli, G.; Gnanaprakasam, A.J.; Mani, G.; Ege, O.; Santina, D.; Mlaiki, N. A Study on Fixed-Point Techniques under the α-ϝ-Convex Contraction with an Application. Axioms 2023, 12, 139. https://doi.org/10.3390/axioms12020139
Nallaselli G, Gnanaprakasam AJ, Mani G, Ege O, Santina D, Mlaiki N. A Study on Fixed-Point Techniques under the α-ϝ-Convex Contraction with an Application. Axioms. 2023; 12(2):139. https://doi.org/10.3390/axioms12020139
Chicago/Turabian StyleNallaselli, Gunasekaran, Arul Joseph Gnanaprakasam, Gunaseelan Mani, Ozgur Ege, Dania Santina, and Nabil Mlaiki. 2023. "A Study on Fixed-Point Techniques under the α-ϝ-Convex Contraction with an Application" Axioms 12, no. 2: 139. https://doi.org/10.3390/axioms12020139
APA StyleNallaselli, G., Gnanaprakasam, A. J., Mani, G., Ege, O., Santina, D., & Mlaiki, N. (2023). A Study on Fixed-Point Techniques under the α-ϝ-Convex Contraction with an Application. Axioms, 12(2), 139. https://doi.org/10.3390/axioms12020139










