Fixed-Point Convergence of Multi-Valued Non-Expansive Mappings with Applications

Abstract

This paper is dedicated to the advancement of fixed-point results for multi-valued asymptotically non-expansive maps regarding convergence criteria in complete uniformly convex hyperbolic metric spaces that are endowed with a graph. The famous fixed-point theorems of Goebel and Kirk, Khamsi and Khan, along with other recent results in the literature can be obtained as corollaries of these main results. A nice graph and an interesting example are also provided in support of the hypothesis of the main results.

1. Introduction

In 1964, Edelstein [1] proposed the existence of a fixed point (FP) in a non-expansive mapping T with a non-empty T-closure. The basic concept of asymptotically non-expansive mappings was first introduced and thoroughly explained by Goebel and Kirk [2]. After this, many authors proved various FP results by using a class of asymptotically non-expansive mappings. Some of these contributions are listed here:

• Nanjaras and Panyanak [3] established the principle of demiclosedness for single-valued asymptotically non-expansive mappings in CAT(0) spaces.
• Alber et al. [4] initiated the idea of total asymptotically non-expansive mappings and approximated the FP for these mappings.
• Strong and weak convergence for asymptotically non-expansive mappings have been established in hyperbolic spaces; for example, see [5,6].

In 1969, Nadler [7] presented an FP result for multi-valued contractions. This article brought a revolution in the area of FP theory, as well as applications in multiple disciplines. (For more details, readers are referred to [8,9].) Khan et al. [10] evaluated the common FPs for the two multi-valued non-expansive mappings in hyperbolic spaces by using a unit-step implicit algorithm. Zhang et al. [11] proved the strong convergence result for multi-valued total Bregmann quasi-asymptotically non-expansive mappings. In [12], Khamsi and Khan generalized the results of [2] by introducing the class of multi-valued asymptotically non-expansive mappings.

In 2008, Jachymski [13] presented an innovative generalization of the Banach contraction principle by merging the notions of FP theory with graph theory. Furthermore, Beg et al. [14] utilized the idea of Jachymski toward the general class of multi-valued contractions. In 2015, Alfuraidan and Khamsi [15] proved an existence result for the newly introduced structure of a monotone, which increased the G-non-expansive mappings in the setting of hyperbolic metric spaces. In [16], Panyanak and Suantai provided an extension of Wangkeeree and Preechasilp’s result [17] by utilizing multi-valued non-expansive mappings. In [18], Anakkamatee and Tongnoi extended Browder’s convergence result for the collection of $\mathfrak{G}$-non-expansive mappings in $CAT\left(0\right)$ spaces. In [19], Chifu et al. applied an FP theorem for an appropriate operator on the Cartesian product of a b-metric space in the presence of a graph. Afterward, numerous FP results for generalized metric spaces have been equipped with graphs and have flourished (see, e.g., [20,21,22,23,24]).

In this article, inspired by the abovementioned developments, some strong convergence theorems for the class of asymptotically $\mathfrak{G}$-non-expansive mappings in the setting of uniformly convex hyperbolic metric space are presented. These results will provide the generalizations of the consequences of Goebel and Kirk [2], Khamsi and Khan [12], and many others.

2. Preliminaries

The theory of multi-valued mappings is a compelling fusion of analysis, topology, and geometry. It has been receiving an degree of important attention by researchers working in a variety of fields in the mathematical sciences. All mappings that are single-valued in traditional analysis are inherently multi-valued, whereas many problems in applied mathematics are multi-valued in nature. For example, the problems of stability and control theory can be solved with the aid of FP methods for multi-valued mappings. The inverse of a single-valued map is the first naturally occurring instance of a set-valued map. The importance of multi-valued mappings can be judged by a beginner when they look at the inverse of basic trigonometric functions (for example, ${sin}^{-1}x$, ${cos}^{-1}x$, etc., in a given domain of 0 to $2\pi$ are multi-valued mappings).

In this article, we consider a useful metric known as the Hausdorff–Pompeiu distance function on the collection of non-empty bounded and closed subsets of a metric space to generalize some FP findings in a traditional single-valued F.P theory.

Consider two non-empty sets X and Y. Suppose we have a function T that maps elements from X to a collection of subsets in Y. For any x in X, $T\left(x\right)$ is a set contained in Y, and this is called the image of x under T. If a point x of X is an element of $Tx$, it is referred to as an FP of T. In the following, some examples of multi-valued mappings have been provided with regard to the existence and uniqueness of their FPs.

Let us start with an illustration of the usual problems involving multi-valued mappings. For the two sets X and Y, a multi-valued mapping is a set valued function from X to $2^Y$ and the power set of Y. Consider a function $T:{\mathbb{R}}_{+}\to 2^{\mathbb{R}}$, such that $Tx=\{\pm y:y\mathrm{is}\mathrm{a}\mathrm{square}\mathrm{root}\mathrm{of}x\}$. Then, T is a multi-valued mapping with

$$\begin{array}{c}\hfill T\left(0\right)=\left\{0\right\}\mathrm{and}T\left(1\right)=\left\{-1,1\right\}.\end{array}$$

Here, it should be noted that $1\in T\left(1\right)$ and $0\in T\left(0\right)$, that is T, have FPs.

Now, for $X=[1,2]$ and $Y=[1,4]$, suppose $F:X\to 2^Y$ is a multi-valued map defined as

$$\begin{array}{c}\hfill F\left(x\right)=\{y\in [1,4];x^2\le y\le 2x\}.\end{array}$$

(1)

Then, F has a unique FP $x=1$, that is, $1\in F\left(1\right)$.

Suppose that $X=[-1,1]$ and $\mathcal{G}:X\to 2^X$ is defined as

$$\begin{array}{c}\hfill \mathcal{G}=\left\{\begin{array}{cc}\left[x^2-\sqrt{x},\sqrt{x}-x^2\right],\hfill & x\in [0,1];\hfill \\ \left[x^2-\sqrt{-x},\sqrt{-x}-x^2\right],\hfill & x\in [-1,0).\hfill \end{array}\right.\end{array}$$

(2)

Then, $\mathcal{G}$ has infinitely many FPs $x\in \mathcal{G}$ for all $x\in \left[\frac{-275}{1250},\frac{275}{1250}\right]$.

Now, if $X=[-1,1]$ and the multi-valued map $H:X\to 2^X$ are defined as

$$H\left(x\right)=\left\{\begin{array}{cc}[x^2,\sqrt{x}]\bigcup [-\sqrt{x},-x^2],\hfill & x\in [0,1];\hfill \\ \left[x^2,\sqrt{-x}\right]\bigcup [-\sqrt{-x},-x^2],\hfill & x\in [-1,0),\hfill \end{array}\right.$$

(3)

then the whole domain of H form the set of FPs.

The graphs of the functions defined by (1)–(3) are depicted below as Figure 1, Figure 2 and Figure 3, respectively. It is evident that these graphs exhibit multi-valued behavior and possess FPs.

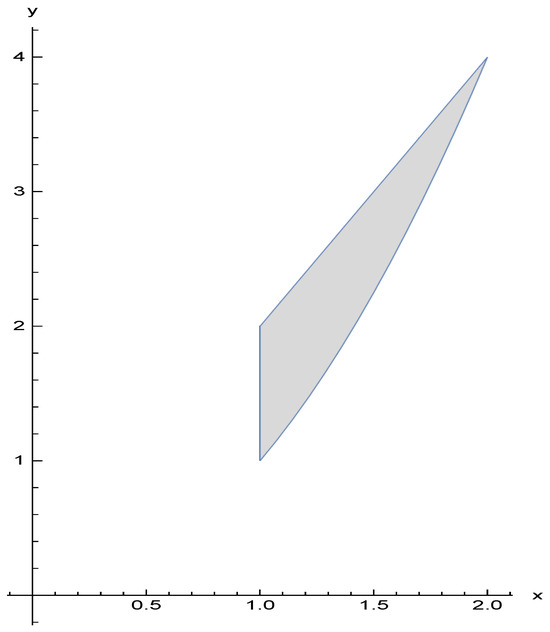
Figure 1. Graphical representation of the unique FPs of the mapping, as defined by (1).

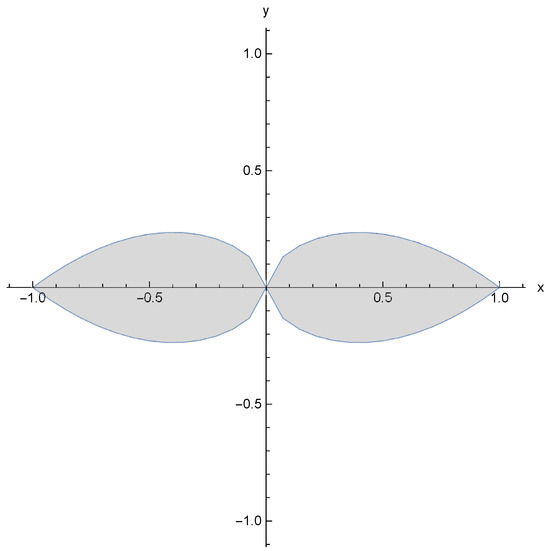
Figure 2. Visualization of the numerous FPs of the mapping, as defined by (2).

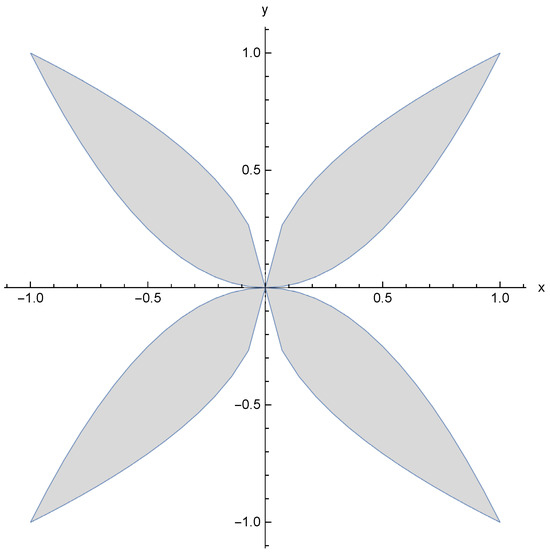
Figure 3. Illustration of the infinitely many FPs of the mapping, as defined by (3).

Consider a metric space $(X,\varrho )$, and let A be any non-empty subset of X. We symbolize a couple of collections of subsets as follows:

• $N\left(A\right)$: all of the non-empty subsets of A;
• $CK\left(A\right)$: all of the non-empty, convex, and compact subsets of A;
• $C\left(A\right)$: all of the non-empty, closed subsets of A;
• $CB\left(A\right)$: all of the non-empty, closed, and bounded subsets of A;
• $CC\left(A\right)$: all of the non-empty, closed, and convex subsets of A;
• $CCB\left(A\right)$: all of the non-empty, closed, convex, and bounded subsets of A.

Definition 1.

Let $A\in N\left(X\right).$ A self map g on A is named a contraction if a constant $k\in [0,1)$ exists such that we have the following:

$$\varrho \left(g\right(x),g(y\left)\right)\le k\varrho (x,y),\forall x,y\in A.$$

If the above inequality is accurate for $k=1$, then the map g is called non-expansive. An FP of g is an element x in A, for which $x=g\left(x\right).$

The generalized multi-valued Hausdorff distance $H:CB\left(X\right)\times CB\left(X\right)\to \mathbb{R}$ is given as follows:

$$\begin{array}{c}\hfill H(A,B)=max\left\{\underset{b\in B}{sup}\varrho (b,A),\underset{a\in A}{sup}\varrho (a,B)\right\},\end{array}$$

where $\varrho (x,A)={inf}_{a\in A}\varrho (x,a)$ and $A,B\in CB\left(X\right)$.

In 1988, Assad [25] initiated the notions of an $\alpha$-general orbit and an $\alpha$-starred general orbit. These concepts were further generalized by Rus [26] in terms of a generalized orbit. Afterward, many authors utilized this idea in subsequent directions (see, for example, [8,27,28]).

Definition 2.

Let $C\in N\left(X\right)$ and $T:C\to N\left(X\right)$ be a multi-valued mapping. For $x\in X$, a generalized orbit of x is the sequence ${\left\{x_n\right\}}_{n\in \mathbb{N}}$ that is generated from $x_0=x$ by $x_{n+1}\in T\left(x_n\right)$ for any nonnegative integer n. Evidently, the generalized orbits generated from x may differ in values for a given $x\in X$.

Remark 1.

It was observed that, for a single-valued mapping T, the generalized orbit coincides with the conventional definition of an orbit.

The class of asymptotically non-expansive mappings has been playing a vital part in the advancement of FP theory due to it being a generalized version of non-expansive mappings ([6,9], and many others). In 2017, Khamsi and Khan [12] extended the idea of asymptotically non-expansive mappings for multi-valued cases. The authors proposed the solutions for some problems that are related to these mappings in the context of [8]. The following definition and theorems have been taken from [12]:

Definition 3.

We say that a mapping $T:X\to N\left(X\right)$ is multi-valued asymptotically non-expansive if there exists a sequence of positive real numbers $k_n$ such that ${lim}_{n\to \infty }{k}_n=1$. In addition, for any generalized orbit $x_n$ of x and for any $x,y\in X$, there exists a generalized orbit $y_n$ of y such that

$$\begin{array}{c}\hfill \varrho (x_{n+h},y_h)\le k_h\varrho (x_n,y),\end{array}$$

where $n,h\in \mathbb{N}$.

In simpler terms, this means that the mapping T does not increase the distances between points in X as they are iterated along their generalized orbits, and the rate at which distances increase is controlled by the sequence $k_n$.

Convexity is an important concept in mathematics and optimization theory that characterizes the curved form of certain geometric shapes or functions. A set or function is said to be convex if every point on a line segment joining two points in the set or on the graph of the function lies within the set or above the graph. The concept of convexity finds broad applications in different areas, including economics, optimization, and physics. For example, convex optimization problems arise in many engineering and financial applications, and convex functions are used to model the behavior of various physical systems.

For the introduction of convex structure in metric spaces, Menger [29] considered the concept of metric segments as a vital component. The element $w:=\chi x\oplus (1-\chi )y$ in the metric segment $[x,y]$ was defined in terms of

$$\varrho (x,w)=(1-\chi )\varrho (x,y)\mathrm{and}\varrho (y,w)=\chi \varrho (x,y),$$

where some $\chi \in [0,1]$ are unique. A metric space along with these groups of segments is understood as a convex metric space. If the subsequent axiom holds

$$\varrho (\chi a\oplus (1-\chi )x,\chi b\oplus (1-\chi \left)y\right)\le \chi \varrho (a,b)+(1-\chi )\varrho (x,y)$$

for all $a,b,x,y\in X$, and $\chi \in [0,1]$, then the space is termed a hyperbolic metric space [30].

Definition 4.

In a hyperbolic metric space $(X,\varrho )$, the modulus of uniform convexity is defined as per the following:

$${\delta }_X(\rho ,\wp )=inf\left\{1-\frac{1}{\rho }\varrho \left(\frac{1}{2}𝚤\oplus \frac{1}{2}𝚥,\ell \right);\varrho (𝚤,\ell )\le \rho ,\varrho (𝚥,\ell )\le \rho ,\varrho (𝚤,𝚥)\ge \rho \wp \right\},$$

which applies for any $\rho >0,\wp >0$ and $𝚤,𝚥,\ell \in X$.

The space is understood as uniformly convex provided that ${\delta }_X(\rho ,\wp )>0$, whenever $\rho >0$ and $\wp >0$.

Throughout this article, our underlying space is supposed to be a complete uniformly convex hyperbolic metric space, which is abbreviated as CUCHMS.

Theorem 1

([12]). For CUCHMS X, the following assertions hold.

1. 

X has the property $\left(R\right)$, i.e., any decreasing sequence of non-empty, convex, bounded, and closed sets that have a non-empty intersection.

2. 

If $Z\in CC\left(X\right),$ then any type function $\eta :X\to [0,\infty )$ attains a minimal point u in Z that is unique, thereby satisfying

$$\begin{array}{c}\hfill \eta \left(u\right)=inf\left\{\eta \right(x);x\in Z\}.\end{array}$$

Furthermore, any minimizing sequence $\left\{u_m\right\}$ in Z is convergent, that is, ${lim}_{m\to \infty }\eta \left(u_m\right)=\eta \left(u\right)$.

3. 

Let $\Omega >0$ and $z\in X$. Suppose $\left\{x_m\right\}$ and $\left\{y_m\right\}$ are any two arbitrary sequences in X satisfying

$$\underset{m\to \infty }{lim\; sup}\varrho (x_m,z)\le \Omega ,\underset{m\to \infty }{lim\; sup}\varrho (y_m,z)\le \Omega ,$$

and

$$\begin{array}{c}\hfill \underset{m\to \infty }{lim}\varrho (\alpha x_m\oplus (1-\alpha )y_m,z)=\Omega ,\end{array}$$

then ${lim}_{m\to \infty }\varrho (x_m,y_m)=0$.

Definition 5.

Consider a multi-valued mapping $T:C\to N\left(C\right)$ and a sequence $\left\{x_n\right\}$ in C. Then, T is called H-continuous if whenever $\left\{x_n\right\}$ converges to x in C, we have

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\varrho (a_n,T\left(x\right))=0,\end{array}$$

for any sequence $\left\{a_n\right\}$, where $a_n$ belongs to the set $T\left(x_n\right)$, for all $n\in \mathbb{N}$.

Remark 2.

1. 

In the case of a compact valued operator T, H-continuity coincides with the lower and upper semi-continuity.

2. 

An asymptotically non-expansive map $T:C\to N\left(C\right)$ always fulfills the criterion of H-continuity.

Theorem 2.

Let $A\in CCB\left(X\right).$ Then, an asymptotically non-expansive map $T:A\to C\left(A\right)$ attains an FP.

According to [13], the following concepts are defined with respect to CUCHMS.

Let $\mathfrak{D}$ symbolize the diagonal of the Cartesian product $X\times X$. Suppose that $\mathfrak{G}=\left(W\right(\mathfrak{G}),\mathcal{E}(\mathfrak{G}\left)\right)$ characterizes a directed graph (whereby $W\left(\mathfrak{G}\right)$ represents vertices, and $\mathcal{E}\left(\mathfrak{G}\right)$ represents edges), which includes all the loops when assuming that $\mathfrak{G}$ does not have any parallel edges, and where the symbol $\tilde{\mathfrak{G}}$ designates the undirected graph associated with $\mathfrak{G}$.

Definition 6.

A self map $\mathfrak{f}$ on X is known as the Banach $\mathfrak{G}$-contraction if it fulfills the following axioms

1. 

The edges of $\mathfrak{G}$ under $\mathfrak{f}$ are preserved, that is, for all elements $\nu ,\omega$ in X, such that

$$\left(\mathfrak{f}\nu ,\mathfrak{f}\omega \right)\in \mathcal{E}\left(\mathfrak{G}\right)whenever\left(\nu ,\omega \right)\in \mathcal{E}\left(\mathfrak{G}\right).$$

2. 

The corresponding weights of edges of $\mathfrak{G}$ under $\mathfrak{f}$ decrease in a subsequent manner, that is, an element $k\in (0,1)$ exists by satisfying

$$\varrho (\mathfrak{f}\nu ,\mathfrak{f}\omega )\le k\varrho (\nu ,\omega )whenever(\nu ,\omega )\in \mathcal{E}\left(\mathfrak{G}\right).$$

3. Convergence Results for Multi-Valued $\mathfrak{G}$-Asymptotically Non-Expansive Mappings

In this section, we define the notion of multi-valued $\mathfrak{G}$-asymptotically non-expansive mappings by combining the concept of asymptotically non-expansive mappings with a graph. We also list two main conditions (namely $\left(\mathcal{A}\right)$ and $\left(\mathcal{B}\right)$), which will be utilized further. In 2017, an extension of Goebel and Kirk’s FP theorem for multi-valued asymptotically non-expansive mappings has been proposed by Khamsi and Khan [12]. Inspired by this work, we are also extending this classical result for the class of multi-valued $\mathfrak{G}$-asymptotically non-expansive mappings in the setting of CUCHMS.

Definition 7

(Multi-valued $\mathfrak{G}$-Asymptotically Non-expansive Mapping). Let $\mathfrak{G}$ represent a directed graph on X. Then, a mapping $\mathcal{P}:X\to C\left(X\right)$ is said to be a multi-valued $\mathfrak{G}$-asymptotically non-expansive mapping if the following conditions hold:

1. 

There exists $\left\{b_m\right\}$ with ${lim}_{m\to \infty }{b}_m=1$;

2. 

$\mathcal{P}$ preserves the edges, that is,

$$\begin{array}{c}\hfill (q,r)\in \mathcal{E}\left(\mathfrak{G}\right)implies(\acute{q},\acute{r})\in \mathcal{E}\left(\mathfrak{G}\right),\end{array}$$

where $\acute{q}$ is an element of $\mathcal{P}\left(q\right)$ and $\acute{r}$ belongs to $\mathcal{P}\left(r\right).$

3. 

Let q and r be any two elements of X. Then, for any generalized orbit $\left\{q_m\right\}$ of q, there exists a generalized orbit $\left\{r_m\right\}$ of r such that $(q_m,r)\in \mathcal{E}\left(\mathfrak{G}\right),$ and

$$\begin{array}{c}\hfill \varrho (q_{m+h},r_h)\le b_h\varrho (q_m,r),form,h\in \mathbb{N}.\end{array}$$

Condition $(\mathcal{A}$). Let $\mathfrak{G}$ represent a directed graph on X. Let $Z\in CC\left(X\right)$ and $\left\{q_m\right\}$ be a generalized orbit of q in X. Then, the type function

$$\begin{array}{c}\hfill \eta \left(q\right)=\underset{m\to \infty }{lim\; sup}\varrho (q_m,q)\end{array}$$

attains a minimum point z in Z, which is unique, that is, for any convergent minimizing sequence $\left\{z_m\right\}$ in Z, where

$$\begin{array}{c}\hfill \underset{m\to \infty }{lim}\eta \left(z_m\right)=\eta \left(z\right).\end{array}$$

Condition ($\mathcal{B}$). Let $\mathfrak{G}$ represent a directed graph on X and $Z\in CCB\left(X\right)$. Let $q\in Z$ and $\left\{q_m\right\}$ be the generalized orbit of q. Then, for $r=\alpha q\oplus (1-\alpha )q_1$, we have

(i) 

$(q,r)\in \mathcal{E}\left(\mathfrak{G}\right)$,

(ii) 

$(q_m,r)\in \mathcal{E}\left(\mathfrak{G}\right)forallm\in \mathbb{N}$.

Theorem 3.

Let $\mathfrak{G}$ be the directed graph on X, and let $Z\in CCB\left(X\right)$, such that $W\left(\mathfrak{G}\right)\subset Z$. Let $\mathcal{P}:Z\to C\left(Z\right)$, and, for any $q\in Z,$ let $\left\{q_m\right\}$ be a generalized orbit of q that satisfies Condition ($\mathcal{A}$), such that $(q_m,q)\in \mathcal{E}\left(\mathfrak{G}\right)$. If $\mathcal{P}$ is an H-continuous $\mathfrak{G}$-asymptotically non-expansive mapping, then $\mathcal{P}$ has an FP.

Proof. 

Suppose that $q\in Z$ and $\left\{q_m\right\}$ is a generalized orbit of $q.$ The boundedness of Z ensures the boundedness of $\left\{q_m\right\}$. Consider a type function $\eta$ produced by $\left\{q_m\right\}$, that is, $\eta \left(q\right)={lim\; sup}_{m\to \infty }\varrho (q_m,q)$. By Condition $\left(\mathcal{A}\right)$, $\eta$ has a unique minimum point $\gamma$ in Z. Let $\gamma =\alpha q\oplus (1-\alpha )q_1$. Then, by Condition $\left(\mathcal{B}\right)$, we have $(q_m,\gamma )\in \mathcal{E}\left(\mathfrak{G}\right)$. Since $\mathcal{P}$ is $\mathfrak{G}$-asymptotically non-expansive, one has

$$\begin{array}{c}\hfill \varrho \left(q_{m+h},{\gamma }_h\right)\le b_h\varrho (q_m,\gamma ),m,h\in \mathbb{N}.\end{array}$$

This ensures that $\eta \left({\gamma }_h\right)\le b_h\eta \left(\gamma \right)$ is for all $h\in \mathbb{N}$. Since ${lim}_{m\to \infty }{b}_m=1$, we achieve that $\left\{{\gamma }_m\right\}$ is a minimizing sequence for $\eta$ as well. Again, by utilizing Condition $\left(\mathcal{A}\right)$, we obtain that $\left\{{\gamma }_m\right\}$ is convergent to $\gamma$. Then, the H-continuity of $\mathcal{P}$ and ${\gamma }_{m+1}\in \mathcal{P}\left({\gamma }_m\right)$ for any $m\in \mathbb{N}$ implies the following:

$$\begin{array}{c}\hfill \underset{m\to \infty }{lim}\varrho ({\gamma }_{m+1},\mathcal{P}\left(\gamma \right))=0.\end{array}$$

Since $\mathcal{P}\left(\gamma \right)$ is closed and $\left\{{\gamma }_m\right\}$ is convergent toward $\gamma$, we determine that z exists in $\mathcal{P}\left(\gamma \right)$, thus indicating that $\gamma$ is the FP of $\mathcal{P}$. □

Before stating the next result, we will form a sequence with the help of generalized orbits and Condition $\left(\mathcal{B}\right)$. This formation will be utilized in the upcoming result.

Let $Z\in CCB\left(X\right)$, $\mathcal{P}:Z\to C\left(Z\right)$ be a $\mathfrak{G}$-asymptotically non-expansive mapping with $q_1\in Z$ and $\alpha \in (0,1)$. Suppose $\left\{q_m^1\right\}$ is a generalized orbit of $q_1$.

Set $q_2=\alpha q_1\oplus (1-\alpha )q_1^1$, then, by Condition $\left(\mathcal{B}\right)$, we have

(i)

$(q_2,q_1)\in \mathcal{E}\left(\mathfrak{G}\right)$;

(ii)

$(q_m^1,q_2)\in \mathcal{E}\left(\mathfrak{G}\right)$.

Assume that $\left\{q_m^2\right\}$ is the generalized orbit of $q_2$. Since $\mathcal{P}$ is a $\mathfrak{G}$-asymptotically non-expansive mapping, we therefore have

$$\varrho (q_{m+h}^1,q_h^2)\le b_h\varrho (q_m^1,q_2),\mathrm{for}\mathrm{all}m\in \mathbb{N}.$$

Set $q_3=\alpha q_2\oplus (1-\alpha )q_1^2$. Then, again by Condition $\left(\mathcal{B}\right)$, we obtain

(i)

$(q_2,q_3)\in \mathcal{E}\left(\mathfrak{G}\right);$

(ii)

$(q_m^2,q_3)\in \mathcal{E}\left(\mathfrak{G}\right);$

and also

$$\varrho (q_{m+h}^2,q_h^3)\le b_h\varrho (q_m^2,q_3).$$

By repeating the above steps, we create a sequence $q_m$ in Z and respectively $\left\{q_m^t\right\}$ for any $t\ge 1$ as the generalized orbit of $q_m,$ thereby satisfying

$$\varrho (q_{m+h}^{t-1},q_h^t)\le b_h\varrho (q_m^{t-1},q_t)$$

and

$$q_{t+1}=\alpha q_t\oplus (1-\alpha )q_t^t.$$

(4)

Theorem 4.

Let $\mathfrak{G}$ be the directed graph on X, and let $Z\in CCB\left(X\right)$. Let $\mathcal{P}:Z\to C\left(Z\right)$ be a $\mathfrak{G}$-asymptotically non-expansive mapping. Assume that $r\in Z$ is an FP of $\mathcal{P}$, thereby satisfying $\mathcal{P}\left(r\right)=\left\{r\right\}$. Assume that

(i) 

${\left\{b_m\right\}}_{m\in \mathbb{N}}$ is the Lipschitz sequence associated with $\mathcal{P}$ and

(ii) 

the series ${\sum }_{m\in \mathbb{N}}(b_m-1)$ is convergent.

Suppose $q_1\in Z$, $\alpha \in (0,1)$, $\left\{q_m^1\right\}$ is a generalized orbit of $q_1$ and $\left\{q_m\right\}$, and let this be the sequence generated by Equation (4), such that $(q_m,r),(q_m^t,r)\in \mathcal{E}\left(\mathfrak{G}\right)$ for each $m,t\in \mathbb{N}$. Then,

$$\begin{array}{c}\hfill \underset{m\to \infty }{lim}\varrho (q_1^m,q_m)=0,\end{array}$$

thus implying ${lim}_{m\to \infty }\varrho (q_m,\mathcal{P}\left(q_m\right))=0$, that is, that $\left\{q_m\right\}$ will be an approximated FP sequence of $\mathcal{P}$.

Proof. 

In view of $\mathcal{P}\left(r\right)=\left\{r\right\},$ we have

$$\varrho (q_{m+h}^t,r)\le b_h\varrho (q_m^t,r).$$

(5)

Using Equation (4) and the definition of CUCHMS, we obtain

$$\begin{array}{ccc}\hfill \varrho (q_{t+1},r)& \le & \alpha \varrho (q_t,r)+(1-\alpha )\varrho (q_t^t,r)\hfill \\ & \le & \alpha \varrho (q_t,r)+(1-\alpha )b_t\varrho (q_t,r)\hfill \\ & =& \alpha \varrho (q_t,r)+b_t\varrho (q_t,r)-\alpha b_t\varrho (q_t,r)\hfill \\ & \le & b_t\varrho (q_t,r).\hfill \end{array}$$

From the above inequality, we obtain

$$\begin{array}{c}\hfill \varrho (q_{t+1},r)-\varrho (q_t,r)\le (b_t-1)\varrho (q_t,r)\le (b_t-1)diam\left(Z\right)\end{array}$$

for any $t\in \mathbb{N}$ and $diam\left(Z\right)=sup\left\{\varrho \right(\omega ,\varpi ):\omega ,\varpi \in Z\}$, which indicates the diameter. As we have

$$\begin{array}{ccc}\hfill \sum _{i=t}^{t+s-1}(b_i-1)& \ge & (b_t-1),\hfill \end{array}$$

we can write

$$\begin{array}{c}\hfill \varrho (q_{t+s},r)-\varrho (q_t,r)\le diam\left(Z\right)\sum _{i=t}^{t+s-1}(b_i-1)\end{array}$$

for any $t,s\in \mathbb{N}.$ By letting s approach infinity, one obtains

$$\begin{array}{c}\hfill \underset{l\to \infty }{lim\; sup}\varrho (q_l,r)-\varrho (q_t,r)\le diam\left(Z\right)\sum _{i=t}^{\infty }(b_i-1).\end{array}$$

Now, by letting t approach infinity, and by using the given assumption, we have

$$\begin{array}{c}\hfill \underset{l\to \infty }{lim\; sup}\varrho (q_l,r)\le \underset{t\to \infty }{lim\; inf}\varrho (q_t,r),\end{array}$$

thus implying the convergence of the sequence $\left\{\varrho (q_t,r)\right\}.$ Assume that ${lim}_{t\to \infty }\varrho (q_t,r)=\mathcal{R}$.

If $\mathcal{R}=0$, then it follows from Inequality (5) that

$$\begin{array}{ccc}\hfill \underset{t\to \infty }{lim\; sup}\varrho (q_t^t,r)& \le & \underset{t\to \infty }{lim\; sup}{b}_t\varrho (q_0^t,r)\hfill \\ & =& \underset{t\to \infty }{lim\; sup}{b}_t\varrho (q_t,r)\hfill \\ & =& 0.\hfill \end{array}$$

Then,

$$\begin{array}{ccc}\hfill \underset{t\to \infty }{lim}\varrho (q_{t+1},r)& =& \underset{t\to \infty }{lim}\varrho (\alpha q_t\oplus (1-\alpha )q_t^t,r)\hfill \\ & \le & \underset{t\to \infty }{lim}\{\alpha \varrho (q_t,r)+(1-\alpha )\varrho (q_t^t,r)\}\hfill \\ & =& 0.\hfill \end{array}$$

By using Theorem 1, ${lim}_{t\to \infty }\varrho (q_t,q_t^t)=0.$

Now, consider the case for $\mathcal{R}>0.$ By repeating the above steps, we have

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim\; sup}\varrho (q_t^t,r)\le \mathcal{R},\underset{t\to \infty }{lim}\varrho (q_t,r)=\mathcal{R}\mathrm{and}\underset{t\to \infty }{lim}\varrho (q_t,q_t^t)=0.\end{array}$$

With the selection of our generalized orbits, we now assert that

$$\begin{array}{c}\hfill \underset{m\to \infty }{lim}\varrho (q_1^m,q_m)=0.\end{array}$$

Evidently, we now have

$$\begin{array}{ccc}\hfill \varrho (q_m,q_1^m)& \le & \varrho \left(q_m,q_m^m\right)+\varrho \left(q_m^m,q_m^{m-1}\right)+\varrho \left(q_m^{m-1},q_1^m\right),\hfill \\ & \le & \varrho \left(q_m,q_m^m\right)+b_m\varrho \left(q_m,q_{m-1}\right)+b_1\varrho \left(q_{m-1}^{m-1},q_m\right),\hfill \\ & \le & \varrho \left(q_m,q_m^m\right)+b_m(1-\alpha )\varrho \left(q_{m-1}^{m-1},q_{m-1}\right)+b_1\alpha \varrho \left(q_m^{m-1},q_{m-1}\right),\hfill \\ & \le & \varrho (q_m,q_m^m)+\left(\underset{t\in \mathbb{N}}{sup}{b}_t\right)\{\varrho \left(q_{m-1}^{m-1},q_{m-1}\right)+\varrho \left(q_m^{m-1},q_{m-1}\right)\}\hfill \end{array}$$

for any $m\ge 1$, which ultimately implies

$$\begin{array}{c}\hfill \underset{m\to \infty }{lim}\varrho (q_1^m,x_m)=0.\end{array}$$

□

4. Some Consequences of the Convergence Results

This section highlights the corollaries derived from the main results. As a consequence of Theorem 4, we obtained the famous result established by Khamsi and Khan (Theorem 2.4, [12]).

Corollary 1.

Let $Z\in CCB\left(X\right)$ and $\mathcal{P}:Z\to C\left(Z\right)$ be assumed as asymptotically non-expansive mappings. Suppose

(i) 

${\left\{b_m\right\}}_{m\in \mathbb{N}}$ is a Lipschitz sequence associated with $\mathcal{P}$, and that

(ii) 

the sequence ${\sum }_{m\in \mathbb{N}}(b_m-1)$ converges.

For a fixed $q_1\in Z$ and $\alpha \in (0,1)$, consider a sequence $\left\{q_m\right\}$ that is generated by

$$q_{t+1}=\alpha q_t\oplus (1-\alpha )q_t^t,$$

where $\left\{q_m^t\right\}$ is a generalized orbit of $q_t$. Then,

$$\begin{array}{c}\hfill \underset{m\to \infty }{lim}\varrho (q_1^m,q_m)=0,\end{array}$$

which implies ${lim}_{m\to \infty }\varrho (q_m,\mathcal{P}\left(q_m\right))=0$, that is, $\left\{q_m\right\}$ is an approximated FP of $\mathcal{P}$.

Proof. 

By assuming $\mathfrak{G}=Z\times Z$, all of the conditions of Theorem 4 are fulfilled, and the process is completed. □

Remark 3.

Theorem 3 is a generalized version of the classical FP result by Goebel and Kirk (Theorem 1, [2]) for the multi-valued mappings that are endowed with graphs and are defined on a nonlinear domain.

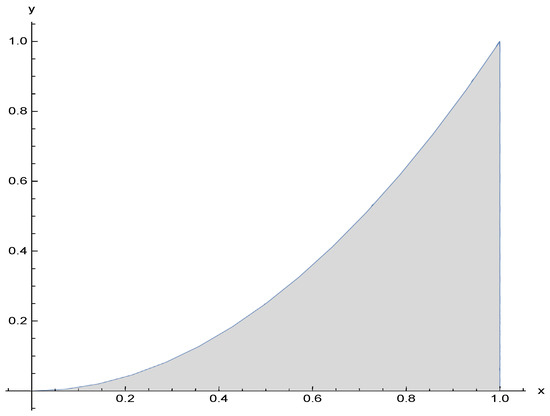
Example 1.

Let $X=\mathbb{R}$ be a CUCHMS and $Z=[0,1]\in CCB\left(X\right)$. Assume that $\mathfrak{G}=\left(W\right(\mathfrak{G}),\mathcal{E}(\mathfrak{G}\left)\right)$ is the directed graph on X with $W\left(\mathfrak{G}\right)=[0,\frac{1}{2}]$, $\mathcal{E}\left(\mathfrak{G}\right)=\left\{\right(q,r);q,r\in W(\mathfrak{G}\left)\right\}$ and $\mathcal{P}:Z\to C\left(Z\right)$ is defined as

$$\begin{array}{c}\hfill \mathcal{P}\left(q\right)=[0,q^2],forallq\in Z.\end{array}$$

(6)

Let $(q,r)\in \mathcal{E}\left(\mathfrak{G}\right)$. For $0\le q^{\prime }\in \mathcal{P}\left(q\right)$ and $r^{\prime }\le \frac{1}{2}\in \mathcal{P}\left(r\right)$, we have $(q^{\prime },r^{\prime })\in \mathcal{E}\left(\mathfrak{G}\right)$. Hence, $\mathcal{P}$ is an example of edge preservation. Now, we show that, for any $q,r\in X$ and any generalized orbit $\left\{q_m\right\}$ of q, there exists a generalized orbit $\left\{r_m\right\}$ of r, such that $(q_m,r)\in \mathcal{E}\left(\mathfrak{G}\right)$, and thus we have

$$\begin{array}{c}\hfill \varrho (q_{m+h},r_h)\le b_h\varrho (q_m,r),form,h\in \mathbb{N}.\end{array}$$

(7)

Let $\left\{q_m\right\}=\{q_0=q,q_1,q_2,\dots \}$ and $\left\{r_m\right\}=\{r_0=r,r_1,r_2,\dots \}$ be generalized orbits of q and r, respectively, where there are $q_{i+1}\in \mathcal{P}\left(q_i\right)$ and $r_{i+1}\in \mathcal{P}\left(r_i\right)$. Take $q_0=\frac{1}{4}$ and $r_0=\frac{1}{2}$, so that $(x_0,y_0)\in \mathcal{E}\left(\mathfrak{G}\right)$. Now, to prove (7), we have multiple cases for values of h.

Case 1:  For $h=0$, (7) becomes

$$\begin{array}{ccc}\hfill \varrho (q_m,r_0)& \le & b_0\varrho (q_m,r),forall(q_m,r)\in \mathcal{E}\left(\mathfrak{G}\right).\hfill \end{array}$$

(8)

Since $r_0=r$, for $b_0=1$, we obtain $\varrho (q_m,r_0)\le \varrho (q_m,r_0)$. Also $r_0,q_0$ and $q_{i+1}\in W\left(\mathfrak{G}\right)$ are for all $i\ge 1$. Thus (8) holds.

Case 2:  For $h=1$, (7) reduces to

$$\begin{array}{c}\hfill \varrho (q_{m+1},r_1)\le b_1\varrho (q_m,r).\end{array}$$

(9)

Now, for $m=0$, we have (9) as $\varrho (q_1,r_1)\le b_1\varrho (q_0,r)$. Using $q_0=\frac{1}{4}$ and $r_0=r=\frac{1}{2}$, we obtain $q_1\in [0,\frac{1}{16}],r_1\in [0,\frac{1}{4}]$, then $\varrho (q_0,r_0)=\frac{1}{4}$ and $\varrho (q_1,r_1)\le \frac{1}{4}$. Thus, we have

$$\begin{array}{c}\hfill \varrho (q_1,r_1)\le \varrho (q_0,r_0).\end{array}$$

For $m=1$, we have (9) as $\varrho (q_2,r_1)\le b_1\varrho (q_1,r)$. For $q_2\in [0,\frac{1}{256}]$ and $r_1\in [0,\frac{1}{4}]$, we have $\varrho (q_2,r_1)\le \frac{1}{4}\le \frac{7}{16}\le \varrho (q_1,r_0)$. Similarly, for $m=2$, we have $\varrho (q_3,r_1)\le \frac{1}{4}\le \frac{127}{256}\le \varrho (q_2,r_0)$, which implies $\varrho (q_3,r_1)\le \varrho (q_2,r_0)$. Thus, we can say that

$$\begin{array}{c}\hfill \varrho (q_{m+1},r_1)\le b_1\varrho (q_m,r),\end{array}$$

where $b_1=1$ implies that (9) holds.

Case 3:  For $h=2$, on similar lines of the abovementioned case, we have

$$\begin{array}{c}\hfill \varrho (q_{m+2},r_2)\le b_2\varrho (q_m,r),\end{array}$$

where $b_2=1$.

Hence, generalizing the above process for $h\in \mathbb{N}$, we have

$$\begin{array}{c}\hfill \varrho (q_{m+h},r_h)\le b_h\varrho (q_m,r),\end{array}$$

where $b_h=1$, for all $h\in \mathbb{N}$ and $(q_m,r)\in \mathcal{E}\left(\mathfrak{G}\right)$. Also, ${lim}_{m\to \infty }{b}_m=1$ implies (7). Thus, $\mathcal{P}$ is a $\mathfrak{G}$-asymptotically non-expansive mapping. Clearly, $0\in Z$ is a FP of $\mathcal{P}$. Thus, satisfying $\mathcal{P}\left(0\right)=\left\{0\right\}$ and ${\left\{b_m\right\}}_{m\in \mathbb{N}}$ is the Lipschitz sequence that is associated with $\mathcal{P}$, and the series ${\sum }_{m\in \mathbb{N}}(b_m-1)$ is convergent. As a result, the presumptions of Theorem 4 are all true. Moreover, suppose $q_1=\frac{1}{4}\in Z,\alpha \in (0,1)$ and $\left\{q_m^1\right\}=\{q_0^1=q_1,q_1^1,q_2^1,\dots \}$, where $q_i^1\in P\left(q_{i-1}^1\right)$ is the generalized orbit of $q_1$ and $q_1^1\in [0,\frac{1}{16}]$. Set

$$\begin{array}{c}\hfill q_2=\alpha q_1+(1-\alpha )q_1^1.\end{array}$$

For $\alpha \in (0,1),q_2\in (0,\frac{5}{16})$ and by Condition $\left(\mathcal{B}\right)$, we have $(q_1,q_2),(q_m^1,q_2)\in E\left(\mathfrak{G}\right)$. Since $\mathcal{P}$ is an $\mathfrak{G}$-asymptotically non-expansive mapping with $b_h=1$, we thus have the inequality

$$\begin{array}{c}\hfill \varrho (q_{m+h}^1,q_h^2)\le b_h\varrho (q_m^1,q_2)\forall h\in \mathbb{N}.\end{array}$$

Now, assume that $q_2=\frac{1}{5}$ and $\left\{q_m^2\right\}$ is its generalized orbit. Then, $q_1^2\in [0,\frac{1}{25}]$ and $q_2^2\in [0,\frac{1}{625}]$. By setting $q_3=\alpha q_2+(1-\alpha )q_2^2$, we have $0<q_3<\frac{126}{625}$. Again, by Condition $\left(\mathcal{B}\right)$, we have $(q_2,q_3),(q_m^2,q_3)\in \mathcal{E}\left(\mathfrak{G}\right)$ and

$$\begin{array}{c}\hfill \varrho (q_{m+h}^2,q_h^3)\le b_h\varrho (q_m^2,q_3).\end{array}$$

Suppose that $q_3=\frac{1}{6}$ and $\left\{q_m^3\right\}$ are its generalized orbit. Then, $q_1^3\in [0,\frac{1}{36}]$. Following the above procedure, we can generalize the inequality as follows:

$$\begin{array}{c}\hfill \varrho (q_{m+h}^t,q_h^{t+1})\le b_h\varrho (q_m^t,q_{t+1}),\end{array}$$

and

$$\begin{array}{c}\hfill q_{t+1}=\alpha q_t+(1-\alpha )q_t^t.\end{array}$$

(10)

Hence, for any $t\ge 1,\left\{q_m^t\right\}$ is the generalized orbit of $q_t$, and $\left\{q_m\right\}$ is the sequence generated by (10), such that $(q_m,r),(q_m^t,r)\in \mathcal{E}\left(\mathfrak{G}\right)$ is for every $m,t\in \mathbb{N}$, and $r=0$ is the FP of $\mathcal{P}$, such that $\mathcal{P}\left(0\right)=\left\{0\right\}$. Clearly, $\varrho (q_1^m,q_m)$ is a decreasing sequence and is bounded below by zero. Therefore, we have

$$\begin{array}{c}\hfill \underset{m\to \infty }{lim}\varrho (q_1^m,q_m)=0,\end{array}$$

which implies ${lim}_{m\to \infty }\varrho (q_m,\mathcal{P}\left(q_m\right))=0$, that is, $\left\{q_m\right\}$ is an approximated FP sequence of $\mathcal{P}$ (Figure 4).

Figure 4. Representation of multi-valued $\mathfrak{G}$-asymptotically non-expansive mapping, as defined by (6).

Open Problem: On similar lines, one can also define the idea of $\mathfrak{G}$-total asymptotically non-expansive mappings and prove convergence theorems in Hadamard spaces, as well as in convex hyperbolic metric spaces.

5. Conclusions

Some thoughtful research for multi-valued mappings happened in the middle of 19th century, which is when mathematicians realized that their needs go far beyond a modest improvement of single-valued mappings. This paper concludes that an H-continuous $\mathfrak{G}$-asymptotically non-expansive multi-valued mapping has an FP under assured circumstances in uniformly convex hyperbolic metric spaces. As a result, the FP theorems provided by Goebel and Kirk [2], Khamsi and Khan [12], and many others have been generalized. Some consequences are also presented, which highlight the practical implications of our findings. Additionally, an application of one of our results is provided in the context of the Nash equilibrium, which underscores the versatility of our contributions. An attractive example, some captivating graphs, and an interesting open problem for Hadamard spaces are also provided to attract new investigations in this field of exploration.