Randić Index of a Line Graph

Abstract

The Randić index of a graph G, denoted by $R\left(G\right)$, is defined as the sum of $1/\sqrt{d\left(u\right)d\left(v\right)}$ for all edges $uv$ of G, where $d\left(u\right)$ denotes the degree of a vertex u in G. In this note, we show that $R\left(L\left(T\right)\right)>\frac{n}{4}$ for any tree T of order $n\ge 3$. A number of relevant conjectures are proposed.

1. Introduction

Let $G=\left(V\right(G),E(G\left)\right)$ be a graph. For a vertex $v\in V\left(G\right)$, $d_G\left(v\right)$ (simply by $d\left(v\right)$) denotes the degree of v in G. The symbol $N_G\left(v\right)$ presents the set of neighbors of the vertex v. The minimum degree and the maximum degree of G are denoted by $\delta \left(G\right)$ and $\mathsf{\Delta }\left(G\right)$, respectively. In 1975, the Randić index $R\left(G\right)$ of a graph G was introduced by Randić [1] as the sum of $\frac{1}{\sqrt{d\left(u\right)d\left(v\right)}}$ over all edges $uv$ of G, i.e.,

$$R\left(G\right)=\sum _{uv\in E\left(G\right)}1/\sqrt{d\left(u\right)d\left(v\right)}.$$

This parameter is quite useful in mathematical chemistry and has been extensively studied, see the monograph [2]. We refer to [3,4,5,6,7] for some recent results. As usual, $P_n$, $C_n$ and $K_n$ denote the path, the cycle and the complete graphs of order n, respectively. In addition, $K_{m,n}$ represents the complete bipartite graph with m and n vertices in its two parts.

Let us recall two classical results on the Randić index of graphs, which are a lower bound and an upper bound in terms of their orders.

Theorem 1

(Bollobás and Erdos [8]). For a connected graph G of order n, $R\left(G\right)\ge \sqrt{n-1}$, with equality, if and only if $G\cong K_{1,n-1}$.

Theorem 2

(Fajtlowicz [9]). For a graph G of order n, $R\left(G\right)\le \frac{n}{2}$ with equality, if and only if each component of G has order at least two and is regular.

The line graph of a graph G, denoted by $L\left(G\right)$, is the graph with $V\left(L\right(G\left)\right)=E\left(G\right)$, in which two vertices are adjacent, if and only if they share a common end vertex in G. The relation between Wiener index of a graph and that of its line graph was investigated in [10,11,12,13].

Interestingly, for a graph G, $R\left(L\right(G\left)\right)$ is usually large contrast to $R\left(G\right)$ (with some exception, $P_n$ for instance). In this note, we investigate the Randić indices of the line graphs of graphs with order given. The following results illustrate that $L\left(K_n\right)$ has the maximum Randić index among all line graphs of graphs with order n.

Theorem 3.

For any graph G of order $n\ge 3$, $R\left(L\left(G\right)\right)\le \frac{n(n-1)}{4}$, with equality, if and only if $G\cong K_n$.

Proof. 

Observe that $K_n$ has the maximum number of edges among all graphs of order n. Thus, the result is an immediate consequence of Theorem 2. □

Our main contribution is to show that $R\left(L\left(T\right)\right)>\frac{n}{4}$ for any tree T of order $n\ge 3$. A number of relevant conjectures are proposed.

2. Results

We begin with a wider family of graphs than line graphs. A graph G is called claw-free if it contains no induced subgraph isomorphic to $K_{1,3}$. It is well-known that every line graph is claw-free. The following lemma is one of our main tools proving Theorem 5.

Lemma 1.

Let $G_1$ and $G_2$ be two disjoint nontrivial connected graphs. If G is a graph obtained from $G_1$ and $G_2$ by identifying a vertex $v_1\in V\left(G_1\right)$ and $v_2\in V\left(G_2\right)$, then

$$R\left(G\right)=R\left(G_1\right)+R\left(G_2\right)-(a+b-c),$$

where

$$a=\frac{1}{\sqrt{d_{G_1}\left(v_1\right)}}\sum _{x\in N_{G_1}\left(v_1\right)}\frac{1}{\sqrt{d_{G_1}\left(x\right)}},$$

$$b=\frac{1}{\sqrt{d_{G_2}\left(v_2\right)}}\sum _{y\in N_{G_2}\left(v_2\right)}\frac{1}{\sqrt{d_{G_2}\left(y\right)}},$$

$$c=\frac{1}{\sqrt{(d_{G_1}\left(v_1\right)+d_{G_2}\left(v_2\right))}}(\sum _{x\in N_{G_1}\left(v_1\right)}\frac{1}{\sqrt{d_{G_1}\left(x\right)}}+\sum _{y\in N_{G_2}\left(v_2\right)}\frac{1}{\sqrt{d_{G_2}\left(y\right)}}).$$

Furthermore, if G is claw-free, then $a+b-c<1$.

Proof. 

The first part of the result is obvious. Next we show the second part. For convenience, let $d_i=d_{G_i}\left(v_i\right)$ for each $i\in \{1,2\}$ and ${\sum }_{x\in N_{G_1}\left(v_1\right)}\frac{1}{\sqrt{d_{G_1}\left(x\right)}}={\sum }_{i=1}^{d_1}\frac{1}{\sqrt{a_i}}$ and ${\sum }_{x\in N_{G_1}\left(v_1\right)}\frac{1}{\sqrt{d_{G_2}\left(y\right)}}={\sum }_{j=1}^{d_2}\frac{1}{\sqrt{b_j}}$.

Since $d_1\ge 1$ and $d_2\ge 1$, we have $\frac{\sqrt{d_1}+\sqrt{d_2}}{\sqrt{d_1+d_2}}>1$. In addition, since G is claw-free, both $N_{G_1}\left(v_1\right)$ and $N_{G_2}\left(v_2\right)$ are cliques, implying that $a_i\ge d_1$ for each i and $b_j\ge d_2$ for each j. Thus, we have

$$\begin{array}{ccc}\hfill a+b-c& =& (\frac{1}{\sqrt{d_1}}-\frac{1}{\sqrt{d_1+d_2}})\sum _{i=1}^{d_1}\frac{1}{\sqrt{a_i}}+(\frac{1}{\sqrt{d_2}}-\frac{1}{\sqrt{d_1+d_2}})\sum _{j=1}^{d_2}\frac{1}{\sqrt{b_j}}\hfill \\ & \le & (\frac{1}{\sqrt{d_1}}-\frac{1}{\sqrt{d_1+d_2}})\sqrt{d_1}+(\frac{1}{\sqrt{d_2}}-\frac{1}{\sqrt{d_1+d_2}})\sqrt{d_2}\hfill \\ & =& 2-\frac{\sqrt{d_1}+\sqrt{d_2}}{\sqrt{d_1+d_2}}\hfill \\ & <& 1.\hfill \end{array}$$

The proof is completed. □

We will also use the following result in the proof of our main theorem.

Theorem 4

(Hansen and Vukicević [14]). Let G be a simple graph. If $d\left(v\right)=\delta \left(G\right)$, then

$$R\left(G\right)-R(G-v)\ge \frac{1}{2}\sqrt{\frac{\delta \left(G\right)}{\mathsf{\Delta }\left(G\right)}}.$$

By the above theorem, if $\delta \left(G\right)>0$, then $R\left(G\right)-R(G-v)>0$ for any vertex $v\in V\left(G\right)$ with $d\left(v\right)=\delta \left(G\right)$.

Theorem 5.

For any tree T of order $n\ge 3$, $R\left(L\left(T\right)\right)>\frac{n}{4}$.

Proof. 

By induction on n. Observe that $L\left(P_n\right)\cong P_{n-1}$ and $L\left(K_{1,n-1}\right)\cong K_{n-1}$. Moreover, $R\left(P_n\right)=\frac{n-3}{2}+\sqrt{2}$ and $R\left(K_n\right)=\frac{n}{2}$. A simple computation shows that the result holds for $T\in \{P_n,K_{1,n-1}\}$. So, assume that $n\ge 5$ and T is neither a star nor a path.

Let P be a longest path of T. Label the vertices of P as $v_0,v_1,\dots ,v_t$ consecutively. Clearly, $t\ge 3$. Observe that all neighbors of $v_1$ except $v_2$ have degree 1. Let $T_{v_1}$ and $T_{v_2}$ be the two components of $T-v_1{v}_2$ containing $v_1$ and $v_2$, respectively. Let $T_1=T\backslash E\left(T_{v_2}\right)$ and $T_2=T\backslash E\left(T_{v_1}\right)$. Let $G_i=L\left(T_i\right)$ for each $i\in \{1,2\}$, and $G=L\left(G\right)$. Note that G is the graph obtained from $G_1$ and $G_2$ by identifying the vertex $v_1{v}_2$. By Lemma 1, we have

$$R\left(G\right)=R\left(G_1\right)+R\left(G_2\right)-(a+b-c),$$

where $a,b$, and c are those defined in the statement of Lemma 1.

By the induction hypothesis, $R\left(G_2\right)>\frac{n-d_1}{4}$, where $d_1=d_T\left(v_1\right)-1$. In addition, $R\left(G_1\right)=\frac{d_1+1}{2}$. We consider two cases.

Case 1.$d_1\ge 2$

Since G is a line graph (so it is claw-free), by Lemma 1, $a+b-c<1$.

$$\begin{array}{ccc}\hfill R\left(G\right)& =& R\left(G_1\right)+R\left(G_2\right)-(a+b-c)\hfill \\ & >& \frac{d_1+1}{2}+\frac{n-d_1}{4}-1\hfill \\ & =& \frac{n}{4}+\frac{d_1}{4}-\frac{1}{}2\hfill \\ & \ge & \frac{n}{4}.\hfill \end{array}$$

Note that if there exists an edge $uv\in T$ with $d_T\left(u\right)\ge 3$ such that all neighbors of u except v have degree 1, then by the argument as in Case 1, we can show that $R\left(G\right)>\frac{n}{4}$. So, in what follows, we may assume that $d_T\left(u\right)=2$ for any vertex $u\in V\left(T\right)$ with all neighbors but one having degree 1.

Case 2.$d_1=1$

Let $d_2=d_T\left(v_2\right)-1$. We consider two subcases.

Subcase 2.1.$d_2=1$

Since $d_G\left(v_1{v}_2\right)=d_1+d_2=2$, we have

$$\begin{array}{ccc}\hfill R\left(G\right)& =& R\left(G_1\right)+R\left(G_2\right)-(a+b-c)\hfill \\ & >& 1+\frac{n-1}{4}-(2-\frac{\sqrt{d_1}+\sqrt{d_2}}{\sqrt{d_1+d_2}})\hfill \\ & \ge & \frac{n-1}{4}+1-(2-\sqrt{2})\hfill \\ & >& \frac{n}{4}.\hfill \end{array}$$

Subcase 2.2.$d_2\ge 2$

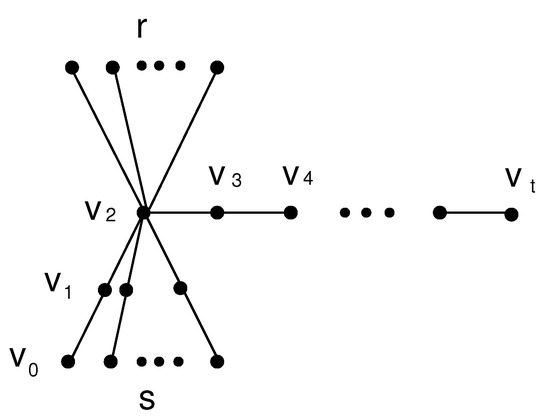
By the choice of P and the remark before Case 2, the component of $T-v_2{v}_3$ containing $v_2$ is a wounded spider, as shown in Figure 1. Denote this component by $W_{r,s}$, where r and s are the numbers of neighbors of $v_2$ having degrees 1 and 2, respectively.

Figure 1. The local structure of T.

Let $T_1$ be the subtree of T obtained from $W_{r,s}$ by joining $v_3$ to $v_2$, and $T_2=T\backslash E\left(W_{r,s}\right)$. Moreover, let $G_i=L\left(T_i\right)$ for each $i\in \{1,2\}$, and let $G=L\left(T\right)$. Clearly, G is obtained from $G_1$ and $G_2$ by identifying the vertex $v_2{v}_3$. By the induction hypothesis, $R\left(G_2\right)>\frac{n-r-2s}{4}$. One can see that

$$R\left(G_1\right)=\frac{s}{\sqrt{r+s+1}}+\frac{\left(\genfrac{}{}{0pt}{}{s}{2}\right)}{r+s+1}+\frac{\left(\genfrac{}{}{0pt}{}{r+1}{2}\right)}{r+s}+\frac{(r+1)s}{\sqrt{(r+s+1)(r+s)}}.$$

(1)

Deleting leaves (minimum degree vertices) of $G_1$ one-by-one, we end up with $K_{r+s+1}$. By Theorem 2.2, we have

$$R\left(G_1\right)>R\left(K_{r+s+1}\right)=\frac{r+s+1}{2}.$$

(2)

Subcase 2.2.1.$r\ge 2$

By (2), $R\left(G_1\right)>\frac{r+s+1}{2}$. By Lemma 1, we have

$$\begin{array}{ccc}\hfill R\left(G\right)& >& R\left(G_1\right)+R\left(G_2\right)-1\hfill \\ & >& \frac{r+s+1}{2}+\frac{n-r-2s}{4}-1\hfill \\ & \ge & \frac{n}{4}.\hfill \end{array}$$

Subcase 2.2.2.$r=0$

Since $d_2=r+s$, $s=d_2\ge 2$. By (1), $R\left(G_1\right)=\frac{s}{\sqrt{s+1}}+\frac{s(s-1)}{2(s+1)}+\frac{s}{\sqrt{(s+1)s}}>\frac{s}{2}+1$ for any $s\ge 2$. By Lemma 1,

$$\begin{array}{ccc}\hfill R\left(G\right)& =& R\left(G_1\right)+R\left(G_2\right)-(a+b-c)\hfill \\ & >& \frac{s}{2}+1+\frac{n-2s}{4}-1\hfill \\ & =& \frac{n}{4}.\hfill \end{array}$$

Subcase 2.2.3.$r=1$

By (1), $R\left(G_1\right)=\frac{s}{\sqrt{s+2}}+\frac{s(s-1)}{2(s+2)}+\frac{1}{s+2}+\frac{2s}{\sqrt{(s+2)(s+1)}}\ge \frac{1+2s}{4}+1=\frac{r+2s}{4}+1$. Thus, by Lemma 1,

$$\begin{array}{ccc}\hfill R\left(G\right)& =& R\left(G_1\right)+R\left(G_2\right)-(a+b-c)\hfill \\ & >& \frac{1+2s}{4}+1+\frac{n-1-2s}{4}-1\hfill \\ & =& \frac{n}{4}.\hfill \end{array}$$

The proof is completed. □

3. Discussion

In this paper, we show that $R\left(L\left(T\right)\right)>\frac{n}{4}$ for any tree T of order $n\ge 3$. For a graph G, $S\left(G\right)$ denotes the graph obtained from G by inserting exactly one vertex into each edge of G. For a positive even integer n, $S{(K_{1,\frac{n}{2}})}^{-}$ denotes the tree obtained from $S(K_{1,\frac{n}{2}})$ by deleting a leaf. Define a function $f\left(n\right)$ as

$$f\left(n\right)=\left\{\begin{array}{cc}\frac{n-3}{4}+\sqrt{\frac{n-1}{2}},\hfill & \mathrm{if} n \mathrm{is} \mathrm{odd}\hfill \\ \frac{n}{4}-\frac{3}{2}+\frac{2}{n}+\sqrt{1-\frac{2}{n}}+\sqrt{\frac{n}{2}}-\sqrt{\frac{2}{n}},\hfill & \mathrm{if} n \mathrm{is} \mathrm{even}.\hfill \end{array}\right.$$

Indeed,

$$f\left(n\right)=\left\{\begin{array}{cc}R(L(S(K_{1,\frac{n-1}{2}}))),\hfill & \mathrm{if} n \mathrm{is} \mathrm{odd}\hfill \\ R(L(S{(K_{1,\frac{n}{2}})}^{-})),\hfill & \mathrm{if} n \mathrm{is} \mathrm{even}.\hfill \end{array}\right.$$

We strongly believe that the following conjectures holds.

Conjecture 1.

For any tree T of order $n\ge 3$, $R\left(L\right(T\left)\right)\ge f\left(n\right)$, with equality, if and only if

$$T\cong \left\{\begin{array}{cc}S(K_{1,\frac{n-1}{2}}),\hfill & if n is odd\hfill \\ S{(K_{1,\frac{n}{2}})}^{-},\hfill & if n is even.\hfill \end{array}\right.$$

Conjecture 2.

For any connected graph G of order $n\ge 3$, $R\left(L\right(G\left)\right)\ge f\left(n\right)$, with equality holds, if and only if

$$T\cong \left\{\begin{array}{cc}S(K_{1,\frac{n-1}{2}}),\hfill & if n is odd\hfill \\ S{(K_{1,\frac{n}{2}})}^{-},\hfill & if n is even.\hfill \end{array}\right.$$

Since every line graph is claw-free, we propose a more general conjecture.

Conjecture 3.

For any connected claw-free graph of order $n\ge 2$, $R\left(G\right)\ge f\left(n\right)$.

A weaker conjecture than the above is the following one.

Conjecture 4.

For any connected claw-free graph of order $n\ge 2$, $R\left(G\right)>\frac{n}{4}$.

As we have seen before, $L\left(P_n\right)\cong P_{n-1}$ for any $n\ge 2$ and $K_{1,3}\cong K_3$. We guess that the following is true.

Conjecture 5.

Let G be a connected graph of order $n\ge 3$. If $\delta \left(G\right)\ge 2$, then $R\left(L\right(G\left)\right)\ge R\left(G\right)$, with equality, if and only if $G\cong C_n$.

The Harmonic index $H\left(G\right)$ of a graph G is defined as $H\left(G\right)={\sum }_{uv\in E\left(G\right)}\frac{2}{d\left(u\right)+d\left(v\right)}$. It is natural that one may consider the same problems for the Harmonic index as we did in this note. Specifically,

Conjecture 6.

$H\left(L\left(T\right)\right)>\frac{n}{4}$ for any tree T of order $n\ge 3$.

If the above conjecture is true, it implies the main result of this note, since $R\left(G\right)\ge H\left(G\right)$ for any graph G.

Recall that for a real number $\alpha$, the general Randić index of a graph G, denoted by $R_{\alpha }\left(G\right)$, is

$$R_{\alpha }\left(G\right)=\sum _{uv\in E\left(G\right)}{\left(d\right(u\left)d\right(v\left)\right)}^{\alpha }.$$

The sum-connectivity index $\chi \left(G\right)$ and the general sum-connectivity index ${\chi }_{\alpha }\left(G\right)$ were proposed by Zhou and Trinajstić in [15,16] and were defined as

$$\chi \left(G\right)=\sum _{uv\in E\left(G\right)}{(d\left(u\right)+d\left(v\right))}^{-\frac{1}{2}}$$

and

$${\chi }_{\alpha }\left(G\right)=\sum _{uv\in E\left(G\right)}{(d\left(u\right)+d\left(v\right))}^{\alpha }.$$

It is interesting to consider the general Randić index and the general sum-connectivity index of a line graph for different value of $\alpha$.