Graph Entropy Based on Strong Coloring of Uniform Hypergraphs

Abstract

The classical graph entropy based on the vertex coloring proposed by Mowshowitz depends on a graph. In fact, a hypergraph, as a generalization of a graph, can express complex and high-order relations such that it is often used to model complex systems. Being different from the classical graph entropy, we extend this concept to a hypergraph. Then, we define the graph entropy based on the vertex strong coloring of a hypergraph. Moreover, some tightly upper and lower bounds of such graph entropies as well as the corresponding extremal hypergraphs are obtained.

1. Introduction

Hypergraphs are an important generalization of ordinary graphs. In this paper, some problems on extremal values of graph entropy based on the strong coloring in k-uniform hypergraphs are studied. Indeed, the colorings for hypergraphs are also a natural extension of colorings for graphs, which have various applications (timetabling and scheduling problems, planning of experiments, multi-user source coding, etc.) and offer rich connections with other combinatorial areas (probabilistic methods, extremal set theory, Ramsey theory, discrepancy theory, etc.).

In information theory, Shannon${}^{’}$s entropy, as a well-known information entropy, was proposed by Shannon [1]. As one of the most important indicators in information theory, it can measure the unpredictability of information contents. Let $p=\{p_1,p_2,\cdots ,p_n\}$ be a probability distribution, where ${\sum }_{i=1}^n{p}_i=1$ and $0\le p_i\le 1$. Shannon${}^{’}$s entropy is defined as

$$I\left(p\right)=-\sum _{i=1}^n(p_{i}log{p}_i).$$

Combining Shannon${}^{’}$s entropy with the probability distribution defined on the vertex set or edge set of a graph, the graph entropy is obtained. Indeed, graph entropy plays an important role in many disciplines such as information theory, biology, chemistry and sociology. It can not only express the structure information contents of a graph but also serve as a complexity measure. Up until now, many graph entropies have been proposed in [2,3,4,5,6,7,8,9,10,11,12,13,14]. For more results on the theory and applications of graph entropies, we refer the reader to [10,13,15,16,17].

In view of the vast amount of existing graph entropies of ordinary graphs, there is little work on graph entropy of hypergraphs [18,19]. Inspired by Mowshowitz [6], who introduced a graph entropy based on the vertex coloring, we define a graph entropy (see Definition 1) based on the strong coloring in a hypergraph.

A hypergraph $H=(V,E)$ with n vertices and m edges consists of a set of vertices $V=\{v_1,v_2,\cdots ,v_n\}$ and a set of edges $E=\{e_1,e_2,\cdots e_m\}$, which is a family of subsets of V such that $e_i\ne \varnothing (i=1,2,\cdots ,m)$ and ${\cup }_i^m{e}_i=V$. A hypergraph in which all edges have the same cardinality k is called k-uniform. A k-uniform hypergraph H is called simple if there are no multiple edges in H, that is, all edges in H are distinct. All hypergraphs considered here are simple and k-uniform with $k\ge 3$. For a k-uniform hypergraph $H=(V,E)$, the degree $d_v$ of a vertex $v\in V$ is defined as $d_v=\left|e_i:v\in e_i\in E\right|$. A vertex of degree one is called a pendent vertex. Otherwise, it is called a non-pendent vertex. An edge $e\in E$ is called a pendent edge if e contains exactly $k-1$ pendent vertices. Otherwise, it is called a non-pendent edge. A walk W of length l in H is a sequence of alternating vertices and edges, i.e., $v_0{e}_1{v}_1{e}_2\cdots e_l{v}_l$, where $\{v_{i-1},v_i\}\subseteq e_i$ for $i=1,\cdots ,l$. If $v_0=v_l$, then W is called a circuit. A walk of H is called a path if no vertices and edges are repeated. A circuit H is called a cycle if no vertices and edges are repeated except $v_0=v_l$. A distance $d(x,y)$ between two vertices x and y is the minimum length of a path which connects x and y. The diameter $d\left(H\right)$ of $H=(V,E)$ is defined by $d\left(H\right)=max\left\{d\right(x,y)\mid x,y\in V\}$. In [20,21,22], more hypergraph concepts are introduced.

Let $H=(V,E)$ be a hypergraph with vertex coloring. A strong k-coloring of H is a partition $(V_1,V_2,\cdots ,V_k)$ of V such that the same color does not appear twice in the same edge. In other words, $\left|e\cap V_i\right|\le 1$ for any edge and any element of the partition. If a partition $(V_1,V_2,\cdots ,V_k)$ of V is a strong k-coloring of H, it is said to be a chromatic decomposition of H. Then set $V_i$ is called a color classe for $1\le i\le k$. The strong chromatic number $\chi \left(H\right)$ is the smallest number k such that H has a strong k-coloring. Define the non-increasing chromatic decomposition sequence of H by ${\pi }_c\left(H\right)=(\left|V_1\right|,\left|V_2\right|,\cdots ,\left|V_k\right|)$ for a chromatic decomposition denoted by c, that is, $\left|V_1\right|\ge \left|V_2\right|\ge \cdots \ge \left|V_k\right|$.

Definition 1.

Let $H=(V,E)$ be a hypergraph with n vertices and m edges. Let $\widehat{V}={\left\{V_i\right\}}_i^{\chi }$ is an arbitrary chromatic decomposition of H and $\chi \left(H\right)=\chi$. Then the graph entropy based on the vertex strong coloring $I_c\left(H\right)$ of H is given by

$$\begin{array}{cc}\hfill I_c\left(H\right)=& \underset{\widehat{V}}{min}\{-\sum _{i=1}^{\chi }\frac{\left|V_i\right|}{n}log\frac{\left|V_i\right|}{n}\}\hfill \\ \hfill =& logn-\underset{\widehat{V}}{max}\{-\frac{1}{n}\sum _{i=1}^{\chi }\left|V_i\right|log\left|V_i\right|\}.\hfill \end{array}$$

(1)

If $h\left(H\right)=\underset{\widehat{V}}{max}{\sum }_{i=1}^{\chi }\left|V_i\right|log\left|V_i\right|$, then $I_c\left(H\right)=logn-\frac{h\left(H\right)}{n}$.

The paper is organized as follows. In Section 2, some concepts and existing results on hypergraphs are given. In Section 3, the extremal properties of graph entropies are studied. The paper finishes with a conclusion in Section 4.

2. Preliminaries

In this section, some basic definitions and results are given.

Definition 2

([19]). Let H be a k-uniform hypergraph with n vertices, m edges and l connected components. The cyclomatic number of H is denoted and defined by $c\left(H\right)=m(k-1)-n+l$. The hypergraph H is called a $c\left(G\right)$-cyclic hypergraph.

A connected hypergraph H does not contain any cycles if and only if $c\left(H\right)=0$.

Definition 3

([23]). Let $G=(V,E)$ be an ordinary graph. For an integer $k\ge 3$, the k-th power of G, denoted by $G^k:=(V^k,E^k)$, is defined as the k-uniform hypergraph with the set of vertices $V^k=V\cup \left({\cup }_{e\in E}\{i_{e,1},\cdots ,i_{e,k-2}\}\right)$ and the set of edges $E^k=\{e\cup \{i_{e,1},\cdots ,i_{e,k-2}\}|e\in E\}$, where $i_{e,1},\cdots ,i_{e,k-2}$ are new added vertices for e.

Definition 4

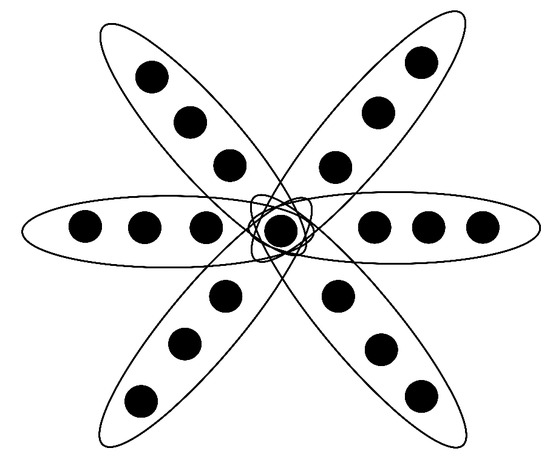
([23]). The k-th power of $S_n$, denoted by $S_n^k$, is called a hyperstar (see Figure 1 for an example).

Figure 1. Hyperstar $S_7^4$.

Definition 5

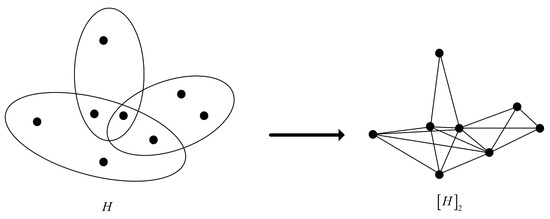
([20]). Let $H=(V,E)$ be a hypergraph. The 2-section of H is the graph, denoted by ${\left[H\right]}_2$, where vertices are the vertices of H and where two distinct vertices form an edge if and only if they are in the same edge of H. An example of 2-section is given in Figure 2.

Figure 2. A 2-section of a hypergraph.

Lemma 1

([20]). The strong chromatic number denoted by $\chi \left(H\right)$ is the smallest k such that H has a strong k-coloring. Then $\chi \left(H\right)$ is the chromatic number of the graph ${\left[H\right]}_2$.

Definition 6

([24]). A graph G with vertex coloring is called color-critical if $\chi \left(G^{{}^{\prime }}\right)<\chi \left(G\right)$ for every proper subgraph $G^{{}^{\prime }}$ of G. If G is a color-critical k-chromatic graph, then G is called critically k-chromatic or simply k-critical.

Lemma 2

([24]). Every k-critical graph, $k\ge 2$, is $(k-1)$-edge-connected.

Definition 7.

A k-uniform hypergraph H with vertex coloring is called color-critical if $\chi \left(H^{{}^{\prime }}\right)<\chi \left(H\right)$ for every k-uniform proper subhypergraph $H^{{}^{\prime }}$ of H. If H is color-critical and k-chromatic, then H is called critically k-chromatic or simplyk-critical.

Some operations [25] of moving edges for hypergraphs are stated as follows.

Definition 8.

Let $r\ge 1$ and $H=(V,E)$ be a hypergraph with $u\in V$ and $e_1,\cdots ,e_r\in E$ such that $u\notin e_i$ for $i=1,\cdots ,r$. Suppose that $v_i\in e_i$ and write $e_i^{{}^{\prime }}=(e\setminus \left\{v_i\right\})\cup \left\{u\right\}(i=1,\cdots ,r)$. Let $H^{{}^{\prime }}=(V,E^{{}^{\prime }})$ be the hypergraph with $E^{{}^{\prime }}=(E\setminus \{e_i,\cdots ,e_r\})\cup \{e_1^{{}^{\prime }},\cdots ,e_r^{{}^{\prime }}\}$. Then $H^{{}^{\prime }}$ is said to be obtained from H by moving edge $(e_1,\cdots ,e_r)$ from $(v_1,\cdots ,v_r)$ to u.

Lemma 3.

Let k-uniform hypergraph H be t-critical $(t>k)$. The graph ${\left[H\right]}_2^{{}^{\prime }}$ is obtained from ${\left[H\right]}_2$ by deleting the vertex whose degree is $k-1$. Then $\chi \left({\left[H\right]}_2^{{}^{\prime }}\right)=\chi \left(H\right)$ and ${\left[H\right]}_2^{{}^{\prime }}$ is t-critical.

Proof. 

By Lemma 1, we have $\chi \left({\left[H\right]}_2\right)=t$. By contradiction, suppose $\chi \left({\left[H\right]}_2^{{}^{\prime }}\right)<t$. If $k-1<\chi \left({\left[H\right]}_2^{{}^{\prime }}\right)<t$, then $\chi \left({\left[H\right]}_2\right)=\chi \left({\left[H\right]}_2^{{}^{\prime }}\right)$, which contradicts with $\chi \left(H\right)=t$. If $\chi \left({\left[H\right]}_2^{{}^{\prime }}\right)<k-1$, then $\chi \left({\left[H\right]}_2\right)\le \chi \left({\left[H\right]}_2^{{}^{\prime }}\right)+1$, which contradicts with $\chi \left(H\right)=t$. Thus, $\chi \left({\left[H\right]}_2\right)=t$.

Now, we prove that ${\left[H\right]}_2^{{}^{\prime }}$ is t-critical. Assume ${\left[H\right]}_2^{{}^{\prime }}$ is not t-critical. Then there is a proper subgraph ${\left[H\right]}_2^{{}^{″}}$ of ${\left[H\right]}_2^{{}^{\prime }}$ such that $\chi \left({\left[H\right]}_2^{{}^{″}}\right)=t$. Any proper subgraph of ${\left[H\right]}_2^{{}^{\prime }}$ can be obtained by deleting vertices whose degree is $k-1$ from the 2-section of the hypersubgraph of hypergraph H. Then, there is a hypersubgraph $H^{{}^{\prime }}$ of H with $\chi \left(H^{{}^{\prime }}\right)=\chi \left({\left[H\right]}_2^{{}^{″}}\right)=t$, which implies that H is not t-critical and this is a contradiction. Hence, ${\left[H\right]}_2^{{}^{\prime }}$ is t-critical. □

3. Extremality of $I_c\left(H\right)$ among k-Uniform $(k\ge 3)$ Hypergraphs

In this section, we investigate the extremality of graph entropy based on the vertex strong coloring among all k-uniform $(k\ge 3)$ supertrees and k-uniform $c\left(H\right)$-cyclic hypergraphs $(k\ge c(H)+2,c(H)\ge 1)$. Assume $\mathbb{X}=\left\{\{x_1,\cdots ,x_n\}\right|x_1\ge \cdots \ge x_n,{\sum }_{i=1}^n{x}_i=N_0,x_i\in Z^{+}(1\le i\le n,N_0\in Z^{+})\}$.

Lemma 4.

Suppose $f\left(X\right)={\sum }_{i=1}^n{x}_{i}log{x}_i$, where $X=\{x_1,\cdots ,x_n\}\in \mathbb{X}$. For any $x_i,x_j\in X$, if $\left|x_i-x_j\right|=0$ or $\left|x_i-x_j\right|=1$, then $f\left(X\right)$ obtains the minimal value.

Proof. 

Suppose $N_0$ is divisible by n. Assume $X_1\in \mathbb{X}$ and $X_1=\{x_1^{\left(1\right)},\cdots ,x_n^{\left(1\right)}\}$. For any $x_i^{\left(1\right)},x_j^{\left(1\right)}\in X_1$, it has $x_i^{\left(1\right)}-x_j^{\left(1\right)}=0$. Suppose $X_2\in \mathbb{X}$ and $X_1\ne X_2=\{x_1^{\left(2\right)},\cdots ,x_n^{\left(2\right)}\}$. Then there are $x_i^{\left(2\right)},x_j^{\left(2\right)}\in X_2$, where $x_j^{\left(2\right)}-x_i^{\left(2\right)}\ge 2$. Let $X_3\in \mathbb{X}$ and $X_3=\{x_1^{\left(2\right)},\cdots ,x_j^{\left(2\right)}-1,\cdots ,x_i^{\left(2\right)}+1,\cdots ,x_n^{\left(2\right)}\}$. Then

$$\begin{array}{ccc}\hfill f\left(X_2\right)-f\left(X_3\right)& =& x_i^{\left(2\right)}log{x}_i^{\left(2\right)}+x_j^{\left(2\right)}log{x}_j^{\left(2\right)}-(x_i^{\left(2\right)}+1)log(x_i^{\left(2\right)}+1)\hfill \\ & -& (x_j^{\left(2\right)}-1)log(x_j^{\left(2\right)}-1)\hfill \\ & =& \left[x_j^{\left(2\right)}log{x}_j^{\left(2\right)}-(x_j^{\left(2\right)}-1)log(x_j^{\left(2\right)}-1)\right]\hfill \\ & -& \left[(x_i^{\left(2\right)}+1)log(x_i^{\left(2\right)}+1)-x_i^{\left(2\right)}log{x}_i^{\left(2\right)}\right]\hfill \\ & =& (log{\xi }_1+\frac{1}{ln2})-(log{\xi }_2+\frac{1}{ln2})\hfill \\ & >& 0,\hfill \end{array}$$

where ${\xi }_1\in (x_j^{\left(2\right)}-1,x_j^{\left(2\right)})$ and ${\xi }_2\in (x_i^{\left(2\right)},x_i^{\left(2\right)}+1)$. So, we obtain $f\left(X_2\right)>f\left(X_3\right)$. This implies that $f\left(X\right)$ attains the minimum value as $X=X_1$.

For the case that $N_0$ is not divisible by n, with the same way as above, we can check that $f\left(X\right)$ attains the minimum value as $X=X_4$, where $X_4\in \mathbb{X}$ and $X_4=\{x_1^{\left(4\right)},x_2^{\left(4\right)}\cdots ,x_n^{\left(4\right)}\}$ satisfying $\left|x_i^{\left(4\right)}-x_j^{\left(4\right)}\right|=1$ or $\left|x_i^{\left(4\right)}-x_j^{\left(4\right)}\right|=0$ for $1\le i,j\le n$. □

Lemma 5.

Let $H=(V,E)$ be a k-uniform hypergraph on n vertices with $m>2$ edges and $\underset{v\in V}{max}d\left(v\right)=2$. Then the number of vertices whose degree is 1 in hypergraph is $n-m+l-c\left(H\right)$ and hypergraph H has, at most, $\lfloor \frac{n-m+l-c\left(H\right)}{k-1}\rfloor$ pendent edges.

Proof. 

Suppose the number of vertices whose degree is 1 in hypergraph H is t, then hypergraph H has, at most, $\lfloor \frac{t}{k-1}\rfloor$ pendent edges. Let the number of vertices whose degree is 2 in hypergraph is x. By $c\left(H\right)=m(k-1)-n+l$ and ${\sum }_{i=1}^n{d}_i=km$, we have

$$\begin{array}{ccc}\hfill km& =& 2x+(n-x),\hfill \\ \hfill x& =& m-l+c\left(H\right).\hfill \end{array}$$

So, the number of vertices whose degree is 1 in hypergraph is $n-m+l-c\left(H\right)$ and hypergraph H has, at most, $\lfloor \frac{n-m+l-c\left(H\right)}{k-1}\rfloor$ pendent edges. □

Lemma 6.

Let $H=(V,E)$ be a k-uniform hypergraph $(k\ge 3)$ on n vertices with m edges and $l=1$ connected components. If $k\ge c\left(H\right)+2$, then $\chi \left(H\right)=k$.

Proof. 

By contradiction, suppose $\chi \left(H\right)>k$ as $k\ge c\left(H\right)+2$. If $\chi \left(H\right)$ is $k+1$, then there exists a subhypergraph $H^{{}^{\prime }}$ of H, which is $(k+1)$-critical. Let $V^{{}^{\prime }}=\{v_1,\cdots ,v_{k+1}\}\subseteq V\left(H^{{}^{\prime }}\right)$ such that $v_i$ is colored with color i. Now, we discuss the following two cases.

$Case$$1.$ There is a vertex set $V^{{}^{\prime }}$ in $H^{{}^{\prime }}$ such that any two vertices in $V^{{}^{\prime }}$ are in the same edge.

Let $H^{{}^{\prime }}=(V_{H^{{}^{\prime }}},E_{H^{{}^{\prime }}})$ be a k-uniform hypergraph of $n^{{}^{\prime }}$ vertices and $m^{{}^{\prime }}$ edges, with $l=1$ connected component. Since hypergraph $H^{{}^{\prime }}$ is k uniform, all vertices of $V^{{}^{\prime }}$ cannot appear in one edge of $H^{{}^{\prime }}$. By the condition that any two vertices in vertex set $V^{{}^{\prime }}$ are in the same edge, there are three vertices in $V^{{}^{\prime }}$ to form a circle of length 3. Such a cycle is denoted by $c_1=v_1{e}_1{v}_2{e}_2{v}_3{e}_3{v}_1$, where $e_1,e_2,e_3\in E_{H^{{}^{\prime }}}$ and $v_1,v_2,v_3\in V^{{}^{\prime }}$. For any $v_i\in V^{{}^{\prime }}\setminus \{v_1,v_2,v_3\}$, we find that there are two vertices of $\{v_1,v_2,v_3\}$ such that the two vertices and the vertex $v_i$ can form a cycle of length 3. Assume $v_2$ and $v_3$ are such two vertices and the cycle is $c_i=v_2{e}_2{v}_3{e}_j{v}_i{e}_i{v}_2$, where $e_i\in E_{H^{{}^{\prime }}}$ is an edge containing $v_i$ and $v_2$, and $e_j\in E_{H^{{}^{\prime }}}$ is an edge containing $v_i$ and $v_3$. If there is not such a cycle $c_i$, then the vertices $v_1,v_2,v_3$ and $v_i$ must be in the same edge, which is a contradiction with $c_1$. So, there must be a cycle $c_i$ in hypergraph $H^{{}^{\prime }}$ for $4\le i\le k+1$.

Let $H_0^{{}^{\prime }}$ be the graph obtained from adding the isolated vertices $v_1^{{}^{\prime }},\cdots ,v_{k-1}^{{}^{\prime }}$. Let $H^{{}^{″}}$ be the k-uniform hypergraph obtained from $H_0^{{}^{\prime }}$ by the following operations of moving edges, i.e., $e_1^{{}^{\prime }}=(e_1\setminus \left\{v_1\right\})\bigcup \left\{v_1^{{}^{\prime }}\right\}$ and $e_i^{{}^{\prime }}=(e_i\setminus \left\{v_i\right\})\bigcup \left\{v_{i-2}^{{}^{\prime }}\right\}(i=4,\cdots ,k+1)$. Then, we see that $H^{{}^{″}}$ is connected and it has no cycles $c_1,c_4\cdots c_{k+1}$. Thus,

$$\begin{array}{ccc}\hfill c\left(H^{{}^{″}}\right)& =& m^{{}^{\prime }}(k-1)-[n^{{}^{\prime }}+k-1]+1,\hfill \\ \hfill n^{{}^{\prime }}+c\left(H^{{}^{″}}\right)& =& m^{{}^{\prime }}(k-1)-k+2\hfill \end{array}$$

and

$$n^{{}^{\prime }}\le m^{{}^{\prime }}(k-1)-k+2.$$

(2)

From $c\left(H^{{}^{\prime }}\right)=m^{{}^{\prime }}(k-1)-n^{{}^{\prime }}+1$ and Inequality (2), we have

$$\begin{array}{ccc}\hfill c\left(H^{{}^{\prime }}\right)& =& m^{{}^{\prime }}(k-1)-n^{{}^{\prime }}+1\hfill \\ & \ge & m^{{}^{\prime }}(k-1)-[m^{{}^{\prime }}(k-1)-k+2]+1\hfill \\ & =& k-1\ge c\left(H\right)+1\ge c\left(H^{{}^{\prime }}\right)+1.\hfill \end{array}$$

Then, we obtain that $c\left(H^{{}^{\prime }}\right)\ge c\left(H^{{}^{\prime }}\right)+1$, which is a contradiction.

$Case$$2.$ There are at least two vertices in $V^{{}^{\prime }}$ which are not in the same edge for any vertex set $V^{{}^{\prime }}$ in $H^{{}^{\prime }}$.

Let ${\left[H^{{}^{\prime }}\right]}_2^{{}^{\prime }}$ be the graph obtained from ${\left[H^{{}^{\prime }}\right]}_2$ by deleting the vertex whose degree is $k-1$. By Lemma 3, we obtain that $\chi \left({\left[H^{{}^{\prime }}\right]}_2^{{}^{\prime }}\right)=\chi \left(H^{{}^{\prime }}\right)$ and ${\left[H^{{}^{\prime }}\right]}_2^{{}^{\prime }}$ is $(k+1)$-critical. By the condition, there are at least two vertices in $V^{{}^{\prime }}$ which are not in the same edge for any vertex set $V^{{}^{\prime }}$ in $H^{{}^{\prime }}$, there are at least two vertices in $V^{{}^{\prime }}$ that are not adjacent. Suppose $v_i$ is not adjacent to $v_j$, where $v_i,v_j\in V^{{}^{\prime }}$. By Lemma 2, ${\left[H^{{}^{\prime }}\right]}_2^{{}^{\prime }}$ is k-edge-connected. Then ${\left[H^{{}^{\prime }}\right]}_2^{{}^{\prime }}$ contains k pairwise edge-disjoint $v_j-v_i$ paths. So, $H^{{}^{\prime }}$ contains k pairwise edge-disjoint $v_j-v_i$ paths. Let $P_1,\cdots ,P_k$ be k pairwise edge-disjoint $v_j-v_i$ paths in $H^{{}^{\prime }}$. Let $H_0^{{}^{\prime }}$ be the graph obtained from adding $k-1$ isolated vertices $v_1^{{}^{\prime }},\cdots ,v_{k-1}^{{}^{\prime }}$. Suppose $P_i$ contains an edge $e_i$ and a vertex $u_i$ such that $u_i\in e_i$ and $u_i\ne v_i,v_j$, where $1\le i\le k-1$. Let $H^{{}^{″}}$ be the k-uniform hypergraph obtained from $H_0^{{}^{\prime }}$ by the following operations of moving edges, i.e., $e_i^{{}^{\prime }}=(e_i\setminus \left\{u_i\right\})\bigcup \left\{v_i^{{}^{\prime }}\right\}(i=1,\cdots ,k-1)$. Then, we see that $H^{{}^{″}}$ is connected and it has no paths $P_1,\cdots P_{k-1}$. Thus,

$$\begin{array}{ccc}\hfill c\left(H^{{}^{″}}\right)& =& m^{{}^{\prime }}(k-1)-[n^{{}^{\prime }}+k-1]+1,\hfill \\ \hfill n^{{}^{\prime }}+c\left(H^{{}^{″}}\right)& =& m^{{}^{\prime }}(k-1)-k+2\hfill \end{array}$$

and

$$n^{{}^{\prime }}\le m^{{}^{\prime }}(k-1)-k+2.$$

(3)

From $c\left(H^{{}^{\prime }}\right)=m^{{}^{\prime }}(k-1)-n^{{}^{\prime }}+1$ and Inequality (3), we have

$$\begin{array}{ccc}\hfill c\left(H^{{}^{\prime }}\right)& =& m^{{}^{\prime }}(k-1)-n^{{}^{\prime }}+1\hfill \\ & \ge & m^{{}^{\prime }}(k-1)-[m^{{}^{\prime }}(k-1)-k+2]+1\hfill \\ & =& k-1\ge c\left(H\right)+1\ge c\left(H^{{}^{\prime }}\right)+1.\hfill \end{array}$$

Then we obtain that $c\left(H^{{}^{\prime }}\right)\ge c\left(H^{{}^{\prime }}\right)+1$, which is a contradiction. □

For the upper bound about $I_c\left(H\right)$, due to the lack of effective analysis methods, we only consider k-uniform hypergraph $H=(V,E)$ on n vertices with $m>2$ edges, where $m\le (2-c\left(H\right))k+{(k-1)}^2-c\left(H\right)$ and $\frac{n-m+1-c\left(H\right)}{k-1}$ is an integer. $(2-c\left(H\right))k+{(k-1)}^2-c\left(H\right)$ is the maximum number of edges when the diameter of $H_1$ is less than or equal to 5, where $H_1$ is a k-uniform hypergraph on n vertices with m edges and the maximum degree 2.

Theorem 1.

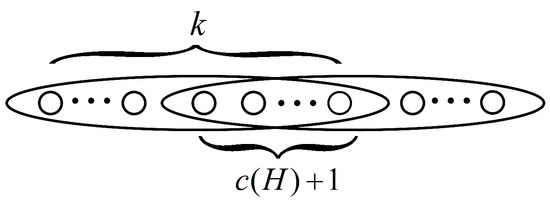
Let $H=(V,E)$ be a k-uniform hypergraph $(k\ge c(H)+2)$ on n vertices with $m>2$ edges, where $\frac{n-m+1-c\left(H\right)}{k-1}$ is an integer and $m\le (2-c\left(H\right))k+{(k-1)}^2-c\left(H\right)$. Then

$$h\left(H\right)\ge r(\lfloor \frac{n}{k}\rfloor +1)log(\lfloor \frac{n}{k}\rfloor +1)+(k-r)\lfloor \frac{n}{k}\rfloor log\lfloor \frac{n}{k}\rfloor$$

with the equality holding if and only if ${\pi }_c\left(H\right)={\pi }_c\left(H_1\right)$, where $r=n-\lfloor \frac{n}{k}\rfloor k$ and $H_1$ is a k-uniform hypergraph with the maximum degree 2, possessing n vertices and m edges, which has $\frac{n-m+1-c\left(H\right)}{k-1}$ pendent edges. Then, we see that there is a hypersubgraph $H^{{}^{\prime }}$ of $H_1$ with $c\left(H^{{}^{\prime }}\right)=c\left(H\right)=c\left(H_1\right)$, where the hypergraph $H^{{}^{\prime }}$ is obtained from jointing two edges by $c\left(H\right)+1$ common vertices (see Figure 3).

Figure 3. The k-uniform $c\left(H\right)$-cyclic hypersubgraph $H^{{}^{\prime }}$ of $H_1$.

Proof. 

By Lemma 6, $\chi \left(H\right)=k$. By Lemma 5, and $\frac{n-m+1-c\left(H\right)}{k-1}$ is an integer, the hypergraph $H_1$ has, at most, $\frac{n-m+1-c\left(H\right)}{k-1}$ pendent edges. For $H_1$ on n vertices with $m>2$ edges and the maximum degree 2, there is $H_1$ that satisfies that the diameter of $H_1$ is less than or equal to 5 because of $m\le (2-c\left(H\right))k+{(k-1)}^2-c\left(H\right)$. By the structure and strong coloring of hypergraph $H_1$, the chromatic decomposition sequences obtained from all strong coloring of k-uniform hypergraph $H_1$ are the same and unique when $\frac{n-m+1-c\left(H\right)}{k-1}$ is an integer and $d\left(H_1\right)\le 5$, which is supposed to be ${\pi }_c\left(H_1\right)=\{\left|V_1\right|,\cdots ,\left|V_k\right|\}$. If n is divisible by k, then $\left|V_1\right|=\cdots =\left|V_k\right|$ in the case of $H_1$. Otherwise, $\left|V_1\right|=\cdots =\left|V_r\right|=\lfloor \frac{n}{k}\rfloor +1$, $\left|V_{r+1}\right|=\cdots =\left|V_k\right|=\lfloor \frac{n}{k}\rfloor$, where $r=n-\lfloor \frac{n}{k}\rfloor k$. Thus, $h\left(H_1\right)=r(\lfloor \frac{n}{k}\rfloor +1)log(\lfloor \frac{n}{k}\rfloor +1)+(k-r)\lfloor \frac{n}{k}\rfloor log\lfloor \frac{n}{k}\rfloor$. In addition, $\left|\left|V_i\right|-\left|V_j\right|\right|\ge 2$ does not hold for any $\left|V_i\right|,\left|V_j\right|\in {\pi }_c\left(H_1\right)$. By Lemma 4, there is no such hypergraph H satisfying $h\left(H\right)<h\left(H_1\right)$. This completes the proof. □

From Theorem 1 and Equality (1), we have the following result.

Theorem 2.

Let $H=(V,E)$ be a k-uniform hypergraph $(k\ge c(H)+2)$ on n vertices with $m>2$ edges, where $\frac{n-m+1-c\left(H\right)}{k-1}$ is an integer and $m\le (2-c\left(H\right))k+{(k-1)}^2-c\left(H\right)$. Then

$$\begin{array}{c}\hfill I_c\left(H\right)\le logn-\frac{r(\lfloor \frac{n}{k}\rfloor +1)log(\lfloor \frac{n}{k}\rfloor +1)+(k-r)\lfloor \frac{n}{k}\rfloor log\lfloor \frac{n}{k}\rfloor }{n},\end{array}$$

the equality holds if and only if ${\pi }_c\left(H\right)={\pi }_c\left(H_1\right)$, where $H_1$ are given in Theorem 1.

From Theorem 2 and Equality (1), we have the following result.

Corollary 1.

Let $H=(V,E)$ be a k-uniform $(k\ge 3)$ supertree on n vertices with $m>2$ edges, where $\frac{n-m+1}{k-1}$ is an integer and $m\le 2k+{(k-1)}^2$. Then

$$\begin{array}{c}\hfill I_c\left(H\right)\le logn-\frac{r(\lfloor \frac{n}{k}\rfloor +1)log(\lfloor \frac{n}{k}\rfloor +1)+(k-r)\lfloor \frac{n}{k}\rfloor log\lfloor \frac{n}{k}\rfloor }{n}\end{array}$$

with the equality holding if and only if ${\pi }_c\left(H\right)={\pi }_c\left(H_3\right)$, where $n=\lfloor \frac{n}{k}\rfloor k+r(0\le r\le k-1)$ and $H_3$ is a k-uniform supertree with the maximum degree 2, possessing n vertices and m edges, which has $\frac{n-m+1}{k-1}$ pendent edges.

Theorem 3.

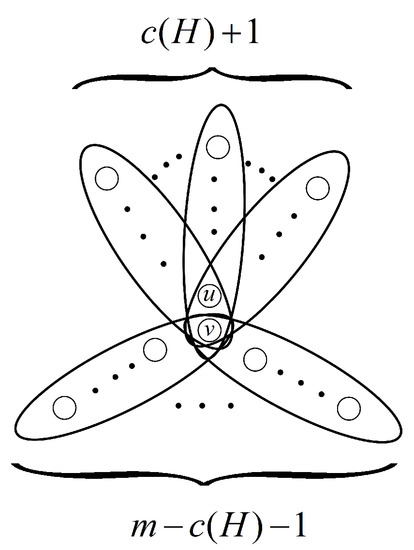
Let $H=(V,E)$ be a k-uniform hypergraph $(k\ge c(H)+2)$ on n vertices with $m>2$ edges. Then

$$h\left(H\right)\le (k-2)mlogm+(m-c(H\left)\right)log(m-c(H\left)\right)$$

with the equality holding if and only if ${\pi }_c\left(H\right)={\pi }_c\left(H_2\right)$, where the hypergraph $H_2$ is obtained from jointing $c\left(H\right)+1$ edges with two common vertices u and v and jointing $m-c\left(H\right)-1$ edges by the vertex v, respectively. (see Figure 4)

Figure 4. The k-uniform $c\left(H\right)$-cyclic hypergraph $H_2$.

Proof. 

By Lemma 6, $\chi \left(H\right)=k$. According to the structure and the strong coloring of a hypergraph, the chromatic decomposition sequence obtained from any strong coloring of $H_2$ is the same and unique, which is denoted by ${\pi }_c\left(H_2\right)=\{\left|V_1\right|,\cdots ,\left|V_k\right|\}$. Then $\left|V_1\right|=\cdots =\left|V_{k-2}\right|=m$, $\left|V_{k-1}\right|=m-c\left(H_2\right)$ and $\left|V_k\right|=1$. So $h\left(H_2\right)=(k-2)mlogm+(m-c\left(H_2\right))log(m-c\left(H_2\right))$. Note that $1\le \left|V_i\right|\le m$ for any strong coloring of a hypergraph. For any $\left|V_i\right|\le \left|V_j\right|$, we see that $\left|V_i\right|=1$ or $\left|V_j\right|=m$. Suppose there is a hypergraph $H=(V,E)$ with $c\left(H\right)=c\left(H_2\right)$ and its coloring c satisfying $h_c\left(H\right)=h\left(H\right)$. Let ${\pi }_c\left(H\right)=\left\{\left|V_1^{{}^{\prime }}\right|,\cdots ,\left|V_k^{{}^{\prime }}\right|\right\}\ne {\pi }_c\left(H_2\right)$. Then there is $\left|V_i^{{}^{\prime }}\right|\le \left|V_j^{{}^{\prime }}\right|$ satisfying $\left|V_j^{{}^{\prime }}\right|<m$ and $\left|V_i^{{}^{\prime }}\right|>1$. So, there are $e_1$ and $e_2$ satisfying $e_1\bigcap e_2\ne \varnothing$. Moreover, there is a vertex $v_1\in e_1$ and a vertex $v_2\in e_2$ satisfying $v_1,v_2\in V_i^{{}^{\prime }}$. Suppose $u\in e_1\bigcap e_2$, then $d\left(u\right)>1$ and $u\in V_j^{{}^{\prime }}$. Let $e_3,\cdots ,e_r$ be the other edges of H containing $v_2$. Let $H^{{}^{\prime }}=(V_{H^{{}^{\prime }}},E_{H^{{}^{\prime }}})$ be a k-uniform hypergraph obtained from H by following operations of moving edges, i.e., $e_2^{{}^{\prime }}=(e_2\setminus \left\{u\right\})\bigcup \left\{v_1\right\}$ and $e^{{}^{\prime }}=(e_i\setminus \left\{v_2\right\})\bigcup \left\{v_1\right\}(i=3,\cdots ,r)$. Obviously, $H^{{}^{\prime }}$ is also a k-uniform $c\left(H\right)$-cyclic hypergraph. Then, color the vertex $v_2$ with the color j noting that its color is i before. Thus, there is a coloring $c_1$ in $H^{{}^{\prime }}$ satisfying ${\pi }_{c_1}\left(H^{{}^{\prime }}\right)=\left\{\left|V_1^{{}^{\prime }}\right|,\cdots ,\left|V_j^{{}^{\prime }}\right|+1,\cdots ,\left|V_i^{{}^{\prime }}\right|-1,\cdots ,\left|V_k^{{}^{\prime }}\right|\right\}$. Then

$$\begin{array}{ccc}\hfill h\left(H\right)-h_{c_1}\left(H^{{}^{\prime }}\right)& =& \left|V_j^{{}^{\prime }}\right|log\left|V_j^{{}^{\prime }}\right|+\left|V_i^{{}^{\prime }}\right|log\left|V_i^{{}^{\prime }}\right|\hfill \\ & -& (\left|V_j^{{}^{\prime }}\right|+1)log(\left|V_j^{{}^{\prime }}\right|+1)-(\left|V_i^{{}^{\prime }}\right|-1)log(\left|V_i^{{}^{\prime }}\right|-1)\hfill \\ & =& \left[\left|V_i^{{}^{\prime }}\right|log\left|V_i^{{}^{\prime }}\right|-(\left|V_i^{{}^{\prime }}\right|-1)log(\left|V_i^{{}^{\prime }}\right|-1)\right]\hfill \\ & -& \left[(\left|V_j^{{}^{\prime }}\right|+1)log(\left|V_j^{{}^{\prime }}\right|+1)-\left|V_j^{{}^{\prime }}\right|log\left|V_j^{{}^{\prime }}\right|\right]\hfill \\ & =& (log{\xi }_1+\frac{1}{ln2})-(log{\xi }_2+\frac{1}{ln2})\hfill \\ & <& 0,\hfill \end{array}$$

where ${\xi }_1\in (\left|V_i^{{}^{\prime }}\right|-1,\left|V_i^{{}^{\prime }}\right|)$ and ${\xi }_2\in (\left|V_j^{{}^{\prime }}\right|,\left|V_j^{{}^{\prime }}\right|+1)$. That is, $h\left(H\right)<h_{c_1}\left(H^{{}^{\prime }}\right)\le h\left(H^{{}^{\prime }}\right)$, which means that $h\left(H\right)$ attains the maximum value as $\pi \left(H\right)=\pi \left(H_2\right)$. □

From Theorem 3 and Equality (1), we have the following result.

Theorem 4.

Let $H=(V,E)$ be a k-uniform hypergraph $(k\ge c(H)+2)$ on n vertices with $m>2$ edges. Then

$$\begin{array}{ccc}& & logn-\frac{(k-2)mlogm+(m-c(H\left)\right)log(m-c(H\left)\right)}{n}\le I_c\left(H\right),\hfill \end{array}$$

the equality holds if and only if ${\pi }_c\left(H\right)={\pi }_c\left(H_2\right)$, where $H_2$ are given in Theorem 3.

From Theorem 4 and Equality (1), we have the following result.

Corollary 2.

Let $H=(V,E)$ be a k-uniform $(k\ge 3)$ supertree on n vertices with m edges. Then

$$logn-\frac{(k-1)mlogm}{n}\le I_c\left(H\right).$$

The equality holds if and only if ${\pi }_c\left(H\right)={\pi }_c\left(S_{m+1}^k\right)$.

4. Conclusions

In this paper, we determine the extremal values for graph entropy based on strong coloring for k-uniform hypergraph H. For k-uniform hypergraph H$(k\ge c(H)+2)$ with n vertices and m edges, when $\frac{n-m+1-c\left(H\right)}{k-1}$ is an integer and $m\le (2-c\left(H\right))k+{(k-1)}^2-c\left(H\right)$, we obtain an upper bound of the graph entropy based on strong coloring by using n and k. For k-uniform hypergraph H$(k\ge c(H)+2)$ with n vertices and m edges, we obtain a lower bound of graph entropy based on strong coloring by using n, k, m and $c\left(H\right)$. Hypergraph is a generalization of a graph. However, there is little research on the entropy of a hypergraph. So, it is meaningful to extend the conclusions of graph entropies based on graphs to hypergraphs in the future.