Abstract
Recently, an extended operator of fractional derivative related to a generalized Beta function was used in order to obtain some generating relations involving the extended hypergeometric functions [1]. The main object of this paper is to present a further generalization of the extended fractional derivative operator and apply the generalized extended fractional derivative operator to derive linear and bilinear generating relations for the generalized extended Gauss, Appell and Lauricella hypergeometric functions in one, two and more variables. Some other properties and relationships involving the Mellin transforms and the generalized extended fractional derivative operator are also given.
Keywords:
gamma and beta functions; Eulerian integrals; generating functions; hypergeometric functions; Appell–Lauricella hypergeometric functions; fractional derivative operators; Mellin transforms Classification:
MSC Primary 26A33, 33C05; Secondary 33C20
1. Introduction, Definitions and Preliminaries
For the sake of clarity and easy readability, we find it to be natural and convenient to divide this introductory section into three parts (or subsections). In Part 1.1, we introduce the extended Beta, Gamma and hypergeometric functions. Part 1.2 deals with the familiar Riemann–Liouville fractional derivative operator and its generalizations, which are motivated essentially by the definition in Part 1.1 for the extended Beta function. In the third subsection (Part 1.3), we then introduce the extended Appell hypergeometric functions in two variables, which were recently investigated in conjunction with the family of the extended Riemann–Liouville fractional derivative operators defined in Part 1.2.
1.1. The Extended Beta, Gamma and Hypergeometric Functions
Extensions of a number of well-known special functions were investigated recently by several authors (see, for example [2,3,4,5,6,7]). In particular, Chaudhry et al. [3] gave the following interesting extension of the classical Beta function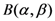 
:
:
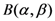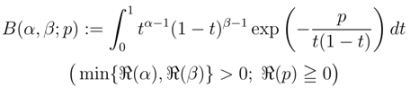
so that, clearly,
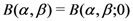
Here, and in what follows, such arguments as (for example)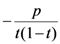 
in the Definition (1.1) are motivated by the connection of the extended Beta function 
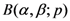with the Macdonald (or modified Bessel) function 
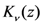(see, for details, [8,9]).
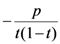in the Definition (1.1) are motivated by the connection of the extended Beta function 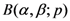with the Macdonald (or modified Bessel) function 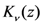(see, for details, [8,9]).Making use of the extended Beta function 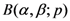defined by (1.1), Chaudhry et al. [8] introduced the extended hypergeometric function as follows:
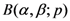defined by (1.1), Chaudhry et al. [8] introduced the extended hypergeometric function as follows: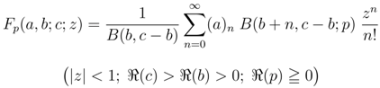
where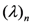 
denotes the Pochhammer symbol or the shifted factorial, which is defined (for 
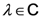and 
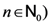by
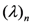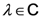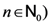denotes the Pochhammer symbol or the shifted factorial, which is defined (for and by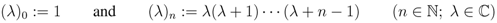
it being understood conventionally that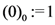 
.
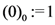.Among several interesting and potentially useful properties of the extended hypergeoemetric function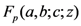 
defined by (1.2), the following integral representation of the Pfaff–Kummer type was also given by Chaudhry et al. [8, p. 592, Equation (3.2)]:
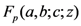defined by (1.2), the following integral representation of the Pfaff–Kummer type was also given by Chaudhry et al. [8, p. 592, Equation (3.2)]: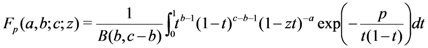
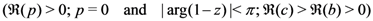
Obviously, for the Gauss hypergeometric function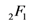 
, we have
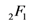, we have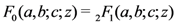
The following further generalizations of the extended Gamma function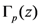 
(see, for details [9]), the extended Beta function 
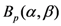and the extended Gauss hypergeometric function 
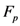were considered more recently by Özergin et al. [7]:
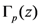(see, for details [9]), the extended Beta function 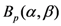and the extended Gauss hypergeometric function 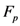were considered more recently by Özergin et al. [7]: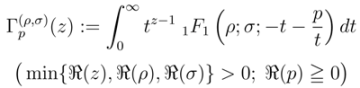
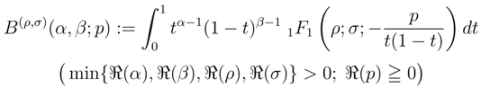
and
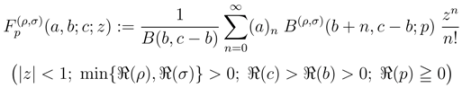
respectively,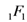 
being the (Kummer’s) confluent hypergeometric function. The following integral representation of the Pfaff–Kummer type was also given by Özergin et al. [7]:
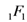being the (Kummer’s) confluent hypergeometric function. The following integral representation of the Pfaff–Kummer type was also given by Özergin et al. [7]: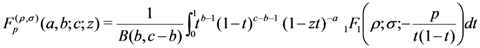
Clearly, since
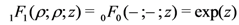
the special cases of Equations (1.6–1.8) when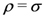 
would immediately yield Equations (1.1), (1.2) and (1.4), respectively.
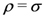would immediately yield Equations (1.1), (1.2) and (1.4), respectively.Throughout our present investigation, it is tacitly assumed that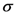 
and various other lower (or denominator) parameters are not zero or negative integers (that is, no zeros appear in the denominators).
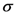and various other lower (or denominator) parameters are not zero or negative integers (that is, no zeros appear in the denominators).1.2. The Riemann–Liouville Fractional Derivative Operator and Its Generalizations
For the Riemann–Liouville fractional derivative operator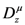 
defined by (see, for example [10, p. 181] [11] and [12, p. 70 et seq.])
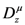defined by (see, for example [10, p. 181] [11] and [12, p. 70 et seq.])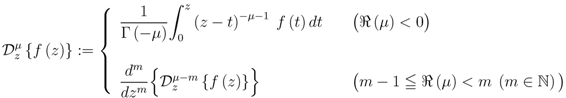
it is known that
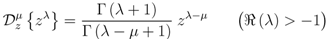
where, and in what follows,
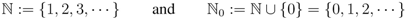
The path of integration in the definition (1.10) is a line in the complex 
-plane from 
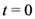to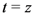 
.
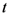-plane from 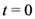to 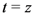.By introducing a new parameter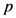 
of the type which is involved in (for example) the Definitions (1.1) and (1.2), Özarslan and Özergin [1] defined the correspondingly extended Riemann–Liouville fractional derivative operator 
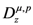by
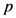of the type which is involved in (for example) the Definitions (1.1) and (1.2), Özarslan and Özergin [1] defined the correspondingly extended Riemann–Liouville fractional derivative operator 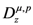by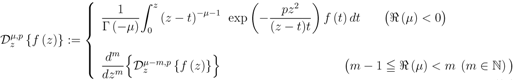
where, as before,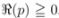 
. The path of integration in the Definition (1.13), which immediately yields the definition (1.10) when 
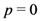, is also a line in the complex 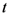-plane from 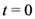to 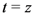. The argument 
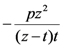in the Definition (1.13) and elsewhere in this paper is obviously necessitated by the applicability of the definition (1.1) of the extended Beta function 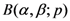when we set
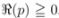. The path of integration in the Definition (1.13), which immediately yields the definition (1.10) when 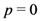, is also a line in the complex 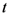-plane from 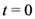to 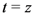. The argument 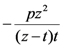in the Definition (1.13) and elsewhere in this paper is obviously necessitated by the applicability of the definition (1.1) of the extended Beta function 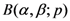when we set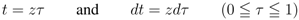
In the case when (for example)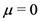 
, we find from the second part of the Definition (1.13) (with 
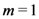) that
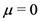, we find from the second part of the Definition (1.13) (with 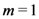) that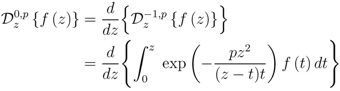
which obviously yields the functio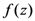n 
when 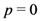. Thus, in general, the natural connection of the Riemann–Liouville fractional derivative operator 
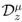defined by (1.10) with ordinary derivatives when the order 
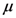is zero or a positive integer is lost by the extended fractional derivative operator in Definition (1.13) and its further generalizations which we have considered in our present investigation.
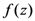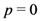when . Thus, in general, the natural connection of the Riemann–Liouville fractional derivative operator 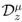defined by (1.10) with ordinary derivatives when the order 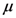is zero or a positive integer is lost by the extended fractional derivative operator in Definition (1.13) and its further generalizations which we have considered in our present investigation.1.3. Extended Appell Hypergeometric Functions in Two Variables
In analogy with the Definition (1.7), and motivated by their Definition (1.13) of the extended Riemann–Liouville fractional derivative 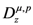, Özarslan and Özergin [1] extended the familiar Appell hypergeometric functions 
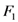and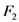 
in two variables as follows:
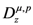, Özarslan and Özergin [1] extended the familiar Appell hypergeometric functions 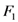and 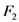in two variables as follows: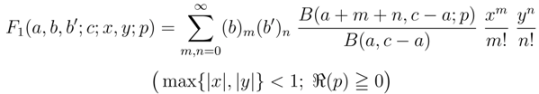
and
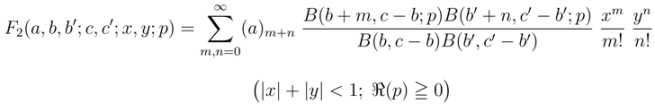
which, in the special case when 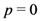, yield the familiar Appell hypergeometric functions 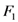and 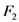in two variables (see [13, p. 14]). For each of these extended Appell hypergeometric functions, such properties as their integral representations and relationships with the extended Riemann–Liouville fractional derivative operator 
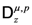defined by (1.13) can also be found in the work of Özarslan and Özergin [1].
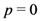, yield the familiar Appell hypergeometric functions 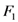and 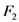in two variables (see [13, p. 14]). For each of these extended Appell hypergeometric functions, such properties as their integral representations and relationships with the extended Riemann–Liouville fractional derivative operator 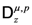defined by (1.13) can also be found in the work of Özarslan and Özergin [1].The aim of this paper is to investigate the various properties of a further generalization of the extended fractional derivative operator 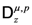defined by (1.13) and apply the generalized operator to derive generating relations for hypergeometric functions in one, two and more variables. We first introduce, in Section 2, the following further generalizations of the extended Appell’s hypergeometric functions:
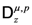defined by (1.13) and apply the generalized operator to derive generating relations for hypergeometric functions in one, two and more variables. We first introduce, in Section 2, the following further generalizations of the extended Appell’s hypergeometric functions: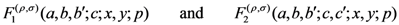
in two variables and the extended Lauricella’s hypergeometric function
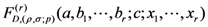
of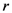 
variables 
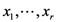are defined and their integral representations are obtained. In Section 3, we introduce and study the properties and relationships associated with the above-mentioned further generalization of the extended fractional derivative operator 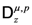defined by Definition (1.13) and apply the generalized operator in order to obtain various generating relations in terms of the generalized extended Appell and Lauricella hypergeometric functions in two and more variables. Section 4 contains some results related to the Mellin transforms and the extended fractional derivative operator. In Section 5, some generating relations for generalized extended hypergeometric functions are obtained via the above-mentioned further generalized fractional derivative operator by following the lines which are detailed in the monograph by Srivastava and Manocha [14]. Finally, in Section 6, we conclude this paper by presenting a number of remarks and observations pertaining to our investigation here.
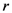variables 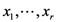are defined and their integral representations are obtained. In Section 3, we introduce and study the properties and relationships associated with the above-mentioned further generalization of the extended fractional derivative operator 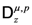defined by Definition (1.13) and apply the generalized operator in order to obtain various generating relations in terms of the generalized extended Appell and Lauricella hypergeometric functions in two and more variables. Section 4 contains some results related to the Mellin transforms and the extended fractional derivative operator. In Section 5, some generating relations for generalized extended hypergeometric functions are obtained via the above-mentioned further generalized fractional derivative operator by following the lines which are detailed in the monograph by Srivastava and Manocha [14]. Finally, in Section 6, we conclude this paper by presenting a number of remarks and observations pertaining to our investigation here.2. The Generalized Extended Appell and Lauricella Functions
Let a function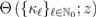 
be analytic within the disk 
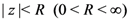and let its Taylor–Maclaurin coefficients be explicitly denoted (for convenience) by the sequence 
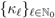. Suppose also that the function 
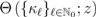can be continued analytically in the right half-plane 
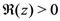with the asymptotic property given as follows:
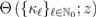be analytic within the disk 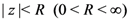and let its Taylor–Maclaurin coefficients be explicitly denoted (for convenience) by the sequence 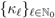. Suppose also that the function 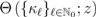can be continued analytically in the right half-plane 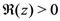with the asymptotic property given as follows: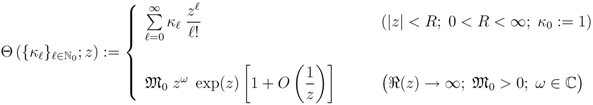
for some suitable constants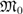 
and 
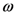depending essentially upon the sequence 
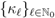. Here, and in what follows, we assume that the series in the first part of the Definition (2.1) converges absolutely when 
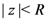for some 
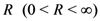and represents the function 
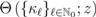which is assumed to be analytic within the disk 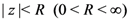and which can be appropriately continued analytically elsewhere in the complex 
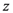-plane with the order estimate provided in the second part of the Definition (2.1). For example, if we choose the sequence 
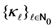to be a suitable quotient of several 
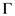-products with arguments linear in 
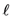so that the function 
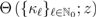becomes identifiable with the familiar Fox–Wright 
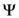-function, we can easily determine the radius 
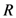of the above-mentioned disk and, moreover, we can then appropriately continue the resulting function 
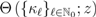analytically by means of a suitable Mellin–Barnes contour integral (see, for details [12, p. 56 et seq.]). Such functions as 
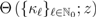can indeed be specified on an ad hoc basis.
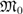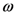and depending essentially upon the sequence 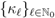. Here, and in what follows, we assume that the series in the first part of the Definition (2.1) converges absolutely when 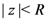for some 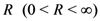and represents the function 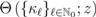which is assumed to be analytic within the disk 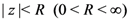and which can be appropriately continued analytically elsewhere in the complex 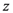-plane with the order estimate provided in the second part of the Definition (2.1). For example, if we choose the sequence 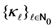to be a suitable quotient of several 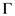-products with arguments linear in 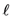so that the function 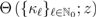becomes identifiable with the familiar Fox–Wright 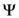-function, we can easily determine the radius 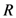of the above-mentioned disk and, moreover, we can then appropriately continue the resulting function 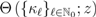analytically by means of a suitable Mellin–Barnes contour integral (see, for details [12, p. 56 et seq.]). Such functions as 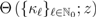can indeed be specified on an ad hoc basis.In terms of the function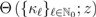 
defined by (2.1), we now introduce a natural further generalization of the extended Gamma function 
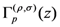, the extended Beta function 
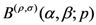and the extended hypergeometric function 
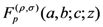by
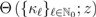defined by (2.1), we now introduce a natural further generalization of the extended Gamma function 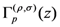, the extended Beta function 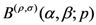and the extended hypergeometric function 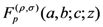by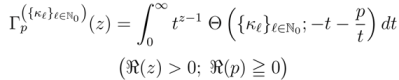
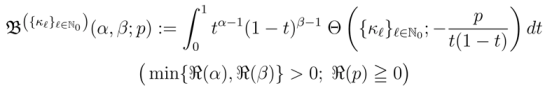
and
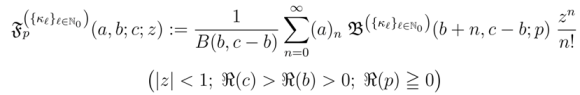
provided that the defining integrals in Definitions (2.2-2.4) exist.
Remark 1. For various special choices of the sequence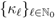 
, the definitions in (2.2–2.4) would reduce to (known or new) extensions of the Gamma, Beta and hypergeometric functions. In particular, if we set
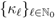, the definitions in (2.2–2.4) would reduce to (known or new) extensions of the Gamma, Beta and hypergeometric functions. In particular, if we set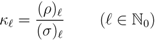
the definitions (2.2–2.4) immediately yield the definitions in (1.5–1.7) for the extended Gamma function 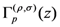, the extended Beta function 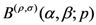and the extended hypergeometric function 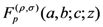, respectively.
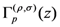, the extended Beta function 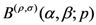and the extended hypergeometric function 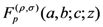, respectively.In terms of the function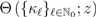 
defined by definition (2.1), it is not difficult to generalize the integral representation definition (1.8) to the following form:
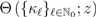defined by definition (2.1), it is not difficult to generalize the integral representation definition (1.8) to the following form: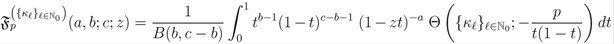
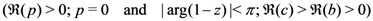
For suitably constrained (real or complex) parameters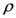 
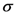and , we propose these further generalizations of the extended Appell’s hypergeometric functions:
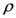and 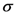, we propose these further generalizations of the extended Appell’s hypergeometric functions: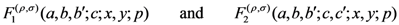
in two variables, and the extended Lauricella’s hypergeometric function:
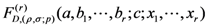
of 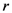variables 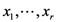, which are defined by
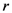variables 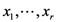, which are defined by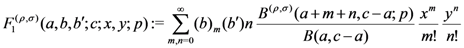
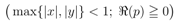
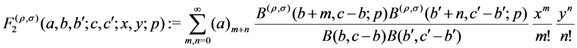
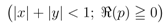
and
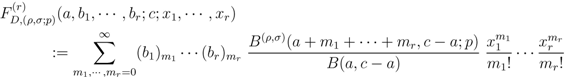
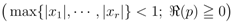
where the generalized extended Beta function 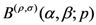is given by Definition (1.6). Clearly, the Definition (2.7) corresponds to the special case of the Definition (2.9) when 
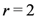. Moreover, in view of the relationship Definition (1.9), the Definitions (2.7) and (2.8) immediately yield the definitions in (1.14) and (1.15) when 
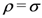. More generally, in terms of the sequence 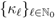defined involved in (2.1), we have the following definitions:
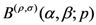is given by Definition (1.6). Clearly, the Definition (2.7) corresponds to the special case of the Definition (2.9) when 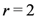. Moreover, in view of the relationship Definition (1.9), the Definitions (2.7) and (2.8) immediately yield the definitions in (1.14) and (1.15) when 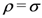. More generally, in terms of the sequence 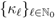defined involved in (2.1), we have the following definitions: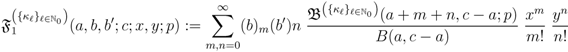
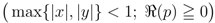
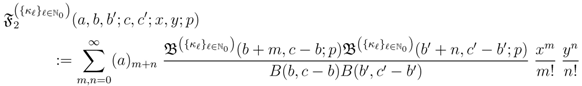
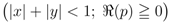
and
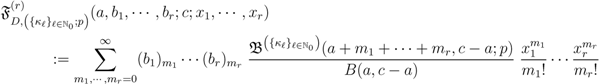
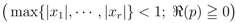
where the generalized extended Beta function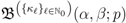 
is given by Definition (2.3).
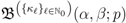is given by Definition (2.3).We now proceed to derive integral representations for the above-defined hypergeometric functions in two and more variables.
Theorem 1. For the generalized extended Appell functions
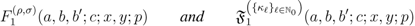
defined by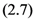 
and 
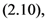the following integral representations hold true:
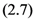and 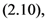the following integral representations hold true: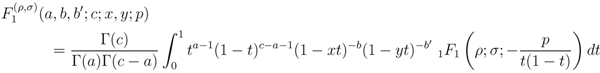
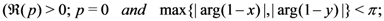
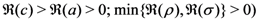
and
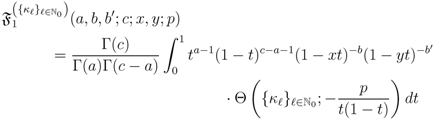
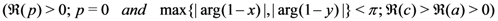
Proof. For convenience, we denote the second member of the Assertion (2.13) by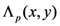 
and assume that 
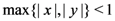. Then, upon expressing
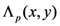and assume that 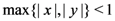. Then, upon expressing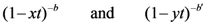
as their Taylor–Maclaurin series, if we invert the order of summation and integration (which can easily be justified by absolute and uniform convergence), we find that
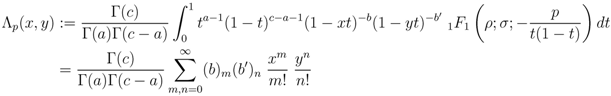
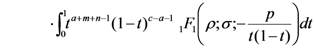
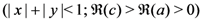
which, in view of the Definitions (1.6) and (2.7), yields the first member of the Assertion (2.13). Our demonstration of the integral Representation (2.13) is completed by applying the principle of analytic continuation, since the integral for 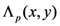above in (2.13) exists under the constraints which are listed already with (2.13).
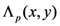above in (2.13) exists under the constraints which are listed already with (2.13).The proof of the Assertion (2.14) runs parallel to that of (2.13) and is based similarly upon the definitions (2.3) and (2.10) instead. The details involved are being omitted.
Theorems 2 and 3 below follow easily from the Definitions (1.6) and (2.3) in conjunction with the Definitions (2.8) and (2.11) and the Definitions (2.9) and (2.12), respectively.
Theorem 2. For the functions
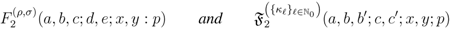
defined by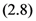 
and 
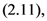respectively, the following integral representations hold true:
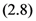and 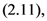respectively, the following integral representations hold true: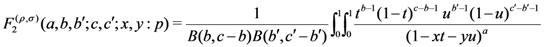
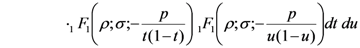
and
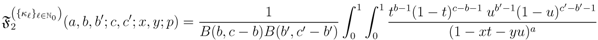
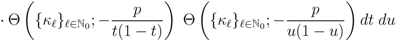
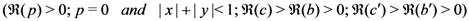
Proof. Since [14, p. 52, Equation 1.6(2)]
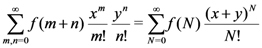
it is easily seen that
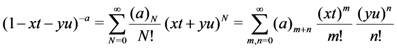
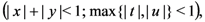
which is rather instrumental in our demonstration of Theorem 2 along the lines of the proof of Theorem 1.
Theorem 3. For the functions
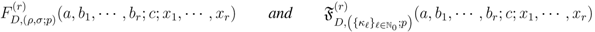
defined by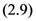 
and 
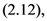respectively, the following integral representations hold true:
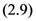and 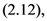respectively, the following integral representations hold true: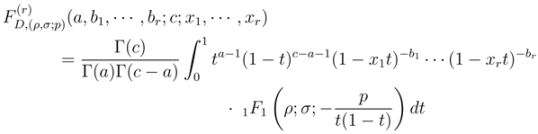
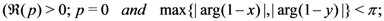
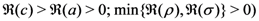
and
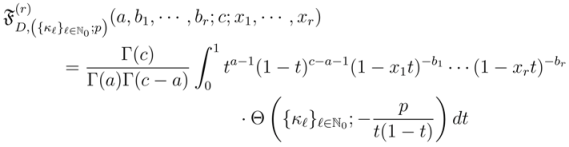
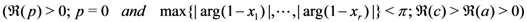
Proof. The proof of Theorem 3 is much akin to that of its special (two-variable) case (that is, Theorem 1) when . We, therefore, omit the details involved.
. We, therefore, omit the details involved.3. Applications of the Generalized Extended Riemann–Liouville Fractional Derivative Operator
Earlier investigations by various authors dealing with operators of fractional calculus and their applications are adequately presented in the recent monograph [12] (see also [15]). The use of fractional derivative in the theory of generating functions is explained reasonably satisfactorily by Srivastava and Manocha (see, for details, [14, Chapter 5]). Here, in this section, we first introduce the following generalizations of the extended Riemann–Liouville fractional derivative operator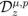 
defined by (1.13):
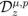defined by (1.13):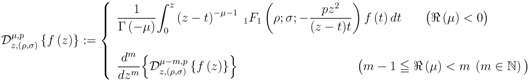
and
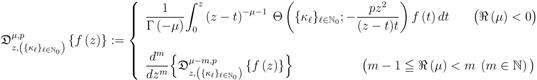
where, as also in (1.13),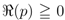 
and the path of integration in each of the Definitions (3.1) and (3.2) is a line in the complex 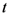-plane from 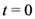to .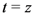
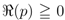and the path of integration in each of the Definitions (3.1) and (3.2) is a line in the complex 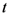-plane from 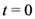to 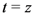.Remark 2. The Definition (3.1) is easily recovered from (3.2) by specializing the sequence 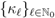as in (2.5). Moreover, by using the specialization indicated in (1.9), the Definition (3.1) reduces immediately to (1.13). For 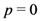, the Definitions (1.13), (3.1) and (3.2) would obviously reduce at once to the familiar Riemann–Liouville Definition (1.10). Each of these and the aforementioned other specializations are fairly straightforward. Henceforth, therefore, we choose to state our results in their general forms only and leave the specializations as an exercise for the interested reader.
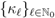as in (2.5). Moreover, by using the specialization indicated in (1.9), the Definition (3.1) reduces immediately to (1.13). For 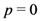, the Definitions (1.13), (3.1) and (3.2) would obviously reduce at once to the familiar Riemann–Liouville Definition (1.10). Each of these and the aforementioned other specializations are fairly straightforward. Henceforth, therefore, we choose to state our results in their general forms only and leave the specializations as an exercise for the interested reader.Making use of the Definition (3.2), we can easily derive the following analogue of the familiar fractional derivative Formula (1.11):
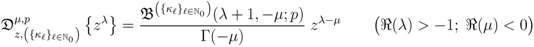
which would readily yield Theorem 4 below.
Theorem 4. In terms of a suitably bounded multiple sequence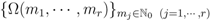 
let the multivariable function 
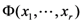be defined by
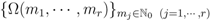let the multivariable function 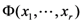be defined by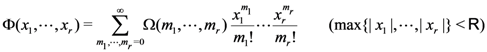
Then
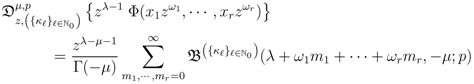
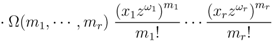
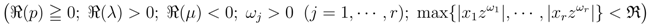
provided that each member of 
exists.
exists.Proof. The Assertion (3.5) of Theorem 4 follows easily from the Definitions (3.2) and (2.3). We, therefore, skip the details involved.
An interesting particular case of the fractional derivative Formula (3.5) asserted by Theorem 4 would occur when we specialize the sequence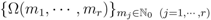 
as follows:
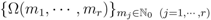as follows: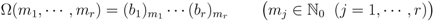
We thus obtain the following interesting generalization of a known result [14, p. 303, Problem 1]:
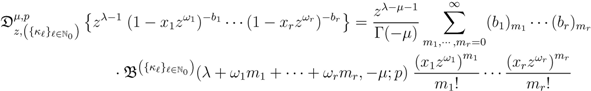
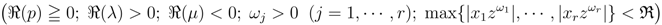
provided that each member of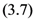 
exists.
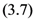exists.Since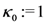 
in the Definition (2.1), in its further special case when
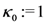in the Definition (2.1), in its further special case when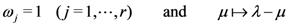
this last result (3.7) can be written, in terms of the generalized extended Lauricella function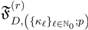 
defined by (2.12), as follows:
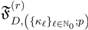defined by (2.12), as follows: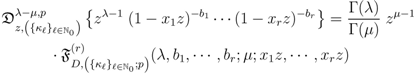
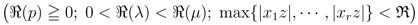
which, for 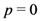or (alternatively) for
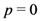or (alternatively) for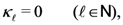
immediately yields the aforementioned known result [14, p. 303, Problem 1].
Yet another result would emerge when, in the two-variable ( 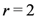) case of the Definition (3.4), we set
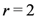) case of the Definition (3.4), we set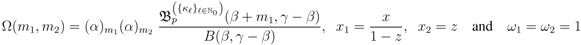
so that, by using the definition (2.4), we have
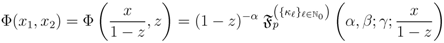
Now, just as in our demonstration of the Assertion (3.5) of Theorem 4, if we apply the fractional derivative formula (3.3) (with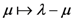 
) to 
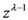times the 
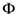-function given by (3.9), we are led to the following result:
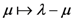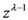) to times the 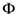-function given by (3.9), we are led to the following result: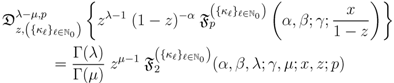
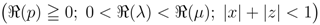
where we have also used the Definition (2.11) for the generalized extended Appell function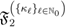 
.
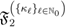.For 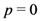or (alternatively) for
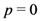or (alternatively) for
this last Formula (3.10) immediately yields a known result [14, p. 289, Equation 5.1(18)].
Remark 3. The Beta function 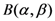defined (for 
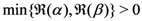) by
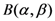defined (for 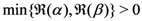) by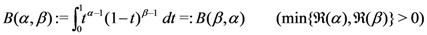
can be continued analytically for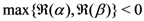 
as follows (see, for example, [14, p. 26, Equation 1.1(48)]):
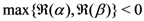as follows (see, for example, [14, p. 26, Equation 1.1(48)]):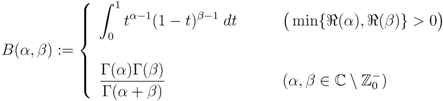
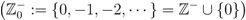
Thus, clearly, in their special cases when
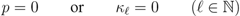
such additional constraints as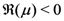 
in (3.3), (3.5) and (3.7), and 
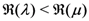in (3.8) and (3.10), can be dropped fairly easily by applying both cases of the definition in (3.2).
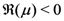in (3.3), (3.5) and (3.7), and 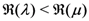in (3.8) and (3.10), can be dropped fairly easily by applying both cases of the definition in (3.2).4. Mellin Transforms of the Generalized Extended Fractional Derivatives
The Mellin transform of a suitably integrable function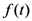 
with index 
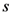is defined, as usual, by
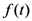with index 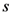is defined, as usual, by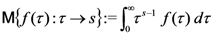
whenever the improper integral in (4.1) exists.
Theorem 5. In terms of the generalized extended Gamma function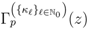 
defined by 
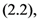the Mellin transforms of the following generalized extended fractional derivatives defined by 
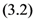are given by
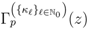defined by 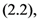the Mellin transforms of the following generalized extended fractional derivatives defined by 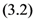are given by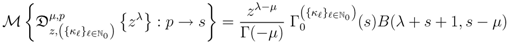
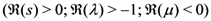
and
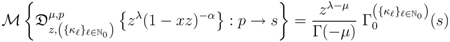
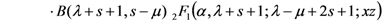
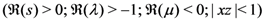
And, more generally, by
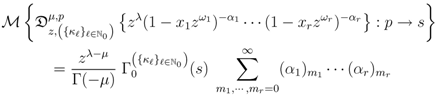
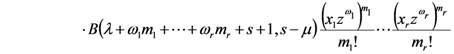
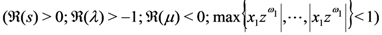
provided that each member of the Assertions (4.2), (4.3) and (4.4) exists, 2F1 being the Gauss hypergeometric function.
Proof. Using the Definition (4.1) of the Mellin transform, we find from (3.2) that
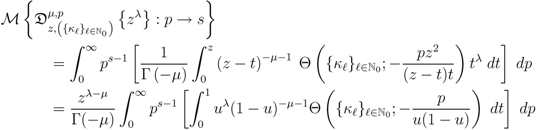
where we have also set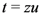 
and 
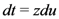in the inner 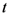-integral. Upon interchanging the order of integration in (4.5), which can easily be justified by absolute convergence of the integrals involved under the constraints state with (4.2), we get
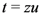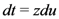and in the inner 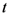-integral. Upon interchanging the order of integration in (4.5), which can easily be justified by absolute convergence of the integrals involved under the constraints state with (4.2), we get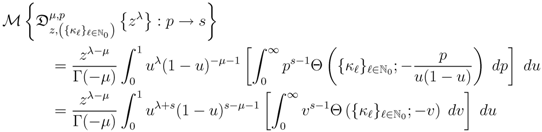
where we obviously have set
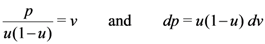
in the inner 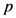-integral. We now interpret the 
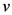-integral and the 
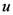-integral in (4.6) by means of the Definitions (2.2) (with 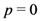) and (3.12), respectively. This evidently completes our derivation of the Mellin transform Formula (4.2) asserted by Theorem 5.
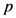-integral. We now interpret the 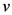-integral and the 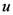-integral in (4.6) by means of the Definitions (2.2) (with 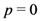) and (3.12), respectively. This evidently completes our derivation of the Mellin transform Formula (4.2) asserted by Theorem 5.Alternatively, by substituting from (3.3) into the left-hand side of (4.2), we have
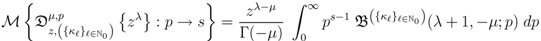
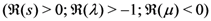
which would lead us once again to the Assertion (4.2) of Theorem 5.
In order to prove the Mellin transform Formula (4.3), we first write
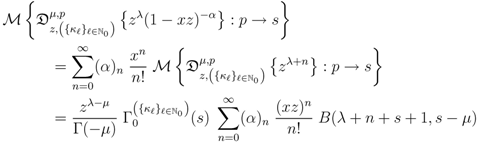
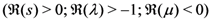
where we have used the already proven Assertion (4.2) of Theorem 5. The Assertion (4.3) of Theorem 5 would now follow upon interpreting the 
-series in the last member of (4.7) as a Gauss hypergeometric function .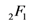
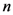-series in the last member of (4.7) as a Gauss hypergeometric function 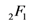.Except for the obvious fact that the single 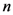-series is to be replaced by the multiple 
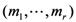-series, the demonstration of the third Assertion (4.4) of Theorem 5 would run parallel to that of the second Assertion (4.3). The details involved may thus be omitted here.
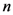-series is to be replaced by the multiple 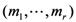-series, the demonstration of the third Assertion (4.4) of Theorem 5 would run parallel to that of the second Assertion (4.3). The details involved may thus be omitted here.The Mellin transform Formula (4.3) corresponds to the case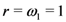 
of the general Result (4.4). Moreover, in its special case when 
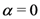(or when 
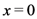), (4.3) would reduce at once to the Mellin transform Formula (4.2).
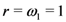of the general Result (4.4). Moreover, in its special case when 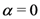(or when 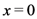), (4.3) would reduce at once to the Mellin transform Formula (4.2).In terms of the Lauricella hypergeometric function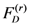 
of 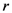variables (see, for details, [14, p. 60, Equation 1.7(4)], the special case of the assertion (4.4) of Theorem 5 when 
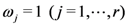yields the following Mellin transform formula:
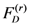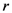of variables (see, for details, [14, p. 60, Equation 1.7(4)], the special case of the assertion (4.4) of Theorem 5 when 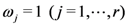yields the following Mellin transform formula: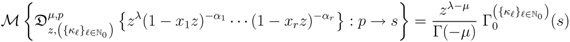
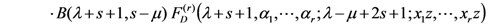
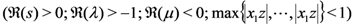
which provides a multivariable hypergeometric extension of the Assertion (4.3) of Theorem 5. In particular, upon setting
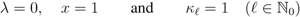
in (4.2), if we make use of the Definition (3.1) (with 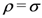), we obtain
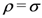), we obtain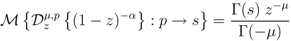
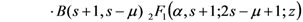
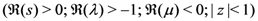
which provides the duly-corrected version of a known result asserted recently by Özarslan and Özergin [1, p. 1832, Theorem 4.2].
5. A Set of Generating Functions
In this section, we derive linear and bilinear generating relations for the generalized extended hypergeometric functions in one, two and more variables (see Section 2) by following the methods which are described fairly adequately in the monograph by Srivastava and Manocha [14, Chapter 5]. Our main results are contained in Theorem 6 below.
Theorem 6. Each of the following generating relations holds true for the generalized extended hypergeometric functions in one and more variables:
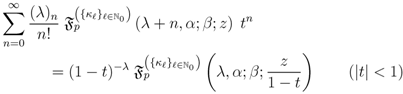
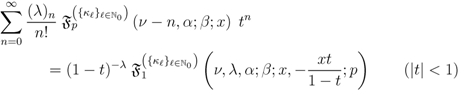
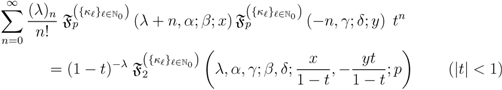
and
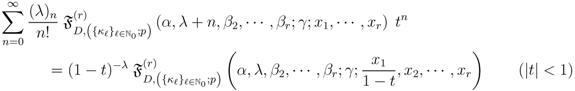
provided that each member of the generating relations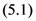 
to 
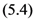exists.
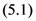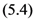to exists.Proof. Our demonstration of Theorem 6 is based upon the generalized extended fractional derivative operator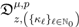 
defined by (3.2). We first rewrite the elementary identity:
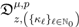defined by (3.2). We first rewrite the elementary identity: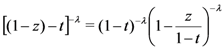
in the following form:
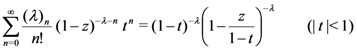
Now, upon multiplying both sides of (5.6) by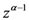 
, if we apply the generalized extended fractional derivative operator 
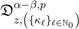on each member of the resulting equation, we find that
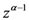, if we apply the generalized extended fractional derivative operator 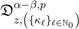on each member of the resulting equation, we find that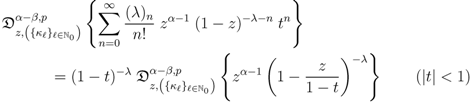
Interchanging the order of fractional differentiation and summation in (5.7), which can be justified when
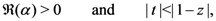
we find from (5.7) that
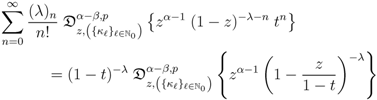
which, by means of some obvious special cases of (3.8), yields the first Assertion (5.1) of Theorem 6 under the constraint derivable by appealing finally to the principle of analytic continuation.
Since
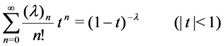
a direct proof of the generating relation (5.1), without using the generalized extended fractional derivative operator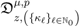 
defined by (3.2), can be given along the following lines:
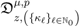defined by (3.2), can be given along the following lines: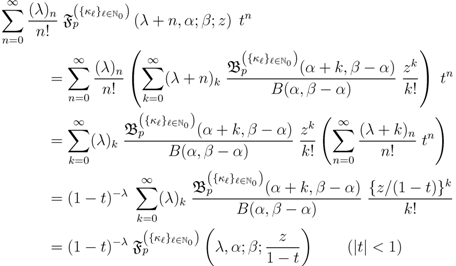
where we have only used the Definition (2.4) in conjunction with the expansion Formula (5.9).
The proof of the second Assertion (5.2) makes similar use of the generalized extended fractional derivative operator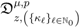 
defined by (3.2) together with the following elementary identity:
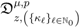defined by (3.2) together with the following elementary identity: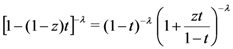
instead of the Identity (5.5).
Next, upon setting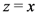 
and 
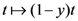in (5.1), if we multiply the resulting equation by 
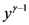and then apply the generalized extended fractional derivative operator 
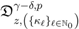together with the elementary Identity (5.11), we find that
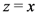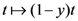and in (5.1), if we multiply the resulting equation by 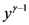and then apply the generalized extended fractional derivative operator 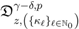together with the elementary Identity (5.11), we find that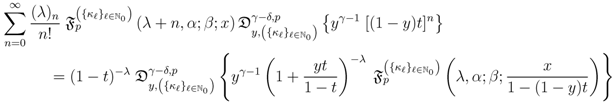
which, in light of (3.10) as well as some obvious special cases of (3.8), leads us eventually to the bilinear generating Relation (5.3) asserted by Theorem 6.
Finally, the proof of the Assertion (5.4) is much akin to that of (5.1). In fact, the role played by the argument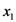 
in (5.4) can be assumed instead by any of the other arguments 
.
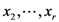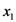in (5.4) can be assumed instead by any of the other arguments 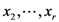.6. Concluding Remarks and Observations
In our present investigation, we have introduced and studied a further generalization of the extended fractional derivative operator related to a generalized Beta function, which was used in order to obtain some linear and bilinear generating relations involving the extended hypergeometric functions [1]. We have applied the generalized extended fractional derivative operator to derive generating relations for the generalized extended Gauss, Appell and Lauricella hypergeometric functions in one, two and more variables. Many other properties and relationships involving (for example) Mellin transforms and the generalized extended fractional derivative operator are also given.
It may be of interest to observe in conclusion that many of the definitions, which we have considered in this paper, can be further extended by introducing one additional parameter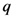 
(with 
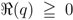. Thus, in terms of the 
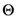-function given by (2.1), we can introduce a further extension of the generalized extended Beta function in (2.3) as follows:
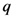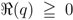(with . Thus, in terms of the 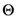-function given by (2.1), we can introduce a further extension of the generalized extended Beta function in (2.3) as follows: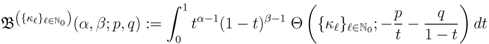
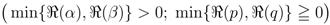
The corresponding further extensions of the Definitions (2.4) and (2.10) to (2.12) are given by
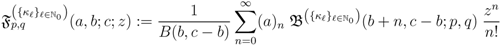
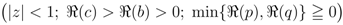
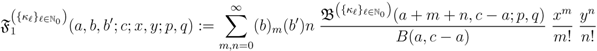
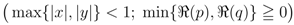
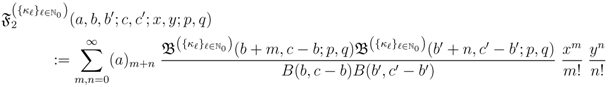
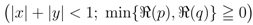
and
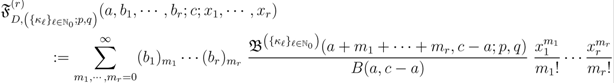
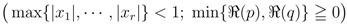
respectively. Moreover, the fractional derivative operator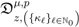 
defined by (3.2) can be further extended as follows:
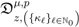defined by (3.2) can be further extended as follows: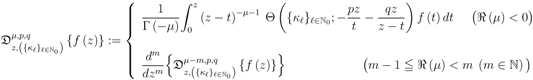
where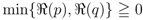 
and, as also in (1.10), (1.13), (3.1) and (3.2), the path of integration in the Definition (6.6) is a line in the complex 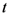-plane from 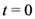to .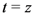
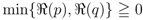and, as also in (1.10), (1.13), (3.1) and (3.2), the path of integration in the Definition (6.6) is a line in the complex 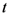-plane from 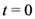to 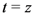.Since
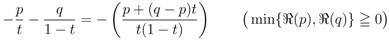
the definitions in (6.1) to (6.6) would obviously coincide with the corresponding definitions in the preceding sections when we set the additional parameter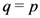 
. Most (if not all) of the properties and results, which we have investigated in this paper in the 
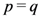case, can indeed be considered analogously for the 
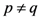case in a rather simple and straightforward manner. The details involved may, therefore, be left as an exercise for the interested reader.
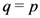. Most (if not all) of the properties and results, which we have investigated in this paper in the 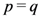case, can indeed be considered analogously for the 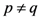case in a rather simple and straightforward manner. The details involved may, therefore, be left as an exercise for the interested reader.References
- Özarslan, M.A.; Özergin, E. Some generating relations for extended hypergeometric function via generalized fractional derivative operator. Math. Comput. Model. 2010, 52, 1825–1833. [Google Scholar] [CrossRef]
- Chaudhry, M.A.; Temme, N.M.; Veling, E.J.M. Asymptotic and closed form of a generalized incomplete gamma function. J. Comput. Appl. Math. 1996, 67, 371–379. [Google Scholar] [CrossRef]
- Chaudhry, M.A.; Qadir, A.; Rafique, M.; Zubair, S.M. Extension of Euler’s beta function. J. Comput. Appl. Math. 1997, 78, 19–32. [Google Scholar] [CrossRef]
- Chaudhry, M.A.; Zubair, S.M. Generalized incomplete gamma functions with applications. J. Comput. Appl. Math. 1994, 55, 99–124. [Google Scholar] [CrossRef]
- Chaudhry, M.A.; Zubair, S.M. On the decomposition of generalized incomplete gamma functions with applications of Fourier transforms. J. Comput. Appl. Math. 1995, 59, 253–284. [Google Scholar] [CrossRef]
- Miller, A.R. Reduction of a generalized incomplete gamma function, related Kampé de Fériet functions, and incomplete Weber integrals. Rocky Mountain J. Math. 2000, 30, 703–714. [Google Scholar] [CrossRef]
- Özergin, E.; Özarslan, M.A.; Altn, A. Extension of gamma, beta and hypergeometric functions. J. Comput. Appl. Math. 2011, 235, 4601–4610. [Google Scholar] [CrossRef]
- Chaudhry, M.A.; Qadir, A.; Srivastava, H.M.; Paris, R.B. Extended hypergeometric and confluent hypergeometric functions. Appl. Math. Comput. 2004, 159, 589–602. [Google Scholar] [CrossRef]
- Chaudhry, M.A.; Zubair, S.M. On a Class of Incomplete Gamma Functions with Applications; CRC Press (Chapman and Hall): Boca Raton, FL, USA, 2002. [Google Scholar]
- Erdélyi, A.; Magnus, W.; Oberhettinger, F.; Tricomi, F.G. Tables of Integral Transforms, Volume II; McGraw-Hill Book Company: New York, NY, USA, 1954. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications, Translated from the Russian: Integrals and Derivatives of Fractional Order and Some of Their Applications (“Nauka i Tekhnika", Minsk, 1987); Gordon and Breach Science Publishers: Reading, UK, 1993. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations. North-Holland Mathematical Studies; Elsevier (North-Holland) Science Publishers: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Appell, P.; Kampé de Fériet, J. Fonctions Hypergéométriques et Hypersphériques: Polynômes d’Hermite; Gauthier-Villars: Paris, France, 1926. [Google Scholar]
- Srivastava, H.M.; Manocha, H.L. A Treatise on Generating Functions; Halsted Press (Ellis Horwood Limited, Chichester), John Wiley and Sons: New York, NY, USA, 1984. [Google Scholar]
- Srivastava, H.M.; Saxena, R.K. Operators of fractional integration and their applications. Appl. Math. Comput. 2001, 118, 1–52. [Google Scholar] [CrossRef]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).