Equations of State of Simple Solids (Including Pb, NaCl and LiF) Compressed in Helium or Neon in the Mbar Range

Abstract

The equations of state measured under ambient temperature in the Mbar range are reviewed, focusing on experiments using diamond anvils cells with a quasi-hydrostatic pressure transmitting medium (helium or neon) and coupled with X-ray diffraction. Equations of state (EoS) parameters are listed with an unified pressure metrology for all data. This metrology is based on the efforts made in the 2000s to update the ruby luminescence pressure scale, after the collection of original data. To complete this database, unpublished P-V data for lead (Pb), sodium chloride (NaCl) and lithium fluoride (LiF) are also provided with the same metrology. Systematic effects of the pressure metrology on the EoS parameters are discussed.

1. Introduction

Ambient temperature equations of state (EoS) $V(P,T=300$ K) describe the evolution of bonding in solids under high compression. In static high-pressure devices such as diamond anvil cells (DACs), the unit cell volume V is measured with X-ray diffraction (XRD) and the pressure P is estimated using a pre-calibrated gauge. In the 2000s, the calibration of the most widely used gauge in DACs, ruby luminescence, has been updated on the basis of new measurements made in quasi-hydrostatic pressure transmitting media [1,2,3,4,5]. It has been suggested that the historical calibration by Mao et al. (hereafter noted as Mao 86) [6] underestimates the pressure by some 8% at 150 GPa, as represented in Figure 1. As a result, the EoS measured under quasi-hydrostatic compression published before, or during the period of ruby metrology updates have to be corrected.

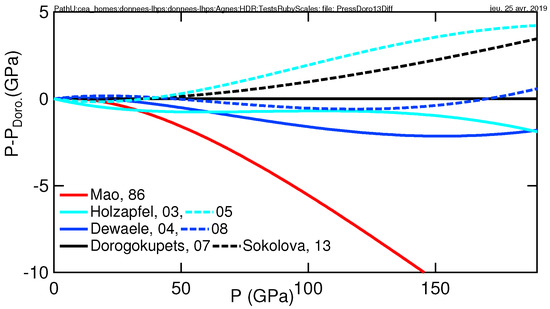
Figure 1. Comparison between calibrations of the ruby luminescence gauge [1,2,3,4,5,6,7]. The reference calibration is [4].

I present here EoS parameters for several simple solids (metals-alkali halides-diamond) measured with similar techniques in the Mbar range, between 2003 and 2012, which originally considered various calibrations of the ruby luminescence gauge. Here, a unified ruby pressure metrology (based on [4]) is used. Corrections to published EoS, subsequent to the update of the ruby scale, are listed in Table 1. In addition, P-V data are provided for some additional compounds: hcp-Pb, NaCl and LiF. NaCl and LiF are standards for static and dynamic compression measurements, and Pb behavior under high compression is typical of post-transition metals, and also used as a standard. These measurements are presented in the third section and compared with literature data. In the last section, the EoS parameters are listed in Table 1 and discussed.

Table 1. Rydberg–Vinet [8] equations of state (EoS) parameters at 300 K for elements and compounds obtained by fitting of the P-V data. $P_{Mao}$ ($P_{Dor}$) indicates that the ruby calibration has been taken from [4,6]. W gauge has been calibrated against ruby in [2]. PTM: pressure transmitting medium. V in Å${}^3$/at or /formula unit, P and $K_0$ in GPa. The numbers in bold have been fixed during the fit. The number in parenthesis indicate fit error bars (95% confidence level). They are of the same value in the third column as in the second column and are not reported. The reference for the published data is provided in the last column.

Element	${\mathit{P}}_{\mathit{M}\mathit{a}\mathit{o}}$ [6]	${\mathit{P}}_{\mathit{D}\mathit{o}\mathit{r}}$ [4]	P	PTM	P	Ref.
or Compound	${\mathit{V}}_0$, ${\mathit{K}}_0$, ${\mathit{K}}_0^{\prime }$	${\mathit{V}}_0$, ${\mathit{K}}_0$, ${\mathit{K}}_0^{\prime }$	Domain		Gauge
Au	16.983(20), 166.4(2.0), 5.47(6)	16.986, 163.4, 6.04	0–131	He	ruby	[9]
Pt	15.099(25), 273.4(2.5), 4.83(8)	15.098, 270.8, 5.50	0–95	He	ruby	[2]
Cu	11.810(15), 135.3(1.5), 4.91(6)	11.81, 133.1, 5.38	0–155	He	ruby	[2]
Ta	18.020(18), 197.9(3.7), 3.17(10)	18.019, 196.1, 3.64	0–90	He	ruby	[2]
Al	16.573(19), 76.32(1.5), 4.16(6)	16.584, 74.2, 4.52	0–155	He	ruby	[2]
W	15.862(16), 298.3(4.1), 3.82(11)	15.858, 298.6, 4.37	0–155	He	ruby	[2]
Co	11.077(12), 197.0(3.2), 3.85(20)	11.077, 194.85, 4.36	0–66	He	ruby	[5]
Ag	17.070(16), 100.2(1.6), 5.70(9)	17.088, 96.6, 6.22	0–124	He	ruby	[5]
Mo	15.569(21), 270.3(3.9), 3.34(12)	15.567, 269.3, 3.87	0–124	He	ruby	[5]
Ni	10.954(18), 177.5(2.4), 4.83(9)	10.952, 176, 5.322	0–157	He	ruby	[5]
Zn	15.147(19), 64.3(1.2), 5.30(10)	15.155, 62.2, 5.705	0–157	He	ruby	[5]
Be	8.133(5), 115.2(1.1), 2.94(5)	8.134, 113.4, 3.29	0–95	He	ruby	[10]
Pb-hcp	28.063(55), 71.8(2.1), 4.40(8)	28.058, 70.0, 4.77	13–131	He	ruby	this work
Re	14.737(20), 350.5(8.0), 3.98(17)	14.734, 350.5, 4.62	0–144	He	W	[11]
$ϵ$-Fe	11.209(50), 164.5(7.9), 4.96(16)	11.177, 168.4, 5.33	17–204	He, Ne	W	[5]
C	5.673(8), 446.8(5.0), 3.01(60)	5.672, 448.9, 3.66	0–151	He, Ne	ruby	[12,13]
KCl-B2	55.98(76), 15.4(2.5), 5.75(15)	56.86, 13.1, 6.21	0–165	He	ruby	[14]
KBr-B2	64.37(81), 14.5(2.5), 5.58(20)	65.29, 12.44, 6.01	0–165	He	ruby	[14]
NaCl-B1	44.90(12), 24.0(8), 5.09(6)	44.93, 23.4, 5.29	0–35	He	ruby	this work
NaCl-B2	42.3, 24.0(1.2), 5.37(20)	42.3, 22.664, 5.735	37–155	He	ruby	this work
LiF	16.371(30), 64.6(1.4), 4.62(60)	16.391, 62.3, 5.01	0–109	He	ruby	this work

2. Methods

The experimental methods are similar for all measurements. Membrane diamond anvil cells with diamonds culets ranging from 400 $\mathsf{\mu }$m to 100 × 300 (central flat × bevel) $\mathsf{\mu }$m diameters are used. The sample, a grain smaller than 5 $\mathsf{\mu }$m, is placed close (a few $\mathsf{\mu }$m) to a pressure gauge and compressed in helium or neon pressure transmitting medium. It is analyzed with angular-dispersive monochromatic X-ray diffraction (XRD), with an X-ray spot size ranging from 6 × 8 $\mathsf{\mu }$m to 2 × 3 $\mathsf{\mu }$m, on high pressure beamlines of the European Synchrotron Radiation Facility (ID30, ID27, ID09). The diffraction geometry (sample to detector distance, detector position and angle) is calibrated using a reference sample. The volume is estimated from fitting of 3 to 8 diffraction lines of the sample in each XRD spectrum, yielding a relative precision of ∼5 × 10${}^{-4}$. The pressure is estimated from the measurement of the luminescence of a ruby gauge, or the XRD signal of an X-ray gauge, here W (tungsten). This X-ray gauge has been calibrated against ruby using the data from [2]. Up to 3 samples have been placed in the same pressure chamber in order to ensure same pressure for calibration cross-check purpose. The pressure is increased with steps of 1 GPa to 4 GPa, with sufficient stabilization time to collect the data with negligible pressure drift (less than 0.5 GPa, estimated by measuring the pressure before and after X-ray exposure). This requires wait time of up to 30 min for low pressure (below 20 GPa) points, and of less than 10 min for highest pressure points. The data collection time is typically 5 min, 1 min for ruby pressure measurement and another 2 min for the X-ray diffraction exposure (including beam search), and 2 min to check the pressure after exposure. In order to diminish the measurement bias due to pressure gradients (which can reach 0.4 GPa at 50 GPa [15]), the gauge was located less than 4 microns away from the sample.

The P-V data have been fitted with a Rydberg–Vinet [8] form:

$$P=3K_0(1-x)x^{-2}exp\left(\frac{3}{2}(K_0^{\prime }-1)(1-x)\right),$$

(1)

with

$$x={\left(\frac{V}{V_0}\right)}^{\frac{1}{3}},$$

the compression $V_0$ volume under ambient conditions, $K_0$ the bulk modulus of the material and $K_0^{\prime }$ its pressure derivative under ambient conditions. The fitted $V_0$ is within experimental error bars of measured volume under ambient conditions, when available. For the same set of parameters ($V_0$, $K_0$, $K_0^{\prime }$), Rydberg–Vinet pressure increases less than Birch–Murnaghan pressure or H02 pressure [16] under extreme compression, it is therefore considered as the most suited for soft solids such as rare-gas solids. It is used here for metals, diamond and alkali halides and its extrapolation beyond the pressure range where the data have been fitted is not fully justified. However, it has been observed that the extrapolation of gold EoS with a Rydberg–Vinet formulation beyond the measured compression range agrees well with measurements carried out later up to 600 GPa [17]. This possibility should be confirmed on other materials. Unless specified, ($V_0$, $K_0$, $K_0^{\prime }$) have been left as free parameters to fit the P-V data.

3. EoS of Pb, NaCl and LiF

3.1. Pb

Lead adopts a fcc phase under ambient conditions and transforms to a hcp phase by cold compression to ∼14 GPa [18]; hcp-Pb partially transforms to a bcc phase above 107 GPa [19]. bcc-Pb is also observed below the melting line around 44 GPa and above, suggesting a negative hcp-bcc Clapeyron slope [20]. P-V data published in the 1990s have been collected with samples compressed directly between the diamond anvils [19,21,22], while Kuznetsov et al. [18] measurements have been performed with a sample compressed in a pressure transmitting medium (NaCl), which was also used as a pressure gauge with Brown scale [23]. The different experimental conditions and techniques yield different scatter of the P-V data (Figure 2). Due to their large scatter and a likely bias due to non-hydrostatic compression [24], I have not taken into account the data of [19,21,22] to obtain EoS parameters.

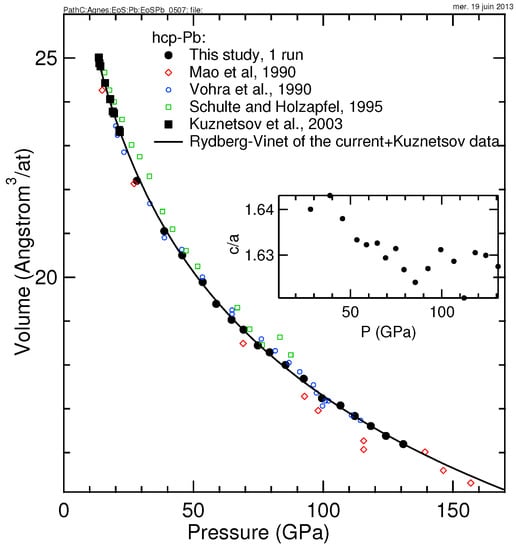
Figure 2. Volume of hcp-Pb volume measured in this study and from the literature [19,21,22]. Inset: c/a ratio measured in this study.

Here, Pb has been compressed in He up to 131 GPa without observing any formation of a bcc phase, indicating that non-hydrostatic compression helps inducing phase transformations, as already noticed for iron [25]. The current (14–131 GPa, see Table 2) and Kuznetsov et al. data have been merged to determine EoS parameters listed in Table 1.

Table 2. Pressure P (from ruby luminescence, with calibration from [4]) and volume V (measured with X-ray diffraction) for hcp-Pb. The data are listed in the order they have been taken.

P (GPa)	V (Å${}^3$/at)
28.16	22.2010
38.74	21.0521
45.62	20.5023
53.51	19.8897
58.77	19.3907
64.69	19.0305
69.24	18.8032
74.79	18.4456
79.34	18.2875
85.48	17.9984
92.47	17.6854
99.5	17.2410
106.6	17.0756
112.2	16.8330
118.3	16.6038
124.2	16.3813
130.8	16.1940

3.2. NaCl

The compression curve of NaCl has been measured in three runs, using helium as pressure medium, reaching 155 GPa (see Figure 3 and Table 3). The low pressure B1 phase transformed to the denser high pressure B2 phase at a pressure between 27 and 36 GPa.

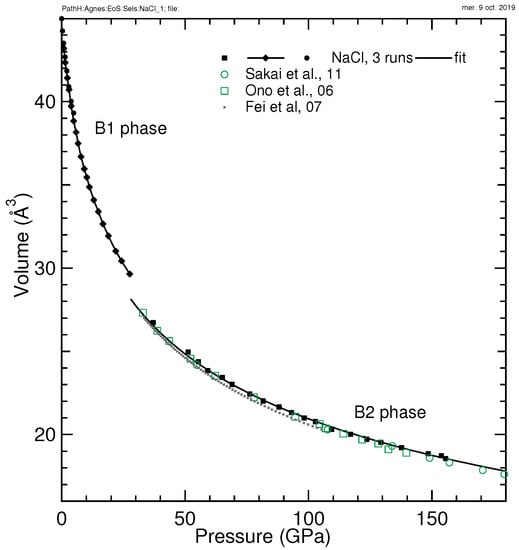
Figure 3. Volume of NaCl measured in this study and in the literature [26,27,28].

Table 3. Pressure P (from ruby luminescence, with calibration from [4]) and volume V (measured with X-ray diffraction) for NaCl (B1 and B2 phases). Each pair of columns corresponds to one experimental run. The data are listed in the order they have been taken.

P (GPa)	V (Å${}^3$/fu) (B1)	P (GPa)	V (Å${}^3$/fu) (B1)	P (GPa)	V (Å${}^3$/fu) (B2)
0.868	43.2022	0.319	44.2471	37.06	26.7309
1.46	42.3505	0.768	43.5143	51.22	24.9611
2.29	41.4177	1.37	42.6836	55.45	24.3764
2.96	40.7222	2.11	41.8422	59.18	23.8456
3.85	39.7304	2.91	40.8914	65.03	23.4403
4.88	38.8363	0.0171	44.9814	69.06	23.0081
5.87	38.1616			76.24	22.4425
6.68	37.4870			81.68	22.0179
7.87	36.6937			88.07	21.6523
9.12	35.9584			93.12	21.3184
10.2	35.4483			98.24	21.0017
11.3	34.8669			102.8	20.7833
13.0	34.0953			109.5	20.3174
14.8	33.3907			117.1	20.0107
16.7	32.6566			123.7	19.7202
18.9	31.9352			129.3	19.5347
21.9	31.0243			137.7	19.2101
24.3	30.4328			148.5	18.8551
27.6	29.6501			153.9	18.7279
				155.6	18.5570

In the literature, EoS measured under non-hydrostatic compression can be found; in particular, two studies in the multi-Mbar range [26,27]. Gold and platinum have been used as X-ray pressure calibrants, respectively, in Ono et al. and Sakai et al. studies. We have taken the calibrations of these gauges from [4] to plot the points in Figure 3. With this calibration, both Ono et al. and Sakai et al. measurements agree correctly with the current data up to 155 GPa. This suggests that non-hydrostatic stress remains weak in NaCl under pressure, as noted by Sakai et al. The P-V data collected using platinum as an X-ray pressure gauge up to 110 GPa in [28] also agree with the current one (the Birch–Murnaghan parameters from Table 1 in [28] have been considered, because there is a likely typographic error in Vinet parameters). The calibration of platinum gauge used by Fei et al. diverges by less than 0.2% with [4] in that range.

The current P-V data, plotted in black in Figure 3, have been used to determine the EoS parameters listed in Table 1. The value of $V_0$ for the B2 phase has been fixed to 42.3 Å${}^3$/at, 5.7% denser than the B1 phase (the relative volume difference measured around 27 GPa), to prevent overfitting.

3.3. LiF

The compression curve of LiF has been measured in three runs (see Table 4). The samples were single crystals, compressed in helium. LiF remained in the B1 phase in the scanned pressure range (0.7–109 GPa). Its compression behavior (see fitting parameters for these three runs in Table 1) agrees well with one recent study up to 92 GPa [29], but not with another one to 37 GPa [30]. The disagreement is more obvious when this EoS is extrapolated in the Mbar range (see Figure 4). It can be noted that in Liu et al. [30], the fitted bulk modulus is 12% higher than its ultrasonic value, 64.3 GPa [31]; the current fitted bulk modulus agrees with the ultrasonic one.

Table 4. Pressure P (from ruby luminescence, with calibration from [4]) and volume V (measured with X-ray diffraction) for LiF. Each pair of columns corresponds to one experimental run. The data are listed in the order they have been taken.

P (GPa)	V (Å${}^3$/fu)	P (GPa)	V (Å${}^3$/fu)	P (GPa)	V (Å${}^3$/fu)
0.722	16.181	21.3	13.3466	0.868	16.0879
1.32	16.040	28.3	12.7874	1.46	15.9574
1.95	15.8910	30.6	12.6060	2.29	15.8032
2.50	15.7684	34.8	12.3274	2.96	15.6871
3.14	15.6498	40.4	12.0328	3.85	15.4849
3.81	15.5367	44.7	11.8066	4.88	15.3078
4.75	15.3677	48.8	11.6103	5.87	15.1685
5.54	15.2234	53.8	11.3973	6.68	15.0231
7.03	14.9857	58.2	11.1980	7.87	14.8317
8.85	14.7288	64.8	10.9605	9.12	14.6591
10.1	14.5479	71.7	10.7381	10.2	14.5370
11.9	14.3310	75.8	10.5914	11.3	14.3930
13.5	14.1368	81.0	10.4369	13.0	14.1842
15.9	13.8710	86.4	10.3086	14.8	13.9848
18.4	13.6116	89.3	10.2328	16.7	13.7792
20.7	13.3988	93.2	10.1232	18.9	13.5672
22.9	13.2003	97.4	10.0220	21.9	13.2994
25.9	12.9683	102.1	9.91426	24.3	13.1015
28.4	12.7853	105.7	9.84496	27.6	12.8561
31.2	12.5880	109.3	9.74253
37	12.2217

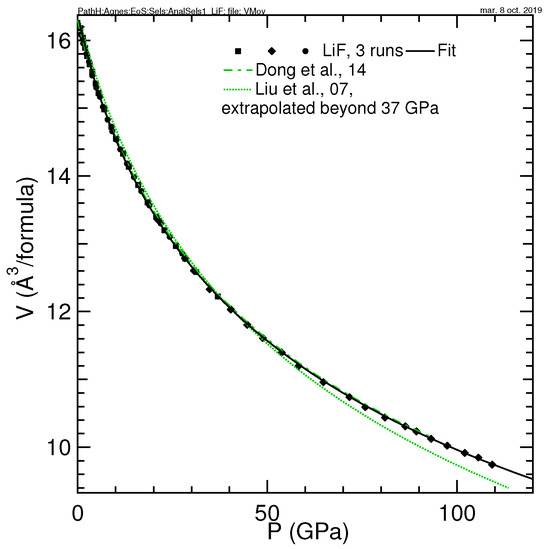
Figure 4. Volume of LiF measured in this study and in the literature [29,30].

4. Equation of State Parameters

The EoS parameters ($V_0$, $K_0$, $K_0^{\prime }$) listed in Table 1 have been obtained for two calibrations of the ruby gauge: Mao 86 [6] and Dorogokupets 07 [4]. This last calibration has been used for Be [10], Re [11], U [32], KCl [14] and KBr [14]. Therefore, no correction of the original publications EoS parameters is needed for these compounds. They have been listed in Table 1 to provide an extended comparison EoS parameters for the two calibrations. To establish their calibration, Mao et al. have compressed a ruby up to 80 GPa together with metals (Cu, Ag) used as primary X-ray gauges in DACs, in argon pressure transmitting medium. Cu and Ag gauges were calibrated using reduced shock waves equations of state. The calibration of [4] has been established by the same method, but using several metals (Au, Pt, Ta, W, Cu, Al [2]) compressed together with ruby in a more hydrostatic helium pressure medium [24].

Table 1 allows extracting trends in the differences between EoS parameters for the two calibrations. Not surprisingly, $V_0$ are identical when the compound volume could be measured close to ambient conditions. The bulk moduli $K_0$ are close within a few percents, because the pressures for the two calibrations are close at moderate compression; the slightly higher value of $K_0$ obtained with Mao 86 calibration is due to the fact that the pressure is slightly higher up to 9 GPa, although not noticeably with the scale of Figure 1. The parameter which differs the most is $K_0^{\prime }$: it is higher with Dorogokupets calibration than Mao calibration, because the pressure is higher in the Mbar range, the domain that places the most constraints on the value of $K_0^{\prime }$. The difference reaches 0.65 (out of 3.01, a 22% increase) for the most incompressible element, diamond. The relative variation of $K_0^{\prime }$ is smaller for softer solids such as aklali halides ($K_0^{\prime }$ of B2-NaCl higher by 7% for Dorogokupets scale than Mao 86 scale). It has already been noted that $K_0^{\prime }$ is more sensitive to the pressure scale for incompressible solids [1], which can easily been explained by a derivation of the Rydberg–Vinet EoS formulation. Reciprocally, a precise measurement of $K_0^{\prime }$ for a hard material would provide a tight constraint on the high pressure metrology.